Смежные и вертикальные углы. Видеоурок. Геометрия 7 Класс

На данном уроке мы рассмотрим и уясним для себя понятие смежные углы. Рассмотрим теорему, которая их касается. Введем понятие «вертикальные углы». Рассмотрим опорные факты, касающиеся этих углов. Далее сформулируем и докажем два следствия об угле между биссектрисами вертикальных углов. В конце занятия рассмотрим несколько задач, посвященных этой теме.

Начнем наш урок с понятия «смежные углы». На рисунке 1 изображен развернутый угол ∠АОС и луч ОВ, который делит данный угол на 2 угла.

                                

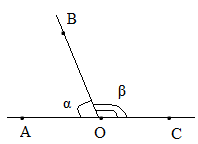
Рис. 1. Угол ∠АОС

Рассмотрим углы ∠АОВ и ∠ВОС. Вполне очевидно, что они имеют общую сторону ВО, а стороны АО и ОС являются противолежащими. Лучи ОА и ОС дополняют друг друга, а значит, они лежат на одной прямой. Углы ∠АОВ и ∠ВОС являются смежными.

Определение: Если два угла имеют общую сторону, а две другие стороны являются дополняющими лучами, то данные углы называются смежными.

Теорема 1: Сумма смежных углов – 180^о.

                              

Рис. 2. Чертеж к теореме 1

∠МОL + ∠LON = 180^o. Данное утверждение является верным, так как луч OL делит развернутый угол ∠MON на два смежных угла. То есть мы не знаем градусных мер ни одного из смежных углов, а знаем лишь их сумму – 180^о.

Рассмотрим пересечение двух прямых. На рисунке изображено пересечение двух прямых 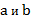 в точке О.

    

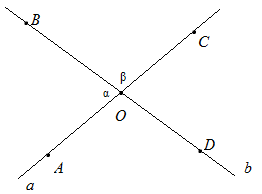
Рис. 3. Вертикальные углы ∠ВОА и ∠СОD

Определение: Если стороны одного угла являются продолжением второго угла, то такие углы называются вертикальными. Именно поэтому на рисунке изображено две пары вертикальных углов: ∠АОВ и ∠СОD, а также ∠AOD и ∠ВОС.

Теорема 2: Вертикальные углы равны.

Используем рисунок 3. Рассмотрим развернутый угол ∠АОС. ∠АОВ = ∠АОС – ∠ВОС = 180

о – β. Рассмотрим развернутый угол ∠ВОD. ∠CОD = ∠BОD – ∠BОС = 180^о – β.

Из этих соображений мы делаем вывод, что ∠АОВ = ∠СОD = α. Аналогично, ∠AOD = ∠ВОС = β.

Следствие 1: Угол между биссектрисами смежных углов равен 90^о.

                             

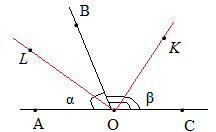
Рис. 4. Чертеж к следствию 1

Поскольку ОL – биссектриса угла ∠ВОА, то угол ∠LOB = 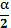 , аналогично ∠ВОК =  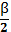. ∠LOK = ∠LOB + ∠BOK =  + 

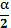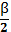
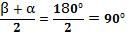  =  . Сумма углов α + β равна 180^о, поскольку данные углы – смежные.

Следствие 2: Угол между биссектрисами вертикальных углов равен 180^о.

                  

Рис. 5. Чертеж к следствию 2

KO – биссектриса ∠AOB, LO – биссектриса ∠COD. Очевидно, что ∠KOL = ∠KOB + ∠BOC + ∠COL = 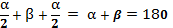 ^o. Сумма углов α + β равна 180^о, так как данные углы – смежные.

Рассмотрим некоторые задачи:

Пример 1:

Найдите угол, смежный с ∠АOС, если ∠АOС = 111^о.

Решение:

Выполним чертеж к задаче:

                             

Рис. 6. Чертеж к примеру 1

Решение

Поскольку ∠АОС = β и ∠СOD = α смежные углы, то α + β = 180^о. То есть 111^о + β = 180^о.

Значит, β = 69^о.

Этот тип задач эксплуатирует теорему о сумме смежных углов.

Пример 2:

Один из смежных углов прямой, каким (острым, тупым или прямым) является другой угол?

Решение:

Если один из углов прямой, а сумма двух углов 180^о, то и другой угол тоже прямой. Эта задача проверяет знания о сумме смежных углов.

Пример 3:

Верно ли, что если смежные углы равны, то они прямые?

Решение:

Составим уравнение: α + β = 180^о, но поскольку α = β, то β + β = 180^о, значит, β = 90^о.

Ответ: Да, утверждение верно.

Пример 4:

Даны два равных угла. Верно ли, что и смежные им углы тоже будут равны?

Решение:

                                                   

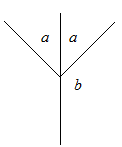
Рис. 7. Чертеж к примеру 4

Если два угла равны α, то соответствующие им смежные углы будут 180^о – α. То есть они будут равны между собой.

Ответ: Утверждение верно.

 

Список рекомендованной литературы

1. Александров  А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.
3. \Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. – М.: Просвещение, 2010.

 

Рекомендованные ссылки на интернет-ресурсы

1. Измерение отрезков (Источник).
2. Обобщающий урок по геометрии в 7-м классе (Источник).
3. Прямая линия, отрезок (Источник).

 

Рекомендованное домашнее задание

1. № 13, 14. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. – М.: Просвещение, 2010.
2. Найдите два смежных угла, если один из них в 4 раза больше другого.
3. Дан угол. Постройте для него смежный и вертикальный углы. Сколько таких углов можно построить?
4. * В каком случае получается больше пар вертикальных углов: при пересечении трех прямых в одной точке или в трех точках?

interneturok.ru

Смежные и вертикальные углы, их свойства.

по теме: Смежные и вертикальные углы, их свойства.

(3 занятия)

В результате изучения темы нужно:

УМЕТЬ:

— понятия: смежных и вертикальных углов, перпендикулярных прямых

— различать понятия смежные и вертикальные углы

— теоремы смежных и вертикальных углов

-решать задачи с использованием свойств смежных и вертикальных углов

— свойства смежных и вертикальных углов

-строить смежные и вертикальные углы, перпендикулярные прямые

ЛИТЕРАТУРА:

1. Геометрия. 7 класс. Ж. Кайдасов, Г. Досмагамбетова, В. Абдиев. Алматы «Мектеп». 2012

2. Геометрия. 7 класс. К.О.Букубаева , А.Т. Миразова. Алматы «Атамұра». 2012

3. Геометрия. 7 класс. Методическое руководство. К.О.Букубаева. Алматы «Атамұра». 2012

4. Геометрия. 7 класс. Дидактический материал. А.Н.Шыныбеков. Алматы «Атамұра». 2012

5. Геометрия. 7 класс. Сборник задач и упражнений. К.О.Букубаева, А.Т.Миразова. Алматы «Атамұра». 2012

Помни, что работать нужно по алгоритму!

Не забывай проходить проверку, делать пометки на полях,

заполнять рейтинговый лист темы.

Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.

Будь объективен во время взаимопроверки, это поможет и тебе, и тому,

кого ты проверяешь.

ЖЕЛАЮ УСПЕХА!

ЗАДАНИЕ №1.

1. Прочитай определение и выучи (2б):

Определение. Углы, у которых одна сторона общая, а две другие стороны являются дополнительными лучами, называются смежными.

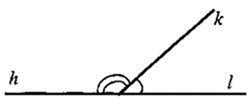
2) Выучи и запиши в тетрадь теорему : (2б)

Сумма смежных углов равна 180.

Дано:

∠АОД и ∠ДОВ –данные смежные углы

ОД — общая сторона

Доказать:

∠АОД + ∠ДОВ = 180

Доказательство:

На основе аксиомы III_{4 :}

_{∠АОД + ∠ДОВ = ∠АОВ.}

∠АОВ — развернутый. Следовательно,

∠АОД + ∠ДОВ = 180

Теорема доказана.

3) Из теоремы следует: (2б)

1) Если два угла равны, то смежные с ними углы равны;

2) если смежные углы равны, то градусная мера каждого из них равна 90°.

Запомни!

Угол, равный 90°, называется прямым углом.

Угол, меньше 90°, называется острым углом.

Угол, больше 90° и меньше 180°, называется тупым углом.

Прямой угол Острый угол Тупой угол

Так как сумма смежных углов равна 180°, то

1) угол, смежный с прямым углом, прямой;

2) угол, смежный с острым углом, тупой;

3) угол, смежный с тупым углом, острый.

4) Рассмотри образец решения задачи:

а) Дано: ∠h k и ∠kl — смежные; ∠h k больше ∠kl на 50° .

Найти: ∠h k и ∠kl.

 

Решение: Пусть ∠kl = х, тогда ∠h k = х + 50°. По свойству о сумме смежных углов ∠kl + ∠h k = 180°.

х + х + 50° = 180°;

2х = 180° — 50°;

2х = 130°;

х = 65°.

∠kl = 65°; ∠h k = 65°+ 50° = 115°.

Ответ: 115° и 65°.

б)  Пусть ∠kl = х, тогда ∠h k = 3х

х + 3х = 180°; 4х = 180°; х = 45°; ∠kl = 45°; ∠hk = 135°.

Ответ: 135° и 45°.

5) Работа с определением смежных углов: (2 б)

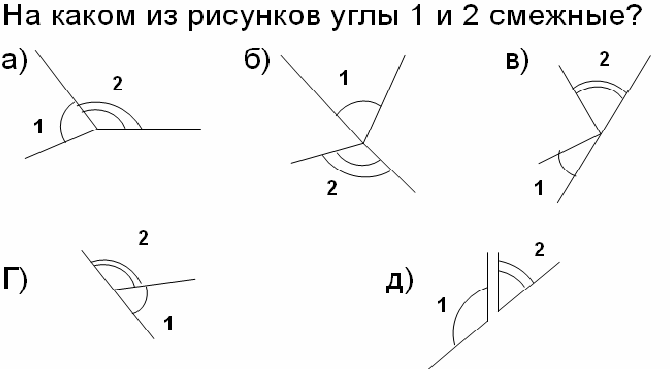
6) Найди ошибки в определениях: (2б)

Пройди проверку №1

Задание №2

1)Построй 2 смежных угла так, чтобы их общая сторона проходила через точку C и сторона одного из углов совпадала с лучом AB.(2б)

2). Практическая работа на открытие свойства смежных углов: (5б)

Ход работы

1. Построй угол  смежный углу а, если а: острый, прямой, тупой.

2. Измерь величины углов.

3.Данные измерений занеси в таблицу.

4. Найди соотношение между величинами углов а и .

5. Сделай вывод о свойстве смежных углов.

Пройди проверку №2

Задание №3

1. Начертите неразвернутый ∠АОВ и назовите лучи, являющиеся сторонами этого угла.

2. Проведите луч О, являющийся продолжение луча ОА, и луч ОД, являющийся продолжение луча ОВ.

3. Запишите в тетради: углы∠ АОВ и ∠СОД называются вертикальными. (3б)

4. Выучи и запиши в тетрадь: (4б)

Определение: Углы, у которых стороны одного из них являются дополнительными лучами другого, называются вертикальными углами.

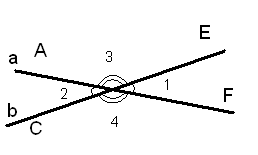
<1 и <2, <3 и <4 вертикальные углы

Лучи OF и OA ,OC и OE являются попарно дополнительными лучами.

Теорема: Вертикальные углы равны.

Доказательство.

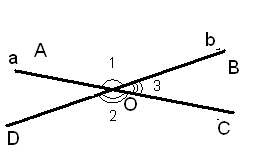
Вертикальные углы образуются при пересечении двух прямых. Пусть прямые а и b пересекаются в точке О. ∠ 1 и ∠2 –вертикальные углы.

∠АОС-развернутый, значит ∠АОС= 180°. Однако ∠ 1+ ∠ 2=∠АОС, т.е.

∠ 3+ ∠ 1=180°, отсюда имеем:

∠ 1= 180 — ∠ 3. (1)

Также имеем, что ∠ДОВ= 180°, отсюда ∠ 2+ ∠ 3=180°, или ∠ 2=180°-∠ 3. (2)

Так как в равенствах (1) и (2) прямые части равны, то ∠ 1=∠ 2.

Теорема доказана.

5). Работа с определением вертикальных углов :(2б)

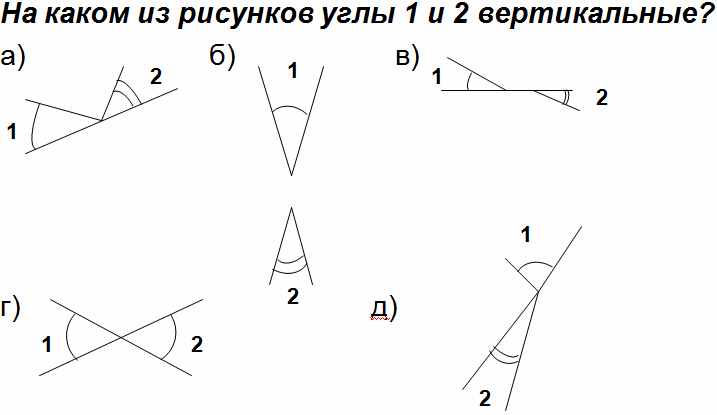
6) Найди ошибку в определении:(2б).

Пройди проверку №3

Задание №4

1)Практическая работа на открытие свойства вертикальных углов:(5б)

Ход работы:

1.Построй угол β вертикальный углу α, если α:

острый, прямой, тупой.

2.Измерь величины углов.

3.Данные измерений занеси в таблицу

4.Найди соотношение между величинами углов α и β.

5.Сделай вывод о свойстве вертикальных углов.

2)Доказательство свойств смежных и вертикальных углов . (3б)

2) Рассмотри образец решения задачи.

Задача. Прямые АВ и СД пересекаются в точке О так, что ∠AOД = 35°. Найдите углы АОС и ВОС.

 

 

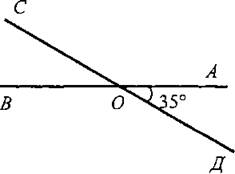
Решение:

1) Углы АОД и АОС смежные, поэтому ∠BOC = 180° — 35° = 145°.

2) Углы АОС и ВОС также смежные, поэтому ∠BOC = 180° — 145° = 35°.

Значит, ∠BOC = ∠АОД = 35°, причем эти углы являются вертикальными. Вопрос: верно ли утверждение, что любые вертикальные углы равны?

3) Решение задач на готовых чертежах: (3б)

1. Найти углы АОВ, АОD, COD.

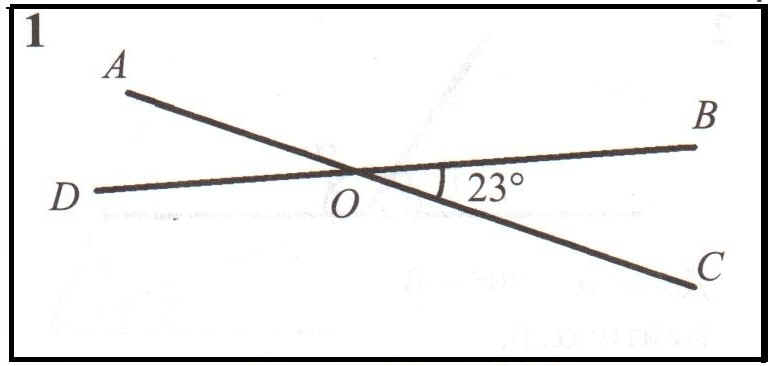
3) Найти углы BOC, FOA.: ( 3б)

 

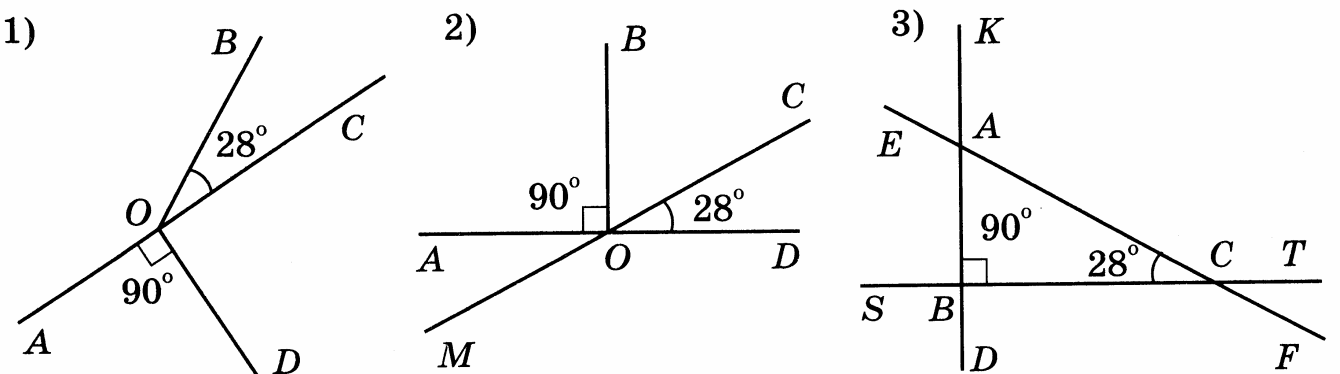
3. Найди на рисунке смежные и вертикальные углы. Пусть известны величины двух углов, отмеченных на чертеже, 28? и 90?. Можно ли найти величины остальных углов, не выполняя измерений (2б)

Пройди проверку №4

Задание №5

Проверь свои знания, выполнив проверочную работу №1

Задание №6

1) Самостоятельно докажи свойства вертикальных углов и запиши эти доказательства в тетрадь. (3б)

Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые.

2 ) Реши на выбор две задачи:

1.Градусные меры смежных углов относятся как 7:2. Найдите эти углы.(2б)

2.Один из углов, образовавшихся при пересечении двух прямых, в 11 раз меньше другого .Найдите каждый из углов.(3б)

3.Найдите смежные углы ,если их разность и их сумма относятся как 2:9.(3б)

Задание №7

Молодец! Можешь приступать к проверочной работе №2.

Проверочная работа №1.

Реши на выбор любой из вариантов (10б)

Вариант 1

1.Ученик, отвечая на вопросы учителя, дал соответствующие ответы. Проверьте, верны ли они, пометив в третьем столбике словом «ДА», «НЕТ», «НЕ ЗНАЮ». В случает «НЕТ» запишите там же верный ответ или добавьте недостающее.

<1 и <2,

<3 и <2,

г) <1 и <3. Какие это углы?

Смежные

д) Начертите ( на глаз) угол в 30° и <ABC, смежный с данным

е) Какие углы называются вертикальными?

Два угла называются вертикальными, если орни равны.

ж) Из точки А провести две прямые, перпендикулярные прямой а

Можно провести только одну прямую.

2. Назовите вертикальные углы на данном рисунке.

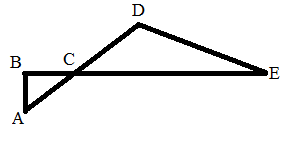
Вариант 2

1.Ученик, отвечая на вопросы учителя, дал соответствующие ответы. Проверьте, верны ли они, пометив в третьем столбике словом «ДА», «НЕТ», «НЕ ЗНАЮ». В случает «НЕТ» запишите там же верный ответ или добавьте недостающее.

<1 и <4,

<2 и <4

Д) <1 и < 3 смежные ?

Нет. Они вертикальные

Е) Какие прямые называются перпендикулярными?

Две прямые называются перпендикулярными, если они пересекаются под прямым углом

Ж) Начертите вертикальные углы так, чтобы их стороны были перпендикулярными прямыми.

2. Назовите вертикальные углы на данном рисунке.

Итого:10 баллов

«5»-10баллов;

«4»-8-9 баллов;

«3»-5-7 баллов .

Проверочная работа №2.

Реши на выбор любой вариант

Вариант I

1. Найдите смежные углы, если их разность и их сумма относятся как 2:9. (4б)

2. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 240°, меньше суммы двух других.(6б)

Вариант II

1) Найдите смежные углы, если их разность и их сумма относятся как 5:8(4б)

2) Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 60°, больше суммы двух других.(6б)

Итого:10 баллов

«5»-10баллов;

«4»-8-9 баллов;

«3»-5-7 баллов .

РЕЙТИНГОВЫЙ ЛИСТ

по теме : «Смежные и вертикальные углы, их свойства »

Ф.И. __________________________________________, класс _____

1

2 б

2 б

2 б

2 б

2б

2

2б

5б

3

3 б

4б

2б

2б

4

5б

3б

3б

3б

2б

5

7б

3б

6

3б

2б

3б

7

4б

6б

Итого

72 б

ИТОГО: 76 баллов

«5» — 72 — 60 б;

«4» — 59 — 436;

«3» — 42 – 38 б.

«2» — 38 б. и менее

 

infourok.ru

Смежные и вертикальные углы

Начальные сведения об углах

Пусть нам даны два произвольных луча. Наложим их начала друг на друга. Тогда

Определение 1

Углом будем называть два луча, которые имеют одно и тоже начало.

Определение 2

Точка, которая является началом лучей в рамках определения 3, называется вершиной этого угла.

Угол будем обозначать следующими тремя её точками: вершиной, точкой на одном из лучей и точкой на другом луче, причем вершина угла записывается в середине его обозначения (рис. 1).

Определим теперь, что такое величина угла.

Для этого необходимо выбрать какой-то «эталонный» угол, который мы будем принимать за единицу. Чаще всего таким углом является угол, который равен $\frac{1}{180}$ части развернутого угла. Такую величину называют градусом. После выбора такого угла мы проводим с ним сравнение углов, величину которого нужно найти.

Существуют 4 вида углов:

Определение 3

Угол называется острым, если он меньше $90^0$.

Определение 4

Угол называется тупым, если он больше $90^0$.

Определение 5

Угол называется развернутым, если он равен $180^0$.

Определение 6

Угол называется прямым, если он равен $90^0$.

Помимо таких видов углов, которые описаны выше, можно выделять виды углов по отношению их друг к другу, а именно вертикальные и смежные углы.

Смежные углы

Рассмотрим развернутый угол $COB$. Из его вершины проведем луч $OA$. Этот луч разделит первоначальный на два угла. Тогда

Определение 7

Два угла будем называть смежными, если одна пара их сторон является развернутым углом, а другая пара совпадает (рис. 2).

В данном случае углы $COA$ и $BOA$ являются смежными.

Теорема 1

Сумма смежных углов равняется $180^0$.

Доказательство.

Рассмотрим рисунок 2.

По определению 7, в нем угол $COB$ будет равняться $180^0$. Так как вторая пара сторон смежных углов совпадает, то луч $OA$ будет разделять развернутый угол на 2, следовательно

$∠COA+∠BOA=180^0$

Теорема доказана.

Рассмотрим решение задачи с помощью данного понятия.

Пример 1

Найти угол $C$ из рисунка ниже

Решение.

По определению 7 получаем, что углы $BDA$ и $ADC$ являются смежными. Следовательно, по теореме 1, получим

$∠BDA+∠ADC=180^0$

$∠ADC=180^0-∠BDA=180〗0-59^0=121^0$

По теореме о сумме углов в треугольнике, будем иметь

$∠A+∠ADC+∠C=180^0$

$∠C=180^0-∠A-∠ADC=180^0-19^0-121^0=40^0$

Ответ: $40^0$.

Вертикальные углы

Рассмотрим развернутые углы $AOB$ и $MOC$. Совместим их вершины между собой (то есть наложим точку $O’$ на точку $O$) так, чтобы никакие стороны этих углов не совпали. Тогда

Определение 8

Два угла будем называть вертикальными, если пары их сторон являются развернутыми углами, а их величины совпадают (рис. 3).

В данном случае углы $MOA$ и $BOC$ являются вертикальными и углы $MOB$ и $AOC$ также вертикальные.

Теорема 2

Вертикальные углы равняются между собой.

Доказательство.

Рассмотрим рисунок 3. Докажем, к примеру, что угол $MOA$ равняется углу $BOC$.

По определению 7, видим, что углы $AOM$ и $MOB$, а также углы $COB$ и $MOB$ будет являться смежными. Обозначим угол $MOB$ через $β$. По теореме 1, получим

$∠AOM+β=180^0$

$∠AOM=180^0-β$

С другой стороны

$∠COB+β=180^0$

$∠COB=180^0-β$

Получаем, что

$∠AOM=∠COB$

Теорема доказана.

Рассмотрим решение задачи с помощью данного понятия.

Пример 2

Найти угол $COB$ из рисунка ниже

Решение.

По определению 8 получаем, что углы $AOD$ и $COB$ являются вертикальными. Следовательно, по теореме 2, получим

$∠COB=∠AOD=54^0$

Ответ: $54^0$.

Пример смешанной задачи

Пример 3

Найти угол $COB$ из рисунка ниже

Решение. По определению 8 получаем, что углы $FAO$ и $COD$ являются вертикальными. Следовательно, по теореме 2, получим

$∠FAO=∠COD=25^0$

По определению 7 получаем, что углы $BOF$ и $BOC$ являются смежными. Следовательно, по теореме 1, получим

$∠BOF+∠BOC=180^0$

$∠BOC=180^0-∠BOF=180^0-55^0-25^0=100^0$

Ответ: $100^0$.

spravochnick.ru

Вертикальные углы — это… Что такое Вертикальные углы?

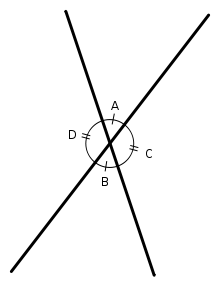Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая — из C и D.

В геометрии, два угла называются вертикальными, если они созданы пересечением двух прямых и не являются прилегающими. Такие углы имеют общую вершину. Они имеют одинаковую градусную меру и могут рассматриваться как равные.

Теорема о вертикальных углах

Если две прямые пересекаются в точке, образуются четыре угла. Несмежные углы называются вертикальными или противоположно вертикальными углами. Также, каждая пара прилегающих углов образует прямую, а эти углы называются смежными^[1]. Поскольку каждая пара вертикальных углов является смежными к прилегающим, то градусные меры вертикальных углов — равны.

Алгебраическое решение вертикальных углов

Например, угол A на рисунке — неизвестен. Обозначим A = x. Если два прилегающих угла образуют прямую, то они — смежные. Тогда, градусная мера C = 180 − x. Аналогично, градусная мера D = 180 − x. Углы C и D имеют одинаковую меру, которая равна 180 — x и являются вертикальными. Поскольку, угол B является смежным для обоих углов C и D, для того, чтобы вычислить размер B можно использовать градусную меру любого из них. Используя меру угла C или угла D, найдём градусную меру угла B = 180 — (180 — x) = 180—180 + x = x. Отсюда, оба угла A и B имеют г

См. также

Литература

1. ↑ Euclid The Elements. — c. 300 BC. Proposition I:13.

Ссылки

dic.academic.ru

Решение задач по теме «Смежные и вертикальные углы»

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Тип урока: урок закрепления нового материала

Цели урока:

• Образовательные: повторить и закрепить понятия о смежных и вертикальных углах;
• Развивающие: развивать умение анализировать условие задачи;
• Воспитательные: воспитание аккуратности (аккуратное выполнение чертежей на доске и в тетрадях, рациональное распределение записей).

Структура урока:

• I этап. Организационный момент
• II этап. Актуализация опорных знаний
• III этап. Закрепление изученного материала
• IV этап. Зарядка для глаз
• V этап. Самостоятельная работа
• VI этап. Домашнее задание
• VII этап. Итог урока

Ход урока

I. Организационный момент

(Слайд 1-2)

Приветствие, сообщение темы, целей и задач. 
Учитель: Вам было задано домашнее задание: повторить п.14 и 15, ответить на вопросы 1, 2, 3, 6, 7. Сейчас проверим, как вы подготовились к уроку.

II. Актуализация опорных знаний

(Слайд 3)

Вопрос: Какие углы называются смежными? (Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными полупрямыми)

Вопрос. Из рисунка назвать смежные углы. (Ответ: ∠АОВ и ∠ВОС – смежные углы)

Вопрос. Какая сторона у них общая? (Ответ: ОВ – общая сторона.)

Вопрос. Назвать дополнительные полупрямые. (Ответ. ОС и ОА – дополнительные полупрямые.)

(Слайд 4) Вопрос. Какими свойствами обладают смежные углы?

Ответ.

• Сумма смежных углов равна 180° (теорема)

∠1 + ∠2 = 180°

• Если два угла равны, то и смежные с ними углы равны.
• Если угол не развернутый, то его градусная мера меньше 180°.
• Угол, смежный с прямым, есть прямой угол.

(Слайд 5)

Вопросы. Могут ли два смежных угла быть равными:

а) 75° и 80°; Ответ: (нет, т.к.75° + 80°=155°)
б) 94° и 96°; Ответ: (нет, т.к. 94° + 96°= 190°)
в) 83° и 97°? Ответ: (да, т.к. 83° + 97°= 180°)

(Слайд 6)

Устно.

Дано: ∠АОВ а ∩ АО а ∩ ОВ ∠3 = ∠4	Доказательство. 1. ∠3 смежный с ∠1, ∠4 смежный с ∠2 . 2. Т.к. ∠3 = ∠4 (по условию), то ∠1 = ∠ 2, как углы, смежные равным углам. (по свойству смежных углов).
Доказать ∠1 = ∠2

(Слайд 7)

Вопрос. Какие углы называются вертикальными?

(Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого).

∠ 1 и ∠ 3 – вертикальные углы

∠ 2 и ∠ 4 – вертикальные углы

(Слайд 8)

Вопрос. Каким свойством обладают смежные углы?

Ответ. Вертикальные углы равны. (теорема)

∠ 1 = ∠ 3

∠ 2 = ∠ 4

III этап. Закрепление изученного материала. Решение задач.

(Слайд 9)

№3 (учебник)

Дано: ∠1 и ∠2– смежные ∠1 больше ∠2 в 2 раза	Решение. 1. Пусть ∠2 = х, тогда ∠1=2х 2. Т.к. ∠1 + ∠2 = 180°(по теореме о смежных углах), то х + 2х = 180° 3х = 180°, ⇒ х =180°: 3, х = 60°. 3. Следовательно: ∠2 = 60°, ∠1 = 2∙60°= 120° Ответ: ∠1= 120°, ∠2= 60°,
Найти ∠1 и ∠2

(Слайд 10)

№6(2)

Дано: ∠1 и ∠2 – смежные ∠1 : ∠2 = 3 : 7	Решение. 1. Пусть х. – коэффициент пропорциональности. Тогда ∠1 = 3х, ∠2 = 7х (по условию задачи) 2. Т.к ∠1 + ∠2 = 180°(по теореме о смежных углах), то 3х + 7х = 180°, 10х = 180°, х = 18°. 3. Следовательно: ∠1 =3 ∙ 18°=54°, ∠2 =7 ∙ 18°=126° Ответ: 54°; 126°.
Найти ∠1 и ∠2

(Слайд 11)

Дано: ∠1 и ∠2 – смежные ∠2 составляет 0,2 от∠1	Решение 1. Пусть ∠1 = х, тогда ∠2 = 0,2х (по условию). 2. Т.к. ∠1 + ∠2 = 180° (по теореме о смежных углах), то х + 0,2х =180°, 1,2х = 180°, х = 150°, 3. Следовательно: ∠1=150°, ∠2= 0,2∙ 150°= 30°. Ответ: 150°, 30°
Найти ∠1 и ∠2

(Слайд 12)

Дано: а ∩ b ∠2 меньше ∠1 в 4 раза	Решение 1. Пусть ∠2 = х , тогда ∠1 = 4х (по условию), 2. Т.к. ∠1+ ∠2 = 180° (по теореме о смежных углах), то 4х + х = 180°, 5х = 180°, х = 36°. 3. Следовательно: ∠2 = 36°, ∠1 = 4∙36° = 144° ∠3= ∠1, ∠4= ∠2 (по теореме о вертикальных углах), значит ∠3= 144°, ∠4=36°. Ответ: 144°, 36°, 144°, 36°.
Найти ∠1, ∠2, ∠3 и ∠4

(Слайд 13)

Дано: AС ∩ ВD = O ∠ВОС = 23°	Решение 1. ∠АОD = ∠ВОС = 23° (по теореме о вертикальных углах) 2. ∠АОВ + ∠ВОС = 180° (по теореме о смежных углах). Следовательно: ∠АОВ =180°– ∠ВОС, т.е. ∠АОВ =180° – 23° = 157° 3. ∠СОD = ∠АОВ = 157° (по теореме о вертикальных углах). Ответ: 157°, 157°, 23°.
Найти: ∠СОD, ∠АОВ, ∠АОD.

(Слайд 14)

Устно. Вопрос. Назовите смежные и вертикальные углы.

Ответ.

Смежные углы:∠ АОМ и ∠ АОD, ∠АОD и ∠NОD, ∠NОD и ∠NОМ, ∠NОМ и ∠АОМ .

Вертикальные углы: ∠АОМ и ∠NОD, ∠АОD и ∠NОМ. 

IV этап. Зарядка для глаз

(Слайд 15)

V этап. Самостоятельная работа (на листочках).

Вариант 1	Вариант 2
№1. Один из углов, получившихся при пересечении двух прямых, равен 87°. Найдите остальные углы.	№1. Один из углов, получившихся при пересечении двух прямых, равен 118°. Найдите остальные углы.
№2. Разность смежных углов равна 50°. Найдите меньший угол.	№2. Один из смежных углов в 4 раза меньше другого. Найдите больший угол.

Ответы

Вариант 1	Вариант 2
№1. 93°, 87°, 93°.	№1. 62°, 118°, 62°
№2. 75°.	№2. 36°.

VI этап. Домашнее задание.

1. §2. Пункты 14-15.
2. Задачи на стр. 26. № 6(4), № 12.

VII этап. Итог урока.

• Повторили понятия смежных и вертикальных углов
• Научились решать задачи, используя знания о смежных и вертикальных углах.
• Стали еще на одну ступеньку выше в изучении геометрии.

urok.1sept.ru

Смежные и вертикальные, центральные и вписанные углы

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

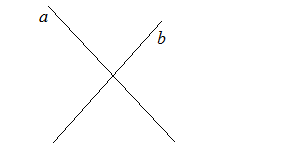
На рисунке углы a и b являются смежными, смежные и углы b и c, и углы c и d, и углы a и d.

Сумма смежных углов равна 180˚. Исходя из этого, можно говорить о свойствах смежных углов:

1. если два угла равны, то смежные с ними углы равны;
2. угол, смежный с прямым углом, является прямым углом;
3. угол, смежный с тупым, является острым, а смежный с ним острый – тупым.

Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми (лучами) сторон другого.

На рисунке углы α и d являются вертикальными. Вертикальными также являются и углы с и d.

Вертикальные углы равны. Исходя из этого, можно говорить о свойствах вертикальных углов:

Две пересекающиеся прямые образуют и смежные, и вертикальные углы. Смежные углы дополняют друг друга до 180˚. Угловая мера меньшего из них называется углом между прямыми.

Вспомним, что биссектриса угла – это луч. Который делит угол на два равные угла. У вертикальных углов биссектрисы лежат на одной прямой. Биссектрисы смежных углов взаимно перпендикулярны. Биссектриса угла обладает свойством: каждая её точка находится на одинаковом расстоянии сторон угла.

Понятия центрального и вписанного угла связаны с понятием окружность.

Окружность – это геометрическая фигура, которая состоит из всех точек плоскости, находящихся на данном расстоянии от данной точки. Эта точка называется центром окружности.

Центральный угол в окружности – это плоский угол с вершиной в её центре. Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу. Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Конспект урока по геометрии на тему: Смежные и вертикальные углы

УРОК № 7 (27.09.16)

Предмет: геометрия, 7 кл.

Тема урока: «Смежные и вертикальные углы»

Цели:

— ввести понятия смежных и вертикальных углов;

— рассмотреть их свойства;

— развивать умение сравнивать, выявлять закономерности, обобщать;

— воспитывать потребность в доказательных рассуждениях;

— воспитывать аккуратность при выполнении рисунков,

— ответственное отношение к учебному труду.

Тип урока: урок изучения нового материала

Оборудование: учебник «геомтерия 7-9 кл», рабочая тетрадь, линейка, доска, раздаточный материал.

ХОД УРОКА

I. Организационный момент. Приветствие, определение отсутствующих, подготовка к работе.

II. Актуализация знаний. Сегодня мы повторим виды углов, их свойства и добавим к знаниям об углах ещё два вида. Чтобы не забыть старых знакомых, выполним устно задания

1. Назвать вид каждого угла и указать градусную меру.

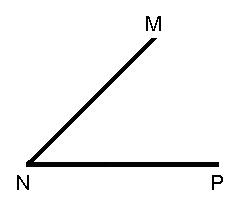
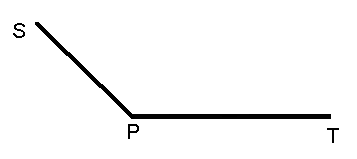
2) Дано: АОD = 8DОВ. Найти: DОВ

3) а) АОЕ=30⁰

ЕОС=20°

AOC=?

б) АОС=70°

АОЕ=50°

ЕОС=?

II. Изучение нового материала. Решение задач.

Решая 1 и 2 задачу, мы встретились с углами, которые носят название смежные и вертикальные. Это и есть тема нашего урока. Сегодня мы рассмотрим их определения и свойства.

Введение понятия «смежные углы».

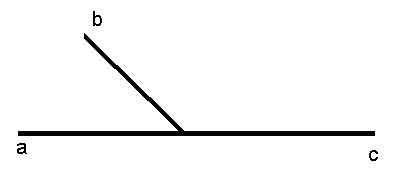
1. Практическая работа. Построим прямую АD и отметим точку С, лежащую между точками А и D. Проведём луч СВ. Получились два угла: АСВ и ВСD. Такие углы принято называть смежными.

Попробуем сформулировать определение смежных углов, но сначала ответим на вопросы:

а) назовите стороны каждого из углов;

б) как связаны между собой стороны смежных углов?;

в) выделить особенности смежных углов (одна сторона общая, две другие являются продолжениями одна другой).

Обратить внимание на слово «смежные» — находящиеся рядом («межа»).

Далее прочитать определение смежных углов в учебнике, подчеркнув те условия, которые должны удовлетворять смежные углы.

2. Усвоение понятия смежных углов.

Найдите пары смежных углов и объясните, почему они смежные.

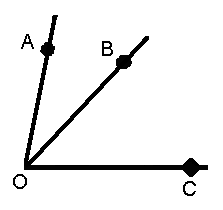
3. Сформулировать свойство смежных углов. (Предложить это сделать самим учащимся, вспомнив 3 задачу).

4. Закрепление понятия и свойства смежных углов.

Решить из учебника задачи № 55 (на доске и в тетрадях), № 59,60 — устно. Разобрать задачу из раздаточного материала.

5. Введение понятия вертикальных углов.

Практическая работа:

1) проведите луч ОС, являющийся продолжением луча ОА и луч ОD, являющийся продолжением луча ОВ;

2) запишите в тетради: углы АОВ и СОD называются вертикальными.

Вопрос: Сколько пар вертикальных углов образуется при пересечении двух прямых?

Попробуем сформулировать определение вертикальных углов, ответив на вопросы:

1) назвать стороны каждого вертикального угла;

2) как связаны стороны вертикальных углов между собой?

3) выделить особенности вертикальных углов (1-я сторона 1-го угла является продолжением стороны второго, 2-я сторона 1-го угла является продолжением стороны второго).

Далее прочитать определение вертикальных углов в учебнике, подчеркнув те условия, которые должны удовлетворять вертикальные углы.

6. Усвоение понятия вертикальных углов.

Указать пары вертикальных углов на рисунке и объяснить, почему они вертикальные.

7. Обоснование того факта, что вертикальные углы равны, вначале можно провести на конкретном примере:

Задача. Прямые АВ и СD пересекаются в точке О так, что угол АОD равен 35⁰.

Найдите углы АОС и ВОС,

Задачу решить по готовому чертежу.

Вопрос: верно ли утверждение, что любые вертикальные углы равны?

Далее учащиеся самостоятельно разбирают доказательство свойства вертикальных углов по рис. 41 в учебнике и записывают в тетрадях.

8. На закрепление свойств вертикальных и смежных углов решить
№65 (а) устно, №66 (б; в) — письменно.

III. Тест. Итог урока.

1. Являются ли смежными углы: а) DОС и DОЕ; б) DОС и СОВ; в) DОЕ и АОВ?

2. Являются ли вертикальными углы: а) DОЕ и СОА; б) DОА и АОВ;

в) АОВ и DОЕ?

Обсудить с детьми вопросы: 1) что нового вы узнали сегодня на уроке? 2) что было самое трудное на уроке? 3) что помогло с этой трудностью справиться?

IV. Домашнее задание. П. 11 выучить определения, № 55,56,58,61.

Раздаточный материал

Смежные и вертикальные углы.

Правила. Смежными называются углы, у которых одна сторона общая, а две  
другие стороны расположены на одной прямой (являются дополняющими  
лучами).            Вертикальными называются углы, у которых стороны одного угла  
являются продолжением второго угла. 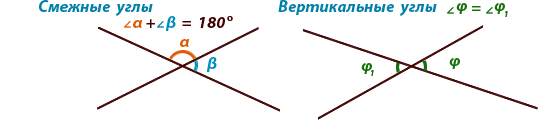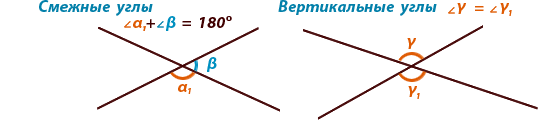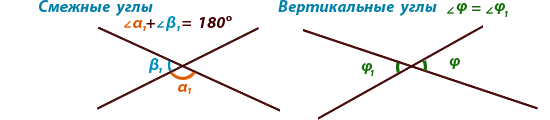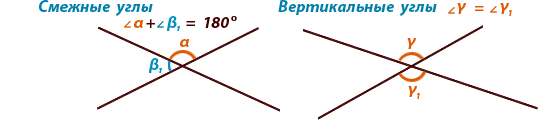                 Сумма смежных углов равна 180°,  

                                                  а 

вертикальные углы равны друг другу.    

         Пример решения задачи на нахождение смежных углов:

Найдем смежные углы,    α   и    β,   если    α   в два раза больше    β.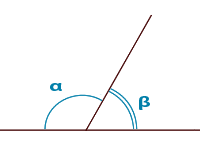  
  
Р е ш е н и е :  

 α   =   2 •  β     —   по условию задачи ;  

 α +  β   =   180 °     —   сумма смежных углов ;  

2 •  β +  β   =   180 °     —   замена   α   на   2β ;    

      3 •  β   =   180 ° ;                     

 β   =   180 ° : 3   =   60 °   ;  

       α   =     2 •  β     =     2 • 60 °     =     120 ° .    

      О т в е т :      α   =   120 ° ,      β     =   60 ° .    

infourok.ru