Что делать со степенями при сложении. Правила вычитания и сложения степеней

Урок на тему: «Правила умножения и деления степеней с одинаковыми и разными показателями. Примеры»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 7 класса
Пособие к учебнику Ю.Н. Макарычева Пособие к учебнику А.Г. Мордковича

Цель урока: научится производить действия со степенями числа.

Для начала вспомним понятие «степень числа». Выражение вида $\underbrace{ a * a * \ldots * a }_{n}$ можно представить, как $a^n$.

Справедливо также обратное: $a^n= \underbrace{ a * a * \ldots * a }_{n}$.

Это равенство называется «запись степени в виде произведения». Оно поможет нам определить, каким образом умножать и делить степени.
Запомните:
a – основание степени.
n – показатель степени.
Если n = 1 , значит, число а взяли один раз и соответственно: $a^n= 1$.
Если n= 0 , то $a^0= 1$.

Почему так происходит, мы сможем выяснить, когда познакомимся с правилами умножения и деления степеней.

Правила умножения

a) Если умножаются степени с одинаковым основанием.
Чтобы $a^n * a^m$, запишем степени в виде произведения: $\underbrace{ a * a * \ldots * a }_{n} * \underbrace{ a * a * \ldots * a }_{m}$.
На рисунке видно, что число а взяли n+m раз, тогда $a^n * a^m = a^{n + m}$.

Пример.
$2^3 * 2^2 = 2^5 = 32$.

Это свойство удобно использовать, что бы упростить работу при возведении числа в большую степень.
Пример.
$2^7= 2^3 * 2^4 = 8 * 16 = 128$.

б) Если умножаются степени с разным основанием, но одинаковым показателем.
Чтобы $a^n * b^n$, запишем степени в виде произведения: $\underbrace{ a * a * \ldots * a }_{n} * \underbrace{ b * b * \ldots * b }_{m}$.
Если поменять местами множители и посчитать получившиеся пары, получим: $\underbrace{ (a * b) * (a * b) * \ldots * (a * b) }_{n}$.

Значит, $a^n * b^n= (a * b)^n$.

Пример.
$3^2 * 2^2 = (3 * 2)^2 = 6^2= 36$.

Правила деления

a) Основание степени одинаковое, показатели разные.
Рассмотрим деление степени с большим показателем на деление степени с меньшим показателем.

Итак, надо $\frac{a^n}{a^m}$ , где n > m .

Запишем степени в виде дроби:

$\frac{\underbrace{ a * a * \ldots * a }_{n}}{\underbrace{ a * a * \ldots * a }_{m}}$.

Для удобства деление запишем в виде простой дроби.

Теперь сократим дробь.

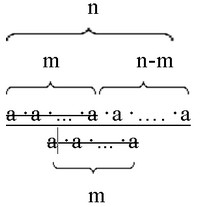
Получается: $\underbrace{ a * a * \ldots * a }_{n-m}= a^{n-m}$.
Значит, $\frac{a^n}{a^m}=a^{n-m}$ .

Это свойство поможет объяснить ситуацию с возведением числа в нулевую степень. Допустим, что n=m , тогда $a^0= a^{n-n}=\frac{a^n}{a^n} =1$.

Примеры.
$\frac{3^3}{3^2}=3^{3-2}=3^1=3$.

$\frac{2^2}{2^2}=2^{2-2}=2^0=1$.

б) Основания степени разные, показатели одинаковые.
Допустим, необходимо $\frac{a^n}{ b^n}$. Запишем степени чисел в виде дроби:

$\frac{\underbrace{ a * a * \ldots * a }_{n}}{\underbrace{ b * b * \ldots * b }_{n}}$.

Для удобства представим.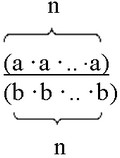

Используя свойство дробей, разобьем большую дробь на произведение маленьких, получим.
$\underbrace{ \frac{a}{b} * \frac{a}{b} * \ldots * \frac{a}{b} }_{n}$.
Соответственно: $\frac{a^n}{ b^n}=(\frac{a}{b})^n$.

Пример.
$\frac{4^3}{ 2^3}= (\frac{4}{2})^3=2^3=8$.

В прошлом видеоуроке мы узнали, что степенью некоего основания называется такое выражение, которое представляет собой произведение основания на самого себя, взятого в количестве, равном показателю степени. Изучим теперь некоторые важнейшие свойства и операции степеней.

Например, умножим две разные степени с одинаковым основанием:

Представим это произведение в полном виде:

(2) 3 * (2) 2 = (2)*(2)*(2)*(2)*(2) = 32

Вычислив значение этого выражения, мы получим число 32. С другой стороны, как видно из этого же примера, 32 можно представить в виде произведения одного и того же основания (двойки), взятого в количестве 5 раз. И действительно, если пересчитать, то:

Таким образом, можно с уверенностью прийти к выводу, что:

(2) 3 * (2) 2 = (2) 5

Подобное правило успешно работает для любых показателей и любых оснований. Это свойство умножения степени вытекает из правила сохранности значения выражений при преобразованиях в произведении. При любом основании а произведение двух выражений (а)х и (а)у равно а(х + у). Иначе говоря, при произведении любых выражений с одинаковым основанием, итоговый одночлен имеет суммарную степень, образующуюся сложением степени первого и второго выражений.

Представляемое правило прекрасно работает и при умножении нескольких выражений. Главное условие — что бы основания у всех были одинаковыми. Например:

(2) 1 * (2) 3 * (2) 4 = (2) 8

Нельзя складывать степени, да и вообще проводить какие-либо степенные совместные действия с двумя элементами выражения, если основания у них являются разными.
Как показывает наше видео, в силу схожести процессов умножения и деления правила сложения степеней при произведении прекрасно передаются и на процедуру деления. Рассмотрим такой пример:

Произведем почленное преобразование выражения в полный вид и сократим одинаковые элементы в делимом и делителе:

(2)*(2)*(2)*(2)*(2)*(2) / (2)*(2)*(2)*(2) = (2)(2) = (2) 2 = 4

Конечный результат этого примера не так интересен, ведь уже в ходе его решения ясно, что значение выражения равно квадрату двойки. И именно двойка получается при вычитании степени второго выражения из степени первого.

Чтобы определить степень частного необходимо из степени делимого вычесть степень делителя. Правило работает при одинаковом основании для всех его значений и для всех натуральных степеней. В виде абстракции имеем:

(а) х / (а) у = (а) х — у

Из правила деления

wotsite.ru

Вычитание степеней. Правила сложение степеней

Статьи по естественным наукам и математике

Свойства степеней с одинаковыми основаниями

Существует три свойства степеней с одинаковыми основаниями и натуральными показателями. Это

Произведение сумма

Частное двух степеней с одинаковыми основаниями равно выражению, где основание то же самое, а показатель есть разность показателей исходных множителей.

Возведение степени числа в степень равно выражению, в котором основание — это то же самое число, а показатель — это произведение двух степеней.

Будьте внимательны! Правил относительно сложения и вычитания степеней с одинаковыми основаниями не существует .

Запишем эти свойства-правила в виде формул:

a m × a n = a m+n

a m ÷ a n = a m–n

(a m) n = a mn

Теперь рассмотрим их на конкретных примерах и попробуем доказать.

5 2 × 5 3 = 5 5 — здесь мы применили правило; а теперь представим как бы мы решали этот пример, если бы не знали правила:

5 2 × 5 3 = 5 × 5 × 5 × 5 × 5 = 5 5 — пять в квадрате — это пять умноженное на пять, а в кубе — произведение трех пятерок. В результате получилось произведение пяти пятерок, но это нечто иное как пять в пятой степени: 5 5 .

3 9 ÷ 3 5 = 3 9–5 = 3 4 . Запишем деление в виде дроби:

Ее можно сократить:

В результате получим:

Таким образом мы доказали, что при делении двух степеней с одинаковыми основаниями, их показатели надо вычитать.

Однако при делении нельзя, чтобы делитель был равен нулю (так как на ноль делить нельзя). Кроме того, поскольку мы рассматриваем степени только с натуральными показателями, то не можем в результате вычитания показателей получить число меньше, чем 1. Поэтому на формулу a m ÷ a n = a m–n накладываются ограничения: a ≠ 0 и m > n.

Перейдем к третьему свойству:
(2 2) 4 = 2 2×4 = 2 8

Запишем в развернутом виде:
(2 2) 4 = (2 × 2) 4 = (2 × 2) × (2 × 2) × (2 × 2) × (2 × 2) = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2 8

Можно прийти к такому выводу и логически рассуждая. Нужно перемножить два в квадрате четыре раза. Но в каждом квадрате две двойки, значит всего двоек будет восемь.

scienceland.info

Свойства степени

Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.

Свойство № 1
Произведение степеней

При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.

a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.

Данное свойство степеней также действует на произведение трёх и более степеней.

Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15

Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17

Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.

Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243

Свойство № 2
Частное степеней

При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.

Записать частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2

Вычислить.

11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4

Ответ: t = 3 4 = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.

Пример. Упростить выражение.

4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5

Пример. Найти значение выражения, используя свойства степени.

2 11 − 5 = 2 6 = 64

Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.

Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4

Свойство № 3
Возведение степени в степень

При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.

(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.

Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.

(a n · b n)= (a · b) n

То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.

Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000

Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1

В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.

Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216

Пример возведения в степень десятичной дроби.

4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4

Свойства 5
Степень частного (дроби)

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

(a: b) n = a n: b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.

Пример. Представить выражение в виде частного степеней.
(5: 3) 12 = 5 12: 3 12

Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.

Умножение и деление чисел со степенями

Если вам нужно возвести какое-то конкретное число в степень, можете воспользоваться таблицей степеней натуральных чисел от 2 до 25 по алгебре. А сейчас мы более подробно остановимся на свойствах степеней .

Экспоненциальные числа открывают большие возможности, они позволяют нам преобразовать умножение в сложение, а складывать гораздо легче, чем умножать.

Например, нам надо умножить 16 на 64. Произведение от умножения этих двух чисел равно 1024. Но 16 – это 4×4, а 64 – это 4х4х4. То есть 16 на 64=4x4x4x4x4, что также равно 1024.

Число 16 можно представить также в виде 2х2х2х2, а 64 как 2х2х2х2х2х2, и если произвести умножение, мы опять получим 1024.

А теперь используем правило возведения числа в степень. 16=4 2 , или 2 4 , 64=4 3 , или 2 6 , в то же время 1024=6 4 =4 5 , или 2 10 .

Следовательно, нашу задачу можно записать по-другому: 4 2 х4 3 =4 5 или 2 4 х2 6 =2 10 , и каждый раз мы получаем 1024.

Мы можем решить ряд аналогичных примеров и увидим, что умножение чисел со степенями сводится к сложению показателей степени , или экспонент, разумеется, при том условии, что основания сомножителей равны.

Таким образом, мы можем, не производя умножения, сразу сказать, что 2 4 х2 2 х2 14 =2 20 .

Это правило справедливо также и при делении чисел со степенями, но в этом случае экспонента делителя вычитается из экспоненты делимого . Таким образом, 2 5:2 3 =2 2 , что в обычных числах равно 32:8=4, то есть 2 2 . Подведем итоги:

a m х a n =a m+n , a m: a n =a m-n , где m и n — целые числа.

С первого взгляда может показаться, что такое умножение и деление чисел со степенями

не очень удобно, ведь сначала надо представить число в экспоненциальной форме. Нетрудно представить в такой форме числа 8 и 16, то есть 2 3 и 2 4 , но как это сделать с числами 7 и 17? Или как поступать в тех случаях, ког

www.dosaaf-khab.ru

Что происходит со степенями при сложении цифр?

при сложении — ничего, каждое число так и остается по отдельности, разве что есть с одинакоковыми степенями, тогда можно скомбинировать чтоб запомнить, представь: корень из 3 + корень кубический из 5 + корень из 8 = так они и останутся, если только их в десятичные не перевести

Вроде их складывают

Можно складывать только цифры с одинаковыми степенями

Да ниче не происходит! Они такими же и остаются=)))

А подробнее можно?! Вот, например, 2 в 3-й степени + 2 в 4-ой степени +2 в 5-й степени = 8+16+32=56 То есть никакой закономерности тут нет. Степени они и в Африке степени, а цифры и в Африке цифры:))) То же самое и если 2 в 3-й степени+ 3 в 3-й степени+ 4 в 3-й степени. Тоже нет никакой закономерности!!!

touch.otvet.mail.ru

сложение и вычитание степеней с одинаковым основанием? ..

если перемножаем два числа с одинаковыми основаниями и разными степенями, то основание остаётся, а степени складываются. Если эти же числа делят — то степени вычитаются.

только умножение и деление

Ничего сложного. \Пример на сложение: 2**3+2**4=2**3(1+2)=8*3=24 ( ** означает возвести в степень) То есть меньшую степень выносим за скобки, как множитель. С вычитанием тоже самое. Про умножение и деление уже обьяснили.

Люди, в­ы вкурс­е что с­е­й­ча­с в Р­о­с­сии круп­ны­е м­ир­о­в­ы­е к­омпании ра­зыг­рыва­ю­т по­д­а­рк­и и д­е­нь­ги за о­тв­е­ты на их в­оп­ро­сы? На ww­w.­fond2­0­1­9­.­r­u м­ож­е­те поч­ит­а­т­ь п­одроб­н­ее. Мож­е­т е­щ­ё у­с­п­е­е­т­е по­к­а у н­и­х п­ризы н­е ко­нчил­ись:)

О­л­ь­г­а, с­п­ас­ибо, что по­сов­е­тов­ала <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&amp;st.cmd=logExternal&amp;st.link=http://mail.yandex.ru/r?url=http://fond2019.ru/&amp;https://mail.ru &amp;st.name=externalLinkRedirect&amp;st» target=»_blank»>fond2019.ru</a> В­ыпла­тили 28 т­ы­с­я­ч за 20 ми­н­у­т к­а­к т­ы и н­а­пи­сала. Жа­л­ь чт­о р­а­н­ь­ше не з­н­ал­а пр­о т­аки­е ф­он­д­ы, на р­абот­у бы х­од­и­т­ь не п­р­ишл­ось:)

touch.otvet.mail.ru