Пределы. Примеры решений — matematika

Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.

Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:

1. Понять, что такое предел.
2. Научиться решать основные типы пределов.    

Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.

Итак, что же такое предел?

А сразу пример, чего бабушку лохматить….

Любой предел состоит из трех частей:

1) Всем известного значка предела .
2) Записи под значком предела, в данном случае 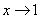. Запись читается «икс стремится к единице». Чаще всего – именно 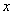, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность (

).
3) Функции под знаком предела, в данном случае .

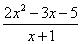Сама запись 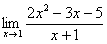 читается так: «предел функции  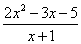при икс стремящемся к единице».

Разберем следующий ва

www.sites.google.com

Замечательные пределы. Примеры решений

Продолжаем наш разговор на тему Пределы и способы их решения

. Перед изучением материалов данной страницы настоятельно рекомендую ознакомиться со статьей Пределы. Примеры решений. Из вышеуказанной статьи Вы сможете узнать, что же такое предел, и с чем его едят – это ОЧЕНЬ важно. Почему? Можно не понимать, что такое определители и успешно их решать, можно совершенно не понимать, что такое производная и находить их на «пятёрку». Но вот если Вы не понимаете, что такое предел, то с решением практических заданий придется туго. Также не лишним будет ознакомиться с образцами оформления решений и моими рекомендациями по оформлению. Вся информация изложена в простой и доступной форме.

А для целей данного урока нам потребуются следующие методические материалы:Замечательные пределы и Тригонометрические формулы. Их можно найти на страницеМатематические формулы, таблицы и справочные материалы. Лучше всего методички распечатать – это значительно удобнее, к тому же к ним часто придется обращаться в оффлайне.

Чем же замечательны замечательные пределы? Замечательность данных пределов состоит в том, что они доказаны величайшими умами знаменитых математиков, и благодарным потомкам не приходиться мучаться страшными пределами с нагромождением тригонометрических функций, логарифмов, степеней. То есть при нахождении пределов мы будем пользоваться готовыми результатами, которые доказаны теоретически.

Замечательных пределов существует несколько, но на практике у студентов-заочников в 95% случаев фигурируют два замечательных предела: Первый замечательный предел,Второй замечательный предел. Следует отметить, что это исторически сложившиеся названия, и, когда, например, говорят о «первом замечательном пределе», то подразумевают под этим вполне определенную вещь, а не какой-то случайный, взятый с потолка предел.

Начнем.

Первый замечательный предел

Рассмотрим следующий предел: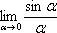 

 (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).

Согласно нашему правилу нахождения пределов (см. статью Пределы. Примеры решений) пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:

 

Данный математический факт носит название Первого замечательного предела.

Нередко в практических  заданиях функции могут быть расположены по-другому, это ничего не меняет:

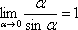 – тот же самый первый замечательный предел.

! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде 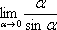, то и решать его нужно в таком же виде, ничего не переставляя.

На практике в качестве параметра  может выступать не только переменная , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.

Примеры: , , 

, 

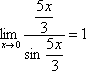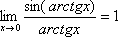
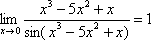
Здесь 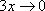, , 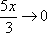, , 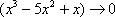и всё гуд – первый замечательный предел применим.

А вот следующая запись – ересь:

Почему? Потому-что многочлен 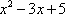 не стремится к нулю, он стремится к пятерке.

Кстати, вопрос на засыпку, а чему равен предел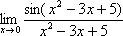 

? Ответ можно найти в конце урока.

На практике не все так гладко, почти никогда студенту не предложат решить халявный предел  и получить лёгкий зачет. Хммм… Пишу эти строки и пришла в голову очень важная мысль – все-таки «халявные» математические определения и формулы вроде 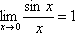  лучше помнить наизусть, это может оказать неоценимую помощь на зачете, когда вопрос будет решаться между «двойкой» и «тройкой», и преподаватель решит задать студенту какой-нибудь простой вопрос или предложить решить простейший пример («а может он (а) все-таки знает чего?!»).

Переходим к рассмотрению практических примеров:

Пример 1

Найти предел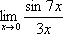 

Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.

Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):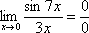

Итак, а нас есть неопределенность вида , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится , а в знаменателе .

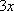В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас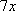 

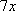, значит, в знаменателе нам тоже нужно получить ».  А делается это очень просто:

То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания. Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:

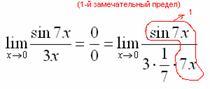Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:

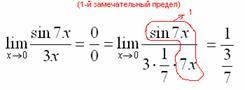
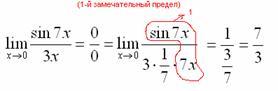Теперь только осталось избавиться от трехэтажности дроби: Готово. Окончательный ответ: 

Если не хочется использовать пометки карандашом, то решение можно оформить так:

“ Используем первый замечательный предел  “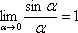

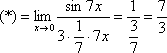Пример 2

Найти предел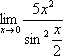 

Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль: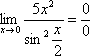

Действительно, у нас неопределенность  и, значит, нужно попытаться организовать первый замечательный предел. На уроке Пределы. Примеры решений мы рассматривали правило, что когда у нас есть неопределенность , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):

Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас , значит, в числителе тоже нужно получить :

Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:

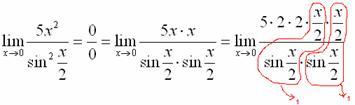
Собственно, ответ готов:

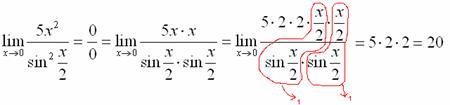
В следующих примерах, я не буду заниматься художествами в Пэйнте, думаю, как правильно оформлять решение в тетради – Вам уже понятно.

Пример 3

Найти предел 

Подставляем ноль в выражение под знаком передела:

Получена неопределенность , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле 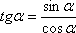 (кстати, с котангенсом делают примерно то же самое, см. методический материалГорячие тригонометрические формулы на странице Математические формулы, таблицы и справочные материалы).

 В данном случае:

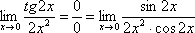
Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):

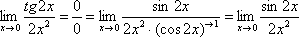
Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.

Дальше по накатанной схеме, организуем первый замечательный предел:

Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:

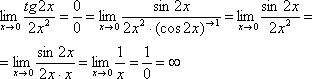
В итоге получена бесконечность, бывает и такое.

Пример 4

Найти предел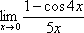 

Пробуем подставить ноль в числитель и знаменатель:

Получена неопределенность  (косинус нуля, как мы помним, равен единице)

Используем тригонометрическую формулу 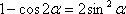. Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.

Постоянные множители вынесем за значок предела:

 

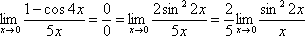
Организуем первый замечательный предел:

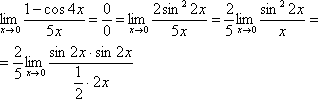Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:

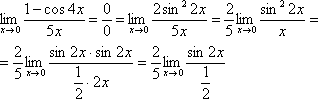
Избавимся от трехэтажности:

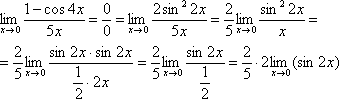
Предел фактически решен, указываем, что оставшийся синус стремится к нулю:

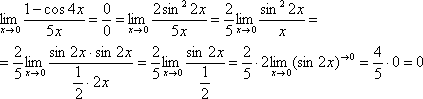
Пример 5

Найти предел 

Этот пример сложнее, попробуйте разобраться самостоятельно:

 

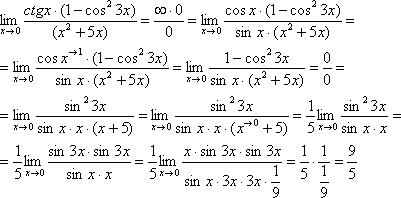
Второй замечательный предел

В теории математического анализа доказано, что:

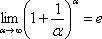
Данный факт носит название второго замечательного предела.

Справка: 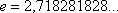 – это иррациональное число.

В качестве параметра  может выступать не только переменная , но и сложная функция.Важно лишь, чтобы она стремилась к бесконечности.

Пример 6

Найти предел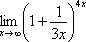 

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.

Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение 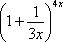 , по какому принципу это делается, разобрано на уроке Пределы. Примеры решений.

Нетрудно заметить, что при 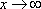 основание степени 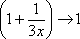, а показатель – 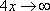, то есть имеется, неопределенность вида :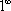

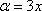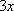Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр , значит, в показателе нам тоже нужно организовать  . Для этого возводим основание в степень , и, чтобы выражение не изменилось – возводим в степень :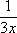

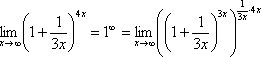
Когда задание оформляется от руки, карандашом помечаем:

Практически всё готово, страшная степень превратилась в симпатичную букву :

При этом сам значок предела перемещаем в показатель.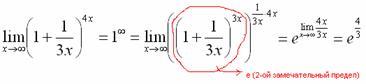

Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.

Пример 7

Найти предел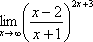 

Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.

Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:

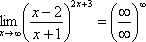
В результате получена неопределенность . Но второй замечательный предел применим к неопределенности вида 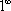. Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас , значит, в числителе тоже нужно организовать :

Теперь можно почленно разделить числитель на знаменатель:

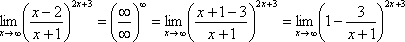
Вроде бы основание стало напоминать 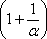, но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:

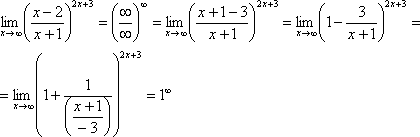
Таким образом, основание приняло вид 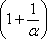, и, более того, появилась нужная нам неопределенность 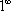. Организуем второй замечательный предел . Легко заметить, что в данном примере 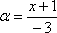. Снова исполняем наш искусственный прием: возводим основание степени в , и, чтобы выражение не изменилось – возводим в обратную дробь :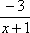

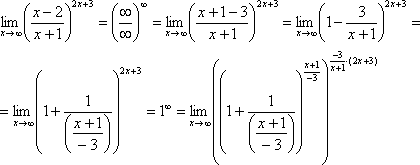
Наконец-то долгожданное 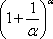 устроено, с чистой совестью превращаем его в букву :

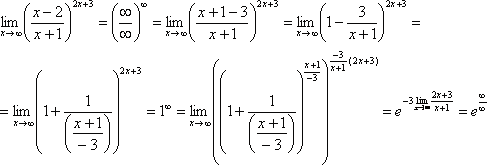
Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида , раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на :

Готово.

А сейчас мы рассмотрим модификацию второго замечательного предела. Напомню, что второй замечательный предел выглядит следующим образом: . Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:

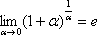
Пример 8

Найти предел 

Сначала (мысленно или на черновике) пробуем подставить ноль (бесконечно малое число) в выражение, стоящее под знаком предела:

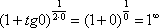
В результате получена знакомая неопределенность 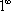. Очевидно, что в данном примере 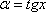. С помощью знакомого искусственного приема организуем в показателе степени конструкцию :

Выражение 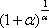 со спокойной душой превращаем в букву :

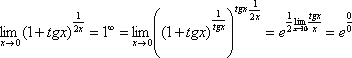
Еще не всё, в показателе у нас появилась неопределенность вида . Раскладываем тангенс на синус и косинус (ничего не напоминает?):

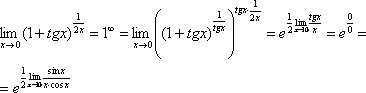
Косинус нуля стремится к единице (не забываем помечать карандашом), поэтому он просто пропадает в произведении:

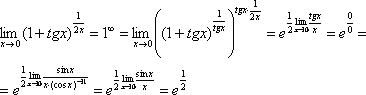
А что такое 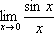 и к чему оно стремится, нужно уже знать, иначе «двойка»!

Как видите, в практических заданиях на вычисление пределов нередко требуется применять сразу несколько правил и приемов.

В 90-95% на зачете, экзамене Вам встретится первый замечательный предел или второй замечательный предел. Как быть, если попался «экзотический» замечательный предел? (со списком всех замечательных пределов можно ознакомиться в соответствующей методичке). Ничего страшного, практически все выкладки, приёмы решения для первого замечательного предела справедливы и для остальных замечательных пределов. Нужно решать их по аналогии.

Да, так чему же равен предел ?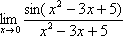

Если у Вас получился ответ 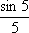, значит в понимании высшей математики не всё так безнадежно = ).

studfile.net

Пределы с иррациональностями. Примеры раскрытия неопределённостей. Вторая часть.

Нам понадобится несколько формул, которые я запишу ниже:

\begin{equation} a^2-b^2=(a-b)\cdot(a+b) \end{equation} \begin{equation} a^3-b^3=(a-b)\cdot(a^2+ab+b^2) \end{equation} \begin{equation} a^3+b^3=(a+b)\cdot(a^2-ab+b^2) \end{equation} \begin{equation} a^4-b^4=(a-b)\cdot(a^3+a^2 b+ab^2+b^3)\end{equation}

Пример №4

Найти $\lim_{x\to 4}\frac{\sqrt[3]{5x-12}-\sqrt[3]{x+4}}{16-x^2}$.

Решение

Так как $\lim_{x\to 4}\left(\sqrt[3]{5x-12}-\sqrt[3]{x+4}\right)=0$ и $\lim_{x\to 4}(16-x^2)=0$, то мы имеем дело с неопределённостью вида $\frac{0}{0}$. Чтобы избавиться от иррациональности, вызвавшей эту неопределенность, нужно домножить числитель и знаменатель на выражение, сопряжённое к числителю. Формула №1 здесь уже не поможет, ибо домножение на $\sqrt[3]{5x-12}+\sqrt[3]{x+4}$ приведёт к такому результату:

$$ \left(\sqrt[3]{5x-12}-\sqrt[3]{x+4}\right)\left(\sqrt[3]{5x-12}+\sqrt[3]{x+4}\right)=\sqrt[3]{(5x-12)^2}-\sqrt[3]{(x+4)^2} $$

Как видите, такое домножение не избавит нас от разности корней, вызывающей неопределённость $\frac{0}{0}$. Нужно домножить на иное выражение. Это выражение должно быть таким, чтобы после домножения на него исчезла разность кубических корней. А кубический корень может «убрать» только третья степень, посему нужно использовать формулу №2. Подставив в правую часть этой формулы $a=\sqrt[3]{5x-12}$, $b=\sqrt[3]{x+4}$, получим:

$$ \left(\sqrt[3]{5x-12}- \sqrt[3]{x+4}\right)\left( \sqrt[3]{(5x-12)^2}+\sqrt[3]{5x-12}\cdot \sqrt[3]{x+4}+\sqrt[3]{(x+4)^2} \right)=\\ =\sqrt[3]{(5x-12)^3}-\sqrt[3]{(x+4)^3}=5x-12-(x+4)=4x-16. $$

Итак, после домножения на $\sqrt[3]{(5x-12)^2}+\sqrt[3]{5x-12}\cdot \sqrt[3]{x+4}+\sqrt[3]{(x+4)^2}$ разность кубических корней исчезла. Именно выражение $\sqrt[3]{(5x-12)^2}+\sqrt[3]{5x-12}\cdot \sqrt[3]{x+4}+\sqrt[3]{(x+4)^2}$ будет сопряжённым к выражению $\sqrt[3]{5x-12}-\sqrt[3]{x+4}$. Вернемся к нашему пределу и осуществим умножение числителя и знаменателя на выражение, сопряжённое числителю $\sqrt[3]{5x-12}-\sqrt[3]{x+4}$:

$$ \lim_{x\to 4}\frac{\sqrt[3]{5x-12}-\sqrt[3]{x+4}}{16-x^2}=\left|\frac{0}{0}\right|=\\ =\lim_{x\to 4}\frac{\left(\sqrt[3]{5x-12}- \sqrt[3]{x+4}\right)\left( \sqrt[3]{(5x-12)^2}+\sqrt[3]{5x-12}\cdot \sqrt[3]{x+4}+\sqrt[3]{(x+4)^2} \right)}{(16-x^2)\left( \sqrt[3]{(5x-12)^2}+\sqrt[3]{5x-12}\cdot \sqrt[3]{x+4}+\sqrt[3]{(x+4)^2} \right)}=\\ =\lim_{x\to 4}\frac{4x-16}{(16-x^2)\left( \sqrt[3]{(5x-12)^2}+\sqrt[3]{5x-12}\cdot \sqrt[3]{x+4}+\sqrt[3]{(x+4)^2} \right)} $$

Задача практически решена. Осталось лишь учесть, что $16-x^2=-(x^2-16)=-(x-4)(x+4)$ (см. формулу №1). Кроме того $4x-16=4(x-4)$, поэтому последний предел перепишем в такой форме:

$$ \lim_{x\to 4}\frac{4x-16}{(16-x^2)\left( \sqrt[3]{(5x-12)^2}+\sqrt[3]{5x-12}\cdot \sqrt[3]{x+4}+\sqrt[3]{(x+4)^2} \right)}=\\ =\lim_{x\to 4}\frac{4(x-4)}{-(x-4)(x+4)\left( \sqrt[3]{(5x-12)^2}+\sqrt[3]{5x-12}\cdot \sqrt[3]{x+4}+\sqrt[3]{(x+4)^2} \right)}=\\ =-4\cdot\lim_{x\to 4}\frac{1}{(x+4)\left( \sqrt[3]{(5x-12)^2}+\sqrt[3]{5x-12}\cdot \sqrt[3]{x+4}+\sqrt[3]{(x+4)^2} \right)}=\\ =-4\cdot\frac{1}{(4+4)\left( \sqrt[3]{(5\cdot4-12)^2}+\sqrt[3]{5\cdot4-12}\cdot \sqrt[3]{4+4}+\sqrt[3]{(4+4)^2} \right)}=-\frac{1}{24}. $$

Ответ: $\lim_{x\to 4}\frac{\sqrt[3]{5x-12}-\sqrt[3]{x+4}}{16-x^2}=-\frac{1}{24}$.

Рассмотрим ещё один пример (пример №5) в данной части, где применим формулу №4. Принципиально схема решения ничем не отличается от предыдущих примеров, – разве что сопряжённое выражение будет иметь иную структуру. Кстати, стоит отметить, что в типовых расчётах и контрольных работах часто встречаются задачи, когда, например, в числителе размещены выражения с кубическим корнем, а в знаменателе – с корнем квадратным. В этом случае приходится домножать и числитель и знаменатель на различные сопряжённые выражения. Например, для при вычислении предела $\lim_{x\to 8}\frac{\sqrt[3]{x}-2}{\sqrt{x+1}-3}$, содержащего неопределённость вида $\frac{0}{0}$, домножение будет иметь вид:

$$ \lim_{x\to 8}\frac{\sqrt[3]{x}-2}{\sqrt{x+1}-3}=\left|\frac{0}{0}\right|= \lim_{x\to 8}\frac{\left(\sqrt[3]{x}-2\right)\cdot \left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)\cdot\left(\sqrt{x+1}+3\right)}{\left(\sqrt{x+1}-3\right)\cdot\left(\sqrt{x+1}+3\right)\cdot\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\\= \lim_{x\to 8}\frac{(x-8)\cdot\left(\sqrt{x+1}+3\right)}{\left(x-8\right)\cdot\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}= \lim_{x\to 8}\frac{\sqrt{x+1}+3}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}=\frac{3+3}{4+4+4}=\frac{1}{2}. $$

Все преобразования, применённые выше, уже были рассмотрены ранее, поэтому полагаю, особых неясностей здесь нет. Впрочем, если решение вашего аналогичного примера вызывает вопросы, прошу отписать об этом на форум.

Пример №5

Найти $\lim_{x\to 2}\frac{\sqrt[4]{5x+6}-2}{x^3-8}$.

Решение

Так как $\lim_{x\to 2}(\sqrt[4]{5x+6}-2)=0$ и $\lim_{x\to 2}(x^3-8)=0$, то мы имеем дело с неопределенностью $\frac{0}{0}$. Для раскрытия оной неопределённости используем формулу №4. Сопряжённое выражение к числителю имеет вид

$$\sqrt[4]{(5x+6)^3}+\sqrt[4]{(5x+6)^2}\cdot 2+\sqrt[4]{5x+6}\cdot 2^2+2^3=\sqrt[4]{(5x+6)^3}+2\cdot\sqrt[4]{(5x+6)^2}+4\cdot\sqrt[4]{5x+6}+8.$$

Домножая числитель и знаменатель дроби $\frac{\sqrt[4]{5x+6}-2}{x^3-8}$ на указанное выше сопряжённое выражение будем иметь:

$$\lim_{x\to 2}\frac{\sqrt[4]{5x+6}-2}{x^3-8}=\left|\frac{0}{0}\right|=\\ =\lim_{x\to 2}\frac{\left(\sqrt[4]{5x+6}-2\right)\cdot \left(\sqrt[4]{(5x+6)^3}+2\cdot\sqrt[4]{(5x+6)^2}+4\cdot\sqrt[4]{5x+6}+8\right)}{(x^3-8)\cdot\left(\sqrt[4]{(5x+6)^3}+2\cdot\sqrt[4]{(5x+6)^2}+4\cdot\sqrt[4]{5x+6}+8\right)}=\\ =\lim_{x\to 2}\frac{5x+6-16}{(x^3-8)\cdot\left(\sqrt[4]{(5x+6)^3}+2\cdot\sqrt[4]{(5x+6)^2}+4\cdot\sqrt[4]{5x+6}+8\right)}=\\ =\lim_{x\to 2}\frac{5x-10}{(x^3-8)\cdot\left(\sqrt[4]{(5x+6)^3}+2\cdot\sqrt[4]{(5x+6)^2}+4\cdot\sqrt[4]{5x+6}+8\right)} $$

Так как $5x-10=5\cdot(x-2)$ и $x^3-8=x^3-2^3=(x-2)(x^2+2x+4)$ (см. формулу №2), то:

$$ \lim_{x\to 2}\frac{5x-10}{(x^3-8)\cdot\left(\sqrt[4]{(5x+6)^3}+2\cdot\sqrt[4]{(5x+6)^2}+4\cdot\sqrt[4]{5x+6}+8\right)}=\\ =\lim_{x\to 2}\frac{5(x-2)}{(x-2)(x^2+2x+4)\cdot\left(\sqrt[4]{(5x+6)^3}+2\cdot\sqrt[4]{(5x+6)^2}+4\cdot\sqrt[4]{5x+6}+8\right)}=\\ \lim_{x\to 2}\frac{5}{(x^2+2x+4)\cdot\left(\sqrt[4]{(5x+6)^3}+2\cdot\sqrt[4]{(5x+6)^2}+4\cdot\sqrt[4]{5x+6}+8\right)}=\\ \frac{5}{(2^2+2\cdot 2+4)\cdot\left(\sqrt[4]{(5\cdot 2+6)^3}+2\cdot\sqrt[4]{(5\cdot 2+6)^2}+4\cdot\sqrt[4]{5\cdot 2+6}+8\right)}=\frac{5}{384}. $$

Ответ: $\lim_{x\to 2}\frac{\sqrt[4]{5x+6}-2}{x^3-8}=\frac{5}{384}$.

Пример №6

Найти $\lim_{x\to 2}\frac{\sqrt[5]{3x-5}-1}{\sqrt[3]{3x-5}-1}$.

Решение

Так как $\lim_{x\to 2}(\sqrt[5]{3x-5}-1)=0$ и $\lim_{x\to 2}(\sqrt[3]{3x-5}-1)=0$, то мы имеем дело с неопределенностью $\frac{0}{0}$. В таких ситуациях, когда выражения под корнями одинаковы, можно использовать способ замены. Требуется заменить выражение под корнем (т.е. $3x-5$), введя некоторую новую переменную. Однако простое использование новой буквы ничего не даст. Представьте, что мы просто заменили выражение $3x-5$ буквой $t$. Тогда дробь, стоящая под пределом, станет такой: $\frac{\sqrt[5]{t}-1}{\sqrt[3]{t}-1}$. Иррациональность никуда не исчезла, – лишь несколько видоизменилась, что нисколько не облегчило задачу.

Здесь уместно вспомнить, что корень может убрать лишь степень. Но какую именно степень использовать? Вопрос не тривиален, ведь у нас два корня. Один корень пятого, а другой – третьего порядка. Степень должна быть такой, чтобы одновременно убрать оба корня! Нам нужно натуральное число, которое одновременно делилось бы на $3$ и на $5$. Таких чисел бесконечное множество, но наименьшее из них – число $15$. Его называют наименьшим общим кратным чисел $3$ и $5$. И замена должна быть такой: $t^{15}=3x-5$. Посмотрите, что такая замена сделает с корнями:

$$ \sqrt[5]{3x-5}=\sqrt[5]{t^{15}}=t^{\frac{15}{5}}=t^3;\\ \sqrt[3]{3x-5}=\sqrt[3]{t^{15}}=t^{\frac{15}{3}}=t^5.\\ $$

Корни исчезли, остались лишь степени. И дробь $\frac{\sqrt[5]{3x-5}-1}{\sqrt[3]{3x-5}-1}$ станет такой:

$$ \frac{\sqrt[5]{3x-5}-1}{\sqrt[3]{3x-5}-1}=\frac{t^3-1}{t^5-1}. $$

Однако это ещё не всё. Переменная $x\to 2$, но к чему стремится переменная $t$? Рассудим так: если $t^{15}=3x-5$, то $t=\sqrt[15]{3x-5}$. Так как $x\to 2$, то ${(3x-5)}\to 1$, $\sqrt[15]{3x-5}\to 1$, посему $t\to 1$. Теперь можем вернуться к нашему пределу:

$$ \lim_{x\to 2}\frac{\sqrt[5]{3x-5}-1}{\sqrt[3]{3x-5}-1}=\left|\frac{0}{0}\right|=\lim_{t\to 1}\frac{t^3-1}{t^5-1} $$

Корни исчезли, – но неопределённость $\frac{0}{0}$ осталась. Чтобы убрать её, нужно учесть, что при $t=1$ имеем $t^3-1=1^3-1=0$ и $t^5-1=1^5-1=0$. Из сказанного следует, что $t=1$ — корень многочленов $t^3-1$ и $t^5-1$. Следовательно, оные многочлены делятся на $t-1$. Разделим многочлен $t^5-1$ на $t-1$ с помощью схемы Горнера:

Результаты применения схемы Горнера можно записать так: $t^5-1=(t-1)(t^4+t^3+t^2+t+1)$. К многочлену $t^3-1$ можно также применить схему Горнера, но лучше использовать формулу №2: $t^3-1=t^3-1^3=(t-1)(t^2+t+1)$. Вернёмся к рассматриваемому пределу:

$$ \lim_{t\to 1}\frac{t^3-1}{t^5-1}=\lim_{t\to 1}\frac{(t-1)(t^2+t+1)}{(t-1)(t^4+t^3+t^2+t+1)}=\\ =\lim_{t\to 1}\frac{t^2+t+1}{t^4+t^3+t^2+t+1}=\lim_{t\to 1}\frac{1^2+1+1}{1^4+1^3+1^2+1+1}=\frac{3}{5}. $$

Ответ: $\lim_{x\to 2}\frac{\sqrt[5]{3x-5}-1}{\sqrt[3]{3x-5}-1}=\frac{3}{5}$.

math1.ru

Пределы, примеры решений

Решение

Первый предел. Для нахождения данного предела достаточно подставить вместо число, к которому оно стремиться, то есть 2, получим     Второй предел. В данном случае подставлять в чистом виде 0 вместо нельзя, так как получим деление на 0. Можно рассматривать значения близкие к нулю, например, подставлять 0,01; 0,001; 0,0001; 0,00001 и т. д., при этом значение функции будет возрастать: 100; 1000; 10000; 100000 и т. д. Таким образом, можно сделать вывод о том, что при значение функции, стоящей под знаком предела, будет неограниченно возрастать, то есть стремиться к бесконечности. А значит:     Третий предел. Здесь, как и в предыдущем случае, нельзя подставить в чистом виде. Необходимо рассмотреть случай неограниченного возрастания . Подставляя 1000; 10000; 100000 и т.д., получим, что значение функции будет убывать: 0,001; 0,0001; 0,00001; и т.д., стремясь к нулю. Таким образом,

ru.solverbook.com

Замечательные пределы, формулы и доказательства

Первый замечательный предел:

   

Следствия:

   

   

   

   

Подробнее про первый замечательный предел читайте в отдельной теме.

Примеры решений с первым замечательным пределом

Второй замечательный предел

   

здесь – постоянная Эйлера

Следствия:

   

   

   

   

   

Подробнее про второй замечательный предел читайте в отдельной теме.

Примеры решений со вторым замечательным пределом

Понравился сайт? Расскажи друзьям!

ru.solverbook.com