Смешанные числа, перевод смешанного числа в неправильную дробь и обратно

В этом материале мы разберем такое понятие, как смешанные числа. Начнем, как всегда, с определения и небольших примеров, потом поясним связь смешанных чисел и неправильных дробей. После этого мы изучим, как правильно выделять целую часть из дроби и получать в результате целое число.

Понятие смешанного числа

Если мы возьмем сумму n+ab, где значением n может быть любое натуральное число, а ab представляет из себя правильную обыкновенную дробь, то мы можем записать то же самое, не используя плюс: nab. Возьмем конкретные числа для ясности: так, 28+57 – это то же самое, что и 2857. Запись дроби рядом с целым числом принято называть смешанным числом.

Определение 1

Смешанное число представляет собой такое число, которое равно сумме натурального числа n с правильной обыкновенной дробью ab. В таком случае n является целой частью числа, а ab – его дробной частью.

Из определения следует, что любое смешанное число равно тому, что получится в результате сложения его целой и дробной части. Таким образом, будет выполняться равенство nab=n+ab.

Его также можно записать в виде n+ab=nab.

Какие можно привести примеры смешанных чисел? Так, к ним относится 518, при этом пятерка – это его целая часть, а одна восьмая – дробная. Еще примеры: 112, 2343453, 34000625.

Выше мы писали, что в дробной части смешанного числа должна стоять только правильная дробь. Иногда можно встретить записи вида 5223, 7572. Они не являются смешанными числами, т.к. их дробная часть неправильная. Их нужно понимать как сумму целой и дробной части. Такие числа можно привести к стандартному виду записи смешанных чисел, выделив целую часть из неправильной дроби и добавив ее к 5 и 75 в этих примерах соответственно.

Числа вида 0314также не относятся к смешанным. Здесь не выполняется первая часть условия: целая часть должна быть представлена только натуральным числом, а нуль им не является.

Как соотносятся между собой неправильные дроби и смешанные числа

Эту связь проще всего проследить на конкретном примере.

Пример 1

Возьмем целый торт и еще три четверти такого же. Согласно правилам сложения, у нас на столе находится 1+34 торта. Эту сумму можно представить в виде смешанного числа как 134 торта. Если мы возьмем целый торт и тоже разрежем его на четыре равные части, то у нас на столе будет 74 торта. Очевидно, что от разрезания количество не увеличилось, и 134=74.

Наш пример доказывает, что в виде смешанного числа можно представить любую неправильную дробь.

Вернемся к нашим 74 торта, оставшимся на столе. Сложим из его кусочков один торт обратно (1+34). У нас опять будет 134.

Ответ: 74=134.

Мы поняли, как приводить неправильную дробь к виду смешанного числа. Если в числителе неправильной дроби стоит такое число, которое можно разделить на знаменатель без остатка, то можно сделать это, и тогда наша неправильная дробь станет натуральным числом.

Пример 2

Например,

84=2, так как 8:4=2.

Как перевести смешанное число в неправильную дробь

Чтобы успешно решать задачи, полезно уметь производить и обратное действие, то есть делать из смешанных чисел неправильные дроби. В этом пункте мы разберем, как правильно это сделать.

Для этого нужно воспроизвести следующую последовательность действий:

1. Для начала представляем имеющееся смешанное число nab как сумму целой и дробной части. Получается n+ab

2. Далее заменяем целую часть на дробь со знаменателем, равным единице (то есть записываем n как n1).

3.После этого выполняем уже знакомое действие – складываем две обыкновенные дроби n1 и ab. Получившаяся в результате неправильная дробь и будет равной смешанному числу, данному в условии.

Разберем это действие на конкретном примере.

Пример 3

Представьте 537 в виде неправильной дроби.

Решение 

Выполняем последовательно шаги указанного выше алгоритма. Наше число 537 – это сумма целой и дробной части, то есть 5+37. Теперь пятерку запишем в виде 51. У нас получилась сумма 51+37.

Последний шаг – сложение дробей, имеющих разные знаменатели:

51+37=357+37=387

Все решение к краткой форме можно записать как 537=5+37=51+37=357+37=387.

Ответ: 537=387.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Таким образом, с помощью указанной выше цепочки действий мы можем перевести любое смешанное число nab в неправильную дробь. У нас получилась формула nab=n·b+ab, которую мы и будем брать для решения дальнейших задач.

Пример 4

Представьте 1525 в виде неправильной дроби.

Решение

Возьмем указанную формулу и подставим в нее нужные значения. У нас n=15, a=2, b=5, следовательно, 1525=15·5+25=775.

Ответ: 1525=775.

Как выделить из неправильной дроби целую часть

Обычно мы не указываем неправильную дробь в качестве итогового ответа. Принято доводить вычисления до конца и заменять ее либо натуральным числом (разделив числитель на знаменатель), либо смешанным числом. Как правило, первый способ используется, когда разделить числитель на знаменатель можно без остатка, а второй – если такое действие невозможно.

Когда мы выделяем из неправильной дроби целую часть, мы просто заменяем ее равным смешанным числом.

Разберем, как именно это делается.

Определение 2

Любая неправильная дробь ab –это смешанное число qrb. Здесь q представляет собой неполное частное, а r – это остаток от ab. Таким образом, целая часть смешанного числа есть неполное частное от деления ab, а дробная – это остаток.

Приведем доказательство этого утверждения.

Нам требуется пояснить, почему qrb=ab. Для этого смешанное число qrb надо представить в виде неправильной дроби, выполнив все шаги алгоритма из предыдущего пункта. Поскольку – неполное частное, а r – остаток от деления a на b, то должно выполняться равенство a=b·q+r.

Таким образом, q·b+rb=ab поэтому qrb=ab. Это и есть доказательство нашего утверждения. Подытожим:

Определение 3

Выделение целой части из неправильной дроби ab осуществляется таким образом:

1) производим деление a на b с остатком и записываем неполное частное q и остаток r отдельно.

2) Записываем результаты в виде qrb. Это и есть наше смешанное число, равное исходной неправильной дроби.

Пример 5

Представьте 1074 в виде смешанного числа.

Решение

Делим 104 на 7 столбиком:

Деление числителя a=118 на знаменатель b=7 дает нам в итоге неполное частное q=16 и остаток r=6.

В итоге мы получаем, что неправильная дробь 1187 равна смешанному числу qrb=1667.

Ответ: 1187=1667.

Нам осталось посмотреть, как заменить неправильную дробь натуральным числом (при условии, что ее числитель делится на знаменатель без остатка).

Для этого вспомним, какая связь существует между обыкновенными дробями и делением. Из этого можно вывести равенства: ab=a:b=c. Получается, что неправильную дробь ab можно заменить натуральным числом c.

Пример 6

Например, если в ответе получилась неправильная дробь 273, то можем записать вместо нее 9, поскольку273=27:3=9.

Ответ: 273=9.

Презентация «Сложение и вычитание смешанных чисел с разными знаменателями»

библиотека
материалов

Содержание слайдов

Номер слайда 1

Тема: Сложение и вычитание смешанных чисел с разными знаменателями»

Номер слайда 2

ДРОБИ. Дроби всякие нужны, Дроби всякие важны. Дробь учи, тогда сверкнёт удача. Если дроби будешь знать , Точно смысл их понимать, Станет легкой даже сложная задача.

Номер слайда 3

Устный счет мы проведем и рекорды все побьем 1. Найди ошибку:

Номер слайда 4

Представь в виде неправильной дроби:

Номер слайда 5

Выдели целую часть из неправильной дроби:

Номер слайда 6

Вставь пропущенный числитель, чтобы получились верные равенства:

Номер слайда 7

Выполните действия:

Номер слайда 8

Вычислите:

Номер слайда 9

Тема урока: Мама купила кг. моркови и кг. свеклы.

Номер слайда 10

Алгоритм сложения смешанных чисел Привести дробные части к общему знаменателю Отдельно сложить целые и дробные части Правильная дробь Неправильная дробь Выделить целую часть и прибывать ее к целой части суммы записать ответ

Номер слайда 11

Алгоритм вычитания Привести дробные части к общему знаменателю Дробная часть уменьшаемого меньше дробной части вычитаемого да нет Занять единицу из целой части Отдельно вычесть целые и дробные части Результат записать в виде смешанного числа Сократить дробную часть ЗАПИСАТЬ ОТВЕТ

Номер слайда 12

Ручки в руки мы возьмем. Смело порешаем и ответы мы узнаем. Найди значение выражения:

Номер слайда 13

Чтоб в царство знаний нам попасть самостоятельно нам надо порешать. Из учебника: № 376 1 строчка – I-В 377 2 строчка – II-В

Номер слайда 14

1 вариант Р Е Т И А Я П Ц 2 вариант Г И Ф О М Л Р А

Номер слайда 15

ПРОВЕРЬ СЕБЯ: Т Р А П Е Ц И Я Л О Г А Р И Ф М

Номер слайда 16

Подведем итог: Я доволен собой, у меня все получилось !!! Я старался, но у меня не все получилось!!!

Дроби.

Смешанные числа.

Позитивный настрой учащихся. Просмотр мультфильма «Путешествие капельки»

Эта капля попала сегодня к нам на урок, она будет помогать вам и мне определять, что у вас получилось и над чем надо поработать. Я думаю, она много узнает нового и в конце урока мы отправим ее дальше путешествовать.

Актуализация жизненного опыта.

Целеполагание Прием «Облака мыслей»

— Приведите первые, пришедшие в голову мысли по данной картинке?

(К)Обсуждение лексической темы, на материале задания №1 учебника.

При утечке из крана воды за сутки набегает примерно 10 литров — целое ведро. Сколько вёдер воды утечёт без пользы за неделю? Месяц? Какой вред это наносит природе? Как утечка воды отразится на семейном бюджете?

Беседа о ценности водных ресурсов, о необходимости бережного отношения к ним.

(ФО) Прием «Символ воды» У каждого ученика имеется лист самооценивания, взаимооценивания (пустой сосуд), где за правильный ответ каждого задания рисуется капелька.

(КП)Послушайте стихотворение и выполните задание.

Вода в морях и океанах,

Озерах, реках и прудах.

И без нее не обойтись нам

Ни в селах, и ни в городах.

Цените воду, берегите:

Природой дан нам дар такой.

(П) Работа с диаграммой.

Извлекаем из круговой диаграммы информацию о воде.

1\100; 4/100; 97/100; 2 ⅛ ; 3/100; 67/67;

Даны дроби, выпишите те, которые показывают состав пресной и соленой воды.

Пресная вода 3%. = 3/100

Соленая вода 97% = 97/100

-Как называются данные дроби? -Какие еще знаете? (ФО)Самооценивание. Прием «Символ воды»

АМО «Капля за каплей» (авторский АМО)

Цель: повторить материал предыдущих уроков. (Ученики в парах по очереди, называют термин, понятие из изученного раннее материала –правильные и неправильные дроби.

(ФО) Взаимооценивание. Прием «Символ воды»

Введение в новую тему.

АМО «Заблудившееся число».

Учащиеся определяют число, с которым еще не работали. (И)Вернемся к предыдущему заданию.

1\100; 4/100; 97/100; 2 ⅛ ; 3/100; 67/67;

-Как можно сгруппировать эти числа? —

Найдите лишнее число. (число 2 ⅛)

(ФО) Самоценивание. Прием «Символ воды»

Постановка темы и цели (проблемная ситуация).

– Какова тема и цель сегодняшнего урока?

• Закрепить знания о дробях.

• Познакомиться с понятием смешанного числа.

АМО «Таблица предположений»:

Что вы знаете по теме?  Что интересует?    Каким будет результат?

Даю учащимся время на заполнение таблицы, выборочно проверяю таблицы: из каждой пары учащихся по одному человеку (все, большинство, некоторые).

(ФО) Самоценивание. Прием «Символ воды»

Деление на группы

(И) У каждого ученика индивидуальное задание по картинке.

       

      

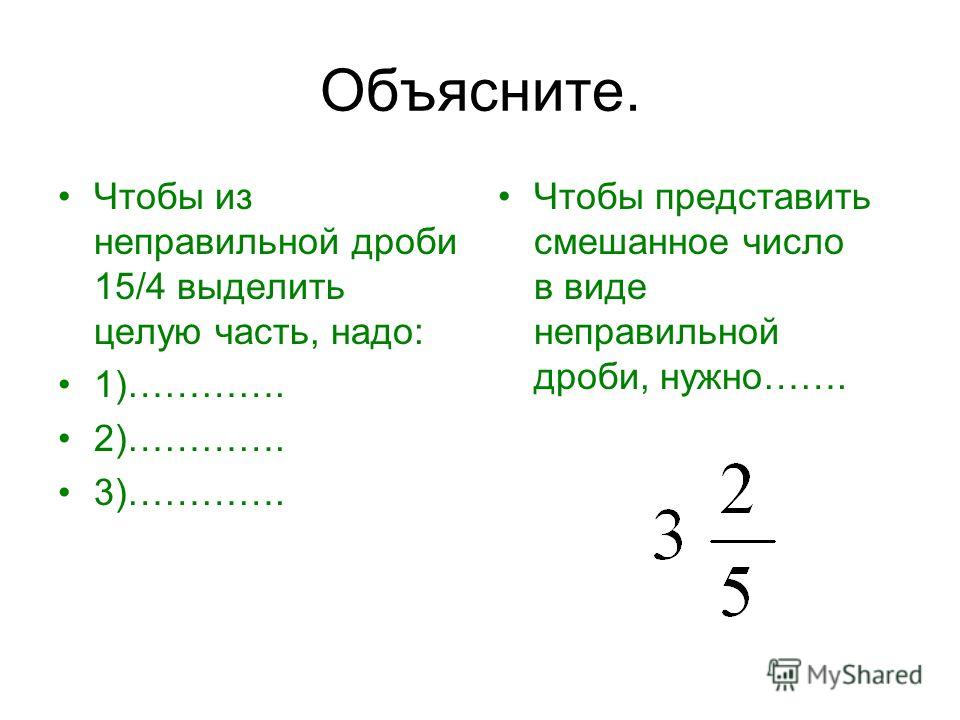
Запиши дроби, соответствующие закрашенным частям каждой из диаграмм.

Самопроверка по эталону.

Формируются группы по знаменателям:

1группа (знаменатель дроби 4)

2группа (знаменатель дроби 6)

3группа (знаменатель дроби 5)

АМО «Добавь следующее»

Задание:Начерти числовой луч. Прими за единицу столько клеток тетради, чему показывает полученный знаменатель.Отметь дробь на луче и добавь долю, чтобы приравнять к 1.Записать в виде суммы дробей.

1группа     2группа       3группа

Дескрипторы — используют дробь закрашенной фигуры;

— отмечают на числовом луче дроби;

— определяют дробь, которую надо добавить;

— записывают сумму и находят результат.

(ФО) Самоценивание. Прием «Символ воды»

(Г)АМО «Идеал» Обучающиеся в группах обсуждают вопросы по заданию учебника. Предлагается рассмотреть №2 учебника

— Сколько третьих долей отмечено на чертеже?

Запиши в виде неправильной дроби.

Можно ли записать, что 5/3 = 3/3 + 2/3 = 1 + 2/3?

«Идеал»

Интересно в чем проблема? (начинается со слов как)

Давайте найдем, как можно больше решений этой проблемы.

Есть ли хорошие решения?

А теперь выберем единственное решение.

Любопытно, а как это будет выглядеть на практике? Планируется работа по претворению выбранного решения в жизнь.

ФО: Наблюдение учителя словесное оценивание. Прием «Символ воды»

– Все ли дроби можно представить в виде суммы целого числа единиц и правильной дроби? – Сумму 1+ 2/3 принято записывать короче. А как его прочитать?

Памятка  Смешанными числами называются числа, состоящие из целой и дробной части   

 

Сборник контрольных работ по математике, (5 класс)

Контрольная работа по математике №1. 5 класс.

Цель: проверить уровень усвоения ГОСО по курсу математики 4 класса:

-решение задачи на нахождение скорости, времени, расстояния;

-выполнение арифметических действий с многозначными числами;

-знание порядка действий;

-знание формул для нахождения периметра и площади прямоугольника и умение применять их при решении геометрической задачи;

-умение находить неизвестный компонент уравнения.

1 вариант

1. Реши задачу:

1. Выполни действия:

5847 + 6132 18619 х 39

49524 – 2615 19776 : 309

2. Реши уравнение:

х – 135 = 5095 : 5

3. Выполни порядок действий:

(450 – 230) : 20 + 49 х 3

4.Из пункта А одновременно в противоположных направлениях выехали два велосипедиста. Скорость первого велосипедиста 23 км/ч, а скорость другого 36 км/ч. На каком расстоянии друг от друга будут велосипедисты через 7 часов?

5. Дан квадрат со стороной 12 см. Найдите ширину прямоугольника, площадь которого равна площади квадрата, а длина прямоугольника на 3 см меньше стороны квадрата.

2 вариант

1. Реши задачу:

1. Выполни действия:

80256 : 192 56789 — 2374

72512 х 27 2894 + 8972

2. Реши уравнение:

х + 137 = 1485 : 5

3. Выполни порядок действий:

270 : (120 – 90) + 140 х 4

4. Из двух городов, находящихся на расстоянии 540 км друг от друга, выехали одновременно навстречу друг другу велосипед и мотоцикл. Они встретились через 18 часов. Велосипед шел со скоростью 11 км/ч. С какой скоростью ехал мотоцикл?

5. Дан прямоугольник, длина которого 60 см, а ширина 15 см. Найди длину другого прямоугольника, площадь которого равна площади данного, а его ширина на 5 см меньше ширины первого прямоугольника.

 

Критерии оценивания
«5»	22-23 баллов
«4»	16-21 балла
«3»	13-15 баллов

 

 

Распределение заданий по содержанию и уровню сложности

Содержательная линия	Воспроизведение знаний	Применение знаний	интеграция	% отношение
Действия с многозначными числами	№1,	№3		40 %
Уравнение	№2	№4		40%
Площади			№5	20%
Итого	40 %	40 %	20 %	100 %

Содержательная матрица и критерии оценивания

№	Характеристика задания	Проверяемые элементы	Балл за выполнение проверяемого элемента	Балл за выполненное задание
1	Выполнение действий с многозначными числами	Выполнение сложения Выполнение вычитания Выполнение умножения Выполнение деления	1 1 1 1	4
2	Решение уравнения	Нахождение неизвестного члена уравнения. Вычислительные навыки	2 2	4
3	Выполнение действий с многозначными числами	Знание порядка действий Выполнение сложения Выполнение вычитания Выполнение умножения Выполнение деления	1 1 1 1 1	5
4	Решение задач	Краткая запись условия задачи Решение задачи Запись ответа	1 3 1	5
5	Решение задачи	Знание формулы вычисления площади прямоугольника, квадрата Умение выражать неизвестную длину (ширину) через известную площадь Вычислительные навыки	2   2 1	5

Контрольная работа по математике №2. 5 класс.

Тема: Буквенные выражения. Уравнения.

Цель: проверить уровень усвоения ГОСО по следующим вопросам:

-буквенные выражения и нахождение их значений

-решение уравнений

-упрощение выражений

-действия с натуральными числами

Текст работы:

Вариант 1 1. Найдите значение выражения: а+37+в при а=13 ,в=28 2. Упростить выражение: (23х-81+42Х)∙3 3. Упростите выражение 39х+18х-27х+56 и найдите его значение при х=12 4. Решите задачу, составив уравнение: Папа, сын и дочка собрали 99 кг свеклы. Сын собрал в два раза больше, чем дочь, а папа в три раза больше, чем сын. Сколько кг свеклы собрал каждый из них. 5.Решите задачу: Длина прямоугольной ванной комнаты равна 4 м, ширина в два раза меньше длины, а высота на 50 см больше ширины. Сколько штук облицовочной плитки понадобится для стены, если размер плитки 50х50 см?

Вариант 2 1. Найдите значение выражения: а+87+в при а=21, в=47 2. Упростить выражение: 4∙(31Х-17+54х) 3.Упростите выражение 43у-14у+39у-18 и найдите его значение при у=12 4. Решите задачу, составив уравнение: Петя, Костя и Гена нашли 112 грибов. Петя нашел в три раза меньше, чем Костя и в четыре раза меньше, чем Гена. Сколько грибов нашел каждый мальчик 5.Решите задачу: Ширина кабинета 4м, а длина на 2м 60см больше ширины, а высота на 3м 60 см меньше длины. Сколько рулонов обоев понадобится для оклеивания стен, если в одном рулоне 10 квадратных метров обоев?

 

 

Критерии оценивания
«5»	20-21 баллов
«4»	16-19 баллов
«3»	11-15 баллов

 

 

 

Распределение заданий по содержанию и уровню сложности.

Содержание	Воспроизведение знаний	Применение знаний	Интеграция	%
Буквенные выражения	№1, №2	№3		60%
Уравнение		№4		20%
Формулы			№5	20%
Итого	40%	40%	20%	100%

Критерий оценивания по проверяемым элементам.

№ задания	Характеристика задания	Проверяемые элементы	Балл за выполнение проверяемого элемента	Балл за выполнение задания
1	Упрощение выражений	Подстановка численных значений Вычислительные навыки	1 2	3
2	Упрощение выражений	Применение распределительного закона умножения Приведение подобных	2 2	4
3	Упрощение выражений	Приведение подобных Вычислительные навыки	2 2	4
4	Задача на составление уравнения	Составление уравнения Решение уравнения Запись ответа	2 2 1	5
5	Задача на нахождение площади	Знание формулы площади прямоугольника Решение задачи Вычислительные навыки	1 2 2	5

Контрольная работа № 3. 5 класс

Тема: Угол. Окружность. Круг.

Цель: проверить уровень усвоения ГОСО:

-знание понятий угол, окружность, круг;

-измерять величину угла с помощью транспортира;

-строить угол заданной величины;

Текст работы:

Вариант 1		Вариант 2
№ 1. Начерти в тетради, обозначь углы и запиши их градусную меру: острый угол и прямой тупой и развёрнутый
№2. Реши задачу: Диаметр окружности равен 8 см, Радиус окружности равен 3см Найди длину радиуса и начерти Найди длину диаметра и начерти окружность. окружность. №3.Выполни:
Угол АОВ- развёрнутый, Найдите градусную меру угла EFK, АОС = 500. Найти градусную меру угла если угол EFN прямой, а угол KFN = 550 СОВ. Определите вид угла. Определите вид угла. C K N А О В Е F
№ 4.Найдите градусную меру угла DBE, если АВС – прямой угол(рис. А) СВD – прямой угол (рис. Б) начертите рисунок в тетради. А Д С Д 350 Е
200
В 150 С		А В Е
№5. Реши задачу с помощью уравнения: Угол MOK равен 1200, внутри угла Угол АОВ равен 1500, внутри угла проведен луч OD. проведен луч OD. Угол MOD больше угла DOK на 500. Угол АОК больше угла DOK на 400. Сколько градусов содержит угол DOK? Сколько градусов содержит угол DOK? А М Д Д В К О О

Критерии оценивания
«5»	22-23 баллов
«4»	16-21 балла
«3»	12-15 баллов

Распределение заданий по содержанию и уровню сложности

Содержательная линия	Воспроизведение знаний	Применение знаний	интеграция	% отношение
Угол	№1	№3, №4	№5	80 %
Окружность и круг	№2			20 %
Итого	40 %	40 %	20 %	100 %

Содержательная матрица и критерии оценивания

№	Характеристика задания	Проверяемые элементы	Балл за выполнение проверяемого элемента	Балл за выполненное задание
1	Изображение угла и запись в градусной мере	Знание понятий угол Умение построить угол Умение изображать угол Умение измерять величину угла	1 1 1 1	4
2	Построение окружности, измерение радиуса и диаметра	Знание понятия окружность, радиус, диаметр. Умение изображать окружность.	2 2	4
3	Вычисление градусной меры угла	Знание видов углов и их градусных мер Вычисление градусной меры	2 2	4
4	Решение геометрической задачи	Знание видов углов. Нахождение суммы двух данных углов. Нахождение искомого угла	1 2 2	5
5	Решение геометрической задачи с помощью уравнения	Краткая запись условия задачи. Составление уравнения по условию задачи. Решение уравнения. Запись ответа	1 2 2 1	6

Контрольная работа №4 по теме «Делители чисел» , 5 класс

Цель: проверить уровень усвоения ГОСО:

-знание понятий делители чисел

-знание понятий кратные чисел

-знание понятий простые числа

-знание понятий составные числа

-знание понятий чётные и нечетные числа

— знание признаков делимости на 2 3 5 9

— знание свойства деления суммы на число

-умение применять свойства деления суммы на число

Текст работы:

Вариант 1		Вариант 2
№1 а) Запишите все делители чисел 6, 11, 23, 38, 62 7, 14, 25, 45, 84
б) Подчеркните простые числа 21,13,72,19,81,23 34,29,31,49,11,18
№3 а) Какие из чисел 896, 975, 1002, 2379, 4568, 9694, 9999 являются чётными нечётными б) Выпишите из чисел 94673, 28624, 33460, 54745, 63785, 73688, 83840 числа, делящиеся на 5 на 2 в) Выпишите числа, делящиеся на 9 на 3 из чисел

Открытый урок по теме «Решение задач на умножение обыкновенных дробей и смешанных чисел».

• Презентации
• Открытый урок по теме «Решение задач на умножение обыкновенных дробей и смешанных чисел».

Автор публикации: Хыдырбек А.Х.

Дата публикации: 10.04.2016

Краткое описание:



1

Открытый урок по теме «Решение задач на умножение обыкновенных дробей и смешанных чисел». Учитель Хыдырбек А. 5 класс 9

2

I.Организационный момент. Для начала вспомним тему нашего урока: Каждый может за версту Видеть дробную черту. Над чертой – числитель, знайте, Под чертою – знаменатель. Дробь такую непременно Надо звать обыкновенной. Посмотрите, что за дробь – Дробь обыкновенная. Проведем сегодня с ней Действие ? … умножение!!! Тема урока – умножение обыкновенных дробей и смешанных чисел.Благодаря этой рекламе сайт может продолжать свое существование, спасибо за просмотр.

3

Тема урока: Умножение обыкновенных дробей и смешанных чисел. Цели урока: Обучающие: Закрепление у учащихся умений использовать правила умножения дробей и смешанных чисел, Воспитательные: содействовать в развитии познавательной активности, чувства ответственности, культуры общения, развивать математическую речь, творческие способности учащихся при решении задач на дроби, доказывать, сравнивать, совершенствовать умение применять имеющиеся знания в разных ситуациях. Развивающие: содействовать в развитии  логического мышления, памяти, внимания, воображения, мыслительной деятельности, обобщения. развивать математическую речь, творческие способности учащихся при решении задач на дроби, совершенствовать умение применять имеющиеся знания в разных ситуациях.

4

План урока: I.ОРГАНИЗАЦИОННЫЙ МОМЕНТ. II.УСТНАЯ РАБОТА. III.БУКВЕННЫЙ ДИКТАНТ. IV.ИНДИВИДУАЛЬНАЯ РАБОТА. V.РАБОТА В ПАРАХ. VI.ФИЗКУЛЬТМИНУТКА VII.РЕШЕНИЕ ЗАДАЧ. VIII.ДОМАШНЕЕ ЗАДАНИЕ. XI.РЕФЛЕКСИЯ

5

Считайте, ребята, скорее считайте. Хорошее дело смелей умножайте. Плохие дела поскорей вычитайте. Скорее работу свою начинайте! Эпиграфом к уроку я взяла такие слова из китайской мудрости: “Я слышу – я забываю, Я вижу – я запоминаю, Я делаю – я усваиваю”

6

II. Актуализация ЗУН. Устная работа + письменная Для начала откройте тетради, запишите сегодняшнее число.   Ребята, давайте поиграем в игру «Ромашка». Помним правила? Итак, начнем:

7

1 2 3 11 10 9 8 7 6 5 4 Ромашка:

8

III Буквенный диктант Отвечайте про себя, запишите лишь первую букву в тетрадь. Получится слово. В математике есть целые числа, а есть… Дробь вида называется … В данном уравнении х + 3= 7 нужно найти неизвестное…  Значение буквы, при котором из уравнения получается верное числовое равенство — …  Раздел математики — …(наука о числах). Получилось слово….

9

В.-1 на «3» В.- 2 на «4» В.-3 на «5»

10

V. Работа в парах Стр.:173 №596(1-3) №596(3-6)

11

VI Физкультминутка. Дружно с вами мы считали и про числа рассуждали, А теперь мы дружно встали, свои косточки размяли. На счет раз кулак сожмем, на счет два в локтях сожмем. На счет три — прижмем к плечам, на 4 — к небесам Хорошо прогнулись, и друг другу улыбнулись Про пятерку не забудем — добрыми всегда мы будем. На счет шесть прошу всех сесть. Числа, я, и вы, друзья, вместе дружная 7-я.

12

VII Решение задач Решение задач – практическое искусство, подобное плаванию, катанию на лыжах и коньках, игре на пианино и фортепьяно. Всему этому можно научиться. «Если Вы хотите  научится плавать, то смело входите в воду, а если научится решать задачи, то решайте их» — советовал учащимся известный математик Джорж Пойа в своей книге «Как решить задачу». Решение любой, достаточно трудной задачи требует напряженного труда, воспитывает волю, упорство, развивает любознательность, смекалку. Проверим?

13

В бутылке литра сока. Сколько сока в 5 таких бутылках? За 1 час автоматическая линия производит центнера пластмассы. Сколько пластмассы линия производит за часа. Сколько км проедет велосипедист за ч., если будет двигаться со скоростью 12 км/ч.

14

VIII. Домашнее задание Вот закончился урок, Подведём сейчас итог, Мы много вспомнили, друзья, Без этого никак нельзя. Правила мы повторили, На практике их применили Задачи, находя решенье, Развивают мышленье, Память и внимание, Закрепляли знания. А теперь, внимание, Домашнее задание: Стр. 173 № 592

15

IХ. Рефлексия. — Выберите фразу, которая отражает ваше настроение на уроке: У меня всё получилось! Были небольшие трудности Было трудно, надо поработать

16

17

А теперь задачи на логику: Кирпич весит 2 кг и еще полкирпича. Сколько весит кирпич? Пара лошадей пробежала 40 км. Сколько км пробежала каждая лошадь? У семи братьев по одной сестре. Сколько всего детей? К Айболиту на прием пришли звери. Все, кроме двух, собаки. Все, кроме двух, кошки. Все, кроме двух, зайцы. Сколько животных пришло к Айболиту? Зайцы пилят бревно. Они сделали 12 распилов. Сколько получилось чурбанов?

18

Правило сравнения- Сравнить дроби.

19

Даны дроби, нужно их сгруппировать в 3 колонки: правильные, неправильные и смешанные дроби.

20

Как неправильную дробь представить в виде смешанного числа? Представь:

21

Как смешанное число представить в виде неправильной дроби? Представь:

22

Как сложить обыкновенные дроби? А если знаменатели разные? Сложи: 1) 2)

23

Как вычитают обыкновенные дроби? А если знаменатели разные? Вычти: 1) 2)

24

Как вычитают смешанные числа? Вычти:

25

Как вычитают из натурального числа обыкновенную дробь? Вычти:

26

Как умножают обыкновенные дроби? Выполни умножение:

27

Как умножают смешанные числа? Выполни умножение:

28

Как умножить обыкновенную дробь на натуральное число? Выполни умножение:

29

30

31

Ejercicio de Представьте в виде смешанных чисел

Ejercicio de Представьте в виде смешанных чисел

Búsqueda avanzada

 

¡Terminado!

Estilo del cuadro de texto:

Fuente: AldrichAmatic SCAnnie Use Your TelescopeArchitects DaughterArialBaloo PaajiBangersBlack Ops OneBoogalooBubblegum SansCherry Cream SodaChewyComic NeueComing SoonCovered By Your GraceCrafty GirlsCreepsterDancing ScriptEscolarExo 2Fontdiner SwankyFreckle FaceFredericka the GreatFredoka OneGloria HallelujahGochi HandGrand HotelGurmukhiHenny PennyIndie FlowerJolly LodgerJust Me Again Down HereKalamKrankyLobsterLobster TwoLove Ya Like A SisterLuckiest GuyMountains of ChristmasNeuchaOpen SansOrbitronOswaldPacificoPatrick HandPernament MarkerPinyon ScriptRanchoReenie BeanieRibeye MarrowRock SaltRusso OneSacramentoSatisfySchoolbellShadows Into Light TwoSpecial EliteUbuntuUnkemptVT323Yanone Kaffeesatz    Tamaño: 89101112131416182022242832364050607080px

Color de fuente&nbsp  Color de fondo&nbsp  Color del borde

Opacidad del fondo: 0. 00.10.20.30.40.50.60.70.80.91.0
Tamaño del borde: 012345678910
Esquinas redondeadas: 02468101216202430
Alineación de texto: CentroIzquierdaDerechaJustificar

 

    Últimos comentarios

 

Por favor, permite el acceso al micrófono
Mira en la parte alta de tu navegador. Si ves un mensaje pidiendo tu permiso para acceder al micrófono, por favor permítelo.

Cerrar

100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.

— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?

— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.

Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.

Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.

— Расскажите поподробнее?

— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.

— Система оценивания останется прежней?

— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.

Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.

— А апелляция?

— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.

— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?

— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.

— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?

— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.

— На сколько процентов будет обновлена база вопросов?

— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.

— По вашему мнению система справится с возможными хакерскими атаками, взломами?

— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.

Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.

— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?

— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.

— Сколько человек будет сидеть в одной аудитории?

— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.

— Будут ли ужесточены требования по дисциплине, запрещенным предметам?

— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.

Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.

— А наблюдатели будут присутствовать во время сдачи тестирования?

— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.

— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?

— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.

Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.

— Сколько средств выделено на проведение ЕНТ в этом году?

Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.

— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?

— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.

Использование смешанных чисел для представления неправильных дробей

В сегодняшнем посте мы узнаем о смешанных числах , которые намного легче интерпретировать, чем неправильные дроби, которые они представляют.

Мы собираемся рассмотреть несколько примеров упражнений , и , задач , над которыми вы можете работать в Smartick, и типы чисел, с которыми вы можете работать в этих упражнениях. Вы сможете делать их практически не задумываясь!

Неправильные дроби как смешанное число

Помните, что смешанное число — это числовой способ представления дроби, превышающей единицу (неправильная дробь), или, другими словами, представления дробей, в которых числитель больше знаменателя.

Начнем с примера:

• Если вы посмотрите на неправильную дробь ⁶⁷ ⁄ ₁₃ , будет непросто представить себе число, которое она представляет, поскольку оно больше единицы (поскольку числитель больше знаменателя, 67 > 13).
• Но если вы конвертируете в смешанное число , вы сможете понять, какое число оно представляет, гораздо легче.
• Для этого первое, что вам нужно сделать, это разделить числитель дроби на знаменатель, чтобы узнать, сколько целых единиц содержит число.

• Поскольку 65 = 13 x 5, мы можем разделить 67 на 65 и 2, и одна из частей будет делиться на 13, а другая — нет:

• Теперь очень легко записать смешанное число : сначала мы записываем целое число, а затем дробь, которая меньше единицы:

• Используя это представление, легко увидеть, что число состоит из 5 целых единиц и 2 тринадцатых другой единицы.

Теперь мы рассмотрим несколько примеров упражнений и задач со смешанными числами, над которыми вы можете работать в Smartick.

Пример 1: Упражнение со смешанными числами

В первом типе упражнений мы можем попрактиковаться в написании смешанного числа из его представления в виде круговых диаграмм . Как видите, в этом примере показан полностью окрашенный круг и 1 равная часть из 4 другого окрашенного круга.

Таким образом, легко увидеть, что число, представленное графически, равно 1 ¹ ⁄ ₄ :

Пример 2: Упражнение со смешанными числами

Во втором типе упражнений мы собираемся использовать пиццу, чтобы научиться преобразовывать неправильную дробь в смешанное число .Как вы можете видеть в примере, у нас есть 2 целых пиццы и три четверти другой пиццы.

Вы легко можете увидеть, что ¹¹ ⁄ ₄ пиццы — это 2 целые пиццы и ³ ⁄ ₄ другой пиццы. Другими словами, смешанное число, которое соответствует неправильной дроби ¹¹ ⁄ ₄ , равно 2 ³ ⁄ ₄ .

Так легче интерпретировать, не правда ли?

Пример 3: Упражнение со смешанными числами

В третьем типе упражнений мы практикуем в написании неправильных дробей и смешанных чисел, представляя их круговыми диаграммами .В этом примере вы можете увидеть 2 полных круга и 2 равные части из 3 других.

Теперь представлено смешанное число 2 ² ⁄ ₃ , а представленная неправильная дробь — ⁸ ⁄ ₃ :

Пример 4: Проблема со смешанными числами

Наконец, давайте посмотрим на пример от Smartick, в котором мы работаем со смешанными числами для решения задач .

Давайте посчитаем, сколько кругов Альби должен пробежать вокруг своей планеты.Поскольку он должен пробежать на 12 кругов больше, чем Алан, а Алан должен пробежать ⁹ ⁄ ₁₀ круга, все, что нам нужно сделать, это добавить 12 и ⁹ ⁄ ₁₀ .

Представить результат в виде смешанного числа очень просто, потому что вам даже не нужно ничего делать, чтобы сложить 12 и ⁹ ⁄ ₁₀ , вам просто нужно написать целое число, а затем дробь: 12 ⁹ ⁄ ₁₀ .

Следовательно, мы можем сказать, что Альби должен пробежать 12 ⁹ ⁄ ₁₀ кругов вокруг своей планеты.

И на сегодня все!

Что вы думаете об этом сообщении? Действительно быстро и легко решить эти упражнения, используя смешанные числа, не так ли?

Если вы хотите и дальше изучать и практиковать начальную математику, войдите в Smartick и попробуйте наш метод обучения бесплатно.

Подробнее:

Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создавать максимально качественные математические материалы.

Правильные дроби, неправильные дроби и смешанные числа — математика 3-го класса

Правильные дроби, неправильные дроби и смешанные числа

1/2 , 1/4 , 2/3 и 5/6 — все это примеры дробей.

Дроби говорят нам о частях целого.

Числитель сообщает вам количество равных частей, которые у вас есть,

Знаменатель показывает количество равных частей, на которые делится целое.

Обратите внимание, что числители всех этих дробей меньше знаменателей. 🤔

Когда числитель меньше знаменателя , тогда у вас есть правильная дробь .

Но это не всегда так. 🙀

Иногда получаются дроби вроде 3/2, 4/3, 5/4, и 8/6.

Если числитель больше или равен знаменателю , то получается неправильная дробь .

👉 Неправильные дроби относятся к чему-то, что больше или равно 1.

Неправильные дроби

Допустим, у вас есть одна целая пицца плюс половина пиццы. 😛

Вы можете выразить это, используя неправильные дроби.

Вы знаете, как это сделать? 🤔

🤓 Обратите внимание, как можно разрезать всю пиццу на два ломтика.

Каждый фрагмент составляет 1/2 от целого . 😃

🤔 Сколько всего у вас кусочков пиццы?

Верно!

У вас 3 половинки пиццы .😜 Это 3 раза 1/2 !

Вы можете выразить это как неправильную дробь :

Как мы это получили?

Только представьте, что складывает 3 половинки вместе .

1 / 2 + 1 / 2 + 1 / 2 = /2 000 000

Сумма этих дробей составляет 3/2 .

Так мы получили 3 / 2 !

Это неправильная дробь.

Другой пример

Давайте посмотрим на другой пример. 😎

Какую неправильную дробь показывает эта модель?

Есть 3 целых и , каждое целое разделено на 4 равные части .

Это означает, что знаменатель будет 4 .

👉 11 деталей окрашены.

Это наш числитель !

Неправильная дробь для этой модели — 11/4 .

Смешанные числа

Другой способ выразить неправильную дробь — использовать смешанное число . 😎

Смешанное число представляет собой целое число и правильную дробь вместе.

Давайте еще раз посмотрим на последний пример.

Сколько целых квадратов у вас раскрашено? 🤔

Верно!

👉 У вас 2 целых квадрата имеют цвет .

Какая дробь может представлять третий квадрат? 🤔

Верно!

👉 3 части из 4 окрашены в цвет .

Это означает, что 3/4 третьего квадрата окрашены.

Когда вы объединяете целых и дробную часть , вы получаете смешанное число !

Вот как можно написать смешанное число 2 3/4 .

Это части смешанного числа:

Обзор типов дробей

Теперь вы знаете, что у нас 3 вида дробей .

Как превратить неправильные дроби в смешанные числа

Мы можем использовать неправильную дробь или смешанное число, чтобы показать одно и то же значение.💪

Мы видели это в примере выше. Одна и та же модель представляет как 11/4 , так и 2 3/4 . 😎

Вы всегда можете превратить неправильную дробь в смешанное число. 😎

👉 Чтобы превратить неправильную дробь в смешанное число r , разделите числитель на знаменатель .

11 ÷ 4 = смешанное число

👉 Частное целого числа является целым числом .

👉 остаток является числителем дроби .

👉 Затем просто скопируйте r неправильной дроби.

Давайте посмотрим на другой пример. 😎

Что такое 10/3 , записанное как смешанное число?

🤓 Разделите числитель на знаменатель.

Вы получаете:

Это означает 10/3 = 3 1/3 .

Как превратить смешанные числа в неправильные дроби

👉 Чтобы превратить смешанные числа в неправильную дробь s , умножить целое на знаменатель .

👉 Затем прибавьте результат к числителю.

👉 Эта сумма является числителем неправильной фракции n .

👉 Затем просто скопируйте знаменатель дроби смешанного числа.

Давайте посмотрим на другой пример. 😎

Что такое 1 5/8 , записанное как неправильная дробь?

🤓 Умножьте целую часть числа на знаменатель, а затем добавьте числитель.

Вы получаете:

Это означает 1 5/8 = 13/8 .

Отличная работа!

Теперь вы знаете неправильные дроби и смешанные числа. 🎉

Смотри и учись

Готовы ли вы попрактиковаться? 💪

Смешанные числа и неправильные дроби

Смешанное число — это комбинация целого числа и дроби. Например, если у вас есть два целых яблока и одно половинное яблоко, вы можете описать это как 2 + ¹ /2 яблока или 2 ¹ /2 яблока.

Запись смешанных чисел в виде дробей

Это смешанное число также можно выразить дробью. Каждое целое яблоко содержит две половинки яблока. Ваши два целых яблока — это также четыре половинных яблока. Четыре половинки яблока плюс одна половина яблока — это пять половинных яблок. Итак, у вас есть ⁵ /2 яблок.

Другими словами: , чтобы превратить смешанное число в дробь, умножьте целое число на знаменатель (нижняя часть) и прибавьте результат к числителю (верхняя часть).

2 ¹ /2 =?
Умножьте целое число на знаменатель.
Целое число равно 2.
Знаменатель 2.
2 x 2 = 4.
Добавьте результат в числитель:
Числитель 1.
4 + 1 = 5
В числителе 5. В знаменателе останется 2
2 ¹ /2 = ⁵ /2

Другой пример

Давайте попробуем другой пример:

5 ² /3 =?
Умножьте целое число на знаменатель.
Целое число равно 5.
Знаменатель 3.
5 x 3 = 15.
Добавьте результат в числитель:
Числитель 2.
15 + 2 = 17
В числителе 17. В знаменателе останется 3
5 ² /3 = ¹⁷ /3

Правильные и неправильные дроби

Дробь, в которой числитель меньше знаменателя, например ¹ /3 или ² /5, называется . правильная дробь. Дробь, числитель которой больше или равен знаменателю, например ⁵ /2, ¹⁷ /3 или ⁶ /6, называется неправильной дробью . (Другими словами, дробь со значением меньше 1 является правильной дробью. Дробь со значением больше или равным 1 является неправильной дробью.)

Как мы показали выше, смешанные числа могут быть записываются в виде неправильных дробей. Точно так же неправильные дроби могут быть записаны как смешанные числа.

Запись неправильных дробей как смешанных чисел

Чтобы записать неправильную дробь как смешанное число, разделите числитель (верхняя часть) на знаменатель (нижняя часть).Частное — это целое число, а остаток — это числитель.

Как бы вы выразили ¹⁷ /4 смешанным числом?
Разделите числитель на знаменатель:
17 ÷ 4 = 4, с остатком 1
Частное, 4, является целым числом. Остаток 1 — числитель. В знаменателе остается 4.
¹⁷ /4 = 4 ¹ /4

Еще два примера

Давайте попробуем еще пару примеров:

¹⁴ /9 =?
Разделите числитель на знаменатель:
14 ÷ 9 = 1, с остатком 5
Частное 1 — это целое число.Остаток 5 — числитель. В знаменателе остается 9.
¹⁴ /9 = 1 ⁵ /9

Если остатка нет, просто возьмите частное как целое число:

²⁰ /5 =?
Разделите числитель на знаменатель:
20 ÷ 5 = 4
Частное 4 — это целое число. Остатка нет.
²⁰ /5 = 4

Наименьшее общее умножение дробей и смешанных чисел

.com / ipa / 0/9/3/3/4/5 / A0933459.html

4.2. Правильные дроби, неправильные дроби и смешанные числа

Цели обучения

• уметь различать правильные дроби, неправильные дроби и смешанные числа
• уметь преобразовывать неправильную дробь в смешанное число
• уметь преобразовывать смешанное число в неправильную дробь

Теперь, когда мы знаем, что такое положительные дроби, мы рассматриваем три типа положительных дробей: правильные дроби, неправильные дроби и смешанные числа.

Положительные правильные дроби

Определение: положительная правильная фракция

Дроби, у которых целое число в числителе строго меньше целого числа в знаменателе, называются положительными собственными дробями . На числовой строке правильные дроби расположены в интервале от 0 до 1. Положительные собственные дроби всегда меньше единицы.

Закрашенный кружок в позиции 0 указывает, что 0 включен, в то время как белый кружок в позиции 1 указывает, что 1 не включен.

Некоторые примеры положительных собственных дробей:

\ (\ dfrac {1} {2} \), \ (\ dfrac {3} {5} \), \ (\ dfrac {20} {27} \) и \ (\ dfrac {106} {255 } \)

Обратите внимание, что \ (1 <2 \), \ (3 <5 \), \ (20 <27 \) и \ (106 <225 \).

Положительные неправильные фракции

Определение: положительные неправильные дроби

Дроби, в которых целое число в числителе больше или равно целому числу в знаменателе, называются положительными неправильными дробями .В числовой строке неправильные дроби лежат справа (включительно) от 1. Положительные неправильные дроби всегда больше или равны 1.

Примеры положительных неправильных дробей:

\ (\ dfrac {3} {2} \), \ (\ dfrac {8} {5} \), \ (\ dfrac {4} {4} \) и \ (\ dfrac {105} {16 } \)

Обратите внимание, что \ (3 \ ge 2, 8 \ ge 5, 4 \ ge 4 \) и \ (105 \ ge 16 \).

Положительные смешанные числа

Определение: смешанные положительные числа

Число в форме \ (\ text {ненулевое целое число} + \ text {правильная дробь} \) называется положительным смешанным числом .Например, 2 \ (\ dfrac {3} {5} \) — смешанное число. В числовой строке смешанные числа расположены в интервале справа от (включительно) 1. Смешанные числа всегда больше или равны 1.

Связь положительных неправильных дробей и положительных смешанных чисел

Связь между неправильными дробями и смешанными числами подтверждается двумя фактами. Во-первых, неправильные дроби и смешанные числа расположены в одном интервале числовой строки.Второй факт, что смешанные числа представляют собой сумму натурального числа и дроби, можно увидеть, сделав следующие наблюдения.

Разделите все количество на 3 равные части.

Теперь рассмотрим следующие примеры, наблюдая за соответствующими заштрихованными областями.

В заштрихованной области две трети или \ (\ dfrac {2} {3} \).

\ (2 (\ dfrac {1} {3}) = \ dfrac {2} {3} \)

Есть 3 одной трети, или \ (\ dfrac {3} {3} \), или 1.

\ (3 (\ dfrac {1} {3}) = \ dfrac {3} {3} \) или 1

Таким образом,

\ (\ dfrac {3} {3} = 1 \)

Неправильная дробь = целое число.

Есть 4 1/3, или \ (\ dfrac {4} {3} \), или 1 и \ (\ dfrac {1} {3} \).

\ (4 (\ dfrac {1} {3}) = \ dfrac {4} {3} \) или 1 и \ (\ dfrac {1} {3} \)

Термины 1 и \ (\ dfrac {1} {3} \) могут быть представлены как \ (1 + \ dfrac {1} {3} \) или \ (1 \ dfrac {1} {3} \)

Таким образом,

\ (\ dfrac {4} {3} = 1 \ dfrac {1} {3}.\)

правильная дробь = смешанное число.

Есть 5 1/3, или \ (\ dfrac {5} {3} \), или 1 и \ (\ dfrac {2} {3} \).

\ (5 (\ dfrac {1} {3}) = \ dfrac {5} {3} \) или 1 и \ (\ dfrac {2} {3} \)

Термины 1 и \ (\ dfrac {2} {3} \) могут быть представлены как \ (1 + \ dfrac {2} {3} \) или \ (1 \ dfrac {2} {3} \).

Таким образом,

\ (\ dfrac {5} {3} = 1 \ dfrac {2} {3} \).

Неправильная дробь = смешанное число.

Есть 6 1/3, или \ (\ dfrac {6} {3} \), или 2.

\ (6 (\ dfrac {1} {3}) = \ dfrac {6} {3} = 2 \)

Таким образом,

\ (\ dfrac {6} {3} = 2 \)

Неправильная дробь = целое число.

Следующий важный факт проиллюстрирован предыдущими примерами.

Смешанное число = натуральное число + правильная дробь
Смешанное число — это сумма натурального числа и правильной дроби. Смешанное число = (натуральное число) + (правильная дробь)

Например, \ (1 \ dfrac {1} {3} \) можно выразить как \ (1 + \ dfrac {1} {3} \). Дробь \ (5 \ dfrac {7} {8} \) может выражаться как \ (5 + \ dfrac {7} {8} \).

Важно отметить, что такое число, как \ (5 + \ dfrac {7} {8} \), не указывает на умножение , а не . Чтобы указать умножение, нам нужно будет использовать символ умножения (например, \ (\ cdot \))

Пример \ (\ PageIndex {1} \)

\ (5 \ dfrac {7} {8} \) означает \ (5 + \ dfrac {7} {8} \), а , а не \ (5 \ cdot \ dfrac {7} {8} \), что означает 5-кратное \ (\ dfrac {7} {8} \) или 5 умноженное на \ (\ dfrac {7} {8} \).

Таким образом, смешанные числа могут быть представлены неправильными дробями, а неправильные дроби могут быть представлены смешанными числами.

Преобразование неправильных дробей в смешанные числа

Чтобы понять, как можно преобразовать неправильную дробь в смешанное число, давайте рассмотрим дробь \ (\ dfrac {4} {3} \).

\ (\ begin {array} {rcl} {\ dfrac {4} {3}} & = & {\ underbrace {\ dfrac {1} {3} + \ dfrac {1} {3} + \ dfrac {1 } {3}} _ {1} + \ dfrac {1} {3}} \\ {} & = & {1 + \ dfrac {1} {3}} \\ {} & = & {1 \ dfrac { 1} {3}} \ end {array} \)

Мы можем проиллюстрировать процедуру преобразования неправильной дроби в смешанное число на этом примере.Однако преобразование проще выполнить путем деления числителя на знаменатель и использования результата для записи смешанного числа.

Преобразование неправильной дроби в смешанное число
Чтобы преобразовать неправильную дробь в смешанное число, разделите числитель на знаменатель.

Целая часть смешанного числа является частным.
Дробная часть смешанного числа — это остаток, записанный над делителем (знаменателем неправильной дроби).

Образец набора A

Преобразует каждую неправильную дробь в соответствующее смешанное число.

\ (\ dfrac {5} {3} \) Разделить 5 на 3.

Решение

Несобственная дробь \ (\ dfrac {5} {3} = 1 \ dfrac {2} {3} \).

Образец набора A

\ (\ dfrac {46} {9} \) Разделим 46 на 9.

Решение

Несобственная дробь \ (\ dfrac {46} {9} = 5 \ dfrac {1} {9} \).

Образец набора A

\ (\ dfrac {83} {11} \) Разделим 83 на 11.

Решение

Несобственная дробь \ (\ dfrac {83} {11} = 7 \ dfrac {6} {11} \).

Образец набора A

\ (\ dfrac {104} {4} \) Разделим 104 на 4.

Решение

\ (\ dfrac {104} {4} = 26 \ dfrac {0} {4} = 26

Несобственная дробь \ (\ dfrac {104} {4} = 26 \).

Практический набор A

Преобразует каждую неправильную дробь в соответствующее смешанное число.

\ (\ dfrac {9} {2} \)

Ответ

\ (4 \ dfrac {1} {2} \)

Практический набор A

\ (\ dfrac {11} {3} \)

Ответ

\ (3 \ dfrac {2} {3} \)

Практический набор A

\ (\ dfrac {14} {11} \)

Ответ

\ (1 \ dfrac {3} {11} \)

Практический набор A

\ (\ dfrac {31} {13} \)

Ответ

\ (2 \ dfrac {5} {13} \)

Практический набор A

\ (\ dfrac {79} {4} \)

Ответ

\ (19 \ dfrac {3} {4} \)

Практический набор A

\ (\ dfrac {496} {8} \)

Ответ

62

Преобразование смешанных чисел в неправильные дроби

Чтобы понять, как преобразовать смешанное число в неправильную дробь, вспомним

смешанное число = (натуральное число) + (правильная дробь)

и рассмотрите следующую диаграмму.

Напомним, что умножение описывает повторное сложение.

Обратите внимание, что \ (\ dfrac {5} {3} \) можно получить из \ (1 \ dfrac {2} {3} \), используя умножение следующим образом.

Умножить: \ (3 \ cdot 1 = 3 \)

Складываем: \ (3 + 2 = 5 \). Поместите 5 над 3: \ (\ dfrac {5} {3} \)

В этом примере проиллюстрирована процедура преобразования смешанного числа в неправильную дробь.

Преобразование смешанного числа в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь,

Умножьте знаменатель дробной части смешанного числа на целую часть числа.
Добавьте к этому произведению числитель дробной части.
Поставьте этот результат над знаменателем дробной части.

Образец набора B

Преобразует каждое смешанное число в неправильную дробь.

\ (5 \ dfrac {7} {8} \)

Решение

1. Умножить: \ (8 \ cdot 5 = 40 \)
2. Складываем: \ (40 + 7 = 47 \)
3. Поместите 47 над 8: \ (\ dfrac {47} {8} \)

Таким образом, \ (5 \ dfrac {7} {8} = \ dfrac {47} {8} \).

Образец набора B

\ (16 \ dfrac {2} {3} \)

Решение

1. Умножить: \ (3 \ cdot 16 = 48 \).
2. Добавить: \ (48 + 2 = 50 \)
3. Поместите 50 над 3: \ (\ dfrac {50} {3} \)

Таким образом, \ (16 \ dfrac {2} {3} = \ dfrac {50} {3} \)

Практический набор A

Преобразует каждое смешанное число в соответствующую неправильную дробь.

\ (8 \ dfrac {1} {4} \)

Ответ

\ (\ dfrac {33} {4} \)

Практический набор A

\ (5 \ dfrac {3} {5} \)

Ответ

\ (\ dfrac {28} {5} \)

Практический набор A

\ (1 \ dfrac {4} {15} \)

Ответ

\ (\ dfrac {19} {15} \)

Практический набор A

\ (12 \ dfrac {2} {7} \)

Ответ

\ (\ dfrac {86} {7} \)

Упражнения

Для следующих 15 задач определите каждое выражение как правильную дробь, неправильную дробь или смешанное число.

Упражнение \ (\ PageIndex {1} \)

\ (\ dfrac {3} {2} \)

Ответ

неправильная дробь

Упражнение \ (\ PageIndex {2} \)

\ (\ dfrac {4} {9} \)

Упражнение \ (\ PageIndex {3} \)

\ (\ dfrac {5} {7} \)

Ответ

собственная фракция

Упражнение \ (\ PageIndex {4} \)

\ (\ dfrac {1} {8} \)

Упражнение \ (\ PageIndex {5} \)

\ (6 \ dfrac {1} {4} \)

Ответ

смешанное число

Упражнение \ (\ PageIndex {6} \)

\ (\ dfrac {11} {8} \)

Упражнение \ (\ PageIndex {7} \)

\ (\ dfrac {1,001} {12} \)

Ответ

неправильная дробь

Упражнение \ (\ PageIndex {8} \)

\ (191 \ dfrac {4} {5} \)

Упражнение \ (\ PageIndex {9} \)

\ (1 \ dfrac {9} {13} \)

Ответ

смешанное число

Упражнение \ (\ PageIndex {10} \)

\ (31 \ dfrac {6} {7} \)

Упражнение \ (\ PageIndex {11} \)

\ (3 \ dfrac {1} {40} \)

Ответ

смешанное число

Упражнение \ (\ PageIndex {12} \)

\ (\ dfrac {55} {12} \)

Упражнение \ (\ PageIndex {13} \)

\ (\ dfrac {0} {9} \)

Ответ

собственная фракция

Упражнение \ (\ PageIndex {14} \)

\ (\ dfrac {8} {9} \)

Упражнение \ (\ PageIndex {15} \)

\ (101 \ dfrac {1} {11} \)

Ответ

смешанное число

Для следующих 15 задач преобразуйте каждую неправильную дробь в соответствующее смешанное число.

Упражнение \ (\ PageIndex {16} \)

\ (\ dfrac {11} {6} \)

Упражнение \ (\ PageIndex {17} \)

\ (\ dfrac {14} {3} \)

Ответ

\ (4 \ dfrac {2} {3} \)

Упражнение \ (\ PageIndex {18} \)

\ (\ dfrac {25} {4} \)

Упражнение \ (\ PageIndex {19} \)

\ (\ dfrac {35} {4} \)

Ответ

\ (8 \ dfrac {3} {4} \)

Упражнение \ (\ PageIndex {20} \)

\ (\ dfrac {71} {8} \)

Упражнение \ (\ PageIndex {21} \)

\ (\ dfrac {63} {7} \)

Ответ

9

Упражнение \ (\ PageIndex {22} \)

\ (\ dfrac {121} {11} \)

Упражнение \ (\ PageIndex {23} \)

\ (\ dfrac {165} {12} \)

Ответ

\ (13 \ dfrac {9} {12} \) или \ (13 \ dfrac {3} {4} \)

Упражнение \ (\ PageIndex {24} \)

\ (\ dfrac {346} {15} \)

Упражнение \ (\ PageIndex {25} \)

\ (\ dfrac {5,000} {9} \)

Ответ

\ (555 \ dfrac {5} {9} \)

Упражнение \ (\ PageIndex {26} \)

\ (\ dfrac {23} {5} \)

Упражнение \ (\ PageIndex {27} \)

\ (\ dfrac {73} {2} \)

Ответ

\ (36 \ dfrac {1} {2} \)

Упражнение \ (\ PageIndex {28} \)

\ (\ dfrac {19} {2} \)

Упражнение \ (\ PageIndex {29} \)

\ (\ dfrac {316} {41} \)

Ответ

\ (7 \ dfrac {29} {41} \)

Упражнение \ (\ PageIndex {30} \)

\ (\ dfrac {800} {3} \)

Для следующих 15 задач преобразуйте каждое из смешанных чисел в соответствующую неправильную дробь.

Упражнение \ (\ PageIndex {31} \)

\ (4 \ dfrac {1} {8} \)

Ответ

\ (\ dfrac {33} {8} \)

Упражнение \ (\ PageIndex {32} \)

\ (1 \ dfrac {5} {12} \)

Упражнение \ (\ PageIndex {33} \)

\ (6 \ dfrac {7} {9} \)

Ответ

\ (\ dfrac {61} {9} \)

Упражнение \ (\ PageIndex {34} \)

\ (15 \ dfrac {1} {4} \)

Упражнение \ (\ PageIndex {35} \)

\ (10 ​​\ dfrac {5} {11} \)

Ответ

\ (\ dfrac {115} {11} \)

Упражнение \ (\ PageIndex {36} \)

\ (15 \ dfrac {3} {10} \)

Упражнение \ (\ PageIndex {37} \)

\ (8 \ dfrac {2} {3} \)

Ответ

\ (\ dfrac {26} {3} \)

Упражнение \ (\ PageIndex {38} \)

\ (4 \ dfrac {3} {4} \)

Упражнение \ (\ PageIndex {39} \)

\ (21 \ dfrac {2} {5} \)

Ответ

\ (\ dfrac {107} {5} \)

Упражнение \ (\ PageIndex {40} \)

\ (17 \ dfrac {9} {10} \)

Упражнение \ (\ PageIndex {41} \)

\ (9 \ dfrac {20} {21} \)

Ответ

\ (\ dfrac {209} {21} \)

Упражнение \ (\ PageIndex {42} \)

\ (5 \ dfrac {1} {16} \)

Упражнение \ (\ PageIndex {43} \)

\ (90 \ dfrac {1} {100} \)

Ответ

\ (\ dfrac {9001} {100} \)

Упражнение \ (\ PageIndex {44} \)

\ (300 \ dfrac {43} {1,000} \)

Упражнение \ (\ PageIndex {45} \)

\ (19 \ dfrac {7} {8} \)

Ответ

\ (\ dfrac {159} {8} \)

Упражнение \ (\ PageIndex {46} \)

Почему \ (0 \ dfrac {4} {7} \) не считается смешанным числом?

Подсказка:

См. Определение смешанного числа.

Упражнение \ (\ PageIndex {47} \)

Почему 5 считается смешанным числом?

Подсказка:

См. Определение смешанного числа.

Ответ

… потому что его можно записать как \ (5 \ dfrac {0} {n} \), где \ (n \) — любое положительное целое число.

Проблемы с калькулятором
Для следующих 8 задач используйте калькулятор для преобразования каждого смешанного числа в соответствующую неправильную дробь.

Упражнение \ (\ PageIndex {48} \)

\ (35 \ dfrac {11} {12} \)

Упражнение \ (\ PageIndex {49} \)

\ (27 \ dfrac {5} {61} \)

Ответ

\ (\ dfrac {1,652} {61} \)

Упражнение \ (\ PageIndex {50} \)

\ (83 \ dfrac {40} {41} \)

Упражнение \ (\ PageIndex {51} \)

\ (105 \ dfrac {21} {23} \)

Ответ

\ (\ dfrac {2,436} {23} \)

Упражнение \ (\ PageIndex {52} \)

\ (72 \ dfrac {605} {606} \)

Упражнение \ (\ PageIndex {53} \)

\ (816 \ dfrac {19} {25} \)

Ответ

\ (\ dfrac {20,419} {25} \)

Упражнение \ (\ PageIndex {54} \)

\ (708 \ dfrac {42} {51} \)

Упражнение \ (\ PageIndex {55} \)

\ (6,012 \ dfrac {4,216} {8,117} \)

Ответ

\ (\ dfrac {48,803,620} {8,117} \)

Упражнения для обзора

Упражнение \ (\ PageIndex {56} \)

Округлите 2 614 000 до ближайшей тысячи.

Упражнение \ (\ PageIndex {57} \)

Найдите товар. \ (1,004 \ cdot 1,005 \)

Ответ

1 009 020

Упражнение \ (\ PageIndex {58} \)

Определите, делится ли 41826 на 2 и 3.

Упражнение \ (\ PageIndex {59} \)

Найдите наименьшее общее кратное 28 и 36.

Ответ

252

Упражнение \ (\ PageIndex {60} \)

Укажите числитель и знаменатель дроби \ (\ dfrac {12} {19} \).

NumberNut.com: Дроби и десятичные знаки: Дроби: Смешанные числа

Теперь вы знаете о правильных дробях с числителями вверху и знаменателями внизу. Дроби могут быть положительными или отрицательными. До сих пор мы просто смотрели на дроби, меньшие единицы. Не имело значения, была ли это половина (1/2) или девятьсот девяносто девять тысячных (999/1000), значения все равно были меньше единицы.

Если у вас дробная часть больше единицы, она может быть в двух форматах. Смешанные числа содержат целое число, за которым следует дробь (2 1/2). Вы бы сказали «два с половиной». Другой формат — это неправильная дробь , где числитель больше знаменателя (5/2). Математики сказали бы, что это пять половин. В ваших задачах вы найдете оба типа дробей. Оба этих примера представляют одно и то же значение (2 1/2 = 5/2). Вот почему …

• 2 1/2 — это столько же, сколько два целых объекта и половина одной трети.
• Вы также можете разбить эти два целых объекта пополам.Если бы у каждого объекта было две половины, то два объекта дали бы вам четыре части (2×2 = 4).
• Это означает, что у вас есть четыре половинки от целых объектов и половина третьей.
• Всего у вас будет пять половинок. Вы можете записать пять половинок как 5/2.

Как мы только что сказали вам, смешанное число — это целое число, в правой части которого написана дробь.
• 2 1/2, 5 8/13, 6 4/7

Обычно дробь записывается в простейшей форме.
• 6 4/7 правильных
• 6 8/14 неправильных (необходимо уменьшить)

У вас могут возникнуть проблемы с просьбой упростить смешанные числа.Не волнуйся. Обычно вас не беспокоит целое число. Когда вы упрощаете, беспокойтесь о дроби.

Пример:
Упростить 8 4/8
• Позаботьтесь об упрощении дроби 4/8.
• Разделим на общий множитель 4 и получим 1/2.
• Упрощенное смешанное число — 8 1/2.

Другой формат дроби больше единицы — неправильная дробь . Их называют «неправильными», потому что дроби всегда должны записываться с числителем (число вверху), которое меньше знаменателя (число внизу).2/3 — правильная дробь. 3/2 — неправильная дробь, потому что 3> 2. Они полезны во многих задачах, когда вы складываете дроби и вычитаете дроби. Вы также будете использовать неправильные дроби при работе с обратными .

1/3 — неправильная дробь? № 1 <3.

Является ли величина, обратная 8/11, неправильной дробью? Да. Обратное — 11/8. 11/8 — неправильная дробь.

Итак, мы можем получить неправильную дробь, найдя обратную.Возможно, вам также понадобится составить неправильную дробь из смешанного числа. Мы только что сделали это выше, но давайте сделаем это еще раз …

Пример:
Запишите 2 1/2 как неправильную дробь.
• Два эквивалента — 2/1 или 4/2. Если вы не уверены, проверьте с помощью деления.
• Перепишите смешанное число как сложную задачу. 2 1/2 = 2 + 1/2
• Подставьте новое значение два. 2 + 1/2 = 4/2 + 1/2
• Использование небольшого сложения дробей … 4/2 + 1/2 = 5/2
• 5/2 — неправильная дробь, эквивалентная 2 1 / 2.

Как найти простейшую форму смешанного числа?

Обновлено 30 ноября 2020 г.

Лиза Мэлони

Смешанное число — это любое выражение, которое объединяет целое число, равное или больше 1, плюс дробное напоминание. Например, 1 5/8 и 3 2/3 — смешанные числа. Обычно смешанное число — это самый простой способ выразить неправильную дробь, в которой числитель или верхнее число больше знаменателя или нижнего числа. Но вы все равно должны обратить внимание на дробную часть смешанного числа.Если это неправильная дробь или она не выражена в наименьших числах, вы можете упростить все смешанное число.

Смешанные числа, содержащие неправильные дроби

Обратите внимание на дробную часть смешанного числа. Если числитель этой дроби больше знаменателя, это неправильная дробь, и вы можете упростить всю смешанную дробь, работая с делением, которое представляет неправильная дробь.

Пример. Рассмотрим смешанную дробь

4 \ enspace \ frac {11} {3}

Произведите деление, представленное дробной частью вашего смешанного числа; в данном случае 11/3.Не выражайте ответ в виде десятичной дроби. Вместо этого рассчитывайте его только до целого числа и любого остатка.

\ frac {11} {3} = 11 ÷ 3 = 3 \ text {остаток} 2

Добавьте целое число из шага 1 к целому компоненту исходного смешанного числа. В этом случае целое число из исходного смешанного числа было 4, поэтому у вас есть:

4 + 3 = 7

Установите остаток от шага 1 как дробь, используя тот же знаменатель, что и исходный смешанный. номер.Чтобы продолжить пример, ваша новая дробь — 2/3.

Соедините две части смешанного числа: целое число, которое теперь равно 7 (из шага 2), и дробь, которая теперь равна 2/3 (из шага 3). Итак, ваше новое смешанное число —

7 \ enspace \ frac {2} {3}

Смешанные числа не в наименьшем значении

Рассмотрим смешанное число, дробная часть которого не является неправильной дробью, но не в низкие сроки тоже. Вот некоторые примеры: 2 11/33 или 6 4/8.В каждом случае числитель и знаменатель дроби имеют по крайней мере один общий множитель больше 1.

Рассмотрим последний случай, 6 4/8, в качестве примера. Сократите дробную часть до наименьших членов, определив, а затем вычленив и исключив наибольший общий фактор.

Составьте список множителей для числителя дроби, а затем список множителей для знаменателя:

Наибольший общий множитель или наибольший множитель, присутствующий в обоих числах, равен 4.

Выложите множитель 4 из числителя и знаменателя дроби или, другими словами, разделите оба числа на 4. Это даст вам:

\ frac {4 ÷ 4} {8 ÷ 4}

\ frac {1} {2}

Поскольку вы разделили числитель и знаменатель на одинаковую величину, вы не изменили значение дроби; но вы написали это самым простым языком.

Помните, что изначально вы имели дело со смешанным числом. Вы только временно проигнорировали компонент целого числа, чтобы иметь дело с дробью.Итак, добавьте целое число обратно, чтобы получить окончательный результат:

6 \ Enspace \ frac {1} {2}

Изменение между неправильной дробью и формой смешанного числа — математический класс [видео 2021]

Что такое смешанное число?

Смешанные числа — это дроби, содержащие числитель, знаменатель и целое число. Эти типы дробей содержат целые наборы и часть оставшегося набора. Примером смешанного числа может быть 4 3/4.

Смешанные числа используются для представления окончательного ответа при работе с дробями.Они также полезны при сложении и вычитании дробей.

Переход от неправильной дроби к смешанному числу

Проблема с этими двумя различными формами дробей заключается в возможности простого преобразования между ними. При преобразовании неправильной дроби в смешанное число мы будем думать о столбце дроби как о делении. Например, используя неправильную дробь 12/8, мы разделим числитель 12 на знаменатель 8.

Чтобы преобразовать неправильную дробь в смешанное число, мы начнем с деления числителя на знаменатель.Как только вы закончите деление, ваше частное станет вашим целым числом. Ваш остаток также станет вашим числителем, и вы сохраните тот же знаменатель.

Если посмотреть на пример, 12 будет делиться на 8 один раз, а 4 останется в качестве остатка. Это сделает наше смешанное число 1 4/8.

Пример, неподходящий для смешанного

Давайте посоветуемся с моим другом Адамом, который работает на местной фабрике по производству печенья. Адам проводит свой день, складывая вкусное печенье в коробки, каждая из которых может вместить 10 печенек.

Поскольку он работает стабильно, машина внезапно ускоряется. Адам понимает, что у него закончились коробки. В панике он нажимает кнопку аварийной остановки. Адам должен достать достаточно коробок, чтобы упаковать целую кучу печенья. Он считает файлы cookie и видит, что 78 файлов cookie помещаются в коробки, в которых содержится только 10 файлов cookie в каждой. Адам знает, что это будет дробь 78/10.

Адаму нужно изменить эту неправильную дробь на смешанное число, чтобы он мог видеть, сколько коробок ему нужно.Адам начинает с деления числителя 78 на знаменатель 10. 10 разделит на 78 7 раз. После вычитания остаток будет 8.

Адам теперь может видеть, что частное 7 станет его целым числом, остаток 8 станет числителем, а знаменатель останется 10.

Смешанное число Адама будет 7 8/10 . Адам видит, что он сможет заполнить 7 полных коробок и 8 из 10 печенья в следующем ящике. Когда он упаковывает последнее печенье, он нажимает кнопку пуска, и машина начинает посылать другие файлы cookie по конвейеру.

Переход от смешанного числа к неправильной дроби

Иногда при работе с дробями вам необходимо использовать неправильную дробь. Чтобы заменить смешанное число на неправильную дробь, мы умножим целое число на знаменатель. Затем мы добавим это значение и числитель. Это значение станет вашим новым числителем, и вы сохраните тот же знаменатель.

Смешанный с неподходящим примером

Давайте посетим местные футбольные поля, где Джеймс создает молодежную футбольную лигу.Джеймс ставит по 8 детей в каждую команду, и у него остается еще 3 ребенка. В настоящее время у него 9 3/8 команд. Джеймс знает, что это означает, что у него 9 полных команд и 3 ребенка из 8 оставшихся.

Джеймс хочет знать, сколько детей записалось на футбол, если у него 9 команд 3/8. Для начала Джеймс умножает целое число на знаменатель 8, что равняется 72.

Теперь, используя это значение, 72, он прибавит числитель 3, что равно 75.

Джеймс знает, что он останется прежним. знаменатель.Итак, дробь, представляющая количество игроков, играющих в футбол в этом сезоне, составляет 75/8.

Резюме урока

Итак, рассмотрим неправильную дробь . — это дробь, числитель которой больше знаменателя. Смешанные числа — это дроби, содержащие числители, знаменатели и целые числа.

Чтобы преобразовать неправильную дробь в смешанное число, мы начнем с деления числителя на знаменатель. Как только вы закончите деление, ваше частное станет вашим целым числом, ваш остаток станет вашим числителем, и вы сохраните тот же знаменатель.

Чтобы преобразовать смешанное число в неправильную дробь, умножьте целое число на знаменатель. Затем вам нужно добавить это значение и числитель. Это новое значение станет вашим числителем, и вы также сохраните тот же знаменатель.