Открытый урок по алгебре и началам анализа в 10-м классе по теме «Метод математической индукции»
Цели:
Дидактические:
- обеспечить в ходе урока усвоение метода математической индукции;
- сформировать умение применять этот метод для доказательства тождеств, неравенств, задач на делимость, логических задач.
Воспитательные:
- формирование научного мировоззрения;
- формирование интереса к исследовательской деятельности;
- формирование культуры речи;
- формирование умения корректно высказывать точку зрения.
Развивающие:
- развитие у школьников умение выделять главное, существенное в изучаемом материале;
- умение сравнивать, обобщать, логически излагать свои мысли;
- формирование интеллектуальных чувств (новизны, интереса, удивления).
Форма обучения:
Урок лекция, беседа. Объяснение нового материала
Материально-техническое обеспечение:
Мультимедийное оборудование, опорный конспект урока (Приложение 2). Презентация по данной теме (Приложение 1).
Ход урока
I. Актуализация знаний
При изучении явлений в любой области знаний – будь, то математика или история, физика или медицина, астрономия или экономика всюду и всегда основным этапом является установление определенных закономерностей связывающих отдельные элементы изучаемого явления. Мы подмечаем определенную связь между элементами изучаемого явления справедливого для многих частных случаев, затем распространяем на все случае вообще, устанавливая тем самым общий закон, раскрывающий сущность данного явления.
Все утверждения можно разделить на общие и частные. Например, утверждение “Во всяком параллелограмме диагонали делятся в точке пересечения пополам”, является общим, так как относится ко всему множеству параллелограммов. В то же время утверждение “В параллелограмме ABCD диагонали делятся в точке пересечения пополам”, является частным, так как относится к конкретному параллелограмму ABCD.
На основе частных утверждений делают некоторые предположения (гипотезы) о справедливости какого либо утверждения. Иногда эти предположения оказываются верными, иногда ошибочными.
Многие свойства чисел сначала были открыты путем наблюдений, задолго до того как истинность была строго доказана.
II. Основная часть урока
Переход от частных утверждений к общим называют индукцией (от латинского слова inductio – наведение). Например, знаменитый математик XVII в. П.Ферма, проверив, что числа
, , , , простые, сделал по индукции предположение, что для всех n=1,2,3,… числа вида , простые. Однако это предположение оказалось неверным, так как в XVIII веке Л. Эйлер нашел, что — составное число. Как видим, индукция не является методом доказательства, а лишь помогает сформулировать неизвестный результат в виде некоторой гипотезы, справедливость которой надо потом доказать.
В случае когда утверждение касается конечного числа объектов, его можно доказать, проверяя для каждого объекта.
В чем же заключается суть исследования которое позволяет доказать или опровергнуть математическое утверждение? Ответ мы найдем при разборе следующей задачи.
Задача
Перед нами последовательность нечетных чисел натурального ряда.
1,3,5,7,9,11,13…Чему равна сумма n первых членов этой последовательности?
Решение
Составим суммы одного, двух, трех, и т.д. первых членов данной последовательности:
S1=1;
S2=1+3=4;
S3=1+3+5=9;
S4=1+3+5+7=16;
S5=1+3+5+7+9=25;
Заметим, что
S1=12;
S2=4=22;
S3=9=32;
S4=16=42;
S5=25=52;
На основе этих наблюдений мы можем высказать предположение, что
Sn=1+3+5+7+…+(2n-1)=n2 (1)
Верно ли это предположение при любом целом положительном n?
Лучше пойдем по иному пути в поисках общего доказательства высказанного нами утверждения.
Предположим, что формула (1) верна для n=k, где kN, то есть
1+3+5+7+…+(2k-1)=k2 (2)
Докажем ее справедливость и для числа, непосредственно следующего за k, для числа n=k+1.
Sk+1=1+3+5+7+…+(2k-1)+(2k+1)=(k+1)2 (3)
Заменим на основе равенства (2) Sk=1+3+5+7+…+(2k-1) на k2.
Sk+1= Sk +(2k+1)= k2 +(2k+1)= (k+1)2 (3)
Мы пришли к очень важному выводу:
Если наше предположение верно для некоторого натурального k, то оно непременно остается верным для следующего целого числа k+1.
Мы уверены, что предположение верно, для n=1,2,3,4,5. Будучи верным, для 5 оно на основе полученного вывода оно должно быть верным и для следующего целого числа 6, будучи верным, для 6 оно должно быть верным и для 7 и так далее. Предположение верно для всех натуральных чисел.
Данное решение может быть укорочено. При переходе, от какого либо произвольного натурального числа k к следующему за ним натуральному числу k+1 нужно ли проверять наше предположение для n=5,4,3,2. Достаточно быть уверенным в том, что оно справедливо для n=1. И тогда мы скажем: если предположение верно для n=1, то оно на основе доказанного верно и для n=2, если оно верно при n=2, то оно верно и для n=3 и так далее.
Решая эту задачу, мы познакомились с очень важным методом доказательства. Такой можно было бы назвать “переходом от k к k+1”, но обычно его называют методом математической или полной индукции.
В основе этого метода лежит принцип математической индукции, который заключается в следующем.
Утверждение P(n) справедливо для всякого натурального n, если:
- Оно справедливо для n=1 или для наименьшего из натуральных чисел при котором закономерность имеет смысл.
- Из справедливости утверждения, для какого либо произвольного натурально n=k, следует его справедливость для n=k+1.
Само доказательство методом математической индукции состоит из следующих частей.
- Проверяют справедливость гипотезы для наименьшего из натуральных чисел при котором гипотеза имеет смысл (базис).
- Сделав предположение, что гипотеза верна для некоторого значения k, стремятся доказать справедливость ее для k+1.
- Если такое доказательство удалось довести до конца, то, на основе принципа математической индукции можно утверждать, что высказанная гипотеза справедлива для любого натурального числа n.
III. Закрепление материала
Применим метод математической индукции к решению следующей задачи.
Задача
Доказать, что , при n2.
Решение
- Гипотеза имеет смысл при n2. Проверим верность утверждения при n=2
- Предположим, что при n=k>2, . Докажем, что .
- На основе принципа математической индукции можно утверждать, что высказанная гипотеза справедлива для любого натурального числа n2.
, 57=19? 3
Гипотеза оказалось справедливой и при n=k+1
При доказательстве гипотезы методом математической индукции очень важно выполнение всех его составляющих.
Рассмотрим следующие примеры.
- При отсутствии первого шага можно “доказать”, что числа вида 2n-1 являются четными при nN.
- В поисках формулы дающий только простые числа Л. Эйлер подверг испытанию трехчлен
Пусть при n=k утверждение верно, то есть
2k-1 четное число.
Проверим верность утверждения при n=k+1
2(k+1)-1=2k+2-1=(2k-1)+2
По предположению индукции 2k-1 четное число,
следовательно число (2k-1)+2 тоже четное.
Отсутствие первого шага приводит к ошибке.
P(n)=n2+n+41
Этот трехчлен давал простые числа при всех
значениях n от 1 до 39:
P(2)=22+2+41=47;
P(3)=32+3+41=53;
…
P(39)=392+39+41=1601;
P(40)=402+40+41=1641=412.
Обратите внимание, что отсутствие второго шага приводит к неверному результату
Метод математической индукции можно эффективно использовать для формул вычисления сумм, когда число слагаемых зависит от n, для доказательство тождеств и неравенств, задач на делимость, логических задач.
Задача
Каждый человек в мире пожал какое-то количество рук. Докажите, что число людей пожавших нечетное число рук – четно.
Решение
Пронумеруем все рукопожатия в мире от первого (его не обязательно должны были совершить Адам и Ева) до произвольного натурального n. Очевидно, что при n=1 утверждение задачи справедливо. Предположим, что оно верно при каком-то n=k, то есть количество людей участвовавших в рукопожатиях с номерами от 1 до k и сделавших нечетное количество рукопожатий, четно.
Докажем справедливость этого утверждения для n=k+1, возможны три варианта осуществления k+1 рукопожатия: друг другу пожимают руки:
- два особых человека;
- два неособых человека;
- один особый и один неособый человек.
В каждом из этих трех случаев количество особых людей либо уменьшается на два, либо увеличивается на два, либо неизменяется.
Утверждение доказано.
IV. Итоги урока
Вывод
Метод математической индукции не дает ни каких указаний, как построить гипотезу. Вопрос о том, как возникает гипотеза, принадлежит к той области, в которой нет никаких общих правил, здесь делает свое дело эксперимент, аналогия, конструктивная индукция.
Без индукции было бы невозможно творчество ни в математике, ни в физике, ни в любой иной области науки.
“Понимание и умение правильно применять принцип математической индукции, является хорошим критерием логической зрелости, которая совершенно необходима математику” А.Н. Колмогоров
Домашнее задание
- Доказать неравенство , где x-1, x0, nN, n>1.
- Доказать, что сумма квадратов чисел натурального ряда от 1 до n, равна , то есть 12+22+32+…+n2=
Это неравенство называется неравенством Бернулли.
urok.1sept.ru
План-конспект урока алгебры (10 класс) по теме: Разработка урока по математике в 10 классе «Метод математической индукции»
Тема: Метод математической индукции.
(10 класс)
Цель урока: Рассмотреть суть метода математической индукции. Научить применять его при доказательстве некоторых утверждений.
Ход урока.
1.Устно
2.Объяснение материала
3.Закрепление материала
4.Домашнее задание
5.Итог урока.
1.Устно
а) Приведите примеры утверждений.
б) Какие виды утверждений вы знаете?
(общие и частные)
в) Приведите примеры общих утверждений.
г) Приведите примеры частных утверждений.
2.Обьяснение материала
В математике на основе частных утверждений делают некоторые предположения
О справедливости какого-либо общего утверждения. Переход от частных утверждений к общим называют индукцией.
Джузеппе Пеано показал, что для дедуктивного построения арифметики натуральных чисел достаточно четырех аксиом. Так аксиома 4 у него говорит : Если какая-либо теорема о свойствах натуральных чисел доказывает для единицы и если из допущения, что она верна для натурального числа и, следует, что она верна для всех натуральных чисел.
ПРИМЕР. Найти формулу для вычисления суммы k первых нечетных чисел.
Попробуем подсчитать такую сумму для некоторых значений k:
k=1; 1=1=12;
k=2; 1+3=4=22;
k=3; 1+3+5=9=32;
k=4; 1+3+5+7=16=42;
Таким образом, 1+3…+(2n-1)+(2n+1)=(n+1)2.
Получим:
1+3+…+(2n-1)+(2n+1)=n2+(2n+1)=(n+1)2, ч.т.д.
Знаменитый математик 17 века Пьер Ферма высказал предположение, что простыми являются все числа вида 22n+1.Он показал, что первые пять числе 220+1=3, 221+1=5,222+1=17, 223+1=257, 224+1=65537 – простые и сделая по индукции предположение, что для всех n числа вида 22n+1- простые.
Однако это предположение оказалось не верным, т.к. в 18 веке Л.Эйлер нашёл, что 225+1=4294967297=641∙4700417 – составное число.
Итак, индукция не является методом доказательства, а лишь помогает сформулировать неизвестный результат в виде некоторой гипотезы, справедливость которой потом надо доказать.
Идея последовательного перехода от натурального числа n к следующему за ним числу n+1 осуществляется в строгой форме в одном из самых важных методов математических доказательств называется методом математической индукции.
В основе этого метода лежит принцип математической индукции, заключающийся в следующем:
Утверждения P(n) справедливо для всякого натурального n, если:
1)Оно справедливо для n=1;
2)Из справедливости утверждения для какого-либо произвольного натурального n=k следует его справедливость для n=k+1.
3. Закрепление материала.
ПРИМЕР. Методом математической индукции докажите справедливость равенства:
12+32+52+…+(2n-1)2=n2n-1(2n+1)3
Доказательство:
- При n=1, 12=12∙1-1(2∙1+1)3=1
2.Пусть при n=k верно неравенство:
12+32+…+(2k-1)2=k2k-12k+13
3.Докажем верность равенству при n=k+1
12+32+…+ (2k-1)2+ (2k+1)2=k2k-1(2k+1)3+(2k+1)2=
= (2k+1)[k2k-1+32k+1]3=2k+12k2-k+6k+33=
= 2k+12k2+5k+33=2k+1k+1(2k+3)3, ч.т.д.
ПРИМЕР. Докажите, что n3- n делится на 3 любых натуральных значениях n.
Доказательство:
1.При n=1 12-1=0 – делится на 3
2. Пусть при n=k (k3-k) – делится на 3, т.е. k3-k=3m
3. Докажем, что (k+1)3-(k+1) – делится на 3.
(k+1)3-(k+1)=k3+3k2+3k+1-k-1=k3- k+3k2+k=3m+3(k+k) делится на 3, т.к. k3-k делится на 3 и k2+k делится на 3, ч.т.д.
4.Домашнее задание.
№1. Методом математической индукции докажите справедливость неравенства:
1∙2∙3+2∙3∙4+…+n (n+1)(n+2)=14n(n+1)(n+2)(n+3)
№2. Докажите, что сумма кубов трех последовательных натуральных чисел делится на 9.
5.Итог урока.
-В чем же заключается методов математической индукции.
nsportal.ru
«Метод математической индукции» (10 класс)
Конспект урока
(1 час)
Тема: Первые представления о методе математической индукции
Цели:
Формирование у учащихся понятие о методе математической индукции, сформулировать принцип математической индукции;
Развитие умения сравнивать и обобщать, познавательные интересы учащихся;
Методы: репродуктивный, объяснительно-иллюстративный, эвристический.
Средства: презентация.
Формы проведения урока: устная, коллективная.
План урока:
Организационный момент;
Целеполагание;
Актуализация знаний;
Введение новой темы;
Закрепление;
Итог урока;
Запись домашнего задания;
Организационный момент.
Вид доски
Организационный момент.
У: «Здравствуйте, садитесь»
Тема: «Первые представления о методе математической индукции»
Слайд №1

Целеполагание.
У: «Сегодня мы начинаем изучать очень интересный метод решения задач. Сначала, вспомним некоторые сведения, которые вы уже изучали»
Актуализация знаний.
У: «Какие числа называются чётными (нечётными)?»
«Какое число называется простым (составным)?»
«Какое множество называется конечным (бесконечным)?»
«Назовите формулу суммы 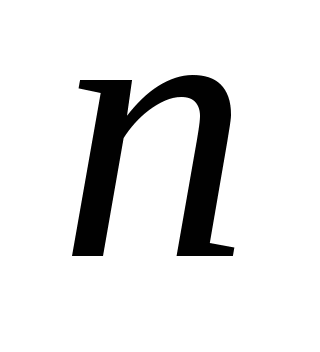 членов арифметической прогрессии?»
членов арифметической прогрессии?»
Д: «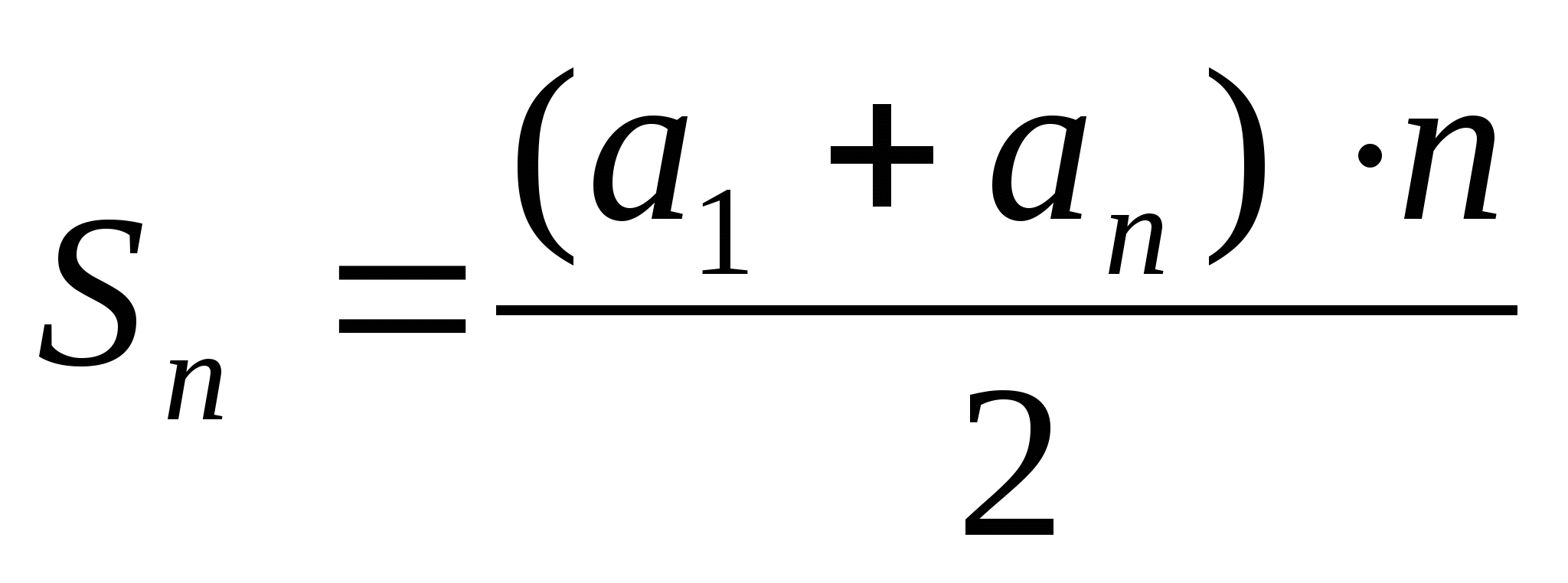 »
»
Слайд №2
Введение новой темы.
У: « Все утверждения можно разделить на общие и частные.
Как вы понимаете, какие утверждения называются общими (частными)?»
На доске записаны утверждения. Отнесите каждое из них к общим или частным утверждениям.
Слайд № 3
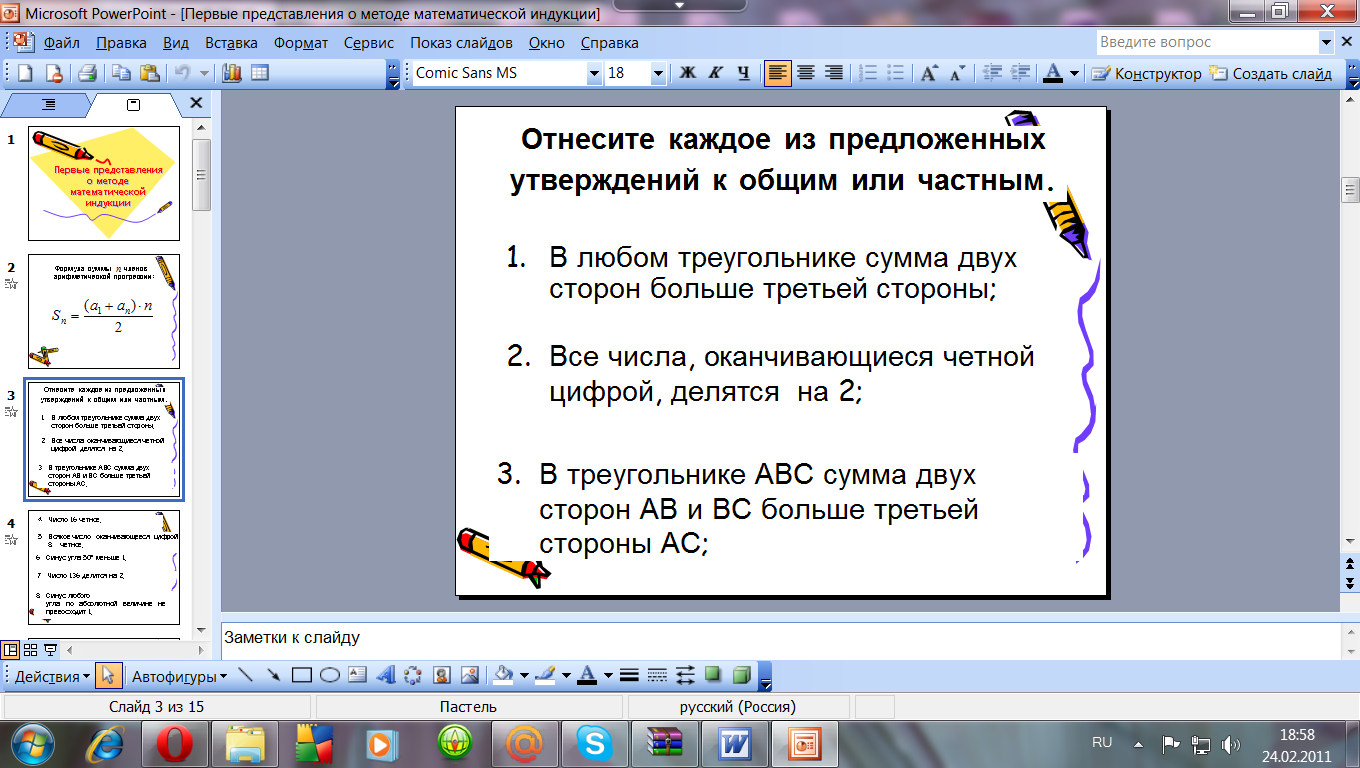
Слайд № 4
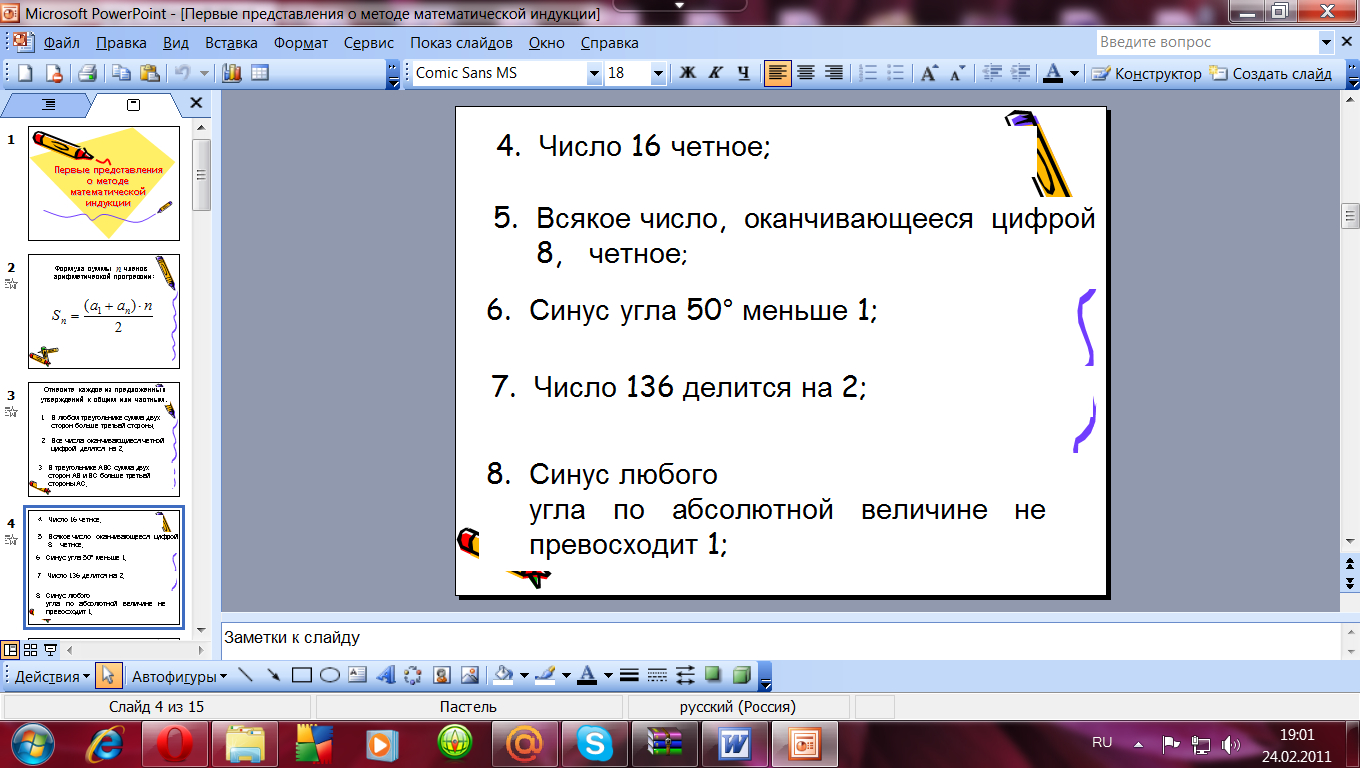
У: «Поднимите руку, кто знает, как называется переход от общих утверждений к частным?» (Дедукция)
«Как называется переход от частного к общему?» (Индукция)
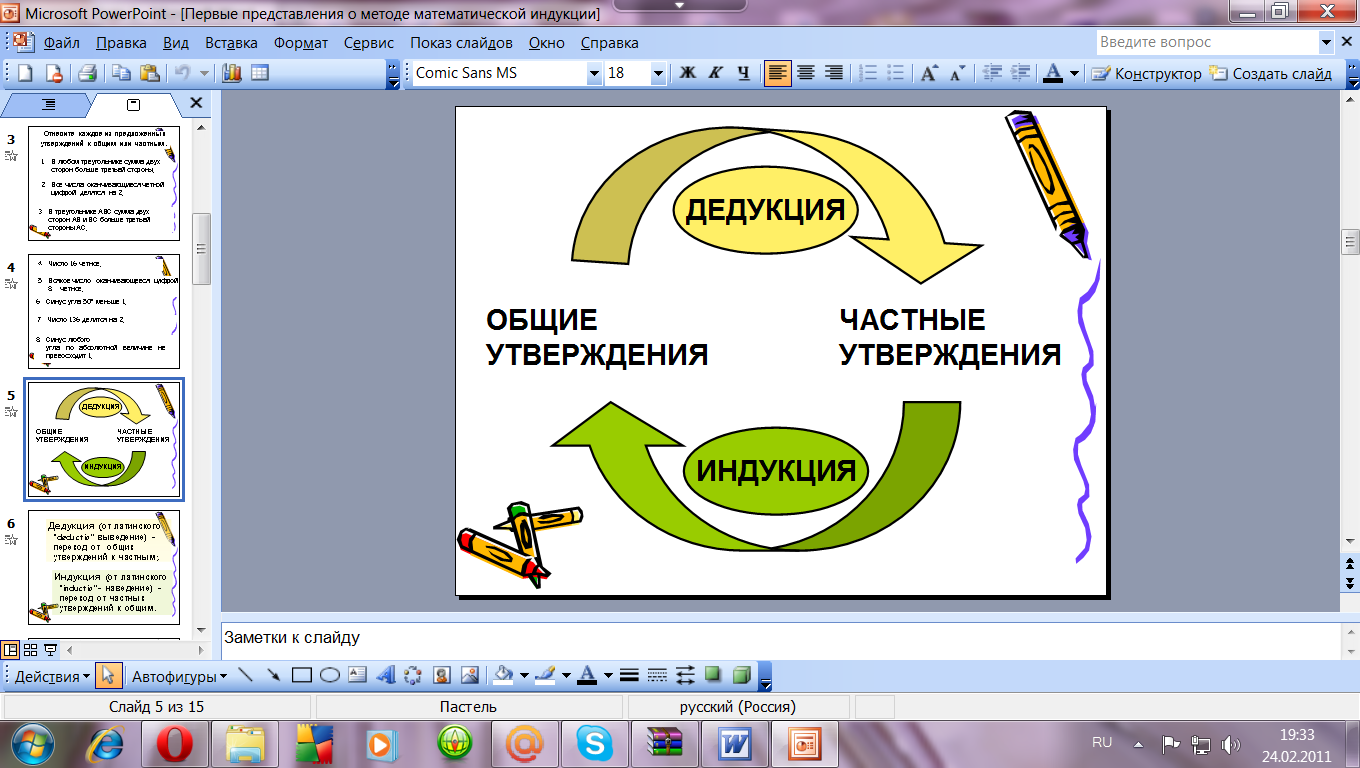
«Переход от общих утверждений к частным называется дедукцией (от латинского “deductio”- выведение), а переход от частных утверждений к общим, называется индукцией (от латинского “inductio”- наведение).
То есть в дедуктивном методе рассуждений исходным моментом является общее утверждение, а заключительным – частный результат. Если же, опираясь на ряд частных результатов, делается общий вывод, то говорят, что используется индуктивный метод рассуждений»
«Попробуйте привести пример дедуктивного рассуждения?»
Дети приводят примеры.
(Если в треугольнике сумма двух сторон больше третьей стороны, то в треугольнике АВС сумма двух сторон АВ и ВС больше третьей стороны АС)
«Попробуйте привести пример индуктивного рассуждения?»
Дети приводят примеры.
(Если в треугольнике АВС сумма двух сторон АВ и ВС больше третьей стороны АС, то в любом треугольнике сумма двух сторон больше третьей стороны)
Слайд № 5
Слайд № 6

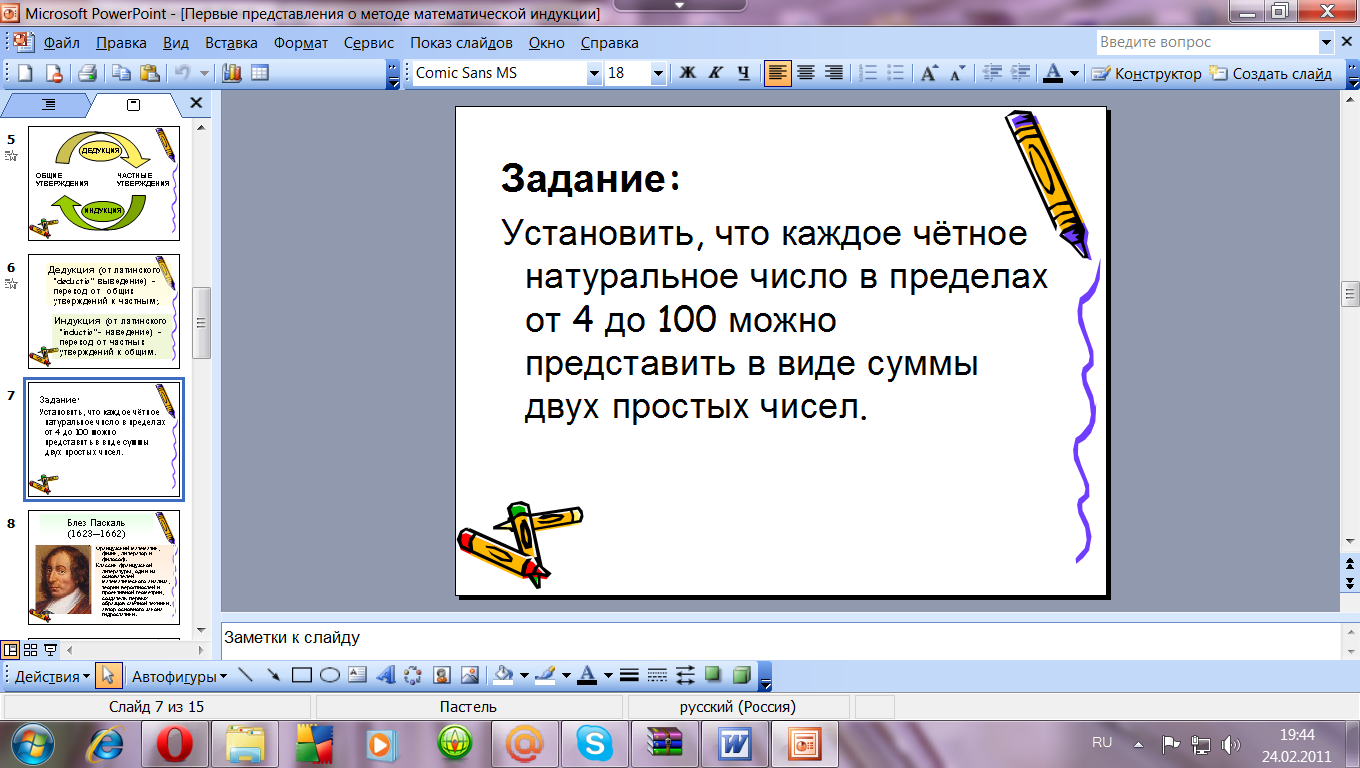
У: « Рассмотрим ещё один интересный пример рассуждения по индукции.
Требуется установить, что каждое чётное натуральное число в пределах от 4 до 100 можно представить в виде суммы двух простых чисел.
Переберём числа и выпишем соответствующие суммы.
Назовите по порядку чётные натуральные числа, начиная с 4. (Дети называют числа, учитель выписывает)
Представьте в виде суммы двух простых чисел. (Дети предлагают варианты)
4 = 2 + 2 12 = 5 + 7 94 = 5 + 89
6 = 3 + 3 14 = 7 + 7 96 = 7 + 89
8 = 5 + 3 16 = 3 + 13 98 = 19 + 79
10 = 5 + 5 18 = 5 + 13 … 100 = 3 + 97
Эти равенства (мы выписали не все за экономией времени) показывают, что сформулированное общее утверждение верно. Итак, что мы доказали?
Д: «Что любое чётное число в пределах от 4 до 100 можно представить в виде суммы двух простых чисел»
У: «Оно было доказано перебором всех частных случаев. Для конечного или бесконечного множества мы доказали утверждение?»
Д: «Для конечного»
У: «Это, так называемая, полная индукция, когда общее утверждение доказывается для конечного множества элементов, перебором всех элементов.
А что делать, если общее утверждение относится не к конечному, а к бесконечному множеству?»
Дети предлагают варианты, идёт обсуждение.
У: «Рассмотреть по отдельности каждый элемент бесконечного множества не возможно. В таких случаях общее утверждение может быть только угаданным, полученным неполной индукцией»
Слайд № 7
4 = 2 + 2 12 = 5 + 7 94 = 5 + 89
6 = 3 + 3 14 = 7 + 7 96 = 7 + 89
8 = 5 + 3 16 = 3 + 13 98 = 19 + 79
10 = 5 + 5 18 = 5 + 13…100 = 3 +97
У: «Приведём пример.
Рассмотрим суммы первых 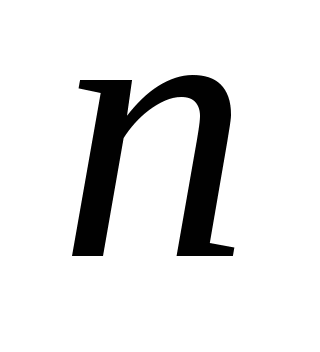 нечётных натуральных чисел. Чему они равны?»
нечётных натуральных чисел. Чему они равны?»
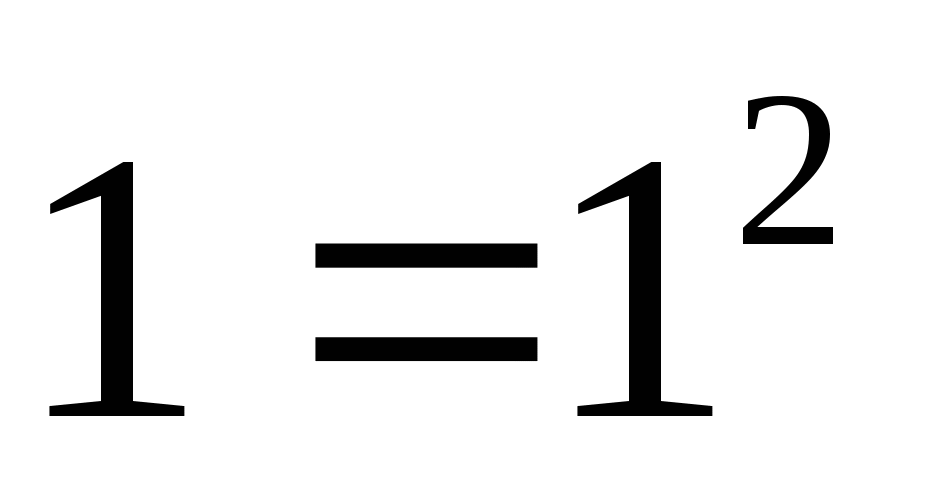
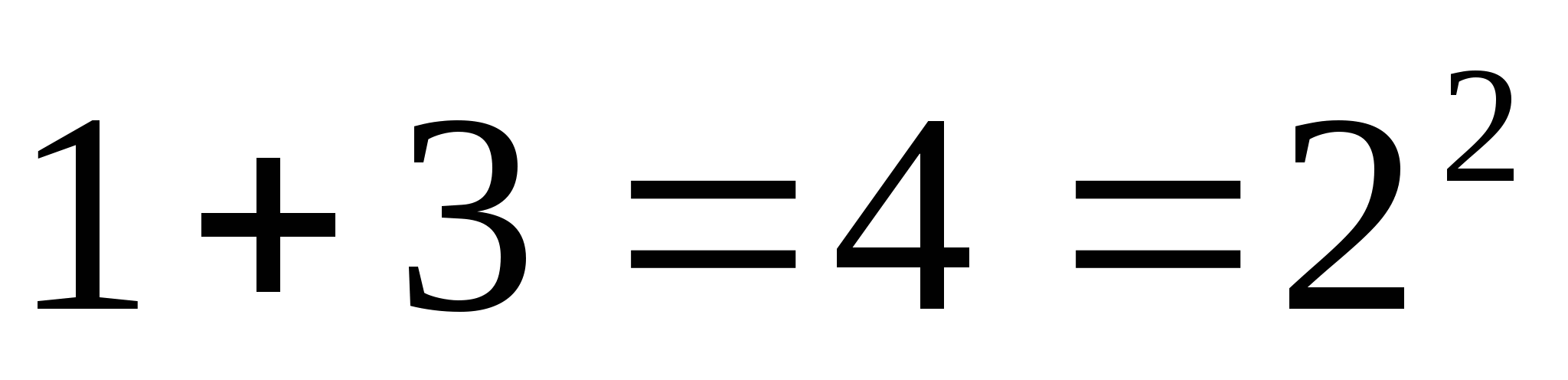
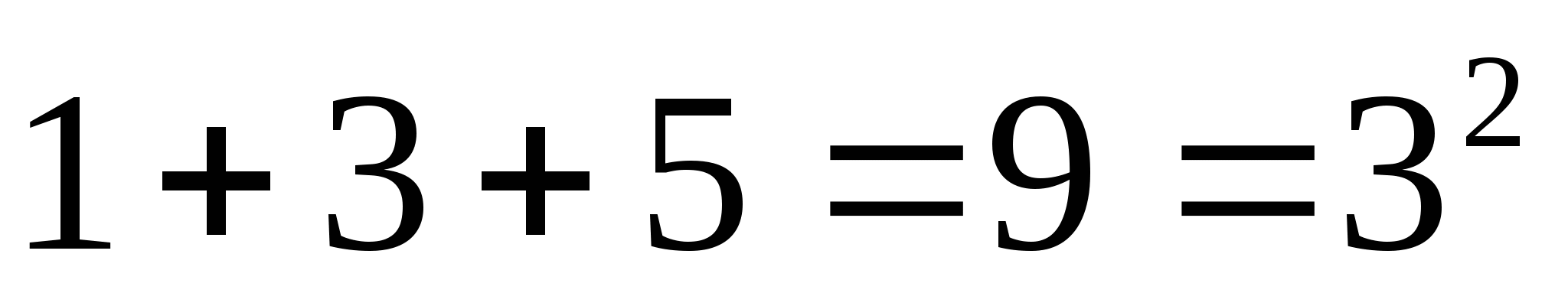
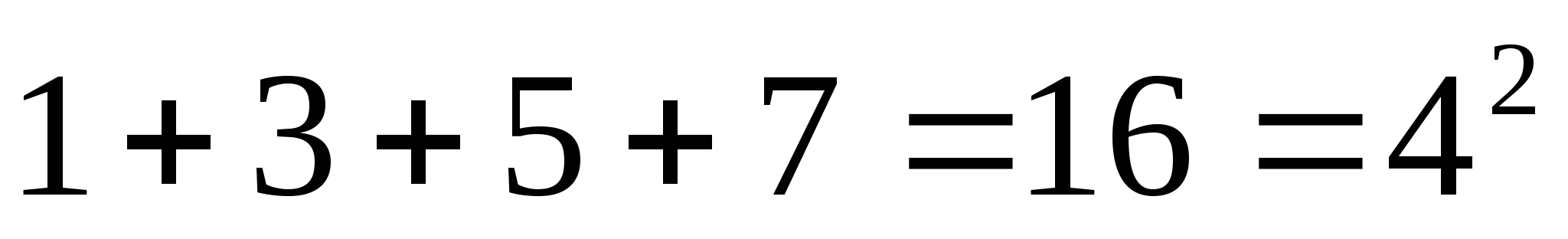
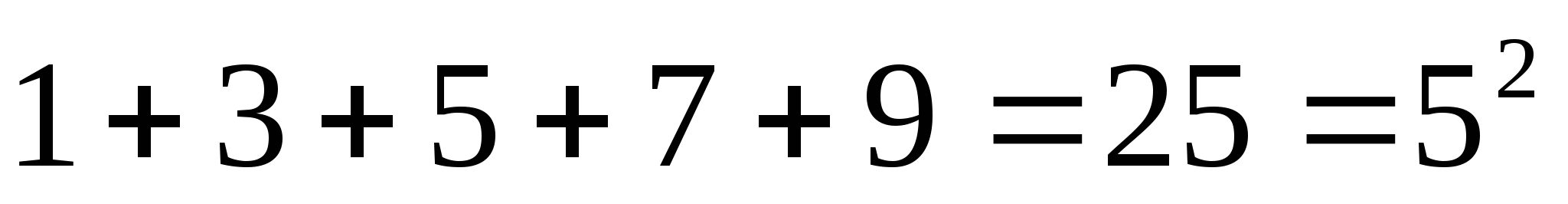
У: «Какую гипотезу можно выдвинуть?»
Д: «Что сумма первых 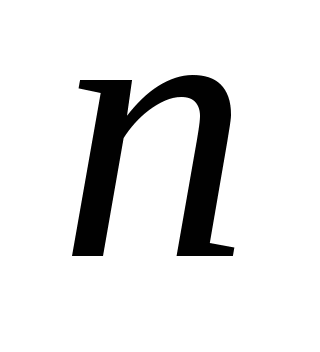 нечётных чисел равна
нечётных чисел равна 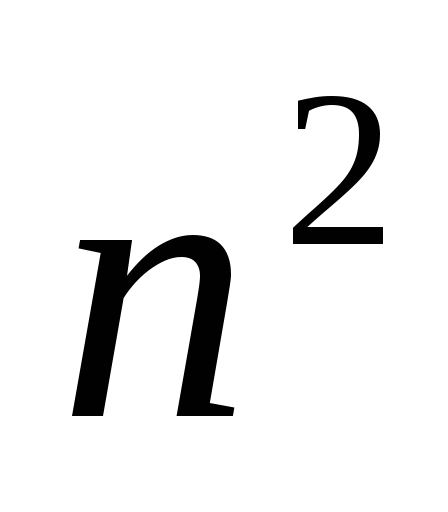 »
»
У: «Проверим её для шести и семи слагаемых»
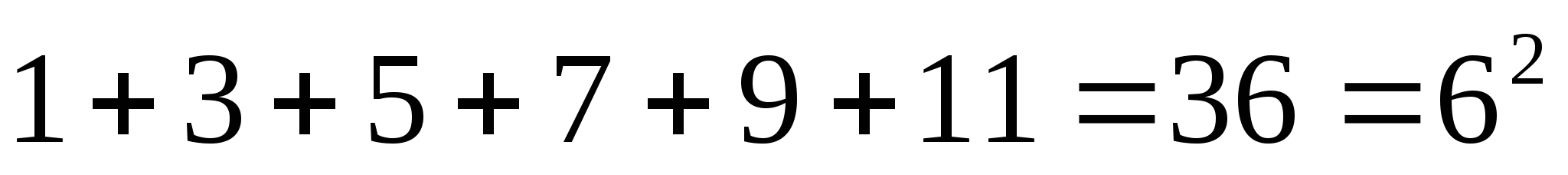
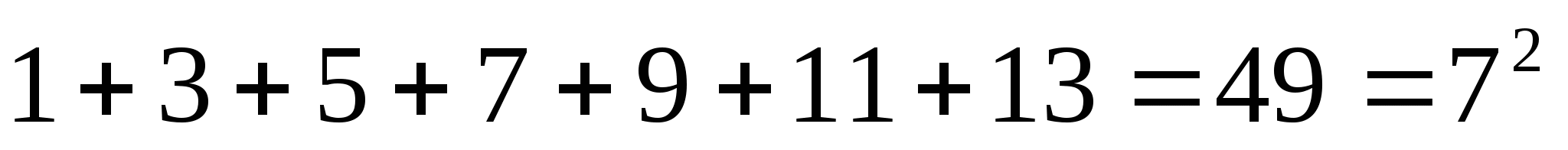
«Гипотеза подтвердилась. Но утверждение не доказано. Как можно доказать данное утверждение? (используя формулу суммы 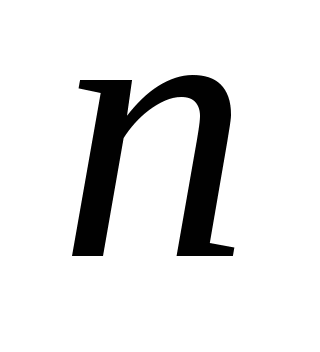 членов геометрической прогрессии)
членов геометрической прогрессии)
Чему равен n-й член геометрической прогрессии?»
Д: « »
»
«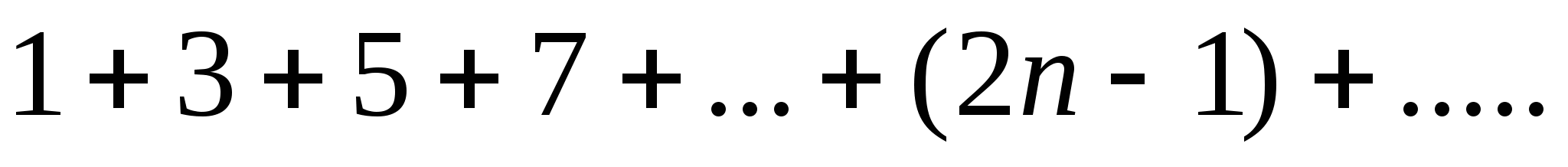
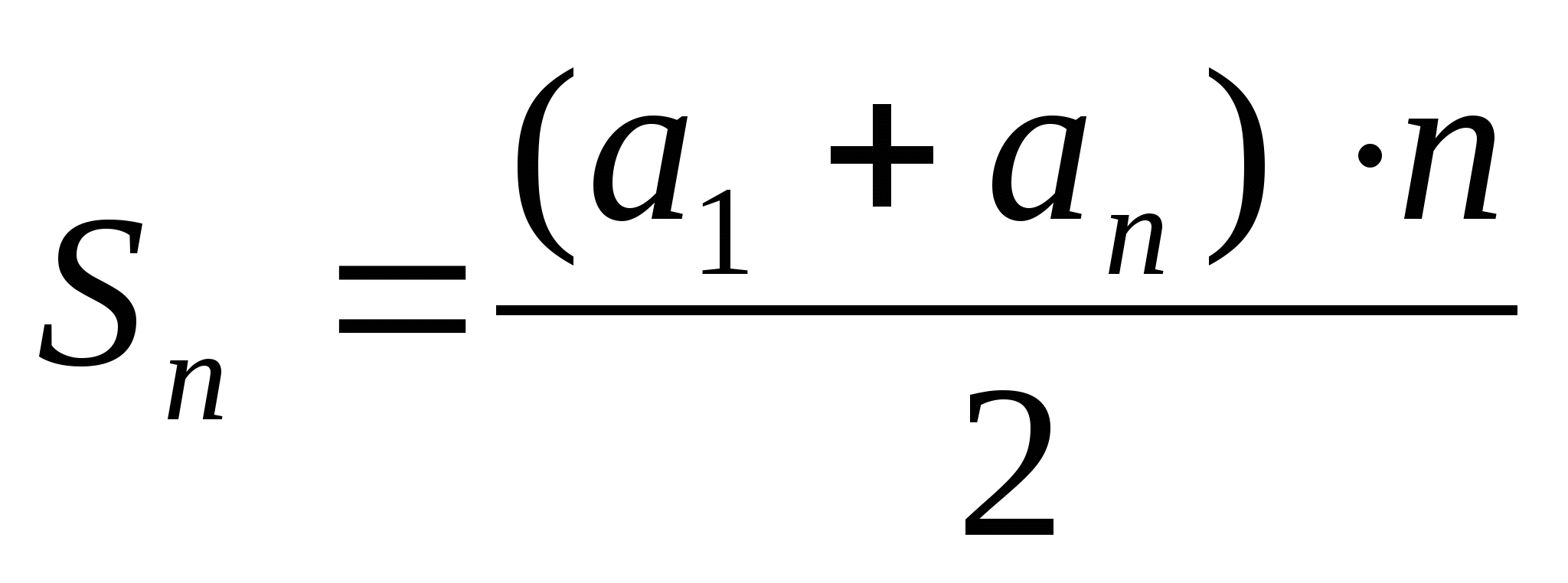 =
=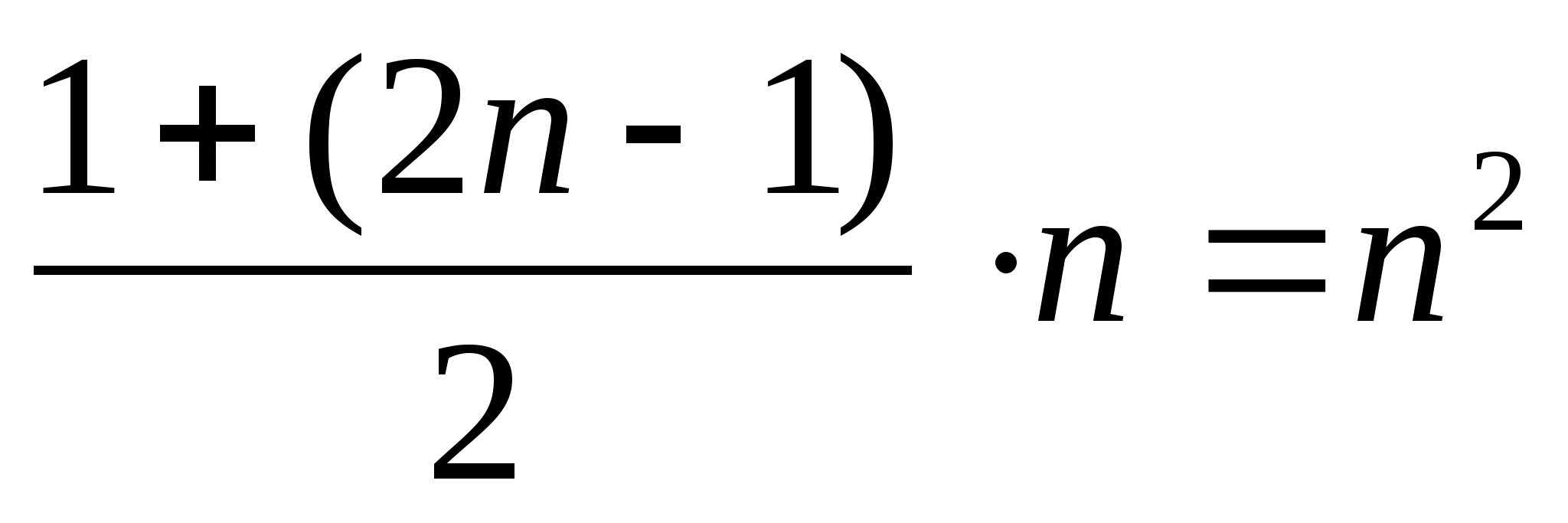 »
»
Утверждение доказано»
Пример 1.
Суммы первых 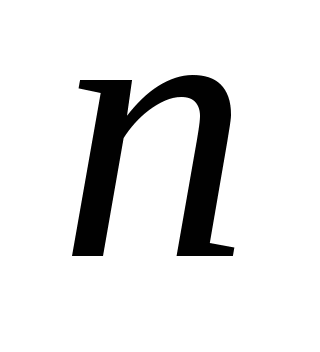 нечётных натуральных чисел:
нечётных натуральных чисел:
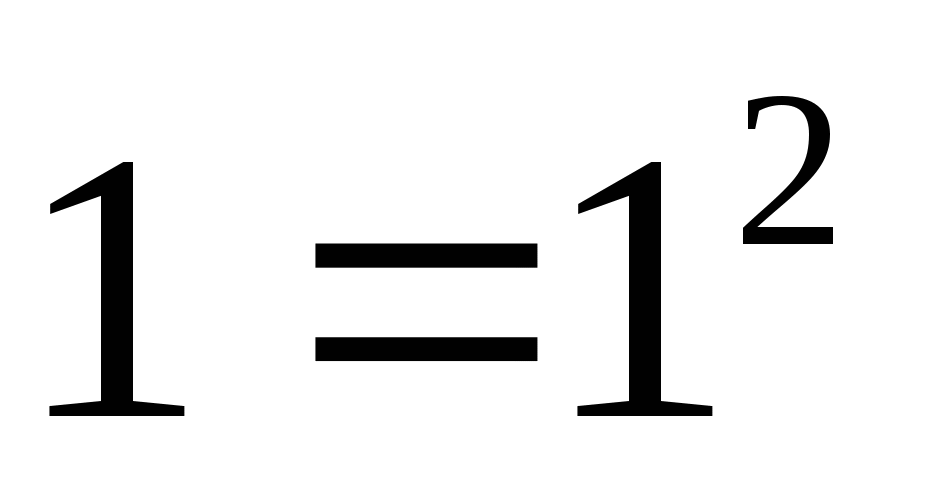
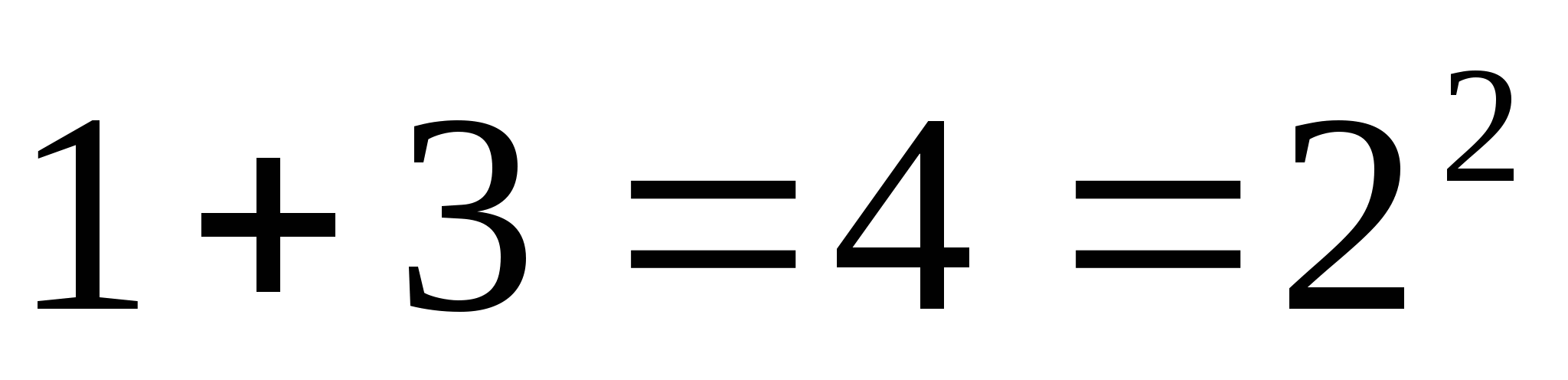
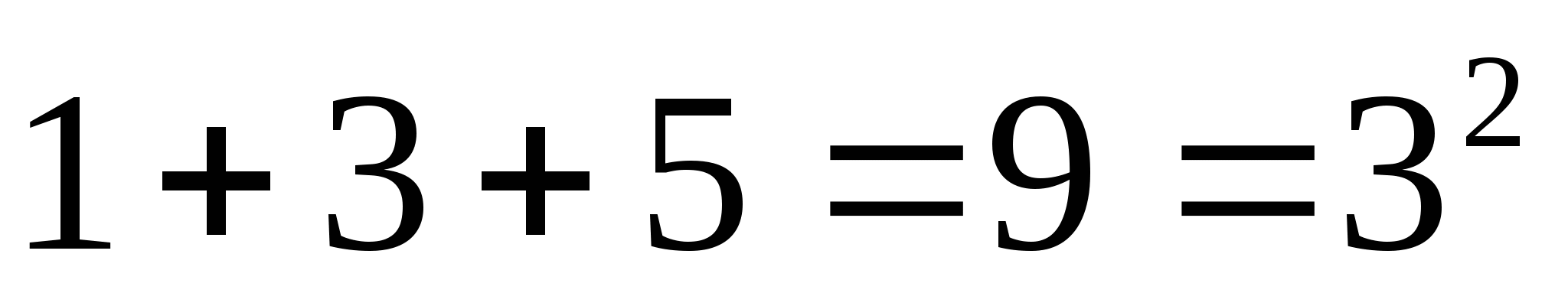
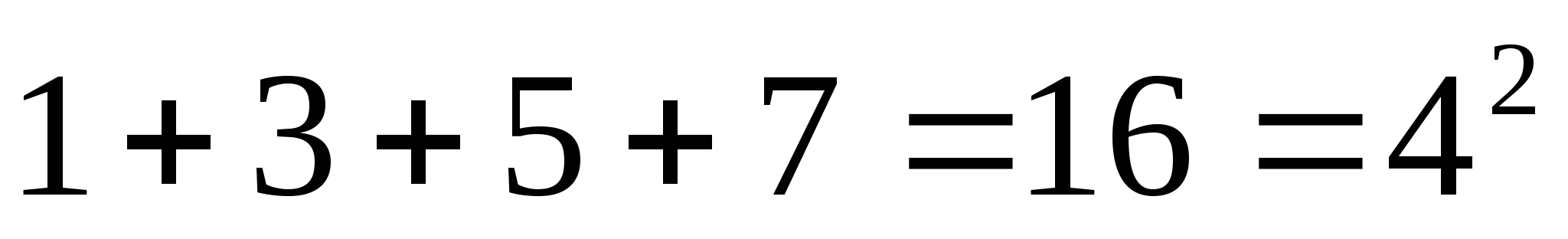
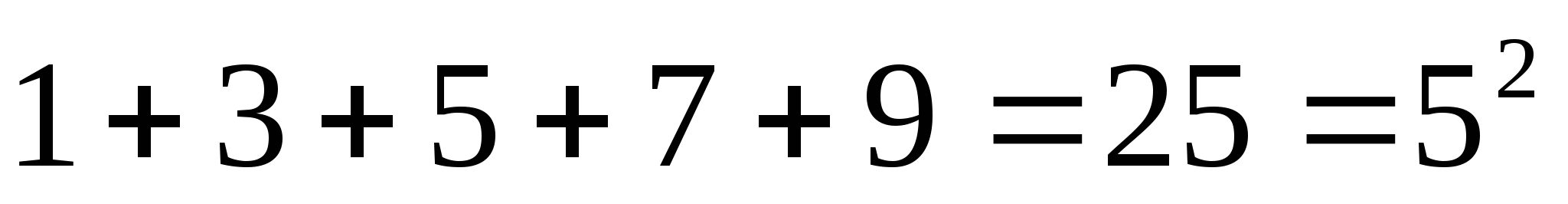
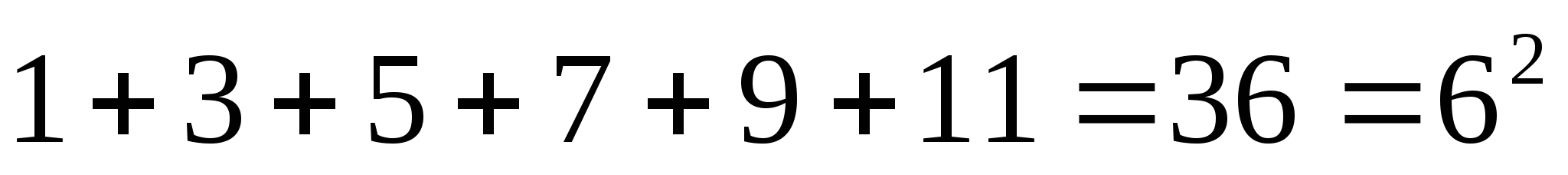
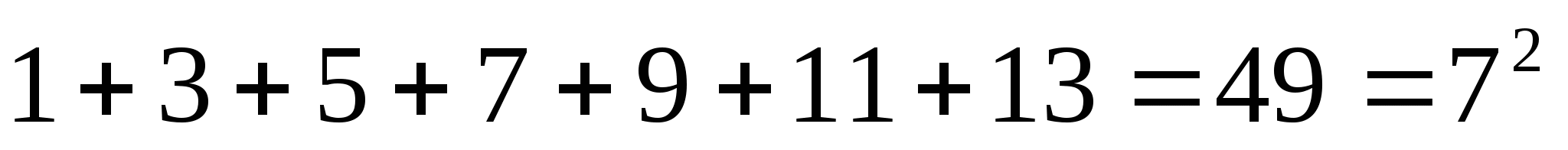
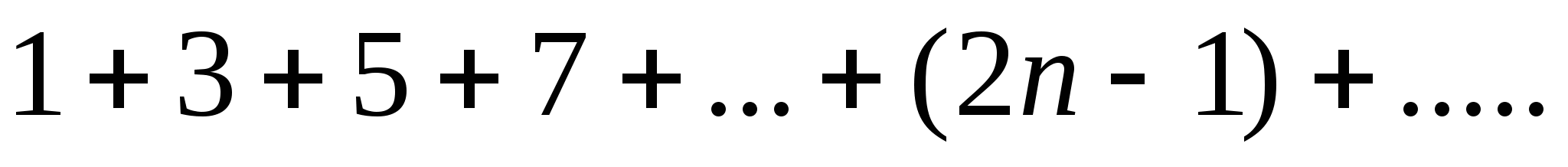
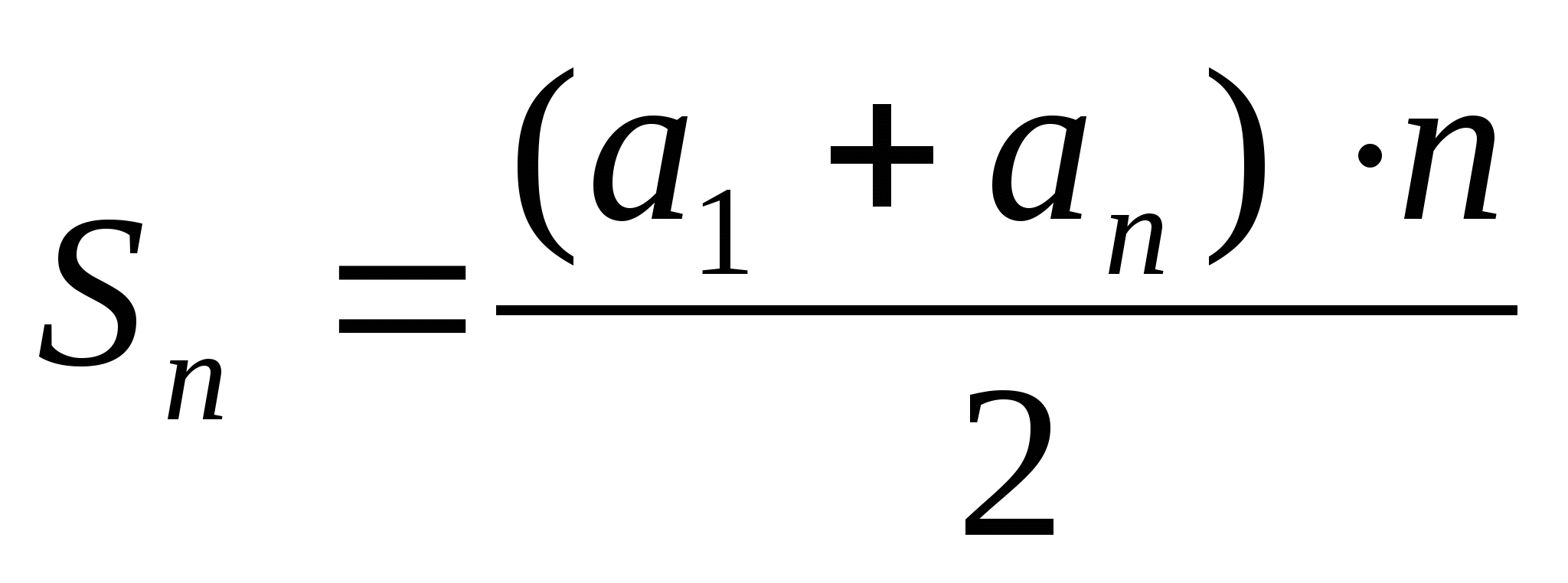 =
=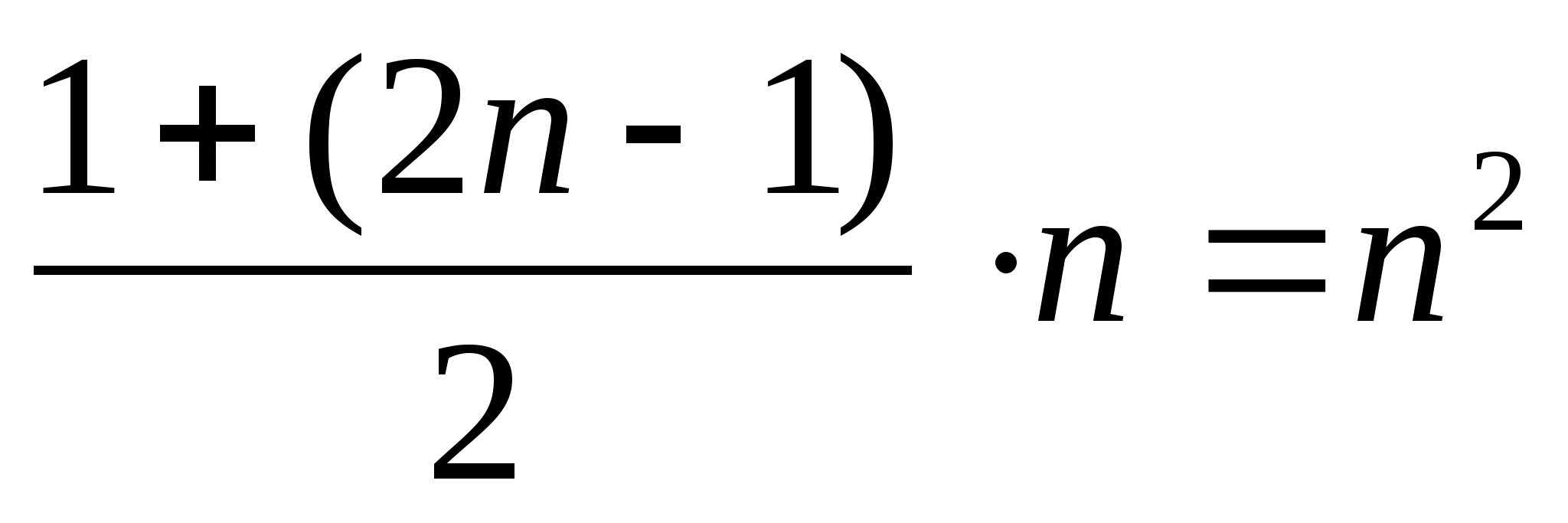 .
.
Утверждение доказано.
У: «Рассмотрим другой пример.
Последовательность задана формулой 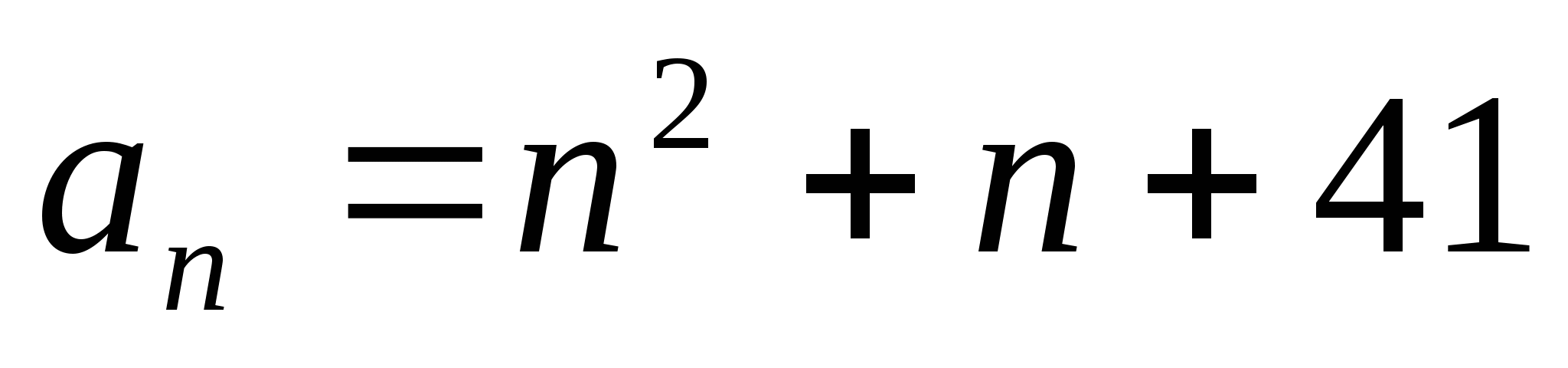 .
.
Выпишем её первые четыре члена:
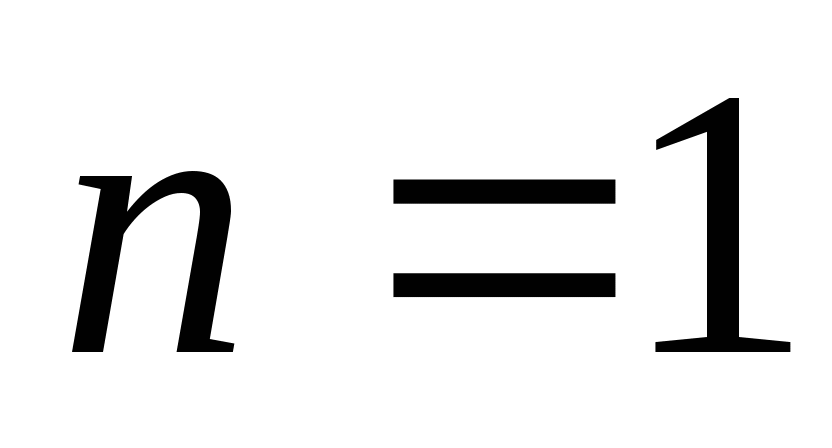
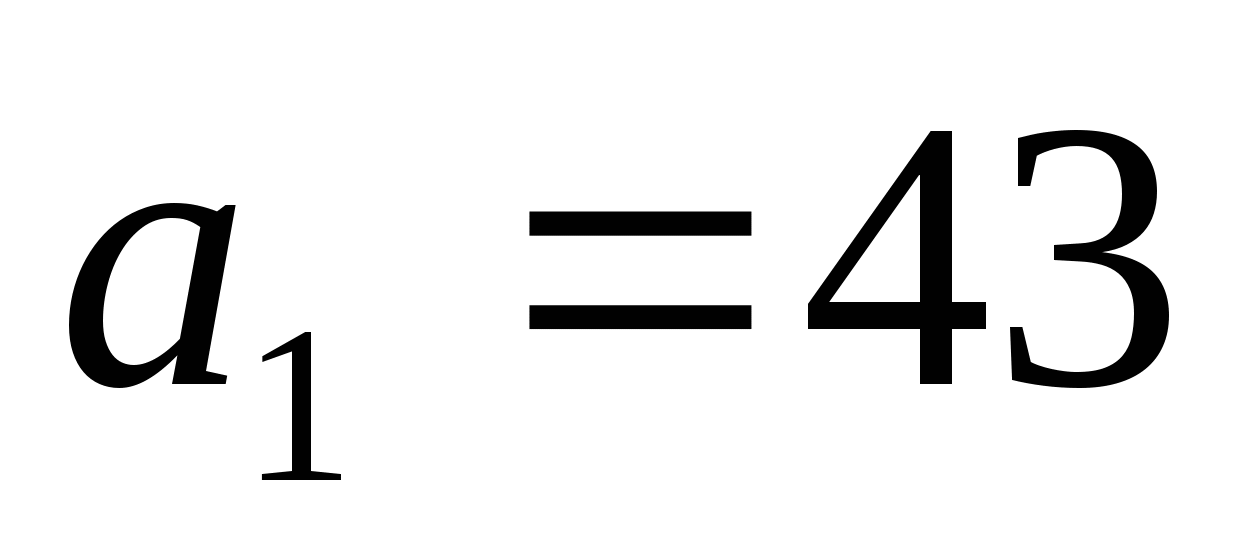 — простое
— простое
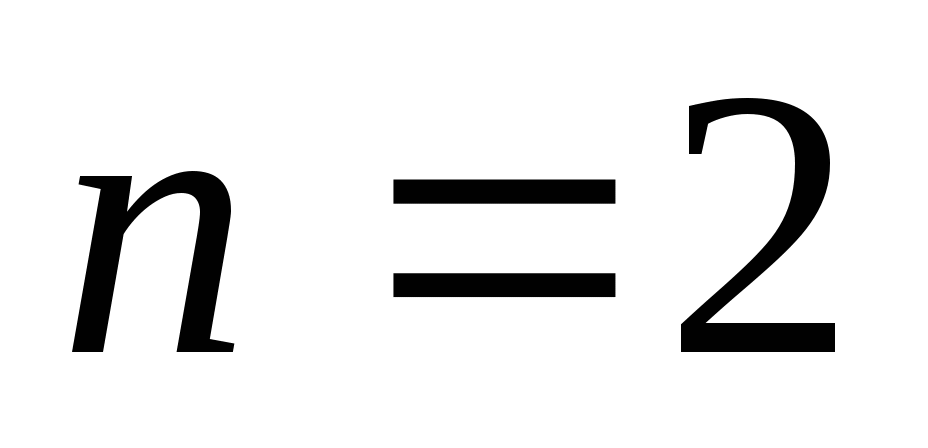
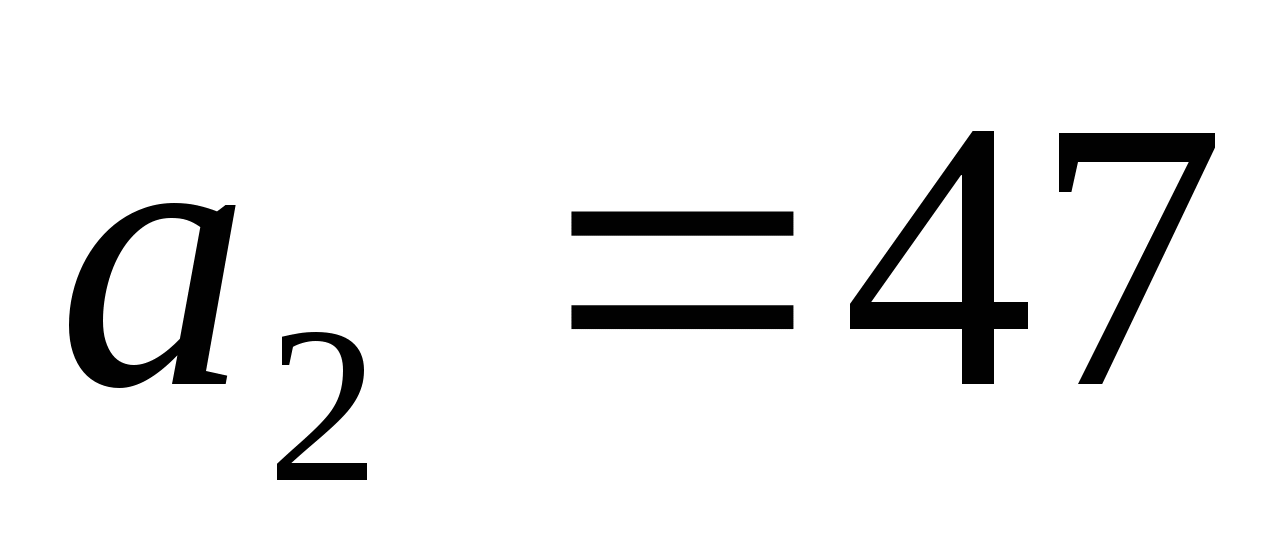 — простое
— простое
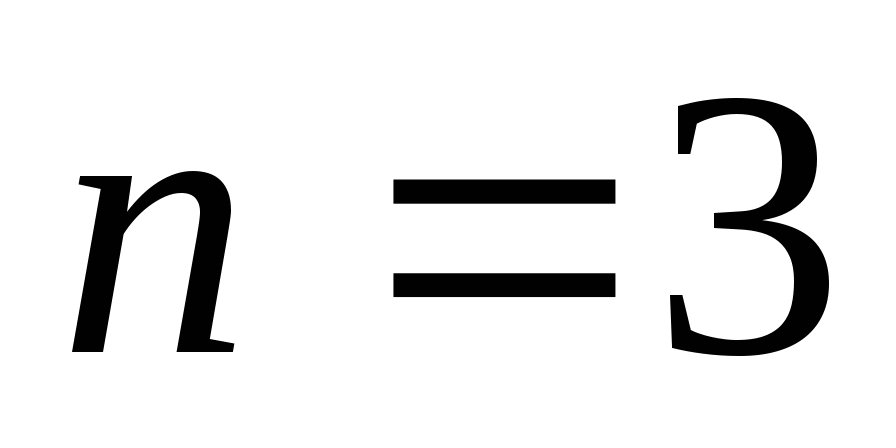
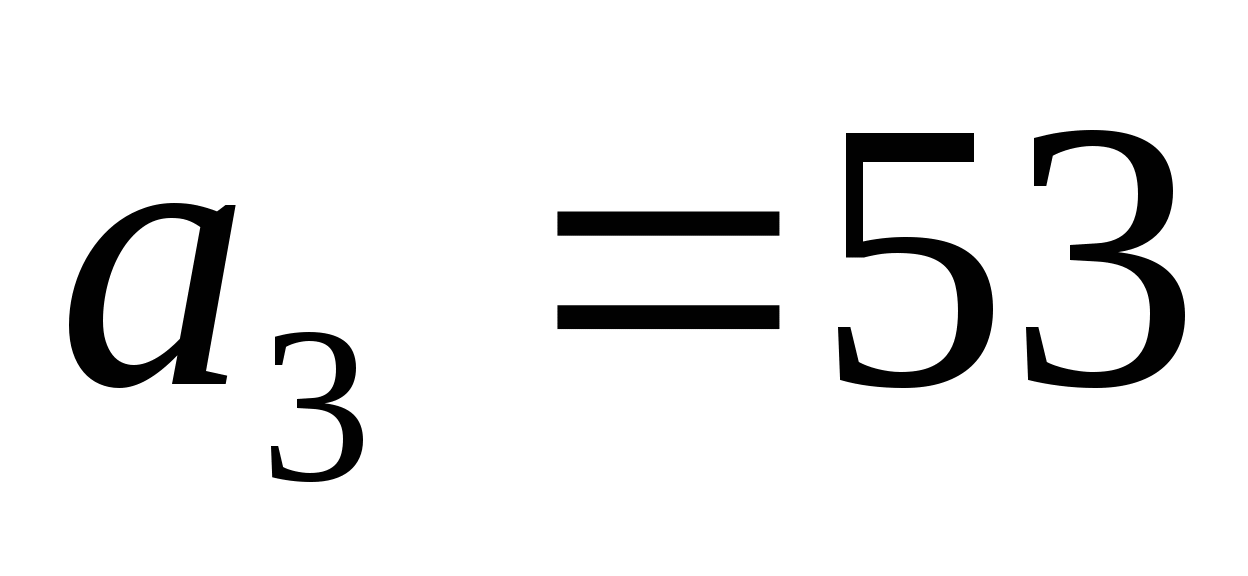 — простое
— простое
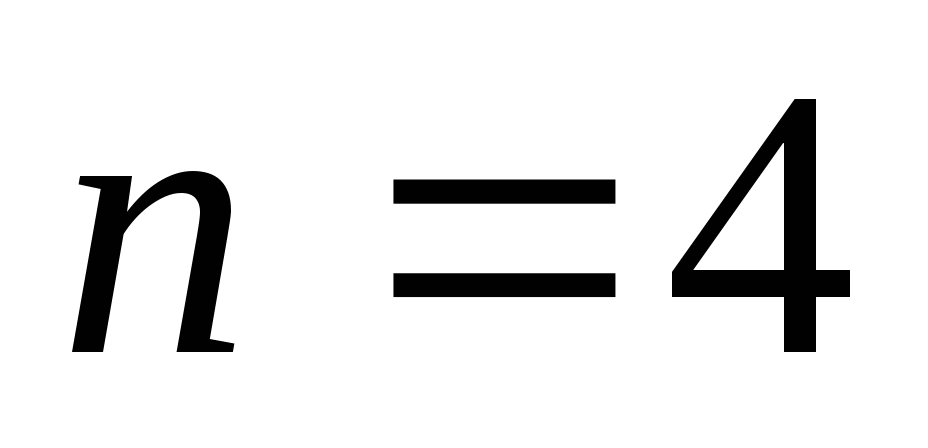
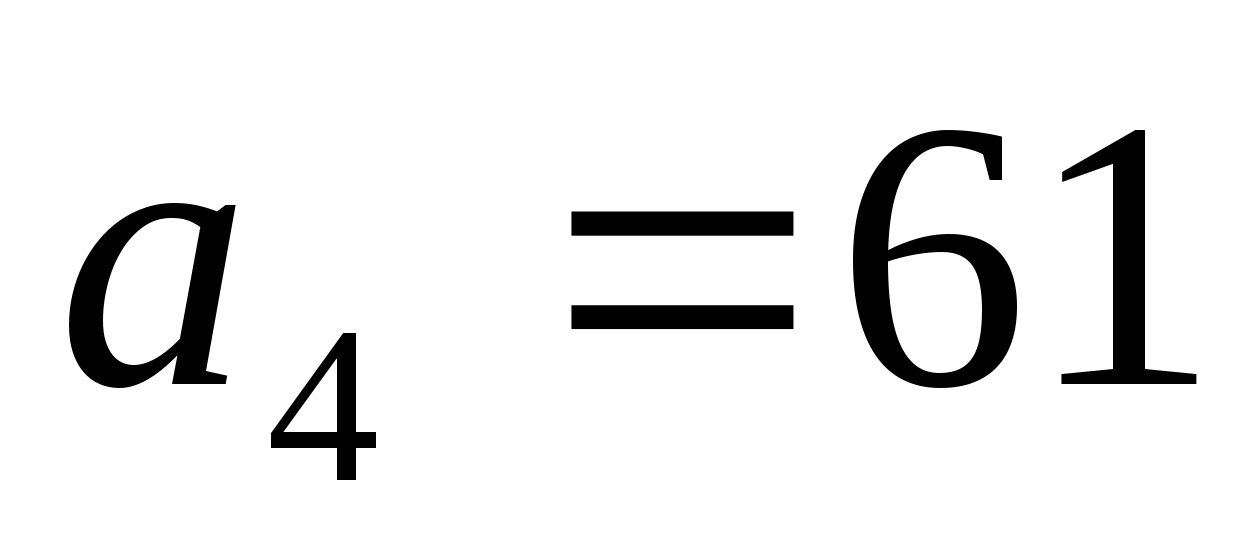 — простое
— простое
Какие получили числа?»
Д: «Простые»
У: «Какой вывод можно сделать?» (какую гипотезу можно выдвинуть?)
Д: « Вся последовательность 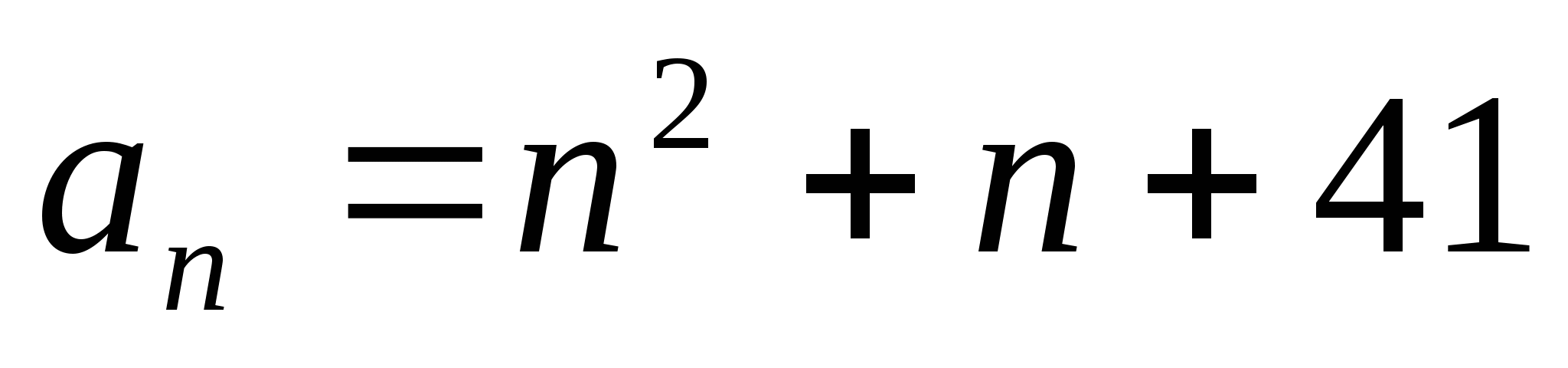 состоит из простых чисел»
состоит из простых чисел»
У: «Попробуем рассмотреть, например, 41-й член данной последовательности,  .
.
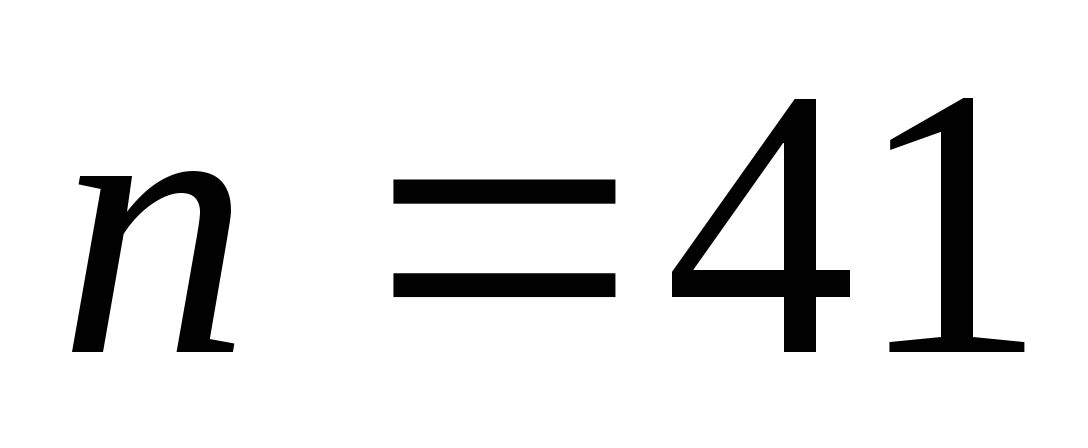
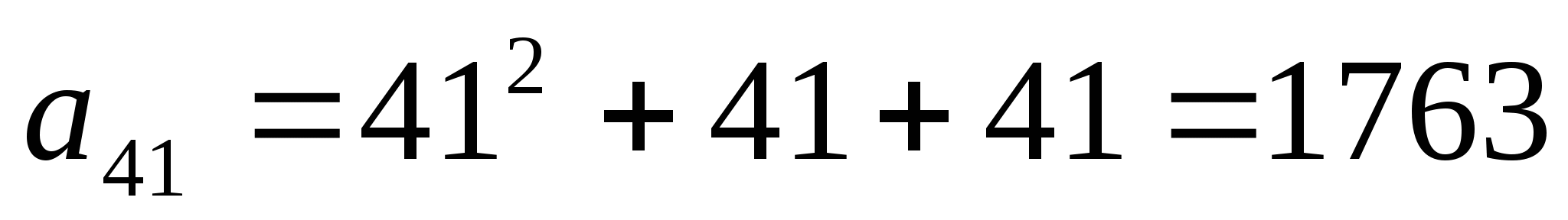 — составное.
— составное.
«Можем ли мы теперь сделать вывод о том, что все числа в данной последовательности простые?»
Д: «Нет»
У: «Нам нужно найти метод, который позволит доказывать утверждения для всех натуральных чисел. Какие будут идеи? Как узнать, справедливо ли это утверждение вообще?»
Дети высказывают предложения.
Пример 2.
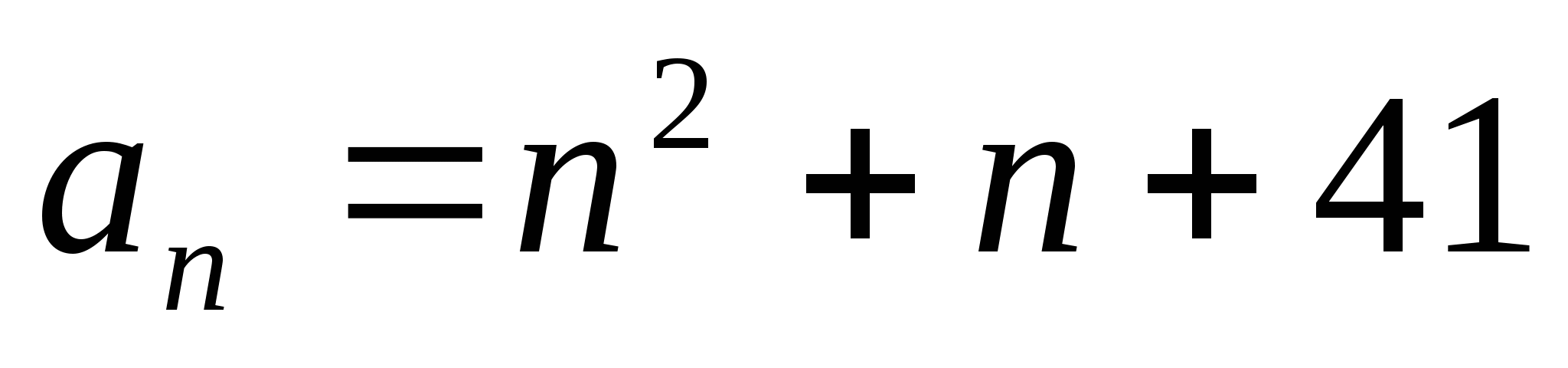
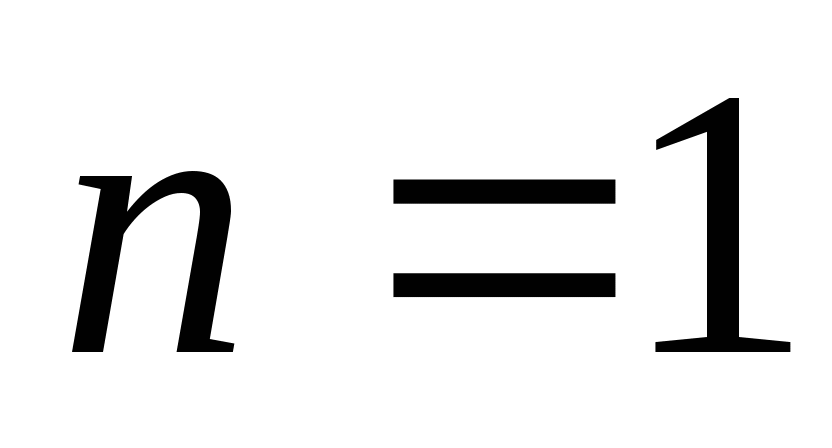
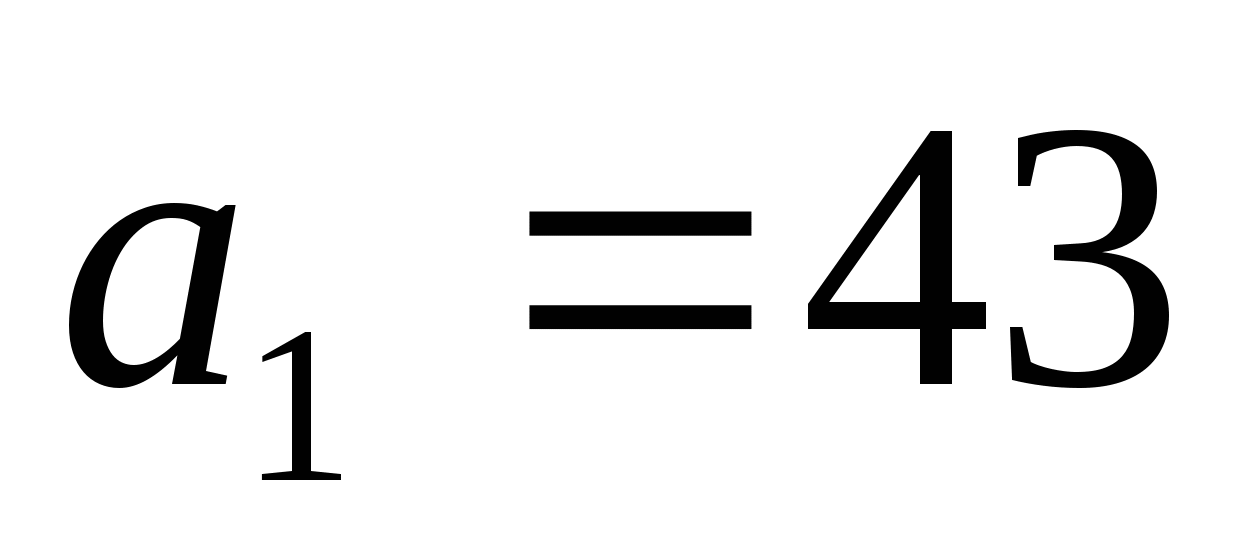 — простое
— простое
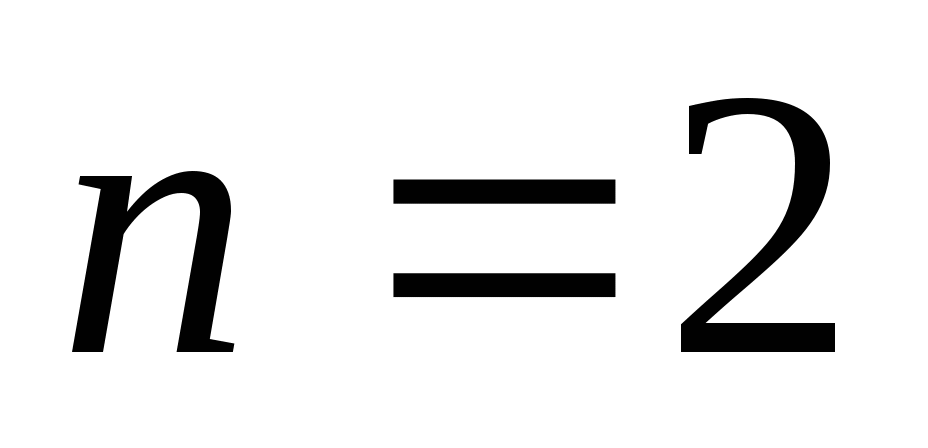
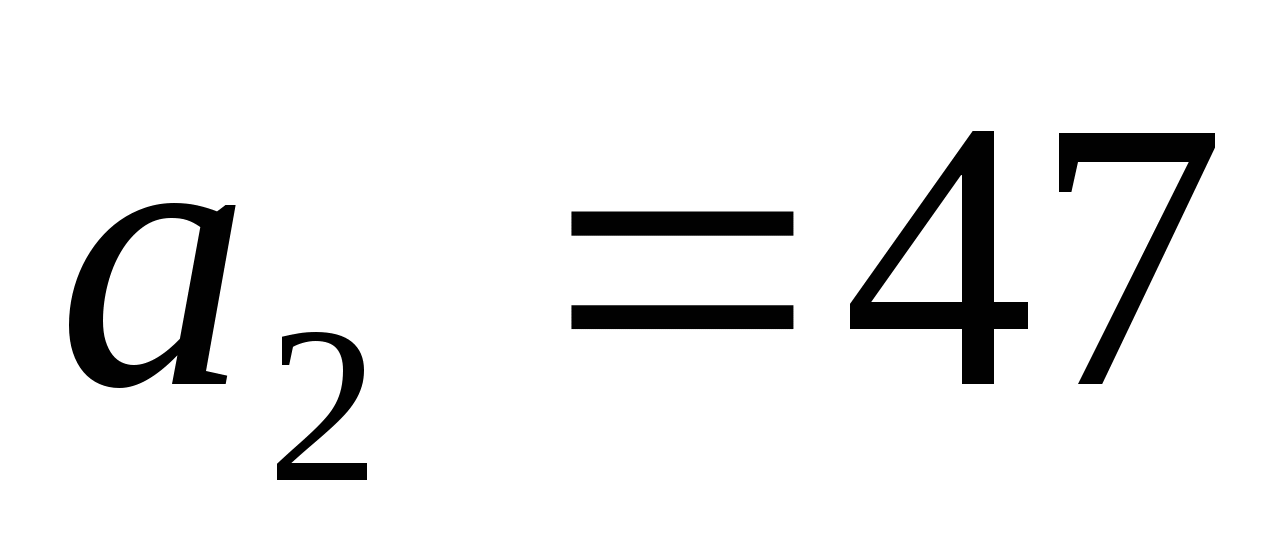 — простое
— простое
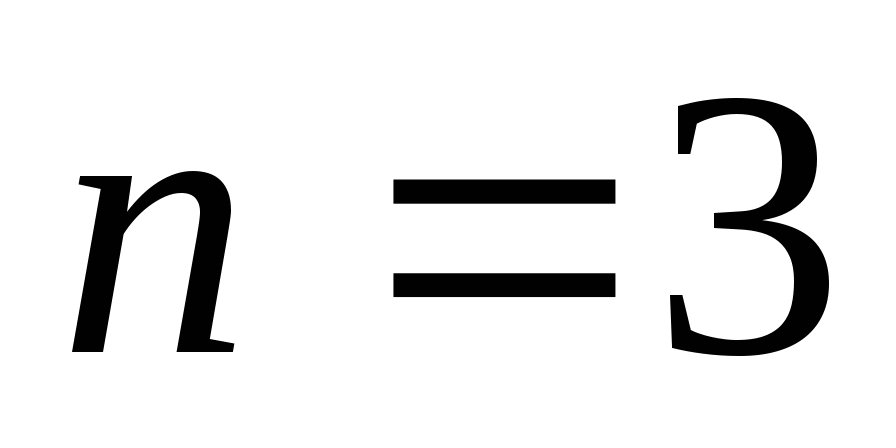
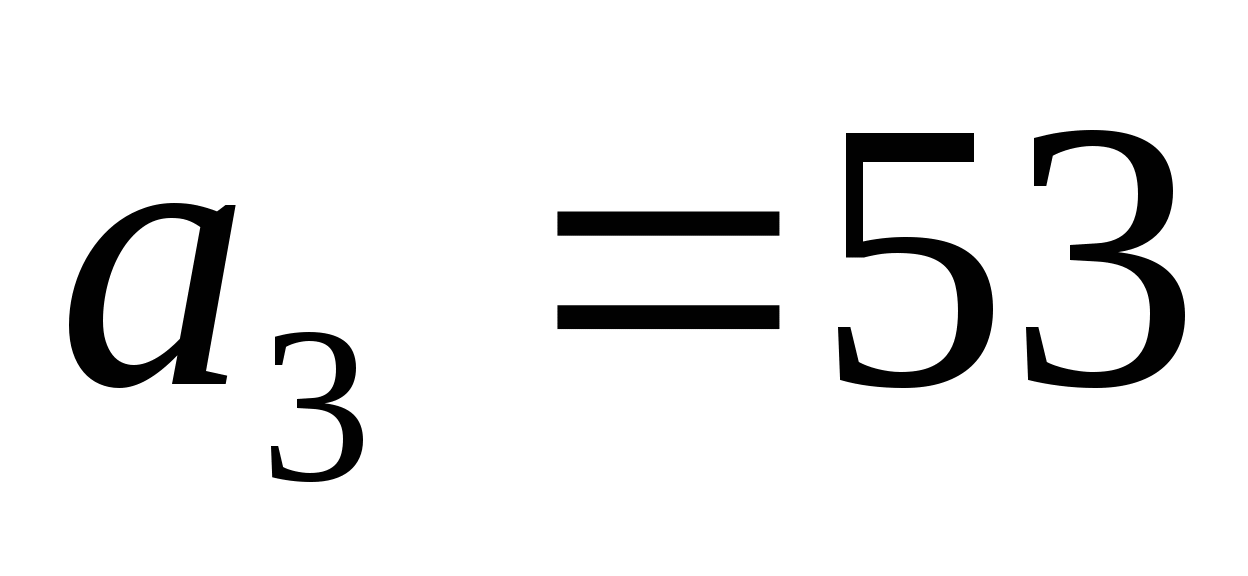 — простое
— простое
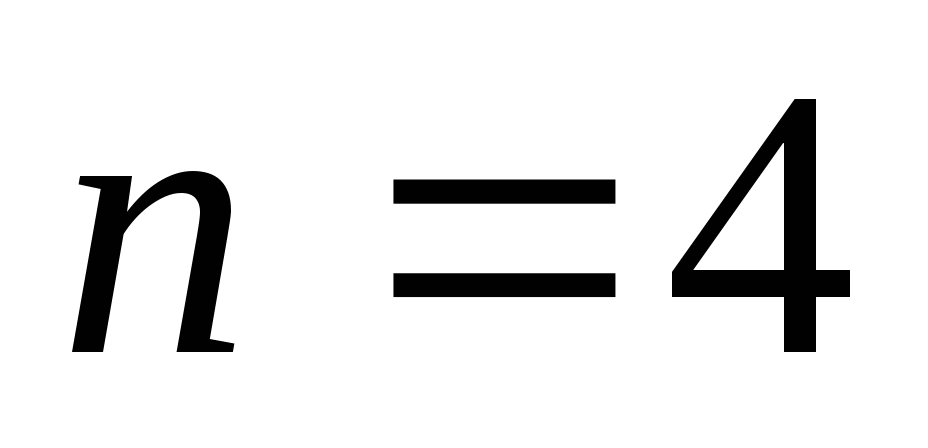
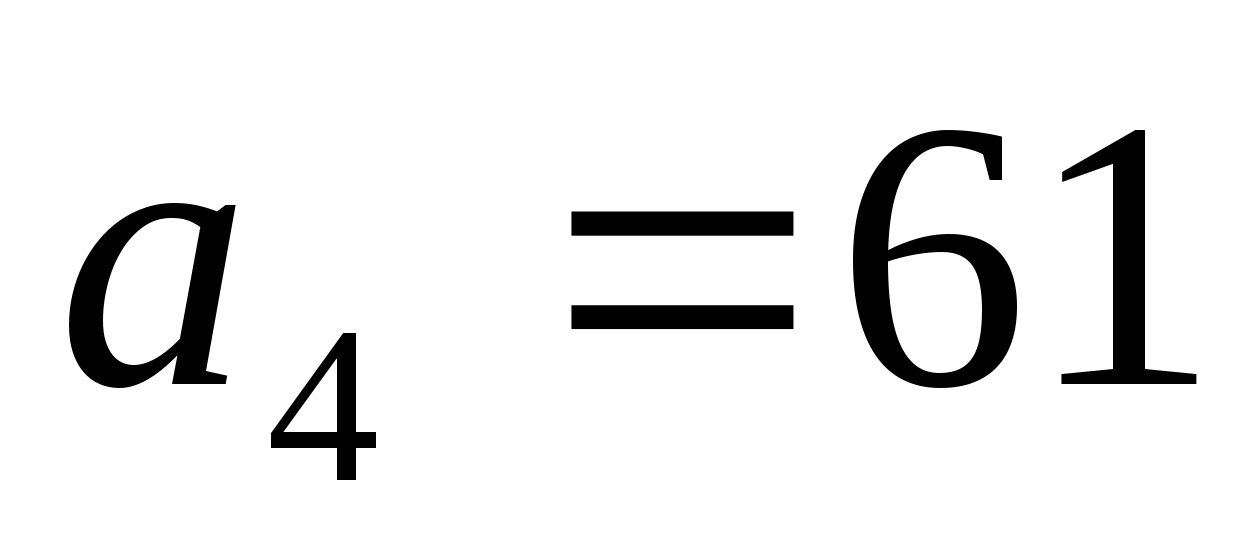 — простое
— простое
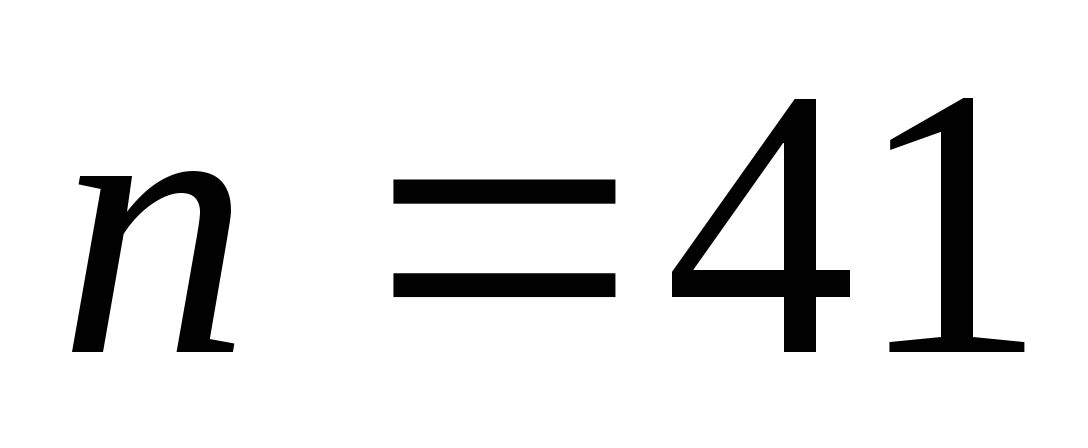
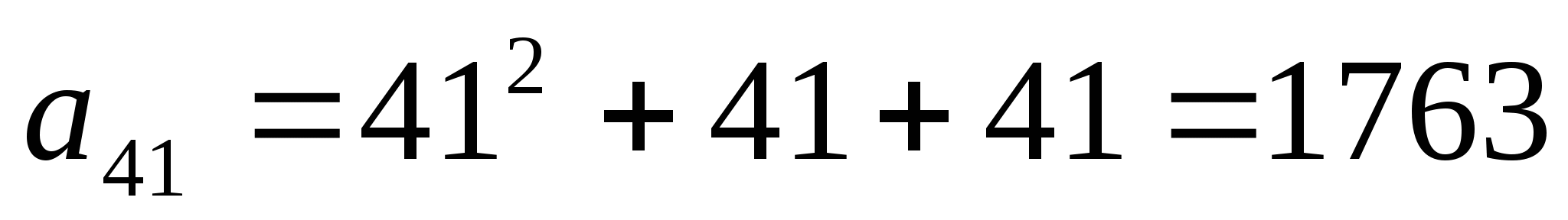 — составное.
— составное.
У: «Веря в непогрешимость индукции, ученые иногда допускали грубые ошибки. К середине семнадцатого столетия в математике накопилось немало ошибочных выводов. Стала сильною ощущаться потребность в научно обоснованном методе, который позволял бы делать общие выводы на основании рассмотрения нескольких частных случаев. И такой метод был разработан. Основная заслуга в этом принадлежит французским математикам Блезу Паскалю (1623—1662) и Рене Декарту(1596—1649), а также швейцарскому математику Якобу Бернулли (1654—1705).
Слайд № 8
Слайд № 9
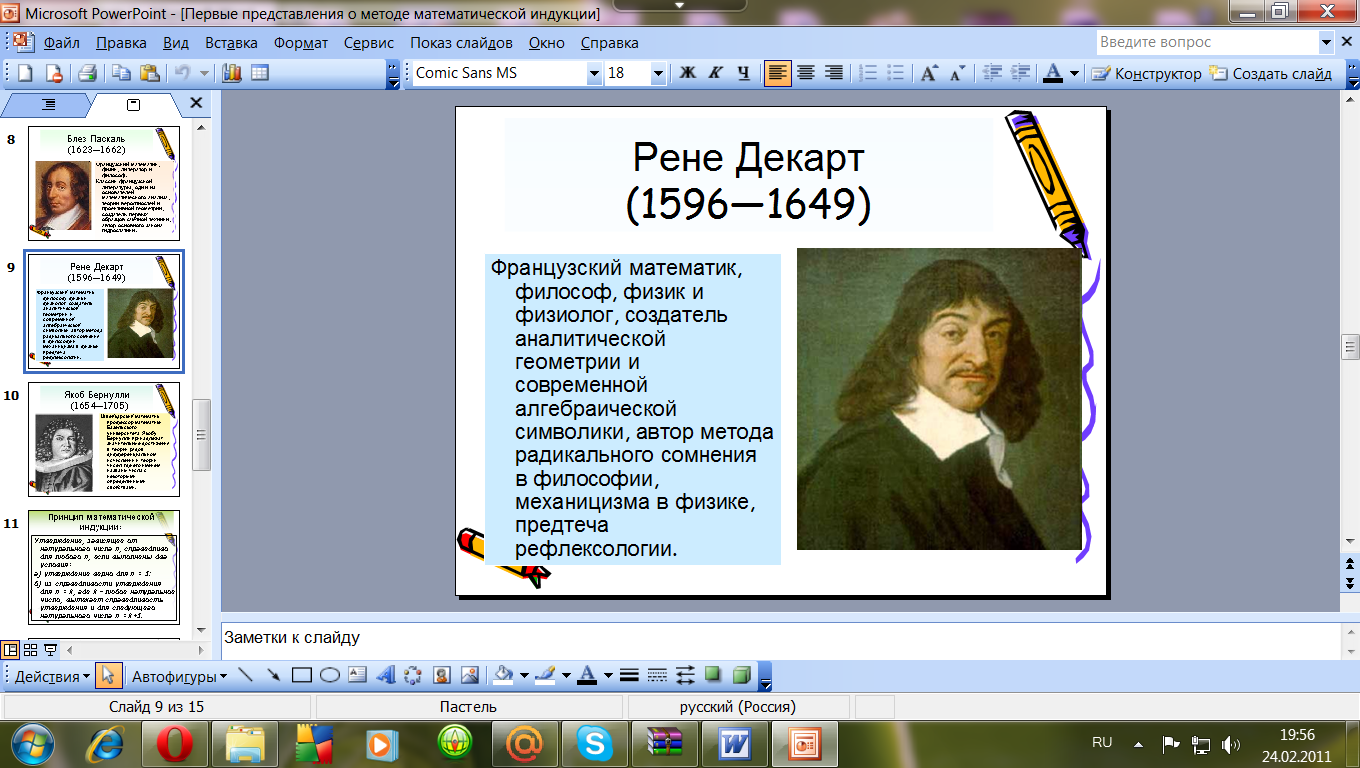
Слайд № 10
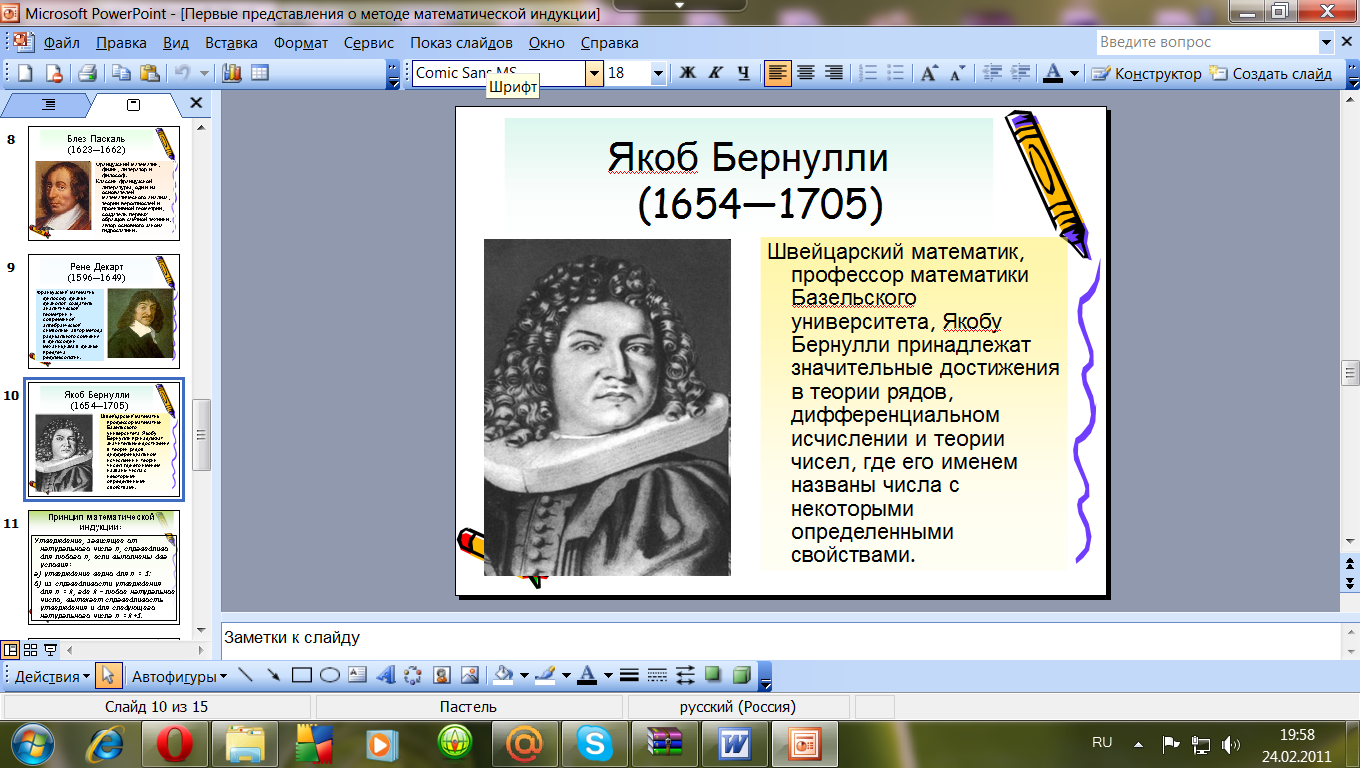
Этот метод называется «Метод математической индукции»
Суть его заключается в следующем:
(учитель показывает на предыдущем примере)
Проверяем истинность утверждения для 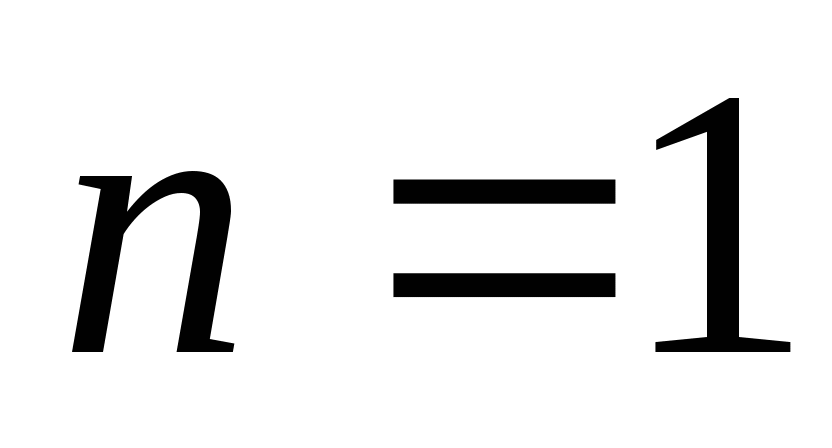 . Затем предполагаем, что утверждение истинно для некоторого натурального числа
. Затем предполагаем, что утверждение истинно для некоторого натурального числа 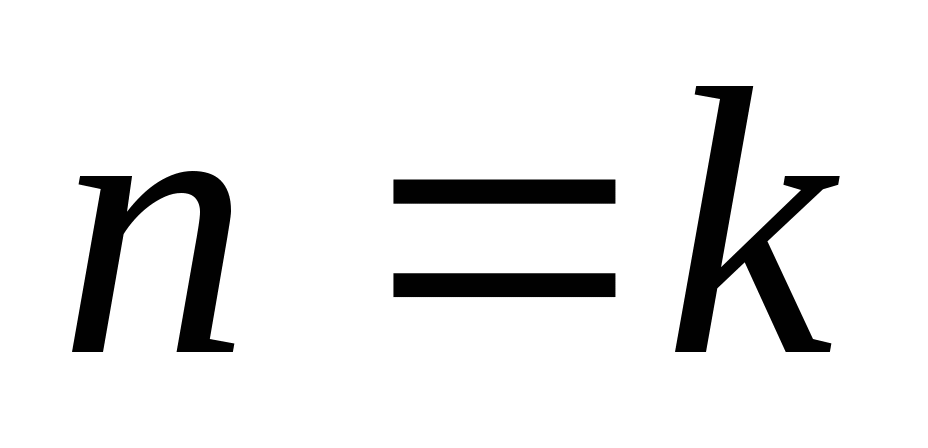 (опять возвращается к примеру).
(опять возвращается к примеру).
В нашем случае, предполагаем, что вся последовательность 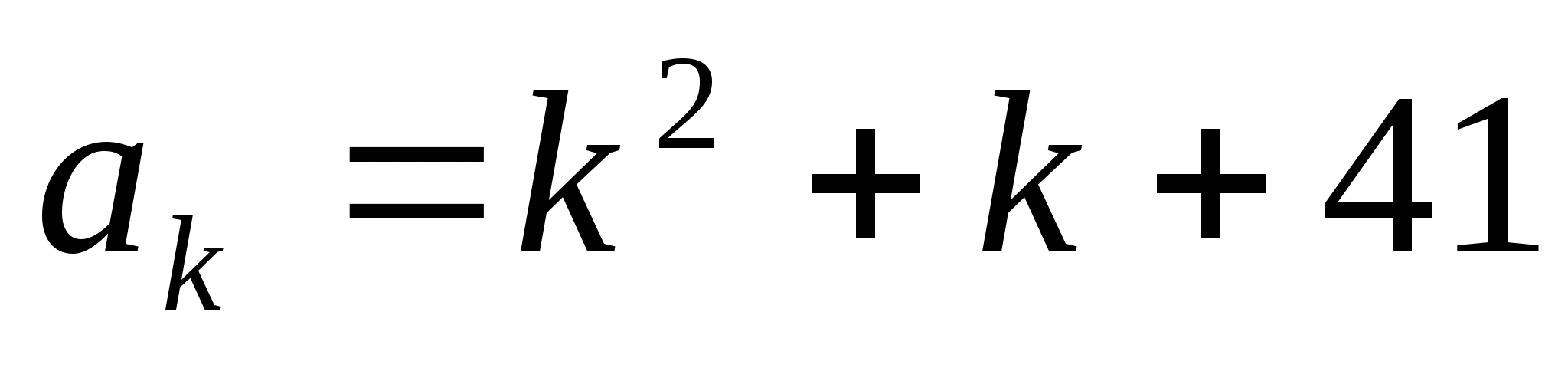 состоит из простых чисел, то есть утверждение верно для некоторого
состоит из простых чисел, то есть утверждение верно для некоторого  . Затем доказываем, что утверждение верно и для следующего натурального числа
. Затем доказываем, что утверждение верно и для следующего натурального числа 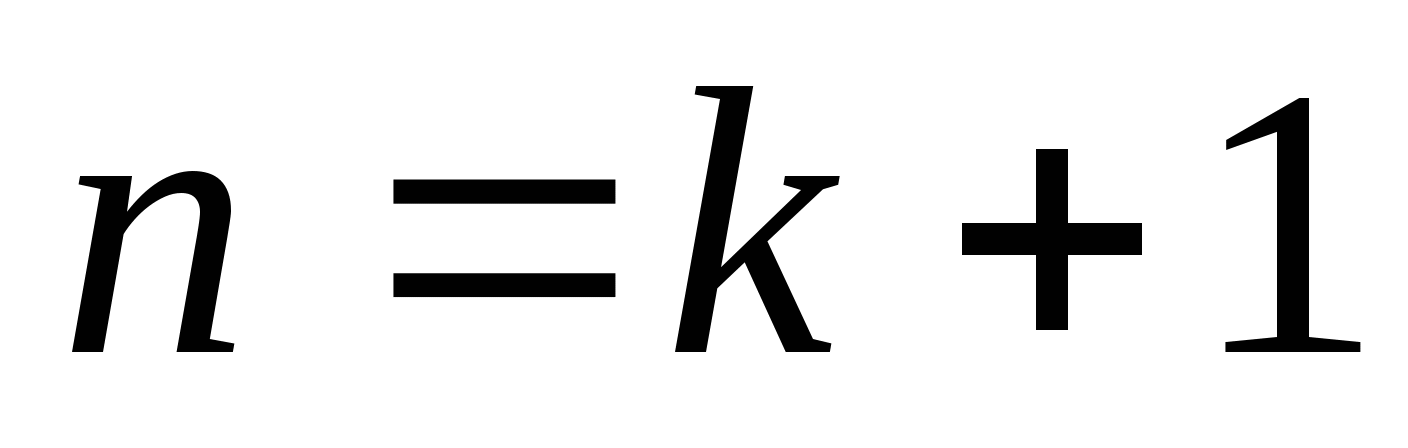 , то есть, что вся последовательность
, то есть, что вся последовательность  состоит из простых чисел. Доказываем это утверждение, используя предположение.
состоит из простых чисел. Доказываем это утверждение, используя предположение.
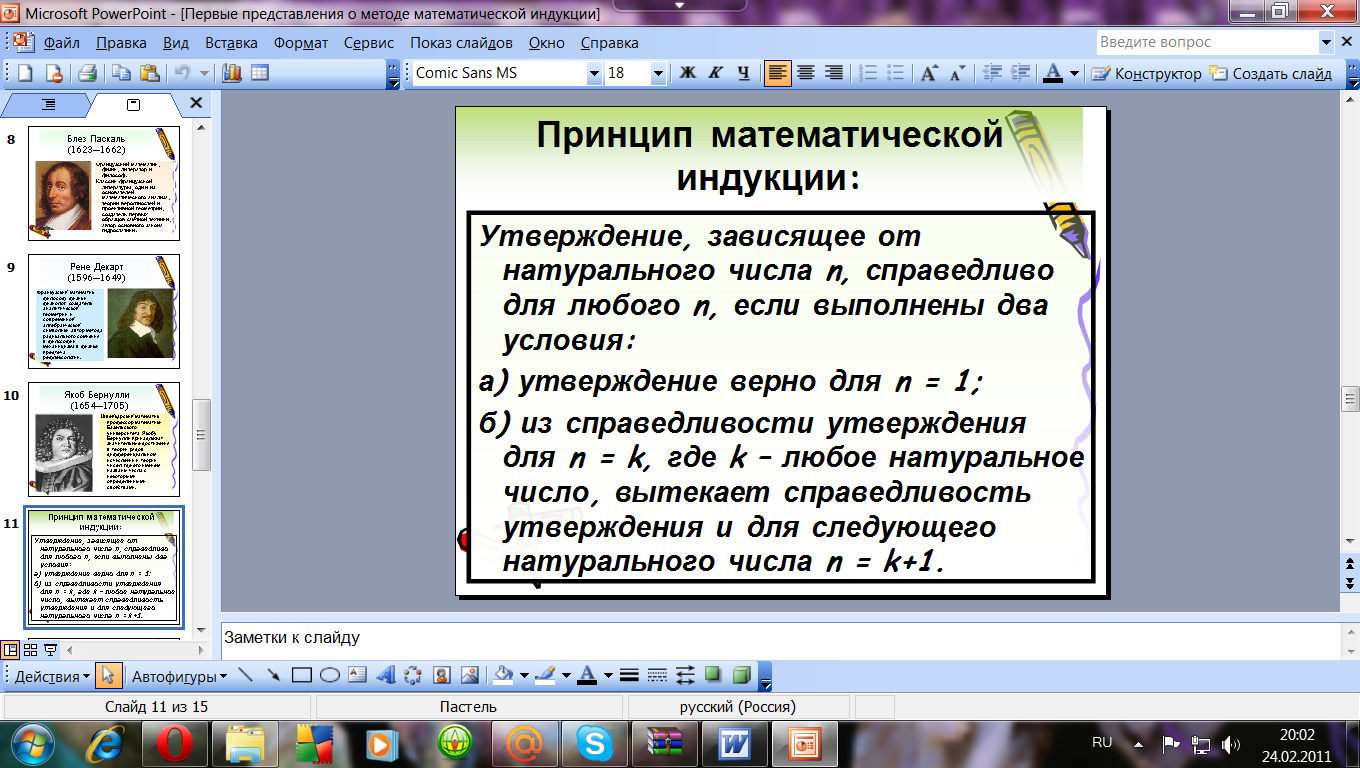
Итак, принцип математической индукции звучит так:
Утверждение, зависящее от натурального числа n, справедливо для любого n, если выполнены два условия:
а) утверждение верно для n = 1;
б) из справедливости утверждения для n = k, где k – любое натуральное число, вытекает справедливость утверждения и для следующего натурального числа n = k+1»
У: «Проверка истинности утверждения Т(1) называется началом индукции, предположение об истинности Т(k) называют индуктивным предположением, а доказательство истинности Т(k+1) на основе истинности Т(k) называют шагом индукции»
Метод математической индукции.
пусть верно при 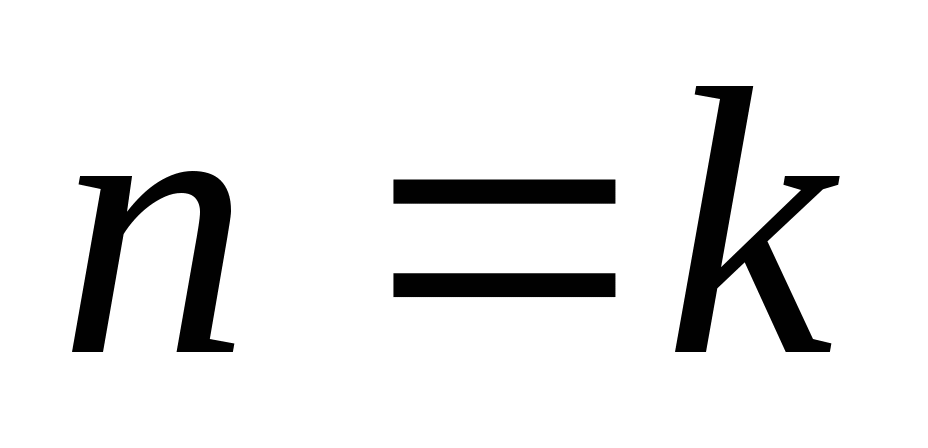 , докажем, что
, докажем, что 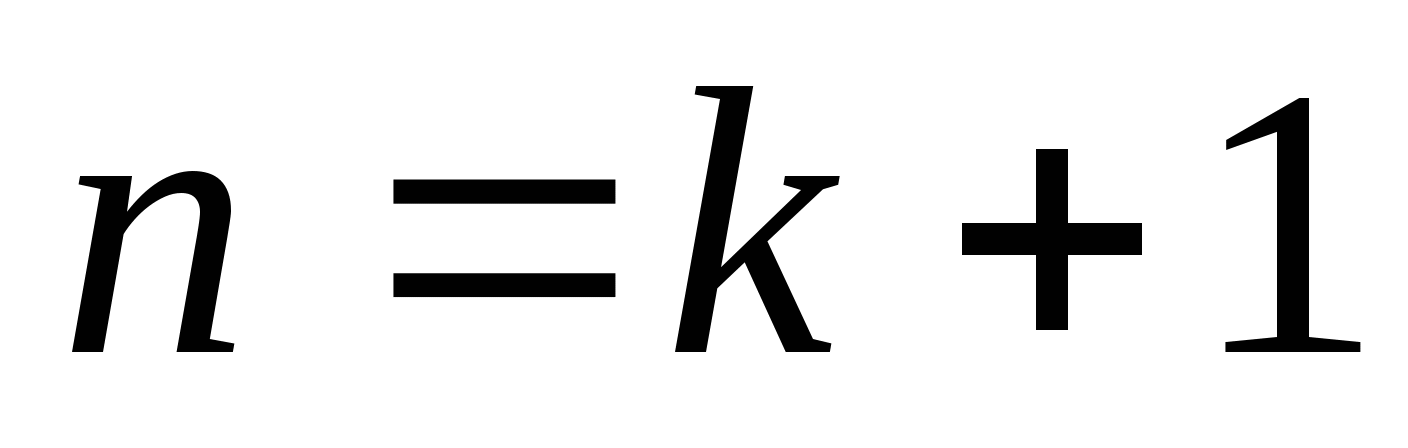
1) 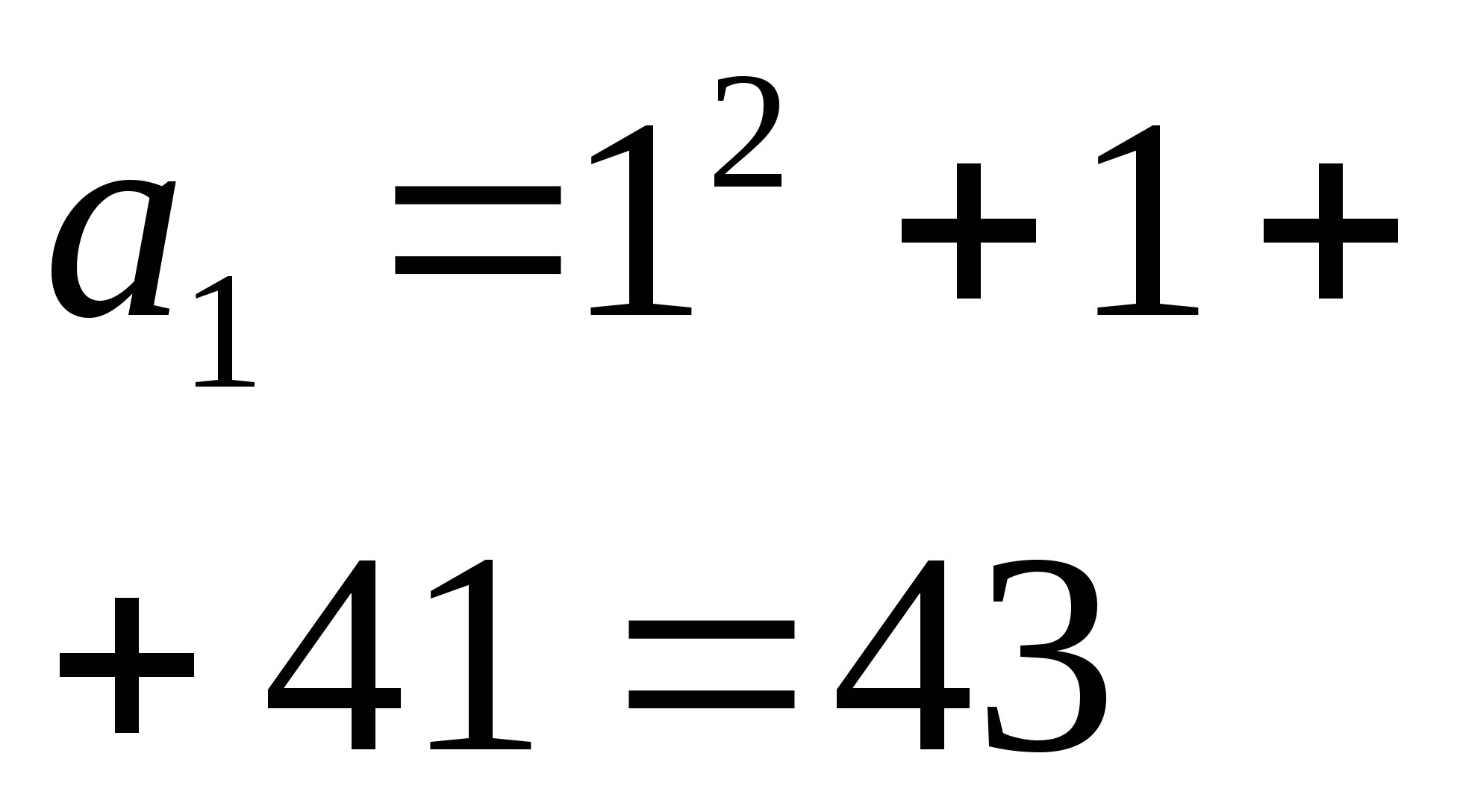
2) 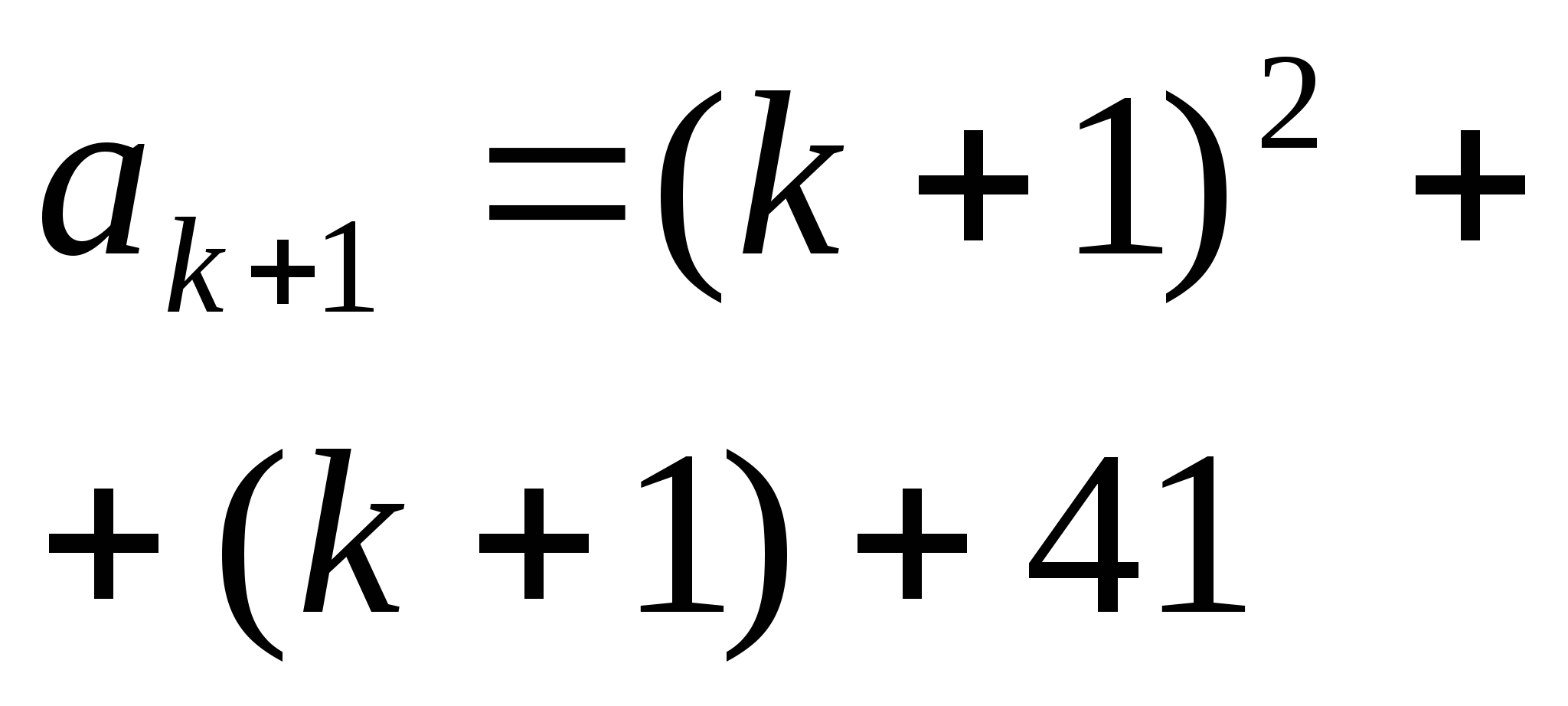
Слайд № 11
Слайд № 12
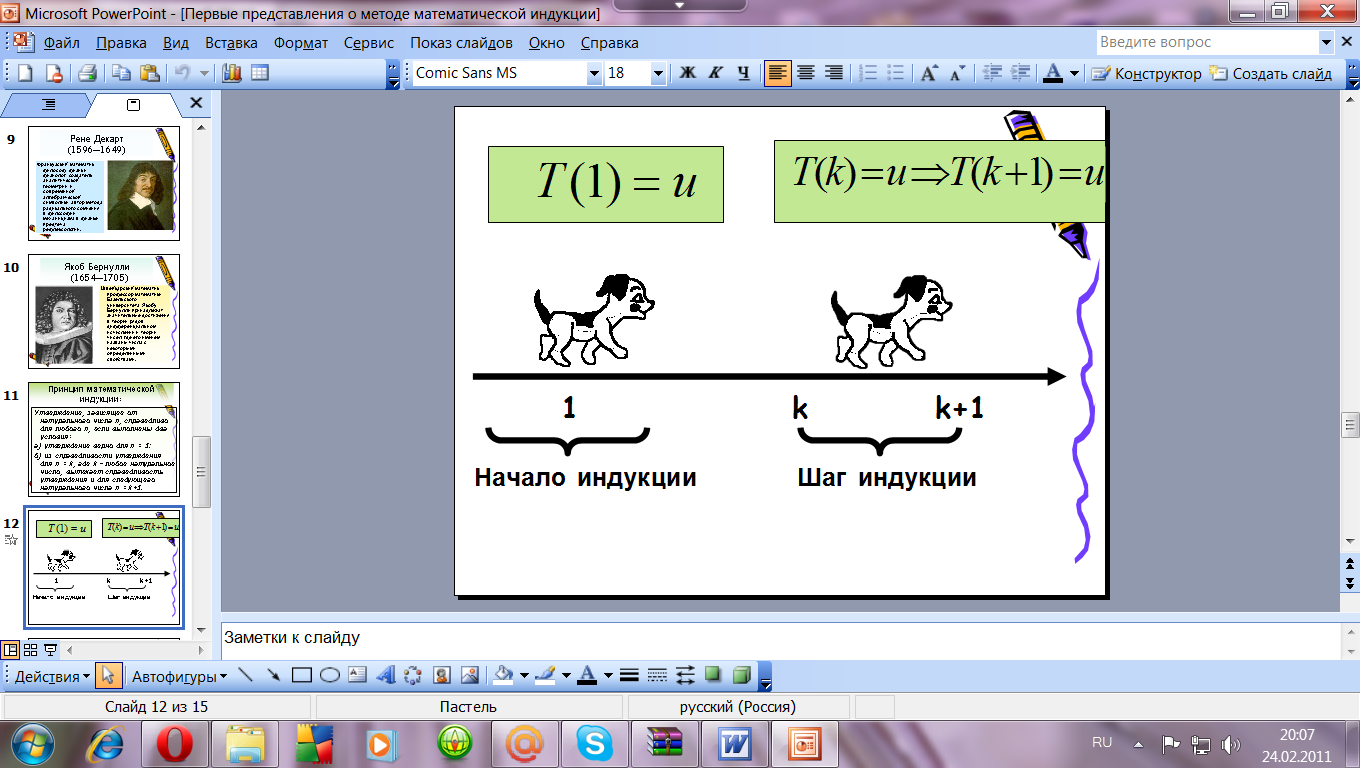
Слайд № 13
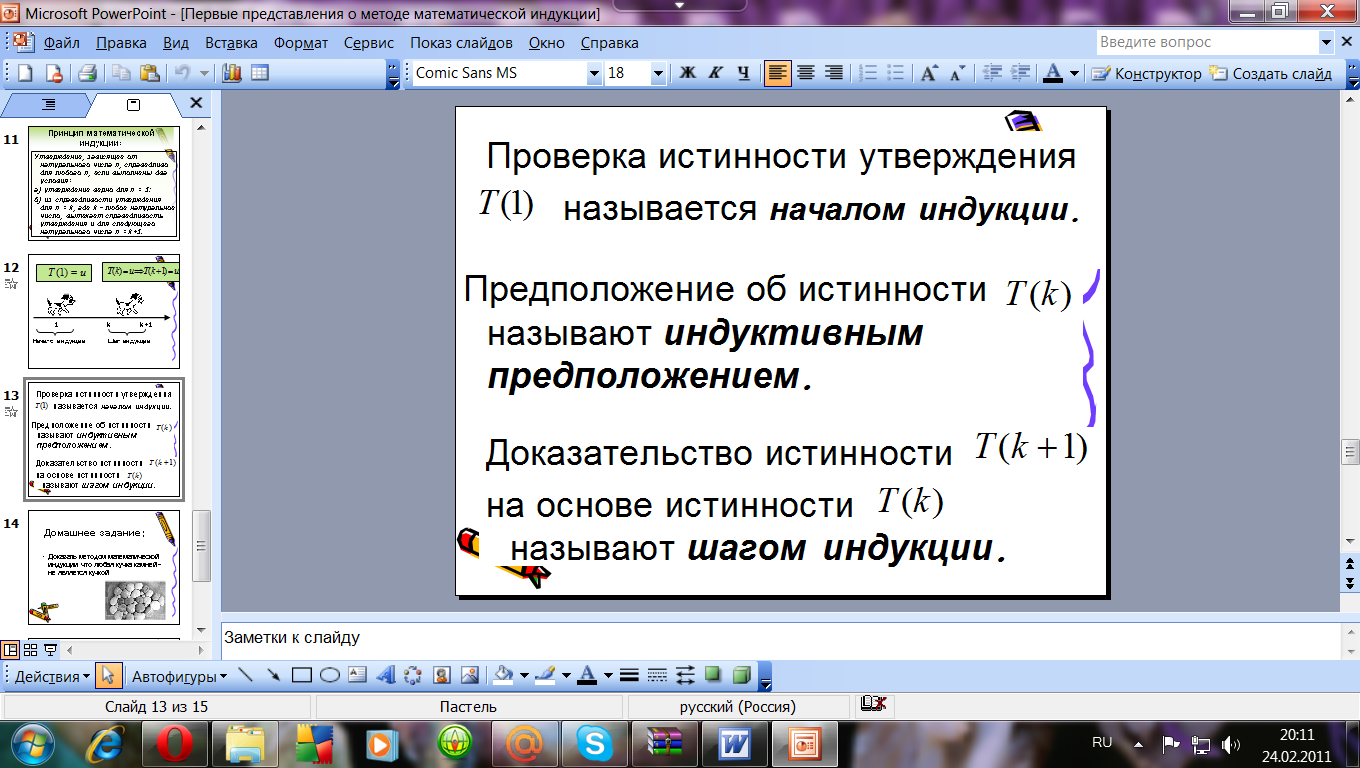
5.) Закрепление.
У: «Теперь рассмотрим на конкретном примере применение данного метода.
Вернемся к примеру, который мы с вами сегодня доказали с помощью формулы суммы 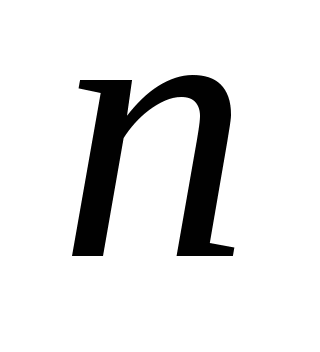 членов геометрической прогрессии.
членов геометрической прогрессии.
Докажите, что сумма первых 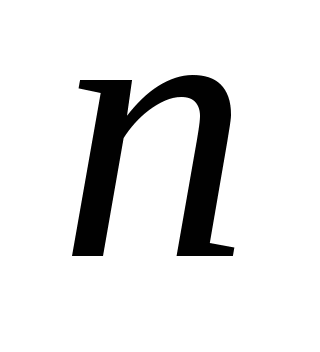 нечётных натуральных чисел равна
нечётных натуральных чисел равна 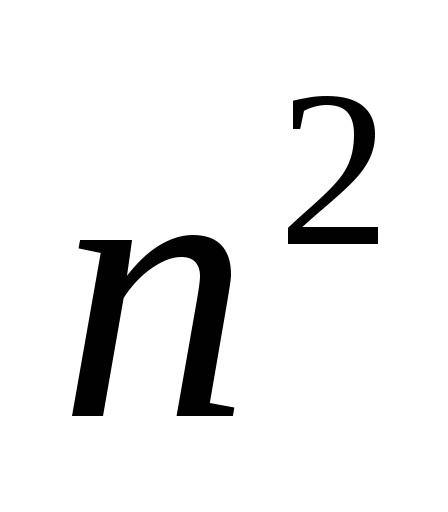 »
»
Доказательство.
 . Проверим, что
. Проверим, что  . Очевидно, это равенство верно;
. Очевидно, это равенство верно;пусть для некоторого
 ,
,  , докажем, что оно верно для некоторого
, докажем, что оно верно для некоторого  то есть
то есть — верно.
— верно.
Имеем: 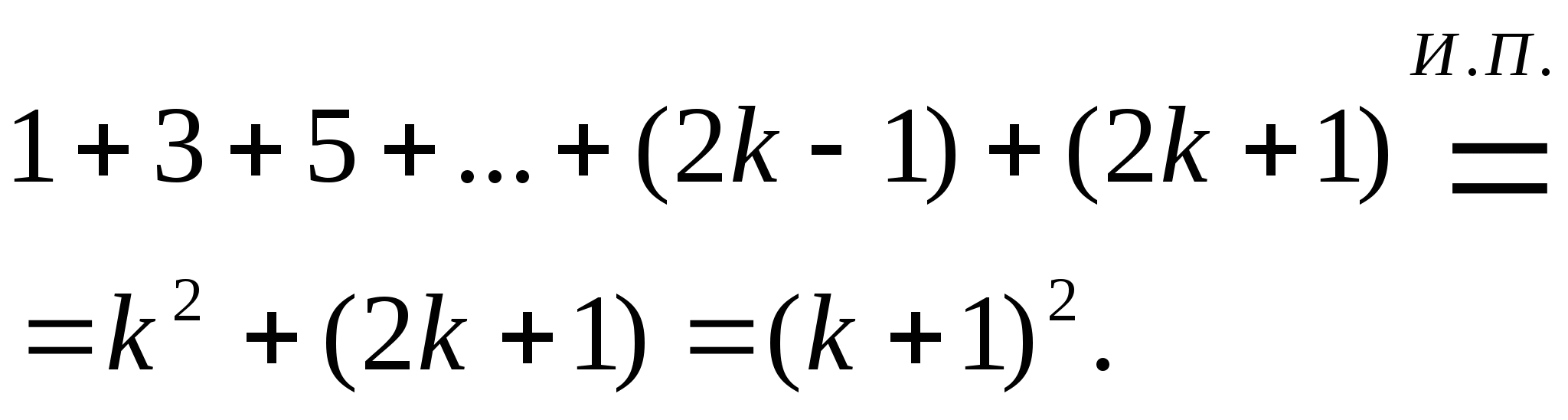
В силу метода математической индукции, утверждение верно для всех 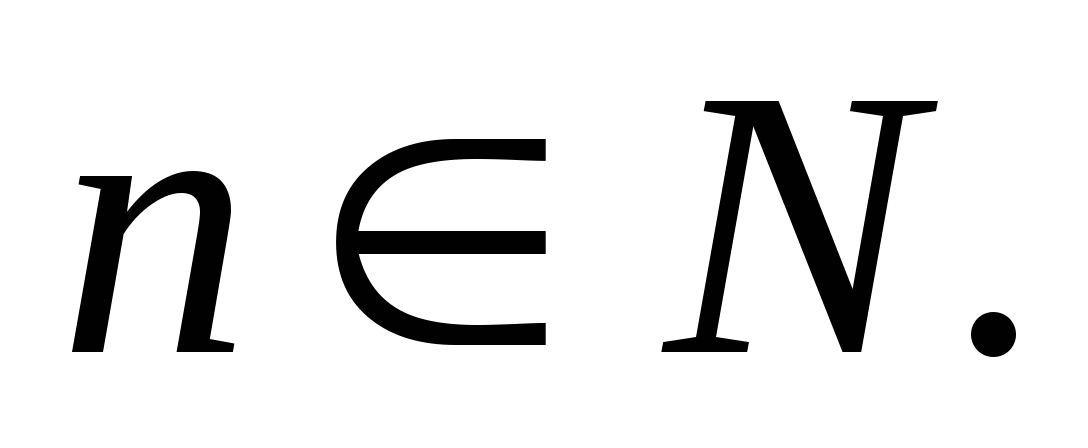
Задание 1.
Докажите, что сумма первых 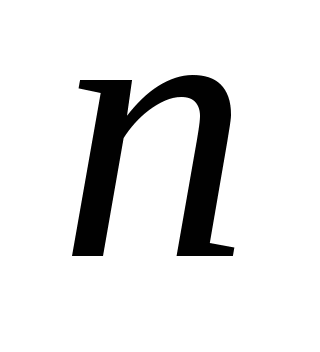 нечётных натуральных чисел равна
нечётных натуральных чисел равна 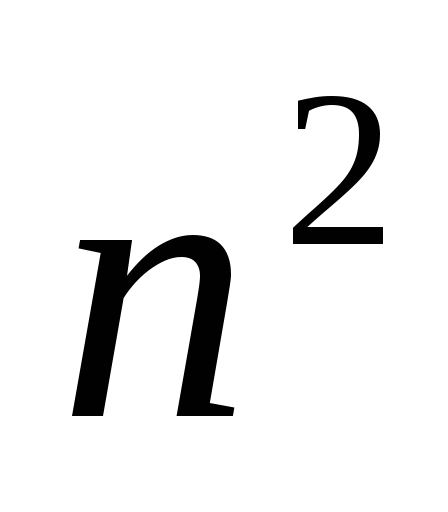 .
.
Доказательство.
 . Проверим, что
. Проверим, что  . Очевидно, это равенство верно;
. Очевидно, это равенство верно;пусть для некоторого
 ,
,  , докажем, что оно верно для некоторого
, докажем, что оно верно для некоторого  то есть
то есть — верно.
— верно.
Имеем: 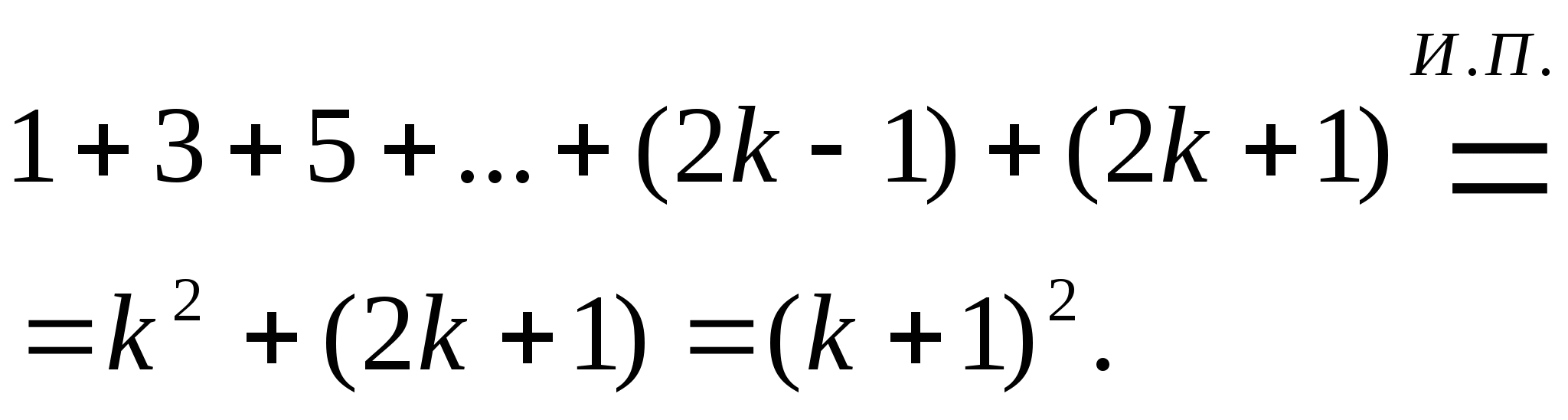
В силу метода математической индукции, утверждение верно для всех 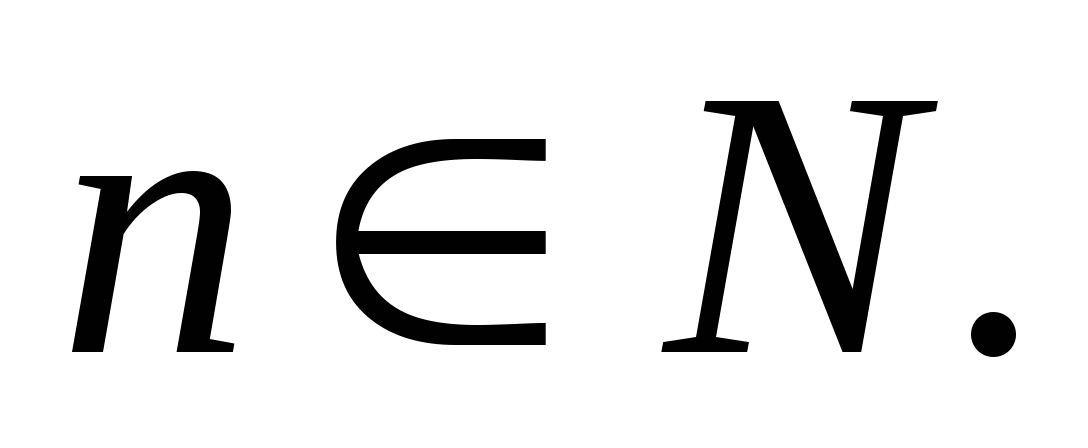
Итог урока.
У: «Чем мы сегодня занимались на уроке?»
Д: «Мы изучали метод математической индукции, решили несколько примеров с помощью этого метода»
Запись домашнего задания.
У: «Домашнее задание:
Доказать методом математической индукции, что любая кучка камней – не является кучкой»
Слайд № 14
infourok.ru
Урок в 10 классе по теме «Метод математической индукции»
Урок по теме: «метод математической индукции»
Тип: усвоения новых знаний.
Организация: дети сидят как обычно.
Цель: Организовать деятельность учащихся по обеспечению максимального усвоения темы. учащихся.
Задачи урока:
Образовательная: сформировать умение решать задачи, используя метод математической индукции.
Развивающая: развитие мышления учащихся.
Воспитательная: воспитание дисциплинированности, собранности требовательности к себе при организации рабочего труда учащегося, отношения к другим людям через такие качества, как терпимость, деликатность и доброжелательность при анализе ответов товарищей по классу, чувства коллективизма и взаимопомощи.
Этапы урока:
1. Организационный этап
2. Этап подготовки к активному сознательному усвоению знаний
3. Организация деятельности по получению знаний.
4. Этап закрепления знаний
5. Контроль и коррекция знаний
6. Рефлексия.
Ход урока
1этап.Организационный этап – 2 мин.
Задачи:
• определение целей и задач урока (предварительная организация внимания учащихся, которая способствует созданию необходимого делового и психологического контакта между учителем и учащимися)
• подготовка учащихся к продуктивной работе на уроке
• развитие внимания к действиям учителя
• подготовка учащихся к общению на уроке.
• воспитание дисциплинированности, собранности требовательности к себе при организации рабочего труда учащегося.
Учитель: Здравствуйте дети, наш урок сегодня уроке мы познакомимся с методом математической индукции, прежде всего быть внимательным и активным, помните, что все мы учимся и можем ошибаться, мы помогаем друг другу, принимаем помощь друг друга.
2.Этап подготовки к активному сознательному усвоению знаний (этап актуализации знаний) — 5 мин.
Задачи:
• мотивирование учащихся на самостоятельную продуктивную деятельность
• актуализация опорных знаний и умений сравнивать и на основе этого делать самостоятельные выводы.
• воспитание отношения к другим людям через такие качества, как терпимость, деликатность и доброжелательность при анализе ответов товарищей по классу.
Учитель. Рассмотрим пример
ПРИМЕР. Найти формулу для вычисления суммы k первых нечетных чисел.
1+3+5+7+….Предложите свои способы нахождения этой суммы
Рассмотрим рисунок
Сделайте вывод…..
Итак, эта сумма равна 16 , если k=4
3этап. Организация деятельности по получению знаний-10 мин
Задачи:
• Организация деятельности учащимся по применению знаний при решении задач,
• развитие мышления учащихся при закреплении умений сравнивать и обобщать знания,
• развитие эмоциональной сферы во время работы, воспитание дисциплинированности, собранности требовательности к себе.
• воспитание отношения к другим людям через такие качества, как терпимость, деликатность и доброжелательность при анализе ответов товарищей по классу.
Учитель. Попробуем подсчитать такую сумму для некоторых значений kработает на доске)
k=1; 1=1=12;
k=2; 1+3=4=22;
k=3; 1+3+5=9=32;
k=4; 1+3+5+7=16=42;
Таким образом, 1+3…+(2n-1)+(2n+1)=(n+1)2.
Получим:
1+3+…+(2n-1)+(2n+1)=n2+(2n+1)=(n+1)2, ч.т.д.
В математике на основе частных утверждений делают некоторые предположения о справедливости какого-либо общего утверждения. Переход от частных утверждений к общим называют индукцией.
Знаменитый математик 17 века Пьер Ферма высказал предположение, что простыми являются все числа вида 22n+1. Он показал, что первые пять числе 220+1=3, 221+1=5,222+1=17, 223+1=257, 224+1=65537 – простые, и рассуждая по индукциирешил, что для всех n числа вида 22n+1- простые. Однако это предположение оказалось не верным, т.к. в 18 веке Л.Эйлер нашёл, что 225+1=4294967297=641∙4700417 – составное число.
Итак, индукция не является методом доказательства, а лишь помогает сформулировать неизвестный результат в виде некоторой гипотезы, справедливость которой потом надо доказать.
Идея последовательного перехода от натурального числа n к следующему за ним числу n+1 осуществляется в строгой форме в одном из самых важных методов математических доказательств, который называется методом математической индукции.
Запишем в тетрадях
В основе этого метода лежит принцип математической индукции, заключающийся в следующем: (запись на доске)
Утверждения P(n) справедливо для всякого натурального n, если:
1)Оно справедливо для n=1;
2)Из справедливости утверждения для какого-либо произвольного натурального n=k следует его справедливость для n=k+1.
4 этап. Закрепление знаний -15 мин
Задачи:
• Организация групповой деятельности учащимся по закреплению знаний,
• развитие мышления учащихся при закреплении умений сравнивать и обобщать знания,
• воспитание дисциплинированности, собранности требовательности к себе при организации рабочего труда группы учащихся.
3. Закрепление материала: №6.6(а). Учитель предлагает попробовать решить в тетрадях, затем показывает решение примера на интерактивной доске.
ПРИМЕР. Методом математической индукции докажите справедливость равенства:
12+32+52+…+(2n-1)2=
Доказательство:
При n=1, 12=

2.Пусть при n=k верно неравенство:
12+32+…+(2k-1)2=
3.Докажем верность равенству при n=k+1
12+32+…+ (2k-1)2+ (2k+1)2= 2=
2=
= (2k+1)
=  , ч.т.д.
, ч.т.д.
Учитель: Метод математической индукции используется для доказательства тождеств, доказательства неравенств и решения задач на делимость.
Решите, работая парами №6.9,6.10(а),6.11(а). дается время для решения, затем ученики по желанию приглашаются к доске.
6 этап. Контроля, коррекции и оценки знаний. – 3 мин
Задачи:
• контроль ЗУН и анализ обнаруженных пробелов и ошибок и определение путей их устранения, формирование у учащихся навыков правильного воспроизведения своих ЗУН.
• развитие активность мышления и его самостоятельность, глубину, широту, систематичность и т.д.,
• воспитание отношения к другим людям через такие качества, как терпимость, деликатность и доброжелательность при анализе ответов товарищей по классу.
Решите самостоятельно №6.12(а)
7 этап. Рефлексия.
Задачи:
• закрепление, уточнение и систематизация знаний учащихся:
-слабые учащиеся лучше осознают материал,
-успевающие учащиеся убеждаются в правильности усвоения материала.
Учитель предлагает ученикам, которые справились с решением, рассказать своё решение, предварительно решение сканируется и выводится на интерактивную доску.
Учитель: объясните, как доказать тождество методом математической индукции?
Учитель сообщает, что домашнее задание будет дано на следующем уроке.
multiurok.ru
Метод математической индукции — Презентации по алгебре
Метод математической индукции — Презентации по алгебреЗагрузка. Пожалуйста, подождите…
На сайте 2297 презентаций по 20 предметам
Для какого класса нужно больше презентаций?^
Слайды:

Описание:
При подаче сложного материала концентрация внимания учащихся снижается, и тема не усваивается в полном объеме. Оживить урок, повысить мотивацию к обучению и привнести соревновательный дух в учебный процесс поможет использование мультимедийных презентаций, сделанных самими учениками.
В презентации «Метод математической индукции» рассматривается индуктивный метод математического исследования. С помощью диаграмм показано отличие индуктивного метода от метода дедукции, а также приведены примеры полной и неполной индукции. Наглядно демонстрируется несостоятельность математического утверждения, полученного методом неполной индукции. Вводятся понятия базиса математической индукции, индукционного шага и разбирается принцип математического доказательства гипотезы на бесконечном множестве элементов.
Содержание:
- В основе математического исследования лежит
- Дедуктивный метод
- Индуктивный метод
- Пример рассуждения по индукции
- Пример 1
- Пример 2
- Метод математической индукции
- Составляющие метода математической индукции
- Принцип математической индукции
Информация:
Предмет: Алгебра
Аудитория: 10 класс
Количество слайдов: 15
Автор: Кондратьева Анастасия
Скачать презентацию «Метод математической индукции»
Понравилась презентация? Тогда скачайте ещё эти:
▲ наверх
prezented.ru
Факультативное занятие по теме «Применение математической индукции» (10-й класс)
Цель: показать применение метода математической индукции для доказательства формул и решения задач на делимость.
Ход занятия
1. Вспомним, в чем же состоит суть метода математической индукции?
Доказательство методом математической индукции состоит из двух частей:
доказать или проверить справедливость утверждения при n =1;
предположить, что утверждение справедливо для n =k ,где k N, и доказать справедливость утверждения для n =k+1.
2.Доказательство формулы n -го члена арифметической прогрессии
a = a + (n-1)d
В 9 классе эту формулу получили, увидев следующую закономерность:
а= a+ d
a= a+ d = a+2d
a= a+ d = a+3d и т. д.
То есть от частных утверждений пришли к общему выводу.
Но мы знаем, что если утверждение справедливо в целом ряде частных случаев, оно может быть несправедливо вообще.
(На предыдущем занятии рассматривали такой пример, когда значение трехчлена x + x + 41 при x = 0,1,2,…39 является простым числом, а при x = 40 40 + 40 + 41 = 41 — составное число.)
Итак, доказательство:
1) n = 1 a= a — верно.
2) n = k a= a + (k-1)d , докажем справедливость формулы при n =k+1,то есть формула должна выглядеть следующим образом a = a + (k + 1-1)d = a + kd.
По определению арифметической прогрессии a =a + d= a + (k-1)d + d = a+ d(k-1+1) = a + kd. Таким образом, формула доказана (доказательство выполняется учеником).
3. Перейдем к задачам на делимость.
На доске восстанавливается треугольник Паскаля (работает ученик)
Пока восстанавливается треугольник Паскаля, с помощью формул сокращенного умножения раскрываются скобки в первых двух выражениях, в следующих двух пользуемся коэффициентами из треугольника:
(a + b) =
(k + 1) =
(a + b) =
(k + 1) =
Предлагаются задачи на делимость:
а) доказать, что число n- n nN делится на 3;
б) доказать, что число n — n nN делится на 5;
в) доказать, что nN число 3+2 делится на 7;
г) доказать, что nN число 11+12 делится на 133.
Решение:
б) 1) при n =1 1-1=0, 0 делится на 5.
2) пусть при n =k k-k делится на 5,тогда при n =k+1
(k+1)- (k+1) = k+ 5k+ 10 k+ 10k+ 5k + 1- k — 1=
k- k + 5k+ 10 k+ 10k+ 5k = (k- k) + 5(k+ 2 k+ 2k+ k) кратно 5, так как каждое слагаемое кратно 5.
Утверждения в задачах а), б) верны. Лейбниц одно время считал, что любое число вида
n — n , где k =1,2,3,… делится на число (2k+1). Однако позже сам обнаружил, что 2 — 2 не делится на 9.
Еще один пример. Ферма пришел к выводу, что числа вида 2+ 1 – простые и проверил справедливость вывода для n =0,1,2,3,4. А в 1732 году Эйлер доказал, что число 2+ 1 = 4294967297 – составное, так как делится на 641.
в) 1) при n =1 3+2= 27 +8 = 35, 35 делится на 7.
2) пусть при n =k 3+2 делится на 7, тогда при n =k+1
3 +2= 3+2= 3•3+ 2·2 = 9•3 +2•2 =
2(3+2) + 7·3 делится на 7, так как каждое слагаемое делится на 7.
г) решается аналогично в).
4. Итог занятия. Сегодня с помощью метода математической индукции определяли делимость чисел и еще раз убедились в том, что нельзя делать общий вывод (без доказательства) на основании справедливости частных утверждений.
urok.1sept.ru
План-конспект урока по алгебре (10 класс) на тему: Разработка урока по математике в 10 классе «Метод математической индукции»
Тема: Метод математической индукции.
(10 класс)
Цель урока: Рассмотреть суть метода математической индукции. Научить применять его при доказательстве некоторых утверждений.
Ход урока.
1.Устно
2.Объяснение материала
3.Закрепление материала
4.Домашнее задание
5.Итог урока.
1.Устно
а) Приведите примеры утверждений.
б) Какие виды утверждений вы знаете?
(общие и частные)
в) Приведите примеры общих утверждений.
г) Приведите примеры частных утверждений.
2.Обьяснение материала
В математике на основе частных утверждений делают некоторые предположения
О справедливости какого-либо общего утверждения. Переход от частных утверждений к общим называют индукцией.
Джузеппе Пеано показал, что для дедуктивного построения арифметики натуральных чисел достаточно четырех аксиом. Так аксиома 4 у него говорит : Если какая-либо теорема о свойствах натуральных чисел доказывает для единицы и если из допущения, что она верна для натурального числа и, следует, что она верна для всех натуральных чисел.
ПРИМЕР. Найти формулу для вычисления суммы k первых нечетных чисел.
Попробуем подсчитать такую сумму для некоторых значений k:
k=1; 1=1=12;
k=2; 1+3=4=22;
k=3; 1+3+5=9=32;
k=4; 1+3+5+7=16=42;
Таким образом, 1+3…+(2n-1)+(2n+1)=(n+1)2.
Получим:
1+3+…+(2n-1)+(2n+1)=n2+(2n+1)=(n+1)2, ч.т.д.
Знаменитый математик 17 века Пьер Ферма высказал предположение, что простыми являются все числа вида 22n+1.Он показал, что первые пять числе 220+1=3, 221+1=5,222+1=17, 223+1=257, 224+1=65537 – простые и сделая по индукции предположение, что для всех n числа вида 22n+1- простые.
Однако это предположение оказалось не верным, т.к. в 18 веке Л.Эйлер нашёл, что 225+1=4294967297=641∙4700417 – составное число.
Итак, индукция не является методом доказательства, а лишь помогает сформулировать неизвестный результат в виде некоторой гипотезы, справедливость которой потом надо доказать.
Идея последовательного перехода от натурального числа n к следующему за ним числу n+1 осуществляется в строгой форме в одном из самых важных методов математических доказательств называется методом математической индукции.
В основе этого метода лежит принцип математической индукции, заключающийся в следующем:
Утверждения P(n) справедливо для всякого натурального n, если:
1)Оно справедливо для n=1;
2)Из справедливости утверждения для какого-либо произвольного натурального n=k следует его справедливость для n=k+1.
3. Закрепление материала.
ПРИМЕР. Методом математической индукции докажите справедливость равенства:
12+32+52+…+(2n-1)2=n2n-1(2n+1)3
Доказательство:
- При n=1, 12=12∙1-1(2∙1+1)3=1
2.Пусть при n=k верно неравенство:
12+32+…+(2k-1)2=k2k-12k+13
3.Докажем верность равенству при n=k+1
12+32+…+ (2k-1)2+ (2k+1)2=k2k-1(2k+1)3+(2k+1)2=
= (2k+1)[k2k-1+32k+1]3=2k+12k2-k+6k+33=
= 2k+12k2+5k+33=2k+1k+1(2k+3)3, ч.т.д.
ПРИМЕР. Докажите, что n3- n делится на 3 любых натуральных значениях n.
Доказательство:
1.При n=1 12-1=0 – делится на 3
2. Пусть при n=k (k3-k) – делится на 3, т.е. k3-k=3m
3. Докажем, что (k+1)3-(k+1) – делится на 3.
(k+1)3-(k+1)=k3+3k2+3k+1-k-1=k3- k+3k2+k=3m+3(k+k) делится на 3, т.к. k3-k делится на 3 и k2+k делится на 3, ч.т.д.
4.Домашнее задание.
№1. Методом математической индукции докажите справедливость неравенства:
1∙2∙3+2∙3∙4+…+n (n+1)(n+2)=14n(n+1)(n+2)(n+3)
№2. Докажите, что сумма кубов трех последовательных натуральных чисел делится на 9.
5.Итог урока.
-В чем же заключается методов математической индукции.
nsportal.ru
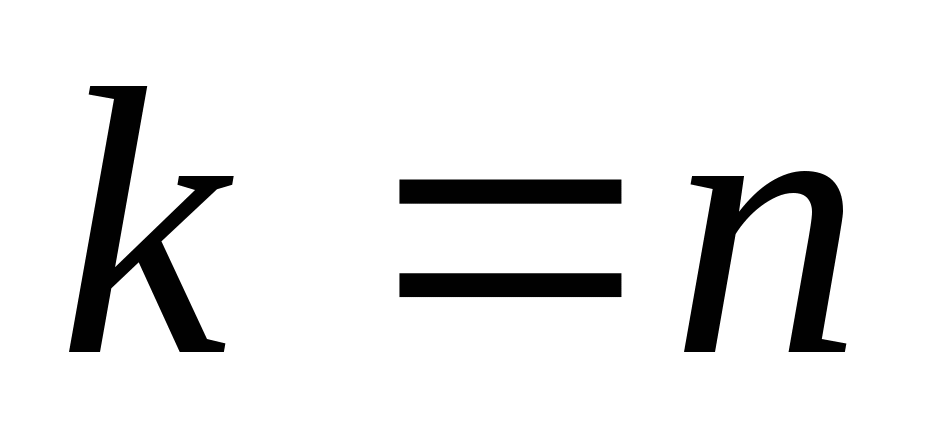 ,
, 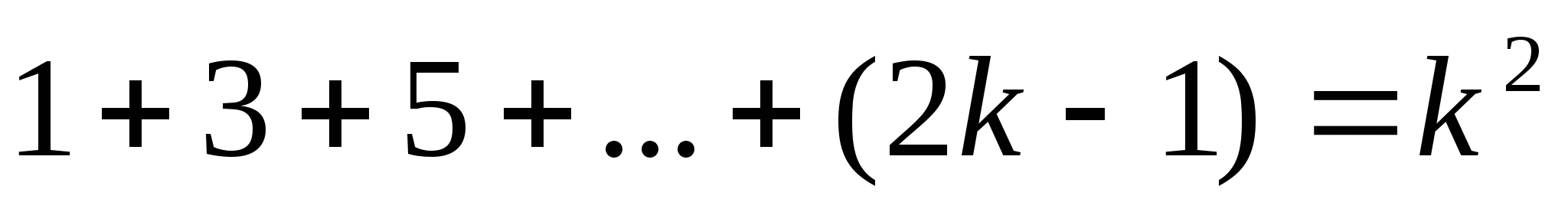 , докажем, что оно верно для некоторого
, докажем, что оно верно для некоторого 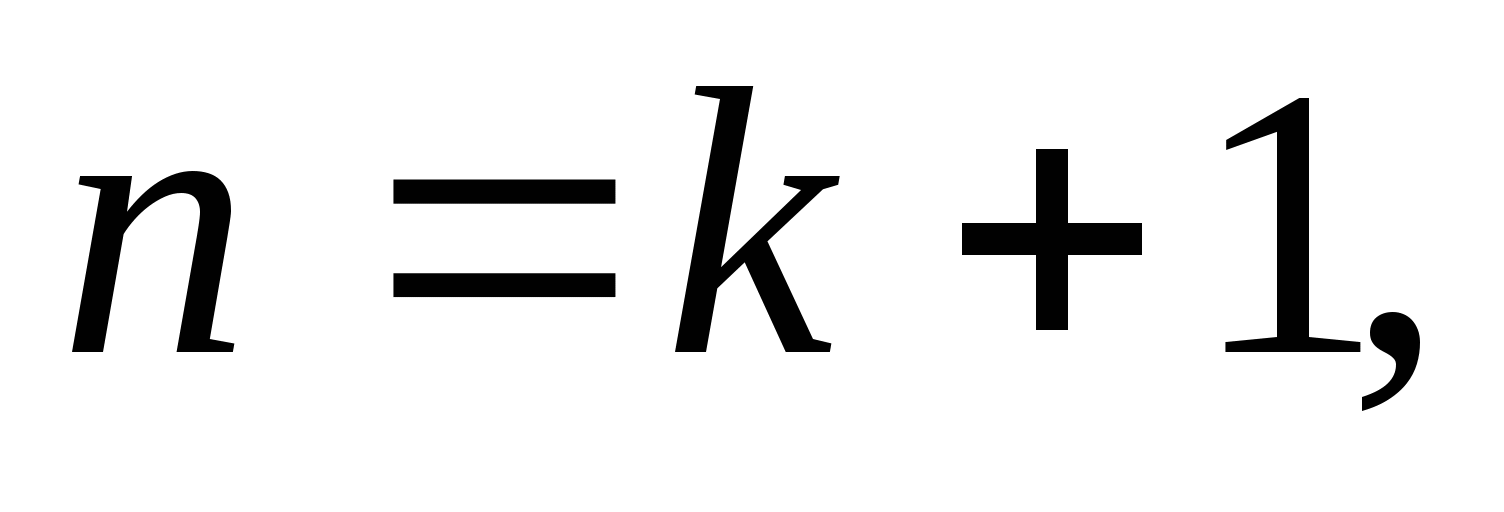 то есть
то есть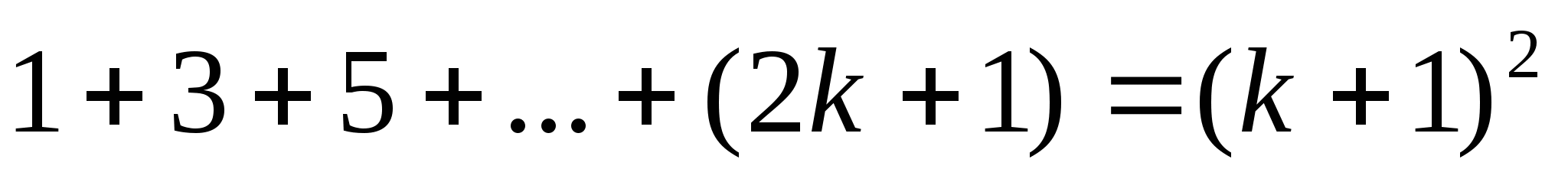 — верно.
— верно.