Раскрытие скобок. Видеоурок. Математика 6 Класс

Тема: Решение уравнений

Урок: Раскрытие скобок

 

Как раскрыть скобки, перед которыми стоит знак «+». Использование сочетательного закона сложения.

Если к числу нужно прибавить сумму двух чисел, то можно к этому числу прибавить сначала первое слагаемое, а затем второе.

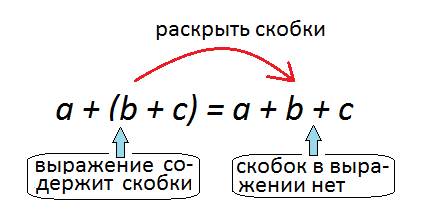
Слева от знака равно выражение со скобками, а справа – выражение без скобок. Значит, при переходе от левой части равенства к правой произошло раскрытие скобок.

Рассмотрим примеры.

Пример 1.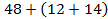

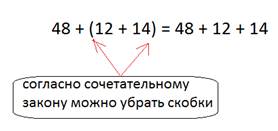
Раскрыв скобки, мы изменили порядок действий. Считать стало удобнее.

Пример 2.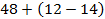

Пример 3.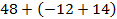

Заметим, что во всех трех примерах мы просто убирали скобки. Сформулируем правило:

Замечание.

Если первое слагаемое в скобках стоит без знака, то его надо записать со знаком «плюс».

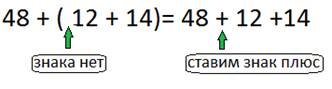
Пример 1.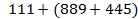

Можно выполнить пример по действиям. Сначала к 889 прибавить 445. Это действие в уме выполнить можно, но это не очень просто. Раскроем скобки и увидим, что изменённый порядок действий значительно упростит вычисления.

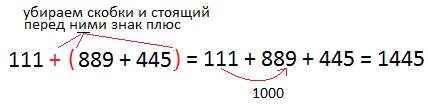
Пример 2.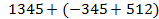

Если следовать указанному порядку действий, то нужно сначала из 512 вычесть 345, а затем к результату прибавить 1345. Раскрыв скобки, мы изменим порядок действий и значительно упростим вычисления.

Иллюстрирующий пример и правило.

Рассмотрим пример: 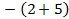.  Найти значение выражения можно, сложив 2 и 5, а затем взять полученное число с противоположным знаком. Получим -7.

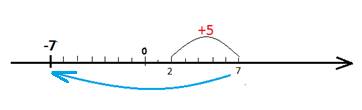
С другой стороны, тот же самый результат можно получить, сложив числа, противоположные исходным.

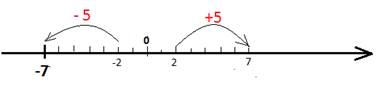
Сформулируем правило:

Как не менять знаки внутри скобок?

Всех нас учат менять знаки при раскрытии скобок или закрывании части выражения в скобки, если перед скобками стоит знак минус. Давайте рассмотрим этот нудный процесс на полуживых примерах.

11-(2+5-4) = 11-3 = 8

Перед выражением в скобках стоит знак минус, это значит, что при раскрытии скобок нужно поменять все знаки на противоположные у всех чисел, которые находятся внутри скобок. Этот же пример, но уже без скобок.

11-(2+5-4) = 11-2-5+4 = 9-5+4 = 4+4 = 8

Теперь попробуем взять часть выражения в скобки. Рассмотрим другой пример.

1+2+3+4 = 10

Естественно, вы спросите: «Где же здесь знак минус?!» Не переживайте, сейчас появится.

1+2-(-3-4) = 3-(-7) = 3+7 = 10

Я поставил перед скобками знак минус и поменял знаки перед числами внутри скобок. При раскрытии скобок я снова поменял знак на противоположный, поскольку у меня перед скобками стоит знак минус. В итоге результат остался неизменным.

Теперь более заковыристый пример.

17-6+9 = 20
17-(6-9) = 17-(-3) = 17+3 = 20

Как видите, сплошная головная боль получается, если вдруг перед скобками появляется знак минус. Как не менять знаки внутри скобок? Очень просто — не нужно ставить минус перед скобками. Вот смотрите, как это делается.

17-6+9 = 17+(-6+9) = 17+(3) = 17+3 = 20

Теперь рассмотрим два последних примера под микроскопом. В первом случае я поставил первую скобку после знака минус. Я словно ножом разрезал отрицательное число на две части — знак минус и положительное число. Знак минус оказался перед скобкой, а положительно число — внутри скобок. Посмотрите.

17-(6……..

Фактически мы в скобки заключаем положительное число, которое до этого было отрицательным. Изменение знака перед первым числом внутри скобок прошло на полном автопилоте без всякого нашего вмешательства. Такой себе автомат по обрезанию знака минус у чисел. А вот с остальными числами, попадающими в такие скобки, уже возникают проблемы. Знаки у них нужно менять вручную.

Во втором случае я поставил открывающую скобку перед знаком минус. Фактически я заключаю в скобки отрицательное число вместе со знаком минус. Вот как это выглядит первоначально.

17(-6………

Теперь между числом 17 и скобкой нет никакого знака, что в математике подразумевает умножение. Но мне не нужно ничего умножать. Чтобы ответ при решении примера оставался прежним, я ставлю перед скобкой дополнительный знак «плюс».

17+(-6………

Вот теперь всё правильно записано. Перед скобками появляется знак полюс и знаки перед числами внутри скобок менять не нужно. Никакого математического преступления я не совершаю, просто грамотно избавляюсь от лишних действий по замене знаков внутри скобок. Почему математики всегда так не делают? Их никто этому не учил. Если этого нет в учебной программе, то и учить вас этому никто не будет. Математику мало знать, нужно ещё уметь нею пользоваться.

Раскрытие скобок

Часто при решении примеров удобно раскрыть скобки в выражении, нежели подсчитывать их значения. Сегодня на уроке мы рассмотрим, как правильно раскрывать скобки.

Итак, рассмотрим случаи, когда перед скобками стоит знак «+». Для этого воспользуемся хорошо известным для вас сочетательным свойством сложения:

Если к числу нужно прибавить сумму двух чисел, то можно сначала к этому числу прибавить первое слагаемое, а затем второе.

Обратите внимание, на экране записано два выражения соединённых знаком равенства. Вот только левая часть равенства содержит скобки, а правая – без скобок. Говорят, что при переходе от левой части равенства к правой произошло раскрытие скобок.

Рассмотрим ещё одно выражение:

Как вы думаете, можно ли его преобразовать в выражение без скобок?

Можно. Вы знаете, что вычитание можно заменить сложением. Так и поступим, заменим в этом выражении вычитание сложением.

И давайте попробуем преобразовать ещё два выражения со скобками: 

Опустим все промежуточные рассуждения и приравняем начальные и конечные части равенств.

Обратите внимание, перед каждой из скобок стоит знак «+».

Сделаем

вывод:

Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках.

Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».

Задание

Раскройте скобки и найдите значения выражений.

Мы разобрали случаи, когда перед скобками стоит знак «+». А как же поступить, если перед скобками стоит знак «».

Давайте рассмотрим выражение: – (2 + 3).

Найти значение этого выражения можно, сложив 2 и 3, а затем взять полученное число с противоположным знаком.

Тот же самый результат можно получить и другим способом. Для этого мы сложим числа противоположные исходным.

Сформулируем правило:

Если перед скобками стоит знак «–», то скобки и этот знак «минус» можно убрать, а знаки перед числами внутри скобок изменить на противоположные.

Например, раскроем скобки в выражениях.

Задание

Раскройте скобки и найдите значения выражений.

Для раскрытия скобок в выражениях, содержащих умножение числа на сумму, используется

распределительное свойство умножения:

По правилам умножения рациональных чисел, если a > 0, то знаки слагаемых b и c не изменятся, а если a <0, то изменятся на противоположные.

Например

Итоги

Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках.

Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».

Если перед скобками стоит знак «–», то скобки и этот знак «минус» можно убрать, а знаки перед числами внутри скобок изменить на противоположные.

Числовые выражения, порядок действий, раскрытие скобок

Тестирование онлайн

• Порядок действий

Числовые выражения

Из чисел, знаков действий и скобок можно составить различные числовые выражения. Например,

Если в выражении встречается деление на ноль, возведение нуля в нулевую или отрицательную степень, то выражение не имеет смысла. Например, выражение не имеет смысла.

Скобки

Отрицательное число записывается в скобках

Если забыть написать скобки, то числовое выражение меняет смысл

Отрицательное число можно не брать в скобки только в том случае, когда оно находится на первой позиции в математическом выражении

Скобками могут обособляться целые числовые выражения

Слагаемые. Раскрытие скобок

Плюс на плюс дает плюс

Плюс на минус или наоборот дает минус.

Минус на минус дает плюс.

Если перед скобкой стоит плюс, то все слагаемые при раскрытии скобок сохраняют свои знаки

Если перед скобкой стоит минус, то все слагаемые при раскрытии скобок меняют знаки на противоположные

Порядок действий

Первостепенно выполняются действия в скобках, затем умножение и деление, в последнюю очередь — сложение и вычитание.

Урок на тему:»Раскрытие скобок»

Конспект открытого урока

в 6классе по математике:

» Раскрытие скобок»

учитель Булдакова Л.П

МОБУ «Новочеркасская СОШ»

2014 год

Конспект открытого урока по теме » Раскрытие скобок»

Цели и задачи урока:

Закрепить умение раскрывать скобки при упрощении выражений, при решении уравнений;

Проверить прочность ЗУН по теме.

Развивать познавательную активность учащихся.

Развивать умение формулировать проблему и строить высказывания. Развивать математическое мышление, внимание, память.

Тип урока: урок закрепления .

Вид урока: : урок-путешествие в мир » Математики»

Ход урока

1. Организационный момент: вступительное слово учителя, постановка целей и задач урока.

— Сегодня мы проведем урок под девизом: «Математику уже затем учить следует, что она ум в порядок приводит». М. Ломоносов.

Будем думать.

Будем решать.

Будем друг другу

Во всем помогать.

По какой теме работали на предыдущем уроке? ( Раскрытие скобок)

Где мы применяли данное правило.

— при преобразовании выражений;

— при решении уравнений.

Итак, сегодняшний наш урок мы проведем, путешествуя по стране «Математика» в поисках умения раскрывать скобки.

Значит тема нашего урока «Раскрытие скобок».

Путешествовать будем по станциям:

1 » Пораскинь Мозгами»

2.» Блиц- опрос»

2.» Мост дружбы»

4.Станция » Уравнений».

5. Пункт размышлений. Итог нашего путешествия

А для того чтобы отправиться в путь , проверим, все ли готовы?

Каким правилом будем пользоваться при раскрытии скобок?(опрос правила)

1. Актуализация знаний . » Пораскинь Мозгами»

а) проверка домашнего задания — обменяться тетрадями, и по слайду проверить № 525.- выставить оценку;

б) работа в парах.

Соедините линиями условие из левого столбика с соответствующим ему правильным ответом из правого столбца.(Приложение 1)

1. a + (b – c) A) a – b – c

2 .a – (b +c) Б) – а + b — c

3.a – (b – c) В) a – b + c

4.– (a – b) – c Г) – a – b – c

5. – a + ( — b – c) Д) a+ b – c

Учащиеся самостоятельно работают в парах вспоминают правила и проверяют ( по слайду) -оценка;

Зачем вообще нужно раскрывать скобки? (Когда есть скобки, есть момент какой-то незавершенности, какой- то тайны. Это – как закрытая дверь, за которой находится что-то интересное.)

Небольшой экскурс в историю:

Фигурные скобки появляются в сочинениях Виета (1593). Широкое применение скобки получили лишь в первой половине XVIII века, благодаря Лейбницу и еще больше Эйлеру.

2.станция БЛИЦ — ОПРОС.

1) блиц — опрос Прежде чем начнем — небольшая справка

Что такое » Блиц»? Как вы думаете?

блиц – слово немецкого происхождения и в переводе означает молния

Это значит отвечать должны быстро, четко и ясно

1. Как сложить два числа с одинаковым знаком?

2.как сложить два числа с разными знаками?

3.какой знак получается при умножении дух отрицательных чисел?

4.Какой знак получается при умножении чисел с разными знаками?.

2) Проведем устную разминку.(презентация- устный счет)

( в это время несколько уч-ся у доски по карточкам)

3 станция. Мост дружбы «Сделал сам – проверь соседа»

1.Раскройте скобки и найдите значения выражений:(приложение 1)

а) 5,7 + (8,3 – 4,5)‏ а)4,3-(-6,7+5)

б) 3,5 – (2а – 1,5)‏ б) -1,7-(у+2,3)

в) m+(13-m) в)-(2.5 +d)-3,5

г) (2-4у) +(-у-3) г) -(5х+3) -(4 +2х)

Проверяют и оценивают друг — друга.

— Таким образом, правила раскрытия скобок помогут нам решать примеры, и упрощать выражения.

А для того чтобы вам легче было запомнить правило раскрытия скобок, предлагаю вам вот такое стихотворение:

Если перед скобкой минус,(приложение 2)

Он ведёт себя как вирус.

Скобки сразу все съедает,

Всем, кто в скобках, знак меняет.

Ну, а если плюс стоит,

Он все знаки сохранит!

Физминутка (для глаз)

Где же нам потребуются знания правил раскрытия скобок? Конечно же при решении уравнений.

4.Следующая станция Станция Уравнений»

Решить:

Далее учащиеся самостоятельно решают уравнение , применяя правила раскрытия скобок. ( комментируют решение по слайду)

(-х -4 ) — ( -2х -20) =10

-х -4 +2х +20 =10

-х +2х = 10 +4 -20

х = — 6

А теперь у вас карточки — решить уравнение и проверить ответ по листу самоконтроля. (Приложение 3)

( дополнительно » Лови ошибку») Найти ошибку в решении уравнений

1 вариант 2 вариант

-(х+3)-2х =15 2х-3(х+5)=5

х+3-2х=15 2х-х+5=5

-х=15-3 х+5=5

х=-12 х=0

Правильное решение

-х-3-2х=15 2х-3х-15=5

-3х=15+3 -х=15+5

-3х=18 -х =20

х =-6 х =-20

Тестовая работа(при наличии времени)(проверка)

5 станция. Пункт размышлений.( подведение итогов)

Рефлексия: Мне все понятно

Мне не все ясно, но я постараюсь,

Мне нужна помощь.

Работа с оценочным листом.

Лист самоконтроля ученика:

Д/з

Устная раб

Соедини линией

Работа у доски

Мост дружбы

Станция Уравнений

Лови ошибку

Тестовая работа

итоговая

Задание на дом: № 530; 538.