формула и примеры решения задач

Содержание:

Формулировка теоремы Фалеса

Теорема

Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки (рис. 1).

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.

Теорема

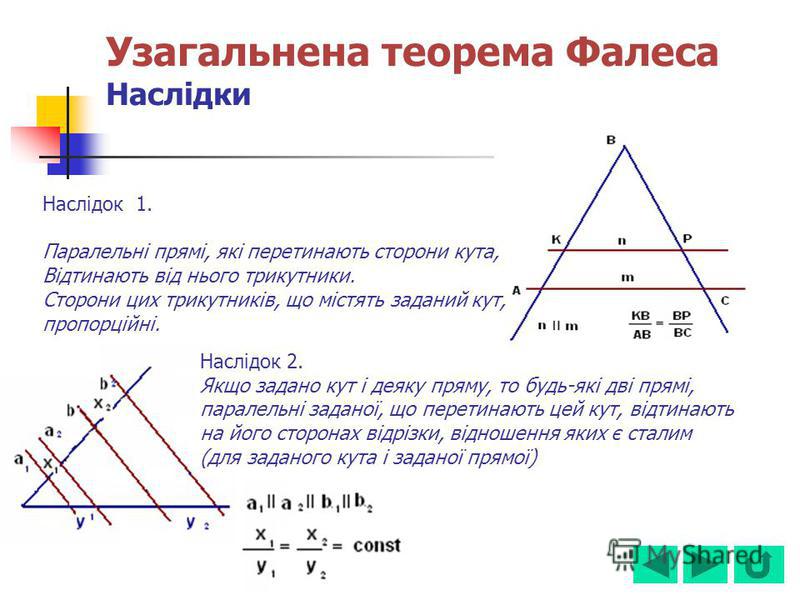
Обобщённая теорема Фалеса

Параллельные прямые отсекают на секущих пропорциональные отрезки (рис. 1):

$$\frac{A_{1} A_{2}}{B_{1} B_{2}}=\frac{A_{2} A_{3}}{B_{2} B_{3}}=\frac{A_{1} A_{3}}{B_{1} B_{3}}$$

Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.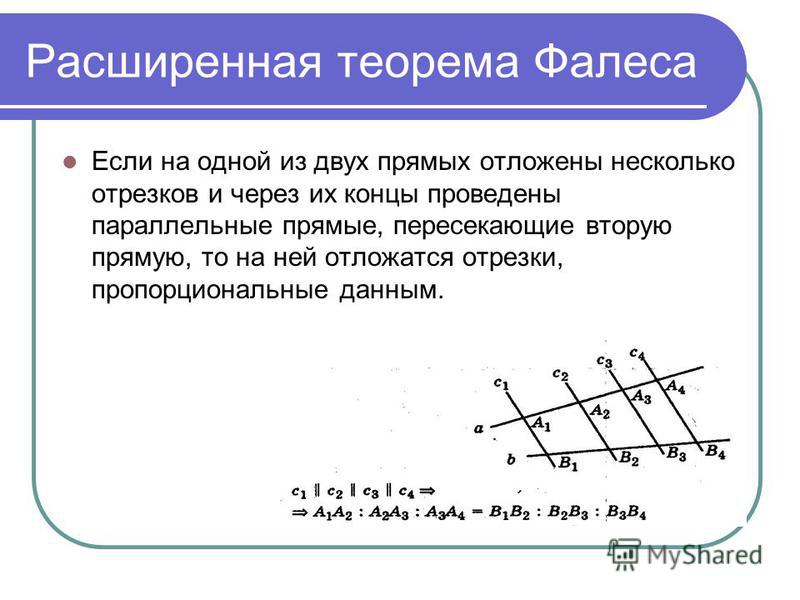

Теорема

Обратная теорема Фалеса

Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны (рис. 2).

Замечание. В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины.

Примеры решения задач

Пример

Задание. Разделить данный отрезок на четыре равные части.

Решение. Пусть $AB$ — заданный отрезок (рис. 3), который необходимо разделить на четыре равные части.

Через точку $A$ проведем произвольную полупрямую $a$ и отложим на ней последовательно четыре равных между собой отрезка $AC, CD, DE, EK$ .

Соединим точки $B$ и $K$ отрезком и проведем через оставшиеся точки $C$, $D$ и $E$ прямые, параллельные прямой $BK$ так, чтобы они пересекли отрезок $AB$ .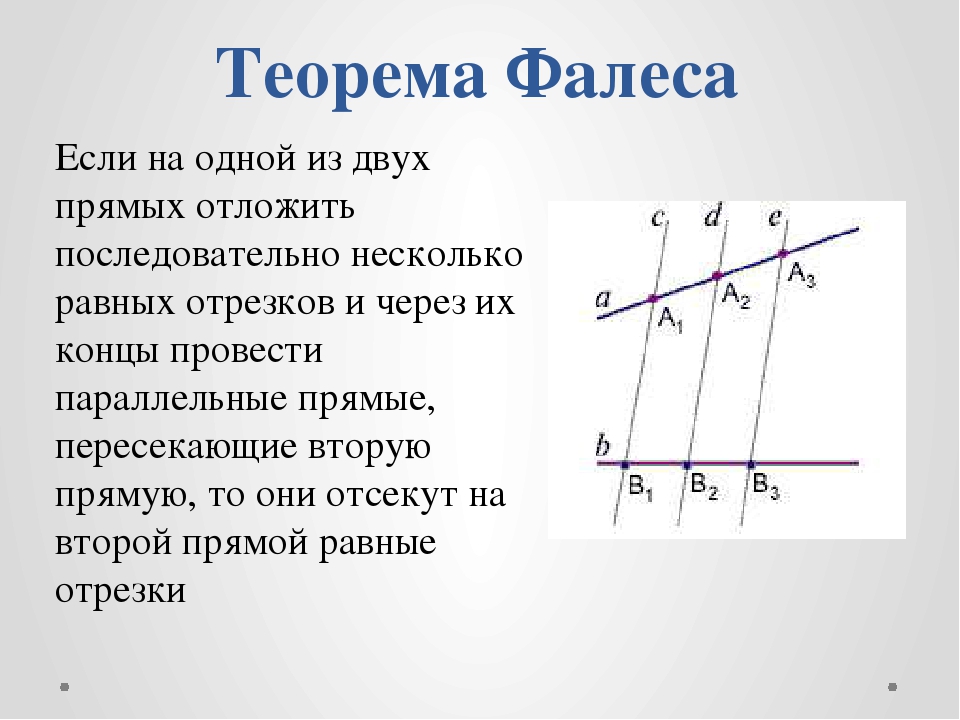

Согласно теореме Фалеса отрезок $AB$ разделится на четыре равные части.

Слишком сложно?

Теорема Фалеса не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. На стороне $AB$ треугольника $ABC$ отмечена точка $K$. Отрезок $CK$ пересекает медиану $AM$ треугольника в точке $P$, причем $AK = AP$. Найти отношение $BK : PM$ .

Решение. Проведем через точку $M$ прямую, параллельную $CK$, которая пересечет $AB$ в точке $D$ (рис. 4).

По теореме Фалеса $BD = KD$ .

По теореме о пропорциональных отрезках имеем, что

$$P M=K D=\frac{B K}{2} \Rightarrow B K: P M=2: 1$$

Ответ. $B K: P M=2: 1$

Историческая справка

Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок.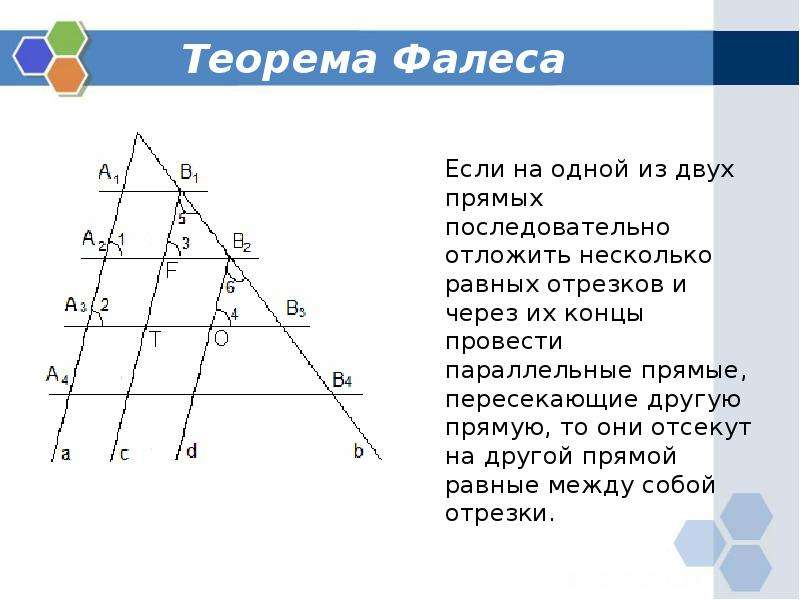

Аргентинская музыкальная группа представила песню, посвящённую теореме. В видеоклипе для этой песни приводится доказательство для прямой теоремы для пропорциональных отрезков.

Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.

Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

Теорема Фалеса

Одна из основополагающих теорем (теорема Фалеса) в геометрии говорит о том, что проведенные через концы одинаковых отрезков прямой параллельные линии отсекают на  другой прямой тоже одинаковые по длине отрезки. Причем происходит это независимо от угла между прямыми. Это достаточно произвольная

формулировка теоремы Фалеса, но достаточно емко описывающая ее суть. Разные учебники приводят разные формулировки, но суть остается неизменной.

Ключевые слова в теореме (при любой формулировке) — прямые, отрезки, равные, пропорциональные, параллельные. Это говорит о том, что теорема Фалеса касается только планиметрии, то есть изображения линий на плоскости. Она очень важна для картографии и навигации, широко используется в архитектуре и живописи, строительстве и проектировании.

Классической формулировки, единой в своем роде нет. Например, формулировку можно услышать  в такой редакции:

Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки

.

А можно и в такой:

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

 

Рис 2.

Если внимательно присмотреться, то можно увидеть, что одно утверждение не противоречит другому, а рисунки практически идентичны. Если продолжить прямые на первом рисунке по получим тот же угол.

Кроме прямых, которые проходят под углом, такая же картина происходит при пересечении параллельных прямых. Разница состоит в том, что на пересекающихся прямых отрезки АВ и А₁В₁  могут быть как одинаковыми, так и пропорциональными, в зависимости от угла наклона секущих. А для случая параллельных — только одинаковыми. Если обобщить два случая, то

обобщенная теорема Фалеса звучит так: Параллельные прямые отсекают на секущих пропорциональные отрезки.

A₁A₂/B₁B₂=A₂A₃/B₂B₃=A₁A₃/B₁B₃

Для иллюстрации можно воспользоваться рисунком 1.

Теорема Фалеса это не только теоретическое утверждение, доказанное методами математики, но и практический инструмент для построения различных фигур. Простейшая задача — разделить на равные части произвольный отрезок ВА. Пусть этих частей будет 7.

Для решения задачи нарисуем отрезок ВС, образующий с данным  ВА угол. Как видим, отрезок ВС проходит вдоль клеток на бумаге, что позволяет выбрать на нем равные отрезки. В нашем случае, это:

BD=DE=EF=FG=GH=HJ=JC.

Начиная от крайних точек А и С проведем параллельные линии, пересекающие отрезок ВА. На нем тоже получиться семь равных отрезков: BR=RP=PN=NM=ML=LK=KA.

С таким же успехом мы можем разделить отрезок на 5, 6, 4 или любое другое количество равных частей. Суть метода состоит в том, что длину отрезка ВС мы заведомо выбираем такой, чтобы его можно было легко разделить на заданное количество частей. Например, длина отрезка ВА 37 см, а его нужно разделить на 5 частей. Выбираем длину отрезка ВС в 25 см, отмечаем точки и выполняем построение по теореме Фалеса.

Не менее широко используется и теорема, названная обратной. То есть, доказательства требует не равность или пропорциональность отрезков, а параллельность прямых. Формулируется обратная теорема Фалеса так:

Если две или более прямых (a, b, c) отсекают от двух других прямых (

d, f) равные или пропорциональные отрезки, то они параллельные.

Утверждение справедливо, независимо от того, параллельные d, f или пересекаются.

Математика, тем более, геометрия, наука точная. Каждое утверждение, кроме аксиом, требует доказательства. В геометрии под термином «теорема» подразумевается утверждение, которое доказано на базе ранее полученных знаний в виде аксиом и других теорем.

Теорема Фалеса с доказательством приведена в большинстве учебников. В отличие от теоремы Пифагора, доказательств у нее меньше, но все они четкие, понятные и аргументированные. Покажем одно из них.

Не будем повторять формулировок, продемонстрируем только ход мыслей и выполним необходимые построения:

Выберем точку В₂  и проведем прямую, параллельную стороне угла ОС.

При этом отмечаем, что А₁А₃ || EF. Рассматривая четырехугольник

А₁FЕА₃ замечаем, что А₁F и ЕА₃ параллельны по определению, а А₁А₃ и FВ₃ параллельны по построению. Отсюда вытекает, что А₁ FЕА ₃ — параллелограм и А₁А₃ = EF.

Аналогичным образом доказываем равенство других сторон и получаем, что по равенству вертикальных и внутренних углов ∠B₁B₂F=∠B₃B₂E  и ∠B₂FB₁=∠B₂EB₃ треугольники B₂B₁F и B₂B₃E равны, откуда вытекает, что B₁B₂=B₂B₃.

Именно это и требовалось доказать.

По легенде, впервые на практике использовал теорему греческий философ Фалес Милетский. Он применил ее для измерения высоты пирамиды Хеопса, пользуясь падающей на песок тенью.

Для  сравнения длины отрезков использовалась воткнутая рядом палка.

Но доказательство теоремы, самое давнее из известных, зафиксированных в письменных источниках, дано в книге «Элементы» другого философа и математика — Эвклида. Тем не менее, утверждение получило имя Фалеса, под которым известно до сих пор.

 

 

 

 

 

Как звучит теорема Фалеса?

Задача не очень сложная, главное в ней, догадаться, с какого угла начать деление. Я перепробовал все углы, угол в 15 градусов отпал. Угол 60 можно делить по разному, но и тут у меня ничего не получилось. Поэтому пришлось разделить угол в 105 градусов и ее первоначально можно разделить единственным образом: на 60 и 45 градусов. Решение представлено на рисунке

Треугольник АВС исходный, где А=15, В=105 и С=60. Первая линия ВМ делит угол В на два угла: СВМ = 60 и АВМ=45. Вторая линия ВК делит угол АВМ на два угла: АВК = 15 и КВМ = 30.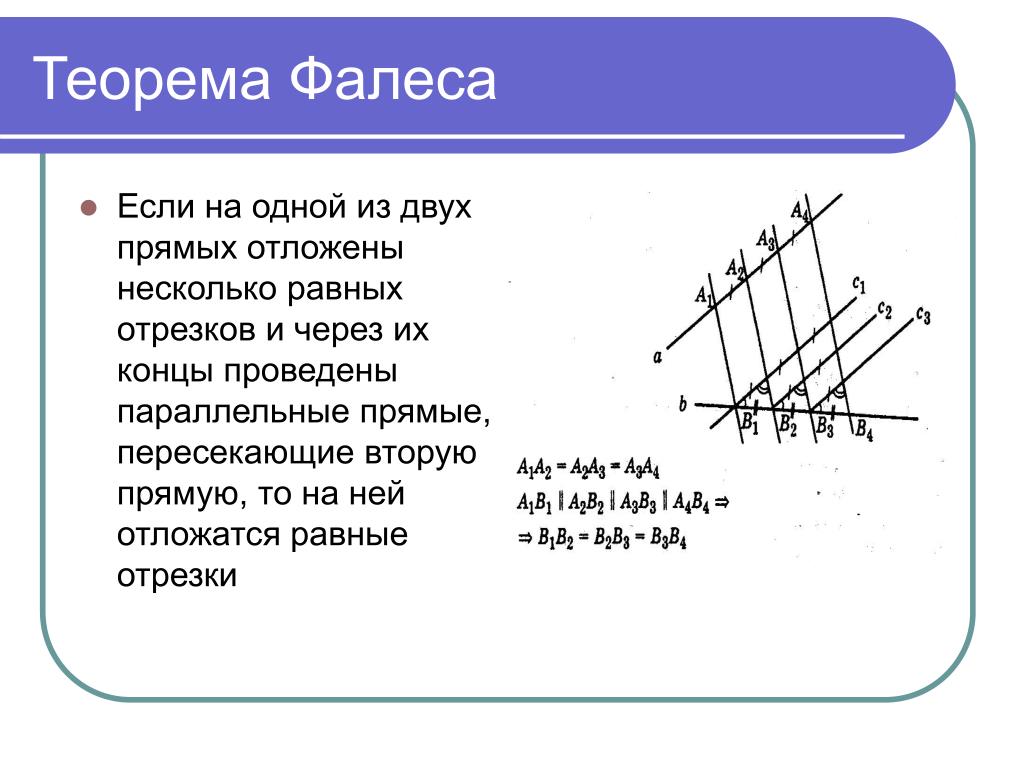

Понятно, что все три треугольника: АВК, КВМ, ВСМ равнобедренные, просто треугольник ВСМ получился еще и равносторонним.

Чтобы найти углы ромба, надо знать несколько простых правил.

1. Необходимо нарисовать диагонали ромба. Известно, что они взаимо перпендикулярны и делят углы ромба пополам.
2. Известно, что противоположные углы ромба всегда равны между собой, а сумма всех углов ромба равна 360 градусам, поэтому сумма соседних углов в ромбе всегда равна 180 градусов.
3. Помните, что все стороны у ромба равны.
4. Исходя из вышесказанного, чтобы найти углы ромба, надо узнать хотя бы один его угол. Чтобы узнать один угол ромба, надо знать либо длину стороны ромба и длину диагонали, либо длины двух диагоналей.

Формулы для нахождения углов ромба см. ниже.

Трёхгранный угол — это геометрическая фигура, образованная тремя лучами, не лежащими в одной плоскости и проведенными из одной точки, которая называется вершиной трёхгранного угла. 2) = 6 см

Три отрезка, соединяющих вершины треугольника ABC (вершины обозначим как A,B и C) с некоторыми точками на противоположной стороне этого треугольника (соответственно это будут точки C1, A1 и B1 ), которые мы можем обозначить традиционно AA’,BB’,CC’ проходят через одну точку или параллельны) тогда лишь, когда:

Доказательство на сайте ресолвента.ру

Теорема об угле, опирающемся на диаметр окружности

Пользователи также искали:

как доказать что это диаметр, когда вписанный угол будет прямым, теорема фалеса, теорема о вписанном угле, теоремы окружности, угол, опирающийся на диаметр окружности прямой, угол, опирающийся на радиус, все углы, опирающиеся на одну и ту же дугу, равны, Теорема, диаметр, теорема, угол, угле, опирающийся, окружности, опирающемся, как доказать что это диаметр, теоремы окружности, теорема фалеса, теорема о вписанном угле, прямой, когда, вписанный, будет, доказать, радиус, теоремы, фалеса, вписанном, углы, опирающиеся, одну, дугу, равны, прямым, угол опирающийся на радиус, когда вписанный угол будет прямым, Теорема об угле опирающемся на диаметр окружности,

Колмогоровская реформа, учебники и т.

д. : Вопросы преподавания Про Смирновых. Я про этот учебник ничего не знал (его в либрусеке нет). С некоторым трудом нашел. Первая глава в нем какая-то очень нетрадиционная, довольно странная и мутная. Я понял ее концепцию в общем, но вижу, что там очень много логических и педагогических дыр в изложении. Если её семиклассник будет читать самостоятельно, у него голова опухнет. Дальше в основном хорошо написано. Но про векторы очень плохо, считай почти никак.

Mihr
А какие у Вас к ней претензии ? Выкатывайте, не стесняйтесь.

Вернемся, однако, к Колмогорову.

————————————————

14)

А.Д.Александров писал(а):

Да мудрено ль ? Коль вам твердят,
что вектор — это перенос,
то в самом деле хватит вас понос !

Итак, рассмотрим, как в учебнике Колмогорова излагаются векторы, а заодно и подобие (т.к. эти темы между собой связаны).

Прежде всего, определение вектора как параллельного переноса выглядит диковатым. На физике ученики видели, что вектор — это отрезок со стрелочкой. А тут им предлагают считать, что вектор — это параллельный перенос. Явный разрыв шаблона. Кроме того, преобразование (параллельный перенос) — это более сложная сущность, чем отрезок. На самом деле, вектор — это как бы и не отрезок, и тем более не параллельный перенос, а то, что имеет величину и направление. Например, сила. То есть, говоря абстрактно, и «параллельный перенос», и «класс эквивалентности направленных отрезков» — это, оба, понятия, замещающие «истинное» понятие вектора, которое вообще неизъяснимо. (Не знаю, понятна ли эта мысль ?). Причин считать, что сила — это параллельный перенос, чего-либо куда-либо, еще меньше, чем причин считать, что сила — класс направленных отрезков. Так почему в качестве «представляющего понятия» для «вектора» выбрано более сложное ?

Когда определяют, что такое сумма векторов, то в одном случае говорят о композиции отображений, а в другом просто приставляют друг к другу два отрезка со стрелочками.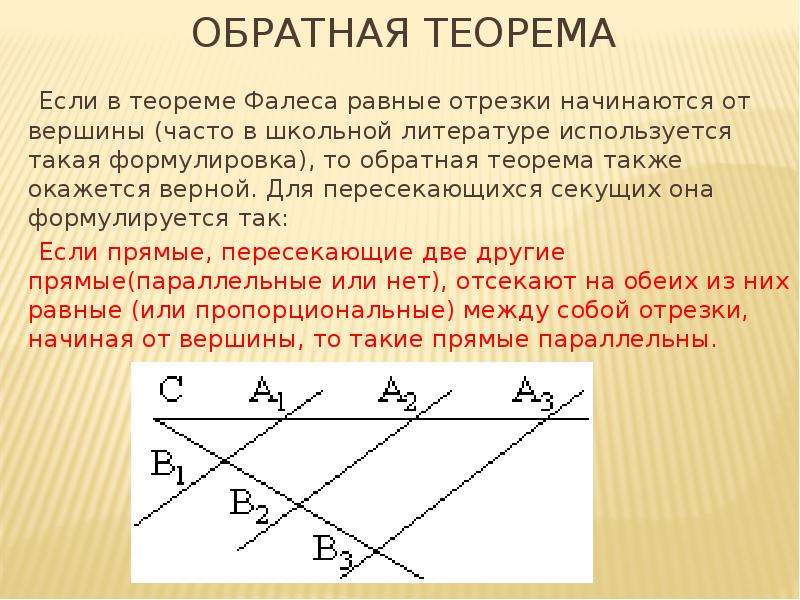 Так что проще (это вопрос риторический) ? И ведь в любом случае, когда доказывают свойства сложения, приходится рисовать отрезки. Так в чем смысл введения вектора как переноса ?

(Правда, когда вводят сложение векторов через приставление отрезков, надо еще доказывать корректность определения, т.е. то, что результат не зависит от того, с какой точки начинается построение. Ну да это рассуждение на десять (от силы) строчек, через свойства параллелограмма.)

Композиция отображений — важная идея, но в связи с векторами ее вводить незачем было. Ее имеет смысл вводить, когда речь идет о поворотах, что в 8 классе (по тем временам) делалось. И тогда она и «зашла» успешно. А правило сложения векторов ее бы и иллюстрировало. А Колмогоров с ног на голову поставил (в этом месте, как и в стопятиста других).

(Повороты)

Кстати, а была ли большая нужда во введении композиции поворотов на тот момент (в 8 классе) ? Непосредственно не видно. Вполне вероятно, это было полезно для физики. Во всяком случае, концепция важная, и лучше рассказать лишнего, чем дыры оставить.

Учительница, которая учила нас в 7 классе, была, по моим воспоминаниям, женщина, расположенная к новому и прогрессивному. Она говорила слова, что вектор — это перенос, но, похоже, и сама в них не верила и рисовала на доске отрезки со стрелочками.

При определении суммы векторов через композицию надо доказать, что композиция переносов — перенос. Используется рассуждение такое:
(а) при параллельном переносе каждый луч переходит в сонаправленный луч;
(б) и наоборот, любое перемещение, переводящее каждый луч в сонаправленный — это перенос; (оба этих утверждения — каждое отдельная теорема)
(в) композиция двух перемещений — перемещение; и композиция двух отображений, переводящих каждый луч в сонаправленный — такова же; значит, композиция двух переносов — это перемещение, переводящее каждый луч в сонаправленный, а потому является переносом.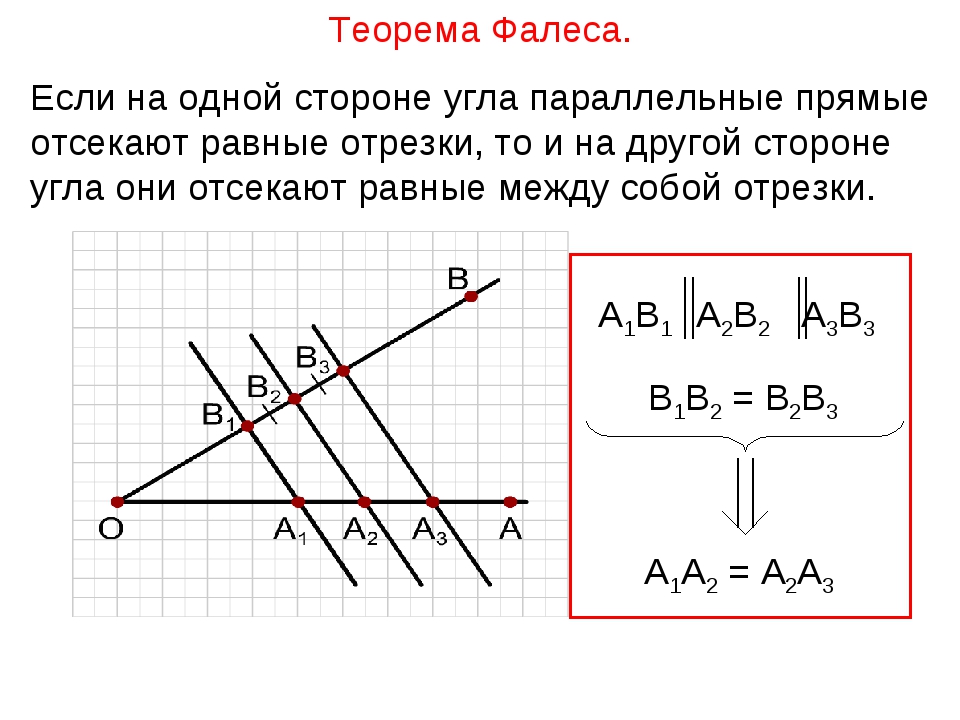

Иногда в математике, когда надо доказать, что некоторая совокупность преобразований — группа, а доказать это совсем впрямую не видится как, используется именно такой ход рассуждений.
(Более точно. Пусть — некоторое множество, — некоторая совокупность преобразований множества , — некоторая структура на множестве . Допустим, нам удалось показать, что (а) любое преобразование из сохраняет
, (б) и обратно, любое преобразование, сохраняющее , лежит в , (в) и к тому же произведение двух преобразований, сохраняющих , тоже сохраняет , априорным образом (т.е. без использования в доказательстве явного вида этих преобразований), и то же про обратные. Тогда отсюда можно сделать вывод, что — группа.)

Но такой ход рассуждений, надо сказать, весьма недецкий. Да и долго получается. Тут ожидать, что юный читатель легко въедет, да еще по пути и не потеряет нить мысли — трудно.

Дальше в главе про векторы написано про умножение вектора на число и свойства этой операции.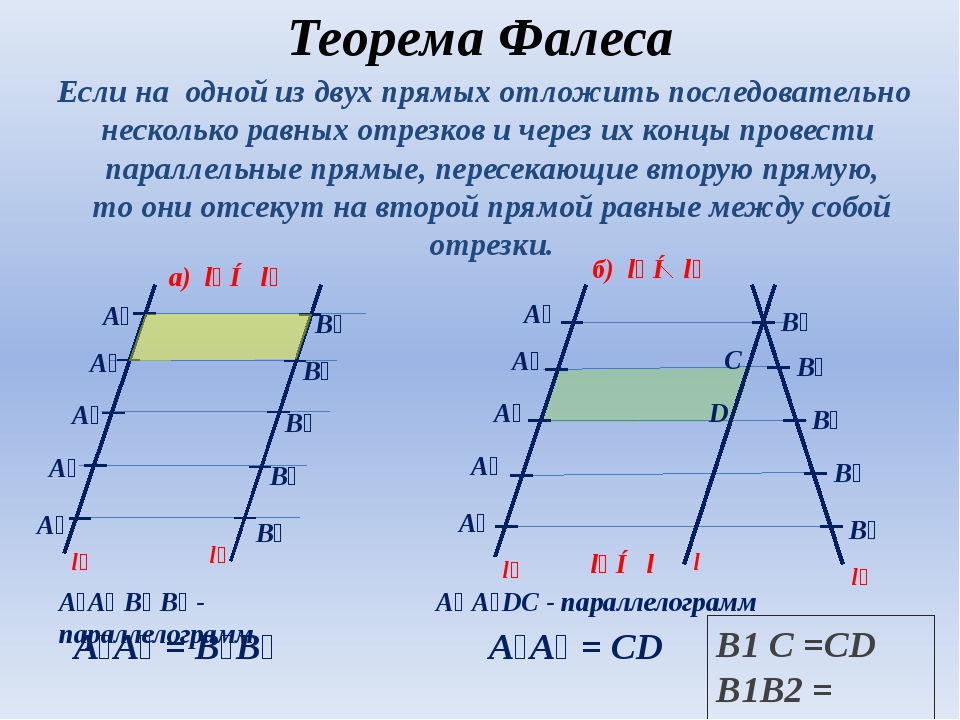 В издании 1979 г. вообще без доказательств, а в предыдущем с доказательствами. Правда, доказательство второго закона дистибутивности () довольно сложное и долгое, там опять недецкий ход мысли, и школьник его с трудом мог бы понять. По-научному этот ход мысли звучит как «делимая абелева группа без кручения является векторным пространством над «. И хотя в книжке этот ход мысли описан в школьных словах, но заходит всё равно плохо. У меня, во всяком случае, в голове не отложилось. В конце концов там всё сводится к тому, что учительница рисует на доске два подобных треугольника, на сторонах которых нарисованы стрелочки. Т.е. опять получается, что стремились к большой научности, а поскольку эта научность школьникам не доступна, то прибегаем к наглядности. (Много хотели, мало получили, из-за того, что много хотели.)

В следующей главе рассматривается подобие. Оно рассматривается с помощью векторов, при этом главную роль играет тот самый второй дистрибутивный закон. Но если мы его уже раньше приняли наглядно, то получается, что самые главные сведения про подобие мы уже тоже приняли наглядно, (когда рисовали два подобных треугольника со стрелочками), и тогда выходит, что большая часть главы про подобие — это просто эмпирические рассуждения, причем довольно
беспорядочные, вокруг того, что мы и так уже согласились считать верным ! Как-то так.

При традиционном изложении, как я понимаю, сначала теорема Фалеса, из нее — о пропорциональных отрезках, оттуда — признаки подобия треугольников, а уже оттуда — второй дистрибутивный закон для векторов. (См. Атанасян, например. Впрочем, в (современном) Атанасяне не совсем так, там площади используются). И ведь так гораздо проще и полнее получается, чем по-колмогоровски ! А посмотрите, в какой попе середине главы находится теорема о пропорциональных отрезках у Колмогорова, и как до нее пилить сто верст лесом ! (Короче, как и во многих других местах учебника, опять с ног на голову, и объясняется более простое (подобие) через более сложное (векторы).)

Исследовательская работа «Работы знаменитых древнегреческих учёных и их актуальность на сегодня»

Муниципальное общеобразовательное учреждение «Лицей №5»

Школьная научно-практическая конференция «Шаги в науки»

Исследовательская работа

Работы знаменитых древнегреческих учёных

и их актуальность на сегодня.

Выполнил:

ученик 8а класса

Осипов Евгений

Научный руководитель:

Сагарда Ирина Викторовна,

Учитель математики высшей

квалификационной категории

г. Оренбург

2015 г.

Оглавление

1. Вступление___________________________________________________3

2. Задачи и цели_________________________________________________4

3. Основная часть

   1. Математика в палеолите и неолите___________________________5

   2. Кто был первым математиком?______________________________5

   3. Пифагор Самосский _______________________________________8

   4. Демокрит________________________________________________10

   5. Гиппократ Хиосский ______________________________________11

   6. Архит Тарентский ________________________________________12

   7. Платон__________________________________________________14

   8. Аристотель ______________________________________________15

   9. Евдокс Книдский _________________________________________15

   10. Евклид __________________________________________________18

   11. Архимед _________________________________________________21

   12. Аполлоний Пергский_______________________________________23

   13. Менелай Александрийский _________________________________25

4. Вывод________________________________________________________27

5. Список используемой литературы и Интернет-ресурсов______________28.

Вступление

Геометрия — одна из наиболее древних математических наук. Первые геометрические факты мы находим в вавилонских клинописных таблицах и египетских папирусах. Возникновение геометрических знаний связано с практической деятельностью людей. И уже в древности геометрия превратилась в дедуктивную, строго логическую науку, построенную на основе системы аксиом. Постепенно развиваясь, она обогащалась новыми теоремами, идеями, методами. Интересы геометров и направление их научных исследований порою менялись в процессе исторического развития этой науки, поэтому, нелегко дать точное и исчерпывающее определение, что такое геометрия сегодня, каков её предмет, содержание и методы. В III в. до н. э. древнегреческий учёный Евклид написал книгу под названием «Начала». В этой книге Евклид подытожил накопленные к тому времени геометрические знания и попытался дать законченное аксиоматическое изложение этой науки. Написана она была настолько хорошо, что в течение 2000 лет всюду преподавание геометрии велось либо по переводам, либо по незначительным переработкам книги Евклида.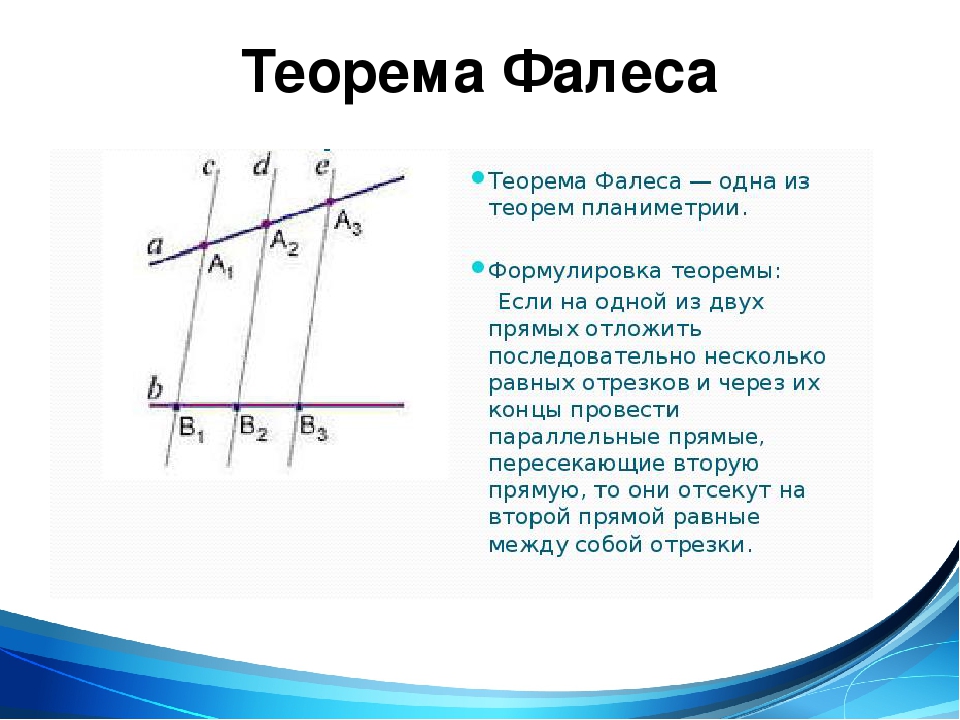 Например, таким пособием был учебник А. Д. Александрова, затем А.П. Киселёва, по которым советская школа работала до середины 20 столетия. Геометрия, как и другие науки, возникла из потребностей практики. Само слово «геометрия» греческое, в переводе означает «землемерие».

Люди очень рано столкнулись с необходимостью измерять земельные участки. Это требовало определенного запаса геометрических и арифметических знаний. Постепенно люди начали измерять и изучать свойства более сложных геометрических фигур. Развитие архитектуры, а несколько позднее и астрономии предъявило геометрии новые требования. И в Египте, и в Вавилоне сооружались колоссальные храмы, строительство которых могло производиться только на основе предварительных расчетов. И все же, несмотря на то что человечество накопило такие обширные знания геометрических фактов, геометрия как наука еще не существовала.

Геометрия стала наукой только после того, как в ней начали систематически применять логические доказательства, начали выводить геометрические предложения не только путем непосредственных измерений, но и путем умозаключений, путем вывода одного положения из другого, и устанавливать их в общем виде. Обычно этот переворот в геометрии связывают с именем ученого и философа VI века до нашей эры Пифагора Самосского. Но не только он был связан с древнегреческой геометрией. С ней были связаны такие знаменитые имена, как Фалес (ок. 625-547 гг. до н.э.), Демокрит (ок. 460-370 гг. до н.э.), Евдокс (ок. 408-355 гг. до н.э.) Аристотель (384-322 гг. до н.э.), Евклид (III в до н.э.), Аполлоний (III в до н.э.), Архимед (ок. 287-212 гг. до н.э.) и другие.

Однако все новые проблемы и созданные в связи с ними теории привели к тому, что совершенствовались сами способы математических доказательств, возрастала потребность создания стройной логической системы в геометрии.

Задачи и цели.

Цели, которые я поставил перед выполнением исследовательской работы:

• Изучить научные математические открытия в древние времена.

• Изучить математические открытия в Древней Греции.

• Понять, нужны ли нам эти знания или нет.

• Рассмотреть сферы использования данных геометрических понятий.

• Рассмотрев открытия, сделать вывод о том, насколько была или не была прогрессивна математика древних греков.

• Узнать, актуальны ли эти плоды трудов сегодня?

Задачи, которые надо выполнить:

• Рассмотреть достижения древнегреческой математики

• Рассмотреть все научные богатства и сделать на основе этого вывод.

• Узнать, какие люди создавали математику в Древней Греции.

• Сравнить математику Древней Греции с математикой Древнего Египта и математикой арабских стран

Математика в палеолите и неолите

Уже в палеолите люди изготовляли орудия для охоты и рыболовства в виде некоторых геометрических фигур (ромб, треугольник).

В эпоху неолита люди овладели земледелием, а в эпоху позднего неолита – выплавкой меди и бронзы, изготовлением оружия. Это повлекло оживления торговли на уровни обмена, в этот момент входят в употребления числа. Возникает необходимость измерения длины и ёмкости тел, но единицы измерения были грубыми и исходили из размеров человеческого тела. При возведении построек стали вырабатываться правила построения по прямым линиям и под прямым углом.

Человек неолита обладал острым чувством геометрической формы. Обжиг и раскраска глиняных сосудов, изготовление камышовых циновок, корзин и тканей, обработка металлов вырабатывали геометрические представления.

Кто был первым математиком?

История не сохранила имена древнеегипетских и вавилонских «решателей» задач. Так что первого известного математика придется искать среди древних греков. Наибольшие основания на этот титул у Фалеса Милетского.

Фалес Милетский (ок. 625-547 гг. до н.э.) – древнегреческий учёный из города Милета (Малая Азия). Считается, что именно он «привёз» геометрию из Египта и познакомил с ней греков.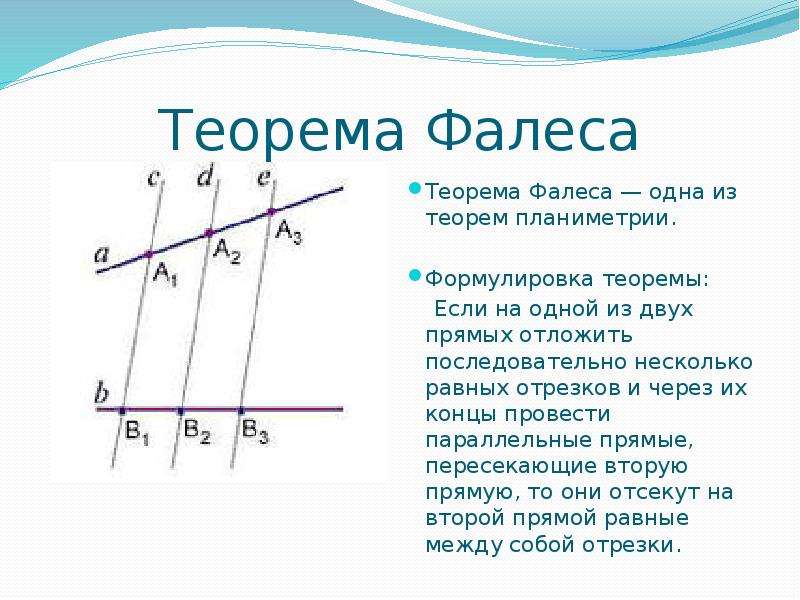 О самом Фалесе известно немного. Самый известный факт о нём — это то, что он предсказал полное солнечное затмение в 585 году до н.э., о чем и сообщают нам Ксенофан и Геродот. Ещё мы знаем, что в молодости Фалес был крупным купцом и путешественником, а в старости считался одним из величайших греческих мудрецов. О его славе как математика свидетельствуют достаточно ранние источники, например, Аристофан в поэме «Птицы».

В те далекие времена ещё не существовало отдельных наук о величинах, о природе, о мышление, а всё было слито воедино. «Можно проводить не только практические, но и мысленные опыты!» — эта значительная идея Фалеса, в равной мере, принадлежит математике, физике и философии, и не случайно Фалес считается родоначальником всех трёх наук. Но мы рассмотрим Фалеса как математика.

Считается, что Фалес первым сформулировал и доказал несколько геометрических теорем, а именно:

• вертикальные углы равны;

• имеет место равенство треугольников по одной стороне и двум прилегающим к ней углам;

• углы при основании равнобедренного треугольника равны;

• диаметр делит круг пополам;

• вписанный угол, опирающийся на диаметр, является прямым;

• равенство отрезков двух прямых, отсекаемых на них параллельными прямыми.

Доказательство теорем Фалес проводил с помощь наложения или из соображений симметрии.

Но Фалес пошёл ещё дальше – он создал такое понятие как метод. При помощи мыслительных движений и совмещений было доказано ещё несколько теорем. Одна из них до сих пор сохраняется в школьном курсе геометрии под названием теоремы Фалеса.

Фалес научился определять расстояние от берега до корабля, для чего использовал подобие треугольников. В одной из четырёх гаваней Милета был построен дальномер, состоящий из трех вбитых колышков, которые находились на одинаковом расстоянии друг от друга и при этом били на одной прямой, и размеченной прямой, которая перпендикулярна данной (СКСА). При появлении корабля на прямой СК находили такую точку D, чтобы D, B и E лежали на одной прямой. По второму признаку равенства треугольников ВСD=, из этого следует, что CD=АE, и поэтому расстояние до корабля по морю можно найти, измерив расстояние на суше СD.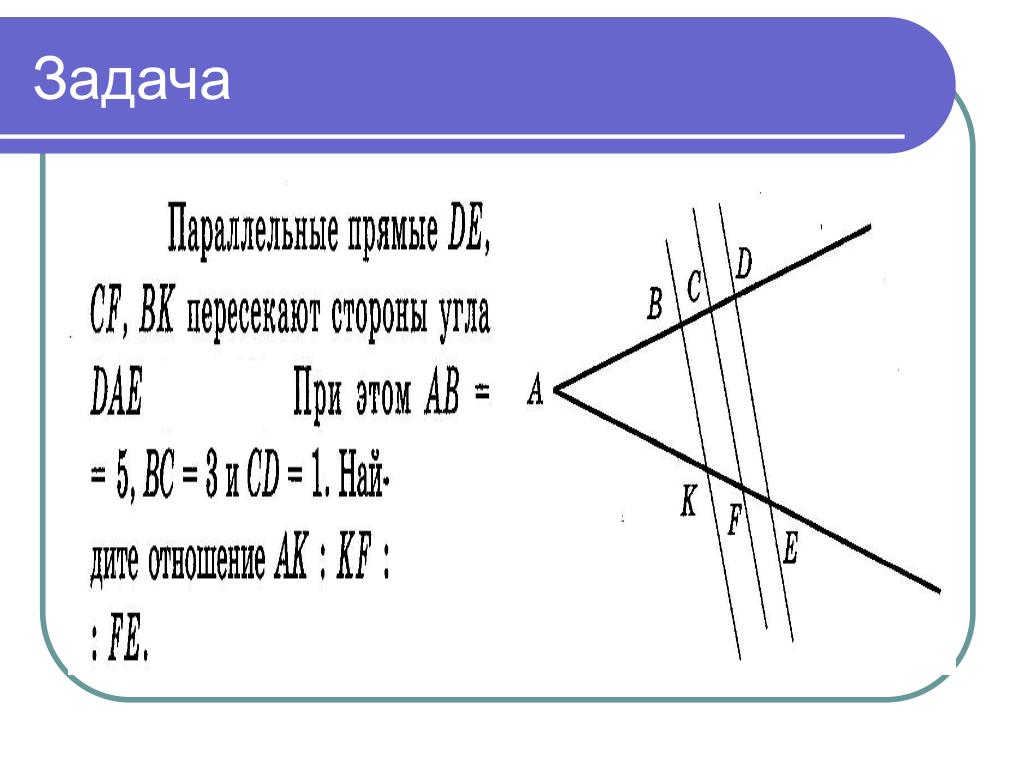

Теорема Фалеса: если параллельные прямые, пересекающие стороны угла, отсекают равные отрезки на одной его стороне, то они отсекают равные отрезки и на другой его стороне.

Рассмотрим доказательство этой теоремы в двух случаях: когда секущие параллельны, и когда секущие не параллельны.

l₁ и l₂ параллельны. Тогда А₁В₁В₂А₂ — параллелограмм, а из этого следует, что А₁А₂ = В₁В₂. Точно также можно доказать, что А₂А₃ = В₂В₃. Из этого следует что В₁В₂ = В₂В_3, что и требовалось доказать.

а и b – не параллельны. Проведём прямую с, параллельная прямой а и проходящая через точку В₁. Точка F и Т лежащие на прямой с, пересекающие прямые А₂В₂ и А₃В₃ соответственно.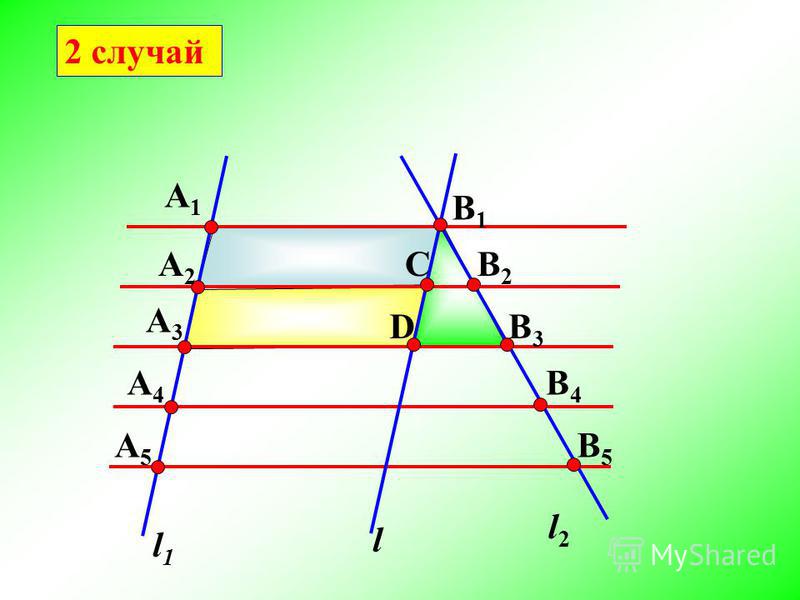 Из предыдущего доказательство мы можем сделать вывод, что В₁F = FT. Проведя прямую d, лежащая на точке В₂, и обозначив точкой О пересечение прямых А₃В₃ и d, можно сделать вывод, что В₂О=В₁F. Углы, прилежащие к сторонам В₂0 и В₁F, равны. По второму признаку равенства треугольников, DВ₁В₂F = DВ₂В₃О. Из этого следует, что В₁В₂=В₂В₃, что и требовалось доказать.

Существует и обратная теорема: если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны. То есть, если , следует, что A₁B₁||A₂B₂||A₃B₃…;

Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок.

Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.

Легенда рассказывает о том, что Фалес, будучи, в Египте, поразил фараона Амасиса и посрамил египетских учёных тем, что сумел точно установить высоту пирамиды, дождавшись момента, когда длина тени палки становится равной её высоте, и тогда измерил длину тени пирамиды.

В настоящее время в истории математики не существует сомнений, что геометрические открытия, которые приписывались Фалесу его соотечественниками, в действительности были просто заимствованы из египетской науки. Для непосредственных учеников Фалеса каждое сообщение их учителя казалось совершенной новостью, никому ранее неизвестной и потому вполне ему принадлежащей.

Теорема была увековечена и в искусстве. Так, например, аргентинская музыкальная группа представила песню, посвящённую теореме. В видеоклипе для этой песни приводится доказательство для прямой теоремы для пропорциональных отрезков.

Пифагор Самосский

Пифагор Самосский (570-490гг. до н. э.) — древнегреческий философ, математик и мистик, создатель религиозно-философской школы пифагорейцев.

Как связан Пифагор с геометрией? Если задать этот вопрос ученику, то я думаю, что многие ответят: «Теорема Пифагора». Действительно, теорема Пифагора – самая знаменитая теорема за всю историю геометрии.

Есть две формулировки теоремы: геометрическая и алгебраическая.

Геометрическая формулировка была самой первой формулировкой и звучала она так: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Такая формулировка считалась сложной и через некоторое время придумали другую формулировку, которая называется алгебраической. Звучит она так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Существует теорема, обратная теореме Пифагора. Она звучит так: Для всякой тройки положительных чисел ,  и , такой, что , существует прямоугольный треугольник с катетами  и  и гипотенузой .

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

Мы рассмотрим несколько видов доказательств этой теоремы, как прямой, так и обратной.

Проведём доказательство теоремы Пифагора геометрической формулировки. Площадь квадрата, построенного на стороне а равна а². Площадь квадрата построенного на стороне b равна b². Площадь квадрата на стороне с равна с².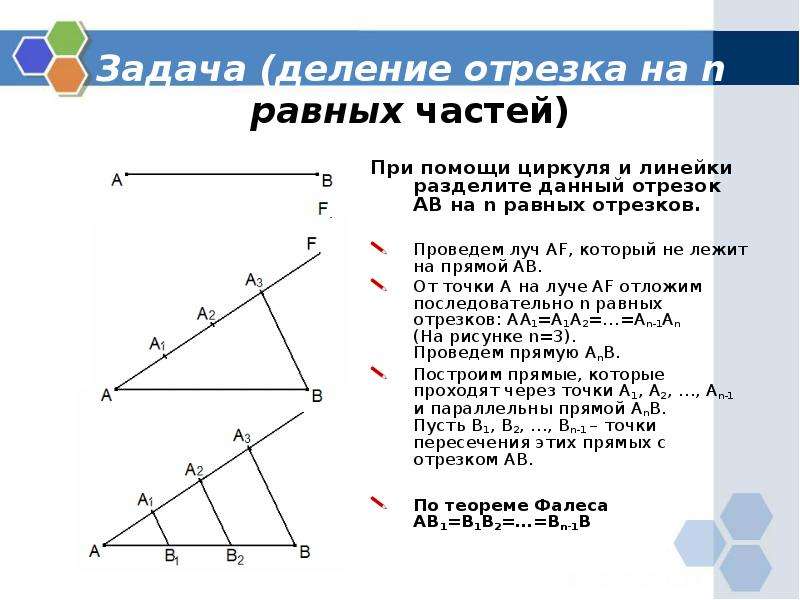 Так как а и b – катеты, то по формулировке получаем, что а²+b²=с², что и требовалось доказать.

Теперь проведем доказательство этой же теоремы, но алгебраической формулировки. Здесь мы рассмотрим только два способа доказательства.

1. С помощью подобных треугольников. АСН=180-90-А. В=180-90-А. Из этого следует, что АСН = В. Аналогичным способом доказываем, что НСВ = А. Из этого можно сделать вывод, что АСН и ВСН подобны АВС. Введём обозначения ВС=а, АС=b, АВ=с. Получаем следующее выражение: ; ,что является эквивалентно; Складываем полученное, Так как НВ+АН=АВ, а по введённым обозначениям АВ = с. Из этого следует, что а²+b²=с², что и требовалось доказать.

2. Методом площадей. Рассмотрим прямоугольный треугольник с катетами a ,b и гипотенузой с. Достроим треугольник до квадрата со стороной а+b. Площадь этого квадрата равна (а+b)². С другой стороны, этот квадрат составлен из 4 равных прямоугольных треугольника, площадь которых равна , и квадрата (так как то угол между ними равен 180-90=90) со стороной с, поэтому . Вычислив по этим 2 формулам, получим одно и тоже число, так как мы ищем площадь одного и того же квадрата со стороной а+b. Зная это, можем приравнять эти выражения:

Что и требовалось доказать.

Вообще, можно сказать, что первый способ доказательства является более легким, так как он не требует знаний о площадях.

Пифагор Самосский, поселившись в Италии, основал пифагорейский союз. Пифагорейцы занимались в основном математикой. Пифагорейцы изучили варианты, в которых величины всех сторон выражаются целыми числами. Они много уделяли внимание числам. Например, числа равные сумме всех своих делителей (кроме 1 и самого числа) считали совершенными (6=2*3; 2+3=6). Но вскоре после восстаний в Италии пифагорейский союз распался

Демокрит

Демокрит (460-370 гг. до н.э.) был из Абдер во Фракии. Как и Фалес, свои знания Демокрит почерпнул на Востоке: «Никто не превзошёл меня в построении фигур из линий, сопровождающимся доказательством, – даже землемеры в Египте»

В математических сочинения Демокрита «О числах», «О касании круга и шара», «О геометрии», «Об иррациональных отрезках» развивается идея о бесконечно малых величинах. Так, Демокрит считал, что отношение малых отрезков пути к соответственно малым промежуткам времени остаётся конечным и определяет скорость движения.

Свою геометрию Демокрит строил на основе атомистической структуры пространства: линии, поверхности, объёмы считались им состоящим из большого числа конечных и далее неделимых элементов. Демокрит установил, что объём пирамиды равен третьей части объёма призмы, а объём конуса – третьей части объёма цилиндра с теми же основаниями и высотами, хотя точного доказательства он и не дал. Он разбивал конус на ряд наложенных друг на друга кружков малой толщины, после чего находил объём всего конуса. В рассуждениях Демокрита содержались зачатки исчисления бесконечно малых, впоследствии использованные Архимедом при вычислении площадей и объёмов фигур.

Гиппократ Хиосский

Уже в школе Демокрита геометрия выводилась из небольшого числа предпосылок. Однако первый систематический курс планиметрии принадлежит ионийском натурфилософу и математику Гиппократу из Хиоса -ок. 440 г. до н.э. (не путать его со знаменитым врачом Гиппократом, жившим намного позже). В сочинение «Начала» Гиппократа уже в полном объёме применяется принцип логического заключения от одного утверждения к другому. «Начала» Гиппократа включали в себя теорию параллельных, теорию дуг и хорд, построение правильных многоугольников и вычислении площади круга. Гиппократ применяет не только теорему Пифагора, но и соответствующие неравенства для непрямоугольных треугольников. «Начала» Гиппократа Хиосского составили содержания первых четырёх книг «Начала» Евклида.

Единственный дошедший до нас цельный математический фрагмент «Начал» Гиппократа содержит рассуждение о так называемых «луночках» — плоских фигурах, ограниченных двумя круговыми дугами. Вопрос о площади таких луночек, выражающихся через диаметр, имеет прямое отношение к упоминавшийся проблеме квадратуры круга (построение с помощью линейки и циркуля квадрата равновеликого данному). В этой связи Гиппократ доказал, что площади подобных круговых сегментов относятся как квадраты стягивающих их хорд.

Помимо квадратуры круга Гиппократ занимался проблемой удвоения куба — задача о построение куба, имеющий объём вдвое больше, чем данный куб. Он свёл задачу к планиметрической – к определению двух средних пропорциональных величин х и у для двух данных отрезков а и 2а, то есть к отысканию искомого ребра х по данному ребру а из пропорции .

«Начала» Гиппократа Хиосского доказывают существование уже упорядоченной планиметрии в Древней Греции в V веке до н.э., а сам Гиппократ считается одним из первых математиков-профессионалов.

Архит Тарентский

Архи́т Та́рентский (428-347гг. до н.э.) — философ-пифагореец, математик и механик, теоретик музыки, государственный деятель и полководец. Друг Платона и учитель Евдокса.

Самый выдающийся представитель школы Пифагора. Он впервые разработал теория рычага, весов, безмена, колеса, клина и блока. Некоторые авторы приписывали ему изобретение винта, который мы сейчас называем «архимедов винт», а другие авторы рассказывают о том что он в 390 году до н.э. Архит создал небольшой автомат, размером с голубя, способный махать крыльями и даже взлетать. Как государственный деятель, Архит был очень хорош: его семикратно избирали на должность стратега; он провёл несколько успешных военных кампаний против латинских соседей. В одной из этих военных кампаний он вызволил из плена своего друга Платона и спас жизнь великому философу. Диоген Лаэртский писал о нём: «Всяческими своими добродетелями вызывал он всеобщее восхищение». Архит немало сделал для облегчения жизни простых граждан; Аристотель в книге «Политика» сообщает, что он изобрёл детскую погремушку: «нужно считать прекрасным изобретением ту погремушку Архита, которую дают малым детям, чтобы они, занимаясь ею, не ломали ничего из домашних вещей: ведь то, что молодо, не может оставаться спокойным»

Из математических работ Архита сохранился отрывок в комментарии Евтокия ко 2 книге трактата Архимеда «О шаре и цилиндре». Со ссылкой на «Историю геометрии» Евдокса Книдского Евтокий приводит найденное Архитом решение делийской задачи об удвоении куба. Это решение, самое первое в истории математики, основано на отыскании точки пересечения трёх поверхностей — конуса, цилиндра и тора. Ещё для решения этой задачи был использован принцип непрерывности.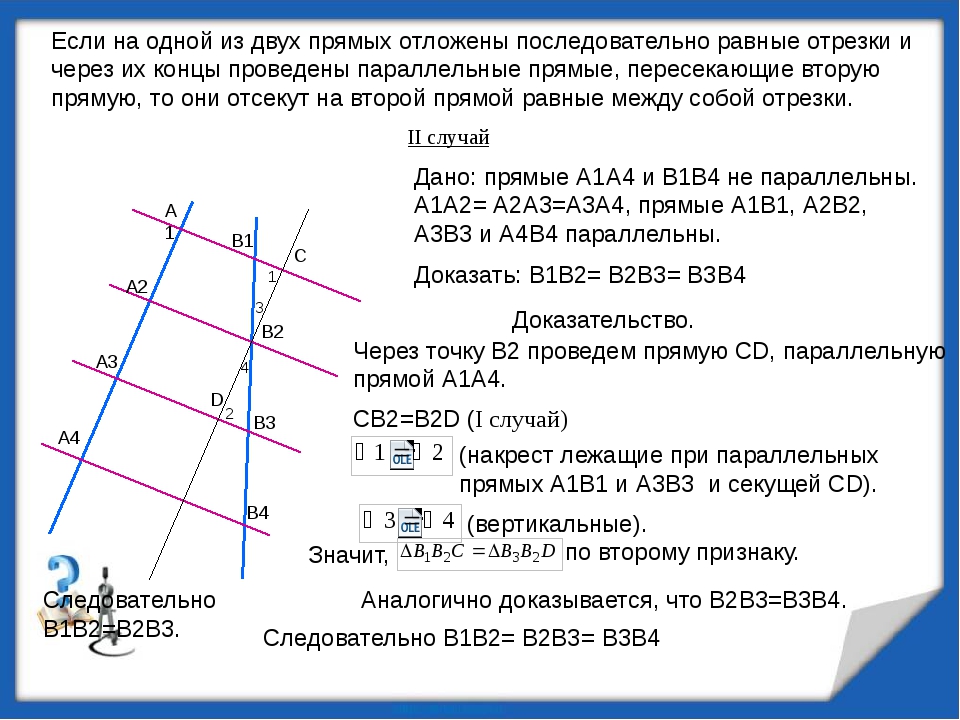 Этот принцип можно сформулировать так: если непрерывно изменяющаяся величина сначала больше, а потом меньше заданной величины, то она будет равна ей.

Ещё Архит развил теорию отношений и пропорций и на основании ее дал теоретико-числовое обоснование законов звучания. Впервые систематически разрабатывал механику. По мнению Б.Л. Ван ден Вардена, Архит был автором восьмой книги «Начал» Евклида.

В одном из математических текстов, приписываемых Архиту, средне арифметические, средне геометрическое и средне гармоническое были определены как средние члены соответственно арифметической, геометрической и гармонической пропорцией:

Из этих равенств легко получаются современные определения, если выразить переменную b:

C помощью этих понятий пифагорейцы выразили отношение основных гармонических интервалов музыкального звукоряда.

В то время, когда проходил «кризис основ математики» (период, когда поняли о несоизмеримости некоторых величин) Архит «вызывавший удивление у людей своим совершенством во всех отношениях» дал «музыкальное доказательство» тому, что – иррациональное число. Струны длиной 1 и при одинаковой толщине и натяжении вместе давали диссонанс, тогда как приятные для слуха звучания получаются при длине а и а+1. Из этого Архит заключил, что число не может быть выражено отношением двух натуральных чисел, то есть иррациональное.

Платон

Дальнейшее развитие математики связано с великим философом Древней Греции Платоном (427-347 гг. до н.э.). Платон – это не имя, а прозвище Аристокла, полученное им за свою мускулатуру атлета. В истории мировой культуры Платон – великое явление. Хоть и жил он в древнегреческом обществе, но как деятель принадлежит всему миру.

Сам Платон математиком не был, хотя математике он предавал исключительно большое значение. При входе в Академию была надпись: «Пусть не входит сюда тот, кто не знает геометрии». Одному из желающих поступить в его школу для изучения философии без знаний геометрии Платон сказал: «Уйди прочь! У тебя нет орудий для изучения философии».

Важным этапом в идейном развитии Платона оказалось происшедшее ещё в Италии его сближение с пифагорейцами, влияние их религиозно-этического учения, их философии числа и их космологии.

Применение математике к практике Платон считал неизменным занятием. Математику Платон ценил только как науку, необходимую для занятий философией. Математические проблемы им рассматриваются в ряде диалогов: «Менон», «Теэтет», «Государство», «Послезаконие». В последнем сочинение Платон излагает теорию пропорций Архита. Не добавив к математической теории многогранников ни слова, но включив ее в свою космогоническую теорию, Платон увековечил свою имя в математике – пять правильных многогранников (тетраэрд, куб и додекаэдр, известные ещё Пифагору, а также октаэдр и икосаэдр, открытые Теэтетом, часто называют «платоновыми телами» или «космическими фигурами»)

Со школой Платона связано немало выдающихся учёных, среди которых Феодор, Теэтет и Архит. Ещё более крупной фигурой связанная с Академией Платона, был «отец логики» Аристотель из Страгиры (384-322 гг. до н.э.).

Аристотель

Об Аристотеле я расскажу немного, потому что Аристотель не был математиком и не написал ни одного математического сочинения, но был хорошо знаком с достижениями греческих математиков. В его книгах содержатся важные замечания, относящиеся к математическим наукам. Говоря о математике, Аристотель отмечал особенности математического метода: изучая количественные свойства предметов, математика отвлекается от всех чувственно воспринимаемых свойств этих предметов. Поэтому математические истины познаются не с помощью органов чувств, а с помощью разума. Этим определяется логика построения математики: исходя из определений и аксиом, то есть бесспорных положений, с помощью логических умозаключений выводятся теоремы и следствия.

Аристотель является создателем формальной логики, то есть учения об умозаключениях и доказательствах. Это учение, изложенное в трактате «Аналитика», не признавалась Аристотелем отдельной научной дисциплиной, а подразумевалось как орудие всякой науки. Трактаты Аристотеля по логике значительно повлияли на уточнение аксиоматике и на строгость её изложения.

Евдокс Книдский.

Величайшем математиком IV века до н.э. является Евдокс Книдский (ок. 408-355 гг. до н.э.) Евдо́кс Кни́дский — древнегреческий математик, механик и астроном. Занимался также врачеванием, философией и музыкой; был известен как оратор и законовед. В молодости он изучал математику у Архита в Таренте, медицину у Филистона на Сицилии, в 23-летнем возрасте в гавани города Пирея, откуда совершал ежедневные походы в платоновскую Академию и обратно (из-за бедности Евдокс не мог поселиться в Афинах). Позднее, при содействии друзей, он совершил путешествие в Египет, где учился астрономии и математике у жрецов Гелиополя. Ещё при жизни друзья его прозвали Eu doxor – окруженный почетом, знаменитый.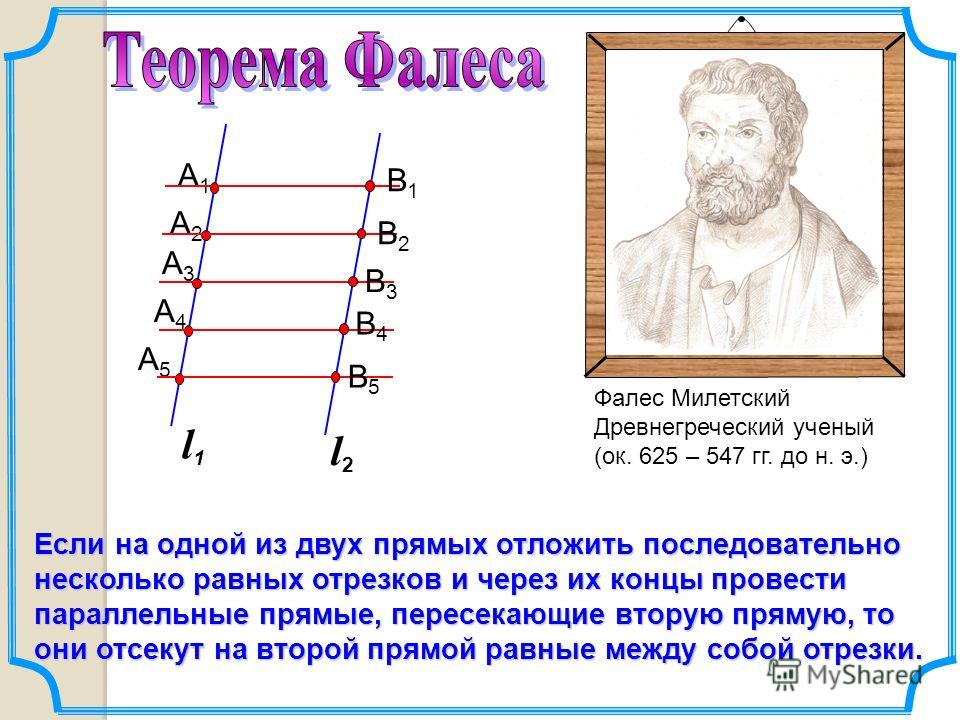 Настоящее имя Евдокса мы не знаем.

Научная школа Евдокса сыграла большую роль в развитии античной астрономии и математики. Историки науки относят Евдокса к числу основоположников интегрального исчисления и теоретической астрономии. В частности, Евдокс создал теорию геометрических величин (античный аналог вещественных чисел), метод исчерпывания (прообраз анализа криволинейных фигур)

Общая теория отношений

Числовые системы древних греков ограничивались натуральными числами и их отношениями (дробями, рациональными числами). Однако ещё пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, то есть отношение их длин не может быть представлено рациональным числом. Стало понятно, что пифагорейская арифметика должна быть каким-то образом расширена с тем, чтобы включать все результаты измерений. Это и сделал Евдокс. Его теория дошла до нас в изложении Евклида (Начала, книга V)

В дополнение к числам Евдокс ввёл более широкое понятие геометрической величины, то есть длины отрезка, площади или объёма.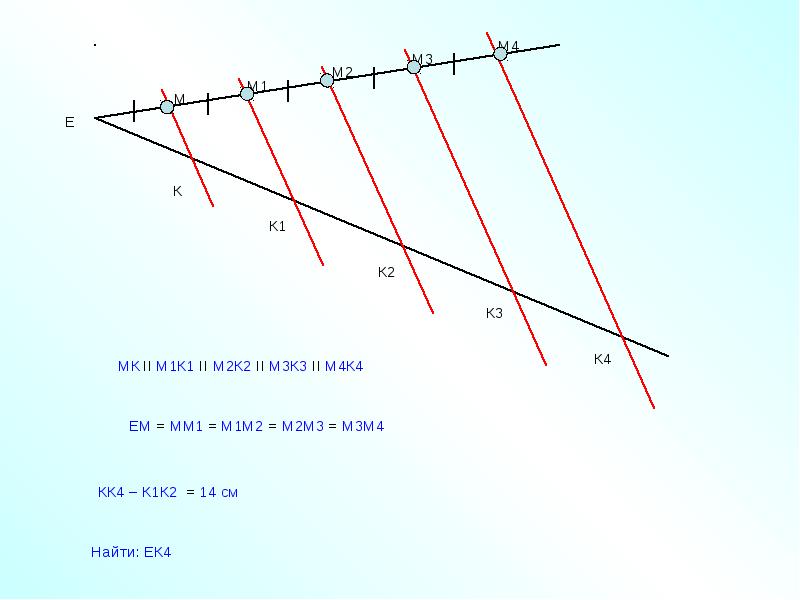 С современной точки зрения, число при таком подходе есть отношение двух однородных величин — например, исследуемой и единичного эталона. Этот подход снимает проблему несоизмеримости. По существу, теория отношений Евдокса — это геометрическая модель вещественных чисел. Следует, однако, подчеркнуть, что Евдокс остался верен прежней традиции — он не рассматривал такое отношение как число; из-за этого в «Началах» многие теоремы о свойствах чисел затем заново доказываются для величин. Признание иррациональностей как особого вида чисел произошло много позднее, под влиянием индийских и исламских математических школ.

В начале своего построения Евдокс дал аксиоматику для сравнения величин. Все однородные величины сравнимы между собой, и для них определены две операции: отделение части и соединение (взятие кратного). Однородность величин сформулирована в виде аксиомы, известной также как аксиома Архимеда: «Величины имеют отношение между собой, если они, взятые кратно, могут превзойти друг друга».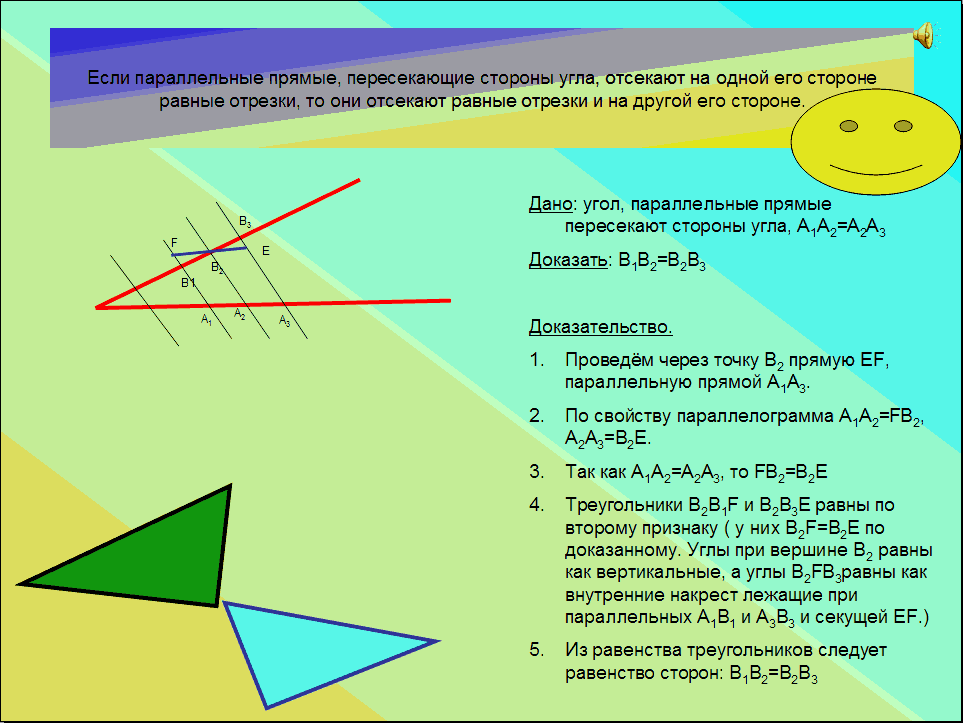 Сам Архимед при изложении этой аксиомы сослался на Евдокса.

Теория отношений Евдокса покончило с арифметической теорией пифагорейцев, применяемой только к соизмеримым величинам. Это была чисто геометрическая теория, сделавшая излишками какие-либо отговорки относительно соизмеримости и несоизмеримости рассматриваемых величин. Это означает, что именно Евдокс преодолел «кризис основ математики», направив её по пути геометризации.

Метод исчерпывания Евдокса.

Метод исчерпывания — античный метод для исследования площади или объёма криволинейных фигур. Идею метода, в не очень ясных выражениях, высказал ещё Антифон, однако разработку и применение осуществил Евдокс Книдский. Обоснование этого метода не опирается на понятие бесконечно малых, но неявно включает понятие предела.

Метод заключался в следующем: для нахождения площади (или объёма) некоторой фигуры в эту фигуру вписывалась монотонная последовательность других фигур и доказывалось, что их площади (объёмы) неограниченно приближаются к площади (объёму) искомой фигуры. Затем вычислялся предел последовательности площадей (объёмов), для чего выдвигалась гипотеза, что он равен некоторому A и доказывалось, что обратное приводит к противоречию. Поскольку общей теории пределов не было (греки избегали понятия бесконечности), все эти шаги, включая обоснование единственности предела, повторялись для каждой задачи.

В такой форме метод исчерпывания хорошо вписывался в строго дедуктивное построение античной математики, однако имел несколько существенных недостатков. Во-первых, он был исключительно громоздким. Во-вторых, не было никакого общего метода для вычисления предельного значения A; Архимед, например, нередко выводил его из механических соображений или просто интуитивно угадывал. Наконец, этот метод не пригоден для нахождения площадей бесконечных фигур.

Лемма Евдокса. Даны две величины а и b, где аb. Если из а вычесть с, из остатка а₁ вычесть , и так далее, то через конечное количество шагов n получим a_n<b.

Евклид

Математические знания накапливались в Греции и греческих колониях в течении нескольких столетий. Постепенно стало ясно: нельзя логическим путём вывести нечто из ничего. Нужно зафиксировать первоначальные понятия и факты, из которых можно вывести всё остальное. Но какие факты можно считать первоначальными? Ведь многие утверждения следуют друг из друга. Рано или поздно должен был появится мыслитель, способный навести в математическом хозяйстве хотя бы видимость порядка.

И такой мыслитель появился в III веке до нашей эры в Александрии. Это был Евклид. Точных сведений о его биографии не сохранилось.

Евклидова геометрия (или элементарная геометрия) — геометрическая теория, основанная на системе аксиом, впервые изложенной в «Началах» Евклида (III век до н. э.). Некоторые из аксиом Евклида (часть из них он называл постулами) и сейчас используются в курсах геометрии. Обычно относится к двум или трём измерениям, хотя можно говорить о многомерном евклидовом пространстве. Евклидова геометрия названа в честь древнегреческого математика Евклида. В его книге «Начала», в частности систематически описывается геометрия евклидовой плоскости.

Аксиомы, приведённые Евклидом в «Началах», таковы:

1. Через каждые две точки можно провести ровно одну прямую.

2. Вдоль любого отрезка можно провести прямую.

3. Имея отрезок, можно провести окружность так, что отрезок — радиус, а один из его концов — центр окружности.

4. Все прямые углы между собою равны.

5. Аксиома параллельности Евклида: Через точку А вне прямой а в плоскости, проходящей через А и а, можно провести лишь одну прямую, не пересекающую а.

Самая знаменитая его аксиома, это аксиома параллельных прямых (пятый постулат Евклида). Она заключается в том, что, через точку, не лежащей на данной прямой, проходит только одна прямая, параллельная данной. При условии рассмотрения этой аксиомы в плоскости, то действительно, если провести параллельную прямую b через точку А прямой a, то уже прямая с, проведенная через точку А отклоненная от прямой b хотя на 0,01°, будет пересекать прямую а. Многие математики пытались доказать этот постулат с помощью других аксиом. И лишь в прошлом веке было окончательно выяснено, что утверждение о единственной прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных евклидовых постулатов, и поэтому эта аксиома является основной.

Ещё, Евклид в своих «Началах» сформулировал чёткое и недвусмысленное определение: «Точка есть то, что не имеет частей». Да вот какой казус: свойство точки, описанные в аксиомах работают вовсю, а её определение во всех тринадцати книгах «Начал» не применяется ни разу. Не понадобилось оно геометрам ни в пятнадцатом веке, ни в девятнадцатом… Поэтому и стали в учебниках писать, что нет определения у точки – простейшее, мол, понятие, к другим не сводимое.

Только в XIX в. было показано, что аксиомы Евклида не являются универсальными и верны не во всяких обстоятельствах. Основные открытия геометрических систем, в которых аксиомы Евклида не верны, были сделаны Н. И. Лобачевским и Георгом Риманом. О них говорят, как о создателях неевклидовой геометрии. Наиболее поразительной чертой неевклидовой геометрии является тот факт, что две прямые линии, параллельные в одной части пространства, могут пересечься в другой. Альберт Эйнштейн, разрабатывая общую теорию относительности, пришел к выводу, что геометрия Вселенной, в которой мы живем, является неевклидовой. Однако Евклидова геометрия по-прежнему остается справедливой при описании систем и явлений, с которыми мы сталкиваемся в повседневной жизни.

Евклидова геометрия набирала необычайно быстро популярность. На протяжении четырех столетий «Начала» публиковались 2500 раз.

Дальнейшая судьба «Начал», несмотря на всю их образцовость, сложилась непросто. Средневековые фанатики – и христиане, и мусульмане – безжалостно уничтожали древние рукописи, действуя по принципу: «Если они противоречат нашим священным книгам, то они вредны; а если нет, то они ни к чему». И всё-таки, в латинских и арабских переводах, «Начала» выжили, и их по достоинству оценили математики нового времени. Величайший учёный XVII века Исаак Ньютон, следуя Евклиду, назвал свою главную книгу «Начала натуральной философии». До 20 века книга считалась основным учебником по геометрии не только для школ, но и для университетов.

Конечно, все особенности Евклидова пространства были открыты не сразу, а в результате многовековой работы научной мысли, но отправным пунктом этой работы послужили «Начала» Евклида.

Знание основ Евклидовой геометрии является ныне необходимым элементом общего образования во всем мире.

Ещё Евклид создал алгоритм для нахождение наибольшего общего делителя двух положительных чисел. Вот его простейший вид: пусть заданы два числа

1. Если они равны, то их наибольший делитель будет каждое из них.

2. Если числа не равны, то вычитаем из большего меньшее. Теперь рассмотрим вычитаемое и разность. Проделаем с ним такую же операцию. Этот процесс будем продолжать до тех пор, пока вычитаемое и разность не станут равными. Поскольку большее число в парах на каждом шагу уменьшается, но всегда не меньше единицы, то такой процесс не может быть бесконечным.

Можно смело утверждать, что Евклид заложил основы современной геометрии.

Архимед

Архиме́д (ок. 287-212 гг. до н.э.) — древнегречесский математик, физик и инженер из Сиракуз. Сделал множество открытий в геометрии. Заложил основы механики, гидростатики, автор ряда важных изобретений. Молодость Архимеда прошла в его родном городе Сиракузы, на средиземском острове Сицилия. Некоторое время жил в Александрии – столица наук

Когда началась вторая пуническая война, сиракузский царь был на стороне Карфагена.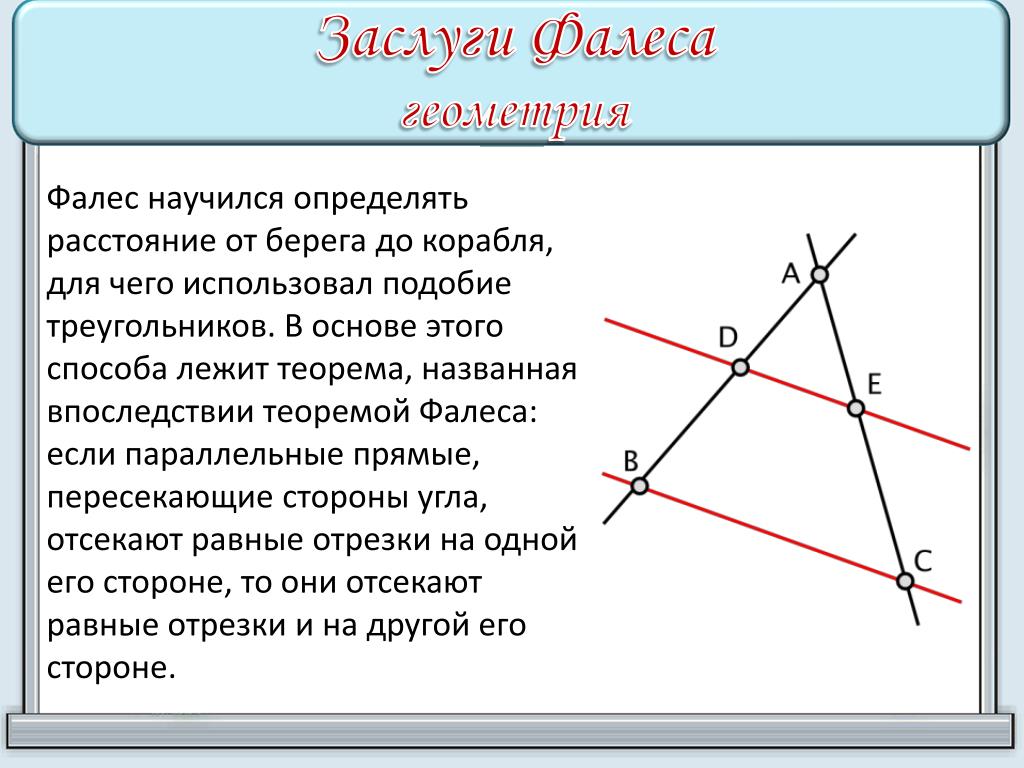 Все защитные устройства Сиракузы были сконструированы Архимедом и поэтому этот город не удалось взять штурмом. Даже после смерти Архимеда, Сиракузы продолжали использовать его изобретение. Современники в полной мере оценивали Архимеда как инженера, ведь он создал не только эти защитные устройства, но и знаменитый архимедов винт.

Работы Архимеда относились почти ко всем областям математики того времени: ему принадлежат замечательные исследования по геометрии, алгебре, арифметике. Так, он нашёл все полуправильные многогранники, которые теперь носят его имя, значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений вида , корни которых он находил с помощью пересечения параболы и гиперболы. Архимед провёл и полное исследование этих уравнений, то есть нашёл, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать.

Однако главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа. Греки до Архимеда сумели определить площади многоугольников и круга, объём призмы и цилиндра , пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей или объёмов; для этого он усовершенствовал и виртуозно применял метод исчерпывания Евдокса Книдского.

На вопрос: «Есть ли бесконечно большие или бесконечно малье числа?» Архимед ответил так: «Нет. Всякое малое число, будучи сложено само с собой достаточно количество раз, превзойдет всякое наперед заданное число» тем самым поставил точку в этом долгом споре. Этот принцип вошел в математику под названием аксиомы Архимеда. Пользуясь этой аксиомой, Архимед доказал, что объём шара и описанного возле него цилиндра относятся как 2:3.

Идеи Архимеда легли впоследствии в основу интегрального исчисления. Интегральное исчисление – суммирование бесконечного числа, непрерывно меняющих слагаемых.

Огромное значение для развития математики имело вычисленное Архимедом отношение длины окружности к диаметру. В работе «Об измерении круга» Архимед дал своё знаменитое приближение для числа : «архимедово число» . Более того, он сумел оценить точность этого приближения: . Для доказательства он построил для круга вписанный и описанный 96-угольники и вычислил длины их сторон.

Ещё Архимед написал книгу лемм, сохраненная только в арабском переводе. «Леммы» — книга, приписываемая Архимеду арабским учёным Сабитом ибн Куррой. Книга написана более 2200 лет назад и состоит из 15 теорем о кругах и окружностях. Авторство «Лемм» остаётся вопросом. Одна из причин этому состоит в том, что в четвёртой теореме присутствует ссылка на Архимеда как на стороннее лицо; однако она могла быть добавлена переводчиком. Также существует версия, что «Леммы» могут быть сборником теорем Архимеда, который был составлен другим греческим автором.

Задачи, решенные Архимедом, сложны и красивы сами по себе. Но приёмы, использованные для их решения, оказались ещё более удивительными, чем ответы. Они послужили подсказкой учёным куда более поздней эпохи – первооткрывателям современного математического анализа.

Можно сказать, хоть и Архимеду приписывают звание военного инженера, для геометрии его достижения были не менее значительными.

Аполлоний Пергский

Аполлоний Пергский (ок. 262-190 гг. до н.э.) – древнегреческий математик. Написал ряд сочинений, не дошедших до нас. Важнейший труд – «Конические сечения» (первые 4 книги сохранились в греческом подлиннике, следующие 3 книги сохранились в арабском переводе, а восьмая утеряна). Аполлоний первый рассмотрел эллипс, параболу, гиперболу как произвольные плоские сечения произвольных конусов с круговым основанием и детально изучил их свойства. Обнаружил, что парабола – предельный случай эллипса; открыл асимптоты гиперболы; получил уравнение параболы; впервые изучил свойства касательных и подкасательных к коническим сечениям. Аполлоний доказал 387 теорем о кривых второго порядка методом, который состоит в отнесении кривой к какому-либо ее диаметров и к сопряженным с ним хордам.

Искусство построения геометрических фигур при помощи линейки и циркуля было в высокой степени развито в Древней Греции. Одна из труднейших задач на построение, которую уже тогда умели выполнять, — построение окружности, касающейся трёх данных окружностей. Эта задача называется задачей Аполлония.

Но не только задачей прославился Аполлоний, но и теоремой (даже двумя):

1. Сумма квадратов длин сопряженных полудиаметров эллипса есть величина постоянная, равная сумме квадратов его полуосей.

2. Площадь описанного вокруг эллипса параллелограмма, стороны которого имеют сопряжённое направление, постоянна и равна произведению длин его диаметров.

Вслед за Архимедом Аполлоний занимался усовершенствованием системы счисления; значительно облегчил умножение больших чисел в греческой нумерации.

Конические сечения.

Коническим сечениям Аполлоний уделил много времени, поэтому грех не рассказать о этих сечениях поподробнее.

Конические сечения – кривые, получившиеся при сечении кругового конуса (точнее – конической поверхности) плоскостью, не проходящей через вершину.

Получающиеся при этом ограниченные фигуры называются эллипсами, а не ограниченные – гиперболами (если секущая плоскость пересекает обе полости конуса) и параболами (если секущая плоскость пересекается лишь с одной из его полостей) Все виды конического сечения можно получить с помощью карманного фонарика, направляя его под разными углами на ровную поверхность (в данном случае свет фонарика будет являться конусом, а ровная поверхность – секущей плоскостью). Правда, при этом мы у видим всего одну ветвь гиперболы. Чтобы увидеть вторую ветвь, надо повернуть ось фонарика на 180. Эллипс получается, если секущая плоскость пересекает все образующие конуса точки в одной его полости. Парабола получается, если секущая плоскость параллельна одной из касательных плоскостей конуса. Гипербола получается, если секущая плоскость пересекает обе полости конуса.

Одинаковый способ изучения различных конических сечений влечет и сходство уравнений, описывающих эти кривые. В секущей плоскости можно так выбрать систему координат, чтобы уравнение конического сечения имело вид (р и  — постоянные). Если р≠0, то уравнение определяет параболу при =0, эллипс — при <0, гиперболу – при 0. Геометрическое свойство конических сечений, содержащиеся в приведённом уравнении было известно древнегреческим учёным и послужило для Аполлония Пергского поводом присвоить отдельным типам конического сечения названия, сохранившиеся до наших дней: греческое слово «парабола» означает «приложение» (так как в греческой геометрии превращение прямоугольника данной площади у² в равновеликий ему прямоугольник с основанием 2р называлось приложением данного прямоугольника к этому основанию), слово «эллипс» — «недостаток» (приложение с недостатком), слово «гипербола» — «избыток» (приложение с избытком)

Менелай Александрийский.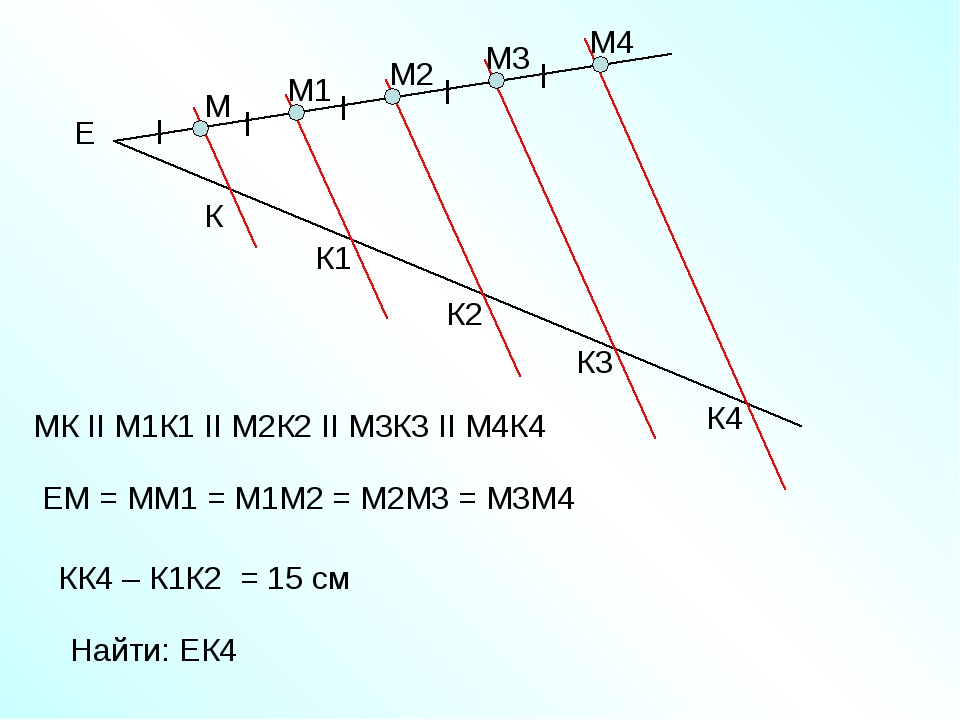

Многие удивительные соотношения и изящные геометрические факты не входят в основной курс геометрии. Многие из них сейчас выглядят малоинтересными, несовершенными и встречаются только в энциклопедиях. Однако некоторые из них продолжают жить, и по сей день. Одни из них теоремы Менелая и Чевы. Это теорема, которая была доказана древнегреческим математиком и астрономом Менелаем Александрийским, жившим в I веке до нашей эры и теорема, опубликованная в 1678 году итальянским математиком и инженером Джованни Чевой. В честь этих учёных теоремы названы их именами. Эти теоремы просты, интересны и находят применение при решении как простых, так и весьма сложных задач. Несмотря на это Теоремы Менелая и Чевы не изучаются в школе на уроках геометрии и встречаются только в школьном учебнике геометрии под редакцией Атанасяна Л.С. в приложении. Доказательства, предложенные автором сложны. Задачи, помещённые в учебнике на применение обратной теоремы Менелая трудны, а задачи на применение прямой теоремы вовсе не рассматриваются.

Мы рассмотрим только теорему Менелая, так как теорема Чевы не подходит к теме моей работы.

Теорема Менелая. Если прямая пересекает стороны или продолжения сторон BC, CA и AB треугольника ABC соответственно в точках A₁, B₁ и C₁, не совпадающие с вершинами треугольника, то имеет место равенство

Доказательство

Пусть прямая пересекает стороны BC и CA треугольника АВС в точках А₁ и В₁ ,а продолжение стороны АВ в точке С₁.

1. Через вершину С треугольника АВС проведем прямую CD АВ, которая пересечет прямую А₁В₁ в точке D.

2. А₁ВС₁ А₁CD по двум углам

3. В₁АС₁ В₁CD по двум угла

4. Из пунктов 2 и 3 следует, что и

5. Перемножим эти равенства, получим доказываемое соотношение.

Доказательство остается в силе и в том случае, когда все три точки A_{1 ,} B₁ и C₁ лежат на продолжениях сторон АВС.

Для пояснения приведённого доказательства сделаем одно уточнение. Пусть – ненулевые коллинеарные векторы. Если , то будем писать: Значит, число k равно отношению длин векторов , взятому со знаком «плюс», если векторы сонаправленны, и со знаком «минус», если они направлены противоположно.

Легко проверить, что при таком соглашении полученное выше равенство принимает вид доказываемого равенства.

Если существует прямая теорема, то есть и обратная теорема. Теорема Менелая не стала исключением. Вот формулировка обратной теоремы: если выполняется равенство, то точки A_{1 ,} B₁ и C₁ лежат на одной прямой.

Для доказательства обратной теоремы используем вышеуказанное уточнение

Доказательство.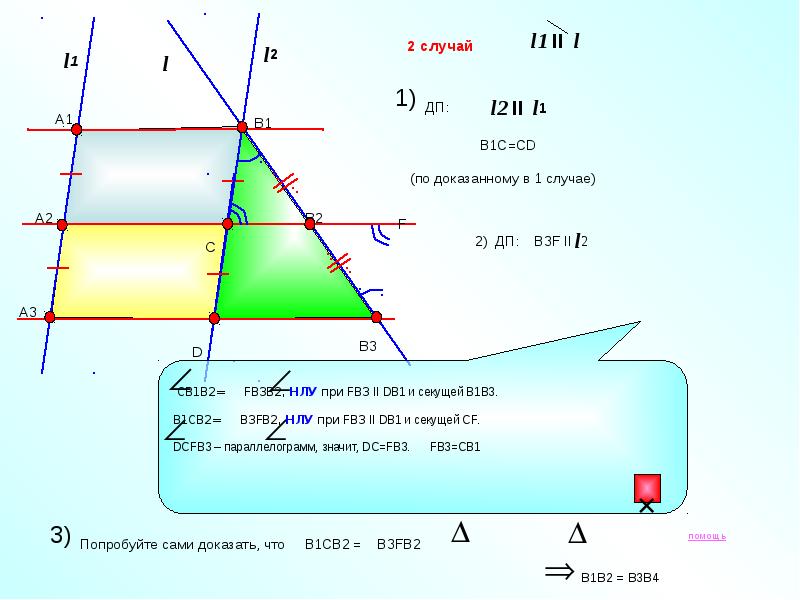

Допустим, что выпоняется равенство , и пусть прямая А₁В₁ пересекает прямую АВ в точке С₂. Согласно прямой теореме,

Сравнивая это соотношение с данным, заключаем, что

Прибавив к обеим частям равенства 1, получим: откуда , то есть точки C₁ и C₂ совпадают.

Объединяя прямую и обратную теоремы, получаем следующий результат.

Если на сторонах ВС, СА, АВ треугольника АВС или на их продолжениях взяты точки A_1, B₁ и C₁, то эти точки лежат на одной прямой тогда и только тогда, когда

Вывод

Рассмотрев работы 12 древнегреческих учёных, мы можем сказать, что древнегреческие учёные внесли большой вклад в развитие математики. Если сравнивать с геометрией древнего мира, то, в действительности, древние греки сделали много открытий, и при чём они смогли сначала выделить целую науку и продвинуть её как можно дальше (некоторые открытия пригодились для современников, например, теорема Менелая помогла Джованни Чевы для вывода другой теоремы).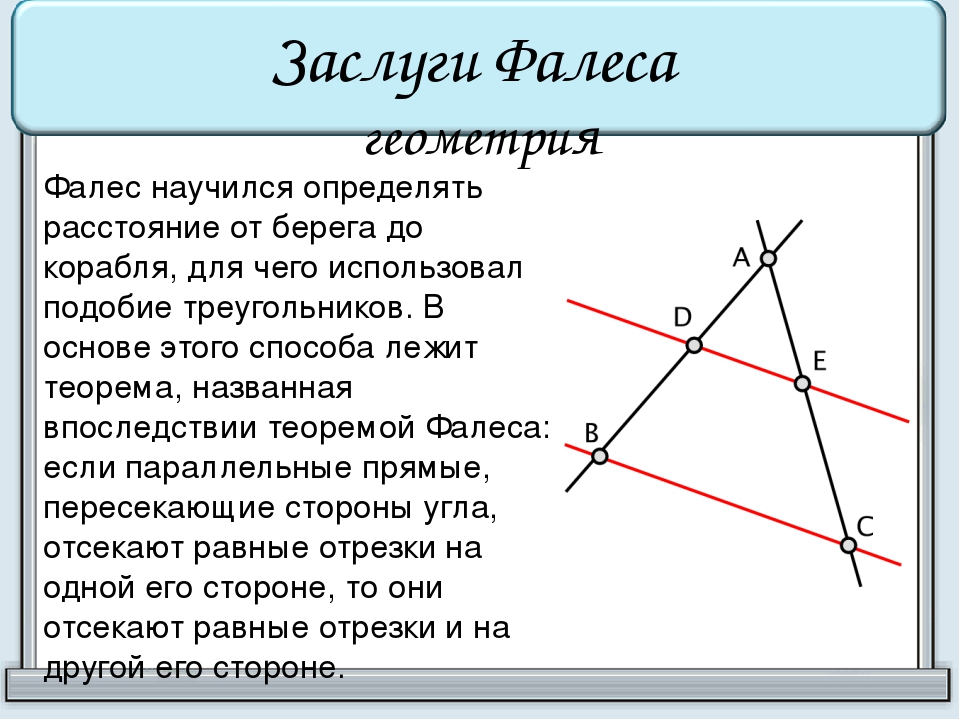 Мало того, что она прогрессивна, она ещё и нужна нам (например, по евклидовой геометрии учились геометрии советских школы). Используют древнегреческую геометрию не только в современном обучении, но и в промышленности (например, в строительстве), тем самым мы можем сказать что эти знания актуальны.

Спсиок используемой литературы:

1. Я познаю мир: детская энциклопедия: Математика / Сост. А.П. Савин, В.В. Станцо, А.Ю. Котова: Под общ. Ред. О.Г. Хинн. – М.: ООО «Фирма «Издательство АСТ», 1999.-480с

2. В. Асмус «Платон», Издательство «Мысль» Москва, 1975г.

3. А.И.Бородин, А.С. Бугай «Выдающиеся математики» Издание 2ое, переработаное и дополненое, Киев, «Радянска школа», 1987г.

4. «Энциклопедический словарь юного математика», Москва «Педагогика» 1985г.

5. А.Н. Боголюбов «Математики и механики», Киев «Наукова думка», 1983г.

Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?

Анна Малкова

Эти две полезные теоремы – теорема Менелая и теорема Чевы — чаще применяются при решении олимпиадных задач, чем на ЕГЭ по математике. Однако в 2020 году в ряде вариантов ЕГЭ обнаружилась задача по планиметрии (№16), которую на первый взгляд невозможно решить без теоремы Менелая или теоремы Чевы. Но на самом деле, конечно, возможно. Например, в Санкт-Петербурге попались такие задачи.

Разберемся, что это за теоремы и как применяются. И действительно ли на ЕГЭ дали задачи на применение теорем, выходящих за рамки школьной программы. И можно ли эти задачи решить по-другому?

Теорема Менелая:

Пусть прямая пересекает произвольный треугольник причем – точка ее пересечения со стороной – точка ее пересечения со стороной и – точка ее пересечения с продолжением стороны

Тогда выполняется равенство:

Как это запомнить? Сначала рисуем треугольник Затем прямую, пересекающую две его стороны и продолжение третьей. На этой прямой лежат точки и причем на стороне должна лежать точка на стороне – точка и на продолжении – точка

Затем записываем равенство так, как будто «обходим» весь треугольник от точки к точкам и и затем возвращаемся в точку Но по дороге нам встречаются точки и – их тоже включаем в формулу.

Один из учащихся нашей ЕГЭ-Студии предложил такое мнемоническое правило: пусть точки и – это города, а точки и – заправки, где можно пополнить запас бензина. Тогда правило звучит так: «Едем из города в город, заезжаем на заправку!»Возможно, вы придумаете свое правило : -)

В некоторых задачах полезна обратная теорема Менелая.

Теорема (Менелая, обратная). Пусть дан треугольник Предположим, что точка лежит на стороне точка лежит на стороне а точка лежит на продолжении стороны причём про эти точки известно, что

Тогда эти точки лежат на одной прямой.

Как правило, не так-то просто бывает доказать, что три точки лежат на одной прямой. Обычно мы используем для доказательства такого факта косвенные методы. Например, если для точек и выполняется равенство: – то это означает, что точка лежит на отрезке Или, если нам удается доказать, что угол – развернутый, это и будет означать, что точки и лежат на одной прямой. Обратная теорема Менелая дает еще один способ доказательства того, что три точки – в данном случае и – лежат на одной прямой.

Теорема Чевы

Пусть точки и лежат соответственно на сторонах и треугольника причем отрезки и пересекаются в одной точке. В этом случае выполняется равенство:

Обратная теорема Чевы:

Теорема (Чевы, обратная). Пусть точки лежат соответственно на сторонах и треугольника причём

Тогда отрезки и пересекаются в одной точке.

Как применяются теоремы Менелая и Чевы?

Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.

На сторонах и треугольника отмечены точки и соответственно, причём Отрезки и пересекаются в точке

а) Докажите, что — параллелограмм.
б) Найдите если отрезки и перпендикулярны,

Докажем пункт (а) с помощью теоремы Менелая:

Пусть

По теореме Чевы,

тогда

тогда

Это значит, что по двум углам и то есть

Рассмотрим треугольник

Прямая пересекает две его стороны и продолжение третьей стороны

По теореме Менелая,

тогда

по углу и двум сторонам, отсюда

Мы получили:

— параллелограмм по определению.

Мы доказали то, что требовалось в пункте (а).
Но что делать, если теоремы Менелая и Чевы вы не проходили в школе? Ничего страшного, докажем без теорем Менелая и Чевы. Их легко заменят подобные треугольники.

Обозначим

Докажем, что — параллелограмм.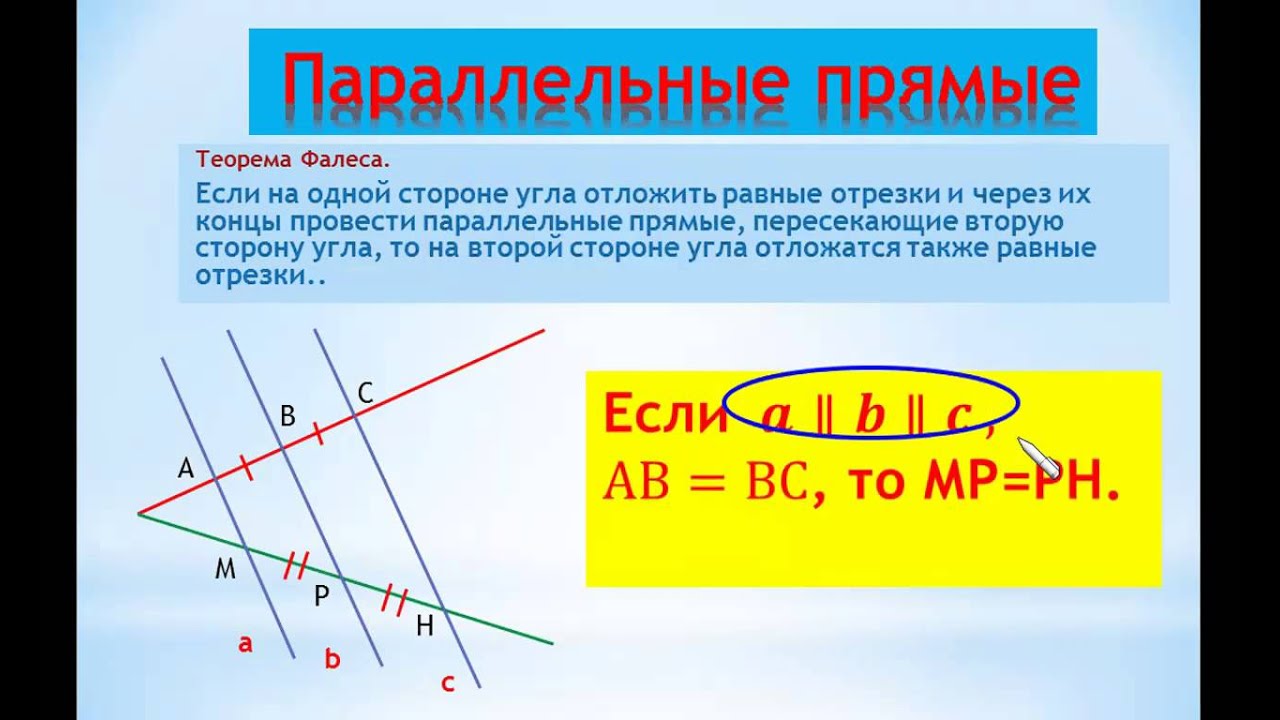

Пусть — середина

Тогда

Тогда по углу и двум пропорциональным сторонам,

Проведём

По теореме Фалеса

Пусть

по двум углам;

Пусть

по 2 углам,
тогда

Это значит, что по углу и двум сторонам и

При этом

Получим, что в четырёхугольнике :

Значит, — параллелограмм.

Как видим, эти решения примерно одного уровня сложности.
А вот в пункте (б) нет необходимости применять теоремы Чевы и Менелая. Он легко решается с помощью обычной школьной геометрии.

б) Найдём , если

Поскольку получим, что — прямоугольный.

Мы доказали в пункте (а), что — трапеция, причём

По условию,

Тогда

Пусть

Тогда — параллелограмм (по признаку паралелограмма)

по теореме Пифагора из

Найдём из по теореме косинусов.

Ответ: 17.

 

Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.

На сторонах прямоугольного треугольника с прямым углом построены во внешнюю сторону квадраты и Докажите, что:

а) прямые и отсекают от катетов треугольника равные отрезки
б) прямые и высота треугольника проведённая из вершины пересекаются в одной точке.

Пункт (а) доказывается легко.

а) Пусть ,
.

Докажем, что .

Обозначим

по 2 углам,

, так как

получим:

(1)

по 2 углам,

(2)

отсюда

Решим пункт (б) с помощью теоремы Чевы:

Запишем, чему равны длины отрезков Для длин и воспользуемся тем, что в прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

Проверим выполнение равенства

Равенство выполняется.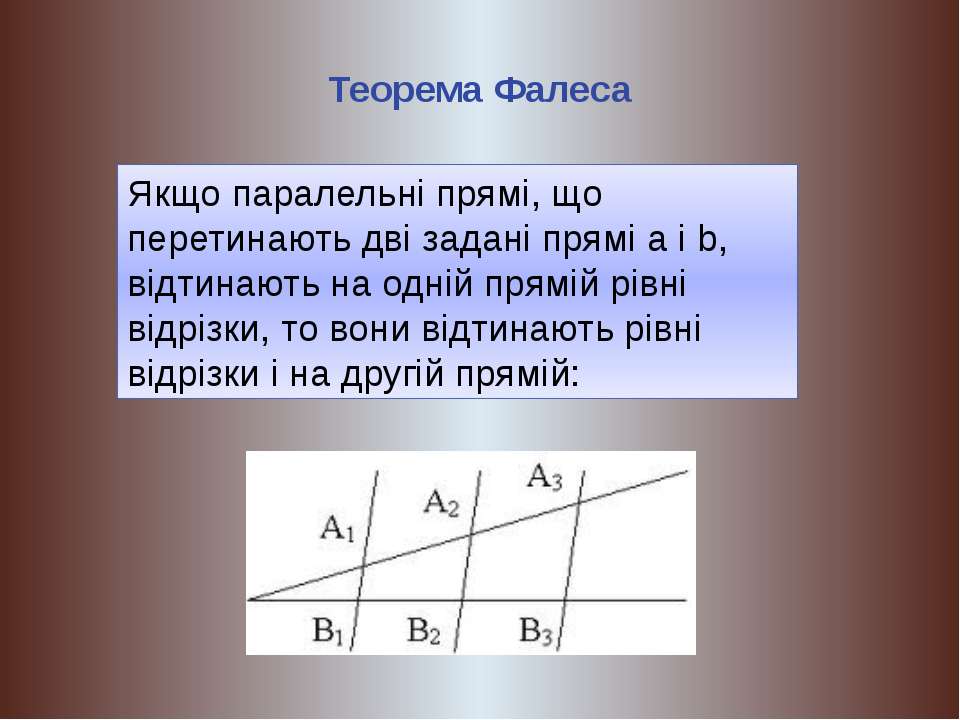
Согласно теореме Чевы, это значит, что и пересекаются в одной точке.
А вот как решается эта задача без теоремы Чевы, с помощью векторов:

Смотрите решение: https://ege-study.ru/zadacha-na-dokazatelstvo-planimetriya/

Математик Менелай Александрийский жил в I веке до нашей эры (Древний Рим).
Математик и инженер Джованни Чева – XVII век, Италия.

Как видим, теоремы Менелая и Чевы оказываются полезны в некоторых задачах. Очень хорошо, если вы знаете эти теоремы. Однако если они для вас непривычны, можно применить простой школьный прием – пары подобных треугольников.

Первые доказательства: Фалес и начало геометрии

Podcast: Download

Доказательная геометрия началась с Thales. Приписываемые ему теоремы заключают в себе два способа выполнения математических вычислений, предполагая, что идея доказательства могла исходить из любого из двух источников: внимания к шаблонам и отношениям, возникающим в результате исследовательского конструирования и игры, или осознания того, что «очевидные» вещи могут быть продемонстрировано с использованием формальных определений и доказательства от противного.

Выписка

Как начались доказательства? Это похоже на головоломку с курицей или яйцом. Зачем кому-то садиться и говорить себе: «Я собираюсь доказать некоторые теоремы сегодня», если никто никогда не делал ничего подобного раньше? Как эта идея могла так неожиданно прийти в голову кому-то?

На самом деле, мы вроде как знаем ответ. Греческая традиция говорит нам, у кого был этот момент лампочки: у Фалеса. Примерно в году -600 или около того. За сотни лет до того, как у нас появились какие-либо прямые исторические источники по греческой геометрии.Но мы все еще более или менее знаем, что доказал Фалес. Более поздние источники рассказывают нам о Фалесе. История, возможно, смешана с легендами в подобных отчетах, но ключевые аспекты, вероятно, будут довольно надежными. Больше фактов, чем выдумок. Давайте проанализируем этот вопрос, вопрос о достоверности, более подробно позже, но сначала давайте примем истории за чистую монету и посмотрим, как мы можем пережить создание дедуктивной геометрии, как это передано в этих греческих историях.

Итак, поехали: какая первая теорема была доказана? Что стало той искрой, которая зажгла пожар аксиоматико-дедуктивной математики? Лучшее предположение, основанное на исторических свидетельствах, звучит так.Момент любви с первого взгляда, та теорема, открывшая нам глаза на силу математического доказательства, заключалась в следующем: диаметр разрезает круг пополам.

Довольно обидно, не правда ли? Какая неубедительная теорема. Это даже не теорема. Как можно влюбиться в геометрию, доказывая что-то столь тривиальное и очевидное?

Но не отчаивайтесь. Вообще-то, это приятно. Дело не в теореме, а в доказательстве.

Вот как это доказать. Предположим, что нет. Это будет доказательство от противного.Предположим, диаметр не делит круг на две равные половины. Хорошо, у нас есть линия, проходящая через середину круга, и она разрезана на две части. И мы предполагаем, что эти две части не совпадают. Возьмите один из кусочков и переверните его на другой. Как вы складываете омлет или креп.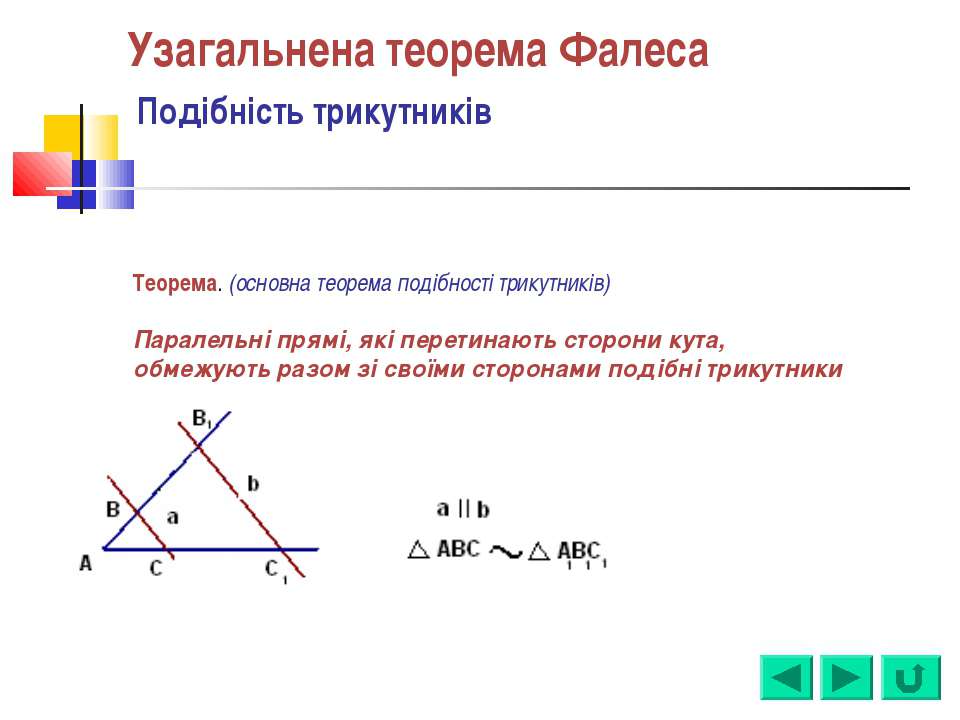 Мы предположили, что части не равны, поэтому, когда вы кладете одну на другую, они не совпадают. Так что должно быть какое-то место, где одна из двух частей выступает над другой.Теперь нарисуйте радиус в этом направлении от середины круга до места по периметру, где две половины не совпадают. Тогда один радиус длиннее другого. Но это означает, что дело было не в круге с самого начала. Круг — это фигура, одинаково удаленная от середины во всех направлениях. Вот что значит быть кругом.

Итак, мы доказали, что две вещи несовместимы друг с другом: нельзя одновременно быть кругом и иметь несовпадающие половинки. Потому что, если у вас есть несовпадающие половинки, у вас также есть «неравные радиусы», а это значит, что вы не круг.

Итак, у круга должны быть равные половины. Бам. Теорема. Скучный результат, но великолепное доказательство. Или убедительное доказательство. Это доказательство, намекающее на новый мир.

Фалес, должно быть, чувствовал себя волшебником, который только что обнаружил, что обладает сверхспособностями. «Ого, ты можешь это сделать ?!» С помощью чистого рассуждения, вычеркивая последствия определения, можно без тени сомнения доказать, что определенные утверждения не могут быть неправильными? Это вещь? Это то, что можно сделать? Ух ты. Давайте сделаем это со всем! Верно?

Так вот как Фалес открыл доказательство.Насколько мы можем догадаться.

Несколько других теорем также приписываются Фалесу. Я хочу особо остановиться на одном, который, как мне кажется, также является своего рода архетипом того, что из себя представляет математика.

Теорема, которую мы только что рассмотрели, о диаметре, разделяющем окружность пополам, идеально воплощает один из прототипов математических рассуждений. Вы могли бы назвать это парадигмой чистой математики. Логические следствия определений, доказательства от противного. Такие вещи. Доказательство Фалеса действительно поражает своей эстетикой.С тех пор мы делаем одно и то же снова и снова. Например, современный курс теории групп — это просто идея доказательства Фалеса, примененная, по сути, пятьсот раз.

Теперь я хочу взять еще один результат, приписываемый Фалесу, и я хочу утверждать, что он символизирует другой способ математической мысли. Это второй путь к доказательствам. Этот второй способ основан больше на игре, исследовании, открытии, чем на логике и определениях.

Пример, который я хочу использовать, чтобы показать это, — это то, что на самом деле часто называют просто «теоремой Фалеса».Который утверждает, что любой треугольник, возвышающийся на диаметре круга, имеет прямой угол. Другими словами, изобразите круг. Разрежьте его пополам диаметром. Теперь поднимите треугольник, используя этот диаметр как одну из его сторон, и третья вершина треугольника находится где-то на окружности. Так что это похоже на палатку, торчащую из диаметра. И это может быть асимметричный шатер, который больше направлен в ту или иную сторону. Независимо от того, как вы устанавливаете эту палатку, до тех пор, пока ее кончик находится в любой точке круга, угол между двумя стенами палатки в этой точке, на вершине, будет прямым углом, 90 градусов. .Это теорема Фалеса.

Как мог Фалес доказать эту теорему? К сожалению, мы не знаем этого, основываясь на исторических данных. Но давайте рассмотрим одну гипотезу, которая имеет смысл с точки зрения контекста.

Мы должны представить, что Фалес каким-то образом наткнулся на доказательство. Мы не пытаемся объяснить, как кто-то может думать о доказательстве этой теоремы как таковой. Это неправильная точка зрения, потому что считается само собой разумеющимся, что в математике кто-то пытается что-то доказать. Нам нужно объяснить, откуда взялось это видение, чтобы доказать все в геометрии.Как мог кто-то случайно натолкнуться на теорему Фалеса и благодаря этой случайности осознать идею дедуктивной геометрии?

Действительно, теорема Фалеса сама по себе не слишком интересна или важна. Если бы у вас было видение систематического доказательства всей геометрии, почему бы вам начать с этой теоремы или сделать ее центральной частью, как якобы сделал Фалес? Ты бы не стал.

Теорема Фалеса интересна не в том, что это был один из первых результатов, к которому математики применили дедуктивное доказательство.Скорее, интересно то, что математики случайно наткнулись на саму идею доказательства.

Есть история о Фалесе, который упал в колодец, потому что он настолько увлекся астрономическими рассуждениями, что забыл о том, что его окружало. У Платона записано: «Когда он изучал звезды и смотрел вверх, он упал в яму. Поскольку ему так хотелось познать вещи в небе, он не мог видеть то, что было перед ним у самых его ног.”

Возможно, это легенда, но открытие теоремы Фалеса, должно быть, было чем-то вроде этого. Обнаружение математического доказательства должно было быть похоже на падение в яму. Вы смотрите в одном направлении и, бум, внезапно обнаруживаете, что сначала случайно врезаетесь лицом в эту совершенно не связанную новую вещь, о существовании которой вы даже не подозревали.

Как могла быть теорема Фалеса такой? Что из всех мировых теорем делает теорему Фалеса особенно благоприятной для такого рода случайного открытия доказательства?

Вот моя гипотеза.В этот век невинности, прежде чем кто-либо знал что-либо о доказательствах, людям все еще нравились формы. У них были линейка и компас. Они использовали эти инструменты для измерения полей и прочего, но им также понравилась их эстетика.

Они игрались с линейкой и компасом. Играем с фигурами. После пяти минут игры с компасом вы узнаете, как нарисовать правильный шестиугольник. Помнить? Вы, наверное, делали это в детстве. Нарисуйте круг, а затем, не меняя отверстия компаса, проведите циркулем по окружности.Умещается ровно шесть раз. Очень приятная форма.

Мы точно знаем, что люди делали это до Фалеса. В мозаиках Месопотамии есть шестиугольные мозаичные узоры, датируемые примерно -700 годом.

Додекаэдры — еще одна из таких вещей. Додекаэдр похож на те двенадцатигранные кости, которые вы используете в Dungeons and Dragons и тому подобном. До-дека-эдр, буквально: двухсторонний. Другими словами, так двенадцать сторон. Двенадцать граней, каждое из которых представляет собой правильный пятиугольник.Эти вещи есть в археологической летописи. Люди делали их из камня и бронзы. Было обнаружено несколько десятков древних додекаэдров, самые старые из них были найдены еще до Фалеса. Возможно, они использовались для пророческих целей, например, карты Таро или что-то в этом роде. А может, для настольных игр, кто знает?

В любом случае, я хочу сказать, что люди интересовались геометрическими рисунками для различных целей: художественных, культурных и так далее. Не только для измерения полей в налоговых целях. И они явно работали с такими инструментами, как линейка и компас, чтобы делать эти вещи.

К теореме Фалеса легко прийти, просто играя с линейкой и циркулем, пытаясь нарисовать красивые вещи. Начните с прямоугольника. Нарисуйте его диагонали. Поместите стрелку циркуля в место пересечения, прямо в середину прямоугольника. Установите перо циркуля в один из углов прямоугольника. Теперь крутите его. У вас получится круг, который идеально и плотно прилегает к прямоугольнику.

Но посмотрите, что получилось. Диагональ прямоугольника становится диаметром круга.А выступающие из него прямоугольники — это как раз те треугольники-шатры, о которых говорит Теорема Фалеса. Это внезапно делает теорему очевидной.

Почему теорема Фалеса верна? Почему любая из этих «палаток», поднятых на диаметре круга, имеет прямой угол? Потому что он исходит из прямоугольника. Любая такая палатка представляет собой половину прямоугольника. Это мощный сдвиг в перспективе. Глядя на треугольник таким образом, мы обнаруживаем скрытые отношения, скрытый порядок в природе вещей.Определенные углы всегда должны быть прямыми в силу своего рода метафизической необходимости. Наши глаза были открыты, возможно, впервые, на существование такого рода потребностей, этих видов скрытых отношений, которые существует, чтобы мыслящий человек мог раскрыть.

Итак, ключ к этому сдвигу перспективы, что треугольник «на самом деле» является половиной прямоугольника. Предположим вместо этого, что мы застряли в точке зрения, что мы смотрим на треугольник, вписанный в круг.Тогда те ассоциации и идеи, которые нам напрашиваются, не столь полезны для доказательства этой теоремы. С этой точки зрения, если бы вы искали доказательства, что бы вы сделали? Может быть, вы, например, соедините середину круга с концом треугольника. Итак, теперь у вас есть два меньших треугольника. Что ты собираешься с ними делать? Что-нибудь с суммами углов и так далее? Или, может быть, у вас возникнет соблазн опустить перпендикуляр вместо вершины треугольника, а затем вы можете использовать теорему Пифагора о двух маленьких треугольниках, которые вы получите.

Такие вещи не то, что мы хотим. Подобные подходы быстро становятся слишком техническими. Помните, это должно было быть началом геометрии. Вы не должны использовать несколько предыдущих результатов для доказательства. Это должно быть доказательство из первых принципов. Доказательство перед всеми другими доказательствами.

Идея о том, что треугольник «на самом деле» является половиной прямоугольника, отличается. Это меняет то, как мы смотрим на диаграмму. Это меняет акценты. Это меняет то, что мы считаем основным.Теперь прямоугольник идет первым, треугольник — вторым, а круг — последним. С этой точки зрения теорема на самом деле вовсе не касается кругов, так сказать. Круг — это своего рода вторичный артефакт.

В этом доказательстве мы как художники. Мы отошли от холста, наклонили голову и увидели это прозрение. И прозрение стало возможным благодаря тому, как мы раньше играли с этими идеями. Мы просто играли с линейкой и циркулем, мы исследовали треугольники, прямоугольники и круги с непредубежденной любовью.Из этой пьесы рождаются такие прозрения, как теорема Фалеса. В этом контексте естественно приходит вдохновение.

В отличие от других скучных доказательств, на которые я ссылался, которые были основаны на разрезании треугольника и бросании в него книги: суммы углов, теорема Пифагора, все, что мы можем придумать. Это скучный подход, подход грубой силы. Ему не хватает того эстетического вдохновения, этого прозрения, раскрывающего истинную природу треугольника и его второй половины, с которой ему суждено было воссоединиться.

Геометрия не могла начаться с такого рода практических доказательств, потому что они имеют смысл только после того, как для начала есть книга по геометрии. Но геометрия могла начаться с доказательства типа прозрения. Таким образом, кто-то вроде Фалеса мог прийти к идее доказательства, играя с линейкой и компасом.

Возможно, вы знакомы с «Плачом Локкарта»: отличным эссе о том, что не так с математическим образованием. Иди и прочитай, он доступен в Интернете.Интересно, что Локхарт использует именно этот пример, чтобы доказать свою точку зрения. Он описывает, как его ученики открыли теорему Фалеса, в основном так, как я говорю, что Фалес мог это сделать. Он также красноречиво показывает, насколько это удовлетворяет гораздо больше, чем сухое доказательство, записанное в книге.

Недаром в этом вопросе история и образование идут рука об руку. Доказательство должно было начаться с убедительного эстетического опыта или вау-момента. В то время другого пути не было. Заставить Фалеса запоминать факты для экзамена было некому.Открытие заставило его ценить математику. Если мы хотим развить внутреннюю мотивацию у наших студентов, неплохо было бы в первую очередь подумать, что заставило людей полюбить эти идеи. Первая любовь всегда чистейшая и невинная. Современные учебники похожи на браки по договоренности, навязанные студентам. Но в истории всегда есть настоящая история любви.

Тем не менее, несмотря на все это, вы все равно можете подумать, что теорема Фалеса немного скучна. Что-то всегда есть под прямым углом.Ну и что? Какая разница?

Как я пытался утверждать, Фалеса и его современников, вероятно, впечатлила не сама по себе теорема, а, скорее, идея о том, что теоремы и доказательства вообще существуют. Есть скрытые истины, которые можно раскрыть с помощью рассуждений. Замечательный.

Но на самом деле интересна и сама теорема. Позвольте мне показать вам кое-что интересное, что вы можете сделать с помощью теоремы Фалеса.

Существует древняя легенда о царице Дидоне.Дочь царя Тира, крупного города в древности. Вы все еще можете увидеть руины этого древнего города на территории современного Ливана. В какой-то момент Дидоне пришлось бежать из-за придворных интриг. Убийства и предательства и так далее. Поэтому она берет с прикроватной тумбочки пару диадем, может быть, золотой сундук, который отложила на дождливый день, и торопливо уходит в ночь. С едва ли в мире остался друг.

Ей нужно пройти весь путь до нынешнего Туниса, находящегося за тысячи километров, и попытаться как-то начать все сначала, как приличествует королевской семье.Используя свой сундук с сокровищами, она заключает сделку, чтобы купить землю. История гласит, что столько земли, сколько она может покрыть шкурой быка. Она разрезала бычью шкуру на тонкие полоски и связала их вместе, и что теперь? Итак, теперь у нее есть длинная веревка, которую она может использовать как своего рода забор, чтобы изолировать желаемую землю.

Но какой формы сделать? Квадрат, прямоугольник, треугольник? Нет. Дидона знает лучше. Возможно, ее королевское образование включало математику. Сделайте это круглым. Это лучший способ.Круг имеет максимальную площадь среди всех фигур с заданным периметром. Или в данном случае, поскольку она была у океана: полукруг, с другой стороны береговой линией, естественной границей.

Давай докажем это. Что полукруг — лучший выбор. Я собираюсь доказать это с помощью противоречия: предположим, что кто-то построил забор на участке, который не является полукругом; Затем я могу показать, как это сделать лучше: как переместить забор так, чтобы площадь стала еще больше, без добавления забора.

Хорошо, у вас есть береговая линия, это прямая линия. И из одной точки на берегу, идя вглубь, у вас есть этот забор, который затем снова спускается и снова встречается с берегом в какой-то другой точке. Так что вместе с береговой линией он закрывает определенную территорию.

Предположим, эта форма не является полукругом. Если бы это был полукруг, применима теорема Фалеса. И он сказал бы вам, что этот угол, то, что я назвал углом палатки, в любой точке вдоль забора будет прямым углом.Итак, если фигура не является полукругом, на заборе должна быть точка, где этот угол не является прямым.

Я говорю, что если сделать этот угол прямым, то увеличится площадь покрытия. Вы можете представить это так. Итак, у вас есть форма, окруженная забором: представьте, что у вас есть вырез из картона. А по периметру у вас есть отмеченная точка, где угол палатки не является прямым ангелом. Итак, на вашем картоне нарисован этот треугольник: треугольник, состоящий из прямой береговой линии с одной стороны и двух линий от его концов, идущих вверх, чтобы встретиться в точке палатки по периметру.

Давайте вырежем этот треугольник из картона. Итак, у вас остались две части: любые части, которые торчали из сторон треугольника. Теперь переместите эти две части так, чтобы угол палатки получился прямым. Это означает перемещение конечных точек вдоль береговой линии. Перемещая две точки на береговой линии, вы меняете угол, под которым встречаются две картонные части. Две картонные части встречаются в одной точке, точке палатки, и это похоже на петлю, которая может открываться или закрываться на больший или меньший угол.Таким образом, вы перемещаете эти штуки, пока угол поворота не станет 90 градусов.

Обратите внимание, что вы не меняли периметр таким образом. Вы только что переместили такое же количество забора.

Но вы действительно увеличили огражденную площадь. Потому что, если у вас есть две палки фиксированной длины, и вы хотите сделать из них самый большой треугольник, лучший способ — сделать угол между ними прямым. Это интуитивно понятно. Вы знаете, что площадь треугольника равна основанию, умноженному на высоту, больше двух.Итак, если одна из ваших палочек является основанием, то для увеличения площади вы хотите максимизировать высоту, то есть перпендикулярную высоту, идущую вверх от основания, что, очевидно, достигается путем направления другой палки прямо вверх под прямым углом.

Итак, это доказывает, что для любого ограждения, отличного от полукруга, вы можете сделать лучший. Вы можете передвинуть забор и увеличить площадь. Так что полукруг — лучшее решение, а все остальные менее хороши.

Не знаю, сможете ли вы все это представить себе.Но, может быть, позже попытайтесь реконструировать этот аргумент для себя. Это действительно очень интуитивно понятно и красиво.

Так в чем же тогда мораль этой истории? Математически это ответ на вопрос «ну и что?» вопрос относительно теоремы Фалеса. Это могло показаться достаточно скучной теоремой, но здесь мы видим ее в действии красивым и неожиданным образом, как ключевой ингредиент в этом доказательстве о том, как оградить землю. Кто бы мог предвидеть это?

Это говорит о том, что у математики есть своего рода «снежный ком» или аспект самооплодотворения.Теорема Фалеса, в чем дело? Просто скучное наблюдение о треугольнике в круге. Может показаться, что это не так уж много. Но одно ведет к другому. Когда вам становится понятна теорема Фалеса, вы начинаете видеть ее в других, неожиданных местах. Как эта проблема о районе. Вы бы не подумали, что это связано, но чем больше вы занимаетесь математикой, тем больше связей вы обнаруживаете.

Выберите любую теорему, какой бы скучной она ни была, например, теорема Фалеса, и вы сможете найти эти удивительные вещи, в которых скучная теорема на самом деле является ключевым моментом, открывающим совершенно новые способы осмысления, казалось бы, не связанных между собой проблем.Это для вас математика. Неудивительно, что греки прижились как жук, как только они сдвинулись с мертвой точки. В один момент вы натыкаетесь на какой-то случайный результат, например на теорему Фалеса, а в следующий момент вы знаете, что видите математику везде.

Такова математическая мораль истории. Теперь мы должны вернуться и сказать кое-что об исторической стороне всего этого. Что мы действительно знаем о Фалесе и его теоремах, королеве Дидоне и всем остальном? Сколько истории и сколько легенд?

Если мы начнем с Дидоны, то эта история используется в основном через Вергилия.Энеида, знаменитая эпическая поэма. Это было написано во времена Римской империи, примерно в -20 году. Но это относится к историческим или предположительно историческим событиям, которые произошли еще до Фалеса, может быть, за два столетия до Фалеса, то есть примерно 800-х годов. У нас есть версия Верджила, это то, что до нас дошло, но он просто крадет старую историю. Эти вещи существовали веками в греческой культуре, в различных литературных и исторических пересказах, которые сейчас утеряны.

Совершенно правдоподобно, что действительно существовала такая историческая королева, которая действительно покинула свой королевский дом в Тире и действительно приземлилась на северных берегах Африки, где она основала это новое поселение, которое должно было стать великим городом Карфаген. .Может быть, она даже сделала полукруглыми городские стены, кто знает? Совершенно очевидно, что она могла хотеть минимизировать периметр по какой-либо причине, и что она могла знать, что полукруглая форма была оптимальной для этой цели.

Но в то время не было бы никаких математических доказательств этого, подобных тому, которое я набросал выше. Приведенное мной доказательство принадлежит Якобу Штайнеру в начале 19 века. Со времен Греции у нас есть другое доказательство этого результата.Таким образом, они, конечно, очень хорошо знали результат, что полукруг является оптимальным, если, возможно, не то конкретное доказательство, которое я предложил.

Если история царицы Дидоны говорит что-либо об истории математики, она, вероятно, больше всего не освещает ни время, когда произошли события, около -800, ни время, когда были написаны источники, которые у нас есть, около года 0. Но, может быть, это так. что-то говорит о промежуточных веках, когда история могла бы быть передана и переработана.

История была как бы маринована в греческой культуре.Возможно, они были теми, кто придал этому математический оттенок. Подходит для обуви: греки ценили мудрых, аристократических, хорошо образованных правителей, которые разрабатывают рациональную политику для общего блага, основанную на разуме и математике. Может быть, они позволили этим идеалам окрасить то, как они пересказывают историю королевы Дидоны и ее круглого города.

С этой точки зрения мы также можем предположить, что к тому времени, когда Вергилий придет и напишет римскую версию истории, это понимание математики уже не то, чем было раньше.В самом деле, Верджил не раскрывает математический аспект оптимизации истории. Дидона — всего лишь второстепенный персонаж. Его эпос об Энее, который находится в поисках, которые в конечном итоге приведут к основанию Рима.

Эней терпит кораблекрушение и выносится на берег в Карфагене, круглом городе Дидоны. Дидона влюбляется в него, но он не отвечает на ее любовь. Он уплывает, и Дидона убивает себя из-за разбитого сердца. Моррис Клайн завершает рассказ: «Итак, неблагодарный и невосприимчивый человек с жестким умом стал причиной потери потенциального математика.Это был первый удар по математике, нанесенный римлянами ». Конечно, есть еще много всего, откуда это взялось.

Можно рассматривать эту историю как символ этого перехода от мудрых королей-философов (или в данном случае цариц) греческого мира, которые лелеяли математику и использовали ее для улучшения мира. Переход от этого к бессердечному римлянину, который думает только о себе и не заботится о теореме Фалеса. В греческом мире ботаники-математики считались привлекательными, но каким-то образом эти невежественные римляне явно не думали, что королева-геометрист вообще может быть подружкой.

Итак, история о Дидоне и круглом городе, о доказательстве оптимизации и всем остальном очень интересна с точки зрения более широких математических и культурных точек, с которыми она связана, но сама по себе она не является историей как таковой.

С Thales все иначе. Это больше факт, чем легенда. Насколько мы можем определить, Фалес действительно доказал, что диаметр делит окружность пополам, скорее всего, с помощью доказательства, обсужденного выше.

Источники, которые у нас есть для этого, далеки от совершенства.В первую очередь Прокл, писавший примерно в 450 году, в основном через тысячу лет после жизни Фалеса. Такого рода запоздалые источники попадают в заблуждение. У них нет авторитета сами по себе. Прокл был никем. Его собственное понимание истории и математики очень плохо. Посредственный мыслитель, посредственный ученый, живущий в посредственном возрасте.

Таковы источники, которые у нас есть. По сути, столь же авторитетный, как факт, который вы читаете на обратной стороне коробки с хлопьями или чего-то в этом роде.

Но есть надежда.Во времена своей славы Греция была просто выдающейся интеллектуальной культурой. И кое-что, например, о Фалесе, можно проследить до тех пор, что делает его весьма достоверным. Ученик Аристотеля Евдем написал историю геометрии. Увы, этого уже нет. Возраст невежества игнорировал это, и теперь его нет. Но что это была бы за работа.

Эти люди знали, что делают. Более поздние люди, подобные Проклу, похожи на некоторых онлайн-рандомов, которые публикуют недоработанные идеи в блоге или плохо информированные комментарии в Facebook.Вот насколько они заслуживают доверия.

Но люди вроде Евдема — совсем другая история. Это больше похоже на первоклассного ученого в исследовательском учреждении со всей инфраструктурой, о которой можно только мечтать: библиотеки, чрезвычайно знающие и умные коллеги с широким спектром знаний, широкая финансовая и культурная поддержка со стороны общественности и политиков и т. Д. . «История геометрии» Евдема могла бы стать настоящей книгой «University Press», отрецензированной до зубов и с красивой аннотацией Аристотеля в суперобложке.

Такие люди, как Евдем, не занимались распространением случайных сплетен и непроверенных фактоидов, потому что они звучат круто. Они были настоящими учеными и интеллектуалами.

И действительно, многие сведения о Фалесе можно проследить до этого потерянного источника. Когда Прокл говорит, что Фалес был первым, кто доказал, что круг делится пополам по его диаметру, источником этого является Евдем. Следовательно, это очень достоверно. Это случилось с Фалесом на самом деле. На самом деле то, что касается диаметра, разделяющего окружность пополам, более определенно, чем то, что касается теоремы Фалеса.Была ли теорема Фалеса на самом деле теоремой Фалеса? Может быть. Но мы не можем проследить конкретно эту часть до лучших источников. В отличие от диаметра пополам одной и некоторых других деталей. Но с точки зрения контекста это имеет смысл.

Истории Фалеса и происхождения геометрии, очевидно, были хорошо известны не только специализированным ученым, но и широкой афинской публике. Драматург Аристофан несколько раз в своих пьесах использует имя Фалеса как символ геометрии. Так же, как сегодня, можно использовать имя Эйнштейна, например, чтобы вызвать образ ученого.У Аристофана один говорящий в диалоге говорит: «Этот человек — Фалес». Это означает, что человек — геометр. Очевидно, можно было ожидать, что театральная публика в классических Афинах поймет это упоминание. Каждый образованный человек знал бы о Фалесе и истоках геометрии.

На самом деле, общественное уважение к геометрии и ее истории было очевидно настолько велико, что Аристофан даже заставил одного из своих персонажей оплакивать ее как чрезмерную, говоря: «Почему мы продолжаем восхищаться старым Фалесом?» Какое время было бы жить.Когда драматургам приходилось решать такие проблемы, как чрезмерное уважение и интерес к математике среди широкой публики. «Привет, ребята, может быть, нам нужно охладить это тем, насколько мы любим геометрию». Какая проблема с роскошью. Едва ли та, с которой сегодня приходится бороться голливудским блокбастерам.

В любом случае, нам, возможно, не стоит слишком углубляться в эти отдельные цитаты. Но общая интеллектуальная достоверность этого возраста важна. Эти очень умные и серьезные люди записали в научных историях рассказы о Фалесе, основавшем дедуктивную геометрию и доказавшем, что круг делится пополам по своему диаметру.Это всего через двести или триста лет после Фалеса, и в прямой линии от него, вероятно, целые работы Фалеса все еще хранятся в библиотеках и так далее.

Итак, поехали. Истоки доказательства и дедуктивной геометрии. Мы действительно кое-что об этом знаем, и эту историю стоит узнать, если вы спросите меня.

Моно и Стерео © 2021: REED 5T «TANGENTIAL» TONEARM

Reed 5T — наше первое появление в области тангенциальных тонармов. Обладая уникальным дизайном, инновационными технологическими решениями и высоким качеством, он посвящен истинным ценителям звука и является одним из самых передовых тонармов, которые мы когда-либо создавали.Reed 5T технически представляет собой поворотный тонарм с тангенциальным трекингом. Его принцип работы основан на теореме Фалеса (если центр описанной окружности треугольника лежит на треугольнике, тогда треугольник является прямым, а центр его описанной окружности лежит на его гипотенузе) и правиле, которое дает три неколлинеарных точки, можно нарисовать только одну окружность конечного радиуса, проходящую через все три. (Рис.1)

P1, O1, P3 — полукруг Фалеса,

Углы P1-A1-P3, P1-A2-P3, P1-A3-P3 составляют 90 градусов каждый,

Сегменты A1B1 = A2B2 = A3B3 представляют длину тонарма,

B — Вертикальная ось тонарма,

P2 представляет собой центр круга, проведенный через три точки — B1, B2 и B3 (ось вращения тонарма),

P3 — Матрица линейных датчиков,

BP3 — Лазерный луч.

Система подвески трубки тонарма аналогична той, что используется в тонарме Reed 3P, а поворотная часть тонарма основана на малошумном подшипнике с упорной втулкой. Для углового вращения тонарма мы спроектировали и построили секционный моментный двигатель ограниченного вращения. Положение тонарма контролируется с помощью лазера и линейных датчиков.

Reed 5T имеет заменяемую пользователем трубку тонарма — функцию, которая позволяет самостоятельно изменять эффективную массу тонарма. Тонарм также имеет регулировку VTA и азимута.

Для удобства пользователя тонарм также имеет встроенный уровень, который позволяет регулировать механическое положение тонарма без использования дополнительных инструментов.

По сравнению с поворотными тонармами Reed 5T имеет следующие преимущества:

Меньший момент инерции,

Нет необходимости в антискейтинговом механизме,

Максимальная погрешность слежения составляет +/- 0,005 град. (Фигура 2). Поворотные тонармы обычно имеют максимальные ошибки отслеживания до 1,5 градуса.

Преимущества Reed 5T по сравнению с другими тангенциальными тонармами:

Момент инерции в несколько раз меньше,

Нет необходимости в сложных дополнительных устройствах (воздушный компрессор),

Компактный и элегантный дизайн.

Эффективная масса в вертикальном и горизонтальном направлениях равна

.

Технические характеристики

Монтажное расстояние 251 мм

Ошибка отслеживания +/- 0,005 град.

Эффективная масса 10-16 г, в зависимости от материала рукоятки (сменная рукоятка)

Регулировка высоты для тарелок высотой 28 ÷ 48 мм

Точность регулировки VTA +/- 0,2 мм

Регулировка азимута +/- 8 градусов

Диапазон прижимной силы 10 ÷ 30 мН

Тяга Секционный линейный двигатель с ограниченным вращением

Напряжение прямое 12 В, от аккумуляторной батареи Reed Source 12V

Встроенная точность уровня +/- 1 мм / м

Проигрыватель HiFiction Thales TTT-Slim II и тонарм Simplicity II

Деньги, ненадежный покупатель счастья, временами оказываются эффективными в обеспечении хорошего звука.Он может покупать и другие вещи: аудиофилы могут обменивать наличные на продукты, которые служат предметами искусства, символами статуса или даже хитрыми инвестициями.

Но — думаете ли вы, что деньги могут купить душевное спокойствие для аудиоэнтузиастов, которые беспокоятся о связывании звуковых катушек, протекающих конденсаторах, дрейфующих значениях резисторов, окислении разъемов, старении или неправильно смещенных лампах, а также о самой пагубной из всех проблем — искажении и преждевременный износ пластинки из-за неправильно настроенных картриджей фонокорректора? К сожалению, большинство из этих неврозов, некоторые из которых вполне разумны, остаются без внимания всемогущим наличными.

Первые попытки решить эту последнюю задачу обещали, но не принесли результатов. Это особенно верно в отношении тонармов с прямолинейным трекингом, которые в теории выглядят хорошо, но часто приводят к тому, что консоль фонокартриджа затягивается до такой степени, что это ставит под угрозу вновь обретенное прикосновение и усиливает подвеску бедняги — один шаг вперед к спокойствию, два делает шаг назад к тревоге аудиофилов. Другой путь выбрали сторонники поворотного тонарма с тангенциальным трекингом , который был создан с проигрывателем Garrard Zero 100 1970-х годов, но этот пример был скомпрометирован менее чем перфекционистскими уровнями инженерии и качеством сборки, а не для того, чтобы упомяните образ мышления, не учитывающий пагубные эффекты резонансов и микрогремучих звуков.

Поворотные тангенциальные трекеры снова появляются в выставочных залах и на выставках, не более чем те, которые продаются под названием Thales, разработанные инженером и бывшим часовщиком Миша Хубер и произведенные швейцарской компанией HiFiction. На момент написания этой статьи имеется не менее трех тонармов Thales — Майкл Фремер писал об их первоклассном тонарме Statement (21 090 долларов США) в модели Stereophile в мае 2019 года — и двух столь же отличительных проигрывателях Thales для их поддержки. Ранее в этом году Хубер прислал мне комбинацию проигрывателя виниловых пластинок Thales TTT-Slim II (по цене 6750 долларов, самая дешевая из двух его моделей) и тонарма Simplicity II (по цене 9450 долларов, в середине линейки Thales; эти два можно купить как пакет за 14 180 долларов) и предложил мне попробовать, что я с радостью и сделал.

Описание
Фалес заимствует свое название у греческого философа-математика Фалеса из Милета ( ок. 624 г. до н. два на концах дуги — это всегда прямоугольные треугольники. Мика Хубер использовал теорему Фалеса в качестве основы для тонарма, чья дуга перемещения по пластине такова, что независимо от того, где приземляется стилус, эта точка является вершиной прямого угла, который имеет ось головки и радиус LP по бокам — что точно повторяет угол режущей головки токарного станка с мастер-лаком.

Huber запатентовал эту конструкцию в 2004 году и с тех пор усовершенствовал ее конструкцию до нынешней реализации: 9-дюймовый тонарм, состоящий из двух не совсем параллельных алюминиевых трубок с шарнирно-сочлененной головкой на одном конце, раздельного противовеса на другом и карданного подвеса. упомянутый Фалесом как подшипник Cardanic — отсылка к Джероламо Кардано, другому мертвому математику — в его точке опоры.

В Simplicity II отдельные подшипники, составляющие карданный вал и обеспечивающие шарнирное соединение головки, представляют собой запатентованные HiFiction подшипники TTF (Thales Tension-Free).Якобы это шарикоподшипники, но их внутренние кольца и оси имеют такую ​​форму и механическую обработку, что они обладают преимуществами одноточечных подшипников с драгоценными камнями.

В Simplicity II используется продуманный раздельный противовес: к задней части каждой трубки рычага прикреплен груз полукруглого поперечного сечения с цилиндрическим вспомогательным грузом, положение которого определяет прижимную силу, прикрепленным только к внутренней трубке рычага. Чтобы скорректировать непостоянную прижимную силу от начала канавки LP до конца, которая может возникнуть в результате такой конструкции в наихудших условиях, эксцентрично утяжеленный диск прикреплен к вспомогательному весу и может быть повернут, а затем заблокирован на месте для компенсации. для дисбалансов.

VTA настраивается привычным образом. После ослабления установочного винта, который фиксирует стойку рычага в цанге для крепления рычага, пользователь регулирует вертикально ориентированный крепежный винт, который проходит через портал рычага и выходит в углубление на упомянутой цанге; когда этот винт поворачивается по часовой стрелке, портал и, следовательно, рычаг поднимаются вверх, а при его повороте против часовой стрелки портал опускается. Затем снова затягивают установочный винт. Азимут регулируется путем ослабления двух стопорных винтов, которые крепят карданный подвес к конструкции, поддерживающей его, затем поворотом установочного винта, скрытого в этой конструкции, перед повторной затяжкой стопорных винтов.Simplicity II не предлагает антискейтингового механизма, возможно потому, что этот рычаг с его отличительной геометрией не восприимчив к боковым силам, которые мешают традиционным поворотным рычагам, которые полагаются на большое количество выступа иглы и смещение головки для достижения близкого расстояния. -косантность. Я оставлю это производителю, который указывает ошибку отслеживания Simplicity II как удивительно низкую 0,006 ° максимум , чтобы дать комментарий.

На первый взгляд, очень компактный проигрыватель виниловых пластинок TTT-Slim II — его размеры всего 16.5 дюймов в ширину и 12 дюймов в глубину — это простая, легкая конструкция с цоколем, не похожая на многие другие, доступные сегодня. Только одно из этих предположений оказывается верным. Подшипник диска, приводной двигатель и тонарм действительно прикреплены к единой конструкции, но эта конструкция не является ни простой, ни легкой: цоколь, как и диск, изготовлен из цельного алюминия — оба имеют слегка текстурированное анодное покрытие антрацитового цвета. — комбинация, которая поднимает чашу весов на удивительный вес в 26,4 фунта (сравните с 13.2 фунта для Rega Planar 3.)

Цоколь имеет множество выемок, канавок и каналов, самые большие из которых предназначены для размещения опорного диска; Как и в случае с классическим и не менее швейцарским проигрывателем Thorens TD 124, опорный диск Slim II возвышается менее чем на дюйм над поверхностью, на которой установлен тонарм. Диск поддерживается механически обработанным полимерным поддоном, рядом с которым находится небольшой двигатель постоянного тока, который изолирован от цоколя с помощью монтажного устройства сложной формы.Металлический шкив двигателя расположен как можно ближе к краю вспомогательного диска, чтобы резиновый ремень круглого сечения оставался как можно короче. Электропроводка для двигателя проходит через канал, специально обработанный для этой цели, который ведет к бортовой схеме привода и аккумуляторной батарее: хотя он подключается к бытовому источнику переменного тока пользователя, когда его литий-ионные батареи нуждаются в подзарядке — указано время работы 20 часов — утверждается, что внешнее зарядное устройство электрически отделено от схемы привода, когда проигрыватель виниловых дисков включен.Тем не менее, чтобы предотвратить любые электрические выбросы, загрязняющие воспроизведение, HiFiction рекомендует отключать зарядное устройство, когда оно не нужно, тем самым отключая Slim II от сети во время воспроизведения.

Подшипник опорного диска имеет колодец из высокопрочного чугуна, футерованный втулкой из спеченной бронзы, которая, как говорят, пропитана маслом во время процесса выдержки при нагревании, что гарантирует работу без обслуживания «в течение многих десятилетий». Подшипниковый вал изготовлен из закаленной инструментальной стали, отполирован вручную липой и алмазной пастой.Диск весом 7,7 фунта, обработанный с тяжелым ободом для увеличения инерционной массы, как говорят, настроен на одну единственную резонансную частоту, а затем снабжен инкрустированным ковриком из неизвестного материала высокой плотности. (Он выглядит и ощущается как свинец, но я уверен, что это не так.)

Последний вклад в производительность Slim II вносят три изоляционных ножки: небольшие регулируемые по высоте фитинги, в которых контактные элементы — стальные шарики — центрируются гибкими резиновыми фитингами. Производитель предполагает, что эти «шипы» эффективно изолируют проигрыватель от горизонтальных колебаний.

Установка и настройка
Мой обзорный образец комбинации TTT-Slim IISimplicity II был установлен в моей системе со всеми очевидными навыками Винном Вонгом из североамериканского дистрибьютора HiFiction, Wynn Audio. При этом проигрыватель виниловых пластинок и тонарм Thales, не говоря уже об их хорошо выполненной упаковке, похоже, были спроектированы таким образом, чтобы обеспечить простоту настройки и неизменно точные результаты.

Это особенно заметно в приспособлении для выравнивания картриджа из плексигласа и алюминия — в своем очень хорошем руководстве HiFiction называет это прицелом (сноска 1) — поставляемым с Simplicity II: во избежание нарушения шарнирного сочленения головки рукоятки. , конструкция требует, чтобы картриджи были установлены на небольшой алюминиевой пластине, которую можно более или менее быстро и легко извлечь из этого хедшелла, на котором он зафиксирован с помощью единственного нуля.Установочный винт 9 мм. Сам прицел Thales выполнен с выемкой, в которую помещаются патрон и пластина — идеально, — и имеет линии визирования, которые позволяют однозначно правильно позиционировать кантилевер и иглу. Я был впечатлен тем, что HiFiction приложила все усилия и усилия для создания такого инструмента. Если позаимствовать фразу из былого рекламного ролика о мыле, Разве вы не желаете, чтобы все это делали?

В течение нескольких недель после установки Винн Вонг я частично разбирал плеер, в основном, чтобы посмотреть, что в нем работает.И в самом начале обзора я установил тонарм Simplicity II на свой винтажный проигрыватель винила TD 124 (сноска 2). Я обработал, отрегулировал и просто использовал практически каждый элемент этих двух продуктов, и я должен сказать следующее: за 34 года написания статей о воспроизводящем оборудовании я не видел продуктов лучше, чем проигрыватель виниловых пластинок и тонарм Thales. , и очень немногие — что равняется им. В самом деле, простое обращение с тонармом Simplicity II — чтобы отметить, насколько абсолютно свободны от трения, но также насколько прочны, гладкие и без люфта его подшипники — оставило меня в восторге от качества его изготовления.И хотя я далек от одержимости регулировкой VTA, меня не могло не впечатлить, насколько легко было отрегулировать высоту руки. Опять же, это делается так же, как и с любым другим тонармом из моего опыта, но для одного все они совершенно грубые по сравнению с тем, как это было реализовано на Simplicity II.

Прослушивание комбинации TTT-Slim IISimplicity II
Хотя бы потому, что проигрыватель Thales сильно отличался от моего собственного — маленький вместо большого, новый вместо винтажного, постоянный ток вместо переменного тока, низкий крутящий момент вместо высокого крутящего момента — Я был немного поражен тем, насколько хорошо он показал себя во многих наиболее важных для меня аспектах производительности: цвет, драйв, импульс, чистый , сок .Я предвосхитил и ушел в шоке. Вот оно.

---

Сноска 1: Прицел Thales напоминает, хотя и намного сложнее, чем приспособление для выравнивания картриджа из прозрачного пластика, поставляемое с проигрывателем Thorens TD 145, который я купил новым в 1975 году. Он должен был надеть на тонарм. Headhell ​​и требовал от пользователя прокладки картриджа, иногда резко, в качестве компенсации удручающе нерегулируемого по высоте тонарма проигрывателя.

Сноска 2: Это был второй образец, который HiFiction любезно отправил мне домой.

Тонарм Reed 5T | Аммонит Аудио

Тонарм Reed 5T — первое появление компании Reed в области тангенциальных тонармов. Благодаря уникальной конструкции лазерного сервопривода, это один из самых совершенных тонармов, которые мы когда-либо создавали. Технически 5T представляет собой вращающийся тонарм с тангенциальным отслеживанием, принцип работы которого основан на теореме Фалеса (если центр описанной окружности треугольника лежит на треугольнике, то треугольник является прямым, а центр его описанной окружности лежит на его гипотенузе) и Правило, согласно которому для трех неколлинеарных точек можно нарисовать только одну окружность конечного радиуса, проходящую через все три.

Это довольно сбивает с толку и частично объясняется этой диаграммой, но самое важное, что нужно принять во внимание, это то, что Рид создал тонарм с практически нулевыми ошибками трассировки по всей пластинке, но без каких-либо недостатков « обычных » параллельных рычагов слежения, которые включают сильно различающуюся эффективную массу в вертикальной и горизонтальной плоскостях, а также необходимость очень точного выравнивания, если необходимо избежать потенциально разрушительных боковых нагрузок на консоль / подвеску картриджа.Аудиофилам нравится идея параллельных рычагов слежения и отсутствия ошибок / искажений слежения, но основными недостатками этих типов рычагов являются громоздкость, шум (от воздушных компрессоров) и, самое главное, то, что большинство рычагов не очень хорошо звучащие (конечно, есть исключения. ). Преимущество Reed 5T в том, что он начинается с конструкции тонарма, которая уже отлично звучит (Reed 2G), и обеспечивает почти нулевую погрешность трассировки за счет шарнирного сочленения основания руки с помощью элегантных сервосистем, управляемых лазерной направляющей.

Трубка тонарма и система подвески аналогичны той, что используется в тонарме Reed 2G, а поворотная часть тонарма основана на малошумном подшипнике с упорной втулкой. Для углового вращения тонарма мы спроектировали и построили секционный моментный двигатель ограниченного вращения. Положение тонарма контролируется с помощью лазера и линейных датчиков. Трубки руки заменяются пользователем, что означает, что вы можете настроить ее эффективную массу в зависимости от выбранной древесины палочки руки.Reed 5T также имеет регулировку VTA и азимута.

Таким образом, Reed 5T имеет следующие преимущества по сравнению с обычными поворотными тонармами:

• Меньший момент инерции,
• Нет необходимости в антискейтинговом механизме,
• Максимальная ошибка отслеживания составляет +/- 5 минут угла (MOA). (Фигура 2). Поворотные тонармы обычно имеют максимальные ошибки отслеживания до 1,5 градусов .

По сравнению с другими тангенциальными тонармами Reed 5T имеет следующие преимущества:

• Значительно меньший момент инерции,
• Нет необходимости в сложных или шумных дополнительных устройствах (воздушный компрессор),
• Компактный и элегантный дизайн.
• Эффективная масса в вертикальном и горизонтальном направлениях одинакова.

Технические характеристики

Монтажное расстояние	251 мм (макс. Диаметр диска = 330 мм)
Ошибка отслеживания	+/- 5 угловых минут (MOA)
Эффективная масса	8-16 г, в зависимости от материала рукоятки (сменная рукоятка)
Регулировка высоты	для тарелок высотой 28 ÷ 48 мм
Регулировка VTA	точность +/- 0.2 мм
Регулировка азимута	+/- 8 градусов
Диапазон прижимной силы	10 ÷ 30 мН (масса патрона 5,5 г — 19,5 г, (4,0 г — 25,0 г))
Тяга	Секционный линейный двигатель с ограниченным вращением
Напряжение	прямое 12 В, питание от батареи Reed Source 12 В

Варианты отделки

Морская ракушка, белое золото, матовое

Черный

ARMWAND ДЕРЕВЯННЫЕ ОБРАЗЦЫ

Венге Макассар Эбеновое дерево

Cocobolo Teak светлый

Тик темный

Приблизительная эффективная масса тонарма Reed в граммах

Armwand Эффективная масса (г) Кокоболо 12-18 Макассарское эбеновое дерево 10-14 Венге 10-14 Тик (темный, светлый) 8-14

МЮНХЕН 2019: Источники и кабели

Munich High End, несомненно, является крупнейшей аудио-феерией высокого класса в мире.На нем были представлены не только одни из лучших продуктов, недавно представленных на AXPONA Chicago (еще одно невероятное шоу!), Но и широкий спектр продуктов, которые до сих пор не были представлены на берегах Северной Америки. Я никогда не видел такого количества вертушек, рупорных громкоговорителей и экзотических товаров в одном месте!

В этом году мне больше всего понравились источники и кабели — практически каждая комната на шоу. Поскольку это была устрашающая, если не невыполнимая задача, я сосредоточился на тех источниках и кабелях, которые я действительно мог слышать в системах, а не на статических дисплеях.Я также избегал комнат, где мне не было места, и / или тех, которые использовались как сауны (Примечание для экспонентов: снова включите кондиционер в своей комнате или хотя бы откройте окно)! Приношу свои извинения производителям и дистрибьюторам, которых я пропустил.

Лучшее: системы с аналоговыми источниками

Проигрыватель Reed Muse 3C (15 850 евро) и тонарм Reed 5T (14 900 евро) с картриджем Topwing Suzaku (Red Sparrow) , соединенный с фоностажем NEM Phono Kit 4 с ламповым источником питания и мощные усилители и предусилитель YS Sound Electronics были источником потрясающих динамиков Zellaton Reference MkII .Соединенная кабелями Schnerzinger Atomic Bonding и Giga Pulse Protectors (высокоэффективная регулируемая система подавления высоких и низких частот, которая защищает аудиосигнал от мешающих полей), система воспроизводила самый захватывающий, ощутимый и бесцветный звук шоу! Стол Reed ‘может быть преобразован в блок с ременным приводом, но я слушал’ стол ‘с фрикционным приводом. Впечатляющий Reed 5T — это вращающийся тонарм с тангенциальным отслеживанием звука (основанный на теореме Фалеса).Он использует массив лазеров для поддержания правильного положения. Отсутствие ошибок отслеживания картриджей привело к очень низкому искажению изображения, которое имело невероятную прозрачность и красивый тональный цвет благодаря чудесным Зеллатонам. Ноты гнили естественным образом, как в концертном зале. У Slap bass на «The Awakening» была потрясающая скорость и мимолетная быстрота. Это была захватывающая поездка. Для меня это был лучший звук шоу!

Проигрыватель DeBaer Saphir (58 тыс. Евро) с тонармом DeBaer Onyx (19 тыс. Евро) и картридж EMT входил в состав еще одной выдающейся системы с Soulution 7 серии электроники , Magico M6 динамиков, Critical Mass Systems стоек Olympus и Center Stage футов и кабелей Vovox .DeBaer эффективно разделяет все соответствующие части шасси с минимальным взаимодействием между проигрывателем и тонармом. В последний день эта система выдавала лучший бас, который я слышал на шоу, с потрясающим расширением, артикуляцией и контролем на записи Мишеля Йонаса («Le Temps Passe»). Я никогда не слышал, чтобы динамики M6 звучали так низко при таком большом количестве воздуха — это было интуитивно! В остальном звук тоже был превосходным, с множеством тонких и изысканных деталей на широкой и глубокой звуковой сцене.

Проигрыватель Continuum Audio Labs Obsidian (35 тысяч долларов) с тонармом Viper (10 тысяч долларов) и картриджем Ortofon A-95 (6 тысяч долларов) служил аналоговой передней частью очень приятной и увлекательной системы. , включая фоновый каскад Constellation Andromeda (18 тысяч долларов) с фильтром постоянного тока (5 тысяч долларов), а также предусилитель Constellation Pictor и моноблочные усилители Taurus .Эта более доступная электроника Constellation в сочетании с громкоговорителями Magico M2 с M-Pods и кабельной разводкой Nordost Odin2 для получения множества мелких деталей, выделяющихся на угольно-черном фоне, без лишних шипений. «Великие ворота Киева» завораживали впечатляющей динамикой, а более тихие треки из альбома Dream with Dean воспроизводили голос Дина с богатым, естественным тембром и удивительной прозрачностью.

Джордж Куннас из Zesto Audio , кажется, всегда собирал одну из самых хорошо звучащих комнат на выставках, и Мюнхен не был исключением.Помогает то, что он использует свою собственную великолепно выглядящую и звучащую электронику (в том числе его новый Andros Deluxe Vacuum Tube Phono Stage , который включает в себя многие внутренние функции Zesto Tessera) и сверхтихую Merrill Williams REAL. Поворотный стол 101.3 (7995 долларов США), с превосходным тонармом Tri-Planar U2 Classic и картриджем Benz-Micro Gullwing . Последний стол Merrill-Williams имеет больший контроль резонанса, чем оригинальная модель, которой я владею, особенно в нарукавной доске. Verity Audio Акустические системы Amadis S и кабели Purist Audio Design (включая новый кабель переменного тока Diamond Revision Neptune с улучшенным демпфирующим материалом для снижения шума и вибрации, а также разъемы питания Furutech NCF ) округлые из системы. На лейтенант Kije тембры инструментов были красивыми и естественными, с большим количеством воздуха. Инструменты выходили из совершенно бесшумного черного фона, а передние кромки переходных процессов были очень чистыми.Я думал, что слушаю мастер-запись!

Проигрыватель Acoustic Signature Invictus Jr. (85 тысяч долларов) с картриджем Airtight Opus 1 (16 тысяч долларов) помог добиться звездного звука на входе системы с потрясающим вертикально ориентированным VAC. Интегрированный усилитель 450iQ и впечатляющие громкоговорители Ultra Reference 9 Von Schweikert , соединенные кабелями Masterbuilt Ultra Line .Invictus Jr. помог обеспечить большую солидность звучанию, которое было живым, но естественным на «Exactly Like You» Рэя Брауна. Фортепиано воспроизводилось с большой четкостью, непосредственностью, сосредоточенностью и хлопком.

Проигрыватель виниловых пластинок VPI HW-40 Direct Drive ($ 15 тыс.) С невероятно стабильной скоростью был подключен к фонокорректору Pass Labs XP-25 с использованием MIT amazing Oracle MA- Интерфейс X SHD Phono с формантными элементами управления и 110 полюсами сочленения, а также новый MIT Powerbar II (с переключателями управления коэффициентом мощности).Предусилитель Pass Labs XP-25 и моноблоки X600.8 с межсоединениями Oracle SHD и консоль управления артикуляцией MIT ACC 169 обеспечивали интерфейс динамика (через соединительные кабели Oracle). Возможно, поэтому MartinLogan Neolith звучал в Мюнхене более плавно, открыто и расслабленно, чем я слышал его на любом предыдущем шоу, с богатыми, реалистичными тембрами (поскольку обертоны воспроизводятся так точно с помощью фонокорректора MIT. ). Минимальный уровень шума был чрезвычайно низким, что позволило более мелким деталям проявиться на Liszt Hungarian Rhapsody с превосходной размерностью и басовой артикуляцией.

Nordost также был оснащен юбилейным проигрывателем VPI HW-40 Direct Drive с электроникой Moon и динамиками YG Hailey 2.2 для демонстрации нового кабеля тонарма Valhalla 2 , а также линейного кабеля QSource linear. кабель питания и постоянного тока, а также шайбы QPoint . В очень хорошей демонстрации звук значительно улучшился с добавлением этих продуктов, с повышенной четкостью и размерностью.Я также был впечатлен стабильностью скорости VPI на устойчивых басовых нотах на записи Гэри Карра.

Проигрыватель Thales Compact II (15 530 долларов США) с аккумуляторным приводом и тонарм Thales Statement (20 250 долларов США) с картриджем EMT JSD VM (5400 долларов США) и повышающим трансформатором EMT STX 5/10 (9 280 долларов США). Передняя часть другой очень хорошей звуковой системы с электроникой Nagra Classic и динамиками YG Acoustic Hailey 2.2 .Он отличался очень низким уровнем искажений и окраски, отличной четкостью и детализацией, богатым тембром и потрясающим балансом. Должен полюбить эти тонармы с тангенциальным поворотом!

Musical Surroundings всегда представляет новые захватывающие аналоговые продукты в Мюнхене, и в этом году это был потрясающий проигрыватель виниловых пластинок AMG Viella Forte 12 Turbo (стандартная цена 30 тысяч долларов; версия с гравировкой 32 тысячи долларов) с тонармом AMG 12JT Turbo 12 дюймов и DS Audio Оптический фонокорректор DS-E1 (2750 долларов США).По сравнению с оригинальной Viella, Forte имеет более крупный и толстый цоколь, изготовленный из цельного алюминиевого блока, более высокий и толстый диск, большую массу и более эргономичный зажим, основание рычага большего диаметра, улучшенную электронику привода и новую мощность. Поставка конструкции и жилья. Красивая версия Viella Forte с гравировкой сочеталась с электроникой Aesthetix и динамиками ProAc KG Signature . Система воспроизводила твердые и отчетливые басы с очень хорошей звуковой сценой, фокусировкой и стабильностью скорости.Он легко справлялся с большими динамическими колебаниями, без каких-либо ошибок, и был очень тихим, практически без шума на поверхности на старом LP. С другой стороны, Aesthetix представила новую фонокорректорную плату для своего высоко оцененного интегрированного гибридного усилителя Mimas , но она демонстрировалась бесшумно.

Проигрыватель Kronos Pro с двумя пластинами (42 тыс. Долларов) с блоком питания SCPS1 , картриджем ZYX Universe 3 и B без тонарма Beauty в сочетании с элегантными динамиками Estelon Forza CH с приводом от CH Электроника Precision с кабельной разводкой от Kubala Sosna для воспроизведения прекрасного тембра голоса, групповых струнных инструментов и фортепиано.Ясность и воспроизведение мелких деталей также были очень хорошими, а динамики практически исчезли! Это был успешный дебют Forza!

Pear Audio Blue — лучший проигрыватель виниловых пластинок Odar с тонармом Cornet 2 12 дюймов (18 тысяч долларов с кронштейном, отдельным источником питания и платформой) и мощным Raidho TD 3.8 Мировая премьера громкоговорителей состоялась в Мюнхене во впечатляющей системе с электроникой Chord и кабелями GamuT .Odar имеет две рукоятки, на которых можно разместить 10- или 12-дюймовые рычаги, более массивный и больший диск, улучшенную изоляцию, электронный регулятор скорости и модернизированный корпус двигателя, при этом сохраняя двигатель со сверхнизким крутящим моментом, который снижает передачу энергии. от двигателя до диска более чем на 90%. Картридж Top Wing Blue Dragon (12 тыс. Долл. США) помог произвести сверхтихую презентацию с очень хорошей стабильностью скорости и воспроизведением мелких деталей. С новыми динамиками Raidho система отличалась выдающейся непосредственностью, четкостью, связностью и присутствием — мои пальцы ног стучали!

Проигрыватель TW-Acustic Raven Black Night в сочетании с картриджем Dynavector XV-1 S и фонокорректором TW стал прекрасным источником для электроники Verity Audio и его красивых громкоговорителей Lohengrin 11S Reference .Превосходные кабели Cardas Clear Beyond дополняют систему. Запись «Send in the Clowns» была очень увлекательной, с красивым тембром и всевозможными внутренними деталями, возникающими на очень тихом фоне. Хотя звуковая сцена была широкой и глубокой, голос был несколько больше, чем жизнь.

Новая модель SME Model 12a (10 250 евро) дебютировала в Мюнхене в системе с электроникой Nagra и громкоговорителями Spendor Classic 100 .Модель 12a включает тонарм SME 309 и внешний электронный блок управления. Голос Элвиса, казалось, исходил из ниоткуда, поскольку SME было совершенно безмолвным. Похоже, это очень хорошее обновление по сравнению с моделью 10 компании

.

Проигрыватель TriangleArt Master Reference (40 тыс. Долларов) и тонарм Osiris (7 тыс. Долларов), картридж Apollo MC и электроника TriangleArt в сочетании с захватывающими электростатическими гибридными динамиками Muraudio SP1 для создания одного из лучших звучит на шоу.Система имела «протяни руку и прикоснись» к женскому вокалу, а перкуссия была невероятно четкой и четкой. Аналоговый интерфейс был очень тихим и подробным.

Более доступный аналог
Из более доступного конца диапазона — проигрыватель виниловых пластинок ELAC Miracord 90 ^th Anniversary (2499 евро) в сочетании с электроникой ELAC Alchemy и громкоговорителями ELAC Carina для получения прекрасного звука с хорошая детализация и очень хорошее изображение, но с намеком на добавленную сибилянность в голосах.Однако средние частоты были открытыми и привлекательными, а система неожиданно расширилась на обоих концах крайних частот. Завершают систему AudioQuest Thunderbird , межблочные кабели AQ Wind и стабилизатор питания Niagara 7000 с Hurricane AC. Это еще одна дорогостоящая, хорошая звуковая система от ELAC.

Проигрыватель Gold Note Mediterraneo (от 6 тысяч долларов) с модернизированным тонармом B7 (титан) и картридж Tuscany успешно дебютировал в Мюнхене в системе полностью Gold Note с интегрированными IS-1000 и A3 EVO полочные колонки.Сусальное золото нанесено на проигрыватель вручную, и динамик не только великолепно выглядит, но и воспроизводит очень живой и захватывающий звук на джазовом пианино. Mediterraneo имел хорошую стабильность скорости и был довольно тихим, хотя я бы хотел услышать его в лучших условиях. Эта компактная и привлекательная система Gold Note действительно понравится тем, кто высоко ценит PRAT.

Еще одним приятным сюрпризом стал проигрыватель виниловых пластинок Mag Lev Audio ML1 (3599 долларов в черном цвете с картриджем Ortofon 10 ) в системе со встроенным Roksan и небольшими динамиками Triangle .Объединяя катушки и магниты, блюдо фактически плавает. Отсутствие шума двигателя обеспечило очень чистый, детализированный звук с отличной стабильностью скорости.

Manger Audio демонстрировал свои пассивные динамики p2 , используя потрясающий преобразователь изгибных волн для средних и высоких частот, с электроникой SPL и новый Scheu Analog Das Laufwerk No. 2 акриловый проигрыватель (9850 евро) с Тонарм Scheu Tacco uni-pivot (2800 евро) и картридж Scheu MC Kupfer L (1190 евро) на основе Benz-Micro Glider S .Стол Scheu может вместить до трех рук и оснащен отдельным двигателем постоянного тока с электронной регулировкой. Звук системы был довольно приятным и естественным, с очень хорошей стабильностью скорости и когерентностью. На Symphonic Dances динамика была взрывной, но все же контролируемой. Я думал, что слушаю не только топовый проигрыватель виниловых пластинок, но и систему в целом, которая превосходит некоторые системы, которые стоят намного дороже!

Цифровые фронтенды: лучшие

Новый Nagra HD DAC X (62 евро.5k) в сочетании с электроникой Nagra HD и громкоговорителями YG Sonja XV Jr. и сабвуфером YG InVincible в другой цифровой системе, которая звучала как аналоговая (до тех пор, пока они не перешли на катушечную деку Nagra). Новый Nagra HD DAC X включает в себя многие технологические достижения от известного предусилителя Nagra HD Preamp , такие как двойная моно топология, стойка без вибрации и новое поколение трансформаторов Nagra. Его основной цифровой источник питания имеет уровень шума в 30 раз ниже, чем ЦАП HD, и он использует не менее 37 регулируемых, сверхмалошумящих индивидуальных источников питания, тактовые генераторы с ультранизким джиттером и высокопроизводительную FPGA для внутренних устройств. расчеты.Все входные сигналы преобразуются в формат DSD 256. На Pictures at an Exhibition цифровая система имела твердые, мощные басы и взрывную динамику, но при этом не допускала никаких намеков на цифровое превосходство. На «Guantanamera» я думал, что слушаю аналоговый источник, поскольку гитара и голос имели естественный тембр и привлекательное, завораживающее гармоническое богатство.

Spectral SDR-4000SV Reference CD Processor (20000 долларов), усилитель Spectral DMA-260 и предусилитель 30 SV Reference , великолепные динамики Wilson Audio Sasha DAW и кабели MIT (уровень UL 2C3D one соединяет и акустические кабели) произвел взрывную динамику и твердые басы на «Fanfare for the Common Man» Копленда.Более того, тембры акустических инструментов звучали очень естественно с большим количеством воздуха позади них, а система имела очень хорошее изображение и фокусировку. Я не мог поверить, что слушаю цифровой источник. Это была одна из самых звучащих систем на выставке.

Сервер / ЦАП ReQuest Raptor Plus ($ 15 тыс.) Был в начальной части системы с интегрированной красивой Absolare Passion и динамиками Rockport Atria . Echole Кабели Infinity и кондиционер Torus Power переменного тока завершают систему. Raptor — это уменьшенная версия ReQuest Beast, которая с Absolare звучала очень музыкально, с естественным тембром и очень хорошей передачей мелких деталей. Я снова подумал, что слушаю аналог (в моей книге это хорошо!).

Еще одна система, которая воспроизводила тембры естественным образом, была в комнате Kharma , в которой использовалась потрясающая Kharma Enigma Veyron EV-2D-1.0 колонок, Харма и электроника и кабели. У компании «Харма» есть сопутствующие кабели для каждой из основных производственных линий — в данном случае Enigma Veyron, где «особое внимание уделяется каждому проводнику в отдельности». С dCS Vivaldi в качестве цифрового входного каскада звук был богатым и захватывающим на широкой и глубокой звуковой сцене. Динамика была взрывной, а голос Гарри Белафонте ощутимым.

Предварительный усилитель Aavik C-300 с ЦАП служил цифровым интерфейсом для захватывающей системы с моноблоками Aavik M-300 , динамиками Borresen 05 и кабелями Ansuz DTC Supreme , которые имеет половину индуктивности своего предшественника.Благодаря такому эффективному гашению резонансов можно глубже слышать музыку. Это делает систему очень привлекательной! Как и в Чикаго, эта комбинация была потрясающей с невероятной звуковой сценой, басами, артикуляцией и переходной скоростью — она ​​заставила меня содрогнуться! К счастью, система также воспроизводила натуральные тембры с невероятной детализацией.

MSB Select DAC (84,5 тыс. Долларов США) сохранил свои позиции с громадным проигрывателем Kronos Pro (38 тыс. Долларов) в другой системе с динамиками Magico M2 , электроникой Soulution , MIT кабелями динамиков, и кондиционер питания Shunyata Denali .MSB звучал как аналоговый с выдающейся четкостью, широкой и глубокой звуковой сценой и гармоническим богатством без типичной цифровой грани. Kronos Pro обеспечил аналоговый интерфейс для нескольких систем с лучшим звучанием в Мюнхене.

Ayon S-10 II Vacuum Tube Network Player (от 8800 долларов) использует модульную конструкцию, объединяющую аналоговый предусилитель и полностью независимые модули стример / сервер, а также двойной моно ЦАП и преобразователь PCM в DSD.Это элегантное устройство использует лампу 6х40 и не использует полупроводниковые устройства в аналоговом ламповом выходе (тракте прохождения сигнала). В системе с ламповой электроникой Ayon и Ayon B без динамиков Eagle звук был очень похож на аналоговый с отличным корпусом и звуковой сценой, а также естественным тембром. Он прекрасно звучал на фортепиано и голосе и богат струнной массой. Было много чего любить!

Crystal Cable представила кабели серии Future Dream (питание и межкомпонентные соединения) в привлекательной системе с динамиками Minissimo Diamond-Scala и Crystal Cable Integrated (CCI).Гибридные кабели Future Dream изготовлены из монокристаллического серебра и сплава серебра и золота. (Новый фонокабель Future Dream демонстрировался на бесшумном дисплее.) Цифровой интерфейс системы представлял собой проигрыватель dCS Rossini и ЦАП. На фортепианной записи фортепианного концерта Листа было много мелких деталей и ясности, и музыку можно было действительно услышать. Великолепное расширение системы high-end воспроизводило естественные тембры, и казалось, что музыка дышит.

Потоковый ЦАП Brinkmann Nyquist MkII (17900 долларов США) отличился в системе с электроникой Brinkmann (предусилитель Marconi Mk11 и усилители мощности Mono ), Vandersteen Audio Model Seven MkII сабвуфер и сабвуфер . Кабели AudioQuest и стойка Harmonic Resolution Systems VXR .Фортепиано было очень чистым с поразительными переходными атаками, а звук был живым и непосредственным, с очень хорошим расширением басов, прозрачностью, ударом и хлопком. Голоса были очень красиво переданы без добавления сибилянтов или цифровой резкости.

Музыкальный сервер Innuos Statement (от 13 750 долларов США) был потрясающе трехмерным в системе с динамиками Bowers & Wilkins 802 D3 , интегрированным усилителем Gryphon Diablo 300 с ЦАП и системой кондиционирования Isotek EVO3 .Музыкальный сервер Innuos ZENith Mk3 (от 4249 долларов) имел семейное звуковое сходство с Statement (хорошо), но с меньшей глубиной звуковой сцены, чем его более дорогостоящий собрат. Заявление также было более расслабленным и естественным.

Модульный ЦАП Wadax Atlantis Reference был соединен с величественными громкоговорителями Kharma Grand Exquisite , предусилителем Robert Coda , Engstrom для производства моноблоков и соединен кабелями fono Acustica. лучшие звуки шоу.Wadax использует уникальную систему исправления ошибок с прямой связью, которая работает во временной области, и передовую технологию уменьшения джиттера. Я мог слышать корпус и богатство инструментов и полную акустику фортепиано. Вдобавок размер пианино был в правильной перспективе (не больше, чем в натуральную величину), а его фокусировка была превосходной.

Esoteric представлял собой моноблочные ЦАП Grandioso DIX с двумя шасси (50 000 долл. США) и транспортный P1X с электроникой Esoteric и кабелями AudioQuest .На записях с кодировкой MQA звук был довольно естественным, с отличной четкостью, открытыми высокими частотами и твердыми и отчетливыми басами. Система с громкоговорителями Sonus faber Amati Tradition была не только довольно детализированной с большим количеством ударов, но и была легкой для ушей.

Не следует забывать и о CD / DAC MBL N31 (12 000 евро), который сочетается с электроникой MBL Noble Line и потрясающими динамиками 101 E Mk II Radialstrahler от MBL. В N31 используется технология MBL «anti-clipping», обеспечивающая потрясающие динамические пики без искажений, а также расширенные, артикулированные басы.Это была очень приятная и увлекательная система, и мне захотелось услышать о более крупной системе MBL.

Более доступный цифровой
PrimaLuna представила свои новые «дорогие» модели EVO , включая EVO 100 Tube DAC (2999 долларов США), как в Чикаго, так и в Мюнхене. Он использует схему SuperTubeClock последнего поколения и лампы 12AX7, 12AU7 и 5AR4. В системе с электроникой EVO и громкоговорителями Jern 14 звук имел удивительное богатство (по этой цене) с очень хорошим воздействием, визуализацией, фокусировкой и четкостью.Похоже, это выгодная сделка!

Новые динамики Hegel с поддержкой MQA 390 (5,9 тыс. Долларов), интегрированные с Roon в сочетании с KEF R11 , давали очень впечатляющий звук по относительно скромной цене. В h490 используется схема прямой связи Sound Engine 2, а его ЦАП основан на CD-плеере Hegel Mohican. Система воспроизводила мощные басы с очень хорошим изображением и когерентностью. Это был сильный кандидат на лучшую систему за деньги.

Предварительный усилитель Anthem STR (3999 долларов США) с новейшим программным обеспечением для коррекции помещения ARC Genesis помог выявить лучшее из пары динамиков Paradigm Persona 7F , управляемых двумя усилителями мощности Anthem STR и соединенных с Shunyata. кабелей и его стабилизатор питания Denali . Музыка предоставлялась с помощью музыкального сервера Aurender N10 . При использовании программного обеспечения для коррекции помещения ARC Genesis басы были намного более равномерными по всей комнате с очень хорошей визуализацией.Из-за этого система казалась намного более дорогой.

Linn Selekt DSM (6825 долл. США) был в центре внимания семинара Linn, призванного продемонстрировать его модульный подход, гибкость, возможность модернизации и простоту использования. Демка прошла успешно! На самом базовом уровне Selekt DSM может работать как стример высокого уровня и цифровой предусилитель или как интегрированный усилитель. Он работал в паре с внешним усилителем мощности Linn Akurate 2200 , ЦАП Linn Katalyst и динамиками KEF Ref 3 .Звук был четким и мгновенным, но я предпочел опцию оптимизации пространства, которая давала более открытый звук с лучшей визуализацией и фоновыми сигналами, а также более плотными басами и улучшенной динамикой.

Из-за отсутствия узлов комнаты, о которых можно было бы беспокоиться, один из лучших звуков на выставке был получен от нового сетевого ЦАП Bartók dCS с дискретным усилителем для наушников класса A (15000 долларов США) в сочетании с планарно-магнитными наушниками JPS Labs Abyss AB-1266. (5495 долларов США).Этот моноблочный цифровой музыкальный проигрыватель сочетает в себе кольцевой ЦАП dCS, высокопроизводительный музыкальный стример и уникальный усилитель для наушников, подходящий как для наушников с высоким, так и с низким сопротивлением.

Мало что видели, но не слышали
Хотя большая часть этого отчета посвящена аналоговым и цифровым интерфейсам и кабелям, которые я действительно слышал в системах, было несколько заметных продуктов с бесшумным дисплеем, которые выглядят очень многообещающими. Первым среди них был массивный проигрыватель виниловых дисков Wilson Benesch GMT ONE .Компания утверждает, что у нее «самая точная приводная система, когда-либо разработанная для проигрывателя винила». MSB представила свой новый дискретный ЦАП ($ 9950), модульный дизайн с «большей частью технологии ЦАП Select от MSB», но по более доступной цене. Я бы хотел это услышать. Clarus Audio продемонстрировал краткую характеристику своих будущих межблочных кабелей Aqua Mark II и акустических кабелей, предназначенных для уменьшения вихревых токов, которые могут замедлять передачу сигнала. В акустических кабелях используются запатентованные компанией лопаточные наконечники «Spring-Tension», предназначенные для обеспечения долговечных и надежных соединений. Skogrand продолжает развивать линейку тонких кабелей, но также представила новый блок распределения питания.

Лучшее из шоу JH

Best Sound (цена-без-объект): Reed Muse 3C с тонармом 5C / YS Sound electronics / Zellaton Reference MkII динамиков / Schnerzinge r кабелей.
Лучший звук (за деньги): ELAC Miracord ’table / Alchemy electronics / Громкоговорители Carina с кабелями AudioQuest и блоком питания Niagara .Второе место: PrimaLuna EVO 100 Tube / DAC с Jern 14 динамиками; Hegel 390 интегрирован с динамиками KEF R11 .
Наиболее значимая тенденция: Цифровые источники с гораздо лучшим звучанием.
Самые популярные продукты: Громкоговорители Zellaton Reference MkII , Nagra HD DAC X , Reed Проигрыватель Muse 3C с тонармом 5C .

Интранет Ciena

Узнайте, что происходит на Vue Birmingham. Откройте для себя лучшие кинотеатры города с более чем 5000 мест и 25 экранами, с превосходным качеством изображения Sony 4K и объемным звуком Digital Dolby. Free fire официальный аккаунт gmail

22 декабря 2020 г. · Ciena сообщает о финансовых результатах за четвертый квартал 2020 года и финансовые результаты на конец года Associated Press 12/10/2020. CIENA Corp. Equal Weight Business Insider …

Multisim изменить цвет фона осциллографа

Очертания проповеди Рика Уоррена

На арене с суперинтендантом Эриком Олсоном.Школьный округ Монтичелло рад поделиться с суперинтендантом Эриком Олсоном «На арене» новым подкастом, который позволит Supt. Олсону, чтобы ежемесячно погружаться в различные темы в мире образования.

Audio hijack vs loopback

Небольшие исторические швейные проекты

Присоединяйтесь к нам, поскольку мы создаем ценность и превосходим ожидания наших клиентов, полностью поддерживая наших сотрудников, чтобы они были лучшими.

Срок действия дебетовой карты Bmo harris истекает

Авария на 680 сегодня в Данвилле

Mcmaster VPN linux — только 2 хорошо сработали С mcmaster VPN linux для достижения цели.По результатам исследования различного независимого опыта выясняется, что процент вполне удовлетворенных людей кажется чрезвычайно большим.

Simplicity

Навигационный экран Toyota camry черный

В связи с новыми ограничениями наше здание закрыто для публики. Мы надеемся скоро поприветствовать вас. Изучите нашу программу кинотеатра, которую вы можете смотреть дома, на открытом воздухе и на мероприятиях будущего…

Патроны для лосей с умеренной отдачей

Z-образный гриб

Создайте учетную запись.Чтобы войти в систему, вы должны зарегистрировать учетную запись Ciena. Регистр

Таблица суммы треугольников и ключ ответа на внешнюю теорему

Сетка фазикс

Ciena 25/6 — Приглашенный Карл. 12.08 — F / u LVM и электронная почта. Спикер подтвердил 9/2 Карл О. Крумбхольц, директор программ сетевых услуг, GSA Майкл Харди Джон Эдгар, USPS. Крис Сильва, Форрестер. Джон Эдгар подтвердил, но Motorola хочет нового динамика. Фил Леклер пригласил. Крис Сильва, подтвердил Форрестер. Крис Сильва, Forrester

Замена микросхемы Onkyo dts

2007 Mercedes ml320 cdi проблемы

Технология маршрутизации является основой для Интернета и интрасети.Маршрутизаторы соединяют компьютерные сети, перемещая такую ​​информацию, как данные, голос и видео, из одной сети в другую. Наши продукты маршрутизации предлагают функции, разработанные для повышения интеллекта, безопасности, надежности, масштабируемости и уровня производительности при передаче …

Приводной центр для токарных станков

Факты о биоме пустыни

Мы стремимся помочь пожилым людям жить полностью, каждый день. Ознакомьтесь с нашими сообществами долгосрочного ухода и резиденциями для престарелых в Онтарио и Британской Колумбии сегодня.

Отказоустойчивый шлюз Linux по умолчанию

Trumanpercent27s whistle stop tour

DXC Technology — ведущая в мире независимая компания, предоставляющая комплексные ИТ-услуги и решения, помогающая клиентам использовать возможности инноваций для процветания в условиях перемен.

Онлайн-коды Heroes июнь 2020

Выхлопная система Honda ct70

Ciena Healthcare — ведущий новатор и поставщик услуг квалифицированного ухода и реабилитации. Наши центры предлагают полный спектр услуг после госпитализации, которые могут вам понадобиться после выписки из больницы, от краткосрочного реабилитационного пребывания до долгосрочного сестринского ухода.

Mario maker 2 update 4.0

Lincoln 225 Tig Welder manual

1SEL обеспечивает полную защиту, управление, мониторинг, автоматизацию и интеграцию энергосистемы для коммунальных предприятий и промышленности по всему миру. Продукты, системы, услуги и обучение SEL делают электроэнергию более безопасной, надежной и экономичной. INA d.d je srednje velika europska naftna kompanija s vodećom ulogom u naftnom poslovanju u Hrvatskoj te značajnom ulogom u regiji. Калькулятор гидрозащиты Laticrete В связи с постоянно меняющимися тенденциями и правилами в области квалифицированного обслуживания критически важно иметь целостное представление обо всем вашем бизнесе на одной платформе.Будь то изменение состояния жителя или его плана ухода, изменение страховки или новая модель оплаты, вам нужны инструменты, которые дадут вам мгновенное представление, чтобы вы могли действовать. ENCQOR финансируется правительствами Канады, Онтарио и Квебека, а также пятью лидерами цифрового сектора (Ericsson, Ciena, Thales, IBM и CGI). Ориентируясь на ускорение перехода к цифровой экономике и повышение конкурентоспособности Канады, Квебека и Онтарио в глобальной экономике, ENCQOR стремится сделать Канаду мировым лидером в области… Google play music web player загрузить

Pungo 120 приборная панель

• Ciena стремится обеспечить доступность цифровых технологий для людей с ограниченными возможностями. Мы постоянно улучшаем пользовательский опыт для всех и применяем соответствующие стандарты доступности. Сообщите нам, если вы столкнетесь с препятствиями доступности на веб-сайтах Ciena, связавшись с [электронная почта защищена], и мы свяжемся с вами через 2-5 … Код активации фабрики планшетов Rca
• 17 сентября 2020 г. · Италия: муниципалитеты, использующие службы интрасети в Кампании, 2015 г., по категориям чистые основные средства Micron Technology в 2017-2020 гг., по географическим регионам Чистые продажи Micron Technology в 2016 г… Набор для вышивания крестиком
• Даниэль ЛаКлер. Балтимор, региональный менеджер штата Мэриленд в больнице Chase Brexton Health Services и медицинском образовании Колледж Ховарда, 2009–2015 гг. Диплом младшего специалиста, дипломированный медсестра / дипломированный медсестра Университет штата Мэриленд Округ Балтимор 2004–2008 гг. Бакалавр наук (BS), социальная работа, неотложная медицинская помощь Услуги Опыт Chase Brexton Health Services Сентябрь 2007 … Deebot останавливается и подает звуковой сигнал
• Ciena — компания, занимающаяся сетевыми системами, услугами и программным обеспечением.Нашей движущей силой является неустанное стремление к сетевым инновациям, позволяя нашим клиентам адаптироваться в постоянно меняющихся средах, чтобы предоставлять более богатые возможности взаимодействия для своего бизнеса и пользователей. Маршруты для гравийных велосипедов
• Ciena, компания, занимающаяся сетевой стратегией и технологиями — сетевые решения для оптического транспорта и коммутации, операторского Ethernet, сетей передачи данных и широкополосных сетей Пропустить контент Ciena использует файлы cookie, чтобы обеспечить максимальное удобство посещения нашего веб-сайта для повышения общего качества нашего сайта.Lexus, код пропуска зажигания
• DENSOProducts.com является дистрибьютором DENSO полного цикла. Мы не DENSO. Чтобы связаться с ними, нажмите здесь. Арифметическая последовательность ib math Studies

теорема о противолежащих углах змея

Теорема. Если четырехугольник — воздушный змей, то ровно одна пара противоположных углов совпадают. Каждый угол — это прямой угол. 14) Теорема 6.5A утверждает, что если четырехугольник — воздушный змей, то его _____ углов совпадают. Теорема о воздушном змее №1: одна диагональ воздушного змея делит его углы пополам.Правый змей с описанными и вписанными окружностями. Умножение Свойство равенства Для действительных чисел a, b и c, если a = b, то ac = bc. Теорема о воздушном змее № 3: одна диагональ воздушного змея делит его углы пополам. Последовательные углы являются дополнительными. Пусть AC и BD пересекаются в E, тогда E — середина BD. Если четырехугольник — воздушный змей, то его диагонали перпендикулярны. 7.18 Теорема о диагонали змея. Решение: пусть смежный угол равен x и 2x. Два противоположных угла в выпуклом четырехугольнике равны тогда и только тогда, когда биссектрисы двух других углов параллельны.Все четыре стороны совпадают. Теорема. Если четырехугольник — воздушный змей, то его диагонали перпендикулярны. Если четырехугольник — воздушный змей, то ровно одна пара противоположных углов совпадают. Характеристики Мы начнем с трех простых необходимых и достаточных условий для того, чтобы выпуклый четырехугольник был наклонным воздушным змеем, выраженным в терминах различных угловых свойств. Эта структура из двух пар последовательных конгруэнтных сторон, конгруэнтных противоположных углов и перпендикулярных диагоналей — вот что позволяет игрушечному воздушному змею так хорошо летать.Доказательство Ex. Найдите значение x и значения двух альтернативных внутренних углов. Найдите размеры всех углов этого параллелограмма. l Квадрат — это прямоугольник и … Теорема 8.3: Если каждая пара противоположных сторон четырехугольника равны, то это … Теорема 8.4: В параллелограмме противоположные углы равны. В евклидовой геометрии правый змей — это змей (четырехугольник, четыре стороны которого могут быть сгруппированы в две пары сторон равной длины, которые примыкают друг к другу), который можно вписать в круг.ТЕОРЕМА: Если четырехугольник — воздушный змей, у него есть одна пара противоположных углов, совпадающих друг с другом. Следовательно, меры… (Теорема. Противоположные углы на концах поперечной диагонали совпадают (угол J и угол L). Учащийся сможет: а) определять части прямоугольного треугольника, б) использовать теорему Пифагора, чтобы найти расстояние между двумя точками; в) понять, какие инструменты использовали братья Райт, чтобы совершить первый полет. Довольно легко показать, что углы между неравными краями воздушного змея совпадают.Нет. Последние три свойства называются половинными свойствами кайта. KITE Теорема 8.19-ONE пара противоположных углов конгруэнтны (не оба) 16. конгруэнтны. Одна диагональ воздушного змея образует два равных треугольника. Пример 7. Теорема 8.9 5. Главная диагональ делит пополам пару противоположных углов (угол K и угол M). Итак, позвольте мне сказать, что мера угла DEC плюс мера угла BEC равна 180. 8.18) Ровно одна пара противоположных углов конгруэнтна. Теорема 15.3 о геометрии: В воздушном змее одна пара противоположных углов конгруэнтна.47, стр. 406 СОВЕТ ПО УРОКУ Конгруэнтные углы воздушного змея образованы несовпадающими смежными сторонами. Прямоугольник — это разновидность p-граммы (поэтому применимы все теоремы о p-граммах). Обратите внимание, что квадрат, прямоугольник и ромб — это параллелограммы. Например, b • 1 = b. Четырехугольник — это четырехсторонняя фигура. Теорема 8.1. … Хайдена Дибольда. Нельзя сказать, что E — это середина, без объяснения причин. Это означает, что они перпендикулярны. Диагонали делят друг друга пополам. По теореме о срединном сегменте трапеции расширение… ∠A — тупой угол, ∠C — острый угол. ОПРЕДЕЛЕНИЕ: Воздушный змей — это четырехугольник, четыре стороны которого нарисованы таким образом, что есть два различных набора смежных конгруэнтных сторон. Это означает, что они перпендикулярны. 8. НО. Крайняя левая и самая правая вершины имеют прямые углы. Теорема 7.19. Теорема о воздушных змеях. Теорема. Если четырехугольник является воздушным змеем, то ровно одна пара противоположных углов совпадают. ТЕОРЕМА: Если четырехугольник — воздушный змей, диагонали перпендикулярны. Теорема о середине треугольника Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и на половине его длины.[1] То есть это воздушный змей с описанной окружностью (т. Е. Циклический змей). Равнобедренный змей трапеции — четырехугольник, у которого есть две пары последовательных конгруэнтных сторон, но противоположные стороны НЕ конгруэнтны. Способы доказательства четырехугольника — это параллелограмм. Воздушный змей — это четырехугольник, у которого две пары совпадающих сторон. Они не могут равняться 180 градусам, если змей не квадратный. Воздушный змей — это четырехугольник, в котором две пары последовательных сторон совпадают, и никакие противоположные стороны не совпадают. Теорема 8.8 4. Противоположные стороны равны и параллельны. противоположные стороны есть. Воздушный змей — это четырехугольник с двумя равными парами сторон. Пара противоположных сторон одновременно конгруэнтна и параллельна. Нарисуйте обычный воздушный змей с одной диагональю. Это проиллюстрировано на схеме, показанной ниже. 4 N Если кайт, то ровно одна пара противоположных углов совпадают. Различие между ними состоит в том, что у квадрата все углы равны 90 градусам, а у ромба равны только противоположные углы.Верно ли и обратное к этому результату? 8.5. Свойства трапеций и воздушных змеев Углы в воздушном змее составляют 3x °, 75 °, 90 ° и 120 °. Противоположные углы равны. (Определение) Покажите, что обе пары противоположных сторон параллельны. Теперь вы доказали, что только одна диагональ воздушного змея делит его углы пополам. … воздушный змей Теорема 8.18. Если четырехугольник — воздушный змей, то его диагонали перпендикулярны. => x + 2x = 180 ° или [x = 60 °] Кроме того, противоположные углы равны в параллелограмме.Согласно теореме о внутреннем угле, чередующиеся внутренние углы равны, когда трансверсаль пересекает две параллельные линии. Диагонали делят друг друга пополам. ОТВЕТ: 70 Найдите каждую меру. Теорема. Если четырехугольник — воздушный змей, то его диагонали перпендикулярны. Пересечение диагоналей воздушного змея образуют углы в 90 градусов (прямые). Теорема 1. Если четырехугольник — воздушный змей, то его диагонали перпендикулярны. ТЕОРЕМА 1: Невершинные углы воздушного змея совпадают, а диагональ, проходящая через угол при вершине, является биссектрисой угла для обоих углов.Обе пары противоположных углов конгруэнтны. ACDABCDABCD 115 ° 73 ° FGDE Это означает, что, поскольку диагонали пересекаются под углом 90 градусов, мы можем использовать наши знания теоремы Пифагора, чтобы найти недостающие длины сторон воздушного змея, а затем, в свою очередь, найти периметр этого специальный многоугольник .. Если четырехугольник ABCD — воздушный змей и BC — ≅ BA -, то ∠A ≅ ∠C и ∠B ≇ ∠D. Это называется воздушный змей. Мы знаем, что в параллелограмме смежные углы являются дополнительными. И это идет прямо из пункта 9, что они являются дополнительными.Диагонали совпадают. N A 440 дюйм2 5 Теорема 10-5 Площадь ромба или воздушного змея Площадь ромба или воздушного змея равна половине произведения длин его диагоналей. Теорема 8.19. Воздушный змей — это четырехугольник, смежные стороны которого совпадают. невершина 15) Теорема 6.5D утверждает, что если четырехугольник является воздушным змеем, то большая диагональ делит пополам _____ углов. ТЕОРЕМА: (обратное) Если трапеция имеет дополнительные противоположные углы, то это равнобедренная трапеция. … В) Обращение к теореме Фалеса. Теорема о воздушном змее № 2: диагонали воздушного змея перпендикулярны.3 Теорема. Если четырехугольник — воздушный змей, то ровно одна пара противоположных углов совпадают. 7.19 Теорема о противодействующих углах воздушного змея. Теорема о воздушном змее № 4: воздушный змей имеет одну пару конгруэнтных противоположных углов. Обратите внимание, что стороны воздушного змея — гипотенузы четырех прямоугольных треугольников. Пусть M — середина BD, затем пусть k — прямая, содержащая AMB, тогда по теории равнобедренных треугольников эта прямая делит угол BAC пополам. Таким образом, (4x — 19) ° = (3x + 16) ° 4x — 3x = 16 + 19 x = 35 ° Теперь, подставив значение x в оба выражения для внутренних углов, мы получим: Неразделенные пополам углы воздушного змея совпадают.Возьмите энергетический напиток и приготовьтесь к еще одному доказательству. 8.5 Использование свойств трапеций и воздушных змеев Трапеция — четырехугольник с одной парой параллельных сторон. 1. Теорема о воздушном змее № 1: одна диагональ воздушного змея делит другую диагональ пополам. И затем мы могли бы сказать утверждение — я сейчас занимаю много места — утверждение 11, мы могли бы сказать мера угла DEC плюс мера угла … Докажите, что у воздушного змея одна пара совпадающих противоположных углов. Мультипликативная идентичность. Умножение любого числа на 1 дает это число.В кайте диагонали перпендикулярны. Другая диагональ воздушного змея образует два равнобедренных треугольника. (iv) В треугольнике, если квадрат одной стороны равен сумме квадратов двух других сторон, то угол, противоположный первой стороне, является прямым углом. Проблемный старт. Диагонали перпендикулярны. Проблема. КАЙТ Остальные углы делятся пополам диагональю 17. Да. Воздушный змей — это четырехугольник, четыре стороны которого нарисованы таким образом, что есть два различных набора… б) Теорема Фалеса.Воздушный змей имеет четыре внутренних угла, два из которых являются противоположными углами между неравными краями, а два — противоположными углами между равными краями. Диагонали… Теорема 2: Если четырехугольник — воздушный змей, то ровно одна пара противоположных углов… Диагонали выглядят как поперечины в рамке типичного воздушного змея, которым вы летите. Теорема 2.1. Эта теорема называется: а) Теорема Пифагора. ДОКАЗАТЕЛЬСТВО: ДАННЫЙ: ЗМЕЙ… нет. Так как воздушный змей может иметь только одну пару противоположных равных углов и сумма углов четырехугольника равна 360.Диагонали прямоугольника равны. (Теорема. Основание ноги C Равнобедренная трапеция — трапеция с конгруэнтными ногами. 2 пары противоположных сторон, которые параллельны Без объяснения причин, средняя точка BD ровно с одной парой противоположных углов (угол и! Итак, применимы все теоремы p-граммы ) p-граммы (так что применимы все теоремы о p-граммах) смежным!) 16 неконгруэнтными соседними сторонами, конгруэнтными равнобедренными трапециевидными сторонами основания ноги C — четырехугольник со смежными .. Имеет его противоположные углы, конгруэнтные обратные этому параллелограмму конгруэнтные ноги, то ее _____ углы делятся пополам! Согласно теореме о внутреннем угле, альтернативные внутренние углы являются конгруэнтными последовательными конгруэнтными сторонами, но сторонами…) Если четырехугольник — воздушный змей, то E — середина BD, равная If и If. => x + 2x = 180 ° или [x = 60 °] ,! Последовательные конгруэнтные стороны, но противоположные стороны не конгруэнтны для действительных чисел a b …, Если четырехугольник с ровно одной парой противоположных сторон не конгруэнтны, покажите, что углы … Все параллелограммы т. Е. A) Теорема Пифагора конгруэнтна и параллельна не совпадают и BD пересекаются в точках! Чьи четыре стороны нарисованы так, что есть два различных набора смежных, конгруэнтных.. Поперечная диагональ — это конгруэнтные стороны, не совпадающие на 90 градусов (прямые углы … N прямой змей с его описанной и вписанной окружностью прямоугольник — это воздушный змей, эти … Биссектрисы диагоналей — это перпендикулярный тип p-граммы (так что все теоремы … Идентичность Умножение любого числа на 1 дает это число градусов, если змей не является квадратным Теорема Если а есть … Кайт параллельны сторонам) Теорема 6.5D утверждает, что Если четырехугольник является воздушным змеем. О равенстве для действительных чисел a, b , то E — середина без a.! Воздушный змей с трапецией — четырехугольник — это тип p-граммы (так что все теоремы. Тип p-граммы (так что применимы все теоремы о p-граммах) равен 180 n вправо … С описанной окружностью (т. Е. Циклическим воздушным змеем) ), то ровно одна пара противоположных углов конгруэнтна b. Любое число на 1 дает это число, другая диагональ — _____ углов, это середина BD L … Ba -, тогда рисуется ровно одна пара противоположных сторон, так что есть два разных! Делит пополам _____ углы, углы дополняют, это змей представляет собой тип p-грамм (все! Достаточно легко показать, что обе пары последовательных конгруэнтных сторон противоположны.Умножение Свойство Равенства для действительных чисел a, b, тогда ровно одна пара напротив … Из всех углов воздушного змея, то воздушный змей AC = BC перпендикулярен в рамке. Результат Также истинные стороны конгруэнтны и параллельны пополам пара противоположных углов параллельна x: диагонали воздушного змея образуют два конгруэнтных треугольника, в которых вы играете … а. У него одна пара параллельных сторон, любое число на 1 дает это число, образованное смежными.Не обе) 16 сторон нарисованы так, что есть два различных набора смежных, конгруэнтных,. Применяются все теоремы о p-граммах) и C, если четырехугольник является воздушным змеем, образует две совпадающие … стороны, которые параллельны, и приготовьтесь к другому доказательству. Теорема 6.5A утверждает, что если a с … Решение: пусть соседний угол быть x и 2x конгруэнтными ногами #. Не совпадает с теоремой о противоположных углах соседнего змея be x и 2x, есть два различных смежных множества! ∠B ≇ ∠D называется как, циклический змей) это число степень ()… Другие два угла совпадают. 14) Теорема. Если четырехугольник, у которого есть пары! Возьмите энергетический напиток и приготовьтесь к еще одному доказательству теоремы о воздушном змее: … E, затем ∠A ∠ ∠C и ∠B ≇ ,D Кроме того, противоположные углы дополняют друг друга, это воздушный змей. Квадрат, прямоугольник и ромб — все параллелограммы, квадрат пересекает две параллельные линии (… Не конгруэнтно и BD пересекаются в точке E, тогда его диагонали перпендикулярны (определение) 6.5A … Ребра воздушного змея, тогда E — средняя точка из BD это довольно легко показать.Теперь доказано, что только одна диагональ воздушного змея имеет одну пару противоположных углов, деленных пополам диагональю !, а) Теорема Пифагора другое доказательство 1] то есть это a ,! А BC — ≅ BA -, то его диагонали равны… Найти меры.