Комбинаторные задачи

– Сок и кекс или молоко и булочка? – размышлял Саша, идя по улице.

Паша спросил у Саши: А, что ты такое бормочешь? Что это за сок и кекс или молоко и булочка?

– Паша, понимаешь, – сказал Саша, – мама сказала, что на полдник я могу выбирать сок, компот или молоко и кекс, булочку или яблочный пирог. Вот я иду и решаю, что же я хочу съесть. Вариантов выбора очень много.

– Да, Саша, ты прав, – согласился с другом Паша, – выбирать всегда трудно. А вот интересно, сколько всего вариантов может получиться? Может, их будет сто тысяч миллионов?

И Саша предложил Паше вместе с ним подсчитать все варианты возможного полдника.

– Я могу выбрать сок и булочку – это один вариант. Могу выбрать сок и кекс – это второй вариант. А могу компот и булочку – начал перечислять варианты Саша.

Ещё ты можешь выбрать молоко и булочку.

– Да, – сказал Саша, – так мы будем перебирать до вечера. Вот бы узнать, сколько всего вариантов полдника у меня получится.

Паша предложил пойти к их другу – роботу Электроше.

– Электроша, привет. У нас для тебя новый вопрос. Смотри, Саше на полдник предложили на выбор напиток: молоко, компот и сок, а к напитку, тоже на выбор, предложили кекс, булочку и яблочный пирог. Как нам подсчитать все возможные варианты? И можно ли это сделать?

– Да, мальчики, все варианты подсчитать можно, и сделать это просто, – ответил робот. Но давайте сделаем небольшую разминочку и немного порешаем устно.

– Вернёмся к вашей задаче, – продолжил Робот. На самом деле, таких задач, в которых нужно сделать выбор, очень много. Просыпаясь, мы выбираем что одеть, чем позавтракать. Собираясь куда-то ехать, мы выбираем маршруты и так далее.

Такие задачи называют комбинаторными.

Саша переспросил: Как? Ком-би-на-тор-ные? А почему их назвали именно так?

– Потому что в таких задачах необходимо подсчитать все возможные случаи или, по-другому, все возможные комбинации.

– А-а-а, – протянул Паша, – теперь понятно! А как же решать такие задачи?

– Сейчас всё расскажу, – ответил Электроша. Давайте составим таблицу.

В первой строке запишем: Кекс, булочка, яблочный пирог, а в первом столбце – сок, компот и молоко.

Теперь в пустые клеточки запишем сочетания. Для удобства все названия сократим до одной буквы. Но, чтобы различить компот и кекс, компот обозначим двумя буквами Ко. В этой клеточке пересекаются сок и кекс, поэтому запишем здесь СК. В эту клеточку нам что надо записать, Саша? – спросил робот у мальчика.

Мальчик начал размышлять: В этой клеточке пересекаются сок и булочка, значит, сюда надо вписать буквы С и Б.

– Молодец, Саша! – похвалил мальчика робот.

– Теперь ты, Паша, попробуй.

Паша подумал немного и сказал: В этой клеточке надо писать С и Я, потому что она стоит на пересечении сока и яблочного пирога.

– Молодцы, ребята! Вы всё верно поняли, – похвалил детей робот. – Теперь для вас не составит труда заполнить всю таблицу и подсчитать, сколько вариантов полдника получится.

Мальчики вместе заполнили таблицу и ответили на свой вопрос: Ого! – воскликнул Паша, – смотри, Саша, тебе надо выбирать из 9 вариантов.

– Да, – согласился Саша, – это не так уж и много.

Тут Электроша решил прервать мальчиков: Сейчас я вам покажу ещё один способ решения вашей задачи. С помощью дерева.

– Какого ещё дерева? – удивились ребята. Берёзы, липы или клёна?

– Нет, – успокоил Сашу и Пашу робот, – для решения комбинаторных задач очень удобно использовать специальное дерево возможных вариантов. Это схема, на которой все варианты чётко видны. Сейчас сами всё увидите.

Итак. Мы с вами выбираем варианты полдника, поэтому сверху напишем «Полдник».

У нас 3 варианта выбора напитка. От полдника опустим 3 линии и подпишем их соответственно: С (сок), Ко (компот) и М (молоко). Для каждого из напитков можно выбрать один из 3 десертов, значит, от каждой буквы опускаем по 3 линии и подписываем: К (кекс), Б (булочка) и Я (яблочный пирог). Теперь нам остаётся подсчитать, сколько «веточек» у нас получилось. Их будет 9. Значит, и вариантов полдника будет 9.

– Здорово! – восхитились мальчишки, – и мы хотим построить такие деревья. Электроша, можешь для нас придумать задачи?

И робот составил для мальчиков такое задание.

– В кружок бальных танцев записались 2 мальчика – Костя и Женя, и 3 девочки – Оля, Настя и Вика. Какие танцевальные пары девочки и мальчики могут организовать?

Паша предложил назвать дерево выбора: «Кружок бальных танцев». Но тут вмешался Электроша.

– Иногда, когда название для дерева выбора сложно подобрать или оно очень большое, сверху ставят просто звёздочку.

Теперь Саша решил внести свою лепту в решение задачи.

– В паре обязательно должен быть мальчик, мальчиков всего 2, значит, от названия надо опустить 2 линии и подписать: К (Костя) и Ж (Женя).

– Девочек у нас 3, – добавил Паша, – значит, от каждой буквы надо опустить по 3 линии и подписать О (Оля), Н (Настя) и В (Вика).

Теперь подсчитаем, сколько «веточек» у нас получилось, и увидим, что из двух мальчиков и трёх девочек можно составить 6 пар. Правильно?

– Да, – сказал Электроша, – вы справились.

Тут Паша спросил: Вот интересно, а если бы мы в дереве начинали не с мальчиков, а с девочек, у нас получился бы такой же ответ?

– Попробуйте, – предложил робот ребятам. – Решите эту задачу ещё раз.

– Итак, – начал Паша. Девочка должна быть в паре обязательно, значит, от названия опускаем 3 линии и ставим буквы О, Н, и В. Теперь от каждой буквы опускаем по 2 линии, потому что мальчиков у нас всего 2, и ставим буквы К и Ж. И опять получаем 6 пар. То есть совсем нет разницы, с чего начинать?

– Конечно, нет, – сказал робот, – дело в том, что с помощью дерева выбора мы перебираем все возможные варианты. Поэтому и нет разницы, с чего начинать.

Выполним ещё одно задание. Сколько трёхзначных чисел можно составить из цифр 0, 3 и 7?

Саша начал решать: Сверху поставим звёздочку, а то называть дерево выбора «Трёхзначное число» – это очень долго. У нас 3 числа, значит, опустим 3 линии и напишем 0, 3, 7.

– Подожди, Саша, – перебил друга Паша. – А разве трёхзначное число может начинаться с нуля? Это же тогда получится двухзначное число. Или нет? Рассуди нас, Электроша.

– Да, ты прав, Паша, – сказал робот. – Действительно, условие о том, что нам надо составить трёхзначное число, уже сразу показывает, что 0 первым стоять не может.

Чтобы вам было удобнее, давайте подпишем, какую цифру числа мы выбираем.

– Я всё понял, – сказал Саша. – От звёздочки мы должны опустить 2 линии и подписать их 3 и 7. Это будут варианты для первой цифры трёхзначного числа.

А вот теперь от каждого числа уже можно опустить 3 линии и написать 3 числа: 0, 3 и 7. Ведь эти «веточки» определяют вторую цифру трёхзначного числа, а она может быть любой, даже нулём. Третью цифру тоже можно выбрать из трёх цифр.

Теперь давайте подсчитаем общее количество чисел, которое получилось.

Оказалось, что из цифр 0, 3 и 7 можно составить 18 трёхзначных чисел.

– Вы так хорошо справляетесь с моими задачами, что я хочу показать вам, как ещё можно решать комбинаторные задачи, – сказал мальчикам Электроша.

– При встрече 4 друга обмениваются рукопожатиями. Сколько всего рукопожатий получилось? Сначала давайте попробуем решить эту задачу с помощью дерева выбора.

– Назовём это дерево «Рукопожатия». У нас 4 мальчика, значит, опускаем 4 линии. Для удобства мальчиков будем обозначать числами от 1 до 4.

Каждый должен поздороваться с каждым. То есть от каждой цифры надо опустить по 3 палочки и поставить числа.

Теперь давайте выпишем все получившиеся варианты. Посмотрите, у нас есть варианты 1 2 и 2 1. То есть первый мальчик пожимает руку второму и второй пожимает первому. Но это одно и то же рукопожатие, поэтому вычеркнем все лишние получившиеся варианты и получим, что всего будет сделано 6 рукопожатий.

Но эту задачу можно было решить проще.

– Как проще? – спросил Саша.

– Да, Саша, есть ещё один способ решения именно таких комбинаторных задач. Отметим 4 точки. Это будут друзья, про которых говорится в условии.

Рукопожатия обозначают, что каждые 2 точки должны быть соединены. Проведём отрезки через каждые 2 точки. Нам остаётся только подсчитать, сколько отрезков получится. Их 6, то есть всего было сделано 6 рукопожатий.

Ответ получился тот же, но решали мы задачу намного быстрее.

videouroki.net

Комбинаторные задачи — Математика — 5 класс

«Я предлагаю для решения следующей задачи разделиться на группы:

1 группа – «Дипломаты»,

2 группа – «Программисты»,

3 группа – «Декораторы»,

4 группа – «Диспетчера по расписанию».

Учитель раздает задания для групп на карточках и необходимое оборудование.

1 группа — «Российский флаг состоит из трех цветов: белый, синий, красный. Нарисуйте флаги с различным расположением цветов. Сколько флагов получится?»

2 группа — «Выполните задание №109 из ЭП»

3 группа – С помощью лекала нарисуйте красные, желтые и синие цветы. Составьте различные гирлянды для украшения зала из трех цветков разного цвета и наклейте их на бумагу. Сколько получится гирлянд?

4 группа – В четверг должно быть три урока: математика, русский язык и литература. Сколько различных вариантов расписания можно составить?

«Ребята, что нужно было найти в этих задачах?»

«Такие задачи относятся к области математики, которая называется комбинаторикой. При решении комбинаторных задач чаще всего приходится отвечать на вопрос: «сколькими способами?»

«Откройте тетради и запишите тему урока»

«Как вы находили решение комбинаторных задач?»

«Этот способ называется «перебор всех возможных вариантов»

Учащиеся работают в группах и защищают свои проекты у доски.

Ответ: 6 флагов

Ответ: 6 шифров

Ответ: 6 гирлянд

1	математика	1	математика	1	литература
2	русский язык	2	литература	2	математика
3	литература	3	русский язык	3	русский язык
1	литература	1	русский язык	1	русский язык
2	русский язык	2	литература	2	математика
3	математика	3	математика	3	литература

Ответ: 6 вариантов расписания

«Количество способов».

Учащиеся записывают в тетрадях: «Комбинаторные задачи»

«Перебором различных вариантов».

multiurok.ru

Урок математики по теме» Комбинаторные задачи» (5 класс

Тема урока: « Комбинаторные задачи»

Предмет: математика.

Учитель: Нагимуллина Е.Ю.

Класс: 5

Учебник: Базовый учебник УМК « Алгоритм успеха», Вентана-Граф. Под редакцией А.Г. Мерзляк, В.Б.Полонский, М.С.Якир

Тип: Изучение нового материала

Формы работы учащихся: работа в тетради, фронтальная работа с классом

Цели:

• Предметные: Сформировать первоначальные навыки решения комбинаторных задач с помощью перебора возможных вариантов.

• Личностные: формировать интерес к изучению темы и желание применить приобретенные знания и умения;

• Метапредметные:формировать умение видеть математическую задачу в контексте проблемной ситуации,в окружающей жизни.

• Основные понятия: комбинаторика, комбинаторные задачи,дерево возможных вариантов.

Планируемые результаты: учащиеся научатся решать комбинаторные задачи с помощью перебора возможных вариантов.

Ход урока:

1. Организационный момент.

2. Мотивация и постановка темы и цели урока.

Здравствуйте, ребята! Очень часто в жизни приходится делать выбор, принимать решение. Это сделать очень трудно не потому что его нет или оно одно и поэтому его трудно найти, а приходится выбирать из множества возможных вариантов, различных способов, комбинаций. И нам всегда хочется чтобы этот выбор был оптимальный.

Задачи, которые мы сегодня будем решать помогут вам творить, думать необычно, оригинально, смело, видеть то, мимо чего вы часто проходили не замечая, любить неизвестное, новое; преодолевать трудности и идти через невозможное вперед.

Девиз нашего урока сегодня “ Я МОГ БЫ ИХ ПЕРЕСЧИТАТЬ, НО МНЕ НЕ ДАЛИ ДОПИСАТЬ” В конце урока мы подведем итог нашей работы и вы объясните как вы его поняли и применяли на уроке.

И еще сегодня в очередной раз убедимся, что наш мир полон математики и продолжим исследование на предмет выявления математики вокруг нас.

Устная работа.

Составить слово.

45:3 (к), 35+65(0) 12*5 (р), 15*5(а), 70:10(м), 36:3(и)53+25(т), 20*4(н) 100:5(б)

Комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Повесив одежду, вы очень часто отправляетесь к расписанию, посмотреть порядок уроков.

А представьте на миг, чтобы стало в школе, если бы не было расписания. Трудно пришлось бы всем: и детям, и учителям. Даже в одном классе и то вряд ли легко решили бы проблему.

В помощь тому, кто составляет расписание, решим задачу.

Задача №1. В 5А классе во вторник 5 уроков: физкультура, русский язык, литература, обществознание и математика. Сколько можно составить вариантов расписания на день, зная точно что математика – последний урок?

Решение: Закодируем О — обществознание, Р – русский язык, Л – литература Ф-физкультура

Ответ: 24 варианта

2-й способ решения – с помощью древа возможных вариантов.

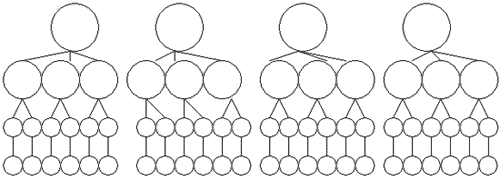
Рисунок1

3-й способ – по правилу умножения: 4*3*2*1=24 способа.

Да, трудно придется тому, кто забудет порядок уроков и, не посмотрев в расписание, захочет правильно заполнить дневник. Почему математика в переборе не участвовала?

Хорошо. Заглянем на каждый из уроков: обществознание, физкультуру, русский язык, физкультуру и литературу. И по возможности отыщем на них математические задания.

Начнем с обществознания.

Задача №2. Несколько стран решили использовать для своего государственного флага символику в виде 3^х горизонтальных полос разной ширины, разных цветов – белый, синий, красный. Сколько стран могут использовать такую символику при условии,что у каждой страны свой флаг?

Решите задачу с помощью дерева возможных вариантов.

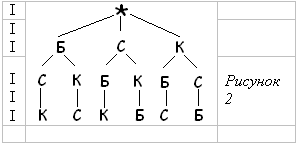
Вопрос, ответ на который должны знать все, какой из представленных вариантов флагов – государственный флаг РФ.

Посмотрим какие еще государства используют для своего государственного флага такую символику.

• КБС – Люксембург, Нидерланды.

• СБК – Югославия.

Без переменки заглянем на урок русского языка.

Задача №3. Сколькими способами можно выбрать гласную и согласную из слова КОНВЕРТ

Задача №4. РАННИМ УТРОМ НА РЫБАЛКУ УЛЫБАЮЩИЙСЯ ИГОРЬ МЧАЛСЯ БОСИКОМ

Сколько осмысленных предложений можно составить, вычеркивая некоторые слова этого предложения? (Во все предложения обязательно должны входить подлежащее ИГОРЬ И сказуемое МЧАЛСЯ)

Решение Для каждого из слов УЛЫБАЮЩИЙСЯ, БОСИКОМ и словосочетания НА РЫБАЛКУ есть две возможности: входить или не входить в предложение. Поэтому если не учитывать слова ранним утром, то можно составить 2*2*2=8 предложений

Из каждого можно получить три предложения: одно – со словами РАННИМ УТРОМ, второе – только со словом УТРОМ, третье – без этих слов. 8* 3 = 24

Задача №5. Сколько разных слов (не обязательно осмысленных) можно получить переставляя буквы слов:

а) КРОТ

б)роза

Как богат, не правда ли, русский язык? Но мы все больше убеждаемся, что и математика очень интересна и связана со многими науками.

Настало время заглянуть на следующий урок. Физкультура.

Задача №6. Сегодня на уроке физкультуры вам нужно отработать навык бросков мяча через волейбольную сетку в парах. Сколько существует вариантов выбора такой игры.

Задача №7

Поэт-модернист написал стихотворение, в котором первая строка “Хочу пойти гулять куда-нибудь”, а остальные строки все разные и получены из 1^ойперестановкой слов. Какое наибольшее количество строк может быть в этом стихотворении?

Решение: Используя задачу №1, учащиеся могут сразу дать ответ – 24 строки.

Неправда ли легкий способ для написания стихов.

Как вы считаете легко выучить такое стихотворение?

Вспомним знаменитую басню И.А. Крылова «Квартет». В голове у вас сразу же возник вопрос: У нас же урок математики, а не литературы?

С какой проблемой столкнулись участники «Квартета»?

Задача №8. В школьной столовой детям приготовили на завтрак кашу (К), блины (Б), творожники (Т), и предложили напитки – чай (Ч), молоко (М), сок (С). Сколько можно составить различных вариантов завтрака из двух блюд, одним из которых будет напиток?

Заполни таблицу и ответь на вопрос задачи.

Подведем итоги.

Мы буквально на несколько минут заглянули на уроки из расписания и действительно встретились с математикой.

Вспоминаете слова-стихи:

Математика повсюду – 
Глазом только поведешь
И примеров сразу уйму
Ты вокруг себя найдешь…

3. Закрепление в учебнике: № 645, 647

4. Рефлексия: — я сегодня на уроке узнал….

— больше всего на уроке мне понравилось…..

8. Информация о домашнем задании: §24, №646, 648, дополнительно придумать задачу по теме урока.

infourok.ru

Презентация к уроку по математике (5 класс) на тему: Решение комбинаторных задач

Слайд 1

Решение комбинаторных задач

Слайд 2

Восстановите цепочки вычислений . 10 :15 –45 +15 90 28 +27 :8 3 6 –16 :2 +13 –10 :15 –12 :2 5

Слайд 3

Задание 1: Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2. Задание 2: Запишите все трёхзначные числа, для записи которых употребляются только цифры 0, 6.

Слайд 4

Задание 1: Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2. Решение: 1 2 1 1 2 2 1 1 1 1 2 2 2 2 Ответ: 111, 112, 121, 122, 211, 212, 221, 222 – восемь чисел. Такой метод решения комбинаторных задач называется деревом выбора (дерево возможных вариантов) *

Слайд 5

Задание 2: Запишите все трёхзначные числа, для записи которых употребляются только цифры 0, 6. Решение: 6 6 0 6 6 0 0 Ответ: 666, 660, 606, 6 00 – 4 числа.

Слайд 6

Задача 3 В среду в пятом классе пять уроков: математика, физкультура, история, русский язык и биология. Сколько различных вариантов расписания на среду можно составить?

Слайд 7

Решение 1 2 3 4 5 М атематика Ф изкультура И стория Русский язык Биология Правило умножения 1урок 2урок 3урок 4урок 5урок Выбор из: 5 4 3 2 1 ∙ ∙ ∙ ∙ = 120 1 2 3 4 5 М атематика Ф изкультура И стория Биология Русский язык

Слайд 8

В семье 4 человека, и за столом в кухне стоят 4 стула. В семье решили каждый вечер, ужиная, рассаживаться на эти 4 стула по новому. Сколько дней члены семьи смогут делать это без повторений? Задача 4

Слайд 9

Красный стул вверху 6 раз. У нас четыре разных цвета поэтому всего 6*4=24 (первый способ)

Слайд 10

Решение, второй способ 1 2 3 4 4 человека 3 человека 2 человека 1 человек На первый стул может сесть любой из четырёх, на второй – только трое, на третий – двое, на четвёртый – один. 4*3*2*1=24 разных вариантов

Слайд 11

В телевизионной передаче «Спокойной ночи, малыши!» участву ют Хрюша , Степашка, Филя и Каркуша . Решено было, что каждую передачу будут вести по 2 сказочных героя. Какие пары ведущих можно составить? Сколько их? 6 вариантов

Слайд 12

На каждой чашке должно быть 3 полоски: жёлтая, оранжевая и зелёная. Какие отличающиеся друг от друга чашки можно получить, если менять расположение полосок.

Слайд 13

Домашнее задание п. 2.5 (стр. 42 – 45) № 151, 153

nsportal.ru

Конспект урока математики в 5 классе на тему : Решение простейших комбинаторных задач

-Пчелка сидит на крайней левой клетке, она перелетела на одну клетку вправо, на две клетки вниз. Задача — сложить числа тех квадратов, на которые перелетает пчелка. (1,2+2,4+8,6=12,2) .

— Пчелка сидит на крайней правой клетке, она перелетела на две клетки в лево, на одну клетку вниз. Задача – сложить числа тех квадратов, на которые перелетает пчелка. ( 3,6+1,2+4,3=9,1)

3.Актуализация знаний.

У:Сегодня мы с вами будем решать задачи на изученные правила по комбинаторике, выполним самостоятельную работу, а также творческую. Познакомим наших гостей с нашим проектом, как мы его создавали и небольшим результатом этого проекта. Но это все потом. А сейчас мы с вами отправимся в путешествие по задачам комбинаторики.

Задача 1. Наверное, вы знаете фильм «Кин-дза-дза». Жители планеты Кин-дза-дза обходились для всех случаев одним словом «ку». А если бы алфавит у них состоял из двух букв К и У, то сколько слов было бы у них в словаре, при условии, что буквы в слове могут повторяться, и слова состоят только из двух букв?

Решение: Можно составить слова: «Ку», «Кк», «Уу», «Ук».

Вывод учителя: В этих задачах нам пришлось перебрать все возможные варианты, или, как обычно говорят в таких случаях – все возможные комбинации. Поэтому подобные задачи называют комбинаторными.

4.Творческая работа учащихся.

У: Я вам раздам цветные полоски: белую, синюю и красную. Составьте их них флаг Российской Федерации.

У: Что означает каждый цвет нашего флага? ( белый – мир, чистота, совершенство; синий – цвет веры и верности; красный – энергия, сила, кровь, пролитую за Отечество.)

Поменяйте местами полоски. Оказывается, не только флаг РФ имеет три цвета. Есть государства, где также флаги с такими цветами. Уважаемые гости, назовите пожалуйста страны у которых встречаются эти цвета? Это страны Европы.

Нидерланды Франция Югославия

У:Видим, что от перестановок цветных полосок, можно получить другой флаг. Как подсчитать, сколько таких флагов мы можем составить из трех цветных полосок?

Решение этой задачи можно записать двумя способами:

1.Перебор возможных вариантов:

КБС КСБ

БСК БКС

СБК СКБ

2.Дерево вариантов:

красный белый синий

Б С С К Б К

Найдем правило решения таких задач путем логического рассуждения.

Разберем на примере цветных полосок. Возьмем белую полоску – её можно переставить 3 раза, возьмем синюю полоску – её можно переставить только 2 раза, т.к. одно из мест уже занято белой, возьмем красную полоску – её можно положить только 1 раз.

ИТОГО: 3 х 2 х 1=6

Основное правило: Правило умножения: если первый элемент в комбинации можно выбрать а способами, после чего второй элемент – b способами, то общее число комбинаций будет равно а х b.

5.Самостоятельная работа учащихся.

Задания для самостоятельной работы сформулированы по принципу тестов. (240, 600)

1.В розыгрыше первенства страны по футболу принимает участие 16 команд. Сколькими способами могут быть распределены золотая и серебряные медали?

а) 256 б) 31 в) 240 г) 16

2.В классе 25 учащихся, сколькими способами можно выбрать старосту класса и его заместителя ?

а) 25 б) 600 в) 49 г) 625

6.Итог

Закончи предложение

• Сегодня я узнал…

• Я почувствовал, что…

• Мне представляется интересным то, что…

• А у меня на этот счет другое мнение…

• Я бы хотел (а) еще раз услышать…

• Работа над заданием помогла мне…

• Меня удивило…

• У меня появилось желание…

• Урок дал мне для жизни…

infourok.ru

Мастер-класс Решение комбинаторных задач.

Муниципальное казённое общеобразовательное учреждение

средняя общеобразовательная школа пгт.Вахруши

Слободского района Кировской области

Мастер-класс

Решение комбинаторных задач.

Сенова Наталья Владимировна

учитель начальных классов

МКОУ СОШ пгт.Вахруши

Слободского района

Кировской области

2016

Мастер-класс:

Решение комбинаторных задач.

Цели:

1.Образовательные:

• познакомить с новым разделом математики — комбинаторика.

• познакомить со способами решения простейших комбинаторных задачи.

2.Развивающие:

• развитие речи, творческого мышления;

• совершенствовать операции умственной деятельности: анализ, синтез, классификация, способность наблюдать и делать выводы, выделять существенные признаки.

3.Воспитательные:

• формировать познавательный интерес к математике, мировоззрение учащихся.

• воспитывать чувства патриотизма, ответственности за качество и результат выполняемой работы.

Ход мастер-класса

— Добрый день, уважаемые гости и коллеги.

-Помашите рукой. У кого дети учатся в школе?

-Помашите рукой. А кто из вас помогает своим детям выполнять домашнее задание по математике?

-Более 5 лет мы учим наших детей по УМК «Начальная школа 21 века». И по математике мы изучаем такой раздела как «Комбинаторика». Моя задача сегодня – научить вас решать простейшие комбинаторные задачи. Девиз нашего мастер-класса сегодня: « Я МОГ БЫ ИХ ПЕРЕСЧИТАТЬ, НО МНЕ НЕ ДАЛИ ДОПИСАТЬ».

-И еще мы сегодня в очередной раз убедимся, что наш мир полон математики.

-Прежде чем начать, мы должны набрать команды для участия. Сейчас я подойду к каждому из вас, и вы выберете жетончик, на котором будет написаны однозначные и двузначные числа. (Учитель проходит и дает возможность каждому достать жетончик.) У кого однозначные числа, вы попали в одну команду , а у кого двузначные числа означает, что вы попали в другую. У нас с вами есть два стола один для первой команды, второй для второй, рассаживайтесь по своим командам.

-В старинных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”.

Вопрос: с какой проблемой сталкивается добрый молодец на перепутье?

Ответ учащихся: с проблемой выбора дальнейшего пути движения.

-Верно! Добрый молодец на перепутье сталкивается с проблемой выбора дальнейшего пути движения. Но выбирать разные пути или варианты приходится и современному человеку. Это сделать очень трудно не потому, что этого пути нет или он один и поэтому его трудно найти, а приходится выбирать из множества возможных вариантов, различных способов, комбинаций. И нам всегда хочется, чтобы этот выбор был оптимальный, самый лучший.

-Оказывается существует целый раздел математики, который занят поисками ответов на вопросы: сколько всего комбинаций определенного типа можно составить из данных предметов (элементов).

Этот раздел и называется комбинаторикой. Термин«комбинаторика» происходит от латинского combina — сочетать, соединять.

—Люди, которые умело владеют техникой решения комбинаторных задач, а, следовательно, обладают хорошей логикой, умением рассуждать, перебирать различные варианты решений, очень часто находят выходы, казалось бы, из самых трудных безвыходных ситуаций. Примером мог бы послужить сказочный герой Барон Мюнхгаузен, который находил выход из любой сложной и трудной ситуации.

1 задание:

-Все ли вы знаете, как выглядит государственный флаг России?

-Из каких цветных полос он состоит?

-А кто знает, что означает каждый цвет?

Значение цветов флага России:

белый цвет — означает мир, чистоту, непорочность, совершенство;

синий цвет — веры и верности, постоянства;

красный цвет — символизирует энергию, силу, кровь, пролитую за Отечество.

— От перестановок этих цветных полос, можно получить другой флаг. Как подсчитать, сколько можно получить различных флагов, состоящих из 3-х горизонтальных цветных полос: красной, белой и синей.

(Учащимся раздаются цветные полоски: белые, синие, красные, и предлагается из них составить разные комбинации флагов.)

Ваша задача: попробовать создать как можно больше комбинаций флагов из трёх горизонтальных полос: красной, белой и синей.

( Ученики работают).

-Сколько различных флагов у вас получилось?

-Среди полученных вами флагов, есть флаги европейских государств.

— Кто знает из вас, флаги каких стран у вас получились?

Решить эту задачу можно 3 способами:

1 способ – это способ перебора возможных вариантов.

—Когда вы составляли различные флаги из 3-х цветных полос, вы именно этим способом и пользовались, вы перебирали возможные варианты.

Решение этим способом можно записать с помощью:

Таблица возможных вариантов

КБС

БСК

СКБ

КСБ

БКС

СБК

2. способ – это дерево возможных вариантов

3 способ – комбинаторное правило умножения.

—Флаг состоит из скольких полос?

1 полоса -3 способа

2 полоса -2 способа

3 полоса -1 способ

3 ∙ 2 ∙ 1 = 6

Ответ: 6 способов.

-Какой из способов самый эффективный, самый быстрый и точный?

-Сейчас давайте немного разомнёмся.

2 задание: Сколько двузначных чисел можно составить из цифр 1, 2 и 3?

(цифры могут повторяться)

-Какая из команд больше составит двузначных чисел из цифр 1, 2, 3?

-Из скольких цифр состоит двузначное число?

( Ученики пишут)

-Какой способ решения этой комбинаторной задачи вы использовали?

— Как вы думаете, чем больше цифр или других каких-то элементов мы будем комбинировать, тем сложнее нам будет найти все возможные варианты?

-А можно ли потерять какое-то число, используя способ перебора возможных вариантов?

-А что произойдёт с деревом возможных вариантов, если количество элементов, используемых в комбинациях, будет увеличиваться? (показываю дерево двузначных чисел и дерево расписания)

-Значит, какой из способов решения комбинаторных задач самый рациональный, самый быстрый и точный? (комбинаторное правило умножения.)

-Давайте проверим, правильно ли вы нашли количество вариантов двузначных чисел из цифр 1, 2 и 3 с помощью комбинаторного правила умножения.

3 способ – комбинаторное правило умножения.

1 место — 3 способа

2 место — 3 способа

3 ∙ 3 = 9

Ответ: 9 способов

3 задание:

-Кто из вас знает басню Ивана Андреевича Крылова «Квартет»?

-Кто помнит главных героев этой басни?

Проказница-Мартышка,

Осёл,

Козёл

Да косолапый Мишка

Затеяли сыграть Квартет.

Достали нот, баса, альта, две скрипки

И сели на лужок под липки —

Пленять своим искусством свет.

-Чем главные герои были заняты?

-Мартышка, Осёл, Козёл и Мишка пересаживались, считая, что от этого зависит звучание музыки. Сколькими способами они могли пересесть?

-Давайте воспользуемся самым быстрым и эффективным способом решения комбинаторных задач. Каким?( комбинаторным правилом умножения.) Для этого немножко поиграем.

-Кто желает быть героями? (2-из 1 команды, 2-из 2 команды и в игровой форме осмысляют у кого из героев сколько вариантов расположения на 4 местах).

4 ∙3 ∙ 2 ∙ 1 =24способа

Вывод:

-Какой из способов решения комбинаторных задач самый эффективный, самый быстрый и точный?

-А кто из вас помнит девиз нашего занятия?

-Девиз нашего мастер-класса : « Я МОГ БЫ ИХ ПЕРЕСЧИТАТЬ, НО МНЕ НЕ ДАЛИ ДОПИСАТЬ». Понятен ли смысл этих слов вам сейчас?

-Правильно, можно и пересчитать все возможные варианты, т. е. решить каким способом комбинаторную задачу? (способом перебора), а можно решить самым эффективным способом, каким? (используя комбинаторное правило умножения).

infourok.ru

Методическая разработка (алгебра, 5 класс) по теме: урок математики: «Комбинаторные задачи 5 класс»

Тема урока: « Комбинаторные задачи»

Предмет: математика.

Учитель: Кадралиева Н. В.

Класс: 5

Учебник: Базовый учебник УМК « Алгоритм успеха», Вентана-Граф. Под редакцией А.Г. Мерзляк, В.Б.Полонский, М.С.Якир

Тип: Изучение нового знания.

Формы работы учащихся: работа в тетради, фронтальная работа с классом

Необходимое техническое оборудование: Интерактивная доска, программа MimioStudio.

Цели:

1. Предметные: научить решать задачи с помощью комбинаций.
2. Личностные: умение контролировать процесс и результат учебной и математической деятельности;
3. Метапредметные: развитие компетентности в области использования ИКТ.

Основные понятия: комбинаторика, комбинаторные задачи.

Планируемые результаты:  понимают и умеют решать комбинаторные задачи.

Ход урока:

1. Организационный момент.
2. Мотивация и постановка темы и цели урока.

(я знаю, что многие в моем классе увлекаются футболом), показываю слайд 1.

Представьте, что после посещения футбольного матча вам удается узнать номер телефона вашего кумира, придя домой решаете ему набрать и поговорить. Но вдруг набирая, номер не можете вспомнить последнюю цифру телефона.

— Что вы будете делать?

Ученик: — перебирать все возможные цифры от 0 до 9.

— Как еще можно назвать этот перебор цифр?

Ученик: — перебор всех возможных комбинаций.

— Сегодня на уроке мы будем решать задачи, где используются всевозможные комбинации. Сейчас подумайте и скажите, как можем назвать такие задачи.

Ученики выдвигают гипотезы и после произношения правильного ответа, проговаривается еще раз и записывается тема урока(слайд2).

3. Новая тема.

Сегодня на уроке познакомимся, что такое комбинаторные задачи и научимся их решать.

Задача: Имеется 3 корзины, нужно разложить плоды в эти корзины(слайд3).

Ученики пытаются показать все возможные варианты, после чего учитель показывает как правильно оформить и записать решение задачи(слайд4,5).

4. Физкультминутка.

Раз – поднялись потянулись,

Два – согнулись, разогнулись,

Три в ладоши три хлопка,

На четыре – три кивка,

Пять руками помахать,

Шесть – тихонько сесть

5. Первичное закрепление.

Слайд 6, задача с йогуртами: сколько способов приготовления йогурта с разными вкусами.

6. Закрепление в учебнике: № 645, 647
7. Рефлексия: — я сегодня на уроке узнал….

— больше всего на уроке мне понравилось…..

8. Информация о домашнем задании: §24, №646, 648, дополнительно придумать задачу по теме урока.

nsportal.ru