Применение производной в различных областях науки
Министерство образования Саратовской области
Государственное автономное профессиональное образовательное учреждение Саратовской области «Энгельсский политехникум»
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В РАЗНИЧНЫХ ОБЛАСТЯХ НАУКИ
Выполнила: Саркулова Нургуля Сергеевна
студентка группы КШИ-216/15
(Конструирование, моделирование и
технология швейных изделий)
Научный руководитель:
Вербицкая Елена Вячеславовна
преподаватель математики ГАПОУ СО
«Энгельсский политехникум»
2016
Введение
Роль математики в различных областях естествознания очень велика. Недаром говорят «Математика – царица наук, физика ее правая рука, химия – левая».
Предмет исследования – производная.
Ведущая цель — показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.
Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.
Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.
Ключевой и тематический вопросы данного реферата:
1. История возникновения производной.
2. Зачем изучать производные функций?
3. Где используются производные?
4. Применение производных в физике, химии, биологии и других науках.5. Выводы
Я решила написать работу на тему «Применение производной в различных областях науки», потому что считаю эту тему очень интересной, полезной и актуальной.
В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.
Применение производной в различных областях науки
Из курса алгебры старших классов мы уже знаем, что производная — это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.
Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.
Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Физический смысл производной: производная функции y=f(x) в точке x0 – это скорость изменения функции f(x) в точке x0.

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.
Геометрический смысл производной состоит в том, что производная функция в точке x0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x0.

Термин производная и современные обозначения y’ , f ‘ ввёл Ж.Лагранж в 1797г.
Российский математик 19 века Панфутий Львович Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, например, как располагать своими средствами для достижения наибольшей выгоды».
С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:
Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;
Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;
Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.
При изучении любой темы у учеников возникает вопрос: «Зачем нам это надо?» Если ответ удовлетворит любопытство, то можно говорить о заинтересованности учеников. Ответ для темы «Производная» можно получить, зная, где используются производные функций.
Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.
Производная в алгебре:
1. Касательная к графику функции 
Касательная к графику функции f, дифференцируемой в точке xо, — это прямая, проходящая через точку (xо; f(xо)) и имеющая угловой коэффициент f ′(xо).
y = f(xо) + f ′(xо) (x – xо)
2. Поиск промежутков возрастания и убывания функции
Функция y=f(x) возрастает на интервале X, если для любых  и
и  выполняется неравенство
выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции.
Функция y=f(x) убывает на интервале X, если для любых  и
и  выполняется неравенство
выполняется неравенство  . Другими словами – большему значению аргумента соответствует меньшее значение функции.
. Другими словами – большему значению аргумента соответствует меньшее значение функции.

3. Поиск точек экстремума функции
Точку 
 . Значение функции в точке максимума называют максимумом функции и обозначают
. Значение функции в точке максимума называют максимумом функции и обозначают  .
. Точку  называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство
называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство  . Значение функции в точке минимума называют
. Значение функции в точке минимума называют
 .
. Под окрестностью точки  понимают интервал
понимают интервал  , где
, где  — достаточно малое положительное число.
— достаточно малое положительное число.
Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.

4. Поиск промежутков выпуклости и вогнутости функции
График функции  , дифференцируемой на интервале
, дифференцируемой на интервале  , является на этом интервале выпуклым, если график этой функции в пределах интервала
, является на этом интервале выпуклым, если график этой функции в пределах интервала  лежит не выше любой своей касательной (рис. 1).
лежит не выше любой своей касательной (рис. 1).
График функции  , дифференцируемой на интервале
, дифференцируемой на интервале 
 лежит не ниже любой своей касательной (рис. 2).
лежит не ниже любой своей касательной (рис. 2). 
Точкой перегиба графика функции  называется точка
называется точка  , разделяющая промежутки выпуклости и вогнутости.
, разделяющая промежутки выпуклости и вогнутости.
5. Поиск точек изгиба функции

Производная в физике:
1. Скорость как производная пути 
2. Ускорение как производная скорости  a =
a = 
3. Скорость распада радиоактивных элементов  = — λN
= — λN
А так же в физике производную применяют для вычисления:
Скорости материальной точки 
Мгновенной скорости как физический смысл производной
Мгновенное значение силы переменного тока
Мгновенное значение ЭДС электромагнитной индукции 
Максимальную мощность 
Производная в химии:
И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.
Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. V (t) = p ‘(t)
Количествов-ва в момент времени t0
p = p(t 0)
Функция
Интервал времени
∆t = t– t0
Приращение аргумента
Изменение количества в-ва
∆p= p(t0+ ∆ t ) – p(t0)
Приращение функции
Средняя скорость химической реакции
∆p/∆t
Отношение приращёния функции к приращёнию аргумента
Производная в биологии:
Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.
Р = х‘ (t)
Производная в географии:
Производная помогает рассчитать:
1. Некоторые значения в сейсмографии
2. Особенности электромагнитного поля земли
3. Радиоактивность ядерно- геоифзичексих показателей
4.Многие значения в экономической географии
5.Вывести формулу для вычисления численности населения на территории в момент времени t.
у’= к у
Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует
Производная в электротехнике:
В наших домах, на транспорте, на заводах : всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.
Количественной характеристикой электрического тока является сила тока.
В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.
В электротехнике в основном используется работа переменного тока.
Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.
Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.
Производная в экономике:
Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.
Производная в экономике решает важные вопросы:
1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?
2. Увеличится или уменьшится выручка фирмы при увеличение цены на её продукцию?
Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления.
Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.
ВЫВОД: производная успешно применяется при решении различных прикладных задач в науке, технике и жизни
Как видно из вышеперечисленного применение производной функции весьма многообразно и не только при изучении математики, но и других дисциплин. Поэтому можно сделать вывод, что изучение темы: «Производная функции» будет иметь своё применение в других темах и предметах.
Мы убедились в важности изучения темы «Производная», ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.
В заключении я хочу вам прочитать стихотворение:
“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.
Так сказал американский математик Морис Клайн.
Список используемой литературы:
1. Богомолов Н.В., Самойленко И.И. Математика. — М.: Юрайт, 2015.
2. Григорьев В.П., Дубинский Ю.А, Элементы высшей математики. — М.: Академия, 2014.
3. Баврин И.И. Основы высшей математики. — М.: Высшая школа, 2013.
4. Богомолов Н.В. Практические занятия по математике. — М.: Высшая школа, 2013.
5. Богомолов Н.В. Сборник задач по математике. — М.: Дрофа, 2013.
6. Рыбников К.А. История математики, «Издательство Московского университета», М, 1960.
7. Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В. – М.: Издательский центр «Академия», 2010
8. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия. – М.: Издательский центр «Академия», 2016
Периодические источники:
Газеты и журналы: «Математика», «Открытый урок»
Использование ресурсов сети Интернет, электронных библиотек:
https://ru.wikipedia.org/wiki
http://dic.academic.ru/
http://urokmatem.ru
www:egetutor.ru
matematika-na5.norod.ru
Проект на тему: Применение производной в различных областях науки
Министерство образования Саратовской области
Государственное автономное профессиональное образовательное учреждение Саратовской области «Энгельсский политехникум»
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В РАЗНИЧНЫХ ОБЛАСТЯХ НАУКИ
Выполнила: Вербицкая Елена Вячеславовна
преподаватель математики ГАПОУ СО
«Энгельсский политехникум»
2016
Введение
Роль математики в различных областях естествознания очень велика. Недаром говорят «Математика – царица наук, физика ее правая рука, химия – левая».
Предмет исследования – производная.
Ведущая цель — показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.
Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.
Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.
Ключевой и тематический вопросы данного реферата:
1. История возникновения производной.
2. Зачем изучать производные функций?
3. Где используются производные?
4. Применение производных в физике, химии, биологии и других науках.
5. Выводы
Я решила написать работу на тему «Применение производной в различных областях науки», потому что считаю эту тему очень интересной, полезной и актуальной.
В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.
Применение производной в различных областях науки
Из курса алгебры старших классов мы уже знаем, что производная — это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.
Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.
Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.
Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Физический смысл производной: производная функции y=f(x) в точке x0 – это скорость изменения функции f(x) в точке x0.
Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.
Геометрический смысл производной состоит в том, что производная функция в точке x0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x0.
Термин производная и современные обозначения y’ , f ‘ ввёл Ж.Лагранж в 1797г.
Российский математик 19 века Панфутий Львович Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, например, как располагать своими средствами для достижения наибольшей выгоды».
С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:
- Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;
- Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;
- Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.
При изучении любой темы у учеников возникает вопрос: «Зачем нам это надо?» Если ответ удовлетворит любопытство, то можно говорить о заинтересованности учеников. Ответ для темы «Производная» можно получить, зная, где используются производные функций.
Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.
Производная в алгебре:
1. Касательная к графику функции
Касательная к графику функции f, дифференцируемой в точке xо, — это прямая, проходящая через точку (xо; f(xо)) и имеющая угловой коэффициент f ′(xо).
y = f(xо) + f ′(xо) (x – xо)
2. Поиск промежутков возрастания и убывания функции
Функция y=f(x) возрастает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Функция y=f(x) убывает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.
3. Поиск точек экстремума функции
Точку называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают .
Точку называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .
Под окрестностью точки понимают интервал , где — достаточно малое положительное число.
Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.
4. Поиск промежутков выпуклости и вогнутости функции
График функции , дифференцируемой на интервале , является на этом интервале выпуклым, если график этой функции в пределах интервала лежит не выше любой своей касательной (рис. 1).
График функции , дифференцируемой на интервале , является на этом интервале вогнутым, если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).
Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.
5. Поиск точек изгиба функции
Производная в физике:
1. Скорость как производная пути
2. Ускорение как производная скорости a =
3. Скорость распада радиоактивных элементов = — λN
А так же в физике производную применяют для вычисления:
Скорости материальной точки
Мгновенной скорости как физический смысл производной
= |
|
| – мгновенная скорость, м/с | |
Δt |
Мгновенное значение силы переменного тока
Мгновенное значение ЭДС электромагнитной индукции
Максимальную мощность
Производная в химии:
И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.
Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. V (t) = p ‘(t)
Понятие на языке химии | Обозначение | Понятие на языке математики |
Количество в-ва в момент времени t0 | p = p(t 0) | Функция |
Интервал времени | ∆t = t– t0 | Приращение аргумента |
Изменение количества в-ва | ∆p= p(t0+ ∆ t ) – p(t0) | Приращение функции |
Средняя скорость химической реакции | ∆p/∆t | Отношение приращёния функции к приращёнию аргумента |
Производная в биологии:
Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.
Р = х‘ (t)
Производная в географии:
Производная помогает рассчитать:
1. Некоторые значения в сейсмографии
2. Особенности электромагнитного поля земли
3. Радиоактивность ядерно- геоифзичексих показателей
4.Многие значения в экономической географии
5.Вывести формулу для вычисления численности населения на территории в момент времени t.
у’= к у
Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует
Производная в электротехнике:
В наших домах, на транспорте, на заводах : всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.
Количественной характеристикой электрического тока является сила тока.
В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.
В электротехнике в основном используется работа переменного тока.
Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.
Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.
Производная в экономике:
Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.
Производная в экономике решает важные вопросы:
1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?
2. Увеличится или уменьшится выручка фирмы при увеличение цены на её продукцию?
Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления.
Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.
ВЫВОД: производная успешно применяется при решении различных прикладных задач в науке, технике и жизни
Как видно из вышеперечисленного применение производной функции весьма многообразно и не только при изучении математики, но и других дисциплин. Поэтому можно сделать вывод, что изучение темы: «Производная функции» будет иметь своё применение в других темах и предметах.
Мы убедились в важности изучения темы «Производная», ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.
В заключении я хочу вам прочитать стихотворение:
“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.
Так сказал американский математик Морис Клайн.
Список используемой литературы:
1. Богомолов Н.В., Самойленко И.И. Математика. — М.: Юрайт, 2015.
2. Григорьев В.П., Дубинский Ю.А, Элементы высшей математики. — М.: Академия, 2014.
3. Баврин И.И. Основы высшей математики. — М.: Высшая школа, 2013.
4. Богомолов Н.В. Практические занятия по математике. — М.: Высшая школа, 2013.
5. Богомолов Н.В. Сборник задач по математике. — М.: Дрофа, 2013.
6. Рыбников К.А. История математики, «Издательство Московского университета», М, 1960.
7. Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В. – М.: Издательский центр «Академия», 2010
8. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия. – М.: Издательский центр «Академия», 2016
Периодические источники:
Газеты и журналы: «Математика», «Открытый урок»
Использование ресурсов сети Интернет, электронных библиотек:
https://ru.wikipedia.org/wiki
http://dic.academic.ru/
http://urokmatem.ru
www:egetutor.ru
matematika-na5.norod.ru
Применение производной. Построение графиков с применением производных
Математика берет свои истоки со времен Античности. Благодаря ней архитектура, строительство и военное дело дали новый виток развития, достижения, которые были получены с помощью математики, привели к движению прогресса. И по сей день математика остается главной наукой, которая встречается во всех остальных отраслях.
Чтобы быть образованными, дети с первого класса начинают постепенно вливаться в эту среду. Очень важно разбираться в математике, так как она, в той или иной степени, встречается каждому человеку на протяжении всей его жизни. В этой статье будет разобран один из ключевых элементов — нахождение и применение производных. Не всякий человек может представить, насколько широко используется это понятие. Рассмотрим более 10 применений производных в определенных областях или науках.
Применение производной к исследованию функции
Производная — это такой предел отношения приращения функции к увеличению ее аргумента, когда показатель аргумента стремится к нулю. Производная — незаменимая вещь при исследовании функции. Например, с помощью нее можно определить возрастание и убывание последней, экстремумы, выпуклости и вогнутости. Дифференциальные исчисления входят в обязательную программу обучения студентов 1 и 2 курса математических вузов.

Область определения и нули функции
Первый этап любого исследования графика начинается с выяснения области определения, в более редких случаях — значения. Область определения задается по оси абсциссы, если говорить другими словами, то это числовые значения на оси OX. Часто область определения уже задана, но если она не задана, то следует оценить значение аргумента х. Допустим, если при каком-то значениях аргумента функция не имеет смысла, то этот аргумент исключается из области определения.
Нули функции находятся простым способом: функцию f(x) следует приравнивнять к нулю и решить полученное уравнение относительно одной переменной x. Полученные корни уравнения являются нулями функции, то есть в этих x функция равна 0.
Возрастание и убывание
Применение производной для исследования функций на монотонность может рассматриваться с двух позиций. Монотонная функция — это категория, которая имеет только положительные значения производной, либо только отрицательные. Простыми словами — функция только возрастает или только убывает на всем исследуемом промежутке:
- Параметр возрастания. Функция f(x) будет возрастать, если производная f`(x) больше нуля.
- Параметр убывания. Функция f(x) будет убывать, если производная f`(x) меньше нуля.
Касательная и угловой коэффициент
Применение производной к исследованию функции определяется еще и касательной (прямой, направленной под углом) к графику функции в данной точке. Касательная в точке (x0) — прямая, которая проходит через точку и принадлежит функции, координаты которой (x0, f(x0)), и имеющая угловой коэффициент f`(x0).
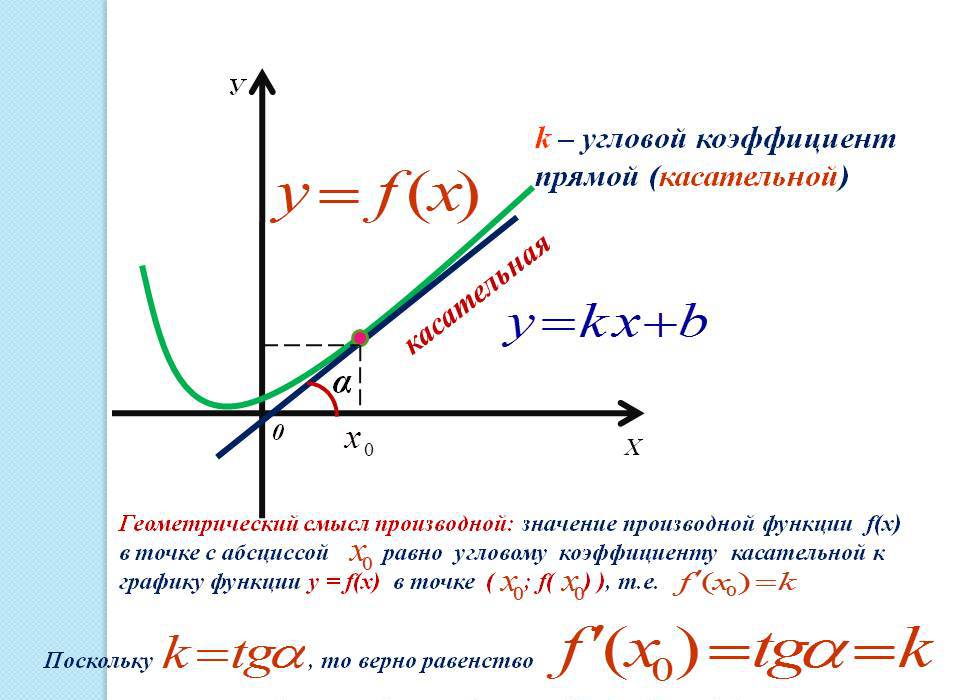
y = f(x0) + f`(x0)(x — x0) — уравнение касательной к данной точке графика функции.
Геометрический смысл производной: производная функции f(x) равняется угловому коэффициенту образованной касательной к графику этой функции в данной точке x. Угловой коэффициент, в свою очередь, равняется тангенсу угла наклона касательной к оси ОХ (абсцисс) в положительном направлении. Это следствие является основополагающим к применению производной к графику функции.
Точки экстремума
Применение производной к исследованию включает в себя нахождение точек максимума и минимума.
Для того чтобы найти и определить точки минимума и максимума, необходимо:
- Отыскать производную функции f(x).
- Приравнять полученное уравнение к нулю.
- Найти корни уравнения.
- Определить точки максимума и минимума.
Чтобы найти экстремумы функции:
- Отыскать точки минимума и максимума по способу выше.
- Подставить эти точки в первоначальное уравнение и высчитать yнаиб. и yнаим.
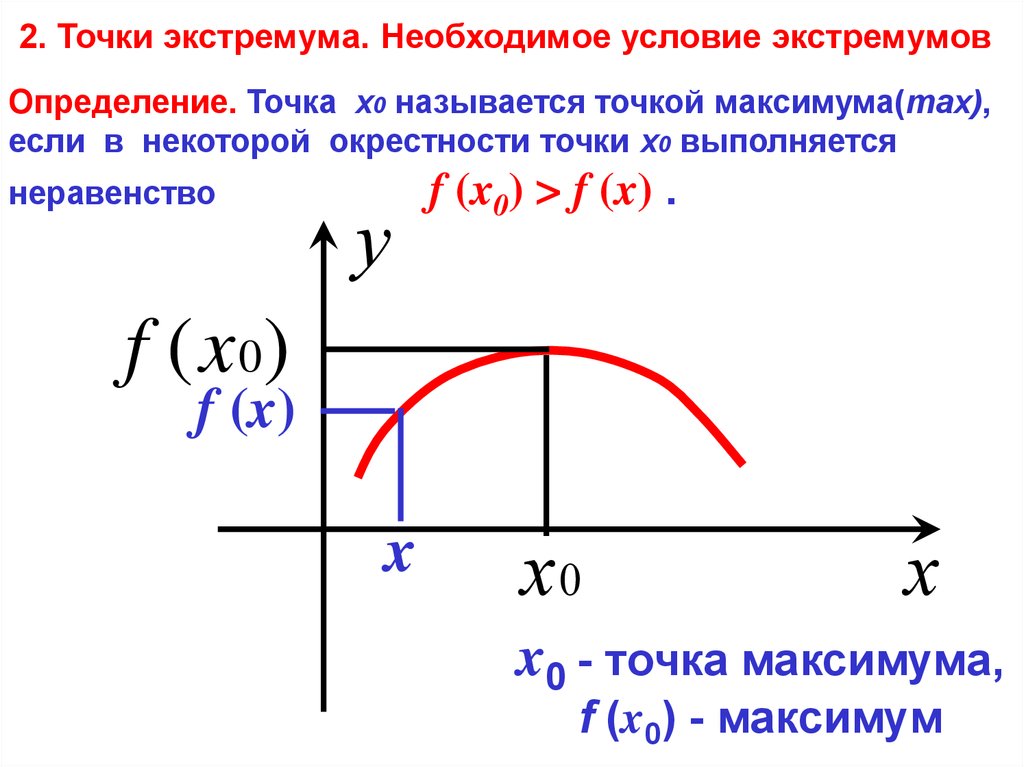
Точка максимума функции — это наибольшее значение функции f(x) на промежутке, другими словами xнаиб.
Точка минимума функции — это наименьшее значение функции f(x) на промежутке, другими словами xнаим.
Точки экстремума — то же самое, что и точки максимума и минимума, а экстремум функции (yнаиб. и унаим) — значения функций, которые соответствуют точкам экстремума.
Выпуклости и вогнутости
Определить выпуклость и вогнутость можно, прибегая к применению производной для построения графиков:
- Функция f(x), исследуемая на промежутке (a, b), является вогнутой, если функция расположена ниже всех своих касательных, находящихся внутри этого интервала.
- Функция f(x), исследуемая на промежутке (a, b), является выпуклой, если функция расположена выше всех своих касательных, находящихся внутри этого интервала.
Точка, которая разделяет выпуклость и вогнутость, называется точкой перегиба функции.
Чтобы найти точки перегиба:
- Найти критические точки второго рода (вторую производную).
- Точками перегиба являются те критические точки, которые разделяют два противоположенных знака.
- Вычисление значений функций в точках перегиба функции.
Частные производные
Применение производных такого типа есть в задачах, где используется больше одной неизвестной переменной. Чаще всего такие производные встречаются при построении графика функции, если быть точнее, то поверхности в пространстве, где вместо двух осей — три, следовательно, три величины (две переменные и одна постоянная).

Основное правило при вычислении частных производных — выбираем одну переменную, а остальные рассматриваем как постоянные. Следовательно, при вычислении частной производной постоянная величина становится как-будто числовым значением (во многих таблицах производных они обозначаются как C = const). Смысл такой производной — это скорость изменения функции z = f(x, y) по оси OX и OY, то есть характеризует крутизну впадин и выпуклостей построенной поверхности.
Производная в физике
Применение производной в физике имеет широкое распространение и значение. Физический смысл: производная пути по времени — скорость, а ускорение — производная скорости по времени. Из физического смысла можно провести множество ответвлений в различные разделы физики, при этом полностью сохраняя смысл производной.
С помощью применения производной находятся такие величины:
- Скорость в кинематике, где вычисляется производная от пройденного пути. Если находится вторая производная от пути или первая производная от скорости, то находится ускорение тела. Помимо этого, возможно нахождение мгновенной скорости материальной точки, однако для этого необходимо знать приращение ∆t и ∆r.
- В электродинамике: вычисление мгновенной силы переменного тока, а также ЭДС электромагнитной индукции. Вычисляя производную, можно найти максимальную мощность. Производная от количества электрического заряда — сила тока в проводнике.

Производная в химии и биологии
Химия: производная используется для определения скорости протекания химической реакции. Химический смысл производной: функция p = p(t), в данном случае p — количество вещества, которое вступает в химическую реакцию во времени t. ∆t — приращение времени, ∆p — приращение количества вещества. Предел отношения ∆p к ∆t, при котором ∆t стремится к нулю, называется скоростью протекания химической реакции. Среднее значение химической реакции — отношение ∆p/∆t. При определении скорости необходимо точно знать все необходимые параметры, условия, знать агрегатное состояние вещества и среду протекания. Это довольно большой аспект в химии, который широко применяется в различных отраслях и деятельности человека.
Биология: понятие производной используют при вычислении средней скорости размножения. Биологический смысл: имеем функцию y = x(t). ∆t — приращение по времени. Тогда с помощью некоторых преобразований получаем функцию y`= P(t) = x`(t) — активность жизнедеятельности популяции времени t (средняя скорость размножения). Такое применение производной позволяет вести статистику, отслеживать темпы размножения и так далее.

Производная в географии и экономике
Производная позволяет географам решать такие задачи, как нахождение численности населения, вычислять значения в сейсмографии, рассчитать радиоактивность ядерно-геофизических показателей, вычислить интерполяцию.
В экономике важную часть расчетов занимает дифференциальное исчисление и вычисление производной. В первую очередь это позволяет определить пределы необходимых экономических величин. Например, наибольшую и наименьшую производительность труда, издержки, прибыль. В основном эти величины рассчитываются по графикам функций, где находят экстремумы, определяют монотонность функции на нужном участке.
Заключение
Роль данного дифференциального исчисления задействована, как было отмечено в статье, в различных научных структурах. Применение производных функций — важный элемент в практической части науки и производства. Не зря нас в старшей школе и университете учили строить сложные графики, исследовать и работать над функциями. Как видим, без производных и дифференциальных исчислений невозможно было бы рассчитать жизненно важные показатели и величины. Человечество научилось моделировать различные процессы и исследовать их, решать сложные математические задачи. Действительно, математика — царица всех наук, потому что эта наука лежит в основе всех других естественных и технических дисциплин.
Глава . Производная и ее применение
§1. Производная функции
1. Определение производной
При
изучении зависимостей, описывающих
различные социально-экономические
процессы, часто возникает вопрос об
определении темпов изменения тех или
иных показателей, характеризующих эти
процессы (темпы роста национального
дохода, темпы роста цен, темпы изменения
занятости населения, и пр.). Если динамика
процесса описывается дискретной моделью,
где время принимает только целочисленные
значения, то в момент времени  состояние
процесса может характеризоваться
значением
состояние
процесса может характеризоваться
значением 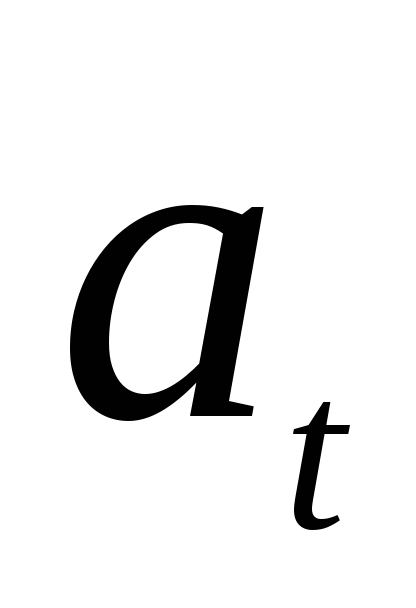 некоторого
экономического показателя (например,
некоторого
экономического показателя (например, 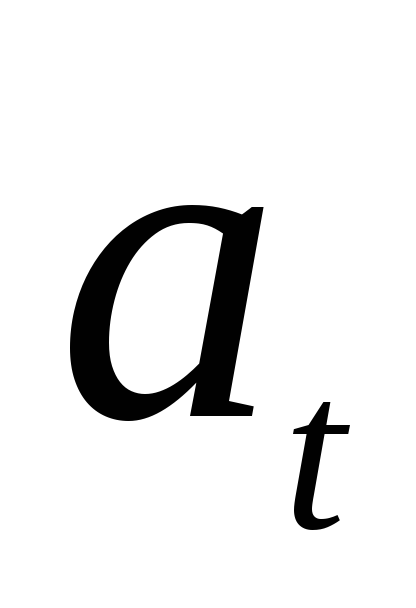 ‑ уровень производства в
некоторой отрасли).
‑ уровень производства в
некоторой отрасли).
Средним
темпом изменения дискретной переменной 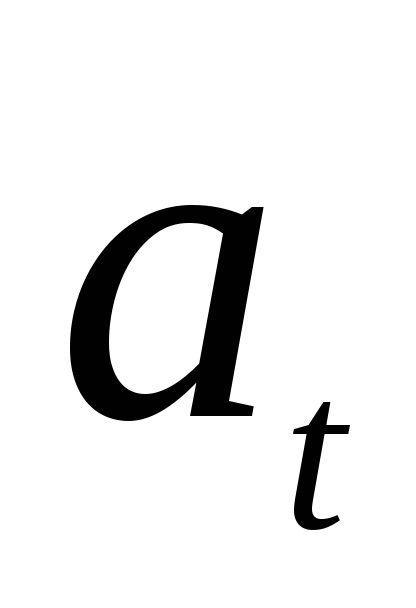 за период
за период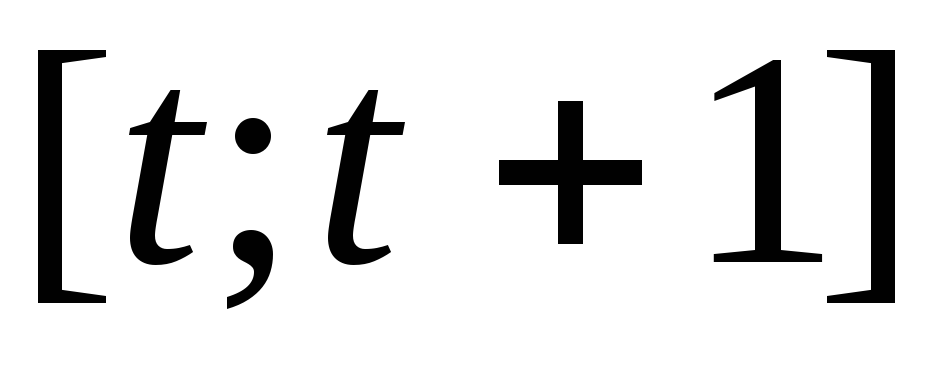 называется относительное изменение
этой переменной в течение этого периода:
называется относительное изменение
этой переменной в течение этого периода:
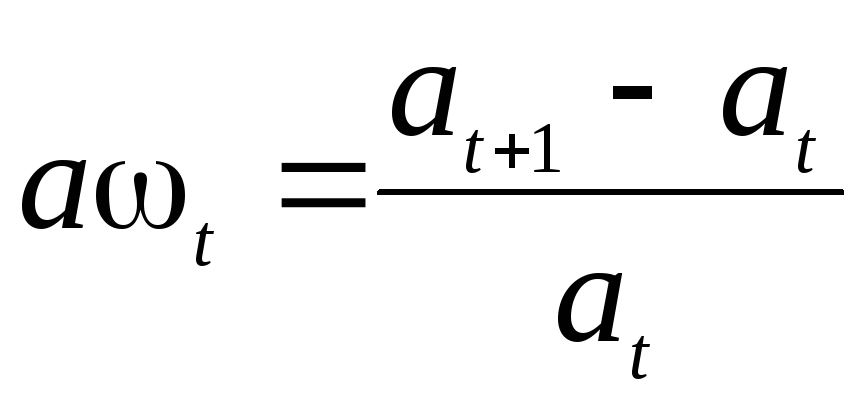 .
.
Этот показатель может быть выражен в процентах; в этом случае относительное изменение определяется по формуле
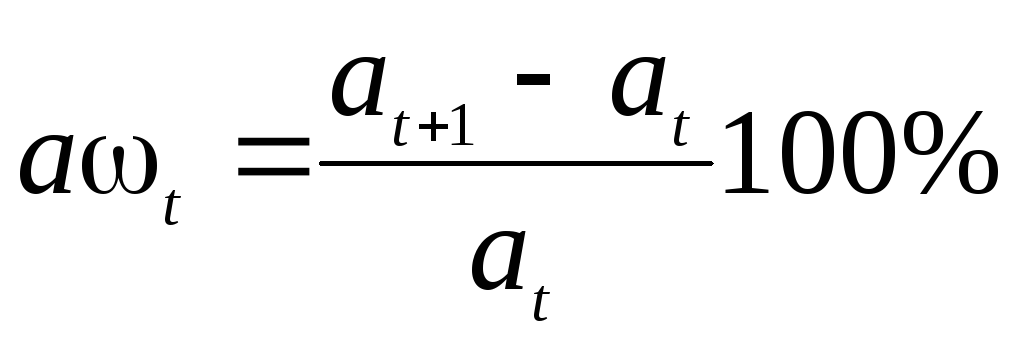 .
.
Поскольку разность
значений дискретной переменной 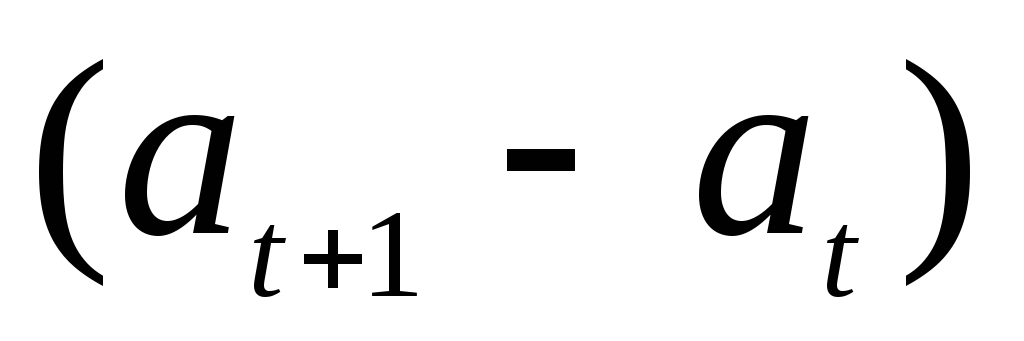 представляет собойприращение
переменной
представляет собойприращение
переменной 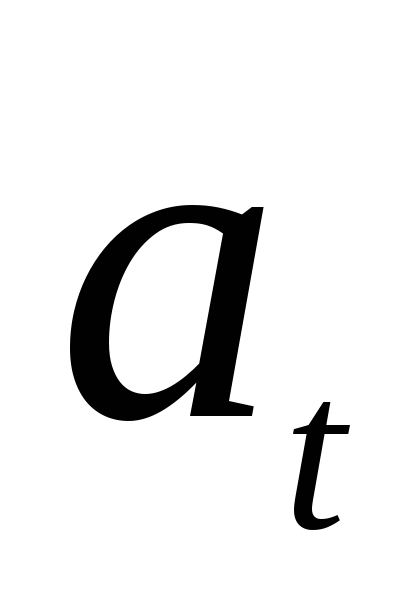 за один
период
за один
период 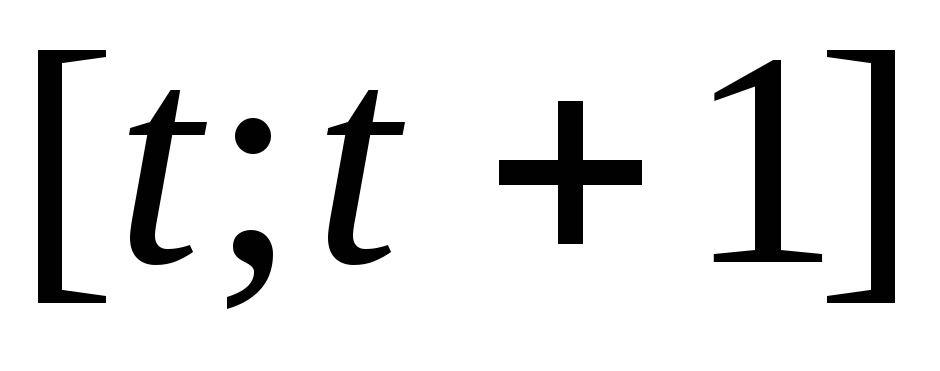 ,
то темп прироста за этот период равен
соответствующему приращению переменной,
деленному на значение переменной в
начале периода.
,
то темп прироста за этот период равен
соответствующему приращению переменной,
деленному на значение переменной в
начале периода.
Существенно, что темп изменения имеет размерность 1/время. Поэтому его значения будут различаться, если, например, в одном случае за единицу измерения времени взять месяц, а в другом ‑ год.
Пример
Если банк начисляет ежемесячно 5% от суммы вклада, который был в начале января, то к концу года клиент банка (вкладчик) получит суммарный доход от вклада в размере 60%.
Часто
для описания динамики того или иного
экономического процесса удобно
использовать непрерывную модель, где
время изменяется не скачками, а непрерывно.
В этом случае состояние процесса в
момент времени  может характеризоваться значением
некоторой функции
может характеризоваться значением
некоторой функции 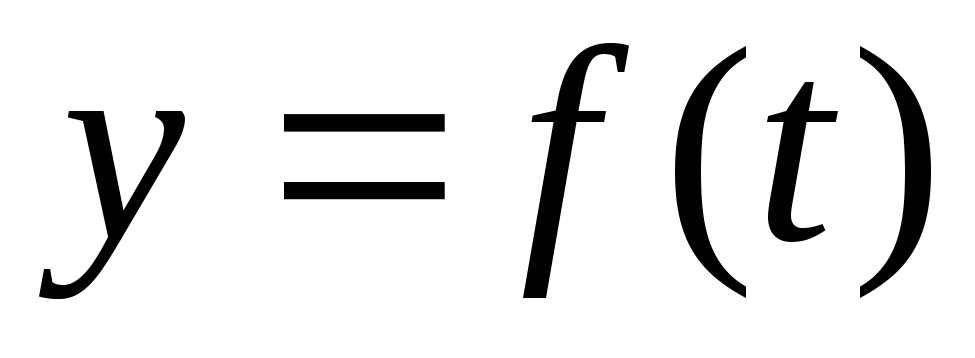 , заданной,
например, на отрезке
, заданной,
например, на отрезке 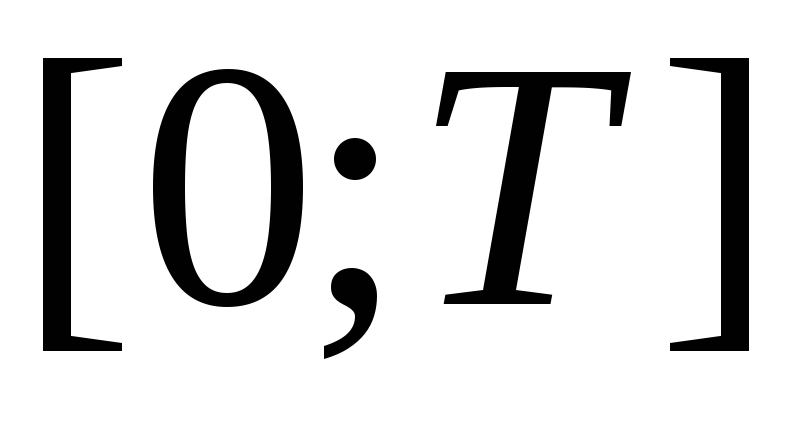 .
.
Средней
скоростью изменения функции 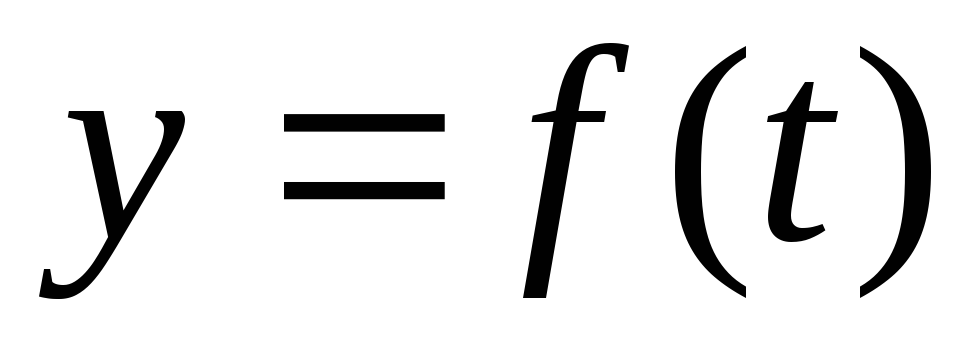 за период
за период 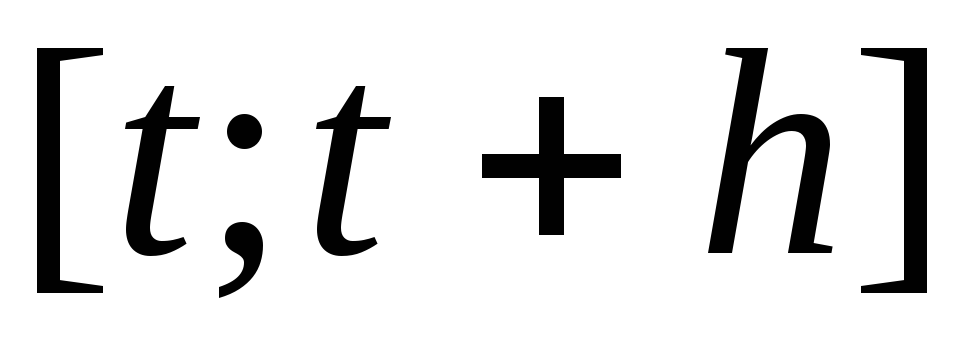 называется отношение приращения этой
переменной за период
называется отношение приращения этой
переменной за период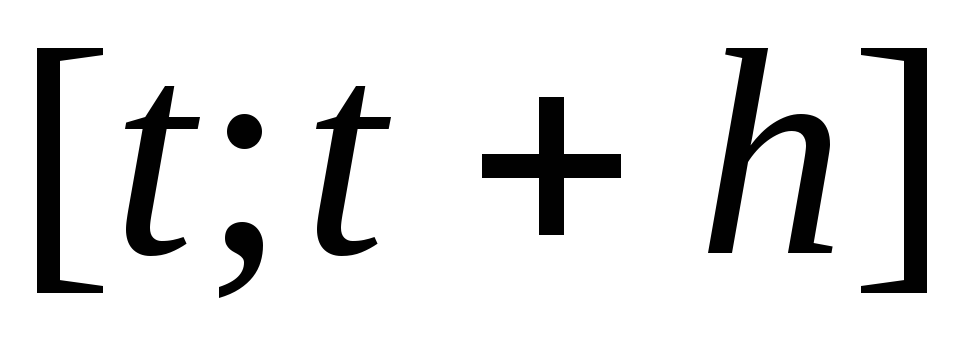 к продолжительности этого периода
к продолжительности этого периода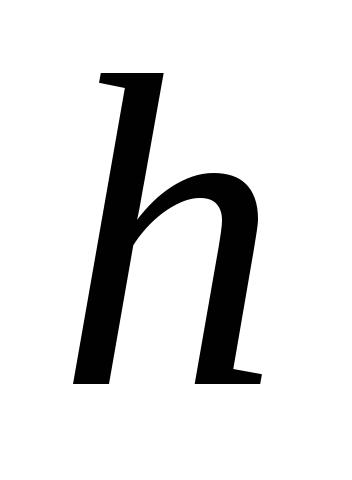 .
.
Поскольку
приращение функции 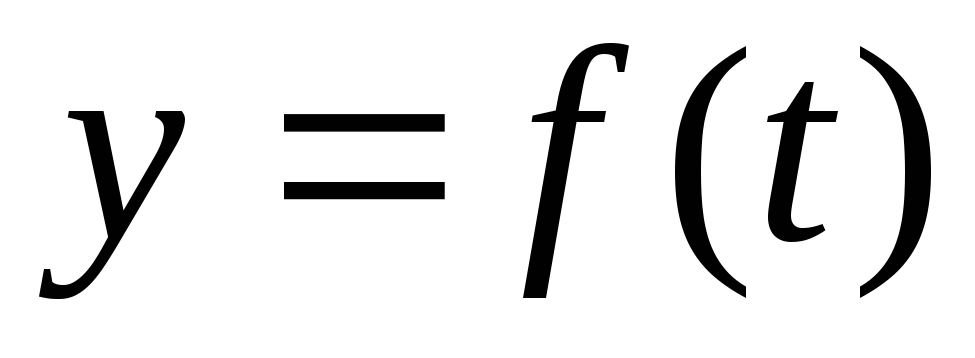 за период
за период 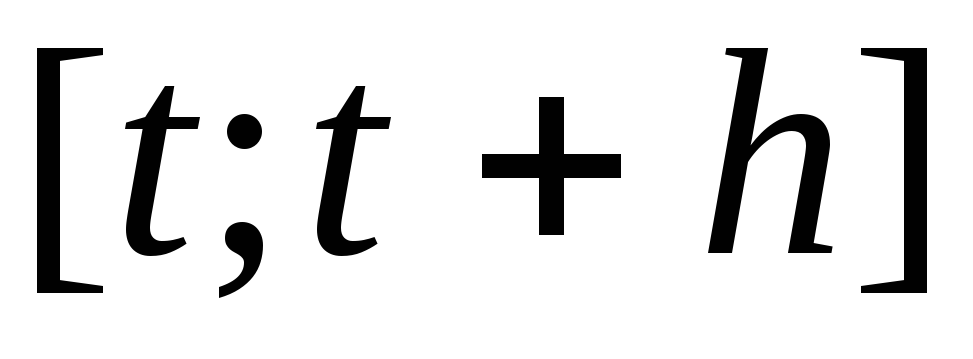 равно разности значений функции
равно разности значений функции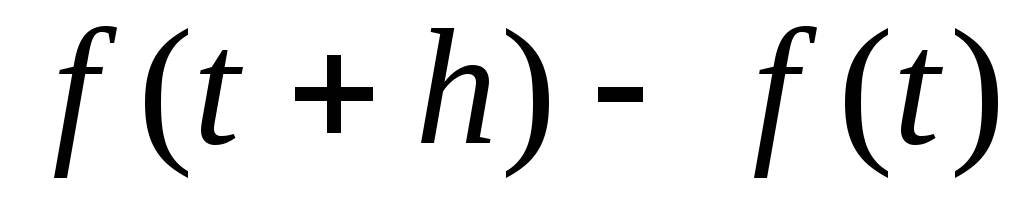 , то средняя
скорость изменения функции
, то средняя
скорость изменения функции 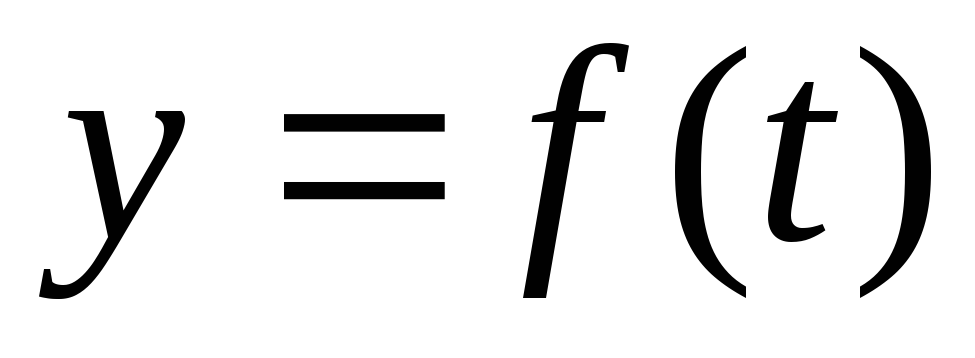 за период
за период 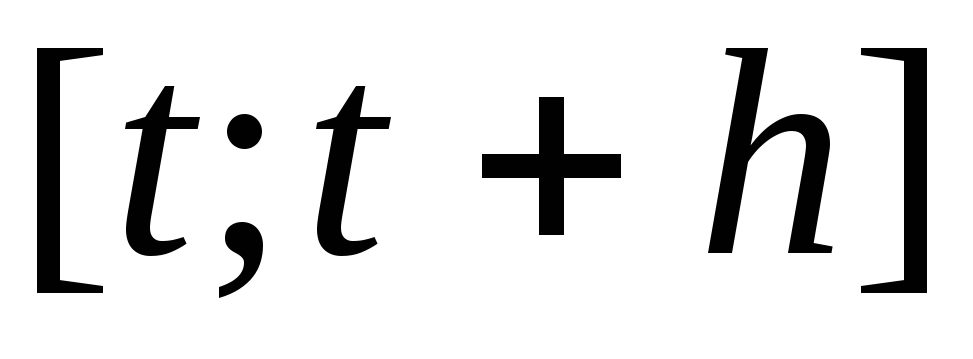 вычисляется так:
вычисляется так:
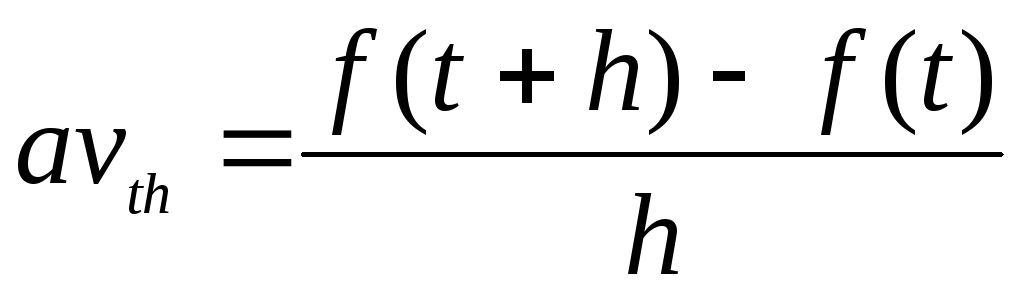 .
.
Средним
темпом изменения функции 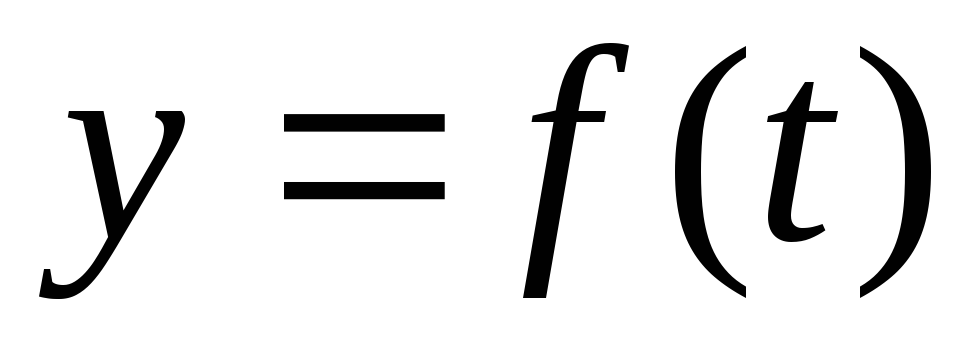 за период
за период 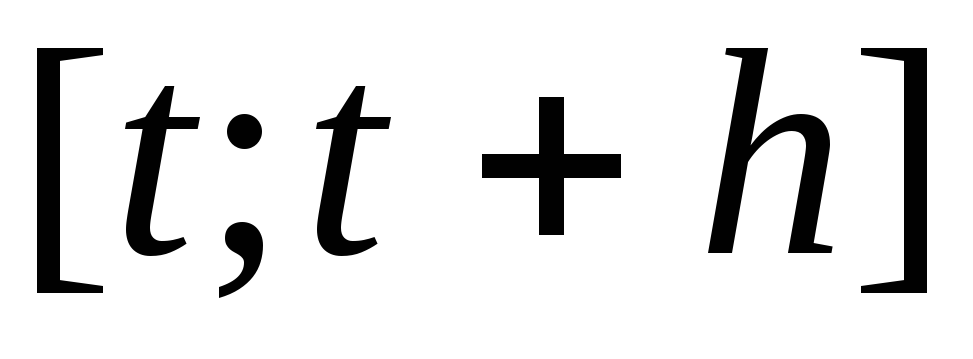 называется относительное изменение
этой переменной в течение этого периода:
называется относительное изменение
этой переменной в течение этого периода:
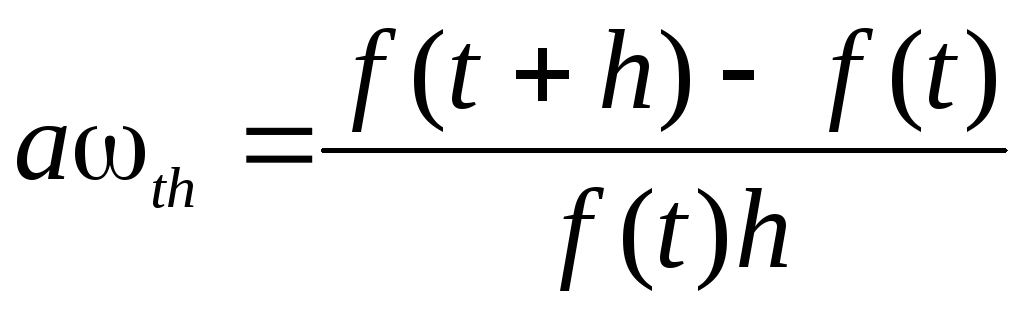 .
.
Таким
образом, средний
темп изменения функции 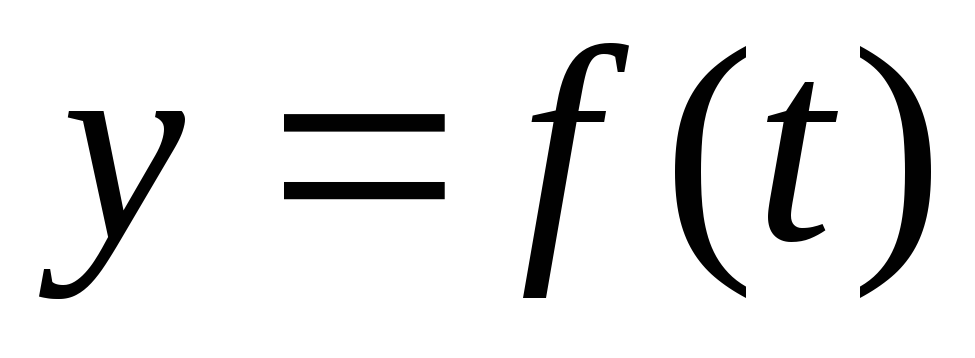 за период
за период 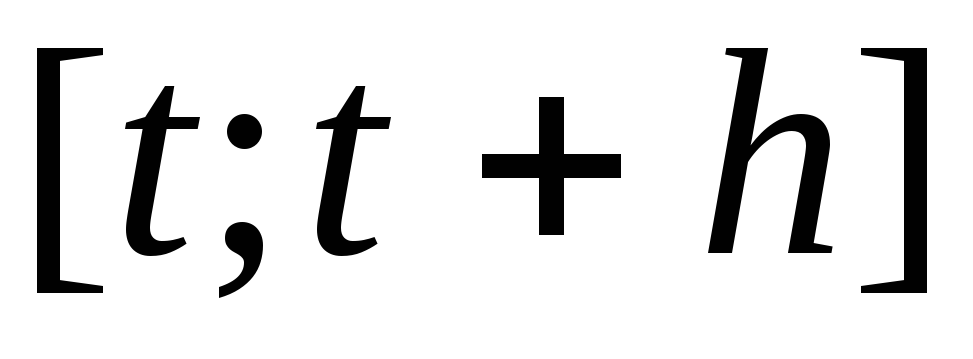 равен средней скорости изменения этой
функции, деленной на значение функции
в начале периода.
равен средней скорости изменения этой
функции, деленной на значение функции
в начале периода.
Мгновенной
скоростью изменения функции 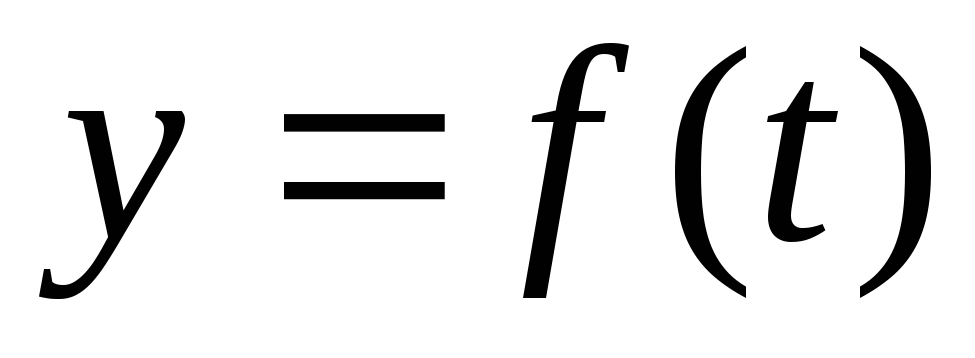 в момент
времени
в момент
времени  называется предел средней скорости
изменения этой функции за период
называется предел средней скорости
изменения этой функции за период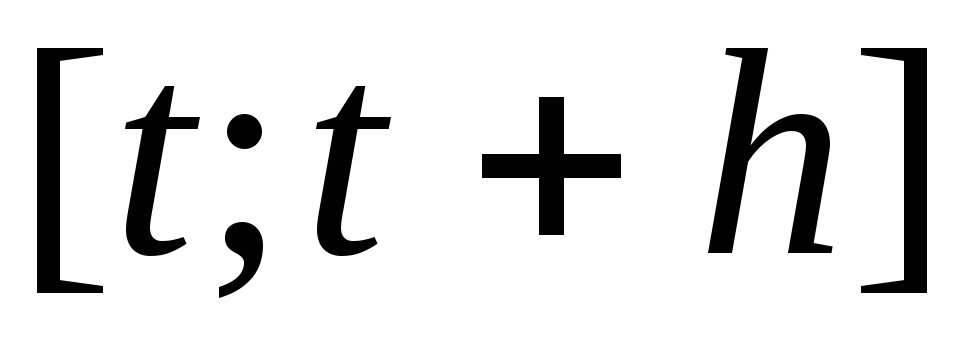 при стремлении продолжительности
периода
при стремлении продолжительности
периода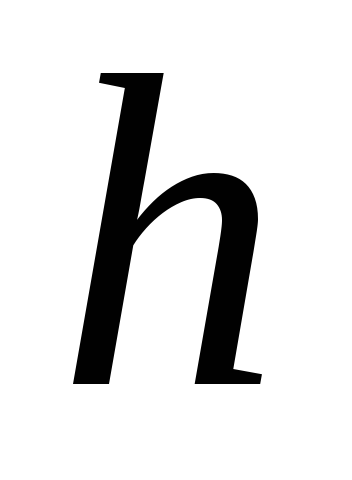 к нулю:
к нулю:
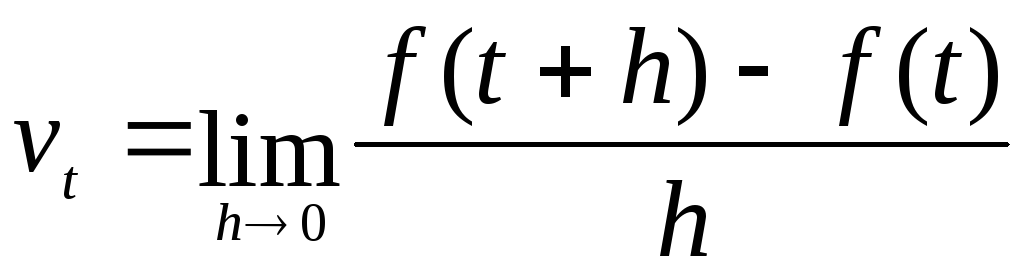 .
.
Мгновенным
темпом изменения функции 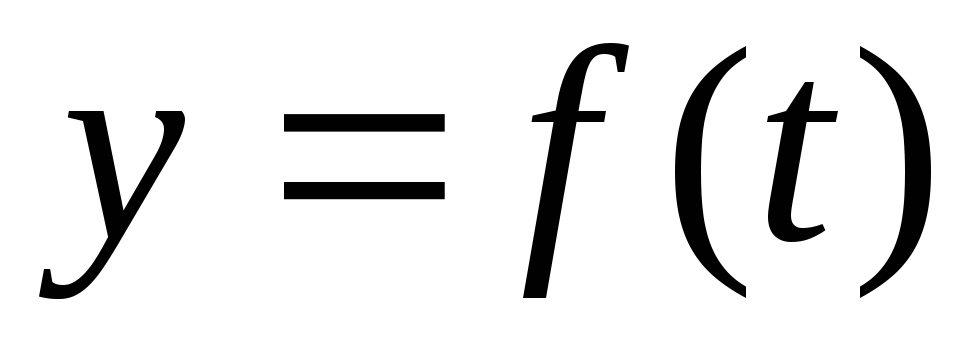 в момент
времени
в момент
времени  называется
предел среднего темпа изменения этой
функции за период
называется
предел среднего темпа изменения этой
функции за период 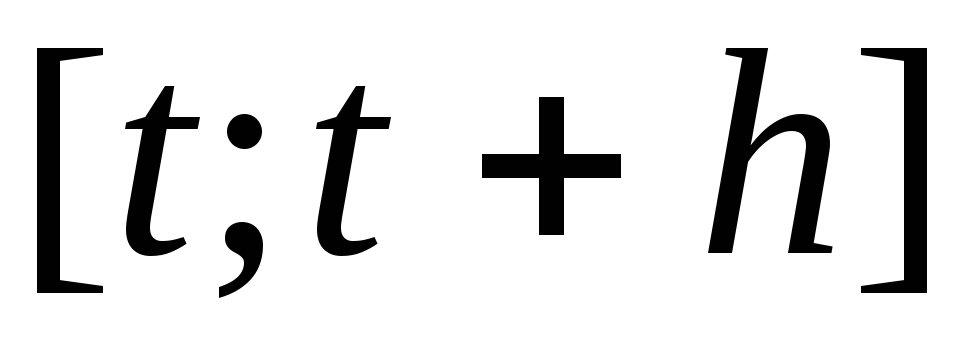 при стремлении продолжительности
периода
при стремлении продолжительности
периода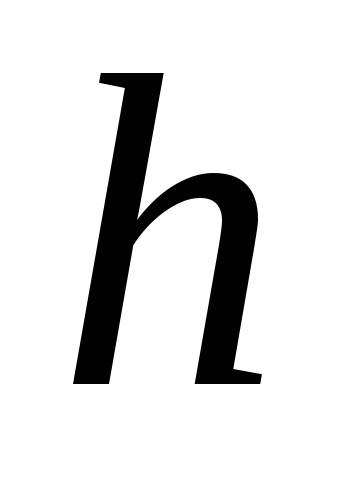 к нулю:
к нулю:
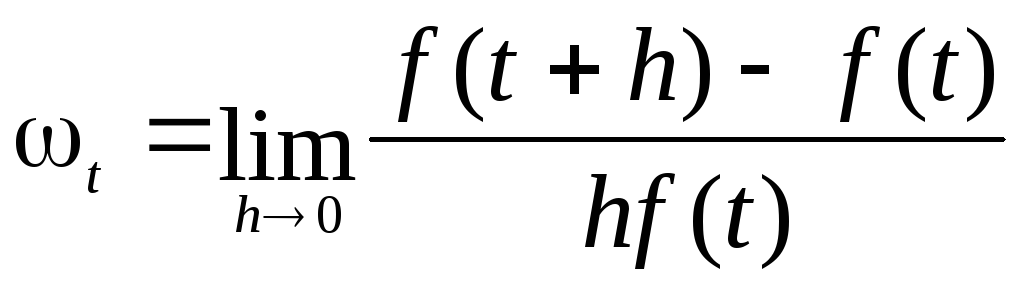 .
.
Таким
образом, мгновенный
темп изменения функции 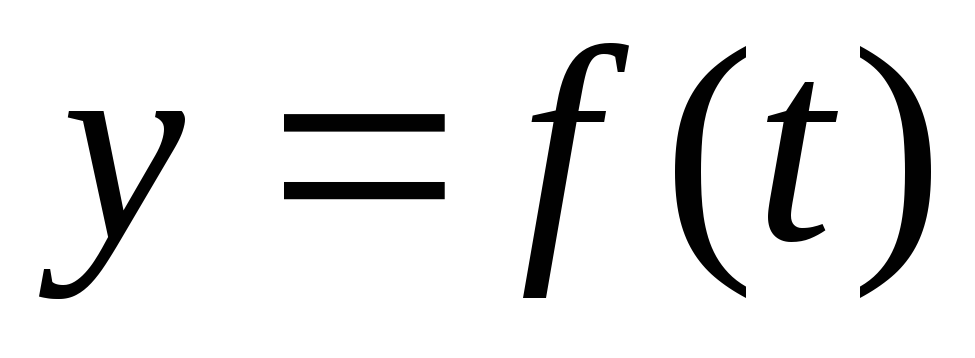 в момент
времени
в момент
времени  связан как
с мгновенной скоростью изменения
функции, так и со значением функции в
этот момент:
связан как
с мгновенной скоростью изменения
функции, так и со значением функции в
этот момент:
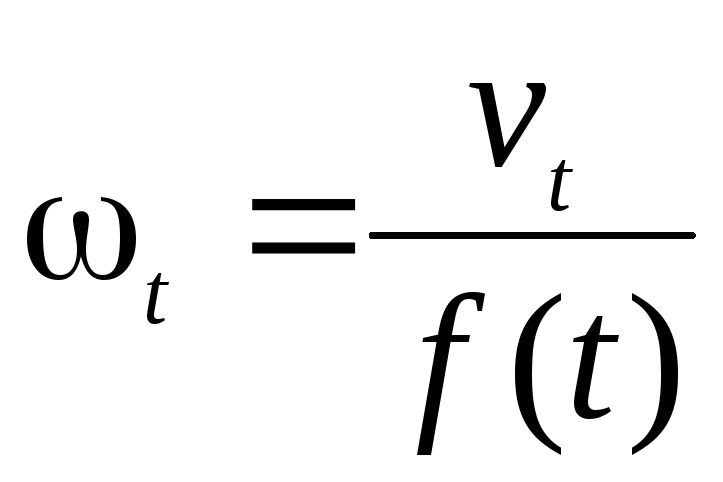 .
.
Задача об определении скорости изменения функции приводит к одному из важнейших понятий математического анализа ‑ к понятию производной. Сначала это понятие применялось при решении различных задач механики. Однако со временем производная и основанный на ней аппарат исследования функций стали использоваться и в других науках, в том числе в экономике, социологии и менеджменте.
Пусть
функция y =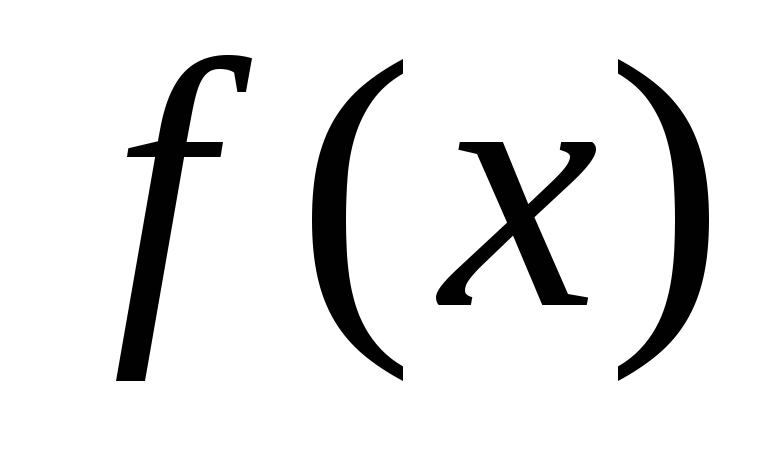 определена в окрестности точкиx0,
определена в окрестности точкиx0, 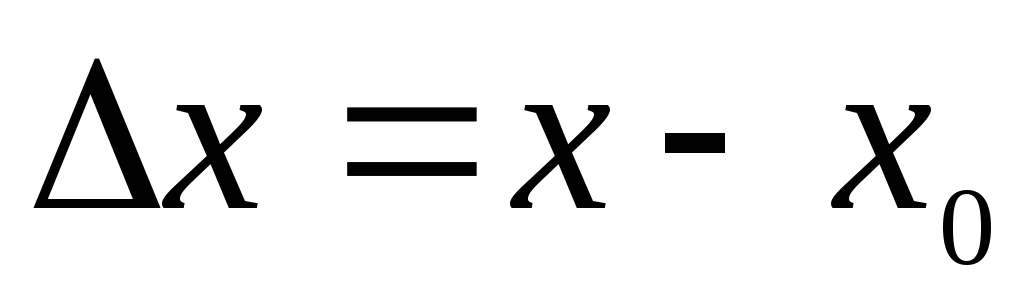
приращение аргумента x,
приращение аргумента x, 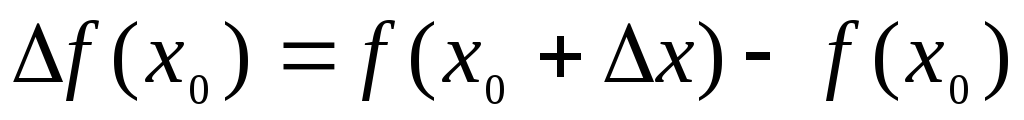
приращение функции.
приращение функции.
Производной функции 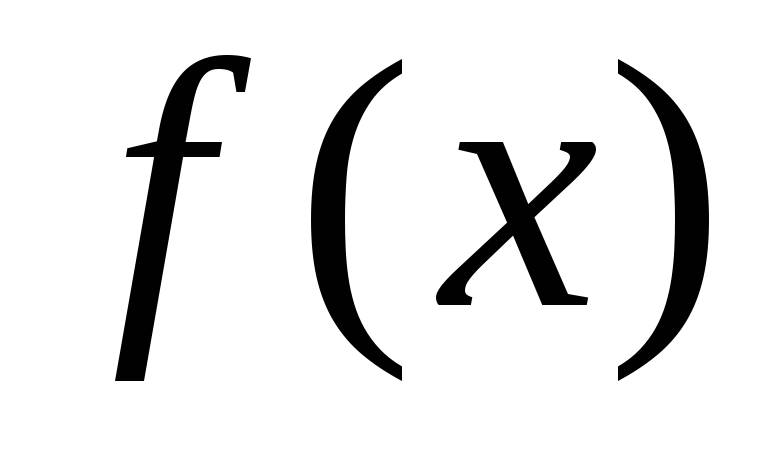 в точкеx0 называется конечный предел
в точкеx0 называется конечный предел 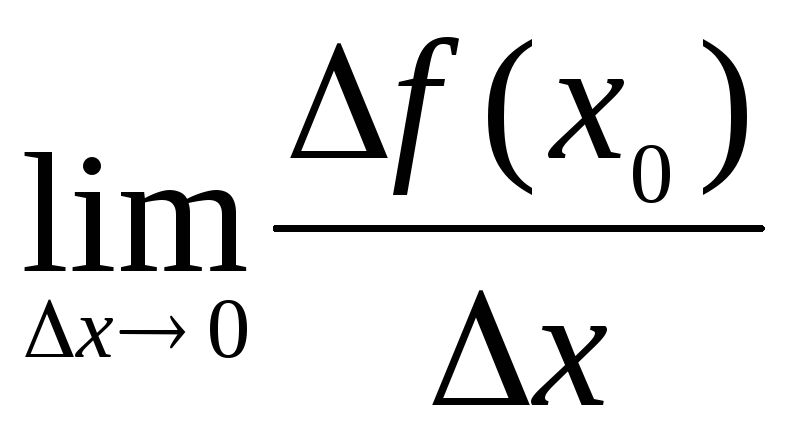 ,
если он существует.
,
если он существует.
Производная
функции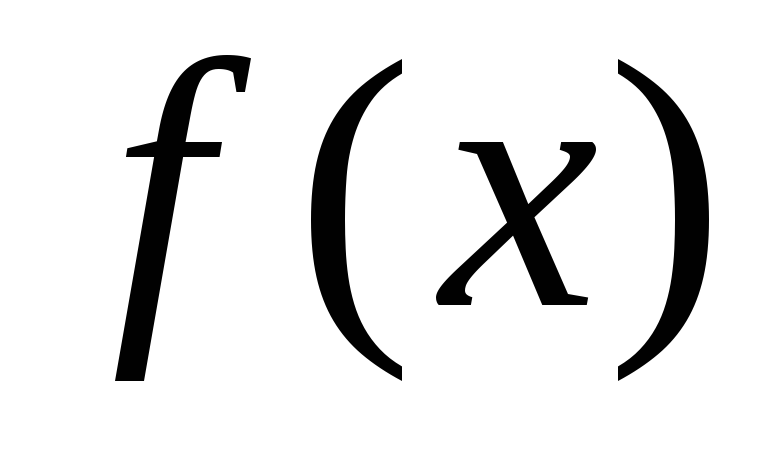 в
точкеx0 обозначается
в
точкеx0 обозначается 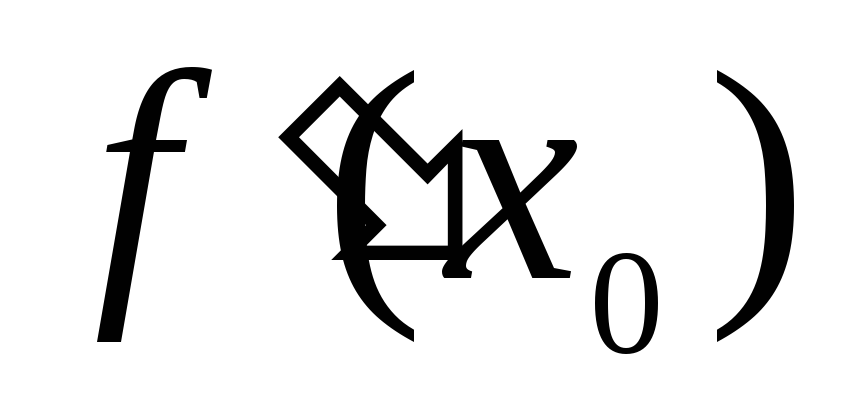 или
или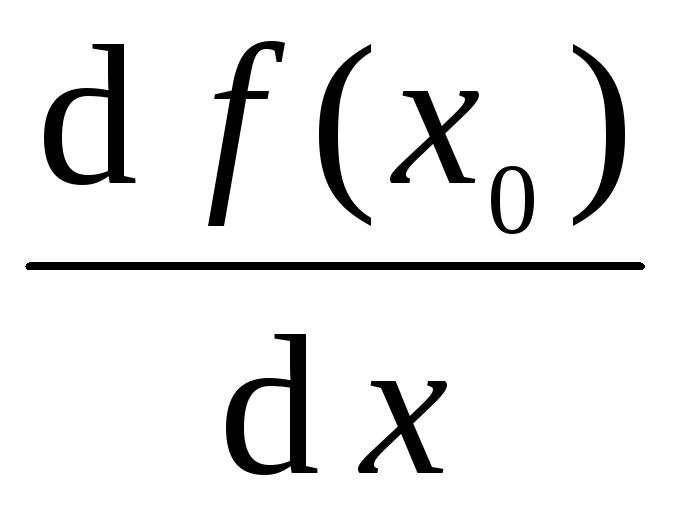 .
Черезy
или
.
Черезy
или 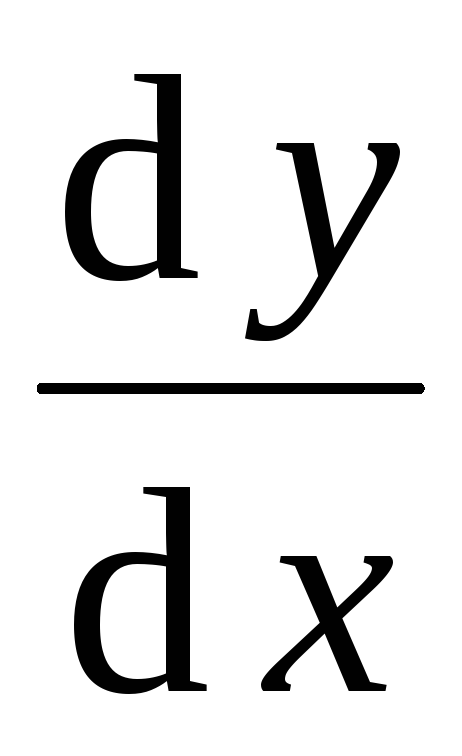 обозначают производную функцииy =
обозначают производную функцииy =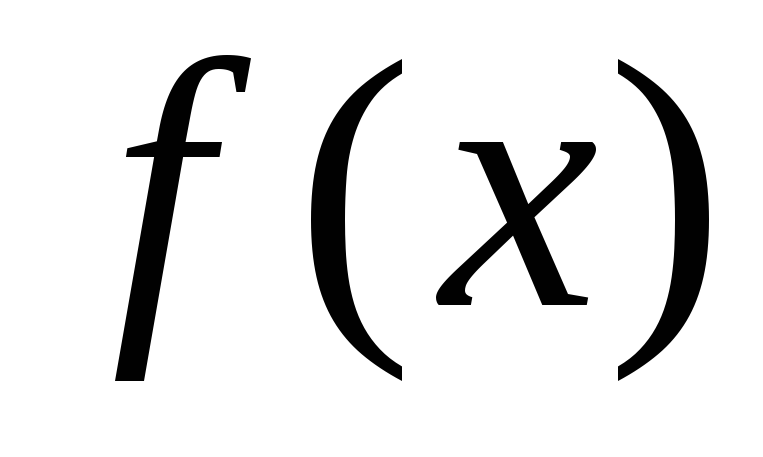 в точкеx.
в точкеx.
Экономический смысл производной
Мгновенный
темп изменения функции 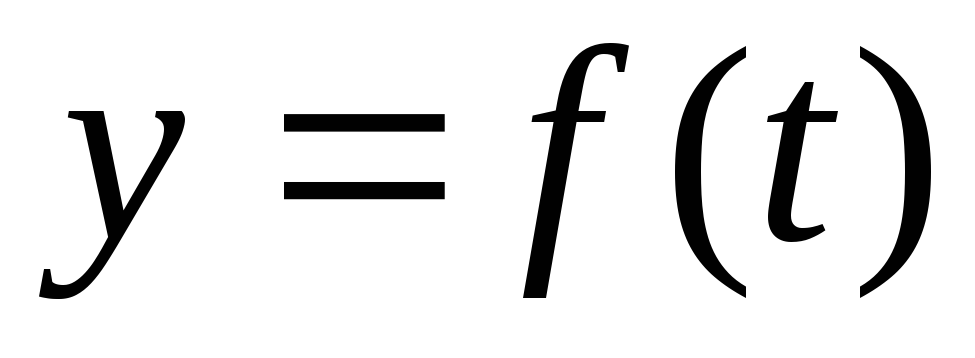 в момент
времени
в момент
времени  равен
производной (мгновенной скорости
изменения функции), деленной на значение
функции в этот момент. Эта формула
выражает экономический смысл производной.
равен
производной (мгновенной скорости
изменения функции), деленной на значение
функции в этот момент. Эта формула
выражает экономический смысл производной.
Замечание
Пусть
предел в определении 1 равен +∞ (или –
∞). В этом случае говорят, что производная 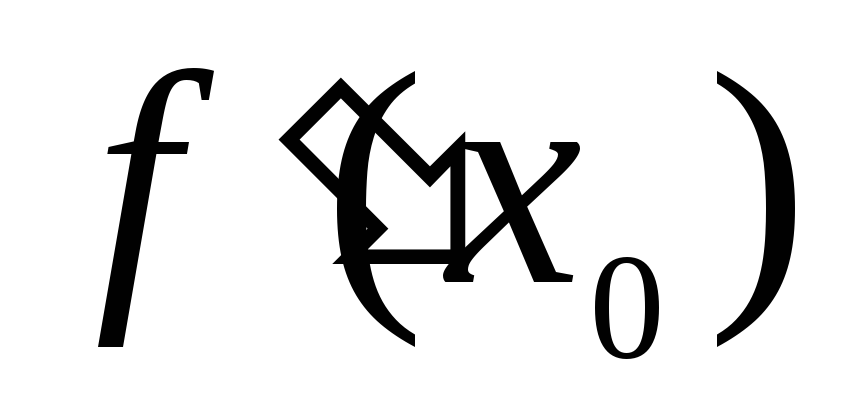 =+∞
(или – ∞).
=+∞
(или – ∞).
В определении производной предполагалось, что предел
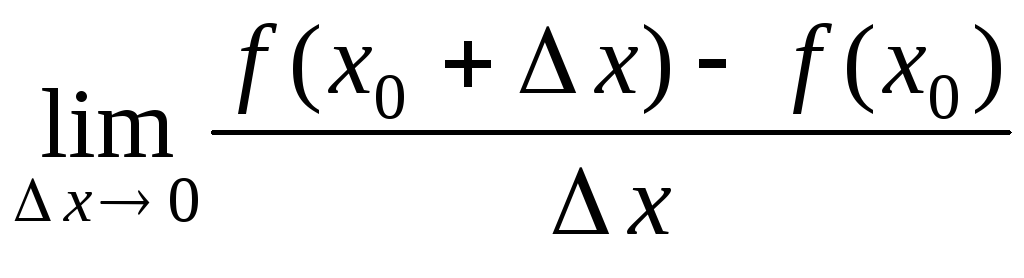
не
зависит от знака приращения 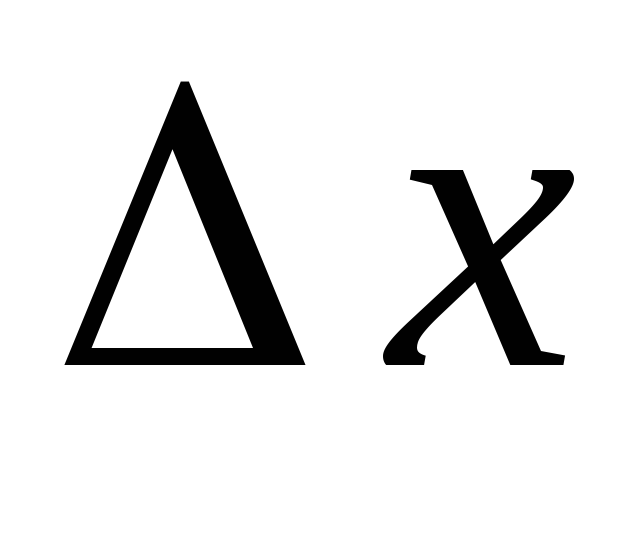 при стремлении
при стремлении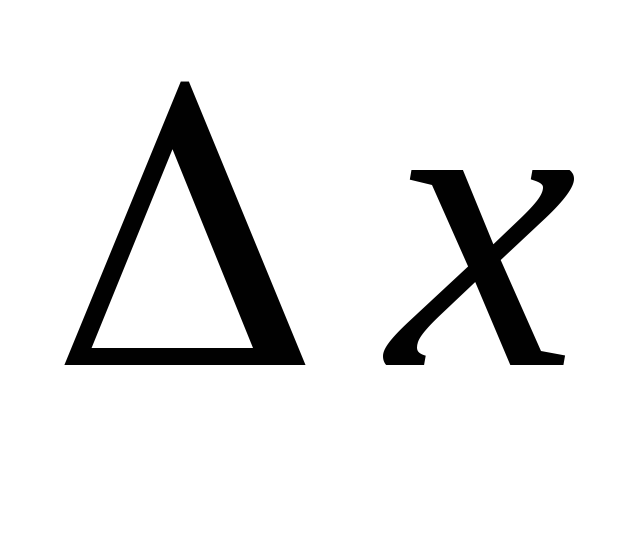 к нулю. Если же в указанном определении
потребовать, чтобы
к нулю. Если же в указанном определении
потребовать, чтобы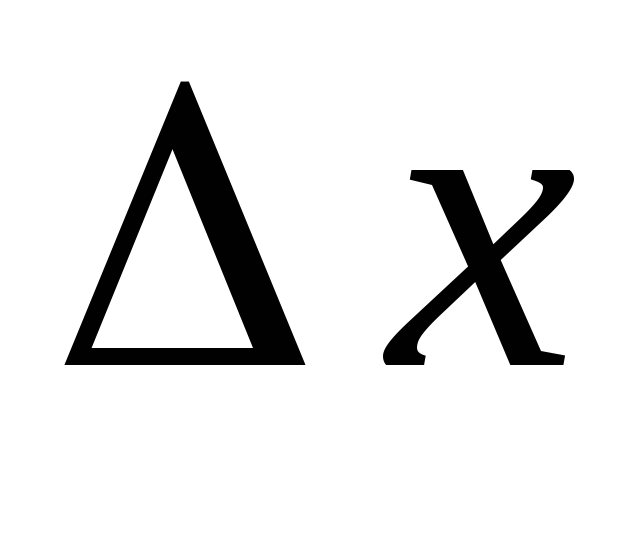 было только одного знака, то придем к
понятию односторонней производной.
было только одного знака, то придем к
понятию односторонней производной.
Правой
производной функции 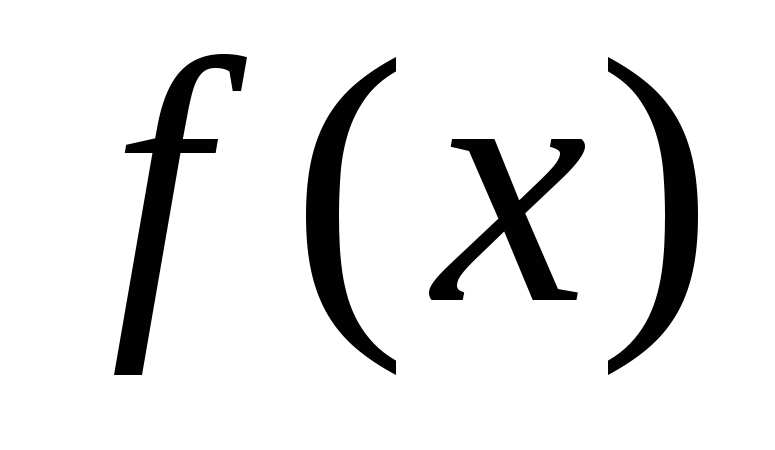 в точке
в точке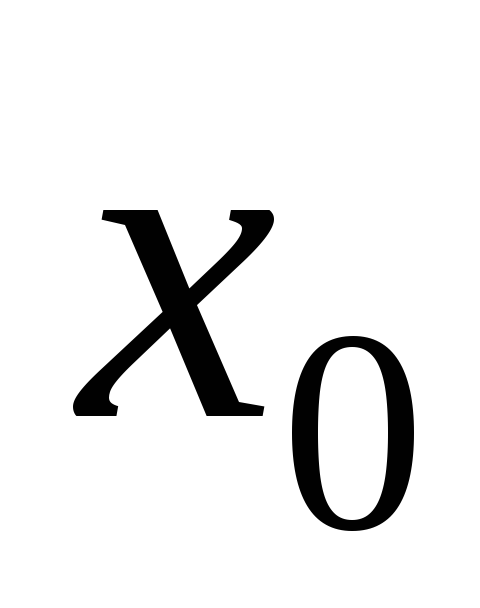 называется предел
называется предел
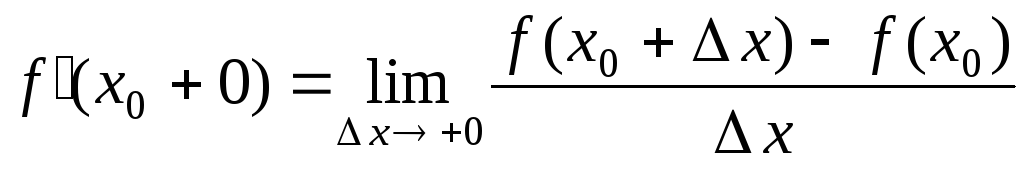 ,
,
если
он существует. Аналогично определяется левая
производная 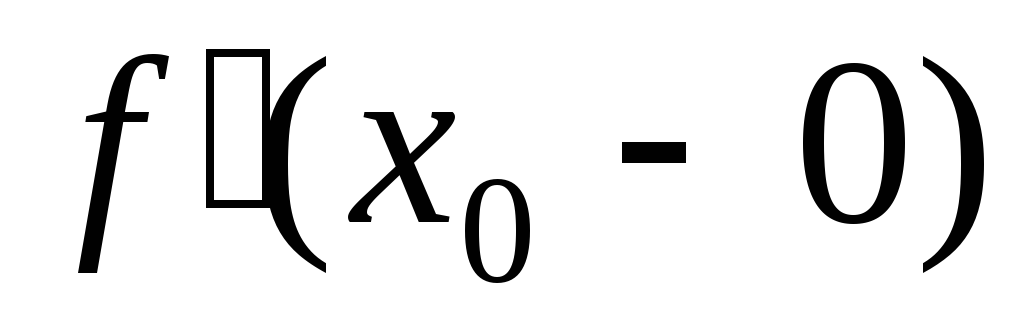 .
Правая и левая производные называются
ееодносторонними производными.
.
Правая и левая производные называются
ееодносторонними производными.
Ясно,
что если функция 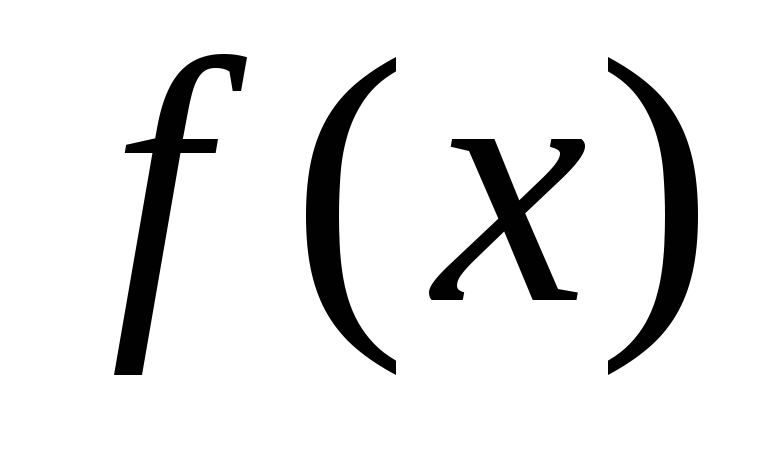 имеет в точке
имеет в точке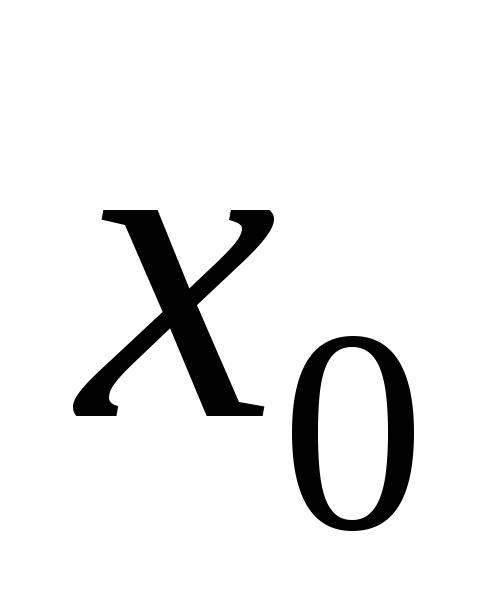 обычную производную, то она имеет и обе
односторонние производные и все они
совпадают. В то же время функция может
иметь односторонние производные и не
иметь производной
обычную производную, то она имеет и обе
односторонние производные и все они
совпадают. В то же время функция может
иметь односторонние производные и не
иметь производной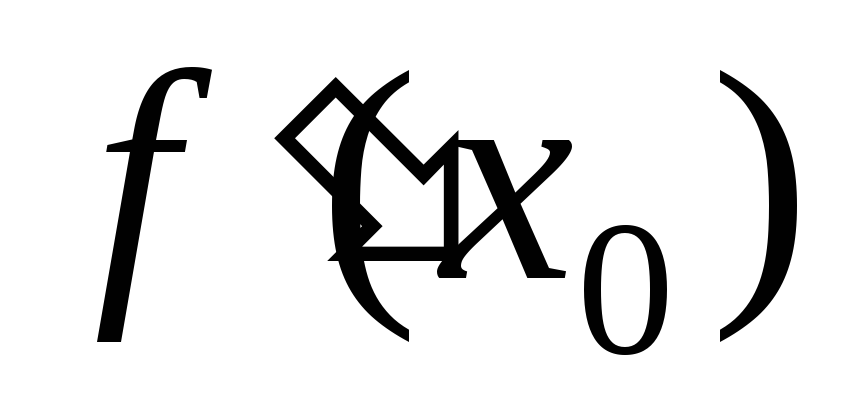 .
Например, ранее упомянутая функция
.
Например, ранее упомянутая функция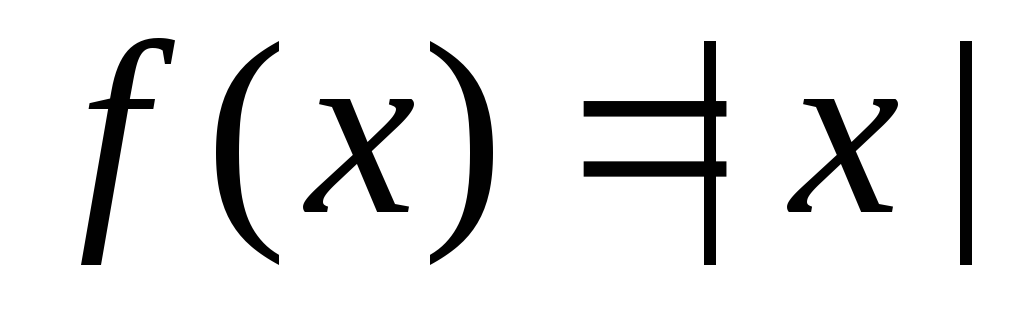 в точке
в точке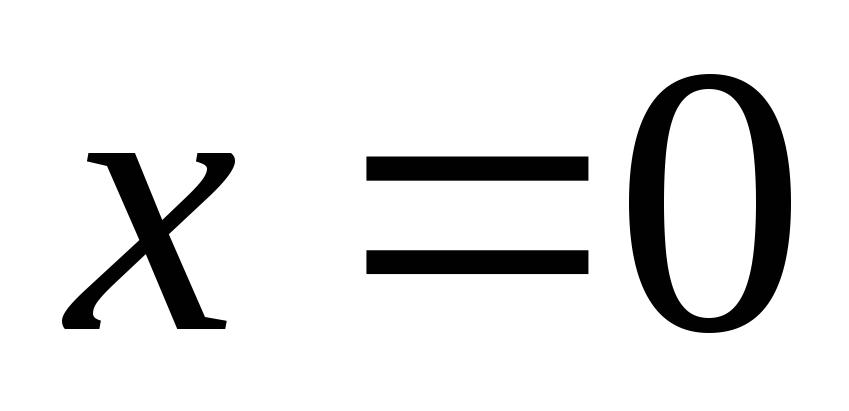 имеет односторонние производные
имеет односторонние производные
Если для любого достаточно малого Δx выполняется равенство
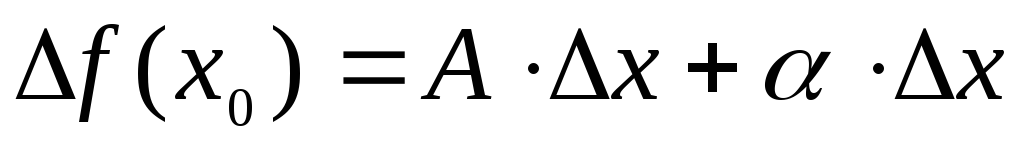 ,
,
где A постоянная, α бесконечно малая функция при Δx→0, то функция f(x) называется дифференцируемой в точке x0 (см. рис. 1а). Величина A∙Δx называется дифференциалом функции f(x) в точке x0 и обозначается символом df(x0). Дифференциал функции y = f(x) в точке x обозначается символом dy.
Если
функция 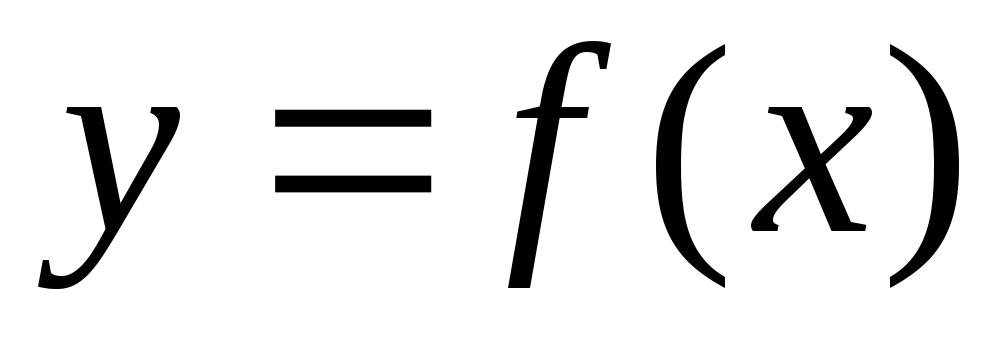 дифференцируема в точке
дифференцируема в точке 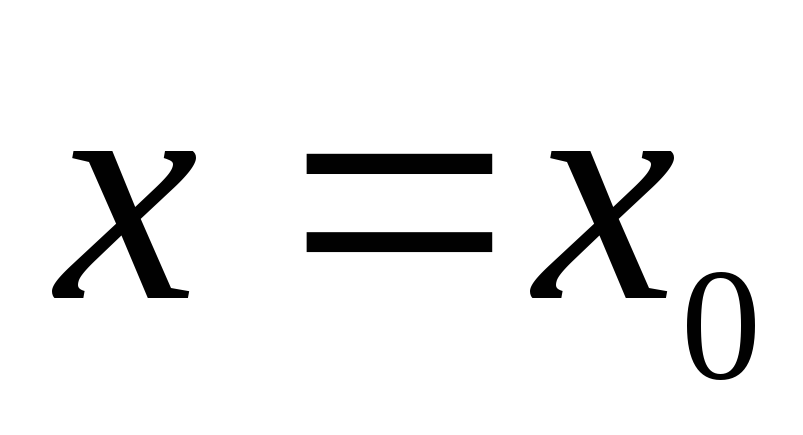 , то замена
этой функции линейной функцией
, то замена
этой функции линейной функцией 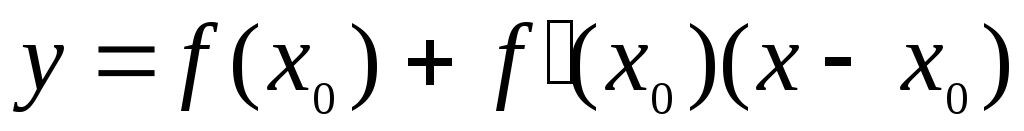 называетсялинеаризацией
функции
называетсялинеаризацией
функции 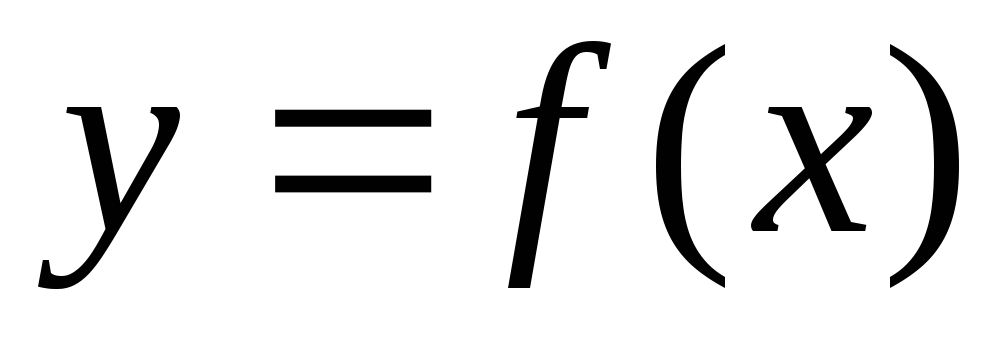 вблизи точки
вблизи точки 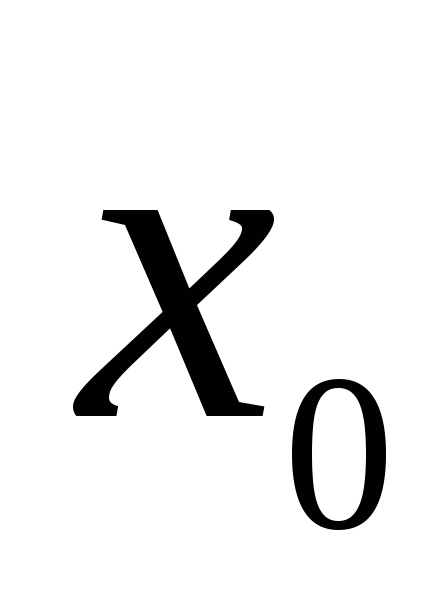 .
Сказанное означает, что при линеаризации
функции вблизи точки
.
Сказанное означает, что при линеаризации
функции вблизи точки 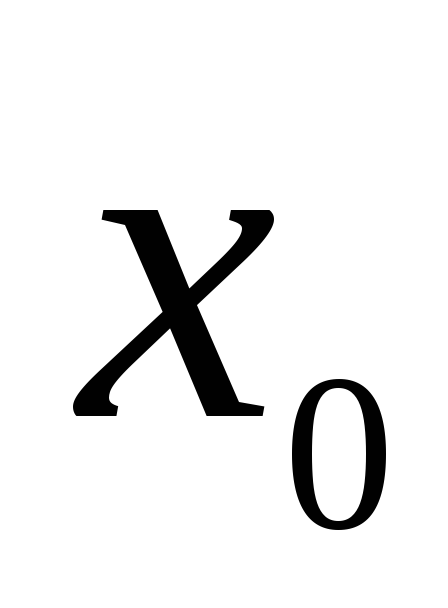 происходит
замена графика функции ее касательной.
происходит
замена графика функции ее касательной.
ТЕОРЕМА 1. Функция y = f(x) имеет в точке x (конечную) производную в том и только в том случае, если она дифференцируема в этой точке. При этом верно равенство
dy = f ′ (x) dx. (1)
В силу этой теоремы выражения “функция дифференцируема» и «функция имеет производную» означают одно и то же.
Пример (правило семидесяти)
Если
при перерасчете суммы вклада банк
использует сложные проценты, то время
удвоения первоначальной суммы вклада
вычисляется по формуле 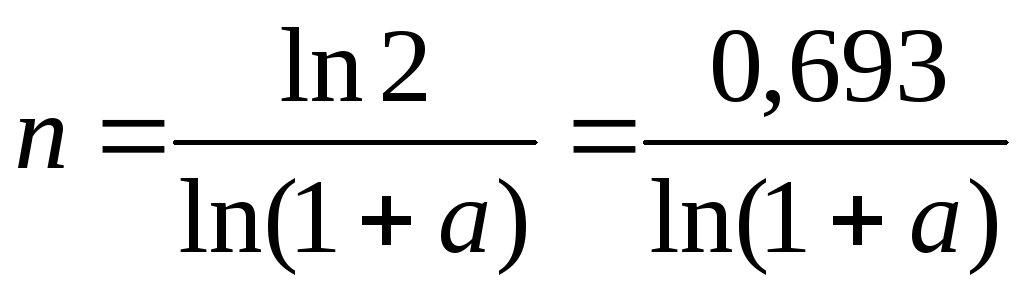 .
Если, ставка процента низкая, то для
оценки времени удвоения можно использовать
формулу линеаризации
.
Если, ставка процента низкая, то для
оценки времени удвоения можно использовать
формулу линеаризации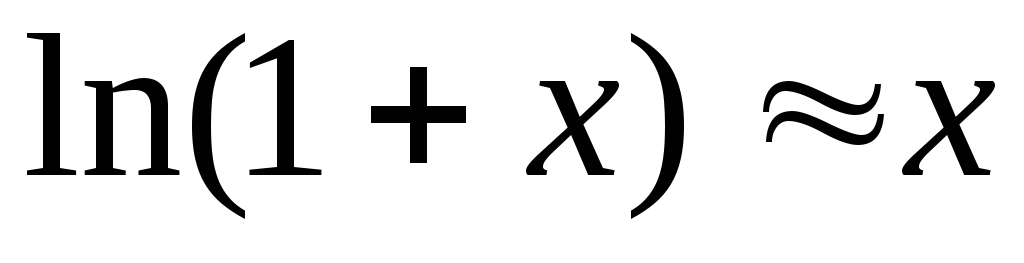 ,
которая приводит к следующему результату:
,
которая приводит к следующему результату:
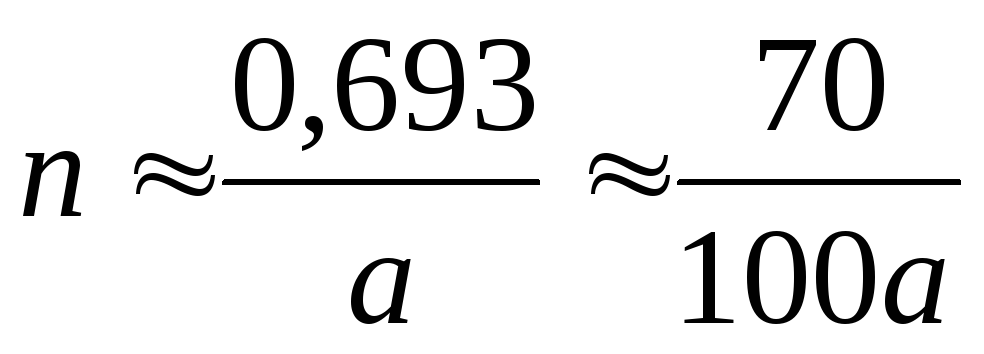 .
.
Итак,
при малой процентной ставке время
удвоения вклада приблизительно равно
дроби, в числителе которой ‑ число
семьдесят, а в знаменателе ‑
относительный прирост вклада, выраженный
в процентах (100 ).
Эта оценка в финансовом менеджменте
известна какправило
семидесяти. Если,
например, банк ежемесячно начисляет 5%
от суммы вклада (a = 0,05),
то время удвоения примерно равно
70/5=14,что хорошо согласуется с точным
результатом
).
Эта оценка в финансовом менеджменте
известна какправило
семидесяти. Если,
например, банк ежемесячно начисляет 5%
от суммы вклада (a = 0,05),
то время удвоения примерно равно
70/5=14,что хорошо согласуется с точным
результатом 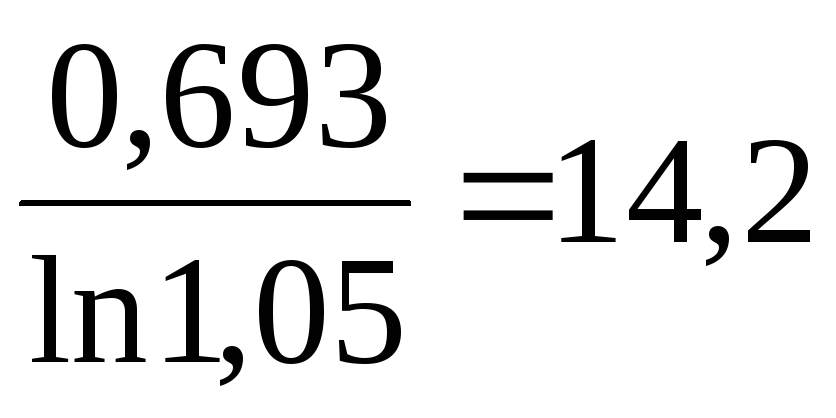 .
.
Применение производной к исследованию функций
Одними из основных аспектов применения производной к исследованию функции являются: исследование функции на возрастание и убывание, исследование функций на выпуклость и вогнутость, нахождение точек экстремума функции, а также наибольшего и наименьшего значения функции. Рассмотрим их отдельно.
Экстремумы функции
Определение 1
Точки $x_0$ называются точками экстремума функции, если они являются точками максимума и минимума для функции $f(x)$.
Определение 2
$x_0$ называется критической точкой функции $f(x)$, если:
1) $x_0$ — внутренняя точка области определения;
2) $f'(x_0)=0$ или не существует.
Для исследования функции на существование точек экстремума, мы будем использовать теорему о достаточных условиях существования экстремума:
Теорема 1
Достаточное условие экстремума
Пусть точка $x_0$ является критической для функции $y=f(x)$ и лежит в интервале $(a,b)$. Пусть на каждом интервале $\left(a,x_0\right)\ и\ (x_0,b)$ производная $f'(x)$ существует и сохраняет постоянный знак. Тогда:
1) Если на интервале $(a,x_0)$ производная $f’\left(x\right)>0$, а на интервале $(x_0,b)$ производная $f’\left(x\right)
2) Если на интервале $(a,x_0)$ производная $f’\left(x\right)0$, то точка $x_0$ — точка минимума для данной функции.
3) Если и на интервале $(a,x_0)$, и на интервале $(x_0,b)$ производная $f’\left(x\right)>0$ или производная $f’\left(x\right)
Схема исследования функции на экстремум
1) Найти область определения функции $f(x)$;
2) Найти производную $f'(x)$;
3) Найти точки, в которых выполняется равенство $f’\left(x\right)=0$;
4) Найти точки, в которых $f'(x)$ не существует;
5) Отметить на координатной прямой все найденные точки и область определения данной функции;
6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;
7) Сделать выводы о наличии максимумов и минимумов на каждом промежутке, используя теорему 2.
Монотонность функции
Определение 3
Функция $y=f(x)$, определенная на промежутке $X$, называется возрастающей, если для любых точек $x_1,x_2\in X$ при $x_1
Определение 4
Функция $y=f(x)$, определенная на промежутке $X$, называется возрастающей, если для любых точек $x_1,x_2\in X$ при $x_1f(x_2)$.
Определение 5
Функция $y=f(x)$, определенная на промежутке $X$, называется неубывающей, если для любых точек $x_1,x_2\in X$ при $x_1
Определение 6
Функция $y=f(x)$, определенная на промежутке $X$, называется невозрастающей, если для любых точек $x_1,x_2\in X$ при $x_1
Схема исследования функции на возрастание и убывание
1) Найти область определения функции $f(x)$;
2) Найти производную $f'(x)$;
3) Найти точки, в которых выполняется равенство $f’\left(x\right)=0$;
4) Найти точки, в которых $f'(x)$ не существует;
5) Отметить на координатной прямой все найденные точки и область определения данной функции;
6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;
7) Сделать вывод: на промежутках, где $f’\left(x\right)0$ функция возрастает.
Наибольшее и наименьшее значение функции
Определение 7
Функция $y=f(x)$, определенная на промежутке $X$, достигает своего наибольшего значения, если существует точка $x_0\in X$, такая, что для всех $x\in X$ выполняется неравенство
\[f\left(x\right)\le f(x_0)\]Определение 8
Функция $y=f(x)$, определенная на промежутке $X$, достигает своего наименьшего значения, если существует точка $x_0\in X$, такая, что для всех $x\in X$ выполняется неравенство
\[f\left(x\right)\ge f(x_0)\]Схема нахождения наибольшего и наименьшего значений функции $f(x)$ на отрезке $[a,b]$
1) Найти производную $f'(x)$;
2) Найти точки, в которых производная $f’\left(x\right)=0$;
3) Найти точки, в которых производная $f'(x)$ не существует;
4) Выбрать из полученных в пунктах 2 и 3 точек те, которые принадлежат отрезку $[a,b]$;
5) Вычислить значение функции в точках, полученных в пункте 4, а также на концах отрезка $[a,b]$;
6) Выбрать из полученных значений наибольшее и наименьшее значение.
Выпуклость и вогнутость функции
Определение 9
Функция $y=f(x)$, определенная на промежутке $X$, называется выпуклой, если для любых точек $x_1,x_2\in X$ выполняется неравенство
\[f\left(\frac{x_1+x_2}{2}\right)\le \frac{{f(x}_1)+f(x_2)}{2}\]Определение 10
Функция $y=f(x)$, определенная на промежутке $X$, называется вогнутой, если для любых точек $x_1,x_2\in X$ выполняется неравенство
\[f\left(\frac{x_1+x_2}{2}\right)\ge \frac{{f(x}_1)+f(x_2)}{2}\]Замечание 1
Если в определении выпуклости и вогнутости функции нестрогие знаки заменить на строгие, то мы получим, соответственно, определение строго выпуклой и строго вогнутой функции.
Схема исследования функции на возрастание и убывание
1) Найти область определения функции $f(x)$;
2) Найти вторую производную $f»(x)$;
3) Найти точки, в которых выполняется равенство $f»\left(x\right)=0$;
4) Найти точки, в которых $f»(x)$ не существует;
5) Определить знак производной $f»(x)$ на каждом получившемся промежутке;
6) Сделать вывод: на промежутках, где $f»\left(x\right)0$ функция вогнута.
Задачи на применение производной
Пример 1
Исследовать функцию на возрастание, убывание, выпуклость, вогнутость и наличие точек максимумов и минимумов:$f(x)=\frac{x^2-2x+1}{4}$
Решение:
1) Область определения — все действительные числа;
2) $f’\left(x\right)=\frac{2x-2}{4}=\frac{x-1}{2}$;
3) $f’\left(x\right)=0$;
\[\frac{x-1}{2}=0\] \[x=1\]4) $f'(x)$ существует во всех точках области определения;
5) Координатная прямая:

Рисунок 1.
6) Определить знак производной $f'(x)$ на каждом промежутке:
\[f’\left(x\right) >0,\ при\ (1,+\infty )\] \[f’\left(x\right)7) Изобразим все на одном рисунке:
Рисунок 2.
Получаем:
Функция убывает, при $\left(-\infty ,1\right)$, функция возрастает, при $(1,+\infty )$.
Точка $x=1$ — точка минимума, точки максимума нет.
8) $f»\left(x\right)=\frac{1}{2}>0$
Функция вогнута на всей области определения.
Методическая разработка по алгебре (11 класс) на тему: Применение производной
Тема: « Применение производной»
Цели урока: — обобщить и систематизировать знания, умения и навыки
учащихся по применению производной;
— совершенствовать навыки решения задач с применением производной;
— развивать логическое мышление;
— формировать навыки самоконтроля.
Оборудование: интерактивная доска, карточки с разноуровневыми заданиями, ОК « Применение производной».
Ход урока: 1. Организационный момент.
Учитель сообщает учащимся тему урока, цель и поясняет, что во время урока учащиеся могут использовать раздаточный материал, который находится у них на партах (ОК), задания для обобщения полученных знаний, они выбирают самостоятельно уровня усвоения изученной темы:
А «3» — желтая карточка
В «4» — синяя карточка
С «5» — красная карточка
Проверяя выполненную работу учащиеся самостоятельно оценивают свою работу.
2. Повторение теоретического материала.
Какие исследования можно проводить с использование производной?
-Составление касательной к графику функции
— Нахождение промежутков возрастания и убывания функции
— Определение критических точек функции. Нахождение экстремумов функции
— Нахождение наибольшего и наименьшего значения функции на отрезке ( интервале)
— Решение некоторых текстовых задач
— Проведение полного исследования функции, для более точного построения графика. ( Слайд 1)
Применение производной в высшей математике для определения выпуклости и вогнутости графика функции, вычислении производных высших порядков.
3. Обобщение полученных знаний.
1. Составление графика уравнения касательной к графику функцииf(x), проходящей через точку с абсциссой х0.
а) f(x) = х3 + х – 5 х0 = 1
(один ученик у доски с подробным объяснением, остальные в своих тетрадях)
Что позволяет определить значение производной в точке х0?
б) работа в рабочих тетрадях по карточкам с разноуровневым заданием с последующей проверкой ( Слайд 2)
2. Нахождение промежутков возрастания и убывания функции.
Один ученик ( из группы А)с места воспроизводит план нахождения промежутков возрастания и убывания функции.
От чего зависит возрастание и убывание функции на промежутке?
а) Найти промежутки монотонности функции f(x) = x4 — 4×3 +10
(один ученик у доски с подробным объяснением , остальные в своих тетрадях)
б) работа в рабочих тетрадях по дифференцированным карточкам с последующей проверкой ( Слайд 3)
3. Определение критических точек функции.
Какие точки называются критическими точками? Какая точка называется точкой максимума , точкой минимума? Перечислите основные этапы нахождения критических точек.
а) Найдите критические точки функции и вычислите экстремумы функции
f(x) = x4+ 2×2 + 1 (один ученик у доски с подробным объяснением , остальные в своих тетрадях)
б) самостоятельная работа по дифференцированным карточкам с последующей проверкой ( Слайд 4)
4.Нахождение наибольшего и наименьшего значения функции на отрезке.
Один ученик с места воспроизводит план нахождения наибольшего и наименьшего значения функции на отрезке.
а) найдите сумму наибольшего и наименьшего значения функции f(x) = 2×4 -8x на отрезке[ -2; 1]
(один ученик у доски с подробным объяснением, остальные в своих тетрадях) б) самостоятельная работа по дифференцированным карточкам с последующей проверкой ( Слайд 5)
4.Применение производной в ЕГЭ.
Выполнение заданий Слайда 6 с последующей проверкой.
5.Итог урока
Объявить и прокомментировать оценки учащихся работающих у доски.
Все учащиеся выставляют оценки на полях своих рабочих тетрадей и сдают тетради на проверку и подтверждение оценок с последующим выставлением в журнал.
6.Домашнее задание.
Задание б) из карточек разноуровневого задания.
Применение производной для исследования функций на монотонность и экстремумы. Алгебра, 10 класс: уроки, тесты, задания.
| 1. |
Исследование свойств функции
Сложность: лёгкое |
4 |
| 2. |
Определение знака производной
Сложность: лёгкое |
2 |
| 3. |
Точки экстремума
Сложность: лёгкое |
1 |
| 4. |
Интервалы монотонности дробной функции
Сложность: среднее |
0,5 |
| 5. |
Монотонность функции в зависимости от параметра
Сложность: среднее |
3 |
| 6. |
Характер монотонности
Сложность: среднее |
4 |
| 7. |
Точки экстремума
Сложность: среднее |
2 |
| 8. |
Производная в доказательстве неравенства
Сложность: сложное |
5 |
| 9. |
Характер монотонности заданной функции
Сложность: сложное |
3 |
| 10. |
Нахождение параметра из отрезка убывания функции
Сложность: сложное |
4 |