Действия с нулём

В математике число ноль занимает особое место. Дело в том, что оно, по сути дела, означает «ничто», «пустоту», однако его значение действительно трудно переоценить. Для этого достаточно вспомнить хотя бы то, что именно с нулевой отметки начинается отсчет координат положения точки в любой системе координат.

 

Ноль широко используется в десятичных дробях для определения значений «пустых» разрядов, находящихся как до, так и после запятой. Кроме того, именно с ним связано одно из основополагающих правил арифметики, гласящее о том, что на ноль делить нельзя. Его логика, собственно говоря, проистекает из самой сути этого числа: действительно, невозможно представить, чтобы некая отличное от него значение (да и само оно – тоже) было разделено на «ничто».

Примеры вычисления

С нулем осуществляются все арифметические действия, причем в качестве его «партнеров» по ним могут использоваться целые числа, обычные и десятичные дроби, причем все они могут иметь как положительное, так и отрицательное значение. Приведем примеры их осуществления и некоторые пояснения к ним.

Сложение

При прибавлении нуля к некоторому числу (как целому, так и к дробному, как к положительному, так и к отрицательному) его значение остается абсолютно неизменным.

Пример 1

Двадцать четыре плюс ноль равняется двадцать четыре.

24 + 0 = 24

Пример 2

Семнадцать целых три восьмых плюс ноль равняется семнадцать целых три восьмых.

Вычитание

При вычитании нуля из некоторого числа (целого, дробного, положительного или отрицательного) оставляет его полностью неизменным.

Пример 1

Две тысячи сто пятьдесят два минус ноль равняется две тысячи сто пятьдесят два.

2152

– 0 = 2152

Пример 2

Сорок одна целая три пятых минус ноль равняется сорок одна целая три пятых.

Умножение

При умножении любого числа (целого, дробного, положительного или отрицательного) на ноль получается ноль.

Пример 1

Пятьсот восемьдесят шесть умножить на ноль равняется ноль.

586 × 0 = 0

Пример 2

Ноль умножить на сто тридцать пять целых шесть седьмых равняется ноль.

0 × 135 = 0

Пример 3

Ноль умножить на ноль равняется ноль.

0 × 0 = 0

Деление

Правила деления чисел друг на друга в тех случаях, когда одно из них представляет собой ноль, различаются в зависимости от того, в какой именно роли выступает сам ноль: делимого или делителя?

В тех случаях, когда ноль представляет собой делимое, результат всегда равен ему же, причем вне зависимости от значения делителя.

Пример 1

Ноль разделить на двести шестьдесят пять равняется ноль.

0 : 265 = 0

Пример 2

Ноль разделить на семнадцать пятьсот девяносто шестых равняется ноль.

Делить ноль на ноль согласно правилам математики нельзя. Это означает, что при совершении такой процедуры частное является неопределенным. Таким образом, теоретически оно может представлять собой абсолютно любое число.

0 : 0 = 8 ибо 8 × 0 = 0

В математике такая задача, как деление нуля на ноль, не имеет никакого смысла, поскольку ее результат представляет собой бесконечное множество. Это утверждение, однако, справедливо в том случае, если не указаны никакие дополнительные данные, которые могут повлиять на итоговый результат.

Таковые, при их наличии, должны состоять в том, чтобы указывать на степень изменения величины как делимого, так и делителя, причем еще до наступления того момента, когда они превратились в ноль. Если это определено, то такому выражению, как ноль разделить на ноль, в подавляющем большинстве случаев можно придать некий смысл.

simple-math.ru

Деление на ноль. Увлекательная математика :: SYL.ru

Число 0 можно представить, как некую границу, отделяющую мир реальных чисел от мнимых или отрицательных. Благодаря двусмысленному положению, многие операции с этой числовой величиной не подчиняются математической логике. Невозможность деления на нуль – яркий тому пример. А разрешенные арифметические действия с нулем могут быть выполнены с помощью общепринятых определений.

История нуля

Ноль является точкой отсчета во всех стандартных системах исчисления. Европейцы стали использовать это число сравнительно недавно, но мудрецы Древней Индии пользовались нулем за тысячу лет до того, как пустое число стало регулярно использоваться европейскими математиками. Ещё раньше индийцев ноль являлся обязательной величиной в числовой системе майя. Этот американский народ использовал двенадцатеричную систему исчисления, а нулем у них начинался первый день каждого месяца. Интересно, что у майя знак, обозначающий «ноль», полностью совпадал со знаком, определяющим «бесконечность». Таким образом, древние майя делали вывод о тождественности и непознаваемости этих величин.

Математические действия с нулем

Стандартные математические операции с нулем можно свести к нескольким правилам.

Сложение: если к произвольному числу добавить ноль, то оно не изменит своего значения (0+x=x).

Вычитание: при вычитании нуля из любого числа значение вычитаемого остается неизменным (x-0=x).

Умножение: любое число, умноженное на 0, дает в произведении 0 (a*0=0).

Деление: ноль можно разделить на любое число, не равное нулю. При этом значение такой дроби будет 0. А деление на ноль запрещено.

Возведение в степень. Это действие можно выполнить с любым числом. Произвольное число, возведенное в нулевую степень, даст 1 (x⁰ =1).

Ноль в любой степени равен 0 (0^а=0).

При этом сразу возникает противоречие: выражение 0⁰ не имеет смысла.

Парадоксы математики

О том, что деление на ноль невозможно, многие знают со школьной скамьи. Но объяснить причину такого запрета почему-то не получается. В самом деле, почему формула деления на ноль не существует, а вот другие действия с этим числом вполне разумны и возможны? Ответ на этот вопрос дают математики.

Все дело в том, что привычные арифметические действия, которые школьники изучают в начальных классах, на самом деле далеко не так равноправны, как нам кажется. Все простые операции с числами могут быть сведены к двум: сложению и умножению. Эти действия составляют суть самого понятия числа, а остальные операции строятся на использовании этих двух.

Сложение и умножение

Возьмем стандартный пример на вычитание: 10-2=8. В школе его рассматривают просто: если от десяти предметов отнять два, останется восемь. Но математики смотрят на эту операцию совсем по-другому. Ведь такой операции, как вычитание, для них не существует. Данный пример можно записать и другим способом: х+2=10. Для математиков неизвестная разность – это просто число, которое нужно добавить к двум, чтобы получилось восемь. И никакого вычитания здесь не требуется, нужно просто найти подходящее числовое значение.

Умножение и деление рассматриваются так же. В примере 12:4=3 можно понять, что речь идет о разделении восьми предметов на две равные кучки. Но в действительности это просто перевернутая формула записи 3х4=12.Такие примеры на деление можно приводить бесконечно.

Примеры на деление на 0

Вот тут и становится понемногу понятным, почему нельзя делить на ноль. Умножение и деление на ноль подчиняется своим правилам. Все примеры на деление этой величины можно сформулировать в виде 6:0=х. Но это же перевернутая запись выражения 6 * х=0. Но, как известно, любое число, умноженное на 0, дает в произведении только 0. Это свойство заложено в самом понятии нулевой величины.

Выходит, что такого числа, которое при умножении на 0 дает какую-либо осязаемую величину, не существует, то есть данная задача не имеет решения. Такого ответа бояться не следует, это естественный ответ для задач такого типа. Просто запись 6:0 не имеет никакого смысла, и она ничего не может объяснить. Кратко говоря, это выражение можно объяснить тем самым бессмертным «деление на ноль невозможно».

Существует ли операция 0:0? Действительно, если операция умножения на 0 законна, можно ли ноль разделить на ноль? Ведь уравнение вида 0х 5=0 вполне легально. Вместо числа 5 можно поставить 0, произведение от этого не поменяется.

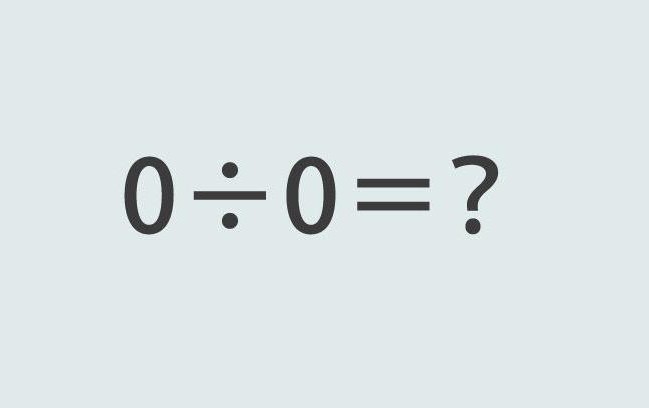
Действительно, 0х0=0. Но поделить на 0 по-прежнему нельзя. Как было сказано, деление – это просто обратная операция умножения. Таким образом, если в примере 0х5=0, нужно определить второй множитель, получаем 0х0=5. Или 10. Или бесконечность. Деление бесконечности на ноль — как вам это понравится?

Но если в выражение подходит любое число, то оно не имеет смысла, мы не можем из бесконечного множества чисел выбрать какое-то одно. А раз так, это значит и выражение 0:0 не имеет смысла. Получается, что на ноль нельзя делить даже сам ноль.

Высшая математика

Деление на ноль — это головная боль для школьной математики. Изучаемый в технических вузах математический анализ немного расширяет понятие задач, которые не имеют решения. Например, к уже известному выражению 0:0 добавляются новые, которые не имеют решения в школьных курсах математики:

• бесконечность, разделенная на бесконечность: ∞:∞;
• бесконечность минус бесконечность: ∞−∞;
• единица, возведенная в бесконечную степень: 1^∞;
• бесконечность, умноженная на 0: ∞*0;
• некоторые другие.

Элементарными методами решить такие выражения невозможно. Но высшая математика благодаря дополнительным возможностям для ряда подобных примеров дает конечные решения. Особенно это видно в рассмотрении задач из теории пределов.

Раскрытие неопределенности

В теории пределов значение 0 заменяется условной бесконечно малой переменной величиной. А выражения, в которых при подставлении нужного значения получается деление на ноль, преобразовываются. Ниже представлен стандартный пример раскрытия предела при помощи обычных алгебраических преобразований:

Как видно в примере, простое сокращение дроби приводит ее значение к вполне рациональному ответу.

При рассмотрении пределов тригонометрических функций их выражения стремятся свести к первому замечательному пределу. При рассмотрении пределов, в которых знаменатель обращается в 0 при подставлении предела, используют второй замечательный предел.

Метод Лопиталя

В некоторых случаях пределы выражений можно заменить пределом их производных. Гийом Лопиталь – французский математик, основоположник французской школы математического анализа. Он доказал, что пределы выражений равны пределам производных этих выражений. В математической записи его правило выглядит следующим образом.

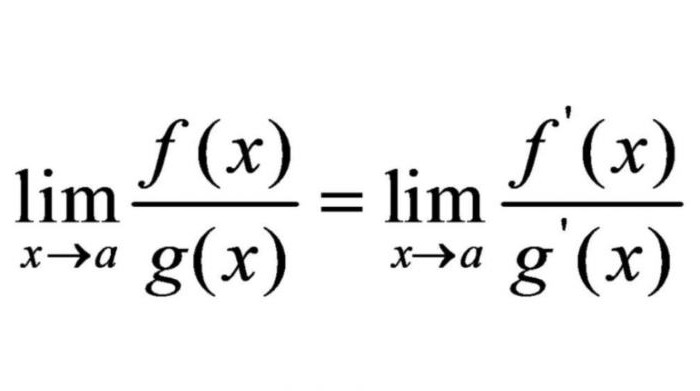
В настоящее время метод Лопиталя с успехом применяется при решении неопределенностей типа 0:0 или ∞:∞.

www.syl.ru

Решение примеров с нулем

Цель:

• Закрепить умение решать примеры с нулем.
• Работать над развитием логического мышления.
• Воспитывать самостоятельность.
• Прививать интерес к предмету.

Оборудование:

1. знаки + – : х ,
2. карточки с геометрическими заданиями,
3. табличка для гимнастики глаз, солнышко, круги.

Ход урока

1. Организационный момент. (Эмоциональный настрой на урок.)

Я желаю тебе сегодня добра,
Ты желаешь мне сегодня добра.
Если тебе будет трудно
Я помогу!

2. Сообщение темы и цели урока.

Сегодня на уроке будем решать примеры с нулем. Работать будем под девизом:

“Давайте, ребята, учиться считать:
Делить, умножать, прибавлять, вычитать (хором, учитель показывает на знаки).
Запомните, все, что без точного счета,
Не сдвинется с места любая работа”.

3. Вступительная беседа.

Загадка.

Пришла, улыбнулась –
Утихли метели
Позванивать стал колокольчик капели (весна).

– По каким признакам узнали?

– Назовите еще признаки весны.

Посмотрите, к нам в гости тоже пришло солнышко. Оно улыбается, радуется весне.

– Из каких геометрических фигур состоит солнышко? (Круг.)

– Какой первый весенний праздник приближается ? (8 Марта.)

– Подумайте, какая получится цифра, если взять два круга ? (8.)

4. Устный счет.

1) 16, 50, 2, 63, 80, 48, 76, 8, 100

– Показать однозначные числа.

– Показать двузначные числа.

– Круглые десятки.

– Числа, полученные при умножении на 8 (16, 48, 8, 80 )

– Числа !6:, 48, 8, 80 уменьшить в 8 раз.

2)

8…0 = 8 8…0 = 0 8…0 = 8

5. Работа в тетрадях.

1) Чистописание: 8 (прописать 5 раз, подчеркнуть лучшую).

2) Математический диктант.

– Записать соседей числа 8.

– Число, в котором 8 десятков.

– Число, состоящее из 8 десятков и 8 единиц.

– Любое двузначное число, оканчивающееся 8.

– Любое двузначное число, где первое число 8.

3) Задача. М. Н. Перова. Математика 4 кл. стр. 142, № 27 (Показ фартуков, которые шьют в школе.)

– Чтение детьми.

– Чтение учителем.

– Краткая запись.

Д. – 80 ф.

Я. – ? в 8 раз меньше

Сколько всего фартуков сшили ?

– Можем сразу найти, сколько сшили всего фартуков? (Нет.)

– Почему? (Не знаем сколько для яслей.)

– Сможем найти сколько сшили для яслей? (Да.)

– Каким действием? (:)

– А теперь сможем ответить на вопрос задачи? (Да.)

– Каким действием? (+ )

– Какая задача? (Составная.)

1) 80 ф. : 8 = 10 ф. – для яслей

2) 80 ф. + 10 ф.= 90 ф.

Ответ: 90 фартуков всего.

6. Физминутка.

Мы по городу гуляли,
Свежим воздухом дышали,

пауза дышим
Собирали мы цветы
Небывалой красоты. улыбнулись

7. Гимнастика для глаз.

– На что похожа фигура? (8.)

– Проследить путь птички только глазами. (Учитель указкой показывает движения.)

8. Примеры с нулем. Стр . 140, № 13.

(75 – 13) х 0 = 0 (48 – 39 ) х 0 = 0 0 : (84 – 79 ) = 0

0 х 7 + 78 = 78 0 : (28 : 4 ) = 0 9 х 0 + 31 = 31

 Самостоятельно.

2 х 0 + 42 = 42

0 х 6 + 37 = 37

0 х 4 + 98 = 98

– Найти примеры с одинаковым ответом и взять их в кружок.

9. Геометрический материал.

– Сколько кругов всего? (9 )

– Сколько пересекающихся? (8 )

Самостоятельно (у детей карточки ).

– Заштриховать круги, находящиеся внутри квадрата.

10. Итог урока.

Нарисовать в тетради цветочек, состоящий из двух восьмерок.

urok.1sept.ru

Примеры от 0 до 10 — методическая рекомендация. Математика, 1 класс.

1.	Домино	1 вид — рецептивный	лёгкое	1 Б.	Сложение двух чисел с использованием картинки, до 10.
2.	Число 0	2 вид — интерпретация	лёгкое	3 Б.	Разность двух одинаковых чисел, вычитание 0, сложение числа и 0, до 10.
3.	Переместительный закон	2 вид — интерпретация	лёгкое	2 Б.	Применение переместительного закона.
4.	Сумма двух одинаковых слагаемых	2 вид — интерпретация	лёгкое	2 Б.	Сумма двух одинаковых слагаемых, до 10.
5.	Примеры с одинаковыми ответами	2 вид — интерпретация	среднее	4 Б.	Выбор примеров с одинаковыми ответами, до 6.
6.	Выбор примеров	2 вид — интерпретация	среднее	4 Б.	Выбор примеров, в которых значения сумм равны данному числу, до 7.
7.	Заполнение таблицы (сумма)	2 вид — интерпретация	среднее	4 Б.	Вычисление двух сумм, до 8.
8.	Пропущенное число (сумма)	2 вид — интерпретация	среднее	2 Б.	Нахождение первого слагаемого, до 10.
9.	Пример из трёх чисел	2 вид — интерпретация	среднее	3 Б.	Пример из трёх чисел, до 9.
10.	Пропущенное число (разность)	2 вид — интерпретация	среднее	2 Б.	Пропущенное вычитаемое, до 10.
11.	Число как сумма двух слагаемых	2 вид — интерпретация	среднее	2 Б.	Число как сумма двух слагаемых, до 10.
12.	Пропущенные знаки	2 вид — интерпретация	сложное	10 Б.	Три числа, до 9.
13.	Пропущенное число (три числа)	2 вид — интерпретация	сложное	4 Б.	Пропущенное число, до 10.
14.	Ответы в порядке возрастания	2 вид — интерпретация	сложное	4 Б.	Следует решить 3 примера, ответы расположить в порядке возрастания.
15.	Четыре числа	2 вид — интерпретация	сложное	5 Б.	Цепочка действий сложения и вычитания.

www.yaklass.ru

Примеры от 0 до 10. Математика, 1 класс: уроки, тесты, задания.

1.	Домино Сложность: лёгкое	1
2.	Число 0 Сложность: лёгкое	3
3.	Переместительный закон Сложность: лёгкое	2
4.	Сумма двух одинаковых слагаемых Сложность: лёгкое	2
5.	Примеры с одинаковыми ответами Сложность: среднее	4
6.	Выбор примеров Сложность: среднее	4
7.	Заполнение таблицы (сумма) Сложность: среднее	4
8.	Пропущенное число (сумма) Сложность: среднее	2
9.	Пример из трёх чисел Сложность: среднее	3
10.	Пропущенное число (разность) Сложность: среднее	2
11.	Число как сумма двух слагаемых Сложность: среднее	2
12.	Пропущенные знаки Сложность: сложное	10
13.	Пропущенное число (три числа) Сложность: сложное	4
14.	Ответы в порядке возрастания Сложность: сложное	4
15.	Четыре числа Сложность: сложное	5

www.yaklass.ru