Сложные примеры по математике, которые вгоняют в краску неучей
Когда дело касается чисел, математика никогда не подводит. В нашем современном изменчивом мире она единственная царица наук, чьи законы систематизированы и не изменяют себе. Потому очень важно дружить с ее правилами и не давать извилинам одеревенеть. А чтобы проверить, в рабочем ли состоянии твоя голова, предлагаем попробовать решить сложные примеры по математике.
© DepositphotosСложные примеры по математике
1. Казалось бы, пример состоит из одних девяток — что же тут сложного? Пожалуй, для тех, кто знает все основные операции и порядок их выполнения, это задание и вправду будет слишком простым. Или нет? Что ж, попробуй решить, не допустив ни одной ошибки.
2. Калькулятор в сторону! Следующее задание вобрало в себя еще больше математических операций. Пусть пример и состоит из одних троек, но будет посложнее предыдущего с девятками.
3. И последнее по порядку, но не по сложности. Попробуй выяснить, каким значениям равны А, В и C. Найди число, скрывающееся за вопросительным знаком. Удачи!
ОТВЕТЫ
1. Если освежить в памяти школьные знания об основных операциях, то решить этот пример не составит труда. Выглядит решение следующим образом: 9 + (9 ÷ 9) + (9 × 9) – 9 = 9 + 1 + 81 – 9 = 82.
© Depositphotos2. В этом задании скобки — это лишь отвлекающий маневр. На самом деле каждую операцию можно решить по порядку: 3 ÷ 3 (3 × 3) × 3 ÷ 3 + 3 = 1 × 9 × 3 ÷ 3 + 3 = 27 ÷ 3 + 3 = 9 + 3 = 12.
© Depositphotos3. Сначала выясняем, что A = 39 ÷ 3 = 13. Затем оказывается, что B = (25 + 13) ÷ 2 = 38 ÷ 2 = 19. Тогда очевидно, что C = 50 – 6 – 19 = 25. Остается решить последний пример: 13 + 19 + 25 = 57.
© DepositphotosУвенчались успехом твои старания или нет? Как бы там ни было, обязательно делись своими результатами в комментариях!
Редакция Офигенно
Это творческая мастерская, работники которой не спят днем и ночью, генерируя новые идеи. Если судьба занесла тебя на «Офигенно», значит, ты попал в особый мир, который заставит тебя переживать самые разнообразные эмоции — от желания разбить монитор до слёз восторга! Как бы то ни было, заверяем тебя: здесь ты найдешь миллион уникальных историй со всех уголков мира!
Если судьба занесла тебя на «Офигенно», значит, ты попал в особый мир, который заставит тебя переживать самые разнообразные эмоции — от желания разбить монитор до слёз восторга! Как бы то ни было, заверяем тебя: здесь ты найдешь миллион уникальных историй со всех уголков мира!
Простые примеры по математике
Математика – наука, областью применения которой являются не только исследования в сфере сугубо количественных отношений, но также изучение порядка, структуры и пространственных форм объективно существующего мира, сложившихся в течение тысячелетий существования человечества на основе самых разнообразных операций по измерению, подсчёту и описанию тех или иных реальных объектов. Являясь мощнейшим средством успешного разрешения практически любых задач научно-прикладного характера, математика одновременно представляет собой универсальный язык науки, а значит, и важнейшую составляющую общемировой культуры.
Округление чисел
Разложение на множители
Сравнение дробейСокращение и расширение
Сложение и вычитание
Умножение дробей
Деление дробей
Большие числа
Математика принадлежит к разряду точных наук и по праву занимает в нем лидирующие позиции. Она не терпит спекуляций и произвола в толковании различных закономерностей, их логическом обосновании. Она – само воплощение жесткой логики и упорядоченности, взаимозависимости происходящих в окружающем мире событий и явлений. Помогая людям в постижении мира, она позволяет им все больше узнавать о законах его развития, поскольку абсолютно все законы имеют математическое выражение, подчиняясь царящему в математике порядку.
Она не терпит спекуляций и произвола в толковании различных закономерностей, их логическом обосновании. Она – само воплощение жесткой логики и упорядоченности, взаимозависимости происходящих в окружающем мире событий и явлений. Помогая людям в постижении мира, она позволяет им все больше узнавать о законах его развития, поскольку абсолютно все законы имеют математическое выражение, подчиняясь царящему в математике порядку.
Изучая математику, мы, как правило, не можем выбрать время для того, чтобы больше узнать о её роли в нашей повседневной жизни и тесной взаимосвязи с различными сферами человеческой жизнедеятельности. Между тем, именно математика является, по сути, началом начал если не всего, то очень многого. Задавшись целью изучать мир во всем его разнообразии, мы рано или поздно, но непременно обнаруживаем, что в повседневной жизни математика играет роль не менее значимую, чем в узких областях точных и прикладных наук. С ней приходится сталкиваться ежеминутно, а следовательно, определенный багаж математических знаний и навыков необходим каждому из нас.
Применение математики безмерно расширяет возможности познания. Ныне просто невозможно назвать область знаний, которая в той или иной мере не была бы основана на математических понятиях и методах. Трудно переоценить прикладную роль математики в исследованиях естественнонаучного, инженерно-технического и гуманитарного генезиса. А основной причиной, обуславливающей математизацию различных областей повседневной жизнедеятельности человека, является способность математики предлагать четкие модели для постижения окружающей нас действительности.
Практически в каждой из профессий не обойтись без математических знаний и навыков. В первую очередь это, разумеется, относится к специальностям, непосредственно сопряженным с технико-экномической сферой. Математика – язык техники и естествознания, а потому овладение инженерными и естественно-прикладными специальностями немыслимо без профессиональных знаний, основанных на математике.
|
|
Порядок действий в Математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Операции действия:
- сложение (+)
- вычитание (-)
- умножение (*)
- деление (:)
Операции отношения:
- равно (=)
- больше (>)
- меньше (<)
- больше или равно (≥)
- меньше или равно (≤)
- не равно (≠)
Сложение — операция, которая позволяет объединить два слагаемых.
- Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.
Вычитание — действие, обратное сложению.
- Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.
Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
- Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
- 3 * 4 = 3 + 3 + 3 + 3
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.
Поэтому и множитель, и множимое называют сомножителями.
Деление — арифметическое действие обратное умножению.
- Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.
В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.
Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.
Возведение степень — операция умножения числа на самого себя несколько раз.
Основание степени — число, которое повторяется сомножителем определённое количество раз. 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
При знаке квадратного корня показатель корня принято опускать: √16 = 4.
3√8 = 2 — корень третьей степени называется — кубическим.
Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
- действия выполняются по порядку слева направо
- сначала выполняется умножение и деление, а затем — сложение и вычитание.
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо. Сначала умножение или сложение? — Умножаем, потом складываем. |
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
Как решаем:
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Ответ: 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Как рассуждаем:
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Ответ: 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
- Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:
8 — 2 * 3 = 8 — 6 = 2.
Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.
Подставляем полученные значения в исходное выражение:
10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Как решаем:
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
2 + 3 = 5.
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
Пример 1. Вычислить (4 + 1) * 3 + 62 : 3 — 7.
Вычислить (4 + 1) * 3 + 62 : 3 — 7.
Как решаем:
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
(4 + 1) * 3 + 36 : 3 — 7.
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
(4 + 1) * 3 + 36 : 3 — 7 = 3 * 3 + 36 : 3 — 7 = 9 + 12 — 7 = 14.
Ответ: (3 + 1) * 2 + 62 : 3 — 7 = 14.
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Говорим о математике на английском ‹ engblog.ru
Многие считают, что их жизнь никак не связана с математикой и им не нужно разбираться в дебрях данной темы на английском. Но цифры окружают нас везде: номера телефонов, кредитных карт, рейсов, не говоря уже о датах. Сегодняшний материал будет полезен всем: увлеченным энтузиастам математики и далеким от мира точных наук гуманитариям.
Сегодняшний материал будет полезен всем: увлеченным энтузиастам математики и далеким от мира точных наук гуманитариям.
Хотелось бы начать с числительных (numerals), ведь это первое, с чем мы сталкиваемся в математическом контексте. Напомню, что числительные бывают двух видов: количественные (отвечают на вопрос «сколько?») и порядковые (отвечают на вопрос «который по счёту?»).
Давайте обратим особое внимание на произношение тех или иных числительных, так как этот, казалось бы, простой момент иногда вызывает замешательство даже у опытных «пользователей» языка.
| Тип | Правило | Пример | Особенность |
|---|---|---|---|
| Сотни | And между сотнями и десятками. | “101 (one hundred and one) Dalmatians” is my favourite cartoon. | – |
| Тысячи | And не ставится между тысячами и сотнями. | The population of my village is almost 6500 (six thousand five hundred) people. 1 253 (one thousand two hundred and fifty-three) candidates passed this exam last year. | Американцы иногда произносят тысячи и сотни так: 1500 = fifteen hundred = 15 сотен. |
| Сотни и десятки тысяч | And между сотнями тысяч и десятками тысяч. | The population of Liverpool is 466 415 (four hundred and sixty-six thousand, four hundred and fifteen) people. | Американцы используют and намного реже британцев. Так, они сказали бы: 466 415 = four hundred sixty-six thousand, four hundred fifteen. |
| Миллионы | And не ставится между миллионами и тысячами. | There are 2 629 743 (2 million, 6 hundred and 29 thousand, 7 hundred and 43) seconds in one month. | – |
| Миллиарды | And не ставится между миллиардами и миллионами. | The world population was 5 320 816 000 (5 billion, 3 hundred and 20 million, 8 hundred and 16 thousand) people in 1990. | – |
Ряд чисел (series of numbers): произнося ряд чисел, из которых состоит банковский счет, номер кредитной карты или телефона, мы называем каждую цифру отдельно. При этом ноль произносится как oh в британском варианте, и как zero – в американском:
His credit card number is 5368 7208 0944 0699 (five three six eight, seven two oh/zero eight…). – Номер его кредитной карты – 5368 7208 0944 0699.
При этом, если в номере телефона присутствуют две одинаковые цифры, стоящие рядом, говорится, например double nine:
My friend’s number is 2290 4566 (double two nine oh four five double six). – Телефон моего друга – 2290…
Называя десятичные дроби (decimals), мы используем слова nought (британский английский) и zero (американский английский): 10. 39 (ten point thirty-nine) – десять целых и тридцать девять сотых. Более подробно ознакомиться с особенностями произношения дробных числительных можно в нашей статье.
39 (ten point thirty-nine) – десять целых и тридцать девять сотых. Более подробно ознакомиться с особенностями произношения дробных числительных можно в нашей статье.
Указывая ту или иную дату, мы, конечно же, очень далеки от математики, однако дата – одна из самых популярных сфер употребления числительных. Если вам необходимо освежить в памяти, как именно указываются даты в английском, то советую прочитать статью «Даты и порядковые числительные в английском языке».
И наконец переходим к математическим действиям (mathematical operations): сложению (addition), вычитанию (subtraction), умножению (multiplication) и делению (division).
- To add to / to plus – прибавлять.
- To minus / to subtract from – вычитать.
- To multiply by – умножать.
- To divide by – делить.
- To equal – равняться
| Действие | Пример по-английски | Перевод |
|---|---|---|
Пример: 7 + 8 = 15 | 7 plus/and 8 equals/is 15. Add 7 to 8 and you’ll get 15. | 7 прибавить 8 равняется 15. Прибавь 7 к 8 и получишь 15. |
Пример: 23 – 3 = 20 | Twenty-three minus three equals/is twenty. If you subtract 3 from 23, the answer is 20. | 23 минус 3 будет 20. Если отнимешь 3 от 23, ответ будет 20. |
Пример: 6 * 4 = 24 | 6 multiplied by 4 / 6 times 4 equals/is 24. Multiply 6 by 4 and you’ll get 24. | 6 умножить на 4 равно 24. Умножь 6 на 4 и получишь 24. |
Пример: 9 ÷ 3 = 3 | 9 divided by 3 equals/is 3. If you divide 9 by 3, the answer is 3. | 9 разделить на 3 равно 3. Если разделить 9 на 3, ответ будет 3. |
Глоссарий на тему «Математика»
- To do sums / to solve problems – решать примеры, задачи.

He is the best at doing sums in our class. – Он решает примеры лучше всех в нашем классе.
- Сommon denominator – общий знаменатель.
The task is to reduce to the common denominator. – Задача – привести к общему знаменателю.
- Difference – разность.
The difference of 15 and 10 is 5. – Разность пятнадцати и десяти – пять.
- Equation /ɪˈkweɪʒ(ə)n/ – уравнение.
Solve the equation. – Решите уравнение.
- Improper fraction – неправильная дробь.
“Improper fractions” are not an easy topic for him. – «Неправильные дроби» – непростая тема для него.
- Mixed fraction – смешанная дробь.
He knows exactly what a mixed fraction is. – Он точно знает, что такое смешанная дробь.
- Numerator /ˈnjuːməˌreɪtə(r)/ – числитель.

Numerator is the number above the line in a common fraction showing how many of the parts indicated by the denominator are taken. – Числитель – это число над линией простой дроби, показывающее сколько частей, указанных знаменателем, взято.
- Quotient /ˈkwəʊʃ(ə)nt/ – частное (при делении).
Quotient is a result obtained by dividing one quantity by another. – Частное – это значение, полученное путем деления некого числа на другое.
- Remainder – остаток.
Remainder is the number that is left over in a division in which one quantity does not exactly divide another – Остаток – это число, которое осталось в результате деления, когда одно число не делится на другое без остатка.
- Сube root of – корень кубический из.
Find the cube root of 15. – Найдите кубический корень из 15.
- Inequality /ˌɪnɪˈkwɒləti/ – неравенство.

Inequality is the relation between two expressions that are not equal. – Неравенство – это соотношение между двумя выражениями, которые не являются одинаковыми.
- Equality /ɪˈkwɒləti/ – равенство.
Equality is the condition of being equal in number or amount. – Равенство – это идентичность числа или величины.
- Mathematical sign – математический знак.
Minus is an example of a mathematical sign. – Минус – это пример математического знака.
- Multiplication table – таблица умножения.
Schoolchildren learn the multiplication table all over the world. – Школьники по всему миру учат таблицу умножения.
- Parentheses /pəˈrenθəsɪs/ или round brackets – круглые/овальные скобки.
Parentheses are widely used in mathematics. – Круглые скобки широко используются в математике.

- Right angle – прямой угол.
The right angle is 90˚ (degrees). – Прямой угол равняется 90 градусам.
И в завершение статьи хотелось бы предложить вам пройти небольшой тест. Но не волнуйтесь! Это не урок математики! 🙂
ТестГоворим о математике на английском
А еще мы публикуем много интересных статей в блоге нашей школы. Вот некоторые из них:
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Как простой математический пример на порядок действий озадачил Сеть
Простая задача по математике на порядок действий разделила пользователей англоязычного твиттера. Любопытные комментаторы пытаются найти правильный ответ примера для младших классов, используя разные, порой несуществующие математические правила. В споре поучаствовал и актёр Тайка Вайтити, но не попал в «список отличников».
Пример со скобками 28 ноября опубликовал пользователь твиттера с ником MIR (@1RealMir) — комментатор запостил фотографию задания и предложил своим подписчикам поделиться полученными ответами. Задача включала в себя вычитание в скобках и сложение за скобками — автор использовал простые числа, поэтому основной трудностью примера был порядок действий.
2+5×(8−5) — так выглядел пример.
MIR
Какой ответ вы получили?
Твит развирусился, став для части комментаторов настоящей головоломкой. Одним из самых популярных ответов оказалось число 21 — те, кто в ходе решения получил такую цифру, поделились порядком действий. Так, блогерка Tara Dublin (Taylor’s Version) (@taradublinrocks) расписала этапы решения задачки по очереди — сначала девушка сложила цифры за скобками, затем выполнила вычитание в скобках и в конце умножила числа друг на друга.
Tara Dublin (Taylor’s Version)
2+5×(8−5)
1) 2+5 = 7
2) 8−5 = 3
3) 7×3 = 21
Вторым популярным ответом стало число 17 — его получила другая половина комментаторов, тоже поделившаяся ходом решения. Как оказалось, ответившие 17 использовали иной порядок действий — после вычитания в скобках фанаты арифметики выполнили умножение и только потом — сложение.
Kiarrie Gates
2+5×(8−5)
2+5×(3)
2+15
17
На пост обратил внимание даже новозеландский актёр и кинорежиссёр Тайка Вайтити. В шуточном твите он предположил, что правильный ответ — 3.
Taika Waititi
Что за чертовщина — всё это не имеет смысла. Там стоит число 7, а рядом в скобках 3. Можно прочитать, как «7, но на самом деле это 3», так что верное решение — 3.
На самом деле решение задачи кроется в школьном правиле из начальных классов, порядке действий, которое гласит — вначале выполняются действия в скобках, затем приоритет достаётся умножению и делению, а в конце решаются сложение и вычитание. Применяя математические правила, пример решается простым образом — первым выполняется вычитание в скобках, затем умножение, и после последнего действия, сложения, получаем правильный ответ — 17.
Впрочем, споры вокруг задания продолжаются — пользователи Сети, получившие разные ответы, настаивают на своей правоте.
Ранее Medialeaks рассказал, как простая задача на логику вывела из строя трёх инженеров. Молодые специалисты три минуты пытались понять, как из двух цифр 100 получить двести, используя одну чёрточку.
О том, зачем пользователи Сети ищут слово «цвет» в «Яндексе», читайте в материале Medialeaks. Участники флешмоба таким образом гадают, как на палитре выглядит их настроение.
Самостоятельные работы по математике за 5 класс к учебнику Виленкина Н.
 Я. за 1, 2, 3 и 4 четверти
Я. за 1, 2, 3 и 4 четвертиДата публикации: .
Самостоятельные на темы: «Натуральные числа и их обозначения», «Сложение и вычитание натуральных чисел», «Сравнение натуральных чисел», «Отрезок, прямая, луч», «Умножение натуральных чисел», «Деление натуральных чисел», «Выражения и уравнения», «Квадрат и куб числа», «Окружность и круг», «Обыкновенные дроби», «Сравнение дробей» и др.
Некоторые понятия к учебному материалу.
1. Натуральные числа – используются для счета предметов в повседневной жизни.2. Отрезок. Длина отрезка – расстояние между его крайними точками, концами. Обозначается заглавными латинскими буквами, например AB.
3. Шкала – специальная линейка с делениями (штрихами).
4. Единичный отрезок – отрезок с длиной равной единице.
5. Меньше и больше. Меньше, число, которое при счете называется раньше. Больше, число, которое при счете называется позже.
6. Слагаемые числа – числа, которые складываются.

7. Вычитание. Число из которого вычитают – это уменьшаемое. Число, которое вычитается – это вычитаемое. В итоге получаем разность.
Самостоятельная работа №1 (входная работа на повторение)
Вариант I.
1. Определение числа.
а) Определите натуральное число, которое следует за числом 699.б) Определите натуральное число, которое на две единицы меньше числа 1001.
в) Определите натуральное число, которое на единицу больше числа 239 999.
г) Определите натуральное число, которое на единицу меньше числа 394 000.
2. Решите задачу.
В городском сквере посажено 340 деревьев. А в парке посажено 270 деревьев. На сколько деревьев больше в городском сквере, чем в парке?3. Решите примеры.
| а) 492 + 1 220 = | б) 3 495 — 593 = |
| в) 5112 : 6 = | г) 56 * 23 = |
Вариант II.
1. Определение числа.
а) Определите натуральное число, которое следует за числом 879.б) Определите натуральное число, которое на единицу меньше числа 2 000.

в) Определите натуральное число, которое на единицу больше числа 722 999.
г) Определите натуральное число, которое на единицу меньше числа 24 000.
2. Решите задачу.
Рыбаки за первую неделю поймали 395 кг рыбы, а за вторую неделю – 239 кг. На сколько кг было поймано меньше за вторую неделю, чем за первую?3. Решите примеры.
| а) 638 + 1 445 = | б) 6 112 — 2 598 = |
| в) 2688 : 3 = | г) 24 * 45 = |
Вариант III.
1. Определение числа.
а) Определите натуральное число, которое следует перед числом 699.б) Определите натуральное число, которое на единицу меньше числа 3 000.
в) Определите натуральное число, которое на единицу больше числа 28 999.
г) Определите натуральное число, которое на единицу меньше числа 12 000.
2. Решите задачу.
В огороде посадили 2 грядки помидор. С первой грядки было собрано 427 помидор, а со второй грядки – 311. На сколько меньше помидор было собрано со второй грядки, чем с первой?3. Решите примеры.
Решите примеры.
| а) 455 + 3 412= | б) 5 332 — 593 = |
| в) 3648 : 8 = | г) 29 * 41 = |
Самостоятельная работа №2 на тему: «Натуральные числа и их обозначения»
Вариант I.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 20;б) число 49.
2. Представьте следующие словосочетания в числовом виде.
а) Шесть миллиардов пятьсот три тысяча семь.б) На единицу больше чем пятьсот девять тысяч девятьсот девяносто девять.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 2, 3 и 7.b) 4, 0 и 9.
Вариант II.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 60;б) число 38.
2. Представьте следующие словосочетания в числовом виде.
а) Восемь миллиардов триста одна тысяча три.
б) На единицу больше чем сто девять тысяч девятьсот девяносто девять.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 1, 3 и 9.b) 2, 4 и 0.
Вариант III.
1. Запишите следующие числа 3 раза подряд и запишите полученное в результате число в виде словосочетания.
а) число 30;б) число 58.
2. Представьте следующие словосочетания в числовом виде.
а) Два миллиарда шестьсот два миллиона триста.б) На единицу больше чем семьсот пять тысяч девятьсот девяносто восемь.
3. Определите все возможные трехзначные числа, состоящие из следующих чисел (числа не должны повторяться).
a) 5, 2 и 8.b) 1, 3 и 0.
Самостоятельная работа №3
Вариант I.
1. Переведите из одной единицы измерения в другую.
| а) 8 дм 43 см = … см | б) 5 км 549 м = … м |
| в) 7 см 18 мм = … мм | г) 249 см =… дм … см |
2. Начертите отрезок AB, равный 17 см 5 мм. Отметьте на нем точки C и D.
AC равно 10 см 4 мм, CD равно 4 см 9 мм. Чему равна длина отрезка DB?
Начертите отрезок AB, равный 17 см 5 мм. Отметьте на нем точки C и D.
AC равно 10 см 4 мм, CD равно 4 см 9 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 18 столбах, расстояние между столбами составляет пять метров. Каково расстояние между шестым и четырнадцатым столбами?4. Начертите четырехугольник ABCD. Отметьте точкой T середину стороны BC. Соедините точки B и D, А и T. Выпишите все многоугольники, которые образовались.
Вариант II.
1. Переведите из одной единицы измерения в другую.
| а) 4 дм 23 см = … см | б) 25 км 50 м = … м |
| в) 16 см 65 мм = … мм | г) 456 см =… дм … см |
2. Начертите отрезок AB, равный 15 см 4 мм, отметьте на нем точки C и D. AC равен 8 см 2 мм, CD равен 3 см 7 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 19 столбах, расстояние между столбами составляет 4 метра. Каково расстояние между третьим и восьмым столбами?
Каково расстояние между третьим и восьмым столбами?4. Начертите четырехугольник ABCD. Отметьте середину AB и поставьте точку N. Проведите отрезки DN и АС. Выпишите все многоугольники, которые образовались.
Вариант III.
1. Переведите из одной единицы измерения в другую.
| а) 19 дм 5 см = … см | б) 21 км 678 м = … м |
| в) 43 см 8 мм = … мм | г) 503 см =… дм … см |
2. Начертите отрезок AB, равный 13 см 2 мм, отметьте на нем точки C и D. AC равен 7 см 3 мм. CD равен 3 см 6 мм. Чему равна длина отрезка DB?
3. Решите задачу.
Перед домом построили забор. Забор держится на 16 столбах, расстояние между столбами составляет 3 метра. Каково расстояние между пятым и одиннадцатым столбами?4. Начертите четырехугольник ABCD. Отметьте середину CD и поставьте точку М. Проведите отрезки BM и АС. Выпишите все многоугольники, которые образовались.
Самостоятельная работа №4 на тему: «Сравнение натуральных чисел»
Вариант I.

1. Сравните числа.
| а) 3 485 660 … 3 458 660 | б) 303 559 … 330 559 |
| в) 2 596 440 … 2 569 440 | г) 45 696 … 44 696 |
2. Представьте в виде двойного неравенства: 18 т 347 кг … 18 т 4 ц 59 кг … 18 568 кг.
Вариант II.
1. Сравните числа.
| а) 34 686 887 … 34 868 887 | б) 3 855 … 3 585 |
| в) 40 955 999 … 40 595 999 | г) 455 776 … 445 776 |
2. Представьте в виде двойного неравенства: 13 км 845 м … 14675 м … 13 км 845 м 3 дм.
Вариант III.
1. Сравните числа.
| а) 678 881 … 687 881 | б) 782 223 … 728 223 |
| в) 2 490 606 … 2 490 660 | г) 13 799 … 13 977 |
2. Представьте в виде двойного неравенства: 15 т 475 кг … 15657 кг … 157 ц 35 кг.
Самостоятельная работа №5 на тему: «Сложение и вычитание натуральных чисел»
Вариант I.

1. Выполните сложение.
| а) 348 588 667 + 239 586 394 = | б) 93 955 483 + 495 868 991 = |
| в) 23 394 596 + 5 697 345 = | г) 3 949 532 + 405 669 = |
2. Выполните вычитание.
| а) 348 588 667 — 283 745 733 = | б) 93 955 483 — 22 394 583 = |
| в) 23 394 596 — 192 485 = | г) 3 949 532 — 4 348 483 = |
3. Решите задачу.
Мастерская закупила 560 гаек. На ремонт первой машины потребовалось 203 гайки, а на ремонт второй машины – еще 293 гайки. Сколько гаек осталось в мастерской?4. Решите задачу.
В концертном зале стояло 454 стула. Для проведения концерта принесли 123 новых стула, а после антракта – еще 13 стульев. Сколько всего стульев стало в концертном зале?Вариант II.
1. Выполните сложение.
| а) 3 484 558 + 9 499 834 = | б) 93 955 483 + 394 585 665 = |
| в) 3 495 863 + 35 384 588 = | г) 5 697 291 + 34 405 669 = |
2. Выполните вычитание.
Выполните вычитание.
| а) 4 856 342 — 3 495 384 = | б) 283 495 864 — 232 485 965 = |
| в) 5 965 493 — 3 449 594 = | г) 23 455 303 — 19 485 588 = |
3. Решите задачу.
В рулоне было смотано 327 м ленты. В первый день использовали 103 м, а во второй день – ещё 205 м. Сколько метров осталось в рулоне?4. Решите задачу.
В магазине находилось 4 т 150 кг сахара. В первый день привезли 340 кг сахара, а во второй день – еще 4 ц сахара. Сколько кг сахара стало в магазине?Вариант III.
1. Выполните сложение.
| а) 2 399 388 + 239 586 394 = | б) 435 483 + 495 868 991 = |
| в) 34 567 784 + 13 412 345 = | г) 6 563 544 + 23 876 554 = |
2. Выполните вычитание.
| а) 455 586 661 — 283 745 733 = | б) 40 954 586 — 22 394 583 = |
| в) 495 568 222 — 448 568 338 = | г) 3 949 532 — 2 349 588 = |
3. Решите задачу.
Решите задачу.
4. Решите задачу.
На складе находилось 3 т и 450 кг муки. В первый день привезли 560 кг, через неделю привезли еще 5 ц муки. Сколько кг муки стало на складе?Самостоятельная работа №6
Вариант I.
1. Найдите значение выражения: ( а + 46 ) : ( b — 48 ), если а = 35 и b = 57.
2. Упростите выражения.
а) с + 239 — 93;б) 485 — 483 + d.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. К нему прибавили число 194, а потом прибавили ещё число 110 и получили число 322. Какое число было задумано?4. Решите уравнения.
a) (305 — ( ( 45 + х ) — 32 ) + 96 = 223;б) 38 + ( 69 — y ) + 74 = 172.
Вариант II.
1. Найдите значение выражения: ( а — 34 ) * ( b + 9 ), если а = 60 и b = 11.
2. Упростите выражения.
а) 594 — 69 — а;б) 149 + b — 54.

3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. Из этого числа вычли число 424, а затем прибавили число 392. В итоге, получилось число 632. Какое число было задумано?4. Решите уравнения.
a) 209 — ( ( 145 + х ) — 12 ) + 96 = 123;б) 18 + ( 159 — y ) + 34 = 172.
Вариант III.
1. Найдите значение выражения: ( а — 68 ) : b + 2 339, если а = 92 и b = 8.
2. Упростите выражения.
а) с + 239 — 193;б) 485 — d + 384.
3. Составьте уравнение для решения задачи и решите его.
Было задумано некоторое число. Из этого числа вычли число 209, а затем прибавили число 47. В итоге, получилось число 217. Какое число было задумано?4. Решите уравнения.
a) ( 111 — ( 45 + х ) ) + 96 = 123;б) 29 + ( 59 — y ) + 15 = 72.
После завершения второй четверти, учащиеся должны:
1. уметь умножать натуральные числа и использовать эти знания;
2. уметь производить деление натуральных чисел, в том числе и деление с остатком, и использовать эти навыки при решении задач;
3. знать распределительное свойство умножения, уметь применять это свойство при устных вычислениях и при решении задач;
знать распределительное свойство умножения, уметь применять это свойство при устных вычислениях и при решении задач;
4. знать, что такое возведение числа в степень. Понимать, что такое корень и куб числа;
5. понимать, что такое формула, и как производить вычисления по формуле.
Самостоятельная работа №7 на тему: «Действия с натуральными числами. Умножение»
Вариант I.
1. Выполните умножение.
| а) 283 * 46 = | б) 29 * 473 = | в) 841 * 93 = | г) 19 * 632 = |
| д) 570 * 340 = | е) 930 * 730 = | ж) 5100 * 360 = | з) 560 * 230 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 491 * 4 * 200 =б) 4 * 324 * 25 * 300 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 35 * 34 = | 34 * 33 = | 34 * 36 = | 32 * 32 = |
4. Решите задачу.
В двухэтажной школе всего 32 кабинета и в каждом кабинете по 12 парт. В трехэтажной школе 45 кабинетов и в каждом кабинете по 14 парт. Сколько всего парт необходимо городским школам, если в городе 8 двухэтажных и 5 трехэтажных школ?
В трехэтажной школе 45 кабинетов и в каждом кабинете по 14 парт. Сколько всего парт необходимо городским школам, если в городе 8 двухэтажных и 5 трехэтажных школ?Вариант II.
1. Выполните умножение.
| а) 342 * 57 = | б) 64 * 268 = | в) 342 * 89 = | г) 32 * 864 = |
| д) 920 * 560 = | е) 470 * 990 = | ж) 2300 * 630 = | з) 430 * 540 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 376 * 4 * 500 =б) 4 * 265 * 25 * 200 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 85 * 84 = | 84 * 83 = | 84 * 86 = | 82 * 82 = |
4. Решите задачу.
В поселке построено 18 домов. Из них 4 трехэтажных, 6 двухэтажных, остальные одноэтажные дома. В трехэтажных домах – 18 окон, в двухэтажных – 14 окон, в одноэтажных – 8 окон. Сколько окон необходимо для 4 таких же посёлков?Вариант III.
1. Выполните умножение.
| а) 563 * 24 = | б) 32 * 441 = | в) 324 * 87 = | г) 23 * 728 = |
| д) 220 * 680 = | е) 240 * 580 = | ж) 7500 * 290 = | з) 920 * 630 = |
2. Умножьте числа, используя наиболее удобный порядок действий.
а) 25 * 376 * 4 * 300 =б) 4 * 641 * 25 * 100 =
3. Расположите уравнения в порядке убывания, не производя никаких действий.
| 65 * 64 = | 64 * 63 = | 64 * 66 = | 62 * 62 = |
4. Решите задачу.
В один мешок помещается 26 кг картофеля, или 34 кг муки, или 38 кг сахара. Сколько всего весит груз, если в машину погрузили 32 мешка картофеля, 38 мешков муки и 52 мешка сахара?Самостоятельная работа №8 на тему: «Деление натуральных чисел»
Вариант I.
1. Выполните деление.
| а) 475 860 : 5 = | б) 8 412 : 4 = | в) 492 000 000 : 1 000 = |
| г) 270 930 : 3 = | д) 386 240 : 5 = | е) 19 688 : 23 = |
2. Решите уравнения.
Решите уравнения.
| а) X : 85 = 2 210 | б) 36 690 : Y = 10 | в) 792 : X = 4 |
| г) 15 * ( 39 : X ) = 45 | д) Y : 42 = 168 | е) 65 065 : Y = 1 001 |
3. Решите задачу.
Фермеру необходимо вспахать поле размером 318500 м. За сколько дней он вспашет поле, если известно, что за день он может вспахать 45 500 м?4. Остаток равен 18, неполное частное – 35 и делитель – 23. Найдите делимое.
Вариант II.
1. Выполните деление.
| а) 489 560 : 5 = | б) 36 690 : 3 = | в) 657 000 : 1 000 = |
| г) 960 552 : 6 = | д) 522 240 : 2 = | е) 67 065 : 85 = |
2. Решите уравнения.
| а) X : 26 = 456 | б) 4 760 : Y = 85 | в) 792 : X = 8 |
| г) 35 * ( 54 : X ) = 315 | д) Y : 3 = 3015 | е) 524 : Y = 131 |
3. Решите задачу.
Станок производит 1200 заготовок за 1 час. Сколько минут нужно машине, чтобы приготовить 48 000 заготовок?
Сколько минут нужно машине, чтобы приготовить 48 000 заготовок?4. Остаток равен 33, неполное частное – 41 и делитель – 25. Найдите делимое.
Вариант III.
1. Выполните деление.
| а) 236 560 : 4 = | б) 36 690 : 6 = | в) 612 345 000 : 1 000 = |
| г) 960 440 : 8 = | д) 678 350 : 2 = | е) 31 464 : 69 = |
2. Решите уравнения.
| а) X : 25 = 14 | б) 1 820 : Y = 28 | в) 1 836 : X = 6 |
| г) 52 * Y = 468 | д) Y : 3 = 7 659 | е) 1048 : Y = 131 |
3. Решите задачу.
Комбайн убирает 30 га пшеницы за 1 час. Сколько дней ему нужно, чтобы убрать площадь равную 1200 га, если в день он будет работать по 10 часов?4. Остаток равен 24, неполное частное – 25 и делитель – 28. Найдите делимое.
Самостоятельная работа №9 на темы: «Выражения, уравнения и решение уравнений», «Квадрат и куб числа»
Вариант I.
1. Решите примеры.
Решите примеры.
б) 152 =
в) 73 =
г) ( 14 + 7 )2 — ( 5 + 13 )2 + 287 =
2. Упростите выражение и найдите его значение при с=34: 47с + 34 — 58 + 12с — 58.
3. Решите уравнения.
а) 15 * х = 945б) 3 * y — 45 = 44
4. Решите задачу.
Бабушка и внучка слепили 124 пельмени. Сколько пельменей слепили бабушка и сколько внучка, если бабушка лепила в 3 раза быстрее, чем внучка?Вариант II.
1. Решите примеры.
а) 472 — ( 29 + 124 : 4 ) — 72 : 8 =б) 182 =
в) 63 =
г) ( 5 + 27 )2 — ( 4 + 12 )2 — 64 =
2. Упростите выражение и найдите его значение при с=12: 19с + 57 — 58с + 29с — 38 + 5с.
3. Решите уравнения:
а) 15 * х = 180б) 12 * y + 36 = 96
4. Решите задачу.
Инженер и студент отремонтировали 248 приборов. Инженер ремонтировал приборы в 3 раза быстрее, чем студент. Сколько приборов починил каждый?Вариант III.
1. Решите примеры.
а) 365 + ( 299 — 342 : 2 ) * 5 — 687 : 3 =б) 172 =
в) 83 =
г) ( 4 + 7 )2 — ( 5 + 23 )2 + 787 =
2. Упростите выражение и найдите его значение при с=12: 47 + 56с — 6с + 34 — 12с.
3. Решите уравнения.
а) 32 * х = 1280б) 8 * y + 36 = 356
4. Решите задачу.
Портной и его ученик сшили 213 фартуков. Портной работал в 2 раза быстрее, чем его ученик. Сколько фартуков сшил портной, а сколько ученик?Самостоятельная работа №10 на темы: «Окружность и круг». «Обыкновенные дроби»
Вариант I.
1. Нарисуйте окружность с центром в точке X и радиусом 4 см 6 мм. Нарисуйте отрезок CD так, чтобы он проходил через центр окружности и пересекал ее в точках C и D. Как называются отрезки СX и СD? Определите их длину.
2. Решите задачу.
Оля нашла 26 грибов, из них 18 маслят. Какую часть грибов составляют маслята?3. Решите задачу.
Рыбаки поймали 112 кг рыбы. Из них 10⁄28 – караси. Сколько карасей поймали рыбаки?
Сколько карасей поймали рыбаки?4. Решите задачу.
Коля прочитал 85 страниц журнала, что составило 5⁄12 от общего числа страниц. Сколько страниц в журнале?Вариант II.
1. Нарисуйте окружность с центром в точке Y и радиусом 3 см 8 мм. Нарисуйте отрезок EF так, чтобы он проходил через центр окружности и пересекал ее в точках E и F. Как называются отрезки YE и EF? Определите их длину.
2. Решите задачу.
Коля собрал в корзину 31 фрукт, из них 22 фрукта – это груши. Какую часть собранных фруктов составляют груши?3. Решите задачу.
Школьники собрали 104 кг овощей. 13⁄26 от общего числа овощей составляют помидоры. Сколько кг помидор собрали школьники?4. Решите задачу.
Мастер отремонтировал 35 приборов, что составило 5⁄12 от общего количества приборов. Сколько всего приборов надо отремонтировать мастеру?Вариант III.
1. Нарисуйте окружность с центром в точке Z и радиусом 2 см 6 мм. Нарисуйте отрезок GH так, чтобы он проходил через центр окружности и пересекал ее в точках G и H. Как называются отрезки GZ и GH? Определите их длину.
Нарисуйте отрезок GH так, чтобы он проходил через центр окружности и пересекал ее в точках G и H. Как называются отрезки GZ и GH? Определите их длину.
2. Решите задачу.
У Саши есть 29 карандашей. Из них 19 карандашей – это простые карандаши. Какую часть карандашей составляют цветные карандаши?3. Решите задачу.
Мастер сделал 312 деталей. Из них 3⁄24 часть деталей – деревянные. Сколько деревянных деталей сделал мастер?4. Решите задачу.
Ребята из 5 класса собрали 32 кг ягод. Это составляет 3⁄24 от всего количества собранных ягод. Сколько всего ягод было собрано?Самостоятельная работа №11 на тему: «Сравнение дробей»
Вариант I.
1. Задан луч длиной в 12 единиц. Отметьте на числовом луче:
| а) 2⁄12 части | б) 6⁄12 части | 2⁄3 части | 5⁄4 части |
2. Сравните дроби.
б) 21⁄45 и 15⁄26
3. Найдите три решения неравенства.
а) 21⁄22< x < 22⁄22б) 7⁄11 < z < 8⁄11
4. При каких значениях х:
а) дробь х⁄22 будет правильной?б) дробь 15⁄х будет неправильной?
Вариант II.
1. Задан луч длиной в 15 единиц. Отметьте на числовом луче:
| 4⁄15 части | 3⁄15 части | 3⁄5 части | 2⁄3 части |
2. Сравните дроби.
а) 26⁄34 и 15⁄17б) 22⁄49 и 18⁄21
3. Найдите три решения неравенства.
а) 19⁄20 < x < 20⁄20б) 7⁄9 < z < 8⁄9
4. При каких значениях y:
При каких значениях y:
б) дробь 23⁄y будет неправильной?
Вариант III.
1. Задан луч длиной в 18 единиц. Отметьте на числовом луче:
| 2⁄18 части | 6⁄18 части | 2⁄3 части | 5⁄6 части |
2. Сравните дроби.
а) 26⁄31 и 18⁄19б) 23⁄41 и 17⁄18
3. Найдите три решения неравенства.
а) 9⁄10< y < 10⁄10б) 5⁄7 < z < 6⁄7
4. При каких значениях z:
а) дробь z⁄29 будет правильной?б) дробь 13⁄z будет неправильной?
Самостоятельная работа №12 на тему: «Сложение и вычитание обыкновенных дробей»
Вариант I.

1. Решите примеры.
а) 26⁄31 + 18⁄31 — 6⁄31;б) 17⁄125 — 5⁄125 + 106⁄125;
в) 19⁄39 + ( 18⁄39 — 6⁄39 ) — 13⁄39;
2. Решите уравнения.
а) x + 6⁄18 = 16⁄18б) 13⁄25 — ( y + 6⁄25 ) = 4⁄25
3. Решите задачу.
Первый спортсмен пробежал 5⁄7 км, а второй спортсмен за тоже время пробежал 6⁄7 км. На сколько метров больше пробежал первый спортсмен?4. Решите задачу.
Из мешка взяли 2⁄9 части муки, а потом – ещё 3⁄9 части. В мешке осталось 14 кг. Сколько кг муки было в мешке?Вариант II.
1. Решите примеры.
а) 15⁄38 + 12⁄38 — 11⁄38;б) 23⁄192 — 8⁄192 + 48⁄192;
в) 19⁄56 + ( 21⁄56 — 12⁄56 ) — 16⁄56;
2. Решите уравнения.
Решите уравнения.
б) 18⁄23 — ( 7⁄23 + y ) = 5⁄23
3. Решите задачу.
Расстояние от дачи до пруда равно 3⁄5 км, а от дачи до леса равно 4⁄5 км. На сколько метров расстояние от дачи до пруда больше, чем расстояние от дачи до леса?4. Решите задачу.
Из погреба вытащили 3⁄12 части картофеля, а потом – ещё 2⁄12 части. После этого в погребе осталось 56 кг картофеля. Сколько картофеля было в погребе?Вариант III.
1. Решите примеры.
а) 19⁄28 + 12⁄28 — 16⁄28;б) 13⁄176 — 11⁄176 + 49⁄176;
в) 27⁄42 + ( 12⁄42 — 6⁄42 ) — 12⁄42;
2. Решите уравнения.
Решите уравнения.
б) 28⁄35 — ( y + 16⁄35 ) = 4⁄35
3. Решите задачу.
Расстояние от школы до больницы равно 8⁄9 км, а от школы до бассейна равно 4⁄9 км. На сколько метров расстояние от школы до больницы больше, чем расстояние от школы до бассейна?4. Решите задачу.
Из рулона отрезали 3⁄8 части ткани, а потом – ещё 2⁄8 части. После этого в рулоне осталось 32 метра ткани. Сколько метров ткани было в рулоне?Самостоятельная работа №13 на тему: «Сложение и вычитание смешанных чисел»
Вариант I.
1. Решите примеры.
а) 4 19⁄28 + 6 12⁄28;б) 5 13⁄176 — 2 11⁄176;
в) 12 27⁄43 + 3 12⁄43.
2. Решите уравнения.
б) 7 14⁄16 — y = 3 11⁄16;
в) y + 18 27⁄53 = 24 13⁄53;
3. Решите задачу.
В первый день в мастерской использовали 23 3⁄18 метра проволоки, а во второй день – ещё 18 2⁄18 части. После этого в рулоне осталось 32 метра проволоки. Сколько метров проволоки было в рулоне?Вариант II.
1. Решите примеры.
а) 3 13⁄22 + 3 12⁄22;б) 8 15⁄126 — 4 15⁄126;
в) 13 22⁄49 + 3 14⁄49.
2. Решите уравнения.
а) 2 18⁄43 + х = 3 4⁄43;б) 17 15⁄19 — y = 12 12⁄19;
в) y — 18 38⁄56 = 24 27⁄56.
3. Решите задачу.
В первый день в школе покрасили 17 5⁄23 метра коридора, а во второй день – ещё 23 4⁄23 метра. Сколько метров было покрашено за 2 дня?Вариант III.
1. Решите примеры.
а) 5 19⁄23 + 6 12⁄23;б) 7 13⁄48 — 3 11⁄48;
в) 82 25⁄78 + 34 12⁄78
2. Решите уравнения.
а) 6 17⁄29 + х = 23 4⁄29;б) 8 15⁄128 — y = 6 12⁄128;
в) y — 18 38⁄47 = 5 27⁄47.
3. Решите задачу.
Фермер убрал 13 6⁄13 метра грядки в первый день, а на следующий день – ещё 18 3⁄13 метра. После двух дней работы осталось убрать 6 метров. Какова длина грядки?Самостоятельная работа №14 на темы: «Десятичная запись дробных чисел».
 «Сравнение десятичных дробей»
«Сравнение десятичных дробей» Вариант I.
1. Заданные дроби представьте, как десятичные дроби.
а) 5 59⁄10б) 6 1⁄100
в) 17 137⁄1000
2. Сравните числа.
а) 5,596 и 5,629б) 7,34 и 7,339
в) 0,684 и 0,6840
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 92 ц; 887 кг; 14 т 12 кг;б) представьте в квадратных дециметрах: 8 м 2; 57 см 2; 8 м2 77 дм2.
4. Отметьте точки: 0,2; 0,8; 1,1; 2,3; 2,1; 3,7 на числовом отрезке, равном 5 единицам.
Вариант II.
1. Заданные дроби представьте, как десятичные дроби.
а) 18 59⁄1000б) 7⁄10
в) 7 137⁄100
2. Сравните числа.
а) 35,97 и 35,971б) 8,449 и 8,540
в) 0,92 и 0,920
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 3 ц; 239 кг; 23 т 28 кг;б) представьте в квадратных дециметрах: 13 м 2; 2 см 2; 87 м2 32 дм2.

4. Отметьте точки: 0,5; 0,7; 1,1; 2; 2,3; 3,5 на числовом отрезке, равном 6 единицам.
Вариант III.
1. Заданные дроби представьте, как десятичные дроби.
а) 15 43⁄100б) 9 23⁄1000
в) 5⁄10
2. Сравните числа.
а) 29,345 и 29,354б) 171,89 и 171,889
в) 0,93 и 0,930
3. Переведите из одной единицы измерения в другую.
а) представьте в тоннах: 18 ц; 56 кг; 3 т 9 кг;б) представьте в квадратных дециметрах: 4 м 2; 23 см 2; 2 м2 56 дм2.
4. Отметьте точки: 0,4; 0,5; 1,4; 1,9; 2,4; 3,0 на числовом отрезке, равном 4 единицам.
Самостоятельная работа №15 на темы: «Сложение и вычитание десятичных дробей». «Округление чисел»
Вариант I.
1. Решите примеры на сложение десятичных дробей.
а) 29,3 + 4,35 =б) 68,9 + 19,1 =
в) 0,68 + 6,4 =
2. Решите примеры на вычитание десятичных дробей.
а) 35,1 — 13,2 =б) 37 — 27,3 =
в) 13,28 — 5,327 =
3. Решите задачу:
Решите задачу:
4. Округлите:
а) целую часть числа 2539,48190 до сотен, до десятков, до единиц;б) дробную часть числа 2539,48190 до тысячных, до сотен, до десятков.
Вариант II.
1. Решите примеры на сложение десятичных дробей.
а) 79,3 + 8,15 =б) 18 + 8,8 =
в) 0,93 + 23,4 =
2. Решите примеры на вычитание десятичных дробей.
а) 48,2 — 4,98 =б) 96 — 48,6 =
в) 37,67 — 13,168 =
3. Решите задачу.
В первом пакете было 15,7 кг песка, во втором – на 350 г больше, чем в первом. В третьем – на 1200 г меньше, чем в первом. Сколько кг песка в трех пакетах?4. Округлите:
а) целую часть числа 3462,9470 до сотен, до десятков, до единиц;б) дробную часть числа 3462,9470 до тысячных, до сотен, до десятков.
Вариант III.
1.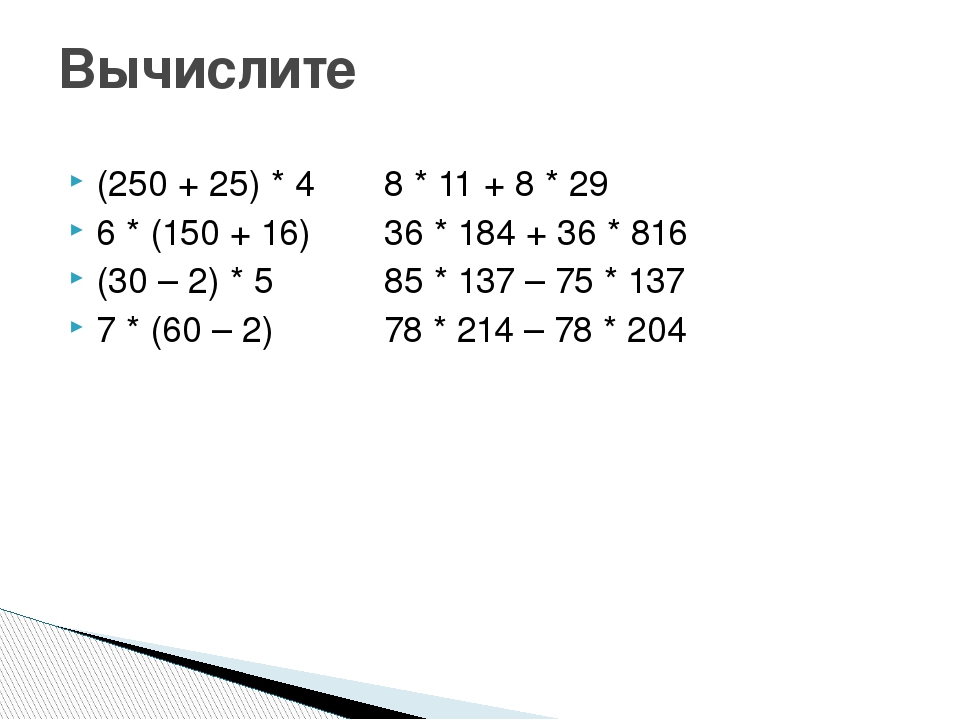 Решите примеры на сложение десятичных дробей.
Решите примеры на сложение десятичных дробей.
б) 8 + 47,7 =
в) 0,123 + 23,942 =
2. Решите примеры на вычитание десятичных дробей.
а) 69,2 — 7,88 =б) 91,76 — 18,6 =
в) 8,94 — 5,452 =
3. Решите задачу.
3 дня бабушка пекла блины. В первый день она использовала 1,2 кг муки, во второй день – на 500 г меньше, чем в первый день, а на третий день – на 300 г больше, чем во второй день. Сколько муки она использовала за три дня?4. Округлите:
а) целую часть числа 4392,73910 до сотен, до десятков, до единиц;б) дробную часть числа 4392,73910 до тысячных, до сотен, до десятков.
Самостоятельная работа №16 на тему: «Умножение десятичных дробей на натуральные числа»
Вариант I.
1. Выполните умножение.
| а) 8,3 * 8 = | б) 7,12 * 34 = | в) 0,235 * 93 = | г) 1,93 * 100 = |
2. Найдите значение выражения: х + ( 3,74х — 1,474х ) при х=3; 100; 374; 1000.
3. Решите задачу.
4. Решите задачу.
Машина проехала 360 км за 6 часов. Какое расстояние она преодолеет, передвигаясь с той же скоростью, за 1⁄4 часа, за 2 1⁄3 часа?Вариант II.
1. Выполните умножение.
| а) 7,48 * 12 = | б) 3,57 * 7 = | в) 0,873 * 87 = | г) 1,698 * 1000 = |
2. Найдите значение выражения: 5х + ( 6,59х + 2,483х ) при х=5; 100; 324; 1000.
3. Решите задачу.
Одновременно в противоположных направлениях из города выехали 2 машины. Скорость первой машины составляет 54,7 км/ч, а скорость второй – 76,2 км/ч. Какое расстояние будет между ними через 3 часа?4. Решите задачу.
Велосипедист преодолел 72 км за 3 часа. Какое расстояние он преодолеет, перемещаясь с той же скоростью, за 5⁄6 часа, за 2 1⁄3 часа?Вариант III.
1. Выполните умножение.
| а) 9,4 * 6 = | б) 8,34 * 56 = | в) 0,517 * 62 = | г) 6,787 * 1000 = |
2. Найдите значение выражения: ( 8,45х — 3,594х ) — х при х=8; 100; 843; 1000.
3. Решите задачу.
Одновременно навстречу друг другу из двух городов выехали мотоциклы. Расстояние между городами составляет 234,8 км. Скорость первого мотоциклиста составляет 34,5 км/ч, а скорость второго – 56,2 км/ч. Какое расстояние будет между ними через 2 часа?4. Решите задачу.
Моторная лодка прошла 24 км за 2 часа. Какое расстояние она пройдет, перемещаясь с той же скоростью, за 1⁄4 часа, за 3 1⁄3 часа?Самостоятельная работа №17 на тему: «Деление десятичных дробей на натуральные числа»
Вариант I.
1. Выполните деление.
| а) 2,729 : 6 = | б) 283,85 : 4 = | в) 4 : 13 = | г) 0,095 : 10 = |
2. Решите уравнения.
| а) 5X — 0,4 = 23,6 | б) 48,2 : Y = 10,4 |
3. Решите задачу.
За два дня рабочие отремонтировали 3,6 км дороги. В первый день они отремонтировали 1/4 части дороги. Сколько км дороги они отремонтировали во второй день?4. Решите задачу.
4 класс и 5 класс собирали макулатуру. Пятиклассники собрали в 2 раза больше макулатуры, чем ребята из 4 класса. Вместе они собрали 239,7 кг. Сколько кг собрали ребята из 5 класса и сколько ребята из 4 класса?Вариант II.
1. Выполните деление.
| а) 5,837 : 7 = | б) 291,49 : 5 = | в) 5 : 18 = | г) 0,023 : 10 = |
2. Решите уравнения.
| а) 8X + 2,8 = 18,6 | б) 28,1 : Y = 12,4 |
3. Решите задачу.
За два дня бригада собрала 147,6 кг ягод. В первый день они собрали 4/9 части урожая ягод. Сколько кг ягод они собрали во второй день?4. Решите задачу.
Две бригады собирали картофель. Первая бригада собрала в 3 раза больше картофеля, чем вторая. Обе бригады вместе собрали 49,6 ц урожая. Сколько центнеров картофеля собрали первая бригада и сколько вторая бригада?
Первая бригада собрала в 3 раза больше картофеля, чем вторая. Обе бригады вместе собрали 49,6 ц урожая. Сколько центнеров картофеля собрали первая бригада и сколько вторая бригада?Вариант III.
1. Выполните деление.
| а) 4,752 : 9 = | б) 472,49 : 6 = | в) 7 : 19 = | г) 0,044 : 10 = |
2. Решите уравнения.
| а) 5X + 2,5 = 24 | б) 14,2 : Y = 3,4 |
3. Решите задачу.
За 2 дня мотоциклист преодолел 394,1 км. В первый день он проехал 4⁄7 части пути. Сколько км он проехал во второй день?4. Решите задачу.
Мама собрала в 5 раз больше ягод, чем дочка. Вместе они собрали 34,5 кг ягод. Сколько ягод собрала мама и сколько дочка?Самостоятельная работа №18 на тему: «Среднее арифметическое»
Вариант I.
1. Найдите среднее арифметическое четырех чисел: 4,5; 5,6; 4,9; 5,1.
2. Решите задачу.
В течение часа машина двигалась со скоростью 67,5 км/ч, в течение второго часа – со скоростью 51,6 км/ч. В течение третьего часа её скорость составила 72,3 км/ч. Какова средняя скорость машины? Сколько км она преодолела за 3 часа?
В течение третьего часа её скорость составила 72,3 км/ч. Какова средняя скорость машины? Сколько км она преодолела за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 14,5. Первое число – 14,1, а второе число на 0,8 больше третьего числа. Назовите эти числа.4. Решите задачу.
Расстояние между двумя деревнями равно 340 км. Автомобиль преодолел половину пути со скоростью 58 км/ч, а вторую половину – со скоростью 49 км/ч. Какова средняя скорость автомобиля на протяжении всего пути?Вариант II.
1. Найдите среднее арифметическое четырех чисел: 12,3; 12,9; 11,6; 13,1.
2. Решите задачу.
В течение первого часа спортсмен шел со скоростью 11,2 км/ч, в течение второго часа – со скоростью 10,7 км/ч, а в течение третьего часа его скорость составила 9,8 км/ч. Какова средняя скорость спортсмена? Какое расстояние он прошел за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 28,5. Первое число – 28,2, а второе на 0,9 больше третьего числа. Назовите эти числа.
Назовите эти числа.4. Решите задачу.
Расстояние между двумя городами составляет 52 км. Первую половину пути велосипедист передвигался со скоростью 18 км/ч, а вторую половину – со скоростью 22 км/час. Какова средняя скорость велосипедиста на всем протяжении пути?Вариант III.
1. Найдите среднее арифметическое четырех чисел: 9,1; 9,9; 11,1; 10,7.
2. Решите задачу.
В течение первого часа лодка двигалась со скоростью 15,5 км/ч, во второй час движения её скорость составила 17,4 км/ч, а в течение третьего часа – 12,7 км/ч. Какая средняя скорость лодки? Сколько км она преодолела за 3 часа?3. Решите задачу.
Среднее арифметическое трех чисел составляет 13,2. Первое число – 13,9, а второе – на 0,7 больше третьего числа. Назовите эти числа.4. Решите задачу.
Расстояние между двумя деревнями составляет 24 км. Первую половину пути пешеход двигался со скоростью 8 км/ч, а вторую половину – со скоростью 9 км/ч. Какова средняя скорость пешехода на всем протяжении пути?Самостоятельная работа №19 на тему: «Проценты, задачи на проценты»
Вариант I.

1. Решите задачу.
В спортивной секции занимается 60 учеников, из них 70% составляют девочки. Сколько мальчиков занимается в спортивной секции?2. Решите задачу.
Ребята четвертых и пятых классов собирали макулатуру. Ребята пятого класса собрали 150 кг макулатуры, что составило 60% общего веса собранной макулатуры. Сколько кг макулатуры собрали ребята?3. Решите задачу.
Из 15 кг яблок получается 12 кг яблочного пюре. Каков процент выхода пюре из яблок?Вариант II.
1. Решите задачу.
В 5 классе числится 30 учеников, 60% из них – мальчики. Сколько девочек учится в 5 классе?2. Решите задачу.
2 бригады собирали помидоры. Первая бригада собрала 320 кг помидор, что составило 40% от общего урожая. Сколько всего помидор собрали обе бригады?3. Решите задачу.
Из 60 семян взошли 55 растений. Найдите процент всхожести семян.Вариант III.
1. Решите задачу.
В школе работает 40 человека. Из них 80% – женщины. Сколько мужчин работает в школе?2. Решите задачу.
Решите задачу.
3. Решите задачу.
При перемалывании 40 кг зерна получили 25 кг муки. Найдите процент выхода муки.Wolfram | Alpha Примеры: математика
Другие примеры
Элементарная математикаВыполняйте основную арифметику. Работайте с дробями, процентами и подобными основами. Решите проблемы с числовыми значениями и словами.
Выполните точную арифметику с дробями:
Еще примеры
Другие примеры
Алгебра Находите корни и расширяйте, факторизуйте или упрощайте математические выражения — от многочленов до полей и групп.
Еще примеры
Другие примеры
Исчисление и анализ Вычисляйте интегралы, производные и пределы, а также анализируйте суммы, произведения и ряды.
Решите обыкновенное дифференциальное уравнение:
Еще примеры
Другие примеры
Геометрия Вычисляет свойства геометрических объектов различных типов в 2-, 3-х или более высоких измерениях. Изучайте и применяйте идеи из многих областей геометрии.
Изучайте и применяйте идеи из многих областей геометрии.
Вычислить свойства геометрической фигуры:
Постройте коническое сечение и определите его тип:
Вычислить свойства многогранника:
Еще примеры
Другие примеры
Дифференциальные уравнения Решайте дифференциальные уравнения любого порядка. Изучите решения и графики семейств решений. Задайте начальные условия, чтобы найти точные решения.
Изучите решения и графики семейств решений. Задайте начальные условия, чтобы найти точные решения.
Решите линейное обыкновенное дифференциальное уравнение:
Решите нелинейное уравнение:
Еще примеры
Другие примеры
Построение и графика Визуализируйте функции, уравнения и неравенства. Сделайте это в 1, 2 или 3 измерениях. Сделайте полярные и параметрические графики.
Сделайте это в 1, 2 или 3 измерениях. Сделайте полярные и параметрические графики.
Постройте область, удовлетворяющую множеству неравенств:
Еще примеры
Другие примеры
Числа Работа с разными числами. Проверьте принадлежность к большим множествам, таким как рациональные числа или трансцендентные числа. Преобразование между базами.
Проверьте принадлежность к большим множествам, таким как рациональные числа или трансцендентные числа. Преобразование между базами.
Вычислить десятичное приближение к указанному количеству цифр:
Преобразуйте десятичное число в другое основание:
Еще примеры
Другие примеры
Тригонометрия Выполняйте тригонометрические вычисления и исследуйте свойства тригонометрических функций и тождеств.
Вычислить значения тригонометрических функций:
Решите тригонометрическое уравнение:
Еще примеры
Другие примеры
Линейная алгебра Исследуйте и вычисляйте свойства векторов, матриц и векторных пространств.
Вычислить свойства вектора:
Вычислить свойства матрицы:
Определите, является ли набор векторов линейно независимым:
Еще примеры
Другие примеры
Теория чисел Анализировать целые числа; подмножества целых чисел, включая простые числа; и связанные идеи.
Вычислить разложение на простые множители:
Решите диофантово уравнение:
Еще примеры
Другие примеры
Дискретная математика Исследуйте последовательности и повторения, решайте общие задачи комбинаторики и вычисляйте свойства графов и решеток.
Вычислите возможную формулу и продолжение для последовательности:
Проанализируйте граф, заданный правилами смежности:
Еще примеры
Другие примеры
Комплексный анализ Анализируйте функции и выражения, содержащие мнимые числа или комплексные переменные.
Вычислить свойства функции сложной переменной (используйте переменную z ):
Вычислить остаток функции в точке:
Еще примеры
Другие примеры
Прикладная математика Выполнять численный анализ и оптимизацию систем и объектов, включая упаковку и покрытие объектов и систем управления.
Свернуть или развернуть функцию:
Численно интегрируйте функции, которые не могут быть объединены символически:
Еще примеры
Другие примеры
Логика и теория множеств Оценивать выражения логической логики и выражения, включающие множества и операторы множеств. Решите булевы уравнения. Вычислить таблицы истинности. Сгенерируйте диаграммы Венна.
Решите булевы уравнения. Вычислить таблицы истинности. Сгенерируйте диаграммы Венна.
Еще примеры
Другие примеры
Математические функции Изучите свойства математических функций, такие как непрерывность, сюръективность и четность.Используйте известные специальные функции или теоретико-числовые функции.
Выполняйте вычисления со специальными функциями:
Выполните вычисления с теоретико-числовыми функциями:
Найдите представления для функции:
Еще примеры
Другие примеры
Математические определения Запрашивайте различные определения и описания в математике.
Найдите информацию о математической концепции:
Еще примеры
Другие примеры
Известные математические задачи Соберите информацию об известных проблемах, гипотезах, теоремах и парадоксах. Узнайте о них и их разработчиках.
Узнайте о них и их разработчиках.
Получите информацию о математической гипотезе:
Получите историческую информацию о теореме:
Еще примеры
Другие примеры
Непрерывные дроби Compute; узнать об алгоритмах, определениях и вовлеченных теоремах; или найдите свойства непрерывных дробей.
Найдите представление числа в виде непрерывной дроби:
Найдите определения терминологии непрерывной дроби:
Найдите статьи о непрерывных дробях по автору:
Еще примеры
Другие примеры
Статистика Вычислять свойства наборов данных, выполнять статистический вывод или моделировать данные. Работайте с распределениями вероятностей и случайными величинами.
Работайте с распределениями вероятностей и случайными величинами.
Вычислить основную описательную статистику для набора данных:
Найдите размер выборки, необходимый для оценки биномиального параметра:
Еще примеры
Другие примеры
Вероятность Вычислить вероятности наступления определенных событий. Вычисляйте совместные, непересекающиеся или условные вероятности и применяйте их к реальным ситуациям.
Вычисляйте совместные, непересекающиеся или условные вероятности и применяйте их к реальным ситуациям.
Вычислите вероятность объединения событий:
Вычислите вероятности подбрасывания монеты:
Еще примеры
Другие примеры
Общая математика ядра Получите информацию об общих основных стандартах математики для детей от детского сада до восьмого класса.
Вычислить выражение (CCSS.Math.Content.6.EE.A.2c):
Выполните несколько операций с рациональными числами (CCSS.Math.Content.7.NS.A.2c):
Еще примеры
Wolfram | Alpha Примеры: математические функции
Другие примеры
Домен и диапазон Вычислить область определения и диапазон математической функции.
Вычислить область определения функции:
Вычислить диапазон функции:
Вычислить область и диапазон функции нескольких переменных:
Еще примеры
Другие примеры
Приемлемость и сюръективность Определите инъективность и сюръективность математической функции.
Определите, является ли данная функция инъективной:
Определите, является ли данная функция сюръективной:
Еще примеры
Другие примеры
Непрерывность Определите непрерывность математической функции.
Определите, является ли функция непрерывной:
Найдите разрывы функции:
Еще примеры
Другие примеры
Периодические функции Вычислить период периодической функции.
Вычислить период периодической функции:
Найдите периоды функции нескольких переменных:
Еще примеры
Четные и нечетные функции
Определите четность математической функции.
Определите, является ли функция четной или нечетной:
Еще примеры
Другие примеры
Специальные функции Вычислить свойства нескольких семейств специальных функций.
Вычислить свойства специальной функции:
Численно оцените специальную функцию:
Выполняйте вычисления со специальными функциями:
Еще примеры
Другие примеры
Теоретико-числовые функции Получите информацию об арифметических функциях, таких как функция Эйлера и Мёбиуса, и используйте их для вычисления свойств положительных целых чисел.
Получите информацию о теоретико-числовой функции:
Выполните вычисления с теоретико-числовыми функциями:
Еще примеры
Другие примеры
Формулы представления Вычислить альтернативные представления математической функции.
Найдите представления функции данного типа:
Еще примеры
Wolfram | Alpha Примеры: Элементарная математика
Другие примеры
АрифметикаВыполнение нескольких арифметических операций.
Еще примеры
Другие примеры
Фракции Выполняет арифметические действия с дробями.
Выполните точную арифметику с дробями:
Еще примеры
Другие примеры
Проценты Вычислить проценты или решить проблемы увеличения / уменьшения процента.
Преобразуйте дробь в процент:
Рассчитайте процент от количества:
Рассчитайте цену со скидкой:
Еще примеры
Другие примеры
Место значение Изучите диаграммы разрядов для десятичных чисел.
Показать значения разряда для числа:
Найдите значение конкретной цифры числа:
Еще примеры
Другие примеры
Число Тип Арифметика Выполнять вычисления по знакам, категориям и типам чисел.
Еще примеры
Wolfram | Примеры альфа: исчисление и анализ
Другие примеры
Интегралы Вычислить определенные и неопределенные интегралы от функций. Интегрировать по одной или нескольким переменным.
Интегрировать по одной или нескольким переменным.
Вычислить неопределенный интеграл:
Вычислить определенный интеграл:
Вычислить неправильный интеграл:
Еще примеры
Другие примеры
Производные Возьмем производную от функций одного или нескольких переменных. Вычислить частную производную выражений с более чем одной переменной.
Вычислить частную производную выражений с более чем одной переменной.
Вычислить производную функции:
Вычислить высшие производные:
Вычислить частные производные:
Еще примеры
Другие примеры
Пределы Исследуйте предельное поведение функции, когда она приближается к единственной точке или асимптотически приближается к бесконечности.
Вычислить односторонний предел:
Еще примеры
Другие примеры
Последовательности Вычисляйте и исследуйте последовательности целых чисел или других числовых значений. Найдите продолжения и формулы для известных или неизвестных последовательностей.
Найдите продолжения и формулы для известных или неизвестных последовательностей.
Вычислите возможную формулу и продолжение для последовательности:
Еще примеры
Другие примеры
Суммы Вычислить значение проиндексированных сумм или сумм последовательностей значений. Вычислить бесконечные суммы и найти условия сходимости.
Вычислить бесконечные суммы и найти условия сходимости.
Еще примеры
Другие примеры
ПродуктыВычислить индексированный продукт путем умножения конечного или бесконечного числа членов.
Вычислить проиндексированный продукт:
Вычислить бесконечное произведение:
Еще примеры
Другие примеры
Расширения серий Найдите серию Тейлора, серию Лорана и многое другое по любому вопросу.
Найдите расширение ряда Тейлора:
Укажите центральную точку и порядок расширения:
Еще примеры
Другие примеры
Приложения исчисления Используйте инструменты вычисления, такие как интегралы и производные, для вычисления свойств кривых, поверхностей, твердых тел и плоских областей.
Вычислите площадь, ограниченную двумя кривыми:
Найдите точки перегиба функции:
Еще примеры
Другие примеры
Векторный анализ Примените ротор, градиент и другие дифференциальные операторы к скалярным и векторным полям.
Вычислить градиент функции:
Вычислить альтернативные формы выражения векторного анализа:
Еще примеры
Другие примеры
Интегральные преобразования Вычислить преобразование Фурье, преобразование Лапласа и другие интегральные преобразования функций.
Вычислить преобразование Фурье:
Вычислить преобразование Лапласа:
Еще примеры
Другие примеры
Домен и диапазон Вычислить область и диапазон реальных математических функций. Нанесите домен и диапазон на числовую линию.
Нанесите домен и диапазон на числовую линию.
Вычислить область определения функции:
Вычислить диапазон функции:
Еще примеры
Другие примеры
Непрерывность Найдите разрывы и непрерывные интервалы функции. Также определите, являются ли определенные разрывы устранимыми или бесконечными из-за асимптоты.
Также определите, являются ли определенные разрывы устранимыми или бесконечными из-за асимптоты.
Определите, является ли функция непрерывной:
Найдите разрывы функции:
Еще примеры
22 примера математики в повседневной жизни — StudiousGuy
По мнению некоторых, математика — это просто использование сложных формул и вычислений, которые никогда не будут применяться в реальной жизни. Но математика — это универсальный язык, который применяется практически во всех сферах жизни. Да! Вы правильно прочитали; все время соблюдаются основные математические концепции. Вы были бы удивлены, если бы увидели, как математика возникает из неожиданных ситуаций.
Но математика — это универсальный язык, который применяется практически во всех сферах жизни. Да! Вы правильно прочитали; все время соблюдаются основные математические концепции. Вы были бы удивлены, если бы увидели, как математика возникает из неожиданных ситуаций.
Давайте продолжим, чтобы узнать о реальных жизненных ситуациях, в которых применяется математика.
1. Составление текущих бюджетовСколько я должен потратить сегодня? Когда я смогу купить новую машину? Стоит ли экономить больше? Как я смогу оплачивать свои EMI? Такие мысли обычно приходят нам в голову.Самый простой ответ на такие вопросы — математика. Мы составляем бюджеты на основе простых расчетов с помощью простых математических понятий. Так что нельзя сказать, что я никогда не буду изучать математику! Все, что нас окружает, так или иначе связано только с математикой.
Заявление:
- Основные математические операции (сложение, вычитание, умножение и деление)
- Расчет процентов
 Конструктивное назначение
Конструктивное назначение Знаете что, математика — это основа любого строительства. Множество расчетов, составление бюджетов, постановка целей, оценка стоимости и т. Д. Выполняются на основе математических расчетов. Если вы не верите, спросите любого подрядчика или строителя, и они объяснят, насколько важна математика для выполнения всех строительных работ.
Заявка:
- Оценка стоимости и прибыли
Мне нужно уменьшить количество жира в организме! Смогу ли я когда-нибудь обрести тело своей мечты? Как? Когда? Смогу ли я нарастить мышцы? Здесь используется простая концепция — математика. Да! основываясь на простых математических представлениях, мы можем ответить на вышеупомянутые вопросы. Мы устанавливаем свой распорядок в соответствии с расписанием тренировок, подсчитываем количество повторений во время упражнений и т. Д., Просто основываясь на математике.
Заявление:
- Основные математические операции (сложение, вычитание, умножение и деление)
- Логические и аналогичные рассуждения
Дизайн интерьера кажется увлекательной и интересной карьерой, но знаете ли вы точную реальность? Чтобы преуспеть в этой области, необходимо следовать множеству математических концепций, расчетов, бюджетов, оценок, целей и т. Д. Дизайнеры интерьера планируют интерьер на основе расчетов площади и объема, чтобы рассчитать и оценить правильную планировку любого помещения или здания. Такие концепции составляют важную часть математики.
Заявка:
5.Моделирование Так же, как дизайн интерьера, математика также является важным понятием дизайна одежды. От измерения, оценки количества и качества одежды, выбора цветовой гаммы, оценки стоимости и прибыли до производства ткани в соответствии с потребностями и вкусами клиентов, математика используется на каждом этапе.
Заявка:
- Основные математические операции
Наиболее очевидное место, где вы могли бы увидеть применение основных математических понятий, — это ближайший продуктовый магазин и супермаркет. Такие схемы, как «Фиксированная скидка 50%», «Купи один, получи один бесплатно» и т. Д. Можно встретить в большинстве магазинов. Покупатели посещают магазины, видят такие схемы, оценивают количество, которое нужно купить, вес, цену за единицу, расчет скидок и, наконец, общую цену продукта и покупают его.Расчеты производятся на основе основных математических представлений. Таким образом, и здесь математика составляет важную часть нашей повседневной жизни.
Заявление:
7. Готовка и выпечка На вашей кухне также выполняется математика. Для приготовления или выпечки чего-либо выполняется ряд шагов, в которых сообщается, какое количество продукта нужно использовать для приготовления, пропорции различных ингредиентов, способы приготовления, используемую посуду и многое другое. Они основаны на разных математических концепциях. Развлекайте детей на кухне, пока они что-нибудь готовят, — это увлекательный способ объяснить математику, а также основные методы приготовления пищи.
Они основаны на разных математических концепциях. Развлекайте детей на кухне, пока они что-нибудь готовят, — это увлекательный способ объяснить математику, а также основные методы приготовления пищи.
Заявка:
8. СпортМатематика улучшает когнитивные навыки человека и навыки принятия решений. Такие навыки очень важны для спортсмена, потому что с их помощью он может принимать правильные решения для своей команды. Если у человека нет таких способностей, он не сможет дать правильных оценок.Таким образом, математика также является важной частью спортивной сферы.
Заявка:
- Математические операции и алгоритм
В настоящее время управление временем — одна из самых сложных задач, с которой сталкивается множество людей. Человек хочет выполнить несколько заданий за ограниченное время. Не только руководство, некоторые люди даже не могут считывать время на аналоговых часах. Такие задачи можно решить только путем понимания основных понятий математики. Математика не только помогает нам понять, как управлять временем, но и ценить его.
Такие задачи можно решить только путем понимания основных понятий математики. Математика не только помогает нам понять, как управлять временем, но и ценить его.
Заявка:
- Основные математические операции
«Скорость, время и расстояние» Все эти три вещи изучаются на математических предметах, которые являются основами вождения независимо от вида транспорта. Математика помогает нам ответить на следующий вопрос;
- Какой должна быть скорость, чтобы преодолеть определенное расстояние?
- Сколько времени это займет?
- Повернуть налево или направо?
- Когда увеличивать или уменьшать скорость?
Заявка:
11.Автомобильная промышленность Различные компании-производители автомобилей производят автомобили в соответствии с требованиями клиентов. У каждой компании есть своя категория автомобилей: от микрокаров до роскошных внедорожников. В таких компаниях используются базовые математические операции для получения информации о различных требованиях клиентов.
У каждой компании есть своя категория автомобилей: от микрокаров до роскошных внедорожников. В таких компаниях используются базовые математические операции для получения информации о различных требованиях клиентов.
Заявка:
12. Компьютерные приложенияВы когда-нибудь задумывались, как работает компьютер? Насколько легко он выполняет каждую задачу в правильной последовательности действий? Простая причина этого — применение математики.Области математики и вычислений пересекаются как в компьютерных науках. Изучение компьютерных приложений практически невозможно без математики. Такие концепции, как вычисления, алгоритмы и многие другие, составляют основу для различных компьютерных приложений, таких как powerpoint, word, excel и т. Д., Которые невозможно запустить без математики.
Заявки:
13. Планирование поездки Нам всем наскучила однообразная жизнь, и мы хотим уехать в долгий отпуск. Для этого мы должны соответствующим образом все спланировать. Нам нужно подготовить бюджет поездки, количество дней, направления, отели, соответствующим образом скорректировать другую работу и многое другое. А вот и роль математики. Чтобы спланировать успешное путешествие, необходимо следовать основным математическим понятиям и операциям.
Для этого мы должны соответствующим образом все спланировать. Нам нужно подготовить бюджет поездки, количество дней, направления, отели, соответствующим образом скорректировать другую работу и многое другое. А вот и роль математики. Чтобы спланировать успешное путешествие, необходимо следовать основным математическим понятиям и операциям.
Заявка:
14. БольницыКаждая больница должна составить график работы врачей, систематические методы проведения любой серьезной операции, ведение записей о пациентах, записи об успешности операций, количество необходимых машин скорой помощи, обучение использованию лекарств. медсестрам, рецептам, расписанию всех задач и т. д.Все это делается на основе математических концепций.
Заявка:
15. Видеоигры Видеоигры — одно из самых любимых развлечений во всем мире, независимо от того, ребенок вы или взрослый. Студенты обычно пропускают уроки математики, чтобы играть в видеоигры. Но знаете ли вы, что здесь также изучают математику? Здесь они узнают о различных шагах и методах, которым необходимо следовать, чтобы выиграть любую игру.Не только во время игры, но и инженеры, которые представляют разные игры для людей, также следуют различным математическим концепциям.
Студенты обычно пропускают уроки математики, чтобы играть в видеоигры. Но знаете ли вы, что здесь также изучают математику? Здесь они узнают о различных шагах и методах, которым необходимо следовать, чтобы выиграть любую игру.Не только во время игры, но и инженеры, которые представляют разные игры для людей, также следуют различным математическим концепциям.
Заявки:
16. Прогноз погодыПрогноз погоды полностью основан на математической теории вероятностей. Благодаря этому мы узнаем о погодных условиях, например о том, будет ли сегодня солнечный день или пойдет дождь. Итак, в следующий раз, когда вы планируете поездку, не забудьте посмотреть прогноз погоды.
Заявление:
17. База прочих субъектов Хотя математика сама по себе является уникальным предметом. Но вы были бы удивлены, узнав, что он составляет основу для каждого предмета. Такие предметы, как физика, химия, экономика, история, бухгалтерский учет, статистика, фактически, каждый предмет основан на математике. Итак, в следующий раз, когда вы скажете: «Я никогда не буду изучать этот предмет по математике!» помните, эта тема никогда не покинет вас.
Итак, в следующий раз, когда вы скажете: «Я никогда не буду изучать этот предмет по математике!» помните, эта тема никогда не покинет вас.
Заявка:
18. Музыка и танцыМузыка и танцы — одно из самых распространенных детских увлечений. Здесь они также изучают математику во время пения и разучивают различные танцевальные движения. Координация в любом танце может быть достигнута с помощью простых математических шагов.
Заявление:
19. Обрабатывающая промышленностьЧасть математики под названием «Операционные исследования» — важная концепция, которой следуют на каждом производственном предприятии.Эта математическая концепция дает производителю простое представление о выполнении ряда задач в рамках производственной единицы, например,
.- Какое количество производить?
- Какие методы нужно использовать?
- Как увеличить производство?
- Как снизить себестоимость продукции?
- Удаление ненужных задач.

- Следующие методы, такие как целевая себестоимость, калькуляция затрат ABC, составление бюджета по рентабельности и многие другие.
Заявка:
20. Планировка городовГородское планирование включает в себя концепции составления бюджета, планирования, постановки целей и многое другое, что составляет часть математики. Никакая деятельность невозможна без математики.
Заявка:
21. Умение решать проблемыНавыки решения проблем — один из важнейших навыков, которым должен обладать каждый человек, чтобы добиться успеха в жизни.Такие навыки помогают человеку принимать правильные решения в жизни, будь то профессиональные или личные. Все это делается, когда человек имеет правильные знания основных математических понятий.
Заявка:
- Основные математические операции
 Маркетинг
Маркетинг Маркетинговые агентства составляют надлежащие планы относительно того, как продвигать любой продукт или услугу. Такие задачи, как продвижение продукта в Интернете, использование платформ социальных сетей, использование различных методов прямого и косвенного маркетинга, продажа от двери до двери, отправка электронных писем, совершение звонков, предоставление ряда схем, таких как «Купи один, получи один бесплатно», «Фиксированная скидка 50%», предлагая скидки в особых случаях и т. Д.все сделано на основе простых математических понятий. Таким образом, математика присутствует везде.
Заявка:
- Математические операции
SAT Math Примеры вопросов | College Board
Указания и номера вопросов ниже отражают то, с чем студенты столкнутся в день экзамена. Некоторые математические разделы позволяют использовать калькулятор, а другие — нет, как указано в инструкциях.
Откройте Раздел 3 своего листа для ответов, чтобы ответить на вопросы этого раздела.
Для вопросов 1–15 решите каждую проблему, выберите лучший ответ из предложенных вариантов и закрасьте соответствующий кружок на листе для ответов. Для вопросов 16–20 решите проблему и введите свой ответ в сетку на листе для ответов. Пожалуйста, ознакомьтесь с инструкциями перед вопросом 16 о том, как вводить свои ответы в сетку. Вы можете использовать любое доступное место в вашем тестовом буклете для черновой работы.
- Использование калькулятора [разрешено] / [запрещено].
- Все используемые переменные и выражения представляют собой действительные числа, если не указано иное.
- Рисунки, представленные в этом тесте, нарисованы в масштабе, если не указано иное.
- Все фигуры лежат в плоскости, если не указано иное.
- Если не указано иное, область заданной функции f представляет собой набор всех действительных чисел x , для которых является действительным числом.
Каталожный номер
Число дуговых градусов в окружности 360.
Число радианов дуги в окружности
Сумма углов треугольника в градусах равна 180.
Для вопросов, задаваемых студентами, студенты также будут видеть следующие направления:
Для вопросов 16–20 решите проблему и введите свой ответ в сетку, как описано ниже, на листе для ответов.
- Хотя это и не обязательно, рекомендуется написать свой ответ в полях вверху столбцов, чтобы помочь вам правильно заполнить кружки.Вы получите кредит только в том случае, если кружки заполнены правильно.
- Отметьте не более одного кружка в любом столбце.
- Ни один вопрос не имеет отрицательного ответа.
- Для некоторых задач может быть несколько правильных ответов. В таких случаях сетка только один ответ.
- Смешанные числа, например, должны быть разделены на сетку как 3,5 или
(Если ввести в сетку как, оно будет интерпретировано как не - Десятичные ответы: если вы получаете десятичный ответ с большим количеством цифр, чем может вместить сетка, он может быть либо округлен, либо усечен, но он должен заполнять всю сетку.

Если вы будете запрашивать (или были одобрены) для размещения формата, совместимого с вспомогательными технологиями (цифровое тестирование для использования с программой чтения с экрана или другой вспомогательной технологией) для SAT, вы можете также просмотреть примеры математических заданий в их полностью отформатированные версии, отсортированные как вопросы, допускающие использование калькулятора, и вопросы, не разрешающие использование калькулятора.
Обратите внимание, что все условия тестирования, включая запросы на вспомогательные технологии и специальные форматы, должны быть одобрены Службой Совета колледжей для студентов с ограниченными возможностями до начала экзамена.
Тест ACT Практические вопросы по математике
Тест ACT по математике Вопросы для практического теста | ДЕЙСТВОВАТЬ перейти к содержанию act.org, actprofile.org, act.org, actstudent.org, act. alertline.com, services.actstudent.org, карьера4.successfactors.com, Engagement.act.org, discoveractaspire.org, qc.vantage.com , myworkkeys.act.org, twitter.com, facebook.com, youtube.com, plus.google.com, linkedin.com, preview.act.org, workreadycommunities.org, pearson.com, instagram.com, actaspire.org, run2.careerready101.com, run2.keytrain.com, лидерствоblog.act.org
alertline.com, services.actstudent.org, карьера4.successfactors.com, Engagement.act.org, discoveractaspire.org, qc.vantage.com , myworkkeys.act.org, twitter.com, facebook.com, youtube.com, plus.google.com, linkedin.com, preview.act.org, workreadycommunities.org, pearson.com, instagram.com, actaspire.org, run2.careerready101.com, run2.keytrain.com, лидерствоblog.act.org
Тестовые подсказки
Настоящий тест по математике ACT содержит 60 вопросов, на которые нужно ответить за 60 минут.
- Внимательно прочтите каждый вопрос, чтобы убедиться, что вы понимаете тип требуемого ответа.
- Если вы решите использовать калькулятор, убедитесь, что это разрешено, он работает в день проверки и имеет надежные батареи.
- Используйте свой калькулятор с умом.
- Решите проблему.
- Найдите ваше решение среди вариантов ответа.

- Убедитесь, что вы ответили на заданный вопрос.
- Убедитесь, что ваш ответ разумный.
- Проверьте свою работу.
Наконечники калькулятора
- Ознакомьтесь с последней информацией о разрешенных и запрещенных калькуляторах.
- Вы не обязаны пользоваться калькулятором. Все проблемы решаются без калькулятора.
- Если вы регулярно используете калькулятор в своей математической работе, воспользуйтесь уже знакомым вам калькулятором при прохождении теста по математике. Использование более мощного, но незнакомого калькулятора вряд ли даст вам преимущество перед обычным калькулятором.
Щелкните по выбранным буквам ниже, чтобы просмотреть правильный ответ и пояснения.
Для полного взаимодействия с Практикой просмотрите эту страницу на планшете или настольном устройстве.
НАПРАВЛЕНИЯ: Решите каждую задачу, выберите правильный ответ, а затем закрасьте соответствующий овал в своем ответе.
Не зацикливайтесь на проблемах, которые отнимают слишком много времени. Решите столько, сколько сможете; затем вернитесь к остальным за то время, которое у вас осталось для этого теста.
Вам разрешается использовать калькулятор в этом тесте. Вы можете использовать свой калькулятор для решения любых задач по вашему выбору, но некоторые из них лучше всего решать без использования калькулятора.
Примечание. Если не указано иное, следует исходить из следующего.
- Иллюстративные фигуры НЕ обязательно выполнены в масштабе.
- Геометрические фигуры лежат на плоскости.
- Слово строка обозначает прямую линию.
- Слово среднее обозначает среднее арифметическое.
Это действие откроет новое окно.Вы хотите продолжить?
Если вы заходите на этот сайт из-за пределов США, Пуэрто-Рико или территорий США, перейдите на неамериканскую версию нашего веб-сайта.
 Можно настроить диапазон числел и ответов: до 10, до 20, до 100, примеры с трёхзначными, четёрыхзначными и пятизначными сичлами. Настраивается сложность примеров: с переходом через десяток или без перехода, сложение или вычитание, действия с «удобными» числами или примеры повышенной сложности…
Можно настроить диапазон числел и ответов: до 10, до 20, до 100, примеры с трёхзначными, четёрыхзначными и пятизначными сичлами. Настраивается сложность примеров: с переходом через десяток или без перехода, сложение или вычитание, действия с «удобными» числами или примеры повышенной сложности…