Динамика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Основы динамики
К оглавлению…
Если в кинематике только описывается движение тел, то в динамике изучаются причины этого движения под действием сил, действующих на тело.
Динамика – раздел механики, который изучает взаимодействия тел, причины возникновения движения и тип возникающего движения. Взаимодействие – процесс, в ходе которого тела оказывают взаимное действие друг на друга. В физике все взаимодействия обязательно парные. Это значит, что тела взаимодействуют друг с другом парами. То есть всякое действие обязательно порождает противодействие.
Сила – это количественная мера интенсивности взаимодействия тел. Сила является причиной изменения скорости тела целиком или его частей (деформации). Сила является векторной величиной. Прямая, вдоль которой направлена сила, называется линией действия силы.
Сила, оказывающая на тело такое же действие, как и все силы, действующие на него, вместе взятые, называется равнодействующей силой. Она равна векторной сумма всех сил, действующих на тело:
Чтобы найти векторную сумму нескольких сил нужно выполнить чертеж, где правильно нарисовать все силы и их векторную сумму, и по данному чертежу с использованием знаний из геометрии (в основном это теорема Пифагора и теорема косинусов) найти длину результирующего вектора.
Виды сил:
1. Сила тяжести. Приложена к центру масс тела и направлена вертикально вниз (или что тоже самое: перпендикулярно линии горизонта), и равна:
где: g — ускорение свободного падения, m — масса тела. Не перепутайте: сила тяжести перпендикулярна именно горизонту, а не поверхности на которой лежит тело. Таким образом, если тело лежит на наклонной поверхности, сила тяжести по-прежнему будет направлена строго вниз.
Не перепутайте: сила тяжести перпендикулярна именно горизонту, а не поверхности на которой лежит тело. Таким образом, если тело лежит на наклонной поверхности, сила тяжести по-прежнему будет направлена строго вниз.
2. Сила трения. Приложена к поверхности соприкосновения тела с опорой и направлена по касательной к ней в сторону противоположную той, куда тянут, или пытаются тянуть тело другие силы.
3. Сила вязкого трения (сила сопротивления среды). Возникает при движении тела в жидкости или газе и направлена против скорости движения.
4. Сила реакции опоры. Действует на тело со стороны опоры и направлена перпендикулярно опоре от нее. Когда тело опирается на угол, то сила реакции опоры направлена перпендикулярно поверхности тела.
5. Сила натяжения нити. Направлена вдоль нити от тела.
6. Сила упругости. Возникает при деформации тела и направлена против деформации.
Обратите внимание и отметьте для себя очевидный факт: если тело находится в покое, то равнодействующая сил равна нулю.
Проекции сил
К оглавлению…
В большинстве задач по динамике на тело действует больше чем одна сила. Для того чтобы найти равнодействующую всех сил в этом случае можно пользоваться следующим алгоритмом:
- Найдем проекции всех сил на ось ОХ и просуммируем их с учетом их знаков. Так получим проекцию равнодействующей силы на ось ОХ.
- Найдем проекции всех сил на ось OY и просуммируем их с учетом их знаков. Так получим проекцию равнодействующей силы на ось OY.
- Результирующая всех сил будет находится по формуле (теореме Пифагора):
При этом, обратите особое внимание на то, что:
- Если сила перпендикулярна одной из осей, то проекция именно на эту ось будет равна нулю.
- Если при проецировании силы на одну из осей «всплывает» синус угла, то при проецировании этой же силы на другую ось всегда будет косинус (того же угла). Запомнить при проецировании на какую ось будет синус или косинус легко.
 Если угол прилежит к проекции, то при проецировании силы на эту ось будет косинус.
Если угол прилежит к проекции, то при проецировании силы на эту ось будет косинус. - Если сила направлена в ту же сторону что и ось, то ее проекция на эту ось будет положительной, а если сила направлена в противоположную оси сторону, то ее проекция на эту ось будет отрицательной.
Законы Ньютона
К оглавлению…
Законы динамики, описывающие влияние различных взаимодействий на движение тел, были в одной из своих простейших форм, впервые четко и ясно сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год), поэтому эти законы также называют Законами Ньютона. Ньютоновская формулировка законов движения справедлива только в
Есть и другие ограничения на применимость законов Ньютона. Например, они дают точные результаты только до тех пор, пока применяются к телам, скорости которых много меньше скорости света, а размеры значительно превышают размеры атомов и молекул (обобщением классической механики на тела, двигающиеся с произвольной скоростью, является релятивистская механика, а на тела, размеры которых сравнимы с атомными — квантовая механика).
Первый закон Ньютона (или закон инерции)
Формулировка: В ИСО, если на тело не действуют никакие силы или действие сил скомпенсировано (то есть равнодействующая сил равна нулю), то тело сохраняет состояние покоя или равномерного прямолинейного движения.
Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией. Поэтому первый закон Ньютона называют законом инерции. Итак, причиной изменения скорости движения тела целиком или его частей всегда является его взаимодействие с другими телами. Для количественного описания изменения движения тела под воздействием других тел необходимо ввести новую величину – массу тела.
Масса – это свойство тела, характеризующее его инертность (способность сохранять скорость постоянной). В Международной системе единиц (СИ) масса тела измеряется в килограммах (кг). Масса тела – скалярная величина. Масса также является мерой количества вещества:
Второй закон Ньютона – основной закон динамики
Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела и сила.
Формулировка: Ускорение, приобретаемое телом в ИСО, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе этого тела:
Однако при решении задач по динамике второй закон Ньютона целесообразно записывать в виде:
Если на тело одновременно действуют несколько сил, то под силой в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил. Если равнодействующая сила равна нолю, то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения, т.к. ускорение будет нулевым (первый закон Ньютона).
Третий закон Ньютона
Формулировка: В ИСО тела действуют друг на друга с силами, равными по модулю и противоположными по направлению, лежащими на одной прямой и имеющими одну физическую природу:
Эти силы приложены к разным телам и поэтому не могут уравновешивать друг друга.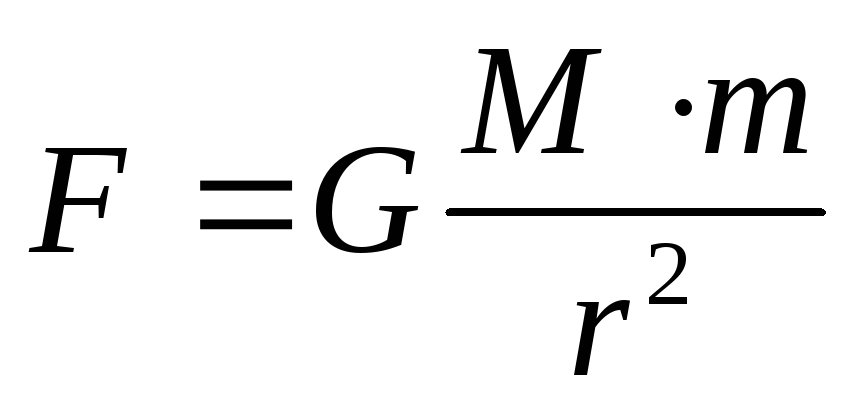 Обратите внимание, что складывать можно только силы, которые одновременно действуют на одно из тел. При взаимодействии двух тел возникают силы, равные по величине и противоположные по направлению, но складывать их нельзя, т.к. приложены они к разным телам.
Обратите внимание, что складывать можно только силы, которые одновременно действуют на одно из тел. При взаимодействии двух тел возникают силы, равные по величине и противоположные по направлению, но складывать их нельзя, т.к. приложены они к разным телам.
Алгоритм решения задач по динамике
Задачи по динамике решаются с помощью законов Ньютона. Рекомендуется следующий порядок действий:
1. Проанализировав условие задачи, установить, какие силы действуют и на какие тела;
2. Показать на рисунке все силы в виде векторов, то есть направленных отрезков, приложенных к телам, на которые они действуют;
3. Выбрать систему отсчета, при этом полезно одну координатную ось направить туда же, куда направлено ускорение рассматриваемого тела, а другую – перпендикулярно ускорению;
4. Записать II закон Ньютона в векторной форме:
5. Перейти к скалярной форме уравнения, то есть записать все его члены в том же порядке в проекциях на каждую из осей, без знаков векторов, но учитывая, что силы, направленные против выбранных осей будут иметь отрицательные проекции, и, таким образом, в левой части закона Ньютона они будут уже вычитаться, а не прибавляться. В результате получатся выражения вида:
В результате получатся выражения вида:
6. Составить систему уравнений, дополнив уравнения, полученные в предыдущем пункте, в случае необходимости, кинематическими или другими простыми уравнениями;
7. Провести далее все необходимые математические этапы решения;
8. Если в движении участвует несколько тел, анализ сил и запись уравнений производится для каждого из них по отдельности. Если в задаче по динамике описывается несколько ситуаций, то подобный анализ производится для каждой ситуации.
При решении задач учитывайте также следующее: направление скорости тела и равнодействующей сил необязательно совпадают.
Сила упругости
К оглавлению…
Деформацией называют любое изменение формы или размеров тела. Упругими называют такие деформации, при которых тело полностью восстанавливает свою форму после прекращения действия деформирующей силы. Например, после того, как груз сняли с пружины, её длина в недеформированном состоянии не изменилась. При упругой деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Ее называют силой упругости. Простейшим видом деформации является деформация одностороннего растяжения или сжатия.
При упругой деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Ее называют силой упругости. Простейшим видом деформации является деформация одностороннего растяжения или сжатия.
При малых деформациях модуль силы упругости пропорционален деформации тела. При этом сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации, и может быть рассчитана по формуле:
где: k – жесткость тела, х – величина растяжения (или сжатия, другими словами: деформации тела), она равна модулю разности между конечной и начальной длиной деформируемого тела. Важно, что величина растяжения или сжатия не равна ни начальной, ни конечной длине тела в отдельности. Жесткость не зависит ни от величины приложенной силы, ни от деформации тела, а определяется только материалом, из которого изготовлено тело, его формой и размерами. В системе СИ жесткость измеряется в Н/м.
Утверждение о пропорциональности силы упругости и деформации называют законом Гука. В технике часто применяются спиралеобразные пружины. При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром.
В технике часто применяются спиралеобразные пружины. При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром.
Таким образом, у каждого конкретного тела (а не материала) есть своя жесткость и она не изменяется для данного тела. Таким образом, если у Вас в задаче по динамике несколько раз растягивали одну и ту же пружину Вы должны понимать, что ее жесткость во всех случаях была одна и та же. С другой стороны если в задаче было несколько пружин разных габаритов, но, например, все они были стальные, то тем не менее у них у всех будут разные жесткости. Так как жесткость не является характеристикой материала, то ее нельзя найти ни в каких таблицах. Жесткость каждого конкретного тела будет либо Вам дана в задаче по динамике, либо ее значение должно стать предметом некоторых дополнительных изысканий при решении данной задачи.
При сжатии сила упругости препятствует сжатию, а при растяжении – препятствует растяжению. Рассмотрим также то, как можно выразить жесткость нескольких пружин соединенных определённым образом. При параллельном соединении пружин общий коэффициент жесткости рассчитывается по формуле:
При последовательном соединении пружин общий коэффициент жесткости может быть найден из выражения:
Вес тела
К оглавлению…
Силу тяжести, с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни в неправильном смысле, под весом подразумевается масса, однако это не так.
Весом тела называют силу, с которой тело действует на опору или подвес. Вес – сила, которая, как и все силы, измеряется в ньютонах (а не в килограммах), и обозначается P. При этом предполагается, что тело неподвижно относительно опоры или подвеса. Согласно третьему закону Ньютона вес зачастую равен либо силе реакции опоры (если тело лежит на опоре), либо силы натяжении нити или силе упругости пружины (если тело висит на нити или пружине). Сразу оговоримся — вес не всегда равен силе тяжести.
Сразу оговоримся — вес не всегда равен силе тяжести.
Невесомость – это состояние, которое наступает, когда вес тела равен нолю. В этом состоянии тело не действует на опору, а опора на тело.
Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Перегрузка рассчитывается по формуле:
где: P – вес тела, испытывающего перегрузку, P0 – вес этого же тела в состоянии покоя. Перегрузка – безразмерная величина. Это хорошо видно из формулы. Поэтому не верьте писателям-фантастам, которые в своих книгах измеряют ее в g.
Запомните, что вес никогда не изображается на рисунках. Он просто вычисляется по формулам. А на рисунках изображается сила натяжения нити либо сила реакции опоры, которые по третьему закону Ньютона численно равны весу, но направлены в другую сторону.
Итак, отметим еще раз три существенно важных момента в которых часто путаются:
- Несмотря на то, что вес и сила реакции опоры равны по величине и противоположны по направлению, их сумма не равна нулю.
 Эти силы вообще нельзя складывать, т.к. они приложены к разным телам.
Эти силы вообще нельзя складывать, т.к. они приложены к разным телам. - Нельзя путать массу и вес тела. Масса – собственная характеристика тела, измеряется в килограммах, вес – это сила действия на опору или подвес, измеряется в Ньютонах.
- Если надо найти вес тела Р, то сначала находят силу реакции опоры N, или силу натяжения нити Т, а по третьему закону Ньютона вес равен одной из этих сил и противоположен по направлению.
Сила трения
К оглавлению…
Трение – один из видов взаимодействия тел. Оно возникает в области соприкосновения двух тел при их относительном движении или попытке вызвать такое движение. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело.
Сухое трение, возникающее при относительном покое тел, называют трением покоя. Сила трения покоя всегда равна по величине внешней вызывающей силе и направлена в противоположную ей сторону. Сила трения покоя не может превышать некоторого максимального значения, которое определяется по формуле:
Сила трения покоя всегда равна по величине внешней вызывающей силе и направлена в противоположную ей сторону. Сила трения покоя не может превышать некоторого максимального значения, которое определяется по формуле:
где: μ – безразмерная величина, называемая коэффициентом трения покоя, а N – сила реакции опоры.
Если внешняя сила больше максимального значения силы трения, возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. Она всегда направлена в сторону, противоположную направлению движения. Силу трения скольжения можно считать равной максимальной силе трения покоя.
Коэффициент пропорциональности μ поэтому называют также коэффициентом трения скольжения. Коэффициент трения μ – величина безразмерная. Коэффициент трения положителен и меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки их поверхностей. Таким образом коэффициент трения является неким конкретным числом для каждой конкретной пары взаимодействующих тел. Вы не сможете найти его ни в каких таблицах. Для Вас он должен либо быть дан в задаче, либо Вы сами должны найти его в ходе решения из каких-либо формул.
Вы не сможете найти его ни в каких таблицах. Для Вас он должен либо быть дан в задаче, либо Вы сами должны найти его в ходе решения из каких-либо формул.
Если в рамках решения задачи у Вас получается коэффициент трения больше единицы или отрицательный – Вы неправильно решаете эту задачу по динамике.
Если в условии задачи просят найти минимальную силу, под действием которой начинается движение, то ищут максимальную силу, под действием которой, движение ещё не начинается. Это позволяет приравнять ускорение тел к нулю, а значит значительно упростить решение задачи. При этом силу трения полагают равной ее максимальному значению. Таким образом рассматривается момент, при котором увеличение искомой силы на очень малую величину сразу вызовет движение.
Особенности решения задач по динамике с несколькими телами
К оглавлению…
Связанные тела
Алгоритм решения задач по динамике в которых рассматриваются несколько тел связанных нитями:
- Сделать рисунок.

- Записать второй закон Ньютона для каждого тела в отдельности.
- Если нить нерастяжима (а так в большинстве задач и будет), то ускорения всех тел будут одинаковы по модулю.
- Если нить невесома, блок не имеет массы, трение в оси блока отсутствует, то сила натяжения одинакова в любой точке нити.
Движение тела по телу
В задачах этого типа важно учесть, что сила трения на поверхности соприкасающихся тел действует и на верхнее тело, и на нижнее тело, то есть силы трения возникают парами. При этом они направлены в разные стороны и имеют равную величину, определяемую весом верхнего тела. Если нижнее тело тоже движется, то необходимо учитывать, что на него также действует сила трения со стороны опоры.
Вращательное движение
К оглавлению…
При движении тела по окружности независимо от того, в какой плоскости происходит движение, тело будет двигаться с центростремительным ускорением, которое будет направлено к центру окружности, по которой движется тело. При этом понятие окружность не надо воспринимать буквально. Тело может проходить только дугу окружности (например, двигаться по мосту). Во всех задачах этого типа одна из осей обязательно выбирается по направлению центростремительного ускорения, т.е. к центру окружности (или дуги окружности). Вторую ось целесообразно направить перпендикулярно первой. В остальном алгоритм решения этих задач совпадает с решением остальных задач по динамике:
При этом понятие окружность не надо воспринимать буквально. Тело может проходить только дугу окружности (например, двигаться по мосту). Во всех задачах этого типа одна из осей обязательно выбирается по направлению центростремительного ускорения, т.е. к центру окружности (или дуги окружности). Вторую ось целесообразно направить перпендикулярно первой. В остальном алгоритм решения этих задач совпадает с решением остальных задач по динамике:
1. Выбрав оси, записать закон Ньютона в проекциях на каждую ось, для каждого из тел, участвующих в задаче, или для каждой из ситуаций, описываемых в задаче.
2. Если это необходимо, дополнить систему уравнений нужными уравнениями из других тем по физике. Особенно хорошо нужно помнить формулу для центростремительного ускорения:
3. Решить полученную систему уравнений математическими методами.
Так же есть ряд задач на вращение в вертикальной плоскости на стержне или нити. На первый взгляд может показаться, что такие задачи будут одинаковы. Это не так. Дело в том, что стержень может испытывать деформации как растяжения, так и сжатия. Нить же невозможно сжать, она сразу прогибается, а тело на ней просто проваливается.
На первый взгляд может показаться, что такие задачи будут одинаковы. Это не так. Дело в том, что стержень может испытывать деформации как растяжения, так и сжатия. Нить же невозможно сжать, она сразу прогибается, а тело на ней просто проваливается.
Движение на нити. Так как нить только растягиваться, то при движении тела на нити в вертикальной плоскости в нити будет возникать только деформация растяжения и, как следствие, сила упругости, возникающая в нити, будет всегда направлена к центру окружности.
Движение тела на стержне. Стержень, в отличие от нити, может сжиматься. Поэтому в верхней точке траектории скорость тела, прикрепленного к стержню, может быть равна нулю, в отличии от нити, где скорость должна быть не меньше определенного значения, чтобы нить не сложилась. Силы упругости, возникающие в стержне, могут быть направлены как к центру окружности, так и в противоположную сторону.
Поворот машины. Если тело движется по твердой горизонтальной поверхности по окружности (например, автомобиль проходит поворот), то силой, которая удерживает тело на траектории, будет являться сила трения. При этом сила трения направлена в сторону поворота, а не против него (наиболее частая ошибка), она помогает машине поворачивать. Например, когда машина поворачивает направо, сила трения направлена в сторону поворота (направо).
При этом сила трения направлена в сторону поворота, а не против него (наиболее частая ошибка), она помогает машине поворачивать. Например, когда машина поворачивает направо, сила трения направлена в сторону поворота (направо).
Закон всемирного тяготения. Спутники
К оглавлению…
Все тела притягиваются друг к другу с силами, прямо пропорциональными их массам и обратно пропорциональными квадрату расстояния между ними. Таким образом закон всемирного тяготения в виде формулы выглядит следующим образом:
Такая запись закона всемирного тяготения справедлива для материальных точек, шаров, сфер, для которых r измеряется между центрами. Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной. В системы СИ он равен:
Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле или другой планете. Если M – масса планеты, Rп – ее радиус, то ускорение свободного падения у поверхности планеты:
Если M – масса планеты, Rп – ее радиус, то ускорение свободного падения у поверхности планеты:
Если же удалиться от поверхности Земли на некоторое расстояние h, то ускорение свободного падения на этой высоте станет равно (при помощи нехитрых преобразований можно также получить соотношение между ускорением свободного падения на поверхности планеты и ускорением свободного падения на некоторой высоте над поверхностью планеты):
Рассмотрим теперь вопрос об искусственных спутниках планет. Искусственные спутники движутся за пределами атмосферы (если таковая у планеты имеется), и на них действуют только силы тяготения со стороны планеты. В зависимости от начальной скорости траектория космического тела может быть различной. Мы рассмотрим здесь только случай движения искусственного спутника по круговой орбите практически на нулевой высоте над планетой. Радиус орбиты таких спутников (расстояние между центром планеты и точкой где находится спутник) можно приближенно принять равным радиусу планеты Rп. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Скорость спутника на орбите вблизи поверхности (на нулевой высоте над поверхностью планеты) называют первой космической скоростью. Первая космическая скорость находится по формуле:
Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Скорость спутника на орбите вблизи поверхности (на нулевой высоте над поверхностью планеты) называют первой космической скоростью. Первая космическая скорость находится по формуле:
Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу планеты. Для спутников, движущихся по круговым траекториям на значительном удалении от планеты, гравитационное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника в таком случае находится с помощью формулы:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Если речь идёт о планете Земля, то нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6RЗ, период обращения спутника окажется равным 24 часам. {n}Fi$.
{n}Fi$.
Первый закон Ньютона: если на тело не действуют другие тела, то тело движется прямолинейно и равномерно: $\overrightarrow{F} = 0$.
Важно! Если есть ИСО, то любая другая система, движущаяся относительно неё прямолинейно и равномерно, также является инерциальной.
Второй закон Ньютон: ускорение тела прямо пропорционально силе, действующей на него, и обратно пропорционально его массе: $\overrightarrow{a} = \frac{\overrightarrow{F}}{m}$.
Другая запись формулы второго закона Ньютона (основное уравнение динамики): $\overrightarrow{F} = m \overrightarrow{a}$ .
Третий закон Ньютона: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению: $\overrightarrow{F}_{12} = -\overrightarrow{F}_{21}$.
Второй закон Ньютона для системы тел: приращение импульса $\Delta \overrightarrow{P}$ системы тел равно по величине и по направлению импульсу внешних сил, действующих на тело, за то же время: $\Delta \overrightarrow{p} = \overrightarrow{F} \Delta t$.
Границы применимости: справедливы для материальных точек или поступательно движущихся тел; для скоростей много меньше скорости света в вакууме; выполняются в ИСО.
Решение задачи на применение второго закона Ньютона
Глава 7. Вращательное движение. Кинематика и динамика
Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
(7.2) |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7. |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7. |
Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
(7.6) |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (задача 7.1.3), получаем
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.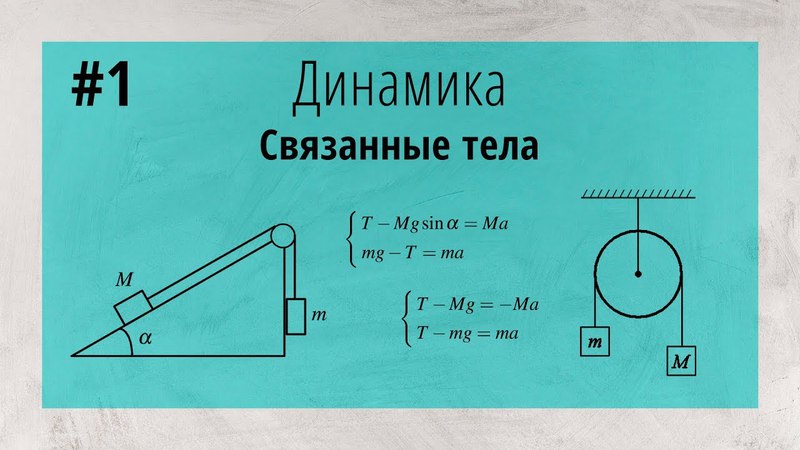 1.5), из формулы (7.5) находим квадрат угловой скорости диска
1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7.5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно
Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия.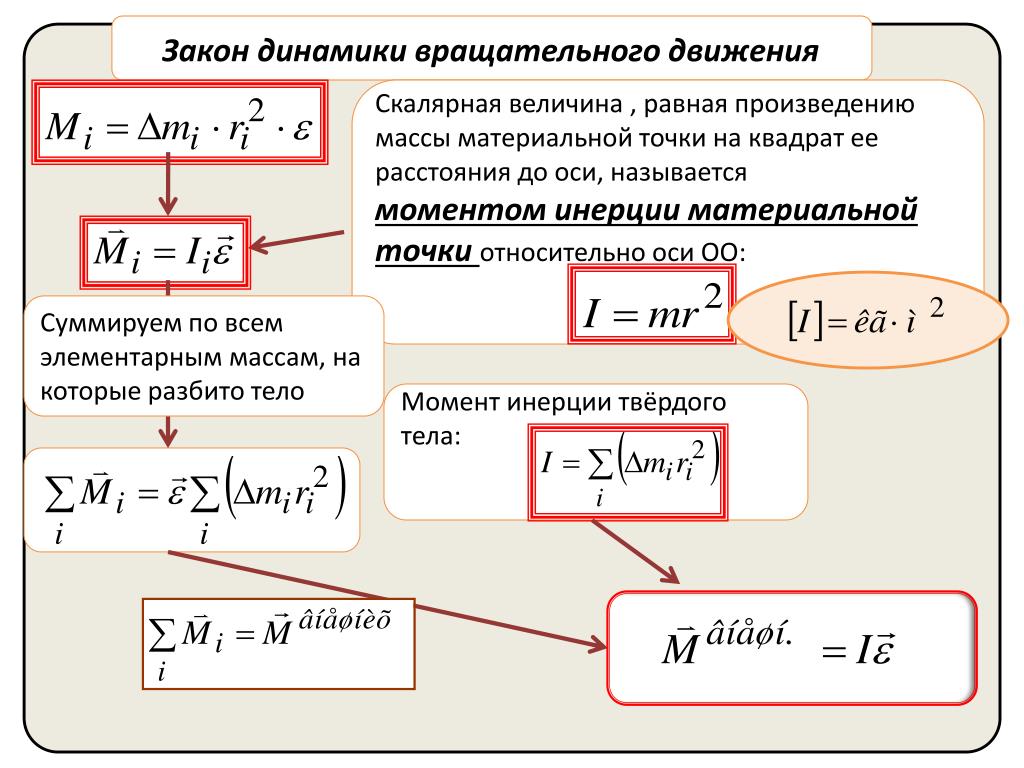 Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7. 2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).
Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7. 2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7.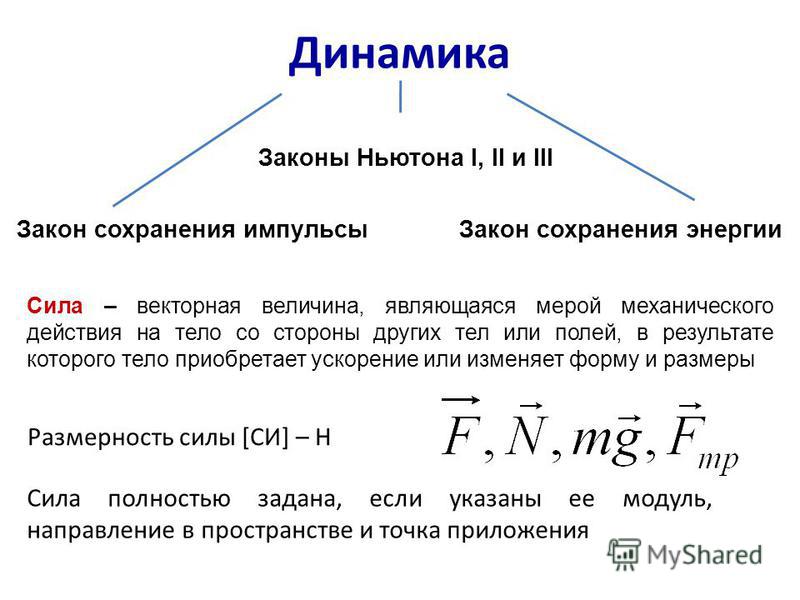 2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7. 2.9 – ответ 1).
2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).
Excel. Часть 2. Статистика
В первом выпуске «Мастерской» об Excel «Важные истории» рассказали о том, как устроена программа, как импортировать и сохранять данные, что такое формулы и функции, как выполнить сортировку и фильтрацию данных. В этот раз – подробнее о списке функций, которые пригодятся журналистам для получения статистических выводов из данных.
Чаще всего дата-журналисты анализируют данные, чтобы найти в них новые тенденции и ответы на вопросы:
- Какие масштабы у явления?
- Какую часть целого составляет то или иное явление?
- Насколько изменилась ситуация по сравнению с предыдущим периодом?
- Ситуация ухудшилась или улучшилась, показали выросли или упали?
Получить ответы на эти вопросы помогают математические и статистические функции Excel.
- Для примера будем использовать набор данных по количеству заболевших коронавирусом в России, собранный Медиазоной на основе данных федерального Роспотребнадзора и его региональных штабов. Исходные данные в формате json можно сказать здесь, а сводные данные по России, переведенные нами в формат xlsx, удобный для работы в Excel, здесь.
Процент от целого
Для того, чтобы получить представление о масштабах явления, принято считать, какую долю целого оно составляет. Например, в исследовании «Важных историй» о насилии над пожилыми говорится о том, что 82,5% таких преступлений совершаются родственниками пострадавших.
С помощью вычисления процента можно посчитать, какая доля выявленных заболевших выздоровела на сегодня в России, согласно официальным данным. Произвести такие расчеты позволяют Google Spreadsheets. Формула для подсчета процента выглядит так: =Часть / Целое * 100. В нашем примере: =Число выздоровевших / Число заболевших * 100.
Формула для подсчета процента выглядит так: =Часть / Целое * 100. В нашем примере: =Число выздоровевших / Число заболевших * 100.
Формула расчета процентного изменения
Прирост или падение. Процентное изменение
Чтобы показать, как ситуация меняется со временем, считают изменение. Например, согласно официальным данным, 7 мая в России выявили на 702 заболевших больше, чем днем ранее – рост продолжается.
Прийти к такому выводу помогает простая формула вычитания: =Новое значение – Старое значение. Например: =Значение за этот год – Значение за предыдущий год. В нашем случае: =Значение за сегодня – значение за вчера. Если число получилось положительным, это указывает на прирост, если отрицательным – на падение.
Чаще всего абсолютные величины не дают нам представления о ситуации: 702 человека – это много или мало? А если днем ранее было выявлено на 471 человека больше, чем до этого, то темпы прироста увеличились или снизились?
В таких случаях показывают процентное изменение, которое тоже может быть положительным или отрицательным – сообщающем о росте или падении. Оно покажет, что 7 мая прирост составил 6,8%, и этот показатель остался на уровне предыдущего дня. Значит темпы прироста не изменились, несмотря на то, что в абсолютных числах в эти дни было выявлено разное количество заболевших людей.
Оно покажет, что 7 мая прирост составил 6,8%, и этот показатель остался на уровне предыдущего дня. Значит темпы прироста не изменились, несмотря на то, что в абсолютных числах в эти дни было выявлено разное количество заболевших людей.
Процентное изменение рассчитывается по формуле: =(Новое значение – Старое значение) / Старое значение * 100. В нашем случае: =(Количество заболевших на сегодня – Количество заболевших на вчера) / Количество заболевших на вчера * 100.
Формула расчета процентного изменения
Среднее арифметическое
Еще одна распространенная операция над данными – это поиск среднего значения. Среднее необходимо, чтобы сделать обобщенный вывод из данных. Например, чтобы узнать, что, в среднем, за последнюю неделю в день выявляли 10 тыс. зараженных.
Формула среднего арифметического выглядит так: =Сумма всех значений / Количество значений. В нашем случае: = Сумма всех новых выявленных случаев заражения за неделю / 7. Чтобы не вводить формулу, можно воспользоваться функцией СРЗНАЧ, которая считает среднее арифметическое. В скобках после функции надо указать диапазон значений, среднее которых мы ищем: =СРЗНАЧ(диапазон).
В скобках после функции надо указать диапазон значений, среднее которых мы ищем: =СРЗНАЧ(диапазон).
Вычислять среднее нужно еще и для того, чтобы увидеть выпадающие значения в ряде чисел, как например, в расследовании «Важных историй» о закупках аппаратов ИВЛ. Если посчитать среднюю цену поставки аппарата ИВЛ и сравнить ее с остальными ценами, это позволит сделать вывод о том, какая часть закупок была совершена по завышенной цене.
Медиана
Существует несколько видов среднего, и не всегда для корректных выводов подходит среднее арифметическое. Иногда, когда значения в наборе данных сильно отличаются – например, в списке зарплат есть очень низкие и очень высокие, среднее арифметическое может искажать картину.
В таких случаях лучше считать медиану. Медиана показывает число в середине упорядоченного набора чисел. Это похоже на границу, которая делит данные пополам: половина данных находится выше нее, а половина – ниже. Рассчитывается она так: =МЕДИАНА(диапазон). В случае с количеством заболевших по дням медиана полезной не будет, но если бы мы работали с данными по возрастам заболевших, можно было бы посчитать не среднее, а медиану. Она показала бы возраст, ниже и выше которого находится равное количество заболевших. Исходя из медианы, можно было бы сказать, что половина заболевших моложе (или старше), например, 45 лет.
Она показала бы возраст, ниже и выше которого находится равное количество заболевших. Исходя из медианы, можно было бы сказать, что половина заболевших моложе (или старше), например, 45 лет.
Мода
Мода в статистике – это еще один вид среднего, она показывает цифру, которая встречается в наборе данных чаще других. Она рассчитывается с помощью соответствующей функции, после которой указывается диапазон значений =МОДА(диапазон).
Среднее, медиана и мода
Вычислять моду из данных о количестве заболевших бесполезно, но если бы мы анализировали, например, данные об оценках студентов за экзамен, мода показала бы самую часто встречающуюся отметку. Если большинство сдали экзамен на пятерки и только пара студентов получили двойки, средняя успеваемость была бы меньше 5, но мода показала бы, что чаще всего студенты получали все-таки наивысшую оценку.
Максимум и минимум
Часто журналистов интересует, когда какое-либо явление достигало своего пика или наоборот оказывалось наименее заметным. В прошлом выпуске мы уже рассказывали, как быстро найти минимум и максимум с помощью сортировки. То же самое можно сделать и с помощью функций МИН и МАКС, после которых в скобках необходимо указать диапазон значений. Например: = МАКС(диапазон). Так можно быстро узнать, что рекорд по выявлению новых случаев заболевания за сутки был поставлен 7 мая.
В прошлом выпуске мы уже рассказывали, как быстро найти минимум и максимум с помощью сортировки. То же самое можно сделать и с помощью функций МИН и МАКС, после которых в скобках необходимо указать диапазон значений. Например: = МАКС(диапазон). Так можно быстро узнать, что рекорд по выявлению новых случаев заболевания за сутки был поставлен 7 мая.
На душу населения
При сравнении данных из разных выборок, например, по разным странам или регионам важно учитывать, что в них проживает разное количество людей, и это влияет на результаты сопоставления. Например, сравнивая масштабы распространения коронавируса в разных странах, часто показывают не только абсолютное количество зараженных, но и показатель в пересчете на душу населения.
Пересчет на душу населения
Формула для подсчета количества случаев в пересчете на душу населения такая: = Количество выявленных заболевших / Численность населения * 100 000. В таком случае полученный результат будет показывать количество выявленных случаев на 100 тыс. населения (иногда считают на 10 тыс. населения, тогда последняя цифра в формуле меняется на 10 000).
населения (иногда считают на 10 тыс. населения, тогда последняя цифра в формуле меняется на 10 000).
Формула темпа роста в процентах и примеры
Понятие показателя темпа роста
Показатель темпа роста может измеряться в процентах или в относительных значениях.
Темп экономического роста напрямую зависит от типа экономического роста. В экономике выделяют два 2 типа экономического роста:
- Экстенсивный тип роста, при которомрост объема производства происходит благодаря внедрению определенного, большого числа факторов (сырья, топлива, рабочей силы, оборудования и др.).
- Интенсивный тип роста увеличивает производственный объем за счет совершенствования качественных показателей (квалификации, технологий, достижений научно-технического прогресса). При данном типе роста изменения происходят посредством улучшения качества, а не количества.
Если в экономике происходит интенсивный тип роста, то темпы могут даже немного снижаться, если сравнивать его с экстенсивным типом. Тем не менее, это не свидетельствует о спаде экономического развития или то, что оно замедляется.
Тем не менее, это не свидетельствует о спаде экономического развития или то, что оно замедляется.
Существует несколько особенностей типов роста:
- В случае экстенсивного типа роста экономика может сохранить пропорции, свои структурные характеристики, при этом продолжить развитие вширь.
- В процессе интенсивного типа роста экономика может стать динамичной благодаря расширению производства, а также по причине прогрессивных структурных перестроек.
Формула темпа роста в процентах
В общем виде формула темпа роста в процентах выглядит следующим образом:
Тр=Pнп/Pкп
Здесь Тр –показатель темпа роста,
Рнп – показатель на начало периода,
Ркп – показатель на конец периода.
Для того, что бы получить более наглядный результат, полученное значение принято умножать на 100%, что бы выразить формулу темпа роста в процентах.
Значения темпа роста
Темп роста отражает динамику, на сколько процентов изменяется (растет) статистический показатель текущего периода при сравнении его со значением предыдущего периода.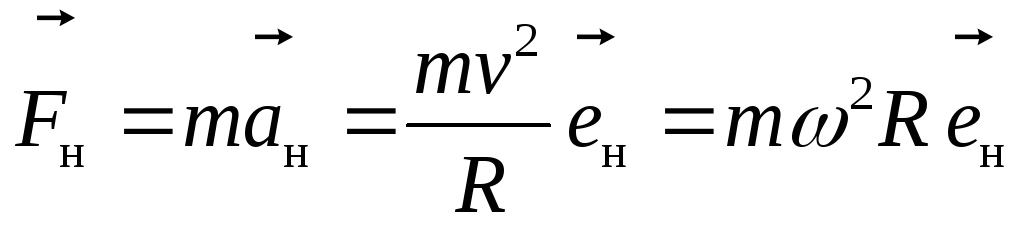
Если использовать различные значения формулы, то можно увидеть 3 варианта динамики значений:
1) Если темп роста больше 100%, то можно наблюдать положительную динамику.
2) Темп роста = 100% не означает никаких изменений.
3) Темп роста меньше 100% свидетельствует об отрицательной динамике.
Темп роста и темп прироста
Часто происходит путаница при определении понятий темпа роста и прироста, так как их формулы легко спутать.
Для того, что бы определить темпа прироста из показателей расчетного периода вычитают показатель базового периода, впоследствии это результат делят на показатель базисного периода и умножают на 100%. В итоге мы получаем значение темпа прироста в процентах.
Для того, чтобы не происходила путаница в этих понятиях, можно отметить, что темп роста показывает увеличение самого показателя, то есть во сколько раз он изменился в определенном временном промежутке.
Темп прироста же показывает, насколько выросло значение показателя за этот период времени (сравнение).
Примеры решения задач
Технологии анализа СМИ и соцсетей
Индекс Цитируемости
Индекс Цитируемости (ИЦ) – показатель качества распространения контента СМИ.
ИЦ учитывает:
- количество ссылок на источник информации в других СМИ и влиятельность* источника, опубликовавшего ссылку;
- социальную влиятельность СМИ (количество likes и shares материалов СМИ в соцмедиа).
ИЦ рассчитывается на базе математико-лингвистического анализа текстов 71 000 открытых источников СМИ и 900 млн. аккаунтов соцмедиа.
Во избежание самоцитирования из анализа исключены ссылки на СМИ, входящие в один медиахолдинг, также объединенные единым брендом и редакцией. Не учитываются показатели посещаемости, тиража или аудитории.
Под ссылками подразумеваются упоминания источника в контексте всех возможных словосочетаний: «в газете … опубликовано интервью», «по сообщению…», «как передали…», «по материалам…» и т. п., а также гиперссылки в интернет-изданиях.
п., а также гиперссылки в интернет-изданиях.
Рейтинги публикуются по следующим категориям:
- газеты, журналы, ТВ и радио федерального уровня;
- интернет;
- региональные СМИ;
- отраслевые СМИ.
Рейтинги по ИЦ публикуются с периодичностью: месяц, квартал, год.
При обработке результатов учитывается написание упоминаемого источника и вариативность синонимичного ряда.
*Влиятельность СМИ — рекурсивно рассчитываемый показатель, отражающий усредненное за год количество и качество ссылок на источник. Показатель рассчитывается ежемесячно на основе анализа материалов 71 000 СМИ за год. Расчет показателя происходит в несколько этапов, на каждом из которых происходит перерасчет и уточнение значения влиятельности. При этом на первом этапе расчета у всех СМИ одинаковая нулевая влиятельность, а после первого этапа влиятельность СМИ фактически равна простому количеству ссылок на это СМИ в других СМИ. На последующих этапах влиятельность СМИ рассчитывается как количество ссылок, умноженное на влиятельность ссылающихся СМИ. Перерасчет происходит до тех пор, пока влиятельность СМИ не перестанет меняться более чем на 0,1%. Таким образом, на последнем шаге получается показатель, который тем больше, чем больше влиятельных СМИ ссылаются на данный источник.
На последующих этапах влиятельность СМИ рассчитывается как количество ссылок, умноженное на влиятельность ссылающихся СМИ. Перерасчет происходит до тех пор, пока влиятельность СМИ не перестанет меняться более чем на 0,1%. Таким образом, на последнем шаге получается показатель, который тем больше, чем больше влиятельных СМИ ссылаются на данный источник.
Сила тяжести, трения, реакции опоры, упругости, Архимеда, сопротивления, вес. Направление, точка приложения, природа возникновения
Тестирование онлайн
Что надо знать о силе
Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:
Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.
Закон Гука
Сила упругости направлена противоположно деформации.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
При параллельном соединении жесткость
Жесткость образца. Модуль Юнга.
Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел здесь.
Вес тела
Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
Формулы определения веса нет. Обозначается эта силы буквой .
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.
Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Сила тяжести действует на тело.
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка — отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
В воздухе силой Архимеда пренебрегаем.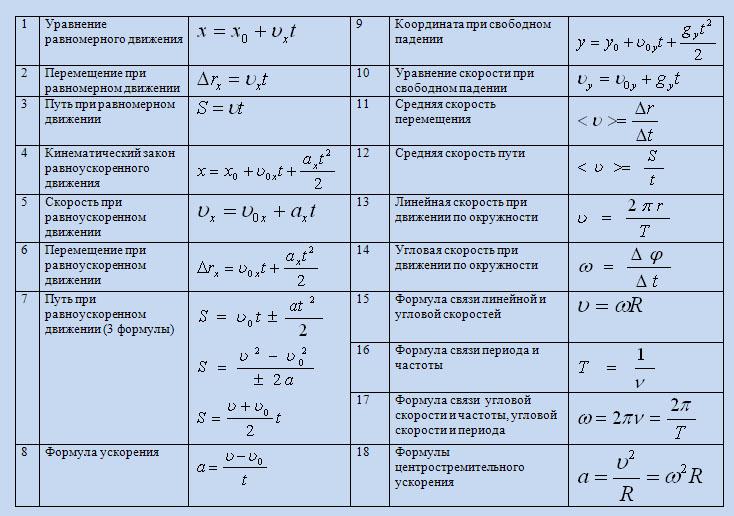
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Рассмотрим взаимное притяжение предмета и Земли. Между ними, согласно закону гравитации возникает сила
А сейчас сравним закон гравитации и силу тяжести
Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.
Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.
При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.
Dynamics | Физика для идиотов
Динамика — это название правил движения. Это то, что, как вы могли подумать, должно было быть выяснено в первую очередь, но не было полностью заблокировано до недавнего времени. При этом правила не сильно изменились и довольно предсказуемы, по крайней мере, в больших масштабах. Кто-то однажды сказал мне, что все, что вам нужно знать для экзамена по динамике, это: и все остальное можно вывести из этого. Я так и не узнал, правы ли они, я узнал и эти, на всякий случай:
Если вы уже знакомы с уравнениями, возможно, вы захотите перейти к следующему разделу, иначе я объясню, откуда они взялись и как их использовать.
При работе с измерениями вы можете использовать скалярные или векторные величины.
Скалярные величины:
- Укажите только величину.
- Энергия, Длина, Масса, Скорость, Температура и Время — все это скалярные величины.

Векторные величины:
- Имеют как величину, так и направление
- Смещение, Сила, Скорость, Ускорение и Импульс — все векторные величины.
Иногда может показаться, что скорость и скорость — одно и то же (часто они равны друг другу), но на самом деле они немного отличаются.Скорость — это то, насколько быстро что-то движется, не имеет значения, идет ли он вверх, вниз, влево или вправо, все, что имеет значение, — это то, как далеко он перемещается за установленное время. Вероятно, лучший способ рассматривать скорость — это если вы думаете или обычная ось x, y. Если тело движется горизонтально по прямой со скоростью 10, затем останавливается и движется в прямо противоположном направлении, при скорости 10, очевидно, произошло изменение, однако скорость этого не отражает. Скорость до разворота такая же, как и после.Однако скорость не та. Если бы мы сказали, что скорость вначале была такой же, как и скорость: 10, тогда, когда тело движется точно в противоположном направлении с той же скоростью, скорость будет -10.
Исаак Ньютон был умным парнем. Мы должны благодарить его за гравитацию (я, вероятно, должен добавить, что он открыл, а не изобрел ее, иначе люди начнут обвинять его каждый раз, когда падают). Больше всего Ньютон известен (помимо случая с яблоком) своими законами движения:
- Частица останется в покое или продолжит движение, если на нее не будет действовать внешняя сила.
- Сила, действующая на объект, равна его массе, умноженной на его ускорение ().
- Каждое действие имеет равную и противоположную реакцию.
Все это нормально, но что на самом деле означают эти законы?
1. Частица останется в покое или продолжит движение, если на нее не будет действовать внешняя сила.
Это просто означает, что если на частицу не действует внешняя сила, она никоим образом не изменит ее движения. Если бы не было трения или сопротивления воздуха, то частица, движущаяся на 5, продолжала бы бесконечно долго.Очевидно, что в реальной жизни этого не происходит из-за сопротивления воздуха и трения, поэтому практически невозможно иметь внешнюю силу на движущуюся частицу.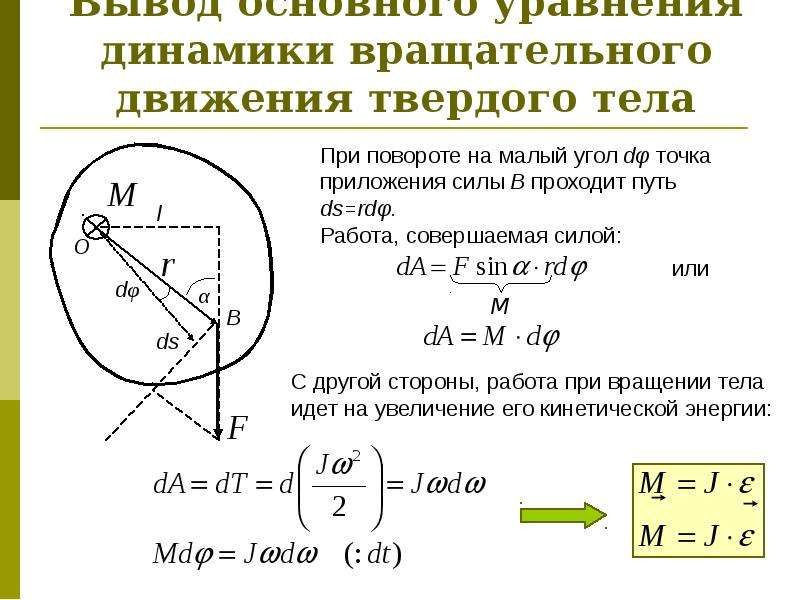 Однако, если вы думаете о неподвижной частице, это имеет гораздо больший смысл. Если к неподвижной частице не приложить силу, она не начнет двигаться.
Однако, если вы думаете о неподвижной частице, это имеет гораздо больший смысл. Если к неподвижной частице не приложить силу, она не начнет двигаться.
2. Сила, действующая на объект, равна его массе, умноженной на его ускорение.
Проще говоря, это, вероятно, одна из самых фундаментальных формул в динамике.Это один из тех, которые часто возникают в Dynamics, и его действительно стоит изучить. Это тоже не так сложно понять. Имеет смысл, что если что-то имеет большую массу, потребуется большая сила, чтобы придать ему такое же ускорение, как и что-то с меньшей массой.
3. Каждое действие имеет равную и противоположную реакцию
Этот закон в основном означает, что если вы толкнетесь о стену, это оттолкнет вас назад, что на самом деле является хорошей работой, потому что иначе вы бы прошли прямо!
У них так много разных названий, что иногда трудно угнаться за ними.Возможно, вы слышали, что их называют кинематическими уравнениями, уравнениями движения, уравнениями SUVAT, а может быть, вы вообще о них не слышали. Прежде всего, давайте взглянем на них:
Прежде всего, давайте взглянем на них:
(1)
(2)
(3)
(4)
(5)
Может показаться, что там есть что вспомнить, но поверьте, это не так сложно, как кажется. Как будто эти уравнения невероятно важны в динамике.
SUVAT Equation 1
Как вы, наверное, уже знаете, скорость, разделенная на время, равна ускорению, а скорость, умноженная на время, равна смещению.Это означает, что на графике зависимости скорости от времени уклон линии равен ускорению, а площадь под линией равна смещению.
Если у вас есть начальная скорость и конечная скорость, график будет выглядеть примерно так:
График, показывающий u против tКак я уже сказал, уклон линии равен ускорению. Так . Переставив это так, чтобы получился объект, мы получаем нашу первую формулу постоянного ускорения:
SUVAT Equation 2
Ладно, один проиграл, осталось четыре!
Мы знаем, что площадь под графиком равна смещению.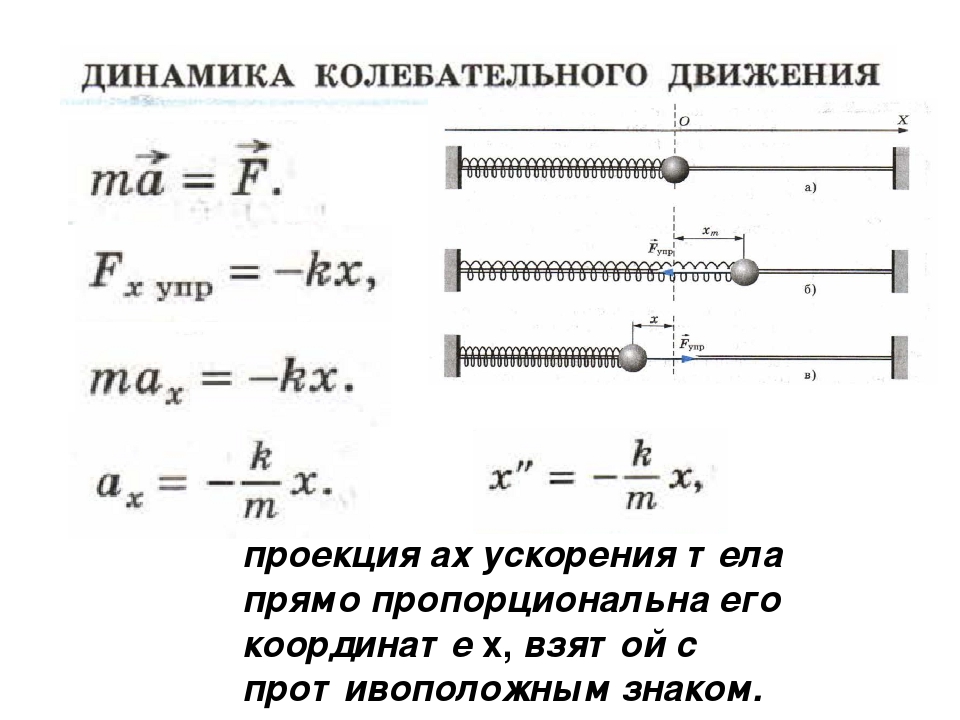 Итак, мы знаем, что умножение на дает нам нижний прямоугольник площади, а деление на 2 дает нам верхний треугольник. Это дает нам:
Итак, мы знаем, что умножение на дает нам нижний прямоугольник площади, а деление на 2 дает нам верхний треугольник. Это дает нам:
Теперь мы уже знаем это, поэтому мы можем переставить это, чтобы получить, а затем подставить это в наше уравнение для смещения. Из этого у нас есть. Если мы просто умножим скобку, которая дает нам нашу вторую формулу:
Для тех из вас, кто любит находить математику там, где это возможно, вам может быть интересно узнать, что это интеграл по отношению к.Если для вас это не имеет смысла, почему бы не заглянуть в замечательный раздел «Интеграция», где все станет ясно!
SUVAT Equation 3
Те из вас, кто увлечен поиском закономерностей, возможно, заметили, что это уравнение очень похоже на предыдущее. Это потому, что он очень похож на предыдущий. Те из вас, кто решил не переходить на страницу интеграции, могут пожалеть об этом сейчас.
Если переставить, чтобы сделать тему, то получится:
Теперь вам просто нужно интегрировать этот результат по времени, чтобы получить наше третье уравнение:
SUVAT Equation 4
Мы уже установили, что площадь под графиком (равная смещению) равна:
Если мы умножим скобку, получим:
, что совпадает с:
Наконец, мы просто разложим это на множители, чтобы получить:
SUVAT Equation 5
Можем переставить, сделать тему:
Затем мы просто подставляем это значение в наше предыдущее уравнение:, что дает нам:
, который можно упростить до,
, а затем
это в конечном итоге дает нам окончательную форму
Вот и все! Эти уравнения определенно стоит изучить, поскольку они полезны снова и снова. Есть несколько правил, например, их можно использовать только в тех случаях, когда есть постоянное ускорение. Это означает, что если ускорение составляет примерно 12 мс -2 , они в порядке, но если ускорение составляет 12 мс -2 , тогда они не будут работать, поскольку ускорение зависит от.
Есть несколько правил, например, их можно использовать только в тех случаях, когда есть постоянное ускорение. Это означает, что если ускорение составляет примерно 12 мс -2 , они в порядке, но если ускорение составляет 12 мс -2 , тогда они не будут работать, поскольку ускорение зависит от.
Большая часть динамики достигается за счет игнорирования сопротивления воздуха, и, хотя это значительно упрощает работу, всегда стоит знать, какое влияние это окажет.Силу сопротивления любого объекта, движущегося в жидкости, можно рассчитать по формуле:
— плотность жидкости (998,2071 кг · м для воды при 30 градусах и 1,204 кг · м для воздуха), — скорость объекта, — площадь поперечного сечения объекта и — коэффициент сопротивления. Коэффициент лобового сопротивления — это число, которое относится к аэродинамике объекта, у куба и шара есть.
Объект, падающий на Землю, в конечном итоге (если он будет падать достаточно долго) достигнет скорости, при которой сила сопротивления равна силе тяжести, тянущей его вниз.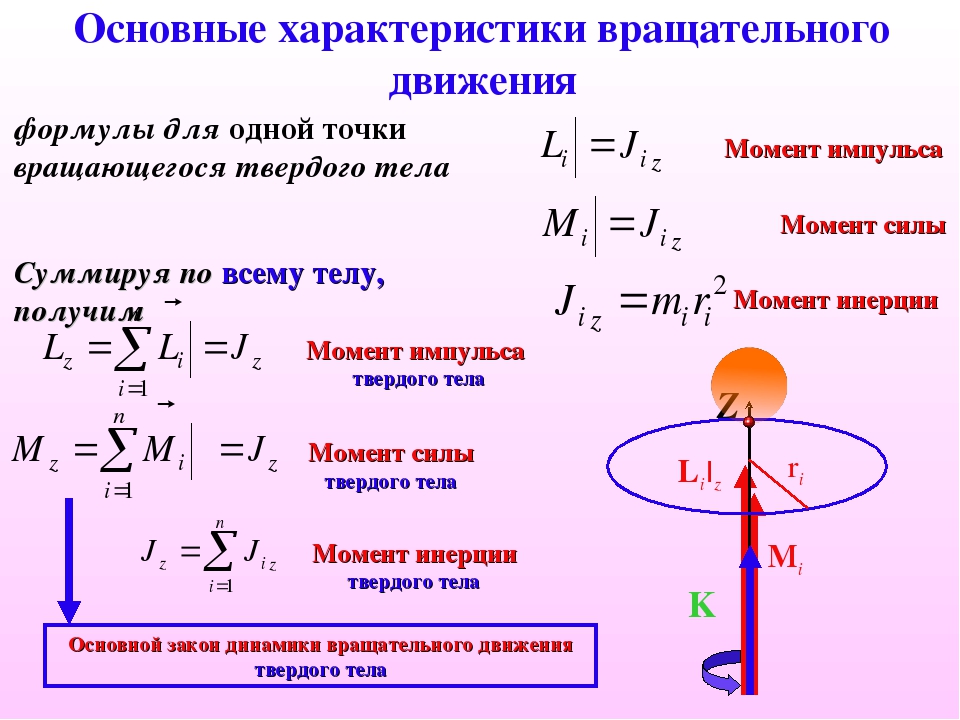 Это называется Конечная скорость , и вы можете получить выражение для этого, приравняв силу сопротивления к, а затем переставив на:
Это называется Конечная скорость , и вы можете получить выражение для этого, приравняв силу сопротивления к, а затем переставив на:
Для человека, падающего в воздухе (сверху), у нас есть 70 кг, площадь 0,5 м и коэффициент сопротивления около 0,8 (приблизительное предположение где-то вокруг углового куба или цилиндра), мы получаем конечную скорость около 53 мс (что оказывается быть довольно хорошей приблизительной оценкой).
Это самый простой экземпляр в динамике.Тело движется по плоской поверхности по прямой. Например:
1. Преподобный ведет машину, как вдруг двигатель перестает работать! Если он едет со скоростью 10 мс –1 , а его замедление составляет 2 мс –2 , сколько времени потребуется машине, чтобы остановиться?
Хорошо, с такого рода проблемами всегда полезно перечислить то, что вы знаете. Нам даны начальная скорость, и ускорение,. Мы также знаем, что если машина собирается финишировать в состоянии покоя, эта конечная скорость должна быть 0 мс -1 . Мы хотим узнать время,. Лично я считаю, что лучше всего изложить эту информацию так:
Мы хотим узнать время,. Лично я считаю, что лучше всего изложить эту информацию так:
u = 10 мс -1
v = 0 мс -1
a = -2 мс -2
t =? с
Отсюда видно, какое уравнение нам нужно. В этом случае мы видим, что нам нужно уравнение. Мы переставляем это так, чтобы получился предмет, давая нам
Наконец, мы помещаем числа в уравнение:
.
2. Майкл выходит на дорогу в 30 метрах от места, где двигатель не работает.Очки преподобного упали, и он не видит Майкла. Остановится ли машина вовремя, чтобы не попасть в Майкла?
Еще раз, лучше всего выложить всю имеющуюся у нас информацию:
u = 10 мс -1
v = 0 мс -1
a = -2 мс -2
t = 5 с
s =? м
На этот раз мы хотим найти смещение s, поэтому нам нужно выбрать уравнение с этим in. Я собираюсь использовать. Я мог бы использовать или, однако, поскольку у нас нет времени, а вместо этого мы разработали это самостоятельно, любая ошибка, сделанная в предыдущих расчетах, будет перенесена в эту.
Опять же, я собираюсь изменить уравнение, на этот раз чтобы дать в качестве предмета. Это хорошая привычка, теперь это может не иметь большого значения, переставляете ли вы уравнение до или после ввода чисел, но с более сложными формулами это может стать действительно беспорядочным, если вы не измените его сначала. Также в экзаменационных ситуациях, если вы допустили ошибку, вы все равно можете получить оценки по методу, если экзаменатор может видеть, что вы сделали.
В любом случае, это дает нам
Подставляя числа в уравнение, получаем:
, чтобы Майкла не ударили! (Уф!)
В приведенном выше примере трение полностью проигнорировано.В реальном мире мы не можем этого сделать (очень удачно, потому что мы все время падали, и люди думали, что мы пьяны). А теперь давайте посмотрим на ситуацию с трением. Коэффициент трения обозначается символом μ. Результирующая (нормальная) сила веса уравновешивает вес автомобиля (поэтому он не едет по дороге). Сила трения равна μ (или μN).
3. Автомобиль преподобного сломался на трассе М1. Ему нужно подтолкнуть его к твердому плечу. Автомобиль весит 5000Н.Rev может толкать около 1800N. Коэффициент трения между автомобилем и дорогой составляет 0,6. Сможет ли Rev подтолкнуть машину к твердой обочине?
Хорошо, в такой ситуации для начала неплохо нарисовать небольшой набросок того, что происходит.
Диаграмма сил, показывающая, что происходит в примере 3.Из этого мы знаем, что для того, чтобы машина двигалась, Rev должен толкать с силой не менее μR. Просто умножив коэффициент трения на результирующую силу, мы обнаружим, что сила трения составляет 3000 Н, поэтому Rev не сможет толкнуть автомобиль на обочину дороги.
4. Бодибилдер случайно проходит мимо и, пытаясь облегчить заторы на постоянно загруженном M1, он решает помочь. Он может толкать с силой 3200Н. Каким будет ускорение машины с учетом того, что бодибилдер и Rev.NB — Принять массу автомобиля 510 кг
Итак, на самом деле ситуация та же, что и раньше, только на этот раз силы не уравновешиваются и будет ускорение. Мы получили это от очень умного Исаака Ньютона.
Мы получили это от очень умного Исаака Ньютона.
Помните, что для определения общей силы необходимо убрать силу трения. Итак, это (3200 + 1800) — 3000. Таким образом, общая сила составляет 2000 Н. Снова нам нужно изменить формулу, чтобы на этот раз в качестве испытуемого использовалось и . Это дает нам. Подставляя числа, получаем:
a = 3.9 мс -2 (2 s.f.)
Это очень похоже на движение по плоской поверхности, только одна или две другие переменные … о, и мы больше не будем говорить об автомобиле Rev, так как я не уверен, что это поможет ему подняться в гору!
В любом случае, боюсь, я немного сбился с пути.Введение «наклонной плоскости» или «уклона», как ее называют большинство из нас, означает, что вам придется освежить свою тригонометрию. С другой стороны, вы узнаете, почему люди годами пытались вбить это в вас! Если вы знакомы со старым добрым порядком операций, все будет в порядке.
Итак, давайте начнем с простого простого примера.
На рисунке выше показан блок, стоящий на склоне. Хорошее место для начала (вероятно, единственное место для начала, если вы хотите получить хоть какой-то шанс получить хоть что-нибудь с вопросом) — это решимость сил.Предполагая, что блок находится в состоянии покоя, мы знаем, что он находится в равновесии, поэтому горизонтальные силы должны быть равны, как и вертикальные силы (если это не один из тех прекрасных левитирующих блоков).
Снарядыничем не отличаются от Движения по прямой, просто вместо того, чтобы тело двигалось слева направо, оно также движется вверх или вниз. Сначала давайте посмотрим на типичный пример движения снаряда:
Мяч брошен под углом 30 °. Имеет начальную скорость 20 мс -1 .Найдите максимальную высоту, которую может достичь мяч.
Ладно, как обычно, рисуем диаграмму:
Пример движения снарядаТеперь давайте перечислим то, что мы знаем:
- u = 20 sin30 мс -1
- v = 0 мс -1
- a = -9,81 мс -2
- с =? м
Теперь мы выбираем одну из кинематических формул, которая даст нам результат наиболее прямым путем, это:, и переставляем ее так, чтобы получился объект:
Затем, наконец, введите числа в уравнение:
и выскакивает ответ:
Смотри, не так ли сложно было? Вопросы о снарядах иногда могут показаться довольно сложными, но если вы не забудете просто использовать тригонометрию для поиска компонентов x и y, вы не ошибетесь.
Иногда вы знаете максимальную высоту, но какой-то другой компонент будет отсутствовать. Например, время, когда мяч находится в воздухе … Опять же, это не проблема, вы просто посмотрите, что вы знаете, , , и воспользуйтесь формулами, чтобы вычислить остальное.
/ / / FORMULA DYNAMICS
Отзывы клиентов — Formula Dynamics USA 22.10.2012 (Quattroporte Sport GT) — Отзыв клиента:
Тормоза Formula Dynamics
Очень низкий износ, отсутствие пыли и скрипа
21.10.2012 (Quattroporte Sport GT) — Отзыв клиента:
Formula Служба поддержки клиентов Dynamics
FD заслужила мое уважение, они действительно заботятся о нас на этом форуме
21.10.2012 (GranTurismo) — Отзыв клиента:
Роторы Formula Dynamics, тормозные магистрали и тормозные колодки из нержавеющей стали
Лучшие вещь, которую я когда-либо делал
06/11/2012 2007 (Quattroporte Sport GT) DuoSelect — Отзыв клиента:
Formula Dynamics Роторы и тормозные колодки
Полное устранение скрипа
06. 09.2012 (GranTurismo) — Отзыв клиента:
09.2012 (GranTurismo) — Отзыв клиента:
Formula Dynamics Бесшумные / малопылящие тормозные колодки с повышенным износом
Он идеален с
31.05.2012 2012 (GranTurismo MC) — Отзыв клиента:
Formula Dynamic s — DBW, ECM, Larini Sports Cats
Автомобиль превратился из забавного в просто потрясающий
26.04.2012 (GranTurismo MC) — Отзыв клиента:
Formula Dynamics — Larini Sports Cats и X-pipe
Это больше, чем я ожидал… Звук нереальный
21.03.2012 2006 (Gransport) — Отзыв клиента:
Formula Dynamics Drive By Wire, ECM, Larini Exhaust, Larini Decats, FD BBK
Автомобиль намного быстрее, чем раньше
16.01.2012 2005 (Gransport) — Отзыв клиента:
Formula Dynamics Drive By Wire
Двигатель чувствует себя более загруженным / быстро реагирует
13.01.2012 (GranTurismo) — Отзыв клиента:
Formula Dynamics Carbon Кевларовые тормозные колодки
Они просто выдающиеся!
28. 04.2011 (Quattroporte) — Отзыв клиента:
04.2011 (Quattroporte) — Отзыв клиента:
Formula Dynamics Drive By Wire, Larini X-Pipe
Убирайтесь к черту с этого забора и немедленно закажите эту вещь!
24.04.2011 (4200) — Отзыв клиента:
Formula Dynamics DBW, Performance Springs, колесные пространства и Larini X-Pipe
Мой Maserati чувствует себя и водит совершенно потрясающе.По ощущениям почти как мой 575M
04/11/2011 (Quattroporte Sport GT) — Отзыв клиента:
Глушители Larini Sport
Я действительно рекомендую выхлопную систему Larini
30.03.2011 (Quattroporte Sport GTS) и 2006 (GranSport) — Отзыв клиента:
Formula Dynamics ECM Performance Chip
«SLAM BAM СПАСИБО, МААМ»
26.03.2011 2008 (QP Sport GTS Automatica) — Отзыв клиента:
Formula Dynamics Drive By Модуль расширения проводов и чип производительности ECM
Он сделает автомобиль более четким и отзывчивым.
26.03.2011 2007 (QP SportGT DuoSelect) — Отзыв клиента:
Larini Sport Cats, Mufflers, X-Pipe
Абсолютно фантастический звук.
25.03.2011 2008 (Quattroporte Sport GT) — Отзыв клиента:
Larini Sport Cats
WHOO HOO !!!! Я их люблю!!!
25.03.2011 2008 (QP SportGT Automatica) — Отзыв клиента:
Larini Sport Cats, глушители, X-Pipe
Сегодня забрал машину !! НЕРЕАЛЬНО КРУТО!!! Я чувствую удар мощности!
25.03.2011 2007 (Quattroporte Sport GT — DuoSelect) — Отзыв клиента:
Запасные роторы Formula Dynamics и тормозные колодки из карбона / кевлара
Пока что никакого визга, и торможение очень плавное и плавное. фирма.
23.03.2011 2006 (4200 Spyder) — Отзыв клиента:
Модуль расширения Formula Dynamics Drive By Wire
Повышение производительности происходит мгновенно, потрясающе и плавно !!
17.03.2011 2004 (4200 Spyder GT — 6-ступенчатая механическая коробка передач) — Отзыв клиента:
Спортивные пружины и стабилизаторы поперечной устойчивости Formula Dynamics
Я очень рекомендую их.
16. 03.2011 (Gransport) — Отзыв клиента:
03.2011 (Gransport) — Отзыв клиента:
Спортивные пружины Formula Dynamics
Они являются обязательным первым шагом и имеют большое значение.
07.03.2011 2006 (Quattroporte) — Отзыв покупателя:
Formula Dynamics Quiet Cermaic Brake Pads
Мои стоковые колодки визжали как свиньи, я пока очень доволен.
03.04.2011 2008 (Quattroporte Sport GTS) — Отзыв клиента:
Модуль расширения привода Formula Dynamics по проводам и чип производительности ECM
Вы должны получить это, оно того стоит.
26.02.2011 2006 (Gransport Spyder) — Отзыв клиента:
Модуль расширения Drive By Wire
Все хорошо, как рекламируется!
08.02.2011 2007 (Quattroporte Sport GT) — Отзыв клиента:
Formula Dynamics Sports Springs
На трассе значительно улучшилась управляемость
28.01.2011 2006 (Quattroporte Sport GT) — Отзыв клиента :
Formula Dynamics Carbon / Kevlar Performance Тормозные колодки
Они останавливаются так хорошо, что пассажиры в моей машине «ухватились за приборную панель»
28. 12.2010 4200 — Отзыв клиента:
12.2010 4200 — Отзыв клиента:
Служба поддержки клиентов
Лучшее обслуживание клиентов на планета!
30.11.2010 2009 (GranTurismo) — Отзыв клиента:
Drive By Wire
Стоимость каждого пенни
28.11.2010 2002 (4200 Cambiocorsa) — Отзыв клиента:
High Performance ECM, Замена фильтра BCM , Выхлопная труба, привод по проводам, спортивные пружины, проставки
У этого купе намного больше крутящего момента и мощности
24.11.2010 2006 (4200 Spyder) — Отзыв клиента:
Модуль расширения привода по проводам
It это как новая машина!
11.06.2010 2009 (GranTurismo 4200 GT) — Отзыв клиента:
Спортивные пружины, роторы / линии / колодки FD
Я очень доволен
18.09.2010 2005 (4200 GT) — Клиент Отзыв:
Larini Exhaust и X-Pipe
Звуковые клипы и видео для выхлопа
06.09.2010 2005 (4200 Cambiocorsa) — Отзыв клиента:
Drive By Wire
FD мод устраняет 0. Задержка на 1-й передаче 25-0,5 секунды
Задержка на 1-й передаче 25-0,5 секунды
24.08.2010 2006 (Gransport F-1) — Отзыв клиента:
Большой тормозной комплект, спортивные пружины
Намного лучше для спортивного вождения
17.07.2010 2005 ( Gransport F-1) — Отзыв клиента:
Модуль расширения Drive By Wire
DBW — это потрясающе
07.01.2010 2006 (Quattroporte Duoselect) — Отзыв клиента:
Большой тормозной комплект
Автомобиль останавливается бесконечно лучше
29.06.2010 2004 (4200 Spyder Cambiocorsa) — Отзыв клиента:
Большой тормозной комплект, нержавеющие задние линии, карбоновые / кевларовые колодки
Большой тормозной комплект FD
18.06.2010 2004 (4200 Cambiocorsa) — Клиент Отзыв:
Sport Springs
Только что были установлены пружины FD
12.04.2010 2004 (4200 Spyder Cambiocorsa) — Отзыв клиента:
Sport Springs, 15-миллиметровые проставки, тормозные колодки Street Performance
Открывается сезон треков! Мой новый / старый Spyder
25. 03.2010 2004 (4200 Spyder Cambiocorsa) — Отзыв клиента:
03.2010 2004 (4200 Spyder Cambiocorsa) — Отзыв клиента:
Sports Springs
Теперь это настоящий спортивный автомобиль со спортивным управлением
14.03.2010 2009 (Quattroporte Sport 4 .7 Automatica) — Отзыв клиента:
Drive By Wire, ECM Performance Chip
Страсть Джеффа к нашим автомобилям искренняя и настоящая
03/10/2010 (Quattroporte Sport) — Отзыв клиента:
Sports Springs
Это dream now
24.02.2010 2005 (Quattroporte Duoselect) — Отзыв клиента:
Проводной привод, модернизированные тормозные шланги
Еще одно потрясающее обновление.
31.01.2010 2005 (Quattroporte GTS Duoselect) — Отзыв клиента:
Sports Springs
Пружины FD настоятельно рекомендуются
28.01.2010 2008 (Quattroporte GTS Automatica) — Отзыв клиента:
ECM Performance Chip, Drive By Wire
Автомобиль теперь зверь
06.01.2010 (Quattroporte) — Отзыв клиента:
Выхлоп Larini и X-Pipe
(не описать словами) УДИВИТЕЛЬНЫЙ !!!
23. 12.2009 2005 (Quattroporte — Duoselect) — Отзыв клиента:
12.2009 2005 (Quattroporte — Duoselect) — Отзыв клиента:
Sports Springs с регулируемыми пружинами Skyhook
FD на 2005 QP с регулируемым Skyhook.
20.12.2009 2008 (Quattroporte Sport — Automatica) — Отзыв клиента:
Sports Springs, Spacers
Джефф из Formula Dynamics действительно знает, как заботиться о своих клиентах
14.12.2009 (4200 F- 1 Cambiocorsa) — Отзыв клиента:
Модуль расширения Drive By Wire и чип производительности ECM
Какая разница !!!!
12/02/2009 2005 (Quattroporte F-1 Duoselect) — Отзыв клиента:
Drive By Wire
Автомобиль более плавный, динамичный и управляемый
25.11.2009 2008 (Quattroporte Sport GTS — Automatica) — Отзыв покупателя:
Поперечины / распорки
Я очень доволен своими обновлениями
25.11.2009 2004 (механическая трансмиссия 4200 Spyder) — Отзыв клиента:
Пружины / распорки стабилизатора поперечной устойчивости
Просто подождите, пока вы попробуете эту настройку на трассе!
25. 11.2009 2004 (механическая коробка передач 4200 Spyder) — Отзыв клиента:
11.2009 2004 (механическая коробка передач 4200 Spyder) — Отзыв клиента:
Пружины Performance, стабилизаторы поперечной устойчивости
В целом настоятельно рекомендуется.
24.11.2009 2008 (Quattroporte Sport GTS — Automatica) — Отзыв клиента:
Поперечины, распорки
Большое улучшение
22.11.2009 2005 (Quattroporte F-1 Duoselect) — Отзыв клиента:
Чип ECM Performance, привод по проводам, пружины Performance, Larini X-Pipe и глушители
Я просто дышу на педаль, и она отрывается
20.11.2009 2002 (4200 F-1 Cambiocorsa) — Отзыв клиента:
Drive By Wire, ECM Performance Chip
Поздравляем с динамикой формулы!
20.11.2009 (Gransport F-1) — Отзыв клиента:
Drive By Wire, ECM Performance Chip, распорка, полная система Larini
Я очень доволен игроком
15.11.2009 2005 (4200 GT ) — Отзыв клиента:
Drive By Wire
Итог еще один довольный клиент FD
13.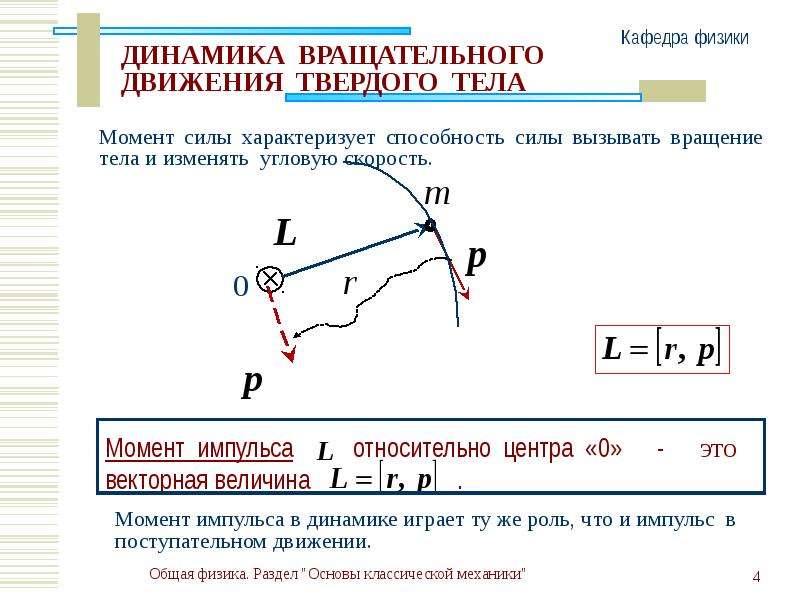 11.2009 (Gransport F-1) — Отзыв клиента:
11.2009 (Gransport F-1) — Отзыв клиента:
FD MODS
Учитывая Ferrari
11.04.2009 2009 2006 (Quattroporte F-1 Duoselect) — Отзыв клиента:
Larini X-Pipe
X-Pipe для QP
31.10.2009 2006 (4200 GranSport) —
Отзыв клиента:
Performance Sports Springs, Drive By Wire, ECM Chip
Продукты Formula Dynamics имеют лучшую поддержку
18.10.2009 (Gransport F-1) — Отзыв клиента:
BMC filter, Larini De-Cat , Drive By Wire, обновление ECM
Отчет о производительности после обновлений FD
14.10.2009 (Gransport F-1) — Отзыв клиента:
Модуль расширения Drive By Wire и чип производительности ECM
Five Stars for Jeff and Formula Динамика!
10.09.2009 2004 (4200) — Отзыв клиента:
Модуль расширения Drive By Wire
Мгновенное подключение — вот как я бы описал эту модификацию.
10.04.2009 2007 (Quattroporte Sport GT Duoselect) — Отзыв клиента:
Чип производительности ECM и модуль расширения привода по проводам
Отчет об установке
16.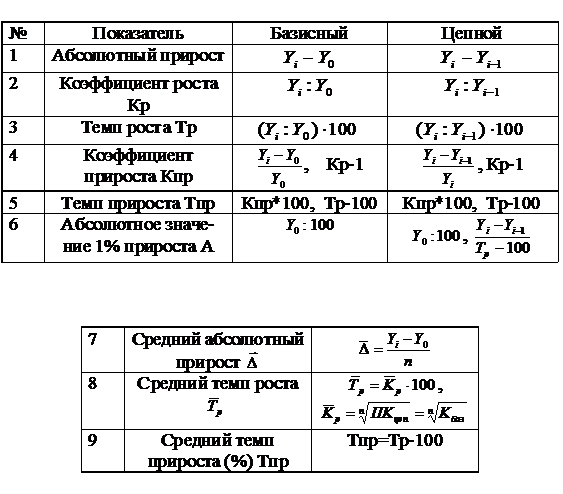 09.2009 2007 (Quattroporte Sport GT) — Отзыв клиента:
09.2009 2007 (Quattroporte Sport GT) — Отзыв клиента:
Drive By Wire
Почему я так долго ждал?
09/12/2009 (4200 Spyder) — Отзыв клиента:
Performance Springs, ECU Chip, Drive By Wire, шины Vredsteiin, проставки, Larini De-Cat
Теперь это самый быстрый и самый маневренный автомобиль, на котором я когда-либо ездил. в собственности
09.04.2009 (Gransport) — Отзыв клиента:
Performance Springs
Formula Dynamics Springs, установленный на GS
17.08.2009 2005 (4200) — Отзыв клиента:
Глушители Larini, Larini X Труба, воздушный фильтр BMC
Коробки Larini и видео X Pipe 3
13.08.2009 2004 (4200 Cambiocorsa) — Отзыв клиента:
Чип производительности ECM, Drive By Wire, Larini De-Cats, X-Pipe
Это необходимо прочитать!
08/12/2009 2008 (Quattroporte Sport GTS) — Отзыв клиента:
Комплект проставок для колеса Performance
Прекрасные ощущения, отличная езда, отличный внешний вид.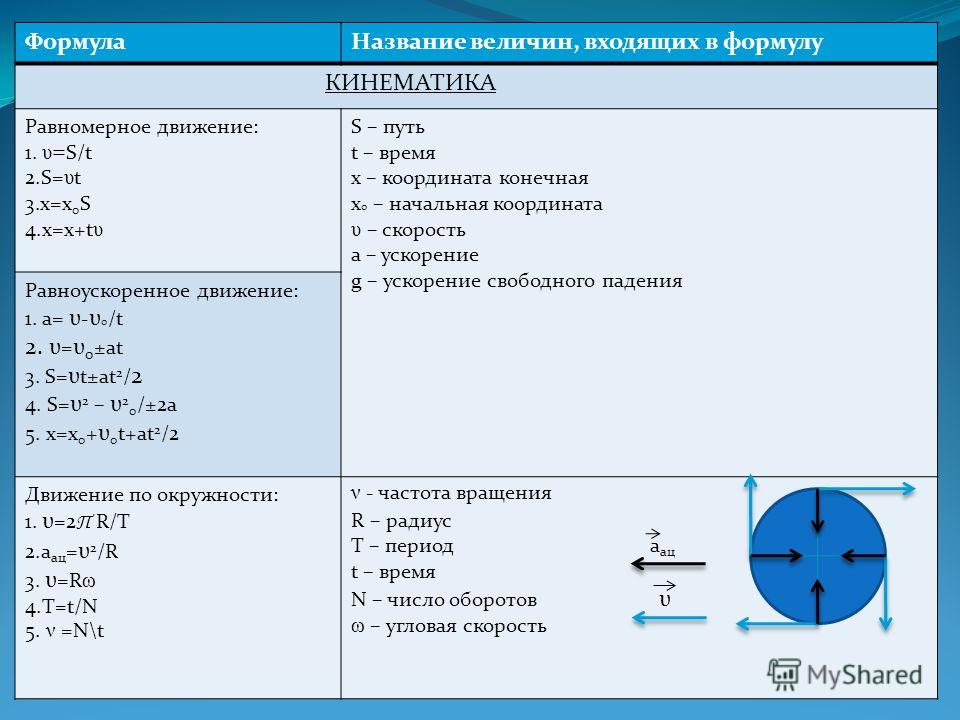
08.06.2009 2005 (Gransport F-1) — Отзыв клиента:
Рукоятки Anti-Sway и Larini Sport De-Cats
Первые впечатления — Новые модификации: Anti-Sway и Sport De-Cat
08 / 05/2009 2004 (Руководство 4200 GT) — Отзыв клиента:
Larini X-Pipe
Существенное улучшение с точки зрения мощности и звука.
08/02/2009 2007 (Quattroporte Sport GT) — Отзыв клиента:
Drive By Wire
Если у вас нет этого
21.07.2009 2007 (Quattroporte Executive GT — Duoselect) — Отзыв клиента:
Performance Springs
Управляется как мечта
17.07.2009 2004 (4200) — Отзыв клиента:
Performance Chip ECM и Drive By Wire
Вау, какая разница
07/05/ 2009 2008 (Quattroporte Sport GTS) — Отзыв клиента:
Larini De-Cat Pipes, Springs, BMI Air filter, DBW, ECM and SS Тормозные магистрали / колодки
Big Thumbs Up to Jeff at Formula Dynamics
07/05/5. 2009 2005 (4200 GT) — Отзыв клиента:
Глушители Larini и фильтр BMC
Еще одно купе GT присоединяется к клубу
07. 02.2009 (GranTurismo) — Отзыв клиента:
02.2009 (GranTurismo) — Отзыв клиента:
.25-миллиметровые проставки
Только что установили проставки 0,25 мм
07.02.2009 2006 (Gransport) — Отзыв клиента:
Куча деталей FD
Это все дорожный автомобиль, который вам когда-либо понадобится
22.06.2009 2009 2008 (Quattroporte Sport GTS) — Отзыв клиента:
Larini De-Cat Трубопроводы, пружины, воздушный фильтр BMI, тормозные магистрали / колодки DBW, ECM и SS
Обновления Gransport.
19.06.2009 (механическая трансмиссия 4200 Spyder) — Отзыв клиента:
Drive By Wire
По ощущениям у автомобиля еще 50 л.с.
18.06.2009 2006 (Gransport F-1) — Отзыв клиента:
Drive By Wire
Поездка в Le Belle Macchine в субботу … для обновления FD DBW
13.06.2009 2004 (4200 Spyder F-1 Cambiocorsa) — Отзыв клиента:
Drive By Wire
Все, что я могу сказать, это ничего себе.
13.06.2009 (Gransport Spyder F-1) — Отзыв клиента:
Drive By Wire, Performance Springs, Larini De-Cats, распорки, воздушный фильтр Performance
Mod Squad спешит на помощь!
06/10/2009 2007 (Quattroporte Executive GT — Duoselect) — Отзыв клиента:
Drive By Wire и ECM Performance Chip
Буквально запрокинут вам голову!
06/09/2009 2005 (Quattroporte Duoselect) — Отзыв клиента:
Drive By Wire
Автомобиль в целом ездит намного лучше
06.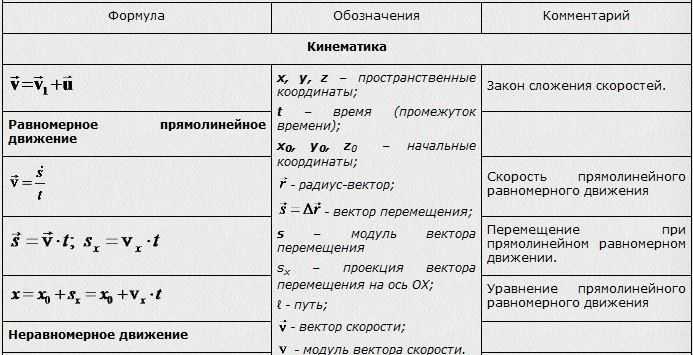 09.2009 2005 (Gransport F-1) — Отзыв клиента:
09.2009 2005 (Gransport F-1) — Отзыв клиента:
Подушечки из карбона / кевлара
Они остановились как чемпион!
06/05/2009 2008 (Quattroporte Sport GTS — Automatica) — Отзыв клиента:
Drive By Wire, ECM Performance Chip
Это просто пипец!
31.05.2009 2005 (Gransport F-1) — Отзыв клиента:
Воздушный фильтр Larini Sport De-Cat Pipes и Performance
Это похоже на новую машину.
24.05.2009 2008 (Quattroporte Sport GTS — Automatica) — Отзыв клиента:
Выхлоп Larini, привод по проводам, чип ECM Performance Chip
Это более чем превзошло мои ожидания!
16.05.2009 2002 (4200 F-1 Cambiocorsa) — Отзыв клиента:
Пружина, колодки, ECM, привод по проводам, колесные проставки, Larini Sport Cats
Управляемость, мощность, трансмиссия и улучшение крутящего момента
04 28/2009 2007 (Quattroporte Executive GT / F-1 Duoselect) — Отзыв клиента:
Чип производительности ECM
ECM того стоит, добавляет значительный импульс!
03. 04.2009 2008 (GranTurismo) — Отзыв клиента:
04.2009 2008 (GranTurismo) — Отзыв клиента:
Performance Chip ECM, Drive By Wire, Larini X-Pipe
New GranTurismo с модами Formula Dynamics
29.11.2008 2006 (GranSport Spyder F- 1) — Отзыв клиента:
Проводная установка привода
Переключение передач происходит очень быстро!
28.08.2008 2002 (4200 Cambiocorsa) — Отзыв клиента:
Выхлопная система Larini
Выхлопная система Larini
27.08.2008 2004 (4200 Cambiocorsa) — Отзыв клиента:
Выхлопная система Larini / Служба поддержки клиентов
Довольный клиент
31.07.2008 2006 (4200 Spyder) — Отзыв клиента:
Выхлоп Larini
I Love Larini
31.07.2008 2003 (4200 GT) — Отзыв клиента:
Sport Springs
Skyhook Coupe GT
07/05/2008 2006 (Gransport Spyder) — Отзыв клиента:
Тормозные колодки
Street Pads Review
25.06.2008 (Quattroporte Sport) — Отзыв клиента:
Quattroporte SportGT Larini Exhaust
Обожаю эти коробки Ларини!
23. 06.2008 (4200) — Отзыв клиента:
06.2008 (4200) — Отзыв клиента:
Спортивные пружины, воздушный фильтр, проводной привод, блок управления двигателем высокой мощности, тормозной комплект
FD, модификации
22.06.2008 2002 (4200 Spyder Cambiocorsa) — Отзыв клиента:
Обслуживание клиентов / установка
Благодаря Джеффу
21.06.2008 2002 (4200 Cambiocorsa) — Отзыв клиента:
Модуль расширения Drive By Wire, High Power ECM
Установлен FD Drive By Wire, ECM
20.05.2008 2006 (Gransport Spyder) — Отзыв клиента:
Служба поддержки / поддержки
Превосходное обслуживание
20.05.2008 (4200 GT) — Отзыв клиента:
Механическая коробка передач 4200 с приводом по проводам, Обзор Sport Springs
Drive By Wire, Springs on Coupe GT Review
18.05.2008 (Gransport F-1) — Отзыв клиента:
4200 Drive By Wire, Sport Springs, тормозной комплект, Обзор воздушного фильтра
Обновление на FD Модификации
12. 05.2008 (4200) — Отзыв клиента:
05.2008 (4200) — Отзыв клиента:
Non Skyhook Springs
Coupe GT Non Skyhook Sport Springs
05.06.2008 2004 (4200 Cambiocorsa) — Отзыв клиента:
Larini Exhaust
Beyond Amazing
05.04.2008 2002 (4200) — Отзыв клиента:
Блок управления двигателем высокой мощности, вилки, тормозные колодки
Влюбился в мой Maserati
30.04.2008 2004 (механическая коробка передач 4200 Spyder) — покупатель Отзыв:
Тормозной комплект, пружины, ECM, воздушный фильтр
Интересный воскресный привод
29.04.2008 2002 (4200 Cambiocorsa) — Отзыв клиента:
Drive By WireEnchancement Module
Установлен привод FD по проводам в эти выходные
20.04.2008 (4200 Cambiocorsa) — Отзыв клиента:
Пружины 4200, ECM, Drive By Wire, Larini, свечи зажигания, воздушный фильтр
Это похоже на то, что у меня новая машина!
19.04.2008 2002 (4200 Cambiocorsa) — Отзыв клиента:
Обзор Drive By Wire
Formula Dynamics Drive By Wire Review
14. 04.2008 2004 (Механическая трансмиссия 4200 Spyder) — Отзыв клиента:
04.2008 2004 (Механическая трансмиссия 4200 Spyder) — Отзыв клиента:
Комплект тормозов, пружины, блок управления двигателем, воздушный фильтр
FD Отзыв о модификации
05.04.2008 (Quattroporte Sport GT) — Отзыв клиента:
Выхлоп Larini
Larini, установленный на Quattroporte Sport GT
31.03.2008 ( Quattroporte Sport GT) — Отзыв клиента:
Выхлоп Larini
Выхлоп Larini на Quattroporte
28.03.2008 (Gransport F-1) — Отзыв клиента:
Выхлоп Larini
Выхлоп Larini
28.03.2008 2003 (механическая коробка передач 4200) — Отзыв клиента:
4200 Sport Springs
Установка пружины
14.02.2008 (4200 GT) — Отзыв клиента:
4200 Springs, Larini, ECM
4200 Coupe GT ECM, Springs, Larini Review
02/03/2008 (4200 Cambiocorsa) — Отзыв клиента:
4200 High Power ECM Chip
Formula Dynamics ECM Chip Review
21.01.2008 2006 (4200) — Отзыв клиента:
4200 Sport Springs
FD Downing Springs
21. 01.2008 (4200) — Отзыв клиента:
01.2008 (4200) — Отзыв клиента:
4200 High Power ECM Chip
Теперь машина тянет!
27.11.2007 2004 (механическая коробка передач 4200 Spyder) — Отзыв клиента:
Микросхема контроллера ЭСУД высокой мощности 4200
4.2L High Power ECM Chip
05.11.2007 2006 (4200) — Отзыв клиента:
4200 Sport Springs
Установлены спортивные пружины
31.07.2007 (Gransport F-1) — Отзыв клиента:
4200 Sport Springs
Gransport с пониженной и угловой нагрузкой
02.01.2007 2002 (4200 Spyder) — Отзыв клиента:
4200 Sport Springs
Открытое письмо Formula Dynamics
20.11.2006 2003 (4200 Механическая коробка передач ) — Отзыв клиента:
4200 Sport Springs
Автоматически скрещенные с моими новыми пружинами Formula Dynamics
11.02.2006 2003 (механическая трансмиссия 4200) — Отзыв клиента:
4200 Sport Springs
Теперь автомобиль справляется!
Qp Formula Dynamics Performance Тормозные роторы
| |||||||||||||||||
|
| ИНФОРМАЦИЯ О ДОСТАВКЕ | ||
| ||
| ИНФОРМАЦИЯ О ГАРАНТИИ | ||
| ||
| ДИЛЕРЫ | ||
| ||
Формулы и версии формул — Управление цепочкой поставок | Динамика 365
- Статья .
- Читать 6 минут

Оцените свой опыт
да Нет
Любой дополнительный отзыв?
Отзыв будет отправлен в Microsoft: при нажатии кнопки «Отправить» ваш отзыв будет использован для улучшения продуктов и услуг Microsoft.Политика конфиденциальности.
Представлять на рассмотрение
Спасибо.
В этой статье
Формула определяет материалы, ингредиенты и результаты конкретного процесса непрерывного производства. Вместе с соответствующим маршрутом формула определяет весь процесс непрерывного производства. Формулы используются для планирования и производства продуктов в непрерывном производстве.
Формула состоит из ингредиентов и количеств, необходимых для производства определенного количества элемента формулы. В зависимости от выполняемой задачи вы можете получить доступ к функциям формулы из управления запасами и складом или из управления информацией о продукте.
Формулы и строки формул
Формула состоит из одной или нескольких строк формулы, которые определяют ингредиенты или элементы, составляющие формулу. Строка формулы может содержать элементы ведомости материалов (BOM), элементы формулы, элементы промежуточного веса, приобретенные элементы, сопутствующие продукты или побочные продукты.Поскольку многие элементы используются в нескольких продуктах, элемент можно использовать в нескольких формулах.
Примером формулы является рецепт печенья с шоколадной крошкой. Ингредиенты для этой формулы состоят из нескольких линий, таких как мука, сахар, яйца, масло и шоколадная стружка. Формула печенья с шоколадной крошкой содержит ингредиенты, которые, вероятно, используются в других формулах. Пока вы готовите печенье с шоколадной крошкой, могут остаться остатки, например, крошки, или некоторые из печенья могут быть пережарены или недоварены.Эти элементы могут быть настроены как побочные продукты или побочные продукты, в зависимости от производственных операций.
Пока вы готовите печенье с шоколадной крошкой, могут остаться остатки, например, крошки, или некоторые из печенья могут быть пережарены или недоварены.Эти элементы могут быть настроены как побочные продукты или побочные продукты, в зависимости от производственных операций.
При создании строки формулы используется тип строки, чтобы указать, как система должна обрабатывать строку при выполнении сводного планирования и создании пакетных заказов. Каждый тип линии дает разный результат. В следующей таблице описаны типы линий, которые вы можете выбрать.
| Тип линии | Описание |
|---|---|
| Товар | Выберите Предмет , если предмет является сырьем или полуфабрикатом, который выбирается из запасов, или когда предмет является услугой. |
| Фантом | Выберите Phantom , если нужно расчленить все элементы формулы нижнего уровня, содержащиеся в строках формулы. Когда вы оцениваете пакетный заказ и элементы формулы разнесены, элементы-компоненты перечисляются в виде строк формулы в пакетном заказе. Дополнительно к производственному маршруту добавляются соответствующие маршруты. Элементы формулы разнесены с использованием текущей конфигурации. При использовании линии Phantom вы можете обрабатывать конфигурации производства и измерения, которые возникают на разных уровнях формулы.Если вы выберете Phantom для продукта на экспресс-вкладке Engineer страницы Released product details , а затем используете этот продукт в формуле, тип строки строки формулы изменится на Phantom . Вы не можете выбрать Phantom для номенклатуры промежуточного веса или для номенклатур, у которых тип производства — Сопутствующий продукт , Побочный продукт или Элемент планирования . Когда вы оцениваете пакетный заказ и элементы формулы разнесены, элементы-компоненты перечисляются в виде строк формулы в пакетном заказе. Дополнительно к производственному маршруту добавляются соответствующие маршруты. Элементы формулы разнесены с использованием текущей конфигурации. При использовании линии Phantom вы можете обрабатывать конфигурации производства и измерения, которые возникают на разных уровнях формулы.Если вы выберете Phantom для продукта на экспресс-вкладке Engineer страницы Released product details , а затем используете этот продукт в формуле, тип строки строки формулы изменится на Phantom . Вы не можете выбрать Phantom для номенклатуры промежуточного веса или для номенклатур, у которых тип производства — Сопутствующий продукт , Побочный продукт или Элемент планирования . |
| Привязка к поставке | Выберите Обособленная поставка , чтобы создать заказ партии, производственный заказ, канбан, заказ на перемещение или заказ на поставку для ингредиента, который содержится в строке формулы.Связанный заказ определяется на основе настроек заказа по умолчанию и типа производства ингредиента и создается при оценке заказа партии. Требуемые количества ингредиентов зарезервированы для заказа партии. |
| Продавец | Выберите Поставщик , если в производственном процессе используется субподрядчик, и вы хотите создать субпроизводство или заказ на поставку для субподрядчика. Услуга или работа, которую выполняет субподрядчик, должны быть созданы с использованием позиции формулы или позиции услуги.Вы можете прикрепить элемент к родительскому элементу в виде строки формулы. Маршрут должен содержать операцию, назначенную операционному ресурсу субподрядчика. Эта операция добавляется к строке формулы с помощью Oper. № поле. |
Формулы
При создании новой формулы необходимо сначала создать версию формулы, прежде чем добавлять элементы строк формулы и их конкретные характеристики. У каждой формулы должна быть хотя бы одна версия.Кнопка Утверждено в версии формулы становится доступной только после успешного сохранения записи версии. Каждая запись версии формулы связана с одним или несколькими сопутствующими и побочными продуктами, которые могут быть произведены при производстве готового продукта. Многие продукты можно изготавливать из одних и тех же ингредиентов в партиях разного размера, в нескольких количествах или с разным выходом. Вы можете создать столько версий формулы, сколько вам нужно.
Для управления несколькими активными версиями формулы используйте диапазоны дат действия или поля количества «от».Несколько активных версий формулы могут существовать только в том случае, если диапазон дат и количество «с» не перекрываются.
В отличие от спецификаций, где одна спецификация часто связана со многими версиями спецификаций, для каждой формулы обычно существует только одна версия формулы. Помните, что только одна версия формулы может быть активирована для измерений покрытия и количества для данного продукта. Однако многие версии формул могут существовать по другим причинам, и вы можете выбрать их вручную при создании заказа на партию.
Утверждение и активация формул и версий формул
Формулы и версии формул должны быть утверждены, прежде чем их можно будет использовать для планирования и производства.Формулы обычно активируются перед использованием. Однако во время производства вы можете выбрать версию формулы, которая утверждена, но не активирована.
Чтобы защитить формулу или версию формулы, вы можете установить Блок редактирования и Блокировать удаление параметров утверждения на странице Параметры управления производством .
Если вы выберете Редактирование блока и формула будет утверждена, никакие поля в строках формулы не могут быть удалены или отредактированы.Однако, если вы удалите утверждение формулы, вы можете удалить и изменить строки формулы. Вы также можете создавать новые формулы и новые версии формул.
При выборе Блокировать удаление утверждения нельзя удалить утверждение утвержденной формулы или версии формулы. Однако вы можете создавать новые формулы и новые версии формул, а также можете удалить активацию версии формулы.
Вы можете добавить больше уровней контроля, используя функцию электронной подписи.Если пользователь настроен так, что во время утверждения формулы требуется электронная подпись, при активации формулы появляется страница Подпись . Пользователь должен быть авторизован для электронной подписи, и сертификат должен быть успешно проверен, прежде чем изменение можно будет зафиксировать. Если подпись не может быть аутентифицирована, утверждение или удаление утверждения отклоняется, а изменение, инициировавшее утверждение или удаление утверждения, возвращается в исходное состояние.
Используйте масштабируемую функцию
Функция масштабирования доступна, только если для всех компонентов позиции в формуле задано значение Переменное потребление .Эта функция недоступна, если для компонентов элемента установлено значение Фиксированное потребление или Шаговое потребление . При использовании функции «Масштабирование» при изменении ингредиента в формуле количество других выбранных ингредиентов корректируется. Размер формулы также корректируется. Аналогичным образом, если вы измените размер формулы, изменится количество всех масштабируемых ингредиентов. Эта функция предназначена специально для создания и обслуживания формул. Он не указывает, будет ли количество ингредиента увеличиваться или уменьшаться в заказе партии.
Использование Шаг потребления
Поэтапное потребление исключает необходимость ввода количества на вкладке Строка формулы для ингредиента. Вместо этого потребление шага настроено так, что оно имеет значение Из серии и значение Количество . Выбирается информация из записи «Шаговое потребление на серию», которая соответствует количеству в заказе партии. Поэтапное потребление полезно, когда скорость потребления не является линейной по отношению к размеру заказа партии и увеличивает требования только при достижении определенного порогового значения количества.Чтобы включить эту функцию для новой формулы, в группе Расчет потребления измените настройку формулы для применимого ингредиента с Стандартный на Шаг . Этот метод потребления указывается на вкладке Настройка страницы Строка формулы .
Уравнения газовой динамики
Уравнения газовой динамикиДалее: MDKC и MDWDF для Up: Приложения в гидродинамике Предыдущая: Уравнение Бургера Поведение одномерной жидкости без потерь описывается следующей системой уравнений сохранения, также известной как уравнения Эйлера :
где — плотность, — объемная скорость, — абсолютное давление, а — полная энергия, внутренняя плюс кинетическая.Три уравнения не являются полными без определяющей связи между четырьмя зависимыми переменными. Люди из WDF в своем трактовке гидродинамики [16] часто не учитывают энергетическое уравнение и делают предположение типа , что существенно сводит систему (В.9) к системе с двумя переменными (в и ). Для газовой динамики мы предполагаем политропное поведение газа [181]:
| (В.10) |
где — постоянная, которая непосредственно следует из термодинамики (равна отношению теплоемкостей [203]).
Прежде чем продолжить, отметим масштабирование зависимых переменных [16,49]; это делается, как и в линейных задачах, обсуждаемых в главах 3 и 5, для оптимизации условия устойчивости результирующей сети. Переменные масштабируются как
Параметры и имеют размеры скорости и давления соответственно и обезразмеривают систему. снова станет отношением пространственного шага / временного шага в программе численного моделирования, а играет роль, аналогичную роли в задаче линии передачи (1 + 1) D, как обсуждалось в §3.7 и следует непосредственно из физических соображений.
Используя определение плотности энергии (B.10), систему (B.9) можно записать в неконсервативной [203] форме (после некоторых утомительных алгебраических манипуляций) как
Проблема здесь в том, что эта система в ее нынешнем виде не подходит для представления схемы, включающей взаимные элементы . Хотя это явно не указано в литературе, решение Fettweis et al.была масштабировать систему (B.9) путем умножения слева на матрицу diag (хотя, как уже упоминалось ранее, они работают с системой двухвариантной гидродинамики или ее аналогами в более высоких измерениях). Масштабированная система принимает вид:
| (В.12) |
Хотя это масштабирование не меняет плавных решений системы (B.9), проблемы могут возникнуть, если ожидаются шоки [181]. Так называемые слабых решений [181] системе (Б.9) (решения с разрывами, которые должны быть описаны с использованием интегральной формулировки (В.9)) не обязательно сохраняются при таком масштабировании. Переменные энтропии, которые будут кратко упомянуты в §B.3.3, позволяют потенциальным способом избежать этих трудностей.
Наконец, используя уравнение сохранения массы для упрощения других уравнений, масштабированная система (B.12) может быть записана в кососамосопряженной форме [181] как:
| (Б.13) |
где симметричные матрицы и определяются как
а — состояние, и . , кроме того, будет положительно определенным, если плотность и давление повсюду положительны. Значение этой асимметрично-самосопряженной формы можно увидеть, взяв внутреннее произведение (В.13) на , и в этом случае мы получаем
| (Б.14) |
Для задачи Коши (т. Е. Задача определяется по всей оси , поэтому граничные условия фактически игнорируются), мы можем интегрировать по области, чтобы получить
| (В.15) |
и поэтому — это глобальная сохраняемая величина. При сравнении (B.14) и (B.15) с (3.3) и (3.5) (в случае без потерь) можно увидеть, что это свойство кососамосопряженности является естественным распространением симметричной гиперболичности на нелинейную кейс.Интересно, что обобщенные определения катушки индуктивности и конденсатора согласно (B.1) и (B.3) полностью соизмеримы; мы увидим это в следующем разделе. Теория кососамосопряженных форм в последнее время заметно активизировалась, в частности, в отношении так называемых энтропийных переменных [68,84,95,180,181,182,183], которые мы кратко рассмотрим в §B.3.3.
Подразделы
Далее: MDKC и MDWDF для Up: Приложения в гидродинамике Предыдущая: Уравнение Бургера Стефан Бильбао 2002-01-22
Решение уравнений через динамику частиц
Эта работа представляет собой удобный способ численного решения нерелятивистского уравнения Шредингера для общей трехчастичной системы, включая полную корреляцию и массовую поляризацию.Можно изучать как кулоновские, так и не кулоновские взаимодействия. Собственный вычислитель основан на рассмотрении динамической системы второго порядка (метод частиц). Матрицу Гамильтона никогда не нужно реализовывать. Волновая функция эволюционирует в сторону стационарного решения, для которого выполняется уравнение Шредингера. Последующие экстраполяции Ричардсона для нескольких сеток затем символически выполняются в Matlab для получения континуального решения. Компьютерный код C протестирован под 64-разрядной версией Linux, и предоставляются версии как с двойной, так и с повышенной точностью.Приведены примеры тестовых прогонов и, по возможности, сравнение с соответствующими значениями в литературе. Компьютерный код небольшой и самодостаточный, что делает его необычайно простым для компиляции и запуска в любой системе. И последовательная, и параллельная работа компьютера проста.
Название программы: corr3p_tr
Идентификатор каталога: AEYR_v1_0
URL-адрес сводки программы: http://cpc.cs.qub.ac.uk/summaries/AEYR_v1_0.html 3 Programable from: 3 Библиотека программ CPC, Королевский университет, Белфаст, Н.Ирландия
Положения о лицензировании: Стандартная лицензия CPC, http://cpc.cs.qub.ac.uk/licence/licence.html
Количество строк в распределенной программе, включая данные тестирования и т. Д .: 15025
Число байтов в распределенной программе, включая тестовые данные и т. Д .: 156430
Формат распределения: tar.gz
Язык программирования: ANSI C.
Компьютер: Linux 64-битный ПК .
Операционная система: Linux 64bit.
RAM: 300 M байтов
Классификация: 2.7, 2.8, 2.9.
Характер задачи: Уравнение Шредингера для произвольной трехчастичной системы решается с использованием конечных разностей и метода быстрых частиц для задачи на собственные значения [20, 21, 23].
Метод решения: Применяется быстрый собственный зольвер (см. Приложение). Этот решатель работает как для симметричных, так и для несимметричных матриц (что позволяет применять более точные несимметричные конечно-разностные выражения на границах).Трехчастичное уравнение Шредингера преобразуется в два основных этапа. Первый шаг — ввести функцию Q (r1, r2, μ) = r1r2 (1 − μ2) φ (r1, r2, μ), где μ = cos (012). Затем точки возврата (r1 = r2, μ = 1) преобразуются в граничные условия. Тогда производные Q непрерывны во всем вычислительном пространстве, и, таким образом, конечно-разностные выражения хорошо определены. Точно так же рассматривается слияние трех частиц (r1 = r2 = 0, μ). Второй шаг — заменить Q (r1, r2, μ) на (2x1x2) −1Q (x1, x2, μ).Пространство (x1, x2, μ) гораздо более подходит для конечно-разностного подхода, поскольку квадратные корни x1 = r1, x2 = r2 позволяют границам уйти намного дальше. Нелинейность x-сетки также приводит к более точному описанию вблизи ядра и более грубому описанию дальше, что приводит к экономии узлов сетки. Кроме того, в отличие от обычной переменной r12, вместо этого мы использовали μ, которая является независимой переменной. Это упрощает математические и численные методы обработки. Естественно, что несколько разных сеток могут работать совершенно независимо друг от друга, что упрощает параллельные вычисления.По результатам нескольких сеток интересующее физическое свойство экстраполируется на пространство континуума. Экстраполяции выполняются в m-скрипте MATLAB, где все вычисления могут быть выполнены символически, поэтому потеря десятичных цифр во время этого процесса сведена к минимуму. Компьютерный код, включая эффекты корреляции и массовую поляризацию, сильно оптимизирован и имеет дело либо с треугольными, либо с квадратичными областями в (x1, x2).
Ограничения: Количество процессорного времени может стать необоснованным для состояний, требующих граничных условий очень далеко за пределами источника.Также, если число обусловленности соответствующей матрицы гамильтониана очень велико, количество итераций будет расти. Использование вычислений с двойной точностью также ограничивает точность экстраполированных результатов примерно до 6–7 десятичных знаков.
Необычные особенности: Численный решатель основан на методе частиц, представленном в [20, 21, 23]. В Приложении мы приводим конкретные детали работы с проблемами собственных значений. Программа использует 64-битную среду (Linux 64bit).Параллельные запуски могут быть выполнены с помощью простого сценария bash.
Дополнительные комментарии: Дискретизированная волновая функция завершена на каждой заданной сетке. Таким образом, новые взаимодействия могут быть добавлены к гамильтониану без необходимости поиска подходящего базиса.
Время работы: Учитывая современный ЦП, такой как Intel Core i5, и внешние граничные условия r1 и r2 ограничены, скажем, 16 атомными единицами, общее время ЦП всего 10 сеток последовательного запуска обычно ограничено до нескольких минут.Тогда можно ожидать около 6–7 правильных цифр в экстраполированном собственном значении. Одна сетка, скажем, h2 = h3 = h4 = 1/16, сходится менее чем за 1 с (с ошибкой в собственном значении около 1 процента). Возможны параллельные запуски, которые еще больше сокращают время ЦП для более сложных задач.
Ссылки: [20] С. Эдвардссон, М. Гулликссон и Дж. Перссон. J. Appl. Мех. ASME, 79 (2012) 021012.
[21] С. Эдвардссон, М. Нойман, П. Эдстром и Х. Олин. Комп. Phys. Commun. 197 (2015) 169.
[23] М. Нойман, С. Эдвардссон, П. Эдстром, Опт. Lett. 40 (2015) 4325.
 Если угол прилежит к проекции, то при проецировании силы на эту ось будет косинус.
Если угол прилежит к проекции, то при проецировании силы на эту ось будет косинус. Эти силы вообще нельзя складывать, т.к. они приложены к разным телам.
Эти силы вообще нельзя складывать, т.к. они приложены к разным телам.
 3)
3) 5)
5)
 При замене с прямой посадкой
При замене с прямой посадкой 7L S, GTS — 575 долларов США за шт.
7L S, GTS — 575 долларов США за шт. 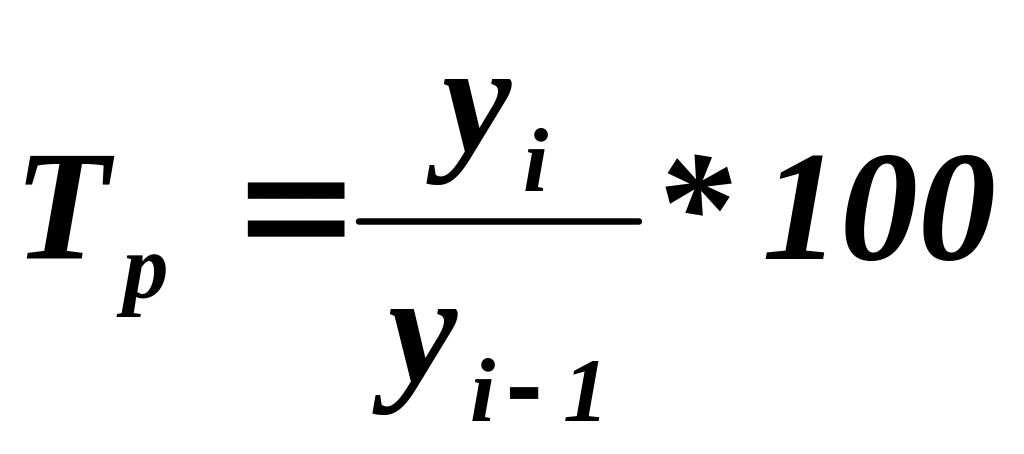 Эти высокопроизводительные роторы с улучшенными характеристиками поперечного сверления, пазов, металлургии и стоимости по сравнению с заводскими деталями OEM являются легким выбором.
Эти высокопроизводительные роторы с улучшенными характеристиками поперечного сверления, пазов, металлургии и стоимости по сравнению с заводскими деталями OEM являются легким выбором. com), банковские переводы или Когда вы будете готовы к покупке, позвоните по телефону (800) 351-8757, чтобы обсудить варианты оплаты и организовать доставку.
com), банковские переводы или Когда вы будете готовы к покупке, позвоните по телефону (800) 351-8757, чтобы обсудить варианты оплаты и организовать доставку. Сюда не входят повреждения от неправильного использования или неправильной установки, а также носимые предметы. Товары, требующие гарантийного обслуживания, будут сфотографированы и отправлены производителю для получения кода разрешения на возврат.Потом отправят в ремонт. Formula Dynamics оставляет за собой право отремонтировать или заменить любой поврежденный элемент по своему усмотрению.
Сюда не входят повреждения от неправильного использования или неправильной установки, а также носимые предметы. Товары, требующие гарантийного обслуживания, будут сфотографированы и отправлены производителю для получения кода разрешения на возврат.Потом отправят в ремонт. Formula Dynamics оставляет за собой право отремонтировать или заменить любой поврежденный элемент по своему усмотрению.