Дифференциал функции
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
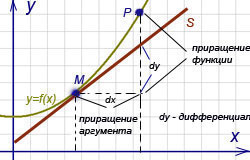
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:
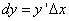
или

или же
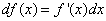
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину 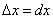
Дифференциал функции в точке x и обозначают
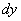
или

Следовательно,
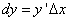 (1)
(1)
или
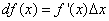 , (2)
, (2)
поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента,
а 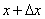
Дифференциал функции можно записать в другой форме:
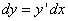 (3)
(3)
или
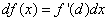 (4)
(4)
Пример 1. Найти дифференциалы функций:
1) 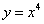 ;
;
2) 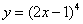 ;
;
3) 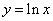 ;
;
4) 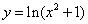
Решение. Применяя формулы дифференцироивания степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:
1) 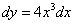 ;
;
2) 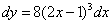 ;
;
3) 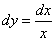 ;
;
4) 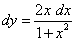 .
.
Найти дифференциалы самостоятельно, а затем посмотреть решения
Пример 2. Найти дифференциал функции
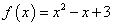
в точке x = 2,
1) выделив линейную часть;
2) по формуле.
Пример 3. Найти дифференциал функции

в точке x.
В основном же задачи на дифференциалы — это более сложные, чем рассмотренные выше для разминки, поэтому стоит посетить страницу с решением задач на дифференциалы сложных функций. Скорее всего, вызывающие у вас трудности задачи именно к таким и относятся.
В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.
Дифференциал обладает свойствами, аналогичными свойствам производной:
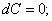 (С – постоянная величина) (5)
(С – постоянная величина) (5)
 (6)
(6)
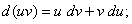
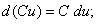 (8)
(8)
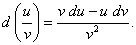 (9)
(9)
Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на  .
.
Одно из особеннейших свойств дифференциала — инвариантность формы дифференциала в случае сложных функций.
Установленное во втором параграфе приближенное равенство

или
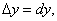
позволяет использовать дифференциал для приближенных вычислений значений функции.
Запишем приближенное равенство более подробно. Так как
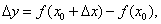
а
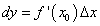
то

или
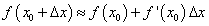 (11)
(11)
Пример 5. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.
Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (11) в данном случае примет вид
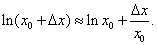
Положим
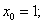
тогда
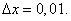
Следовательно,
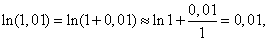
что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.
Пример 6. Пользуясь понятием дифференциала, вычислить приближенно
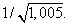
Решение. Число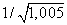 является одним из значений функции
является одним из значений функции

Так как производная этой функции
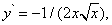
то формула (11) примет вид

Полагая

и
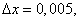
получаем
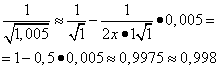
(табличное значение
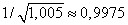 ).
).
Вычислить приближенно самостоятельно, а затем посмотреть решение
Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.
Абсолютная погрешность  приближенного числа
приближенного числа  равна абсолютной величине разности между точным числом
равна абсолютной величине разности между точным числом 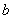 и его приближенным значением:
и его приближенным значением:
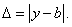 (12)
(12)
Относительной погрешностью 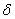 приближенного числа
приближенного числа 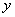 называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
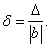 (13)
(13)
Если точное число неизвестно, то
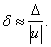 (14)
(14)
Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина 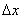 была достаточно малой по сравнению с
была достаточно малой по сравнению с 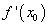 , так как чем меньше
, так как чем меньше  , тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина
, тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина 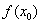
Пример 8. Пользуясь понятием дифференциала, вычислить приближенно 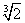 . Оценить точность полученного результата.
. Оценить точность полученного результата.
Решение. Рассмотрим функцию
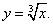
Её производная равна
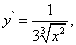
а формула (11) примет вид
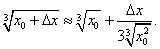
В данном случае было бы нерационально вычислять приближенно  следующим образом:
следующим образом:
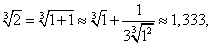
так как значение
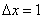
не является малым по сравнению со значением производной в точке
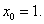
Здесь удобно предварительно вынести из под корня некоторое число, например 4/3. Тогда

Теперь, полагая
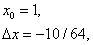
получим

Умножая на 4/3, находим
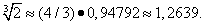
Принимая табличное значение корня
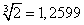
за точное число, оценим по формулам (12) и (13) абсолютную и относительную погрешности приближенного значения:
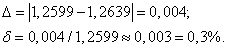

Весь блок «Производная»
Поделиться с друзьями
function-x.ru
Теорема о производной обратной функции (Лекция №6)
ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
Дифференцирование многих функций упрощается, если их предварительно прологарифмировать. Для этого поступают следующим образом. Если требуется найти y‘ из уравнения y=f(x), то можно:
- Прологарифмировать обе части уравнения (по основанию е) ln y = ln f(x) = j(x).
- Продифференцировать обе части равенства, считая ln y сложной функцией от переменной x: .
- Выразить y‘ = y·j'(x) = f(x)·(lnx)’.
Примеры.
- y = xa – степенная функция с
произвольным показателем.
.
ПОКАЗАТЕЛЬНО-СТЕПЕННАЯ ФУНКЦИЯ И ЕЕ ДИФФЕРЕНЦИРОВАНИЕ
Показательно-степенной функцией называется функция вида y = uv, где u=u(x), v=v(x).
Логарифмическое дифференцирование применяется для нахождения производной от показательно-степенной функции.
Примеры.
- .
ТАБЛИЦА ПРОИЗВОДНЫХ
Объединим в одну таблицу все основные формулы и правили дифференцирования, выведенные ранее. Всюду будем полагать u=u(x), v=v(x), С=const. Для производных основных элементарных функций будем пользоваться теоремой о производной сложной функции.
- .
- .
- .
- .
- .
а).
б) .
- .
- .
.
- .
- .
- .
- .
- .
- .
- .
- .
- .
Примеры.
- . Найти y’(–1).
ПОНЯТИЕ ДИФФЕРЕНЦИАЛА ФУНКЦИИ. СВЯЗЬ МЕЖДУ ДИФФЕРЕНЦИАЛОМ И ПРОИЗВОДНОЙ
Пусть функция y=f(x) дифференцируема на отрезке [a; b]. Производная этой функции в некоторой точке х0Î [a; b] определяется равенством
.
Следовательно, по свойству предела
Умножая все члены полученного равенства на Δx, получим:
Δy = f ‘(x0)·Δx + a·Δx.
Итак, бесконечно малое приращение Δy дифференцируемой функции y=f(x) может быть представлено в виде суммы двух слагаемых, из которых первое есть (при f ‘(х0) ≠ 0) главная часть приращения, линейная относительно Δx, а второе – бесконечно малая величина более высокого порядка, чем Δx. Главную часть приращения функции, т.е. f ‘(х0)·Δx называют дифференциалом функции в точке х0 и обозначают через dy.
Таким образом, если функция y=f(x) имеет производную f ‘(x) в точке x, то произведение производной f ‘(x) на приращение Δx аргумента называют дифференциалом функции и обозначают:
Найдем дифференциал функции y= x. В этом случае y‘ = (x)’ = 1 и, следовательно, dy=dx=Δx. Таким образом, дифференциал dxнезависимой переменной xсовпадает с ее приращением Δx. Поэтому формулу (1) мы можем записать так:
Но из этого соотношения следует, что . Следовательно, производную f ‘(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
Ранее мы показали, что из дифференцируемости функции в точке следует существование дифференциала в этой точке.
Справедливо и обратное утверждение.
Если для данного значения x приращение функции Δy = f(x+Δx) – f(x) можно представить в виде Δy = A·Δx + α, где α – бесконечно малая величина, удовлетворяющая условию , т.е. если для функции y=f(x) существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет производную в точке x и f ‘(x)=А.
Действительно, имеем , и так как при Δx→0, то .
Таким образом, между дифференцируемостью функции и существованием дифференциала имеется очень тесная связь, оба понятия равносильны.
Примеры. Найти дифференциалы функций:
- .
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА
Рассмотрим функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной x приращение Δx, тогда функция получит приращение Δy = NM1. Значениям x+Δx и y+Δy на кривой y = f(x) будет соответствовать точка
M1(x+Δx; y+Δy).
Из ΔMNT находим NT=MN·tg α. Т.к. tg α = f ‘(x), а MN = Δx, то NT = f ‘(x)·Δx. Но по определению дифференциала dy=f ‘(x)·Δx, поэтому dy = NT.
Таким образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х.
ТЕОРЕМА ОБ ИНВАРИАНТНОСТИ ДИФФЕРЕНЦИАЛА
Ранее мы видели, что если u является независимой переменной, то дифференциал функции y=f ‘(u) имеет вид dy = f ‘(u)du.
Покажем, что эта форма сохраняется и в том случае, когда u является не независимой переменной, а функцией, т.е. найдем выражение для дифференциала сложной функции. Пусть y=f(u), u=g(x) или y = f(g(x)). Тогда по правилу дифференцирования сложной функции:
.
Следовательно, по определению
, но g‘(x)dx= du, поэтому dy= f'(u)du.
Мы доказали следующую теорему.
Теорема. Дифференциал сложной функции y=f(u), для которой u=g(x), имеет тот же вид dy=f'(u)du, какой он имел бы, если бы промежуточный аргумент u был независимой переменной.
Иначе говоря, форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство дифференциала называется инвариантностью формы дифференциала.
Пример. . Найти dy.
Учитывая свойство инвариантности дифференциала, находим
.
ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛА К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
Пусть нам известно значение функции y0=f(x0) и ее производной y0‘ = f ‘(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x.
Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f‘(x0)·Δx.
Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f‘(x0)·Δx.
Откуда
Примеры.
- y = x2 – 2x. Найти
приближенно, с помощью дифференциала, изменение y (т.е. Δy), когда x изменяется от 3 до 3,01.
Имеем Δy≈dy=f‘(x)·Δx.
f‘(x)=2x – 2 ,f‘(3)=4, Δx=0,01.
Поэтому Δy ≈ 4·0,01 = 0,04.
- Вычислить
приближенно значение функции в точке x = 17.
Пусть x0= 16. Тогда Δx = x – x0= 17 – 16 = 1, ,
.
Таким образом, .
- Вычислить ln 0,99.
Будем рассматривать это значение как частное значение функции y=lnx при х=0,99.
Положим x0 = 1. Тогда Δx = – 0,01, f(x0)=0.
, f ‘(1)=1.Поэтому f(0,99) ≈ 0 – 0,01 = – 0,01.
ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
Пусть функция y=f(x) дифференцируема на некотором отрезке [a; b]. Значение производной f‘(x), вообще говоря, зависит от x, т.е. производная f‘(x) представляет собой тоже функцию переменной x. Пусть эта функция также имеет производную. Дифференцируя ее, получим так называемую вторую производную от функции f(x).
Производная от первой производной называется производной второго порядка или второй производной от данной функции y=f(x) и обозначается y»или f»(x). Итак, y» = (y‘)’.
Например, если у = х5, то y‘= 5x4, а y»= 20x4.
Аналогично, в свою очередь, производную второго порядка тоже можно дифференцировать. Производная от второй производной называется производной третьего порядка или третьей производной и обозначается y»’или f»'(x).
Вообще, производной n-го порядка от функции f(x) называется производная (первая) от производной (n – 1)-го порядка и обозначается символом y(n) или f(n)(x): y(n) = (y(n-1))’.
Таким образом, для нахождения производной высшего порядка от данной функции последовательно находят все ее производные низших порядков.
Примеры.
- Найти производную четвертого порядка функции y= ln x.
.
- .
- Найти производную n-го порядка функции y = ekx.
y‘= k·ekx, y»= k2·ekx, y»’ = k3·ekx, …,y(n) =kn·ekx.
- Найти производную n-го
порядка функции y = sin x.
Имеем
Выясним механический смысл второй производной. (Механический смысл первой производной – скорость).
Пусть материальная точка движется прямолинейно по закону s=s(t), где s – путь, проходимый точкой за время t. Тогда скорость vэтого движения есть v= s'(t) = v(t), т.е. тоже некоторая функция времени.
В момент времени t скорость имеет значение v=v(t). Рассмотрим другой момент времени t+Δt. Ему соответствует значение скорости v1 = v(t+Δt). Следовательно, приращению времени Δt соответствует приращение скорости Δv= v1 – v = v(t + Δt) – v(t). Отношение называется средним ускорением за промежуток времени Δt.
Ускорением в данный момент времени t называется предел среднего ускорения при Δt→0:
.
Таким образом, ускорение прямолинейного движения точки есть производная скорости по времени. Но как мы уже видели, скорость есть производная пути s по времени t: v = s‘. Учитывая это, имеем:
a = v‘(t) = (s‘)’ = s»(t),
т.е. ускорение прямолинейного движения точки равно 2-й производной пути по времени
a = S»(t).
toehelp.ru
Дифференциал сложной функции
Здесь дифференциал записан в том же виде, как и в формуле для
дифференциала функции независимой переменной x, т. е.
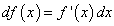 ,
хотя аргумент u является не независимой переменной,
а функцией x.
,
хотя аргумент u является не независимой переменной,
а функцией x.
Следовательно, выражение дифференциала функции в виде произведения производной этой функции на дифференциал её аргумента справедливо независимо от того, является ли аргумент независимой переменной или функцией другой переменной. Это свойство называется инвариантностью (неизменностью) формы дифференциала.
Задание к примерам. Во всех примерах требуется вычислить дифференциал функции двумя способами: выражая его через dx и через du — дифференциал промежуточной переменной u. Проверить совпадение полученных результатов.
Потребуется таблица производных некоторых сложных функций.
Пример 1. Дана функция  .
.
Решение.
Через dx:
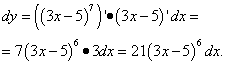
Использовали правило дифференцирования степенной функции.
Через du:
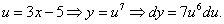
Подставляя в полученное равенство  и
и  , получаем
, получаем
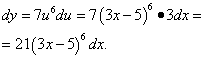
Результаты совпадают.
Пример 2. Дана функция  .
.
Решение.
Через dx:
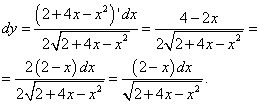
Использовали правило дифференцирования сложной функции квадратного корня.
Через du:
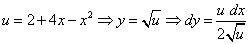 .
.
Подставляя в полученное равенство 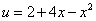 и
и 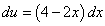 , получаем
, получаем
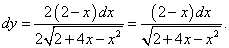
Результаты совпадают.
Пример 3. Дана функция  .
.
Решение.
Через dx:

Использовали правило дифференцирования сложной логарифмической функции.
Через du:
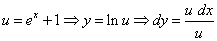 .
.
Подставляя в полученное равенство 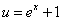 и
и 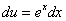 , получаем
, получаем
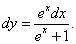
Результаты совпадают.
Пример 4. Дана функция 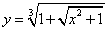 .
.
Решение.
Через dx (в процессе решения для удобства преобразуем корни в степени и обратно):
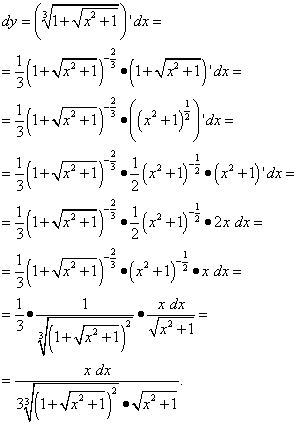
Использовали общее правило дифференцирования сложной функции два раза.
Через du:
 .
.
Подставляя в полученное равенство 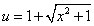 и
и  ,
,
получаем
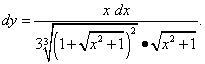
Результаты совпадают.
Пример 5. Дана функция  .
.
Решение.
Через dx:
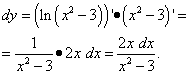
Использовали общее правило дифференцирования сложной функции и правило дифференцирования сложной логарифмической функции.
Через du:
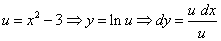 .
.
Подставляя в полученное равенство 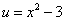 и
и  , получаем
, получаем
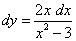 .
.
Результаты совпадают.

Весь блок «Производная»
Поделиться с друзьями
function-x.ru
Дифференциал функции
Дифференциал
(первого порядка) функции 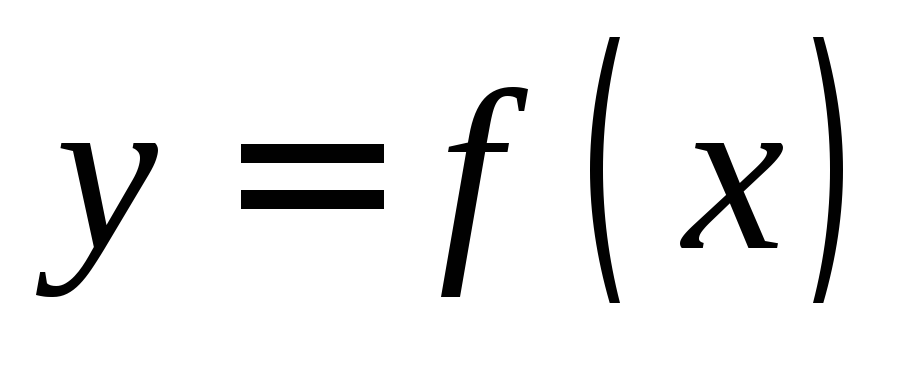 —это главная
часть ее приращения, линейная относительно
приращения аргумента. Дифференциал
аргумента равен его приращению:
—это главная
часть ее приращения, линейная относительно
приращения аргумента. Дифференциал
аргумента равен его приращению: 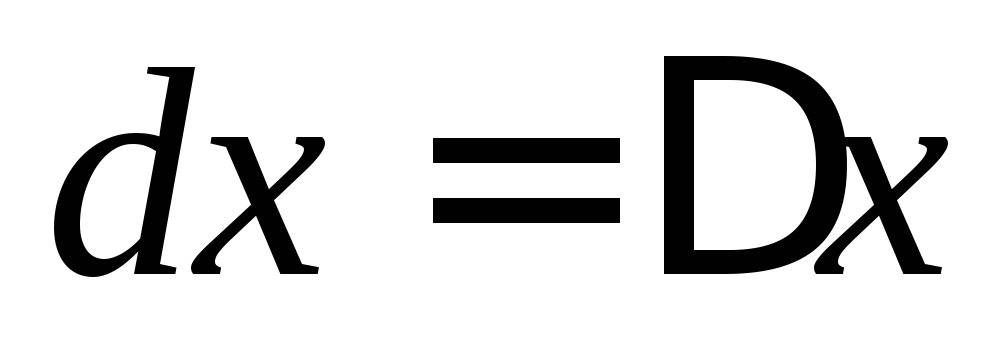 .
Дифференциал функции равен произведению
ее производной на дифференциал аргумента
.
Дифференциал функции равен произведению
ее производной на дифференциал аргумента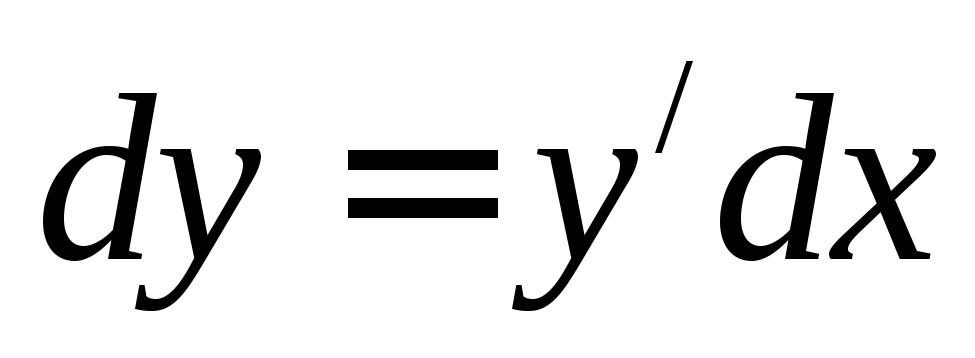 .
.
Основные свойства дифференциала:
1. 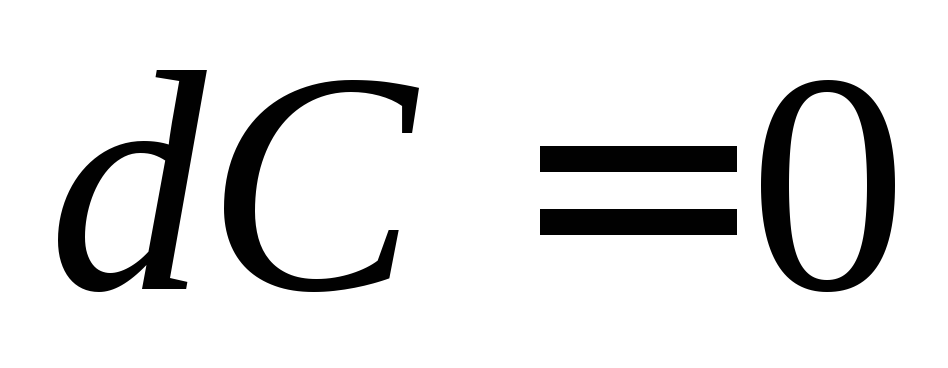 ,
где
,
где -const.
-const.
2. 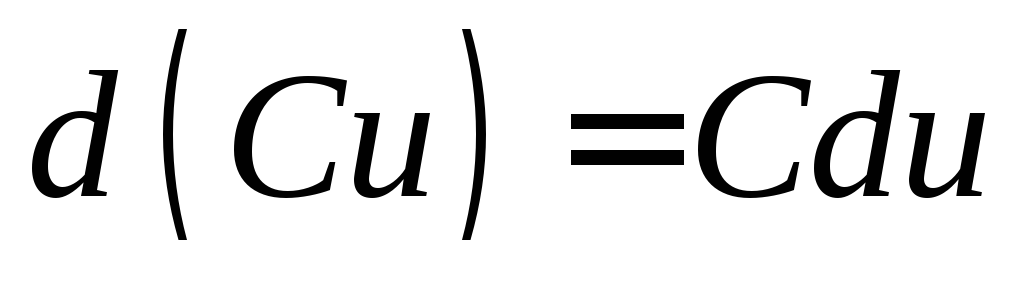 .
.
3. 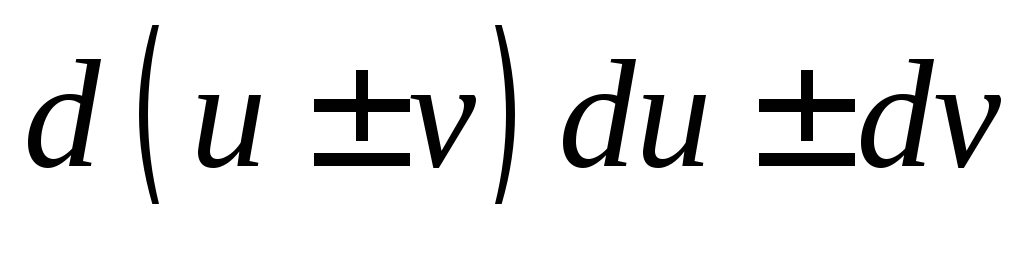 .
.
4. 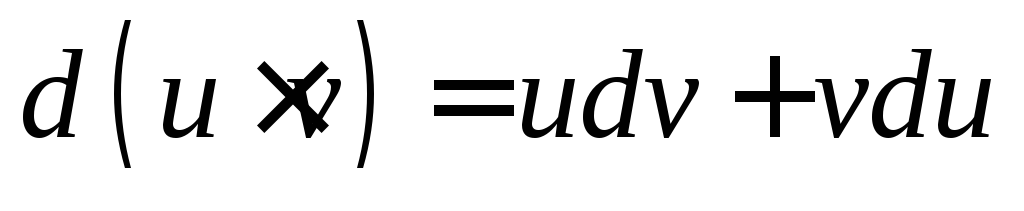 .
.
5. 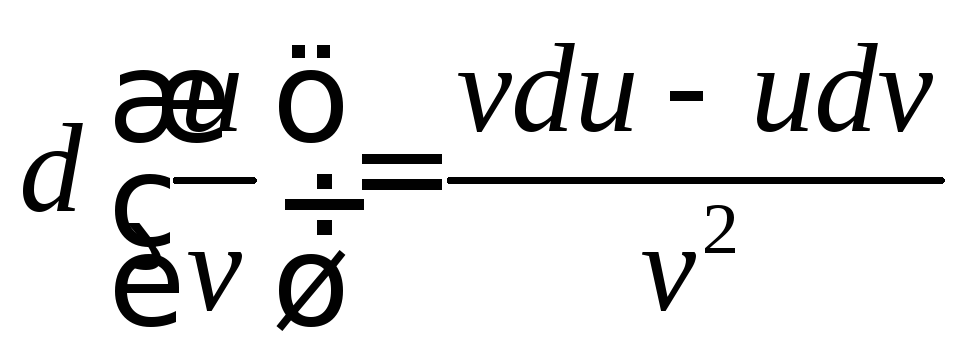 ,
, .
.
6.  ,
,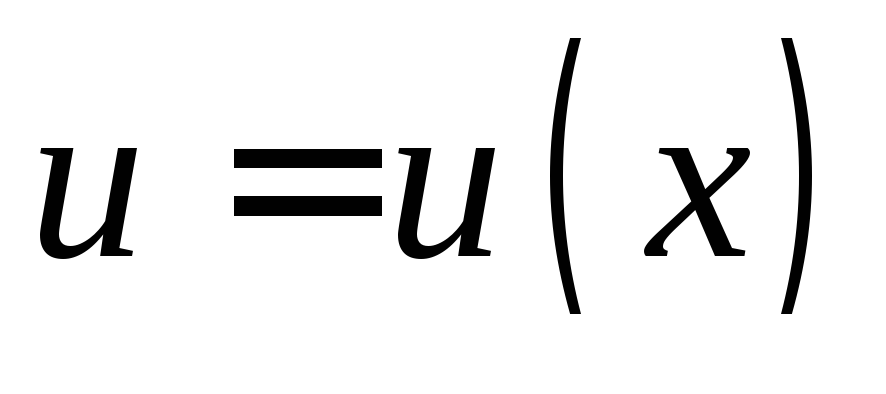 .
Форма дифференциала первого порядка
не зависит от того, является аргумент
функции независимой переменной или
функцией другого аргумента. В этом
состоит свойствоинвариантности
формы дифференциала первого порядка.
.
Форма дифференциала первого порядка
не зависит от того, является аргумент
функции независимой переменной или
функцией другого аргумента. В этом
состоит свойствоинвариантности
формы дифференциала первого порядка.
Дифференциалом
второго порядка функции 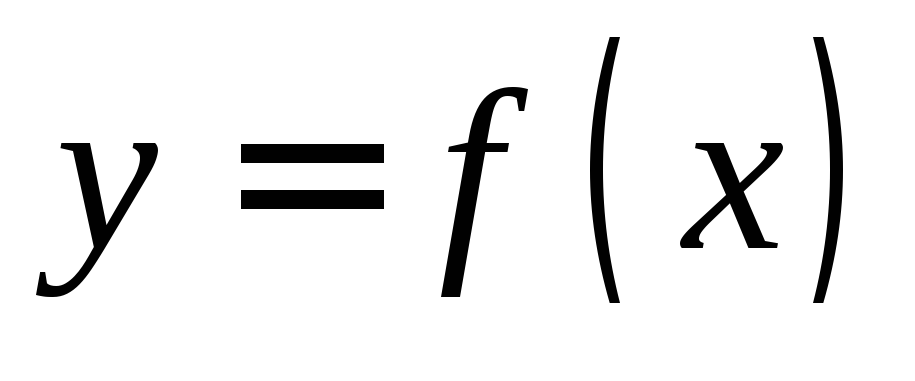 называется дифференциал от дифференциала
первого порядка:
называется дифференциал от дифференциала
первого порядка: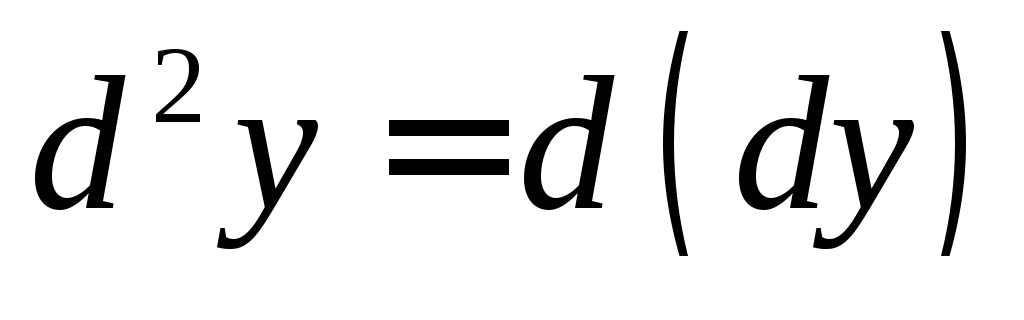 .
.
Аналогично
определяется дифференциал
третьего порядка: 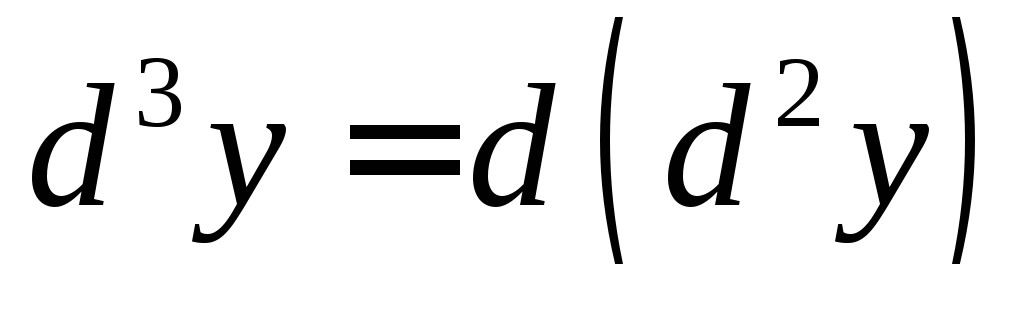 .Дифференциал n-го
порядка:
.Дифференциал n-го
порядка: 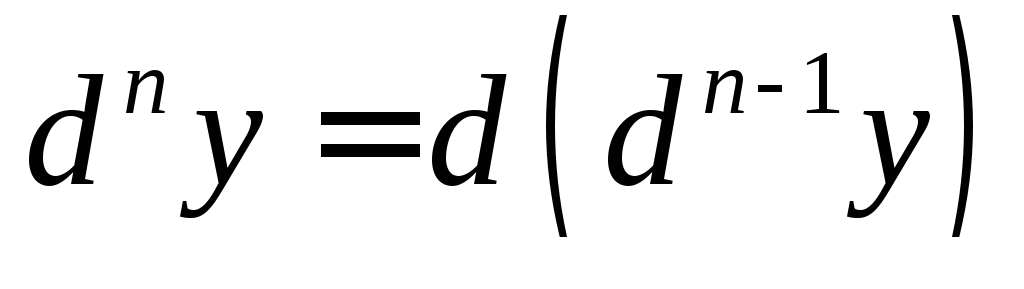 .
.
Если  и
и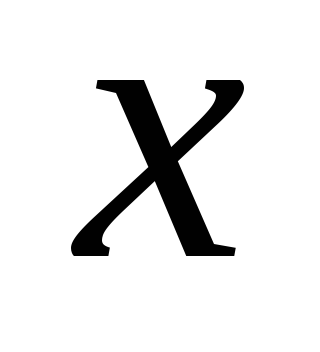 — независимая переменная, то дифференциалы
высших порядков вычисляются по формулам:
— независимая переменная, то дифференциалы
высших порядков вычисляются по формулам:
, 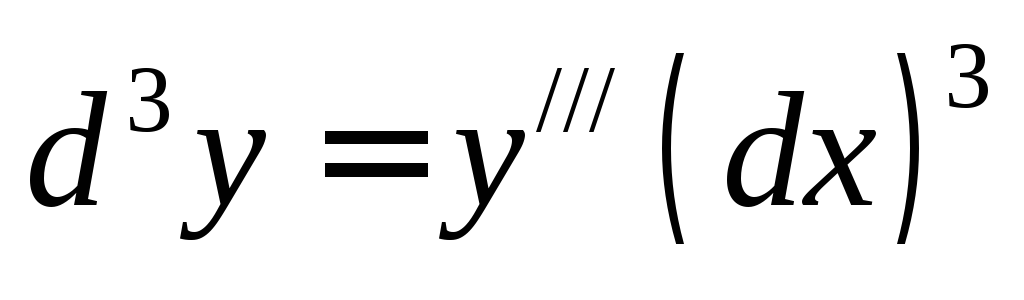 ,…..,
,….., .
.
Если 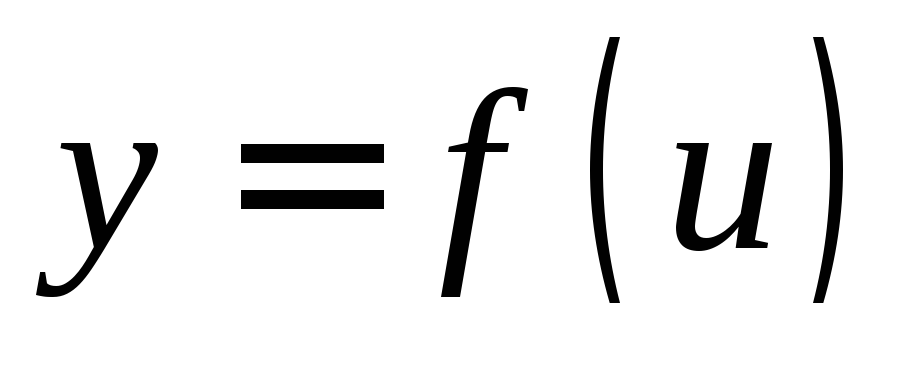 ,
,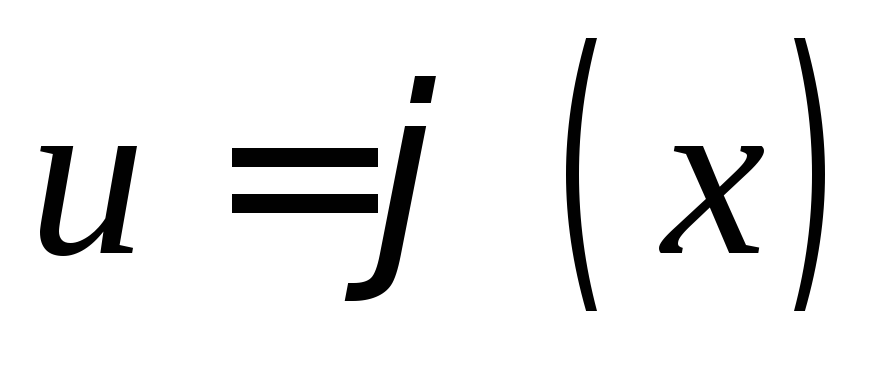 ,
то
,
то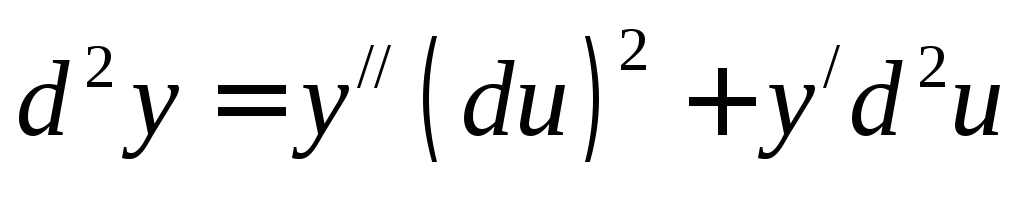 ,
где дифференцирование функции
,
где дифференцирование функции выполняется по переменной
выполняется по переменной .
Это имеет место и для дифференциалов
более высоких порядков.
.
Это имеет место и для дифференциалов
более высоких порядков.
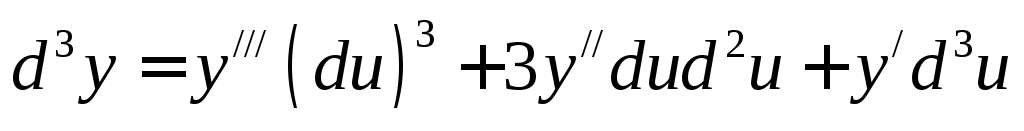 .
.
Дифференциалы второго и более высоких порядков не обладают свойством инвариантности формы.
Геометрически
дифференциал представляет собой
приращение ординаты касательной к
графику функции в точке  .
.
Если
приращение аргумента мало по абсолютной
величине, то 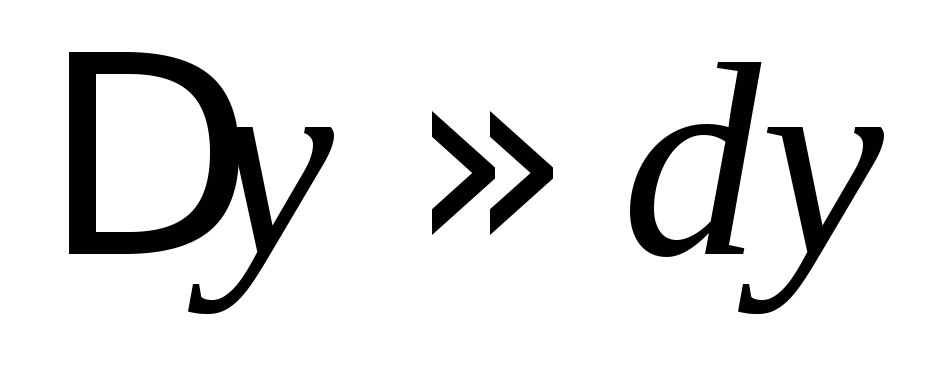 и
и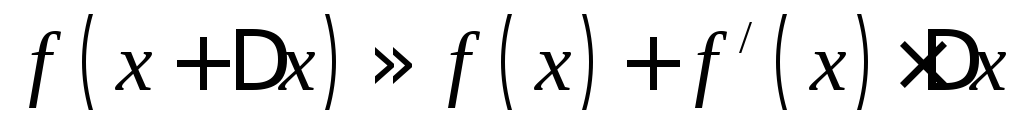 .
Таким образом, дифференциал функции
может применяться для приближенных
вычислений.
.
Таким образом, дифференциал функции
может применяться для приближенных
вычислений.
Абсолютная
величина разности между истинным
значением какой-либо величины 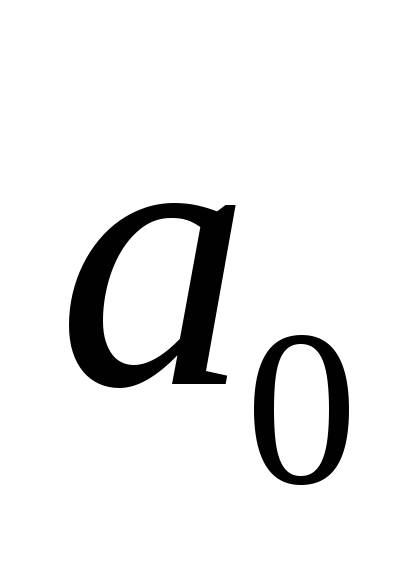 и ее приближенным значением
и ее приближенным значением называется абсолютной погрешностью и
обозначается
называется абсолютной погрешностью и
обозначается 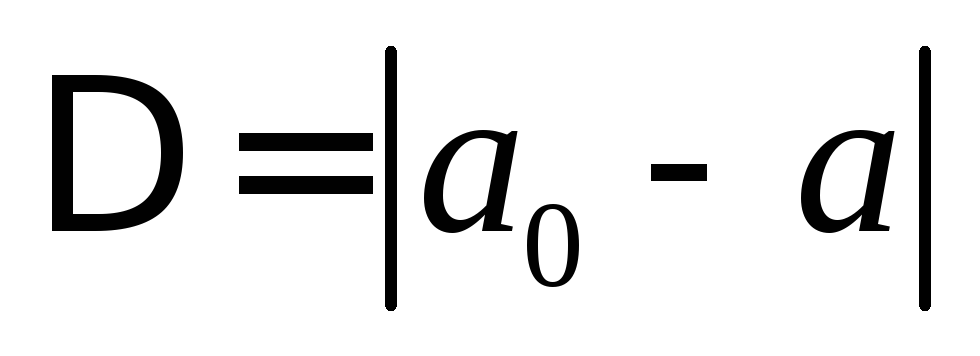 .
.
Абсолютная
величина отношения абсолютной погрешности
к истинному значению называется относительной
погрешностью и обозначается 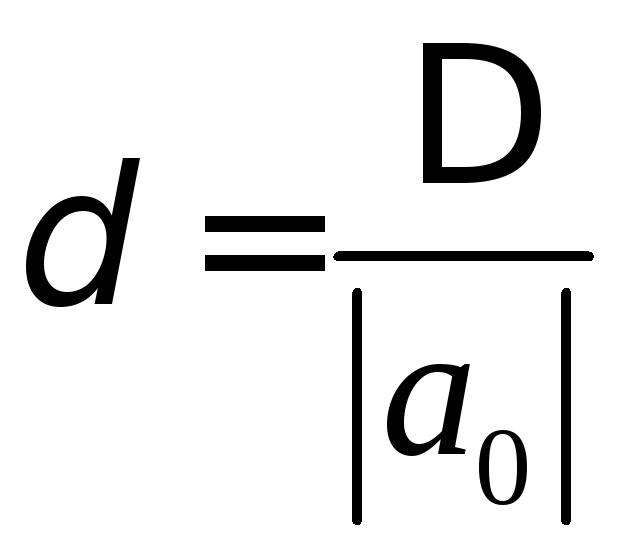 .
Относительная погрешность обычно
выражается в процентах
.
Относительная погрешность обычно
выражается в процентах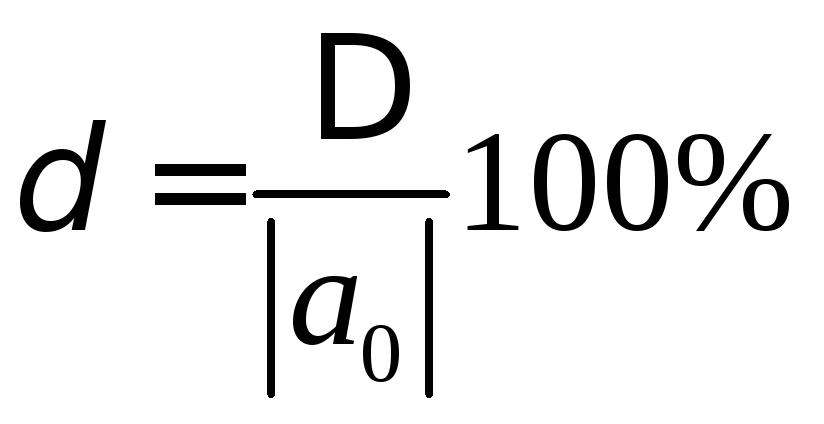 .
.
Если
приращение функции заменить ее
дифференциалом, то получим приближенное
значение приращения 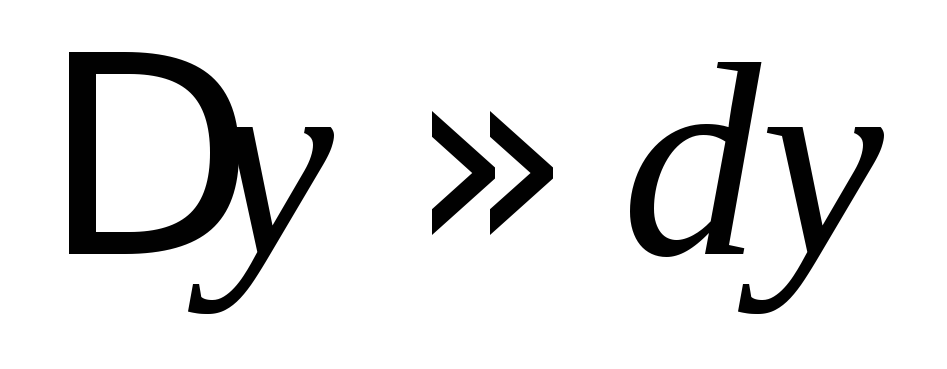 .
В этом случае абсолютная погрешность
равна
.
В этом случае абсолютная погрешность
равна ,
а относительная погрешность будет
,
а относительная погрешность будет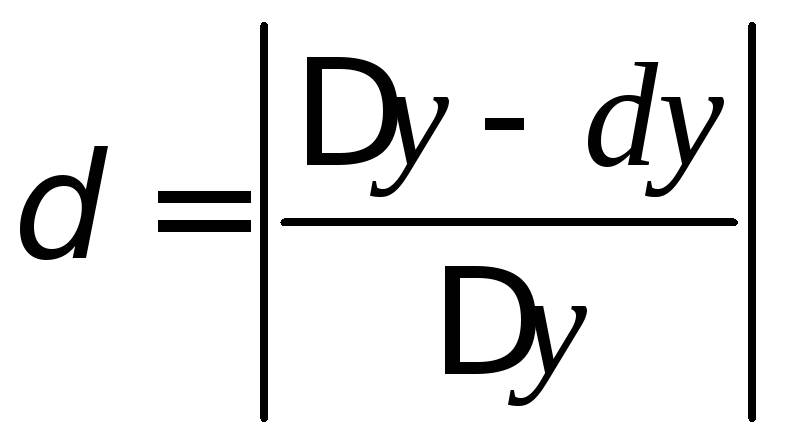 .
.
С
помощью дифференциала функции вычисляют
абсолютную погрешность функции 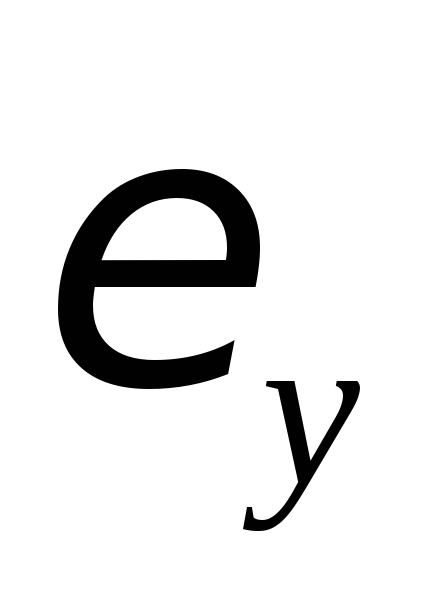 ,
если известна абсолютная погрешность
,
если известна абсолютная погрешность аргумента. В практических задачах
значения аргумента находятся с помощью
измерений, и его абсолютная погрешность
считается известной.
аргумента. В практических задачах
значения аргумента находятся с помощью
измерений, и его абсолютная погрешность
считается известной.
Пусть
требуется вычислить значение функции  при
некотором значении аргумента
при
некотором значении аргумента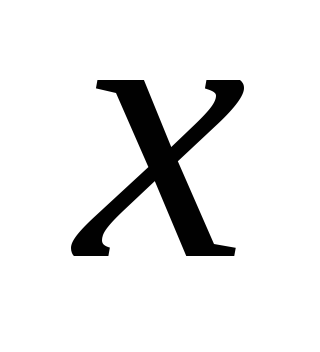 ,
истинная величина которого нам известна,
но дано его приближенное значение
,
истинная величина которого нам известна,
но дано его приближенное значение с абсолютной погрешностью
с абсолютной погрешностью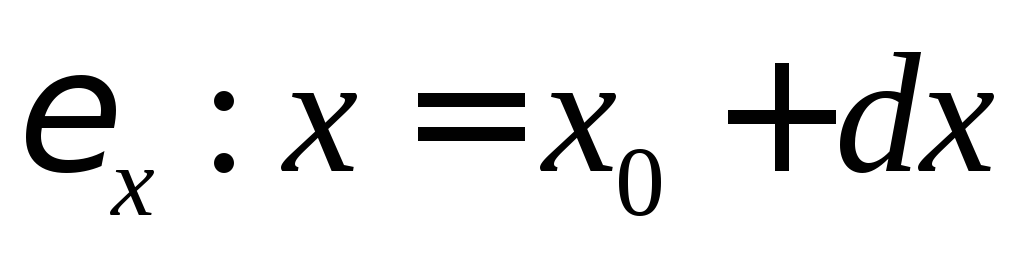 ,
, .
Тогда
.
Тогда
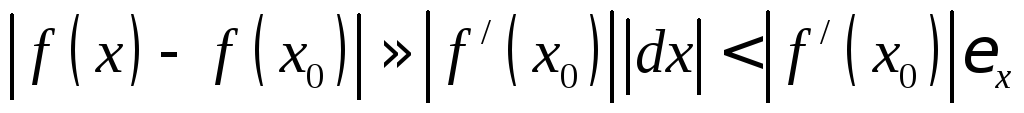 .
.
Отсюда
видно, что 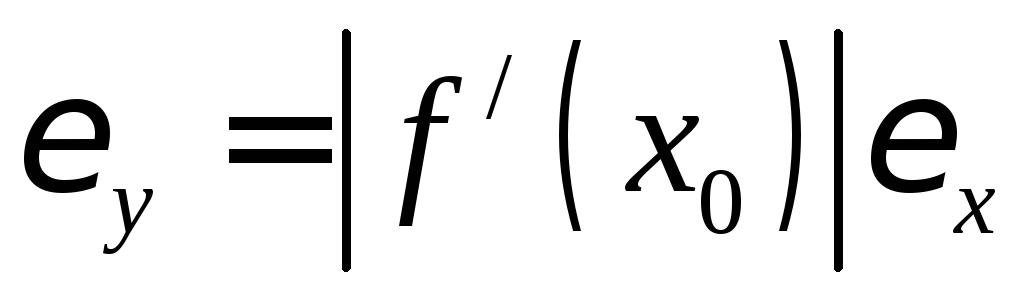 .
.
Относительная
погрешность функции  выражается формулой
выражается формулой
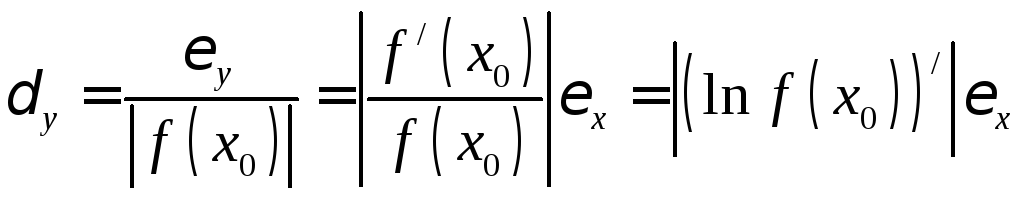 .
.
Пример
1. Найти
дифференциал функции 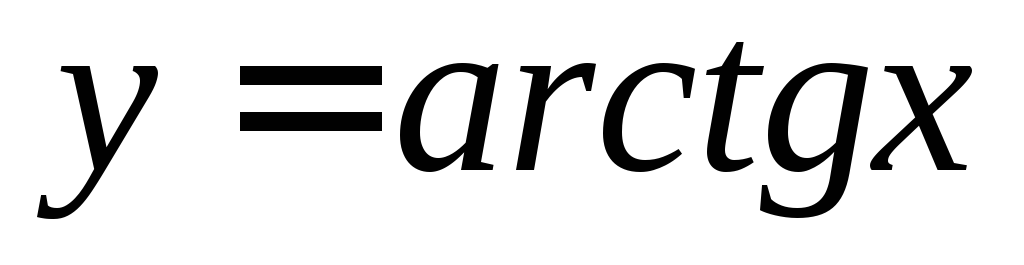 .
.
Решение: 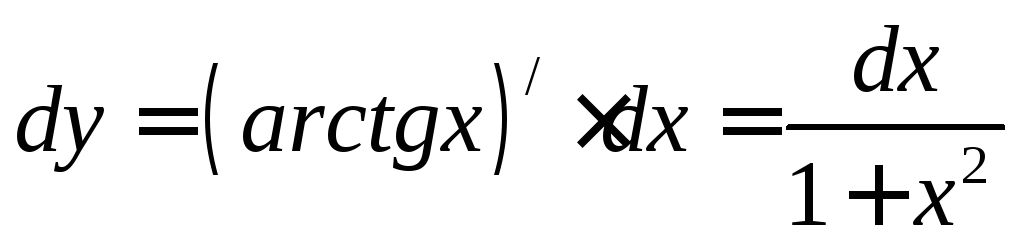 .
.
Пример
2. Найти все
дифференциалы функции 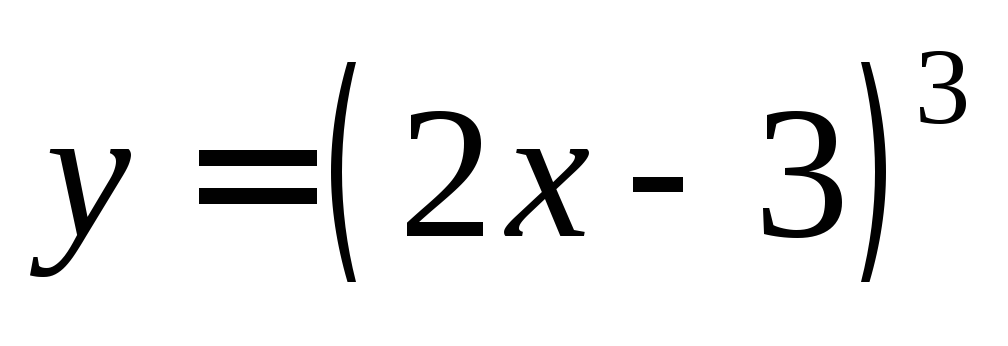 .
.
Решение:  ,
,
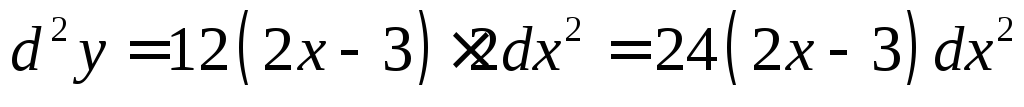 ,
, 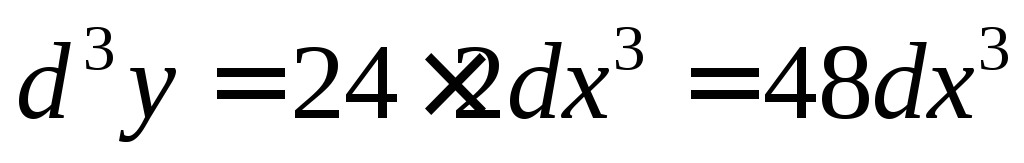 ,
,
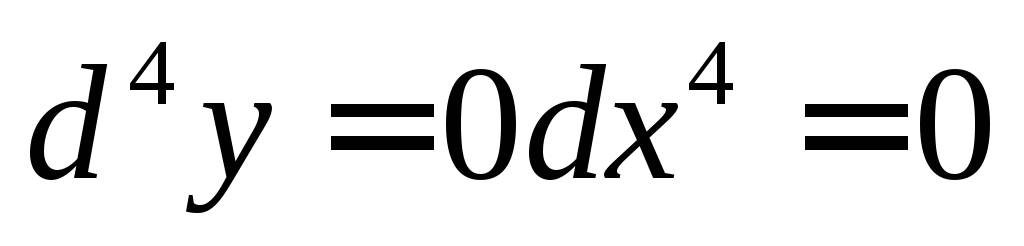 ,
, 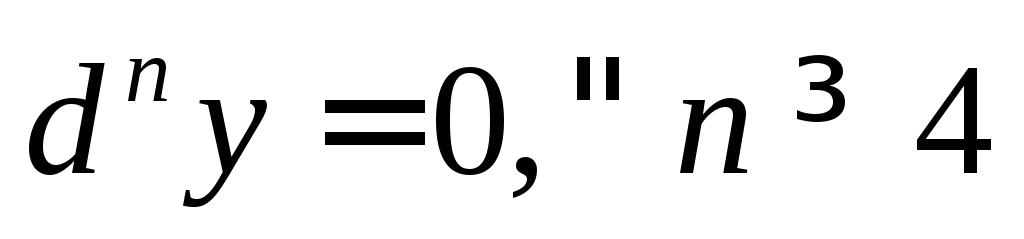 .
.
Пример
3. Найти 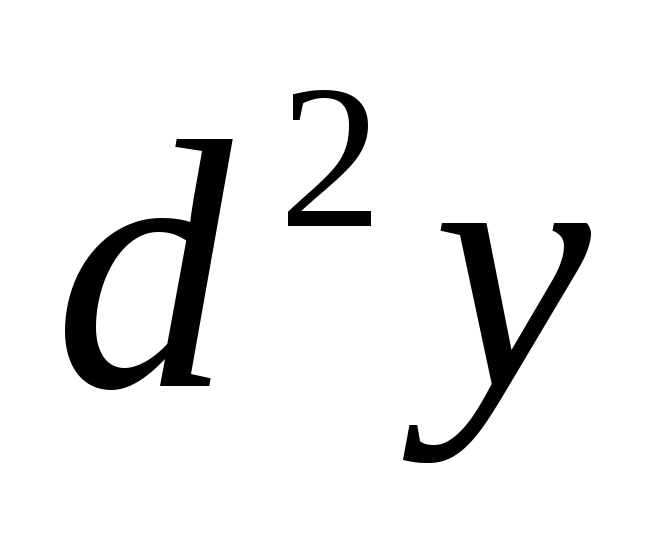 для неявно заданной функции
для неявно заданной функции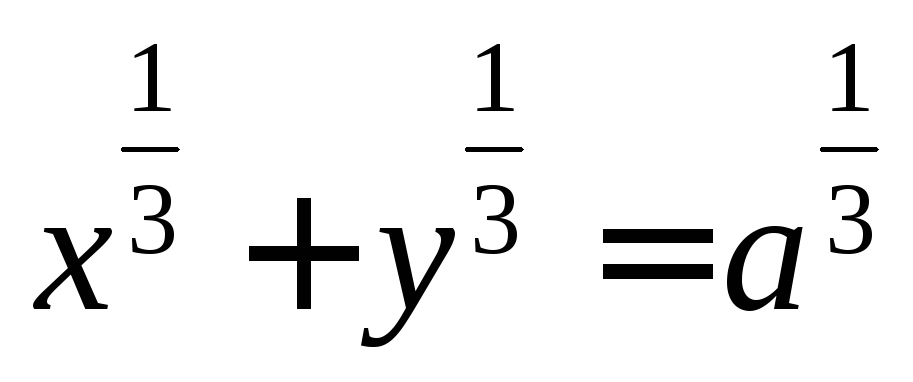 .
.
Решение: Функция задана неявно. Находим первую производную
 ,
тогда
,
тогда  .
.
Вычислим вторую производную
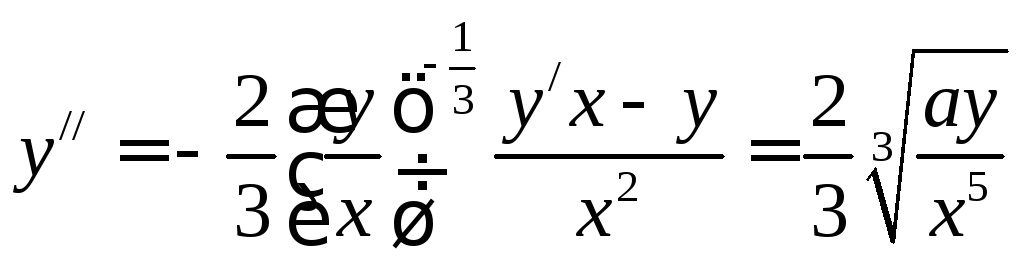 ,
отсюда
,
отсюда  .
.
Пример
4. Выразить
дифференциал сложной функции через
независимую переменную и дифференциал:  ,
,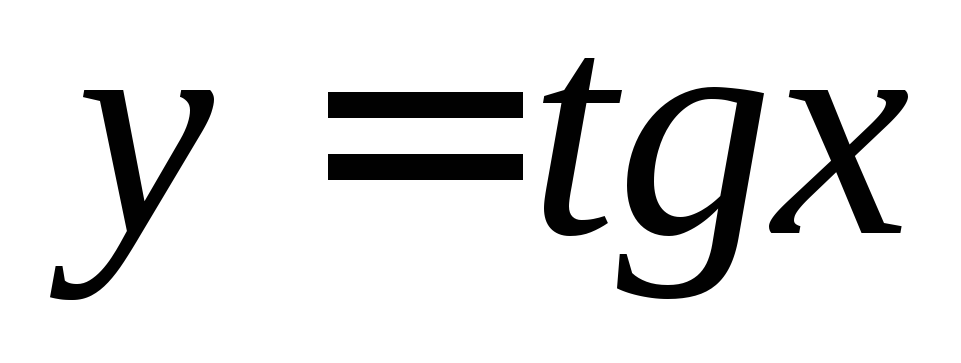 ,
, .
.
Решение: 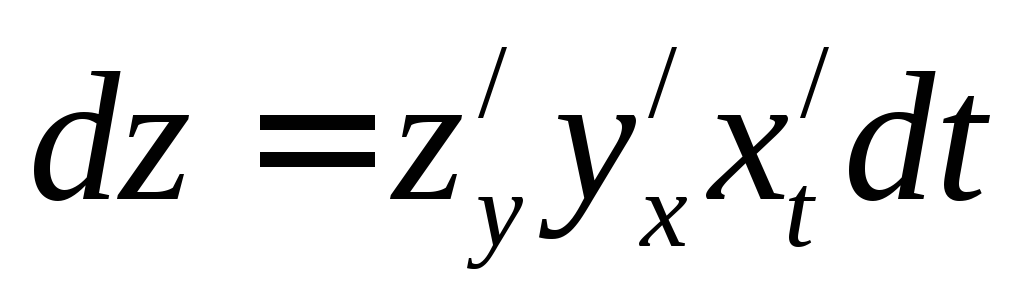 .
. .
.
Пример
5. Вычислить
приближенное значение 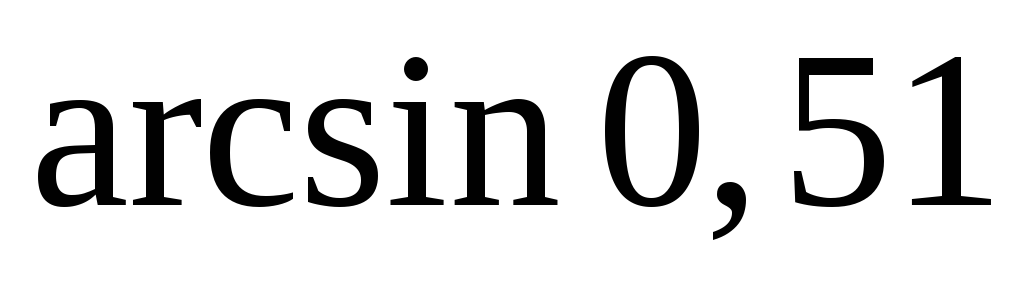 .
.
Решение:
Рассмотрим функцию  .
Полагая
.
Полагая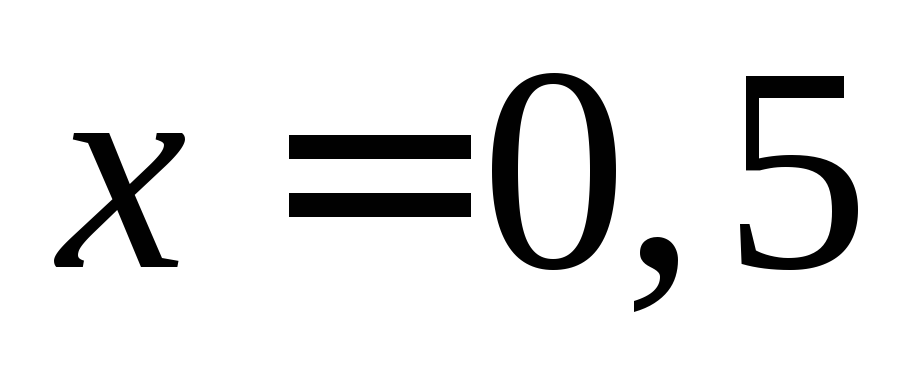 ,
,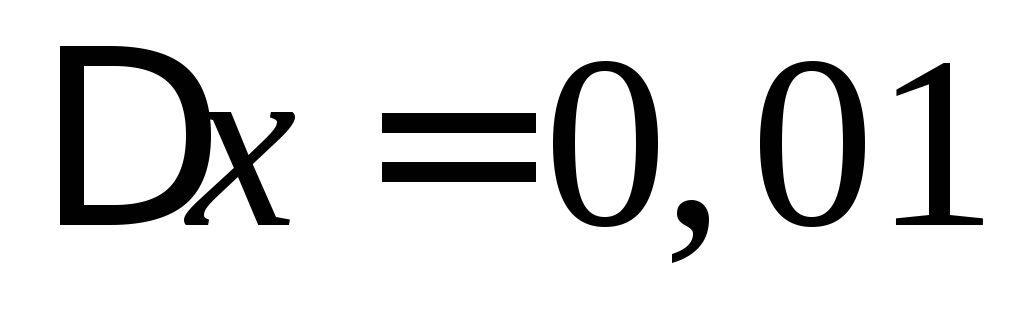 и применяя формулу
и применяя формулу ,
получим:
,
получим:
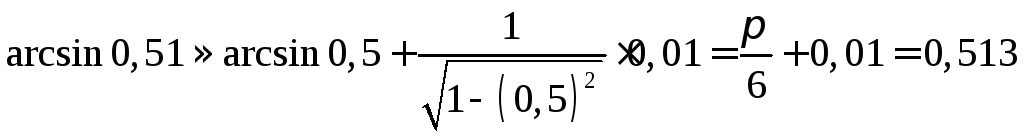 .
.
Пример 6. Вычислить приближенное значение площади круга, радиус которого равен 3,02 м.
Решение:
Воспользуемся формулой 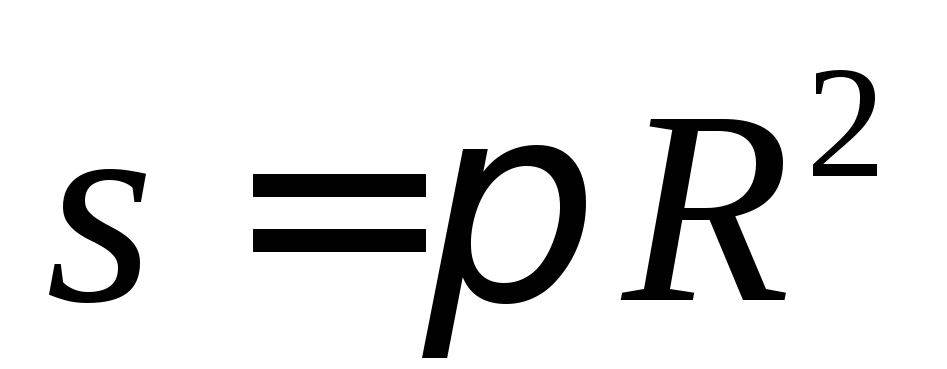 .
Полагая
.
Полагая  ,
, 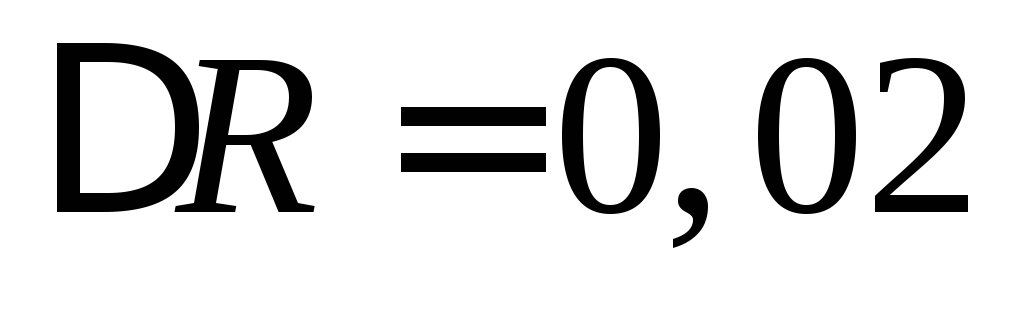 ,
имеем
,
имеем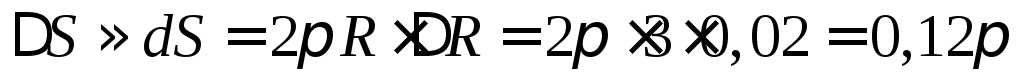 .
Следовательно, приближенное значение
площади круга составляет
.
Следовательно, приближенное значение
площади круга составляет .
.
Пример
7. Для функции 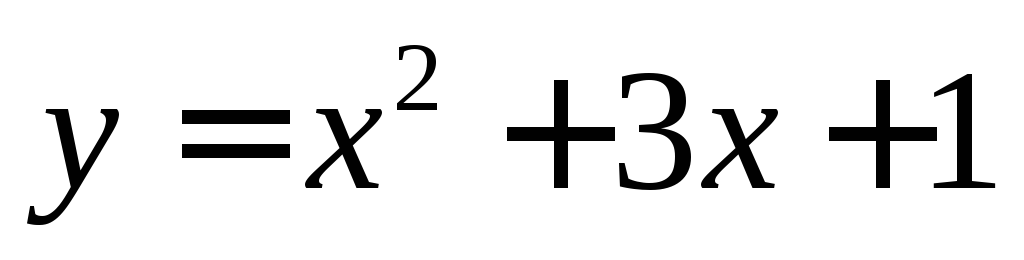 найти приращение ординаты касательной
и приращение функции при переходе
аргумента
найти приращение ординаты касательной
и приращение функции при переходе
аргумента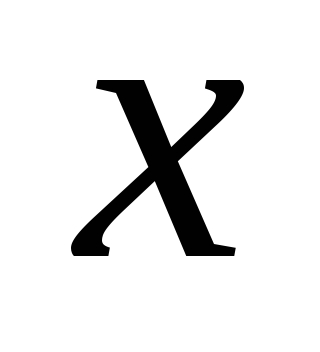 от значения
от значения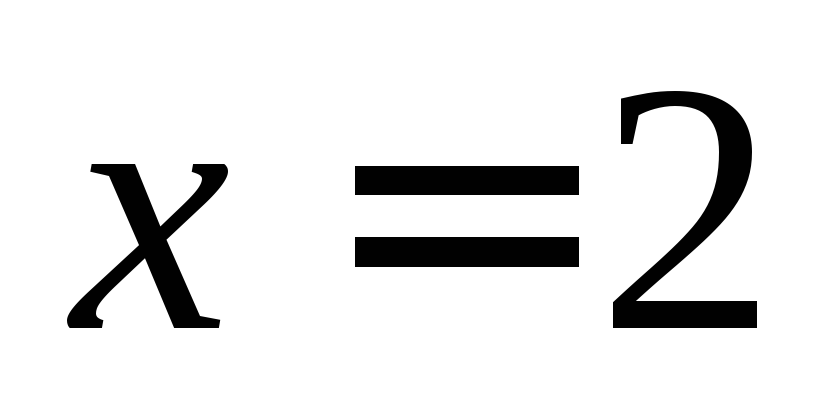 к
к .
.
Решение:
согласно геометрическому смыслу
дифференциала, приращению ординаты
касательной соответствует дифференциал
функции  .
.
При 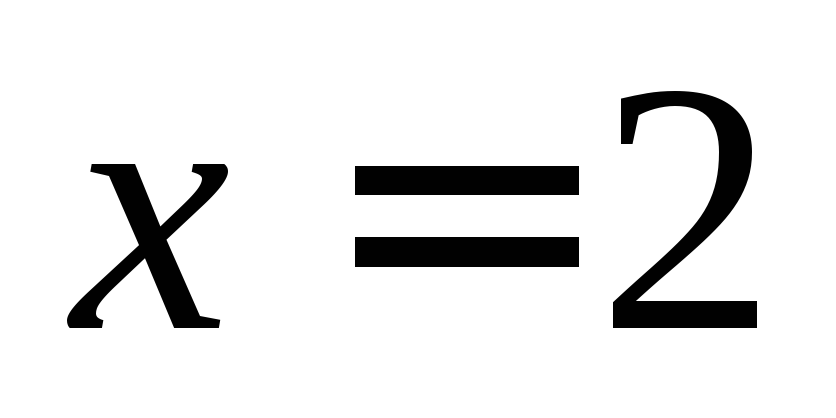 и
и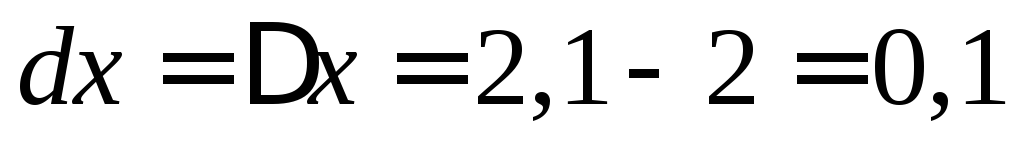 получим
получим .
.
Приращение функции находим по формуле
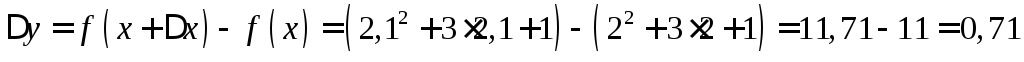 .
.
Следовательно,
приращение ординаты касательной равно
0,7, а приращение функции 0,71. Т. к. 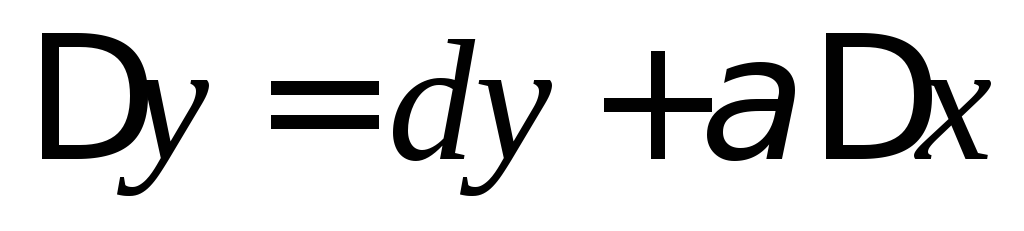 ,
то
,
то .
.
Пример
8. Найти
дифференциал и приращение функции 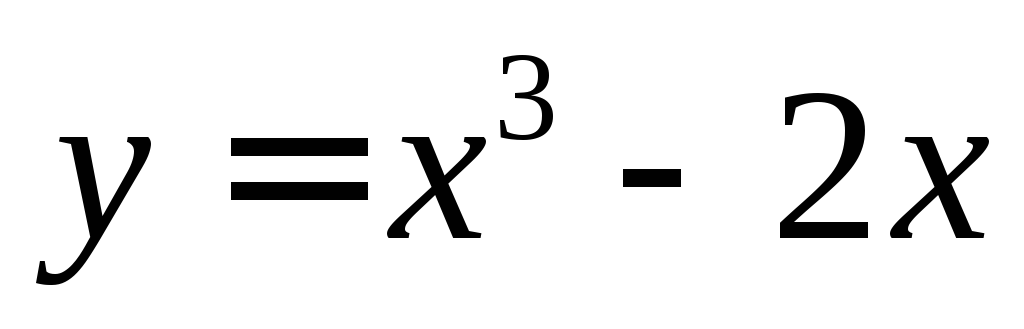 в точке
в точке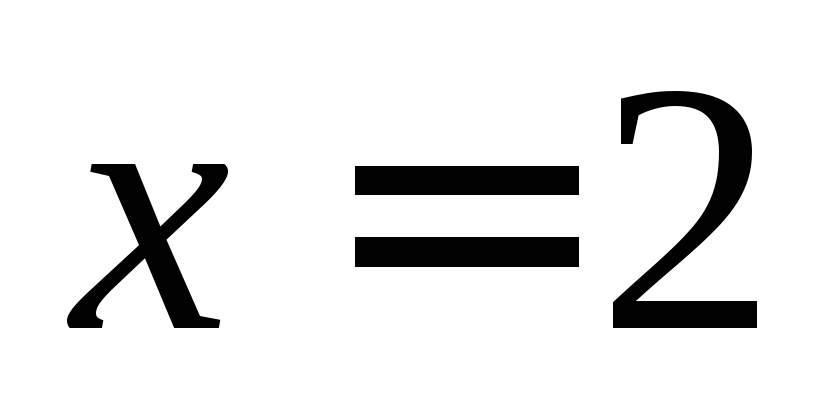 и
и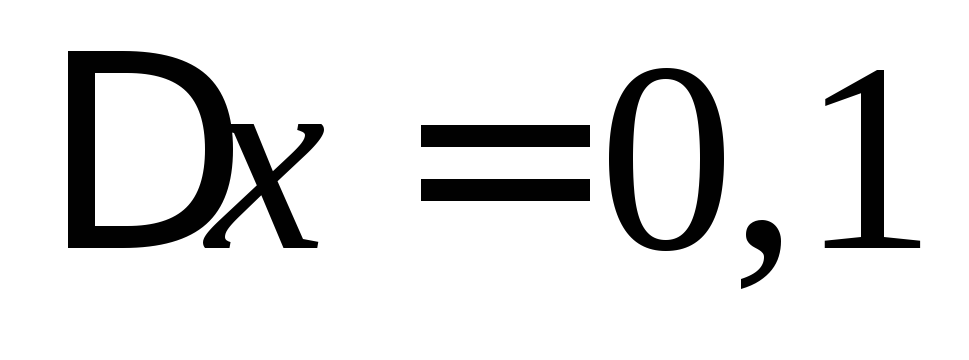 .
Найти абсолютную и относительную
погрешности значения функции при замене
приращения функции ее дифференциалом.
.
Найти абсолютную и относительную
погрешности значения функции при замене
приращения функции ее дифференциалом.
Решение:
Имеем:  ,
,
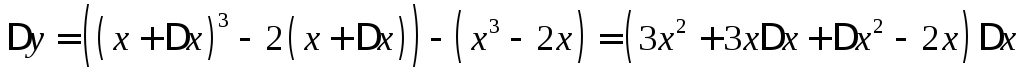 .
.
При 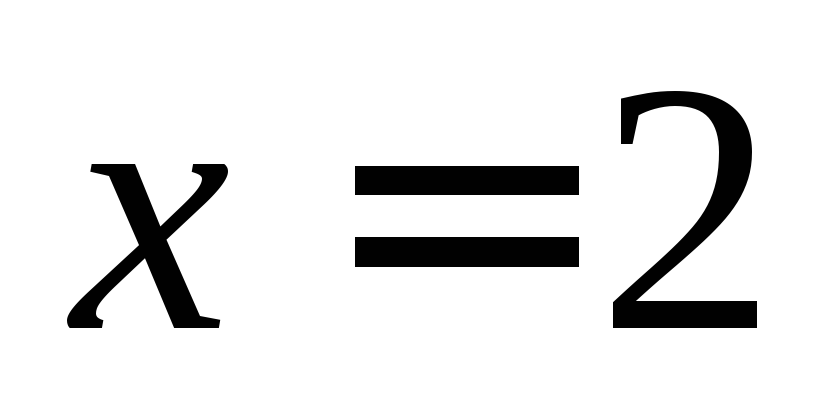 и
и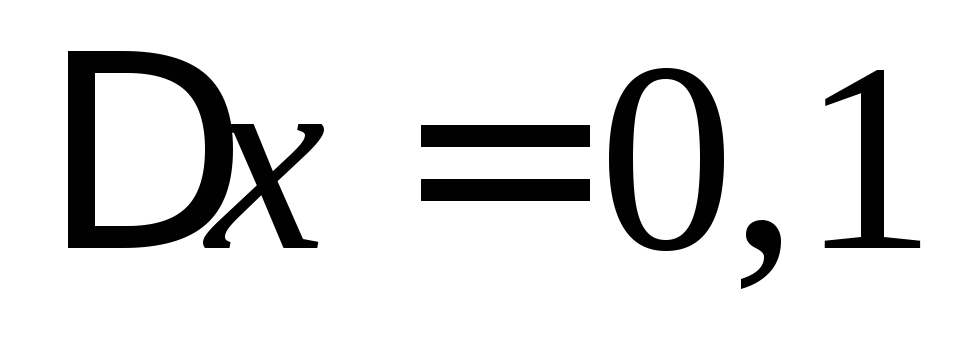 получим:
получим:
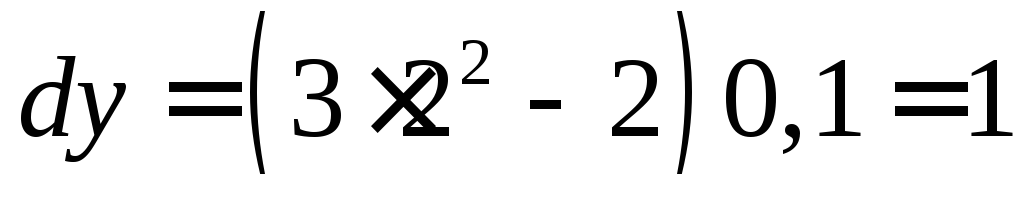 ,
, 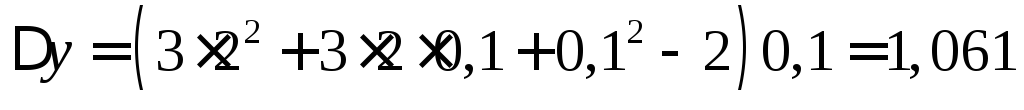 .
.
Абсолютная
погрешность  ,
а относительная погрешность
,
а относительная погрешность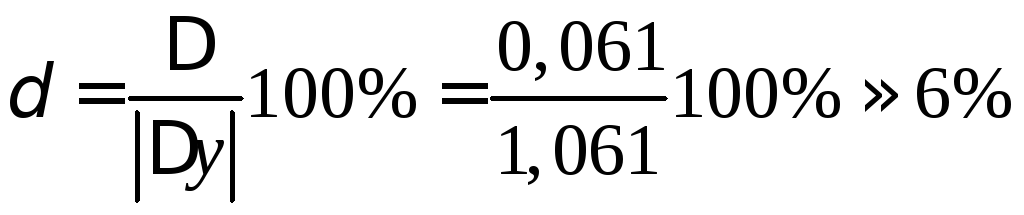 .
.
Пример
9. При измерении
сторона куба 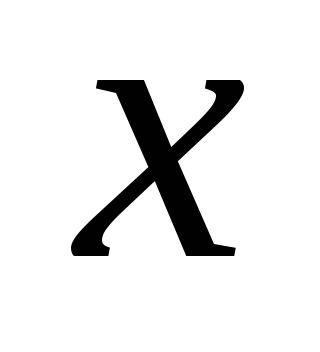 оказалась равной 4 см. При этом максимально
возможная погрешность измерения
оказалась равной 4 см. При этом максимально
возможная погрешность измерения находится в пределах
находится в пределах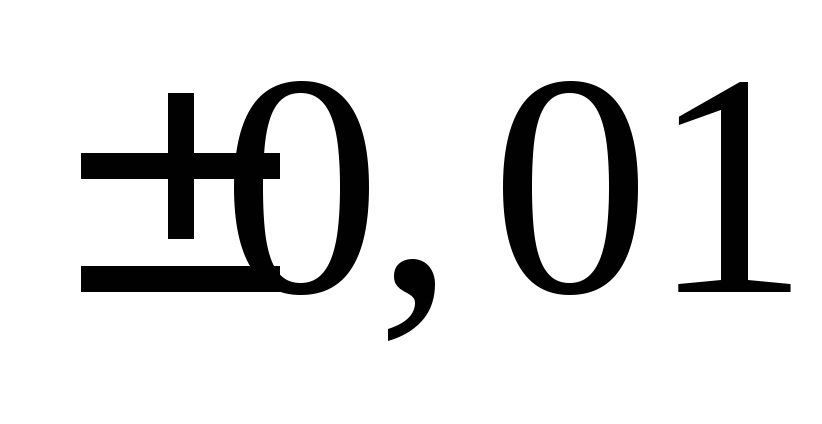 см.
Определить абсолютную и относительную
погрешности при вычислении объема куба.
см.
Определить абсолютную и относительную
погрешности при вычислении объема куба.
Решение:
Объем куба равен 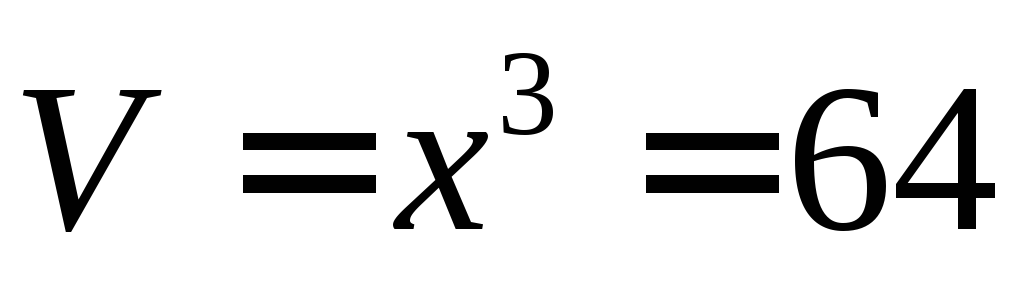 см
см .
.
Возможная
неточность измерения 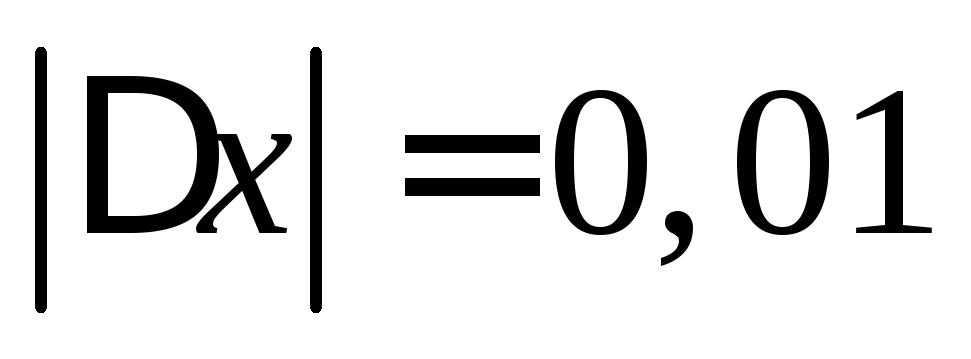 .
.
Отсюда
абсолютная погрешность 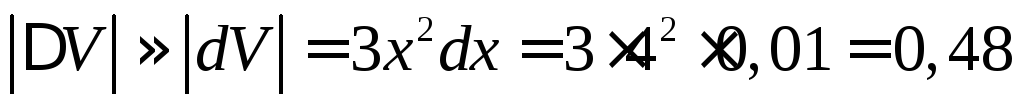 .
.
Относительная
погрешность 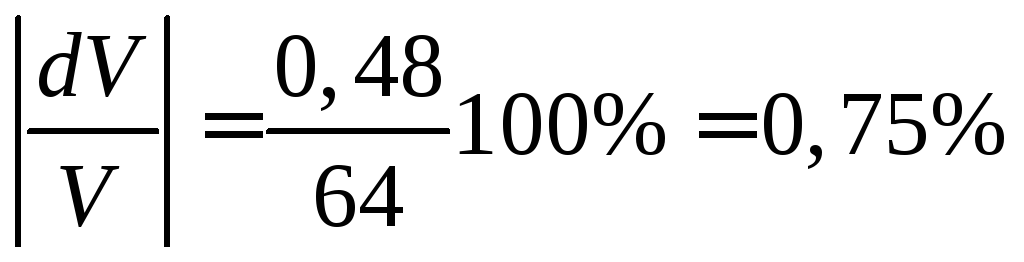 .
.
Пример
10. Найти
приближенно 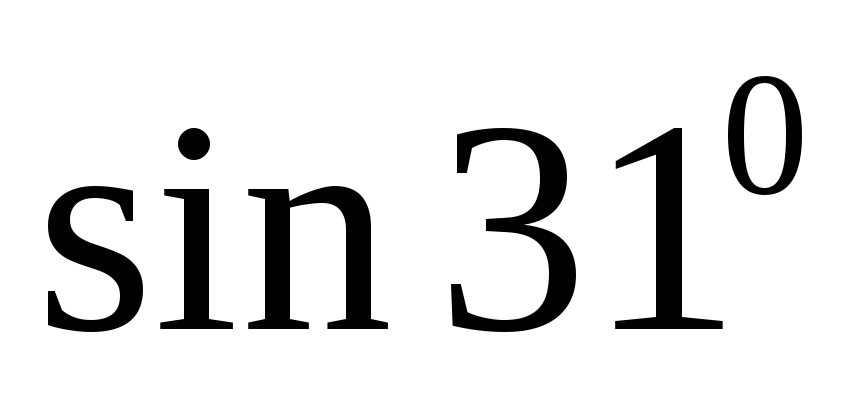 .
.
Решение:
Полагаем  ,
тогда
,
тогда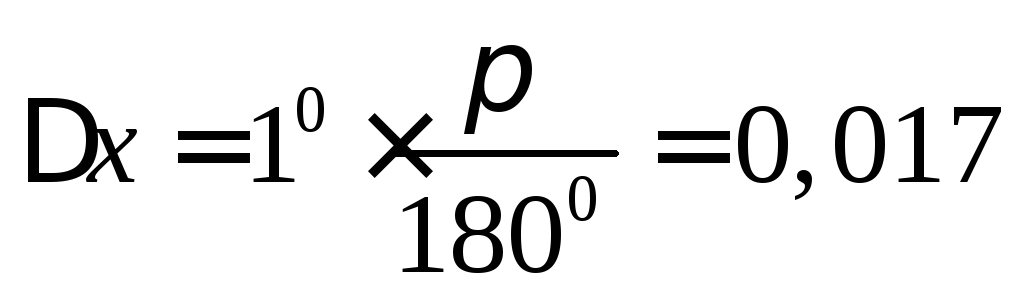 ,
,
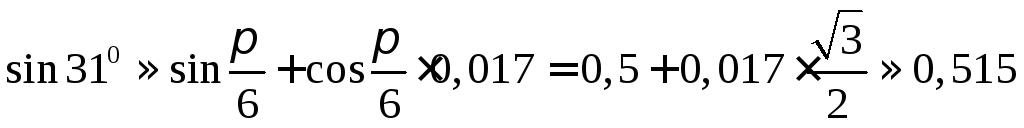 .
.
Если
принять  ,
то
,
то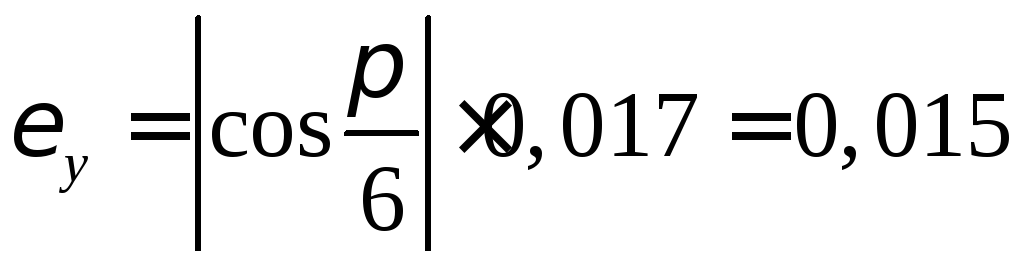 ,
,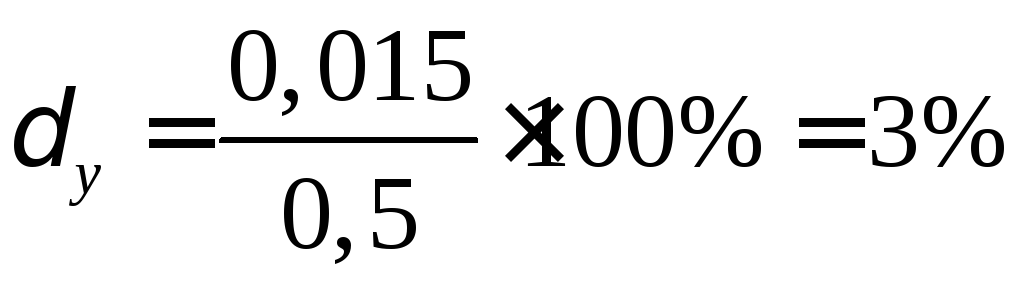 .
.
Найти дифференциалы указанных порядков от функций:
1. 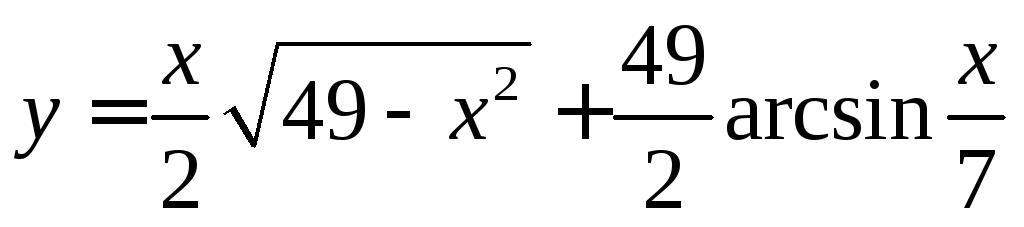 ,
, -?.
Ответ:
-?.
Ответ: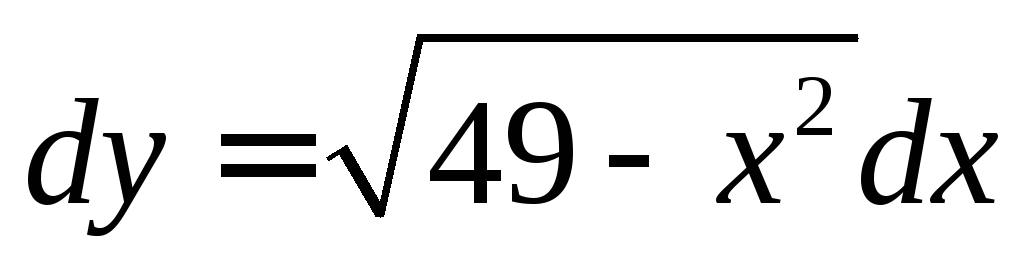 .
.
2. 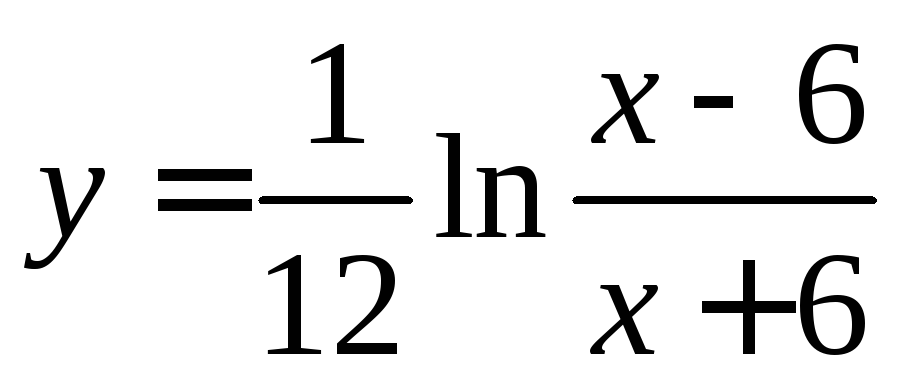 ,
,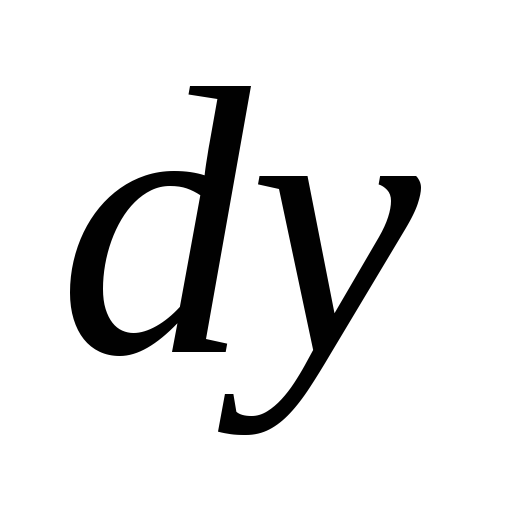 -?
Ответ:
-?
Ответ: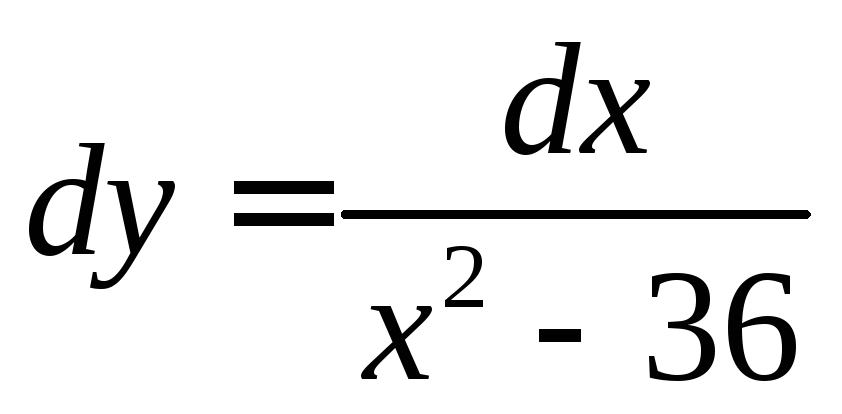 .
.
3. 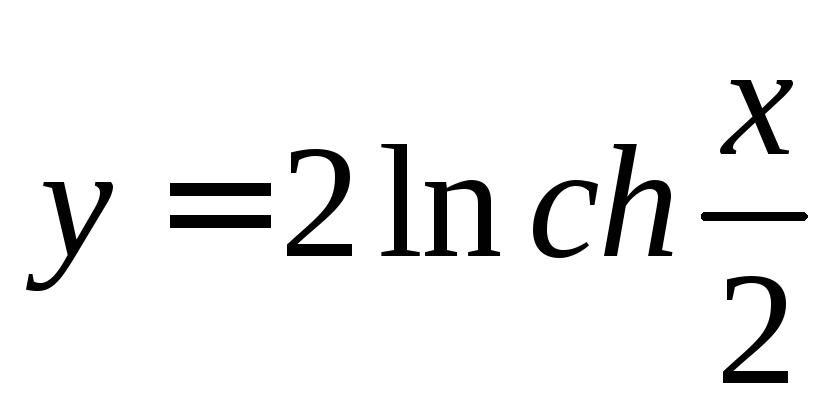 ,
,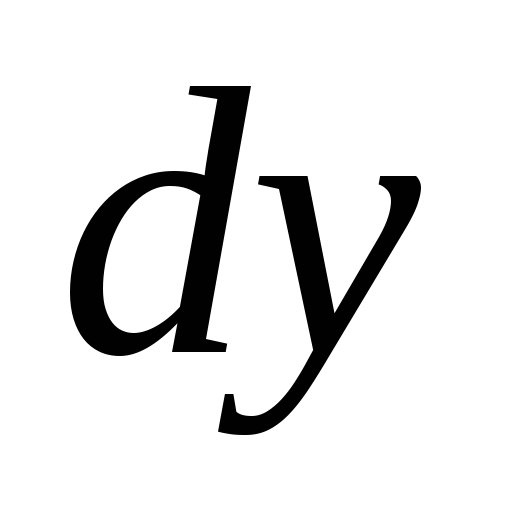 -?
Ответ:
-?
Ответ: .
.
4. 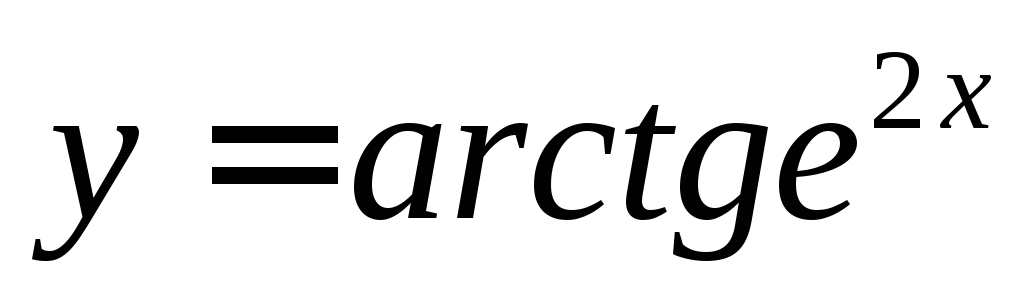 ,
,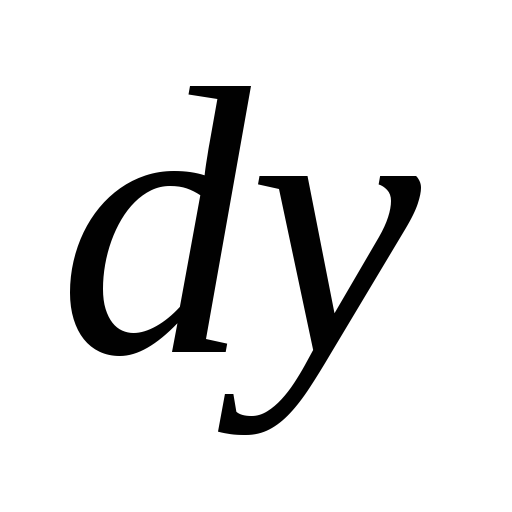 -?
Ответ:
-?
Ответ: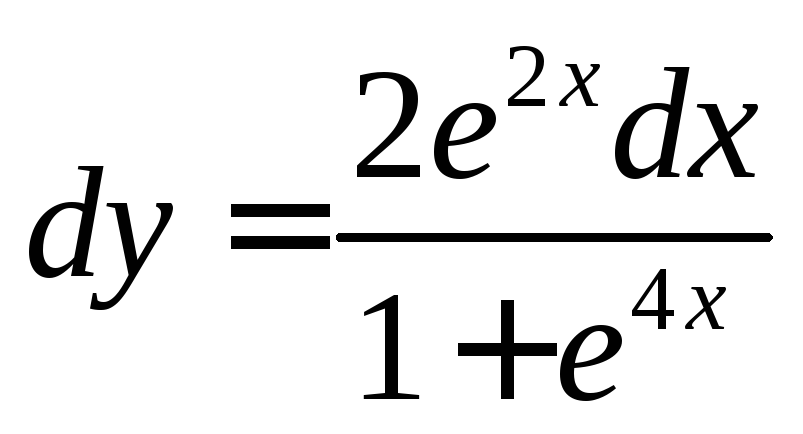 .
.
5. 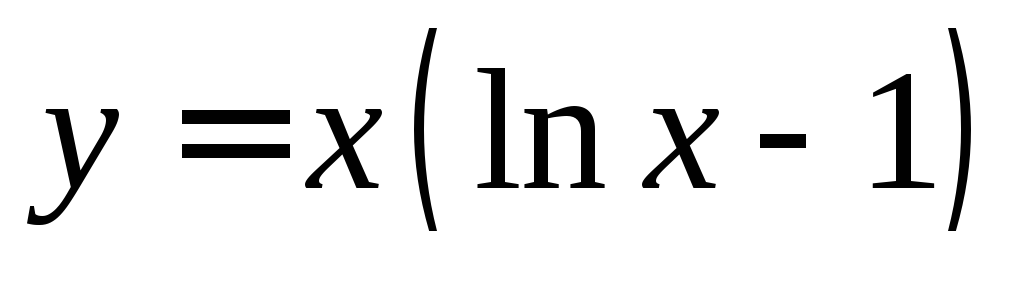 ,
,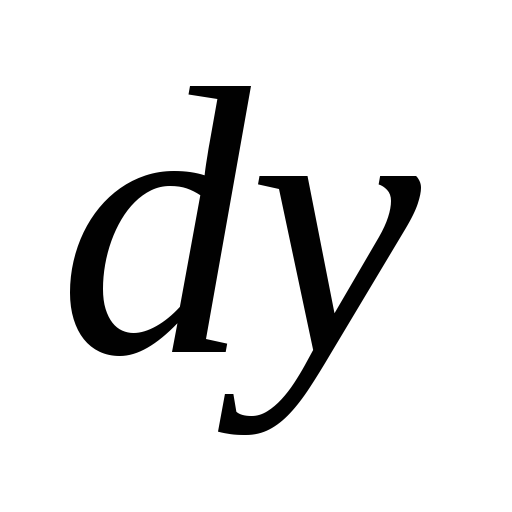 ,
, ,
,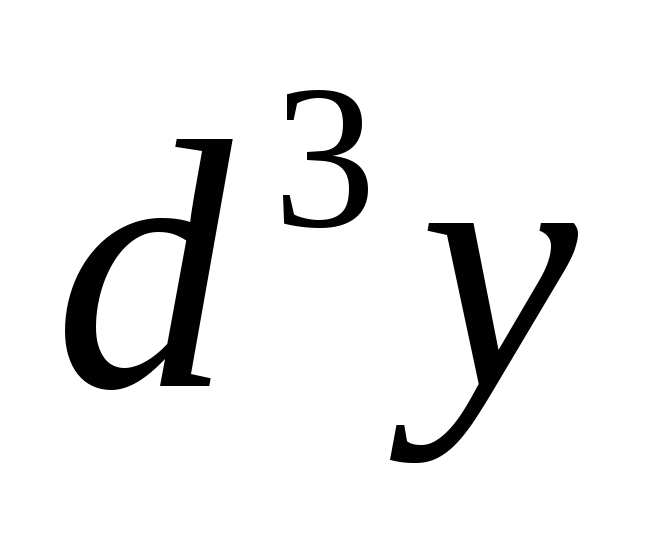 -? Ответ:
-? Ответ: .
.
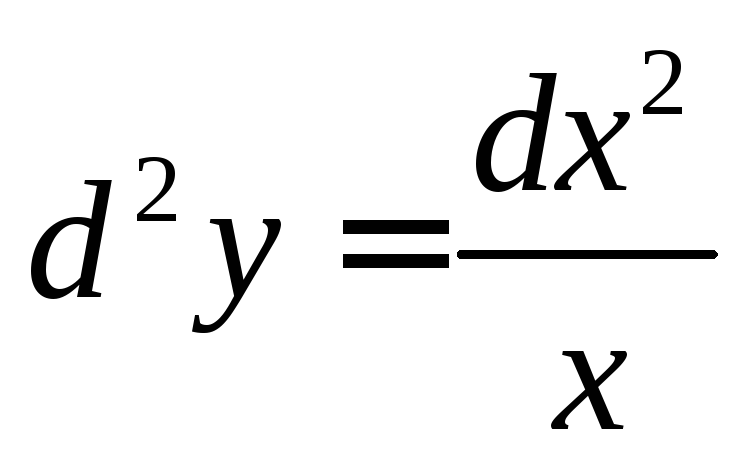 ,
, 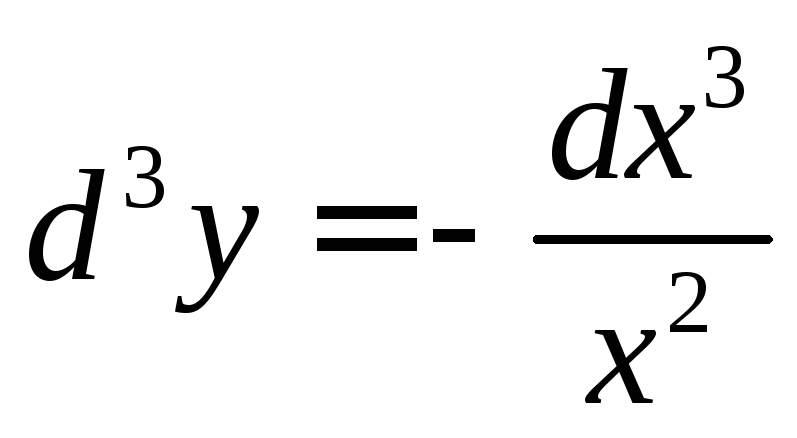 .
.
6. 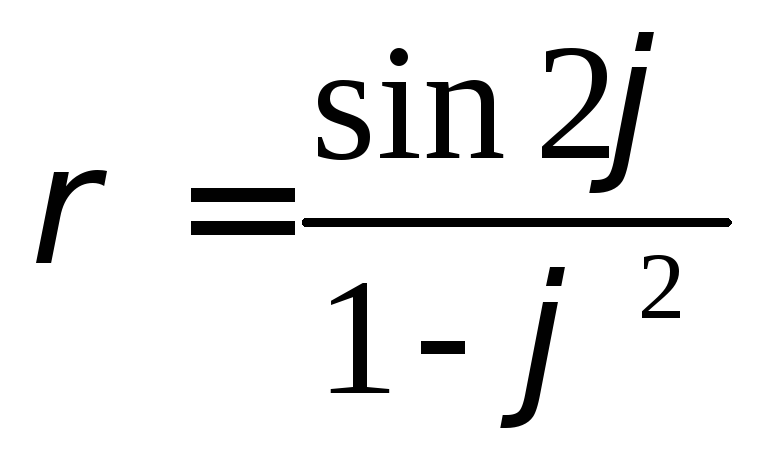 ,
,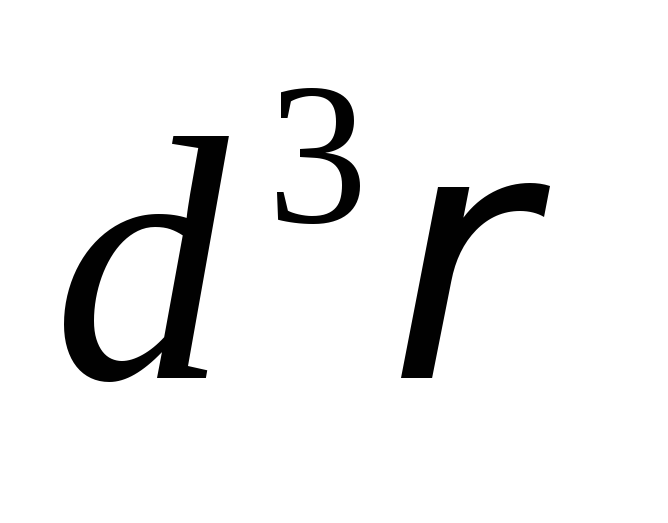 -?
-?
Ответ: 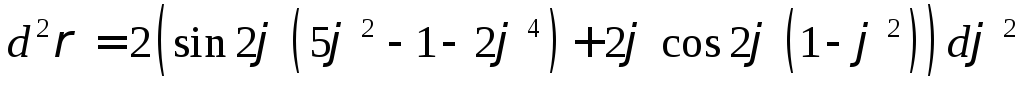 .
.
7. 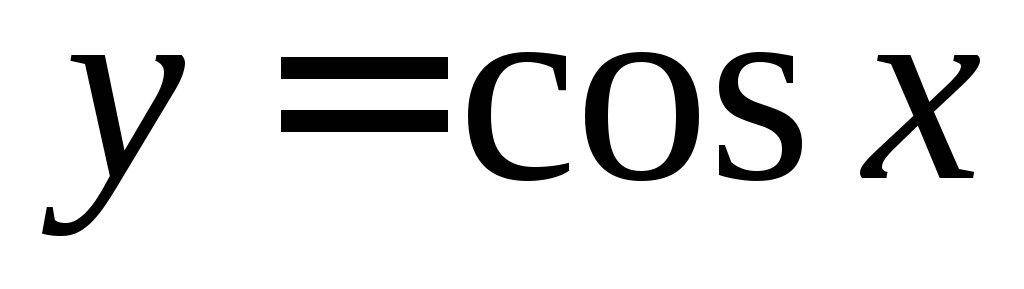 ,
,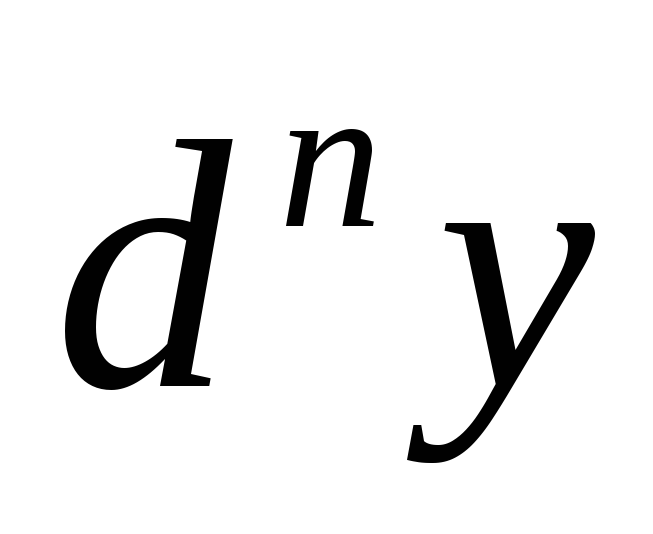 -? Ответ:
-? Ответ: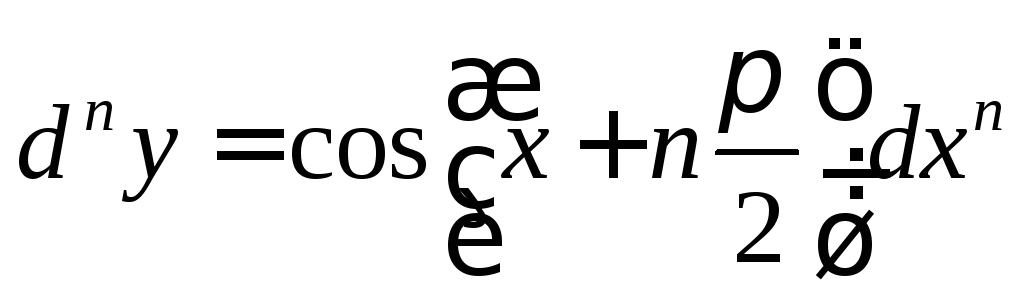 .
.
8. 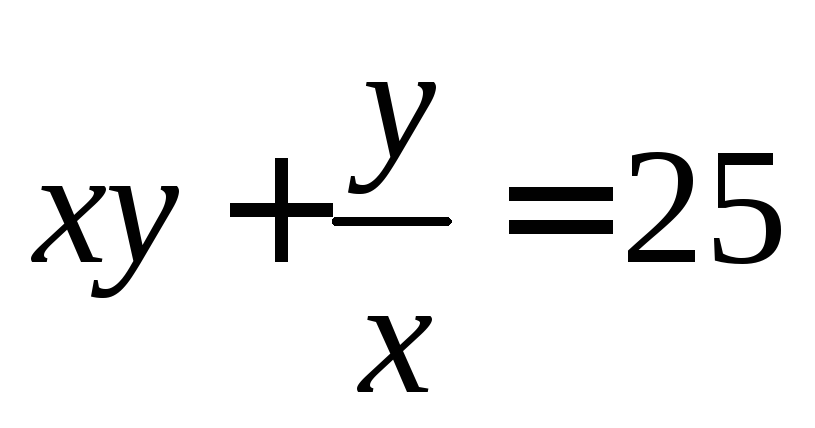 ,
,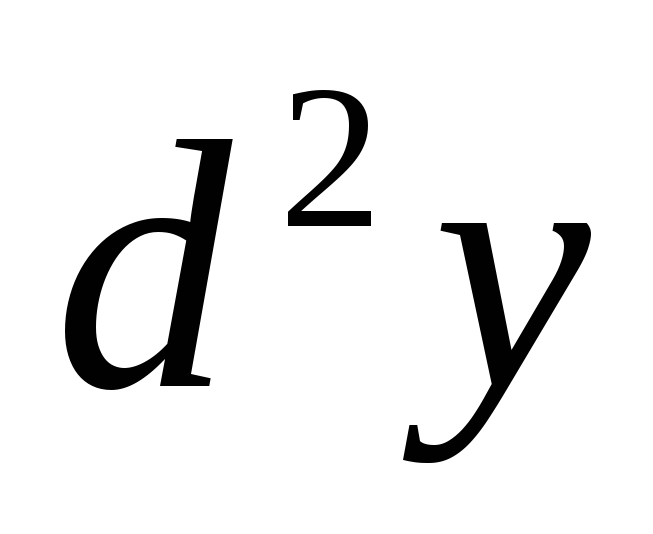 -? Ответ:
-? Ответ: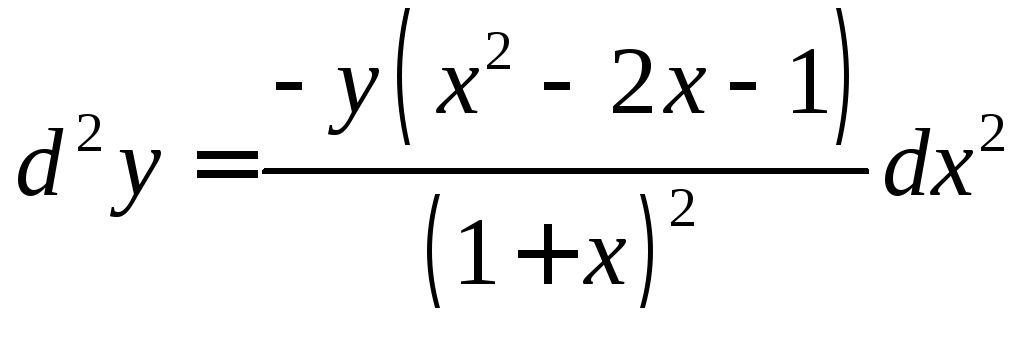 .
.
9. 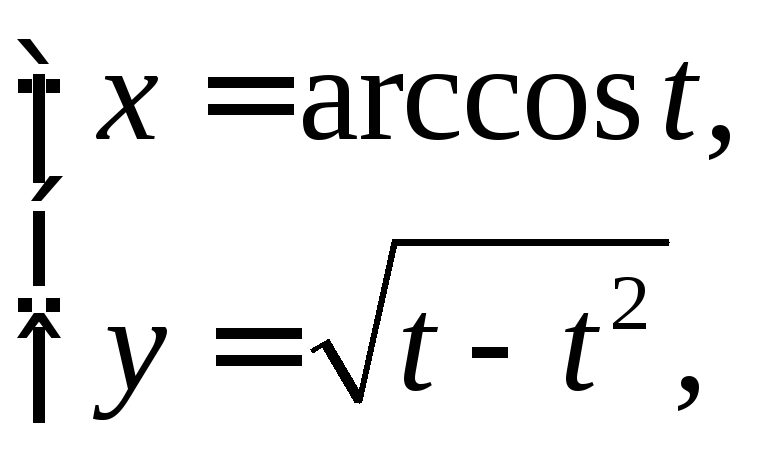
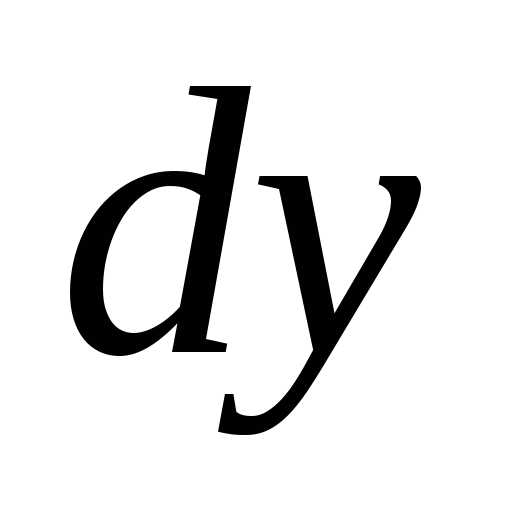 -? Ответ:
-? Ответ: .
.
10. 
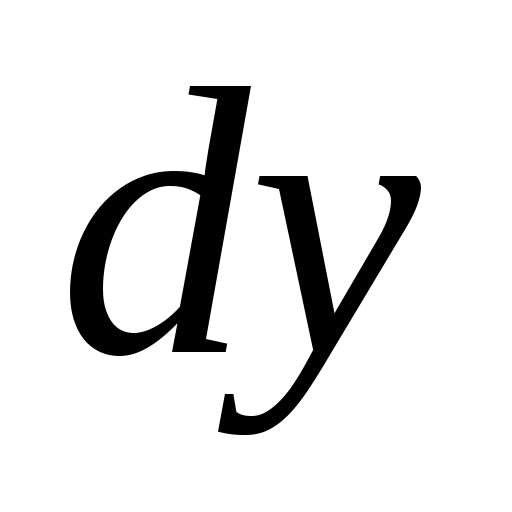 -? Ответ:
-? Ответ: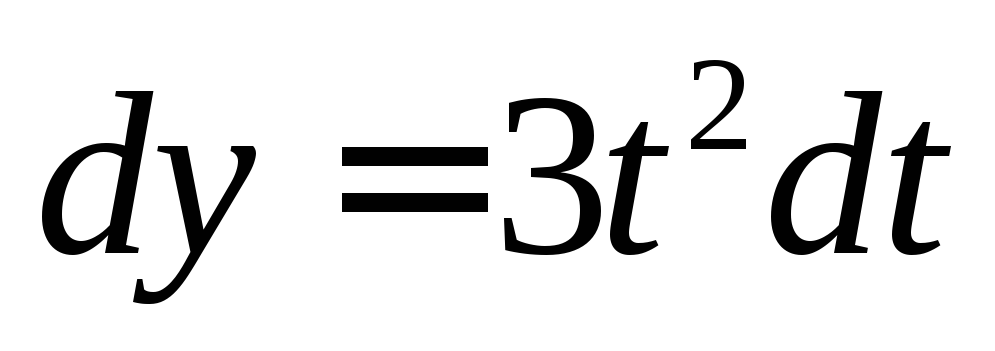 .
.
11.  ,
,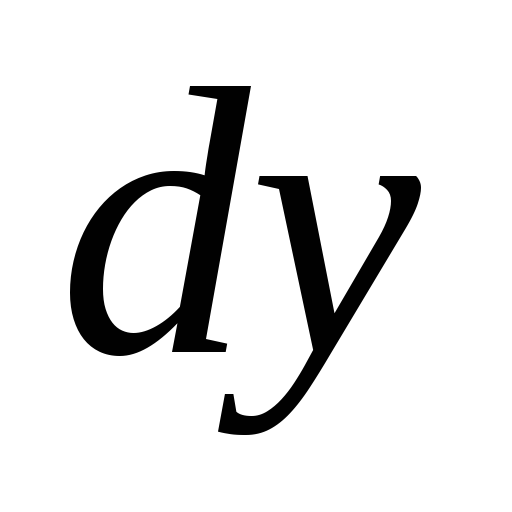 -? Ответ:
-? Ответ: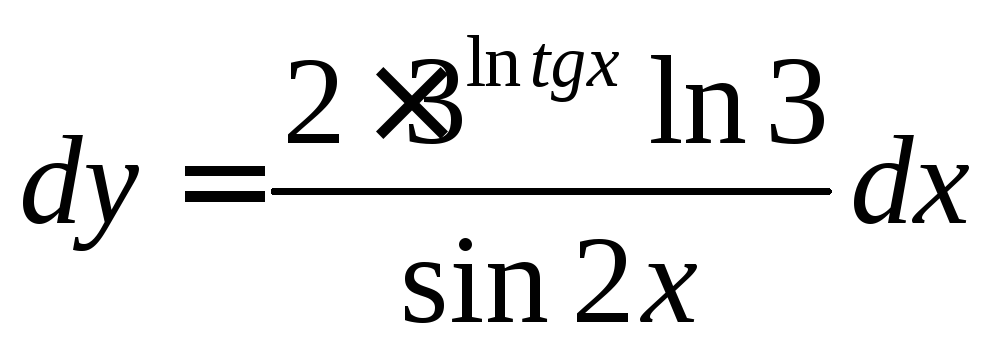 .
.
12. 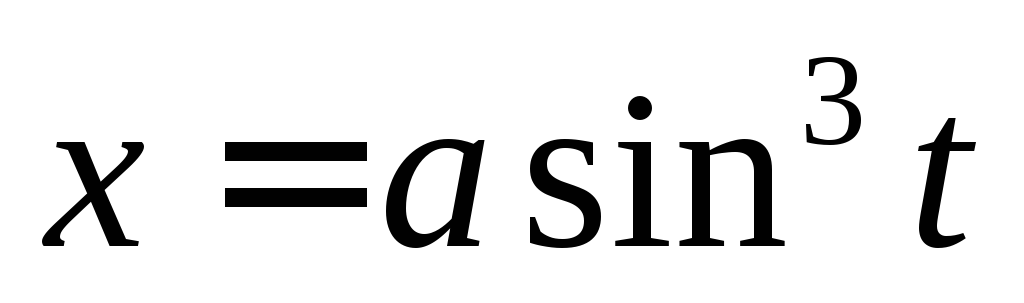 ,
, -? Ответ:
-? Ответ: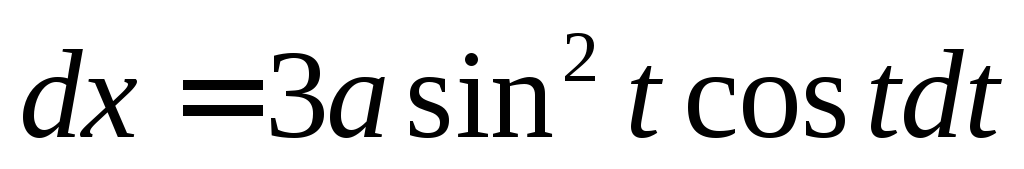 .
.
13. 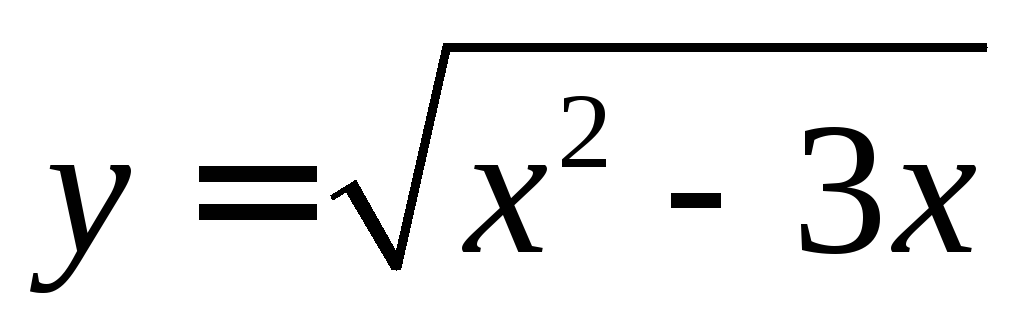 ,
, .
. -?
Ответ:
-?
Ответ: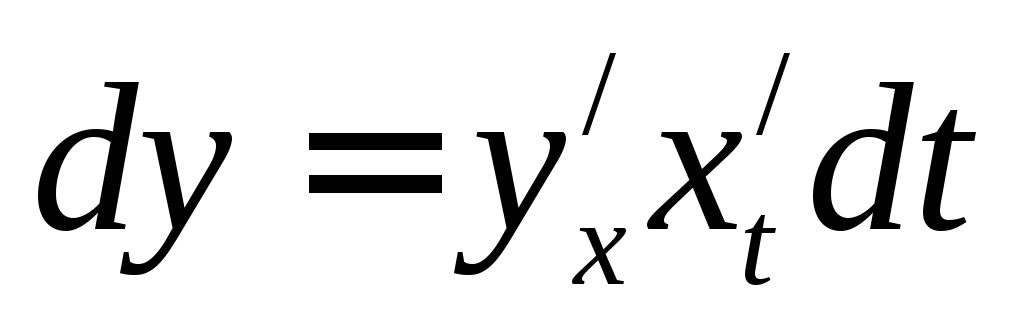 ,
,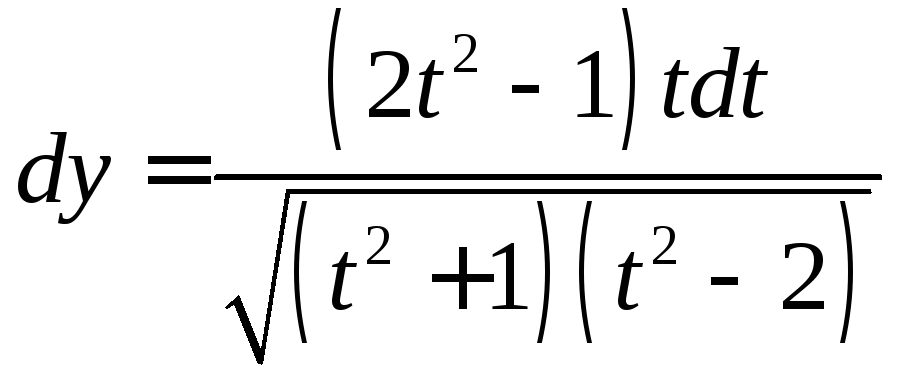 .
.
14. 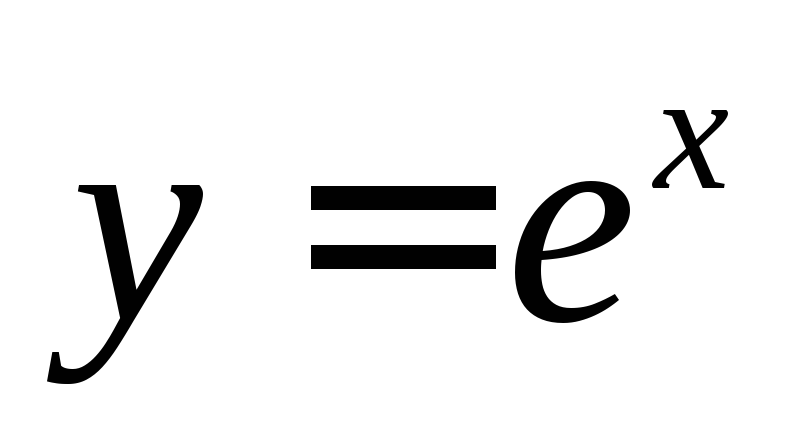 ,
, ,
, -?
-?
Ответ:  ,
,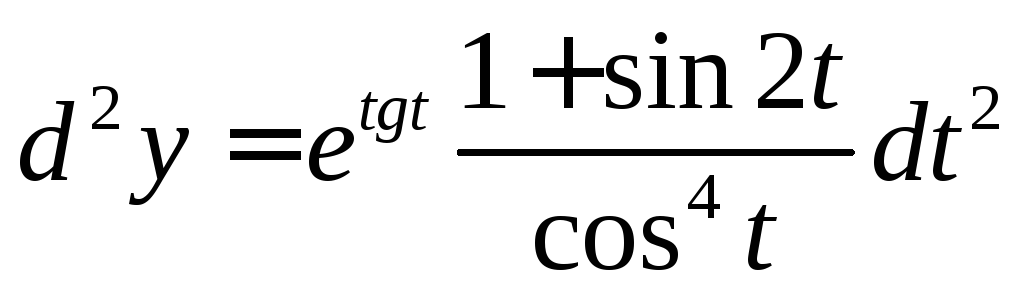 .
.
15. 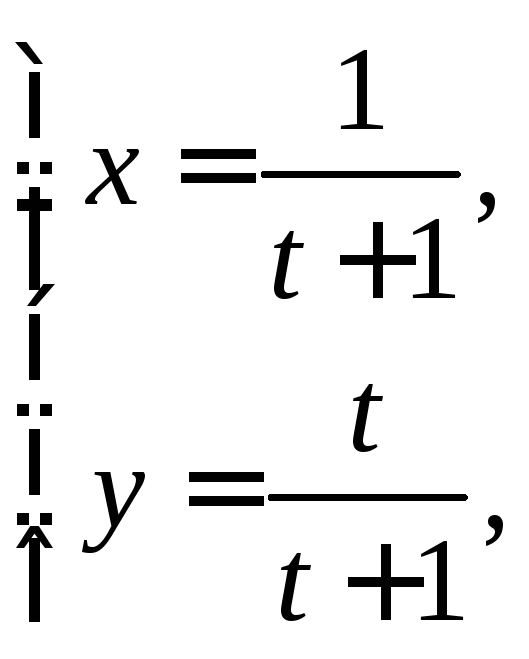
 -?
-?
Найти приближенное значение:
16.  .
Ответ: 0,811.
.
Ответ: 0,811.
17. 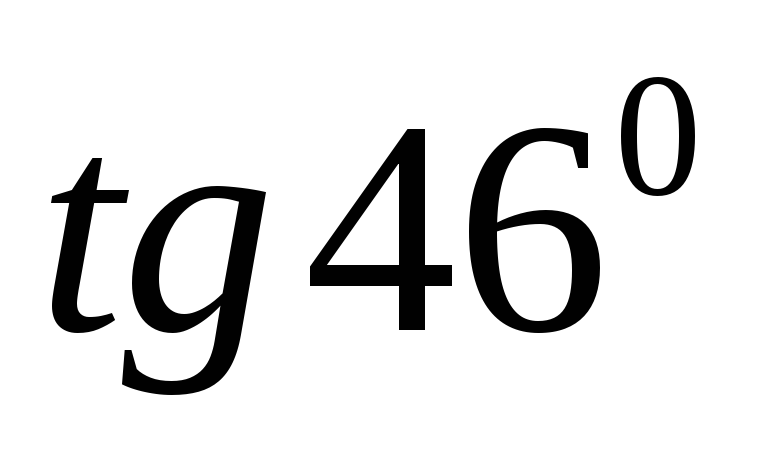 .
Ответ: 1,035.
.
Ответ: 1,035.
18. 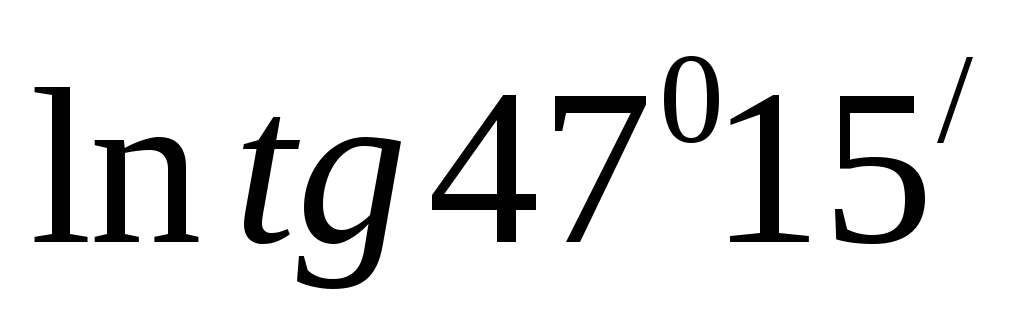 .
Ответ: 0,078.
.
Ответ: 0,078.
19. 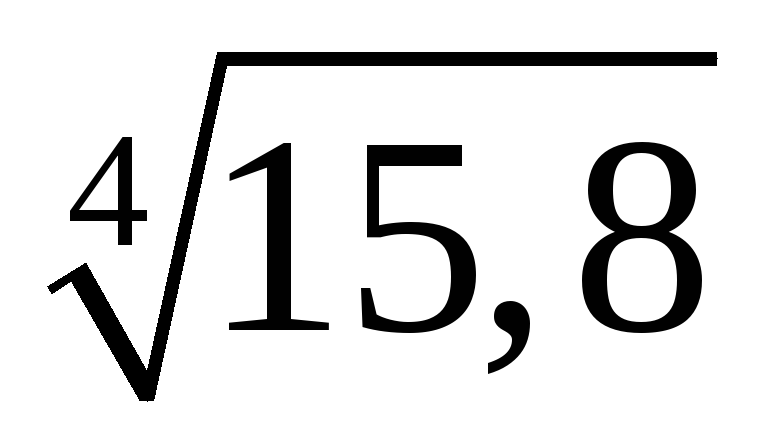 .
Ответ: 1,9938.
.
Ответ: 1,9938.
20. 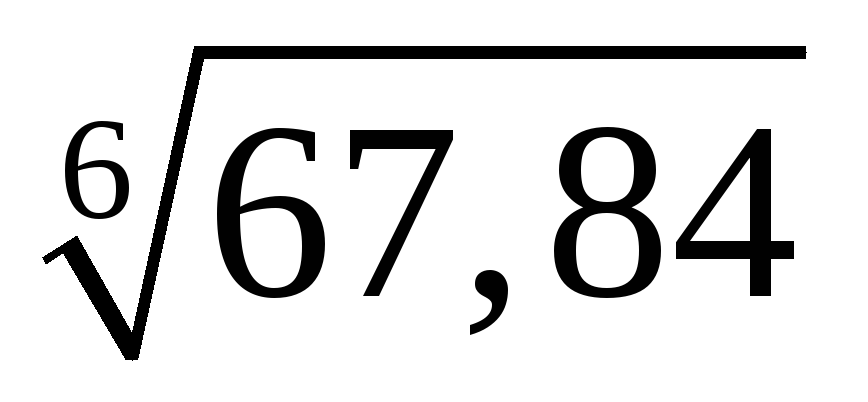 .
Ответ: 2,02.
.
Ответ: 2,02.
21.  .
Ответ:3,03.
.
Ответ:3,03.
22. 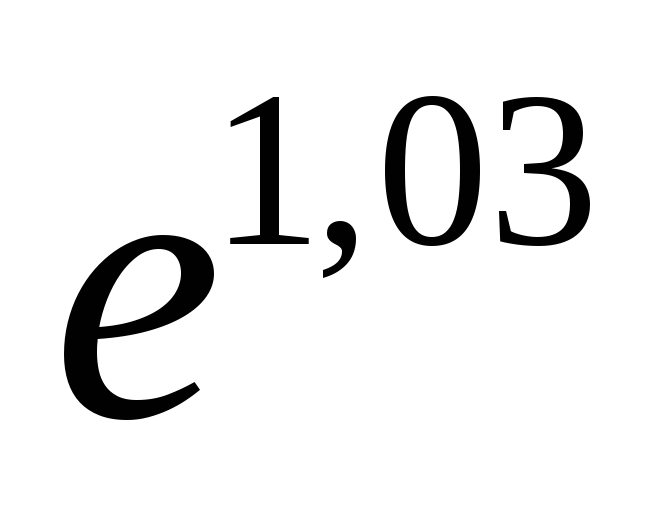 .
Ответ:
.
Ответ: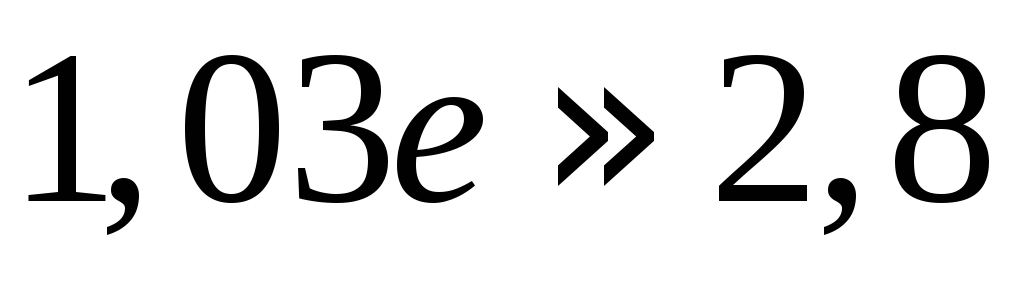 .
.
23. 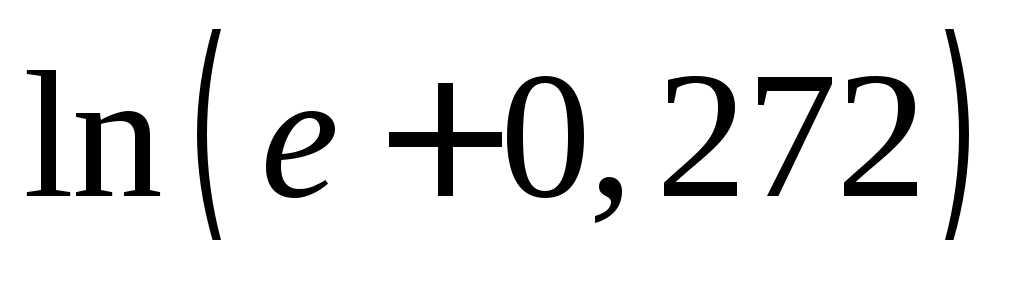 .
Ответ:
.
Ответ: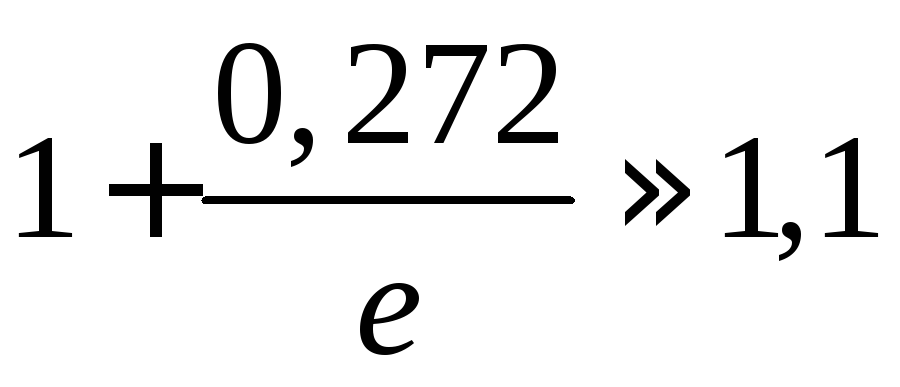 .
.
24. 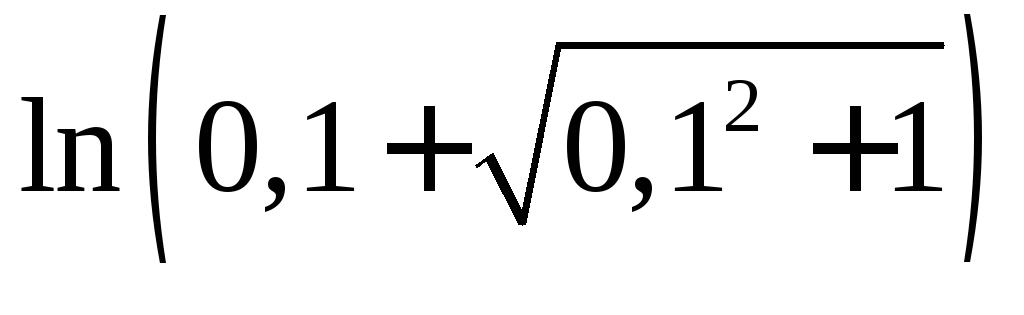 .
Ответ: 0,1.
.
Ответ: 0,1.
25.  .
Ответ:
.
Ответ: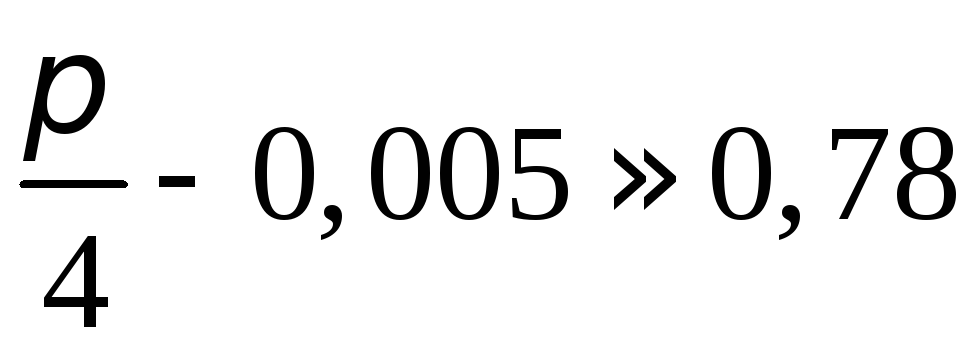 .
.
26.
Определить, на сколько приблизительно
увеличится объем шара, если его радиус 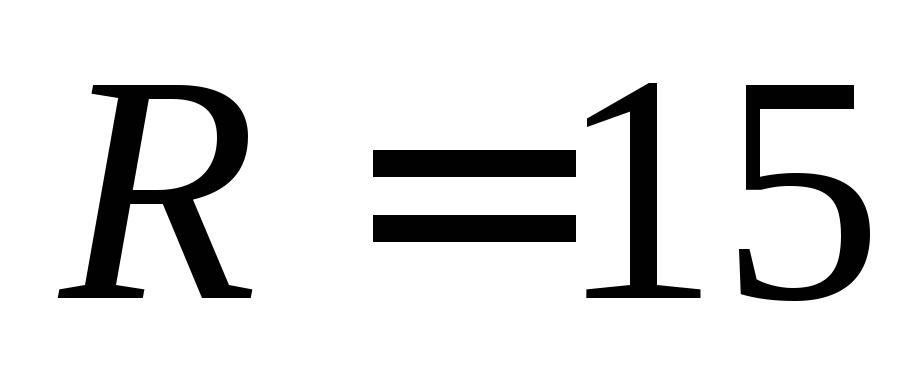 см
увеличить на 0,2см. Ответ: 565
см
увеличить на 0,2см. Ответ: 565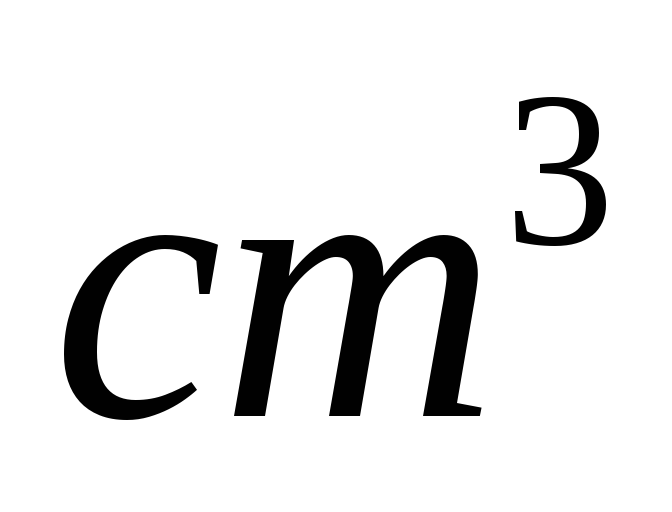 .
.
27.
Вычислить приближенное значение площади
круга, радиус которого равен 3,02 м.
Ответ: 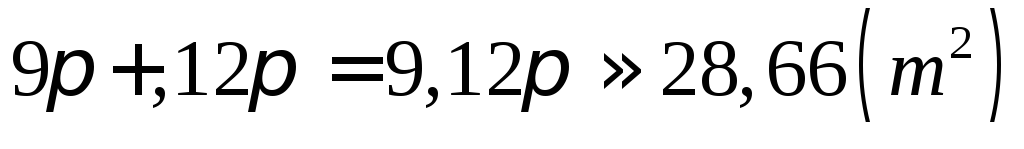 .
.
28.
Сравнить приращение и дифференциал
функции 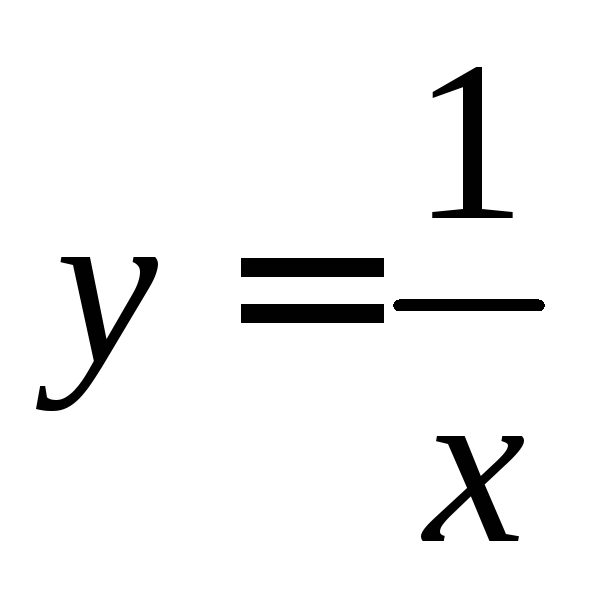 .
.
Ответ: 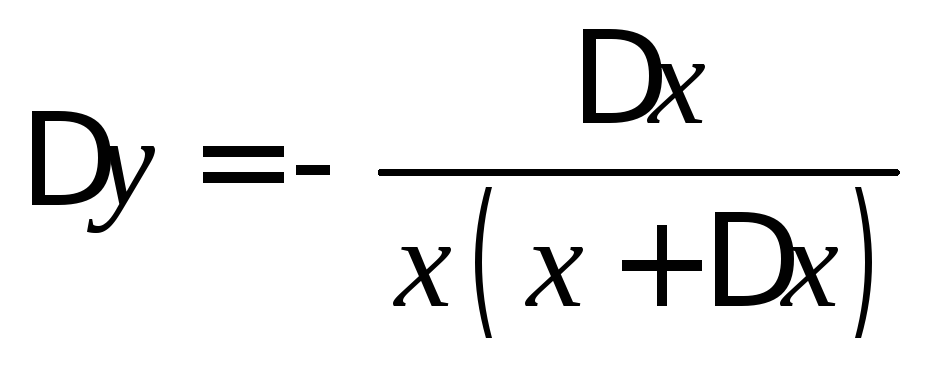 ,
,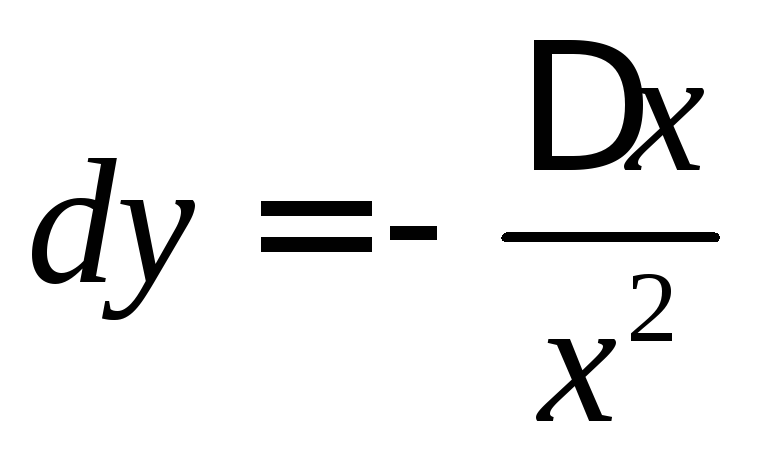 .
.
29.
Вычислить  ,
,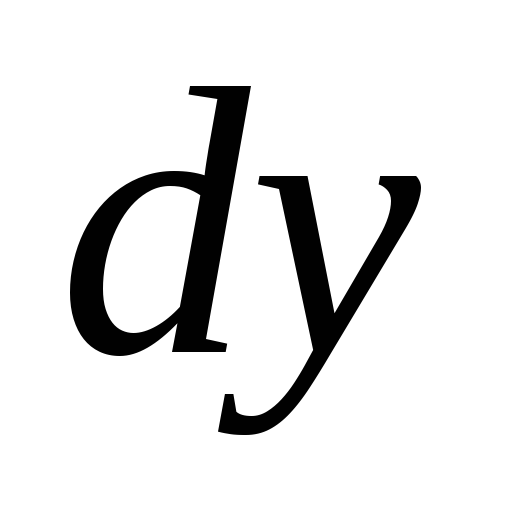 для функции
для функции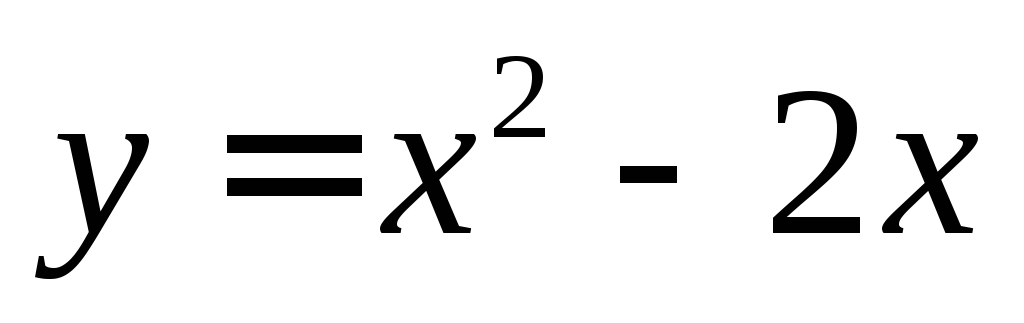 при
при и
и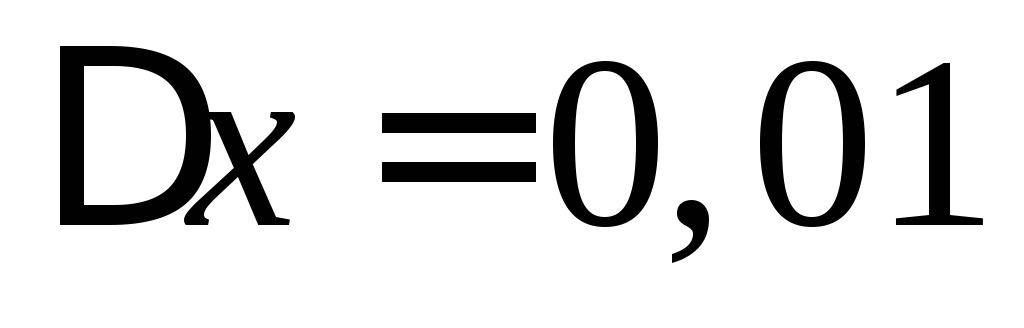 .
.
Ответ:  ,
,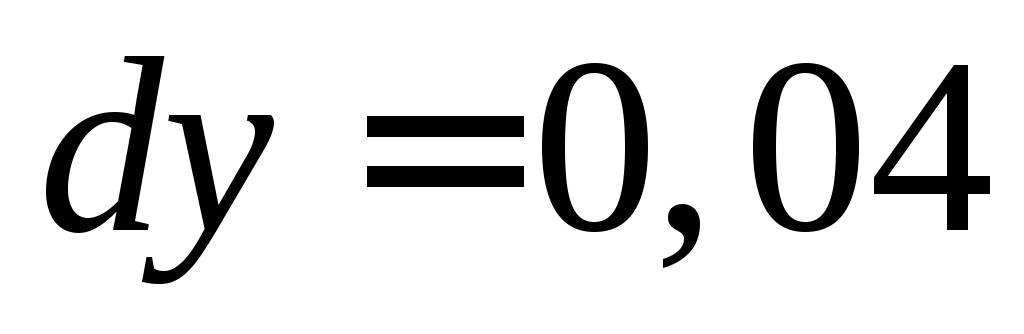 .
.
30. Найти приближенное значение объема шара радиуса 2,01 м.
Ответ: 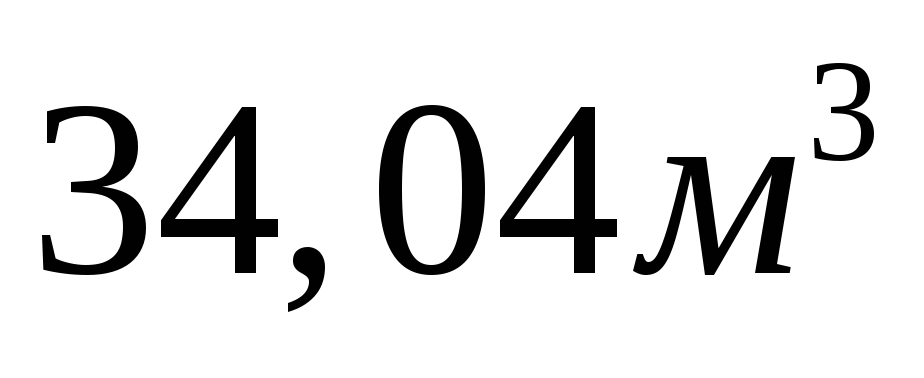 .
.
31.
Найти приближенное значение 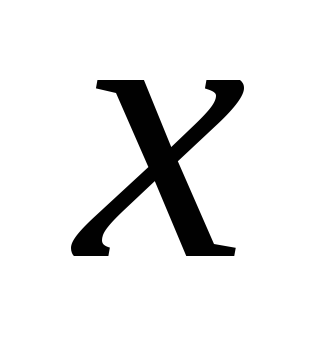 из уравнения:
из уравнения:
 .
Ответ:
.
Ответ: 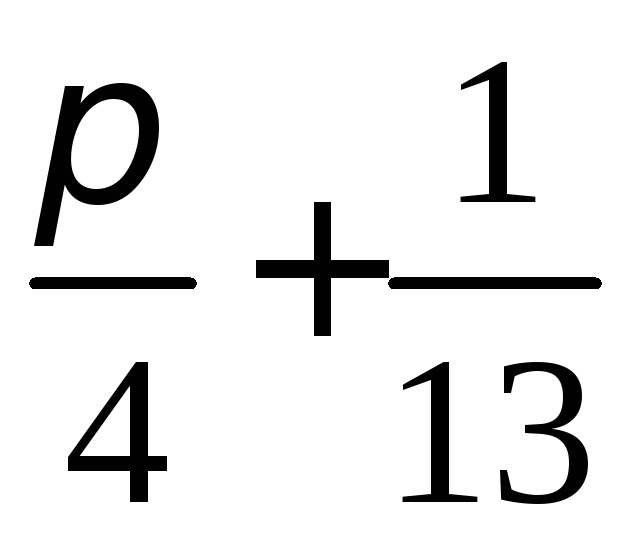 .
.
32.
Найти приближенно значение объема шара
радиуса 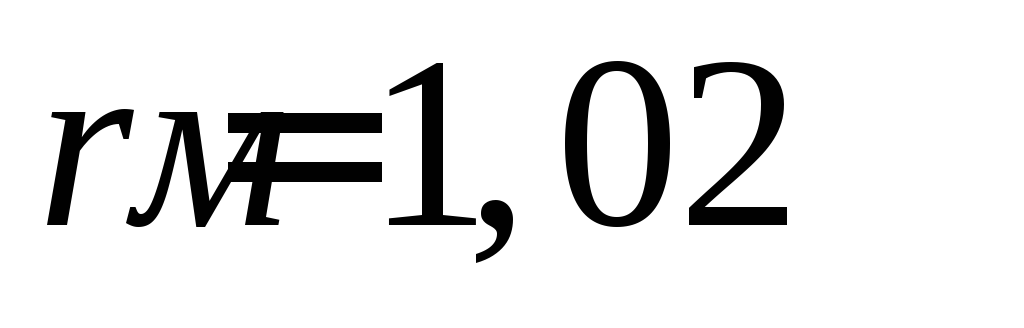 .
.
Ответ: 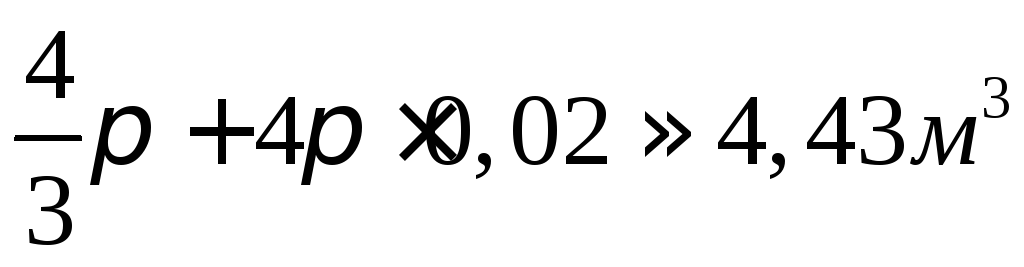 .
.
33.
Ребра куба увеличены на 1см. При этом
дифференциал  объема
объема куба оказался равным 12 см
куба оказался равным 12 см .
Найти первоначальную длину ребер.
Ответ: 2 см.
.
Найти первоначальную длину ребер.
Ответ: 2 см.
34.
Радиус круга увеличен на 1см. Дифференциал
площади круга оказался при этом равным 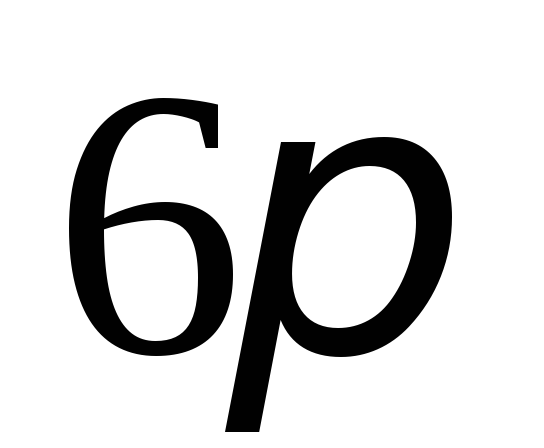 см
см .
Найти первоначальную величину радиуса.
Ответ: 3 см.
.
Найти первоначальную величину радиуса.
Ответ: 3 см.
35.
Определить приблизительно относительную
погрешность при вычислении поверхности
сферы, если при определении ее радиуса
относительная погрешность составила 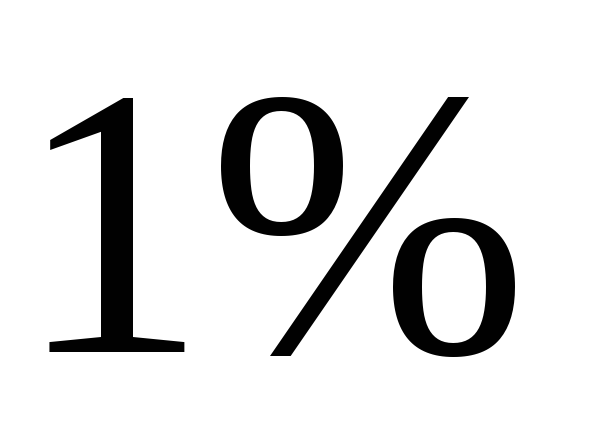 .
Ответ:
.
Ответ: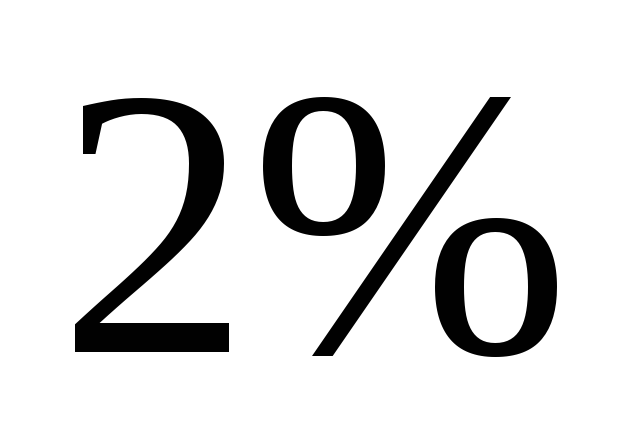 .
.
studfile.net
Дифференциал функции: основные понятия и определения
Пусть функция в точке имеет отличную от нуля производную
Тогда в некоторой окрестности этой точки отношение
где при Тому приращение функции можно представить в виде:
При этом величина является бесконечно малой более высокого порядка, чем и бесконечно малая поэтому величину называют главной частью приращения функции .
Замечание. Дифференциал называют также дифференциалом первого порядка.
Найдем дифференциал независимой переменной то есть дифференциал функции Так как получаем, что
то
То есть дифференциал независимой переменной равен ее приращению:
Тогда формула для дифференциала перепишется в виде:
Таким образом, дифференциал функции равен произведению производной указанной функции на дифференциал независимой переменной.
Геометрический и механический смыслы дифференциала функции
Геометрически дифференциал функции в точке равен приращению ординаты касательной к графику функции в рассматриваемой точке, когда переменная получает приращение .
Механический смысл дифференциала. Пусть материальная точка двигается по закону Дифференциал функции равен:
Для фиксированных значений и – это тот путь, который бы прошла материальная точка за время в случае, если она будет двигаться равномерно и прямолинейно с постоянною скоростью
Стоит отметить, что фактический путь в случае неравномерного движения материальной точки, в отличии от дифференциала не является линейной функцией времени а поэтому отличается от пути Но все же, если время является достаточно малым, то скорость движения существенно не изменяется и поэтому движение точки на промежутке времени от до есть практически равномерным.
Основные формулы дифференциала
Основные формулы, которые связаны с дифференциалами, можно получить, используя связь между дифференциалом функции и ее производной, то есть тот факт, что а также соответствующие формулы для производных.
Рассмотрим две дифференцируемые функции и Тогда имеют место следующие равенства:
ru.solverbook.com
Дифференциалы высших порядков, формулы и примеры решения задач
Пусть функция зависит от переменной и дифференцируема в точке . Может оказаться, что в точке дифференциал , рассматриваемый как функция от , есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала данной функции, который называется дифференциалом второго порядка функции . Дифференциал второго порядка обозначается следующим образом:
Аналогично определяются дифференциалы более высоких порядков.
Получим формулы, выражающие дифференциалы высших порядков. Рассмотрим несколько случаев.
Случай независимой переменной
Пусть — функция независимой переменной , имеющая дифференциалы любого порядка. Первый дифференциал функции
где — некоторое приращение независимой переменной , которое мы задаем сами и которое не зависит от . По определению
Переменной является аргумент . Значит, для дифференциала величина является постоянной и поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка
Для вычисления дифференциала применим формулу дифференциала первого порядка к функции . Тогда получим:
Итак,
Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала
www.webmath.ru