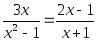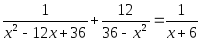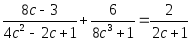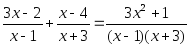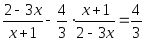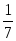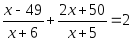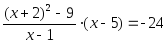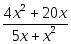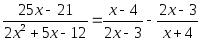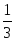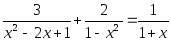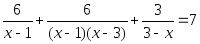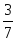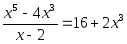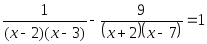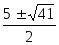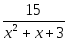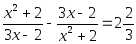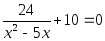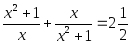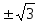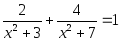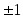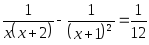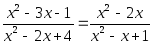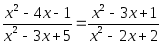Как решать дробные уравнения? | Александр Будников
Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений – дробными уравнениями.
Иногда их называют более научно и солидно — дробные рациональные уравнения. Или дробно-рациональные уравнения. Это сути не меняет.)
Дробные уравнения – незаменимая вещь во многих других темах математики. Особенно – в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:
1. Дроби и действия с дробями и дробными выражениями.
2. Тождественные преобразования уравнений.
3. Решение линейных и квадратных уравнений.
Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем – настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.
Итак, вперёд!
Что такое дробное уравнение? Примеры.
Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби. Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.
Например, вот такое уравнение:
Или такое:
Или вот такое:
И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся. Либо это линейные уравнения, либо квадратные.
Например:
Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей – четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.
Или такое уравнение:
Это обычное квадратное уравнение, несмотря на двойку в знаменателе. Опять же, по причине того, что двойка – не икс, и деления на неизвестное в дроби нету.
В общем, вы поняли.
Как решать дробные уравнения? Убираем дроби!
Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?
Первым делом надо избавиться от дробей!
Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?
Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)
Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:
Первое, что приходит на ум – перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае – при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.
А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?
Давайте его конструировать.) Смотрим ещё раз на уравнение:
Понятно, что в левой части для ликвидации знаменателя нам необходимо умножение на (х+3), а в правой – на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные – не катит. Ничего не поделать, так уж она устроена…)
Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х+3), так и на тройку. Причём очень важно – только с помощью умножения! И какое же это выражение? Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.
Итак, для ликвидации
Умножаем:
Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:
Прошу обратить внимание: скобки (х+3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача – дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок?!
А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:
Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:
2∙3 = х+3
А его (надеюсь) уже решит каждый:
х = 3
Решаем следующий примерчик:
И опять избавляемся от того, что нам не нравится. В данном примере это дробь 20/х. Одна единственная. Для её ликвидации правую часть надо домножить на знаменатель. То есть, просто на х. Но тогда и левую часть тоже надо домножить на х: так уж второе тождественное преобразование требует.
Вот и домножаем! Всю левую часть и всю правую часть:
Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части нашего уравнения мы умножаем на «х».
Вперёд!
А вот теперь – снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 – х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть
Дело всё в том, что частенько после умножения народ записывает левую часть вот так:
Это категорически неверно. Дальше можно уже не решать, да…)
Но у нас всё хорошо, будем дорешивать.
С чистой совестью сокращаем икс справа и получаем уравнение уже безо всяких дробей, в одну строчку.
(9 – х)∙х = 20
Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:
9х – х2 = 20
Переносим всё влево и приводим к стандартному виду:
Получили классическое квадратное уравнение. Но минус перед квадратом икса – нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:
Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:
х1 = 4
х2 = 5
И все дела.)
Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь – квадратным.
А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3=3. Это означает, что икс может быть любым. Какой икс ни возьми – всё равно всё посокращается и останется железное равенство 3=3.
Или наоборот, может получиться какая-нибудь белиберда, типа 3=4. А это будет означать, что корней нет. Какой икс ни возьми – всё сократится и останется бред…
Надеюсь, такие сюрпризы вас уже нисколько не удивят.) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее –
Разумеется, при попытке ликвидации дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.
Раскладываем на множители!
Решаем третье уравнение по списку:
А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить
x(x2+2x)(x+2)
и домножить на эту конструкцию всё уравнение. Математика не возражает.) Но… Может быть, есть выражение попроще?
Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители. Привет седьмому классу!)
А попробуем-ка разложить на множители каждый из знаменателей? Ну, с х и х+2 точно ничего не сделать, а вот х2+2х вполне себе раскладывается! Выносим один икс за скобку и получаем:
х2+2х = х(х+2)
Отлично. Вставим наше разложение в исходное уравнение:
Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и само на себя – на х(х+2).
Вот на х(х+2) и умножаем:
И снова расписываю подробно, дабы не запутаться. В левой части я буду использовать скобки: там
А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем – вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:
Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х – 3) в числителе первой дроби – думаю, уже не стоит объяснять?)
С удовольствием сокращаем все дроби:
(x-3)(x+2) + 3 = x
Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:
x2 + 2x – 3x – 6 + 3 – х = 0
x2 – 2x – 3 = 0
И снова получили квадратное уравнение.) Решаем и получаем два корня:
x1 = -1
x2 = 3
Вот и всё. Это и есть ответ.)
Из этого примера можно сделать важный вывод:
Если знаменатели дробей можно разложить на простые множители – обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!
Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это – дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.) Мы всегда будем от всего этого избавляться.)
Ну что, порешаем?)
Решить уравнения:
Ответы (как обычно, вразброс):
x = 3
x1 = 0,5; x2 = 3
x = 2
х = 6
x = 2,6
x1 = 2; x2 = 5
Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)
Всё решилось? Что ж, здорово! Значит, полпути в решении дробных уравнений мы с вами уже преодолели. Эта первая часть пути – избавление от дробей. Осталась вторая. Не менее важная!
Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение дробных уравнений этого урока вовсе не гарантирует успех в решении всех остальных примеров этой темы. Даже очень простых, подобных этим. К сожалению…
Но об этом – дальше.)
abudnikov.ru
Практика. Решение квадратных и дробно-рациональных уравнений
На этом уроке мы потренируемся решать квадратные и дробно-рациональные уравнения, отработаем различные методы их решения.
Математической моделью практических задач могут быть разные уравнения. В школе мы чаще всего будем сталкиваться с линейными и квадратными уравнениями, которые уже умеем решать. Но иногда могут встречаться и более сложные уравнения. Существуют компьютерные алгоритмы, которые позволяют приближенно найти решение практически любого уравнения, а вот точное решение найти удастся не всегда. На этом уроке мы рассмотрим некоторые приемы, которые позволяют эквивалентными преобразованиями свести более сложные уравнения к тем, которые мы уже умеем решать, – линейным и квадратным.
Задание 1. Решить уравнение:
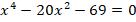
Решение.
Воспользуемся свойством степеней 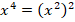 и перепишем уравнение в виде:
и перепишем уравнение в виде:
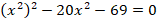
Обратим внимание, что неизвестная величина 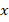 присутствует в уравнении только в составе «конструкции»
присутствует в уравнении только в составе «конструкции» 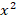 . В таком случае применяют метод замены переменной.
. В таком случае применяют метод замены переменной.
Суть его состоит в том, что эту повторяющуюся конструкцию мы заменяем новой переменной:
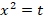
Заменяя 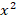 на
на 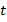 , получаем уравнение:
, получаем уравнение:
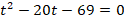
Получили квадратное уравнение. С его решением вы можете ознакомиться ниже.
Решение квадратного уравнения с помощью дискриминанта
Имеем следующее квадратное уравнение:
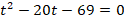
Решим уравнение с помощью дискриминанта. Коэффициенты из общего вида квадратного уравнения:
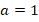
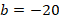
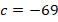
Тогда:
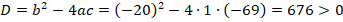
Найдем корни квадратного уравнения:
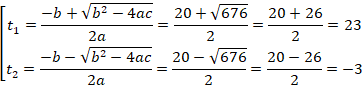
Ответ: 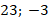 .
.
Далее решения линейных и квадратных уравнений не будут разбираться подробно. Внимание будет сконцентрировано на том, как свести более сложное уравнение к линейному или квадратному. Если же у вас возникают проблемы при решении линейных или квадратных уравнений, пересмотрите соответствующие уроки:
- «Линейное уравнение с одной переменной (Г.Г. Гаицгори)»;
- «Квадратные уравнения».
Решаем уравнение, получаем корни:
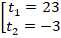
Мы нашли значения 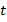 . Но в исходном уравнении фигурировала переменная
. Но в исходном уравнении фигурировала переменная 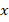 , и решить уравнение – значит, найти значения
, и решить уравнение – значит, найти значения 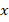 . Вернемся к замене:
. Вернемся к замене:
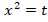
Тогда:

Получили два квадратных уравнения. Первое уравнение 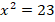 имеет два решения:
имеет два решения:
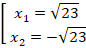
Второе уравнение не имеет действительных корней.
Ответ: 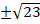 .
.
В процессе решения нам пришлось дважды решать квадратные уравнения: сначала для переменной 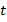 , затем для переменной
, затем для переменной 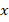 . Поэтому такие уравнения, в которых присутствуют только
. Поэтому такие уравнения, в которых присутствуют только 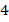 -я и
-я и 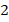 -я степень неизвестной, а также свободный член, называются биквадратными уравнениями, т. е. «дважды квадратными»:
-я степень неизвестной, а также свободный член, называются биквадратными уравнениями, т. е. «дважды квадратными»:
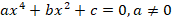
Теперь перейдем к решению дробно-рациональных уравнений. По названию понятно – это те уравнения, которые содержат в себе дробно-рациональные выражения. Если вы забыли, что это за выражения и как с ними работать, рекомендуем пересмотреть соответствующий видеоурок: «Дробно-рациональные выражения».
При решении дробно-рациональных уравнений важно:
- в самом начале найти ОДЗ выражений, которые встречаются в уравнении;
- после нахождения корней нужно проверить, входят ли они в ОДЗ.
Рассмотрим несколько примеров простейших дробно-рациональных уравнений.
Задание 2.Решить уравнение:
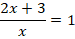
Решение.
Знаменатель дроби не должен равняться нулю, т. е. ОДЗ:
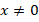
Поскольку 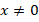 , можем умножить обе части уравнения на
, можем умножить обе части уравнения на 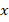 , чтобы избавиться от дроби, тогда:
, чтобы избавиться от дроби, тогда:
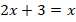
Получили линейное уравнение, решением которого является 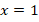 . Это решение входит в ОДЗ, ведь
. Это решение входит в ОДЗ, ведь 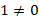 .
.
Ответ: 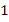 .
.
Задание 3.Решить уравнение:
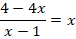
Решение.
Выпишем ОДЗ:
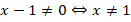
Чтобы избавиться от дроби, умножим обе части уравнения на 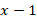 . Мы это можем сделать, поскольку
. Мы это можем сделать, поскольку 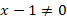 , тогда:
, тогда:
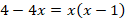
Раскроем скобки, перенесем все слагаемые в одну сторону, приведем подобные слагаемые. Получим квадратное уравнение:
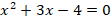
Найдем корни этого уравнения:
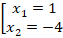
Первый корень не входит в ОДЗ. Поэтому 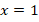 не является решением уравнения.
не является решением уравнения.
Ответ: 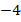 .
.
Решим более сложные дробно-рациональные уравнения.
Задание 4. Решить уравнение:
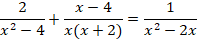
Решение.
Выпишем ОДЗ:
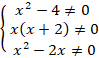
Решим каждое из этих неравенств:
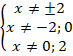
Можем объединить эти неравенства в одно:
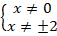
Перенесем все слагаемые в одну сторону:
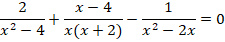
Выполним сложение дробей – для этого разложим знаменатели на множители:
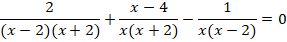
Приведем все дроби к общему знаменателю 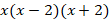 :
:
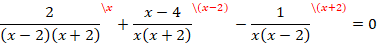
Тогда:
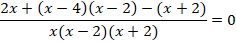
Дробь равна 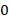 , если ее числитель равен
, если ее числитель равен 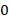 :
:
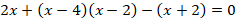
Раскрыв скобки и приведя подобные слагаемые, получаем квадратное уравнение:

Найдем корни квадратного уравнения:
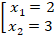
Корень 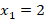 не входит в ОДЗ.
не входит в ОДЗ.
Ответ: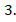
Отметим, что для решения дробно-рациональных уравнений можно использовать разные способы. Первый – это умножить обе части уравнения на некоторые выражения так, чтобы избавиться от дробей. Таким способом мы решили первые два примера с дробно-рациональными выражениями. Второй способ – перенести все слагаемые в одну сторону, преобразовать выражение и приравнять числитель полученной дроби к нулю. Так мы решили последний пример. Вы можете выбрать тот способ, который вам удобнее и понятнее. Главное в каждом из них – не забывать про ОДЗ.
Задание 5. Решить уравнение
interneturok.ru
Решение целых и дробно рациональных уравнений
Давайте познакомимся с рациональными и дробными рациональными уравнениями, дадим их определение, приведем примеры, а также разберем наиболее распространенные типы задач.
Рациональное уравнение: определение и примеры
Знакомство с рациональными выражениями начинается в 8 классе школы. В это время на уроках алгебры учащиеся все чаще начинают встречать задания с уравнениями, которые содержат рациональные выражения в своих записях. Давайте освежим в памяти, что это такое.
Определение 1Рациональное уравнение – это такое уравнение, в обеих частях которого содержатся рациональные выражения.
В различных пособиях можно встретить еще одну формулировку.
Определение 2Рациональное уравнение – это такое уравнение, запись левой части которого содержит рациональное выражение, а правая – нуль.
Определения, которые мы привели для рациональных уравнений, являются равнозначными, так как говорят об одно и том же. Подтверждает правильность наших слов тот факт, что для любых рациональных выражений P и Q уравнения P=Q и P−Q=0 будут равносильными выражениями.
А теперь обратимся к примерам.
Пример 1Рациональные уравнения:
x=1, 2·x−12·x2·y·z3=0, xx2+3·x-1=2+27·x-a·(x+2), 12+34-12x-1=3.
Рациональные уравнения точно также, как и уравнения других видов, могут содержать любое количество переменных от 1 до нескольких. Для начала мы рассмотрим простые примеры, в которых уравнения будут содержать только одну переменную. А затем начнем постепенно усложнять задачу.
Рациональные уравнения делятся на две большие группы: целые и дробные. Посмотрим, какие уравнения будут относиться к каждой из групп.
Определение 3Рациональное уравнение будет являться целым в том случае, если в записи левой и правой его частей содержатся целые рациональные выражения.
Определение 4zaochnik.com
Решение дробных уравнений с преобразованием в квадратные уравнения
Дробным уравнением называется уравнение, в котором хотя бы одно из
слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением
является уравнение 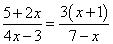 .
.
Решать дробные уравнения удобно в следующем порядке:
- найти общий знаменатель дробей, входящих в уравнение, если каждая дробь имеет смысл,
- заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
- решить получившееся целое уравнение,
- исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решить дробное уравнение:
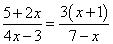 .
.
Решение. Воспользуемся основным свойством дроби с представим левую и правую части этого уравнения в виде дробей с одинаковым знаменателем:
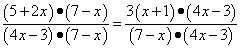 .
.
Эти дроби равны при тех и только тех значениях, при которых равны их числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а следовательно, и уравнение не имеет смысла.
Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение
 .
.
Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение
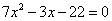 .
.
При решении квадратного уравнения получаем его корни:
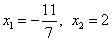 .
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:
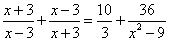 .
.
Решение. Найдём общий знаменатель дробей, входящих в данное дробное уравнение. Общий знаменатель —
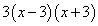 .
.
Заменим исходное уравнение целым. Для этого умножим обе его части на общий знаменатель. Получим:
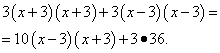
Выполним необходимые преобразования в полученном уравнении и придём к квадратному уравнению
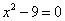 .
.
Решенив квадратное уравнение, получаем его корни:
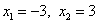 .
.
Если x = -3, то найденный на первом шаге знаменатель обращается в нуль:
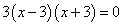 ,
,
то же самое, если x = 3.
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а, поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:
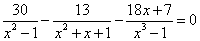 .
.
Решение. Найдём общий знаменатель дробей, входящих в данное уравнение. Для этого знаменатели дробей разложим на множители:
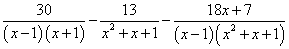 .
.
Общий знаменатель — выражение
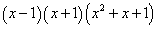
Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:
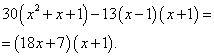
Выполнив преобразования, придём к квадратному уравнению
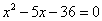 .
.
Решенив квадратное уравнение, получаем его корни:
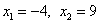 .
.
Ни один из корней не обращает общий знаменатель в нуль. Следовательно, числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:
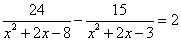 .
.
Решение. Введём новую переменную, обозначив 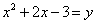 .
Получим уравнение с переменной y:
.
Получим уравнение с переменной y:
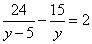 .
.
Корни этого уравнения:

Значит
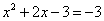 или
или 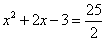 .
.
Из уравнения 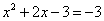 находим, что
находим, что
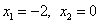 .
.
Из уравнения 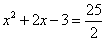 находим, что
находим, что
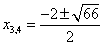 .
.
Итак, данное уравнение имеет четыре корня:
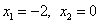 ,
, 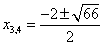 .
.

Другие темы в блоке «Школьная математика»
function-x.ru
Дробно рациональные уравнения. Решения
Уравнение которые можно свести к дроби f(x)/g(x)=0 называется дробно рациональным уравнением.
Решение дробно рациональных уравнений не слишком сложная задача если Вы знаете методику, а она достаточно проста.
Если уравнение имеет несколько слагаемых то переносим их по одну сторону знака равенства и сводим к общему знаменателю. В результате получим дробную функцию f(x)/g(x), которая равна нулю
Следующим шагом находим корни числителя. Отвергаем среди них те, которые не принадлежат области допустимых значений (нули знаменателя) и записываем правильный ответ.
В теории все просто, однако на практике и у школьников и у студентов возникают проблемы при сведены к общему знаменателю, отыскании корней и т.д. Для ознакомления с решением рассмотрим несколько распространенных задач.
Примеры дробно рациональных уравнений
Пример 1. Найти корни уравнения
Решение: По методике переносим слагаемые и сводим к общему знаменателю
Приравниваем числитель и знаменатель к нулю и находим корни. Первое уравнение можем решить по теореме Виета
Второе раскладываем на множители
Если от корней числителя отбросить нули знаменателя то получим только одно решение x=-7.
Внимание: Всегда проверяйте совпадают ли корни числителя и знаменателя. Если такие есть то не учитывайте их в ответе.
Ответ: х=-7.
————————————
Пример 2. Решить уравнение
Решение: Задано дробное рациональное уравнение. Находим сначала корни числителя, для этого решаем квадратное уравнение
Вычисляем дискриминант
и корни уравнения
Получили три нуля числителя .
Квадратное уравнение в знаменателе проще и можем решить по теореме Виета
Числитель и знаменатель не имеют общих корней поэтому все три найденные значения будут решениями.
————————————
Пример 3. Найти корни уравнения
Решение: Переносим слагаемое за знак равенства
и сводим к общему знаменателю
Раскрываем в числителе скобки и сводим к квадратному уравнению
Полученное дробно рациональное уравнение эквивалентно системе двух уравнений
Корни первого вычисляем через дискриминант
Нули второго находим без проблем
Исключаем из решений числителя значение и получим.
Ответ: х=3.
————————————
Задачи на движение
Задача 4. Вертолет пролетел по ветру расстояние 120 км и обратно вернулся, потратив на весь путь 6 час. Найдите скорость ветра если скорость в штиль составляет 45 км/час.
Решение:
Обозначим скорость ветра через х км/час. Тогда за ветром скорость вертолета составит (45+х) км/час, и в обратном направлении (45-х) км/час. По условию задачи вертолет потратил 6 часов на дорогу.
Разделив расстояние на скорость и просуммировав получим время
Получили дробно рациональное уравнение схема решения которого неоднократно повторялась
Решением второго уравнения будут значения x=-45; x=45.
Корни числителя найдем после упрощений
С физических соображений первое решение отвергаем.
Ответ: скорость ветра 15 км/час.
————————————
Задачи о совместной работе
Задача 2. Два лесорубы работая вместе выполнили норму вырубки за 4 дня. Сколько дней нужно на выполнение этой работы каждому лесорубу отдельно если первому для в
yukhym.com
Решение дробных рациональных уравнений
Сегодня мы разберемся, как решать дробные рациональные уравнения.
Посмотрим: из уравнений
(1) 2х + 5 = 3(8 – х),
(2) ,
(3)
(4)
дробными рациональными уравнениями являются только (2) и (4), а (1) и (3) это целые уравнения.
Предлагаю решить уравнение (4), а затем сформулировать правило.
Поскольку уравнение дробное, то надо найти общий знаменатель. В этом уравнении это выражение 6(х – 12)(х – 6). Затем мы умножаем обе части уравнения на общий знаменатель:
После сокращения получаем целое уравнение:
6(х – 6)2 – 6(х – 12)2 = 5(х – 12)(х – 6).
Решив это уравнение надо обязательно проверить не обращают ли полученные корни в нуль знаменатели дробей в исходном уравнении.
Раскрываем скобки:
6х2 – 72х + 216 – 6х2 + 144х – 864 = 5х2 – 90х + 360, упрощаем уравнение: 5х2 – 162х + 1008 = 0.
Находим корни уравнения
D = 6084, √D = 78,
х1= (162 – 78)/10= 84/10 = 8,4 и х2 = (162 + 78)/10 = 240/10 = 24.
При х = 8,4 и 24 общий знаменатель 6(х – 12)(х – 6) ≠ 0, значит эти числа являются корнями уравнения (4).
Ответ: 8,4; 24.
Решив предложенное уравнение, приходим к следующим положениям:
1) Находим общий знаменатель.
2) Умножаем обе части уравнения на общий знаменатель.
3) Решаем полученное целое уравнение.
4) Проверяем, какие из корней обращают общий знаменатель в нуль и исключаем их из решения.
Посмотрим теперь на примере, как работают полученные положения.
Решить уравнение:
1) Общий знаменатель: х2 – 1
2) Умножаем обе части уравнения на общий знаменатель, получаем целое уравнение: 6 – 2(х + 1) = 2(х2 – 1) – (х + 4)(х – 1)
3) Решаем уравнение: 6 – 2х – 2 = 2х2 – 2 – х2 – 4х + х + 4
х2 – х – 2 = 0
х1 = — 1 и х2 = 2
4) При х = -1, общий знаменатель х2 – 1 = 0. Число -1 корнем не является.
При х = 2, общий знаменатель х2 – 1 ≠ 0. Число 2 – корень уравнения.
Ответ: 2.
Как видите, наши положения работают. Не бойтесь, у вас все получится! Самое главное правильно найдите общий знаменатель и аккуратно выполните преобразования. Надеемся, что при решение дробных рациональных уравнений у вас всегда будут получаться правильные ответы. Если у вас остались вопросы или вы хотите попрактиковаться в решении подобных уравнений, записывайтесь на уроки к автору этой статьи, репетитору Валентине Галиневской.
Также рекомендуем посмотреть новый видеоурок по данной теме от нашего репетитора Ольги Лукашонок.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
5. Дробно рациональные уравнения
Дробно рациональные уравнения. Решения
Уравнение
которые можно свести к дроби
f(x)/g(x)=0 называется дробно рациональным
уравнением.
Решение дробно
рациональных уравнений не слишком
сложная задача если Вы знаете методику,
а она достаточно проста.
Если
уравнение имеет несколько слагаемых
то переносим их по одну сторону знака
равенства и сводим к общему знаменателю.
В результате получим дробную функцию
f(x)/g(x), которая равна нулю 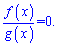
Следующим шагом находим корни числителя. Отвергаем среди них те, которые не принадлежат области допустимых значений (нули знаменателя) и записываем правильный ответ.
В теории все просто, однако на практике и у школьников и у студентов возникают проблемы при сведены к общему знаменателю, отыскании корней и т.д. Для ознакомления с решением рассмотрим несколько распространенных задач.
Примеры дробно рациональных уравнений
Пример
1. Найти корни уравнения 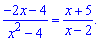
Решение:
По методике переносим слагаемые и сводим
к общему знаменателю 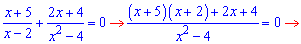
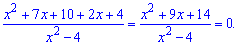
Приравниваем
числитель и знаменатель к нулю и находим
корни. Первое уравнение можем решить
по теореме Виета 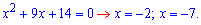
Второе
раскладываем на множители 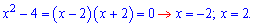
Если от корней числителя отбросить нули знаменателя то получим только одно решение x=-7.
Внимание: Всегда проверяйте совпадают ли корни числителя и знаменателя. Если такие есть то не учитывайте их в ответе.
Ответ: х=-7.
————————————
Пример
2. Решить уравнение 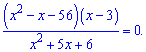
Решение:
Задано дробное рациональное уравнение.
Находим сначала корни числителя, для
этого решаем квадратное уравнение 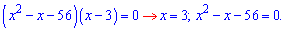
Вычисляем
дискриминант 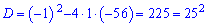
и
корни уравнения 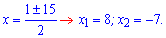
Получили
три нуля числителя 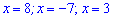 .
Квадратное
уравнение в знаменателе проще и можем
решить по теореме Виета
.
Квадратное
уравнение в знаменателе проще и можем
решить по теореме Виета
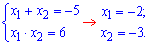
Числитель
и знаменатель не имеют общих корней
поэтому все три найденные значения 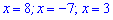 будут
решениями.
будут
решениями.
————————————
Пример
3. Найти корни уравнения 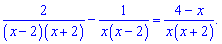
Решение:
Переносим слагаемое за знак равенства 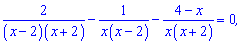 и
сводим к общему знаменателю
и
сводим к общему знаменателю 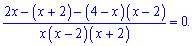
Раскрываем в числителе скобки и сводим к квадратному уравнению
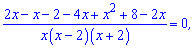
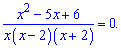
Полученное
дробно рациональное уравнение эквивалентно
системе двух уравнений 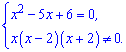
Корни
первого вычисляем через дискриминант 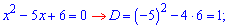
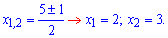
Нули
второго находим без проблем 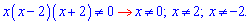
Исключаем
из решений числителя значение 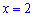 и
получим.
и
получим.
Ответ: х=3.
————————————
Задачи на движение
Задача 4. Вертолет пролетел по ветру расстояние 120 км и обратно вернулся, потратив на весь путь 6 час. Найдите скорость ветра если скорость в штиль составляет 45 км/час.
Решение: Обозначим скорость ветра через х
км/час. Тогда за ветром скорость вертолета
составит (45+х) км/час, и в обратном
направлении (45-х) км/час. По условию
задачи вертолет потратил 6 часов на
дорогу.
Разделив расстояние на
скорость и просуммировав получим время 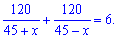
Получили
дробно рациональное уравнение схема
решения которого неоднократно
повторялась 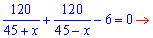
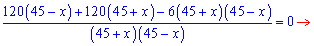
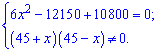
Решением второго уравнения будут значения x=-45; x=45.
Корни
числителя найдем после упрощений 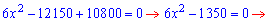
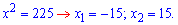
С физических соображений первое решение отвергаем.
Ответ: скорость ветра 15 км/час.
————————————
Задачи о совместной работе
Задача 2. Два лесорубы работая вместе выполнили норму вырубки за 4 дня. Сколько дней нужно на выполнение этой работы каждому лесорубу отдельно если первому для вырубки нормы нужно на 6 дней меньше чем другому?
Решение:
Пусть первый лесоруб выполняет норму
по х дней. Тогда второму необходимо
(х+6) дней.
Это означает что за один
день первый выполнит 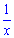 ,
а второй —
,
а второй — 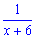 часть всей нормы. По условию выполняют
норму за 4 дня, то есть оба в день могут
выполнить
часть всей нормы. По условию выполняют
норму за 4 дня, то есть оба в день могут
выполнить  нормы. Составляем
и решаем уравнение
нормы. Составляем
и решаем уравнение 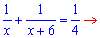
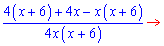
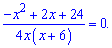
Данное
дробно рациональное уравнение эквивалентно
системе двух уравнений 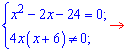
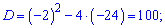
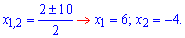
Одно
решение 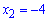 не
соответствует физической сути задачи.
Время второго лесоруба
х+6=6+6=12 (дней)
не
соответствует физической сути задачи.
Время второго лесоруба
х+6=6+6=12 (дней)
Ответ: Работу первый лесоруб выполнит за 6 дней, а второй за 12.
————————————
Подобных дробно рациональных уравнений можно рассмотреть множество, схема их решения неизменна. В теоретических задачах правильно составляйте уравнение и не заблуждайтесь при сведении к общему знаменателю. Все остальное сводится к решению преимущественно линейных или квадратных уравнений.
Следует приобрести навык в решении дробно-рациональных уравнений путём выполнения ряда тренировочных упражнений. Тренировочные упражнения предлагаются трёх уровней сложности: А – обязательный минимум знаний по этой теме, В – упражнения среднего уровня сложности, С – упражнения повышенной степени сложности.
№ | Уравнения | Ответы |
Уровень А | ||
1 |
| 5 |
2 |
| -2; 50 |
3 |
| -9; 1 |
4 |
| -0,5; 1 |
5 |
| 0,5 |
6 |
| -1 |
7 |
| -4,7; -1 |
8 |
| -4; 7 |
9 |
| — |
10 |
| 2 |
№ | Уравнения | Ответы |
Уровень В | ||
1 |
| 7 |
2 |
| -0,25 |
3 |
| Нет корней |
4 |
| 0; 1 |
5 |
| -1; 5 |
6 |
| -1 |
7 | (x+4)(x2-1)
=4x2 + 24x
— | 5 |
8 |
| — |
9 |
| 4 |
10 |
| 1 |
№ | Уравнения | Ответы |
Уровень С | ||
1 |
| -2 |
2 |
| 1; 4; |
3 | x2+x+1= | -2; 1 |
4 |
| 1; 8 |
5 | x2-5x+ | 1; 2; 3; 4 |
6 |
| 2 |
7 |
|
|
8 |
| -3; 1 |
9 |
| 0,2; 1 |
10 |
| Нет корней |
studfile.net

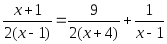
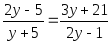
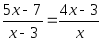
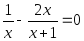
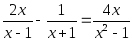
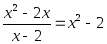
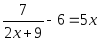
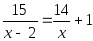
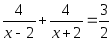
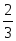 ;
6
;
6