Решение уравнений с дробями — как решать дробные уравнения
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математике, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 — 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x — y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
| Основные свойства дробей |
|---|
|
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Приходите решать увлекательные задачки по математике в детскую школу Skysmart. Поможем разобраться в сложной теме, подтянем оценки и покажем, что математика может быть захватывающим приключением.
Запишите ребенка на бесплатный вводный урок: познакомим с форматом, выявим пробелы и наметим индивидуальную программу обучения.
Ты можешь записаться на онлайн-уроки по математике для учеников 1-11 классов!
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
| Универсальный алгоритм решения |
|---|
|
А теперь еще несколько способов, которые пригодятся ребенку на уроках математики.
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
Как решаем:
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.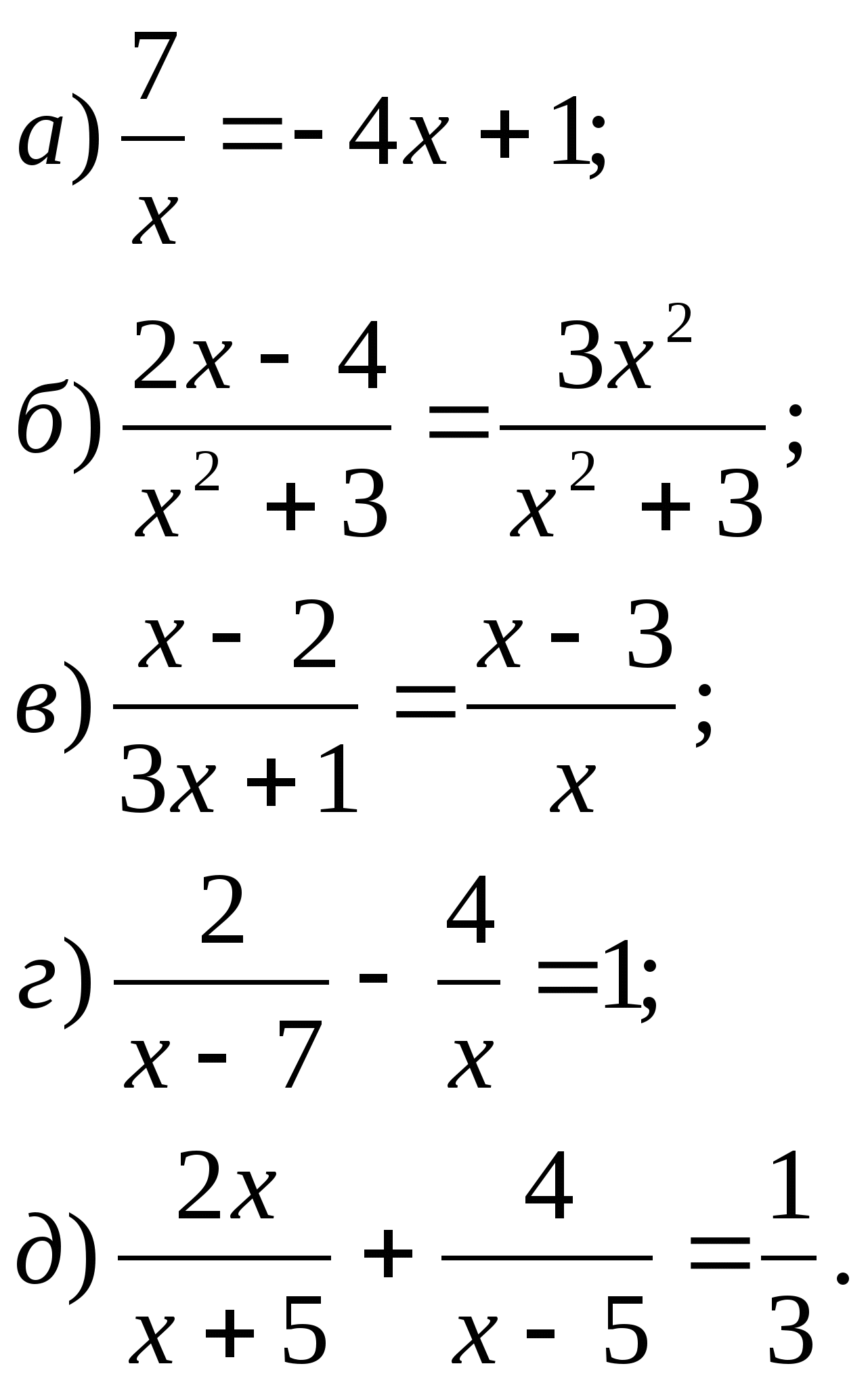
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
| Что еще важно учитывать при решении |
|---|
|
А вот и полезные видео для закрепления материала:
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
Как решаем:
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
1 + 2x = 5х
- Решим обычное уравнение.
5x — 2х = 1
3x = 1
х = 1/3
Ответ: х = 1/3.
Пример 2. Найти корень уравнения
Как решаем:
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
- Переведем новый множитель в числитель..
- Сократим левую часть на (х+2), а правую на 2.
4 = х + 2
х = 4 — 2 = 2
Ответ: х = 2.
Пример 3. Решить дробное уравнение:
Как решаем:
- Найти общий знаменатель:
3(x-3)(x+3)
- Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
3(x+3)(x+3)+3(x-3)(x-3)=10(x-3)(x+3)+3*36
- Выполним возможные преобразования. Получилось квадратное уравнение:
x2-9=0
- Решим полученное квадратное уравнение:
x2=9
- Получили два возможных корня:
x1=−3, x2=3
х = 4 — 2 = 2
- Если x = −3, то знаменатель равен нулю:
3(x-3)(x+3)=0
Если x = 3 — знаменатель тоже равен нулю.
- Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.
Ответ: нет решения.
Если нужно решить уравнение с дробями быстро — поможет онлайн-калькулятор дробей. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Как решать дробные уравнения? | О математике понятно
Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями.
Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями.
Иногда их называют более научно и солидно — дробные рациональные уравнения. Или дробно-рациональные уравнения. Это сути не меняет.)
Дробные уравнения — незаменимая вещь во многих других темах математики. Особенно — в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:
1. Дроби и действия с дробями и дробными выражениями.
2. Тождественные преобразования уравнений.
3. Решение линейных и квадратных уравнений.
Без этих трёх китов браться за решение дробных уравнений слишком уж самонадеянно, я бы сказал. Почему? Да потому, что непонимание, как, скажем, работать с дробями (сокращать, приводить к общему знаменателю и т.д.) автоматически будет приводить к полному провалу и в дробных уравнениях. Намёк понятен?)
Намёк понятен?)
Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем — настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.
Итак, вперёд!
Что такое дробное уравнение? Примеры.
Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби. Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.
Например, вот такое уравнение:
Или такое:
Или вот такое:
И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся. Либо это линейные уравнения, либо квадратные.
Например:
Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей — четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.
Т.е. просто числа. И ни один из знаменателей не содержит иксов.
Или такое уравнение:
Это обычное квадратное уравнение, несмотря на двойку в знаменателе. Опять же, по причине того, что двойка — не икс, и деления на неизвестное в дроби нету.
В общем, вы поняли.
Как решать дробные уравнения? Убираем дроби!
Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?
Первым делом надо избавиться от дробей! Это ключевой шаг в решении любого дробного уравнения, который должен быть освоен идеально. Ибо после того, как все дроби исчезли, уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы уже с вами знаем, что делать.)
Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?
Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)
Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)
Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:
Первое, что приходит на ум — перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае — при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.
А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?
Давайте его конструировать.) Смотрим ещё раз на уравнение:
Понятно, что в левой части для ликвидации знаменателя нам необходимо умножение на (х+3), а в правой — на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)
Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)
Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х+3), так и на тройку. Причём очень важно — только с помощью умножения! И какое же это выражение? Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.
Итак, для ликвидации всех дробей наше уравнение надо умножать на выражение 3(х+3).
Умножаем:
Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:
Прошу обратить внимание: скобки (х+3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача — дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок?!
А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:
Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:
Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:
2∙3 = х+3
А его (надеюсь) уже решит каждый:
х = 3
Решаем следующий примерчик:
И опять избавляемся от того, что нам не нравится. В данном примере это дробь 20/х. Одна единственная. Для её ликвидации правую часть надо домножить на знаменатель. То есть, просто на х. Но тогда и левую часть тоже надо домножить на х: так уж второе тождественное преобразование требует.
Вот и домножаем! Всю левую часть и всю правую часть:
Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части нашего уравнения мы умножаем на «х».
Вперёд!
А вот теперь — снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 — х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть целиком, а не отдельные её кусочки!
Дело всё в том, что частенько после умножения народ записывает левую часть вот так:
Это категорически неверно. Дальше можно уже не решать, да…)
Но у нас всё хорошо, будем дорешивать.
С чистой совестью сокращаем икс справа и получаем уравнение уже безо всяких дробей, в одну строчку.
(9 — х)∙х = 20
Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:
9х — х2 = 20
Переносим всё влево и приводим к стандартному виду:
Получили классическое квадратное уравнение. Но минус перед квадратом икса — нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:
Но минус перед квадратом икса — нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:
Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:
х1 = 4
х2 = 5
И все дела.)
Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь — квадратным.
А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3=3. Это означает, что икс может быть любым. Какой икс ни возьми — всё равно всё посокращается и останется железное равенство 3=3.
Или наоборот, может получиться какая-нибудь белиберда, типа 3=4. А это будет означать, что корней нет. Какой икс ни возьми — всё сократится и останется бред…
Надеюсь, такие сюрпризы вас уже нисколько не удивят. ) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они ко всем видам уравнений относятся. И дробные — не исключение.)
) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они ко всем видам уравнений относятся. И дробные — не исключение.)
Разумеется, при попытке ликвидации дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.
Раскладываем на множители!
Решаем третье уравнение по списку:
А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить
x(x2+2x)(x+2)
и домножить на эту конструкцию всё уравнение. Математика не возражает.) Но… Может быть, есть выражение попроще?
Математика не возражает.) Но… Может быть, есть выражение попроще?
Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители. Привет седьмому классу!)
А попробуем-ка разложить на множители каждый из знаменателей? Ну, с х и х+2 точно ничего не сделать, а вот х2+2х вполне себе раскладывается! Выносим один икс за скобку и получаем:
х2+2х = х(х+2)
Отлично. Вставим наше разложение в исходное уравнение:
Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и само на себя — на х(х+2).
Вот на х(х+2) и умножаем:
И снова расписываю подробно, дабы не запутаться. В левой части я буду использовать скобки: там сумма дробей. В правой части скобки не нужны: там одна дробь. Вот и пишем:
В левой части я буду использовать скобки: там сумма дробей. В правой части скобки не нужны: там одна дробь. Вот и пишем:
А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем — вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:
Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х — 3) в числителе первой дроби — думаю, уже не стоит объяснять?)
С удовольствием сокращаем все дроби:
(x-3)(x+2) + 3 = x
Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:
x2 + 2x — 3x — 6 + 3 — х = 0
x2 — 2x — 3 = 0
И снова получили квадратное уравнение. ) Решаем и получаем два корня:
) Решаем и получаем два корня:
x1 = -1
x2 = 3
Вот и всё. Это и есть ответ.)
Из этого примера можно сделать важный вывод:
Если знаменатели дробей можно разложить на простые множители — обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!
Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это — дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.) Мы всегда будем от всего этого избавляться.)
Ну что, порешаем?)
Решить уравнения:
Ответы (как обычно, вразброс):
x = 3
x1 = 0,5; x2 = 3
x = 2
х = 6
x = 2,6
x1 = 2; x2 = 5
Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)
Всё решилось? Что ж, здорово! Значит, полпути в решении дробных уравнений мы с вами уже преодолели.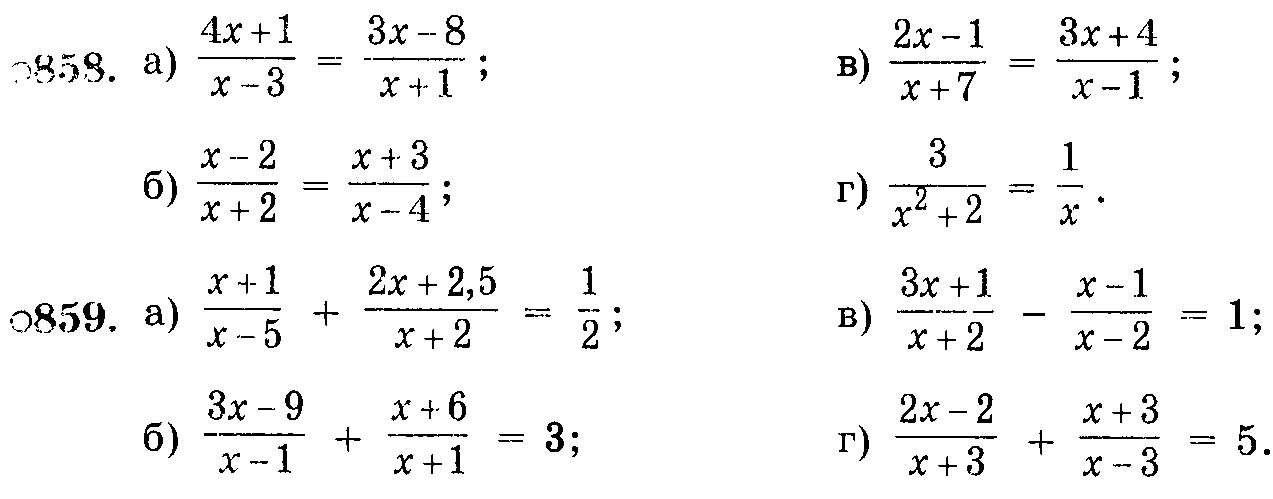 2} +2 $$
2} +2 $$
Алгоритм решения дробного рационального уравнения
Шаг 1. Привести по отдельности левую и правую части уравнения к их общим знаменателям.
Шаг 2. Используя свойство пропорции
$$ \frac{a}{b} = \frac{c}{d} \iff {\left\{ \begin{array}{c} ad = bc \\ b \neq 0 \\ d \neq 0 \end{array} \right.} $$
перейти к целому рациональному уравнению с условиями $\neq$ 0 для знаменателей.
Шаг 3. Решить полученное целое рациональное уравнение.
Шаг 4. Проверить и отбросить те корни целого рационального уравнения, которые превращают знаменатели исходного дробного уравнения в 0.
Шаг 5. Записать оставшиеся корни в ответ. Работа завершена.
Также, при решении дробных рациональных уравнений на шаге 1 и шаге 3 часто используются методы замены переменной, разложении на множители и т.п. (см. §30 данного справочника).
Например:
Решить уравнение $ \frac{1}{5x+12} — \frac{1}{5x-12} = \frac{1}{x^2} $
Шаг 1. 2-x-2}$$
2-x-2}$$
$$ {\left\{ \begin{array}{c} (a+3-5+3a)x-2(a+3)-(5-3a) = ax+3 \\ x \neq -1, x \neq 2 \end{array} \right.} $$
$$ (4a-2)x+a-11 = ax+3 $$
$$ (3a-2)x = 14-a \Rightarrow \left[ \begin{array}{cc} {\left\{ \begin{array}{c} a = \frac{2}{3} \\ 0 \cdot x = 5-\frac{2}{3}, x \in \varnothing \end{array} \right.} \\ {\left\{ \begin{array}{c} a \neq \frac{2}{3} \\ x = \frac{14-a}{3a-2} \end{array} \right.} \end{array} \right. \Rightarrow {\left\{ \begin{array}{c} a \neq \frac{2}{3} \\ x = \frac{14-a}{3a-2} \end{array} \right.} $$
Проверяем условия $x \neq -1, x \neq 2$.
$$ \frac{14-a}{3a-2} \neq -1 \Rightarrow 14-a \neq 2-3a \Rightarrow 2a \neq -12 \Rightarrow a \neq -6 $$
$$ \frac{14-a}{3a-2} \neq 2 \Rightarrow 14-a \neq 6a-4 \Rightarrow 7a \neq 18 \Rightarrow a \neq \frac{18}{7} $$
Ответ:
При a = $\{-6; \frac{2}{3}; \frac{18}{7}\}$ решений нет; при $a \neq \{-6; \frac{2}{3}; \frac{18}{7}\}$ один корень $x = \frac{14-a}{3a-2}$
Пример 2. 2}}{2} = \frac{a(1 \pm \sqrt{5})}{2} $$
2}}{2} = \frac{a(1 \pm \sqrt{5})}{2} $$
2) Накладываем условия $z \neq 0, z \neq \pm a$ на полученные решения.
$$ z = — \frac{a}{4} \neq 0 \Rightarrow a \neq 0, z = -\frac{a}{4} \neq \pm a \Rightarrow a \neq 0 $$
$$ z = \frac{a(1 \pm \sqrt{5})}{2} \neq 0 \Rightarrow a \neq 0 $$
$$ z = \frac{a(1 \pm \sqrt{5})}{2} \neq \pm a \Rightarrow a(1 \pm \sqrt{5}) \neq \pm 2a \Rightarrow a \neq 0 $$
3) Особая точка a = 0.
При a = 0 исходное уравнение является ложным: 0 = 8, решений нет.
4) Возвращаемся к исходной переменной: x = z-2a
$$ x_1 = -\frac{a}{4}-2a = -\frac{9}{4} a $$
$$ x_2 = \frac{a(1-\sqrt{5})}{2}-2a = \frac{a(1-\sqrt{5}-4)}{2} = \frac{a(-\sqrt{5}-3)}{2} $$
$$ x_2 = \frac{a(1+\sqrt{5})}{2}-2a = \frac{a(1+\sqrt{5}-4)}{2} = \frac{a(\sqrt{5}-3)}{2} $$
Ответ:
При a = 0 корней нет
При $a \neq 0$ три корня $x_1 = -\frac{9}{4} a; x_{2,3} = \frac{a(\pm\sqrt{5}-3)}{2}$
Сложные дробные уравнения. Как решать уравнения с дробями
Как решать уравнения с дробями
Уравнения с дробями сами по себе не трудны и очень интересны. Рассмотрим виды дробных уравнений и способы их решения.
Как решать уравнения с дробями – икс в числителе
В случае, если дано дробное уравнение, где неизвестное находится в числителе, решение не требует дополнительных условий и решается без лишних хлопот. Общий вид такого уравнения – x/a + b = c, где x – неизвестное, a,b и с – обычные числа.
Найти x: x/5 + 10 = 70.
Для того чтобы решить уравнение, нужно избавиться от дробей. Умножаем каждый член уравнения на 5: 5x/5 + 5×10 = 70×5. 5x и 5 сокращается, 10 и 70 умножаются на 5 и мы получаем: x + 50 = 350 => x = 350 – 50 = 300.
Найти x: x/5 + x/10 = 90.
Данный пример – немного усложненная версия первого. Тут есть два варианта решения.
- Вариант 1: Избавляемся от дробей, умножая все члены уравнения на больший знаменатель, то есть на 10: 10x/5 + 10x/10 = 90×10 => 2x + x = 900 => 3x = 900 => x=300.

- Вариант 2: Складываем левую часть уравнения. x/5 + x/10 = 90. Общий знаменатель – 10. 10 делим на 5, умножаем на x, получаем 2x. 10 делим на 10, умножаем на x, получаем x: 2x+x/10 = 90. Отсюда 2x+x = 90×10 = 900 => 3x = 900 => x = 300.
Нередко встречаются дробные уравнения, в которых иксы находятся по разные стороны знака равно. В таких ситуация необходимо перенести все дроби с иксами в одну сторону, а числа в другую.
- Найти x: 3x/5 = 130 – 2x/5.
- Переносим 2x/5 направо с противоположным знаком: 3x/5 + 2x/5 = 130 => 5x/5 = 130.
- Сокращаем 5x/5 и получаем: x = 130.
Как решить уравнение с дробями – икс в знаменателе
Данный вид дробных уравнений требует записи дополнительных условий. Указание этих условий является обязательной и неотъемлемой частью правильного решения. Не приписав их, вы рискуете, так как ответ (даже если он правильный) могут просто не засчитать.
Общий вид дробных уравнений, где x находится в знаменателе, имеет вид: a/x + b = c, где x – неизвестное, a, b, c – обычные числа. Обратите внимание, что x-ом может быть не любое число. Например x не может равняться нулю, так как делить на 0 нельзя. Именно это и является дополнительным условием, которое мы должны указать. Это называется областью допустимых значений, сокращенно – ОДЗ.
Обратите внимание, что x-ом может быть не любое число. Например x не может равняться нулю, так как делить на 0 нельзя. Именно это и является дополнительным условием, которое мы должны указать. Это называется областью допустимых значений, сокращенно – ОДЗ.
Найти x: 15/x + 18 = 21.
Сразу же пишем ОДЗ для x: x ≠ 0. Теперь, когда ОДЗ указана, решаем уравнение по стандартной схеме, избавляясь от дробей. Умножаем все члены уравнения на x. 15x/x+18x = 21x => 15+18x = 21x => 15 = 3x => x = 15/3 = 5.
Часто встречаются уравнения, где в знаменателе стоит не только x, но и еще какое-нибудь действие с ним, например сложение или вычитание.
Найти x: 15/(x-3) + 18 = 21.
Мы уже знаем, что знаменатель не может равняться нулю, а значит x-3 ≠ 0. Переносим -3 в правую часть, меняя при этом знак “-” на ”+” и получаем, что x ≠ 3. ОДЗ указана.
Решаем уравнение, умножаем все на x-3: 15 + 18×(x – 3) = 21×(x – 3) => 15 + 18x – 54 = 21x – 63.
Переносим иксы направо, числа налево: 24 = 3x => x = 8.
Мы уже научились решать квадратные уравнения. Теперь распространим изученные методы на рациональные уравнения.
Что такое рациональное выражение? Мы уже сталкивались с этим понятием. Рациональными выражениями называются выражения, составленные из чисел, переменных, их степеней и знаков математических действий.
Соответственно, рациональными уравнениями называются уравнения вида: , где — рациональные выражения.
Раньше мы рассматривали только те рациональные уравнения, которые сводятся к линейным. Теперь рассмотрим и те рациональные уравнения, которые сводятся и к квадратным.
Пример 1
Решить уравнение: .
Решение:
Дробь равна 0 тогда и только тогда, когда ее числитель равен 0, а знаменатель не равен 0.
Получаем следующую систему:
Первое уравнение системы — это квадратное уравнение. Прежде чем его решать, поделим все его коэффициенты на 3. Получим:
Получим:
Получаем два корня: ; .
Поскольку 2 никогда не равно 0, то необходимо, чтобы выполнялись два условия: . Поскольку ни один из полученных выше корней уравнения не совпадает с недопустимыми значениями переменной, которые получились при решении второго неравенства, они оба являются решениями данного уравнения.
Ответ: .
Итак, давайте сформулируем алгоритм решения рациональных уравнений:
1. Перенести все слагаемые в левую часть, чтобы в правой части получился 0.
2. Преобразовать и упростить левую часть, привести все дроби к общему знаменателю.
3. Полученную дробь приравнять к 0, по следующему алгоритму: .
4. Записать те корни, которые получились в первом уравнении и удовлетворяют второму неравенству, в ответ.
Давайте рассмотрим еще один пример.
Пример 2
Решить уравнение: .
Решение
В самом начале перенесем все слагаемые в левую сторону, чтобы справа остался 0. Получаем:
Получаем:
Теперь приведем левую часть уравнения к общему знаменателю:
Данное уравнение эквивалентно системе:
Первое уравнение системы — это квадратное уравнение.
Коэффициенты данного уравнения: . Вычисляем дискриминант:
Получаем два корня: ; .
Теперь решим второе неравенство: произведение множителей не равно 0 тогда и только тогда, когда ни один из множителей не равен 0.
Необходимо, чтобы выполнялись два условия: . Получаем, что из двух корней первого уравнения подходит только один — 3.
Ответ: .
На этом уроке мы вспомнили, что такое рациональное выражение, а также научились решать рациональные уравнения, которые сводятся к квадратным уравнениям.
На следующем уроке мы рассмотрим рациональные уравнения как модели реальных ситуаций, а также рассмотрим задачи на движение.
Список литературы
- Башмаков М.И. Алгебра, 8 класс. — М.: Просвещение, 2004.

- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра, 8. 5-е изд. — М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра, 8 класс. Учебник для общеобразовательных учреждений. — М.: Просвещение, 2006.
- Фестиваль педагогических идей «Открытый урок» ().
- School.xvatit.com ().
- Rudocs.exdat.com ().
Домашнее задание
Дробные уравнения. ОДЗ.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Продолжаем осваивать уравнения. Мы уже в курсе, как работать с линейными уравнениями и квадратными. Остался последний вид – дробные уравнения . Или их ещё называют гораздо солиднее – дробные рациональные уравнения . Это одно и то же.
Дробные уравнения.
Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дроби, а дроби, у которых есть неизвестное в знаменателе . Хотя бы в одном. Например:
Хотя бы в одном. Например:
Напомню, если в знаменателях только числа , это линейные уравнения.
Как решать дробные уравнения ? Прежде всего – избавиться от дробей! После этого уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы знаем, что делать… В некоторых случаях оно может превратиться в тождество, типа 5=5 или неверное выражение, типа 7=2. Но это редко случается. Ниже я про это упомяну.
Но как избавиться от дробей!? Очень просто. Применяя всё те же тождественные преобразования.
Нам надо умножить всё уравнение на одно и то же выражение. Так, чтобы все знаменатели посокращались! Всё сразу станет проще. Поясняю на примере. Пусть нам требуется решить уравнение:
Как учили в младших классах? Переносим все в одну сторону, приводим к общему знаменателю и т.д. Забудьте, как страшный сон! Так нужно делать, когда вы складываете или вычитаете дробные выражения. Или работаете с неравенствами. А в уравнениях мы сразу умножаем обе части на выражение, которое даст нам возможность сократить все знаменатели (т. е., в сущности, на общий знаменатель). И какое же это выражение?
е., в сущности, на общий знаменатель). И какое же это выражение?
В левой части для сокращения знаменателя требуется умножение на х+2 . А в правой требуется умножение на 2. Значит, уравнение надо умножать на 2(х+2) . Умножаем:
Это обычное умножение дробей, но распишу подробно:
Обратите внимание, я пока не раскрываю скобку (х + 2) ! Так, целиком, её и пишу:
В левой части сокращается целиком (х+2) , а в правой 2. Что и требовалось! После сокращения получаем линейное уравнение:
А это уравнение уже решит всякий! х = 2 .
Решим ещё один пример, чуть посложнее:
Если вспомнить, что 3 = 3/1, а 2х = 2х/ 1, можно записать:
И опять избавляемся от того, что нам не очень нравится – от дробей.
Видим, что для сокращения знаменателя с иксом, надо умножить дробь на (х – 2) . А единицы нам не помеха. Ну и умножаем. Всю левую часть и всю правую часть:
Опять скобки (х – 2) я не раскрываю. Работаю со скобкой в целом, как будто это одно число! Так надо делать всегда, иначе ничего не сократится.
Работаю со скобкой в целом, как будто это одно число! Так надо делать всегда, иначе ничего не сократится.
С чувством глубокого удовлетворения сокращаем (х – 2) и получаем уравнение безо всяких дробей, в линеечку!
А вот теперь уже раскрываем скобки:
Приводим подобные, переносим всё в левую часть и получаем:
Но до того мы другие задачи научимся решать. На проценты. Те ещё грабли, между прочим!
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Решение дробно-рациональных уравнений
Справочное пособие
Рациональные уравнения – это уравнения, в которых и левая, и правая части являются рациональными выражениями.
(Напомним: рациональными выражениями называют целые и дробные выражения без радикалов, включающие действия сложения, вычитания, умножения или деления — например: 6x; (m – n)2; x/3y и т. п.)
п.)
Дробно-рациональные уравнения, как правило, приводятся к виду:
Где P (x ) и Q (x ) – многочлены.
Для решения подобных уравнений умножить обе части уравнения на Q(x), что может привести к появлению посторонних корней. Поэтому, при решении дробно-рациональных уравнений необходима проверка найденных корней.
Рациональное уравнение называется целым, или алгебраическим, если в нем нет деления на выражение, содержащее переменную.
Примеры целого рационального уравнения:
5x – 10 = 3(10 – x)
3x
— = 2x – 10
4
Если в рациональном уравнении есть деление на выражение, содержащее переменную (x), то уравнение называется дробно-рациональным.
Пример дробного рационального уравнения:
15
x + — = 5x – 17
x
Дробные рациональные уравнения обычно решаются следующим образом:
1) находят общий знаменатель дробей и умножают на него обе части уравнения;
2) решают получившееся целое уравнение;
3) исключают из его корней те, которые обращают в ноль общий знаменатель дробей.
Примеры решения целых и дробных рациональных уравнений.
Пример 1. Решим целое уравнение
x – 1 2x 5x
— + — = —.
2 3 6
Решение:
Находим наименьший общий знаменатель. Это 6. Делим 6 на знаменатель и полученный результат умножаем на числитель каждой дроби. Получим уравнение, равносильное данному:
3(x – 1) + 4x 5х
—— = —
6 6
Поскольку в левой и правой частях одинаковый знаменатель, его можно опустить. Тогда у нас получится более простое уравнение:
3(x – 1) + 4x = 5х.
Решаем его, раскрыв скобки и сведя подобные члены:
3х – 3 + 4х = 5х
3х + 4х – 5х = 3
Пример решен.
Пример 2. Решим дробное рациональное уравнение
x – 3 1 x + 5
— + — = —.
x – 5 x x(x – 5)
Находим общий знаменатель. Это x(x – 5). Итак:
х 2 – 3х x – 5 x + 5
— + — = —
x(x – 5) x(x – 5) x(x – 5)
Теперь снова освобождаемся от знаменателя, поскольку он одинаковый для всех выражений. Сводим подобные члены, приравниваем уравнение к нулю и получаем квадратное уравнение:
Сводим подобные члены, приравниваем уравнение к нулю и получаем квадратное уравнение:
х 2 – 3x + x – 5 = x + 5
х 2 – 3x + x – 5 – x – 5 = 0
х 2 – 3x – 10 = 0.
Решив квадратное уравнение, найдем его корни: –2 и 5.
Проверим, являются ли эти числа корнями исходного уравнения.
При x = –2 общий знаменатель x(x – 5) не обращается в нуль. Значит, –2 является корнем исходного уравнения.
При x = 5 общий знаменатель обращается в нуль, и два выражения из трех теряют смысл. Значит, число 5 не является корнем исходного уравнения.
Ответ: x = –2
Ещё примеры
Пример 1.
x 1 =6, x 2 = — 2,2.
Ответ:-2,2;6.
Пример 2.
Мы уже научились решать квадратные уравнения. Теперь распространим изученные методы на рациональные уравнения.
Что такое рациональное выражение? Мы уже сталкивались с этим понятием. Рациональными выражениями называются выражения, составленные из чисел, переменных, их степеней и знаков математических действий.
Соответственно, рациональными уравнениями называются уравнения вида: , где — рациональные выражения.
Раньше мы рассматривали только те рациональные уравнения, которые сводятся к линейным. Теперь рассмотрим и те рациональные уравнения, которые сводятся и к квадратным.
Пример 1
Решить уравнение: .
Решение:
Дробь равна 0 тогда и только тогда, когда ее числитель равен 0, а знаменатель не равен 0.
Получаем следующую систему:
Первое уравнение системы — это квадратное уравнение. Прежде чем его решать, поделим все его коэффициенты на 3. Получим:
Получаем два корня: ; .
Поскольку 2 никогда не равно 0, то необходимо, чтобы выполнялись два условия: . Поскольку ни один из полученных выше корней уравнения не совпадает с недопустимыми значениями переменной, которые получились при решении второго неравенства, они оба являются решениями данного уравнения.
Ответ: .
Итак, давайте сформулируем алгоритм решения рациональных уравнений:
1. Перенести все слагаемые в левую часть, чтобы в правой части получился 0.
2. Преобразовать и упростить левую часть, привести все дроби к общему знаменателю.
3. Полученную дробь приравнять к 0, по следующему алгоритму: .
4. Записать те корни, которые получились в первом уравнении и удовлетворяют второму неравенству, в ответ.
Давайте рассмотрим еще один пример.
Пример 2
Решить уравнение: .
Решение
В самом начале перенесем все слагаемые в левую сторону, чтобы справа остался 0. Получаем:
Теперь приведем левую часть уравнения к общему знаменателю:
Данное уравнение эквивалентно системе:
Первое уравнение системы — это квадратное уравнение.
Коэффициенты данного уравнения: . Вычисляем дискриминант:
Получаем два корня: ; .
Теперь решим второе неравенство: произведение множителей не равно 0 тогда и только тогда, когда ни один из множителей не равен 0.
Необходимо, чтобы выполнялись два условия: . Получаем, что из двух корней первого уравнения подходит только один — 3.
Ответ: .
На этом уроке мы вспомнили, что такое рациональное выражение, а также научились решать рациональные уравнения, которые сводятся к квадратным уравнениям.
На следующем уроке мы рассмотрим рациональные уравнения как модели реальных ситуаций, а также рассмотрим задачи на движение.
Список литературы
- Башмаков М.И. Алгебра, 8 класс. — М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра, 8. 5-е изд. — М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра, 8 класс. Учебник для общеобразовательных учреждений. — М.: Просвещение, 2006.
- Фестиваль педагогических идей «Открытый урок» ().
- School.xvatit.com ().
- Rudocs.exdat.com ().
Домашнее задание
Дробно рациональное уравнение приведя. Решение дробно-рациональных уравнений. Как решаются дробно-рациональные уравнения
Решение дробно-рациональных уравнений. Как решаются дробно-рациональные уравнения
Дробным уравнением называется уравнение, в котором хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением является уравнение .
Решать дробные уравнения удобно в следующем порядке:
- найти общий знаменатель дробей, входящих в уравнение, если каждая дробь имеет смысл,
- заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
- решить получившееся целое уравнение,
- исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решить дробное уравнение:
Решение. Воспользуемся основным свойством дроби с представим левую и правую части этого уравнения в виде дробей с одинаковым знаменателем:
.
Эти дроби равны при тех и только тех значениях, при которых равны их
числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а
следовательно, и уравнение не имеет смысла.
Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение
Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение
.
При решении квадратного уравнения получаем его корни:
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное дробное уравнение. Общий знаменатель —
Заменим исходное уравнение целым. Для этого умножим обе его части на общий знаменатель. Получим:
Выполним необходимые преобразования в полученном уравнении и придём к квадратному уравнению
Решенив квадратное уравнение , получаем его корни:
Если x = -3 , то найденный на первом шаге знаменатель обращается в нуль:
,
то же самое, если x = 3 .
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а,
поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное уравнение. Для этого знаменатели дробей разложим на множители:
.
Общий знаменатель — выражение
Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:
Выполнив преобразования, придём к квадратному уравнению
.
Решенив квадратное уравнение , получаем его корни:
.
Ни один из корней не обращает общий знаменатель в нуль. Следовательно, числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:
.
Решение. Введём новую переменную, обозначив . Получим уравнение с переменной y .
§ 1 Целое и дробное рациональные уравнение
В этом уроке разберем такие понятия, как рациональное уравнение, рациональное выражение, целое выражение, дробное выражение. Рассмотрим решение рациональных уравнений.
Рациональным уравнением называют уравнение, в котором левая и правая части являются рациональными выражениями.
Рациональные выражения бывают:
Дробные.
Целое выражение составлено из чисел, переменных, целых степеней с помощью действий сложения, вычитания, умножения, а также деления на число, отличное от нуля.
Например:
В дробных выражениях есть деление на переменную или выражение с переменной. Например:
Дробное выражение не при всех значениях входящих в него переменных имеет смысл. Например, выражение
при х = -9 не имеет смысла, так как при х = -9 знаменатель обращается в нуль.
Значит, рациональное уравнение может быть целым и дробным.
Целое рациональное уравнение — это рациональное уравнение, в котором левая и правая части — целые выражения.
Например:
Дробное рациональное уравнение — это рациональное уравнение, в котором или левая, или правая части — дробные выражения.
Например:
§ 2 Решение целого рационального уравнения
Рассмотрим решение целого рационального уравнения.
Например:
Умножим обе части уравнения на наименьший общий знаменатель знаменателей входящих в него дробей.
Для этого:
1. найдем общий знаменатель для знаменателей 2, 3, 6. Он равен 6;
2. найдем дополнительный множитель для каждой дроби. Для этого общий знаменатель 6 делим на каждый знаменатель
дополнительный множитель для дроби
дополнительный множитель для дроби
3. умножим числители дробей на соответствующие им дополнительные множители. Таким образом, получим уравнение
которое равносильно данному уравнению
Слева раскроем скобки, правую часть перенесем налево, изменив знак слагаемого при переносе на противоположный.
Приведем подобные члены многочлена и получим
Видим, что уравнение линейное.
Решив его, найдем, что х = 0,5.
§ 3 Решение дробного рационального уравнения
Рассмотрим решение дробного рационального уравнения.
Например:
1.Умножим обе части уравнения на наименьший общий знаменатель знаменателей входящих в него рациональных дробей.
Найдем общий знаменатель для знаменателей х + 7 и х — 1.
Он равен их произведению (х + 7)(х — 1).
2.Найдем дополнительный множитель для каждой рациональной дроби.
Для этого общий знаменатель (х + 7)(х — 1) делим на каждый знаменатель. Дополнительный множитель для дроби
равен х — 1,
дополнительный множитель для дроби
равен х+7.
3.Умножим числители дробей на соответствующие им дополнительные множители.
Получим уравнение (2х — 1)(х — 1) = (3х + 4)(х + 7), которое равносильно данному уравнению
4.Слева и справа умножим двучлен на двучлен и получим следующее уравнение
5.Правую часть перенесем налево, изменив знак каждого слагаемого при переносе на противоположный:
6.Приведем подобные члены многочлена:
7.Можно обе части разделить на -1. Получим квадратное уравнение:
8.Решив его, найдем корни
Так как в уравнении
левая и правая части — дробные выражения, а в дробных выражениях при некоторых значениях переменных знаменатель может обратиться в нуль, то необходимо проверить, не обращается ли в нуль при найденных х1 и х2 общий знаменатель.
При х = -27 общий знаменатель (х + 7)(х — 1) не обращается в нуль, при х = -1 общий знаменатель также не равен нулю.
Следовательно, оба корня -27 и -1 являются корнями уравнения.
При решении дробного рационального уравнения лучше сразу указать область допустимых значений. Исключить те значения, при которых общий знаменатель обращается в нуль.
Рассмотрим еще один пример решения дробного рационального уравнения.
Например, решим уравнение
Знаменатель дроби правой части уравнения разложим на множители
Получим уравнение
Найдем общий знаменатель для знаменателей (х — 5), х, х(х — 5).
Им будет выражение х(х — 5).
теперь найдем область допустимых значений уравнения
Для этого общий знаменатель приравняем к нулю х(х — 5) = 0.
Получим уравнение, решив которое, найдем, что при х = 0 или при х = 5 общий знаменатель обращается в нуль.
Значит, х = 0 или х = 5 не могут быть корнями нашего уравнения.
Теперь можно найти дополнительные множители.
Дополнительным множителем для рациональной дроби
дополнительным множителем для дроби
будет (х — 5),
а дополнительный множитель дроби
Числители умножим на соответствующие дополнительные множители.
Получим уравнение х(х — 3) + 1(х — 5) = 1(х + 5).
Раскроем скобки слева и справа, х2 — 3х + х — 5 = х + 5.
Перенесем слагаемые справа налево, изменив знак переносимых слагаемых:
Х2 — 3х + х — 5 — х — 5 = 0
И после приведения подобных членов получим квадратное уравнение х2 — 3х — 10 = 0. Решив его, найдем корни х1 = -2; х2 = 5.
Но мы уже выяснили, что при х = 5 общий знаменатель х(х — 5) обращается в нуль. Следовательно, корнем нашего уравнения
будет х = -2.
§ 4 Краткие итоги урока
Важно запомнить:
При решении дробных рациональных уравнений надо поступить следующим образом:
1.Найти общий знаменатель дробей входящих в уравнение. При этом если знаменатели дробей можно разложить на множители, то разложить их на множители и затем найти общий знаменатель.
2.Умножить обе части уравнения на общий знаменатель: найти дополнительные множители, умножить числители на дополнительные множители.
3.Решить получившееся целое уравнение.
4.Исключить из его корней те, которые обращают в нуль общий знаменатель.
Список использованной литературы:
- Макарычев Ю.Н., Н. Г. Миндюк, Нешков К.И., Суворова С.Б. / Под редакцией Теляковского С.А. Алгебра: учебн. для 8 кл. общеобразоват. учреждений. — М.: Просвещение, 2013.
- Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учеб. для общеобразоват. учреждений. — М.: Мнемозина.
- Рурукин А.Н. Поурочные разработки по алгебре: 8 класс.- М.: ВАКО, 2010.
- Алгебра 8 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворовой / Авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. -Волгоград: Учитель, 2005.
«Рациональные уравнения с многочленами» — одна из самых часто встречающихся тем в тестовых заданиях ЕГЭ по математике. По этой причине их повторению стоит уделить особое внимание. Многие ученики сталкиваются с проблемой нахождения дискриминанта, перенесения показателей из правой части в левую и приведения уравнения к общему знаменателю, из-за чего выполнение подобных заданий вызывает трудности. Решение рациональных уравнений при подготовке к ЕГЭ на нашем сайте поможет вам быстро справляться с задачами любой сложности и сдать тестирование на отлично.
По этой причине их повторению стоит уделить особое внимание. Многие ученики сталкиваются с проблемой нахождения дискриминанта, перенесения показателей из правой части в левую и приведения уравнения к общему знаменателю, из-за чего выполнение подобных заданий вызывает трудности. Решение рациональных уравнений при подготовке к ЕГЭ на нашем сайте поможет вам быстро справляться с задачами любой сложности и сдать тестирование на отлично.
Выбирайте образовательный портал «Школково» для успешной подготовки к единому экзамену по математике!
Чтобы знать правила вычисления неизвестных и легко получать правильные результаты, воспользуйтесь нашим онлайн-сервисом. Портал «Школково» — это единственная в своем роде площадка, где собраны необходимые для подготовки к ЕГЭ материалы. Наши преподаватели систематизировали и изложили в понятной форме все математические правила. Кроме того, мы предлагаем школьникам попробовать силы в решении типовых рациональных уравнений, база которых постоянно обновляется и дополняется.
Для более результативной подготовки к тестированию рекомендуем следовать нашему особому методу и начать с повторения правил и решения простых задач, постепенно переходя к более сложным. Таким образом, выпускник сможет выделить для себя самые трудные темы и сделать акцент на их изучении.
Начните подготовку к итоговому тестированию со «Школково» уже сегодня, и результат не заставит себя ждать! Выберите самый легкий пример из предложенных. Если вы быстро справились с выражением, переходите к более сложной задаче. Так вы сможете подтянуть свои знания вплоть до решения заданий ЕГЭ по математике профильного уровня.
Обучение доступно не только выпускникам из Москвы, но и школьникам из других городов. Уделяйте пару часов в день занятиям на нашем портале, например, и совсем скоро вы сможете справиться с уравнениями любой сложности!
Мы уже научились решать квадратные уравнения. Теперь распространим изученные методы на рациональные уравнения.
Что такое рациональное выражение? Мы уже сталкивались с этим понятием. Рациональными выражениями называются выражения, составленные из чисел, переменных, их степеней и знаков математических действий.
Рациональными выражениями называются выражения, составленные из чисел, переменных, их степеней и знаков математических действий.
Соответственно, рациональными уравнениями называются уравнения вида: , где — рациональные выражения.
Раньше мы рассматривали только те рациональные уравнения, которые сводятся к линейным. Теперь рассмотрим и те рациональные уравнения, которые сводятся и к квадратным.
Пример 1
Решить уравнение: .
Решение:
Дробь равна 0 тогда и только тогда, когда ее числитель равен 0, а знаменатель не равен 0.
Получаем следующую систему:
Первое уравнение системы — это квадратное уравнение. Прежде чем его решать, поделим все его коэффициенты на 3. Получим:
Получаем два корня: ; .
Поскольку 2 никогда не равно 0, то необходимо, чтобы выполнялись два условия: . Поскольку ни один из полученных выше корней уравнения не совпадает с недопустимыми значениями переменной, которые получились при решении второго неравенства, они оба являются решениями данного уравнения.
Ответ: .
Итак, давайте сформулируем алгоритм решения рациональных уравнений:
1. Перенести все слагаемые в левую часть, чтобы в правой части получился 0.
2. Преобразовать и упростить левую часть, привести все дроби к общему знаменателю.
3. Полученную дробь приравнять к 0, по следующему алгоритму: .
4. Записать те корни, которые получились в первом уравнении и удовлетворяют второму неравенству, в ответ.
Давайте рассмотрим еще один пример.
Пример 2
Решить уравнение: .
Решение
В самом начале перенесем все слагаемые в левую сторону, чтобы справа остался 0. Получаем:
Теперь приведем левую часть уравнения к общему знаменателю:
Данное уравнение эквивалентно системе:
Первое уравнение системы — это квадратное уравнение.
Коэффициенты данного уравнения: . Вычисляем дискриминант:
Получаем два корня: ; .
Теперь решим второе неравенство: произведение множителей не равно 0 тогда и только тогда, когда ни один из множителей не равен 0.
Необходимо, чтобы выполнялись два условия: . Получаем, что из двух корней первого уравнения подходит только один — 3.
Ответ: .
На этом уроке мы вспомнили, что такое рациональное выражение, а также научились решать рациональные уравнения, которые сводятся к квадратным уравнениям.
На следующем уроке мы рассмотрим рациональные уравнения как модели реальных ситуаций, а также рассмотрим задачи на движение.
Список литературы
- Башмаков М.И. Алгебра, 8 класс. — М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра, 8. 5-е изд. — М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра, 8 класс. Учебник для общеобразовательных учреждений. — М.: Просвещение, 2006.
- Фестиваль педагогических идей «Открытый урок» ().

- School.xvatit.com ().
- Rudocs.exdat.com ().
Домашнее задание
Сегодня мы разберемся, как решать дробные рациональные уравнения.
Посмотрим: из уравнений
(1) 2х + 5 = 3(8 – х),
(3)
(4)
дробными рациональными уравнениями являются только (2) и (4), а (1) и (3) это целые уравнения.
Предлагаю решить уравнение (4), а затем сформулировать правило.
Поскольку уравнение дробное, то надо найти общий знаменатель. В этом уравнении это выражение 6(х – 12)(х – 6). Затем мы умножаем обе части уравнения на общий знаменатель:
После сокращения получаем целое уравнение:
6(х – 6) 2 – 6(х – 12) 2 = 5(х – 12)(х – 6).
Решив это уравнение надо обязательно проверить не обращают ли полученные корни в нуль знаменатели дробей в исходном уравнении.
Раскрываем скобки:
6х 2 – 72х + 216 – 6х 2 + 144х – 864 = 5х 2 – 90х + 360, упрощаем уравнение: 5х 2 – 162х + 1008 = 0.
Находим корни уравнения
D = 6084, √D = 78,
х 1 = (162 – 78)/10= 84/10 = 8,4 и х 2 = (162 + 78)/10 = 240/10 = 24.
При х = 8,4 и 24 общий знаменатель 6(х – 12)(х – 6) ≠ 0, значит эти числа являются корнями уравнения (4).
Ответ: 8,4; 24.
Решив предложенное уравнение, приходим к следующим положениям :
1) Находим общий знаменатель.
2) Умножаем обе части уравнения на общий знаменатель.
3) Решаем полученное целое уравнение.
4) Проверяем, какие из корней обращают общий знаменатель в нуль и исключаем их из решения.
Посмотрим теперь на примере, как работают полученные положения.
Решить уравнение:
1) Общий знаменатель: х 2 – 1
2) Умножаем обе части уравнения на общий знаменатель, получаем целое уравнение: 6 – 2(х + 1) = 2(х 2 – 1) – (х + 4)(х – 1)
3) Решаем уравнение: 6 – 2х – 2 = 2х 2 – 2 – х 2 – 4х + х + 4
х 2 – х – 2 = 0
х 1 = — 1 и х 2 = 2
4) При х = -1, общий знаменатель х 2 – 1 = 0. Число -1 корнем не является.
При х = 2, общий знаменатель х 2 – 1 ≠ 0. Число 2 – корень уравнения.
Число 2 – корень уравнения.
Ответ : 2.
Как видите, наши положения работают. Не бойтесь, у вас все получится! Самое главное правильно найдите общий знаменатель и аккуратно выполните преобразования . Надеемся, что при решение дробных рациональных уравнений у вас всегда будут получаться правильные ответы. Если у вас остались вопросы или вы хотите попрактиковаться в решении подобных уравнений, записывайтесь на уроки к автору этой статьи, репетитору й.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Сложение и вычитание алгебраических дробей
Мы знаем, что сложение и вычитание арифметических дробей с одинаковыми знаменателями сводится к сложению и вычитанию их числителей, а знаменатель остается тот же самый. Распространяется ли это на алгебраические дроби? Другими словами, будет ли справедливо равенство:
,
какие бы числа a, b, c и n ни были (целые или дробные, положительные или отрицательные)?
Ответ на этот вопрос легко получится, если вспомнить деление многочлена на одночлен: мы знаем, что
(a + b – c) ÷ n = a ÷ n + b ÷ n – c ÷ n
или
;
написав это равенство в обратном порядке, получим:
,
откуда и получим вывод, что сложение и вычитание алгебраических дробей с одинаковыми знаменателями выполняется так же, как и сложение и вычитание арифметических дробей, т. е. складываются или вычитаются числители, а знаменатель остается неизменным.
е. складываются или вычитаются числители, а знаменатель остается неизменным.
Примеры:
[Здесь мы сразу пишем числителя без скобок, т. е. вместо (3x – 2y) – (2x + 5y) + (7 – x) пишем тот многочлен, который получится после раскрытия скобок].
Выполнив затем в числителе приведение подобных членов, мы увидим, что все члены взаимно уничтожаются, и в числителе получается нуль, т. е. в результате получим . Так как при делении нуля на любое число получается нуль, то и окончательный результат = 0, т. е.
.
Если алгебраические дроби имеют различных знаменателей, то, для выполнения их сложения и вычитания, их надо предварительно привести к общему знаменателю. Приведение алгебраических дробей к общему знаменателю выполняется так же, как и для арифметических дробей: надо разложить знаменателей дробей, если это еще не сделано, на множители, при помощи этих множителей надо найти общее наим. кратное (это название здесь имеет условный смысл) для знаменателей всех данных дробей (найти общего знаменателя) и затем надо, пользуясь основным свойством дробей, умножить числителя и знаменателя каждой дроби на одно и то же число, выбранное так, чтобы получился у этой дроби нужный нам и уже найденный общий знаменатель.
Решение решения с дробями — как решать дробные уравнения
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, самых дробей и разницей между ними.
Дробь — это запись числа в математике, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a / b,
- десятичный вид — 0,5.
Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 — 0,3) / 5.
- Алгебраические — состоят из числа.
 Например, (x + y) / (x — y). Значение дроби зависит от данных букв букв.
Например, (x + y) / (x — y). Значение дроби зависит от данных букв букв.
Дробь называют правильным , когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «целых три пятых», а записывается — 2 3 \ 5.
| Основные свойства дробей |
|---|
|
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4 + 5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти.Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражение справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — те, которые совпадают с множеством решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a 0. |
Приходите решать увлекательные задачки по математике в детскую школу Skysmart. Поможем разобраться в сложной теме, подтянем оценки и покажем, что математика может быть захватывающим приключением.
Запишите ребенка на бесплатный вводный урок: познакомим с форматом, выявим пробелы и наметим индивидуальную программу обучения.
Ты можешь записаться на онлайн-уроки по математике для учеников 1-11 классов!
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными . В них всегда есть хотя бы одна дробь с показателем в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные.Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это универсальное уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
| Универсальный алгоритм |
|---|
|
А теперь еще несколько способов, которые пригодятся ребенку на уроках математики.
1. Метод пропорций
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: прекрасное качество равно произведению средних . Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части отображается сумма, которую нужно упростить так, чтобы осталась одна дробь.
Как решаем:
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждого из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
| Что еще важно при решении |
|---|
|
А вот и полезные видео для закрепления материала:
Примеры решения дробных соотношений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1 / x + 2 = 5.
Как решаем:
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
1 + 2x = 5х
- Решим обычное уравнение.
5x — 2х = 1
3x = 1
х = 1/3
Ответ: х = 1/3.
Пример 2. Найти корень уравнения
Как решаем:
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2 (х + 2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
- Переведем новый множитель в числитель ..
- Сократим левую часть на (х + 2), а правую на 2.

4 = х + 2
х = 4 — 2 = 2
Ответ: х = 2.
Пример 3. Решить дробное уравнение:
Как решаем:
- Найти общий знаменатель:
3 (х-3) (х + 3)
- Умножим обе части уравнения на общий знаменатель.Сократим. Получилось:
3 (x + 3) (x + 3) +3 (x-3) (x-3) = 10 (x-3) (x + 3) + 3 * 36
- Выполним возможные преобразования. Получилось квадратное уравнение:
х 2 -9 = 0
- Решим полученное квадратное уравнение:
х 2 = 9
- Получили два преступника корня:
x 1 = −3, x 2 = 3
х = 4 — 2 = 2
- Если x = −3, то знаменатель равенство нулю:
3 (х-3) (х + 3) = 0
Если x = 3 — знаменатель тоже равенство нулю.
- Вывод: числа −3 и 3 не являются коренными уравнениями, значит у данного уравнения нет решения.
Ответ: нет решения.
Если нужно решить уравнение с дробями быстро — поможет онлайн-калькулятор дробей. Воспользуйтесь им, если уже разобрались с темой и щелкаете задач легко и без помощников:
Воспользуйтесь им, если уже разобрались с темой и щелкаете задач легко и без помощников:
Рациональные уравнения (ЕГЭ — 2021)
А вот еще одно уравнение \ (\ displaystyle \ frac {5} {x + 1} + \ frac {4 {x} -6} {(x + 1) \ cdot (x +3)} = 3 \). Это уравнение целое? НЕТ !!! Тут есть деление на переменную \ (\ displaystyle x \), а это говорит о том, что уравнение не целое.Тогда какое же оно? Это дробно рациональное уравнение.
Дробно-рациональное уравнение — рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.
На первый взгляд особой разницы не видно, ну давай попробуем решать его как мы решали целое (линейное) уравнение.
Для начала найдем наименьший общий знаменатель, это будет \ (\ displaystyle (x + 1) \ cdot (x + 3) \).
Важный момент!
В приведенном примере, где было целое уравнение мы не стали член \ (\ displaystyle 13 \) приводить к знаменателю, т. к. умножали все на числа без числа, но тут-то наименьший общий знаменатель \ (\ displaystyle (x + 1) \ cdot (x + 3) \).
к. умножали все на числа без числа, но тут-то наименьший общий знаменатель \ (\ displaystyle (x + 1) \ cdot (x + 3) \).
А это тебе не шутки, переменная в знаменателе!
Решая дробно-рациональное уравнение, обе его части умножаем на наименьший общий знаменатель!
Это надеюсь, ты запомнишь, но давай посмотрим что вышло:
\ (\ displaystyle \ frac {5 (x + 1) \ cdot (x + 3)} {x + 1} + \ frac {(4 { x} -6) \ cdot (x + 1) \ cdot (x + 3)} {(x + 1) \ cdot (x + 3)} = 3 \ cdot (x + 1) \ cdot (x + 3) \).{2}} + 3x = 0. \ End {array} \)
Ну как, это уже попроще выглядит, чем в начале было?
Выносим за скобку общий множитель: \ (\ displaystyle 3x \ cdot (x + 1) = 0 \)
У этого уравнения два решения, его левая сторона принимает нулевое значение при \ (\ displaystyle x = 0 \) и \ (\ Displaystyle х = -1 \).
Вроде бы все, ну ладно давайте напоследок подставим корни \ (\ displaystyle x = 0 \) и \ (\ displaystyle x = -1 \) в исходное уравнение, чтобы проверить, нет ли ошибок. Сначала подставим \ (\ displaystyle 0 \), получается \ (\ displaystyle 3 = 3 \) –нет претензий?
Сначала подставим \ (\ displaystyle 0 \), получается \ (\ displaystyle 3 = 3 \) –нет претензий?
С ним все нормально.А теперь \ (\ displaystyle -1 \), и тут же видим в знаменателе первого члена \ (\ displaystyle -1 + 1 \)!
Но ведь это же будет ноль!
На ноль делить нельзя, это все знают, в чем же дело ???
Дело в ОДЗ! (если забыл что это, повтори тему «ОДЗ»!) Области Допустимых Значений.
Всякий раз, когда ты видишь уравнение, где есть переменные (\ (\ displaystyle x, y \) и т.д.) в знаменателе, прежде всего, нужно найти ОДЗ, найти какие значения может принимать икс, хотя удобнее в ОДЗ написать , чему икс НЕ может быть равен, ведь таких значений не так много, как правило.
Просто запомни, что на ноль делить нельзя ! И перед тем как решать наше уравнение нам следовало сделать так:
ОДЗ: \ (\ displaystyle x + 1 \ ne 0 \) и \ (\ displaystyle x + 3 \ ne 0 \) \ (\ displaystyle \ Rightarrow x \ ne -1 \) и \ (\ Displaystyle х \ ne -3 \).
Если бы мы так написали, то заранее бы знали, что эти ответы стоит исключить и так, из полученных нами ответов \ (\ displaystyle x = 0 \) и \ (\ displaystyle x = -1 \) мы смело исключаем \ ( \ Displaystyle х = -1 \), т.к. он противоречит ОДЗ.
Значит, какой ответ будет у решенного уравнения?
В ответ стоит написать только один корень, \ (\ displaystyle x = 0 \).
Стоит заметить, что ОДЗ не всегда сказывается на ответе , возможны случаи, когда корни, которые мы получили, не попадают под ограничения ОДЗ.
Но писать ОДЗ в дробно рациональных уравнениях стоит всегда — так просто спокойнее, что ты ничего не упустил и да,
ВСЕГДА по окончании решения сверяй свои корни и область допустимых значений!
Как решать дробные уравнения? | О математике понятно
Итак, друзья, продолжаем осваивать решение типов алгебраических уравнений.Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями .
Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями .
Иногда их называют более научно и солидно — дробные рациональные уравнения . Или дробно-рациональные уравнения. Это суть не меняет.)
Дробные уравнения — незаменимая вещь во многих других темах математики. Особенно — в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:
1.Дроби и действия с дробями и дробными выражениями.
2. Тождественные преобразования формул.
3. Решение линейных и квадратных уравнений.
Без этих трёх китов браться за решение дробных соотношений слишком уж самонадеянно, я бы сказал. Почему? Да потому, что непонимание, как, скажем, работать с дробями (сокращать, приводить к общему знаменателю и т.д.) автоматически будет приводить к полному провалу и в дробных уравнениях. Намёк понятен?)
, у кого проблемы хотя бы по одной из вышеперечисленных тем — настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.
Итак, вперёд!
Что такое дробное уравнение? Примеры.
Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби . Обязательно. Причём (важно!) Не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.
Например, вот такое уравнение:
Или такое:
Или вот такое:
И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относится. Либо это линейные уравнения, либо квадратные.
Например:
Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей — четвёрка и пятёрка. Т.е. просто числа . И ни один из знаменателей не содержит иксов.
Или такое уравнение:
Это обычное квадратное уравнение, несмотря на двойку в знаменателе.Опять же, по причине, что двойка — не икс, и деления на неизвестное в дроби нету.
В общем, вы поняли.
Как решать дробные уравнения? Убираем дроби!
Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?
Первым делом надо избавиться от дробей! Это ключевой шаг в решении любого дробного уравнения, который должен быть освоен идеально.Ибо после того, как все дроби исчезли , уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы уже с вами знаем, что делать.)
Но… Как же нам избавиться от дробей ?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?
Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится намного проще и приятнее. )
)
Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:
Первое, что приходит на ум — перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае — при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.
В уравнении нам надо умножить обе части на такое выражение, которое нам позволит сократить все знаменатели.И какое же это выражение?
Давайте его конструировать.) Смотрим ещё раз на уравнение:
Понятно, что в левой части для обозначения знаменателя необходимо умножение на (х + 3) , а в правой — на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)
Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х + 3) , так и на тройку. Причём очень важно — только с помощью умножения! И какое же это выражение? Очевидно, это 3 (х + 3) . То есть, по сути, общий знаменатель дробей.
Причём очень важно — только с помощью умножения! И какое же это выражение? Очевидно, это 3 (х + 3) . То есть, по сути, общий знаменатель дробей.
Итак, для устранения всех дробей уравнение надо умножать на выражение 3 (х + 3) .
Умножаем:
Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:
Прошу обратить внимание: скобки (х + 3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква .Ибо наша основная на данный момент задача — дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок ?!
А вот теперь мы видим, что в левой части сокращается целиком (х + 3) , а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:
Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:
После сокращения получилось безобидное линейное уравнение:
2 ∙ 3 = х + 3
А его (надеюсь) уже решит каждый:
х = 3
Решаем следующий примерчик:
И опять избавляемся от того, что нам не нравится.В данном примере это дробь 20 / х. Одна единственная. Для ее устранения надо часть надо домножить на знаменатель. То есть, просто на х . Но тогда и левую часть тоже надо домножить на х : так уж второе тождественное преобразование требует.
Вот и домножаем! Всю левую часть и всю правую часть:
Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части наши уравнения мы умножаем на «х».
Вперёд!
А вот теперь — снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 — х) я взял в скобки! Почему? Потому что мы умножаем на икс всю левую часть целиком , а не отдельные её кусочки!
Дело всё в том, что частенько после умножения народ записывает левую часть вот так:
Это категорически неверно. Дальше можно уже не решать, да…)
Дальше можно уже не решать, да…)
Но у нас всё хорошо, будем дорешивать.
С чистой совестью сокращаем икс справа и уравнение уже безо всяких дробей, в одну строчку.
(9 — х) ∙ х = 20
Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:
9х — х 2 = 20
Переносим всё влево и приводим к стандартному виду:
Получили классическое квадратное уравнение.Но минус перед квадратом икса — нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнением на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:
Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:
х 1 = 4
х 2 = 5
И все дела.)
Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь — квадратным.
А бывает и так, что после сокращения дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3 = 3. Это означает, что икс может быть любым . Какой икс ни возьми — всё равно всё посокращается и останется железное равенство 3 = 3.
Или наоборот, может получиться какая-нибудь белиберда, типа 3 = 4.А это будет означать, что корней нет. Какой икс ни возьми — всё сократится и останется бред…
Надеюсь, такие сюрпризы вас уже нисколько не удивят.) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они всем видам принадлежностей. И дробные — не исключение.)
Разумеется, при попытке уничтожения дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.
Раскладываем на множители!
Решаем третье уравнение по списку:
А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить
На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить
x ( x 2 +2 x ) ( x +2)
и домножить на эту конструкцию всё уравнение.Математика не возражает.) Но… Может быть, есть выражение попроще?
Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители . Привет седьмому классу!)
А попробуем-ка разложить на множители каждого из знаменателей? Ну, с х и х + 2 точно ничего не сделать, а вот х 2 + 2х вполне себе раскладывается! Выносим один икс за скобку и получаем:
х 2 + 2х = х (х + 2)
Отлично.Вставим наше разложение в исходное уравнение:
Вот теперь всё и прояснилось. ) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х (х + 2). Это выражение короче и прекрасно делится на каждого из знаменателей: и на x , и на (х + 2), и само на себя — на х (х + 2).
) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х (х + 2). Это выражение короче и прекрасно делится на каждого из знаменателей: и на x , и на (х + 2), и само на себя — на х (х + 2).
Вот на х (х + 2) и умножаем:
И снова расписываю подробно, дабы не запутаться.В левой части я буду использовать скобки: там сумма дробей . В правой части скобки не нужны: там одна дробь. Вот и пишем:
А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х (х + 2) . Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем — вторую. Ну, а в правой части, по правилам умножения дробей, просто умножаем числитель:
Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х — 3) в числителе первой дроби — думаю, уже не стоит объяснять?)
С удовольствием сокращаем все дроби:
( x -3) ( x +2) + 3 = x
Раскрываем оставшиеся скобки, приводим и собираем всё слева:
x 2 + 2 x — 3 x — 6 + 3 — х = 0
x 2 — 2 x — 3 = 0
И снова получили квадратное уравнение. ) Решаем и получаем два корня:
) Решаем и получаем два корня:
x 1 = -1
x 2 = 3
Вот и всё. Это и есть ответ.)
Из этого примера можно сделать важный вывод:
Если знаменатели дробей можно разложить на простые множители — обязательно делаем это! Пригодится при снятии дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!
Как вы видите, всё просто и просто логично.Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это — дроби . И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.)
Ну что, порешаем?)
Решить уравнения:
Ответы (как обычно, вразброс):
x = 3
x 1 = 0,5; x 2 = 3
x = 2
х = 6
x = 2,6
x 1 = 2; x 2 = 5
Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)
Всё решилось? Что ж, здорово! Значит, полпути в решении дробных мы с вами уже преодолели. Эта первая часть пути — избавление от дробей. Осталась вторая. Не менее важная!
Эта первая часть пути — избавление от дробей. Осталась вторая. Не менее важная!
Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение дробных действий этого урока вовсе не гарантирует успех в решении всех примеров этой темы. Даже очень простых, подобных этим. К сожалению…
Но об этом — дальше.)
Алгоритм решения дробного рационального уравнения: определение и понятие, примеры.
Понятие дробного рационального уравнения
Если одна из частей уравнения или обе его части — используются рациональные дроби, такое уравнение дробным рациональным уравнением .2} +2 $$
Алгоритм решения дробного рационального уравнения
Шаг 1. Привести по отдельной левую и правую части уравнения к их общим знаменателям.
Шаг 2. Используя свойство пропорции
$$ \ frac {a} {b} = \ frac {c} {d} \ iff {\ left \ {\ begin {array} {c} ad = bc \\ b \ neq 0 \\ d \ neq 0 \ end {array} \ right.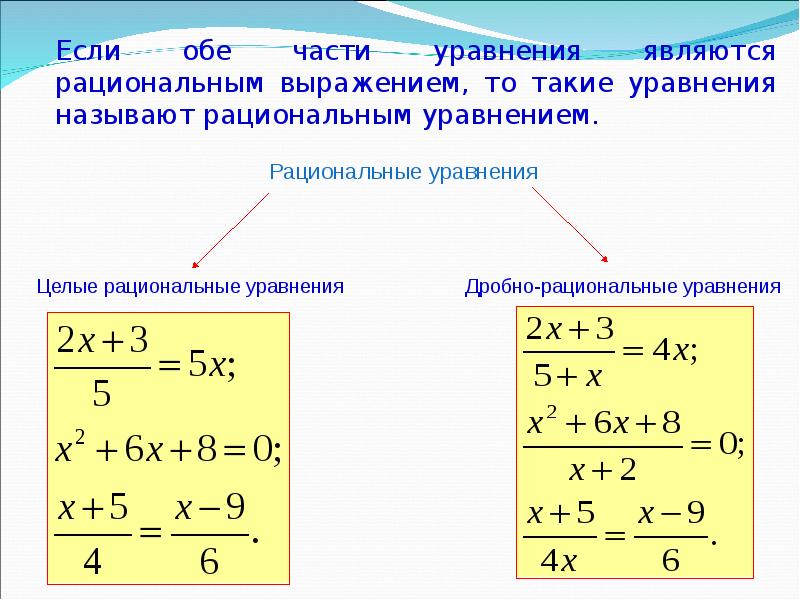 2} $
2} $
Шаг 1.2 = \ frac {144} {49} \ Rightarrow x = \ pm \ sqrt {\ frac {144} {49}} \ Rightarrow x_ {1,2} = \ pm 1 \ frac {5} {7} $
Шаг 4. Полученные корни входят в ОДЗ (не превращают знаменатели в 0).
Шаг 5. Ответ: $ x_ {1,2} = \ pm 1 \ frac {5} {7} $
Примеры
Пример 1. Решите уравнения:
$ а) \ frac {x + 1} {x-4} = \ frac {x + 5} {x-3} + 1 $
$$ \ frac {x + 1} {x-4} = \ frac {x + 5 + (x-3)} {x-3} \ Rightarrow \ frac {x + 1} {x-4} = \ гидроразрыв {2x + 2} {x-3} \ Rightarrow {\ left \ {\ begin {array} {c} (x + 1) (x-3) = (2x + 2) (x-4) \\ x \ neq 3, x \ neq 4 \ end {array} \ right.2-x-6 = 0 \ Rightarrow (x-3) (x + 2) = 0 \ Rightarrow \ left [\ begin {array} {cc} x_1 = -2 \\ x_2 = 3 \ end {array} \ right .
$Корень (-2) не подходит. Остаётся x = 3.
Ответ: 3
Пример 2. При каком x
а) сумма дробей $ \ frac {12} {x + 1} $ и $ \ frac {x + 5} {x-3} $ равна их произведению?
$$ \ frac {12} {x + 1} + \ frac {x + 5} {x-3} = \ frac {12} {x + 1} \ cdot \ frac {x + 5} {x-3 } $$
$$ \ frac {12 (x-3) + (x + 1) (x + 5)} {(x + 1) (x-3)} = \ frac {12 (x + 5)} {(x +1) (x-3)} $$
$$ {\ left \ {\ begin {array} {c} 12x-36 + x ^ 2 + 6x + 5 = 12x + 60 \\ x \ neq -1, x \ neq 3 \ end {array} \ right . 2 \\ x \ neq 0, x \ neq 5 \ end {array} \ right.2-4 \ cdot 7 \ cdot (-141) = 1225 + 3948 = 5173 $$
2 \\ x \ neq 0, x \ neq 5 \ end {array} \ right.2-4 \ cdot 7 \ cdot (-141) = 1225 + 3948 = 5173 $$
$$ x = \ frac {32 \ pm \ sqrt {5173}} {14} $$
Все три корня $ x_1 = 1, x_ {2,3} = \ frac {32 \ pm \ sqrt {5173}} {14} $ подходят.
Ответ: $ \ {1; \ frac {32 \ pm \ sqrt {5173}} {14} \}
долларов СШАРешение задач по математике
Каталог примеров
- Категория: PHP
- Категория: Алгебраические преобразования, уравнения, неравенства
- Как упростить выражение с дробями на тестах по математике
- Решение дробно-рационального уравнения высшей степени замены методом
- Решение неравенств онлайн, пример с высшими степенями
- Решение неравенства с многочленами высших степеней.
- Решение системы неравенств
- Решение уравнения с двумя компонентами
- Решение уравнения с двумя элементами функции
- Решение уравнения с двумя элементами.

- Упростить выражение, примеры. Упростить выражение с дробными функциями
- Упростить выражение наиболее оптимальным способом
- Решение системы неравенств с тремя неравенствами, содержащими квадратичную и кубическую функции
- Возведение одночленов в степень
- Деление простейших рациональных дробей со знаменателями-одночленами степеней.
- Докажите, что при любых значениях истинны неравенства
- Иррациональные уравнения примеры.
- Использование формулы разности кубов при упрощении выражений
- Исследование функций онлайн 4 степени
- Исследование функций онлайн с квадратичной функцией в числителе и знаменателе
- Исследование функций онлайн, квадратичной функции в числителе и знаменателе.
- Исследование функций второй степени и построения ее графика
- Исследовать функцию второй степени и построить ее график
- И исследуем функцию в числителе и линейной в знаменателе
- Исследовать функцию второй степени и построить ее график которой задаются линейные функции
- Как решить кубические уравнения
- Как решить неравенство с дробями
- Нахождение множества решений неравенства
- Необходимо упростить выражение.

- Необходимо построить график графики функций, заданную вот такую формулой
- Нестандартные способы решения квадратных уравнений. Метод 900 замены
- Построить график функции заданной формулой
- Построить график функции, провести ее полное исследование
- Пример упрощенного выражения
- Пример упрощенного выражения
- Пример упрощения выражения
- Пример решения дробно рациональных уравнений
- Примеры решения биквадратных уравнения
- примеры построения графиков
- Примеры решения системы линейных соотношений.
- Провести полное исследование и построить график функции седьмой степени
- Разложение многочлена на множители
- Разложение многочленов на множители. Применение различных способов
- разложить на множители
- Решаем неравенств, имеющих в левой части дробное выражение с квадратичными функциями
- Решаем неравенство с четвертой степенью интервалов
- Решение иррациональных уравнений с переменной z
- Решение биквадратного уравнения методом замены
- Решение биквадратного уравнение методом замены
- Решение биквадратного уравнения методом замены
- Решение биквадратных уравнений в онлайн
- Решение двойного неравенства онлайн с модулем в числителе и знаменателе
- Решение двойных неравенств на тестах по математике
- решение двойного неравенства в математике
- решение двойного неравенства.
 Решение дробно-рациональных соотношений, сводящихся к квадратным задачам
Решение дробно-рациональных соотношений, сводящихся к квадратным задачам - Решение дробно-рациональных соотношений, сводящихся к квадратным задачам
- Решение дробно-рациональных соотношений. округление с недостатком
- Решение иррациональное уравнение с включением.
- Решение иррациональных правил, установленных кубический корень.
- Решение квадратичного неравенства с модулем
- Решение квадратичного неравенств онлайн с модулем
- Решение квадратного неравенства в числителе и знаменателе
- Решение квадратного уравнения методом замены
- Решение квадратного неравенств онлайн с квадратным трехчленом в числителе и знамен
- Решение квадратных уравнений с модулями
- Решение квадратных уравнений с преобразованием и левой правой части уравнения.
- Решение квадратных алгебраических преобразований.
- Решение линейных неравенств онлайн с модулем в знаменателе
- Решение линейных неравенств с дробными выражениями
- Решение линейных неравенств, модуль
- Решение линейных уравнений с дробями в левой и правой части
- Решение линейных уравнений с дробями в левой и правой частях
- Решение на тестах по математике неравенств онлайн, модуль
- Решение на тестах по математике модуль неравенств и кубическую функцию в правой части
- Решение неравенств с кубическими степенями
- Решение неравенств онлайн с дробями наиболее оптимальным способом
- Решение неравенств высших степеней онлайн.

- Решение неравенств онлайн методом замены числа
- Решение неравенств онлайн на тестах по математике, имеющим очень большую степень
- Решение неравенств онлайн с двумя квадратичными функциями в знаменателе
- Решение неравенств онлайн с квадратичными функциями в знаменателе
- Решение неравенств онлайн со сложными дробно-рациональными дробями
- Решение неравенств онлайн, в числителе и знаменателе квадратного трехчленов
- Решение неравенств онлайн, многочлен четвертой степени в левой части
- неравенств онлайн, модули модуль.
- Решение неравенств онлайн, решение неравенств онлайн, функция неравенств онлайн
- Решение неравенств онлайн, решение неравенств онлайн, решение неравенств онлайн. Дробно-рациональное неравенство
- Решение неравенств онлайн. Применение группировки для решения неравенств
- Решение неравенств онлайн. Решение квадратичных неравенств.
- Решение неравенств с выносом за скобки многочлена
- Решение неравенств с квадратичной функцией под модулем.

- Решение неравенств с квадратичной функцией в числителе и знаменателе
- Решение неравенств с квадратичной функцией в числителе и знаменателе.
- Решение неравенств с линейной функцией в правой части
- Решение неравенств с линейными и квадратичными функциями в знаменателе
- Решение неравенств с линейными функциями в модулях
- Решение неравенств с многочленом пятой степени
- Решение неравенств с модулем в модулем.
- Решение неравенств с модулем. Квадратичная функция в модуле.
- Решение неравенств с применением разности кубов
- Решение неравенств с применением формулы сокращенного умножения
- Решение неравенств с применением формулы разности квадратов
- Решение неравенств с применением формулы разности квадратов
- Решение неравенств с применением формул сокращенного умножения
- Решение неравенств устанавливает параметр
- Решение неравенств третьей степени онлайн методом замены
- Решение неравенств четвертой степени заменой
- Решение неравенств, нулевой куб суммы
- Решение неравенств третьей степени в левой части
- Решение неравенств 3 степени
- Решение неравенства онлайн с квадратичной функцией под модулем в левой части и линейной под модулем в правой части
- Решение неравенства онлайн с модулем и квадратичной функции в левой части
- Решение неравенства в левой части сведения онлайн.
 Пример, в котором нужно решить систему
Пример, в котором нужно решить систему - Решение неравенства с 4 квадратичными функциями под модулем
- Решение неравенства с двумя модулями
- Решение неравенства с квадратичной функцией под модулем.
- Решение неравенства с модулем
- Решение неравенства с модулем
- Решение неравенства с модулем в знаменателе
- Решение неравенства с модулем квадратичной функциии в знаменателе
- Решение неравенства с модулем и дробями
- Решение неравенства с одинаковой квадратичной функцией
- Решение неравенства Решение нескольких линейных уравнений с параметром и модулем
- Решение нескольких линейных соотношений с параметром и модулем
- Решение показательных уравнений онлайн с использованием свойств степеней с рациональным показателем и характеристической функцией
- показательных функций онлайн.
- Решение показательных уравнений с линейными функциями в степенях
- Решение примеров с помощью алгоритмов линейных неравенств
- Решение примеров с упрощением радикалов на тестах по математике
- Решение логических уравнений, сводящихся к квадратным
- Решение систем квадратных неравенств
- Решение системных линейных неравенств
- Решение систем линейных соотношений второй степени выражения неизвестной
- Решение систем линейных соотношений с двойными неравенствами
- Решение систем линейных соотношений с дробными коэффициентами
- Решение системных неравенств
- Решение систем неравенств на тестах по математике
- Решение систем неравенств онлайн на тестах по математике
- Решение систем неравенств онлайн с квадратичными функциями
- Решение систем неравенств с квадратичными функциями
- Решающее значение переменных квад систем » Решение систем неравенств c линейными функциями в каждом неравенстве
- Решение систем неравенств c линейными функциями в каждом неравенстве
- Решение систем неравенств с линейными функциями в каждом неравенстве
- Решение систем неравенств c линейными функциями онлайн
- Решение системы неравенств онлайн с квадратичными функциями
- Решение системы неравенств, содержащее куб неравентсво
- Решение сложного дробно-рационального уравнения
- Решение сложного неравенства с формул сокращен Много умножения
- Решение дробно-рациональных неравенств
- Решение квадратного уравнения онлайн
- решение сложных неравенств
- Решение уравнения высших степеней с дробями
- Решение уравнения методом замены размера
- Решение уравнения онлайн с большим числом многочленов
- Решение уравнения Решение уравнения третьей степени с дробной частью
- Решение уравнения третьей степени с дробной частью
- Решение уравнения, которое определяет квадратичные функции
- Решение уравнения с модулем и параметром
- сводящихся к квадратным
- Решение уравнений, сводящихся к квадратным свойствам сокращенного умножения.

- Решение уравнения с заменой числа
- Решение неравенств методом подбора
- Решение неравенства задач на свойства степеней
- Решение неравенства методом интервалов, применив при этом методе группировки слагаемых.
- Решить биквадратное уравнение.
- Решить дробно-рациональное кубическое уравнение наиболее оптимальным способом.
- Решить Дробно-рациональное неравенство онлайн
- Решить дробно-рациональное уравнение высшей степени с дробями.
- Решить квадратное уравнение наиболее оптимальным способом.
- Решить неравенство наиболее оптимальным методом
- Решить неравенство наиболее оптимальным методом
- Решить неравенство наиболее оптимальным методом
- Решить неравенство наиболее оптимальным методом
- Решить неравенство онлайн с многочленом третьей степени
- Решить неравенство онлайн, содержащее многочленов
- Решить неравенство онлайн, содержащее высшие степени
- Решить неравенство онлайн, содержащее высшие степени
- Решить неравенство онлайн, содержащее дробно-рациональные выражения
- Решить неравенство онлайн, содержащееся модуль.

- Решить неравенство онлайн, содержащее произведение многочленов высших степеней.
- Решить неравенство онлайн, содержащее многочленов
- Решить неравенство онлайн, содержащее количество дробно-рациональных функций
- Решить неравенство онлайн. Квадратичная функция.
- Решить неравенство онлайн. Неравенство высших степеней.
- Решить неравенство онлайн. Дробно-рациональные функции
- Решить неравенство оптимальным методом
- Решить неравенство, содержащее дробно-рациональную функцию интервалов
- Решить неравенство, содержащее дробно-рациональную функцию
- Решить неравенство, содержащее дробно-рациональные выражения в и и правой части
- Решить неравенство, содержащее произведение кубической и квадратной функций.
- Решить неравенство, содержащее произведение многочленов.
- Решить неравенство, содержащее количество произведений многочленов
- Решить неравенствую высшую степень методом интервалов
- Решить неравенств наиболее оптимальным способом.

- Решить систему неравенств с модулями
- Решить систему неравенств, существую неравенств второй степени
- Решить систему неравенств.
- Решить систему неравенств.
- Решить систему уравнений с тремя неизвестными методами выражения неизвестной величины
- Решить систему уравнений, выразив x, y, z через u и v.
- Решить уравнение высшей степени
- Решить уравнение высшей степени, используя метод замены числа
- Решить уравнение онлайн, используя замену
- Решить уравнение онлайн, содержащее в левой и правой части дробно-рациональные выражения с квадратичными числами.
- Решить уравнение онлайн, содержащее выражение под модулем в левой и правой части уравнения
- Решить уравнение четвертой степени, используя группировку и выполнение общего множителя
- Тождественное преобразование рациональных выражений с использованием формулы разницы квадратов
- Тождественное преобразование рациональных выражений
- Упросить выразить оптимальным способом
- Упростить выражение примеры
- Упростить выражение примеры.
 Сложение и вычитание рациональных дробей с одинаковыми дробями
Сложение и вычитание рациональных дробей с одинаковыми дробями - Упростить выражение примеры. Упрощение дробно-рациональных выражений.
- Упростить выражение с дробями.
- Упростить выражение с помощью преобразований
- Упростить выражение типичные примеры тестов по математике
- Упростить выражение, содержащее дробные выражения
- Упрощение выражения с радикалами
- Упрощение выражения на тестах по математике доказательство с использованием тождественных преобразований.
- Упрощение выражений на тестах по математике. Сложение и вычитание дробей с разными знаменателями. Простейшие примеры
- Упрощение выражений при умножении рациональных дробей
- Упрощение выражений с корнями
- Упрощение выражений с кубическими корнями
- Упрощение выражений с многоэтажными корнями
- Упрощение выражений с помощью разности квадратов
- Упрощение выражений с помощью формул квадрата.
- Упрощение выражений с помощью формулы разности квадратов
- Упрощение выражений выражений с помощью умножения формулы
- Упрощение выражения формулы разложения квадратного трехчлена на множители
- Упрощение выражений с формулой формулы кубов и куб разности
- Упрощение выражений с формулами радикалов.

- Упрощение выражений с тремя действиями
- Упрощение выражений, возведение рационального выражения в степень.
- Упрощение выражений, сложение рациональных выражений в знаменателе
- Упрощение выражений, деление дроблений многочленов
- Упрощение выражений, эффективность деления рациональных дробей
- Упрощение выражений, степень сглаживания рациональных показателей
- Упрощение выражений, умножение выражений, умножение выражений с квадратичными выражениями.
- Упрощение выражения, содержащего операции деления
- Категория: Другое
- Категория: Логарифмические, показательные уравнения, неравенства
- Категория: Начала анализа
- Задача нахождение числа касательных.
- Исследование и построение графика функции четвертой степени
- Исследование функции онлайн, неограниченной пятой степени в числителе и седьмой в знаменателе.

- Исследование функций с многочленом четвертой степени в знаменателе
- Исследование дробно-дробной функции и построения ее графика
- Исследование онлайн-функций и построение ее графика
- Исследование онлайн-функций с кубом в знаменателе
- Исследование рациональной функции и построение ее графика
- Исследование функций десятой степени
- Исследование функций онлайн с числителем шестой степени
- Исследование функций пятой степени
- Исследование функций пятой степени
- Исследование функций с числителем шестой степени в числителе и знаменателе
- Исследование функции с многочленом шестой степени в числителе
- Исследование функции с числителем пятой степени
- Исследовать график дробно-линейной функции и правильно построить график
- Исследовать функцию 4 степени и построить график
- Исследовать функцию высших степеней и построить ее график
- Исследовать функцию и построить ее график
- Исследовать функцию и построить ее график онлайн.

- Исследуем функцию, заданную многочленом четвертой степени в числителе
- Изуем функцию, в которой в знаменателе произведения функций
- Исследуем функцию, заданную многочленом четвертой степени Построение графика функции с кубом в числителе и знаменателе
- Построение графика дробно-линейной функции
- Построение графика кубической функции
- Построение графика с квадратичными функциями в числителе и знаменателе знаменателе
- Построение графика с кубической функцией в числителе и линейной в знаменателе
- Построение графика с функцией шестой степени в числителе
- Построение графика с полным исследованием
- Постро Построение графика функций в знаменателе
- Построение графика функций с многочленом пятой степени в знаменателе
- Построение графика функций, в знаменателе которого многочлен пятой степени
- Построение графиков на тестах по математике
- Построение графиков функций онлайн.
 Нахождение производной в точке
Нахождение производной в точке - Построить график функции и провести ее полное исследование. Функция дробно-рациональная
- Построить график дробно-линейной функции и провести ее полное исследование.
- Построить график квадратичной функции методом полного исследования
- Построить график кубической функции
- Построить график кубической функции, провести ее полное исследование
- Построить график функции дробной функции, выполнить функцию четвертой степени в знаменателе, проведя полное исследование.
- Построить график функции и провести ее полное исследование
- Построить график функции онлайн, заданной следующей формулой
- Построить график функции пятой степени
- Построить график функции, часть дроби.
- Построить и исследовать график функции, заданной такой формулой.
- Провести исследование функции и построить ее
- Провести исследование функции и построить ее график.
- Провести полное исследование функции.
 После этой исследования построить ее график.
После этой исследования построить ее график. - Производная дроби примеры
- Укажите график нечетной функции
Каждый год выпускники стараются успешно завершить обучение и успешно сдать Поступить в высшие учебные заведения и стать студентами.
Многие ищут решение задач по математике, чтобы к этому подготовиться.
В данный момент аттестация проводится в форме внешнего независимого
оценивания (ЗНО). Результат тестов по математике засчитывается как балл государственной итоговой
аттестации (ДПА). Выпускникам, которые прошли ЕГЭ по математике, алгебре, геометрии выдается сертификат
с его результатов, в соответствии с которым вносится соответствующая запись в дополнение к аттестату.Чтобы набрать количество баллов недостаточно овладеть школьным опытом —
необходимы углубленные знания, практика в решении задач, умение правильно и подробно изложить на бумаге
решение задачи, сопровождая его необходимыми схемами, рисунками, формулами.
Выпускникам, которые прошли ЕГЭ по математике, алгебре, геометрии выдается сертификат
с его результатов, в соответствии с которым вносится соответствующая запись в дополнение к аттестату.Чтобы набрать количество баллов недостаточно овладеть школьным опытом —
необходимы углубленные знания, практика в решении задач, умение правильно и подробно изложить на бумаге
решение задачи, сопровождая его необходимыми схемами, рисунками, формулами.
Этот сайт с решениями задач по математике поможет в комплексной подготовке абитуриента к независимому внешнему тестированию по математике.Он решит с вами задачи, которые предлагают решения школьникам и абитуриентам при поступлении в высшие учебные заведения.
Разбор задач, урокият вам успешно сдать непростые экзамены и легко
овладеть такими науками, как алгебра и геометрия. Вы научитесь выполнять алгебраические преобразования,
сможете упростить любое выражение, изучите алгебраические формулы.Вы успешно освоите решение уравнений,
систем неравенств, систем неравенств (квадратные, иррациональные, показательные,
логарифмические, тригонометрические).
Вы научитесь выполнять алгебраические преобразования,
сможете упростить любое выражение, изучите алгебраические формулы.Вы успешно освоите решение уравнений,
систем неравенств, систем неравенств (квадратные, иррациональные, показательные,
логарифмические, тригонометрические).
Сложности в решение задач на составложление уравнений? На сайте представлены решения задач с полным описанием. Геометрия дается сложнее, чем алгебра? На сайте представлены решения задач из разделов планиметрия и стереометрия, разобраны примеры решения нахождение неизвестных геометрических элементов, площадей фигур, методики доказательств утверждений.
Сайт- хороший помощник при подготовке домашних заданий и подготовке к тестам
Сайт нужен для получения информации лучшего усвоения большего количества,
более глубоких знаний, а также навыков приобретения по полученным знаниям. Специалиста можно найти, обратившись в специальные агентства, поместив объявление в средствах массовой информации
информации.Однако, попав на этот сайт, вы уже нашли то, что искали. У автора — большой опыт подготовки
к ЗНО по математике, ДПА по математике, ЗНО по физике, ДПА по физике. Вы можете посмотреть отзывы на
нашу страницу. Все мои ученики успешно сдавали ЗНО с результатом от 180 баллов, а результат
ДПА всегда был не ниже 9. Поэтому вы можете быть уверены в результативности занятий.
Специалиста можно найти, обратившись в специальные агентства, поместив объявление в средствах массовой информации
информации.Однако, попав на этот сайт, вы уже нашли то, что искали. У автора — большой опыт подготовки
к ЗНО по математике, ДПА по математике, ЗНО по физике, ДПА по физике. Вы можете посмотреть отзывы на
нашу страницу. Все мои ученики успешно сдавали ЗНО с результатом от 180 баллов, а результат
ДПА всегда был не ниже 9. Поэтому вы можете быть уверены в результативности занятий.
Уравнения 5, 6, 7 класса с дробями.Решение
Переменная:Уравнение:
Другие полезные темы:
| Делимся | знаниями |
Если думаешь, что Это интересно для друга, напиши
2021. 01.18 15:44:22 Имя: полич
01.18 15:44:22 Имя: полич
———————————————— ————
Комментарий:
нечем не помогло
========================================
2021.01.18 15:44:21 Имя: полич
———————————————— ————
Комментарий:
нечем не помогло
========================================
2020.12.28 13:12:21 Имя: Надя
———————————————— ————
Комментарий:
Нечего не понятно не калькулятор а говно
========================================
2020.12.28 07:34:19 Имя: Дэнчин
———————————————— ————
Комментарий:
Говно полное
========================================
2020. 12.23 14:32:48 Имя: Соня
12.23 14:32:48 Имя: Соня
———————————————— ————
Комментарий:
ничего не понятно
========================================
2020.12.22 05:51:46 Имя: Елизавета
———————————————— ————
Комментарий:
Нахрена не поняла
========================================
2020.12.21 09:22:45 Имя: валя
———————————————— ————
Комментарий:
уравнения
========================================
2020.12.21 09:22:43 Имя: валя
———————————————— ————
Комментарий:
уравнения
========================================
2020.12.21 09:22:42 Имя: валя
———————————————— ————
Комментарий:
уравнения
========================================
2020. 12.21 09:22:40 Имя: валя
12.21 09:22:40 Имя: валя
———————————————— ————
Комментарий:
уравнения
========================================
2020.12.21 09:22:38 Имя: валя
———————————————— ————
Комментарий:
уравнения
========================================
2020.12.15 08:04:20 Имя: Люда
———————————————— ————
Комментарий:
Помогите решить
========================================
2020.12.11 15:34:17 Имя: М @ ди
———————————————— ————
Комментарий:
Капец просто.С этим калькулятором не работать нужно а в игры играть. 🤮🤢
========================================
2020. 11.29 14:28:52 Имя: Настя
11.29 14:28:52 Имя: Настя
———————————————— ————
Комментарий:
Говно а не помощь
========================================
2020.11.23 16:51:07 Имя: Жыпара
———————————————— ————
Комментарий:
x²-86x + 113
========================================
2020.11.23 16:51:07 Имя: Жыпара
———————————————— ————
Комментарий:
x²-86x + 113
========================================
2020.11.23 16:51:05 Имя: Жыпара
———————————————— ————
Комментарий:
x²-86x + 113
========================================
2020.11. 23 16:51:05 Имя: Жыпара
23 16:51:05 Имя: Жыпара
———————————————— ————
Комментарий:
x²-86x + 113
========================================
2020.11.23 16:51:04 Имя: Жыпара
———————————————— ————
Комментарий:
x²-86x + 113
========================================
2020.11.23 16:51:04 Имя: Жыпара
———————————————— ————
Комментарий:
x²-86x + 113
========================================
2020.11.23 16:51:02 Имя: Жыпара
———————————————— ————
Комментарий:
x²-86x + 113
========================================
2020.11.23 16:51:01 Имя: Жыпара
———————————————— ————
Комментарий:
x²-86x + 113
========================================
2020.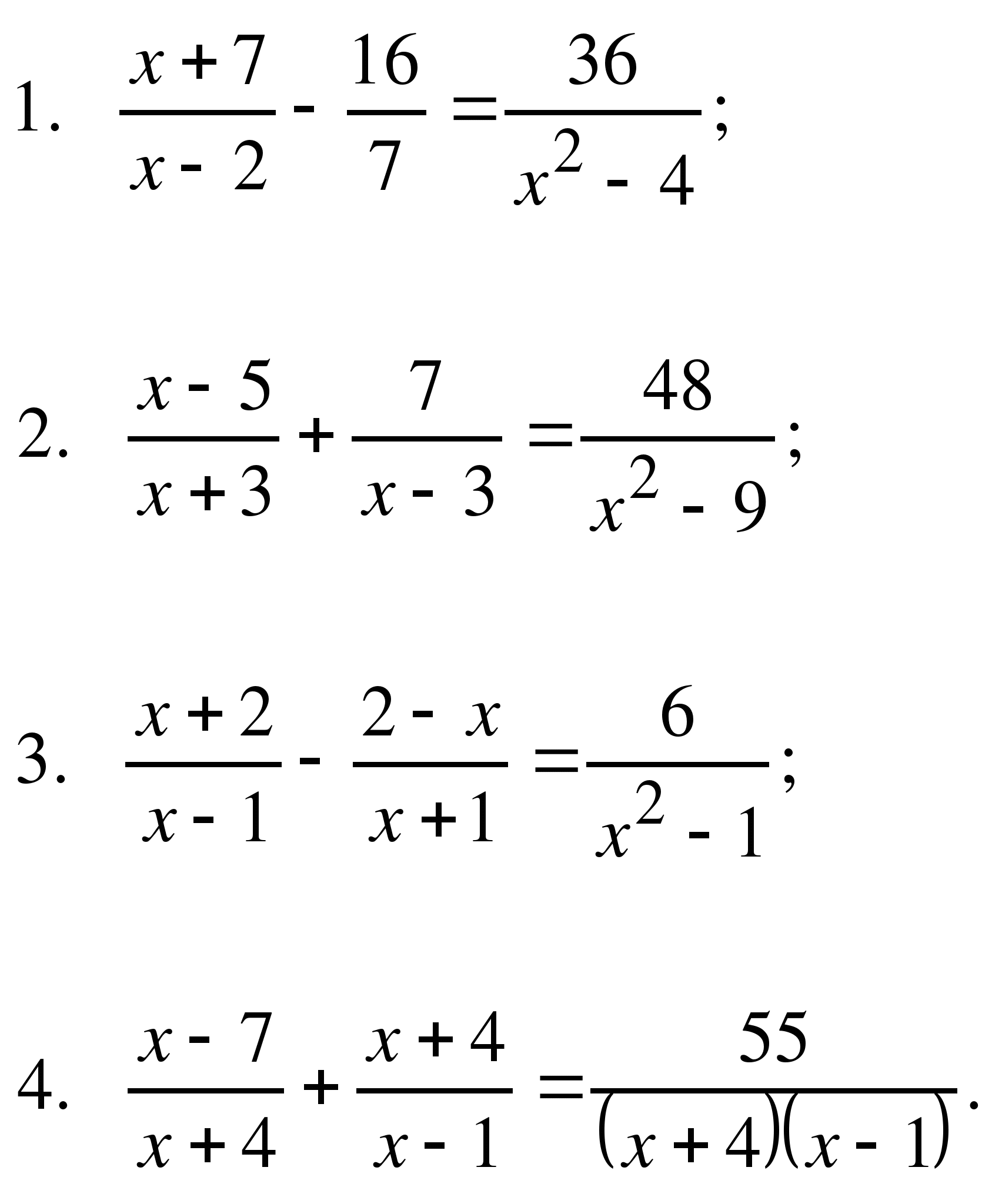 11.09 11:07:06 Имя: Дарья
11.09 11:07:06 Имя: Дарья
———————————————— ————
Комментарий:
Ну и чё? Нехрена не понятно!
========================================
2020.10.26 07:15:32 Имя: Барижат
———————————————— ———
Комментарий:
Налеюсь что правильно
========================================
Дробно рациональное уравнение приведя. Решение дробно-рациональных уравнений. Как решаются дробно-рациональные уравнения
Дробным уравнением называется уравнение, в котором хотя бы одно из слагаемых — дробь, в знаменателе присутствует неизвестное.Например, дробным уравнением является уравнение.
Решать дробные уравнения удобно в следующем порядке:
- найти общий знаменатель дробей, входящего в уравнение, если каждая дробь имеет смысл,
- заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
- решить получившееся целое уравнение,
- исключить из его корней те, которые обращают в нуль общий знаменатель.

Пример 1. Решить дробное уравнение:
Решение.Воспользуемся основным свойством дроби с представим левую и правую части этого уравнения в виде дробей с одинаковым знаменателем:
.
Эти дроби равны при тех и только тех значениях, при которых они равны их числители, знаменатель отличен от нуля. Если знаменатель равенство нулю, то дроби, а Следовательно, и уравнение не имеет смысла.
Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение
Упростив уравнение (раскрыв скобки и приведя членов), получим квадратное уравнение
.
При решение квадратного уравнения получаем его корни:
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, введенный в данное дробное уравнение. Общий знаменатель —
Заменим исходное уравнение целым. Для этого умножим обе его части на
общий знаменатель.Получим:
Для этого умножим обе его части на
общий знаменатель.Получим:
Выполним необходимые преобразования в полученном уравнении и придём к квадратному уравнению
Решенив квадратное уравнение , получаем его корни:
Если х = -3 , то найденный на первом шаге знаменатель обращается в нуль:
,
то же самое, если x = 3 .
Следовательно, числа -3 и 3 не являются коренными исходными уравнениями, а, поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, введенного в данное уравнение. Для этого знаменатели дробей разложим на множители:
.
Общий знаменатель — выражение
Заменим исходное уравнение целым, умножив его части на общий знаменатель. Получим:
Выполнив преобразование, придём к квадратному уравнению
.
Решенив квадратное уравнение , получаем его корни:
.
Ни один из корней не обращает общий знаменатель в нуль. Следовательно, числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:
.
Решение. Введём новую переменную, обозначив. Получим уравнение с переменной г .
§ 1 Целое и дробное рациональные уравнение
В этом уроке разберем такие понятия, как рациональное уравнение, рациональное выражение, целое выражение, дробное выражение.Рассмотрим решение рациональных уравнений.
Рациональным уравнением уравнение, в котором левая и правая части используются рациональными выражениями.
Рациональные выражения бывают:
Дробные.
Целое выражение составлено из чисел, чисел, целых степеней с помощью действий сложения, вычитания, умножения, а также деления на число, отличное от нуля.
Например:
В дробных выражениях есть деление на переменную или выражение с образцом.Например:
Дробное выражение не при всех значениях смысл в нем имеет. Например, выражение
Например, выражение
при х = -9 не имеет смысла, так как при х = -9 знаменатель обращается в нуль.
Значит, рациональное уравнение может быть целым и дробным.
Целое рациональное уравнение — это рациональное уравнение, в левая и правая части — целые выражения.
Например:
Дробное рациональное уравнение — это рациональное уравнение, в или левая, или правая части — дробные выражения.
Например:
§ 2 Решение целого рационального уравнения
Рассмотрим решение целого рационального уравнения.
Например:
Умножим обе части уравнения на наименьший общий знаменатель знаменателей входящего в него дробей.
Для этого:
1. найдем общий знаменатель для знаменателей 2, 3, 6. Он равен 6;
2. найдем дополнительный множитель для каждой дроби. Для этого общего знаменатель 6 делим на каждый знаменатель
дополнительный множитель для дроби
дополнительный множитель для дроби
3. умножим числители дробей на соответствующие им дополнительные множители. Таким образом, получим уравнение
умножим числители дробей на соответствующие им дополнительные множители. Таким образом, получим уравнение
которое равносильно данному уравнению
Слева раскроем скобки, правую часть перенесем налево, изменив знак слагаемого при переносе на противоположный.
Приведем подобных членов многочлена и получим
Видим, что уравнение линейное.
Решив его, найдем, что х = 0,5.
§ 3 Решение дробного рационального уравнения
Рассмотрим решение дробного рационального уравнения.
Например:
1.Умножим обе части уравнения на наименьший общий знаменатель знаменателей в его рациональных дробей.
Найдем общий знаменатель для знаменателей х + 7 и х — 1.
Он равен их произведению (х + 7) (х — 1).
2.Найдем дополнительный множитель для каждой рациональной дроби.
Для этого общего знаменатель (х + 7) (х — 1) делим на каждый знаменатель. Дополнительный множитель для дроби
равен х — 1,
дополнительный множитель для дроби
равенство х + 7.
3.Умножим числители дробей на соответствующие им дополнительные множители.
Получим уравнение (2х — 1) (х — 1) = (3х + 4) (х + 7), которое равносильно данному уравнению
4.Слева и справа умножим двучлен на двучлен и получим уравнение
5.Правую часть перенесенного налево, изменив знак каждого слагаемого при переносе на противоположный:
6.Приведем подобных членов многочлена:
7.Можно обе части разделить на -1.Получим квадратное уравнение:
8.Решив его, найдем корни
Так как в уравнении
левая и правая части — дробные выражения, а в дробных выражениях при некоторых значениях число знаменатель может обратиться в нуль, то необходимо проверить, не обращается ли в нуль при найденных х1 и х2 общий знаменатель.
При х = -27 общий знаменатель (х + 7) (х — 1) не обращается в нуль, при х = -1 общий знаменатель также не равен нулю.
Следовательно, оба корня -27 и -1 являются коренными уравнениями.
При решении дробного рационального уравнения лучше указать сразу область допустимых значений. Исключить те значения, при которых общий знаменатель обращается в нуль.
Рассмотрим еще один пример решения дробного рационального уравнения.
Например, решим уравнение
Знаменатель дроби правой части уравнения разложим на множители
Получим уравнение
Найдем общий знаменатель для знаменателей (х — 5), х, х (х — 5).
Им будет выражение х (х — 5).
теперь найдем область допустимых значений уравнения
Для этого общего знаменателя приравняем к нулю х (х — 5) = 0.
Получим уравнение, решающее которое, найдем, что при х = 0 или при х = 5 общий знаменатель обращается в нуль.
Значит, х = 0 или х = 5 не могут быть корнями нашего уравнения.
Теперь можно найти дополнительные множители.
Дополнительным множителем для рациональной дроби
дополнительным множителем для дроби
будет (х — 5),
и дополнительный множитель дроби
Числители умножим на соответствующие дополнительные множители.
Получим уравнение х (х — 3) + 1 (х — 5) = 1 (х + 5).
Раскроем скобки слева и справа, х2 — 3х + х — 5 = х + 5.
Перенесем слагаемые справа налево, изменив знак переносимых слагаемых:
Х2 — 3х + х — 5 — х — 5 = 0
И после приведения подобных членов получим квадратное уравнение х2 — 3х — 10 = 0. Решив его, найдем корни х1 = -2; х2 = 5.
Но мы уже выложили, что при х = 5 общий знаменатель х (х — 5) обращается в нуль. Следовательно, корнем нашего уравнения
будет х = -2.
§ 4 Краткие итоги урока
Важно запомнить:
При решении дробных действий надо поступить образом:
1.Найти общий знаменатель дробей входного в уравнение. При этом если знаменатели дробей можно разложить на множителей, то разложить их на множители и затем найти общий знаменатель.
2.Умножить две части уравнения на общий знаменатель: дополнительные множители, умножить числители на дополнительные множители.
3.Решить получившееся целое уравнение.
4.Исключить из его корней те, которые обращают в нуль общий знаменатель.
Список использованной литературы:
- Макарычев Ю.Н., Н. Г. Миндюк, Нешков К.И., Суворова С.Б. / Под редакцией Теляковского С.А. Алгебра: учебн. для 8 кл. общеобразоват. учреждений. — М .: Просвещение, 2013. .
- Мордкович А.Г. Алгебра. 8 кл .: В двух частях. Ч.1: Учеб. для общеобразоват. учреждений. — М .: Мнемозина.
- Рурукин А.Н. Поурочные разработки по алгебре: 8 класс.- М .: ВАКО, 2010.
- Алгебра 8 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворовой Авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. -Волгоград: Учитель, 2005.
«Рациональные уравнения с многочленами» — одна из самых часто встречающихся тем в тестовых заданиях ЕГЭ по математике. По этой причине их повторению стоит обратить особое внимание. Многие ученики сталкиваются с проблемой нахождения дискриминанта, имеют показатели из правой части в левую и приведения уравнения к общему знаменателю, из-за чего выполнение подобных заданий трудности трудности.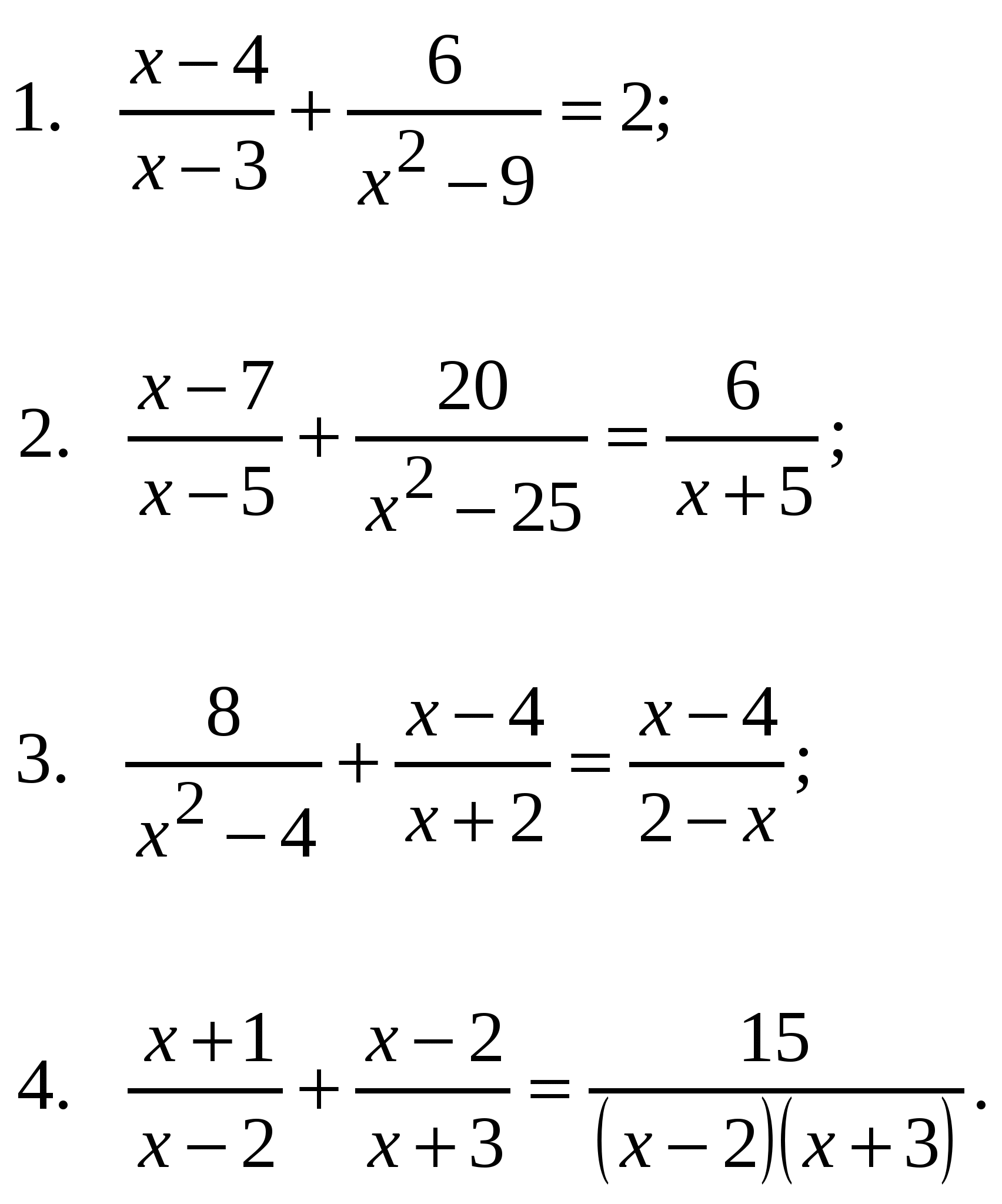 Решение задач при подготовке к ЕГЭ на нашем сайте поможет вам быстро справиться с задачами любой сложности и сдать тестирование на отлично.
Решение задач при подготовке к ЕГЭ на нашем сайте поможет вам быстро справиться с задачами любой сложности и сдать тестирование на отлично.
Выбирайте образовательный портал «Школково» для успешной подготовки к единому экзамену по математике!
Чтобы знать правила вычисления неизвестных и легко получать правильные результаты, воспользуйтесь возможностью нашим онлайн-сервисом. Портал «Школково» — это единственная в своем роде площадка, где собраны необходимые для подготовки к ЕГЭ материалы.Наши преподаватели систематизировали и изложили в понятной форме все математические правила. Кроме того, мы предлагаем школьникам использовать методы в решении типовых уравнений, которые постоянно обновляются и дополняются.
Для более результативной подготовки к тестированию рекомендуем следовать нашему особому методу и начать с повторения правил и решений более простых задач. Таким образом, выпускник включает для себя самые трудные темы и сделать акцент на их изучении.
Начните подготовку к итоговому тестированию со «Школково» уже сегодня, и результат не заставит себя ждать! Выберите самый легкий пример из предложенных. Если вы быстро справились с выражением, переходите к более сложной задаче. Так вы сможете получить свои знания до решения заданий ЕГЭ по математике профильного уровня.
Если вы быстро справились с выражением, переходите к более сложной задаче. Так вы сможете получить свои знания до решения заданий ЕГЭ по математике профильного уровня.
Обучение доступно не только выпускникам из Москвы, но и школьникам из других городов. Уделяйте пару часов в день занятиям на нашем портале, например, и совсем скоро вы сможете справиться с уравнениями любой сложности!
Мы уже научились решать квадратные уравнения.Теперь распространим изученные методы на рациональные уравнения.
Что такое рациональное выражение? Мы уже сталкивались с этим понятием. Рациональными выражениями называются выражения, составленные из чисел, число, их степеней и знаков математических действий.
Соответственно, рациональными уравнениями называются уравнения вида:, где — рациональные выражения.
Раньше мы рассмотрели только рациональные уравнения, которые сводятся к линейным.Теперь рассмотрим и рациональные уравнения, которые сводятся и к квадратным.
Пример 1
Решить уравнение:.
Решение:
Дробь равна 0 тогда и только тогда, когда ее числитель равен 0, а знаменатель не равен 0.
Получаем следующую систему:
Первое уравнение системы — это квадратное уравнение. Прежде чем его решать, поделим все его коэффициенты на 3.Получим:
Получаем два корня:; .
Мне 2 никогда не равно 0, то необходимо, чтобы выполнялись два условия:. Ни один из предложенных выше корней уравнения не совпадает с недопустимыми значениями переменных, которые получились при решении второго неравенства.
Ответ: .
Итак, давайте сформулируем возможные решения рациональных соотношений:
1.Перенести все слагаемые в левую часть, чтобы в правой части получился 0.
2. Преобразовать и упростить левую часть, привести все дроби к общему знаменателю.
3. Полученную дробь приравнять к 0, по следующему алгоритму:.
4. Записать те корни, которые получились в первом уравнении и удовлетворяют второму неравенству, в ответ.
Давайте рассмотрим еще один пример.
Пример 2
Решить уравнение:.
Решение
В самом начале перенесем все слагаемые в левую сторону, чтобы справа остались 0.Получаем:
Теперь приведем левую часть уравнения к общему знаменателю:
Данное уравнение эквивалентно системе:
.Первое уравнение системы — это квадратное уравнение.
Коэффициенты данного уравнения:. Вычисляем дискриминант:
Получаем два корня:; .
Теперь решим второе неравенство: тогда произведение множителей не равно 0 и только тогда, когда ни один из множителей не равен 0.
Необходимо, чтобы выполнялись два условия:. Получаем, что из двух корней первого уравнения подходит только один — 3.
Ответ: .
На этом уроке мы вспомнили, что такое рациональное выражение, а также научились решать рациональные уравнения, которые сводятся к квадратным уравнениям.
На следующем уроке мы рассмотрим рациональные уравнения как модели реальных действий, а также рассмотрим задачи на движение.
Список литературы
- Башмаков М.И. Алгебра, 8 класс. — М .: Просвещение, 2004. .
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра, 8. 5-е изд. — М .: Просвещение, 2010. .
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра, 8 класс. Учебник для общеобразовательных учреждений. — М .: Просвещение, 2006. .
- Фестиваль педагогических идей «Открытый урок» ().
- School.xvatit.com ().
- Rudocs.exdat.com ().
Домашнее задание
Сегодня мы разберемся, как решать дробные рациональные уравнения.
Посмотрим: из формулы
(1) 2х + 5 = 3 (8 — х),
(3)
(4)
дробными рациональными уравнениями являются только (2) и (4), а (1) и (3) это целые уравнения.
Предлагаю решить уравнение (4), а затем включить правило.
уравнение дробное, то надо найти общий знаменатель. В этом уравнении это выражение 6 (х — 12) (х — 6). Затем мы умножаем обе части уравнения на общий знаменатель:
После получения целое уравнение:
6 (х — 6) 2-6 (х — 12) 2 = 5 (х — 12) (х — 6).
Решив это уравнение надо обязательно проверить не обращают ли полученные корни в нуль знаменатели дробей в исходном уравнении.
Раскрываем скобки:
6х 2 — 72х + 216 — 6х 2 + 144х — 864 = 5х 2 — 90х + 360, упрощаем уравнение: 5х 2 — 162х + 1008 = 0.
Находим корни уравнения
D = 6084, √D = 78,
х 1 = (162 — 78) / 10 = 84/10 = 8,4 и х 2 = (162 + 78) / 10 = 240/10 = 24
При х = 8,4 и 24 общий знаменатель 6 (х — 12) (х — 6) ≠ 0, значит эти числа являются корнями уравнений (4).
Ответ: 8,4; 24.
Решив предложенное уравнение, приходим к следующему положениям :
1) Находим общий знаменатель.
2) Умножаем обе части уравнения на общий знаменатель.
3) Решаем полученное целое уравнение.
4) Проверяем, какие из корней обращают общий знаменатель в нуль и исключаем их решения.
Посмотрим теперь на примере, как работают полученные положения.
Решить уравнение:
1) Общий знаменатель: х 2 — 1
2) Умножаем обе части уравнения на общий знаменатель, получаем целое уравнение: 6 — 2 (х + 1) = 2 (х 2 — 1) — (х + 4) (х — 1)
3) Решаем уравнение: 6 — 2х — 2 = 2х 2 — 2 — х 2 — 4х + х + 4
х 2 — х — 2 = 0
х 1 = — 1 и х 2 = 2
4) При х = -1, общий знаменатель х 2 — 1 = 0. Число -1 корнем не является.
При х = 2, общий знаменатель х 2 — 1 ≠ 0.Число 2 — корень уравнения.
Ответ : 2.
Как видите, наши положения работают. Не бойтесь, у вас все получится! Самое главное правильно найдите общий знаменатель и аккуратно провести преобразование .
 Знаменатели при этом пропадут.
Знаменатели при этом пропадут. Как решать уравнения с дробями
Как решать уравнения с дробями

 Решение дробно-рациональных уравнений. Как решаются дробно-рациональные уравнения
Решение дробно-рациональных уравнений. Как решаются дробно-рациональные уравнения
 Например, (x + y) / (x — y). Значение дроби зависит от данных букв букв.
Например, (x + y) / (x — y). Значение дроби зависит от данных букв букв.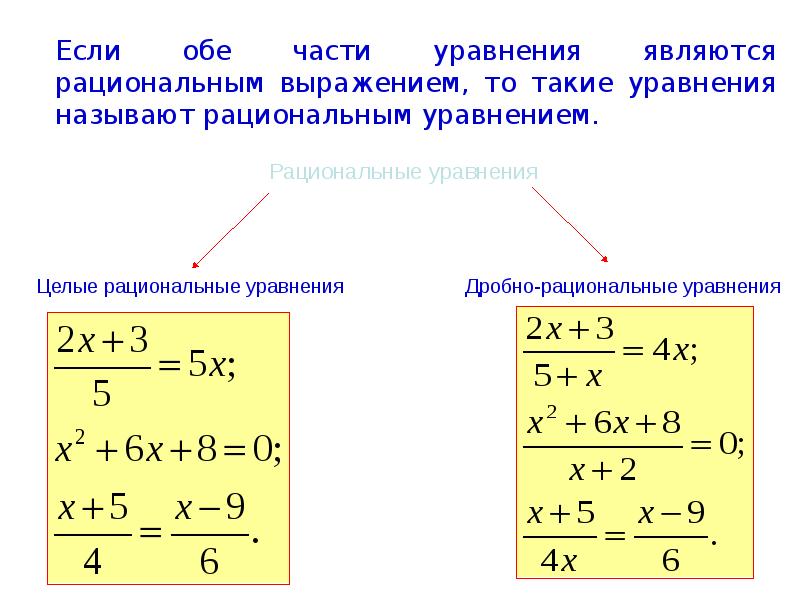



 Решение дробно-рациональных соотношений, сводящихся к квадратным задачам
Решение дробно-рациональных соотношений, сводящихся к квадратным задачам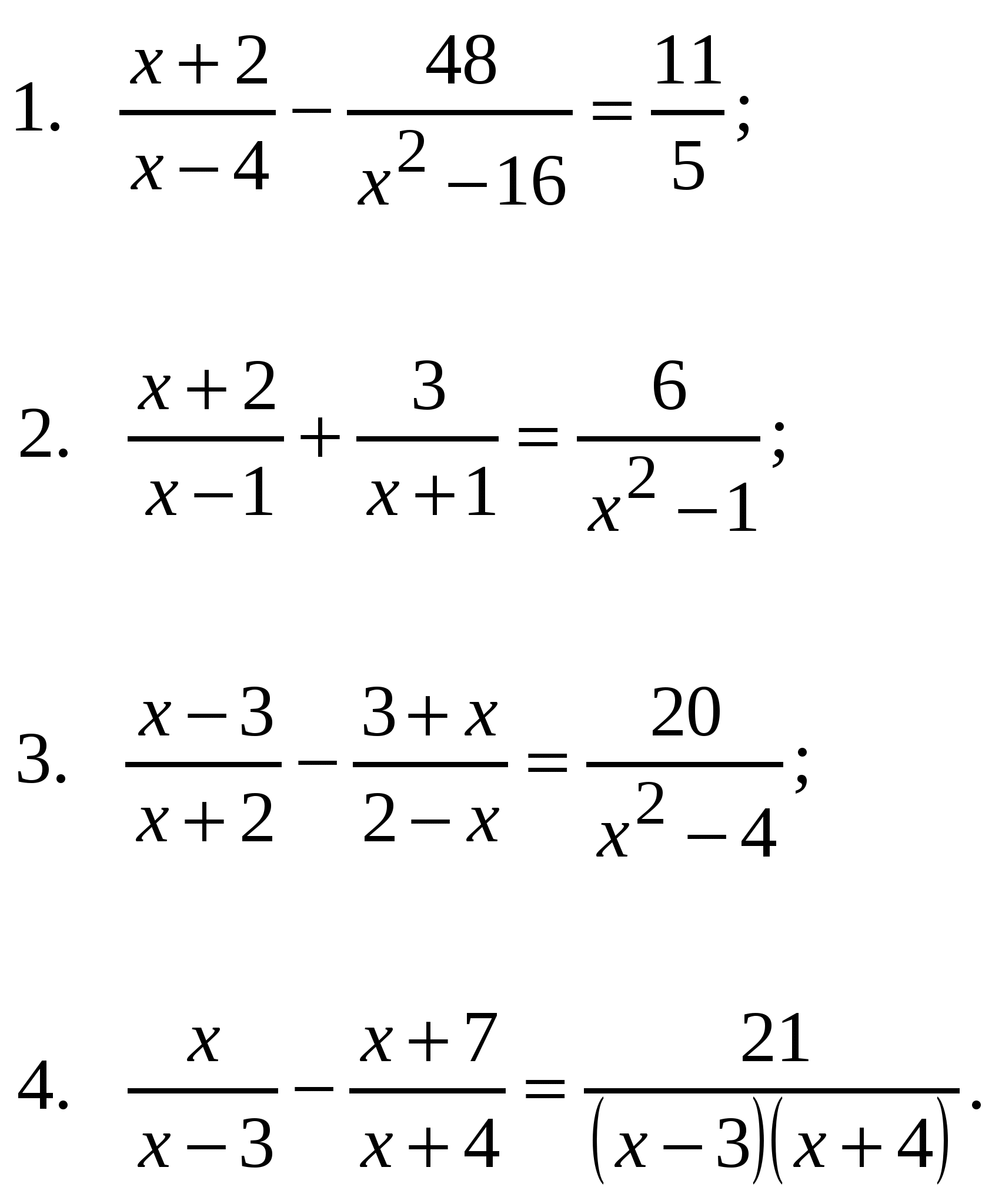

 Пример, в котором нужно решить систему
Пример, в котором нужно решить систему


 Сложение и вычитание рациональных дробей с одинаковыми дробями
Сложение и вычитание рациональных дробей с одинаковыми дробями


 Нахождение производной в точке
Нахождение производной в точке После этой исследования построить ее график.
После этой исследования построить ее график.