Что такое функция общего вида. График четной и нечетной функций
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Доказать, что у = х 4 — четная функция.
Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как : пусть x 1a ;b , а x 2a ;b .
Зависимость переменной y от переменно x, при которой каждому значению х соответствует единственное значение y называется функцией. Для обозначения используют запись y=f(x). У каждой функции существует ряд основных свойств, таких как монотонность, четность, периодичность и другие.
Рассмотри подробнее свойство четности.
Функция y=f(x) называется четной, если она удовлетворяет следующим двум условиям:
2. 3 симметрична относительно начала координат.
3 симметрична относительно начала координат.
Функция — общий вид — Большая Энциклопедия Нефти и Газа, статья, страница 1
Функция — общий вид
Cтраница 1
Функция общего вида, непериодическая. [1]
Для функций общего вида комбинация метода Коши или метода координатного спуска с методами сопряженных направлений приводит к эффективным алгоритмам, так как получающиеся при этом смешанные алгоритмы используют квадратичную аппроксимацию оптимизируемой функции, избегая вместе с тем трудоемких вычислений вторых частных производных. [2]
Элементы с функциями общего вида (2.10) были помимо однородного материала успешно использованы и для решения задач о трещине, вершина которой расположена на границе раздела двух материалов с различными упругими свойствами. Аналогичные функции перемещений могут быть построены и для более сложных элементов, имеющих большее число узлов. [4]
[4]В такой интерпретации функция общего вида принимает вид функции порядковой полезности что не исключает возможности присвоения полезностям товарных наборов числовых значений. [5]
Фурье, способного аппроксимировать функции весьма общего вида. [6]
Для алгоритмов безусловной оптимизации функций общего вида построено довольно много тестовых задач, но даже в этом случае возникают некоторые из трудностей, описанных выше. Например, рассматриваются в основном задачи очень малой размерности; кроме того, не ясно, какие свойства алгоритмов проявляются на выбранных тестовых функциях. [7]
Функция у а является функцией общего вида. [8]
Функция у х ж2 является функцией общего вида. [9]
[9]
Функция у ахг Ьх с есть функция общего вида. Если Ь 0 то у ахг с есть четная функция. [10]
Это не означает, что для функций общего вида порядок сходимости равен 2, хотя так и может случиться. [11]
Рассмотрим числовые примеры на определение ошибок функций общего вида
по заданным ошибкам аргументов. [12]Функция у ах b, b О есть функция общего вида, т.е. не является четной, нечетной. [13]
Функция не является четной и не является нечетной, это функция общего вида. [14]
Функция не является четной, не является нечетной, Это функция общего вида. [15]
Страницы: 1 2 3
Четность-нечетность функции.
 {2}-3, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x. Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией, когда f(-x)=f(x) для любого x из области определения. Такая функция будет симметрична относительно оси Oy.
Функция является нечетной функцией, когда f(-x)=-f(x) для любого x из области определения. {7} является нечетной.
{7} является нечетной.
Периодическая функция
Функция y=f(x), в области определения которой для любого x выполняется равенство f(x+T)=f(x-T)=f(x), называется периодической функцией с периодом T \neq 0.
Повторение графика функции на любом отрезке оси абсцисс, который имеет длину T.
Промежутки, где функция положительная, то есть f(x) > 0 — отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих выше оси абсцисс.
f(x) > 0 на (x_{1}; x_{2}) \cup (x_{3}; +\infty )
Промежутки, где функция отрицательная, то есть f(x) < 0 — отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.
f(x) < 0 на (-\infty; x_{1} ) \cup (x_{2}; x_{3} )
Ограниченность функции
Ограниченной снизу принято называть функцию y=f(x), x \in X тогда, когда существует такое число A, для которого выполняется неравенство f(x) \geq A для любого x \in X.
Пример ограниченной снизу функции: y=\sqrt{1+x^{2}} так как y=\sqrt{1+x^{2}} \geq 1 для любого x. {2}} \neq 1 для любого x \in [-1;1].
{2}} \neq 1 для любого x \in [-1;1].
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0, для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X.
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1.
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) > y(x_{2}).
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) < y(x_{2}).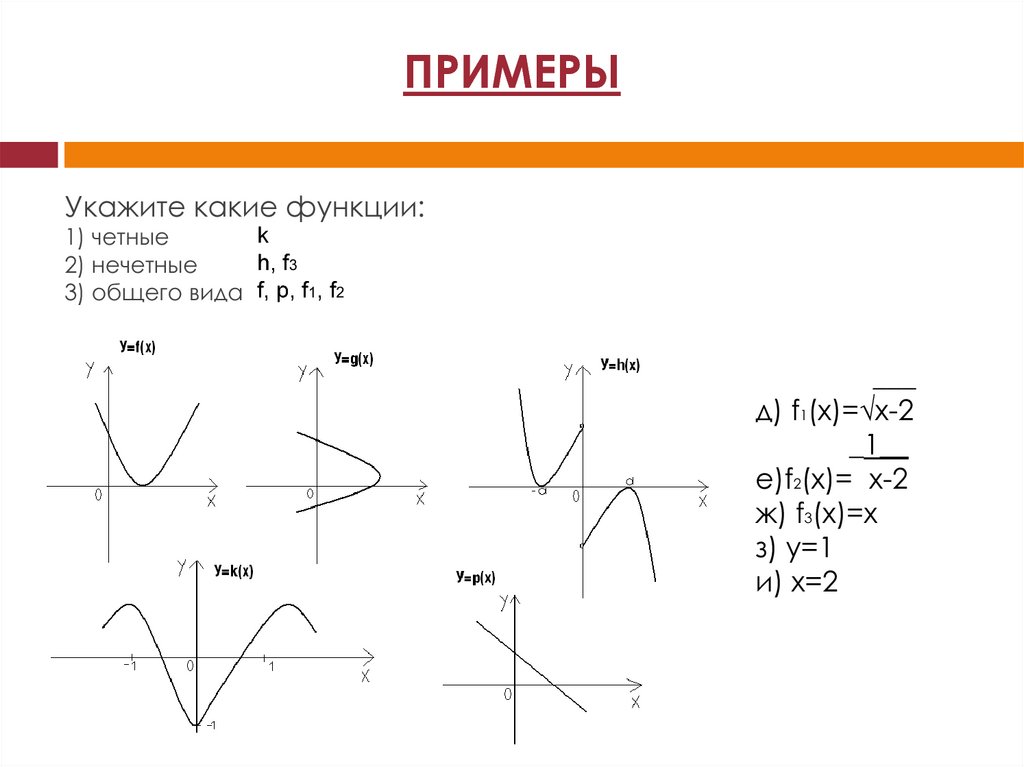
Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0).
а) Если при x > 0 четная функция возрастает, то убывает она при x < 0
б) Когда при x > 0 четная функция убывает, то возрастает она при x < 0
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x < 0
г) Когда нечетная функция будет убывать при x > 0, то она будет убывать и при x < 0
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняться неравенство f(x) > f(x_{0}). y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняется неравенство f(x) < f(x^{0}). y_{max} — обозначение функции в точке max.
y_{max} — обозначение функции в точке max.
Необходимое условие
Согласно теореме Ферма: f'(x)=0 тогда, когда у функции f(x), что дифференцируема в точке x_{0}, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0}.
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f'(x);
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку [a; b];
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции, а большее — наибольшим.
функция общего вида — это… Что такое функция общего вида?
- функция общего вида
- мат.
 general function
general function
Большой англо-русский и русско-английский словарь. 2001.
- функция обслуживания
- функция объема
Смотреть что такое «функция общего вида» в других словарях:
функция — 2.1 функция (function): Реализация в программе алгоритма, по которому пользователь или программа могут частично или полностью выполнять решаемую задачу. Примечания 1 Пользователю нет необходимости вызывать функцию (например, автоматическое… … Словарь-справочник терминов нормативно-технической документации
Функция Грина — используется для решения неоднородных дифференциальных уравнений с граничными условиями (неоднородная краевая задача). Функция Грина это обратный оператор к . Поэтому ее нередко символически обозначают как . Функции Грина полезны в… … Википедия
Функция Дирака — δ функция (или дельта функция, δ функция Дирака, дираковская дельта, Единичная импульсная функция) позволяет записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т.
п.), сосредоточенной или… … Википедия
ОБОБЩЕННАЯ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция удовлетворяющая системе с действительными коэффициентами являющимися функциями действительных переменных хи у В обозначениях исходная система записывается в виде Если коэффициенты Аи Всистемы (1) на всей плоскости Екомплексного… … Математическая энциклопедия
АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция, к рая может быть представлена степенным рядом. Исключит, важность класса А. ф. определяется следующим. Во первых, этот класс достаточно ш и р о к: он охватывает большинство функций, встречающихся в основных вопросах математики и ее… … Математическая энциклопедия
Случайная функция — функция произвольного аргумента t (заданная на множестве Т его значений и сама принимающая или числовые значения или, более общо, значения из какого то векторного пространства) такая, что её значения определяются с помощью некоторого… … Большая советская энциклопедия
ТЕТА-ФУНКЦИЯ — функция, одного комплексного переменного квазидвоякопериодическая целая функция комплексного переменного z, т.
 е. функция имеющая, кроме периода еще квазипериод при прибавлении к poro к значению аргумента значение функции умножается на нек рый… … Математическая энциклопедия
е. функция имеющая, кроме периода еще квазипериод при прибавлении к poro к значению аргумента значение функции умножается на нек рый… … Математическая энциклопедияНечетная функция — f(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
Нечётная функция — f(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
Четная функция — f(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
Чётная функция — f(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
Книги
- Костюм. Стиль, форма, функция, Бруард Кристофер. Что объединяет «молодых старомодников» и конголезских sapeurs, что общего между pijama и баньяном, архитектурой и одеждой? Как связаны парижский щеголь и участники» пятниц без галстуков»?В… Подробнее Купить за 851 руб
- Костюм стиль форма функция, Бруард К.
 . Что объединяет «молодых старомодников» и конголезских sapeurs, что общего между pijama и баньяном, архитектурой и одеждой? Как связаны парижский щеголь и участники» пятниц без галстуков»?В… Подробнее Купить за 491 руб
. Что объединяет «молодых старомодников» и конголезских sapeurs, что общего между pijama и баньяном, архитектурой и одеждой? Как связаны парижский щеголь и участники» пятниц без галстуков»?В… Подробнее Купить за 491 руб - Костюм. Стиль, форма, функция, Бруард Кристофер. Что объединяет`молодых старомодников`и конголезских sapeurs, что общего между pijama и баньяном, архитектурой и одеждой? Как связаны парижский щеголь и участники`пятниц без галстуков`? В этой… Подробнее Купить за 437 грн (только Украина)
Четные и нечетные функции: графики и свойства
Зависимость переменной y от переменно x, при которой каждому значению х соответствует единственное значение y называется функцией. Для обозначения используют запись y=f(x). У каждой функции существует ряд основных свойств, таких как монотонность, четность, периодичность и другие.
Рассмотри подробнее свойство четности.
Четность и нечетность функции
Функция называется четной, если для любого значения х из ее области определения значение – х также принадлежит области определения и верно равенство f( ‑ x)=f(x).
Область определения четной функции симметрична относительно нуля.
График четной функции симметричен относительно оси Оу.
Функция называется нечетной, если для любого значения х из ее области определения значение – х также принадлежит области определения и верно равенство f( ‑ x)= ‑ f(x).
Область определения нечетной функции симметрична относительно нуля.
График нечетной функции симметричен относительно начала координат.
Пример 1. Дан график функции .
Определите по графику четной или нечетной является функция.
Решение. Поскольку график функции симметричен относительно оси Ох, то функция является четной.
Ответ: функция четная
Задание 1. Определите по графику четной или нечетной является функция…
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
Пример 2.
Решение. График нечетной функции симметричен относительно начала координат.
Следовательно, для построения графика нужно отобразить данную часть относительно точки (0; 0):
Задание 2. На рисунке изображена часть графика некоторой функции, область определения которой — промежуток [ ‑ 3; 3]. Постройте график этой функции, если…
1) функция четная
2) функция нечетная
3) функция четная
4) функция нечетная
5) функция четная
6) функция нечетная
7) функция четная
8) функция нечетная
9) функция четная
10) функция нечетная
Пример 3.
Решение. По определению четной функции должно выполняться равенство f( ‑ x)=f(x).
=. Отсюда следует, что функция четная.
Ответ: четная
Задание 3. Определите, является функция четной, нечетной или не является ни четной, ни нечетной…
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
Пример 4.
Решение. Подставим в выражение вместо х значение ‑ х: ==. Отсюда следует, что функция нечетная.
Ответ: нечетная
Задание 4. Определите четность или нечетность функции…
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
Пример 5.
Решение. Поскольку функция f(x) – нечетная, то f( ‑ x)= ‑ f(x).
Т.е. f( ‑ 5)= ‑ f(5)= ‑ 3; f( ‑ 2)= ‑ f(5)=8.
Следовательно, =4( ‑ 3)+8= ‑ 4.
Ответ: ‑ 4
Задание 5. Вычислите…
1) , если f(x) – нечетная функция и f(3)= ‑ 7; f( ‑ 4)=3
2) , если f(x) – четная функция и f(2)=3; f( ‑ 5)=2
3) , если f(x) – четная функция и f(3)= ‑ 7; f( ‑ 4)=5
4) , если f(x) – нечетная функция и f( ‑ 4)=2; f(2)= ‑ 3
5) , если f(x) – нечетная функция и f( ‑ 3)=1; f(2)= ‑ 3
6) , если f(x) – четная функция и f(2)=2; f( ‑ 3)=3
7) , если f(x) – четная функция и f(3)=3; f(5)=2
8) , если f(x) – нечетная функция и f( ‑ 4)=3; f(3)=5
9) , если f(x) – нечетная функция и f( ‑ 3)=3; f(2)= ‑ 3
10) , если f(x) – четная функция и f(‑ 2)=3; f( ‑ 5)=4
Сумма двух четных функций четна, а сумма двух нечетных – нечетна.
Доказательство: f(x)+g(x)=f( ‑ x)+g( ‑ x)=f(x)+g(x).
Произведение двух четных функций является четной функций, произведение двух нечетных функций также является четной функций. Произведение четной и нечетной функции – нечетно.
Доказательство: (fg)( ‑ x)=f( ‑ x)g( ‑ x)=f(x)g(x)=(fg)(x).
Если функция f четна (нечетна), то и функция четна (нечетна).
Доказательство: если функция f четна и f(x)0, то .
Если Х симметрично относительно начала координат, то любая заданная на Х функция f является суммой четной и нечетной функций f=g+h, где , .
Доказательство: , . Отсюда следует, что функция g(x) четна, а функция h(x) нечетна. При этом .
Пример 6. Функции f и g определены на множестве всех действительных чисел. Является ли функция h четной или нечетной, если h(x)=f2(x)g2(x), f – четная функция, g – нечетная?
Решение. Поскольку f – четная функция, g – нечетная, то f2 и g2 – четные функции. Произведение четных функций – функция четная. Следовательно, h(x)=f2(x)g2(x) является четной функцией.
Ответ: четная
Задание 6.
1) h(x)=f(x)g2(x),
f – четная функция, g – нечетная
2) h(x)=f(x)g2(x),
f и g – четные функции
3) h(x)=f(x)+g(x),
f и g – нечетные функции
4) h(x)=f(x)g(x),
f и g – нечетные функции
5) h(x)=f(x)g2(x),
f и g – нечетные функции
6) h(x)=f(x)+g(x),
f и g – четные функции
7) h(x)=f(x)g(x),
f – четная функция, g – нечетная
8) h(x)=f(x)g(x),
f и g – четные функции
9) h(x)=f(x)‑g(x),
f – четная функция, g – нечетная
10) h(x)=f(x)g2(x),
f – нечетная функция, g – четная
Задание 7.
Задание 8. Найдите ось симметрии для графиков функций…
1)
2)
Задание 9. Найдите центр симметрии для графиков функций…
1)
2)
Область определения
функции
– это множество значений аргумента,
для которых существует функция. Пример 6.1.
Найти область определения следующих
функций 1)
,
2),
3). Решение. 1) Функция определена
на всей числовой оси,
,
т.к. нет таких значений аргумента,
для которых не существует значение
функции. 2) функция определена,
если знаменатель дроби не равен нулю,
т.е.
.
Решив квадратное уравнение, найдем. Таким образом,
функция определена для всех значений
,
кромеи. Область определения
данной функции . 3) Функция определена,
если подкоренное выражение
.
Решим это неравенство методом интервалов.
Разложим многочлен на множители .
На числовой оси отметим точки
,
в которых многочлен обращается в нуль
и определим его знак в полученных
интервалах. Таким образом,
. Функция
называется четной (нечетной), если для
любогои выполняется равенство . График четной
функции симметричен относительно оси
. График нечетной
функции симметричен относительно начала
координат. Пример 6.2. Исследовать на четность или нечетность
функции 1)
;
2);
3). Решение. 1) Функция определена
при
.
Найдем. ,
т.е.
.
Значит, данная функция является четной. 2) Функция определена
при ,
т.е.
.
Таким образом, данная функция нечетная. 3) функция определена
для
,
т.е. для ,
.
Поэтому функция не является ни четной,
ни нечетной. Назовем ее функцией общего
вида. Функция
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции. Функции возрастающие
(убывающие) на некотором интервале
называются монотонными. Если функция
дифференцируема на интервалеи имеет положительную (отрицательную)
производную,
то функциявозрастает (убывает) на этом интервале. Пример 6.3.
Найти интервалы монотонности функций 1)
;
3). Решение. 1) Данная функция
определена на всей числовой оси. Найдем
производную
. Производная равна
нулю, если
и.
Область определения – числовая ось,
разбивается точками,на интервалы. Определим знак производной
в каждом интервале. В интервале
производная отрицательна, функция на
этом интервале убывает. В интервале
производная положительна, следовательно,
функция на этом интервале возрастает. 2) Данная функция
определена, если
или . Определяем знак
квадратного трехчлена в каждом интервале. Таким образом,
область определения функции . Найдем производную
,,
если,
т.е.,
но.
Определим знак производной в интервалах. В интервале
производная отрицательна, следовательно,
функция убывает на интервале.
В интервалепроизводная положительна, функция
возрастает на интервале. Точка
называется точкой максимума (минимума)
функции,
если существует такая окрестность точки,
что для всехиз этой окрестности выполняется
неравенство. Точки максимума
и минимума функции называются точками
экстремума. Если функция
в точкеимеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума). Точки, в которых
производная равна нулю или не существует
называются критическими. Концепция функций была разработана в семнадцатом веке, когда Рене Декарт использовал эту идею для моделирования математических отношений в своей книге Геометрия . Термин «функция» был введен Готфридом Вильгельмом Лейбницем через пятьдесят лет после публикации Geometry. Позже Леонард Эйлер формализовал использование функций, когда ввел понятие обозначения функций; у = f (х).Так продолжалось до 1837 года, когда немецкий математик Петер Дирихле дал современное определение функции. В математике функция — это набор входных данных с одним выходом в каждом случае. У каждой функции есть домен и диапазон. Область — это набор независимых значений переменной x для определенного отношения или функции. Проще говоря, домен — это набор значений x, которые генерируют реальные значения y при подстановке в функцию. С другой стороны, диапазон — это набор всех возможных значений, которые может выдать функция. Обозначение можно определить как систему символов или знаков, которые обозначают такие элементы, как фразы, числа, слова и т. Д. Следовательно, обозначение функций — это способ, которым функция может быть представлена с помощью символов и знаков.Нотация функций — это более простой метод описания функции без подробного письменного объяснения. Чаще всего используется обозначение функции f (x), которое читается как «f» или «x». В этом случае буква x, помещенная в круглые скобки, и весь символ f (x) обозначают набор доменов и набор диапазонов соответственно. Хотя f — самая популярная буква, используемая при написании обозначений функций, любая другая буква алфавита также может использоваться как в верхнем, так и в нижнем регистре. Рассмотрим линейную функцию y = 3x + 7. Чтобы записать такую функцию в обозначении функции, мы просто заменяем переменную y фразой f (x), чтобы получить; f (x) = 3x + 7.Эта функция f (x) = 3x + 7 читается как значение f для x или как f для x. В алгебре есть несколько типов функций. К наиболее распространенным типам функций относятся: Линейная функция — это полином первой степени. Линейная функция имеет общий вид f (x) = ax + b, где a и b — числовые значения, а a 0. Полиномиальная функция второй степени известна как квадратичная функция. Общая форма квадратичной функции: f (x) = ax 2 + bx + c, где a, b и c — целые числа и a 0. Это полиномиальная функция от 3 rd градусов, которая имеет форму f (x) = ax 3 + bx 2 + cx + d Логарифмическая функция — это уравнение, в котором переменная отображается как аргумент логарифма. Общая функция функции f (x) = log a (x), где a — основание, а x — аргумент. Экспоненциальная функция — это уравнение, в котором переменная появляется как показатель степени. Экспоненциальная функция представлена как f (x) = a x . f (x) = sin x, f (x) = cos x и т. Д. Являются примерами тригонометрических функций Идентификационная функция такова, что f: A → B и f (x ) = x, ∀ x ∈ A Функция называется рациональной, если R (x) = P (x) / Q (x), где Q (x) ≠ 0. Оценка функции — это процесс определения выходных значений функции. Это делается путем подстановки входных значений в обозначение данной функции. Пример 1 Запишите y = x 2 + 4x + 1, используя обозначение функции, и оцените функцию при x = 3. Решение Учитывая, y = x 2 + 4x + 1 Применяя обозначение функции, получаем f (x) = x 2 + 4x + 1 Оценка: Заменить x на 3 f (3) = 3 2 + 4 × 3 + 1 = 9 + 12 + 1 = 22 Пример 2 Вычислите функцию f (x) = 3 (2x + 1), когда x = 4. Решение Подставьте x = 4 в функцию f (x). f (4) = 3 [2 (4) + 1] f (4) = 3 [8 + 1] f (4) = 3 x 9 f (4) = 27 Пример 3 Запишите функцию y = 2x 2 + 4x — 3 в обозначении функции и найдите f (2a + 3). Решение y = 2x 2 + 4x — 3 ⟹ f (x) = 2x 2 + 4x — 3 Заменить x на (2a + 3). f (2a + 3) = 2 (2a + 3) 2 + 4 (2a + 3) — 3 = 2 (4a 2 + 12a + 9) + 8a + 12 — 3 Пример 4 Представьте y = x 3 — 4x, используя обозначение функции, и решите для y при x = 2. Решение Учитывая функцию y = x 3 — 4x, замените y на f (x), чтобы получить; f (x) = x 3 — 4x Теперь оцените f (x), когда x = 2 ⟹ f (2) = 2 3 — 4 × 2 = 8-8 = 0 Следовательно , значение y при x = 2 равно 0 Пример 5 Найдите f (k + 2) при условии, что f (x) = x² + 3x + 5. Решение Чтобы оценить f (k + 2), замените x на (k + 2) в функции. ⟹ f (k + 2) = (k + 2) ² + 3 (k + 2) + 5 ⟹ k² + 2² + 2k (2) + 3k + 6 + 5 ⟹ k² + 4 + 4k + 3k + 6 + 5 = k² + 7k + 15 Пример 6 Учитывая обозначение функции f (x) = x 2 — x — 4. Найдите значение x, когда f ( x) = 8 Решение f (x) = x 2 — x — 4 Заменить f (x) на 8. 8 = x 2 — x — 4 x 2 — x — 12 = 0 Решите квадратное уравнение путем разложения на множители, чтобы получить; ⟹ (x — 4) (x + 3) = 0 ⟹ x — 4 = 0; x + 3 = 0 Следовательно, значения x при f (x) = 8 равны; х = 4; x = -3 Пример 7 Вычислите функцию g (x) = x 2 + 2 при x = −3 Решение Замените x на -3. г (−3) = (−3) 2 + 2 = 9 + 2 = 11 Обозначения функций можно применять в реальной жизни для оценки математических задач, как показано ниже Примеры: Пример 8 Для производства определенного продукта компания тратит x долларов на сырье и y долларов на рабочую силу. Если себестоимость продукции описывается функцией f (x, y) = 36000 + 40x + 30y + xy / 100.Рассчитайте стоимость производства, если фирма тратит 10 000 и 1 000 долларов на сырье и рабочую силу соответственно. Решение Дано x = 10000 долларов США и y = 1000 долларов США Подставьте значения x и y в функцию производственных затрат ⟹f (10000, 1000) = 36000 + 40 (10000) + 30 (1000) + (10000) (1000) / 100. ⟹ f (10000, 1000) = 36000 + 4000000 + 30000 + 100000 ⟹ 4136000 долларов. Пример 9 Мэри экономит 100 долларов в неделю на предстоящий день рождения. Решение Пусть x = количество недель, а f (x) = общая сумма. Мы можем записать эту проблему в обозначении функции как; f (x) = 100x + 1000 Таким образом, общая сумма составит 3200 долларов. Пример 10 Стоимость разговора в двух мобильных сетях A и B составляет 34 доллара плюс 0.05 / мин и 40 долларов плюс 0,04 / мин соответственно. Решение Следовательно, функция сети A равна f (x) = 0,05x + 34, а функция сети B — f (x) = 0. A ⟹ f (1160) = 0,05 (1160) + 34 = 58 + 34 = 92 доллара США B f (1160) = 0,04 (1160) + 40 = 46,4 + 40 = 86,4 долл. США Следовательно, сеть B является доступной, поскольку ее общая стоимость времени разговора меньше, чем у A. ⟹ 0,05x +34 = 0,04x + 40 ⟹ 0,01x = 6 x = 600 Ежемесячный счет для A и B будет равен, когда среднее количество минут составляет 600. Доказательство: A ⟹ 0,05 (600) +34 = 64 доллара B ⟹ 0,04 (600) + 40 = 64 доллара Пример 11 Определенное число такое, что при его добавлении к 142, результат на 64 раза больше исходного числа. Найдите номер. Решение Пусть x = исходное число, а f (x) будет результатом добавления 142. f (x) = 142 + x = 3x + 64 2x = 78 x = 39 Пример 12 Если произведение двух последовательных положительных целых чисел равно 1122, найдите два целых числа. Решение Пусть x будет первым целым числом; второе целое число = x + 1 Теперь сформируйте функцию как; f (x) = x (x + 1) найти значение x, если f (x) = 1122 Заменить функцию f (x) на 1122 1122 = x (x + 1) 1122 = x 2 + 1 x 2 = 1121 Найдите квадрат обеих сторон функции x = 33 x + 1 = 34 Целые числа 33 и 34. Похоже, вы используете устройство с «узкой» шириной экрана (, т. Теперь нам нужно перейти ко второй теме этой главы.Однако, прежде чем мы это сделаем, нам нужно сделать быстрое определение. Отношение — это набор упорядоченных пар. Это кажется странным определением, но оно нам понадобится для определения функции (что является основной темой этого раздела). Однако, прежде чем мы фактически дадим определение функции, давайте посмотрим, сможем ли мы понять, что такое отношение. Вернитесь к примеру 1 в разделе «Графики» этой главы.2} — 4 \). Вот упорядоченные пары, которые мы использовали. Любые из следующих отношений являются отношениями, потому что они состоят из набора упорядоченных пар. Конечно, есть еще много отношений, которые мы могли бы сформировать из списка упорядоченных пар, приведенного выше, но мы просто хотели перечислить несколько возможных отношений, чтобы привести некоторые примеры. Теперь вы, вероятно, спрашиваете, почему мы заботимся об отношениях, и это хороший вопрос. Некоторые отношения очень специфичны и используются почти на всех уровнях математики. Следующее определение говорит нам, какие отношения являются этими особыми отношениями. Функция — это отношение, для которого каждое значение из набора первых компонентов упорядоченных пар связано ровно с одним значением из набора вторых компонентов упорядоченной пары. Ладно, это полный рот. Посмотрим, сможем ли мы понять, что это значит. Давайте посмотрим на следующий пример, который, надеюсь, поможет нам во всем этом разобраться. Из этих упорядоченных пар мы получаем следующие наборы первых компонентов ( i. Для набора вторых компонентов обратите внимание, что «-3» встречается в двух упорядоченных парах, но мы указали его только один раз. Чтобы понять, почему это отношение является функцией, просто выберите любое значение из набора первых компонентов. Теперь вернитесь к отношению и найдите каждую упорядоченную пару, в которой это число является первым компонентом, и перечислите все вторые компоненты из этих упорядоченных пар.Список вторых компонентов будет состоять ровно из одного значения. Например, давайте выберем 2 из набора первых компонентов. Из отношения мы видим, что существует ровно одна упорядоченная пара с 2 в качестве первого компонента, \ (\ left ({2, — 3} \ right) \). Следовательно, список вторых компонентов (, т.е. список значений из набора вторых компонентов), связанный с 2, представляет собой ровно одно число -3. Обратите внимание, что нас не волнует, что -3 является вторым компонентом второго упорядоченного номинала в отношении.Это вполне приемлемо. Мы просто не хотим, чтобы было больше одной упорядоченной пары с 2 в качестве первого компонента. Мы рассмотрели одно значение из набора первых компонентов для нашего быстрого примера, но результат будет таким же для всех остальных вариантов. Независимо от выбора первых компонентов с ним будет связан ровно один второй компонент. Следовательно, это отношение является функцией. Чтобы действительно почувствовать, что нам говорит определение функции, мы, вероятно, должны также проверить пример отношения, которое не является функцией. Не беспокойтесь о том, откуда взялось это отношение. Из набора первых компонентов выберем 6. Теперь, если мы перейдем к соотношению, мы увидим, что есть две упорядоченные пары с 6 в качестве первого компонента: \ (\ left ({6,10} \ right) \ ) и \ (\ left ({6, — 4} \ right) \). Список вторых компонентов, связанных с 6, будет: 10, -4. Список вторых компонентов, связанных с 6, имеет два значения, поэтому это отношение не является функцией. Обратите внимание на тот факт, что если мы выбрали -7 или 0 из набора первых компонентов, то в списке вторых компонентов, связанных с каждым из них, будет только одно число. Это не имеет значения. Тот факт, что мы нашли даже одно значение в наборе первых компонентов с более чем одним вторым компонентом, связанным с ним, достаточно, чтобы сказать, что это отношение не является функцией. В качестве последнего комментария к этому примеру отметим, что если мы удалим первую и / или четвертую упорядоченную пару из отношения, у нас будет функция! Итак, надеюсь, у вас есть хоть какое-то представление о том, что нам говорит определение функции. Теперь, когда мы заставили вас пройти собственно определение функции, давайте дадим еще одно «рабочее» определение функции, которое будет гораздо более полезным для того, что мы здесь делаем. Фактическое определение работает с отношением. Однако, как мы видели с четырьмя отношениями, которые мы указали до определения функции, и с отношением, которое мы использовали в примере 1, мы часто получаем отношения из некоторого уравнения. Важно отметить, что не все отношения основаны на уравнениях! Отношение из второго примера, например, было просто набором упорядоченных пар, которые мы записали для этого примера, и не было получено из какого-либо уравнения. Однако, как бы то ни было, все функции, которые мы собираемся использовать в этом курсе, основаны на уравнениях. Поэтому давайте напишем определение функции, которая признает этот факт. Прежде чем мы дадим «рабочее» определение функции, мы должны указать, что это НЕ фактическое определение функции, данное выше. Это просто хорошее «рабочее определение» функции, которое связывает вещи с видами функций, с которыми мы будем работать в этом курсе. Функция — это уравнение, для которого любой \ (x \), который может быть вставлен в уравнение, даст ровно один \ (y \) из уравнения. Вот оно. Это определение функций, которые мы собираемся использовать, и, вероятно, будет легче понять, что оно означает. Прежде чем мы исследуем это, обратите внимание, что мы использовали фразу «\ (x \), который может быть подключен» в определении. Далее, имея дело с функциями, мы всегда будем предполагать, что и \ (x \), и \ (y \) будут действительными числами.Другими словами, мы на некоторое время забудем о том, что знаем что-либо о комплексных числах, пока будем заниматься этим разделом. Хорошо, теперь давайте вернемся к определению функции и рассмотрим несколько примеров уравнений, которые являются функциями, и уравнений, которые не являются функциями. «Рабочее» определение функции гласит, что если мы возьмем все возможные значения \ (x \), подставим их в уравнение и решим для \ (y \), мы получим ровно одно значение для каждого значения \ ( Икс\).На этом этапе игры может быть довольно сложно на самом деле показать, что уравнение является функцией, поэтому в основном мы будем обсуждать его. С другой стороны, часто довольно легко показать, что уравнение не является функцией. Итак, нам нужно показать, что независимо от того, какое \ (x \) мы подставляем в уравнение и решаем для \ (y \), мы получим только одно значение \ (y \). Также обратите внимание, что значение \ (y \), вероятно, будет различным для каждого значения \ (x \), хотя это не обязательно. Давайте начнем с того, что подставим некоторые значения \ (x \) и посмотрим, что произойдет. Итак, для каждого из этих значений \ (x \) мы получили единственное значение \ (y \) из уравнения.Теперь этого недостаточно, чтобы утверждать, что это функция. Чтобы официально доказать, что это функция, нам нужно показать, что она будет работать независимо от того, какое значение \ (x \) мы подставляем в уравнение. Конечно, мы не можем подставить в уравнение все возможные значения \ (x \). Это просто невозможно физически. Однако давайте вернемся и посмотрим на те, которые мы подключили. Для каждого \ (x \) после подключения мы сначала умножили \ (x \) на 5, а затем прибавили к нему 1.2} + 1 = 9 + 1 = 10 \ end {align *} \] А теперь давайте немного подумаем о том, что мы делали с оценками. Сначала мы возводили в квадрат значение \ (x \), которое мы подключили. Когда мы возводим в квадрат число, будет только одно возможное значение. Затем мы добавляем к этому 1, но опять же, это даст одно значение. Итак, похоже, что это уравнение также является функцией. Обратите внимание, что получить одинаковое значение \ (y \) для разных \ (x \) — это нормально.2} & = 10 + 1 = 11 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} y = \ pm \ sqrt {11} \ end {align *} \] Теперь помните, что мы решаем для \ (y \), и это означает, что в первом и последнем случаях выше мы фактически получим два разных значения \ (y \) из \ (x \), и поэтому это уравнение НЕ является функцией. Обратите внимание, что у нас могут быть значения \ (x \), которые приведут к единственному \ (y \), как мы видели выше, но это не имеет значения. Если даже одно значение \ (x \) дает более одного значения \ (y \) при решении, уравнение не будет функцией. 2} = 4 \ hspace {0.2} = 4 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} y = \ pm \, 2 \] Итак, это уравнение не является функцией. Напомним, что из предыдущего раздела это уравнение круга. Круги никогда не бывают функциями. Надеюсь, эти примеры позволили вам лучше понять, что такое функция. Теперь нам нужно перейти к так называемой нотации функции . Обозначения функций будут широко использоваться в большинстве оставшихся глав этого курса, поэтому важно понимать их.2} — 5x + 3 \] Буква, которую мы используем, не имеет значения. Важна часть «\ (\ left (x \ right) \)». Буква в скобках должна соответствовать переменной, используемой справа от знака равенства. Очень важно отметить, что \ (f \ left (x \ right) \) на самом деле не что иное, как действительно причудливый способ записи \ (y \). Если вы запомните это, вы можете обнаружить, что работать с обозначениями функций становится немного проще. Кроме того, это НЕ умножение \ (f \) на \ (x \)! Это одна из наиболее распространенных ошибок, которые люди допускают, когда впервые сталкиваются с функциями.2} — 5x + 3 \] и спросите, каково его значение для \ (x = 4 \). В терминах обозначений функций мы будем «спрашивать» об этом, используя обозначение \ (f \ left (4 \ right) \). Итак, когда в скобках есть что-то, кроме переменной, мы действительно спрашиваем, каково значение функции для этой конкретной величины. Теперь, когда мы говорим значение функции, мы действительно спрашиваем, каково значение уравнения для этого конкретного значения \ (x \). Вот \ (f \ left (4 \ right) \).2} — 5} \ right) \) Показать все решения Скрыть все решения
a \ (f \ left (3 \ right) \) и \ (g \ left (3 \ right) \) Показать решение Хорошо, у нас есть две оценки функций, которые нужно выполнить, и у нас также есть две функции, поэтому нам нужно будет решить, какую функцию использовать для оценок. Главное здесь — обратить внимание на букву перед круглой скобкой. Для \ (f \ left (3 \ right) \) мы будем использовать функцию \ (f \ left (x \ right) \), а для \ (g \ left (3 \ right) \) мы будем использовать \ (g \ влево (х \ вправо) \).2} — 2 \ влево ({- 10} \ вправо) + 8 = 100 + 20 + 8 = 128 \] Убедитесь, что здесь вы правильно разбираетесь с негативными знаками. Теперь второй. Мы достигли разницы. Напомним, когда мы впервые начали говорить об определении функций, мы заявили, что будем иметь дело только с действительными числами. Другими словами, мы подставляем только действительные числа и хотим, чтобы в качестве ответов возвращались только действительные числа.2} — 2 \ влево (0 \ вправо) + 8 = 8 \] Опять же, не забывайте, что это не умножение! По какой-то причине ученикам нравится думать об этом как об умножении и получать нулевой ответ. Будь осторожен. Остальные оценки теперь будут немного другими. Как показывает этот, нам не нужно просто указывать числа в скобках. Однако оценка работает точно так же. Мы вставляем \ (x \) справа от знака равенства в скобки.2} — 2t + 8 \] Обратите внимание, что в этом случае это почти то же самое, что и наша исходная функция, за исключением того, что на этот раз мы используем \ (t \) в качестве переменной. Теперь давайте немного посложнее, или, по крайней мере, они кажутся более сложными. Однако все не так плохо, как может показаться. Сначала мы оценим \ (f \ left ({t + 1} \ right) \). Этот работает точно так же, как и предыдущая часть.2} + 1} \ end {выровнять *} \] Оценка функций — это то, чем мы будем много заниматься в следующих разделах и главах, поэтому убедитесь, что вы можете это сделать. Вы обнаружите, что несколько последующих разделов будет очень трудным для понимания и / или выполнения работы, если вы не имеете хорошего представления о том, как работает оценка функций. Пока мы говорим об оценке функций, мы должны теперь поговорить о кусочных функциях . На самом деле мы уже видели пример кусочной функции, даже если в то время мы не называли его функцией (или кусочной функцией).Вспомните математическое определение абсолютной величины. Это функция, и если мы используем обозначение функции, мы можем записать ее следующим образом: Это также пример кусочной функции. Кусочная функция — это не что иное, как функция, которая разбита на части, и какой фрагмент вы используете, зависит от значения \ (x \).2} + 4} & {{\ mbox {if}} t \ le — 4} \\ {10} & {{\ mbox {if}} — 4 15} \ end {array}} \ right. \] оценивают каждое из следующих действий. Прежде чем приступить к оценкам, обратите внимание, что мы используем разные буквы для функции и переменной, чем те, которые мы использовали до этого момента.Это не повлияет на работу оценки. Не зацикливайтесь на том, чтобы видеть \ (f \) для функции и \ (x \) для переменной, что вы не сможете решить любую проблему, в которой нет этих букв. Теперь, чтобы выполнить каждую из этих оценок, первое, что нам нужно сделать, это определить, какому неравенству удовлетворяет число, и оно будет удовлетворять только одному неравенству. Когда мы определяем, какому неравенству удовлетворяет число, мы используем уравнение, связанное с этим неравенством.2} + 4 = 52 \] В этом случае число 1 удовлетворяет среднему неравенству, поэтому мы будем использовать среднее уравнение для оценки. Эта оценка часто вызывает проблемы у студентов, несмотря на то, что на самом деле это одна из самых простых оценок, которые мы когда-либо проводим. Мы знаем, что оцениваем функции / уравнения, подставляя номер переменной. В этом случае нет переменных. Это не проблема. Поскольку переменных нет, это просто означает, что мы на самом деле ничего не подключаем, и получаем следующее: Опять же, как и со второй частью, нам нужно быть немного осторожнее с этой.В этом случае число удовлетворяет среднему неравенству, так как это число со знаком равенства в нем. Затем, как и в предыдущей части, мы получаем Не радуйтесь тому факту, что предыдущие две оценки имели одинаковое значение. Иногда это будет происходить. Для окончательной оценки в этом примере число удовлетворяет нижнему неравенству, поэтому мы будем использовать нижнее уравнение для оценки. Кусочные функции не так часто возникают в классе алгебры, однако они возникают в нескольких местах в более поздних классах, поэтому вам важно понимать их, если вы собираетесь перейти к большему количеству математических классов. В качестве последней темы нам нужно вернуться и коснуться того факта, что мы не всегда можем подключить каждый \ (x \) к каждой функции. Мы кратко говорили об этом, когда давали определение функции, и мы видели пример этого, когда оценивали функции.Теперь нам нужно взглянуть на это немного подробнее. Во-первых, нам нужно избавиться от пары определений. Область уравнения — это набор всех \ (x \), которые мы можем вставить в уравнение и получить действительное число для \ (y \). Диапазон уравнения — это набор всех \ (y \), которые мы когда-либо можем получить из уравнения. Обратите внимание, что мы действительно имели в виду использовать уравнение в определениях выше вместо функций.Это действительно определения уравнений. Однако, поскольку функции также являются уравнениями, мы также можем использовать определения функций. Определение диапазона уравнения / функции для многих функций может быть довольно сложным, поэтому мы не будем вдаваться в подробности. Здесь нас гораздо больше интересует определение областей функций. Согласно определению, домен — это набор всех \ (x \), которые мы можем подключить к функции и получить действительное число. На данный момент это означает, что нам нужно избегать деления на ноль и извлечения квадратных корней из отрицательных чисел.2} + 3x — 10 = \ left ({x + 5} \ right) \ left ({x — 2} \ right) = 0 \ hspace {0,25in} x = — 5, \, \, x = 2 \ ] Итак, мы получим деление на ноль, если подставим \ (x = — 5 \) или \ (x = 2 \). Это означает, что нам нужно избегать этих двух чисел. Однако все остальные значения \ (x \) будут работать, поскольку они не дают деления на ноль. Тогда домен В этом случае у нас не будет задач деления на ноль, так как у нас нет дробей.У нас действительно есть квадратный корень в задаче, поэтому нам нужно позаботиться о том, чтобы извлечь квадратный корень из отрицательного числа. Эта часть будет работать немного иначе, чем предыдущая. В этой части мы определили значение (я) \ (x \), которого следует избегать. В этом случае напрямую получить домен будет так же просто. Чтобы избежать квадратных корней из отрицательных чисел, все, что нам нужно сделать, это потребовать, чтобы Это довольно простое линейное неравенство, которое мы должны решить на данный момент.2} + 4}} \) Показать решение В этом случае у нас есть дробь, но обратите внимание, что знаменатель никогда не будет равен нулю для любого действительного числа, поскольку x 2 гарантированно будет положительным или нулевым, и добавление 4 к этому будет означать, что знаменатель всегда будет минимум 4. Другими словами, знаменатель никогда не будет равен нулю. Итак, все, что нам нужно сделать, это позаботиться о квадратном корне в числителе. Для этого нам потребуется Теперь мы можем фактически подставить любое значение \ (x \) в знаменатель, однако, поскольку у нас есть квадратный корень в числителе, мы должны убедиться, что все \ (x \) удовлетворяют неравенство выше, чтобы избежать проблем.2} — 16}} \) Показать решение В этой заключительной части нам нужно беспокоиться как о квадратном корне, так и о делении на ноль. Давайте сначала позаботимся о квадратном корне, поскольку это, вероятно, наложит наибольшее ограничение на значения \ (x \). Итак, чтобы квадратный корень оставался счастливым (, то есть без квадратного корня из отрицательных чисел), нам потребуется это, Итак, по крайней мере, нам нужно потребовать, чтобы \ (x \ ge \ frac {1} {2} \), чтобы избежать проблем с квадратным корнем.2} — 16 = \ left ({x — 4} \ right) \ left ({x + 4} \ right) = 0 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} x = — 4, \, \, х = 4 \] Теперь обратите внимание, что \ (x = — 4 \) не удовлетворяет неравенству, которое нам нужно для квадратного корня, и поэтому значение \ (x \) уже исключено квадратным корнем. С другой стороны, \ (x = 4 \) удовлетворяет неравенству. Это означает, что можно подставить \ (x = 4 \) в квадратный корень, однако, поскольку это даст деление на ноль, нам нужно будет избегать этого. Тогда домен для этой функции будет Когда у нас есть функция в форме формулы, вычислить ее обычно несложно.{2} + 3x — 4 [/ latex], оцените каждое из следующих значений. Замените [latex] x [/ latex] в функции каждым указанным значением. {2} + 2p [/ latex], решите относительно [латекс] h \ left (p \ right) = 3 [/ latex].{2} + 2p — 3 = 0 && \ text {Вычтите по 3 с каждой стороны}. \\ & \ left (p + 3 \ text {) (} p — 1 \ right) = 0 && \ text {Factor}. \ end {align} [/ latex] Если [латекс] \ left (p + 3 \ right) \ left (p — 1 \ right) = 0 [/ latex], либо [latex] \ left (p + 3 \ right) = 0 [/ latex] или [латекс] \ left (p — 1 \ right) = 0 [/ latex] (или оба они равны 0). Мы установим каждый коэффициент равным 0 и решим для каждого случая [латекс] p [/ латекс]. [латекс] \ begin {align} & p + 3 = 0, && p = -3 \\ & p — 1 = 0, && p = 1 \ hfill \ end {align} [/ latex] Это дает нам два решения.Вывод [латекс] h \ left (p \ right) = 3 [/ latex], когда на входе либо [latex] p = 1 [/ latex], либо [latex] p = -3 [/ latex]. Мы также можем проверить, построив график, как на рисунке 5. График проверяет, что [latex] h \ left (1 \ right) = h \ left (-3 \ right) = 3 [/ latex] и [latex] h \ left (4 \ справа) = 24 [/ латекс]. Учитывая функцию [латекс] g \ left (m \ right) = \ sqrt {m — 4} [/ latex], решите [latex] g \ left (m \ right) = 2 [/ latex]. Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения .Если можно выразить выход функции с помощью формулы , включающей входную величину, то мы можем определить функцию в алгебраической форме. Например, уравнение [латекс] 2n + 6p = 12 [/ латекс] выражает функциональную взаимосвязь между [латексом] n [/ латексом] и [латексом] p [/ латексом]. Мы можем переписать его, чтобы решить, является ли [latex] p [/ latex] функцией [latex] n [/ latex]. Выразите отношение [латекс] 2n + 6p = 12 [/ latex] как функцию [latex] p = f \ left (n \ right) [/ latex], если это возможно. Чтобы выразить взаимосвязь в этой форме, нам нужно иметь возможность записать взаимосвязь, где [latex] p [/ latex] является функцией [latex] n [/ latex], что означает запись в виде [latex] p = [/ latex] выражение, включающее [latex] n [/ latex]. [латекс] \ begin {align} & 2n + 6p = 12 \\ [1 мм] & 6p = 12 — 2n && \ text {Subtract} 2n \ text {с обеих сторон}. \\ [1mm] & p = \ frac {12 — 2n} {6} && \ text {Разделите обе стороны на 6 и упростите}. \\ [1 мм] & p = \ frac {12} {6} — \ frac {2n} {6} \\ [1 мм] & p = 2- \ frac {1} {3} n \ end {align} [/ latex ] Следовательно, [латекс] p [/ latex] как функция [latex] n [/ latex] записывается как [латекс] p = f \ left (n \ right) = 2- \ frac {1} {3} n [/ latex] Важно отметить, что не все отношения, выраженные уравнением, можно также выразить как функцию с формулой.{y} [/ latex], если мы хотим выразить [latex] y [/ latex] как функцию [latex] x [/ latex], не существует простой алгебраической формулы, включающей только [latex] x [/ latex] что равно [латекс] y [/ латекс]. Однако каждый [latex] x [/ latex] действительно определяет уникальное значение для [latex] y [/ latex], и существуют математические процедуры, с помощью которых [latex] y [/ latex] может быть найден с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для [latex] y [/ latex] как функции [latex] x [/ latex], даже если формулу нельзя записать явно. Как мы видели выше, мы можем представлять функции в виде таблиц. И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев.И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов. Функция, которая связывает тип домашнего животного с продолжительностью его памяти, легче визуализировать с помощью таблицы. См. Таблицу ниже. Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений. Здесь вызовем функцию [латекс] П [/ латекс]. Область функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память питомца.Мы можем оценить функцию [latex] P [/ latex] при входном значении «золотая рыбка». Мы бы написали [латекс] P \ left (\ text {goldfish} \ right) = 2160 [/ latex]. Обратите внимание, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции [latex] P [/ latex] кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции. Используя приведенную ниже таблицу, Когда мы вводим 2 в функцию [latex] g [/ latex], мы получаем 6.Когда мы вводим 4 в функцию [latex] g [/ latex], наш результат также равен 6. Используя таблицу из предыдущего примера, оцените [латекс] g \ left (1 \ right) [/ latex]. [латекс] г \ слева (1 \ справа) = 8 [/ латекс] Оценка функции с помощью графика также требует нахождения соответствующего выходного значения для данного входного значения, только в этом случае мы находим выходное значение, глядя на график.Решение функционального уравнения с использованием графика требует нахождения всех экземпляров данного выходного значения на графике и наблюдения за соответствующими входными значениями. Учитывая график ниже, Используя график, решите [латекс] f \ left (x \ right) = 1 [/ latex]. [латекс] x = 0 [/ латекс] или [латекс] x = 2 [/ латекс] Вы можете использовать онлайн-инструмент построения графиков для построения графиков функций, поиска значений функций и оценки функций.2 + x + 4 [/ latex] с использованием обозначения функций. У вас была идея улучшить этот контент? Нам очень понравится ваш вклад. Улучшить эту страницуПодробнее Упорядоченная пара — это набор входов и выходов, представляющий взаимосвязь между двумя значениями.Отношение — это набор входов и выходов, а функция — это отношение с одним выходом для каждого входа. Некоторые отношения имеют смысл, а другие — нет. Функции — это отношения, которые имеют смысл. Все функции являются отношениями , но не все отношения являются функциями. Функция — это отношение, в котором для каждого входа существует только один выход. Вот отображение функций.Домен — это вход или x-значение , а диапазон — это выход или y-значение . Каждое значение x связано только с одним значением y. Хотя входы, равные -1 и 1, имеют одинаковый выход, это отношение по-прежнему является функцией, потому что каждый вход имеет только один выход. Это отображение не является функцией. Вход для -2 имеет более одного выхода. Использование входов и выходов, перечисленных в таблицах, картах и списках, позволяет легко нанести точек на координатную сетку .Используя график точек данных, вы можете определить, является ли отношение функцией, используя тест вертикальной линии . Если вы можете провести вертикальную линию через график и коснуться только одной точки, отношение является функцией. Взгляните на график этой карты отношений. Если бы вы провели вертикальную линию через каждую точку на графике, каждая линия касалась бы только одной точки, так что это отношение является функцией. Специальные функции и их уравнения имеют узнаваемые характеристики. $ f (x) = c $ Значение c может быть любым числом, поэтому график постоянной функции представляет собой горизонтальную линию. Вот график $ f (x) = 4 $ долл. США f (x) = x Для функции идентичности значение x совпадает с значением y. График представляет собой диагональную линию, проходящую через начало координат. долл. США f (x) = mx + b Уравнение, записанное в форме пересечения наклона , является уравнением линейной функции , а график функции представляет собой прямую линию. Вот график $ f (x) = 3x + 4 $ долл. США f (x) = | x | Функцию абсолютного значения легко распознать по V-образному графику. График состоит из двух частей и представляет собой одну из кусочных функций. Это лишь некоторые из наиболее часто используемых специальных функций. Инверсная функция меняет местами входы и выходы.{-1} (x) = \ frac {x + 4} {3} $. Не каждая инверсия функции является функцией, поэтому для проверки используйте тест вертикальной линии. Вы можете складывать, вычитать, умножать и делить функции . Посмотрите на два примера операций функции: Какова сумма этих двух функций? Просто добавьте выражения.{2} + 11x + 28
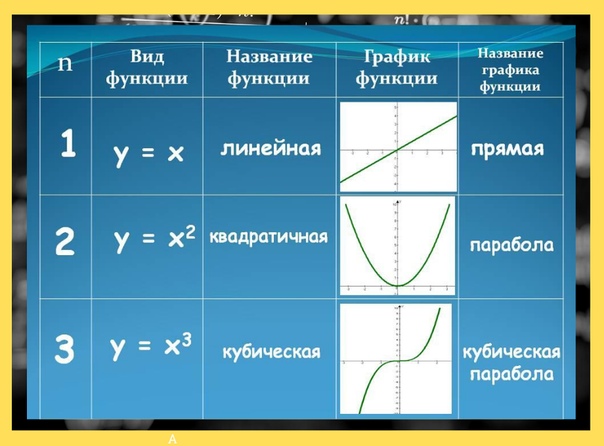
\ end {align} Начнем с того, что отношение — это просто набор или совокупность упорядоченных пар. Ничего особенного в этом нет. Упорядоченная пара, обычно известная как точка, имеет два компонента, которые являются координатами x и y. Это пример упорядоченной пары. Пока числа идут парами, это становится отношением.Если вы можете написать кучу точек (упорядоченных пар), то вы уже знаете, как выглядит отношение. Например, здесь у нас есть отношение, в котором пять упорядоченных пар записаны в нотации множеств с использованием фигурных скобок. Отношение в обозначении набора : Однако, помимо обозначения набора, есть и другие способы записать это отношение. Мы можем отобразить это в таблице, нанести на ось xy и выразить с помощью диаграммы сопоставления. Мы также можем описать область и диапазон данного отношения. Итак, в отношении ниже наш домен и диапазон следующие: При перечислении элементов домена и диапазона избавьтесь от дубликатов и запишите их в порядке возрастания. С другой стороны, функция на самом деле является «особым» видом отношения, потому что она следует дополнительному правилу. Как и отношение, функция — это также набор упорядоченных пар; однако каждое значение x должно быть связано только с одним значением y. Предположим, у нас есть два отношения, записанные в таблицах, Поскольку у нас есть повторения или дубликаты значений x с разными значениями y, это отношение перестает быть функцией. Это отношение определенно является функцией, потому что каждое значение x уникально и связано только с одним значением y. Итак, для краткого обзора, если вы видите какие-либо дубликаты или повторы в значениях x, отношение не является функцией. А как насчет этого примера? Разве это не функция, потому что у нас есть повторяющиеся записи в x? Будьте здесь очень осторожны. Да, у нас есть повторяющиеся значения x, но они связаны с одним и тем же значением y.Точка (1,5) появляется дважды, а точка (3, -8) записывается трижды. Эту таблицу можно очистить, написав единственную копию повторяющихся упорядоченных пар. Теперь отношение явно является функцией! Давайте рассмотрим еще несколько примеров, определив, является ли данное отношение функцией или нет. Пример 1: Является ли отношение, выраженное на диаграмме отображения, функцией? Каждый элемент домена отслеживается до одного-единственного элемента в диапазоне.Однако это нормально, если два или более значений в домене имеют общее значение в диапазоне. То есть, даже несмотря на то, что элементы 5 и 10 в домене имеют одинаковое значение 2 в диапазоне, это отношение по-прежнему является функцией. Пример 2: Является ли отношение, выраженное на диаграмме отображения, функцией? Как вы думаете? Каждое значение в домене указывает на одно значение в диапазоне? Абсолютно! Нет ничего плохого в том, что четыре элемента из домена имеют общее значение в диапазоне.Это также отличный пример функции. Пример 3: Является ли отношение, выраженное на диаграмме отображения, функцией? Грязный? Да! Сбивает с толку? Не совсем. Единственное, что мне нужно, это наблюдать, является ли элемент в домене «жадным», желая быть спаренным с более чем одним элементом в диапазоне. Элемент 15 имеет две стрелки, указывающие как на 7, так и на 9. Это явное нарушение требования быть функцией. Функция ведет себя хорошо, то есть каждый элемент в домене должен указывать на один элемент в диапазоне.Следовательно, это отношение , а не функция . Пример 4: Является ли отношение, выраженное на диаграмме отображения, функцией? Если вы считаете, что пример 3 «плохой», это «еще хуже». Один элемент в домене соединяется с четырьмя элементами в диапазоне. Помните, что если элемент в домене связан с более чем одним элементом в диапазоне, отношение автоматически дисквалифицируется как функция. Таким образом, это отношение абсолютно , а не функция . Пример 5: Является ли диаграмма отображения отношением или функцией? Позвольте мне показать вам этот пример, чтобы выделить очень важную идею о функции, которая обычно игнорируется. Ваш учитель может дать вам что-то подобное, чтобы проверить, обращаете ли вы внимание на детали определения функции. Пока все нормально выглядит. Но есть небольшая проблема. Элемент «2» в домене не связан ни с одним элементом в диапазоне. Вот сделка! Каждый элемент в домене должен иметь какое-то соответствие элементам в диапазоне, по крайней мере, чтобы он мог считаться отношением.Поскольку это не отношение, отсюда следует, что это не может быть функцией. Итак, окончательный ответ: ни ни отношение, ни функция. Функция в среде программирования представляет собой набор инструкций. Программист создает функцию, чтобы избежать повторения одной и той же задачи или уменьшить сложность . Функция должна быть Общий подход к функции состоит в том, чтобы использовать часть аргумента как входов , передать часть 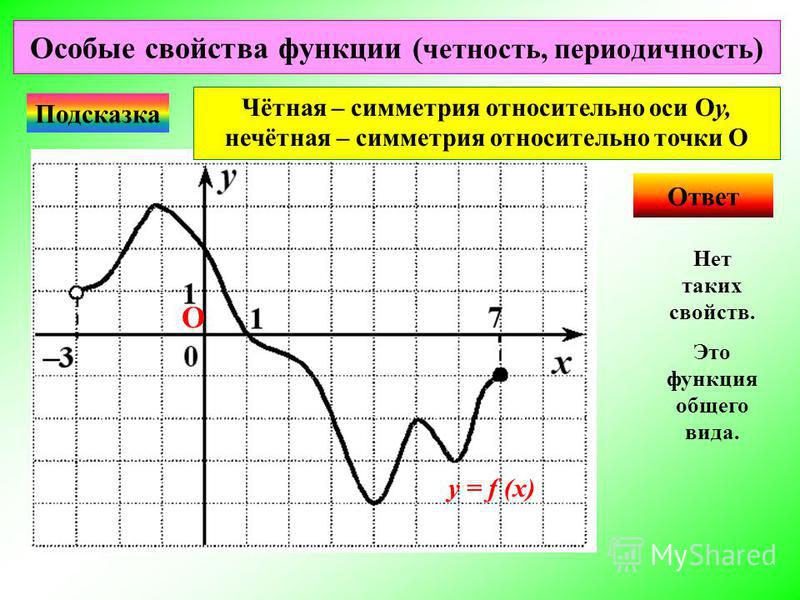 n: линейная функция, квадратичная, кубическая и y=1/x
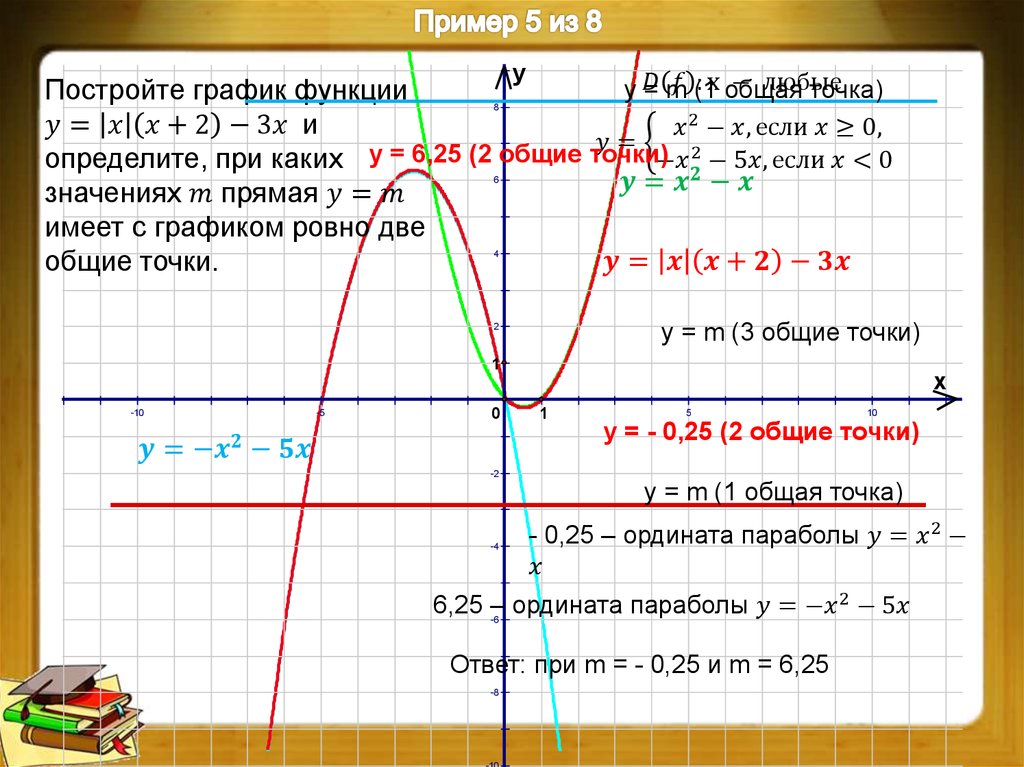
n: линейная функция, квадратичная, кубическая и y=1/xМатериал к уроку «Четные и нечетные функции»

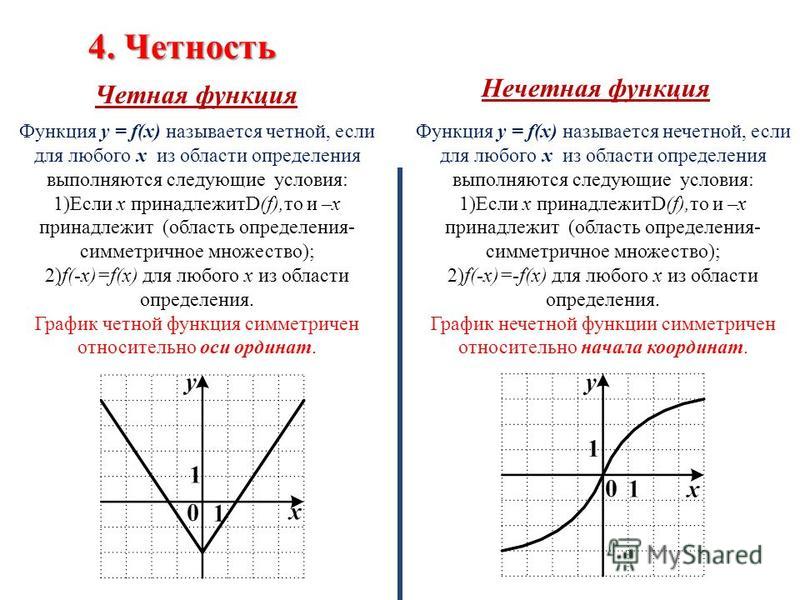
 На рисунке изображена часть графика некоторой функции, область определения которой — промежуток [ ‑ 4; 4]. Постройте график этой функции, если функция нечетная.
На рисунке изображена часть графика некоторой функции, область определения которой — промежуток [ ‑ 4; 4]. Постройте график этой функции, если функция нечетная.
 Определить четность (нечетность) функции .
Определить четность (нечетность) функции .
 Исследовать функцию на четность (нечетность).
Исследовать функцию на четность (нечетность).
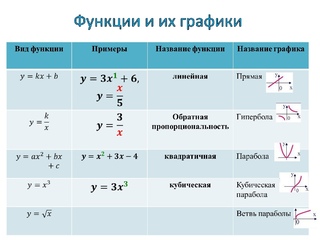 Вычислите , если f(x) – нечетная функция и f( ‑ 5)=3; f(2)= ‑ 8.
Вычислите , если f(x) – нечетная функция и f( ‑ 5)=3; f(2)= ‑ 8.

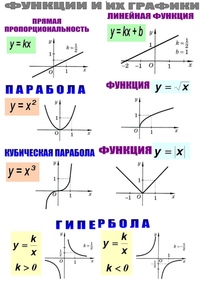
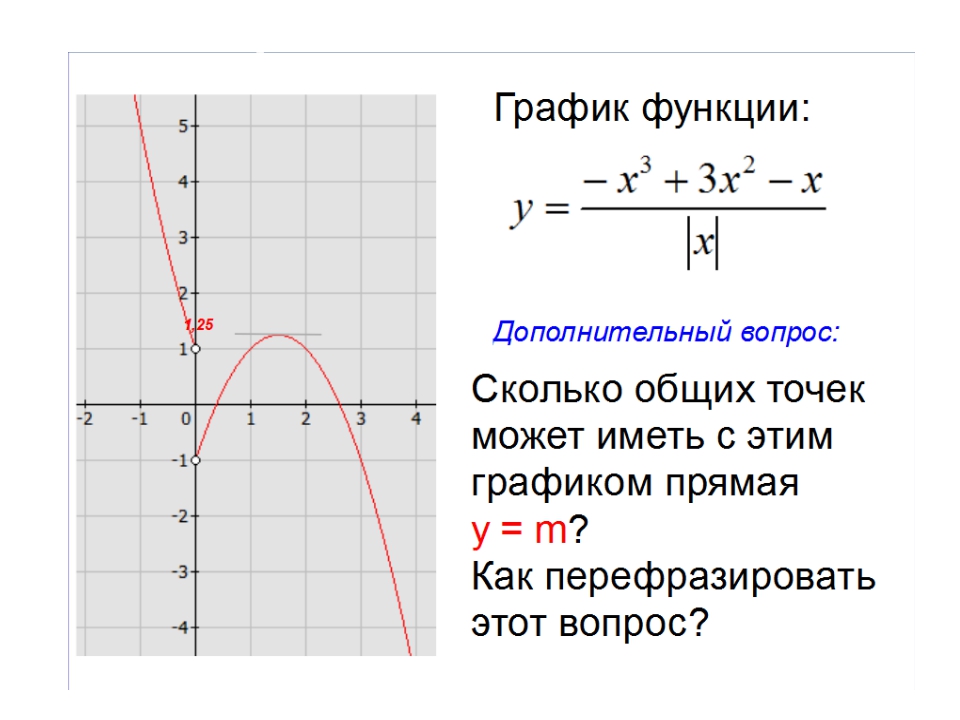 Функции f и g определены на множестве всех действительных чисел. Является ли функция h четной или нечетной, если…
Функции f и g определены на множестве всех действительных чисел. Является ли функция h четной или нечетной, если…
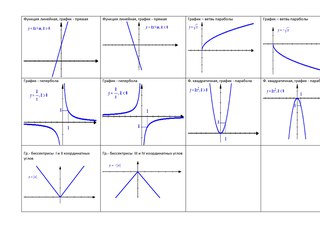 Представьте функцию в виде суммы четной и нечетной функций…
Представьте функцию в виде суммы четной и нечетной функций…
§ 6. Исследование функции.
1. Область определения функции.

2. Исследование функции на четность и нечетность.
3. Исследование функции на монотонность.

4. Исследование функции на экстремум.

— пояснения и примеры
Что такое функция?
 Диапазон функции может быть выражен в виде интервалов или содержать информацию о неравенствах.
Диапазон функции может быть выражен в виде интервалов или содержать информацию о неравенствах. Что такое обозначение функций?
Преимущества использования обозначения функций
 д., мы используем f (x), чтобы избежать путаницы относительно того, какая функция оценивается.
д., мы используем f (x), чтобы избежать путаницы относительно того, какая функция оценивается. Типы функций

Identity Function:
Рациональная функция:
Как оценивать функции?

= 8a 2 + 24a + 18 + 8a + 12-3
= 8a 2 + 32a + 27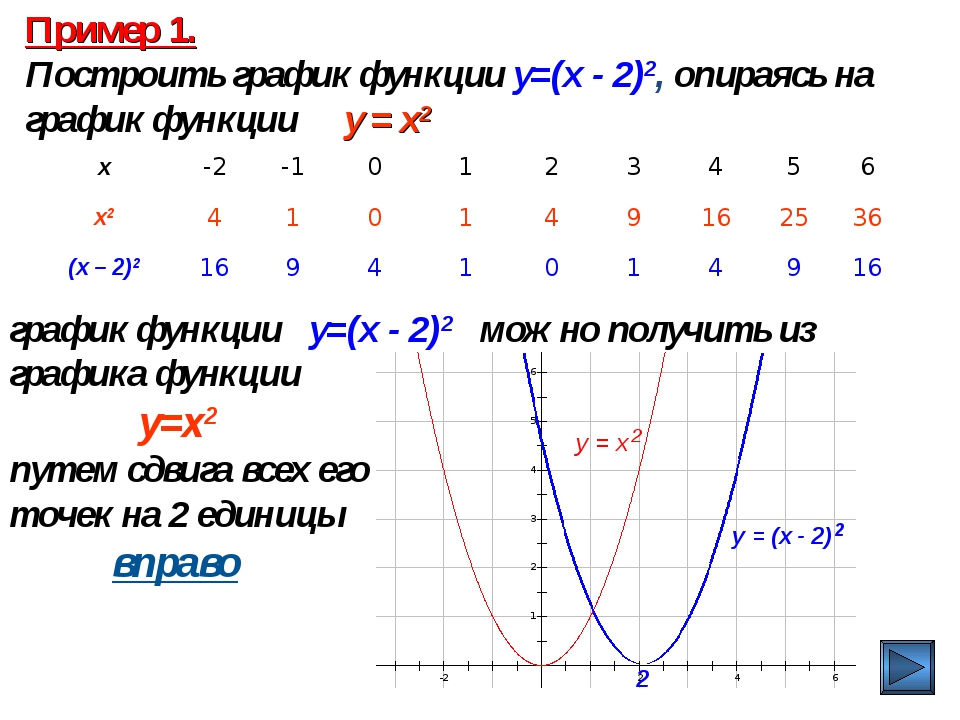

Примеры обозначений функций из реальной жизни
 Если у нее уже есть 1000 долларов, сколько у нее будет через 22 недели.
Если у нее уже есть 1000 долларов, сколько у нее будет через 22 недели.
Теперь оцените функцию, когда x = 22
f (22) = 100 (22) +1000
f (22) = 3200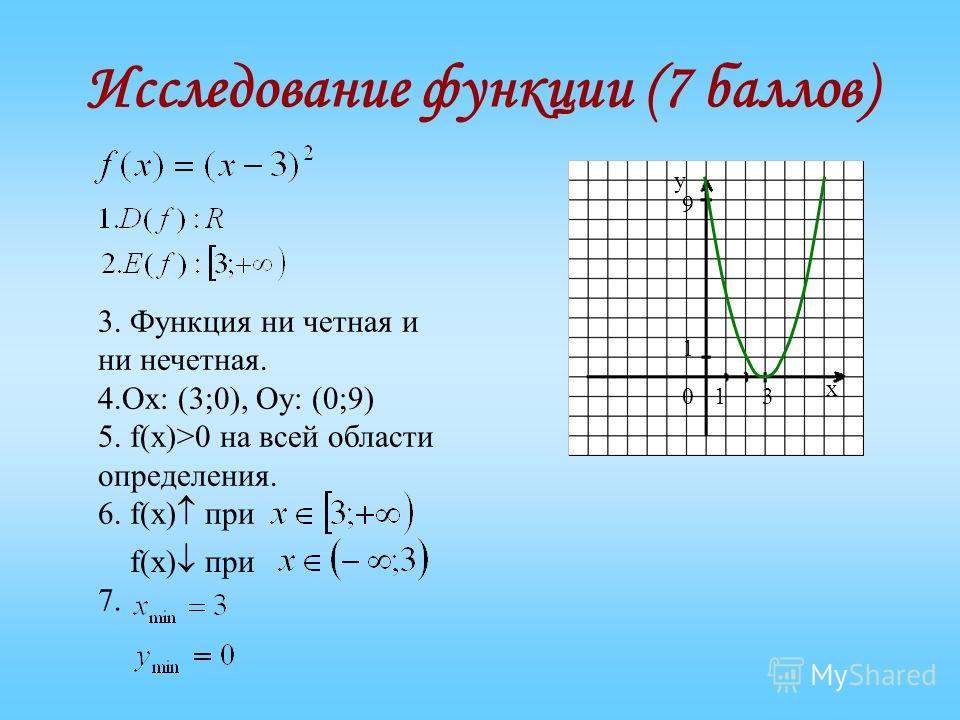 04x + 40 долларов.
04x + 40 долларов.
Определение функции
Показать мобильное уведомление Показать все заметки Скрыть все заметки е. , вероятно, вы используете мобильный телефон).Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. , вероятно, вы используете мобильный телефон).Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. Раздел 3-4: Определение функции
Определение отношения

 Также обратите внимание, что мы также можем получить другие упорядоченные пары из уравнения и добавить их в любое из приведенных выше отношений, если захотим.
Также обратите внимание, что мы также можем получить другие упорядоченные пары из уравнения и добавить их в любое из приведенных выше отношений, если захотим. Определение функции
 {{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{0, — 3,0,5} \ right \} \]
{{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{0, — 3,0,5} \ right \} \]
 {{\ mbox {st}}}} {\ mbox {components:}} \ left \ {{6, — 7,0} \ right \} \ hspace {0.{{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{10,3,4, — 4} \ right \} \]
{{\ mbox {st}}}} {\ mbox {components:}} \ left \ {{6, — 7,0} \ right \} \ hspace {0.{{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{10,3,4, — 4} \ right \} \]
 Это также может быть верно для отношений, которые являются функциями. Они не обязательно должны исходить из уравнений.
Это также может быть верно для отношений, которые являются функциями. Они не обязательно должны исходить из уравнений. «Рабочее определение» функции
 Это имеет тенденцию означать, что не все \ (x \) могут быть включены в уравнение, и это на самом деле правильно. Мы вернемся и обсудим это более подробно в конце этого раздела, однако на данном этапе просто помните, что мы не можем делить на ноль, и если мы хотим, чтобы действительные числа были исключены из уравнения, мы не можем извлечь квадратный корень из отрицательное число. Итак, с этими двумя примерами ясно, что мы не всегда сможем подставить каждое \ (x \) в какое-либо уравнение.
Это имеет тенденцию означать, что не все \ (x \) могут быть включены в уравнение, и это на самом деле правильно. Мы вернемся и обсудим это более подробно в конце этого раздела, однако на данном этапе просто помните, что мы не можем делить на ноль, и если мы хотим, чтобы действительные числа были исключены из уравнения, мы не можем извлечь квадратный корень из отрицательное число. Итак, с этими двумя примерами ясно, что мы не всегда сможем подставить каждое \ (x \) в какое-либо уравнение. 2} = 4 \) Показать все решения Скрыть все решения
Показать обсуждение
2} = 4 \) Показать все решения Скрыть все решения
Показать обсуждение
a \ (y = 5x + 1 \) Показать решение
d \ (f \ left (t \ right) \) Показать решение
e \ (f \ left ({t + 1} \ right) \) и \ (f \ left ({x + 1} \ right) \) Показать решение
Показать все решения Скрыть все решения
Показать обсуждение
c \ (g \ left (1 \ right) \) Показать решение
d \ (g \ left ({15} \ right) \) Показать решение
e \ (g \ left ({21} \ right) \) Показать решение и диапазон
b \ (f \ left (x \ right) = \ sqrt {5 — 3x} \) Показать решение вычисляющих и решающих функций | Колледж алгебры
Результаты обучения
Показать решение Попробуйте
Вычисление функций, выраженных в формулах
Практическое руководство. Для данной функции в форме уравнения напишите ее алгебраическую формулу.
Пример: поиск уравнения функции
Анализ решения
Оценка функции, заданной в табличной форме
Домашнее животное Объем памяти в часах Щенок 0,008 Взрослая собака 0.083 Кот 16 Золотая рыбка 2160 Бета-рыба 3600 Практическое руководство. Для функции, представленной в виде таблицы, определите конкретные выходные и входные значения.
Пример: оценка и решение табличной функции
Показать решение [латекс] n [/ латекс] 1 2 3 4 5 [латекс] g (n) [/ латекс] 8 6 7 6 8 [латекс] n [/ латекс] 1 2 3 4 5 [латекс] g (n) [/ латекс] 8 6 7 6 8 Попробуйте
Поиск значений функций из графика
Пример: чтение значений функций из графика
Показать решение Попробуйте
Попробуйте
Внесите свой вклад!
Функции и взаимосвязи — стало проще
Введение
Что такое функция?
Графические функции
Специальные функции
Постоянная функция
Функция идентификации
Линейная функция
Функция абсолютного значения
Обратные функции
Функциональные операции
Отношения и функции — ChiliMath
Основные идеи и способы записи или представления отношений
Что делает связь функцией?
Примеры того, как определить, является ли отношение также функцией
Функции в программировании на языке R (с примером)
Что такое функция в языке R?
function (arglist) {
# Функция тела
}
В этом руководстве мы изучим важные встроенные функции
R
В R. много встроенных функций. R сопоставляет ваши входные параметры с аргументами своей функции, либо по значению, либо по позиции, а затем выполняет тело функции.Аргументы функции могут иметь значения по умолчанию: если вы не укажете эти аргументы, R примет значение по умолчанию.
Примечание : можно увидеть исходный код функции, запустив имя самой функции в консоли.
Мы увидим три группы функций в действии
- Общая функция
- Математическая функция
- Статистическая функция
Общие функции
Мы уже знакомы с общими функциями, такими как cbind (), rbind (), range () , функции sort (), order ().Каждая из этих функций имеет определенную задачу, принимает аргументы для возврата вывода. Ниже приведены важные функции, которые необходимо знать:
diff () функция
Если вы работаете с временными рядами , вам необходимо зафиксировать ряд, взяв их значения лага . Стационарный процесс обеспечивает постоянное среднее значение, дисперсию и автокорреляцию во времени. Это в основном улучшает предсказание временного ряда. Это легко сделать с помощью функции diff (). Мы можем построить случайные данные временного ряда с трендом, а затем использовать функцию diff () для стабилизации ряда.Функция diff () принимает один аргумент, вектор и возвращает подходящую запаздывающую и повторяемую разницу.
Примечание : Нам часто нужно создавать случайные данные, но для обучения и сравнения мы хотим, чтобы числа были идентичными на разных машинах. Чтобы гарантировать, что все мы генерируем одни и те же данные, мы используем функцию set.seed () с произвольными значениями 123. Функция set.seed () генерируется с помощью процесса генератора псевдослучайных чисел, который заставляет все современные компьютеры иметь одинаковую последовательность. номеров.Если мы не будем использовать функцию set.seed (), у всех будет разная последовательность чисел.
набор. семян (123) ## Создайте данные х = rnorm (1000) ts <- cumsum (x) ## Стационарный сериал diff_ts <- diff (ts) номинал (mfrow = c (1,2)) ## Постройте серию сюжет (ts, type = 'l') сюжет (diff (ts), type = 'l')
length () function
Во многих случаях нам нужно знать длину вектора для вычисления или использования в цикле for.Функция length () подсчитывает количество строк в векторе x. Следующие коды импортируют набор данных автомобилей и возвращают количество строк.
Примечание : length () возвращает количество элементов в векторе. Если функция передается в матрицу или фрейм данных, возвращается количество столбцов.
dt <- автомобили ## числовые столбцы длина (dt)
Выход:
## [1] 1
## числовые строки длина (dt [, 1])
Вывод:
## [1] 50
Математические функции
R имеет массив математических функций.
| Оператор | Описание | abs (x) | Принимает абсолютное значение x |
|---|---|
| log (x, base = y) | Логарифмирует x с основанием y; если основание не указано, возвращает натуральный логарифм |
| exp (x) | Возвращает экспоненту x |
| sqrt (x) | Возвращает квадратный корень из x |
| факториал (x) | Возвращает факториал x (x!) |
# последовательность чисел от 44 до 55, включая увеличенную на 1 x_vector <- seq (45,55, by = 1) #логарифм журнал (x_vector)
Выход:
## [1] 3.806662 3.828641 3.850148 3.871201 3.8 3.
3 3.931826 ## [8] 3.951244 3.970292 3.988984 4.007333
#exponential ехр (x_vector)
# квадратный корень sqrt (x_vector)
Выход:
## [1] 6.708204 6.782330 6.855655 6.928203 7.000000 7.071068 7.141428 ## [8] 7.211103 7.280110 7.348469 7.416198
#факториал факториал (x_vector)
Выход:
## [1] 1.196222e + 56 5.502622e + 57 2.586232e + 59 1.241392e + 61 6.082819e + 62 ## [6] 3.041409e + 64 1.551119e + 66 8.065818e + 67 4.274883e + 69 2.308437e + 71 ## [11] 1.269640e + 73
Статистические функции
R Стандартная установка содержит широкий спектр статистических функций. В этом руководстве мы кратко рассмотрим наиболее важные функции.
Основные статистические функции
Оператор | Описание |
|---|---|
среднее (x) | Среднее значение |
медиана (x) | Медиана x |
var (x) | Отклонение x |
| Стандартное отклонение x | |
шкала (x) | Стандартные оценки (z-значения) x |
квантиль (x) | Квартили x 1 |
Краткое изложение x: среднее, минимальное, максимальное и т. д.. |
скорость <- dt $ скорость скорость # Набор данных о средней скорости автомобилей среднее (скорость)
Выход:
## [1] 15,4
# Средняя скорость набора данных автомобилей медиана (скорость)
Выход:
## [1] 15
# Дисперсия скорости набора данных автомобилей var (скорость)
Выход:
## [1] 27.95918
# Стандартное отклонение скорости набора данных автомобилей sd (скорость)
Вывод:
## [1] 5.287644
# Стандартизация векторной скорости набора данных автомобилей напор (шкала (скорость), 5)
Выход:
## [, 1] ## [1,] -2.155969 ## [2,] -2.155969 ## [3,] -1,588609 ## [4,] -1,588609 ## [5,] -1,399489
# Квантильная скорость набора данных автомобилей квантиль (скорость)
Выход:
## 0% 25% 50% 75% 100% ## 4 12 15 19 25
# Суммарная скорость набора данных автомобилей резюме (скорость)
Выход:
## Мин.1st Qu. Среднее значение 3-го кв. Максимум. ## 4.0 12.0 15.0 15.4 19.0 25.0
К этому моменту мы изучили множество встроенных функций R.
Примечание : будьте осторожны с классом аргумента, то есть числовым, логическим или строковым. Например, если нам нужно передать строковое значение, нам нужно заключить строку в кавычки: «ABC».
Функция записи в R
В некоторых случаях нам нужно написать нашу собственную функцию, потому что мы должны выполнить конкретную задачу, а готовой функции не существует.Пользовательская функция включает имя , аргументов и тело .
function.name <- функция (аргументы)
{
вычисления аргументов
какой-то другой код
}
Примечание : Хорошая практика состоит в том, чтобы назвать пользовательскую функцию отличным от встроенной функции. Это позволяет избежать путаницы.
Функция с одним аргументом
В следующем фрагменте мы определяем простую квадратную функцию. Функция принимает значение и возвращает квадрат значения.2 } # вызов функции и передача значения 4 квадратная функция (4)
Пояснение кода:
# после создания функции
rm (square_function) square_function
На консоли мы видим сообщение об ошибке: Ошибка: объект 'square_function' не найден, что говорит о том, что функция не существует.
Область действия среды
В R среда представляет собой коллекцию объектов, таких как функции, переменные, фрейм данных и т. Д.
R открывает среду при каждом запросе Rstudio.
Доступная среда верхнего уровня - это глобальная среда , которая называется R_GlobalEnv. И у нас есть локальная среда .
Мы можем перечислить содержимое текущей среды.
ls (environment ())
Output
## [1] "diff_ts" "dt" "speed" "square_function" ## [5] "ts" "x" "x_vector"
Вы можете увидеть все переменные и функции, созданные в R_GlobalEnv.
Приведенный выше список будет отличаться для вас в зависимости от исторического кода, который вы выполняете в R Studio.
Обратите внимание, что n, аргумент функции square_function - , не в этой глобальной среде .
Для каждой функции создается новая среда . В приведенном выше примере функция square_function () создает новую среду внутри глобальной среды.
Чтобы прояснить разницу между глобальной и локальной средой , давайте рассмотрим следующий пример
Эта функция принимает значение x в качестве аргумента и добавляет его к определению y снаружи и внутри функции
Функция f возвращает значение вывод 15.Это потому, что y определяется в глобальной среде. Любая переменная, определенная в глобальной среде, может использоваться локально. Переменная y имеет значение 10 во время всех вызовов функций и доступна в любое время.
Посмотрим, что произойдет, если переменная y определена внутри функции.
Нам нужно отбросить `y` перед запуском этого кода с помощью rm r
Вывод также равен 15, когда мы вызываем f (5), но возвращает ошибку, когда мы пытаемся напечатать значение y. Переменная y не входит в глобальную среду.
Наконец, R использует самое последнее определение переменной для передачи внутри тела функции. Давайте рассмотрим следующий пример:
R игнорирует значения y, определенные вне функции, потому что мы явно создали переменную y внутри тела функции.
Функция с несколькими аргументами
Мы можем написать функцию с несколькими аргументами. Рассмотрим функцию под названием «раз». Это простая функция умножения двух переменных.
раз <- функция (х, у) {
х * у
}
раз (2,4)
Вывод:
## [1] 8
Когда писать функцию?
Специалисту по обработке данных необходимо выполнять множество повторяющихся задач.В большинстве случаев мы многократно копируем и вставляем фрагменты кода. Например, перед запуском алгоритма машинного обучения настоятельно рекомендуется нормализовать переменную. Формула для нормализации переменной:
Мы уже знаем, как использовать функции min () и max () в R. Мы используем библиотеку tibble для создания фрейма данных. Tibble пока что является самой удобной функцией для создания набора данных с нуля.
библиотека (табл.) # Создать фрейм данных data_frame <- тиббл ( c1 = rnorm (50, 5, 1.5), c2 = rnorm (50, 5, 1.5), c3 = rnorm (50, 5, 1.5), )
Мы выполним два шага для вычисления функции, описанной выше. На первом этапе мы создадим переменную c1_norm, которая является масштабированием c1. На втором шаге мы просто копируем и вставляем код c1_norm и меняем его с помощью c2 и c3.
Деталь функции со столбцом c1:
Номинатор:: data_frame $ c1 -min (data_frame $ c1))
Знаменатель: max (data_frame $ c1) -min (data_frame $ c1))
Следовательно, мы можно разделить их, чтобы получить нормализованное значение столбца c1:
(data_frame $ c1 -min (data_frame $ c1)) / (max (data_frame $ c1) -min (data_frame $ c1))
Мы можем создать c1_norm, c2_norm и c3_norm:
Создать c1_norm: масштабирование c1 кадр_данных $ c1_norm <- (кадр_данных $ c1 -min (кадр_данных $ c1)) / (макс (кадр_данных $ c1) -min (кадр_данных $ c1)) # показать первые пять значений голова (data_frame $ c1_norm, 5)
Выход:
## [1] 0.3400113 0,4198788 0,8524394 0,4925860 0,5067991
Работает. Мы можем скопировать и вставить
data_frame $ c1_norm <- (data_frame $ c1 -min (data_frame $ c1)) / (max (data_frame $ c1) -min (data_frame $ c1))
, затем измените c1_norm на c2_norm и c1 на c2. Мы делаем то же самое для создания c3_norm
data_frame $ c2_norm <- (data_frame $ c2 - min (data_frame $ c2)) / (max (data_frame $ c2) -min (data_frame $ c2)) data_frame $ c3_norm <- (data_frame $ c3 - min (data_frame $ c3)) / (max (data_frame $ c3) -min (data_frame $ c3))
Мы отлично изменили масштаб переменных c1, c2 и c3.
Однако этот метод подвержен ошибкам. Мы могли скопировать и забыть изменить имя столбца после вставки. Поэтому рекомендуется писать функцию каждый раз, когда вам нужно вставить один и тот же код более двух раз. Мы можем преобразовать код в формулу и вызывать ее, когда это необходимо. Чтобы написать нашу собственную функцию, нам нужно указать:
- Имя: normalize.
- количество аргументов: нам нужен только один аргумент, который является столбцом, который мы используем в наших вычислениях.
- Тело: это просто формула, которую мы хотим вернуть.
Мы будем шаг за шагом создавать функцию normalize.
Шаг 1) Создаем номинатор , то есть. В R мы можем сохранить знаменатель в переменной следующим образом:
nominator <- x-min (x)
Шаг 2) Мы вычисляем знаменатель : . Мы можем воспроизвести идею шага 1 и сохранить вычисление в переменной:
знаменатель <- max (x) -min (x)
Шаг 3) Мы выполняем деление между знаменателем и знаменателем.
normalize <- nominator / denominator
Шаг 4) Чтобы вернуть значение вызывающей функции, нам нужно передать normalize внутри return (), чтобы получить результат функции.
return (normalize)
Шаг 5) Мы готовы использовать функцию, заключив все в скобки.
normalize <- function (x) {
# шаг 1: создайте номинатора
номинатор <- x-min (x)
# шаг 2: создайте знаменатель
знаменатель <- max (x) -min (x)
# шаг 3: разделите знаменатель на знаменатель
нормализовать <- знаменатель / знаменатель
# вернуть значение
вернуть (нормализовать)
}
Давайте протестируем нашу функцию с переменной c1:
normalize (data_frame $ c1)
Работает отлично.Мы создали нашу первую функцию.
Функции - это более комплексный способ выполнения повторяющейся задачи. Мы можем использовать формулу нормализации для разных столбцов, как показано ниже:
data_frame $ c1_norm_function <- нормализовать (data_frame $ c1) data_frame $ c2_norm_function <- нормализовать (data_frame $ c2) data_frame $ c3_norm_function <- нормализовать (data_frame $ c3)
Несмотря на то, что пример прост, мы можем сделать вывод о силе формулы. Приведенный выше код легче читать и особенно избегать ошибок при вставке кодов.
Функции с условием
Иногда нам нужно включить в функцию условия, чтобы код мог возвращать разные выходные данные.
В задачах машинного обучения нам нужно разделить набор данных между набором поездов и набором тестов. Набор поездов позволяет алгоритму учиться на данных. Чтобы проверить производительность нашей модели, мы можем использовать набор тестов, чтобы получить показатель производительности. В R нет функции для создания двух наборов данных. Для этого мы можем написать нашу собственную функцию.Наша функция принимает два аргумента и называется split_data (). Идея проста: мы умножаем длину набора данных (то есть количество наблюдений) на 0,8. Например, если мы хотим разделить набор данных 80/20, а наш набор данных содержит 100 строк, тогда наша функция умножит 0,8 * 100 = 80. 80 строк будут выбраны, чтобы стать нашими обучающими данными.
Мы будем использовать набор данных о качестве воздуха для тестирования нашей пользовательской функции. Набор данных о качестве воздуха состоит из 153 строк. Мы можем увидеть это с помощью кода ниже:
nrow (airquality)
Выход:
## [1] 153
Мы будем действовать следующим образом:
split_data <- function (df, train = TRUE) Аргументы: -df: определить набор данных -train: укажите, возвращает ли функция набор поездов или набор тестов.По умолчанию установлено значение ИСТИНА
У нашей функции два аргумента. Цепочка аргументов - это логический параметр. Если установлено значение ИСТИНА, наша функция создает набор данных поезда, в противном случае - тестовый набор данных.
Мы можем продолжить, как мы делали с функцией normalize (). Мы пишем код, как если бы это был только одноразовый код, а затем оборачиваем все с условием в тело, чтобы создать функцию.
Шаг 1:
Нам нужно вычислить длину набора данных.Это делается с помощью функции nrow (). Nrow возвращает общее количество строк в наборе данных. Мы называем переменную длину.
длина <- nrow (качество воздуха) длина
Вывод:
## [1] 153
Шаг 2:
Мы умножаем длину на 0,8. Он вернет количество строк для выбора. Должно быть 153 * 0,8 = 122,4
total_row <- длина * 0,8 total_row
Вывод:
## [1] 122.4
Мы хотим выбрать 122 строки из 153 в наборе данных о качестве воздуха. Создаем список, содержащий значения от 1 до total_row. Мы сохраняем результат в переменной под названием split
split <- 1: total_row split [1: 5]
Вывод:
## [1] 1 2 3 4 5
split выбирает первые 122 строки из набора данных. Например, мы видим, что наша переменная split собирает значения 1, 2, 3, 4, 5 и так далее. Эти значения будут индексом, когда мы выберем строки для возврата.
Шаг 3:
Нам нужно выбрать строки в наборе данных о качестве воздуха на основе значений, хранящихся в переменной разделения. Это делается так:
train_df <- airquality [split,] head (train_df)
Вывод:
## [1] Ozone Solar.R Wind Temp Месяц День ## [2] 51 13 137 10,3 76 6 20 ## [3] 15 18 65 13,2 58 5 15 ## [4] 64 32 236 9,2 81 7 3 ## [5] 27 NA NA 8.0 57 5 27 ## [6] 58 Н / Д 47 10,3 73 6 27 ## [7] 44 23 148 8,0 82 6 13
Шаг 4:
Мы можем создать тестовый набор данных, используя оставшиеся строки, 123: 153. Это делается с помощью - перед разделением.
test_df <- качество воздуха [-split,] head (test_df)
Вывод:
## [1] Ozone Solar.R Wind Temp Месяц День ## [2] 123 85 188 6,3 94 8 31 ## [3] 124 96 167 6.9 91 9 1 ## [4] 125 78 197 5,1 92 9 2 ## [5] 126 73 183 2,8 93 9 3 ## [6] 127 91 189 4,6 93 9 4 ## [7] 128 47 95 7,4 87 9 5
Шаг 5:
Мы можем создать условие внутри тела функции. Помните, что у нас есть поезд аргументов, который является логическим значением, по умолчанию установленным в ИСТИНА, чтобы вернуть набор поездов. Для создания условия мы используем синтаксис if:
if (train == TRUE) {
train_df <- качество воздуха [сплит,]
возврат (поезд)
} еще {
test_df <- качество воздуха [-split,]
возврат (тест)
}
Вот и все, мы можем написать функцию.Нам нужно только изменить качество воздуха на df, потому что мы хотим попробовать нашу функцию с любым фреймом данных, а не только с качеством воздуха:
split_data <- function (df, train = TRUE) {
длина <- nrow (df)
total_row <- длина * 0,8
split <- 1: total_row
if (train == TRUE) {
train_df <- df [split,]
возврат (train_df)
} еще {
test_df <- df [-split,]
возврат (test_df)
}
}
Давайте попробуем нашу функцию на наборе данных о качестве воздуха.у нас должен быть один набор со 122 строками и тестовый набор с 31 строкой.
поезд <- split_data (качество воздуха, поезд = ИСТИНА) dim (train)
Вывод:
## [1] 122 6
test <- split_data (airquality, train = FALSE) dim (тест)
Выход:
## [1] 31 6
Постоянная функция | Определение | Графики | Примеры
Функции могут быть увеличивающими, убывающими и постоянными.
Мы знаем, что функция - это
- Увеличивается в своей области, если она непрерывно растет слева направо.
- Уменьшается в своем домене, если он непрерывно падает слева направо.
В частности, функция, представляющая прямую линию, увеличивается, когда ее наклон положительный, и уменьшается, когда ее наклон отрицательный.
Но существует ли какая-либо функция, представляющая прямую линию, которая не увеличивается и не убывает?
Да, и такие функции называются постоянными функциями.
Давайте узнаем больше о постоянных функциях здесь.
План урока Что вы подразумеваете под постоянной функцией?Постоянная функция - это линейная функция, диапазон которой содержит только один элемент независимо от количества элементов домена.
Рассмотрим функцию \ [f (x) = 3 \]
В определении (справа) нет переменной.
Это означает, что он всегда будет генерировать результат, равный 3, независимо от того, какое входное значение мы ему дадим.
Следовательно, эта конкретная функция является постоянной функцией.
Таким образом, постоянная функция имеет вид
| \ (f (x) = k \), где \ (k \) - постоянная. |
Графики постоянных функций
Из приведенного выше объяснения, постоянная функция относится к функции с действительным знаком, в определении которой нет переменной.
Рассмотрим постоянную функцию \ (f (x) = 3 \), где \ (f: R \ rightarrow R \).
Это означает, что он всегда будет генерировать результат, равный 3, независимо от того, какое входное значение мы ему дадим.
Таким образом, некоторые точки на его графике могут быть (-1, 3), (2, 3), (4, 3) и т. Д.
Давайте просто нарисуем все такие точки, соединим их и посмотрим, что у нас получится.
Итак, график \ (f (x) = 3 \) представляет собой горизонтальную линию, поскольку координаты y всех точек совпадают (как 3)
Следовательно,
| Графики всех постоянных функций представляют собой горизонтальные линии. |
Характеристики постоянной функции Наклон постоянной функции
Мы знаем, что постоянная функция имеет вид \ (f (x) = k \) (или) \ (y = k \).
Это можно записать как \ (y = 0x + k \).
Сравнивая это с формой пересечения наклона \ (y = mx + b \), мы получаем, что его наклон равен \ (m = 0 \). Таким образом,
| Наклон постоянной функции равен 0 |
Поскольку постоянная функция определена для всех действительных значений \ (x \), ее областью определения является набор всех действительных чисел, \ (\ mathbb {R} \).
Поскольку постоянная функция \ (f (x) = k \) приводит только к одному выходу, то есть \ (k \), ее диапазон - это набор только с одним элементом \ (k \).
| Домен = \ (\ mathbb {R} \) Диапазон = \ (\ {k \} \) |
Помимо этого, некоторые другие характеристики постоянных функций:
- Постоянные функции являются непрерывными, поскольку они представляют собой горизонтальные линии, которые непрерывно проходят с обеих сторон без каких-либо разрывов.
- Постоянные функции измеримы, потому что если \ (f: A \ rightarrow \ {k \} \) является постоянной функцией, то набор обратных изображений для \ (f \) будет либо \ (\ phi \), либо \ (A \ ).
Советы и хитрости
- График постоянной функции никогда не может быть кривой.
- График постоянной функции всегда представляет собой горизонтальную линию. 2 = 1 \)
г) \ (у-2 = 0 \)
д) \ (у = х \)Решение
Сначала мы решаем каждое уравнение относительно \ (y \).2} \)
г) \ (у = 2 \)
д) \ (у = х \)Среди них те, у которых в правой части только константа, есть \ (y = \ pi \) и \ (y = 2 \).
\ (\ следовательно \) Постоянные функции:
б) и г).Что из следующего может представлять постоянную функцию (-ы)?
Решение
Мы знаем, что график постоянной функции всегда представляет собой горизонтальную линию.
Среди приведенных графиков только (d) и (e) являются горизонтальными линиями.
\ (\ следовательно \) Постоянные функции:
(d) и (e).
Интерактивные вопросыВот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Сложные вопросы
- Является ли график вертикальной линии постоянной функцией?
Подсказка: подумайте, не является ли это функцией.Вы можете применить тест вертикальной линии. - Постройте график следующей постоянной функции:
\ [f (x) = \ left \ {\ begin {array} {ll}
1, & x \ in [-1,2] \\
2, & x \ in (2,3]
\ end {array} \ right. \]
Мини-урок был посвящен увлекательной концепции постоянных функций. Математическое путешествие вокруг постоянных функций начинается с того, что студент уже знает, и переходит к творческому созданию новой концепции в молодых умах.Сделано таким образом, чтобы не только было понятно и легко понять, но и навсегда осталось с ними. В этом заключается магия Куэмат.
О компании CuemathВ Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, это логическое мышление и интеллектуальный подход к обучению, в которые мы, в Cuemath, верим.
Часто задаваемые вопросы о постоянных функциях1. Что такое уравнение постоянной функции?
Уравнение постоянной функции имеет вид f (x) = k, где k - постоянная.
2. Как узнать, постоянна ли функция?
Если в определении функции нет переменной, то это постоянная функция.
Например, f (x) = 5 - постоянная функция.
3. Является ли постоянная функция линейной?
Графики как линейных, так и постоянных функций представляют собой прямые линии.
Итак, постоянная функция линейна.
В частности, это всегда горизонтальная линия.
4. Может ли постоянная функция быть на?
Да, постоянная функция f (x) = k может быть включена, если ее codomain такой же, как и ее диапазон (который равен {k}).
5. Какова степень постоянной функции?
Степень постоянной функции равна нулю, поскольку константа k может быть записана как kx 0 .
6. Сюръективна ли функция константы?
Постоянная функция НЕ сюръективна, так как НЕ является однозначной.
7. Что такое постоянная функция и функция идентичности?
Постоянная функция имеет вид f (x) = k, где k - постоянная.
Идентификационная функция имеет вид f (x) = x.
8. Может ли постоянная функция быть 1-1?
Постоянная функция является однозначной только тогда, когда ее домен имеет ровно один элемент.
9. Какая производная постоянной функции?
Производная постоянной функции всегда равна нулю.
- Является ли график вертикальной линии постоянной функцией?
 general function
general function
 е. функция имеющая, кроме периода еще квазипериод при прибавлении к poro к значению аргумента значение функции умножается на нек рый… … Математическая энциклопедия
е. функция имеющая, кроме периода еще квазипериод при прибавлении к poro к значению аргумента значение функции умножается на нек рый… … Математическая энциклопедия . Что объединяет «молодых старомодников» и конголезских sapeurs, что общего между pijama и баньяном, архитектурой и одеждой? Как связаны парижский щеголь и участники» пятниц без галстуков»?В… Подробнее Купить за 491 руб
. Что объединяет «молодых старомодников» и конголезских sapeurs, что общего между pijama и баньяном, архитектурой и одеждой? Как связаны парижский щеголь и участники» пятниц без галстуков»?В… Подробнее Купить за 491 руб