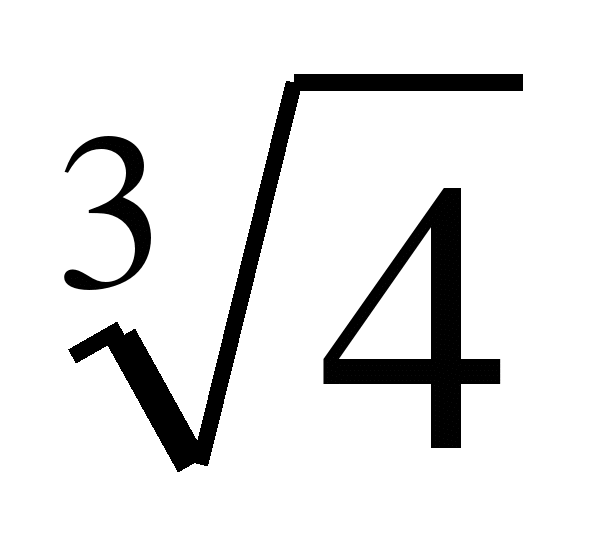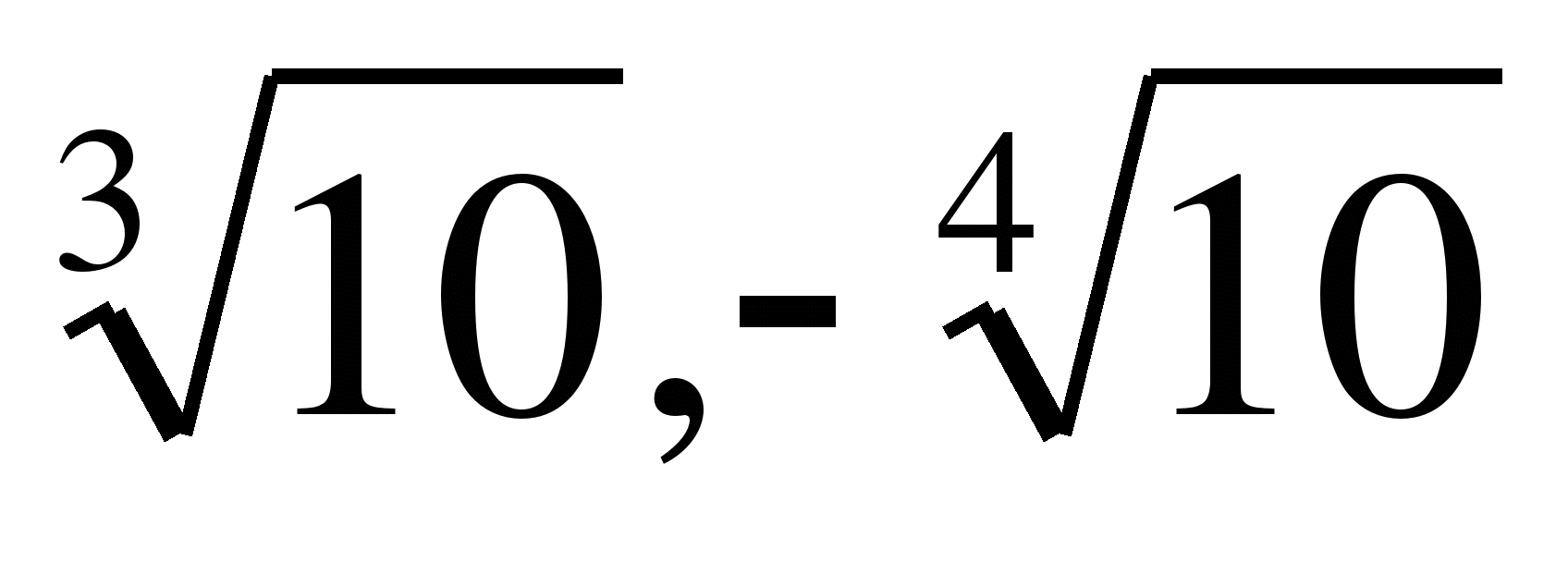Свойства корня n — степени
Вопросы занятия:
· сформулировать и доказать свойства корня n-ой степени из неотрицательного числа, в случае натурального n;
· рассмотреть примеры использования этих свойств на примерах.
Материал урока
Прежде чем перейти к изучению нового материала, давайте повторим основные понятия, с которыми мы познакомились на предыдущих уроках.
Корнем n-ой степени из неотрицательного числа a называют такое неотрицательное число, при возведении которого в степень n получается число а.
Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.
Обозначают:

Число а – это подкоренное число, число n – показатель корня.
На сегодняшнем уроке мы рассмотрим основные свойства операции извлечения корня n-ой степени.
Итак, первое свойство формулируется следующей теоремой.
Теорема 1.
Корень n-ой степени (где n = 2, 3, 4, …) из произведения двух неотрицательных чисел равен произведению корней n-ой степени из этих чисел.

Доказательство.
Введём следующие обозначения:

Нам надо доказать, что для неотрицательных чисел x, y, z выполняется равенство x = yz.
Из определения корня n-ой степени из неотрицательного числа мы знаем:

После замены в равенстве чисел a, b, произведения ab на соответствующие им выражения, получим, что:

Что и требовалось доказать.
Очевидно, что теорема остаётся справедливой и для случая, когда подкоренное выражение представляет собой произведение более чем двух неотрицательных чисел.
Рассмотрим следующее свойство.
Сформулируем теорему.
Теорема 2.
Если a ≥ 0, b>0 и n – натуральное число,

Доказательство.
Доказывать это свойство мы будем аналогично предыдущему. Введём обозначения.

Используя определение корня n-ой степени из неотрицательного числа, можно записать:

Получим:

Что и требовалось доказать.
Давайте рассмотрим несколько примеров.
Пример.

Пример.

Рассмотрим ещё одно свойство корня n-ой степени из неотрицательного числа.
Теорема 3.
Если a ≥ 0, k – натуральное число и n – натуральное число, n > 1, то справедливо равенство:

Другими словами, чтобы возвести корень в натуральную степень достаточно возвести в эту степень подкоренное выражение.
Доказательство.
Эта теорема является следствием теоремы 1. Если k = 3, то получим:

Точно так же можно рассуждать в случае любого другого натурального значения показателя k.
Рассмотрим ещё одно свойство.
Теорема 4.
Если a ≥ 0, k – натуральное число и n – натуральное число, n > 1, то справедливо равенство:

Доказательство этого свойства вы можете провести самостоятельно, оно аналогично доказательству первой и второй теоремы.
Мы с вами научились перемножать, делить, возводить в степень и извлекать корень из корней n-ой степени из неотрицательного числа. А как же складывать и отнимать такие корни? Никак. Их нельзя просто так складывать и вычитать. Надо преобразовывать каждый корень, а затем, если это возможно, складывать полученные результаты.
Рассмотрим это на примере.
Пример.

Рассмотрим ещё одно свойство корней n-ой степени из неотрицательных чисел.
Теорема 5.
Если показатели корня и степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.

Например.

Доказательство.
Введём некоторые обозначения:

Тогда по определению корня n-ой степени из неотрицательного числа, можно записать:

Возведём обе части последнего равенства в одну и ту же степень p, получим:

Итак, получили:

Что и требовалось доказать.
Рассмотрим несколько примеров.
Пример.

Пример.

Пример.

Пример.

Давайте запишем свойства корней энной степени из неотрицательного числа ещё раз:

Обратите внимание, что мы рассматривали с вами свойства корней n-ой степени только из неотрицательных чисел. Потому что корень n-ой степени из отрицательного числа имеет смысл только при нечётных n. Для таких значений показателей корня рассмотренные свойства корней верны и в случае отрицательных подкоренных выражений.
Рассмотрим пример.

videouroki.net
35. Степени и корни. Корень n-й степени
Для всякого числа A Î R определена степень с натуральным показателем An, N Î N.
Число B Î R называется Корнем N-й степени, N Î N, N ³ 2, из числа А, если обозначают
Нахождение корня N-й степени из данного числа А называют Извлечением корня N-й степени Из числа А. Число А, из которого извлекается корень N-й степени, называют Подкоренным выражением, а число N – Показателем корня.
Если то определен для всех A Î R и принимает любые действительные значения.
Если то определен для всех A ³ 0 (A Î R). В курсе элементарной математики рассматривают Арифметическое значение корня, т. е. число
Свойства корней
Пусть A, B Î R, тогда:
1)
2)
3)
4)
5)
6) где A ³ 0 в случае
7) где в случае
8) где в случае
Пример 1. Вычислить
Решение. 1-й способ. Выделим полные квадраты подкоренных выражений:
Тогда получим
2-й способ. Обозначим вычисляемое выражение через A, т. е.
Заметим, что
Возведем обе части полученного равенства в квадрат:
Тогда
Поскольку исходное выражение положительно, в ответе получаем A = 4.
Пример 2. Упростить выражение
Решение. 1-й способ. Используем формулы квадрата разности и суммы, а также свойства корней. Получаем:
2-й способ. При упрощении иррациональных выражений часто бывает эффективным Метод рационализации, основанный на замене переменных.
Введем такую замену переменных, чтобы корни извлеклись:
Заданное выражение приобретает вид
Упрощаем его, используя формулы сокращенного умножения:
Возвращаясь к старым переменным, приходим к ответу
Пример 3. Избавиться от иррациональности в знаменателе:
1) 2) 3)
Решение. 1) Умножим числитель и знаменатель дважды на сопряженные выражения и воспользуемся формулой разности квадратов:
2) Домножим числитель и знаменатель на неполный квадрат разности и воспользуемся формулой суммы кубов:
3) Умножим числитель и знаменатель дважды на сопряженные выражения:
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Понятие корня n-ой степени из действительного числа. Видеоурок. Алгебра 11 Класс
На данном уроке мы рассмотрим понятие корня n-ной степени из действительного числа, дадим строгие определения и решим различные примеры на практическое применение данной конструкции.
Мы довольно долго не знали, что такое корень n-ой степени из действительного числа, и умели обходиться без этого понятия, но потом появились случаи, в которых обойтись без него уже невозможно.
Рассмотрим несколько простейших примеров.
Пример 1: 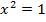
Решение:
Способ 1, аналитический. Перенесем все члены в левую часть уравнения так, чтобы справа остался  :
: 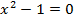 . Далее разложим на множители:
. Далее разложим на множители:  .
.
Каждый множитель приравниваем к нулю:
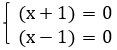
Получаем ответ:

Способ 2, графический. Построим кривую  и прямую
и прямую  (рис. 1). Получим
(рис. 1). Получим  и
и  в точках пересечения графиков.
в точках пересечения графиков.
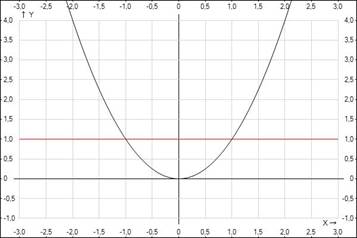
Рис. 1. График уравнений  и
и 
Ответ.  ,
,  .
.
Для решения этой задачи нам не потребовалось никаких новых методов.
Пример 2: 
Решение:
Способ 1. 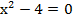 . Разложим на множители:
. Разложим на множители:  . Каждый множитель приравниваем к нулю:
. Каждый множитель приравниваем к нулю:
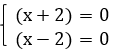
Получаем ответ:

Способ 2, графический. Построим график для системы (рис. 2), где первое уравнение – левая часть заданного выражения ( ), второе – правая (
), второе – правая (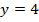 ):
):
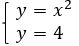
Ответами будут точки пересечения графиков, т. е.  и
и 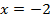 .
.
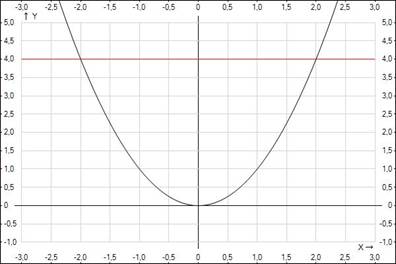
Рис. 2. График уравнений 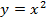 и
и 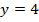
Ответ:  ,
, 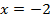 .
.
После решения двух задач нужды в новом слове не обнаружено.
Пример 3: x2=3
Решение:
Способ 1, аналитический. 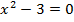 . Пытаемся разложить на множители, но ничего не выходит. Попробуем другой способ.
. Пытаемся разложить на множители, но ничего не выходит. Попробуем другой способ.
Способ 2, графический. Построим график для системы (рис. 3), где первое уравнение – левая часть заданного выражения ( ), второе – правая (
), второе – правая ( ):
):
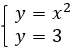

Рис. 3. График уравнений  и
и 
Видим, что графики пересекаются, а значит, ответы все же есть. Назовем их корень квадратный из 3 и минус корень квадратный из 3:

Ответ:  ,
, 
Определение:
Квадратный корень из трех – это иррациональное число, приближенное к десятичной дроби ( ). Так как
). Так как  , в дальнейшем будем считать его арифметическим корнем.
, в дальнейшем будем считать его арифметическим корнем.
Теперь нам нужно определить корень n-ой степени из действительного числа.
Рассмотрим еще один пример.
Пример 4: 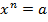 , где
, где  ,
, 

Рис. 4. График функций  и
и 
Уравнение имеет 2 корня:  и
и  .
.
Определение:
Корнем n-ой степени из неотрицательного числа а называют такое неотрицательное число, которое при возведении в степень n дает в результате число a.
Т. е. если  , то
, то 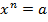 . Из этого следует тождество
. Из этого следует тождество  .
.
Напомним, что у любой функции, в том числе и у данной, есть 2 задачи: прямая (по данному х найти у) и обратная (по данному у, в данном случае равному а, найти х). Если значение а положительное и n четное, то значение у достигается при двух значениях аргумента – положительном и отрицательном. Положительное значение аргумента называется корнем n-ной степени из а, или арифметическим корнем n-ной степени из а.
Перейдем к нечетным степеням. Начнем с  .
.
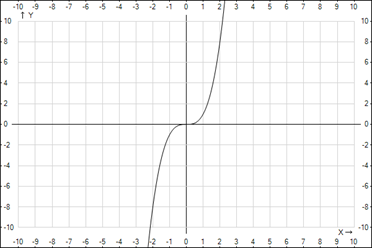
Рис. 5. График функции  , где
, где 
Свойства функции 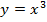 (рис. 5) отличаются от предыдущих. Напомним, что функция нечетная, график ее симметричен относительно начала координат; она принимает все значения от
(рис. 5) отличаются от предыдущих. Напомним, что функция нечетная, график ее симметричен относительно начала координат; она принимает все значения от  до
до  , а значит, любое свое значение у принимает при единственном значении х. Например,
, а значит, любое свое значение у принимает при единственном значении х. Например, 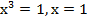 ;
;  ;
; 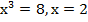 ;
;  ;
; 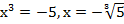 . По графику функции (рис. 5) находим решения.
. По графику функции (рис. 5) находим решения.
Итак, уравнение 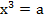 имеет единственный корень. Если этот корень неотрицательный, он называется арифметическим корнем, в противном случае – минус арифметическим корнем.
имеет единственный корень. Если этот корень неотрицательный, он называется арифметическим корнем, в противном случае – минус арифметическим корнем.
Если n – любое нечетное число, график функции  имеет тот же вид и те же свойства, что и
имеет тот же вид и те же свойства, что и 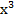 : функция нечетная, график симметричен относительно начала координат, область значений от
: функция нечетная, график симметричен относительно начала координат, область значений от  до
до  , любое значение, в том числе и отрицательное, функция принимает при единственном значении аргумента.
, любое значение, в том числе и отрицательное, функция принимает при единственном значении аргумента.
Определение:
Корнем нечетной степени из отрицательного числа а при 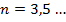 называют такое отрицательное число, которое, будучи возведено в степень n, дает в результате число а. Например,
называют такое отрицательное число, которое, будучи возведено в степень n, дает в результате число а. Например, т. к.
т. к. 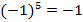 ;
;  т. к.
т. к.  ;
;  т. к.
т. к. 
Понятие корня n-ой степени из действительного числа позв
interneturok.ru
Корень n-ой степени
Вопросы занятия:
· повторить, как извлекается корень n-ой степени из числа;
· повторить свойства арифметического корня n-ой степени;
· показать, как можно применить свойства корня при решении задач.
Материал урока
Определение.
Корнем n-ой степени из числа а называется такое число, энная степень которого равна А.

Говоря о корне энной степени нужно понимать, что показатель корня n является натуральным числом.
Вам хорошо известен такой частный случай корня n-ой степени, как корень второй степени, то есть квадратный корень из числа. Показатель корня в этом случае не пишут.
Определение.
Квадратным корнем из числа называют такое число, квадрат которого равен числу а.

Например,

Ещё одним частным случаем является корень третьей степени, мы привыкли называть его корнем кубическим.
Например,

Вы могли задаться вопросом, почему.

Чтобы ответить на этот вопрос, рассмотрим два случая корня энной степени: где показатель корня является нечётным числом и где показатель корня является чётным числом.


Но чтобы избавиться от неоднозначности в вычислениях, договорились неотрицательный корень n-ой степени обозначать как «корень n-ой степени из а». А отрицательный как «минус корень n-ой степени из а».

Исходя из этой договорённости и становится понятно, что

Из рассмотренных случаев можем сделать заключение, что:

Пример.

Вернёмся к определению корня энной степени

В первую запись вместо можно подставить:

Тогда получаем свойство, которым очень удобно пользоваться при вычислении корня энной степени.
Но ведь корень чётной степени мы договорились считать числом неотрицательным. Поэтому чтобы не возникало путаницы при вычислении корней, вместо этого свойства мы пользовались двумя:

Пример.

Вы видите, что корень энной степени из любого неотрицательного числа а имеет смысл при любых Эн и принимает неотрицательные значения. Такой корень называют арифметическим корнем n-ой степени из числа а.
Любой корень можно выразить через арифметический.
Корни чётных степеней всегда являются арифметическими, ведь подкоренное выражение у них является числом неотрицательным, и под их значениями мы условились понимать неотрицательные числа.
Это же касается корней нечётных степеней из неотрицательных чисел.
А вот, например, корни нечётных степеней из отрицательных чисел можно записать так, при этом вынеся минус перед корнем.

Таким образом, при работе с любым корнем энной степени можно всегда перейти к рассмотрению арифметического корня.
Также при работе с корнями энной степени очень важно знать ещё несколько свойств. Напомним их.

Все эти свойства пригодятся вам при работе с выражениями, содержащими знак корня.
Итоги урока
На этом уроке мы с вами вспомнили, как извлекать корень n-ой степени из числа. Напомнили, что корень n-ой степени из неотрицательного числа считают числом неотрицательным, и называют «арифметическим корнем n-ой степени».
Так корень чётной степени из неотрицательного числа всегда является корнем арифметическим и поэтому равен числу неотрицательному. А корня чётной степени из отрицательного числа не существует. Корень нечётной степени из неотрицательного числа равен числу неотрицательному. Например, корень третьей степени из двадцати семи равен трём.
Ну, а корень нечётной степени из отрицательного числа равен числу отрицательному. Его нужно выражать с помощью арифметического корня n-ой степени, при этом вынося минус из-под знака корня. Также мы напомнили свойства арифметического корня энной степени и применили их на конкретных примерах.


videouroki.net
Корень n-й степени
Определение.
Корнем n-й степени из числа а называется такое число, n-я степень которого равна а, где:
n - показатель корня;
а — выражение, стоящее под знаком корня — подкоренным выражением.
Заметим, что для корня 2 — й степени показатель не пишут, и такой корень называют квадратным корнем.
Рассмотрим примеры:

Заметим, что в зависимости от того чётное или нечётное n, можно получить 1 или 2 значения.
Рассмотрим случай, когда n - нечётное число.

Заметим, что каждому значению а соответствует единственное значение х.
Например:

Рассмотрим случай, когда n - чётное число. Рассмотрим график такой функции:

Если
a>0,
то существует два значения,  и
и
 .
.
Если a=0, то существует только одно значение, x=0.
Вывод:
Корень нечётной степени имеет смысл при любом значении а, а корень чётной степени имеет смысл только при неотрицательных значениях а.
Рассмотрим пример: найти выражения не имеющие смысла.

Не имеют смысла выражения только корень чётной степени, когда подкоренное выражение меньше нуля:


Определение:
Корень n-й степени из а, где a≥0, имеет смысл при любых n. Его называют арифметическим корнем n-й степени.
Найдём значения данных выражений:

Подкоренное выражение a<0 может быть в случае, когда имеем дело с корнем нечётной степени. Но и его можно выразить через арифметический корень этой степени.
Найдём значения выражений:

Пример.
Найти
значение выражения  .
.

videouroki.net
Корень n-ой степени и его свойства.
Корень n-й степени и его свойства. 11 класс.
А.Г. Мордкович. Алгебра и начала анализа.
Цели урока:
Образовательная: расширить и обобщить знания учащихся по данной теме, овладеть свойствами корня п-ой степени.
Развивающая: развитие коммуникативных способностей.
Воспитательная: формирование активной жизненной позиции, умение работать и преодолевать трудности, воспитание интереса к предмету.
Средства обучения: карточки, таблицы.
Тип урока: урок обобщения и систематизации знаний.
Форма обучения: индивидуальная и групповая.
Ход урока
«Мышление начинается с удивления»
Аристотель
Организационный момент: приветствие, выявление готовности учащихся к уроку, постановка цели.
Разминка.
Актуализация опорных знаний.
Обобщение и закрепление материала.
Ход урока.
Вопросы для разминки.
Так называют выражение хn. (степень)
Есть у любого слова, у растения, может быть n-й степени. (корень)
Степень корня, кратная 2. (четная)
Степень корня 2 k+1. (нечетная).
Как можно иначе назвать корень третьей степени? (кубический)
Действие, посредством которого отыскивают корень. (извлечение).
Положительный корень. (арифметический).
Как можно иначе назвать арифметический корень второй степени? (квадратный).
Актуализация опорных знаний.
а) Свойства арифметического квадратного корня:
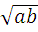 =
= 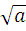 ∙
∙ 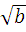 , а ≥ 0 , в ≥0
, а ≥ 0 , в ≥0
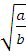 =
= 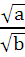 , а≥0, b
, а≥0, b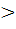 0
0
б) свойства степени с натуральным показателем:
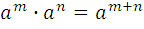
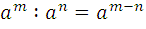
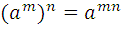
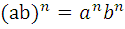
 =
= 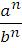
Формирование новых знаний. Аналогично определению квадратного корня из числа a определяется корень n-ной степени из числа а, где n— произвольное натуральное число, n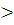 1.
1.
Определение. Корнем n-ной степени из числа а называется такое число, n—ная степень которого равна а.
а) 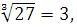
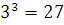
б 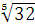 =2,
=2, 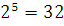
в) 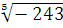 = -3
= -3
Рассмотрим уравнение 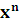 = a. Число корней этого уравнения зависит от n и a.
= a. Число корней этого уравнения зависит от n и a.
Рассмотрим функцию f(x)=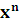 . При x
. При x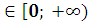 и n –любое число- возрастает, и a
и n –любое число- возрастает, и a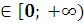 имеет неотрицательный корень и только один x=
имеет неотрицательный корень и только один x=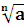 .
.
Определение. Арифметическим корнем n-ной степени из числа a называют неотрицательное число, n -ая степень которого равна a.
При четном n существует два корня n—ной степени из любого положительного числа a, корень четной степени из отрицательных чисел не существует. При нечетном n существует корень n—ной из любого числа a и притом только один.
Краткая запись (в тетради).
n— четное число
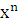 =a, a>0
=a, a>0
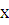 =
=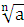
X= —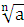
а) 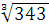 = 7 , 7 =343 в)
= 7 , 7 =343 в)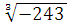 = -3
= -3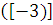 = -243
= -243
основные свойства арифметических корней n-ной степени.
Для любых чисел n € N , k € N, n >1 и k>1 , a>0, b>0 выполняются равенства :
 =
= ∙
∙ ;
; =
=  ;
; =
= ;
;
 =(
=(  ) k
) k >
>  0≤ a a>b
0≤ a a>b
Обобщение и закрепление материала.
Задание 1. Вычислите.
а) 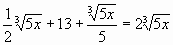
б) 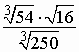
в) 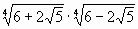
Задание2. Докажите:
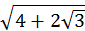 —
—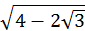 =2
=2
Задание3. Вычислите.
1)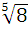 ∙
∙ 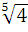 =
= 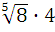 =
= 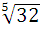 = 2
= 2
2) 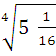 =
= 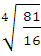 =
= 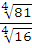 =
= 
3) 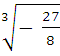 =
= 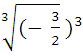 = —
= — 
Трехуровневая самостоятельная работа с целью проверить знания, умения и навыки по теме
« Корень п-ой степени и его свойства»
№ 1. Вычислить (А)
1 вариант 2 вариант
вариант 2 вариант
 ∙
∙  1)
1)  ;
;– 2
 ; 2)
; 2)  ∙
∙  ;
; ; 3) -6 ∙
; 3) -6 ∙  ;
;
№ 2 . Найдите значение выражения (В)

1) 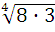 ∙
∙ 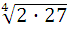 = 1)
= 1) 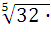 7
7 ∙
∙ 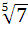
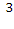 =
=
2) 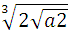 = 2)
= 2)  =
=
№ 3. Упростите (С)
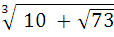
 ∙
∙ 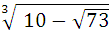
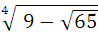 ∙
∙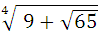
Подведение итогов урока
Проверка работы учащихся: выставление оценок.
infourok.ru
Разработка конспекта урока «Корень n-ой степени и его свойства
Тема: «Корень n-ой степени и его свойства».
Цели урока:
Ввести понятие корня n-ой степени из действительного числа;
Изучить свойства корня n-ой степени.
Задачи урока:
Тип урока: изучение и первичное закрепление новых знаний.
Формы контроля: самопроверка самостоятельно решённых задач, проверка самостоятельной работы преподавателем на оценку.
Оборудование: ноутбук, мультимедийный проектор, экран.
План урока:
организационный момент;
проверка дз;
повторение опорных знаний;
изучение нового материала;
первичное закрепление изученного материала;
самостоятельная работа;
рефлексия;
подведение итогов, дз.
Ход урока.
Приветствие
Здравствуйте, ребята. Сегодня на уроке мы познакомимся со следующими понятиями: корень n-ой степени, арифметический корень n-ой степени из числа, с решениями уравнений вида хn=a.
Проверка дз (один студент решает на доске, у 5 проверяет учитель по тетрадям).
П
 овторить определение квадратного корня из числа а, степени с натуральным, нулевым, целым отрицательным и рациональным показателем.
овторить определение квадратного корня из числа а, степени с натуральным, нулевым, целым отрицательным и рациональным показателем.
аn=а·а·а···а , 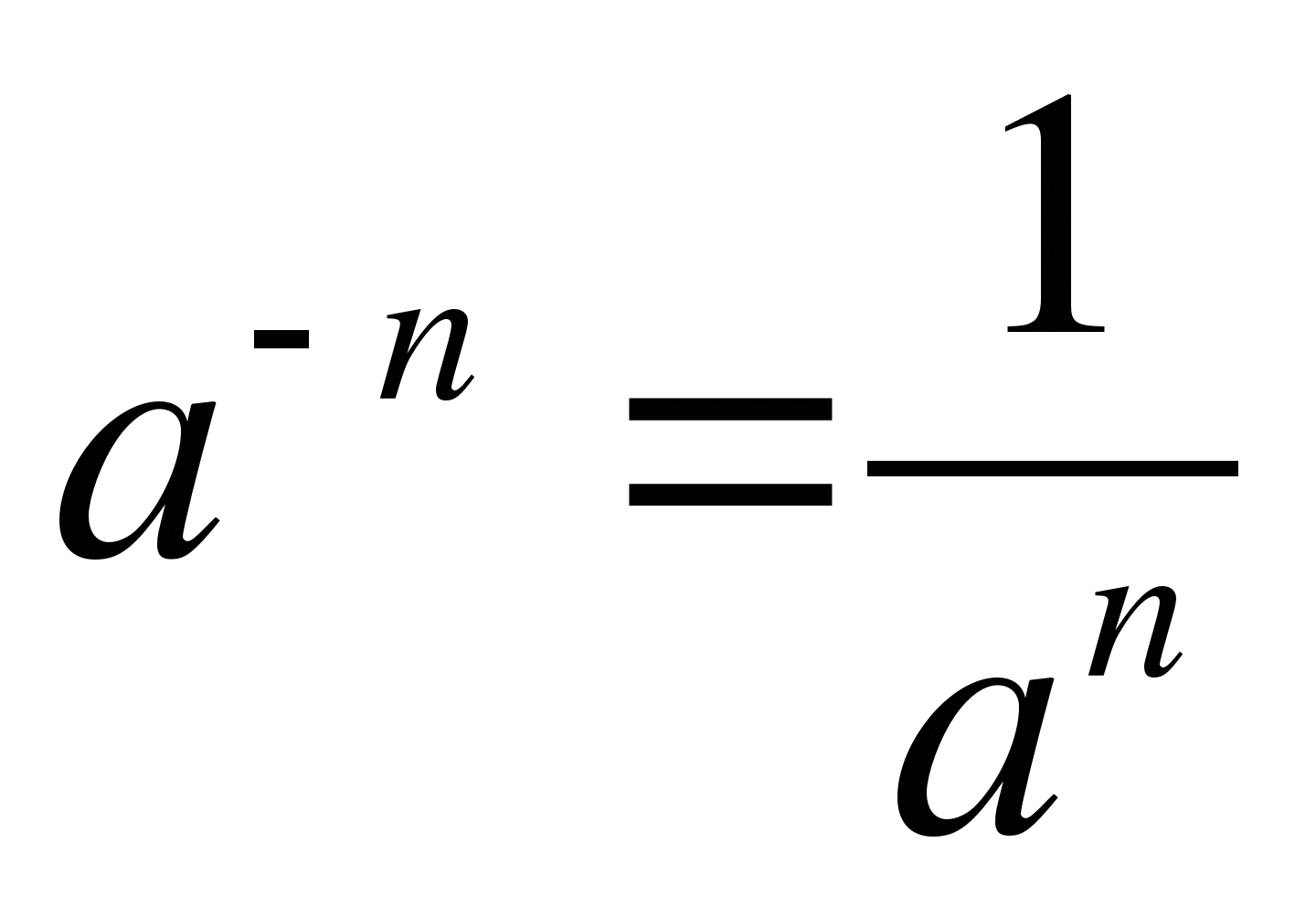 , a≠0, a0=1, a≠0,
, a≠0, a0=1, a≠0,
n
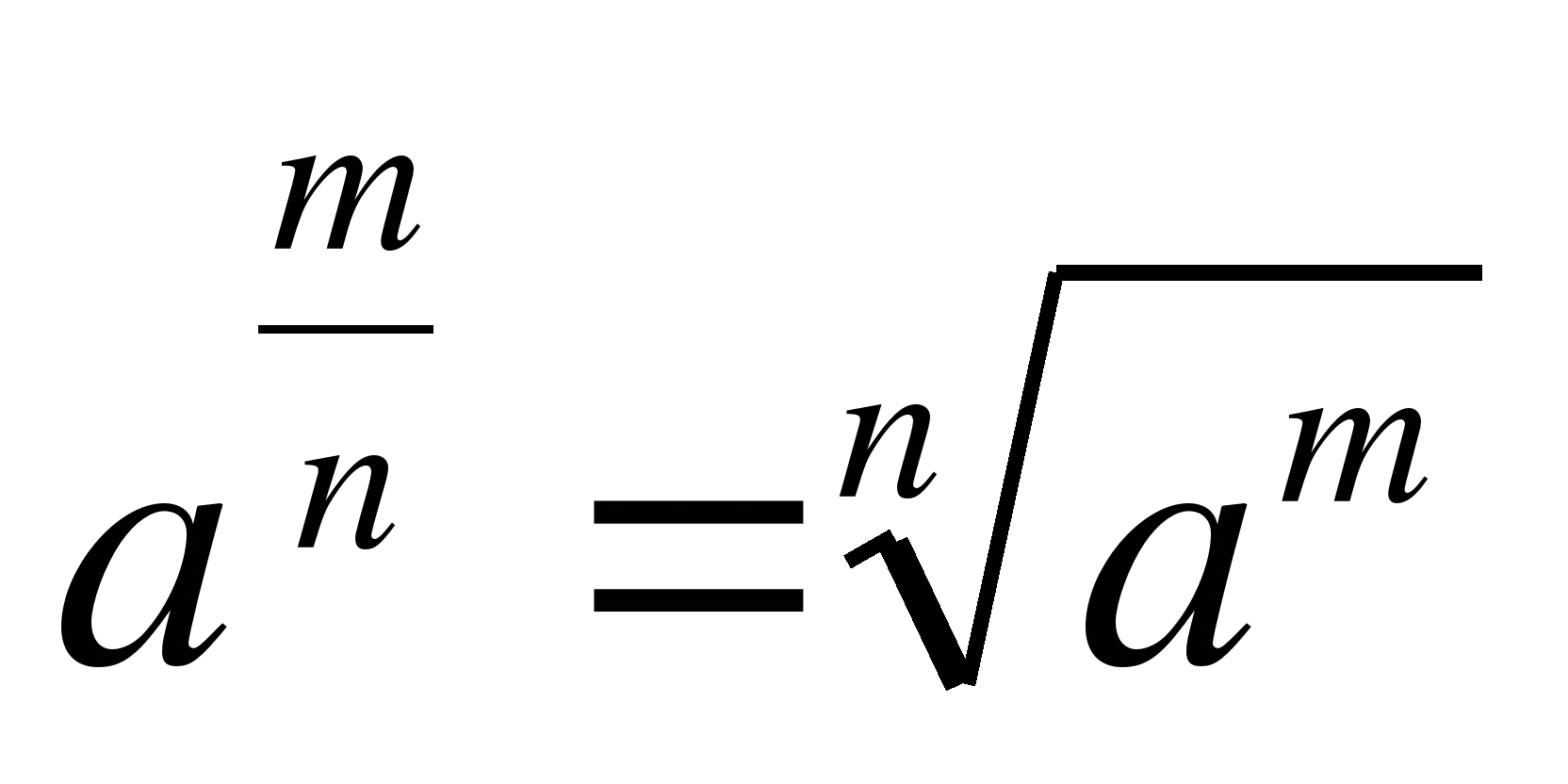 , a>0, mєZ, nєZ, n≥2
, a>0, mєZ, nєZ, n≥2
Повторить свойства степеней с рациональным показателем:
10. ах ·ау=ах+у
20. 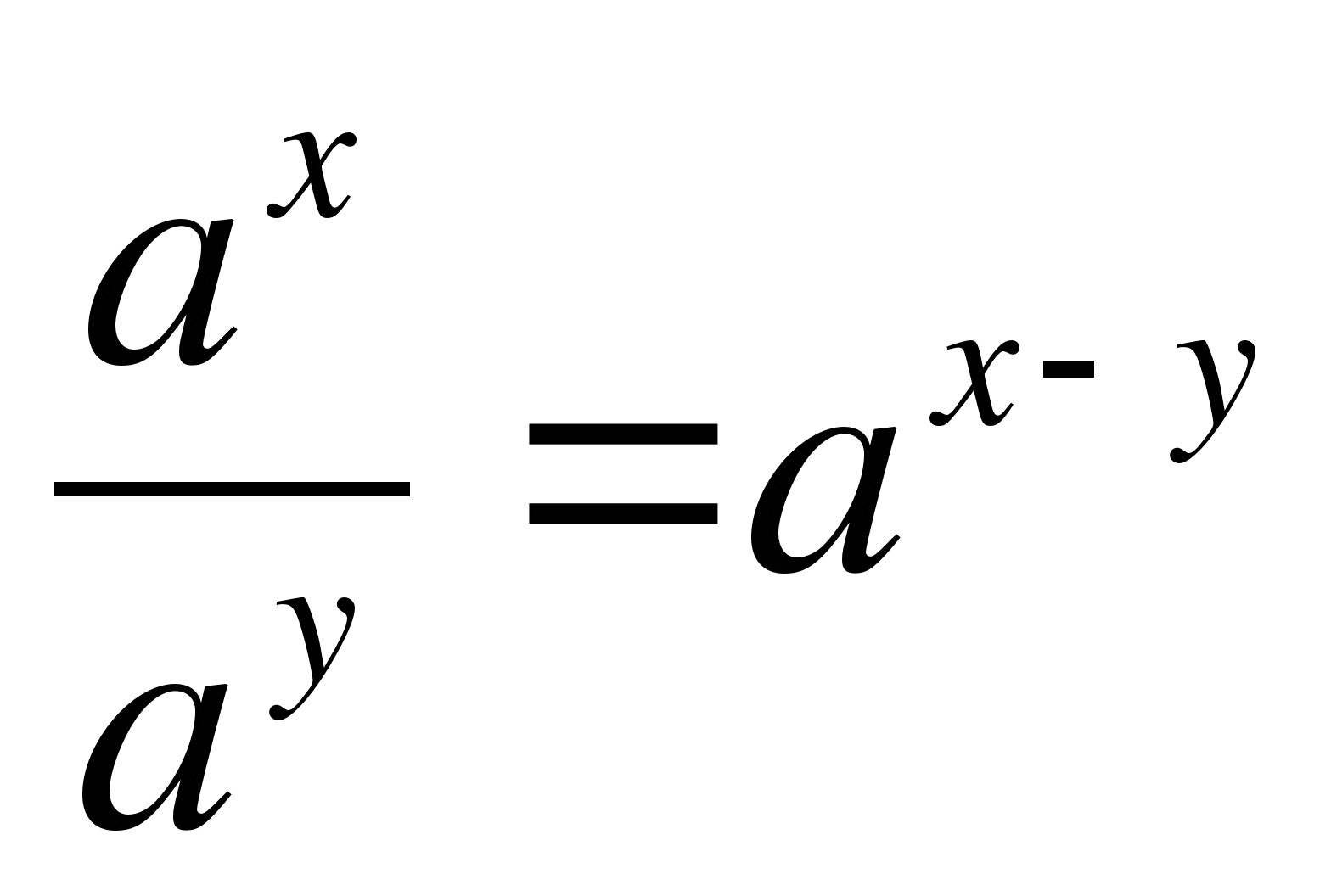
30. 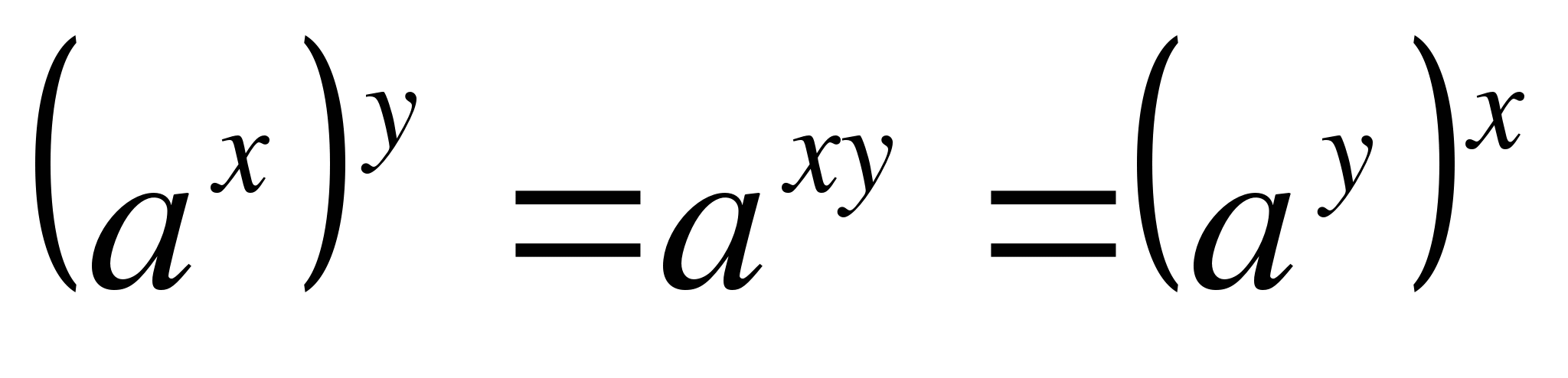
40. 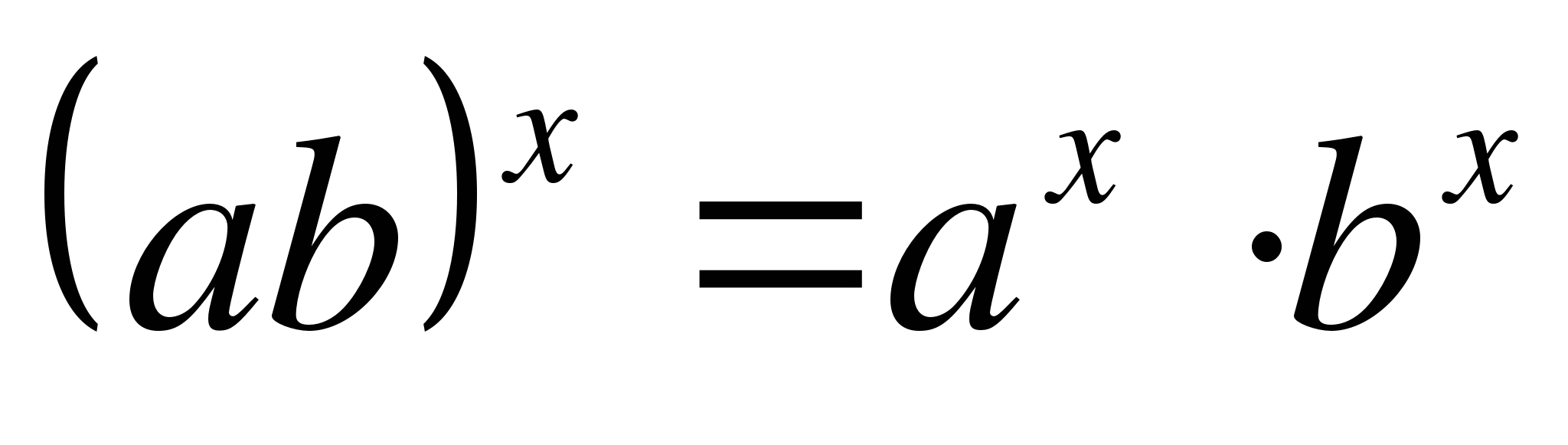
50. 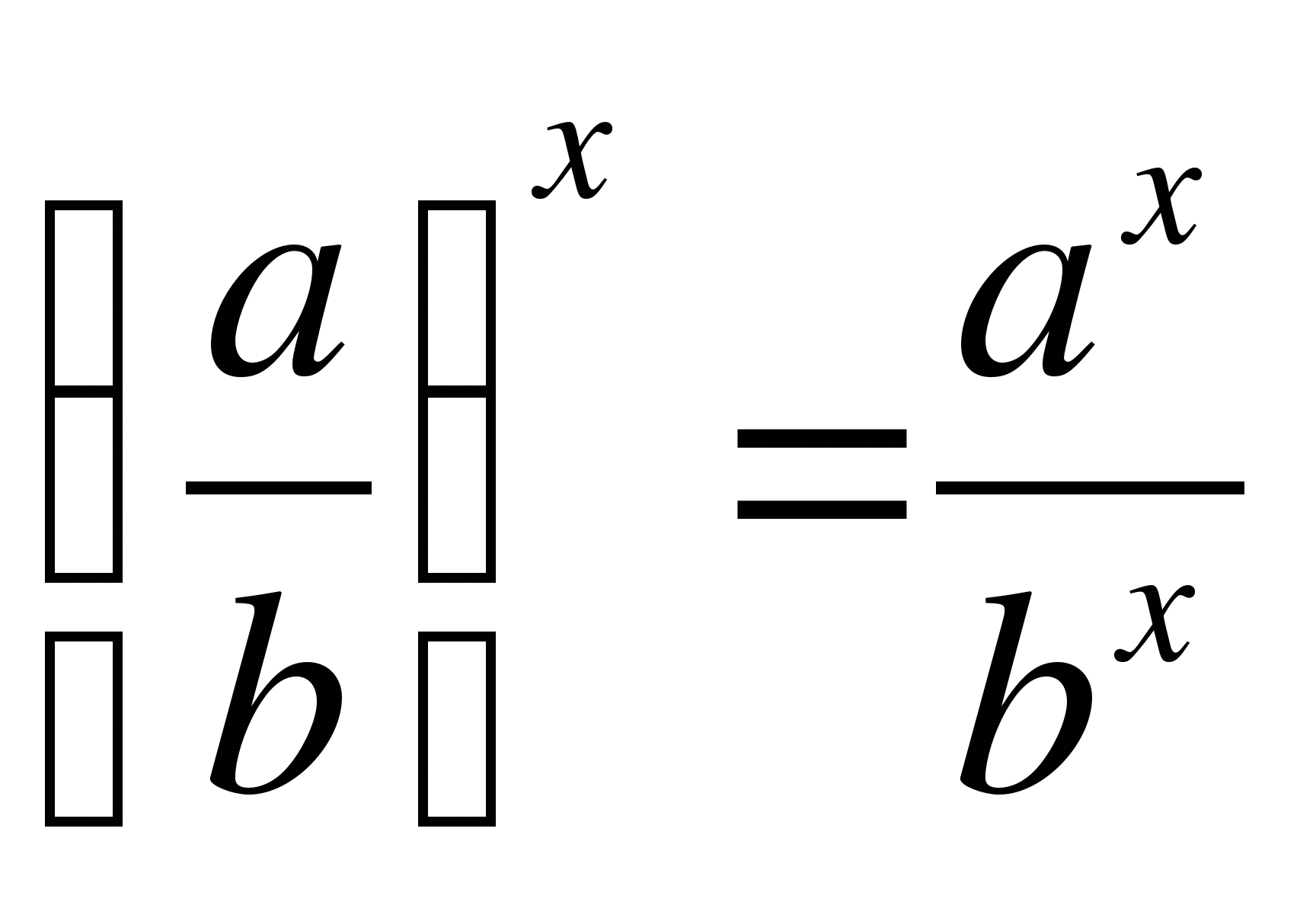
4. Определение. Корнем n-ой степени из числа а называется такое число, n-ая степень которого равна а.
Пример 1. Найти:
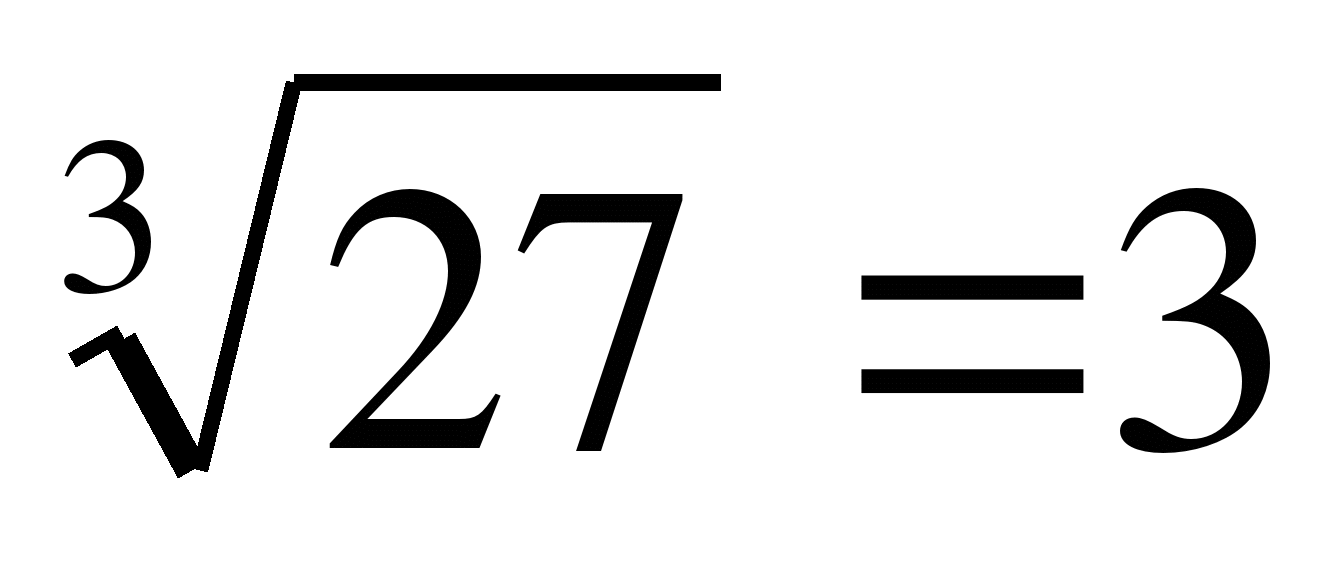 , т.к. 33=27,
, т.к. 33=27, 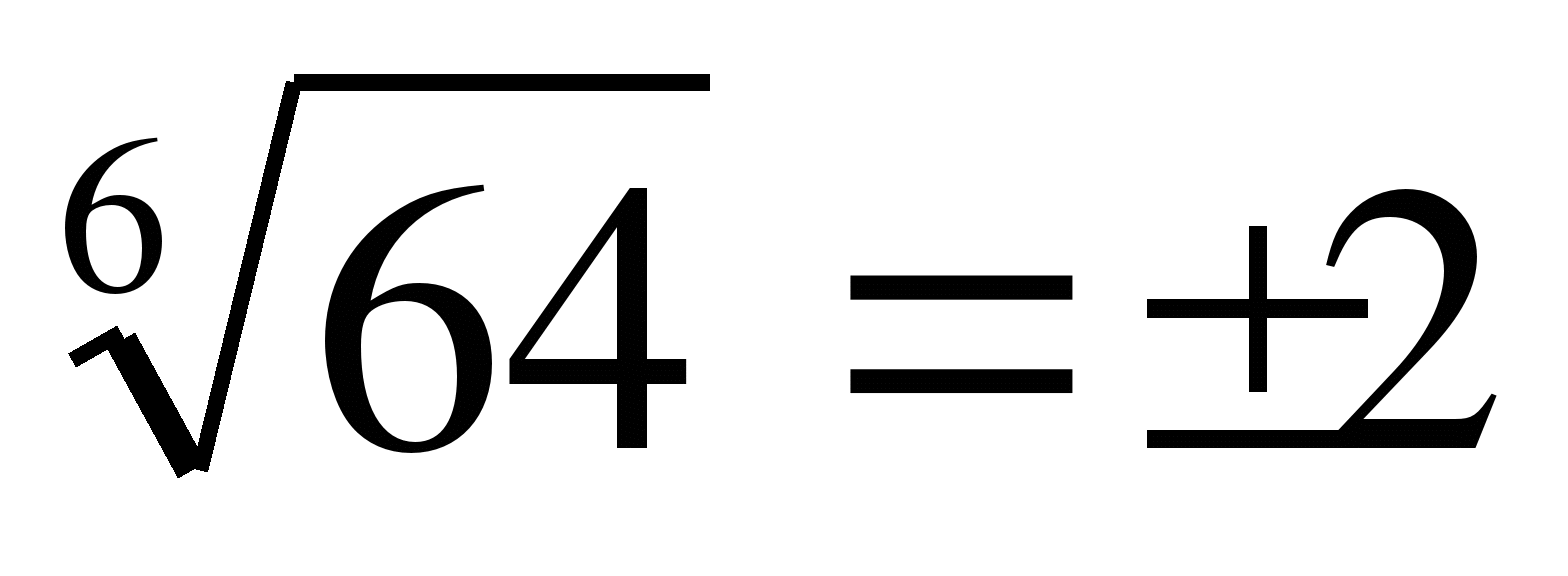 , т.к. 26=64 и (-2)6=64
, т.к. 26=64 и (-2)6=64
Определение. Арифметическим корнем n-ой степени из числа а называется неотрицательное число, n-ая степень которого равна а.
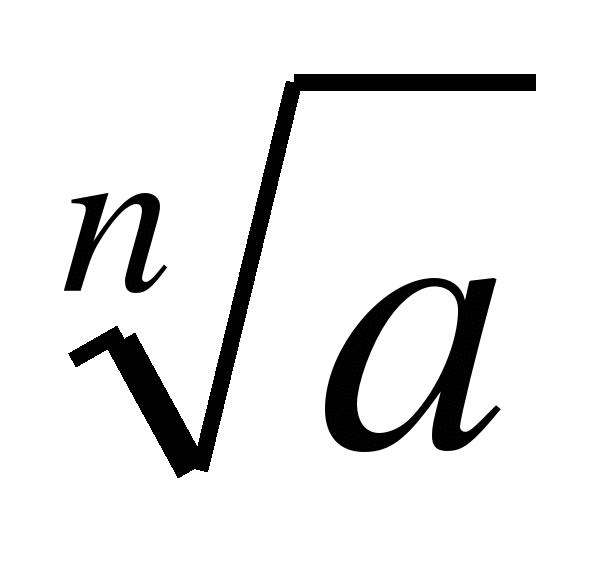 , n – показатель корня, а – подкоренное выражение.
, n – показатель корня, а – подкоренное выражение.
Пример 2. Найти:
а) 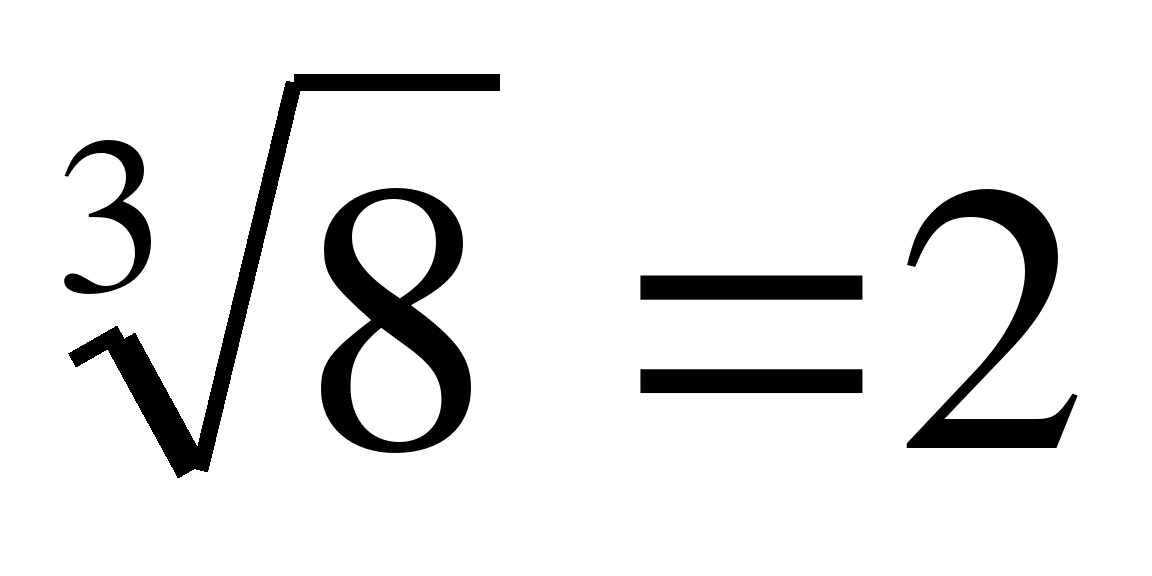 , т.к. 23=8 и 2>0
, т.к. 23=8 и 2>0
б) 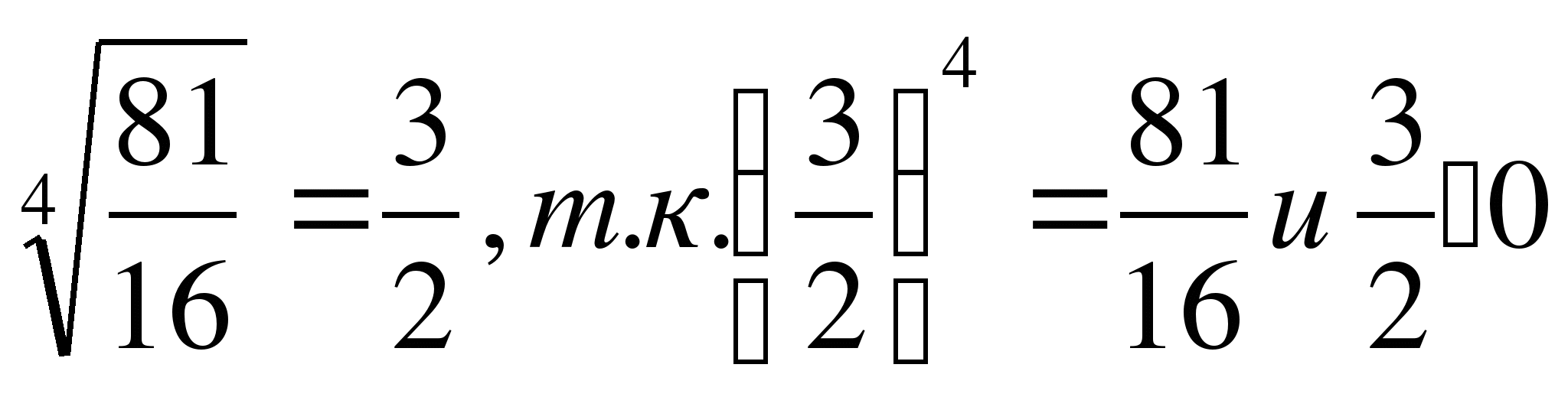
При четном n существует два корня n-ой степени из любого положительного числа а; корень n-ой степени из числа 0 равен 0; корней четной степени из отрицательных чисел не существует.
Пример 3.Уравнение х4=81 имеет два корня: х1=3 и х2=-3, при этом 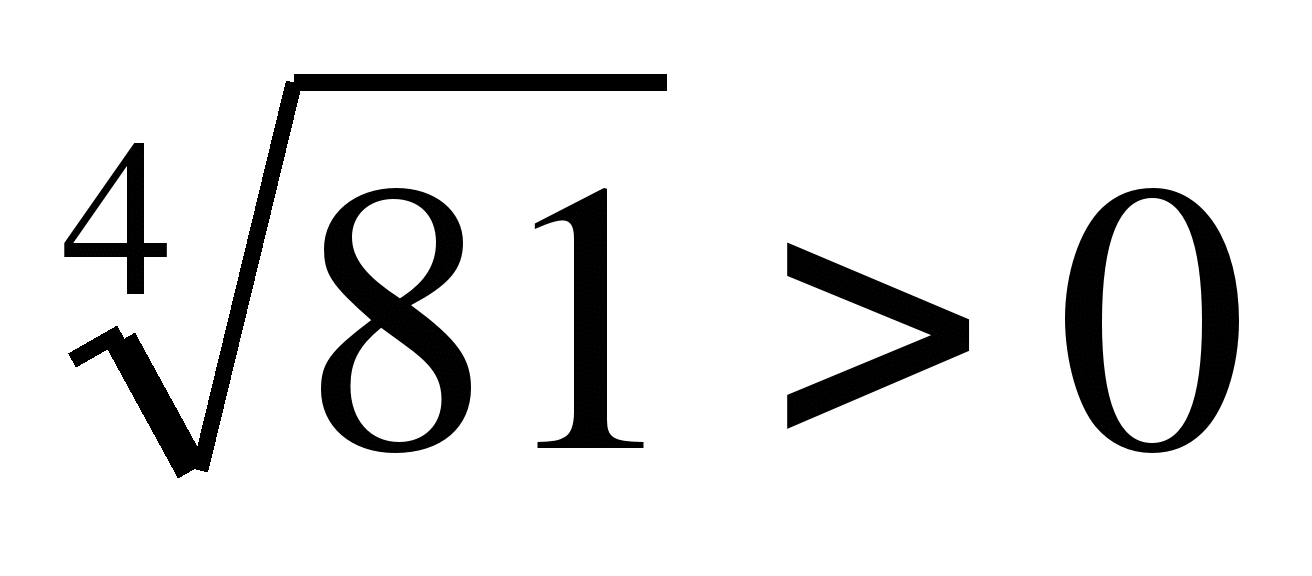 , т.е.
, т.е. 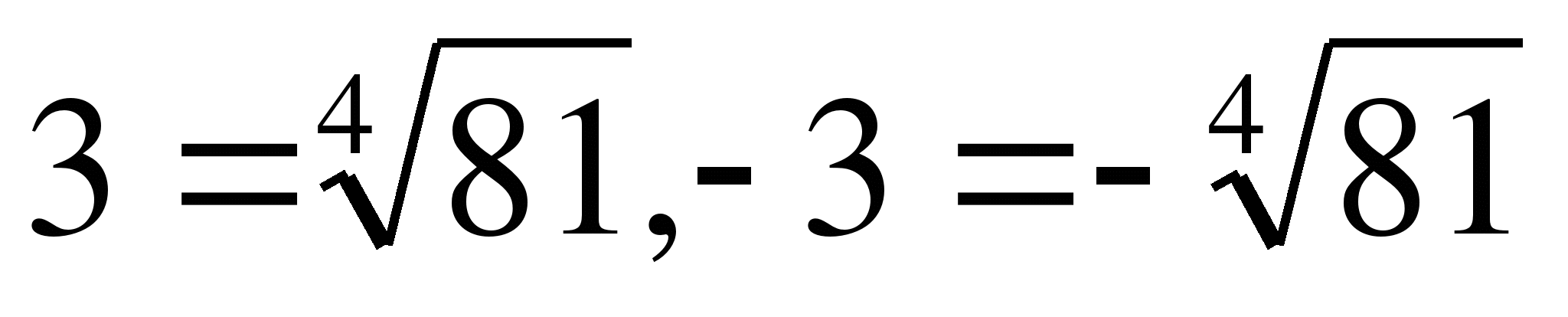
При нечетном n существует корень n-ой степени из любого числа а и притом только 1.
Например, 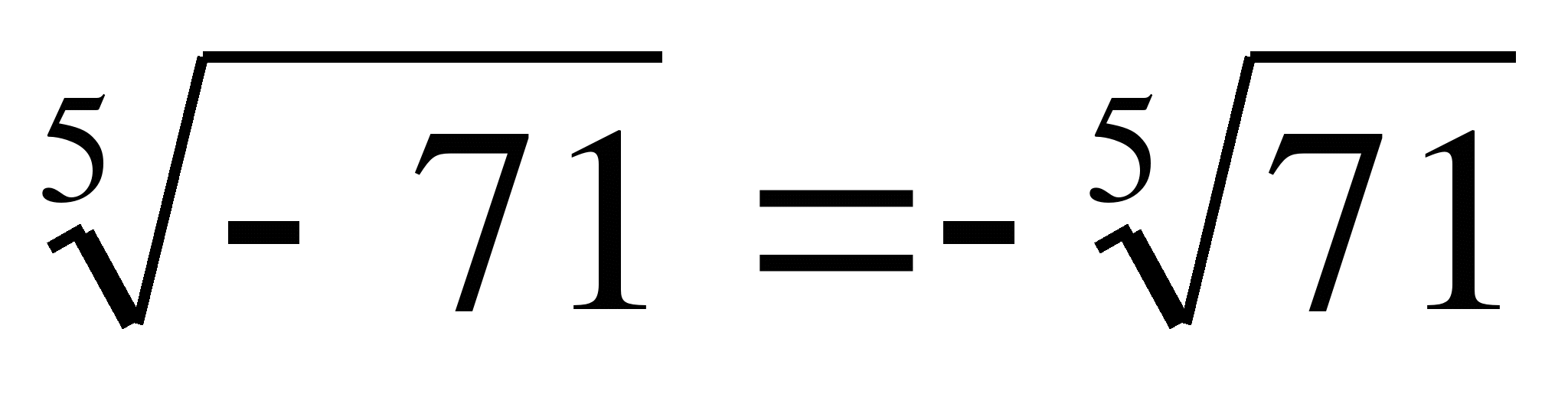 ,
, 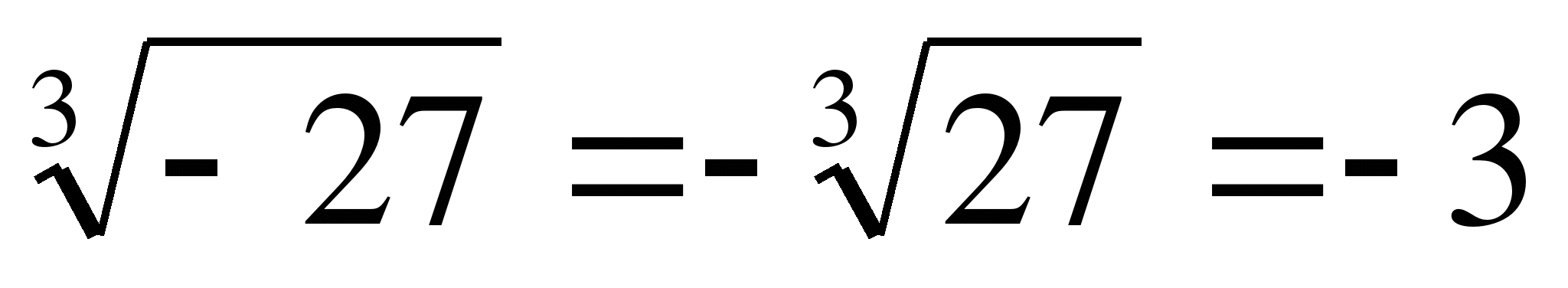
Замечание. Для любого х

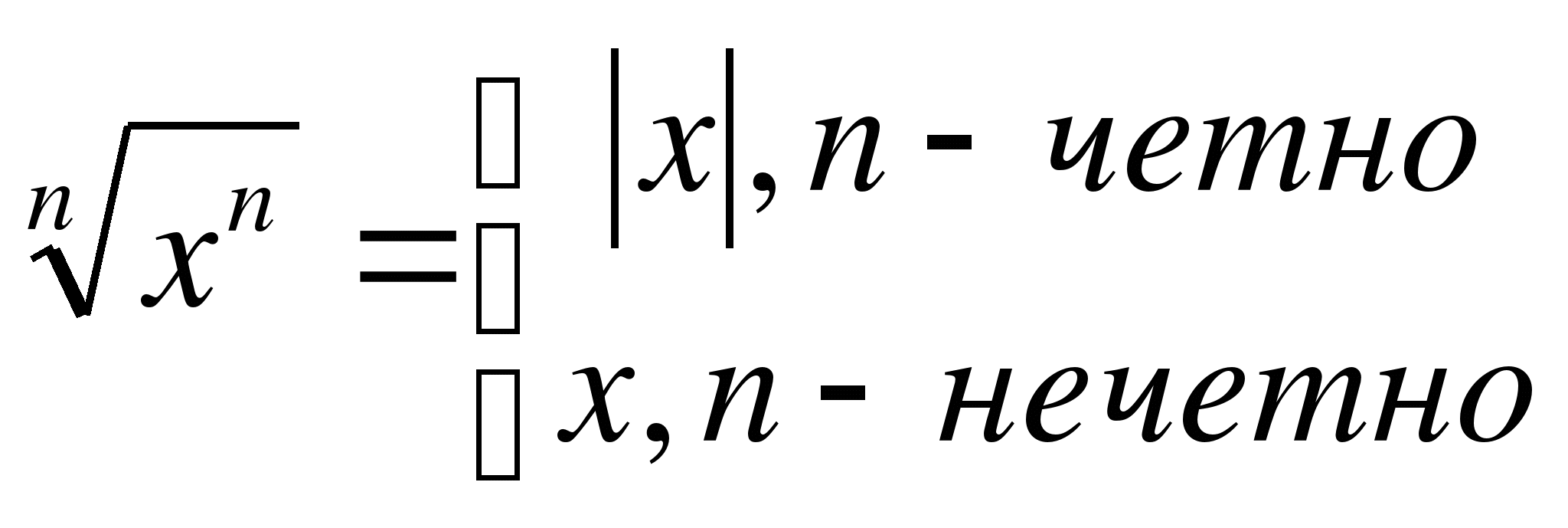
Основные свойства арифметического корня n-ой степени:
10. 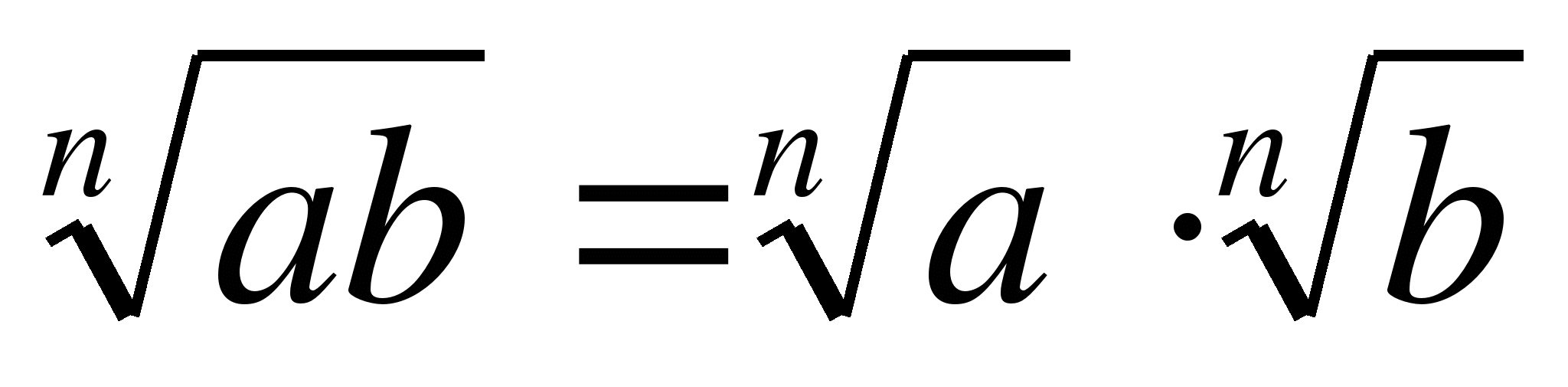
20. 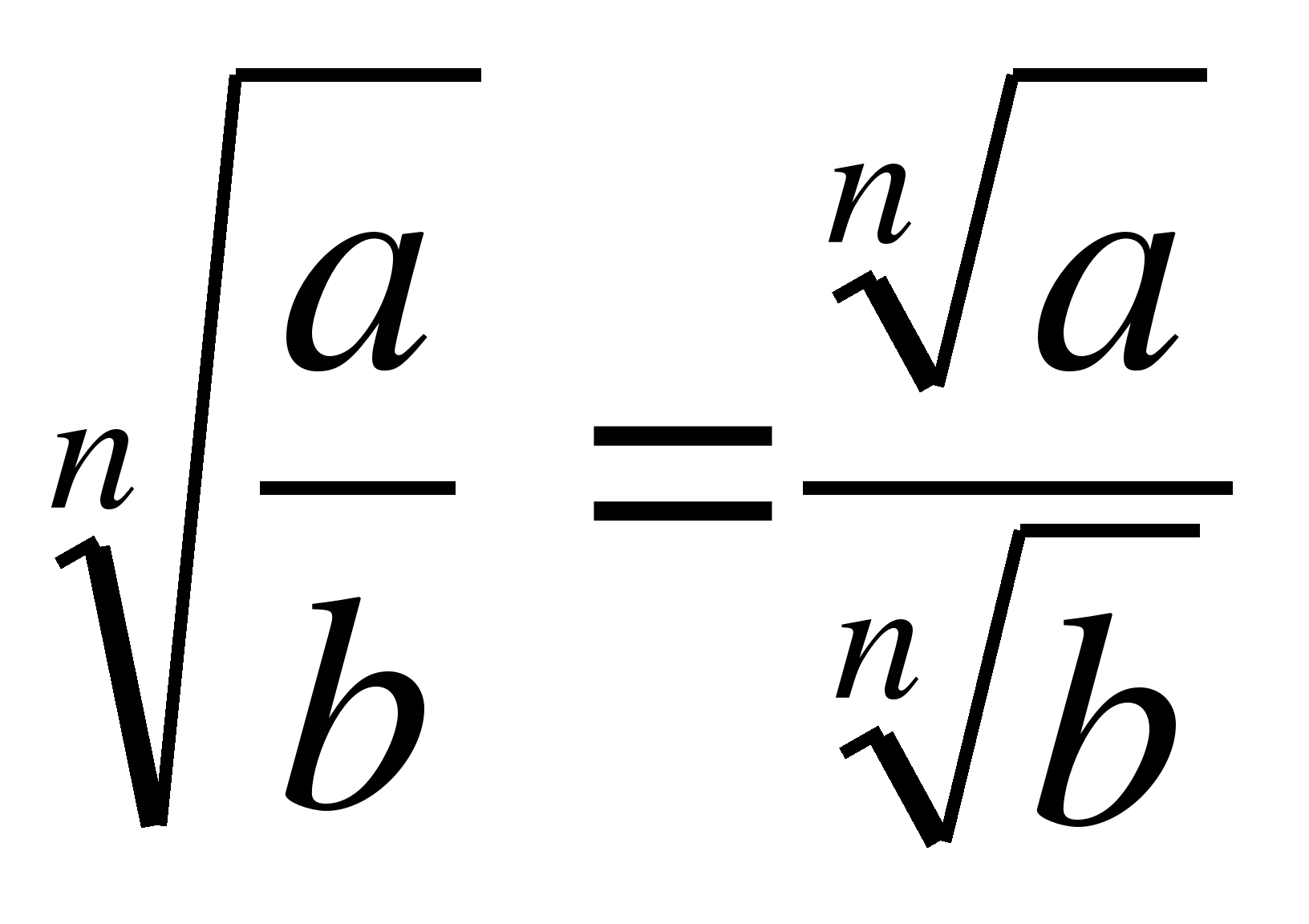
30. 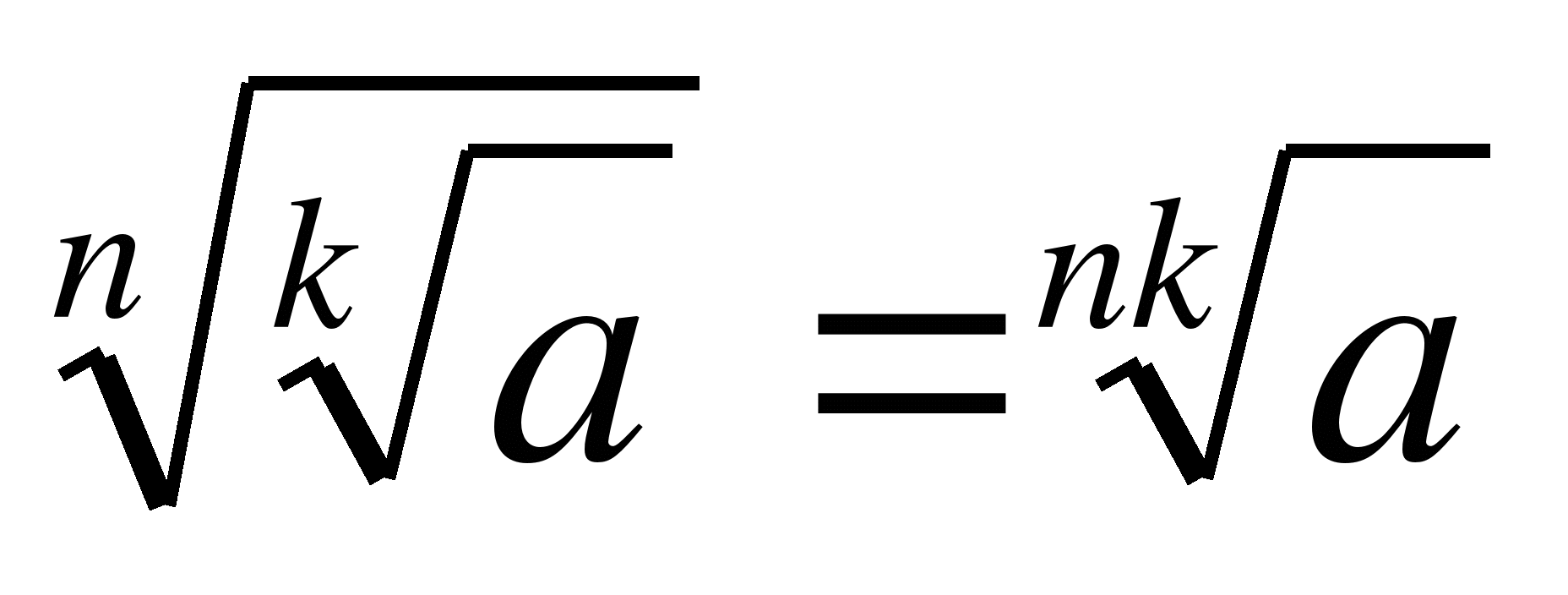
40. 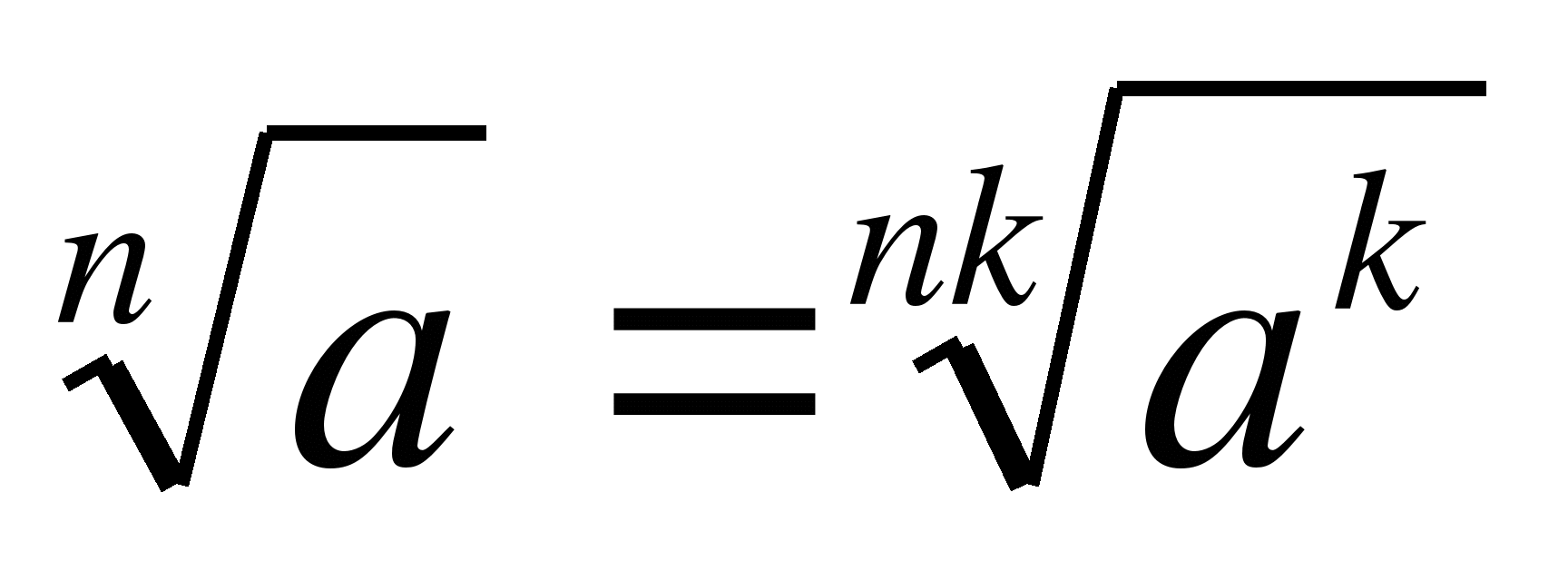
50. 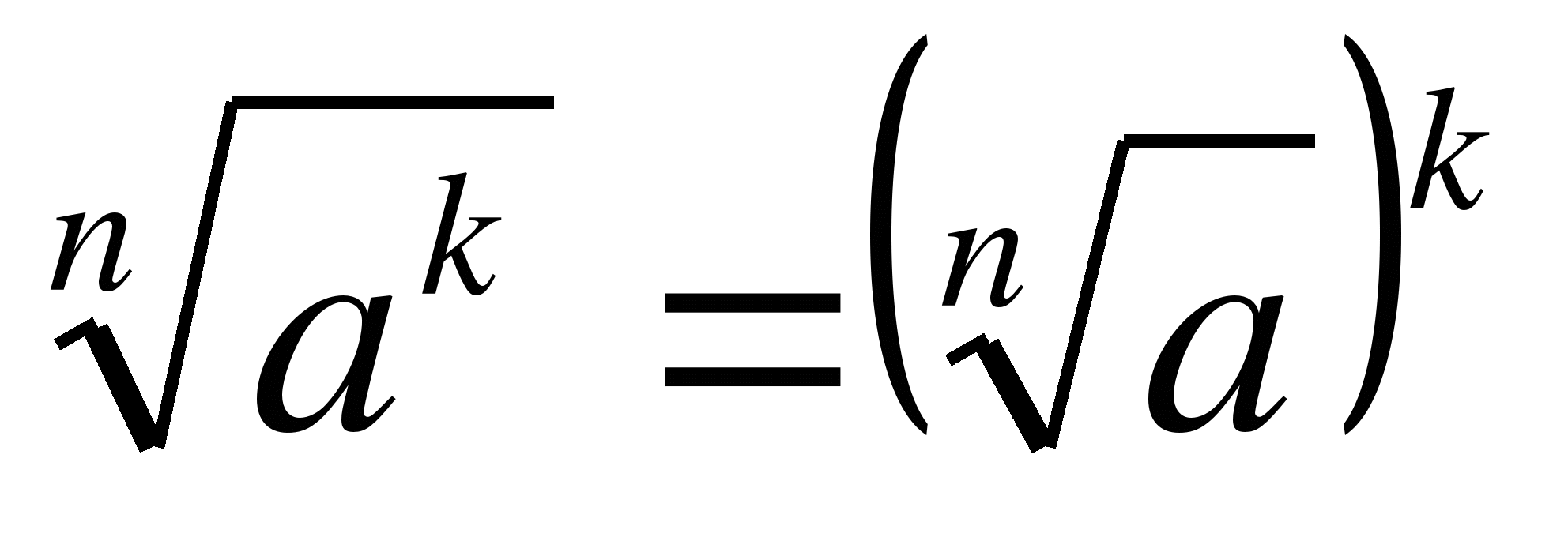
Пример 6. Преобразовать выражения:
а) 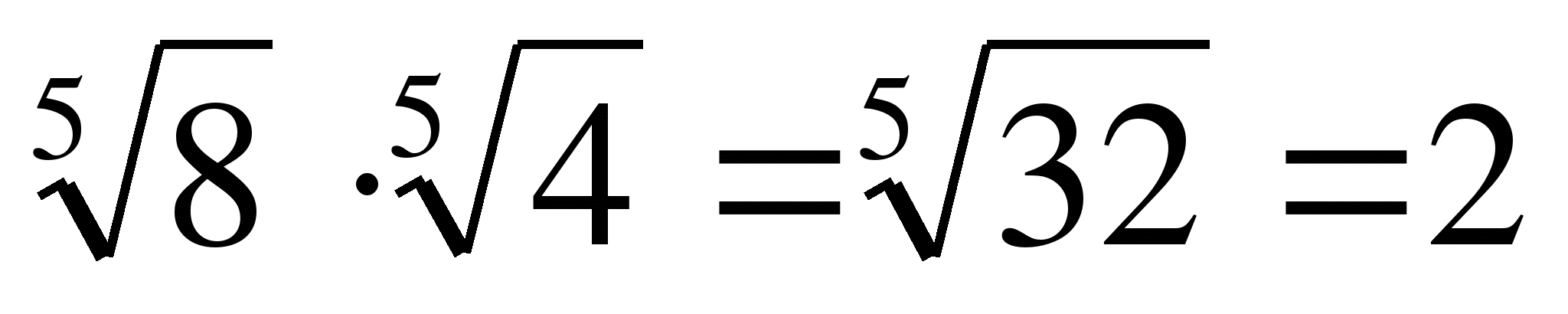
б) 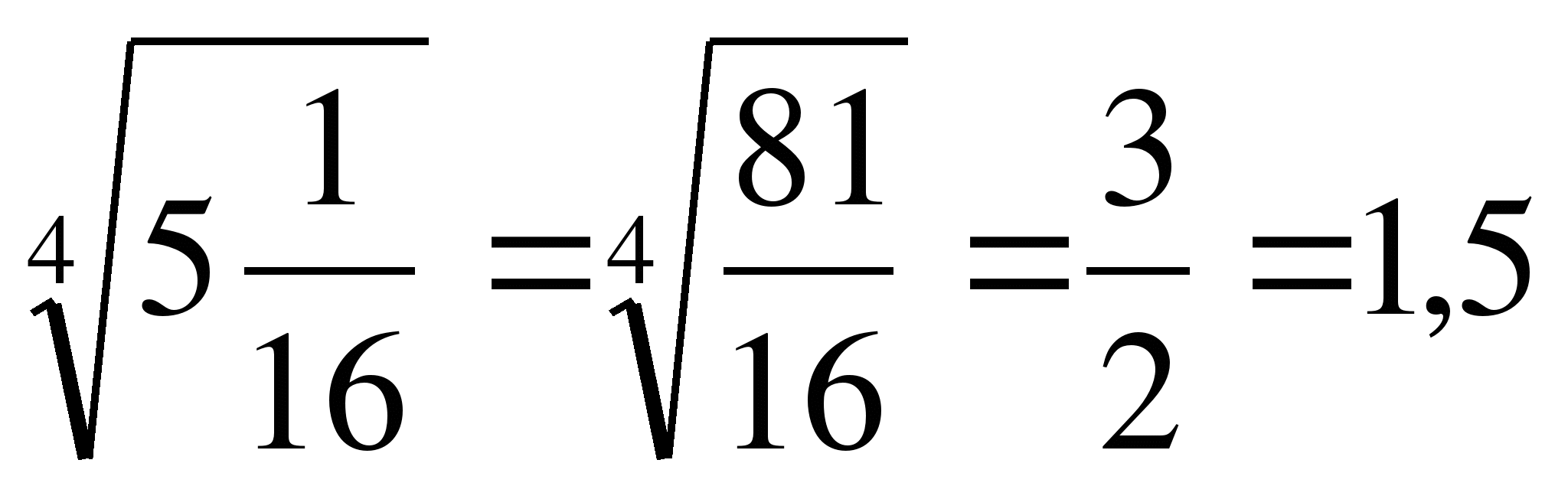
в) 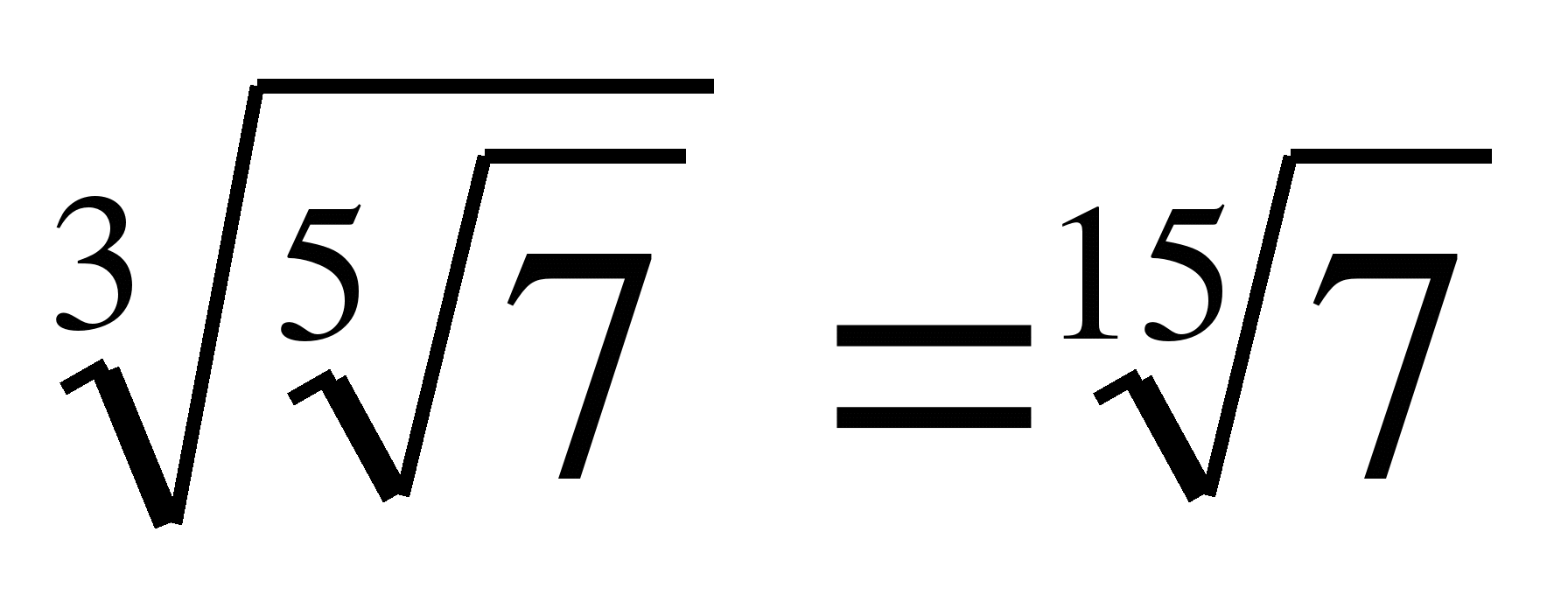
г) 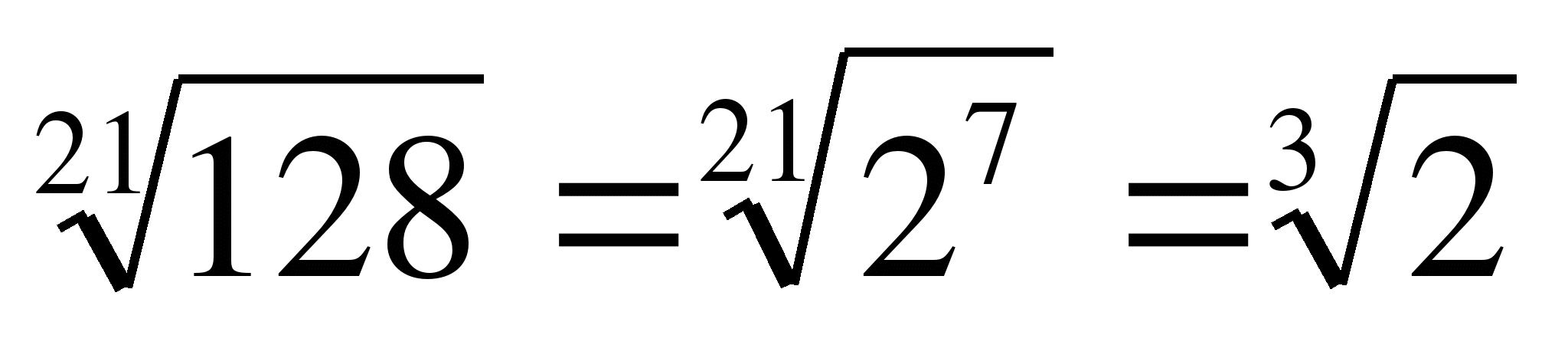
д) 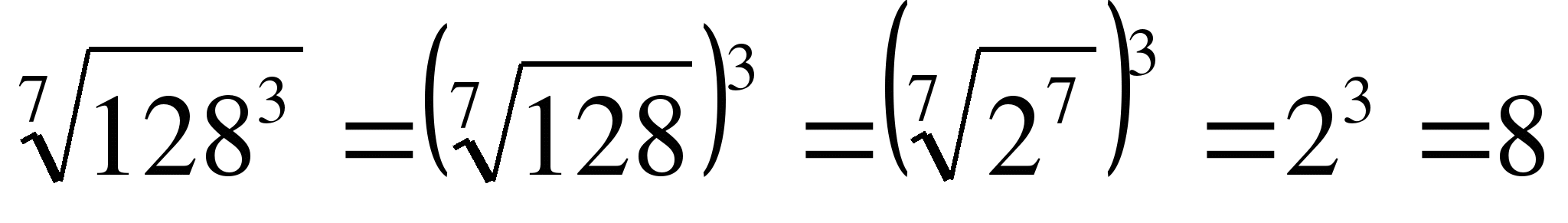
60. Для любых чисел a и b, таких что 0≤a<b, выполняется неравенство: 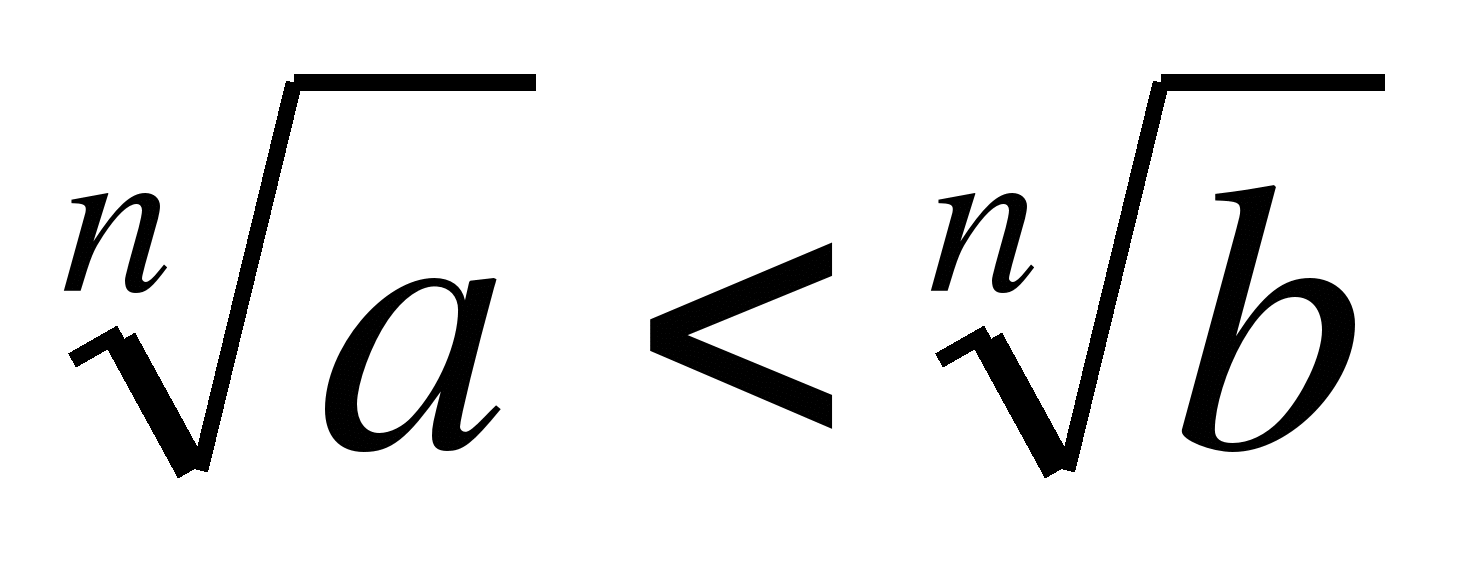
Пример 7. Сравним числа 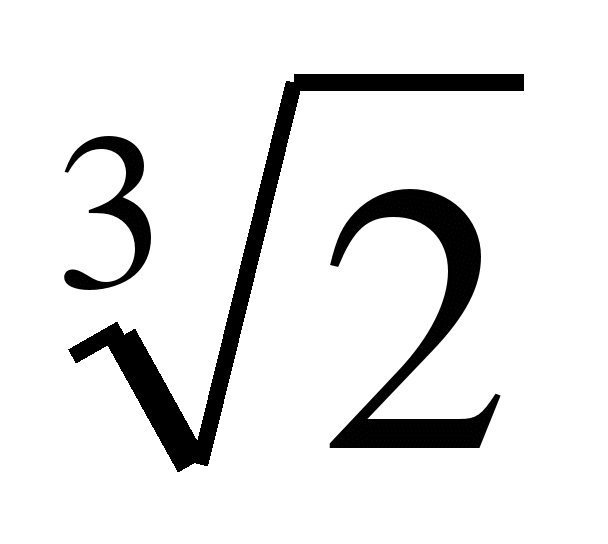 и
и 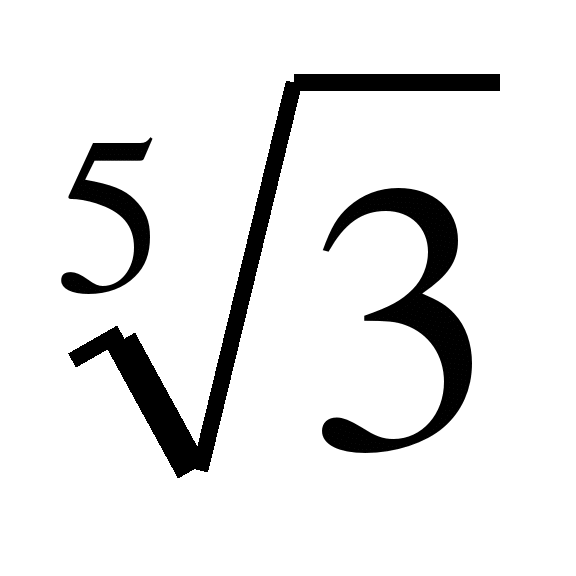 .
.
Решение: 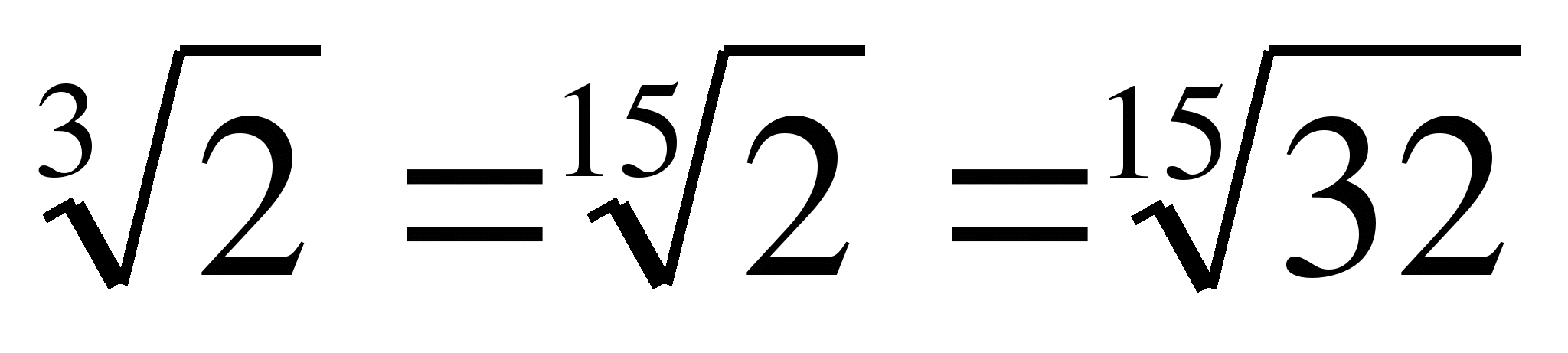 ;
; 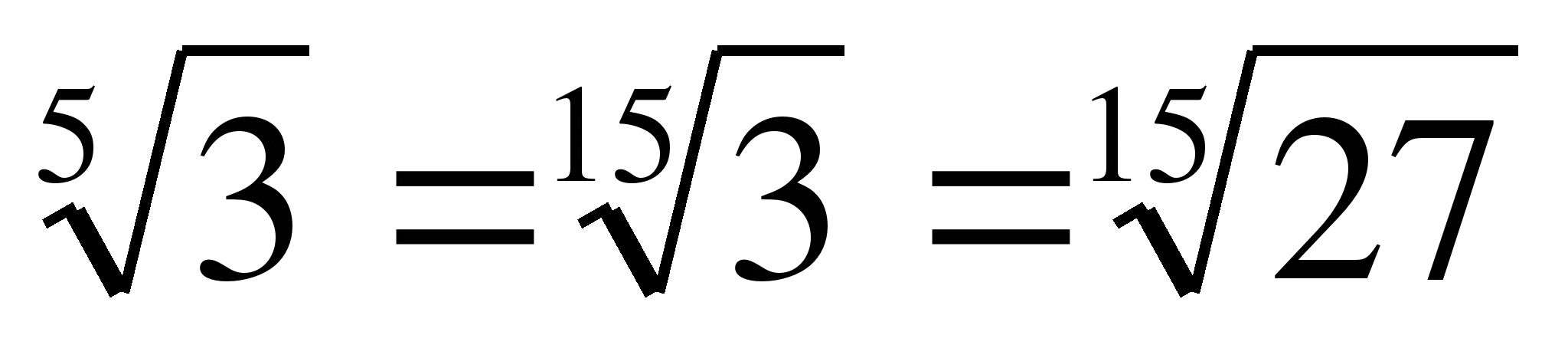 , т.к. 32>27, то
, т.к. 32>27, то 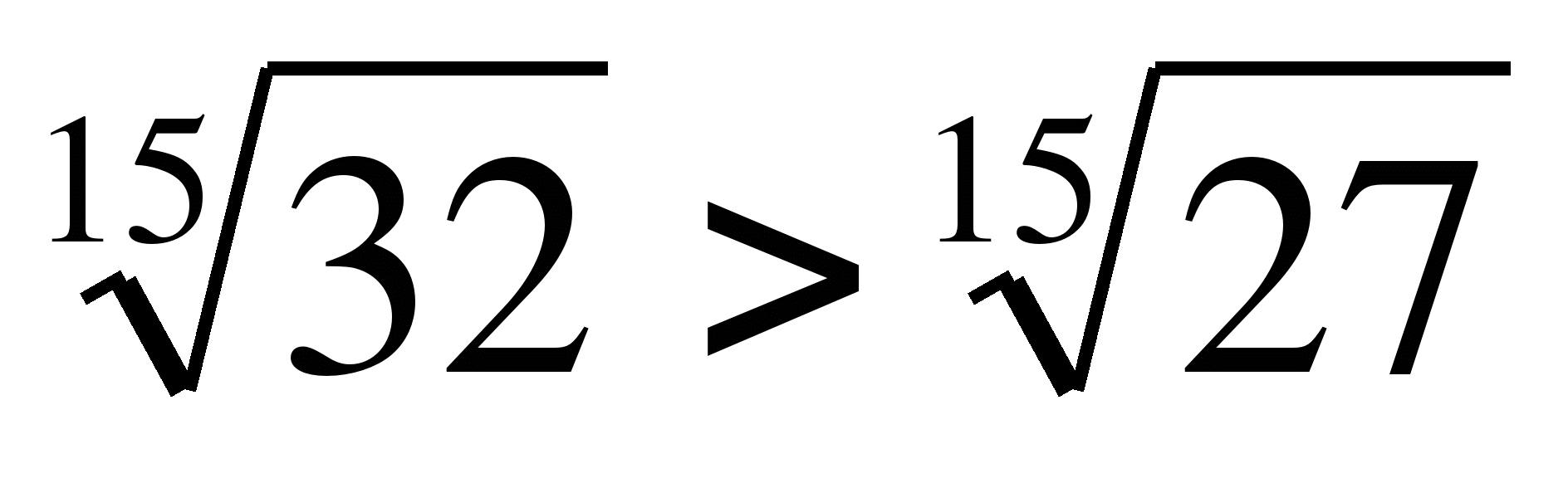
 и
и 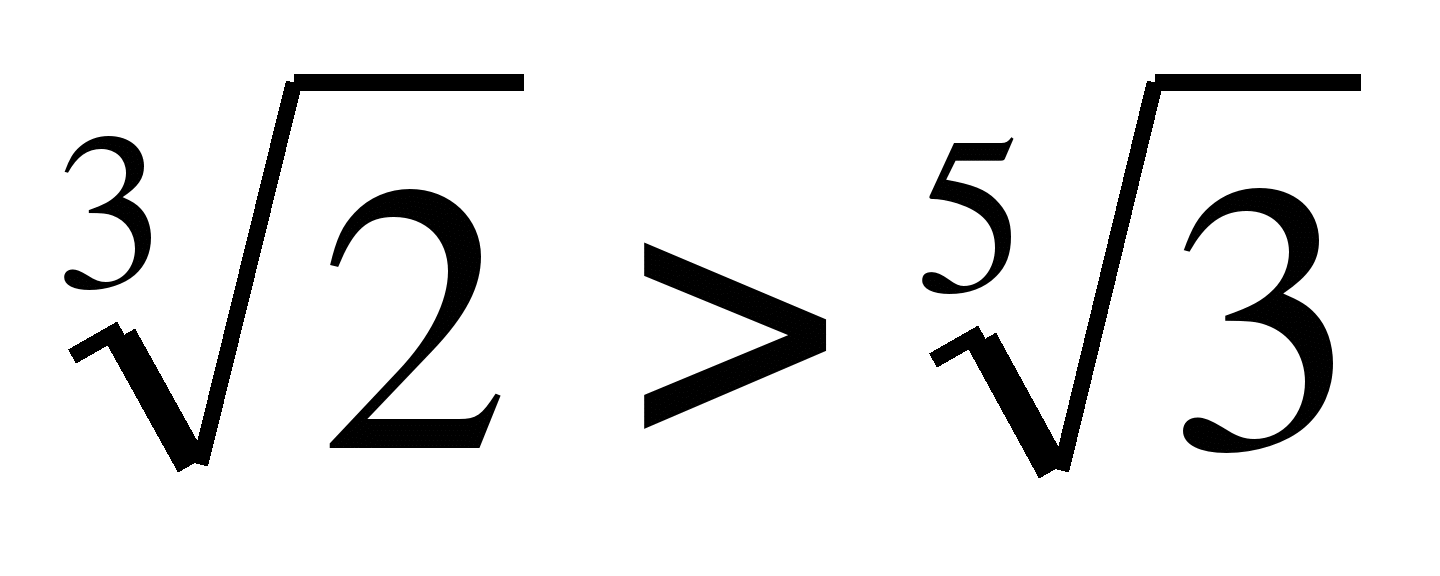
Пример 8. Решить неравенство: x6>20
 Решение: x6-20>0,
Решение: x6-20>0, 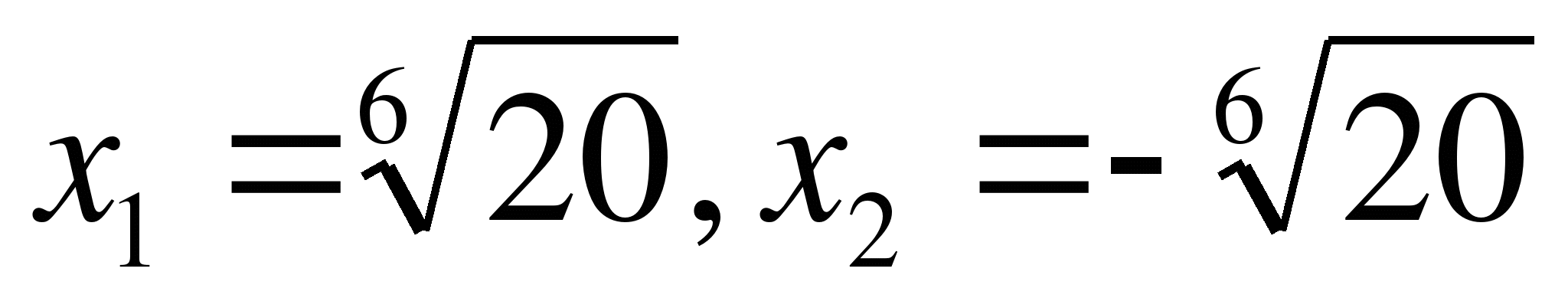




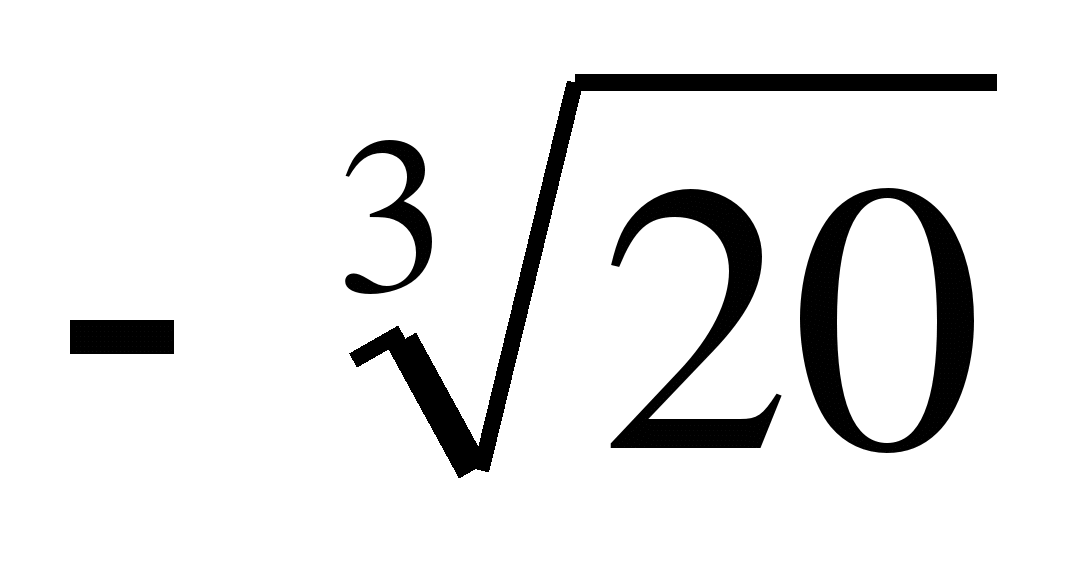
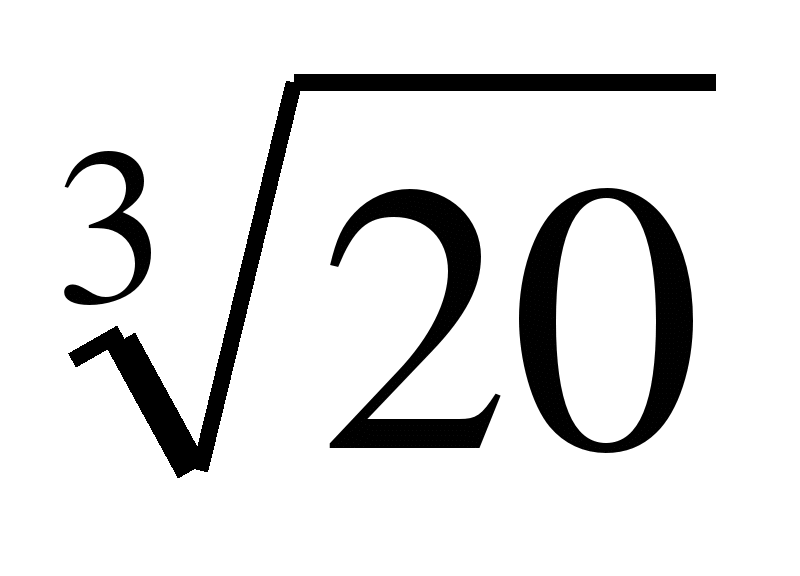
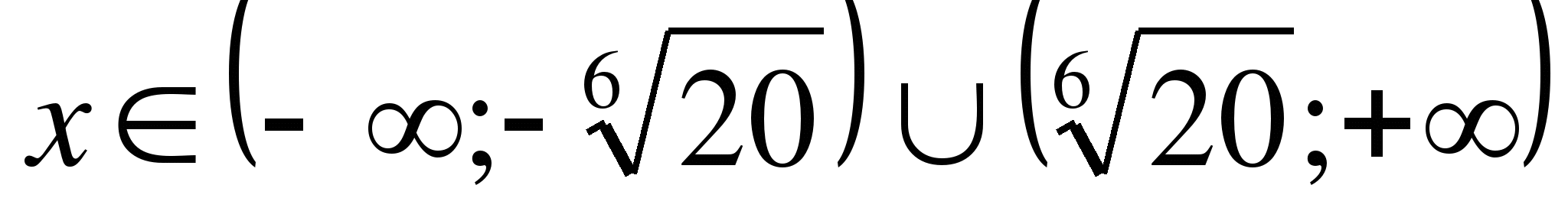
5. Решение примеров на доске (студенты на оценку):
Найдите значение числового выражения:
1) 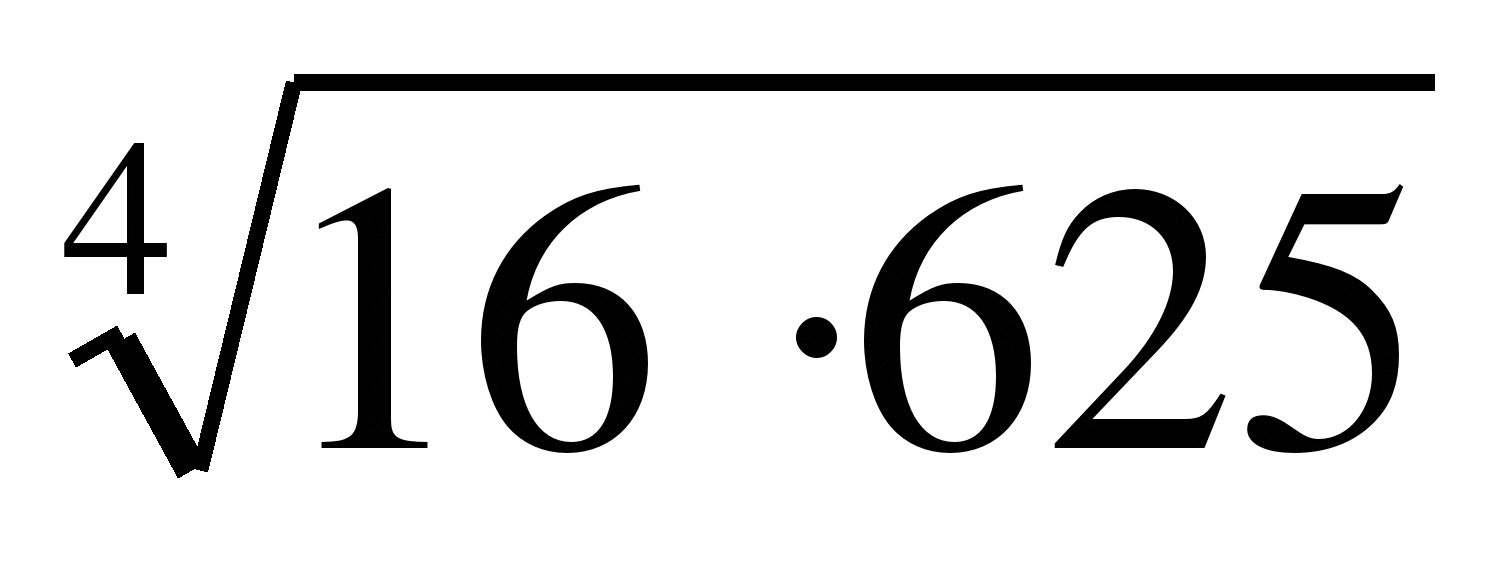 Ответ:10
Ответ:10
2) 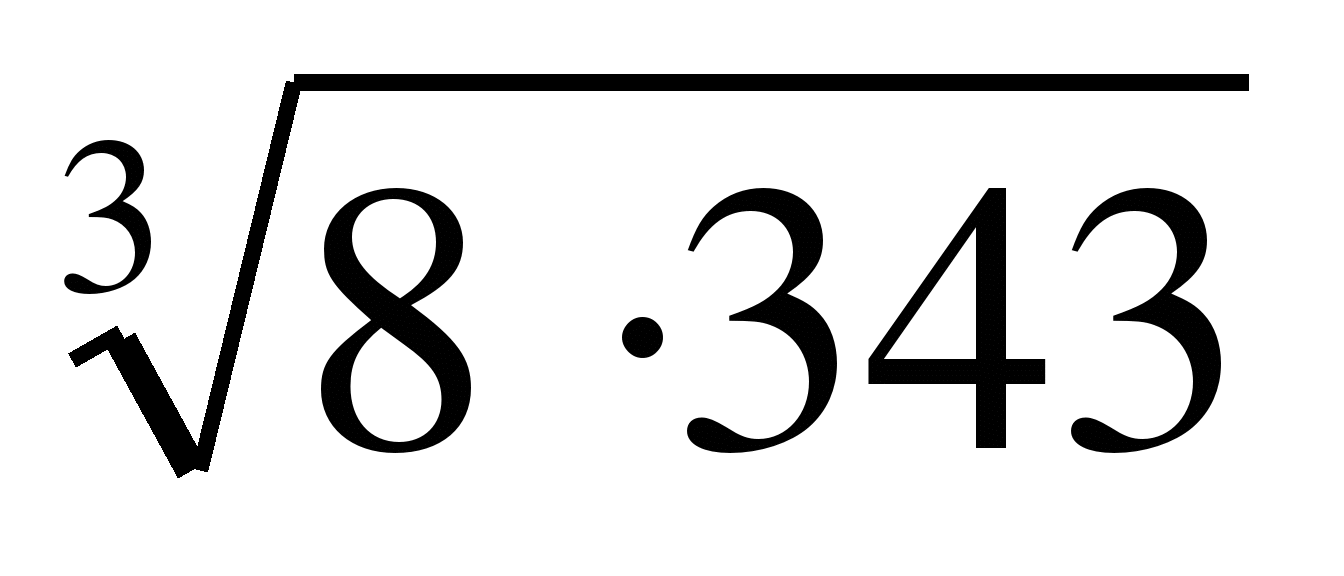 Ответ:14
Ответ:14
3) 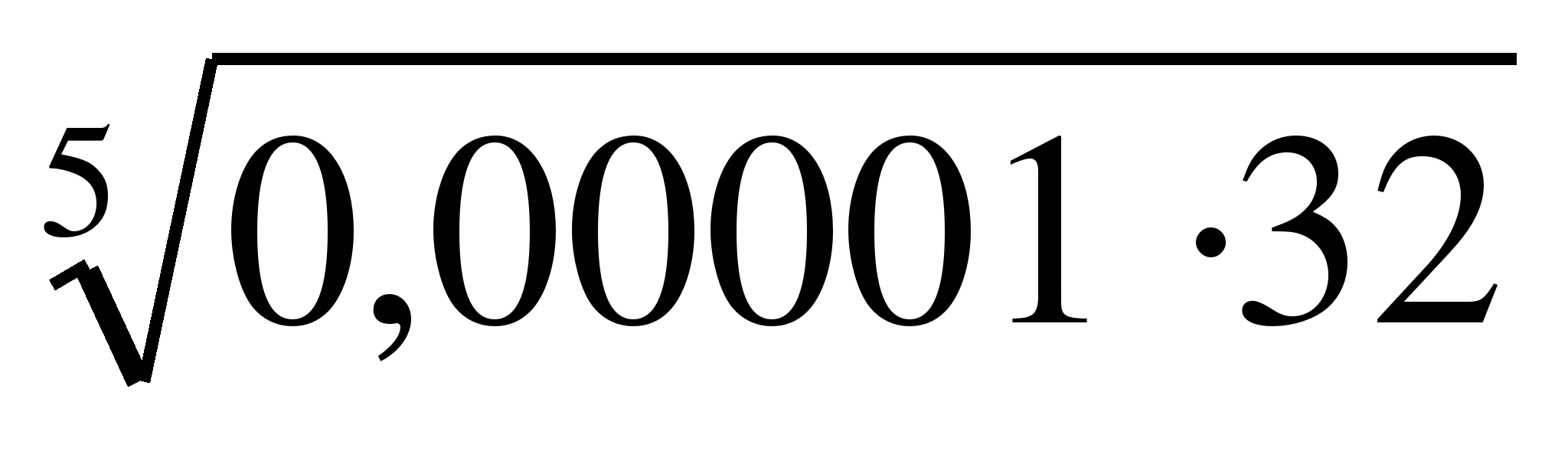 Ответ:0,2
Ответ:0,2
4) 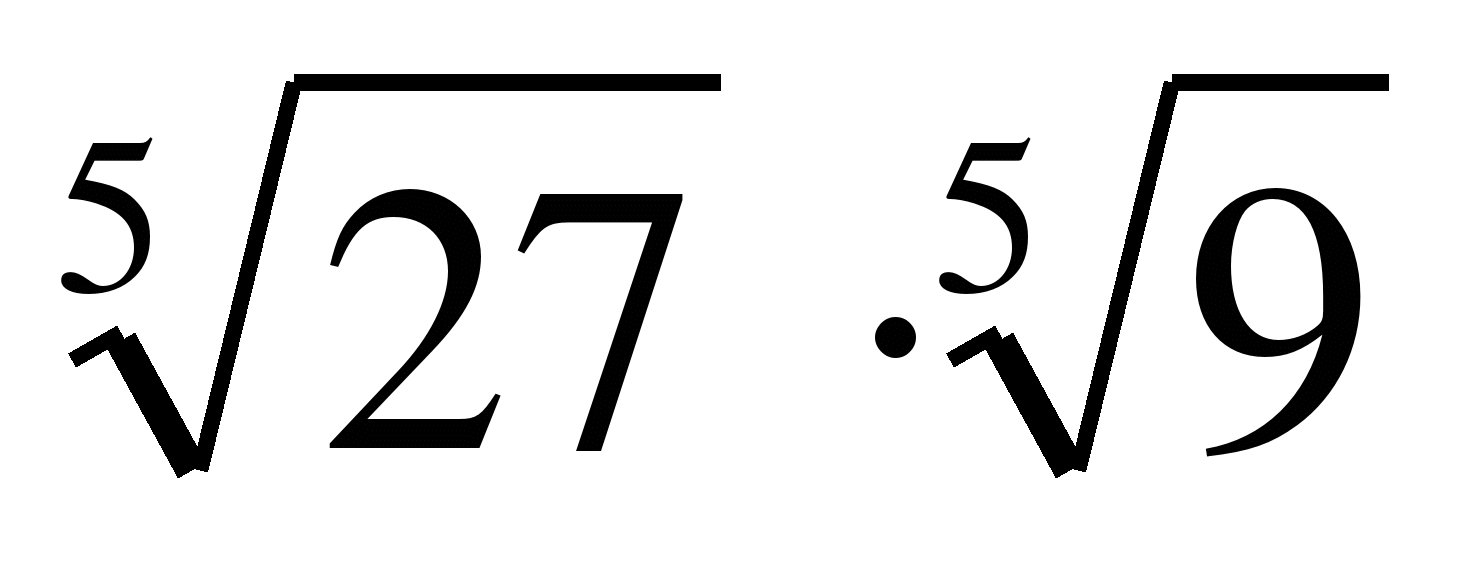 Ответ: 3
Ответ: 3
5) 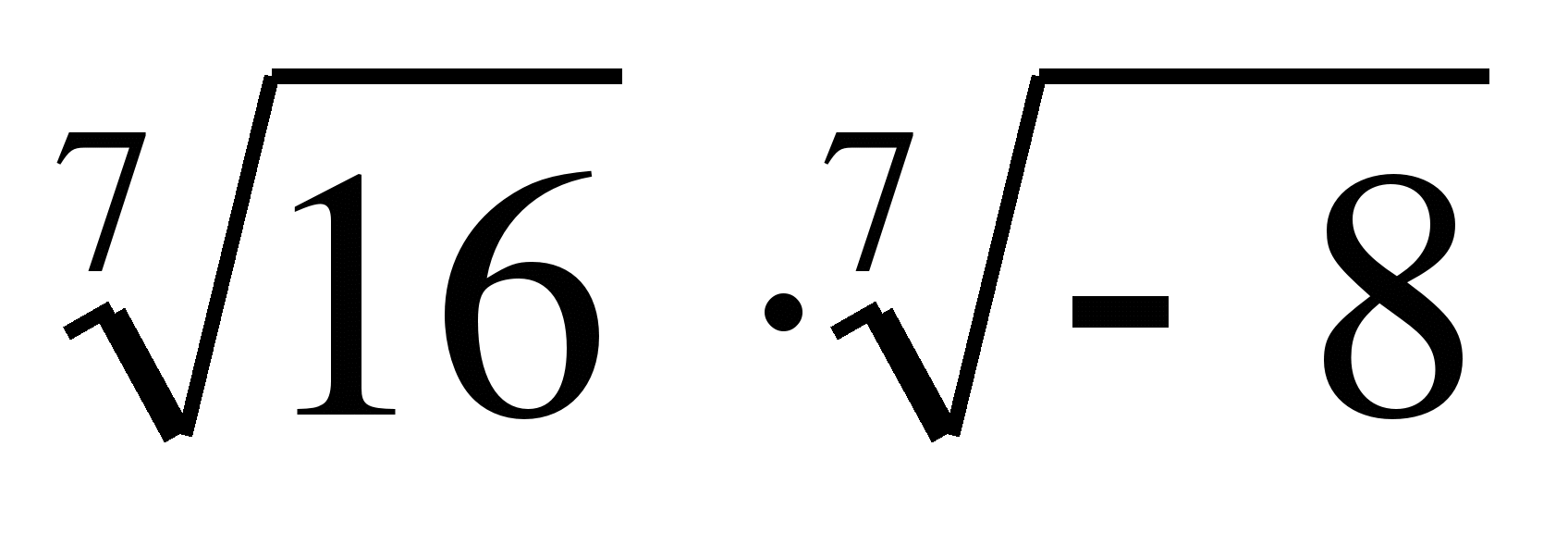 Ответ: -2
Ответ: -2
6) 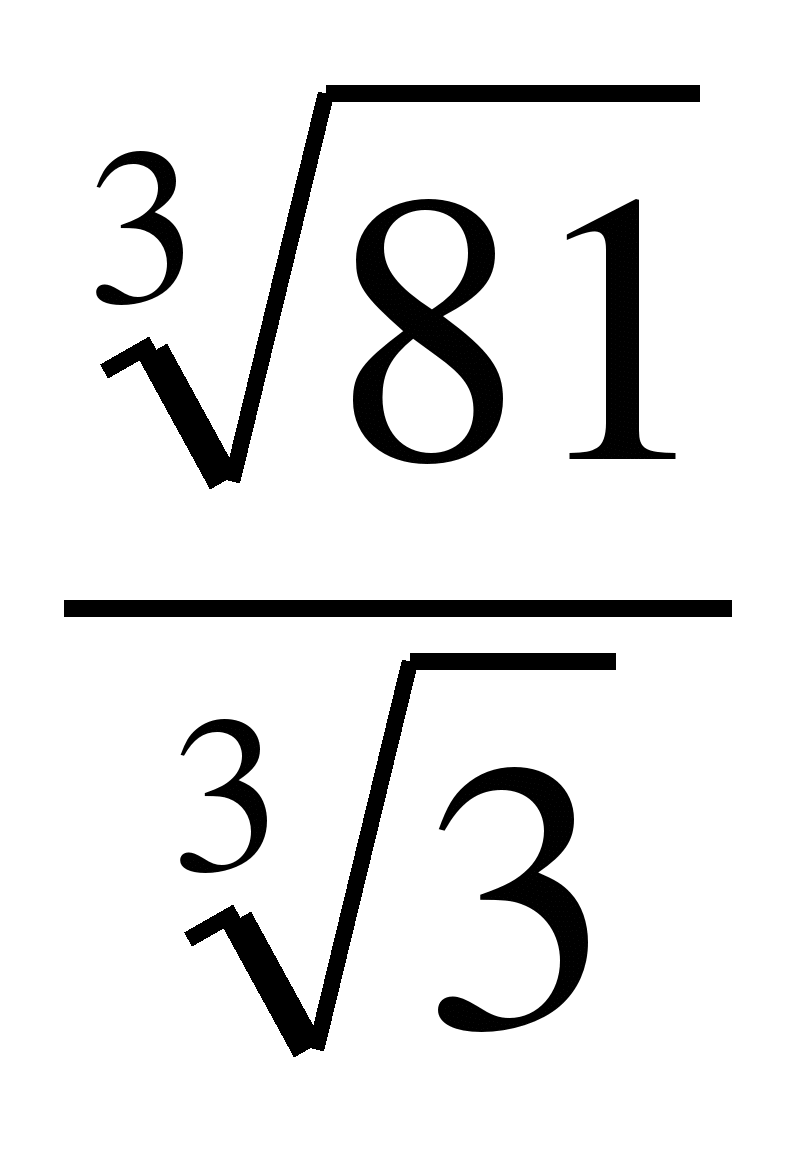 Ответ: 3
Ответ: 3
7) 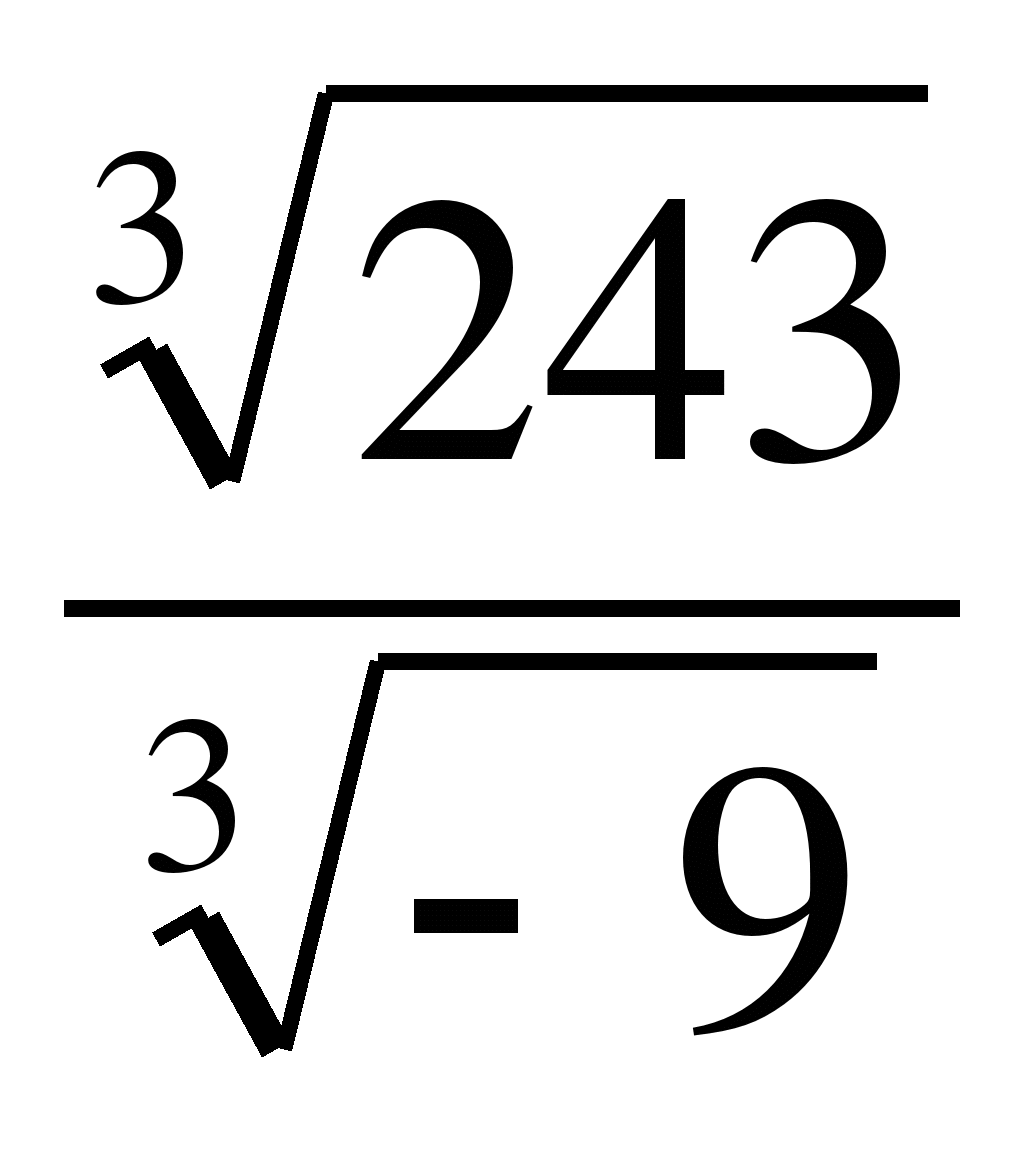 Ответ: -3
Ответ: -3
Сравните числа:
 и
и  ;
; и 1;
и 1; и
и  ;
; и 0.
и 0.
Решите уравнения:
х3=4 Ответ:


х4=10 Ответ:

6. Самостоятельная работа. Критерии оценки: Правильно выполненные 4 задания – “3”. Правильно выполненные 6 заданий – “4”. Правильно выполненные 7 заданий – “5”.
7. Провести рефлексию. Дать студентам возможность проанализировать свои ошибки.
8. Подвести итоги урока.
Записать домашнее задание.
infourok.ru
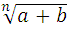 =
=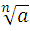 ∙
∙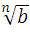 ;
;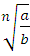 =
= 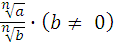 ;
;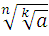 =
=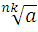 ;
;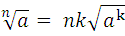
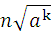 =(
=( 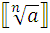 ) k
) k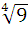 ∙
∙ 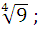 1)
1) 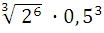 ;
;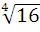 ; 2)
; 2) 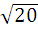 ∙
∙ 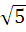 ;
;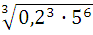 ; 3) -6 ∙
; 3) -6 ∙ 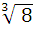 ;
; овторить определение квадратного корня из числа а, степени с натуральным, нулевым, целым отрицательным и рациональным показателем.
овторить определение квадратного корня из числа а, степени с натуральным, нулевым, целым отрицательным и рациональным показателем.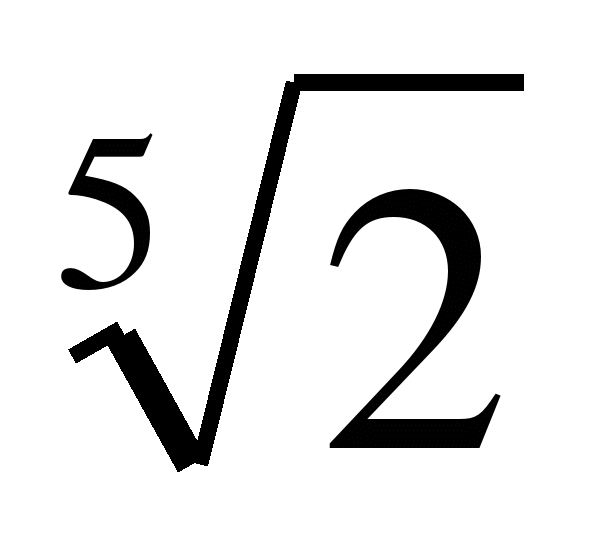 и
и 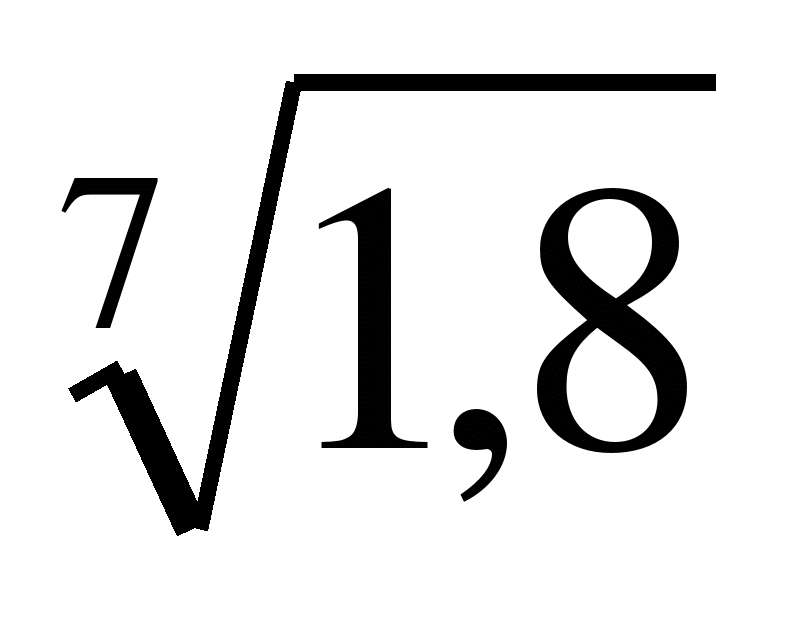 и 1;
и 1;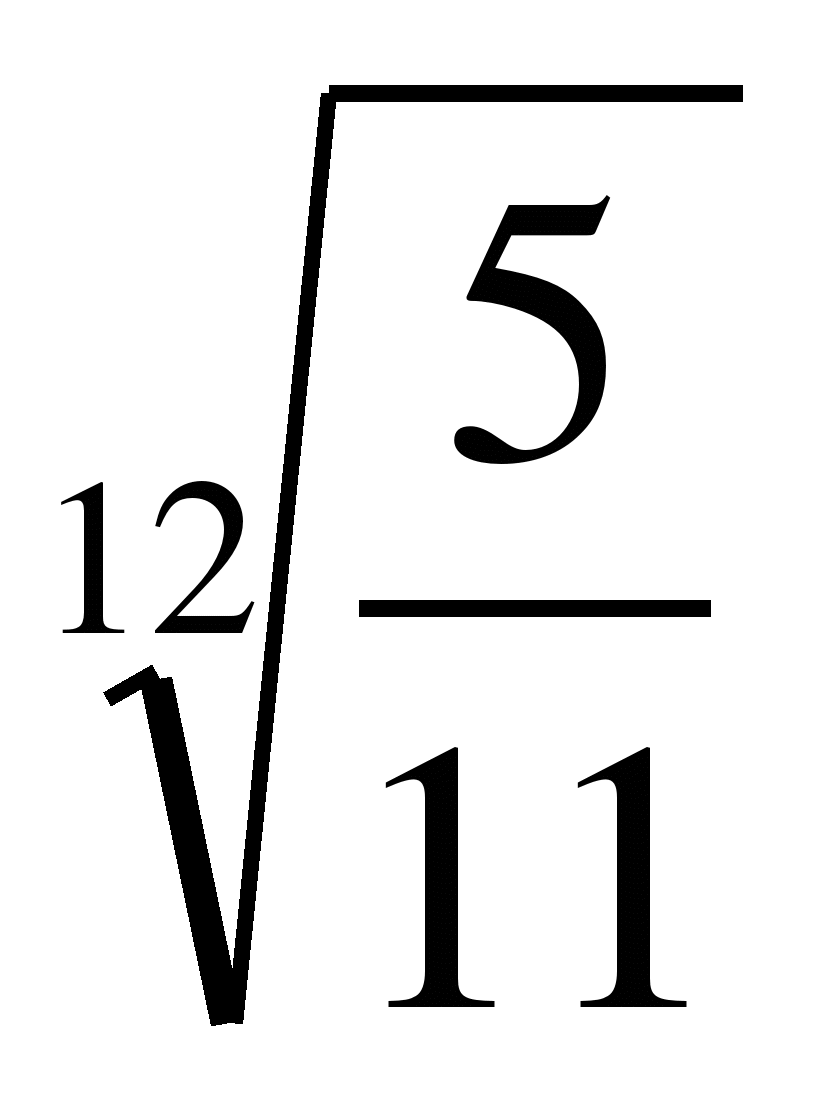 и
и 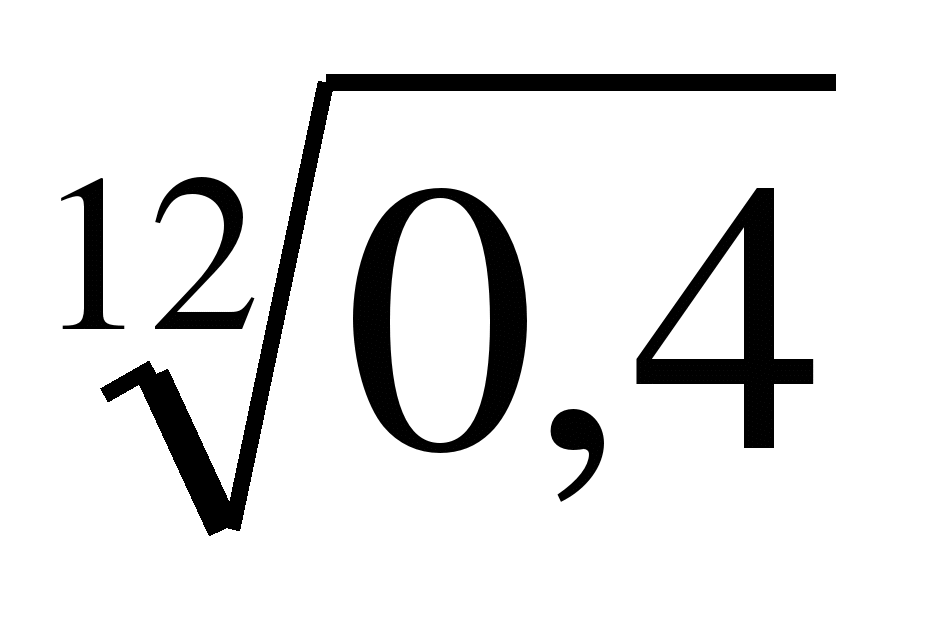 ;
;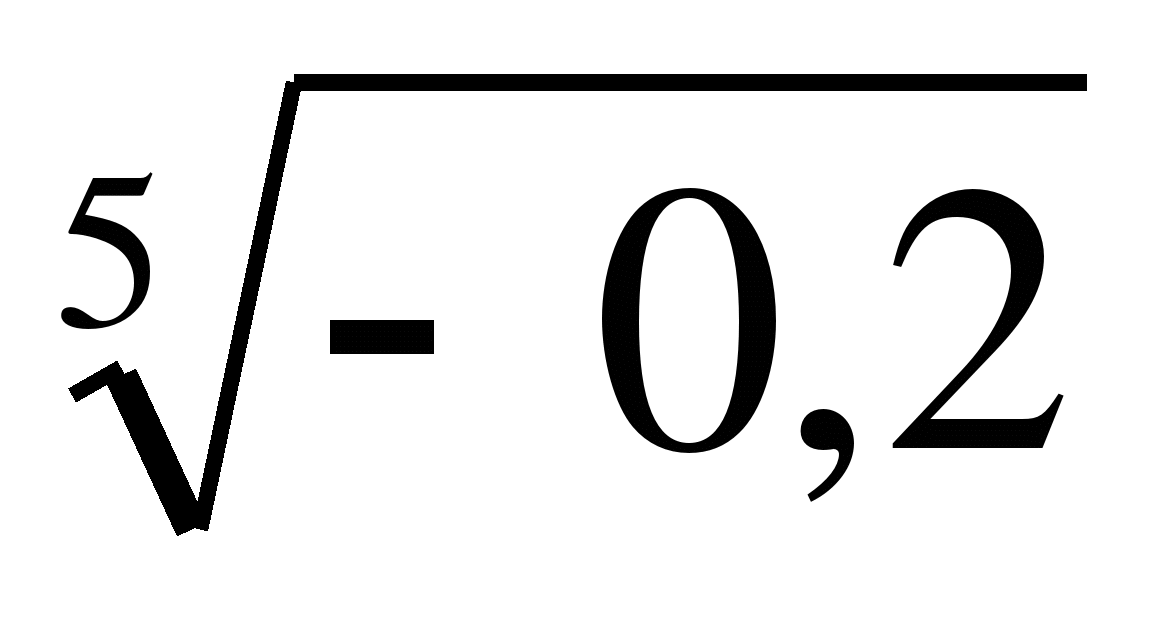 и 0.
и 0.