Подборка материала к ЕГЭ по математике В 11 классе профильный уровень»Задачи на движение по окружности» №11

Задачи на движение по окружности№11 ЕГЭ

1. Задание 11 № 99596

Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?

Решение.

Пусть v км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста равна v + 21 км/ч. Пусть первый раз мотоциклисты поравняются через 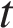 часов. Для того, чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому

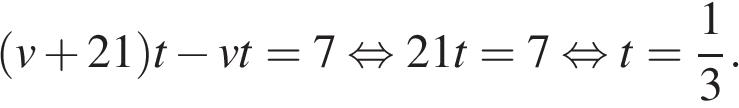
Таким образом, мотоциклисты поравняются через 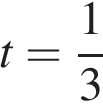 часа или через 20 минут.

 

Ответ: 20.

 

Приведём другое решение.

Быстрый мотоциклист движется относительно медленного со скоростью 21 км в час, и должен преодолеть разделяющие их 7 км. Следовательно, на это ему потребуется одна треть часа.

2. Задание 11 № 99598

Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Решение.

Пусть скорость второго автомобиля равна 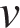 км/ч. За 2/3 часа первый автомобиль прошел на 14 км больше, чем второй, отсюда имеем

 

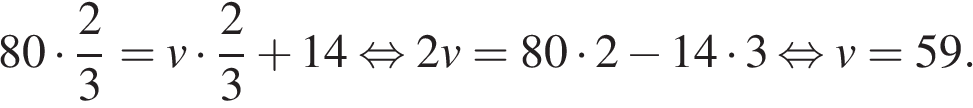
Ответ: 59.

3. Задание 11 № 99599

Из пункта A круговой трассы выехал велосипедист. Через 30 минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.

Решение.

К моменту первого обгона мотоциклист за 10 минут проехал столько же, сколько велосипедист за 40 минут, следовательно, его скорость в 4 раза больше. Поэтому, если скорость велосипедиста принять за x км/час, то скорость мотоциклиста будет равна 4x, а скорость их сближения — 3x км/час.

C другой стороны, второй раз мотоциклист догнал велосипедиста за 30 минут, за это время он проехал на 30 км больше. Следовательно, скорость их сближения составлят 60 км/час.

Итак, 3х = 60 км/час, откуда скорость велосипедиста равна 20 км/час, а скорость мотоциклиста равна 80 км/час.

 

Ответ: 80.

4. Задание 11 № 99600

Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Решение.

Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой – 1 деление/час. До четвертой встречи минутной и часовой стрелок минутная должна сначала 3 раза «обогнать» часовую, то есть пройти 3 круга по 12 делений. Пусть после этого до четвертой встречи часовая стрелка пройдет 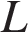делений. Тогда общий путь минутной стрелки складывается из найденных 36 делений, ещё 8 изначально разделяющих их делений (поскольку часы показывают 8 часов) и последних L делений. Приравняем время движения часовой и минутной стрелок:

 

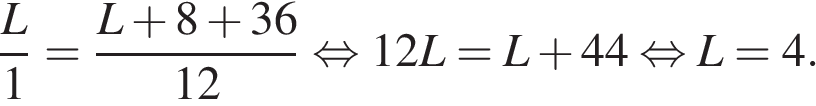
Часовая стрелка пройдет 4 деления, что соответствует 4 часам, то есть 240 минутам.

 

Ответ: 240.

 

Приведем другое решение.

Ясно, что в первый раз стрелки встретятся между 8 и 9 часами, второй раз — между 9 и 10 часами, третий — между 10 и 11, четвертый — между 11 и 12 часами, то есть ровно в 12 часов. Таким образом, они встретятся ровно через 4 часа, что составляет 240 минут.

 

По просьбам читателей помещаем общее решение.

Скорость вращения часовой стрелки равна 0,5 градуса в минуту, а минутной — 6 градусов в минуту. Поэтому когда часы показывают время h часов m минут часовая стрелка повернута на 30h + 0,5m градусов, а минутная — на 6m градусов относительно 12-часового деления.

Пусть в первый раз стрелки встретятся через t₁ минут. Тогда если минутная стрелка еще не опережала часовую в течение текущего часа, то 6m + 6t₁ = 30h + 0,5m + 0,5t₁, т. е. t₁ = (60h − 11m)/11 (*). В противоположном случае получаем уравнение 6m + 6t₁ = 30h + 0,5m + 0,5t₁ + 360, откуда t₁ = (60h − 11m + 720)/11 (**).

Пусть во второй раз стрелки встретятся через t₂ минут после первого, тогда 0,5t₂ = 6t₂ − 360, откуда t₂ = 720/11 (***). Это же верно для каждого следующего оборота.

Поэтому для встречи с номером n из (*) и (**) с учетом (***) имеем соответственно: t_n = (60h − 11m + 720(n − 1))/11 или t_n

 = (60h − 11m + 720n)/11.

5. Задание 11 № 323856

Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.

Решение.

Первый обогнал второго на 3 км за четверть часа, это значит, что скорость удаления (сближения) гонщиков равна 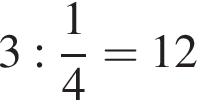 км/ч. Обозначим скорость второго гонщика  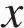км/ч, тогда скорость первого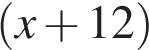 

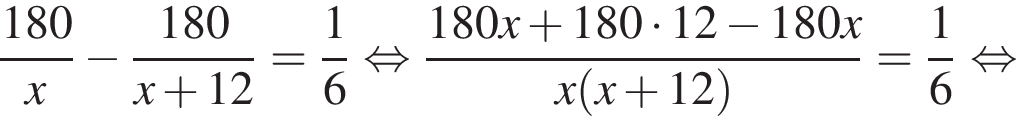
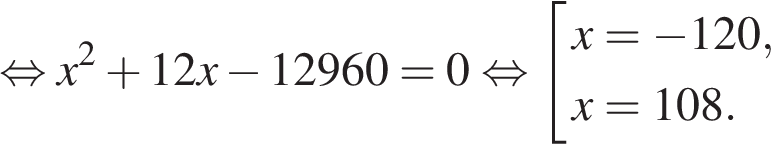
 км/ч. Составим и решим уравнение:

 

Таким образом, скорость второго гонщика равна 108 км/ч.

 

Ответ: 108.

infourok.ru

Методическая разработка по алгебре (11 класс) на тему: Готовимся к ЕГЭ. В13: Задачи на движение

Готовимся к ЕГЭ. В13: Задачи на движение                

Е.С.Пухова,

учитель математики МБОУСОШ №2

г. Апшеронск Краснодарский край

Для педагогов не секрет, что решение текстовых задач вызывало и вызывает затруднение у большей части учащихся. Умение анализировать условие и составлять математическую модель оказывается далеко не под силу каждому. Задачи на движение, совместную работу, смеси и сплавы рассматриваются в школьном курсе математики не один год. Но многие учащиеся из года в год при выполнении домашних работ, контрольных и краевых диагностических работ выбирают задания повышенного уровня С, игнорируя текстовые задачи. Ограниченность во времени при контроле знаний, напряжение и насыщенный объем работ не позволяет полностью свободно поразмыслить над схемой решения задания. С другой стороны развитое логическое мышление, приемы моделирования  позволяет остальным учащимся успешно справиться с задачами такого типа. Вашему вниманию предложены задания по теме, которые можно использовать при различных формах организации работы по подготовке к ЕГЭ.

1. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.

Решение.  Скорость сближения поездов 65 + 35 = 100 (км/ч) =  (м/с). Общий путь за 36 с составляет   * 36 = 1000 (м). Тогда 1000 – 700 = 300 (м) — длина скорого поезда.

Ответ: 300 м

2. Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Комментарий. Не уставайте напоминать учащимся формулу:

Средняя скорость =  .

Ответ: 72 км/ч

3. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.

Решение.  Важно объяснить, что в отличие от задачи 1, придорожный столб зафиксирован. Поезд за 36 с проезжает расстояние, равное собственной длине, со скоростью 80 км/ч = 80 *  (м/с) =   (м/с). Длина поезда * 36 = 800 (м).

Ответ: 800 м

Комментарий. Учащиеся при переводе км/ч в м/с часто путают деление  с умножением величины на 3,6. Не пытайтесь заставить их выучить нужное действие. Проще в соответствии с наименованием (км/ч) умножить величину на 1000 м  и разделить на 3600с. Ошибок будет намного меньше.

4. Дальнобойщик, погрузив груз в фуру, отправился в путь со скоростью 60 км/ч. Через 1 ч он сделал остановку на заправке на 30 мин, а затем продолжил путь с первоначальной скоростью. Через 1 ч после отправки фуры диспетчер склада обнаружил, что он забыл отдать дальнобойщику сопроводительные документы на груз и выехал вдогонку на мотоцикле со скоростью 100 км/ч. Какое расстояние (в километрах) проедет мотоциклист до места встречи?

Решение. Задачи на движение вдогонку встречаются часто. Собака догоняет шляпу, унесенную ветром, ребенок проезжает на велосипеде путь, возвращаясь от конечной точки до равномерно движущихся вслед за ним родителей и т. д.

   В данной задаче путь дальнобойщика равен пути мотоциклиста. Важно не забыть, что дальнобойщик двигался (1+х–0,5) часа, где х ч – время движения мотоциклиста. Решив уравнение 60(х + 0,5) = 100х, х = 0,75, найдем путь мотоциклиста, который равен 75 км.

Ответ: 75 км

5. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

Решение. Пусть х км/ч –скорость второго сухогруза, у км/ч -скорость первого сухогруза. Необходимо найти величину (х–у) км/ч. За 12 мин = 0,2 ч второй сухогруз прошел 0,2х км, что составляет (0,4 + 0,12 + 0,6 + 0,2у) км. (Необходимо помнить о длине второго сухогруза, как в задачах о поездах).

Из уравнения 0,2х = 0,4 + 0,12 + 0,6 + 0,2у  находим х-у = 5,6.

Ответ: на 5,6 км/ч скорость первого сухогруза меньше скорости второго.

6. Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
7. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
8. Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого  — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
9. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Решение. Трудность для учащихся — в круговой трассе.  Пусть х км/ч – скорость второго автомобиля, его путь за 40 мин равен х км. Путь первого автомобиля составил 80* км, что на 1 круг больше. Уравнение 80* — х = 14. Часть учащихся обратят внимание на скорость удаления и составят более простое уравнение: (80 – х) = 14.

Ответ: скорость второго автомобиля 59 км/ч.

10. Теплоход, скорость которого в неподвижной воде равна 25 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 30 часов после отплытия из него. Сколько километров прошел теплоход за весь рейс?
11. Товарный поезд каждую минуту проезжает на 750 м меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
12. Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
13. Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
14. Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.
15. Пристани A и B расположены на озере, расстояние между ними 390 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути остановку на 9 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
16. Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, баржа отправилась назад и вернулась в пункт А в 16:00. Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.
17. Катер проплывает 20 км против течения реки и еще 24 км по течению за то же время, за какое может проплыть по этой реке 9 км. Во сколько раз скорость катера больше скорости реки?

Решение. Как и в задаче 5, не нужно стремиться найти скорости катера и течения реки. Необходимо вычислить отношение , где х км/ч – собственная скорость катера, у км/ч – скорость течения реки. Уравнение + =  после преобразований примет вид: 5у² + 44 ху – 9х² = 0. Разделив обе части уравнения на у² ≠ 0 и обозначив  = m, имеем 9m² — 44m – 5 = 0. m1 = 5, m2 = —  – не соответствует условию задачи. В 5 раз скорость катера больше скорости реки.

Ответ: в 5 раз

   Анализируя работы учащихся, результаты КДР, ГИА, ЕГЭ выпускников, четко прослеживаю более высокий процент выполнения текстовых задач у ребят, обучающихся по УМК А.Г.Мордковича в средней и старшей школе. Эти дети, как правило, успешно справляются с  задачами. Нарастание сложности математических моделей идет постепенно, разнообразен уровневый подбор материала. Учителю необходимо разнообразить подбор материала из других пособий и источников.

nsportal.ru

Урок обобщения и систематизации знаний в 11-м классе по теме «Задачи на движение по прямой». Подготовка к ЕГЭ

При подготовке к ЕГЭ очень часто решение задач на движение вызывает у старшеклассников трудности. Они связаны с тем, что такие задачи они решали давно, в курсе основной школы. Это были в основном задачи на основные типы движения — по прямой, по воде, на среднюю скорость, и совсем редко встречались задачи по замкнутой трассе, на протяженные тела. Повторение темы «Задачи на движение» надо начинать с темы «Задачи на движение по прямой». При этом при решении каждой задачи необходимо учитывать сложности, которые возникают при анализе процесса движения, выполнении чертежа, выборе способа решения и как следствие — создании математической модели задачи.

Цели урока:

• обобщить и систематизировать знания, умения решения задач на движение по прямой;
• познакомить с новым методом решения — методом подобия.

Задачи урока:

• повторить основные формулы пути, движения, на сближение и удаление;
• решить задачи на движение по прямой из открытого банка задач ЕГЭ, применяя различные способы;
• развивать навыки рассуждения, наблюдательности, умения проводить аналогии, обобщать, обосновывать, анализировать, делать выводы;
• формировать сознательное отношение к учебе, подготовке к экзамену.

Содержание урока.

Актуализация знаний.

В 2012 году задание В13 открытого банка задач ЕГЭ по математике включает в себя практически все типы текстовых задач, которые раньше предлагались на вступительных экзаменах в вузы: задачи на движение и работу, задачи на проценты, на растворы, сплавы и смеси, на движение по замкнутой трассе и нахождение средней скорости.

Постановка цели.

Сегодня на уроке мы повторим решение задач на движение по прямой (навстречу и вдогонку), рассмотрим различные способы решения. Познакомимся с новым методом решения.

Повторение теоретического материала.

Вспомним, что при решении задач на движение принимают такие допущения: (Приложение 1.Слайд 4)

движение считается равномерным, если нет специальных оговорок;

изменение направления движения и переходы на новый режим движения считаются происходящими мгновенно;

если два тела начинают движение одновременно (если одно тело догоняет другое), то в случае, если они встречаются, каждое тело с момента выхода и до встречи затрачивает одинаковое время;

если тела выходят в разное время, то до момента встречи из них затрачивает время больше то, которое выходит раньше;

все величины, как правило, положительные (в природе скорость расстояние и время положительны), поэтому можно смело умножать, делить и возводить в квадрат получающиеся уравнения и неравенства, не делая необходимых в таких случаях оговорок.

Полезный совет.

При решении задач на движение, рисуйте картинки. Особенно, когда текст задачи большой и сразу в голове не укладывается. Чаще всего это нужно делать в задачах, где кто-то кого-то догоняет, встречается, или «болтается» между пунктами А и В туда и обратно: На картинке сразу видно, какие отрезки пути можно просчитать. Картинка реально облегчает составление математической модели. Не знаешь, что делать, загляни в Памятку опорного конспекта!

Повторить по опорному конспекту (Приложение 2): взаимосвязь времени, скорости и расстояния; скорость и время удаления (сближения).

Решение задач.

Задача № 1. (Устно) По чертежу найдите скорость сближения и скорость удаления объектов и определите, на каком расстоянии друг от друга они будут через 1 ч после начала движения. (Приложение 1.Слайд 5)

Рисунок 1                                   Рисунок 2

Рисунок 3                            Рисунок 4

Ответ: 1) 20 км/ч, 40 км; 2) 20 км/ч, 80 км; 3) 4 км/ч, 56 км; 4) 4 км/ч, 64 км.

Задача № 2. Расстояние между городами А и В 250 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через два часа после этого навстречу ему из города В выехал со скоростью 85 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся? Ответ дайте в километрах. (Приложение 1.Слайд 6)

Решение:

Выполним чертеж к задаче:

Рисунок 5

В задаче известны скорости каждого автомобиля, движение навстречу друг другу (опорный конспект). Решим задачу по действиям:

2 * 55 = 110 (км) — путь 1-ого автомобиля за 2 часа.

250 — 110 = 140 (км) — расстояние, которое надо проехать 1-ому и 2-ому автомобилю до встречи.

55 + 85 = 140 (км/ч) — скорость сближения.

140 : 140 = 1 (ч) — время встречи.

110 + 55 = 165 (км).

Напомним, что в бланках ЕГЭ ответ должен быть целым числом или конечной десятичной дробью, единицы измерения не пишут.

Ответ: 165 .

Задача № 3. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 112 км. На следующий день он отправился обратно в А со скоростью на 6 км/ч большей прежней. По дороге он сделал остановку на 6 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько и на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. (Приложение 1.Слайд 7)

Решение:

Скорость велосипедиста из В в А на 6 км/ч больше, чем скорость из А в В. Пусть скорость из А в В х км/ч (х >0), тогда (х + 6) км/ч скорость из В в А.

Выполним чертеж к задаче:

Рисунок 6

Составим таблицу. (Приложение 2)

	Скорость v (км/ч)	Время t (ч)	Расстояние s (км)
из А в В	х		112
из В в А	х + 6		112

Зная, что на обратном пути он останавливался на 6 ч и в результате на него он затратил столько же времени, сколько на путь из А в В, составим уравнение:

.

Умножая обе части уравнения на х(х+6), , после решения полученного уравнения приходим к квадратному уравнению . Корни уравнения . Отсюда, , где х₂ = — 14 не удовлетворяет условию х > 0. Скорость из А в В равна 8 км/ч, значит, из В в А: 8 + 6 = 14 (км/ч).

Проверка: 1) 112 : 8 = 14 (ч) — время из А в В

2) 112 : (8 + 6) + 6 =14 (ч) — время из В в А.

Ответ: 14 .

Задача № 4. Из городов А и В навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 10 часов раньше, чем велосипедист приехал в А, а встретились они через 55 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?

Решение:

Ни скорость мотоциклиста и велосипедиста, ни расстояние от А до В нам неизвестны. Мы знаем, что движение обоих равномерное, скорость - постоянная величина. Расстояние зависит от времени, s(t) = vt, где v = const, — функция прямой пропорциональности, графиком которой является прямая. Выполним чертеж к задаче, построив схематические графики движения мотоциклиста и велосипедиста. (Приложение 1.Слайд 8)

Рисунок 7

AR — схематический график движения мотоциклиста, BK — схематический график движения велосипедиста, точка N соответствует моменту их встречи через 55 минут. Пусть х мин (х >0) — время мотоциклиста от момента встречи до прибытия в пункт В., т.е. DR = x минут. Из условия задачи следует, что МК = 600 минут. (Приложение 1.Слайд 9)

Рисунок 8

BD = AC = 55, DR = CM = x. Из подобия двух пар треугольников BDN и CNК, DNR и CAN, получим пропорции: . Откуда Решая пропорцию, приходим к квадратному уравнению, корни которого Отсюда, , что не удовлетворяет условию х >0.

Найдем сколько часов затратил велосипедист на путь из В в А:

55 + 5 = 60 (мин) = 1 (ч), 2) 1 ч + 10 ч = 11 ч.

Метод, которым мы решали, называют методом подобия.

Ответ: 11.

Задача № 5. Расстояние между городами А и В равно 203 км. Из города А в город В выехал автомобиль, а через 3 часа следом за ним со скоростью 110 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С. Ответ в километрах. (Приложение 1.Слайд 10)

Решение:

Выполним чертеж к задаче:

Рисунок 9

Пусть скорость автомобиля х км/ч (х > 0), а искомое расстояние АС = у км. На участке АС движение вдогонку, причем время, затраченное обоими транспортными средствами на этом участке, равно t = АС : 110 = у : 110 (ч). Расстояние, пройденное автомобилем за первые три часа AD = 3х (км). Учитывая, что на участке АС движение вдогонку и в пункте С они встретились, получаем AD = (км). Составим уравнение:

После встречи в пункте С автомобиль и мотоцикл, двигаясь в противоположных направлениях, начинают и заканчивают движение одновременно. Расстояние, которое они проходят за время t = у : 100 (ч), АВ = (км). Зная, что АВ = 203 км, составим уравнение: Составим и решим систему уравнений:

Выражая из каждого уравнения дробь , приравниваем полученные выражения: Решая пропорцию, приходим к квадратному уравнению Корни уравненияОтсюда, . Значит, х = 35, у = 154, т.е. АС = 154 км.

Проверка: 1) 154 : (3 + ) = 35 (км/ч) — скорость автомобиля,

2) 154 : = 110 (км/ч) — скорость мотоциклиста,

3) (35 + 110) = 203 (км) — АВ.

Ответ: 154 .

Самостоятельная работа. (Приложение 1.Слайд 11)

Ответы (Приложение 1.Слайд 12): 1 вариант: № 1 2 , № 2 340 , № 3 10;

2 вариант: № 1 2 , № 2 350 , № 3 11.

Подведение итога урока.

Домашнее задание. (Приложение 3)

Заключительное слово:

На следующих уроках мы продолжим повторение темы «Задачи на движение», где рассмотрим задачи на движение по воде, по замкнутой трассе и протяженных тел, на нахождение средней скорости.

Урок я хочу закончить словами известного математика Дж. Пойа: «Если хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их». (Приложение 1.Слайд 13)

urok.1sept.ru

Тест по алгебре (11 класс) по теме: ЕГЭ Задачи на движение.

Вариант 1. 1.Из города А в город В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 33 км/ч, а вторую половину пути – со скоростью, на 22 км/ч большей скорости первого, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста. Ответ дайте в км/ч. 2. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 104 км. На следующий день он отправился обратно в А со скоростью на 5 км в час больше прежней. По дороге он сделал остановку на 5 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на путь из В в А. (в км/ч). 3.Два велосипедиста одновременно отправились в 117-километровый   пробег.   Первый   ехал   со   скоростью, на 4 км/ч большей, чем скорость второго, и прибыл к фи нишу на 4 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч. 4. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч. 5. Заказ на 130 деталей первый рабочий выполняет на 3 часа быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 3 детали больше? 6.На изготовление 475 деталей первый рабочий затрачивает на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?

Вариант 2. 1.Два велосипедиста одновременно отправились в 110 километровый пробег. Первый ехал со скоростью, ни 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.         2.Моторная лодка прошла против течения реки 72 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 9 км/ч. Ответ дайте в км/ч. 3.От пристани А к пристани В отправился с постоянной скоростью первый теплоход, а через 3 часа после этого следом за ним со скоростью, на 3 км/ч большей, отправился второй. Расстояние между пристанями равно 154 км. Найдите скорость второго теплохода, если в пункт В он прибыл одновременно с первым. Ответ дайте в км/ч. 4.Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 1 деталь больше? 5.На изготовление 99 деталей первый рабочий затрачивает на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий? 6.Первая труба пропускает на 3 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 648 литров она заполняет на 3 минуты быстрее, чем первая труба?

nsportal.ru

Задачи на движение протяженных тел и сложение скоростей

Это один из самых интересных типов текстовых задач на ЕГЭ по математике. Здесь и задачи на движение протяженных тел. И задачи, где два поезда движутся навстречу друг другу (по параллельным путям, конечно). И такие, где один поезд обгоняет другой.

Расскажем о секретах решения таких задач.

Что значит «движение протяженных тел»?

Если в условии задачи поезд проходит расстояние от Санкт-Петербурга до Москвы — длиной самого поезда можно пренебречь. Она намного меньше расстояния между городами. В физике говорят, что поезд в этом случае можно считать материальной точкой. Если же в задаче один поезд проходит мимо другого или поезд проходит через туннель — длину поезда также надо учитывать.

1. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо лесополосы, длина которой равна 500 метров, за 36 секунд. Найдите длину поезда в метрах.

36 секунд, за которые поезд проезжает мимо лесополосы, — это время от момента, когда голова поезда поравнялась с началом лесополосы, до момента, когда хвост поезда поравнялся с концом лесополосы. За это время поезд проезжает расстояние, равное сумме собственной длины и длины лесополосы.

Переведем 36 секунды в часы. 

За это время поезд проехал 

 

Ответ: 300

Задачи на встречное движение или обгон удобно решать в движущейся системе отсчета. 

2. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 60 км/ч и 30 км/ч. Длина пассажирского поезда равна 400 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 38 секундам. Ответ дайте в метрах.

Решим задачу в системе отсчета, связанную с головой пассажирского поезда. Представим, что мы находимся в кабине машиниста неподвижного поезда, а мимо нас проносится скорый поезд. Скорость, с которой один поезд движется относительно другого, равна

Тогда 38 секунд, за которые движущийся поезд проезжает мимо неподвижного, — это время от момента, когда голова первого поезда поравнялась с хвостом второго, до момента, когда хвост первого поезда поравнялся с головой второго (смотри рисунки) За это время скорый поезд проезжает расстояние, равное сумме длин двух поездов.

Переведем 38 секунд в часы:

За это время поезд проехал 

Ответ: 550

3. Два поезда движутся навстречу друг другу со скоростями 56 и 52 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 15 секунд. Найдите длину второго поезда. Ответ выразите в метрах.

Если пассажир находится в первом поезде, то в его системе отсчета второй поезд движется навстречу со скоростью, равной сумме скоростей поездов. Иначе она называется «скорость сближения», и она равна

Переведем эту скорость в метры/минуту.

Мы получили, что со скоростью 1800м/мин мимо пассажира первого поезда проходит весь второй поезд. По условию, это происходит за 

Длина второго поезда равна 

Ответ: 450 м.

4. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 140 метров, второй — длиной 60 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 800 метров. Через 15 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 1000 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

Переведем минуты в часы: 

Пусть и — скорости первого и второго сухогрузов. Будем решать задачу в системе отсчета, связанной с первым сухогрузом. Представьте, что вы находитесь на нем и видите, как второй сухогруз догоняет и обгоняет ваш корабль со скоростью

Расстояние, пройденное вторым сухогрузом, — это сумма расстояний от носа второго сухогруза до кормы первого, длины первого сухогруза, расстояния от его носа первого до кормы второго и длины второго (см. рисунок).

Воспользуемся формулой:

км/ч

На 8 километров в час скорость второго сухогруза больше скорости первого.

Ответ: 8

 

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Материал для подготовки к ЕГЭ (ГИА) по алгебре (11 класс) на тему: Скорость, движение, время. Задачи на движение.

В.К. Кузнецова,

учитель математики ГБОУ «Школа № 329» г.  Москва,

кандидат педагогических наук

Готовимся к ЕГЭ

Скорость, движение, время. Задачи на движение.

В данном пособии собраны задачи на движение. При составлении систем для таких задач обычно не требуется никаких особенных математических знаний. Требуется лишь здравый смысл и понимание того, что

Расстояние = скорость х время

Существуют два подхода к решению задач на движение:

1.  С помощью таблиц — самый распространенный прием, который в большинстве случаев помогает быстро получить уравнение, но не всегда в некоторых задачах этот прием дает положительный результат.
2.  Последовательный анализ условия с привлечением иллюстраций — классический прием из средней школы, о котором к 11-му классу многие забывают.

Обратите внимание: на практике любую задачу B14 можно решить каждым из этих способов. И ответ получится одинаковым. Однако некоторые задачи проще решаются таблицами, а другие — иллюстрациями и анализом. Поэтому какой способ выбрать — зависит исключительно от предпочтений ученика.

Примеры решения задач

Задачи на движение в одном направлении

Задача № 1.

Два человека отправляются одновременно из одного и того же места на прогулку до опушки леса, находящейся в 4,5 км от места отправления. Один идет со скоростью 2,4 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от места отправления произойдет их встреча? Ответ выразите в километрах.

Решение:

Задача № 2

Из пункта  в пункт , расстояние между которыми  км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на  км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт  на  часа позже автомобилиста. Ответ дайте в км/ч.

Решение:

Что здесь лучше всего обозначить за ? Скорость велосипедиста. Тем более, что ее и надо найти в этой задаче. Автомобилист проезжает на  километров больше, значит, его скорость равна .

Нарисуем таблицу. В нее сразу можно внести расстояние — и велосипедист, и автомобилист проехали по  км. Можно внести скорость — она равна  и  для велосипедиста и автомобилиста соответственно. Осталось заполнить графу «время».

Его мы найдем по формуле: . Для велосипедиста получим , для автомобилиста .
Эти данные тоже запишем в таблицу.

Вот что получится:

велосипедист
автомобилист

Остается записать, что велосипедист прибыл в конечный пункт на 4 часа позже автомобилиста. Позже — значит, времени он затратил больше. Это значит:

Решаем уравнение:

Получим:

 Преобразуем:

Найдем дискриминант  и корни:

, .

Ясно, что  не подходит по смыслу задачи — скорость велосипедиста не должна быть отрицательной.

Ответ: скорость велосипедиста 10 км/час.

Задачи на движение вдогонку 

Как и большинство других текстовых задач на движение такие задачи лучше всего решаются с помощью таблиц.

Задача № 3

Данный пример интересен тем, что мы сравниваем время движения двух объектов — мотоциклиста и велосипедиста — при этом сама скорость движения вдогонку нас мало интересует. При этом возникает опасность неправильно составить исходное уравнение.

Решить задачу: из города А в город Б, расстояние между которыми равно 240 км, одновременно выехали велосипедист и мотоциклист. Скорость мотоциклиста на 40 км/ч больше скорости велосипедиста, а в пункт Б он приехал на 8 часов раньше, чем велосипедист. Найдите скорость велосипедиста. Ответ дайте в км/ч.

Ключевое правило при сравнении времени движения следующее:

1. Если в задаче указано общее время движения, то нужно сложить  полученные дроби, отвечающие за время.
2. Если же время движения сравнивается (как в данной задаче), то нужно приравнять их и добавить слагаемое по принципу: «больше = меньше + число» либо «меньше = больше + число».

Последнее правило естественным образом следует из самой терминологии «больше — меньше»: чтобы получить большее число, нужно к меньшему числу прибавить что-то еще. Если же вместо прибавки мы будем вычитать, то получим еще меньшее, что никак не согласуется с условием задачи.

Кроме того, необходимо помнить, что при равном расстоянии (а в задачах B14 расстояния очень часто оказываются равны) объект с большей скоростью накроет это расстояние за меньшее время. И наоборот: чем меньше скорость, тем больше времени потребуется на преодоление пути.

Решение:

Обозначим за х км/ч скорость велосипедиста. Составим таблицу

	V	T	S
Велосипедист	x		240
Мотоциклист	x+40		240

Время мотоциклиста на 8 часов меньше времени велосипедиста.

Составим уравнение:

 

Необходимо помнить, что время велосипедиста больше, чем время мотоциклиста. Поэтому от большей дроби вычитаем меньшую.

Решим уравнение:

Получим, x=20 или x= -60. -60 – посторонний корень. Скорость велосипедиста равна 20 км/ч.

Ответ: 20 км/ч.

nsportal.ru

Задачи повышенной сложности на равнопеременное движение

Этот урок посвящён решению задач по кинематике, а именно на равнопеременное движение. В ходе урока будут подробно показаны решения трёх типовых задач повышенной сложности, которые взяты из сборника задач для подготовки к единому государственному экзамену. Благодаря этому вы сможете научиться делать правильно краткую запись условия, делать поясняющие чертежи, а также применять известные вам формулы для нахождения неизвестных в задаче величин

С какой скоростью начало тело двигаться вверх по наклонной плоскости, если на расстоянии 0,5 м от её основания тело было через 0,5 с и через 2,5 с от начала движения?

Дано: 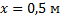 – координата точки, которую тело проходит через время  и ;  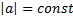– ускорение.

Найти: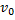

Решение

Координата при равнопеременном движении равна:

 

Данную формулу запишем для 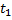 и :

 

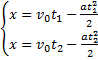
Из условия задачи видно, что:

 

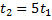
Или:

 

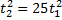
В полученной ранее системе уравнений два неизвестных, 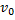и . Если требуется найти 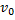, то оптимальным способом решения данной системы будет домножение первого уравнения на 25 и вычитание из него второго уравнения. Тем самым мы уберём слагаемое, которое содержит ускорение a.

 

 

 

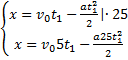
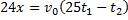
Ответ: .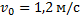

Два мальчика, находящиеся на расстоянии 9,2 м друг от друга, перебрасывают мяч, сообщая ему скорость 11 м/с. Найти максимальную высоту подъёма мяча.

Дано: 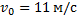; ; 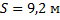 – ускорение равно ускорению свободного падения

Найти:

Решение

На рисунке 1 изображён поясняющий чертёж к задаче.

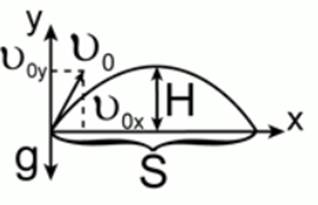
Рис. 1. Иллюстрация к задаче

 

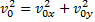
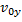 можно найти из уравнения кинематики для движения тела по вертикали:

 

 

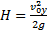
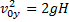
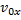 найдём из формулы дальности полёта:

,

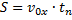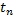 – время полёта.

При симметричной траектории время полёта равно удвоенному времени подъёма до верхней точки (спуска с верхней точки):

 

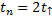
Время подъёма до верхней точки равно:

 

 

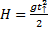
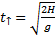
Следовательно:

 

 

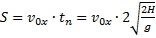
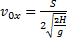
Возведём обе части данного выражения в квадрат:

 

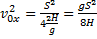
Подставим значения 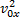 и 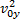 в формулу для квадрата начальной скорости:

 

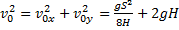
Домножим обе части уравнения на :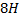

 

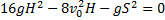
Получили квадратное уравнение относительно H. Следовательно:

 

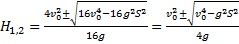
Максимальная высота будет соответствовать выражению:

  

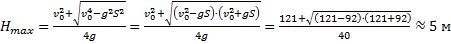
Ответ: .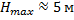

Под каким минимальным углом к горизонту нужно направить ствол орудия, сообщающего снаряду скорость 400 м/с, чтобы поразить цель, расположенную в 4 км от огневой позиции на горе высотой 1,5 км?

Дано: ; ; ;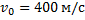

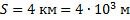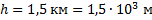Найти: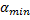

Решение

На рисунке 2 изображён поясняющий рисунок к задаче.

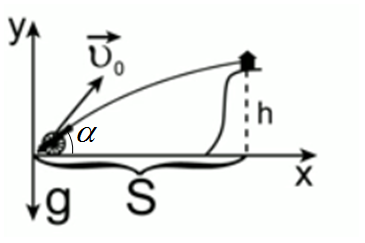
Рис. 2. Иллюстрация к задаче

Для решения данной задачи воспользуемся уравнением для траектории движения тела, брошенного под углом к горизонту:

 ,

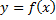где 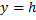 — вертикальная координата цели;  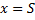– горизонтальная координата цели.

Данное уравнение с подстановкой h и S выглядит следующим образом:

 

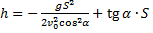
Как известно:

 

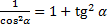
Поэтому:

 

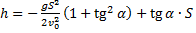
Домножим обе части уравнения на :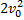

 

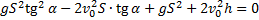
Получили квадратное уравнение относительно :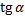

 

 

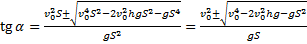
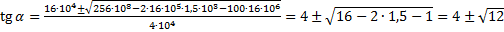
Нам необходимо вычислить минимальный угол, поэтому:

 

 

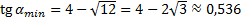
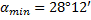
Ответ: .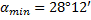

 

Домашнее задание

1. Упражнение 4 стр. 43 – Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10 (см. список рекомендованной литературы)
2. Тело, пущенное вверх вдоль наклонной плоскости со скоростью 1,5 м/с, вернулось обратно со скоростью 1 м/с. Найти среднюю скорость тела на всем пути. Вверх и вниз тело двигалось с постоянным ускорением. 
3. При аварийном торможении автомобиль, двигающийся со скоростью 20 м/с, остановится через 5 с. Найти тормозной путь автомобиля, если его ускорение – 6 м/с.
4. Теннисист при подаче запускает мяч с высоты h над землей. На каком расстоянии от подающего мяч ударится о землю, если начальная скорость равна  и направлена вверх под углом   к горизонту?

 

Список литературы

1. Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
2. А.П. Рымкевич. Физика. Задачник 10–11. – М.: Дрофа, 2006.
3. О.Я. Савченко. Задачи по физике. – М.: Наука, 1988.
4. А.В. Пёрышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
5. Орлов В.А., Демидова М.Ю., Никифоров Г.Г., Ханнанов Н.К. Оптимальный банк заданий для подготовки к ЕГЭ. Единый государственный экзамен 2015. Физика. Учебное пособие. – М.: Интеллект-Центр, 2015.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Eduspb.com (Источник).
2. Интернет-портал Indigomath.ru (Источник).
3. Интернет-портал Natalibrilenova.ru (Источник).

interneturok.ru