Сложение и вычитание дробей с одинаковыми знаменателями: ПРИМЕРЫ

 

Дробью будем называть одну или несколько равных между собой долей одного целого. Дробь записывается с помощью двух натуральных чисел, которые  разделены между собой чертой. Например, 1/2, 2/4, ¾, 5/9 и т.д. 

Цифра, которая записана сверху над чертой, называется числителем дроби, а цифра записанная под чертой, называется знаменателем дроби. Знаменатель дроби показывает, на сколько равных частей было поделено целое. Числитель дроби показывает, сколько таких частей взято.   

Дроби, как и обычные натуральные числа, можно складывать и вычитать между собой. Разберемся, как складывать и вычитать дроби, у которых в знаменателе находится одно и тоже число.

Сложение дробей с одинаковыми знаменателями

Пусть имеется две дроби с одинаковыми знаменателями, например 3/7 и 2/7. Найти их сумму.

Основное правило сложения дробей с одинаковыми знаменателями:

• Для того, чтобы сложить две дроби с одинаковыми знаменателями, необходимо знаменатель оставить без изменения, а числители складываемых дробей сложить между собой как обычные числа.

Вернемся к нашему  примеру, и сложим дроби 3/7 и 2/7. Так как, знаменатели у дробей одинаковые, то можно воспользоваться правилом, написанным выше.

Согласно этому правилу 3/7 + 2/7 будет равняться 5/7.

• 3/7 + 2/7 = (3+2)/7 = 5/7.

Вычитание дробей с одинаковыми знаменателями

Пусть имеется две дроби с одинаковыми знаменателями, например 9/13 и 5/13. Нужно найти их разность.

Основное правило вычитания дробей с одинаковыми знаменателями:

• Для вычитании  дробей с одинаковыми знаменателями, необходимо знаменатель оставить без изменений, а из числителя первой дроби, вычесть числитель второй дроби.

Вернемся к нашему примеру, и вычтем из дроби 9/13  дробь 5/13. Так как знаменатели дробей равны, то можно воспользоваться правилом, написанным выше.

Согласно этому правилу  9/13 –  5/13 будет равняться 4/13.

• 9/13 –  5/13 = (9-5)/13 = 4/13.

Задача-пример на сложение и вычитание дробей

Рассмотрим одну небольшую задачку, на сложение и вычитание дробей.

Бочонок с медом был заполнен на 5/7 от своего объема. Винни-Пух съел за завтраком, 2/7 бочонка, и еще 1/7 бочонка съел Пятачок. Найти сколько меда осталось в бочонке, после завтрака героев.

Сначала определим сколько вместе съели Винни-Пух и Пятачок, для этого сложим две дроби 2\7 и 1/7. 

Так как у дробей одинаковые знаменатели, то воспользуемся правилом сложения дробей с одинаковыми знаменателями.

• 2/7 + 1/7= (2+1)/7 = 3/7.

Теперь вычтем из того, что было в бочонке, то сколько съели Винни-Пух и Пятачок.

Так как дроби снова имеют одинаковые знаменатели, воспользуемся правилом вычитания дробей с одинаковыми знаменателями.

• 5/7 – 3/7 = (5-3)/7 = 2/7.

Это и будет ответом, к нашей задаче.

Нужна помощь в учебе?

Предыдущая тема: Дроби: чтение и сравнение дробей
Следующая тема:&nbsp&nbsp&nbspТочка, отрезок, луч, прямая — числовая прямая | 5 класс

5.4.7. Примеры на сложение и вычитание обыкновенных дробей.

Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 4.8k. Опубликовано 19 ноября 2012

I.  Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

Примеры.

II.  Если нужно сложить дроби с разными знаменателями, то сначала дроби приводят к наименьшему общему знаменателю, а затем складывают дроби с одинаковыми знаменателями.

Примеры.

III.  Чтобы выполнить вычитание дробей с одинаковыми знаменателями, из числителя первой дроби вычитают числитель второй дроби, а знаменатель оставляют тот же.

Примеры.

IV.  Если нужно выполнить вычитание дробей с разными знаменателями, то их сначала приводят к общему знаменателю, а затем выполняют вычитание дробей с одинаковыми знаменателями.

Примеры.

V.  При выполнении действий сложения или вычитания смешанных чисел эти действия выполняют отдельно для целых частей и для дробных частей, а затем результат записывают в виде смешанного числа.

Примеры.

Да, складывать нужно отдельно целые части и отдельно дробные части смешанного числа.

Нет, не нужно расписывать целые и дробные части смешанных чисел по отдельности.

Важно: не начинайте выполнять сложение, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ).

Помним, что единицу можно представить в виде обыкновенной дроби, числитель и знаменатель которой, являются любыми равными друг другу числами.

Важно: не начинайте выполнять вычитание, пока не приведете  дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ) и не убедитесь, что из числителя первой дроби можно вычесть числитель второй дроби. А если нельзя вычесть?

Тогда «занимаете» у целой части уменьшаемого одну целую единицу, представляете ее в виде неправильной дроби с таким же знаменателем (НОЗ),  и добавляете эту неправильную дробь (раздробленную единицу) к дробной части уменьшаемого.

Урок 40. сложение и вычитание дробей — Математика — 6 класс

Математика

6 класс

Урок № 40

Сложение и вычитание дробей

Перечень рассматриваемых вопросов:

• обобщение и систематизация знаний по теме «Сложение и вычитание дробей».

Тезаурус

Сумма дробей с одинаковыми положительными знаменателями есть дробь с тем же знаменателем и числителем, равным сумме числителей.

Разностью двух дробей называют такую дробь, которая в сумме с вычитаемым даёт уменьшаемое.

Наименьший общий положительный знаменатель – это наименьшее положительное число, кратное знаменателям данных дробей.

Наименьшее общее кратное двух чисел – наименьшее натуральное число, которое делится на заданные числа без остатка.

Обязательная литература:

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

На прошлых уроках мы с вами рассматривали, как выполняют сложение и вычитание дробей любого знака. Сегодня вспомним и закрепим эти правила.

Вспомним основные правила сложения и вычитания дробей любого знака.

Правило сложения дробей с одинаковыми знаменателями

Чтобы сложить две дроби с одинаковыми положительными знаменателями, надо сложить их числители, а знаменатель оставить прежним.

Правило сложения дробей с разными знаменателями

Чтобы сложить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сложить полученные дроби.

Правило вычитания дробей с одинаковыми знаменателями

Чтобы вычесть две дроби с одинаковым положительными знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.

Правило вычитания дробей с разными знаменателями

Чтобы найти разность двух дробей с разными знаменателями, надо привести их к общему положительному знаменателю и выполнить вычитание дробей с одинаковыми знаменателями.

Разность дробей a и b равна сумме уменьшаемого и числа, противоположного вычитаемому.

Дроби можно складывать и вычитать по тем же правилам, что и целые числа, то есть сначала определять знак результата, потом выполнять действия с модулями.

Иногда сложение и вычитание дробей выполняется проще, если привести их к наименьшему общему положительному знаменателю.

Дополнительный материал

Решим задачу.

Какую часть пути прошли туристы за три дня?

Решение.

Найдём, какую часть пути туристы прошли в третий день.

Найдём, какую часть пути туристы прошли за три дня.

Для этого сложим все части.

Разбор заданий тренировочного модуля

№ 1. Разместите нужные подписи под изображениями.

Варианты ответов:

Сложение дробей с разными знаками и разными знаменателями.

Сложение отрицательных дробей с разными знаменателями

Вычитание дробей с одинаковыми знаменателями

Для ответа на вопрос задания вспомним действия с рациональными числами и внимательно посмотрим на знаки между предложенными дробями.

Правильный ответ:

1. Вычитание дробей с одинаковыми знаменателями.
2. Сложение дробей с разными знаками и разными знаменателями.
3. Сложение отрицательных дробей с разными знаменателями

№ 2. Вставьте в текст нужные слова.

Чтобы сложить две дроби с разными …, надо привести их к общему положительному … и … полученные дроби.

Варианты слов для вставки:

знаменателями

числителями

знаменателю

числителю

сложить

вычесть

Для ответа на вопрос задания обратимся к теоретическому материалу урока.

Правильный ответ:

Чтобы сложить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сложить полученные дроби.

Сложение дробей — как складывать дроби 🤔

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
2. Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.

Основные свойства дробей 1. Дробь не имеет значения, при условии, если делитель равен нулю. 2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля. 3. Равными называются такие a/b и c/d, если: 4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Как плюсовать дроби

Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.

Свойства сложения

• От перестановки мест слагаемых сумма не меняется: a + b = b + a.
• Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа: (a + b) + c = a + (b + c).
• Если к числу прибавить ноль, получится само число: a + 0 = 0 + a = a
• При сложении числа можно переставлять и объединять в группы, результат от этого не изменится.

Давайте рассмотрим несколько вариантов сложения обыкновенных дробей. 

Сложение дробей с одинаковыми знаменателями

Чтобы получить результат суммы двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.

Не забудьте проверить, можно ли сократить дробь.

Сложение дробей с разными знаменателями

Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:

1. Найдем наименьшее общее кратное (далее — НОК) для определения единого делителя.

Для этого записываем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

• 90 : 15 = 6,
• 90 : 18 = 5.

Полученные числа записываем справа сверху над числителем.

3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.

4. Проверим полученный результат:

• если делимое больше делителя, нужно преобразовать в смешанное число;
• если есть что сократить, нужно выполнить сокращение.
  

Еще раз ход решения одной строкой:

Сложение смешанных чисел

Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

1. Сложить целые части.

2. Сложить дробные части.

Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.

3. Суммируем полученные результаты.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:

Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, нужно решать примеры сложения дробей, как можно чаще.

Запишите вашего ребенка на бесплатный вводный урок математики в детскую школу Skysmart: порешаем задачки на интерактивной платформе, порисуем фигуры на онлайн-доске и покажем, что учиться можно с интересом и в удовольствие.

 

Вычитание дробей с разными, одинаковыми знаменателями

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Есть два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Над чертой принято писать делимое, которое является числителем. А под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
2. Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.

Основные свойства дробей 1. Дробь не имеет значения, при условии, если делитель равен нулю. 2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля. 3. Равными называют a/b и c/d в том случае, если a * d = b * c. 4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Правило вычитания дробей

Вычитание — арифметическое действие, когда от одного числа отнимают другое.

Свойства вычитания:

1. Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое, а после из результата вычесть другое слагаемое:
   a — (b + c) = (a — b) — c,
   a — (b + c) = (a — с) — b.

2. Скобки в выражении (a — b) — c не имеют значения и их можно опустить:
   (a — b) — c = a — b — c.

3. Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся:
   (a + b) — c = (a — c) + b, если a > c или а = с,
   (a + b) — c = (b — c) + a, если b > c или b = с.

4. Если из числа вычесть нуль, получится оно же:
   a — 0 = a.

5. Если из числа вычесть его само, получится нуль:
   a — a = 0.

Вычитание дробей с одинаковыми знаменателями

Для вычитания дробей с одинаковыми знаменателями нужно от числителя первой отнять числитель второй, а знаменатель оставить тот же.

Прежде, чем зафиксировать ответ, важно проверить возможность сокращения.

Рассмотрим это правило на примере:

Вычитание дробей с разными знаменателями

Как вычитать дроби с разными знаменателями? Для этого приводим их к общему знаменателю и гаходим разность числителей.

Рассмотрим пример, в котором нужно найти разность 2/9 и 1/15.

Как решаем:

• Знаменатели разные, значит найдем наименьшее общее кратное (далее — НОК) для определения единого делителя. Для этого записываем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (9, 15) = 3 * 3 * 5 = 45

• Найдем дополнительные множители. Для этого НОК делим на каждый знаменатель:

45 : 9 = 5,

45 : 15 = 3.

• Полученные числа умножим на соответствующие дроби: 

и

• Перейдем к вычитанию заданных чисел:

Ответ: 

Вычитание обыкновенной дроби из натурального числа

Для вычитания из обыкновенной дроби натурального числа необходимо это действие привести к вычитанию обыкновенных дробей.

Разберем для наглядности пример разности 3 и 6/7.

Как решаем:

• Представим натуральное число в виде смешанного — займем единицу и переведем ее в неправильную дробь с тем же знаменателем, что у вычитаемой:

3 = 2 * 7/7.

• Произведем разность:
  

Ответ: две целых одна седьмая.

Вычитание натурального числа из обыкновенной дроби

Для вычитания натурального числа из обыкновенной дроби нужно последовать тому же алгоритму, что и в предыдущем примере. А именно: перевести натуральное число в вид дроби, привести все к единому знаменателю, найти разность.

Рассмотрим пример разности 3 из 83/21.

Как решаем:

3 = 3/1.

А еще можно вот так:

• Представим 83/21 в виде смешанной дроби, для этого разделим делитель на делимое:

 83/21 = 3 * 20/21.

• Произведем вычитание:

3 * 20/21 — 3 = 20/21

Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором.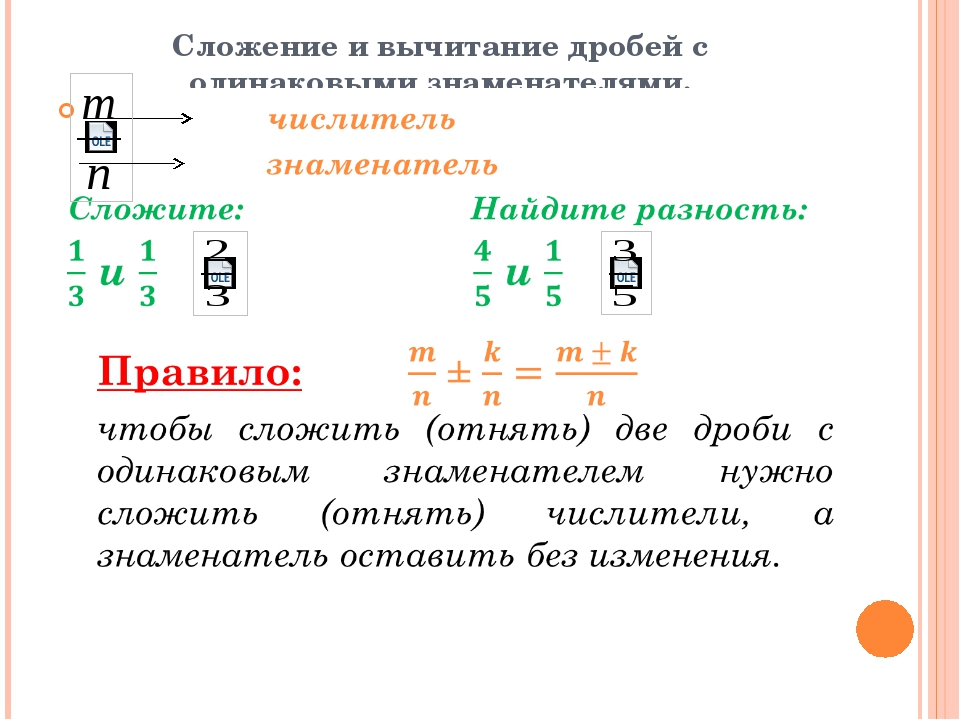 Вот несколько подходящих:

Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, нужно решать примеры сложения дробей, как можно чаще.

Приходите практиковаться в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

 

Сложение и вычитание простых дробей с одинаковыми знаменателями

Описание

Программа формирует примеры на сложение и вычитание простых дробей с одинаковыми знаменателями.

Случайным образом генерируется десять примеров. Ответ каждого предыдущего примера является первым числом следующего, что позволяет сформировать цепочку взаимосвязанных примеров. Итоговый ответ, который печатается в правом нижнем углу страницы, позволяет проверить правильность решения всех примеров без проверки каждого из них. Это дает возможность самостоятельно проверить правильность решения без возможности посмотреть ответ в процессе работы.

Правило сложения / вычитания простых дробей с одинаковыми знаменателями:
для того, чтобы сложить / вычесть две простые дроби с одинаковым знаменателем, необходимо сложить / вычесть числители этих дробей, а знаменатель оставить без изменений.
При необходимости проводится сокращение дроби. Если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную.

Программа написана в Excel с помощью макросов. Примеры генерируются случайным образом, количество генераций не ограничено. Для ознакомления с программой можно скачать образец примеров, которые получаются при использовании программы.
Для получения новой карточки примеров достаточно скачать, нажать на кнопку и распечатать.

Основные виды дробей, их основное свойство, а также все операции, которые можно выполнять с дробями: сокращение, приведение, сравнение, сложение, вычитание, умножение и деление описаны в статье «Математические дроби – просто о сложном».

Другие программы, которые помогут закрепить навыки счета с дробями:

На сайте представлен каталог программ, в котором все программы распределены по группам с указанием различий в программах внутри каждой группы. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

Сложение и вычитание простых дробей

См. также: более сложный уровень — сложение и вычитание дробей с алгебраическими выражениями и переменными.

Для проведения операции вычисления сложения простых дробей руководствуются следующим алгоритмом:

Сложение и вычитание простых дробей с одинаковым знаменателем

Для того, чтобы сложить две простые дроби с одинаковым знаменателем, необходимо сложить числители этих дробей, а знаменатель оставить без изменений.

• Числители каждой из дробей складываются,  а знаменатели остаются без изменения
• При необходимости проводится сокращение дроби
• Если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную

Общая формула сложения простых дробей с одинаковым знаменателем приведена на картинке.

Примеры сложения дробей с одинаковыми знаменателями и их пояснение.

Складываем 2/9 и 5/9

Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители

2+5 = 7

Ответ: 7/9

Складываем 1/8 и 3/8

Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители

1+3=4

Таким образом, 1/8 + 3/8 = 4/8

Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению. Сокращаем числитель и знаменатель на 4

4/8 = 1/2

Ответ: 1/2

Складываем 7/12 + 11/12

Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители

7+11=18

Таким образом, 7/12 + 11/12 = 18/12

Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению. Сокращаем числитель и знаменатель на 6

18/12 = 3/2

Получившаяся дробь является неправильной (числитель больше знаменателя). Преобразуем ее в смешанную

3/2 = 1 1/2

Ответ: 1 1/2

Для того, чтобы вычесть из одной простой дроби другую простую дробь, если обе дроби имеют одинаковый знаменатель, необходимо из числителя первой дроби, вычесть числитель второй дроби, а знаменатель оставить без изменения

• Из числителя первой дроби вычитается числитель второй дроби,  а знаменатели остаются без изменения
• При необходимости проводится сокращение дроби

Примеры вычитания дробей с одинаковыми знаменателями и их пояснение.

Вычитаем: 8/9 — 1/9

Поскольку обе простые дроби имеют общий одинаковый знаменатель, то вычитаем из числителя первой дроби числитель второй дроби

8-1 = 7

Ответ: 8/9 — 1/9 = 7/9

Вычитаем: 7/8 — 1/8

Поскольку обе простые дроби имеют общий одинаковый знаменатель, то вычитаем из числителя первой дроби числитель второй дроби

7-1 = 6

Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению.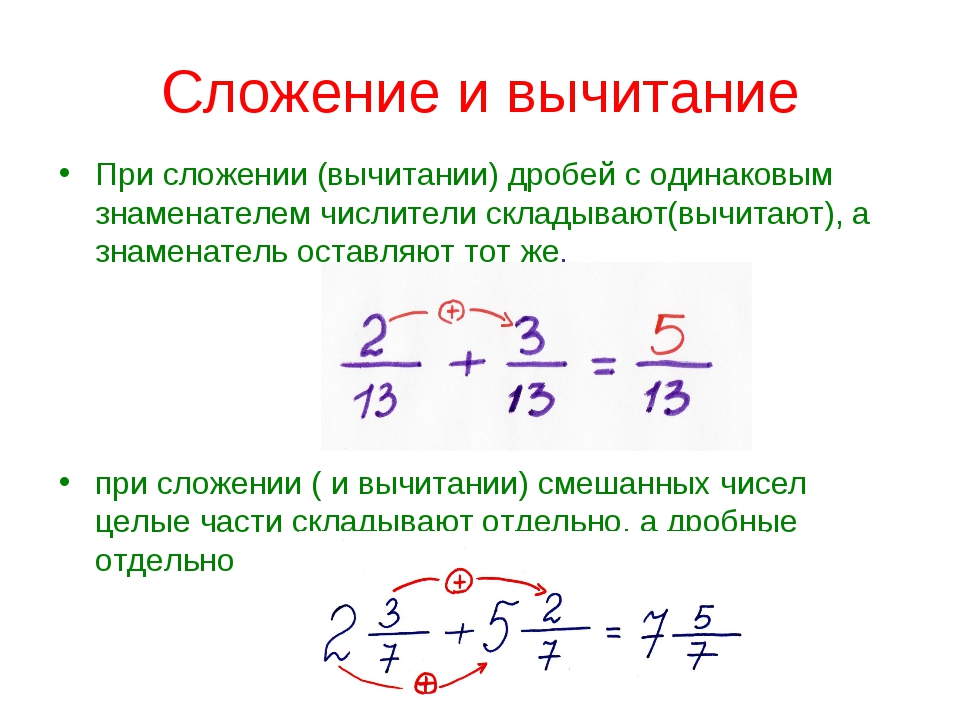 Сокращаем числитель и знаменатель на 2

6/8 = 3/4

Ответ: 7/8 — 1/8 = 3/4

В случае, когда обе дроби имеют разные знаменатели, пользуются правилами, описанными ниже.

Сложение и вычитание простых дробей с разными знаменателями (сложение и вычитание обыкновенных дробей)

Сложение обыкновенных дробей проводится по следующему алгоритму:

• Обе дроби приводятся к общему знаменателю
• Числители каждой из дробей складываются,  а знаменатели остаются без изменения
• При необходимости проводится сокращение дроби
• Если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную

Примеры сложения простых дробей с разными знаменателями с пояснением.

Складываем 1/3 и 1/4

Поскольку знаменатели у обоих дробей — разные, их необходимо привести к общему знаменателю.

В данном случае, наименьшее общее кратное для 3 и 4 — это число 12. Соответственно, числитель и знаменатель первой дроби ( 1/3 ) умножаем на 4, а числитель и знаменатель второй дроби ( 1/4 ) умножаем на 3.

Получаем 4/12 и 3/12

Теперь у нас обе дроби имеют одинаковый знаменатель — 12. Поэтому складываем числители первой и второй дроби

4 + 3 = 7

Знаменатель остается без изменений 4/12 + 3/12 = 5/12

Ответ: 1/3 + 1/4 = 5/12

Складываем 2/3 и 3/4

Поскольку знаменатели у обоих дробей — разные, их необходимо привести к общему знаменателю.

В данном случае, наименьшее общее кратное для 3 и 4 — это число 12. Соответственно, числитель и знаменатель первой дроби ( 1/3 ) умножаем на 4, а числитель и знаменатель второй дроби ( 1/4 ) умножаем на 3.

Получаем 8/12 и 9/12

Теперь у нас обе дроби имеют одинаковый знаменатель — 12. Поэтому складываем числители первой и второй дроби

8 + 9 = 17

Знаменатель остается без изменений 8/12 + 9/12 = 17/12

Полученная дробь является неправильной (числитель больше знаменателя). Преобразуем ее в смешанную

17/12 = 1 5/12

Ответ: 2/3 + 3/4 = 1 5/12

 Скорость поедания яблока | Описание курса | Сложение и вычитание дробей. Додавання і віднімання дробів 

   

Сложение дробей с одинаковыми знаменателями |

Чтобы складывать или вычитать элементы, единицы должны быть одинаковыми. Например, посмотрите на добавляемые ниже элементы.

2 яблока + 3 яблока = 5 яблок

6 апельсинов + 3 апельсина = 9 апельсинов

2 четверти + 5 четвертей = 7 кварталов

2 никеля + 3 никеля = 5 никель

Мы не можем добавлять яблоки и апельсины, если не называем их «фруктами». Точно так же мы не можем добавлять четвертинки и пятаки, если не называем их «центами».В названии дроби знаменателем является единица. Например, в дроби «4 десятых» знаменателем является единица десятых . Следовательно, 4 десятых + 5 десятых = 9 десятых. Посмотрите на пример 1 ниже.

Пример 1: Пицца была разделена на восемь равных частей (ломтиков). Если Дженни съела пять ломтиков, а Эрик — два, то какую часть пиццы они съели вместе?

Анализ: Дженни съела «5 восьмых» пиццы, а Эрик съел «2 восьмых».В каждой из этих дробей знаменателем является единица восьмых . Поскольку обе дроби имеют одинаковые единицы, мы можем сложить их вместе.

Решение: «5 восьмых + 2 восьмых = 7 восьмых».

---

Знаменатель дроби обозначает то, что мы считаем. В примере 1 мы считаем восьмые. Это показано в числовой строке ниже.

Нарисовать числовую прямую не всегда удобно. Итак, нам нужна арифметическая процедура сложения дробей.Задача из примера 1 записана с использованием математической записи ниже:

Знаменатель дроби указывает единицу измерения. Числитель показывает, сколько их. Например, в дроби пять восьмых единица восьмая, а их 5. Для сложения дробей знаменатели должны совпадать с . То есть они должны иметь общий знаменатель .

У этих дробей общий знаменатель (знаменатели совпадают).Если бы знаменатели не были общими, вы не смогли бы сложить эти дроби.

Это приводит нас к следующей процедуре сложения дробей с общим знаменателем.

Процедура: Чтобы сложить две или более дробей с одинаковыми знаменателями, сложите числители и поместите полученную сумму над общим знаменателем. При необходимости упростите результат.

Давайте рассмотрим несколько примеров сложения дробей с помощью этой процедуры.

Пример 2: Сложите эти дроби: Анализ: Сложите числители и поставьте сумму над общим знаменателем 7. Решение:

Пример 3: Сложите эти дроби: Анализ: Сложите числители и поставьте сумму над общим знаменателем, 9 . Решение:

В примере 3 нам нужно было упростить результат: мы сократили шесть девятых до наименьших членов, то есть двух третей.

Пример 4: Сложите эти дроби: Анализ: Сложите числители и поставьте сумму над общим знаменателем, 4 . Решение:

В примере 4 мы упростили результат, преобразовав неправильную дробь в целое число.

Избегайте этой распространенной ошибки!

Некоторые студенты по ошибке складывают знаменатели и числители. Это математически неверно, как показано ниже.

Пример 5: Сложите эти дроби: Решение: Анализ:

Знаменатели не складывать!

Чтобы сложить дроби, складывайте только числители и ставьте сумму над общим знаменателем.

Пока мы добавляли только две дроби за раз. Мы можем сложить более двух дробей, используя описанную выше процедуру. Это показано в примерах ниже.

Пример 6: Сложите эти дроби: Анализ: Сложите числители и поставьте сумму над общим знаменателем, 11 . Решение:

Пример 7: Сложите эти дроби: Анализ: Сложите числители и поставьте сумму над общим знаменателем, 10 . Решение:

Резюме:

Чтобы сложить две или более дробей с одинаковыми знаменателями, сложите числители и поместите полученную сумму над общим знаменателем. При необходимости упростите результат.

---

Упражнения

Указания: складывайте дроби в каждом упражнении ниже. Обязательно упростите ваш результат, если необходимо. Щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ.

Примечание. Чтобы записать дробь в три четверти, введите в форму 3/4.

1.

2.

3.

4.

5.

Сложение дробей

Дробь типа 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.

Три простых шага для сложения дробей:

• Шаг 1. Убедитесь, что нижние числа (знаменатели) совпадают.
• Шаг 2: сложите верхние числа (числители), поместите полученный ответ над знаменателем
• Шаг 3. Упростите дробь (при необходимости)

Пример:

Шаг 1 . Нижние цифры (знаменатели) уже совпадают. Переходите сразу к шагу 2.

Шаг 2 .Сложите верхние числа и поставьте ответ над тем же знаменателем:

.

1 4 + 1 4 знак равно 1 + 1 4 знак равно 2 4

Шаг 3 . Упростим дробь:

2 4 знак равно 1 2

На картинке это выглядит так:

1 4	+	1 4	=	2 4	=	1 2

… и ты видишь как 2 4 проще как 1 2 ? (см. Эквивалентные дроби.)

Пример:

Шаг 1 : Нижние числа разные. Видите, как ломтики бывают разных размеров?

1 3	+	1 6	=	?

Нам нужно сделать их такими же, прежде чем мы сможем продолжить, потому что мы не можем добавить их таким образом.

Число «6» вдвое больше, чем «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю часть первой дроби на 2 , например:

× 2

× 2

Важно: вы умножаете как верхний, так и нижний на одинаковую величину,
, чтобы сохранить значение дроби одинаковым

Теперь дроби имеют одинаковое нижнее число («6»), и наш вопрос выглядит так:

2 6	+	1 6

Нижние числа теперь те же, поэтому мы можем перейти к шагу 2.

Шаг 2 : сложите верхние числа и поместите их над тем же знаменателем:

2 6 + 1 6 знак равно 2 + 1 6 знак равно 3 6

На картинке это выглядит так:

2 6	+	1 6	=	3 6

Шаг 3 : Упростите дробь:

3 6 знак равно 1 2

На картинке весь ответ выглядит так:

2 6	+	1 6	=	3 6	=	1 2

С ручкой и бумагой

А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):

Рифма, которая поможет вам вспомнить

♫ «Если ваша цель — сложение или вычитание,
Нижние числа должны быть одинаковыми!
♫» Измените нижнее значение с помощью умножения или деления,
Но то же самое и к верхнему,
♫ » И не забудьте упростить,
Пока не пришло время прощаться «

Пример:

1 3 + 1 5

Опять же, нижние цифры разные (срезы разного размера)!

1 3	+	1 5	=	?

Но давайте попробуем разделить их на меньшие размеры, чтобы каждый был одинаковым :

5 15	+	3 15

Первая дробь: умножив верхнюю и нижнюю части на 5, мы получили 5 15 :

× 5

× 5

Вторая дробь: умножив верхнюю и нижнюю части на 3, мы получили 3 15 :

× 3

× 3

Нижние числа теперь те же, поэтому мы можем продолжить и сложить верхние числа:

5 15	+	3 15	=	8 15

Результат настолько прост, насколько это возможно, вот и ответ: 8 15

1 3 + 1 5 знак равно 8 15

Делаем знаменатели одинаковыми

В предыдущем примере, как мы узнали, что нужно разрезать их на ¹ / ₁₅ тысяч, чтобы знаменатели совпадали? Мы просто умножили два знаменателя вместе (3 × 5 = 15).

Прочтите о двух основных способах сделать знаменатели одинаковыми здесь:

Они оба работают, используйте тот, который вам больше нравится!

Пример: кексы

Вы хотите приготовить и продать кексы:

• Друг может предоставить ингредиенты, если вы дадите ему ¹ / ₃ продаж
• А рыночный прилавок стоит ¹ / ₄ продаж

Сколько это всего?

Нам нужно добавить ¹ / ₃ и ¹ / ₄

Первые делают нижние числа (знаменатели) одинаковыми.

Умножить верхнюю и нижнюю часть ¹ / ₃ на 4 :

1 × 4	+	1	=	?
3 × 4		4		?

И умножьте верхнюю и нижнюю часть ¹ / ₄ на 3 :

1 × 4	+	1 × 3	=	?
3 × 4		4 × 3		?

Сейчас делаем расчеты:

4	+	3	=	4 + 3	=	7
12		12		12		12

Ответ: 7 12 продаж идет на ингредиенты и рыночные затраты.

Добавление смешанных фракций

У меня есть специальная (более продвинутая) страница о добавлении смешанных дробей.

Сложение и вычитание дробей с одинаковым или близким знаменателем

Когда вы складываете или вычитаете дроби, считайте, что задача проста, когда знаменатели равны или одинаковы. Правила можно кратко изложить ниже.

Шаги по сложению и вычитанию дробей с одинаковым знаменателем

• К ДОБАВИТЬ дробей с одинаковым или одинаковым знаменателем, просто сложите числители, а затем скопируйте общий знаменатель.Всегда сокращайте свой окончательный ответ до самого низкого члена.

• К ВЫЧИТАЙТЕ дробей с одинаковым или одинаковым знаменателем, просто вычтите числители и скопируйте общий знаменатель. Всегда сокращайте свой окончательный ответ до самого низкого члена.

---

Примеры сложения и вычитания дробей с одинаковым знаменателем

Пример 1 : Сложите дроби.

Знаменатели обеих дробей равны 7. Имея одинаковые знаменатели, мы можем легко сложить эти дроби, сложив их числители и скопировав общий знаменатель, равный 7.

Мы также можем показать процесс сложения с помощью кружков.

• Первую дробь \ Large {3 \ over 7} можно представить в виде круга, разделенного поровну на семь частей с тремя частями, заштрихованными красным.

Наблюдайте : Числитель сообщает нам, сколько областей заштриховано, а знаменатель говорит нам, на сколько равных частей разделен круг.

• Таким же образом вторая дробь \ Large {2 \ over 7} выглядит так:

• Поскольку оба круга разделены на семь (7) равных частей, мы должны иметь возможность перекрывать их.Новый круг после добавления имеет пять (5) заштрихованных областей, которые представляют собой скопление и красных и синих фигур.

---

Пример 2 : Сложите дроби.

Давайте сложим эти дроби, используя правило сложения. Снова сложите числители и скопируйте общий знаменатель.

После добавления дробей всегда находите возможность упростить добавленные дроби, уменьшив их до наименьшего члена. Мы можем сделать это, разделив числитель и знаменатель на их наибольший общий делитель.

• Общий делитель — это ненулевое целое число, которое может равномерно делить два или более чисел.
• Наибольший общий делитель (НОД) — это наибольшее число среди общих делителей двух или более чисел.

Очевидно, что числитель и знаменатель имеют общий делитель 2. Однако существует ли число больше 2, которое может также равномерно разделить их обоих?

Да, есть! Число 4 — это наибольший общий делитель 12 и 16.Следовательно, мы будем использовать это число, чтобы уменьшить дробь до наименьшего члена.

Разделите верхнюю и нижнюю часть на GCD = 4 , чтобы получить окончательный ответ.

---

Пример 3: Сложите дроби.

Решение :

Поскольку знаменатели двух дробей равны, сложите числители и скопируйте общий знаменатель.

Верхнее и нижнее числа дроби делятся на 2 и 6. Однако мы всегда хотим, чтобы наибольший общий делитель уменьшал дробь до наименьшего члена.Таким образом, НОД = 6 .

• Разделите верхнее и нижнее числа на 6.

---

Пример 4: Сложите дроби.

Решение :

Знаменатели всех трех дробей совпадают. Правило сложения дробей с равными знаменателями остается в силе!

• Получите сумму трех числителей и скопируйте общий знаменатель.

Наибольший общий делитель числителя и знаменателя равен 5.

• Разделите верх и низ на 5.

---

Пример 5: Вычтите дроби.

На этот раз мы собираемся вычесть числители вместо того, чтобы складывать их.

Глядя на результат после вычитания, всего , общий делитель между числителем и знаменателем равен 1 . Таким образом, окончательный ответ остается \ Large {{3 \ over 5}}. Подумайте об этом, разделив верхнюю и нижнюю части на 1, значение дроби не изменится.

Как это выглядит графически?

Допустим, у вас есть зеленый торт. И вы разрезаете его на 5 равных частей. Это можно представить в виде дроби, равной \ Large {{5 \ over 5}}.

Если вы съели два куска торта (\ Large {- {2 \ over 5}}), у вас должно остаться три оставшихся куска (\ Large {{3 \ over 5}}).

Табличка должна выглядеть примерно так.

---

Пример 6: Вычтите дроби.

У этих двух дробей одинаковые знаменатели, что означает, что мы должны иметь возможность легко вычесть их числители.

Ответ можно еще больше упростить, используя общий делитель 3. Итак, разделите числитель и знаменатель на 3, чтобы уменьшить дробь до наименьшего значения.

---

Пример 7: Вычтите дроби.

Решение :

Поскольку знаменатели двух дробей равны, из вычтите их числителей и скопируйте общий знаменатель.

Числитель и делитель делятся на 3 и 9. Однако мы всегда хотим, чтобы наибольший общий делитель уменьшал дробь до наименьшего члена.Таким образом, НОД = 9 .

• Разделите верхнее и нижнее числа на 9.

---

Пример 8: Вычтите дроби.

Решение :

Вычтите числители и уменьшите полученную дробь до наименьшего члена, используя GCD = 11 .

---

Практика с рабочими листами

---

Возможно, вас заинтересует:

Сложение и вычитание дробей с разными знаменателями
Умножение дробей
Деление дробей
Упрощение дробей
Эквивалентные дроби
Обратное значение дроби

Сложение дробей с одинаковым знаменателем

Сложение дробей с одинаковыми знаменателями

Сложить дроби с одинаковыми знаменателями довольно просто, если следовать правилам.В этом уроке рассматривается сложение дробей с одинаковым знаменателем. Мы включим всю информацию, которая вам понадобится, чтобы упростить работу с проблемами общего знаменателя!

Уравнение выше показывает Правило сложения . Итак, если вы имеете дело с одним и тем же (общим) знаменателем (b), ответ будет суммой числителей (a и c) над их общим знаменателем. Помните, что дробь относится к количеству частей в «целом», а ЦЕЛОЕ, о котором мы говорим, всегда является числом в знаменателе (внизу).Итак, все, что нам нужно сделать, это сложить части и сохранить нашу точку отсчета.

Инструкция по сложению дробей с одинаковым знаменателем

Чтобы сложить дроби, знаменатели должны быть одинаковыми. Выполните следующие шаги, чтобы сложить две дроби.

1. Постройте каждую дробь (при необходимости) так, чтобы оба знаменателя были равны.
2. Сложите числители дробей.
3. Новый знаменатель будет знаменателем построенных дробей.
4. При необходимости сократите или упростите свой ответ.
   • Разложите на множитель числитель.
   • Разложите на множитель знаменатель.
   • Отмена смешивает фракции , которые имеют значение 1.
   • Перепишите ответ в виде упрощенной или сокращенной дроби.
     ПОМНИТЕ: Мы НЕ добавляем знаменатели

Вот и все!

Вот пример сложения дробей с одинаковым знаменателем…

Вы хотите проверить свою работу? Попробуйте наш новый калькулятор сложения дробей для сложения до 5 дробей, целых чисел, смешанных чисел или неправильных дробей с одинаковыми или разными знаменателями.

Теперь, когда у вас есть эта часть сложения дробей, давайте копнем немного глубже …

Вы хотите быть «мастером» дроби? Верно?

Ладно!

Было бы здорово, если бы изложенное выше правило было всем, что вам нужно знать о сложении дробей. Но есть еще несколько вещей, о которых нам нужно поговорить, чтобы завершить этот урок. Итак, приступим к делу.

Щелкните здесь , чтобы узнать, как переписать ответ в виде упрощенной или сокращенной дроби.

Как упростить ответы

Иногда, когда вы добавляете дроби любого типа, вам нужно упростить ответ. На самом деле это означает, что вы должны показывать свои результаты в «наилучшей» возможной дробной форме. В результате есть еще несколько вещей, о которых стоит подумать…

Во-первых, вашим ответом может быть более высокая эквивалентная дробь, которую лучше представить в сокращенной форме. Многие учителя будут настаивать на том, чтобы вы уменьшали дробь, когда это возможно.

Кроме того, сложение двух дробей может привести к так называемой неправильной дроби.Здесь числитель больше знаменателя. Чтобы записать эти ответы в их простейшей форме, вам придется преобразовать их в смешанные числа. Это покажет представление целых частей и дробных частей.

Итак, давайте продолжим некоторую подробную информацию о сложении дробей в этих особых случаях.

Уменьшение дроби до наименьшего эквивалента

Вот ситуация. Вы правильно сложили дроби, но в вашем ответе может не быть наименьшей эквивалентной дроби.Так как же при добавлении дробей убедиться, что ваш ответ отображается в наименьшем эквиваленте?

Давайте воспользуемся простым примером сложения дробей, чтобы вы поняли…

Обратите внимание, что исходный ответ на сложение дробей в нашей задаче — «2/4». Чтобы определить, является ли наш ответ в его простейшей форме, мы должны разложить числитель и знаменатель на его простые числа.

Щелкните здесь, чтобы просмотреть простые числа.

Множители числа — это числа, которые при умножении будут равны этому числу.Самый простой способ убедиться, что вы учли ВСЕ множители числа, содержащегося в дроби, — это разбить их на простые числа.

То, что мы ищем, — это простые числа, которые являются общими множителями как в числителе, так и в знаменателе дроби. Если мы найдем эти общие факторы, мы сможем их исключить. Результатом будет наименьшая дробная эквивалентная дробь.

Поскольку «2» является общим множителем как в числителе, так и в знаменателе нашего примера, это означает, что наш ответ не является дробью в простейшей форме.Следовательно, мы сократим (/) одну из двоек как в числителе, так и в знаменателе, разделив на «2». Результатом является сокращенная дробь в простейшей форме.

Вот правило…

Всегда имейте в виду…

Все, что вы делаете с числителем дроби, вы должны делать и со знаменателем дроби. Поэтому, если вам нужно разделить числитель на число, вы также должны разделить знаменатель на то же число. Таким образом, вы не измените общее значение дроби.

Давайте добавим более жесткую дробь, чтобы убедиться, что вы ее поняли…

В этой задаче «2» и «3» могут быть найдены как множители как в числителе, так и в знаменателе дроби. Обратите внимание, как мы отменяем только один к одному! Сначала мы делим числитель и знаменатель на «2», затем делим числитель и знаменатель на «3». Итак, в числителе осталось 1 x 1 x 3 = 3 , а в знаменателе — 1 x 2 x 2 x 1 = 4 .Это оставляет использование с уменьшенной долей, равной 3/4.

Упростите неправильные дроби

Вы можете помнить, что неправильные дроби — это когда числитель имеет большее значение, чем знаменатель. Поэтому каждый раз, когда вы складываете две дроби и ваш ответ оказывается неправильной дробью, вы должны упростить свой ответ. Результаты будут в виде смешанного числа.

Чтобы преобразовать неправильную дробь в смешанное число, просто разделите числитель на знаменатель.Результатом будет целочисленная часть и дробная часть.

Вот пример…

Как видите, это довольно простая операция. Но имейте в виду, что если нет остатка, ответ — только ВСЕ ЧИСЛО.

Теперь у вас есть несложный способ складывать дроби с одинаковыми знаменателями.

[fusion_separator style_type = ”shadow” top_margin = ”40 ″ bottom_margin =” 40 ″ sep_color = ”” icon = ”” width = ”” class = ”” id = ”” /]

Дополнительная справка

Таблица первичной факторизации

Рабочие листы сложения дробей

Добавление дробей | Как сложить дроби + примеры

Сегодня мы рассмотрим несколько примеров добавления дробей .

Перед тем, как прочитать этот пост, вы можете прочитать предыдущий пост, в котором мы шаг за шагом объясняем, как складывать дроби.

Начнем с простейшего примера:

Сложение дробей с одинаковым знаменателем

Например:

Единственное, что нам нужно сделать, это сложить числители и оставить знаменатель в покое . Ответ: :

.

Сложение чисел и дроби

Например:

Первое, что нам нужно сделать в этом случае, — это преобразовать 2 в дробь.Как вы уже знаете, мы можем просто поставить 1 в знаменателе любого числа, не меняя его значения:

Когда у нас есть две дроби, мы можем начать искать общий знаменатель . В этом примере это довольно просто, потому что этим числом является наименьшее общее кратное 1 и любому числу. Итак:

Теперь нам нужно только умножить 2 на 4, и мы получим:

… и теперь мы добавляем его в нашу задачу сложения:

Сложение дробей с равными простыми знаменателями

Помните, что два числа взаимно просты, если их наибольший общий делитель равен 1 .Например, в задаче:

Знаменатели взаимно простые, потому что:

Проблемы такого рода легко решить, потому что единственное, что нам нужно сделать, чтобы найти новые числители, — это умножить каждый числитель на знаменатель другой дроби, как показано ниже:

А мы просто умножаем знаменатели вместе. Итак, получаем:

и

И осталось сложить две дроби вместе:

Общее сложение дробей

Например:

Нам нужно вычислить наименьшее общее кратное знаменателей :

Что нам делать дальше? Давайте разберемся.Во-первых, давайте посмотрим на дробь:

Чтобы найти числитель , нам нужно разделить НОК на знаменатель дроби:

Нам нужно умножить числитель дроби на 2. Итак:

И мы видим, что новый числитель — 6.

В качестве знаменателя нам просто нужно использовать GCM (18):

Теперь мы проделаем то же самое с другой дробью. Чтобы найти числитель, нам нужно разделить:

И умножаем на числитель:

Затем мы подставляем GCM в качестве знаменателя, что дает нам:

Теперь осталось сложить дроби вместе …

И все!

Фактически мы складываем все дроби таким образом, первые примеры были проще благодаря GCM, с которым было легче работать.Однако способ решения проблем всегда оставался прежним.

Подводя итог, шагов для сложения дробей :

• Найдите GCM двух знаменателей.
• Разделите GCM на знаменатель и умножьте это на числитель, чтобы преобразовать каждую дробь в дробь, в которой GCM является новым знаменателем.
• Когда мы закончили два предыдущих шага со всеми дробями, расположите их все по порядку и сложите их числители.

Если вы хотите продолжить изучение математики, зарегистрируйтесь на Smartick сегодня!

Удачи в добавлении дробей — немного попрактиковавшись, вы увидите, что это совсем несложно, и получите это в кратчайшие сроки!

Подробнее:

Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.

Рабочие листы сложения дробей с одинаковыми знаменателями

Добро пожаловать на нашу страницу сложения дробей с одинаковыми знаменателями.

Здесь вы найдете нашу подборку рабочих листов, призванных помочь вашему ребенку освоить умение складывать дроби с одинаковым знаменателем.

Здесь вы найдете страницы поддержки о том, как складывать и вычитать дроби (с одинаковыми и разными знаменателями).

Если вы хотите использовать наш Калькулятор свободных фракций, чтобы сделать работу за вас, воспользуйтесь ссылкой ниже.

Наш калькулятор дробей позволит вам складывать или вычитать дроби и покажет, как это вычислить.

В противном случае, чтобы получить более подробную поддержку и рабочие листы, продолжайте читать!

Узнайте, как складывать и вычитать дроби с помощью как знаменатели, используя видео ниже.

Здесь вы найдете подборку рабочих листов Free Fraction, предназначенных для помощи ваш ребенок понимает, как складывать дроби с одинаковым знаменателем. Листы отсортированы таким образом, чтобы более легкие были вверху.

Использование этих листов поможет вашему ребенку:

• складывать (и вычитать) дроби с одинаковым знаменателем.
• решает задачу, в которой дан ответ и одно из дополнений отсутствует.

Мы разделили рабочие листы на 3 части:

• Первый раздел содержит добавление дробей с помощью кругов — визуальный способ понять эту концепцию.
• Второй раздел содержит просто добавление дробей с одинаковыми знаменателями без дополнительной поддержки.
• Третий раздел содержит как сложение, так и вычитание дробей с одинаковыми знаменателями.

Отличный способ представить и понять эту концепцию — использовать визуальные представления дробей.

Вопросы на этих листах включают закрашивание различных фракций, а затем определение общей заштрихованной дроби.

Это затем преобразуется в простое предложение сложения дробей!

Первый лист включает использование диаграмм дробей, чтобы увидеть закономерность между сложением и вычитанием дробей.

Остальные 3 листа представляют собой более традиционные задачи с дробями, включающие сложение и вычитание дробей.

Взгляните на еще несколько наших рабочих листов, похожих на эти.

У нас также есть набор рабочих листов, в которых используется вычитание дробей с одинаковыми знаменателями.

Эти листы аналогичны листам на этой странице, но включают вычитание вместо сложения.

Эти листы предназначены для сложения (и вычитания) дробей с разными знаменателями.

Использование этих листов поможет вашему ребенку:

• сложение и вычитание дробей с разными знаменателями;
• примените ваши эквивалентные знания о дробях.

Использование этих листов поможет вашему ребенку:

• понять, что такое дроби;
• соотносят дроби с повседневными предметами и количествами;
• разместить дроби в числовой строке;
Оттенок
• в разных фракциях фигур;
• вычисляют единичные дроби чисел.

Здесь вы найдете бесплатную онлайн-справку по математике Math Salamanders о дробях.

Существует широкий спектр справочных страниц, в том числе справка по следующим вопросам:

• определения фракций;
• эквивалентных дроби;
• преобразование неправильных дробей;
• как складывать и вычитать дроби;
• как переводить дроби в десятичные дроби и проценты;
• как упростить дроби.

Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.

Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.

Урок математики — сложение одинаковых дробей (с общим знаменателем)

Чтобы сложить дроби, нужно выполнить три простых шага:

Шаг 1. Убедитесь, что нижние числа (знаменатели) совпадают.

Шаг 2: Сложите верхних чисел (числителей), поставьте полученный ответ над знаменателем.

Шаг 3. Упростите дробь (при необходимости)

Мы считаем, что дети учатся на множестве примеров в самых разных ситуациях.

Уверен, ты, дорогой читатель, идеален. Однако я видел классы, где единственными примерами дробей были круги и ломтики пиццы. Я также видел слишком много учебников по математике, которые, как мне казалось, не давали достаточно примеров и объяснений, прежде чем ожидал, что ученики решат кучу задач.

Прежде чем вы заставите своих учеников погрузиться в решение задач, попробуйте дополнительный 5-10-минутный мини-урок. Мы сделали это за вас.

Вот вам пара PowerPoints с примерами сложения и сравнения дробей с одинаковыми (общими) знаменателями.

Если вы предпочитаете видео, у нас есть то же самое в видео формате.

Кроме того, я подумал, что упомянул, что мы создаем целый сайт ресурсов для учителей.Ознакомьтесь с гораздо более длинным планом урока по эквивалентным дробям.

Как сложить подобные дроби в видео

Чтобы было понятнее, вот видео, объясняющее, как складывать подобные дроби с примерами:

Завершите свой урок фракциями изучения стиля, играя в Fish Lake

РЫБНОЕ ОЗЕРО

Описание: В Fish Lake игроки тренируются с дробями, изучая стратегии решения математических задач.

Инструкции: MAC OS X, Win 7, Win 8, Win 10.

ПРИМЕЧАНИЕ. Если вы получили сообщение о «неустановленном разработчике», вот как это исправить за 5 секунд или меньше.

---

Рекомендуется для	4-6 классы
Согласование стандартов по математике	5-6 классы
Математические темы	Фракции
Культура	Оджибве
Доступно для	Mac, MAC OS X, Win 7 Win 8, Win 10

---

Скачать для MAC

Скачать для Windows .