Простые уравнения математика тренировочные задания – ЕГЭ 2019, Математика, Простейшие уравнения, Задача 5, Профильный уровень, Задача 4 и 7, Базовый уровень, Рабочая тетрадь, Шестаков С.А., Ященко И.В.

Posted on by alexxlab

Содержание

Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь умножается на А в правой части — смешанное число Его целая часть равна 19, а дробная часть равна Запишем это число в виде неправильной дроби:

Получим:

или

Выбираем меньший корень.

Ответ: — 6,5.

2. Решите уравнение

Возведем в квадрат левую часть уравнения. Получим:

Ответ: — 6

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:

Это довольно простой тип уравнений. Главное — внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.

4. Решите уравнение:

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, \sqrt{\frac{6}{4{x}-54} } =\frac{1}{7}..

Возведём обе части уравнения в квадрат:

Решим пропорцию:

Условие \sqrt{\frac{6}{4{x}-54} } =\frac{1}{7}. при этом выполняется.

Ответ: 87.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

\sqrt{72-x}=x \Leftrightarrow \left\{\begin{matrix} 72-x=x^2\\72-x \geq 0 \\x \geq 0 \end{matrix}\right. \Leftrightarrow

Мы получили, что . Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: или Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов.

\sqrt{45+4x}=x

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение

Вспомним, что Уравнение приобретает вид: Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

откуда

8. Решите уравнение

Представим как

Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

Ответ: 7,5.

9. Решите уравнение

Представим в виде степени с основанием 3 и воспользуемся тем, что


Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел;

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

Область допустимых значений: {{log}_5 \left(4+x\right)=2 } . Значит, {{log}_5 \left(4+x\right)=2 }

Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.

Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом y = {{log}_5 x }



Ответ: 21.

11. Решите уравнение:

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

{{log}_8 \left(x^2+x\right)={{log}_8 \left(x^2-4\right) } }

{{log}_8 \left(x^2+x\right)={{log}_8 \left(x^2-4\right) } }

Ответ: -4.

12. Решите уравнение:

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

Записываем решение как цепочку равносильных переходов.

{{log}_4 b }=\frac{{{log}_2 b }}{{{log}_2 4 }}=\frac{{{log}_2 b }}{2}

{{log}_4 b }=\frac{{{log}_2 b }}{{{log}_2 4 }}=\frac{{{log}_2 b }}{2}

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Получим систему:

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: и

Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену Получим:

cos t=\frac{\sqrt{2}}{2}.

Получаем решения: Вернемся к переменной x.

Поделим обе части уравнения на и умножим на 4.

Первой серии принадлежат решения

Вторая серия включает решения

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это

Ответ: -2.

15. Решите уравнение В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену Получим: Решения этого уравнения:

Вернемся к переменной х:

Умножим обе части уравнения на 4 и разделим на

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

Наименьший положительный корень

Ответ: 2

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Успеха вам в подготовке к ЕГЭ!

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

Задание 7 ЕГЭ по математике базового уровня 2020 :: Бингоскул

Если задание выполнено на отлично, то сможешь получить 1 первичный балл.

На решение отводится примерно 8 минут.

Чтобы решить задание 7 по математике базового уровня нужно знать:

  • Линейное уравнение: ax + b =0
  • Квадратное уравнение: ax2 + bx + c = 0.
  • Алгоритм решения квадратного уравнения:
  1. Найти дискриминат по формуле D = b2 — 4ac
  2. Корни вычисляются по формулам:
    a) D b) D = 0, x = -\frac{b}{2a}
    c) D > 0, x = \frac{-b \pm\sqrt{D}}{2a}
  3. Свойства корней
  4. Свойства логарифмов

 

Таблица кубов натуральных чисел от 10 до 99 и степеней чисел 2 и 3
n12345678910
n31827641252163435127291000
2n2481632641282565121024
3n3927812437292187656119 68359 049

Простейшие рациональные уравнения | Подготовка к ЕГЭ по математике

В Заданиях №5 ЕГЭ по математике проверяется умение решать простейшие рациональные,
иррациональные,
показательные,
логарифмические,
тригонометрические уравнения.

Сейчас мы рассмотрим основные типы рациональных уравнений, которые могут встретится на экзамене.

Загляни сюда, – вдруг узнаешь себя!

Задание 1.

Решить уравнение: \frac{3}{8}x=-3\frac{3}{8}.

Решение: + показать

Задание 2.

Решить уравнение x^2-4=(x-4)^2

   Решение: + показать

Надеюсь, вы не допускаете таких ошибок, как (x-4)^2=x^2-16 или (x-4)^2=x^2+16?

Квадрат разности раскрывается так (согласно формуле (a-b)^2=a^2-2ab+b^2):

(x-4)^2=x^2-8x+16

Тогда мы переходим к следующему уравнению:

x^2-4=x^2-8x+16

Откуда 8x=20

x=2,5

Ответ: 2,5. 

Задание 3.

Решите уравнение (5x-8)^2=(x-4)^2. В ответе укажите наибольший корень, если уравнение имеет несколько корней.

Решение: + показать

Здесь же распространенная ошибка – следующая:

переход к уравнению 5x-8=x-4.

Такое уравнение-то следует, конечно, из исходного, но наряду с ним, вытекает и уравнение 5x-8=-(x-4).

То есть исходное уравнение следует заменить на: 5x-8=\pm(x-4).

Откуда x=1 или x=2

Уравнение можно, конечно, решать и путем раскрытия скобок, что несколько дольше:

25x^2-80x+64=x^2-8x+16

24x^2-72x+48=0

x^2-3x+2=0

x=\frac{3\pm 1}{2}

x=1 или x=2

Больший из корней – 2.

Ответ: 2. 

Задание 4.

Решите уравнение \frac{7}{12}x^2=5\frac{1}{4} . Если уравнение имеет более одного корня, в ответе запишите меньший из корней

Решение: + показать

Переходим к уравнению:

\frac{7}{12}x^2=\frac{21}{4}

Далее обе части разделим на 7 и домножим на 12, то есть домножаем обе части на \frac{12}{7}:

x^2=9

И уж, конечно, нельзя забывать, что уравнение такого типа имеет два корня: x=\pm 3

Меньший из корней – это -3.

Ответ: -3. 

Задание 5.

Найдите корень уравнения (x+2)^3=-343

Решение: + показать

В подобных заданиях совершенно не обязательно помнить формулу  куб суммы (разности). Более того, может встретиться и такое уравнение: (x-2)^5=32… Вы знаете как возводить разность x-2 в пятую степень? Это не требуется. 

Действуем так –  представляем 343 в виде куба – 343=7^3.

Тогда (x+2)^3=-7^3

Извлекаем кубический корень из обеих частей уравнения:

x+2=-7

x=-9

Ответ: -9. 

Задание 6.

Решите уравнение  \frac{13x}{2x^2-7}=1. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Решение: + показать

Уравнение равносильно следующему:

13x=2x^2-7

2x^2-13x-7=0

x=\frac{13\pm\sqrt{169-4\cdot2\cdot (-7)}}{2\cdot 2}

x=\frac{13\pm15}{4}

x=7 или x=-0,5

Меньший из корней – это -0,5.

Ответ: -0,5. 

Задание 7.

Решите уравнение  \frac{x-8}{7x-2}=\frac{x-8}{6x-7} . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Решение: + показать

Уравнение равносильно следующей системе (воспользовались свойством пропорции, а также записали ОДЗ для данного уравнения):

\begin{cases} (x-8)(6x-7)=(x-8)(7x-2),& &6x-7\neq0,& &7x-2\neq0; \end{cases}

В уравнении системы переносим все в левую сторону и выносим x-8 за скобку как общий множитель:

\begin{cases} (x-8)(6x-7-(7x-2))=0,& &6x-7\neq0,& &7x-2\neq0; \end{cases}

\begin{cases} (x-8)(-x-5)=0,& &x\neq \frac{7}{6},& &x\neq \frac{2}{7}; \end{cases}

Откуда x=8 или x=-5. Больший из корней – 8.

Ответ: 8. 


Unknown

Пройдите по теме «Простейшие рациональные уравнения»

 

 

 

Как решать более сложные рациональные уравнения, которые могут встретиться во второй части С ЕГЭ, смотрите здесь.

 

 

 

Задание №7 ЕГЭ по математике базовый уровень

Простейшие уравнения

В задании №7 базового уровня ЕГЭ по математике необходимо решить простейшие уравнения. Для этого нам понадобятся знания логарифмов, степеней и методы решения квадратных уравнений. Перейдем к рассмотрению и разбору подобных примеров.

Разбор типовых вариантов заданий №7 ЕГЭ по математике базового уровня

Вариант 7МБ1

Найдите корень уравнения 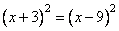 image001

Алгоритм выполнения
  1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
  2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
  3. Преобразовать левую часть.
  4. Преобразовать правую часть.
  5. Решить уравнение относительно x, то есть найти неизвестный множитель.
Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 3)2 = x2 + 2 · x · 3 + 32 = x2 + 6x + 9

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x — 9)2 = x2 — 2 · x · 9 + 92 = x2 — 18x + 81

После преобразования выражение примет вид:

x2 + 6x + 9 = x2 — 18x + 81

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x2 + 6x — x2 + 18x = 81 — 9

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x

2 и x.

x2 + 6x — x2 + 18x = (x2 — x2) + (6x +18x) = 0 + 24x = 24x

Выражение примет вид:

24x = 81 — 9

Преобразуем правую часть. 81 – 9 = 72

Выражение примет вид:

24x = 72

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 72 : 24

x = 3

Решение в общем виде:

Раскроем скобки в уравнении, получим:

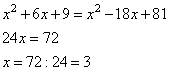
image002

 

 

 

Ответ: 3.

Вариант 7МБ2

Найдите корень уравнения 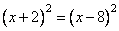 image001

Алгоритм выполнения
  1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
  2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
  3. Преобразовать левую часть.
  4. Преобразовать правую часть.
  5. Решить уравнение относительно x, то есть найти неизвестный множитель.
Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 2)2 = x2 + 2 · x · 2 + 22 = x2 + 4x + 4

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x — 8)2 = x2 — 2 · x · 8 + 82 = x2 — 16x + 64

После преобразования выражение примет вид:

x2 + 4x + 4 = x2 — 16x + 64

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x2 + 4x — x2 + 16x = 64 — 4

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x2 и x.

x2 + 4x — x2 + 16x = (x2 — x2) + (4x +16x) = 0 + 20x = 20x

Выражение примет вид:

20x = 64 — 4

Преобразуем правую часть. 64 — 4 = 60

Выражение примет вид:

20x = 60

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 60 : 20

x = 3

Решение в общем виде:

Раскроем скобки, получим:

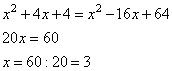
image002

Ответ: 3.

Вариант 7МБ3

Найдите корень уравнения 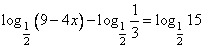 image001

Алгоритм выполнения
  1. Перенести вычитаемое в правую сторону равенства с противоположным знаком.
  2. Преобразовать правую часть с учетом свойства: loga x + loga y = loga (x · y).
  3. Приравнять логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.
  4. Решить уравнение относительно x.
Решение:

Перенесем вычитаемое в правую сторону равенства с противоположным знаком.

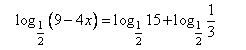
image001

Преобразуем правую часть с учетом свойства: loga x + loga y = loga (x · y).

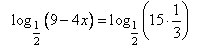
image001

Выполним преобразование:

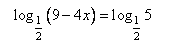
image001

Приравняем логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.

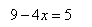
image001

Решим уравнение относительно x.

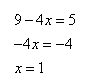
image001

Ответ: 1.

Вариант 7МБ4

Найдите корень уравнения 3x− 3 = 81.

Алгоритм выполнения
  1. Привести выражения в степенях к одинаковому основанию. В данном случае — это 3. Теперь необходимо вспомнить, какой степенью тройки является 81.
  2. Когда основания равны, можно приравнять значения степеней

Если вы забыли, то для этого необходимо делить 81 на 3 до тех пор, пока не получим 3. Чтобы получить три из 81, нам нужно поделить 81 на 3 три раза: при первом делении мы получим 27, при втором — 9, при третьем — три.

Значит, 81 это три в четвертой степени. Запишем это:

Решение:

3x− 3 = 34

х — 3 = 4

Откуда:

х = 7

Ответ: 7

Вариант 7МБ5

Найдите корень уравнения log2( x − 3) = 6 .

Алгоритм выполнения
  1. Логарифм по основанию два показывает нам число, в степень которого нам необходимо возвести основание, то есть двойку, чтобы получить число под логарифмом.
Решение:

x − 3 = 26

x − 3 = 64

x = 67

Ответ: 67

Вариант 7МБ6

Найдите отрицательный корень уравнения x2 − x − 6 = 0.

Алгоритм выполнения
  1. Вычислить дискриминант
  2. Найти корни
  3. Выбрать необходимый корень

D = b2 − 4ac

Решение:

D = -(1)2 − 4 • 1 • (-6) = 25

x = (- b ±√D) : 2a

x = (1 + 5) : 2 = 3

x = (1 — 5) : 2 = -2

Так как нам необходим отрицательный корень — ответ -2

Ответ: -2.

Вариант 7МБ7

Решите уравнение х2 = –2х + 24.

Если уравнение имеет больше одного корня, в ответе укажите больший из них.

Алгоритм выполнения
  1. Переносим влево часть ур-ния, стоящую справа от знака «=». Получаем кв.уравнение стандартного вида.
  2. Поскольку уравнение является приведенным, используем для нахождения корней т.Виета.
  3. Записываем в качестве ответа большее из полученных 2 чисел.
Решение:

х2 = –2х +24

х2 +2х – 24 = 0

По т.Виета х1+х2=–b, x1·x2=c. В нашем ур-нии b=2, c=24. Подбираем подходящую пару чисел, получаем: х1=–6, х2=4.

Поскольку требуется указать больший из корней, то ответом будет 4.

Ответ: 4

Вариант 7МБ8

Найдите корни уравнения 4х–6 = 64.

Алгоритм выполнения
  1. Представляем 64 как степень с основанием 4, т.е. приводим выражения справа и слева к степеням с одинаковым основанием.
  2. Опускаем одинаковые основания и переходим к равенству показателей. Ур-ние стало простейшим линейным.
  3. Находим корень ур-ния.
Решение:

4х–6 = 64

4х–6 = 43

х – 6 = 3

х = 9

Ответ: 9

Вариант 7МБ9

Найдите корень уравнения log3 (2x – 5) = 2.

Алгоритм выполнения
  1. Преобразуем часть уравнения справа от знака «=», используя св-ва логарифмов logxx=1 и logxyn=nlogxy.
  2. Переходим от равенства логарифмов к равенству выражений, стоящих под их знаками.
  3. Решаем полученное линейное ур-ние.
Решение:

log3 (2x – 5) = 2

log3 (2x – 5) = 2 · log33

log3 (2x – 5) = log332

2x – 5 = 32

2x – 5 = 9

2x = 14

x=7

Ответ: 7

Вариант 7МБ10

Найдите корень уравнения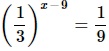
C:\Users\Ксенья\Desktop\матме\4.jpg

Алгоритм выполнения
  1. Преобразовываем обе части ур-ния: приводим их к степеням с основанием 3. Для этого используем св-во степеней (1/а)х=а–х.
  2. Поскольку основания степеней слева и справа в ур-нии теперь одинаковы, то можем их опустить и приравнять показатели.
  3. Решаем полученное линейное ур-ние.
Решение:

–x + 9 = –2

–x = –2–9

x = 11

Ответ: 11

Вариант 7МБ11

Найдите корень уравнения (х – 8)2 = (х – 2)2.

Алгоритм выполнения
  1. Раскрываем скобки слева и справа, используя ф-лу сокращенного умножения (х–у)2=х2–2ху–у2.
  2. Переносим влево часть уравнения справа от знака «=». Справа получаем 0.
  3. Приводим подобные слагаемые. В результате уравнение стало линейным.
  4. Решаем полученное уравнение.
Решение:

(х – 8)2 = (х – 2)2

х2 – 2 · х ·8 + 82 = х2 – 2 · х · 2 + 22

х2 – 16х + 64 = х2 – 4х + 4

х2 – 16х +64 – х2 + 4х – 4 = 0

–12х + 60 = 0

–12х = –60

х = 5

Ответ: 5

Вариант 7МБ12

Найдите корень уравнения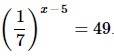
C:\Users\Ксенья\Desktop\матме\6.jpg

Алгоритм выполнения
  1. Преобразовываем обе части ур-ния так, чтобы привести их к степеням с одинаковым основанием 7. Для выражения слева применяем св-во степеней (1/а)х=а–х.
  2. Применяем св-во показат.уравнений: если степени с одинаковыми основаниями равны, то равны и их показатели. Отсюда переходим к линейному ур-нию.
  3. Решаем его.
Решение:

–(x–5) = 2

5 – x = 2

–x = 2 – 5

x = 5 – 2

x = 3

Ответ: 3

Вариант 7МБ13

Решите уравнение х2 – 25 = 0

Алгоритм выполнения
  1. Переносим 25 в правую часть ур-ния.
  2. Выражаем из ур-ния х путем извлечения корня из 25.
  3. Определяем корни, сравниваем их, определяем больший.
Решение:

х2 – 25 = 0

х2 = 25

х = ±√25

х1 = –5, х2 = 5

Для ответа берем 5.

Ответ: 5

Вариант 7МБ14

Найдите корень уравнения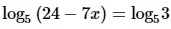
C:\Users\Ксенья\Desktop\матме\8.jpg

Алгоритм выполнения
  1. Применим св-во логарифмических равенств: если логарифмы с одинаковыми основания равны, то равны и их подлогарифменные выражения. В результате получаем равенство из выражений, стоящих под знаком логарифма.
  2. Решаем полученное линейное ур-ние.
Решение:

log5 (24 – 7x) = log5 3

24 – 7x = 3

–7x = 3 – 24

7x = 21

x = 3

Ответ: 3

Вариант 7МБ15

Найдите корень уравнения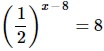
C:\Users\Ксенья\Desktop\матме\9.jpg

Алгоритм выполнения
  1. Приводим обе части ур-ния к степеням с основанием 2. При этом для преобразования выражения слева используем св-во степеней (1/а)х=а–х.
  2. Получив слева и справа степени с одинаковым основанием, опускаем это основание и приравниваем показатели этих степеней. Получаем линейное ур-ние.
  3. Решаем его.
Решение:

2–(x–8) = 23

–x+8 = 3

–x = 3–8

x = 5

Ответ: 5

Вариант 7МБ16

Найдите корень уравнения 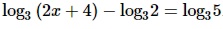C:\Users\Ксенья\Desktop\матме\10.jpg

Алгоритм выполнения
  1. К левой части уравнения применяем св-во логарифмов loga(x/y)=logax–logay.
  2. Поскольку в обеих частях ур-ния имеем логарифмы по одинаковым основаниям, то можем их знаки, оставив только подлогарифменные выражения. Получаем линейное ур-ние.
  3. Решаем его.
Решение:

log3 (2x + 4) – log3 2 = log3 5

log3 (2x + 4)/2 = log3 5

log3 (x + 2) = log3 5

x + 2 = 5

x = 3

Ответ: 3

image_pdfСкачать PDFimage_printРаспечатать

Подготовка к ЕГЭ. Решение простейших уравнений. (задание №5)

Задания для подготовки к ЕГЭ.

Проверяемые элементы содержания и виды деятельности: владение понятием уравнение, область определения уравнения, знание основных типов простейших уравнений, умение решать уравнение.

  1. Най­ди­те ко­рень урав­не­ния hello_html_m592005dc.png.

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

hello_html_1c3bccb7.png

Ответ: −1.

  1. Най­ди­те ко­рень урав­не­ния hello_html_m427bbec8.png.

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

hello_html_38e77d73.png.

Ответ: 4.

  1. Най­ди­те ко­рень урав­не­ния hello_html_m334d1ec0.png.

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

hello_html_m572ddca5.png.

Ответ: 10

  1. Най­ди­те ко­рень урав­не­ния hello_html_m161be751.png.

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

hello_html_m161be751.pnghello_html_m294d7190.png.

Ответ: 4.

  1. Най­ди­те ко­рень урав­не­ния hello_html_14565d98.png.

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

hello_html_m381d73c3.png

Ответ: 8,75

  1. Най­ди­те ко­рень урав­не­ния hello_html_m2c352de5.png.

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

hello_html_5ac6120f.png.

Ответ: 12,5

  1. Най­ди­те ко­рень урав­не­ния: hello_html_7e48f64c.png.

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

hello_html_25a0709.png.

Ответ: 8.

  1. Най­ди­те ко­рень урав­не­ния: hello_html_65e0409c.png

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

hello_html_m74e67406.png

Ответ: 0.

  1. Най­ди­те ре­ше­ние урав­не­ния: hello_html_m2019380c.png

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

hello_html_m55cb1136.png

Ответ: 4.

  1. Най­ди­те ко­рень урав­не­ния hello_html_m12fd21a4.png.

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

hello_html_m22c8f49e.png

Ответ: −124.

  1. Най­ди­те ко­рень урав­не­ния hello_html_m159931e6.png.

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

hello_html_m58433e5c.png

Ответ: 21.

  1. Най­ди­те ко­рень урав­не­ния hello_html_3fae3742.png.

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

hello_html_mb0b2cd8.png.

Ответ: −12.

  1. . Най­ди­те ко­рень урав­не­ния hello_html_m2941142f.png.

Ре­ше­ние.

Ло­га­риф­мы двух вы­ра­же­ний равны, если сами вы­ра­же­ния равны и при этом по­ло­жи­тель­ны:

hello_html_5fb369e3.png

Ответ: 6.

  1. Най­ди­те ко­рень урав­не­ния hello_html_1d5ffa94.png.

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

hello_html_846d335.png

Ответ: −4.

  1. Ре­ши­те урав­не­ние hello_html_m5f83e22e.png.

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

hello_html_3e0effe4.png

Ответ: 5.

  1. Ре­ши­те урав­не­ние hello_html_m3d2e8551.png.

Ре­ше­ние. За­ме­тим, что hello_html_m2ec39c47.pngи ис­поль­зу­ем фор­му­лу hello_html_6d5ca81d.pngИмеем:

 

hello_html_66f9d6d2.png

  1.  

hello_html_m4a206322.png

Ответ: 2.

  1. Най­ди­те ко­рень урав­не­ния hello_html_m76055e5d.png.

Ре­ше­ние.hello_html_m78a7bbc2.pngОтвет:2.

  1. Най­ди­те ко­рень урав­не­ния hello_html_3982ae45.png.

Ре­ше­ние.

Воз­ве­дем в квад­рат:

hello_html_m3fe78db3.png

Ответ: 55

  1. Най­ди­те ко­рень урав­не­ния. hello_html_5c7309d0.png

Ре­ше­ние.

Воз­ве­дем в квад­рат:

hello_html_5c7309d0.png.

Ответ: 38.

  1. Най­ди­те ко­рень урав­не­ния: hello_html_m452ababf.pngЕсли урав­не­ние имеет более од­но­го корня, ука­жи­те мень­ший из них.

Ре­ше­ние.

Воз­ве­дем в квад­рат:

hello_html_m467c70f5.png

Ответ: 8.

  1. Най­ди­те ко­рень урав­не­ния hello_html_m2b82545e.png.

Ре­ше­ние.

Воз­ве­дем в квад­рат:

hello_html_m4bd0f1f1.png

Ответ: 87.

  1. Най­ди­те ко­рень урав­не­ния hello_html_m121be860.png.

Ре­ше­ние.

Воз­ве­дем обе части урав­не­ния в тре­тью сте­пень:

hello_html_14ecc1a5.png

Ответ: 31.

  1. Ре­ши­те урав­не­ние hello_html_7dac47de.png. Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те мень­ший из кор­ней.

Ре­ше­ние.

Воз­ве­дем в квад­рат:

hello_html_m4dc0f373.png

Мень­ший ко­рень равен 1.

Ответ: 1.

  1. Най­ди­те ко­рень урав­не­ния: hello_html_m2aebf8e1.png

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

hello_html_56b17fa8.png.

Ответ: 3.

  1. Най­ди­те ко­рень урав­не­ния: hello_html_4c2f9a63.pngЕсли урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.

Ре­ше­ние.Об­ласть до­пу­сти­мых зна­че­ний: hello_html_m1f062bb9.png. На этой об­ла­сти до­мно­жим на зна­ме­на­тель:

 

hello_html_m410b4224.png

Оба корня лежат в ОДЗ. Мень­ший из них равен −3.

 

 

Ответ: −3.

  1. Най­ди­те ко­рень урав­не­ния: hello_html_m57d3fe35.png. Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те боль­ший из них.

Ре­ше­ние.

Об­ласть до­пу­сти­мых зна­че­ний: hello_html_cd2f858.png.

 

При hello_html_m18b78e8f.pngдо­мно­жим на зна­ме­на­тель:

 

 

hello_html_m1f309a01.png

Оба корня лежат в ОДЗ. Боль­ший из них равен 5.

 

Ответ: 5.

Используемые источники:

  1. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и профильный уровни /И.В.Ященко, И.Р.Высоцкий, А.В.Забелин и др.; под редакцией И.В.Ященко. – М.: Издательство «Экзамен», 2016. – 640 с. (Серия «Банк заданий ЕГЭ»)

  2. Математика. ЕГЭ – 2013: экспресс – курс для подготовки к экзамену/ Дмитрий Гущин. – М, : Издательский дом «Учительская газета», 2013. – 256 с. (Библиотечка «Учительской газеты». Готовимся к ЕГЭ с лучшими учителями России)

  3. http://reshuege.ru/

  1. Ответ: -124

Учебно-методический материал по алгебре (10 класс) на тему: ЕГЭ (ПУ-5) Тригонометрические уравнения. Тренировочные задания.

ЕГЭ (профиль) Задание 5. Тригон. ур-ния.(Тренировочные задания.)

1. Решите уравнение. В ответе запишите наименьший положительный и наибольший отрицательный корень:

а)         б)

в)          г)

д)                 е)

ж)            з)

и)          к)

ЕГЭ (профиль) Задание 5. Тригон. ур-ния.(Тренировочные задания.)

1. Решите уравнение. в ответе запишите наименьший положительный и наибольший отрицательный корень:

а)         б)

в)          г)

д)                 е)

ж)            з)

и)          к)

ЕГЭ (профиль) Задание 5. Тригон. ур-ния.(Тренировочные задания.)

1. Решите уравнение. в ответе запишите наименьший положительный и наибольший отрицательный корень:

а)         б)

в)          г)

д)                 е)

ж)            з)

и)          к)

ЕГЭ (профиль) Задание 5. Тригон. ур-ния.(Тренировочные задания.)

1. Решите уравнение. в ответе запишите наименьший положительный и наибольший отрицательный корень:

а)         б)

в)          г)

д)                 е)

ж)            з)

и)          к)

л)          м)

н)          о)

п)           р)

с)          т)

у)           ф)

х)                 ц)

л)          м)

н)          о)

п)           р)

с)          т)

у)           ф)

х)                 ц)

л)          м)

н)          о)

п)           р)

с)          т)

у)           ф)

х)                 ц)

л)          м)

н)          о)

п)           р)

с)          т)

у)           ф)

х)                 ц)

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *