Равенства и неравенства / Сравнение чисел / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Сравнение чисел
5. Равенства и неравенства

Сначала повтори тему «Больше. Меньше» и вспомни, что такое больше, меньше, поровну, столько же.

---

Рассмотри рисунок.

Сколько синих кругов? 5.

Сколько красных кругов? 5.

Каких кругов больше? Каких меньше?

Синих кругов столько же, сколько красных. Их поровну.

Красных кругов столько же, сколько синих. Их поровну.

Составим запись к рисунку:

5 = 5.

Прочитаем запись: пять равно пяти.

Это равенство.

Запись, в которой есть знак РАВНО, называется РАВЕНСТВОМ.

---

Рассмотри рисунок.

Сколько синих кругов?

5.

Сколько красных кругов? 6.

Каких кругов больше? Красных.

Каких кругов меньше? Синих.

Синих кругов меньше, чем красных. 

Красных кругов больше, чем синих. 

Составим запись к рисунку:

6 > 5

Прочитаем запись: шесть больше пяти.

Это неравенство.

5 < 6

Прочитаем запись: пять меньше шести.

Это неравенство.

Запись, в которой есть знак БОЛЬШЕ  или МЕНЬШЕ, называется НЕРАВЕНСТВОМ.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Уменьшить на… Увеличить на…

Сравнение чисел

Правило встречается в следующих упражнениях:

1 класс

Страница 115, Моро, Волкова, Степанова, Учебник, 1 часть

Страница 21, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 39, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 40, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 46, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 20. Вариант 1. № 1, Волкова, Проверочные работы

Страница 52. Вариант 1. Тест, Волкова, Проверочные работы

Страница 53. Вариант 2. Тест, Волкова, Проверочные работы

Страница 44, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 57, Моро, Волкова, Степанова, Учебник, 2 часть

2 класс

Задание 29, Моро, Волкова, Рабочая тетрадь, 1 часть

Задание 38, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 23. Вариант 2. № 4-5, Моро, Волкова, Проверочные работы

Страница 27. Тест 2. Вариант 2, Моро, Волкова, Проверочные работы

Страница 35. Вариант 2. № 4, Моро, Волкова, Проверочные работы

Страница 55. Вариант 2. № 2, Моро, Волкова, Проверочные работы

Страница 49, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 53, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 67, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

3 класс

Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 53, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 77, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 17, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 56, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 63, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 75, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 19. Вариант 2. № 4, Моро, Волкова, Проверочные работы

Страница 27. Вариант 2. Тест 1, Моро, Волкова, Проверочные работы

Страница 69. Вариант 2. Тест 1, Моро, Волкова, Проверочные работы

4 класс

Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 42, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 61, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 69, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 93, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 39, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 70, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

---

© budu5.com, 2020

Пользовательское соглашение

Copyright

Числовые равенства, свойства числовых равенств

После получения общих сведений о равенствах в математике переходим к более узким темам. Материал этой статьи даст представление о свойствах числовых равенств.

Что такое числовое равенство

Первый раз мы сталкиваемся с числовыми равенствами еще в начальной школе, когда происходит знакомство с числами и понятием «столько же». Т.е. самые примитивные числовые равенства это: 2=2, 5=5 и т.д. И на том уровне изучения мы называли их просто равенствами, без уточнения «числовые», и закладывали в них количественный или порядковый смысл (который несут натуральные числа). Например, равенство 2=2 будет соответствовать изображению, на котором – два цветка и на каждом сидит по две шмеля. Или, к примеру, две очереди, где вторыми по порядку стоят Вася и Ваня.

По мере появления знаний об арифметических действиях числовые равенства становятся сложнее: 5+7=12; 6-1=5; 2·1=2; 21:7=3 и т.п. Затем начинают встречаться равенства, в записи которых участвуют числовые выражения разного рода. Например, (2+2)+5=2+(5+2); 4·(4−(1+2))+12:4−1=4·1+3−1 и т.п. Дальше мы знакомимся с прочими видами чисел, и числовые равенства приобретают все более и более интересный и разнообразный вид.

Определение 1

Числовое равенство – это равенство, обе части которого состоят из чисел и/или числовых выражений.

Свойства числовых равенств

Сложно переоценить значимость свойств числовых равенств в математике: они являются опорой многому, определяют принцип работы с числовыми равенствами, методы решений, правила работы с формулами и многое другое.Очевидно, что существует необходимость детального изучения свойств числовых равенств.

Свойства числовых равенств абсолютно согласованы с тем, как определяются действия с числами, а также с определением равных чисел через разность: число a равно числу bтолько в тех случаях, когда разность a−b есть нуль. Далее в описании каждого свойства мы проследим эту связь.

Основные свойства числовых равенств

Изучать свойства числовых равенств начнем с трех базовых свойств, которые присущи всем равенствам. Перечислим основные свойства числовых равенств:

• свойство рефлексивности: a=a;
• свойство симметричности: если a=b, то b=a;
• свойство транзитивности: если a=b и b=c, то a=c,где a, b и c

Понятие равенства, знак равенства, связанные определения

Материал статьи позволит ознакомиться с математической трактовкой понятия равенства. Порассуждаем на тему сути равенства; рассмотрим его виды и способы его записи; запишем свойства равенства и проиллюстрируем теорию примерами.

Что такое равенство

Само понятие равенства тесно переплетено с понятием сравнения, когда мы сопоставляем свойства и признаки, чтобы выявить схожие черты. Процесс сравнения требует наличия двух объектов, которые и сравниваются между собой. Данные рассуждения наводят на мысль, что понятие равенства не может иметь место, когда нет хотя бы двух объектов, чтобы было что сравнивать. При этом, конечно, может быть взято большее количество объектов: три и более, однако, в конечном, счете, мы так или иначе придем к сравнению пар, собранных из заданных объектов.

Смысл понятия «равенство» в обобщенном толковании отлично определяется словом «одинаковые». О двух одинаковых объектах можно говорить – «равные». Например, квадраты   и . А вот объекты, которые хоть по какому-то признаку отличаются друг от другу, назовем неравными.

Говоря о равенстве, мы можем иметь в виду как объекты в целом, так и их отдельные свойства или признаки. Объекты являются равными в целом, когда одинаковы по всем характеристикам. Например, когда мы привели в пример равенство квадратов, имели в виду их равенство по всем присущим им свойствам: форме, размеру, цвету. Также объекты могут и не быть равными в целом, но обладать одинаковыми отдельными признаками. Например:  и . Указанные объекты равны по форме (оба – круги), но различны (неравны) по цвету и размеру.

Таким образом, необходимо заранее понимать, равенство какого рода мы имеем в виду.

Запись равенств, знак равно

Чтобы произвести запись равенства, используют знак равно (или знак равенства), обозначаемый как =.Такое обозначение является общепринятым.

Составляя равенство, равные объекты размещают рядом, записывая между ними знак равно. К примеру, равенство чисел 5 и 5 запишем как 5=5. Или, допустим, нам необходимо записать равенство периметра треугольника АВС 6 метрам: PАВС=6 м.

Определение 1

Равенство – запись, в которой использован знак равно, разделяющий два математических объекта (или числа, или выражения и т.п.).

Когда возникает необходимость письменно обозначить неравенство объектов, используют знак не равно, обозначаемый как ≠, т.е. по сути зачеркнутый знак равно.

Верные и неверные равенства

Составленные равенства могут соответствовать сути п

Равенство и неравенство. Видеоурок. Математика 1 Класс

Тема: Знакомство с основными понятиями в математике

Урок: Равенство и неравенство

 

На данном уроке мы познакомимся с математическими понятиями: «равенство» и «неравенство».

Попробуйте ответить на вопрос:

У стены стоят кадушки,

В каждой ровно по лягушке.

Если б было пять кадушек,

Сколько б было в них лягушек? (рис. 1)

Рис. 1

В стихотворении говорится, что кадушек было 5, в каждой кадушке по 1 лягушке, никто не остался без пары, значит число лягушек равно числу кадушек.

Обозначим кадушки буквой К, а лягушек – буквой Л.

Запишем равенство: К = Л. (рис. 2)

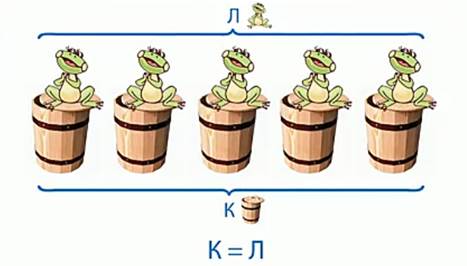
Рис. 2

Сравните по количеству две группы фигур. Фигур много, они разного размера, расположены без порядка. (рис. 3)

 

Рис. 3

Составим из этих фигур пары. Каждый квадрат соединим с треугольником. (рис. 4)

 

Рис. 4

Два квадрата остались без пары. Значит, количество квадратов не равно количеству треугольников. Обозначим квадраты буквой К, а треугольники – буквой Т.

Запишем неравенство: К ≠ Т. (рис. 5)

Рис. 5

Вывод: сравнивать количество элементов в двух группах можно, составляя пары. Если всем элементам хватает пары, то соответствующие числа равны, в этом случае ставим между цифрами или буквами знак равно. Эта запись называется равенством. (рис. 6)

Рис. 6

Если не хватает пары, то есть остаются лишние предметы, то эти числа неравны. Ставим между числами или буквами знак неравно.  Эта запись называется неравенством. (рис. 7)

Рис. 7

Оставшиеся без пары элементы показывают, какое из двух чисел больше и на сколько. (рис. 8)

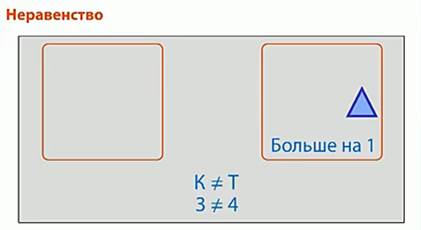
Рис. 8

Способ сравнения групп фигур с помощью составления пар не всегда удобен и занимает много времени. Можно сравнивать числа с помощью числового луча. (рис. 9)

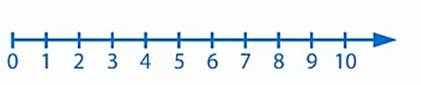
Рис. 9

Сравните данные числа с помощью числового луча и поставьте знак сравнения.

Пример 1

2  ⃞  5

Нужно сравнить числа 2 и 5. Посмотрим на числовой луч. Число 2 находится ближе к 0, чем число 5, или говорят, число 2 на числовом луче левее, чем число 5. Значит, 2 не равно 5. Это неравенство.

2 ≠ 5

Знак «≠» (не равно) лишь фиксирует неравенство чисел, но не указывает, какое из них больше, а какое – меньше.

Из двух чисел на числовом луче меньшее расположено левее, а большее – правее. (рис. 10)

Рис. 10

Можно данное неравенство записать по-другому, используя знак меньше « < » или знак больше  « > » :

2 < 5

Пример 2

7   ⃞  4

На числовом луче число 7 находится правее, чем число 4, следовательно:

7 ≠ 4  и 7 > 4

Пример 3

9  ⃞  9

Числа 9 и 9 равны, поэтому ставим знак =, это равенство:

9 = 9

Сравните количество точек и число и поставьте соответствующий знак. (рис. 11)

Рис. 11

На первом рисунке  нам необходимо поставить знак  = или  ≠ .

Сравниваем две точки и число 2, ставим между ними знак =. Это равенство.

Сравниваем одну точку и число 3, на числовом луче число 1 находится левее, чем число 3, ставим знак ≠.

Сравниваем четыре точки и 4. Между ними ставим знак =. Это равенство.

Сравниваем три точки и число 4. Три точки – это число 3. На числовом луче оно левее, ставим знак ≠. Это неравенство. (рис. 12)

Рис. 12

На втором рисунке между точками и числами надо поставить знаки = , <, >.

Сравним пять точек и число 5. Между ними ставим знак =. Это равенство.

Сравним три точки и число 3. Здесь тоже можно поставить знак =.

Сравним пять точек и число 6. На числовом луче число 5 левее, чем число 6. Ставим знак <. Это неравенство.

Сравним две точки и единицу, число 2 правее на числовом луче, чем число 1. Ставим знак >. Это неравенство. (рис. 13)

Рис. 13

Вставьте в окошко число, чтобы полученное равенство и неравенство стали верными.

1.   ⃞ < 7

Это неравенство. Посмотрим на числовой луч. Раз мы ищем число меньше, чем число 7, значит оно должно быть левее числа 7 на числовом луче. (рис. 14)

 

Рис. 14

В окошко можно вставить несколько чисел. Сюда подходят числа 0, 1, 2, 3, 4, 5, 6. Любое из них можно подставить в окошко и получить несколько верных неравенства. Например, 5 < 7 или 2 < 7

2. 5 >     ⃞

На числовом луче найдём числа, которые будут меньше 5. (рис. 15)

 

Рис. 15

Это числа 4, 3, 2, 1, 0. Следовательно, любое из этих чисел можно подставить в окошко, мы получим несколько верных неравенств. Например, 5 >4, 5 >3

3. 8 =     ⃞

В можно подставить только одно число 8.

8 = 8.

На данном уроке мы познакомились с математическими понятиями: «равенство» и «неравенство», научились правильно расставлять знаки сравнения, потренировались сравнивать группы фигур с помощью составления пар и сравнивать числа с помощью числового луча, что поможет в дальнейшем изучении математики.

 

Список литературы

1. Александрова Л.А., Мордкович А.Г. Математика 1 класс. – М: Мнемозина, 2012.
2. Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
3. Беденко М.В. Математика. 1 класс. – М7: Русское слово, 2012.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Igraem.pro (Источник).
2. Slideshare.net (Источник).
3. Iqsha.ru (Источник).

 

Домашнее задание

1. Какие знаки сравнения вы знаете, в каких случаях они используются? Запишите знаки сравнения чисел.

2. Сравните количество предметов на рисунке и поставьте знак «<», «>» или «=».

 

3. Сравни числа, поставив знак «<», «>» или «=».

5 … 8	9 … 2	5 … 5
10 … 1	7 … 8	3 … 5

Числовые равенства и неравенства | интернет проект BeginnerSchool.ru

Чтобы получить запись, называемую числовым равенством, надо два числовых выражения соединить знаком равенства (=).

Пример:

Представленный пример является верным числовым равенством, но числовое равенство может быть неверным:

Давайте разберем свойства числовых равенств.

1. Если числовое равенство верно, то прибавив к обеим частям этого равенства одно и тоже число мы получим верное числовое равенство.

Например:

Проверим равенство

(12 + 3) = (9 + 6)

12 + 3 = 15 и 9 + 6 = 15

Равенство верно, теперь проверим свойство

(12 + 3) + (5 – 2) = (9 + 6) + (5 – 2)

15 + (5 – 2) = 15 + (5 – 2)

18 = 18

В обоих случаях равенства верны

 

То же самое произойдет, если мы вычтем одно и то же числовое выражение из обеих частей верного числового равенства.

Проверим это свойство на предыдущем примере заменив действие сложение на вычитание:

(12 + 3) – (5 – 2) = (9 + 6) – (5 – 2)

15 + (5 – 2) = 15 + (5 – 2)

12 = 12

Как мы видим равенство верно.

 

2. Если числовое равенство верно, то умножив обе части этого равенства на одно и тоже числовое выражение мы получим верное числовое равенство.

Проверим и это свойство:

(75 – 3) = (15 + 57)

75 – 3 = 72 и 15 + 57 = 72 это равенство верно

(75 – 3) · (10 – 2) = (15 + 57) · (10 – 2)

72 · (10 – 2) = 72 · 8 = 576

576 = 576

Свойство доказано.

3. Если числовое равенство верно, то разделив обе части этого равенства на одно и тоже числовое выражение мы получим верное числовое равенство. Правда, это выражение справедливо только если числовое выражение не равно нулю, так как на ноль делить нельзя.

 

 

Проверим это свойство:

(12 + 3) : (5 – 2) = (9 + 6) : (5 – 2)

15 : 3 = 15 : 3

5 = 5

Что и требовалось доказать.

Если одно числовое выражение не равно другому, то сравним оба выражения поставим между ними знак сравнения – больше (>) или меньше (<). Мы получим числовое неравенство.

(3 · 4) < (3 · 6)

(10 + 25)

Числовые неравенства также могут быть верными и неверными:

(25 – 5) : 5 > 10 – это неравенство неверно

(25 – 5) : 5 < 10 – это неравенство верно

Спасибо, что Вы с нами!

Понравилась статья — поделитесь с друзьями:

Подпишитесь на новости сайта:

Оставляйте пожалуйста комментарии в форме ниже

Равенство и неравенство

Два числовых математических выражения, соединенные знаком «=» называют равенством.

Например: 3 + 7 = 10 — равенство.

Равенство может быть верным и неверным.

Смысл решения любого примера состоит в том, чтобы найти та­кое значение выражения, которое превращает его в верное равенство.

Для формирования представлений о верных и неверных равенствах в учебнике 1 класса используются примеры с окошком.

Например:

Методом подбора ребенок находит подходящие числа и проверяет верность равенства вычислением.

Процесс сравнения чисел и обозначение отношений между ними с помощью знаков сравнения приводит к получению неравенств.

Например: 5 < 7; б > 4 — числовые неравенства

Неравенства также могут быть верными и неверными.

Например:

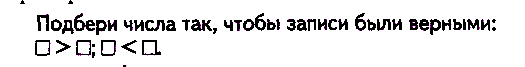
Методом подбора ребенок находит подходящие числа и проверяет верность неравенства.

Числовые неравенства получаются при сравнении числовых выражений и числа.

Например:

При выборе знака сравнения ребенок вычисляет значение выражения и сравнивает его с заданным числом, что отражается в выборе соответствующего знака:

10-2>7 5+К7 7 + 3>9 6-3 = 3

Возможен другой способ выбора знака сравнения — без ссылки на вычисления значения выражения.

Наппимеп:

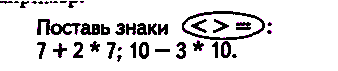
Для постановки знаков сравнения можно провести такие рассуждения:

Сумма чисел 7 и 2 будет заведомо больше, чем число 7, значит, 7 + 2 > 7.

Разность чисел 10 и 3 будет заведомо меньше, чем число 10, значит, 10 — 3 < 10.

Числовые неравенства получаются при сравнении двух числовых выражений.

Сравнить два выражения — значит сравнить их значения. Например:

При выборе знака сравнения ребенок вычисляет значения выражений и сравнивает их, что отражается в выборе соответствующего знака:

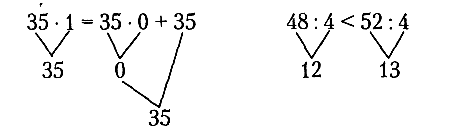
Возможен другой способ выбора знака сравнения — без ссылки на вычисления значения выражения. Например:

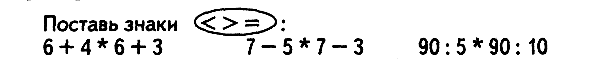
Для постановки знаков сравнения можно провести такие рассуждения:

Сумма чисел 6 и 4 больше суммы чисел 6 и 3, поскольку 4 > 3, значит, 6 + 4 > 6 + 3.

Разность чисел 7 и 5 меньше, чем разность чисел 7 и 3, поскольку 5 > 3, значит, 7 — 5 < 7 — 3.

Частное чисел 90 и 5 больше, чем частное чисел 90 и 10, поскольку при делении одного и того же числа на число большее, частное получается меньшее, значит, 90 : 5 > 90 :10.

Для формирования представлений о верных и неверных равенствах и неравенствах в новой редакции учебника (2001) используются задания вида:

Для проверки используется метод вычисления значения выражений и сравнения полученных чисел.

Неравенства с переменной практически не используются в последних редакциях стабильного учебника математики, хотя в более ранних изданиях они присутствовали. Неравенства с переменными активно используются в альтернативных учебниках математики. Это неравенства вида:

 + 7 < 10; 5 —  > 2;  > 0;  > О

После введения буквы для обозначения неизвестного числа такие неравенства приобретают привычный вид неравенства с переменной:

а + 7>10; 12-d<7.

Значения неизвестных чисел в таких неравенствах находятся методом подбора, а затем подстановкой проверяется каждое подобранное число. Особенность данных неравенств состоит в том, что могут быть подобраны несколько чисел, подходящих к ним (дающих верное неравенство).

Например: а + 7 > 10; а = 4, а = 5 , а = 6 и т. д. — количество значений для буквы а бесконечно, для данного неравенства подхо­дит любое число а > 3; 12 — d < 7; d = 6, d = 7, d = 8, d = 9, d = 10, d = 11, d = 12 — количество значений для буквы d конечно, все значения могут быть перечислены. Ребенок подставляет каждое найденное значение переменной в выражение, вычисляет значение выражения и сравнивает его с заданным числом. Выбираются те значения переменной, при которых неравенство является верным.

В случае бесконечного множества решений или большого количества решений неравенства ребенок ограничивается подбором нескольких значений переменной, при которых неравенство является верным.

Урок математики в 1-м классе по теме «Равенство. Неравенство»

Цели:

• познакомить с терминами « равенство», « неравенство»;
• продолжить работу по формированию умения сравнивать числа и числовые выражения;
• отработать устный счет, формируя вычислительные навыки;
• закрепить пространственные представления;
• развивать двигательную активность;
• провести работу по развитию связной речи.

Ход урока

I. Организационный момент.

II. Подготовительная работа.

Устный счет.

Работа с веером.

– В домике живет цифра 5. Нужно узнать какой цифры не хватает на каждом этаже, чтобы результат был равен 5. (Дети показывают ответ с помощью математического веера.)

– Назовите ответ.

Счет «цепочкой» от 1 до 10 прямой и обратный от 10 до (мячом).

– По очереди посчитайте от 1 до 10.

– Теперь в обратном порядке от 10 до 1.

Работа с математическим набором.

– Откройте математические наборы.

– Положите 4 красных кружка, рядом 1 кружок другого цвета.

– Сколько кружков стало? (5)

– Составьте пример пользуясь цифрами из математического набора. (4+1=5)

– Как записать? (Запись на доске)

– Оставьте цифры 4 и 5.

– Какое число меньше? (4)

– Какую запись записать? (4<5)

– Прочитаем запись. (Четыре меньше пяти.)

– Какое число больше 4? (5)

– Поставьте цифру 5 слева от 4.

– Какой знак между ними поставить? (5>4)

– Прочитайте запись . (Пять больше четырех.)

– Уберите математический набор.

Физминутка. 

Поднимаем плечики, прыгаем кузнечики.
Прыг-скок, прыг-скок.
Сели, покушаем, тишину послушаем.
Тише-тише, высоко прыгаем легко-легко.

III. Основная часть.

Работа на доске.

– Поставьте 3 морковки сверху.

– Поставьте 3 репки снизу.

– Что можно сказать о количестве морковок и репок? (Их поровну. Столько же.)

– Какой знак поставим между цифрами? (Равно.)

Учитель записывает на доске 3=3.

– Это равенство –  тема урока.

– Кто любит грызть морковку? (Зайчик.)

Учитель ставит зайчика к морковкам.

– Какую сказку узнали по картинкам? («Репка»)

Предлагается драматизация сказки «Репка», раздаются сказочные персонажи:

• репка
• дедка
• бабка
• внучка
• Жучка
• кошка
• мышка

– Встаньте по порядку, как стояли сказочные герои в сказке.

Дети проговаривают последовательность персонажей сказки (кто за кем стоит).

– Сколько репок вытащили герои сказки? (1)

– Что нужно сделать с репками, которые расположены на доске? (Убрать 1.)

– Сколько морковок? (3)

– Сколько репок? (2)

– Как узнали? (3-1=2)

На доске запись 3 2

– Какой знак поставим между цифрами? (>)

– Сколько репок? (2)

– Сколько морковок? (3)

– Какой знак поставим между цифрами? (<)

– Это неравенство.

Физминутка.

Еле-еле, еле-еле
Завертелись карусели.
А потом кругом, кругом
И бегом, бегом.
Тише-тише не спешите
Карусель остановите.
Раз-два, раз-два
Вот и кончилась игра.

IV. Закрепление изученного материала.

Работа в учебнике.

– Прочитайте название темы в учебнике. (Равенство. Неравенство.)

– Посмотрите, с какой стороны написаны равенства? (Слева.) Прочитайте.

– С какой стороны в учебнике написаны неравенства? (Справа.) Прочитайте.

V. Рефлексия.

– С какой темой урока вы сегодня познакомились?

– Какой математический знак используется при записи равенства?

– Какие знаки при записи неравенства?

– Что понравилось на уроке?