3}}.$

 

Вычисление определенного интеграла. Формула Ньютона-Лейбница

Решение прикладных задач сводится к вычислению интеграла, но не всегда это возможно сделать точно. Иногда необходимо знать значение определенного интеграла с некоторой степенью точности, к примеру, до тысячной.

Существуют задачи, когда следовало бы найти приближенное значение определенного интеграла с необходимой точностью, тогда применяют численное интегрирование такое, как метод Симпосна, трапеций, прямоугольников. Не все случаи позволяют вычислить его с определенной точностью.

Данная статья рассматривает применение формулы Ньютона-Лейбница. Это необходимо для точного вычисления определенного интеграла. Будут приведены подробные примеры, рассмотрены замены переменной в определенном интеграле и найдем значения определенного интеграла при интегрировании по частям.

Формула Ньютона-Лейбница

Определение 1

Когда функция y=y(x) является непрерывной из отрезка [a; b] ,а F(x) является одной из первообразных функции этого отрезка, тогда

формула Ньютона-Лейбница считается справедливой. Запишем ее так ∫abf(x)dx=F(b)-F(a).

Данную формулу считают основной формулой интегрального исчисления.

Чтобы произвести доказательство этой формулы, необходимо использовать понятие интеграла с имеющимся переменным верхним пределом.

Когда функция y=f(x) непрерывна из отрезка [a; b], тогда значение аргумента x∈a; b, а интеграл имеет вид ∫axf(t)dt и считается функцией верхнего предела. Необходимо принять обозначение функции примет вид ∫axf(t)dt=Φ(x), она является непрерывной, причем для нее справедливо неравенство вида ∫axf(t)dt’=Φ'(x)=f(x).

Зафиксируем, что приращении функции Φ(x) соответствует приращению аргумента ∆x, необходимо воспользоваться пятым основным свойством определенного интеграла и получим

Φ(x+∆x)-Φx=∫ax+∆xf(t)dt-∫axf(t)dt==∫ax+∆xf(t)dt=f(c)·x+∆x-x=f(c)·∆x

где значение c∈x; x+∆x.

Зафиксируем равенство в виде Φ(x+∆x)-Φ(x)∆x=f(c).  По определению производной функции необходимо переходить к пределу при ∆x→0, тогда получаем формулу вида Φ'(x)=f(x). Получаем, что Φ(x) является одной из первообразных для функции вида y=f(x), расположенной на [a; b]. Иначе выражение можно записать

F(x)=Φ(x)+C=∫axf(t)dt+C, где значение C является постоянной.

Произведем вычисление F(a) с использованием первого свойства определенного интеграла. Тогда получаем, что

F(a)=Φ(a)+C=∫aaf(t)dt+C=0+C=C, отсюда получаем, что C=F(a). Результат применим при вычислении F(b) и получим:

F(b)=Φ(b)+C=∫abf(t)dt+C=∫abf(t)dt+F(a), иначе говоря, F(b)=∫abf(t)dt+F(a). Равенство доказывает формулу Ньютона-Лейбница ∫abf(x)dx+F(b)-F(a).

Приращение функции принимаем как Fxab=F(b)-F(a). С помощью обозначения формулу Ньютона-Лейбница принимает вид ∫abf(x)dx=Fxab=F(b)-F(a).

Чтобы применить формулу, обязательно необходимо знать одну из первообразных y=F(x) подынтегральной функции y=f(x) из отрезка [a; b] , произвести вычисление приращения первообразной из этого отрезка. Рассмотрим несколько примером вычисления, используя формулу Ньютона-Лейбница.

Пример 1

Произвести вычисление определенного интеграла ∫13x2dx по формуле Ньютона-Лейбница.

Решение

Рассмотрим, что подынтегральная функция вида y=x2 является непрерывной из отрезка [1;3], тогда и интегрируема на этом отрезке. По таблице неопределенных интегралов видим, что  функция y=x2 имеет множество первообразных для всех действительных значений x, значит, x∈1; 3 запишется как F(x)=∫x2dx=x33+C. Необходимо взять первообразную с С=0, тогда получаем, что F(x)=x33.

Воспользуемся формулой Ньютона-Лейбница и получим, что вычисление определенного интеграла примет вид ∫13x2dx=x3313=333-133=263.

Ответ: ∫13x2dx=263

Пример 2

Произвести вычисление определенного интеграла ∫-12x·ex2+1dx по формуле Ньютона-Лейбница.

Решение

Заданная функция непрерывна из отрезка [-1;2], значит, на нем интегрируема. Необходимо найти значение неопределенного интеграла ∫x·ex2+1dx при помощи метода подведения под знак дифференциала , тогда получаем ∫x·ex2+1dx=12∫ex2+1d(x2+1)=12ex2+1+C.

Отсюда имеем множество первообразных функции y=x·ex2+1, которые действительны для всех x, x∈-1; 2.

Необходимо взять первообразную при С=0 и применить формулу Ньютона-Лейбница. Тогда получим выражение вида

∫-12x·ex2+1dx=12ex2+1-12==12e22+1-12e(-1)2+1=12e(-1)2+1=12e2(e3-1)

Ответ: ∫-12x·ex2+1dx=12e2(e3-1)

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 3

Произвести вычисление интегралов ∫-4-124×3+2x2dx и ∫-114×3+2x2dx.

Решение

Отрезок -4; -12 говорит о том, что функция, находящаяся под знаком интеграла, является непрерывной, значит, она интегрируема. Отсюда найдем множество первообразных функции y=4×3+2×2. Получаем, что

∫4×3+2x2dx=4∫xdx+2∫x-2dx=2×2-2x+C

Необходимо взять первообразную F(x)=2×2-2x, тогда, применив формулу Ньютона-Лейбница, получаем интеграл, который вычисляем:

∫-4-124×3+2x2dx=2×2-2x-4-12=2-122-2-12-2-42-2-4=12+4-32-12=-28

Производим переход к вычислению второго интеграла.

Из отрезка [-1;1] имеем, что подынтегральная функция считается неограниченной, потому как limx→04×3+2×2=+∞, тогда отсюда следует, что необходимым условием интегрируемости  из отрезка. Тогда F(x)=2×2-2x не является первообразной для y=4×3+2×2из отрезка [-1;1], так как точка O принадлежит отрезку, но не входит в область определения. Значит, что имеется определенный интеграл Римана и Ньютона-Лейбница для функции y=4×3+2×2 из отрезка [-1;1].

Ответ: ∫-4-124×3+2x2dx=-28, 

имеется определенный интеграл Римана и Ньютона-Лейбница для функции y=4×3+2×2 из отрезка [-1;1].

Перед использованием формулы Ньютона-Лейбница нужно точно знать о существовании определенного интеграла.

Замена переменной в определенном интеграле

Когда функция y=f(x) является определенной и непрерывной из отрезка [a;b], тогда имеющееся множество [a;b] считается областью значений функции x=g(z), определенной на отрезке α; β с имеющейся непрерывной производной, где g(α)=a и gβ=b, отсюда получаем, что ∫abf(x)dx=∫αβf(g(z))·g'(z)dz.

Данную формулу применяют тогда, когда нужно вычислять интеграл ∫abf(x)dx, где неопределенный интеграл имеет вид ∫f(x)dx, вычисляем при помощи метода подстановки.

Пример 4

Произвести вычисление определенного интеграла вида ∫9181x2x-9dx.

Решение

Подынтегральная функция считается непрерывной на отрезке интегрирования, значит определенный интеграл имеет место на существование. Дадим обозначение, что 2x-9=z⇒x=g(z)=z2+92. Значение х=9, значит, что z=2·9-9=9=3, а при х=18 получаем, что z=2·18-9=27=33, тогда gα=g(3)=9, gβ=g33=18. При подстановке полученных значений в формулу ∫abf(x)dx=∫αβf(g(z))·g'(z)dz получаем, что

∫9181x2x-9dx=∫3331z2+92·z·z2+92’dz==∫3331z2+92·z·zdz=∫3332z2+9dz

По таблице неопределенных интегралов имеем, что одна из первообразных функции 2z2+9 принимает значение 23arctgz3. Тогда при применении формулы Ньютона-Лейбница получаем, что

∫3332z2+9dz=23arctgz3333=23arctg333-23arctg33=23arctg3-arctg 1=23π3-π4=π18

Нахождение можно было производить, не используя формулу ∫abf(x)dx=∫αβf(g(z))·g'(z)dz.

Если при методе замены использовать интеграл вида ∫1x2x-9dx, то можно прийти к результату ∫1x2x-9dx=23arctg2x-93+C.

Отсюда произведем вычисления по формуле Ньютона-Лейбница и вычислим определенный интеграл. Получаем, что

∫9182z2+9dz=23arctgz3918==23arctg2·18-93-arctg2·9-93==23arctg3-arctg 1=23π3-π4=π18

Результаты совпали.

Ответ: ∫9182x2x-9dx=π18

Интегрирование по частям при вычислении определенного интеграла

Если на отрезке [a;b] определены и непрерывны функции u(x) и v(x), тогда их производные первого порядка v'(x)·u(x) являются интегрируемыми, таким образом из этого отрезка для интегрируемой функции u'(x)·v(x) равенство ∫abv'(x)·u(x)dx=(u(x)·v(x))ab-∫abu'(x)·v(x)dx справедливо.

Формулу можно использовать тогда, необходимо вычислять интеграл ∫abf(x)dx, причем ∫f(x)dx необходимо было искать его при помощи интегрирования по частям.

Пример 5

Произвести вычисление определенного интеграла ∫-π23π2x·sinx3+π6dx.

Решение

Функция x·sinx3+π6 интегрируема на отрезке -π2; 3π2, значит она непрерывна.

Пусть u(x)=х, тогда d(v(x))=v'(x)dx=sinx3+π6dx, причем d(u(x))=u'(x)dx=dx, а v(x)=-3cosπ3+π6. Из формулы ∫abv'(x)·u(x)dx=(u(x)·v(x))ab-∫abu'(x)·v(x)dx получим, что

∫-π23π2x·sinx3+π6dx=-3x·cosx3+π6-π23π2-∫-π23π2-3cosx3+π6dx==-3·3π2·cosπ2+π6—3·-π2·cos-π6+π6+9sinx3+π6-π23π2=9π4-3π2+9sinπ2+π6-sin-π6+π6=9π4-3π2+932=3π4+932

Решение примера можно выполнить другим образом.

Найти множество первообразных функции x·sinx3+π6 при помощи интегрирования по частям с применением формулы Ньютона-Лейбница:

∫x·sinxx3+π6dx=u=x, dv=sinx3+π6dx⇒du=dx, v=-3cosx3+π6==-3cosx3+π6+3∫cosx3+π6dx==-3xcosx3+π6+9sinx3+π6+C⇒∫-π23π2x·sinx3+π6dx=-3cosx3+π6+9sincosx3+π6—3·-π2·cos-π6+π6+9sin-π6+π6==9π4+932-3π2-0=3π4+932

Ответ: ∫x·sinxx3+π6dx=3π4+932

как понять и решать неопределенные и определенные интегралы, правила и примеры

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие «интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

«Интеграл»

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a, b и с:

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Урок 25. применение интегралов для решения геометрических и физических задач — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №25. Применение интегралов для решения геометрических и физических задач.

Перечень вопросов, рассматриваемых в теме

1) Знакомство с применением определенного интеграла в различных предметных областях

2) Знакомство с прикладными задачами, связанными с вычислением определенного интеграла в физике, экономике, геометрии.

3) Решение задач, с помощью определенных интегралов

путь, пройденный телом

Прирост численности популяции N(t) за промежуток времени от t₀ до T равен .

Объем тела вращения

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].

Отрезок [a;b] называют основанием этой криволинейной трапеции

формула Ньютона – Лейбница

путь, пройденный телом

Прирост численности популяции N(t) за промежуток времени от t₀ до T равен .

Объем тела вращения

Примеры и разбор решения заданий тренировочного модуля

№1 Найти объем тела вращения вокруг оси 0х , ограниченной прямыми у=0, х=0ю у= х², х=4.

Решение: Построим тело вращения, образованного вращением фигуры вокруг оси 0х

Воспользуемся формулой Ньютона-Лейбница.

и формулой нахождения объемов тел вращения.

Далее подставляем значения в формулу и рассчитываем объем тела вращения.

Ответ 51,2 ед³

№2. Сила в 1 Н растягивает пружину на 3 см. Какую работу она при этом производит?

Решение.

Если F–сила, А – работа S– перемещение, то F = A’(S).

Обратимся к физике.

По закону Гука сила пропорциональна растяжению или сжатию пружины, т. е. F = kx, где k – коэффициент пропорциональности, х – величина растяжения или сжатия.

Используя данные задачи, найдите коэффициент k. Подставим данные в задаче величины в уравнение, выражающее закон Гука. Получим: .

Следовательно, сила, растягивающая нашу пружину, выразится следующим образом:.

Так как сила начинает действовать на пружину в состоянии покоя, то работа

Ответ: 0,015 Дж

№3. Аквариум имеет форму прямоугольного параллелепипеда. Найдем силу давления воды (плотность воды 1000 кг/м³), наполняющей аквариум, на одну из его вертикальных стенок, размеры которой 0,4 м x 0,7 м.

Решение.

Выберем систему координат так, чтобы оси Оy и Оx соответственно содержали верхнее основание и боковую сторону вертикальной стенки аквариума. Для нахождения силы давления воды на стенку воспользуемся формулой

Р=

Стенка имеет форму прямоугольника, поэтому f(x)=0.7x, xϵ [0;0.4]  Так как пределы интегрирования а=0 и b=0,4, то получим:

Ответ: 549 Н

№4 Скорость прямолинейного движения тела выражается формулой . Найти путь, пройденный телом за 5 секунд от начала движения.

Решение.

Физический смысл производной: если тело движется по закону S = S(t), то скорость тела в момент времени t₀ равна значению производной функции S(t) в этой точке, т. е. v = S’(t₀). Тогда обратное утверждение: если скорость движения тела задана уравнением v = v(t), то путь, пройденный телом от момента времени t = a до момента времени t = b равен . Подставим уравнение скорости в формулу и рассчитаем путь.

Ответ 150м

Страница не найдена — ПриМат

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Юлия Стерлянко (8), Денис Стехун (8), Елизавета Савицкая (8), Игорь Любинский (8), Олег Шпинарев (7), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Татьяна Корнилова (6), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2),

5.

Вычисление интегралов | Техническая библиотека lib.qrz.ru

 

Вычисление интегралов

 

Вычисление интегралов в символьном виде

Одна из важнейших операций — вычисление первообразных и определенных интегралов в символьном виде. Первообразная — это функция F(x), удовлетворяющая уравнению

f(x)dx = F(x) + C,

где С — постоянная интегрирования. А вычисление определенного интеграла с пределами — верхним b и нижним а — производится по формуле

f(X)dX = F(b)-F(a)

Заметим, что определенный интеграл может быть представлен как аналитическим, так « численным значением. Для вычисления численных значений определенных интегралов разработан ряд приближенных методов — от простых (прямоугольников и трапеций) до сложных, автоматически адаптирующихся к характеру изменения подынтегральной функции f(x).

Для интегрирования в системе Mathematica используются следующие функции:

• Integrate [f, x] — возвращает первообразную (неопределенный интеграл) подынтегральной функции f по переменной х;
• Integrate [f, {x, xmin, xmax}] — возвращает значение определенного интеграла с пределами от x _min до x _max ;
• Integrate [f, {x, xmin, xmax}, {у, ymin, ymax},…] —возвращает значение кратного интеграла с пределами от x _min до x _max по переменной х, от y _min до y _max по переменной у и т. д. (кратность реально не ограничена).

Обычно функция Integrate применяется в простейшей форме, но она имеет три характерные опции:

Options[Integrate]

{Assumptions -> {}, GenerateConditions->Automatic,

PrincipalValue > False)

Для обозначения бесконечных пределов используется константа Infinity. Эта константа означает положительную бесконечность, для задания отрицательной бесконечности она используется со знаком «минус». Пределы могут задаваться как константами, так и функциями.

Особый интерес, естественно, вызывает применение функции Integrate для вычисления заданных пользователем неопределенных интегралов в символьном виде. Это иллюстрируют примеры на вычисление неопределенных интегралов с алгебраическими подынтегральными функциями, представленные на рис. 4.2.

Здесь входная ячейка в первом примере представлена в формате ввода (Input-Form), а в остальных примерах — в стандартном формате (StandardForm). При записи интегралов последний предпочтителен ввиду большей наглядности, поскольку при этом знаки интеграла имеют естественный математический вид. Обратите внимание на проверку операции интегрирования с помощью дифференцирования в двух последних примерах.

На рис. 4.3 показано еще несколько примеров вычисления неопределенных интегралов. Нетрудно заметить, что интегралы от ряда алгебраических функций дают выражения с тригонометрическими функциями.

Другая группа примеров, представленная на рис. 4.4, показывает нахождение интегралов с тригонометрическими и гиперболическими подынтегральными функциями.

Последний пример показывает, что возможно вычисление списка определенных интегралов, если подынтегральные функции представлены также в виде списка.

Рис. 4.2. Примеры вычисления неопределенных интегралов (начало)

Рис. 4.3. Примеры вычисления неопределенных интегралов (продолжение)

Рис. 4.4. Примеры вычисления неопределенных интегралов (окончание)

 

Вычисление определенных интегралов

Следующая серия примеров (рис. 4.5) иллюстрирует вычисление определенных интегралов в символьном виде. 3,x],y]

x4y/4+y4x/4

( (x3 + y3) dx) dy

x4y/4+y4x/4

Другая серия примеров (рис. 4.8) показывает, как вычисляются двойные и тройные интегралы, пределы которых сами по себе являются функциями.

Рис. 4.8. Примеры вычисления кратных интегралов с пределами-функциями

Хотя вычисление двойного интеграла предусмотрено в синтаксисе функции Integrate, это не всегда дает результат. Как правило, вычисление кратных интегралов лучше производить, используя последовательное вычисление однократных интегралов, вложенных друг в друга. Это и показывают приведенные примеры.

Особые случаи вычисления интегралов

При вычислении сложных интегралов, например не имеющих представления через элементарные функции, система Mathematica 2 обращалась к своим пакетам расширений в попытке найти решение, которое может быть представлено через специальные математические функции. Mathematica 3/4 уже не акцентирует внимание пользователя на своих проблемах и, как правило, выдает результат интегрирования. Однако порой он может иметь довольно необычный вид (рис. 4.9).

Эти примеры наглядно показывают, что вычисление первообразных в системе может дать результаты, далекие от тривиального вычисления неопределенных интегралов, имеющихся в обычных справочниках по математике. Кстати, и при вычислении тривиальных интегралов результат может оказаться иным, чем в справочниках, из-за различных преобразований, примененных для получения конечных формул. Подчас могут потребоваться определенные усилия для получения результата в заданной форме. Как подынтегральное выражение, так и результаты вычислений могут содержать как элементарные, так и специальные математические функции.

Рис. 4.9. Примеры вычисления особых интегралов

В заключение надо отметить, что результаты символьного интегрирования в системах Mathematica 3 и Mathematica 4 нередко различаются. 3}] 0.010582 NIntegrate [l/(x*y) , {х,4,4 .4} , {у, 2, 2. 6}] 0.025006 NIntegrate [Sqrt[2*x+l] ,{x,0,l}] 1.39872

Эти примеры показывают, что функция NIntegrate с успехом может применяться для вычисления как однократных, так и многократных определенных интегралов, в том числе с переменными пределами.

 

формулы, определения, примеры с решением по высшей математике

Вычисления определенного интеграла

Формула ньютона-лейбница

Простым и удобным методом вычисления определенного интеграла

от непрерывной функции является формула Ньютона-Лейбница:

Применяется этот метод во всех случаях, когда может быть найдена первообразная функции

для подынтегральной функции .

Например,

.

При вычислении определенных интегралов широко используется метод замены переменной и метод интегрирования по частям.

Интегрирование подстановкой (заменой переменной)

Пусть для вычисления интеграла

от непрерывной функции сделана подстановка .

Теорема 39.1. Если:

1) функция

и ее производная непрерывны при ;

2) множеством значений функции

при является отрезок ;

3)

и , то

Пусть

есть первообразная для на отрезке . Тогда по формуле Ньютона-Лейбница . Так как , то является первообразной для функции . Поэтому по формуле Ньютона-Лейбница имеем

Формула (39.1) называется формулой замены переменной в определенном интеграле.

Отметим, что:

1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется;
2) часто вместо подстановки

применяют подстановку ;
3) не следует забывать менять пределы интегрирования при замене переменных!

Пример №39. 1.

Вычислить

.

Решение:

Положим

, тогда . Если , то ; если , то . Поэтому

Интегрирование по частям

Теорема 39.2. Если функции

и имеют непрерывные производные на отрезке , то имеет место формула

На отрезке

имеет место равенстве) . Следовательно, функция есть первообразная для непрерывной функции . Тогда по формуле Ньютона-Лейбница имеем:

Следовательно,

Формула (39.2) называется формулой интегрирования по частям для определенного интеграла.

Пример №39.2.

Вычислить

.

Решение:

Положим

Применяя формулу (39.2), получаем

Дополнительный пример №39.3.

Дополнительная лекция: Интегрирование четных и нечетных функций в симметричных пределах

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Другие темы по высшей математике возможно вам они будут полезны:

Определенные интегралы

Возможно, вам сначала захочется прочитать «Введение в интеграцию»!

Интеграция

Integration можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей. Но его часто используют, чтобы найти область под графиком функции следующим образом:
Область может быть найдена путем добавления срезов, ширина которых приближается к нулю : И есть Правила интеграции, которые помогают нам получить ответ.

Обозначение

Символ «Интеграл» — стильная буква «S» (от «Сумма», идея суммирования срезов):

После символа интеграла мы помещаем функцию, интеграл от которой мы хотим найти (называемую интегралом).

А затем закончите с dx , чтобы обозначить, что срезы идут в направлении x (и приближаются к нулю по ширине).

Определенный интеграл

Определенный интеграл имеет начальное и конечное значения: другими словами, существует интервал [a, b].

a и b (называемые пределами, границами или границами) помещаются внизу и вверху буквы «S», например:

Определенный Интегральный (от a до b )		Неограниченный Интегральный (без конкретных значений)

Мы находим Определенный интеграл путем вычисления неопределенного интеграла при a и b с последующим вычитанием:

Пример: Что такое

Нам нужен определенный интеграл , от 1 до 2, из 2x dx

Сначала нам нужно найти Indefinite Integral .

Используя правила интегрирования, находим, что ∫2x dx = x ² + C

Теперь посчитайте, что при 1 и 2:

• При x = 1: ∫2x dx = 1 ² + C
• При x = 2: ∫2x dx = 2 ² + C

Вычесть:

(2 ² + C) — (1 ² + C)

2 ² + К — 1 ² — К

4 — 1 + C — C = 3

И «C» отменяется… так что с определенными интегралами мы можем игнорировать C .

Результат:

Проверить : с такой простой формой попробуем еще вычислить площадь по геометрии:

A = 2 + 4 2 × 1 = 3

Да, у него есть площадь 3.

(Ура!)

Обозначение : Мы можем показать неопределенный интеграл (без + C) внутри квадратных скобок с пределами a и b после, например:

Пример (продолжение)

Хороший способ показать свой ответ:

Давайте попробуем другой пример:

Пример:

Определенный интеграл, от 0. От 5 до 1.0, из cos (x) dx:

(Примечание: x должен быть в радианах)

Неопределенный интеграл : ∫ cos (x) dx = sin (x) + C

Мы можем игнорировать C для определенных интегралов (как мы видели выше) и получаем:

= грех (1) — грех (0,5)

= 0,841 … — 0,479 …

= 0,362 …

И еще один важный пример:

Пример:

Определенный интеграл от 0 до 1 от sin (x) dx:

Неопределенный интеграл : ∫ sin (x) dx = −cos (x) + C

Поскольку мы идем от 0, можем ли мы просто вычислить интеграл при x = 1?

−cos (1) = −0.540 …

Что? Это минус ? Но на графике это выглядит положительно.

Ну … мы сделали ошибку !

Поскольку нам нужно вычесть интеграл при x = 0 . Не следует предполагать, что он равен нулю.

Итак, давайте сделаем это правильно, вычтя одно из другого:

грех (x) dx

= [−cos (x)]

= −cos (1) — (−cos (0))

= -0,540 … — (-1)

= 0.460 …

Так лучше!

Но у нас может быть отрицательные области , когда кривая ниже оси:

Пример:

Определенный интеграл от 1 до 3 от cos (x) dx:

Обратите внимание, что некоторые из них положительные, а некоторые отрицательные.
Определенный интеграл даст чистое значение .

Сделаем расчеты:

= грех (3) — грех (1)

= 0.141 … — 0,841 …

= −0,700 …

Таким образом, отрицательного больше, чем положительного, с чистым результатом -0,700 ….

Итак, нам нужно запомнить одну важную вещь:

f (x) dx = (Площадь над осью x) — (Площадь под осью x)

Попробуйте интегрировать cos (x) с разными начальными и конечными значениями, чтобы увидеть, как работают положительные и отрицательные значения.

Положительная область

Но иногда мы хотим, чтобы вся область обрабатывалась как положительное значение (без вычитания части ниже оси).

В этом случае мы должны вычислить площади отдельно , как в этом примере:

Пример: Какова общая площадь

между y = cos (x) и осью x, от x = 1 до x = 3?

Это похоже на пример, который мы только что сделали, но теперь мы ожидаем, что вся площадь положительна (представьте, что нам нужно было это нарисовать).

Итак, теперь мы должны делать детали отдельно:

• Один для области над осью x
• Один для области ниже оси x

Кривая пересекает ось x при x = π / 2, поэтому мы имеем:

От 1 до π / 2:

cos (x) dx

= грех (π / 2) — грех (1)

= 1 — 0.841 …

= 0,159 …

От π / 2 до 3:

cos (x) dx

= грех (3) — грех (π / 2)

= 0,141 … — 1

= -0,859 …

Последний выходит отрицательным, но мы хотим, чтобы он был положительным, поэтому:

Общая площадь = 0,159 … + 0,859 … = 1,018 …

Это сильно отличается от ответа в предыдущем примере.

непрерывный

О да, функция, которую мы интегрируем, должна быть непрерывной между a и b : без дыр, скачков или вертикальных асимптот (где функция направляется вверх / вниз к бесконечности).

Пример:

Вертикальная асимптота между a и b влияет на определенный интеграл.

Недвижимость

Область выше — область ниже

Интеграл добавляет площадь над осью, но вычитает площадь ниже, для «чистого значения»:

f (x) dx = (Площадь над осью x) — (Площадь под осью x)

Добавление функций

Интеграл от f + g равен интегралу от f плюс интеграл от g :

f (x) + g (x) dx =

ф (х) dx +

г (x) dx

Реверсирование интервала

Изменение направления интервала на противоположное дает отрицательное значение исходного направления.

Интервал нулевой длины

Когда интервал начинается и заканчивается в одном и том же месте, результат равен нулю:

Добавление интервалов

Мы также можем сложить два соседних интервала вместе:

Сводка

Определенный интеграл между a и b — это неопределенный интеграл при b минус неопределенный интеграл при a .

Исчисление I — Вычисление определенных интегралов

Показать мобильное уведомление Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон).Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 5-7: Вычисление определенных интегралов

В этом разделе мы сосредоточимся на том, как мы фактически вычисляем определенные интегралы на практике.б = F \ влево (б \ вправо) — F \ влево (а \ вправо) \]

Чтобы увидеть доказательство этого, см. Раздел «Доказательство различных интегральных свойств» в главе «Дополнительные возможности».

Напомним, что когда мы говорим об антипроизводной функции, на самом деле мы говорим о неопределенном интеграле для функции. Итак, чтобы вычислить определенный интеграл, первое, что мы собираемся сделать, это вычислить неопределенный интеграл для функции.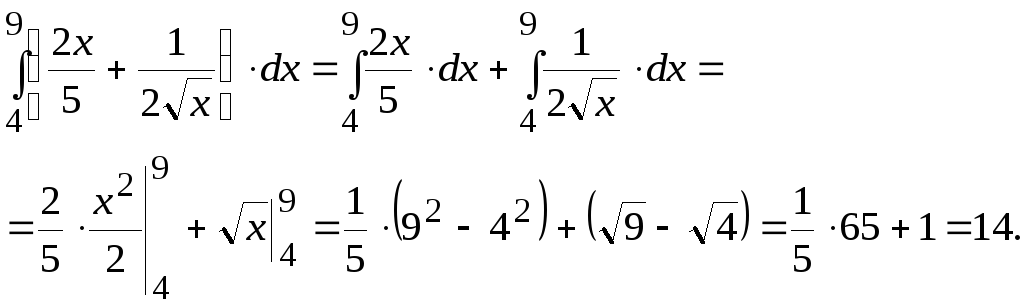 {- 2}} \, dy}} & = \ left .3} — \ frac {1} {1}} \ right) \\ & = \ frac {8} {3} — \ frac {1} {2} — \ frac {1} {3} + 1 \\ & = \ frac {{17}} {6} \ end {align *} \]

Помните, что оценка всегда выполняется в порядке оценки на верхнем пределе минус оценка на нижнем пределе. Также будьте очень осторожны со знаками минус и круглыми скобками. Их очень легко забыть или неправильно использовать и получить неправильный ответ.

Также обратите внимание, что для облегчения вычисления мы немного переписали неопределенный интеграл.{- 2}} \, dy}} \) Показать решение

Этот интеграл здесь, чтобы указать на важность. Напомним, что для того, чтобы мы могли сделать интеграл, подынтегральное выражение должно быть непрерывным в пределах диапазона. В этом случае второй член будет иметь деление на ноль в точке \ (y = 0 \), и поскольку \ (y = 0 \) находится в интервале интегрирования, , т.е. , он находится между нижним и верхним пределом, это подынтегральное выражение равно не непрерывна в интервале интегрирования, поэтому мы не можем сделать этот интеграл.

Обратите внимание, что эта проблема не помешает нам выполнить интеграл в (b), поскольку \ (y = 0 \) не находится в интервале интегрирования.

Итак, что мы узнали из этого примера?

Во-первых, чтобы получить определенный интеграл, первое, что нам нужно сделать, это неопределенный интеграл. Итак, мы не собираемся отказываться от вычисления неопределенных интегралов, они будут в каждом интеграле, который мы будем делать в оставшейся части этого курса, поэтому убедитесь, что вы хорошо умеете их вычислять.

Во-вторых, нам нужно внимательно следить за функциями, которые не являются непрерывными ни в одной точке между пределами интеграции.Также важно отметить, что это будет проблемой только в том случае, если точка (точки) разрыва возникает между пределами интеграции или на самих границах. Если точка разрыва возникает за пределами интегрирования, интеграл все еще может быть вычислен.

В следующих наборах примеров мы не будем уделять слишком много внимания проблемам непрерывности или отсутствию проблем непрерывности, если это не влияет на оценку интеграла. Не позволяйте этому убедить вас, что вам не нужно беспокоиться об этой идее.{{\ pi} / {3} \;} \\ & = — 2 \ cos \ left ({\ frac {\ pi} {3}} \ right) — 5 \ sin \ left ({\ frac {\ pi } {3}} \ right) — \ left ({- 2 \ cos 0 — 5 \ sin 0} \ right) \\ & = — 1 — \ frac {{5 \ sqrt 3}} {2} + 2 \ \ & = 1 — \ frac {{5 \ sqrt 3}} {2} \ end {align *} \]

Сравните этот ответ с предыдущим, особенно с нулевой оценкой. Очень легко выработать привычку записывать ноль при вычислении функции. Это особенно проблема, когда многие из функций, которые мы интегрируем, включают только \ (x \), возведенные в положительные целые числа; эти оценки нулевая конечно.{\, ​​{\ pi} / {4} \;} \\ & = 5 \ left ({\ frac {\ pi} {4}} \ right) — 2 \ sec \ left ({\ frac {\ pi} {4}} \ right) — \ left ({5 \ left ({\ frac {\ pi} {6}} \ right) — 2 \ sec \ left ({\ frac {\ pi} {6}} \ right) )} \ right) \\ & = \ frac {{5 \ pi}} {{12}} — 2 \ sqrt 2 + \ frac {4} {{\ sqrt 3}} \ end {align *} \]

Для оценки напомним, что

\ [\ sec z = \ frac {1} {{\ cos z}} \]

, и поэтому, если мы можем вычислить косинус под этими углами, мы сможем вычислить секанс под этими углами.6} — 10t + \ frac {1} {t} \; dt}} \) Показать решение

Этот интеграл не может быть выполнен. В третьем члене при \ (t = 0 \) есть деление на ноль, а \ (t = 0 \) лежит в интервале интегрирования. Тот факт, что первые два члена могут быть объединены, не имеет значения. Если даже одно слагаемое в интеграле не может быть интегрировано, то и весь интеграл не может быть выполнен.

Итак, на данный момент мы вычислили изрядное количество определенных интегралов. Помните, что большая часть работы по их вычислению — это сначала поиск неопределенного интеграла.{{\, 22}} {{f \ left (x \ right) \, dx}} \) Показать решение

Для этого интеграла обратите внимание, что \ (x = 1 \) не находится в интервале интегрирования, и поэтому нам не нужно беспокоиться об этом в этой части.

Также обратите внимание, что пределы интеграла полностью лежат в диапазоне для первой функции. Для нас это означает, что при выполнении интеграла все, что нам нужно сделать, это вставить первую функцию в интеграл.

Вот интеграл.{{\, 3}} {{f \ left (x \ right) \, dx}} \) Показать решение

В этой части \ (x = 1 \) находится в пределах интегрирования. Это означает, что подынтегральная функция больше не является непрерывной в интервале интегрирования, и это, с нашей точки зрения, сдерживающий фактор. Как отмечалось выше, мы просто не можем интегрировать функции, которые не являются непрерывными в интервале интегрирования.

Кроме того, даже если бы функция была непрерывной при \ (x = 1 \), у нас все еще была бы проблема, заключающаяся в том, что функция на самом деле представляет собой два разных уравнения в зависимости от того, где мы находимся в интервале интегрирования.

Давайте сначала рассмотрим проблему того, что функция не является непрерывной в точке \ (x = 1 \). Как мы увидим, в этом случае, если мы сможем найти способ обойти эту проблему, вторая проблема также будет решена одновременно.

В предыдущих примерах, где у нас были функции, которые не были непрерывными, у нас было деление на ноль, и как бы мы ни старались, мы не можем избавиться от этой проблемы. Деление на ноль — настоящая проблема, и мы действительно не можем ее избежать.{{\, 3}} {{f \ left (x \ right) \, dx}} \]

На каждом из этих интервалов функция непрерывна. Фактически мы можем сказать больше. 2} \ hпространство {0.5} + \ sin \ left (x \ right) \, dx}} = \ cos \ left ({10} \ right) — \ cos \ left (9 \ right) — \ frac {{468559}} {6} = — 78093.09461 \]

Мораль здесь — быть осторожным и не злоупотреблять этими фактами.

Исчисление I — Определение определенного интеграла

Показать мобильное уведомление Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 5-6: Определение определенного интеграла

В этом разделе мы формально определим определенный интеграл и дадим многие свойства определенных интегралов.*} \ right) \ Delta x} \]

Определенный интеграл определяется как предел и сумма, которые мы рассмотрели в предыдущем разделе, чтобы найти чистую площадь между функцией и осью \ (x \). Также обратите внимание, что обозначение для определенного интеграла очень похоже на обозначение для неопределенного интеграла. Причина этого со временем станет очевидной.

Есть также немного терминологии, от которой нам следует избавиться. Число «\ (a \)», которое находится внизу знака интеграла, называется нижним пределом интеграла, а число «\ (b \)» в верхней части знака интеграла называется верхним пределом . 3}}} + \ frac {2}) {n}} \ right)} \ end {align *} \]

Теперь нам нужно взять предел этого.Значит, нам нужно будет «оценить» это суммирование. Другими словами, нам придется использовать формулы, приведенные в обзоре нотации суммирования, чтобы исключить фактическое суммирование и получить формулу для этого общего \ (n \).

Для этого нам нужно признать, что \ (n \) является константой в том, что касается обозначения суммирования. По мере того, как мы перебираем целые числа от 1 до \ (n \) в суммировании, изменяется только \ (i \), и поэтому все, что не является \ (i \), будет постоянным и может быть исключено из суммирования.2}}} \\ & = \ frac {{14}} {3} \ end {align *} \]

Мы видели несколько методов решения этой проблемы с ограничением, поэтому оставим вам проверять результаты.

Вау, это было много работы для довольно простой функции. Есть гораздо более простой способ их оценки, и в конце концов мы до него доберемся. Основная цель этого раздела — разъяснить основные свойства и факты об определенном интеграле. Мы обсудим, как мы вычисляем их на практике, начиная со следующего раздела.{{\, b}} {{f \ left (t \ right) \, dt}} \). Смысл этого свойства в том, чтобы заметить, что, пока функция и пределы совпадают, переменная интегрирования, которую мы используем в определенном интеграле, не повлияет на ответ.

Доказательство свойств 1–4 см. В разделе «Доказательство различных интегральных свойств» в главе «Дополнительные возможности». Свойство 5 доказать непросто, поэтому оно здесь не показано. Свойство 6 не является собственностью в полном смысле этого слова. Это сделано только для того, чтобы признать, что до тех пор, пока функция и ограничения одинаковы, не имеет значения, какую букву мы используем для переменной.{{\, 12}} {{f \ left (x \ right) \, dx}} \). Показать решение

Этот пример в основном является примером свойства 5, хотя в решении также есть несколько вариантов использования свойства 1.

Нам нужно выяснить, как правильно разбить интеграл, используя свойство 5, чтобы мы могли использовать заданные фрагменты информации. Во-первых, заметим, что существует интеграл, в одном из пределов которого стоит «-5». Это не нижний предел, но мы можем использовать свойство 1, чтобы в конечном итоге это исправить.{{\, b}} {{\ left | {f \ left (x \ right) \,} \ right | dx}} \)

См. Доказательство этих свойств в разделе «Доказательство различных интегральных свойств» главы «Дополнительные возможности».

Интерпретации определенного интеграла

Здесь мы можем дать несколько быстрых интерпретаций определенного интеграла.

Во-первых, как мы упоминали в предыдущем разделе, одна из возможных интерпретаций определенного интеграла состоит в том, чтобы дать чистую площадь между графиком \ (f \ left (x \ right) \) и осью \ (x \) на интервал \ (\ left [{a, b} \ right] \).{{\, b}} {{f ‘\ left (x \ right) \, dx}} = f \ left (b \ right) — f \ left (a \ right) \]

— чистое изменение \ (f \ left (x \ right) \) на интервале \ (\ left [{a, b} \ right] \). Другими словами, вычислите определенный интеграл скорости изменения, и вы получите чистое изменение количества. Мы видим, что значение определенного интеграла \ (f \ left (b \ right) — f \ left (a \ right) \) на самом деле дает нам чистое изменение в \ (f \ left (x \ right) \), так что этим утверждением действительно нечего доказывать.{{\, {t_2}}} {{V ‘\ left (t \ right) \, dt}} = V \ left ({{t_2}} \ right) — V \ left ({{t_1}} \ right ) \]

— это чистое изменение объема по мере того, как мы идем от времени \ ({t_1} \) к времени \ ({t_2} \).

Аналогичным образом, если \ (s \ left (t \ right) \) — функция, задающая положение некоторого объекта в момент времени \ (t \), мы знаем, что скорость объекта в любой момент времени \ (t \) равна: \ (v \ left (t \ right) = s ‘\ left (t \ right) \). Следовательно, смещение времени объекта \ ({t_1} \) к времени \ ({t_2} \) составляет

\ [\ int _ {{\, {t_1}}} ^ {{\, {t_2}}} {{v \ left (t \ right) \, dt}} = s \ left ({{t_2}} \ right ) — s \ left ({{t_1}} \ right) \]

Обратите внимание, что в этом случае if \ (v \ left (t \ right) \) одновременно положительно и отрицательно ( i. {{\, v \ left (x \ right)}} {{f \ left (t \ right) \, dt }} = — v ‘\ left (x \ right) f \ left ({v \ left (x \ right)} \ right) \]

Наконец, мы также можем получить версию для обоих пределов, являющихся функциями \ (x \).2}} \ right) \ end {align *} \]

Определенные интегралы

Определенный интеграл функции тесно связан с первообразным и неопределенным интегралом функции. Основное отличие состоит в том, что неопределенный интеграл, если он существует, является вещественным числовым значением, в то время как последние два представляют бесконечное количество функций, которые отличаются только константой. Взаимосвязь между этими понятиями будет обсуждаться в разделе, посвященном фундаментальной теореме исчисления, и вы увидите, что определенный интеграл будет иметь приложения ко многим задачам исчисления.

Развитие определения определенного интеграла начинается с функции f ( x ), которая непрерывна на отрезке [ a, b ]. Данный интервал разбивается на подинтервалы « n », которые, хотя и не обязательно, могут быть взяты равными по длине (Δ x ). Произвольное значение домена, x , _i , выбирается в каждом подынтервале, и определяется его последующее значение функции, f ( x _i ).Определяется произведение каждого значения функции на соответствующую длину подынтервала, и эти произведения « n » складываются для определения их суммы. Эта сумма называется суммой Римана и может быть положительной, отрицательной или нулевой, в зависимости от поведения функции на закрытом интервале. Например, если f ( x )> 0 на [ a, b ], тогда сумма Римана будет положительным действительным числом. Если f ( x ) <0 на [ a, b ], тогда сумма Римана будет отрицательным действительным числом.Сумма Римана функции f ( x ) на [ a, b ] выражается как

Таким образом, сумму Римана можно представить как «сумму n произведений».

Пример 1: Оцените сумму Римана для f ( x ) = x ² на [1,3], используя четыре подинтервала равной длины, где x _i — правое конечная точка на подынтервале и (см. рисунок).

Рисунок 1 Сумма Римана с четырьмя частями.

Поскольку подынтервалы должны иметь одинаковую длину, вы обнаружите, что

Сумма Римана для четырех подинтервалов равна

.

Если количество подинтервалов многократно увеличивать, то в результате длина каждого подынтервала будет становиться все меньше и меньше. Это можно переформулировать следующим образом: если количество подынтервалов неограниченно увеличивается ( n → + ∞), то длина каждого подынтервала приближается к нулю (Δ x → + ∞).Этот предел суммы Римана, если он существует, используется для определения определенного интеграла функции на [ a, b ]. Если f ( x ) определено на закрытом интервале [ a, b ], то определенный интеграл из f ( x ) от a до b определяется как

, если это ограничение выходит за пределы.

Функция f ( x ) называется подынтегральным выражением, а переменная x является переменной интегрирования.Числа a и b называются пределами интегрирования, а a — нижним пределом интегрирования, а b — верхним пределом интегрирования.

Обратите внимание, что символ ∫, используемый с неопределенным интегралом, — это тот же символ, который ранее использовался для неопределенного интеграла функции. Причина этого станет более очевидной в следующем обсуждении фундаментальной теоремы исчисления. Также имейте в виду, что определенный интеграл является уникальным действительным числом и не представляет бесконечное количество функций, которые являются результатом неопределенного интеграла функции.

Вопрос о существовании предела суммы Римана важно рассмотреть, поскольку он определяет, существует ли определенный интеграл для функции на отрезке. Как и в случае с дифференцированием, между непрерывностью и интегрированием существует значительная взаимосвязь, которую можно резюмировать следующим образом: если функция f ( x ) непрерывна на отрезке [ a, b ], то определенный интеграл от f ( x ) на [ a, b ] существует, а f считается интегрируемым на [ a, b ].Другими словами, непрерывность гарантирует, что определенный интеграл существует, но обратное не обязательно верно.

К сожалению, тот факт, что определенный интеграл функции существует на отрезке, не означает, что значение определенного интеграла легко найти.

Некоторые свойства полезны при решении задач, требующих применения определенного интеграла. Некоторые из наиболее распространенных свойств:

1.

2.

3., где c — постоянная

4.

5. Правило суммы:

6. Правило разницы:

7. Если

8. Если

9. Если

10. Если a, b, и c — любые три точки на закрытом интервале, то

11. Теорема о среднем значении для определенных интегралов: если f ( x ) непрерывно на закрытом интервале [ a, b ], то по крайней мере одно число c существует в открытом интервале ( a , b ) такая, что

Значение f ( c ) называется средним или средним значением функции f ( x ) на интервале [ a, b ] и

.

Пример 2: Оценить

Пример 3: Учитывая, что

Пример 4: Учитывая, что

Пример 5 Вычислить

Пример 6: Учитывая, что оценка

Пример 7: Учитывая, что оценка.

Пример 8: Учитывая это, оцените.

Пример 9: При условии, что найти все c значений, которые удовлетворяют теореме о среднем значении для данной функции на отрезке.

По теореме о среднем значении

Поскольку находится в интервале (3,6), заключение теоремы о среднем значении выполняется для этого значения c .

Основная теорема исчисления

Фундаментальная теорема исчисления устанавливает связь между неопределенными и определенными интегралами и вводит методику вычисления определенных интегралов без использования сумм Римана, что очень важно, поскольку вычисление предела суммы Римана может быть чрезвычайно трудоемким и трудным.Утверждение теоремы таково: если f ( x ) непрерывно на интервале [ a, b ], а F ( x ) является любой первообразной f ( x ) на [ a, b ], затем

Другими словами, значение определенного интеграла функции на [ a, b ] — это разность любой первообразной функции, вычисленной на верхнем пределе интегрирования, за вычетом той же первообразной, вычисленной на нижнем пределе интегрирования.Поскольку константы интегрирования одинаковы для обеих частей этой разности, они игнорируются при вычислении определенного интеграла, поскольку они вычитаются и дают ноль. Помня об этом, выберите постоянную интегрирования равной нулю для всех определенных интегральных вычислений после примера 10.

Пример 10: Оценить

Поскольку общая первообразная x ² равна (1/3) x ³ + C , вы обнаружите, что

Пример 11: Оценить

Поскольку первообразная sin x — cos x , вы обнаружите, что

Пример 12: Оценить

(Потому что (первообразная от, и вы обнаружите, что

Пример 13: Оценить

Поскольку первообразная x ² — 4 x + 1 — это (1/3) x ³ — 2 x ² + x , вы обнаружите, что

Определенная интегральная оценка

Многочисленные методы, которые можно использовать для вычисления неопределенных интегралов, также могут использоваться для вычисления определенных интегралов. Методы подстановки и замены переменных, интегрирования по частям, тригонометрических интегралов и тригонометрической подстановки проиллюстрированы в следующих примерах.

Пример 14: Оценить

Использование метода замены с

пределы интегрирования могут быть преобразованы из значений x в соответствующие им значения u . Когда x = 1, u = 3 и когда x = 2, u = 6, вы обнаружите, что

Обратите внимание, что когда метод подстановки используется для вычисления определенных интегралов, нет необходимости возвращаться к исходной переменной, если пределы интегрирования преобразуются в новые значения переменных.

Пример 15: Оценить

Используя метод подстановки с u = sin x + 1, du = cos x dx , вы обнаружите, что u = 1, когда x = π, и u = 0, когда x = 3π / 2; следовательно,

Обратите внимание, что вам никогда не приходилось возвращаться к тригонометрическим функциям в исходном интеграле для вычисления определенного интеграла.

Пример 16: Оценить

Использование интеграции по частям с

вы обнаружите, что

Пример 17: Оценить

Использование интеграции по частям с

Пример 18: Оценить

Пример 19: Оценить.

Пример 20: Оценить.

Поскольку подынтегральное выражение содержит форму a ² + x ² ,

Рисунок 2 Диаграмма для примера 20.

Пример 21: Оценить

Поскольку радикал имеет вид

Рисунок 3 Диаграмма для примера 21. b`

`= F (б) -F (а)`

где

`F (x)` — интеграл от `f (x)`;

`F (b)` — значение интеграла на верхнем пределе, `x = b`; и

`F (a)` — значение интеграла на нижнем пределе, `x = a`.

Это выражение называется определенным интегралом . Обратите внимание, что это не включает константу интеграция и дает нам определенное значение (число) при конец расчета.(n + 1)) / (n + 1) + K` (если `n ≠ -1`)

Когда мы заменяем, мы меняем переменную, поэтому мы не можем используйте одинаковые верхний и нижний пределы. Мы можем либо:

• Выполните задачу как неопределенный интеграл сначала , затем использовать верхний и нижний пределы позже
• Решите проблему, используя новую переменную и новые верхний и нижний пределы
• Показать правильную переменную для верхнего и нижнего предела во время фазы замены.4] `

  `= 0`, как и раньше.

  Этот второй подход будет весьма полезен позже, когда замены становятся более сложными (например, тригонометрические замена).

  Заявление: Работа

  
  Эйнштейн катается на велосипеде.

  В физика, работа выполняется, когда сила, действующая на объект вызывает смещение. (Например, езда на велосипеде.)

  Если сила непостоянна, мы должны использовать интеграцию найти проделанную работу.4] `

  `= 1/24 [16-1]`

  `= 15/24`

  `= 5/8`

  Таким образом, требуется среднее значение 0,625 единиц. Это согласуется с нашей предыдущей оценкой.

  Приложение: смещение

  Если мы знаем выражение, v , для скорость в терминах t , время, мы можем найти смещение (записано s ) движущегося объекта от времени t = a до времени t = b путем интегрирования, как показано ниже:

  `s = int_a ^ bv \ dt`

  Пример 7

  Найдите смещение объект от т = 2 до т = 3, если скорость объект в момент времени t выдается

  `v = (t ^ 2 + 1) / ((t ^ 3 + 3t) ^ 2`

  Ответ

  Чтобы найти смещение, нам нужно оценить:

  `int_2 ^ 3 (t ^ 2 + 1) / ((t ^ 3 + 3t) ^ 2) dt`

  Положим `u = t ^ 3 + 3t`, тогда` du = (3t ^ 2 + 3) dt = 3 (t ^ 2 + 1) dt`

  Так `(du) / 3 = (t ^ 2 + 1) dt`

  Итак имеем:

  `int_2 ^ 3 (t ^ 2 + 1) / ((t ^ 3 + 3t) ^ 2) = 1 / 3int_ (t = 2) ^ (t = 3) 1 / u ^ 2du`

  `= 1 / 3int_ (t = 2) ^ (t = 3) u ^ -2du`

  `= -1 / 3 [1 / u] _ (t = 2) ^ (t = 3)`

  `= -1 / 3 [1 / (t ^ 3 + 3t)] _ 2 ^ 3`

  `= -1 / 3 [1 / (3 ^ 3 + 3 (3)) — 1 / (2 ^ 3 + 3 (2))]`

  `= -1 / 3 [1 / 36-1 / 14]`

  `= 0.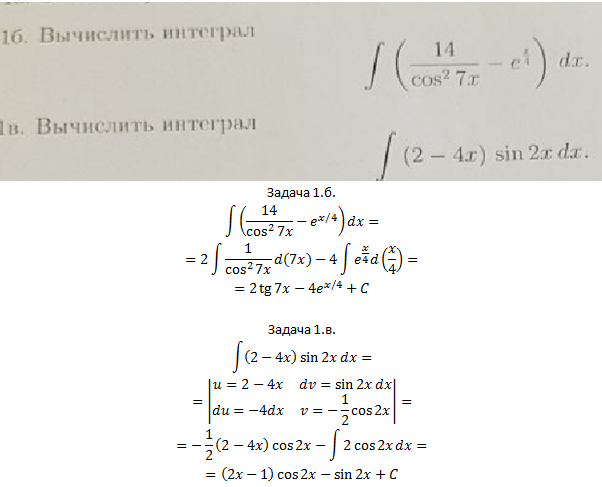 2 + 1`

  Тогда найдем дифференциал:

  `du = 2x \ dx`

  Затем мы могли бы перейти к нахождению интеграла, как мы делали в примерах выше, заменив `2x \ dx` на` du` , а часть квадратного корня на `sqrt u`.2 + 1) \ dx`

  ( Примечание: Исторически все определенные интегралы аппроксимировались численными методами до того, как Ньютон и Лейбниц разработали методы интегрирования, которые мы изучили до сих пор в этой главе.)

  Мы можем использовать два различных численных метода для вычисления интеграла:

  Мы встречаемся с этими методами в следующих двух разделах.

  Определенные интегралы — Исчисление 2

  Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

  Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как как ChillingEffects.org.

  Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

  Чтобы отправить уведомление, выполните следующие действия:

  Вы должны включить следующее:

  Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

  Отправьте жалобу нашему уполномоченному агенту по адресу:

  Чарльз Кон Varsity Tutors LLC
  101 S. Hanley Rd, Suite 300
  St. Louis, MO 63105
  

  Или заполните форму ниже:

  4.7: Определенные интегралы подстановкой.

  Замена определенных интегралов

  Подстановку можно использовать и с определенными интегралами. Однако использование подстановки для вычисления определенного интеграла требует изменения пределов интегрирования.3) \, dx. \]

  Подсказка

  Используйте процесс из примера для решения проблемы.

  Ответ

  \ (\ dfrac {2} {3π} ≈0,2122 \)

  Замена может быть только одним из методов, необходимых для вычисления определенного интеграла. Все свойства и правила интегрирования применяются независимо, и, возможно, потребуется переписать тригонометрические функции с использованием тригонометрического тождества, прежде чем мы сможем применить замену.2} \).

  Подсказка

  Следуйте процедурам из примера для решения проблемы.

  Ответ

  \ [\ dfrac {π} {8} \]

  Как упоминалось в начале этого раздела, экспоненциальные функции используются во многих реальных приложениях. Число e часто ассоциируется со сложным или ускоряющимся ростом, как мы видели в предыдущих разделах о производной.Хотя производная представляет собой скорость изменения или скорость роста, интеграл представляет собой общее изменение или общий рост. Давайте посмотрим на пример, в котором интеграция экспоненциальной функции решает обычное бизнес-приложение.

  Функция цена-спрос сообщает нам о взаимосвязи между объемом спроса и ценой продукта. Как правило, цена снижается по мере увеличения объема спроса. Функция предельная цена-спрос является производной функции цена-спрос и сообщает нам, насколько быстро изменяется цена на данном уровне производства.Эти функции используются в бизнесе для определения эластичности спроса по цене и для помощи компаниям в определении прибыльности изменения уровня производства.

  Пример \ (\ PageIndex {4} \): поиск уравнения цены и спроса

  Найдите уравнение цены и спроса для определенной марки зубной пасты в сети супермаркетов, когда спрос составляет 50 тюбиков в неделю по цене 2,35 доллара за тюбик, учитывая, что предельная цена — функция спроса, \ (p ′ (x), \) для x количество пробирок в неделю, дается как

  \ [p ‘(x) = — 0.