Урок 21. показательная функция — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №21. Показательная функция.
Перечень вопросов, рассматриваемых в теме:
— какая функция называется показательной;
— какие свойства имеет показательная функция в зависимости от ее основания;
— какой вид имеет график показательной функции в зависимости от ее основания;
— примеры реальных процессов, описываемых показательной функцией.
Глоссарий по теме
Функция вида , a>0, а≠1 называется показательной функцией с основанием а.
Функция называется монотонно возрастающей на промежутке <a; b>, если (чем больше аргумент, тем больше значение функции).
Функция называется монотонно убывающей на промежутке <a; b>, если (чем больше аргумент, тем меньше значение функции).
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. учреждений: базовый и профил. уровни 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс.310-314, сс. 210-216.
Открытые электронные ресурсы:
http://fcior.edu.ru/ — Федеральный центр информационно-образовательных ресурсов
http://school-collection.edu.ru/ — Единая коллекция цифровых образовательных ресурсов
Теоретический материал для самостоятельного изучения
1. Определение, свойства и график показательной функции
Определение:
Функция вида y=ах, a>0, а≠1 называется показательной функцией с основанием а.
Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.
Для положительного основания значение степени
ах можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.
Сформулируем основные свойства показательной функции.
1. Область определения.
Как мы уже сказали, степень ах для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D(y)=R.
2. Множество значений.
Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.
Множество значений показательной функции Е(y)=R+, или Е(y)=(0; +∞).
3. Корни (нули) функции.
Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.
4. Монотонность.
При a>1 функция монотонно возрастает.
При 0<a<1 функция монотонно убывает.
5. При любом значении а значение функции y (0) = а0 =1.
6. График функции.
При a>1
Рисунок 1 – График показательной функции при a>1
При 0<a<1
Рисунок 2 – График показательной функции при 0<a<1
Независимо от значения основания а график функции имеет горизонтальную асимптоту y=0. Для 0<a<1 при х стремящемся к плюс бесконечности, для a>1 при х стремящемся к минус бесконечности.
Для 0<a<1 при х стремящемся к плюс бесконечности, для a>1 при х стремящемся к минус бесконечности.
2. Рассмотрим пример исследования функции y=–3х+1.
Решение:
1) Область определения функции – любое действительное число.
2) Найдем множество значений функции.
Так как 3х>0, то –3х<0, значит,
–3х+1<1, то есть множество значений функции y=–3х+1 представляет собой промежуток (-∞; 1).3) Так как функция y=3х монотонно возрастает, то функция y=–3х монотонно убывает. Значит, и функция y=–3х+1 также монотонно убывает.
4) Эта функция будет иметь корень: –3х+1=0, 3х=1, х=0.
5) График функции
Рисунок 3 – График функции y=–3х+1
6) Для этой функции горизонтальной асимптотой будет прямая y=1.
3. Примеры процессов, которые описываются показательной функцией.
1) Рост различных микроорганизмов, бактерий, дрожжей и ферментов описывает формула: N= N0·akt, N– число организмов в момент времени t, t – время размножения, a и k – некоторые постоянные, которые зависят от температуры размножения, видов бактерий. Вообще это закон размножения при благоприятных условиях (отсутствие врагов, наличие необходимого количества питательных веществ и т.п.). Очевидно, что в реальности такого не происходит.
2) Давление воздуха изменяется по закону: P=P0·a-kh, P– давление на высоте h, P0 – давление на уровне моря, h – высота над уровнем моря, a и k – некоторые постоянные.
3) Закон роста древесины: D=D0·akt, D– изменение количества древесины во времени, D0 – начальное количество древесины, t – время, a и k – некоторые постоянные.
4) Процесс изменения температуры чайника при кипении описывается формулой: T=T0+(100– T0)e-kt.
5) Закон поглощения света средой: I=I0·e-ks, s– толщина слоя, k – коэффициент, который характеризует степень замутнения среды.
6) Известно утверждение, что количество информации удваивается каждые 10 лет. Изобразим это наглядно.
Примем количество информации в момент времени t=0 за единицу. Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т.д.
Если предположить, что поток информации изменялся по тому же закону до того года, который принят за начальный, то будем двигаться по оси абсцисс влево от начала координат и над значениями аргумента -10, -20 и т.д. будем наносить на график значения функции уже в порядке убывания — уменьшая каждый раз вдвое.
Рисунок 4 – График функции y=2х – изменение количества информации
Закон изменения количества информации описывается показательной функцией y=2х.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Выберите показательные функции, которые являются монотонно убывающими.
- y=3x-1
- y=(0,4)x+1
- y=(0,7)-х
- y=
- y=3-2х
- y=102x +1
Решение:
Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы. Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: , используя свойство степеней.
Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:
2) 4) 5)
Пример 2.
Найдите множество значений функции y=3x+1– 3.
Решение:
Рассмотрим функцию.
Так как 3x+1>0, то 3x+1– 3>–3, то есть множество значений:
(– 3; +∞).
Пример 3.
Найдите множество значений функции y=|2x– 2|
Рассмотрим функцию.
Ответ: \(x=\left[-1;0\right]\)
Показательная функция
Основные сведения
Показательной функцией назыввается функция вида y = ax, где a > 0 и a ≠ 1.
График функции имеет следующий вид:
Рассмотрим свойства функции:
- Областью определения функции является множество всех действительных чисел R.
- Множеством значений функции являются все положительные числа, т. е. промежуток E(y): (0; +∞).
- Наименьшего и наибольшего значений функция не имеет.
- Функция не является ни нечетной, ни четной. Имеет общий вид.
- Функция непериодическая.
- График функции пересекает координатную ось Oy в точке (0; 1).
- Функция не имеет нулей.
- при a > 1 функция возрастает на всей числовой прямой; при 0 < a < 1 функция убывает на множестве R.

- Функция принимает положительные значения на всей области определения.
Примеры решения задач
Задача 1.
В одной координатной плоскости построить графики функций:
- y=2x
- y=3x
- y=5x
- y=10x
Решение.
Для начала построим график функции y=2x. Для этого найдем значения функции при x = 0, ±1, ±2, ±3.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y(x) | 1 | 2 | 4 | 8 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует и большее значение функции у. Функция y = 2x возрастает на всей области определения D(y)=R, так как основание функции 2 > 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание a (если a>1) показательной функции y = ax, тем ближе расположена кривая к оси Оу.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Задача 2.
В одной координатной плоскости построить графики функций:
Решение.
Для начала построим график функции . Для этого найдем значения функции при x = 0, ±1, ±2, ±3.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y(x) | 8 | 4 | 2 | 1 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует меньшее значение функции y. Функция убывает на всей своей области определения: D(y)=R, так как основание функции 0 < < 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать любое значение: D(y)=R, при этом область значений функции: E(y)=R+.
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.
Чем меньше основание а (при 0 < a < 1) показательной функции y = ax, тем ближе расположена кривая к оси Оу.
Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Задание 3.
Найти область значений функции:
- y = -2x
- y = +1
- y = 3x+1 — 5
Решение.

1. y = -2x
Область значений показательной функции y = 2x – все положительные числа, т. е. 0 < 2x < +∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем: -∞ < 2x < 0.
Ответ: E(y): (-∞; 0).
2. y = +1
0 < < +∞. Тогда, прибавляя ко всем частям двойного неравенства число 1, получаем:
0 + 1 < +1 < +∞ + 1
1 < +1 < +∞
Ответ: E(y): (1; +∞).
3. y = 3x+1 — 5.
Запишем функцию ввиде: y = 3·3x — 5, тогда:
0 < 3x < +∞
умножаем все части двойного неравенства на 3:
0·3 < 3x·3 < (+∞)·3
0 < 3x·3 < +∞
из всех частей двойного неравенства вычитаем 5:
0 — 5 < 3x·3 — 5 < +∞ — 5
-5 < 3x·3 — 5 < +∞
Ответ: E(y): (-5; +∞).
«Показательная функция, ее свойства.
 Простейшие показательные уравнения и неравенства»
Простейшие показательные уравнения и неравенства»МОУ ИРМО «Вечерняя (сменная) общеобразовательная школа»
Открытый урок по алгебре и началам анализа в 12Д классе
Тема: «Показательная функция, ее свойства и график.
Решение простейших показательных уравнений и неравенств»
Учитель первой квалификационной категории, Земляничкина Тамара Михайловна
Тема урока:
«Показательная функция, ее свойства.
Простейшие показательные уравнения и неравенства»
Класс-12Д Учитель-Земляничкина Тамара Михайловна
Дата проведения:06.10.2015г
Тип урока: Урок изучения нового материала.
Оборудование урока: таблицы по алгебре, компьютер , проектор, карточки.
Цели урока:
*Образовательные:
знать график показательной функции и ее свойства и умение применять свойства при решении простейших уравнений и неравенств.
*Развивающие:
развивать умения решать простейшие показательные уравнения и неравенства . Развивать умение рассуждать по аналогии. Прививать интерес к предмету.
*Воспитательные:
формировать культуру общения, уважение друг к другу, культуру математической речи.
План урока:
1.Актуализация знаний.
5.Рефлексия.
6.Домашнее задание.
1.Актуализация знаний
Представьте в виде степени ( проверить ответы)
1/4= 0.25= 1.21= корень 2-й степени из числа 6
1/25= 0.04= 2.25= корень третьей степени из числа 36
1/64= 0.027= 0.125= корень пятой степени из числа 81
. Вычислить:
Повторить свойства степени по таблице и решить примеры на доске. 1. ; б) ; в) ; г) ; д) ; е) ; ж) ; з)
Дополнительные задания для сильных учащихся
2. . ; б) ; в) ; г)
3.
.
.2.Изучение н/м (при обЪяснении использую видеоурок)
На данном уроке мы рассмотрим показательную функцию, ее график и основные свойства. Также научимся решать простейшие показательные уравнения и неравенства.
Также научимся решать простейшие показательные уравнения и неравенства.
1. Опреедление показательной функции, свойства, графики
Рассмотрим основное определение.
Функцию вида , где и называют показательной функцией.
Например: и т. д.
Рассмотрим первый случай, когда основание степени больше единицы: :. График показательной функции, основание степени больше единицы
. Основные свойства данного семейства функций:
Область определения: ;
Область значений: ;
Функция возрастает, т. е. большему значению аргумента соответствует большее значение функции;
Рассмотрим второй случай, когда основание степени меньше единицы :
Например: и т. д.
График показательной функции, основание степени меньше единицы
График показательной функции, основание степени меньше единицы
Свойства данного семейства функций:
Область определения: ;
Область значений: ;
Функция убывает, т. е. большему значению аргумента соответствует меньшее значение функции;
е. большему значению аргумента соответствует меньшее значение функции;
2. Решение элементарных показательных уравнений и неравенств
Решение показательных уравнений и неравенств основывается на свойствах показательной функции.
Пример 1 – решить уравнение:
а)
Ответ: , т. к. показательная функция принимает строго положительные значения.
б)
Ответ: , т. к. показательная функция принимает строго положительные значения.
Пример 2 – решить неравенство:
а)
Ответ: , т. к. показательная функция принимает строго положительные значения.
б)
Ответ: , т. к. показательная функция принимает строго положительные значения.
3. Простейшие показательные уравнения и неравенствав общем виде, конкретные примеры
Рассмотрим простейшие уравнения и неравенства на графике:
а)
б) ,
в) аналогично решить неравенство с основанием 1/3
функция монотонно возрастает на всей области определения
Сделаем вывод:
Рассмотрим простейшие показательные уравнения в общем виде.
Равенство показателей степени при равных основаниях обусловлено свойством показательной функции, а именно ее монотонностью. Это означает, что каждое свое значение функция приобретает при единственном значении аргумента.
Таким образом, получаем методику решения показательных уравнений:
Уравнять основания степеней;
Приравнять показатели степеней;
Рассмотрим простейшие показательные неравенства в общем виде:
* Монотонное возрастание функций данного семейства является ключом к решению показательных неравенств, при условии, что основание степени больше единицы.
*Монотонное убывание функций данного семейства является ключом к решению показательных неравенств, при условии, что основание степени меньше единицы, но больше нуля.
*Методика решения подобных неравенств:
1. Уравнять основания степеней.
2. Сравнить показатели, изменив знак неравенства.
Примеры решения показательных уравнений:
1.
2.
3.
Примеры решения показательных неравенств по учебнику № 466
3.Закрепление . Самостоятельная работа
а) решить уравнения по учебнику № 460 б) решить неравенства по учебнику № 466
4. Итоги урока : Все учащиеся справились с работой.
Итак, мы рассмотрели показательную функцию, ее график и свойства, научились решать простейшие показательные уравнения и неравенства, рассмотрели простейшие показательные уравнения и неравенства в общем виде. На следующем уроке мы рассмотрим приемы решений показательных уравнений и неравенств.
С самостоятельной работой все справились.
5.Рефлексия : Молодцы, все работали хорошо. Какие вопросы вы хотели бы задать?
Урок закончен ,всем спасибо за урок.
6.Домашнее задание
1. Алгебра и начала анализа, 10–11 класс (А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын) 2012г п 35 п36, № 446, 461;467
Колмогоров, А.М. Абрамов, Ю.П. Дудницын) 2012г п 35 п36, № 446, 461;467
Решить уравнение:
а) ; б) ; в) ; г)
Список литературы
Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Mathematics-repetition.com (Источник).
Terver.ru (Источник).
Egesdam.ru (Источник).
Методическая разработка урока (КСП) «Показательная функция»
Қазақстан Республикасының Білім және ғылым министрлігі
Министерство образования и науки Республики Казахстан
ШҚО Білім басқармасы
Управление образования ВКО
«Шығыс Қазақстан технология колледжі» КМҚК
КГКП «Восточно-Казахстанский технологический колледж»
Утверждаю
Методист
_____________ Бекбаева К. Ж
Ж
« ____» _____________20___г.
Разработка
открытого урока по математике
«Ох, уж эта экспонента»
(«Показательная функция, ее график и свойства»)
Преподаватель
Васильева Г.П.
2020
Методическая разработка
открытого урока по математике «Показательная функция, ее свойства и график»
подготовила преподаватель Васильева Г. П.
П.
Пояснительная записка
Тема «Показательная функция» — это классическая тема курса алгебры и начал анализа. Изучение показательной функции предоставляет большие возможности обогатить знания учащихся о функциях вообще, о способах их задания, о связи способа задания функции с ее свойствами. На примере показательной функции можно развить представления о функциях как о модели процессов и закономерных связей явлений.
Тема «Показательная функция» тесно связана с темами «Степени с различными показателями», «Степенная функция», как бы обобщает предметное содержание понятия степень и в тоже время является ступенькой перехода к теме «Логарифмы»
Основная дидактическая единица данной темы -определение
показательной функции, которое формулируется на основе имеющихся у учащихся
знаний о понятии степени. Обоснование свойства монотонности (возрастание,
убывание) также дается на основе ранее изученного материала и иллюстрируется с
использованием частных примеров.
Знания определения и свойств показательной функции будут применены при решении показательных уравнений и неравенств.
Представленный урок – это урок изучения новой темы, на котором в ходе фронтальной работы, учащиеся формулируют определение показательной функции, а затем, выполняя практическую работу в парах (или группах), исследуют функцию, предварительно построив график. Для построения графиков функции предлагается использование программы Excel и графического редактора Desmos Можно использовать любую другую программу для построения графиков, например, Advanced Grapher, а так же построить графики в тетрадях, но построение «вручную» занимает больше времени.
На уроке будет использованы элементы технологий проблемного, адаптивного и витагенного
обучения, КСО и обучения в сотрудничестве – коллективный разбор задач,
совместное выполнение практической работы (в группах). При выполнении
практического построения графиков использована уровневая дифференциация.
Проведение паузы-релаксации реализует применение здоровьесберегающих
технологий.
Формулирование темы занятия предполагается осуществить через побуждающий от проблемной ситуации диалог. Для поддержания внимания использован прием «отсроченная отгадка» и связь с современностью.
Для развития самостоятельности, логического мышления студентов предлагаются проблемно-поисковые ситуации, выполнение нестандартных заданий.
В целях демонстрации связей математики с другими предметами, на уроке будет показано, что само понятие показательной функции и, вытекающее из него, понятие экспоненциальной функции имеют большое практическое приложение, так как описывают законы природы, техники и общества. И это дает возможность формирования у учащихся целостной картины окружающего мира и развития познавательного интереса к математике как науке.
С целью формирования у учащихся представлений о математике как части
общечеловеческой культуры, использованы исторические сведения о числе е и
высказывания ученых о значении математики и, в частности, показательных
функций в исследованиях окружающего мира.
Для проведения контроля уровня понимания изучаемого материала используется техника «Кубик Блюма». Формативное оценивание реализовано в виде выполнения заданий по образцу и тестирования с самооценкой.
Ход урока сопровождается демонстрацией мультимедийной презентацией, что дает возможность наглядно представить материал по теме, оперативно предъявлять задания, корректировать результаты их выполнения и обеспечивает визуальный контроль результатов. Яркое представление материала рассчитано на удержание внимания учащихся при изучении темы, анимационные эффекты помогают более понятно продемонстрировать решения задач. Для более быстрого запоминания понятий, свойств и особенностей решения используется выделение цветом.
Функции и Графики — сайт по математике и не только!!! ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ Всё о Математических функциях и их графиках…
|
Экспоненциальная функция — формула, свойства, график, правила
Экспоненциальная функция — это тип математической функции, которая помогает найти рост или уменьшение населения, денег, цен и т. д., которые растут или уменьшаются экспоненциально. Джонатан читал новостную статью о последних исследованиях роста бактерий. Он читал, что был проведен эксперимент с одной бактерией. После первого часа бактерия удвоилась, и их стало две. После второго часа число было четыре.С каждым часом количество бактерий увеличивалось. Он думал, каково будет количество бактерий через 100 часов, если эта закономерность сохранится.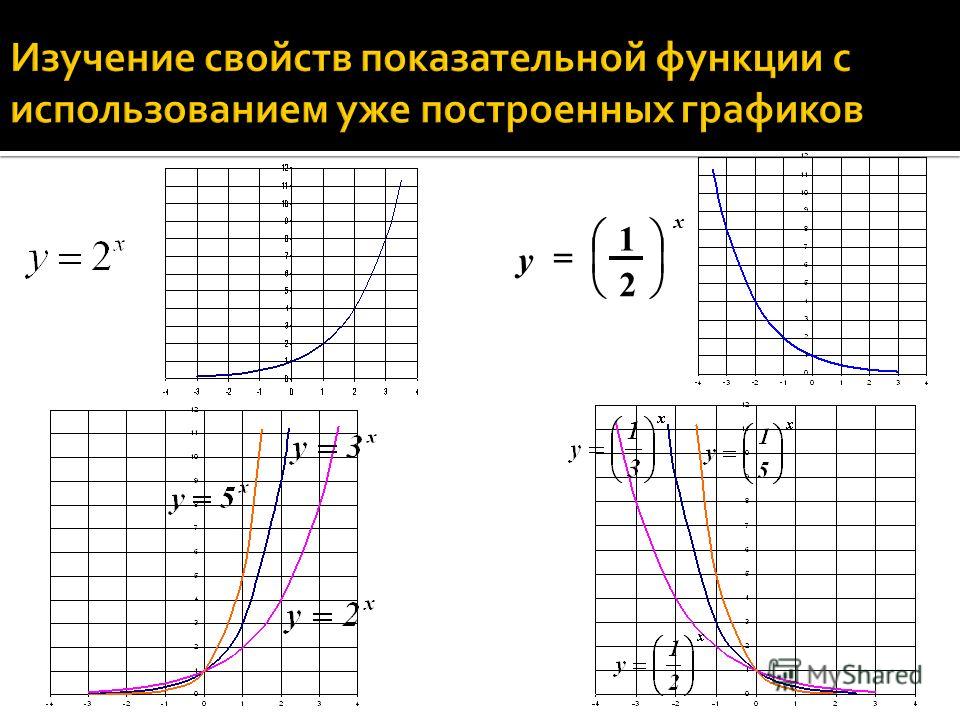 Когда он спросил своего учителя о том же, ответом было понятие экспоненциальной функции.
Когда он спросил своего учителя о том же, ответом было понятие экспоненциальной функции.
Давайте узнаем больше об экспоненциальной функции, а также о ее определении, уравнении, графиках, экспоненциальном росте, экспоненциальном затухании и т. д.
Что такое экспоненциальная функция?
Экспоненциальная функция, как следует из ее названия, включает в себя показатели степени.Но обратите внимание, что экспоненциальная функция имеет константу в качестве основания и переменную в качестве ее показателя, но не наоборот (если функция имеет переменную в качестве основания и константу в качестве показателя степени, то это степенная функция, а не функция). экспоненциальная функция). Показательная функция может быть представлена в одной из следующих форм.
Определение экспоненциальной функции
В математике экспоненциальная функция — это функция формы f (x) = a x , где «x» — переменная, а «a» — константа, которая называется основанием функции и должна быть больше, чем 0.
Примеры экспоненциальной функции
Вот несколько примеров экспоненциальной функции.
- f(x) = 2 х
- f(x) = (1/2) х
- f(x) = 3e 2x
- f(x) = 4 (3) -0,5x
Формула экспоненциальной функции
Базовая экспоненциальная функция по определению имеет вид f(x) = b x , где b — константа, а x — переменная.Одной из популярных экспоненциальных функций является f(x) = e x , где e — «число Эйлера», а e = 2,718… Если мы расширим возможности различных экспоненциальных функций, экспоненциальная функция может включать в себя постоянная как кратная переменной по своей мощности. т. е. экспоненциальная функция также может иметь вид f(x) = e kx . Кроме того, он также может иметь вид f(x) = p e kx , где p — константа. Таким образом, экспоненциальная функция может быть в одной из следующих форм.
- f(x) = b х
- f(x) = аб х
- f(x) = аб сх
- f(x) = е х
- f(x) = e kx
- f(x) = p e kx
Здесь, кроме ‘x’, все остальные буквы являются константами, ‘x’ — переменная, а f(x) — экспоненциальная функция относительно x. Также обратите внимание, что основание каждой экспоненциальной функции должно быть положительным числом.т. е. в приведенных выше функциях b > 0 и e > 0. Также b не должно быть равно 1 (если b = 1, то функция f(x) = b x становится f(x) = 1 и в этом случае функция является линейной, но НЕ экспоненциальной).
Экспоненциальная функция возникает всякий раз, когда значение величины увеличивается при экспоненциальном росте и уменьшается при экспоненциальном затухании. Мы можем увидеть больше различий между экспоненциальным ростом и спадом вместе с их формулами в следующей таблице.
| Экспоненциальный рост | Экспоненциальный спад |
|---|---|
При экспоненциальном росте величина сначала медленно увеличивается, а затем быстро увеличивается. | При экспоненциальном распаде величина сначала очень быстро убывает, а затем медленно. |
| Формулы экспоненциального роста используются для моделирования роста населения, моделирования сложных процентов, определения времени удвоения и т. д. | Экспоненциальный распад полезен для моделирования распада населения, определения периода полураспада и т. д. |
| График функции экспоненциального роста увеличивается. | График функции в экспоненциальном росте убывает. |
При экспоненциальном росте функция может иметь вид:
Здесь b = 1 + r ≈ e k . | При экспоненциальном затухании функция может иметь вид:
Здесь b = 1 — r ≈ e — k . |
В приведенных выше формулах
- a (или) P\(_0\) = начальное значение
- r = Скорость роста
- k = константа пропорциональности
- x (или) t = время (время может быть в годах, днях или (или) месяцах. Все, что мы используем, должно быть согласованным во всей задаче).\infty\) x n /n! = (1/1) — (1/1) + (1/2) — (1/6) + …
Правила экспоненциальной функции
Правила экспоненциальной функции такие же, как правила экспоненты. Вот некоторые правила экспоненты.
- Закон нулевой степени: a 0 = 1
- Закон произведения: a m × a n = a m+n
- Закон частного: a m /a n = a m-n
- Закон Силы Силы: (a m ) n = a mn
- Закон мощности продукта: (ab) m = a m b m
- Закон степени частного: (a/b) m = a m /b m
- Закон отрицательного показателя степени: a -m = 1/a m
Помимо этого, иногда нам нужно использовать формулу преобразования логарифмической формы в экспоненциальную, которая выглядит следующим образом:
- б х = а ⇔ log\(_b\) а = х
Свойство равенства экспоненциальной функции
Согласно свойству равенства показательной функции, если две показательные функции с одним и тем же основанием одинаковы, то их показатели также одинаковы.
 то есть
то естьб \(х_1\) = б \(х_2\) ⇔ \(х_1\) = \(х_2\)
График экспоненциальной функции
Мы можем понять процесс построения графика экспоненциальной функции, взяв несколько примеров. Построим график двух функций f(x) = 2 x и g(x) = (1/2) x . Чтобы построить график каждой из этих функций, мы построим таблицу значений с некоторыми случайными значениями x, нанесем точки на график, соединим их кривой и продолжим кривую на обоих концах.
Вот таблица значений, которые используются для построения графика экспоненциальной функции f(x) = 2 x .
Вот таблица значений, которые используются для построения графика экспоненциальной функции g(x) = (1/2) x .
Примечание: Из двух приведенных выше графиков видно, что f(x) = 2 x увеличивается, тогда как g(x) = (1/2) x уменьшается. Таким образом, график показательной функции f(x) = b x .

- увеличивается, когда b > 1
- уменьшается, когда 0 < b < 1
Домен и диапазон экспоненциальной функции
Мы знаем, что область определения функции y = f(x) — это множество всех значений x (входных данных), где ее можно вычислить, а диапазон — это множество всех значений y (выходных данных) функции.Из графиков f(x) = 2 x и g(x) = (1/2) x в предыдущем разделе видно, что экспоненциальную функцию можно вычислить при всех значениях x. Таким образом, областью определения экспоненциальной функции является множество всех действительных чисел (или) (-∞, ∞). Диапазон экспоненциальной функции можно определить по горизонтальной асимптоте графика, скажем, y = d, и по тому, находится ли график выше y = d или ниже y = d. Таким образом, для экспоненциальной функции f(x) = ab x ,
- Домен — это множество всех действительных чисел (или) (-∞, ∞).
- Диапазон равен f(x) > d, если a > 0, и f(x) < d, если a < 0.

Чтобы понять это, вы можете увидеть пример ниже.
Производная экспоненциальной функции
Вот формулы дифференцирования, которые используются для нахождения производной экспоненциальной функции.
- d/dx (е х ) = е х
- d/dx (a x ) = a x · ln a.
Интегрирование экспоненциальной функции
Вот формулы интегрирования, которые используются для нахождения интеграла экспоненциальной функции.
- ∫ е х dx = е х + С
- ∫ a x dx = a x / (ln a) + C
☛ Связанные темы по экспоненциальной функции:
Часто задаваемые вопросы об экспоненциальной функции
Что такое экспоненциальная функция?
Экспоненциальная функция — это тип математической функции, в которой используются показатели степени.
. Основная экспоненциальная функция имеет вид f(x) = b x , где b > 0 и b ≠ 1,
Основная экспоненциальная функция имеет вид f(x) = b x , где b > 0 и b ≠ 1,Какие формулы экспоненциальной функции?
В формулах показательной функции есть показатели степени. Показательное уравнение может быть представлено в одной из следующих форм.
Каковы правила экспоненциальной функции?
Поскольку экспоненциальная функция включает показатели степени, правила экспоненциальной функции такие же, как и правила показателей степени. Они:
- a м × a n = a m+n
- a м /a n = a m-n
- а 0 = 1
- а -м = 1/а м
- (а м ) н = а мн
- (ab) м = а м б м
- (a/b) м = a м /b м
Как построить график экспоненциальной функции?
Чтобы построить график экспоненциальной функции y = f(x), создайте таблицу значений, взяв несколько случайных чисел в качестве x (обычно мы берем -2, -1, 0, 1 и 2), подставьте каждое из них в функцию чтобы найти соответствующие значения y.
 Затем нанесите точки из таблицы и соедините их кривой. Наконец, удлините кривую на обоих концах.
Затем нанесите точки из таблицы и соедините их кривой. Наконец, удлините кривую на обоих концах.Что такое область экспоненциальной функции?
Экспоненциальная функция f(x) = ab x определена для всех значений x и, следовательно, ее областью определения является множество всех действительных чисел, которые в интервальных обозначениях могут быть записаны как (-∞, ∞).
Каковы свойства экспоненциальной функции?
Свойства экспоненциальной функции могут быть заданы как,
- a м × a n = a m+n
- a м /a n = a m-n
- а 0 = 1
- а -м = 1/а м
- (а м ) н = а мн
- (ab) м = а м б м
- (a/b) м = a м /b м
Для любой показательной функции вида f(x) = ab x , где b > 1, экспоненциальный график возрастает, а для любой показательной функции вида f(x) = ab x , где 0 < b < 1 график уменьшается.

Что такое диапазон экспоненциальной функции?
Диапазон экспоненциальной функции зависит от ее горизонтальной асимптоты, а также от того, лежит ли кривая выше или ниже горизонтальной асимптоты. т. е. для экспоненциальной функции f(x) = ab x диапазон составляет
- f(x) > d, если a > 0 и
- f(x) < d, если a < 0,
где y = d — горизонтальная асимптота графика функции.
Что такое свойство равенства экспоненциальной функции?
Свойство равенства экспоненциальной функции говорит, что если два значения (выхода) экспоненциальной функции равны, то соответствующие входы также равны.т. е. b \(x_1\) = b \(x_2\) ⇔ \(x_1\) = \(x_2\).
Что такое производная показательной функции?
Экспоненциальная функция может иметь форму e x или x . Формулы для нахождения производных этих функций следующие:
- d/dx (е х ) = е х
- d/dx (a x ) = a x · ln a.

Что такое интеграл показательной функции?
Экспоненциальная функция может иметь форму e x или x .Формулы для нахождения интегралов этих функций следующие:
- ∫ е х dx = е х + С
- ∫ a x dx = a x / (ln a) + C
Алгебра. Экспоненциальные функции
Показать мобильное уведомление Показать все примечания Скрыть все примечанияПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 6-1: Экспоненциальные функции
Давайте начнем этот раздел с определения экспоненциальной функции.Икс}\]
, где \(b\) называется основанием , а \(x\) может быть любым действительным числом.
Обратите внимание, что \(x\) теперь находится в показателе степени, а основание является фиксированным числом. Это прямо противоположно тому, что мы видели до сих пор. До сих пор основанием была переменная, в большинстве случаев \(х\), а показателем степени было фиксированное число. Однако, несмотря на эти различия, эти функции оцениваются точно так же, как те, к которым мы привыкли. Вскоре мы увидим несколько примеров экспоненциальных функций.{\ гидроразрыва {1} {2}}} = \ SQRT {- 4} \]
, и, как вы можете видеть, некоторые вычисления функций дают комплексные числа. Мы хотим, чтобы в результате вычисления функции возникали только действительные числа, и поэтому, чтобы убедиться в этом, мы требуем, чтобы \(b\) не было отрицательным числом.
 x}\]
x}\], где \({\bf{e}} = 2.Икс}\). В первом случае \(b\) — это любое число, которое соответствует указанным выше ограничениям, а и — это очень конкретное число. Также обратите внимание, что e не является завершающим десятичным числом.
Эта особая экспоненциальная функция очень важна и естественным образом возникает во многих областях. Как отмечалось выше, эта функция возникает так часто, что многие люди будут думать об этой функции, если говорить об экспоненциальных функциях. Мы увидим некоторые приложения этой функции в последнем разделе этой главы.Икс}\). Показать решение
Давайте сначала создадим таблицу значений для этой функции.
\(х\) -2 -1 0 1 2 \(f(x)\) 0,1353… 0,3679… 1 2.  718…
718…7,389… Чтобы получить эти оценки (за исключением \(x = 0\)) вам нужно будет использовать калькулятор. На самом деле, это часть смысла этого примера. Убедитесь, что вы можете запустить свой калькулятор и проверить эти числа.
Вот набросок этого графика.
Обратите внимание, что это возрастающий график, как и следовало ожидать, поскольку \({\bf{e}} = 2.{1 — х}} — 4\). Показать решение
Вот краткая таблица значений этой функции.
\(х\) -1 0 1 2 3 >\(г(х)\) 32,945… 9,591… 1 -2.  2} — 4\\ & = 5\влево( {7.389} \вправо) — 4\конец{выравнивание*}\]
2} — 4\\ & = 5\влево( {7.389} \вправо) — 4\конец{выравнивание*}\]Обратите внимание, что при вычислении экспоненциальных функций нам сначала нужно возвести в степень, прежде чем умножать на какие-либо коэффициенты (в данном случае 5). Кроме того, мы использовали здесь только 3 знака после запятой, так как мы строим только график. Во многих приложениях мы будем использовать гораздо больше десятичных разрядов в этих вычислениях.
Вот набросок графика.
Обратите внимание, что этот граф нарушает все перечисленные выше свойства.Икс}\). В этой функции происходит гораздо больше, поэтому свойства, описанные выше, не будут выполняться для этой функции.
Исчисление I. Экспоненциальные функции
Показать мобильное уведомление Показать все примечания Скрыть все примечанияПохоже, вы используете устройство с «узкой» шириной экрана ( i.
 е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.Раздел 1-7: экспоненциальные функции
В этом разделе мы рассмотрим одну из наиболее распространенных функций как в исчислении, так и в естественных науках.0} = 1\)
1 \(f\влево( 1 \вправо) = 2\) \(g\влево( 1 \вправо) = \frac{1}{2}\) 2 \(f\влево( 2 \вправо) = 4\) \(g\влево( 2 \вправо) = \frac{1}{4}\) Вот набросок обеих этих функций.

Этот график иллюстрирует некоторые очень хорошие свойства экспоненциальных функций в целом.х}\)
- \(f\влево( 0 \вправо) = 1\). Функция всегда будет принимать значение 1 при \(x = 0\).
- \(f\влево( x \вправо) \ne 0\). Показательная функция никогда не будет равна нулю.
- \(f\влево(х\вправо) > 0\). Показательная функция всегда положительна.
- Два предыдущих свойства можно резюмировать, сказав, что диапазон экспоненциальной функции равен \(\left( {0,\infty } \right)\).
- Область определения экспоненциальной функции: \(\left( { — \infty ,\infty } \right)\).Другими словами, вы можете подставить каждый \(x\) в экспоненциальную функцию.
- Если \(0 < b < 1\), то
- \(f\влево( x \вправо) \to 0{\mbox{as}}x \to \infty \)
- \(f\left( x \right) \to \infty {\mbox{as}}x \to — \infty \)
- Если \(b > 1\), то
- \(f\влево( x \вправо) \to \infty {\mbox{as}}x \to \infty \)
- \(f\left( x \right) \to 0{\mbox{as}}x \to — \infty \)
Все эти свойства будет очень полезно вспоминать время от времени по мере продвижения по этому курсу (и более поздним курсам исчисления, если уж на то пошло…).
 {1 — \frac{t}{2}}}\).
Показать решение
{1 — \frac{t}{2}}}\).
Показать решениеДавайте сначала получим таблицу значений для этой функции.
\(т\) -2 -1 0 1 2 3 \(ч\влево(т\вправо)\) -35,9453 -21.4084 -12,5914 -7,2436 -4 -2,0327 Вот эскиз.
Основной смысл этой проблемы заключается в том, чтобы убедиться, что вы можете выполнить этот тип оценки, поэтому убедитесь, что вы можете получить значения, которые мы изобразили на графике в этом примере. Вам будет предложено провести такую оценку время от времени в этом классе.
Вы будете встречать экспоненциальные функции почти в каждой главе этого курса, поэтому убедитесь, что они вам удобны.

экспоненциальных функций | Примеры и преобразования — видео и стенограмма урока
Отрицательная экспоненциальная функция, отражающая ось Y
Преобразования показательных функций
Вы уже видели одно преобразование показательных функций, отражения.x {/eq}, график будет двигаться вверх. Это движение изменит и горизонтальную асимптоту графика. У родительской функции была горизонтальная асимптота в точке {eq}y=0 {/eq}, и теперь, после этого переноса, асимптота находится в точке {eq}y=4 {/eq}. Родительская функция имела точку пересечения y в точке {eq}(0,1) {/eq}, а теперь точка пересечения находится в точке {eq}(0,5) {/eq}. Это движение графика вверх на четыре позиции. Домен по-прежнему состоит из действительных чисел, но диапазон больше не равен {eq}y\geq0 {/eq}. Теперь диапазон равен {eq}y\geq4 {/eq}.x {/eq} график сдвинется вниз.
 Это движение изменит и горизонтальную асимптоту графика. У родительской функции была горизонтальная асимптота в точке {eq}y=0 {/eq}, и теперь, после этого переноса, асимптота находится в точке {eq}y=-3 {/eq}. Родительская функция имела точку пересечения y в точке {eq}(0,1) {/eq}, а теперь точка пересечения находится в точке {eq}(0,-2) {/eq}. Это движение графика вниз на три позиции. Домен по-прежнему состоит из действительных чисел, но диапазон больше не равен {eq}y\geq 0 {/eq}. Теперь диапазон равен {eq}y\geq -3 {/eq}.{x+3} {/eq}
Это движение изменит и горизонтальную асимптоту графика. У родительской функции была горизонтальная асимптота в точке {eq}y=0 {/eq}, и теперь, после этого переноса, асимптота находится в точке {eq}y=-3 {/eq}. Родительская функция имела точку пересечения y в точке {eq}(0,1) {/eq}, а теперь точка пересечения находится в точке {eq}(0,-2) {/eq}. Это движение графика вниз на три позиции. Домен по-прежнему состоит из действительных чисел, но диапазон больше не равен {eq}y\geq 0 {/eq}. Теперь диапазон равен {eq}y\geq -3 {/eq}.{x+3} {/eq}Поскольку к независимой переменной {eq}x {/eq} было добавлено три, график сдвинется влево. Это движение не изменит горизонтальной асимптоты. Асимптота останется равной {eq}y=0 {/eq}. Родительская функция имела точку пересечения y в точке {eq}(0,1) {/eq}, а теперь точка пересечения находится в точке {eq}(0,8) {/eq}. Домен по-прежнему состоит из действительных чисел, а диапазон по-прежнему равен {eq}y\geq 0 {/eq}. Оба графика будут увеличиваться и будут вогнутыми вверх.

Пример 4
В следующем примере вы увидите, как вычитание числа из независимой переменной {eq}x {/eq} преобразует функцию.{x-4} {/eq}
Поскольку из независимой переменной {eq}x {/eq} было вычтено четыре, график сдвинется вправо. Это движение не изменит горизонтальной асимптоты. Асимптота останется равной {eq}y=0 {/eq}. Родительская функция имела точку пересечения y в точке {eq}(0,1) {/eq}, а теперь точка пересечения находится в точке {eq}(0,\frac{1}{16}) {/eq}. Домен по-прежнему состоит из действительных чисел, а диапазон по-прежнему равен {eq}y\geq 0 {/eq}. Оба графика будут увеличиваться и будут вогнутыми вверх.
Экспоненциальные графики
Чтобы построить график экспоненциальных функций, начните с построения горизонтальной асимптоты и точки пересечения с координатой Y.x-3 {/eq}, точка пересечения y будет {eq}(0,-2) {/eq} после того, как вы подставите {eq}0 {/eq} и решите. Затем вы можете использовать таблицу значений, чтобы определить, будет ли график увеличиваться или уменьшаться, чтобы дать вам представление о форме графика.
 Обратите внимание, является ли функция отрицательной или независимая переменная отрицательна, чтобы также помочь вам узнать положение или направление графика. Если либо функция, либо независимая переменная отрицательны, функция будет уменьшаться по всей своей области определения.
Обратите внимание, является ли функция отрицательной или независимая переменная отрицательна, чтобы также помочь вам узнать положение или направление графика. Если либо функция, либо независимая переменная отрицательны, функция будет уменьшаться по всей своей области определения.Горизонтальные сдвиги влево и вправо
Горизонтальные сдвиги возникают при добавлении или вычитании числа из {eq}x {/eq}, независимой переменной.{x+4} {/экв.}. {eq}4 {/eq} представляет горизонтальное движение графика. В частности, это движение влево, потому что оно было добавлено. Если к независимой переменной {eq}x {/eq} добавить число, то график сдвинется влево. Если из независимой переменной {eq}x {/eq} вычесть число, график сдвинется вправо.
При горизонтальном перемещении горизонтальная асимптота не изменится по сравнению с асимптотой родительской функции. Если родительская функция имеет асимптоту при {eq}y=2 {/eq}, то сдвиг влево или вправо также будет иметь асимптоту {eq}y=2 {/eq}.

Пересечение по оси y изменится при горизонтальном перемещении. Чтобы определить новую точку пересечения y, просто подставьте {eq}0 {/eq} в функцию и найдите y.
Домен и диапазон горизонтального перевода останутся такими же, как и у родительской функции. Функция будет увеличиваться или уменьшаться так же, как и ее родительская функция. Кроме того, вогнутость графика не изменится при горизонтальном преобразовании.
Вертикальные сдвиги вверх и вниз
Вертикальное смещение происходит при добавлении или вычитании числа из функции {eq}f(x) {/eq}.х-2 {/экв}. {eq}2 {/eq} представляет вертикальное движение графика. В частности, это движение вниз, потому что оно было вычтено. Если к функции {eq}f(x) {/eq} добавить число, то график сдвинется вверх. Если из функции {eq}f(x) {/eq} вычесть число, то график сдвинется вниз.
Горизонтальная асимптота будет изменена при вертикальном переносе. Чтобы найти новую асимптоту, вы просто добавляете или вычитаете значение, которое добавляется или вычитается в функции, из горизонтальной асимптоты родителя.
 Если родительская функция имеет асимптоту в точке {eq}y=0 {/eq} и к функции добавлено {eq}2 {/eq}, добавьте {eq}2 {/eq} к исходной асимптоте. Новая асимптота будет расположена в точке {eq}y=2 {/eq}. Если родительская функция имеет асимптоту при {eq}y=-2 {/eq}, а {eq}3 {/eq} было вычтено из функции, то вычтите {eq}3 {/eq} из исходной асимптоты. Новая асимптота будет расположена в точке {eq}y=-5 {/eq}.
Если родительская функция имеет асимптоту в точке {eq}y=0 {/eq} и к функции добавлено {eq}2 {/eq}, добавьте {eq}2 {/eq} к исходной асимптоте. Новая асимптота будет расположена в точке {eq}y=2 {/eq}. Если родительская функция имеет асимптоту при {eq}y=-2 {/eq}, а {eq}3 {/eq} было вычтено из функции, то вычтите {eq}3 {/eq} из исходной асимптоты. Новая асимптота будет расположена в точке {eq}y=-5 {/eq}.Домен останется прежним, но изменится диапазон.Если исходный диапазон был {eq}y\geq -2 {/eq}, а вы опустились на {eq}3 {/eq}, новый диапазон будет {eq}y\geq -5 {/eq}. Перехват y изменится. Чтобы найти новую точку пересечения y, подставьте {eq}0 {/eq} вместо x и найдите {eq}y {/eq}. Если изначально был перехват x, он также изменится.
График по-прежнему будет увеличиваться или уменьшаться, как это делает родительская функция. Вогнутость графика также не изменится от вогнутости родительской функции.
Рефлексивное преобразование
При использовании отрицательной экспоненциальной функции, такой как {eq}y=-2^x {/eq}, график будет отражаться по оси X.
 {x-2}-3 {/экв}.
{x-2}-3 {/экв}.Зеленый график представляет родительскую функцию, а синий график представляет экспоненциальную функцию, сдвинутую вниз на три.
Вертикальный перевод смещен вниз
Краткий обзор урока
Показательная функция — это функция с базовым числом больше единицы и показателем степени, который является переменной. Ключевые особенности экспоненциального — это горизонтальная асимптота , точка пересечения y , иногда точка пересечения x , область значений всех действительных чисел и диапазон, больший или меньший, чем горизонтальная асимптота.Горизонтальная асимптота — это граничная линия, к которой функция будет приближаться и очень близко, но никогда не коснется. Точка пересечения y — это место, где график пересекает ось y. Точка пересечения x — это место, где график пересекает ось x. Домен относится ко всем значениям x, которые дадут значение y.
 Диапазон относится ко всем значениям y. Функция либо возрастает на всей своей области определения, либо убывает, и она вогнута вверх или вогнута вниз . Вогнутость описывает кривизну графика.Ключевые функции могут изменяться в зависимости от преобразований , которые происходят с функцией. Этот урок был посвящен преобразованиям отражений и переводов . Отражения, или отрицательные экспоненциальные функции, переворачивают график по оси x или y, когда перед базовым числом стоит отрицательное значение или перед независимой переменной стоит отрицательное значение. Переводы перемещают графики вверх, вниз, влево или вправо, когда число прибавляется или вычитается из функции или независимой переменной.
Диапазон относится ко всем значениям y. Функция либо возрастает на всей своей области определения, либо убывает, и она вогнута вверх или вогнута вниз . Вогнутость описывает кривизну графика.Ключевые функции могут изменяться в зависимости от преобразований , которые происходят с функцией. Этот урок был посвящен преобразованиям отражений и переводов . Отражения, или отрицательные экспоненциальные функции, переворачивают график по оси x или y, когда перед базовым числом стоит отрицательное значение или перед независимой переменной стоит отрицательное значение. Переводы перемещают графики вверх, вниз, влево или вправо, когда число прибавляется или вычитается из функции или независимой переменной.Экспоненциальные функции и их графики
Экспоненциальные функции
На этом этапе нашего изучения алгебры мы начинаем рассматривать трансцендентные функции или функции, которые, кажется, «выходят за пределы» алгебры.
 Мы изучали функции с переменным основанием и постоянными показателями, такими как x2 или y−3. В этом разделе мы исследуем функции с постоянным основанием и переменными показателями. При заданном вещественном числе b>0, где b≠1, экспоненциальная функцияЛюбая функция с определением вида f(x)=bx, где b>0 и b≠1.имеет вид,
Мы изучали функции с переменным основанием и постоянными показателями, такими как x2 или y−3. В этом разделе мы исследуем функции с постоянным основанием и переменными показателями. При заданном вещественном числе b>0, где b≠1, экспоненциальная функцияЛюбая функция с определением вида f(x)=bx, где b>0 и b≠1.имеет вид,f(x)=bx Экспоненциальная функция
Например, если основание b равно 2, то у нас есть экспоненциальная функция, определяемая выражением f(x)=2x. Здесь мы видим, что показатель степени является переменной. До этого момента рациональные показатели были определены, а иррациональные — нет. Рассмотрим число 27, где показатель степени — иррациональное число в диапазоне
.2,64<7<2,65
Мы можем использовать эти границы для оценки 27,
22.7≈6,26
Следовательно, область определения любой экспоненциальной функции состоит из всех действительных чисел (−∞,∞). Выберите несколько значений для 90 597 x 90 598, а затем определите соответствующие значения 90 597 и 90 598.

xyf(x)=2xSolutions−214y=2−2=122=14(−2, 14)−112y=2−1=121=12(−1, 12)01y=20=1(0, 1)12y =21=2(1, 2)24y=22=4(2, 4)76,26y=27≈6,26(2,65, 6,26)
Поскольку показатели степени определены для любого действительного числа, мы можем нарисовать график, используя непрерывную кривую, проходящую через эти заданные точки:
Важно отметить, что когда x приближается к отрицательной бесконечности, результаты становятся очень маленькими, но никогда не достигают нуля.Например,
f(−5)=2−5=125≈0,03125f(−10)=2−10=1210≈0,0009766f(−15)=2−15=12−15≈.00003052
Это описывает горизонтальную асимптоту при y=0, ось x , и определяет нижнюю границу диапазона функции: (0,∞).
Основание b экспоненциальной функции влияет на скорость ее роста. Ниже мы изобразили y=2x, y=3x и y=10x на том же наборе осей.
Обратите внимание, что все эти экспоненциальные функции имеют одну и ту же точку пересечения и , а именно (0,1).
 Это связано с тем, что f(0)=b0=1 для любой функции, определенной с помощью формы f(x)=bx. Поскольку функции читаются слева направо, они интерпретируются как возрастающие или растущие экспоненциально. Кроме того, любая экспоненциальная функция этой формы будет иметь область определения, состоящую из всех действительных чисел (−∞, ∞), и диапазон, состоящий из положительных значений (0, ∞), ограниченных горизонтальной асимптотой при y = 0.
Это связано с тем, что f(0)=b0=1 для любой функции, определенной с помощью формы f(x)=bx. Поскольку функции читаются слева направо, они интерпретируются как возрастающие или растущие экспоненциально. Кроме того, любая экспоненциальная функция этой формы будет иметь область определения, состоящую из всех действительных чисел (−∞, ∞), и диапазон, состоящий из положительных значений (0, ∞), ограниченных горизонтальной асимптотой при y = 0.Пример 1
Нарисуйте график и определите домен и диапазон: f(x)=10x+5.
Решение:
Часто используется основание 10, особенно в экспоненциальном представлении. Следовательно, 10 называется общим основанием . На самом деле экспоненциальная функция y=10x настолько важна, что вы найдете кнопку 10x, посвященную ей, на большинстве современных научных калькуляторов. В этом примере мы нарисуем базовый график y=10x, а затем сдвинем его вверх на 5 единиц.

Обратите внимание, что горизонтальная асимптота базового графика y=10x была смещена вверх на 5 единиц до y=5 (показано пунктиром).Потратьте минуту, чтобы оценить несколько значений x с помощью своего калькулятора и убедить себя, что результат никогда не будет меньше 5.
Ответ:
Домен: (−∞,∞); Диапазон: (5,∞)
Далее рассмотрим экспоненциальные функции с дробным основанием 0
xyf(x)=(12)xSolutions−24f(12)=(12)−2=1−22−2=2212=4(−2, 4)−12f(12)=(12)−1=1 −12−1=2111=2(−1, 2)01f(12)=(12)0=1(0, 1)112f(12)=(12)1=12(1, 12)214f(12) =(12)2=14(2, 14)
точки построения у нас есть,
При чтении графика слева направо он интерпретируется как экспоненциально убывающий.База влияет на скорость, с которой экспоненциальная функция уменьшается или затухает.
 Ниже мы изобразили y=(12)x, y=(13)x и y=(110)x на одном и том же наборе осей.
Ниже мы изобразили y=(12)x, y=(13)x и y=(110)x на одном и том же наборе осей.Напомним, что x−1=1x, поэтому мы можем выразить экспоненциальные функции с дробными основаниями, используя отрицательные показатели степени. Например,
г(х)=(12)х=1х2х=12х=2-х.
Кроме того, учитывая, что f(x)=2x, мы видим, что g(x)=f(−x)=2−x, и можем считать g отражением f относительно оси y .
Таким образом, дано b>0
И в обоих случаях
Домен:(−∞,∞)Диапазон:(0,∞)y-отрезок:(0,1)Асимптота:y=0
Кроме того, обратите внимание, что графики проходят тест горизонтальной линии, и поэтому экспоненциальные функции являются взаимно однозначными. Мы используем эти базовые графики вместе с преобразованиями для построения графиков экспоненциальных функций.
Пример 2
Нарисуйте график и определите домен и диапазон: f(x)=5−x−10.

Решение:
Начните с базового графа y=5−x и сдвиньте его вниз на 10 единиц.
Пересечение y равно (0,−9), а горизонтальная асимптота равна y=−10.
Ответ:
Домен: (−∞,∞); Диапазон: (−10,∞)
Примечание : Нахождение пересечения графика размером x в предыдущем примере оставлено для последующего раздела этой главы.Сейчас нас больше интересует общий вид экспоненциальных функций.
Пример 3
Нарисуйте график и определите домен и диапазон: g(x)=−2x−3.
Решение:
Начните с базового графа y=2x и определите преобразования.
y=2x Основная графия=−2x Отражение о оси xy=−2x−3 Сдвиг вправо 3 единицы
Обратите внимание, что горизонтальная асимптота остается одинаковой для всех преобразований.
 Чтобы закончить, мы обычно хотим включить y -intercept. Помните, что для нахождения точки пересечения y мы устанавливаем x=0.
Чтобы закончить, мы обычно хотим включить y -intercept. Помните, что для нахождения точки пересечения y мы устанавливаем x=0.г(0)=-20-3=-2-3=-123=-18
Следовательно, точка пересечения y равна (0, −18).
Ответ:
Домен: (−∞,∞); Диапазон: (−∞,0)
Попробуйте! Нарисуйте график и определите домен и диапазон: f(x)=2x−1+3.
Ответ:
Домен: (−∞,∞); Диапазон: (3,∞)
Натуральная основа e
Некоторые числа часто встречаются в обычных приложениях. Одним из таких знакомых чисел является число пи (π), которое, как мы знаем, возникает при работе с кругами. Это иррациональное число имеет специальную кнопку на большинстве калькуляторов π и округляется до пяти знаков после запятой, π≈3,14159.
 Другое важное число e возникает при работе с моделями экспоненциального роста и распада.Это иррациональное число, округленное до пяти знаков после запятой, e≈2,71828. Эта константа естественным образом встречается во многих реальных приложениях и поэтому называется естественным основанием . Иногда e называют постоянной Эйлера в честь Леонарда Эйлера (произносится как «Ойлер»).
Другое важное число e возникает при работе с моделями экспоненциального роста и распада.Это иррациональное число, округленное до пяти знаков после запятой, e≈2,71828. Эта константа естественным образом встречается во многих реальных приложениях и поэтому называется естественным основанием . Иногда e называют постоянной Эйлера в честь Леонарда Эйлера (произносится как «Ойлер»).Рисунок 7.1
Леонард Эйлер (1707–1783)
На самом деле натуральная экспоненциальная функция , е (х) = экс настолько важен, что вы найдете кнопку, посвященную ему, на любом современном научном калькуляторе.(−2)≈0,13534
После того, как вы научились пользоваться своим калькулятором, теперь вы можете рисовать график, нанося точки. (Округлить до сотых.)
xyf(x)=exSolutions−20,14f(−2)=e−2=0,14(−2, 0,14)−10,37f(−1)=e−1=0,37(−1, 0,37)01f(0)= e0=1(0, 1)12,72f(1)=e1=2,72(1, 2,72)27,39f(2)=e2=7,39(2, 7,39)
Нанесите точки и нарисуйте график.

Обратите внимание, что функция аналогична графику y=3x.Домен состоит из всех действительных чисел, а диапазон состоит из всех положительных действительных чисел. Существует асимптота при y = 0 и y -перехват в точке (0,1). Мы можем использовать преобразования, чтобы нарисовать график более сложных экспоненциальных функций.
Пример 4
Нарисуйте график и определите домен и диапазон: g(x)=ex+2−3.
Решение:
Определите основные преобразования.
y=ex Basic graphy=ex+2 Shift влево 2 unitsy=ex+2−3 Shift вниз 3 единиц
Для определения точки пересечения и установите x=0.
г(0)=e0+2−3=e2−3≈4,39
Следовательно, точка пересечения y равна (0,e2−3).
Ответ:
Домен: (−∞,∞); Диапазон: (−3,∞)
Попробуйте! Нарисуйте график и определите домен и диапазон: f(x)=e−x+2.

Ответ:
Домен: (−∞,∞); Диапазон: (2,∞)
Формулы сложных процентов
Экспоненциальные функции появляются в формулах, используемых для расчета процентов, полученных на большинстве обычных сберегательных счетов.Сложные проценты возникают, когда проценты, накопленные за один период, добавляются к основной сумме инвестиций до расчета процентов за следующий период. Сумма, накопленная таким образом с течением времени, моделируется формулой сложных процентов. Формула, которая дает сумму, накопленную за счет получения процентов на основную сумму и процентов с течением времени: A(t)=P(1+rn)nt.:
A(t)=P(1+rn)nt
Здесь сумма А зависит от времени т в годах основной долг Р накапливает сложные проценты по годовой процентной ставке р .Значение n представляет количество начислений процентов в течение года.

Пример 5
Инвестиция в размере 500 долларов США сделана в 6-летний депозитный сертификат, который приносит 412% годовых, которые ежемесячно начисляются. Сколько будет стоить компакт-диск в конце 6-летнего срока?
Решение:
Здесь основная сумма долга P=500 долларов, процентная ставка r=412%=0,045, а поскольку проценты начисляются ежемесячно, n=12.Инвестиции моделируются следующим образом,
А(т)=500(1+0,04512)12т
Чтобы определить сумму на счете через 6 лет, оцените A(6) и округлите до ближайшего цента.
А(6)=500(1+0,04512)12(6)=500(1,00375)72=654,65
Ответ: Компакт-диск будет стоить 654,65 доллара в конце 6-летнего срока.
Далее мы исследуем эффект увеличения на в формуле. Ради ясности мы принимаем P и r равными 1 и вычисляем соответственно.
Годовое начисление процентов
(1+1n)n
Ежегодно (n=1)
(1+11)1=2
Раз в полгода (n=2)
(1+12)2=2,25
Ежеквартально (n=4)
(1+14)4≈2.
 44140
44140Ежемесячно (n=12)
(1+112)12≈2,61304
Еженедельно (n=52)
(1+152)52≈2,69260
Ежедневно (n=365)
(1+1365)365≈2,71457
Ежечасно (n=8760)
(1+18760)8760≈2.71813
Продолжая эту схему, поскольку n увеличивается, скажем, увеличиваясь каждую минуту или даже каждую секунду, мы можем видеть, что результат стремится к естественному основанию e≈2,71828. Начисление процентов каждый момент приводит к формуле непрерывного начисления процентов.
 Формула, которая дает сумму, накопленную за счет непрерывно начисленных процентов: A(t)=Pert.,
Формула, которая дает сумму, накопленную за счет непрерывно начисленных процентов: A(t)=Pert.,А(т)=перт
Здесь P представляет собой первоначальную вложенную основную сумму, r представляет собой годовую процентную ставку, а t представляет собой время в годах, в течение которого инвестиции позволяют непрерывно начислять сложные проценты.
Пример 6
Инвестиции в размере 500 долларов США сделаны в 6-летний CD, который приносит 412% годовых, которые непрерывно начисляются. Сколько будет стоить компакт-диск в конце 6-летнего срока?
Решение:
Здесь основная сумма долга P=500 долларов, а процентная ставка r=412%=0,045. Поскольку проценты начисляются непрерывно, мы будем использовать формулу A(t)=Pert. Инвестиции моделируются следующим образом,
А(t)=500e0.045т
Чтобы определить сумму на счете через 6 лет, оцените A(6) и округлите до ближайшего цента.

А(6)=500е0,045(6)=500е0,27=654,98
Ответ: Компакт-диск будет стоить 654,98 доллара в конце 6-летнего срока.
Сравните два предыдущих примера и обратите внимание, что постоянное начисление процентов может быть не таким выгодным, как кажется. Хотя лучше начислять проценты чаще, разница не так велика.Конечно, процентная ставка является гораздо большим фактором в конечном результате.
Попробуйте! Сколько будет стоить депозитный сертификат на 1200 долларов, приносящий 5,2% годовых с постоянным начислением сложных процентов, в конце 10-летнего срока?
Ответ: $2018,43
Ключевые выводы
- Экспоненциальные функции имеют определения вида f(x)=bx, где b>0 и b≠1.Область состоит из всех действительных чисел (−∞, ∞), а диапазон состоит из положительных чисел (0, ∞).
 Кроме того, все экспоненциальные функции этой формы имеют точку пересечения y (0,1) и являются асимптотическими относительно оси x .
Кроме того, все экспоненциальные функции этой формы имеют точку пересечения y (0,1) и являются асимптотическими относительно оси x . - Если основание экспоненциальной функции больше 1 (b>1), то ее график увеличивается или растет при чтении слева направо.
- Если основанием экспоненциальной функции является правильная дробь (0
- Число 10 называется общим основанием, а число e — натуральным основанием.
- Естественная экспоненциальная функция, определяемая выражением f(x)=ex, имеет график, очень похожий на график g(x)=3x.
- Экспоненциальные функции взаимно однозначны.
Тематические упражнения
f(x)=3x, где f(−2), f(0) и f(2).

f(x)=10x, где f(−1), f(0) и f(1).
g(x)=(13)x, где g(−1), g(0) и g(3).
g(x)=(34)x, где g(-2), g(-1) и g(0).
h(x)=9−x, где h(−1), h(0) и h(12).
h(x)=4−x, где h(−1), h(−12) и h(0).
f(x)=−2x+1, где f(−1), f(0) и f(3).

f(x)=2−3x, где f(−1), f(0) и f(2).
g(x)=10−x+20, где g(−2), g(−1) и g(0).
g(x)=1−2−x, где g(−1), g(0) и g(1).
f(x)=3x−10, где f(3.2).
f(x)=10−x−2, где f(1,5).

f(x)=5−x+3, где f(1.3).
f(x)=(23)x+1, где f(−2,7).
f(x)=(35)−x−1, где f(1.4).
е (х) = (14) х
ч (х) = (13) х
f(x)=(14)x−2
ч(х)=(13)х+2
Часть A: экспоненциальные функции
Оценить.
Воспользуйтесь калькулятором, чтобы вычислить следующие значения с точностью до сотых.
Нарисуйте функцию и определите домен и диапазон. Нарисуйте горизонтальную асимптоту пунктирной линией.
Часть B: Натуральная основа
eНайдите f(−1), f(0) и f(32) для заданной функции.
 Используйте калькулятор, где это уместно, чтобы округлить до ближайшей сотой.
Используйте калькулятор, где это уместно, чтобы округлить до ближайшей сотой. Нарисуйте функцию и определите домен и диапазон.Нарисуйте горизонтальную асимптоту пунктирной линией.
Джим вложил 750 долларов в 3-летний компакт-диск, который приносит 4.
 2% годовых, которые начисляются ежемесячно. Сколько будет стоить компакт-диск в конце 3-летнего срока?
2% годовых, которые начисляются ежемесячно. Сколько будет стоить компакт-диск в конце 3-летнего срока?Хосе инвестировал 2450 долларов в 4-летний депозитный сертификат, который приносит 3,6% годовых и начисляется каждые полгода. Сколько будет стоить компакт-диск в конце 4-летнего срока?
У Джейн есть сбережения в размере 5350 долларов на счете, приносящие 358% годовых, которые начисляются ежеквартально.Сколько будет на счете через 5 лет?
У Билла есть 12 400 долларов на обычном сберегательном счете, приносящий 423% годовых, который начисляется ежемесячно. Сколько будет на счете через 3 года?
Если 85 200 долларов инвестировано в счет, зарабатывающий 5.
 8% годовых, начисляемых ежеквартально, то сколько процентов начисляется за первые 3 года?
8% годовых, начисляемых ежеквартально, то сколько процентов начисляется за первые 3 года?Если 124 000 долларов вложены на счет, приносящий 4,6% годовых с ежемесячным начислением процентов, то сколько процентов будет начислено за первые 2 года?
Билл вложил 1400 долларов в компакт-диск сроком на 3 года, который приносит 4.2% годовых, которые постоянно начисляются. Сколько будет стоить компакт-диск в конце 3-летнего срока?
Brooklyn инвестировал 2850 долларов в 5-летний депозитный сертификат, который приносит 5,3% годовых и постоянно начисляется. Сколько будет стоить компакт-диск в конце 5-летнего срока?
У Омара есть сбережения в размере 4200 долларов на счету, приносящие 438% годовых, которые постоянно начисляются.
 Сколько будет на счету через 212 лет?
Сколько будет на счету через 212 лет?У Нэнси есть сбережения в размере 8 325 долларов на счете, приносящие 578% годовых, которые постоянно начисляются. Сколько будет на счету через 512 лет?
Если 12 500 долларов вложены в счет, зарабатывающий 3.8% годовых, начисляемых непрерывно, то сколько процентов начисляется за первые 10 лет?
Если 220 000 долларов вложены на счет, приносящий 4,5% годовых с постоянным начислением процентов, то сколько процентов будет начислено за первые 2 года?
Население небольшого городка растет согласно функции P(t)=12 500(1.
 02)t, где t представляет время в годах с момента последней переписи. Используйте функцию для определения численности населения в день переписи (когда t = 0) и оцените численность населения через 6 лет с этого времени.
02)t, где t представляет время в годах с момента последней переписи. Используйте функцию для определения численности населения в день переписи (когда t = 0) и оцените численность населения через 6 лет с этого времени.Население небольшого городка уменьшается в соответствии с функцией P(t)=22 300(0,982)t, где t представляет время в годах с момента последней переписи.Используйте функцию для определения численности населения в день переписи (когда t = 0) и оцените численность населения через 6 лет с этого времени.
Уменьшение стоимости нового автомобиля в долларах моделируется по формуле V(t)=28 000(0,84)t, где t представляет количество лет после покупки автомобиля.
 Используйте формулу, чтобы определить стоимость автомобиля, когда он был новым ( t = 0) и стоимость через 4 года.
Используйте формулу, чтобы определить стоимость автомобиля, когда он был новым ( t = 0) и стоимость через 4 года.Количество уникальных посетителей веб-сайта колледжа можно приблизительно оценить по формуле N(t)=410(1,32)t, где t представляет собой количество лет после 1997 года, когда был создан веб-сайт. Примерное количество уникальных посетителей сайта колледжа в 2020 году.
Если не остановить новый штамм вируса гриппа, он может очень быстро распространиться от одного человека к другому.Количество затронутых людей можно смоделировать по формуле P(t)=e0,22t, где t представляет собой количество дней, в течение которых вирус может беспрепятственно распространяться. Оцените количество людей, инфицированных вирусом через 30 дней и через 60 дней.

Если ничего не контролировать, популяция из 24 диких английских кроликов может расти по формуле P(t)=24e0.19t, где время t измеряется в месяцах. Сколько кроликов будет через 312 лет?
Население одного города в 1975 г. составляло 65 000 человек и росло в геометрической прогрессии со скоростью 1,7% в год. В то время прирост населения моделировался по формуле P(t)=65 000e0,017t, где t представляло количество лет, прошедших с 1975 года.В 2000 году перепись определила фактическую численность населения 104 250 человек. Какое население предсказывала модель на 2000 год и какова была фактическая ошибка?
Из-за радиоактивного распада количество 10 миллиграммов йода-131 уменьшается в соответствии с формулой A(t)=10e−0,087t, где t представляет собой время, измеренное в днях.
 Какая часть образца остается через 10 дней?
Какая часть образца остается через 10 дней?Количество клеток в образце бактерий аппроксимируется логистической моделью роста N(t)=1,2×1051+9e−0,32t, где t представляет время в часах. Определите начальное количество клеток, а затем определите количество клеток через 6 часов.
Рыночная доля продукта в процентах приблизительно рассчитывается по формуле P(t)=1002+e−0.44t, где t представляет количество месяцев после запуска агрессивной рекламной кампании. Насколько мы можем ожидать увеличения доли рынка после первых трех месяцев рекламы?
Часть C: Формулы сложных процентов
Почему b = 1 исключено как основание в определении показательных функций? Объяснять.

Объясните, почему экспоненциальная функция формы y=bx никогда не может быть отрицательной.
Исследуйте и обсудите вывод формулы сложных процентов.
Исследуйте и обсудите модель роста логистики.Дайте ссылку на дополнительную информацию по этой теме.
Исследуйте и обсуждайте жизнь и вклад Леонарда Эйлера.
Часть D: Дискуссионная доска
ответы
f(−2)=19, f(0)=1, f(2)=9
г(-1)=3, г(0)=1, г(3)=127
ч(-1)=9, ч(0)=1, ч(12)=13
f(−1)=12, f(0)=0, f(3)=−7
г(-2)=120, г(-1)=30, г(0)=21
Домен: (−∞,∞); Диапазон: (0,∞)
Домен: (−∞,∞); Диапазон: (2,∞)
Домен: (−∞,∞); Диапазон: (0,∞)
Домен: (−∞,∞); Диапазон: (−4,∞)
Домен: (−∞,∞); Диапазон: (−2,∞)
Домен: (−∞,∞); Диапазон: (0,∞)
Домен: (−∞,∞); Диапазон: (−2,∞)
Домен: (−∞,∞); Диапазон: (−3,∞)
Домен: (−∞,∞); Диапазон: (−∞,6)
Домен: (−∞,∞); Диапазон: (−∞,5)
f(−1)≈2.
 37, f(0)=3, f(32)≈6,48
37, f(0)=3, f(32)≈6,48f(−1)≈3,90, f(0)=2, f(32)≈−8,45
f(−1)≈3,72, f(0)=2, f(32)≈1,22
f(−1)≈9.39, f(0)=3, f(32)≈2,05
Домен: (−∞,∞); Диапазон: (−3,∞)
Домен: (−∞,∞); Диапазон: (0,∞)
Домен: (−∞,∞); Диапазон: (1,∞)
Домен: (−∞,∞); Диапазон: (−∞,0)
Домен: (−∞,∞); Диапазон: (−∞,0)
Первоначальное население: 12 500 человек; Население 6 лет спустя: 14 077
Новый: 28 000 долларов США; Через 4 года: 13 940 долларов.
 40
40Через 30 дней: 735 человек; Через 60 дней: 540 365 человек
- Модель
: 99 423 человека; ошибка: 4827 человек
Изначально имеется 12 000 ячеек, а через 6 часов уже 51 736 ячеек.
Графические экспоненциальные функции – объяснение и примеры
График экспоненциальных функций позволяет нам моделировать функции формы x на декартовой плоскости, когда а — действительное число больше 0.

Общие примеры экспоненциальных функций включают 2 x , e x и 10 x . График экспоненциальных функций иногда сложнее, чем график квадратичных или кубических функций, потому что существует бесконечно много родительских функций, с которыми можно работать.
Перед тем, как научиться строить графики экспоненциальных функций, рекомендуется ознакомиться с координатной геометрией и показателями в целом.
Эта тема будет включать в себя информацию о:
- Как график экспоненциальных функций
- 3
- 3 горизонтальные и вертикальные сдвиги
- Отражения
- И сжатие
- графики с таблицами
- 3
- 3
Как графические экспоненциальные функции
Графические функции формы A x , где база, A, является действительным числом больше 0, аналогично построению графиков других функций.
 В частности, важно изучить форму родительской функции. Из этого мы можем делать различные преобразования, в том числе сдвигать график влево и вправо, отражать его и растягивать.
В частности, важно изучить форму родительской функции. Из этого мы можем делать различные преобразования, в том числе сдвигать график влево и вправо, отражать его и растягивать.Y-пересечение
Рассмотрим любую функцию размером x . Независимо от того, какое действительное число мы используем для a, a 0 всегда будет равно 1. Это означает, что, если график не имеет вертикального или горизонтального сдвига, y-пересечение экспоненциальной функции равно 1.
Горизонтальная асимптота
Для какого значения x функция 2 x =0?
Это, конечно, вопрос с подвохом. Функции вида a x всегда строго положительны. Следовательно, любая экспоненциальная функция будет иметь горизонтальную асимптоту в 0, когда x стремится к отрицательной бесконечности.
Это просто причудливый способ сказать, что по мере того, как наши значения x становятся все меньше и меньше, наши значения y становятся все ближе и ближе к нулю.
 Но, что важно, они никогда не достигнут этого.Таким образом, асимптота — это линия, к которой функция приближается бесконечно близко, но на самом деле никогда не касается и не пересекает ее. В этом случае мы видим, что ось x является асимптотой любой экспоненциальной функции (при условии отсутствия вертикального смещения).
Но, что важно, они никогда не достигнут этого.Таким образом, асимптота — это линия, к которой функция приближается бесконечно близко, но на самом деле никогда не касается и не пересекает ее. В этом случае мы видим, что ось x является асимптотой любой экспоненциальной функции (при условии отсутствия вертикального смещения).По мере того, как x стремится к положительной бесконечности, функция будет становиться все больше и больше. На самом деле экспоненциальные функции растут быстрее, чем функции любого другого типа! Вот почему, если мы говорим, что что-то растет «в геометрической прогрессии», это означает, что это быстро складывается.
Вертикальные и горизонтальные сдвиги
Как и в случае с другими функциями, мы можем сдвигать экспоненциальные функции вверх, вниз, влево и вправо, добавляя и вычитая числа из x в родительской функции a x .
В частности, мы можем сдвигать функцию по горизонтали, добавляя числа непосредственно к a в виде a x+b .
 В частности, если b положительно, функция сместит b единиц влево. Если b отрицательно, функция сдвинет |b| единиц вправо. Помните, что вы можете думать о числах, добавленных непосредственно к х, как о чем-то вроде «зеркального мира», где все противоположно тому, что вы ожидаете. Следовательно, отрицательные числа вызывают сдвиг вправо, а положительные числа вызывают сдвиг влево, что противоположно большинству вещей в математике.
В частности, если b положительно, функция сместит b единиц влево. Если b отрицательно, функция сдвинет |b| единиц вправо. Помните, что вы можете думать о числах, добавленных непосредственно к х, как о чем-то вроде «зеркального мира», где все противоположно тому, что вы ожидаете. Следовательно, отрицательные числа вызывают сдвиг вправо, а положительные числа вызывают сдвиг влево, что противоположно большинству вещей в математике.Если мы добавим число c непосредственно к экспоненциальной функции a x как x +c, это вызовет сдвиг по вертикали. Если c положительно, функция будет двигаться вверх на c единиц. Точно так же, если c отрицательно, график сместит |c| единицы вниз.
Обратите внимание, что горизонтальная асимптота функции будет перемещаться вверх и вниз вместе со сдвигом по вертикали. Например, если функция перемещается вверх на две единицы, горизонтальная асимптота сдвинется вверх на две единицы до y=2.
Отражения
Мы также можем отразить экспоненциальную функцию по оси Y или X.

Чтобы отразить функцию по оси y, мы просто умножаем основание a на -1 после возведения в степень x, чтобы получить -a x . Обратите внимание, что функция (-a) x не будет отражать функцию, но полностью изменит функцию, потому что (-a) x изменяется в зависимости от того, является ли x четным или нечетным.
Мы также можем отразить функцию по оси x, умножив x на -1. То есть функция a -x является отражением x по оси x.
Растяжение и сжатие
Умножение f(x)=a x на любое положительное число, кроме единицы, приведет к его растяжению или сжатию. В частности, числа меньше единицы сделают график более плоским, а числа больше единицы сделают его более крутым.
Любое из этих преобразований графа можно комбинировать с другими для создания различных видов экспоненциальных графов.
Графики с помощью таблиц
Хотя все экспоненциальные функции имеют одинаковую общую форму, мы можем создавать более точные функции с помощью таблицы.

Как правило, рекомендуется найти по крайней мере от трех до пяти точек. Включение y-пересечения, одной отрицательной точки и одной положительной точки может помочь нам получить лучшее представление о форме графика. То есть нахождение значений y функции при x=-1, x=0 и x=1 даст нам хорошее представление о том, как должен выглядеть график функции.
Число Эйлера
Число Эйлера, e, является иррациональным числом. Приблизительно до первых трех знаков после запятой это 2,718.Это число имеет множество уникальных свойств и характеристик, в том числе полезно для расчета сложных процентов, и оно почти всегда отображается в виде e x .
Число e также представляет особый интерес в исчислении, поскольку функция e x имеет производную e x . Это означает, что касательная, проведенная к функции e x в любой точке, имеет наклон, равный e x ! Довольно круто!
Число Эйлера также является основанием натурального логарифма, пер.
 Логарифмы — это обратные экспоненциальные функции точно так же, как вычитание является обратным сложением, а деление — обратным умножению.
Логарифмы — это обратные экспоненциальные функции точно так же, как вычитание является обратным сложением, а деление — обратным умножению.Примеры
В этом разделе мы рассмотрим распространенные примеры с экспоненциальными функциями и их пошаговыми решениями.
Пример 1
Постройте график функции y=2 x . Используйте таблицу, чтобы помочь.
Пример 1 Решение
При построении графика экспоненциальной функции наиболее важными моментами являются точка пересечения по оси Y и горизонтальная асимптота.
Мы знаем, что для любой функции a x горизонтальной асимптотой является ось x, y=0. Так как в этой функции нет смещения по вертикали (т. е. в ее конец не добавлены числа), то асимптота не изменилась. Следовательно, эта функция будет стремиться к 0, когда x стремится к отрицательной бесконечности. Он также будет быстро расти до положительной бесконечности, когда x стремится к положительной бесконечности.
Поскольку эта функция не перемещалась ни влево, ни вправо, ни вверх, ни вниз, точка пересечения по оси y также не будет перемещаться.
 Таким образом, как и все другие экспоненциальные функции, y=2 x будет иметь точку пересечения с точкой (0, 1).
Таким образом, как и все другие экспоненциальные функции, y=2 x будет иметь точку пересечения с точкой (0, 1).Теперь мы можем использовать таблицу, чтобы найти еще несколько точек и более точно построить график функции. Давайте найдем значения для -2, -1, 0, 1, 2, 3 и 4.
Когда x=-2, мы имеем y=2 -2 =1/4.
Когда x=-1, мы имеем y=2 -1 =1/2.
Мы уже знаем, что когда x=0, y=1.
Когда x=1, 2, 3 и 4, мы имеем y=2 1 , y=2 2 , y=2 3 и y=2 4 .Эти функции упрощаются до 2, 4, 8 и 16 соответственно.
Теперь мы можем нанести эти точки на декартову плоскость и нарисовать плавную кривую, соединяющую их. Наконец, чтобы закончить наш график, мы можем продолжить левую часть кривой вдоль асимптоты y=0 по мере того, как x становится все меньше и меньше, и продолжить ее до бесконечности по мере того, как x становится все больше и больше.
Пример 2
Постройте график функции y=10 x-1 +3.
 Используйте таблицу, чтобы помочь вам.
Используйте таблицу, чтобы помочь вам.Пример 2 Решение
Эта экспоненциальная функция имеет большее значение, чем та, которую мы рассмотрели в примере 1.Однако, как и прежде, мы начнем с нахождения горизонтальной асимптоты и точки пересечения по оси Y.
Глядя на нашу функцию, мы видим, что основание равно 10 и возведено в степень x-1. То есть функция на единицу правее функции 10 x . Точно так же мы добавляем 3 ко всей функции. Это означает, что функция на три единицы выше родительской функции 10 x . Таким образом, в сумме функция на одну единицу правее и на три единицы выше исходной функции.
Следовательно, наша горизонтальная асимптота также сдвинется вверх на 3 единицы к горизонтальной линии y=3. Теперь мы можем использовать таблицу, чтобы найти точку пересечения по оси Y и другие точки. Рассмотрим x=-1, x=0, x=1, x=2 и x=3.
Когда x=-1, мы имеем y=10 -2 +3. Это равно 1/100+3 или 3,01.
На пересечении оси y, x=0, мы имеем 10 -1 +3.
 Это то же самое, что 1/10+3 или 3,1.
Это то же самое, что 1/10+3 или 3,1.Когда x=1, мы возводим 10 в степень 0, что равно 1. Следовательно, y=1+3=4.
Аналогично, когда x=2, мы имеем 10 1 +3=13.При x=3 имеем 10 2 +3=103.
Эта функция явно растет очень быстро! От x=-1 до x=3 разница почти в 100 раз!
Чтобы закончить построение графика этой функции, мы просто нарисуем горизонтальную асимптоту в точке 3, когда x стремится к минус бесконечности, и нарисуем стрелку, указывающую на бесконечность, когда x становится все больше и больше.
Пример 3
Сравните графики функций f(x)=(1/5)5 x и g(x)=5 x . Используйте таблицу, чтобы помочь вам.
Пример 3 Решение
Начнем с g(x)=5 x , так как это более простая функция. Как и все основные экспоненциальные функции, она имеет горизонтальную асимптоту при y=0 и пересекает ось y в точке (0, 1).
Все значения y в функции f(x) будут составлять 1/5 значений соответствующих значений в g(x).
 Это означает, что функция будет пересекать ось Y в точке (0, 1/5) вместо (0, 1). Однако его горизонтальная асимптота не изменится, поскольку не произошло никакого вертикального смещения.Следовательно, как и g(x), f(x) имеет горизонтальную асимптоту на линии y=0.
Это означает, что функция будет пересекать ось Y в точке (0, 1/5) вместо (0, 1). Однако его горизонтальная асимптота не изменится, поскольку не произошло никакого вертикального смещения.Следовательно, как и g(x), f(x) имеет горизонтальную асимптоту на линии y=0.Теперь давайте сравним две функции в точках x=-1, x=0, x=1 и x=2.
При x=-1 g(x) равно 5 -1 , что равно 1/5. Следовательно, f(x) будет составлять 1/5 от этого при 1/25.
Мы уже обсуждали x=0, так как это точка пересечения с осью y. Функция f(x)=1/5, а g(x)=1.
Когда x=1, g(x)=5 1 , что равно 5. Следовательно, f(x)=1.
Наконец, когда x=2, g(x)=5 2 =25.Функция f(x) будет равна 1/5 от g(x), поэтому f(x)=5.
В этом случае f(x)=g(x-1). Это имеет смысл, потому что, если мы рассмотрим функцию 5 x-1 , мы получим 5 x× 5 1 =1/5(5) x .
График функций выглядит так, как показано ниже.
Пример 4
Постройте график функции y=2(3) x-2 +4.
 Используйте таблицу, чтобы помочь вам.
Используйте таблицу, чтобы помочь вам.Пример 4 Решение
Основание этой функции равно 3.Она возведена в степень x-2, что указывает на сдвиг по горизонтали на 2. Точно так же, поскольку мы добавляем 4 ко всей функции, возникает сдвиг по вертикали на четыре единицы вверх. Однако, в отличие от примера 2, мы также должны учитывать растяжение в 2 раза, указанное цифрой 2 перед 3 x-2 .
Вертикальный сдвиг говорит нам о том, что асимптота также сдвинется вверх на 4 единицы. Следовательно, когда x стремится к минус бесконечности, значения y будут стремиться к положительным 4 вдоль линии y=4.
Теперь мы можем использовать таблицу, чтобы найти значения 1, 2, 3 и 4.Мы используем эти числа вместо -1, 0, 1, 2, потому что они дадут нам показатели степени -1, 0, 1 и 2. Для большинства чисел это самые простые степени для возведения числа, что означает, что они самые простые расчеты. Они также являются одними из самых важных чисел на графике, потому что они находятся вокруг точки пересечения с осью y.

При x=1 имеем 2(3) -1 +4. 3 -1 равно 1/3, поэтому наш ответ равен 4+2/3, что примерно равно 4,66.
При x=2 имеем 2(3) 0 +4=2(1)+4=6.
Теперь, когда x=3, мы имеем 2(3) 1 +4=2(3)+4=10.
Наконец, когда x=4, мы имеем 2(3) 2 +4=22.
Как и в некоторых других примерах, эта функция очень быстро растет и очень быстро становится большой. График ниже моделирует это.
Пример 5
Определите алгебраическое выражение экспоненциального графика, показанного ниже:
Пример 5 Решение
Подсказка говорит нам, что эта функция является экспоненциальной, но форма также указывает на это.Единственная разница между тем, что мы видим, и нормальной экспоненциальной функцией состоит в том, что она отражена по оси X. Это означает, что перед a будет стоять -1.
По мере того, как функция становится все меньше и меньше, значения y стремятся к нулю, но так и не достигают его.
 По мере того, как функция становится все больше и больше, значения y становятся все меньше и меньше. Следовательно, существует горизонтальная асимптота на линии y=0, оси x.
По мере того, как функция становится все больше и больше, значения y становятся все меньше и меньше. Следовательно, существует горизонтальная асимптота на линии y=0, оси x.Эта функция также пересекает ось Y в точке (0, -1).Это означает, что нет никакого сдвига в функции, кроме отражения.
Однако нам нужно найти некоторые другие точки, чтобы определить основание a функции.
Довольно сложно определить числа, которые не лежат на линиях сетки с достаточной точностью. Поэтому мы сосредоточимся на положительных значениях x. Мы видим, что эта линия также пересекает точки (1, -3) и (2, -9). Это означает, что до того, как мы умножим значения x на -1 и отразим их по оси y, 1 = 3 и 2 = 9.Таким образом, a должно быть равно 3.
Таким образом, мы можем заключить, что функция y=3 -x .
Пример 6
Определите алгебраическое представление экспоненциальной функции и ее график, учитывая следующие точки: (-1, 5,5), (0, 6), (1, 7) и (2, 9).

Пример 6 Решение
Поскольку эта функция пересекает ось Y в точке (0, 6), произошел вертикальный сдвиг. В частности, функция переместилась с (0, 1) на (0, 6), что представляет собой сдвиг вверх на 5 единиц.
Горизонтальная асимптота также сдвинется вверх на 5 единиц от y=0 до y=5.
Теперь мы знаем, что функция имеет вид x +5. Чтобы найти x , мы должны вычесть 5 из каждого из заданных значений y. В этом случае мы получаем (-1, 0,5), (0, 1), (1, 2) и (2, 4). Таким образом, основанием является такое число, что 1 = 2, а 2 = 4. Отсюда видно, что а=2.
Теперь у нас достаточно информации для построения графика функции.
Пример 7
Пусть f(x)=(4) x .Пусть g(x) будет отражением f(x) по оси x со сдвигом влево на три единицы. Что такое граф и алгебраическое представление на основе словесного описания. Используйте таблицу, чтобы помочь.
Пример 7 Решение
В этом случае проще всего начать с нахождения алгебраического представления g(x) на основе f(x) и словесного описания.

Отражение по оси Y означает, что вся функция умножается на -1. Таким образом, пока что у нас есть -4 x . Помните, что это не то же самое, что (-4) x .
Так как функция также перемещается на три единицы влево, нам нужно напрямую добавить три к x. Это дает нам g(x)=-4 x+3 .
Теперь мы можем использовать таблицу для поиска точек на этом графике. Давайте рассмотрим, что происходит, когда x=-4, x=-3, x=-2 и x=-1. Опять же, мы выбираем эти точки, потому что они возводят функцию в степени -1, 0, 1 и 2, с которыми легко работать.
Когда x=-4, мы имеем g(x)=-4 -1 =-1/4.
В точке x=-3 получаем g(x)=-4 0 =-1.
Тогда при x=-2 и x=-1 получаем g(x)=-4 1 =-4 и g(x)=-4 2 =-16 соответственно.
Таким образом, наш график выглядит так.
Пример 8
Что произойдет, если a меньше 1? Давайте рассмотрим это, построив график y=(1/2) x .
 Мы будем использовать график, чтобы помочь.
Мы будем использовать график, чтобы помочь.Пример 8 Решение
Вероятно, мы можем догадаться, что поскольку функция не имеет сдвига ни по горизонтали, ни по вертикали, она пересекает ось Y в точке (0, 1).Быстрое решение для x = 0 дает нам y = (1/2) 0 = 1. Следовательно, наша интуиция верна.
Точно так же, поскольку не было никакого сдвига, мы можем предположить, что горизонтальная асимптота — это y=0, ось x.
Рассмотрим некоторые другие точки, включая x=-2, x=-1, x=1 и x=2.
При x=-2 имеем y=(1/2) -2 . Это то же самое, что y=2 2 =4.
Аналогично, x=-1 равно y=(1/2) 1 , что совпадает с y=2 1 =2.
Мы уже знаем, что точка пересечения по оси y равна 0.
Теперь, когда x=1, y=(1/2) 1 =1/2.
Аналогично, когда x=2, y=(1/2) 2 =1/4.
Мы видим, что эта функция аналогична функции y=2 x , перевернутой по оси Y! По мере того как в этом случае x стремится к положительной бесконечности, функция будет все ближе и ближе приближаться к 0.
 Следовательно, мы были правы в том, что горизонтальная асимптота равна y = 0, но она существует, поскольку значения x становятся бесконечно большими, а не бесконечно малыми.
Следовательно, мы были правы в том, что горизонтальная асимптота равна y = 0, но она существует, поскольку значения x становятся бесконечно большими, а не бесконечно малыми.Почему это так?
Напомним, что (1/2)=2 -1 . Следовательно, y=(1/2) x совпадает с y=2 -x . Вспомните ранее, что умножение x на -1 отражает эту функцию (или любую функцию, если уж на то пошло) по оси x. Поэтому имеет смысл, что эти две функции связаны!
Практические задачи
- Постройте график функции y=4 x . Используйте таблицу, чтобы помочь.
- Постройте график экспоненциальной функции, проходящей через точки (0, 2), (1, 3) (2, 5), (3, 9).Затем найдите алгебраическое представление этой функции.
- Каково алгебраическое представление графа, показанного ниже?
- Сравните графики 3 x и (1/3) x .
- Функция 10 x отражается по оси X и смещается на четыре единицы вниз.
 Каков график этой функции? Каково его алгебраическое представление?
Каков график этой функции? Каково его алгебраическое представление?
Ключ к ответу на практическую задачу
-
Алгебраическое представление: 2 x +1. - Это график 2 x-1 +2.
- Эти графики представляют собой один и тот же график, отраженный по оси Y.
- Новое алгебраическое представление равно -10 x -4. График:
График экспоненциальных функций: примеры
Графики Экспоненциальные функции: примеры (стр. 3 из 4)
Разделы: вводные концепции, пошаговые инструкции по построению графиков, Примеры работы
- График и = 2 х + 4
Это стандарт экспоненциальный, за исключением того, что «+ 4» толкает график вверх так что это на четыре единицы выше, чем обычно.

Сначала я вычисляю некоторые точки:
Затем я рисую эти очки:
Студент очень часто вычисляют только и значений для значений x которые близки к нулю.
 Тогда либо они понятия не имеют, где
график идет с левой стороны, и оставьте его висеть там:
Тогда либо они понятия не имеют, где
график идет с левой стороны, и оставьте его висеть там:неверно график …или иначе они опустите график до оси x , как обычно для стандартного экспоненциального графика:
неверно график Но это не стандартный экспоненциальный график; это стандартная экспонента граф поднят на четыре единицы .
 Когда х отрицательно, y = 2 х + 4 не будет
быть очень близким к нулю; вместо этого он будет очень близок к 4,
потому что значения будут «маленькими-маленькими числами,
плюс четыре», что получается чуть-чуть больше
чем четыре.
Когда х отрицательно, y = 2 х + 4 не будет
быть очень близким к нулю; вместо этого он будет очень близок к 4,
потому что значения будут «маленькими-маленькими числами,
плюс четыре», что получается чуть-чуть больше
чем четыре.авторское право Элизабет Стапель 2002-2011 Все права защищены
Чтобы помочь мне с мой график и указать, что я знаю, что y = 2 х + 4 никогда идет ниже (или даже касается, если уж на то пошло) линии y = 4, я буду начертил пунктирную линию на y = 4:
рисунок асимптота может быть полезной Этот заштрихованный линия, указывающая, куда идет график, как x головы в сторону, называется «горизонтальной асимптотой», или просто «асимптота».
 Не обязательно рисовать его, но это может быть полезно,
и можете указать учителю на тесте, что вы знаете
что ты делаешь.
Не обязательно рисовать его, но это может быть полезно,
и можете указать учителю на тесте, что вы знаете
что ты делаешь.Тогда я нарисую экспонента:
график от до = 2 х + 4 - График и = 5 х
Мне нужно помнить, что «отрицательная» экспонента меняет положение на противоположное (по оси x ) в котором мощность на 5 отрицательно.
 Когда значения x отрицательны (то есть, когда я нахожусь в левой части графика),
значение х будет положительным, поэтому график будет быстро расти в левой части.
С другой стороны, когда значения x положительны (т. е. находятся в правой части графика), значение х будет отрицательным, поэтому график будет оставаться очень близко к оси x .
Когда значения x отрицательны (то есть, когда я нахожусь в левой части графика),
значение х будет положительным, поэтому график будет быстро расти в левой части.
С другой стороны, когда значения x положительны (т. е. находятся в правой части графика), значение х будет отрицательным, поэтому график будет оставаться очень близко к оси x .Другими словами, стандартные значения меняются местами:
Затем и = 5 х графики как:
Любой график, похожий на выше (большой слева и ползущий вдоль оси x ) справа) отображает экспоненциальное затухание , а не экспоненциальное рост.
 Чтобы график отображал экспоненциальное затухание, либо показатель степени
является «отрицательным», иначе основание находится между 0
и 1.
Вы должны ожидать, что вам нужно будет определить тип экспоненциального
уравнение из графика. Первые два проработанных примера отображали экспоненциальный
рост; последний пример выше показывает экспоненциальное затухание; и следующее
снова демонстрирует экспоненциальный рост.
Чтобы график отображал экспоненциальное затухание, либо показатель степени
является «отрицательным», иначе основание находится между 0
и 1.
Вы должны ожидать, что вам нужно будет определить тип экспоненциального
уравнение из графика. Первые два проработанных примера отображали экспоненциальный
рост; последний пример выше показывает экспоненциальное затухание; и следующее
снова демонстрирует экспоненциальный рост.Это не то же самое как «2 x + 3″.В «2 х + 3″, стандарт экспонента сдвинута вверх на три единицы. В этом случае смещение во «внутрь» экспоненциальный. Вместо «+ 3» переключение «2 х » на три, «+ 3» смещает «2 х » сбоку на три. Единственный вопрос: сдвиги вбок какие путь, левый или правый? Как я понимаю это прямо, чтобы рассмотреть один из основные точки любой экспоненты.
 Когда мощность равна нулю, экспонента
1.
Для «2 ( х +3) «,
когда мощность равна нулю? Когда х + 3 = 0, значит х = 3. То есть
основная сюжетная точка (0,
1) был сдвинут
в точку (3,
1), поэтому график
был сдвинут на три пункта влево:
Когда мощность равна нулю, экспонента
1.
Для «2 ( х +3) «,
когда мощность равна нулю? Когда х + 3 = 0, значит х = 3. То есть
основная сюжетная точка (0,
1) был сдвинут
в точку (3,
1), поэтому график
был сдвинут на три пункта влево:
<< Предыдущий Топ | 1 | 2 | 3 | 4 | Вернуться к индексу Далее >>
Процитировать эту статью как:
Стапель, Элизабет.


 Например:
Например:

 Этот промежуток времени t0 называется периодом полураспада. Общая формула для этого процесса: m = m0(1/2)—t/t0 , где m0 — первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество. Это явление используют для определения возраста археологических находок. Радий, например распадается по закону: M = M0e—kt, используя данную формулу ученые рассчитали возраст Земли (радий распадается нормально за время равное возрасту Земли).
Этот промежуток времени t0 называется периодом полураспада. Общая формула для этого процесса: m = m0(1/2)—t/t0 , где m0 — первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество. Это явление используют для определения возраста археологических находок. Радий, например распадается по закону: M = M0e—kt, используя данную формулу ученые рассчитали возраст Земли (радий распадается нормально за время равное возрасту Земли).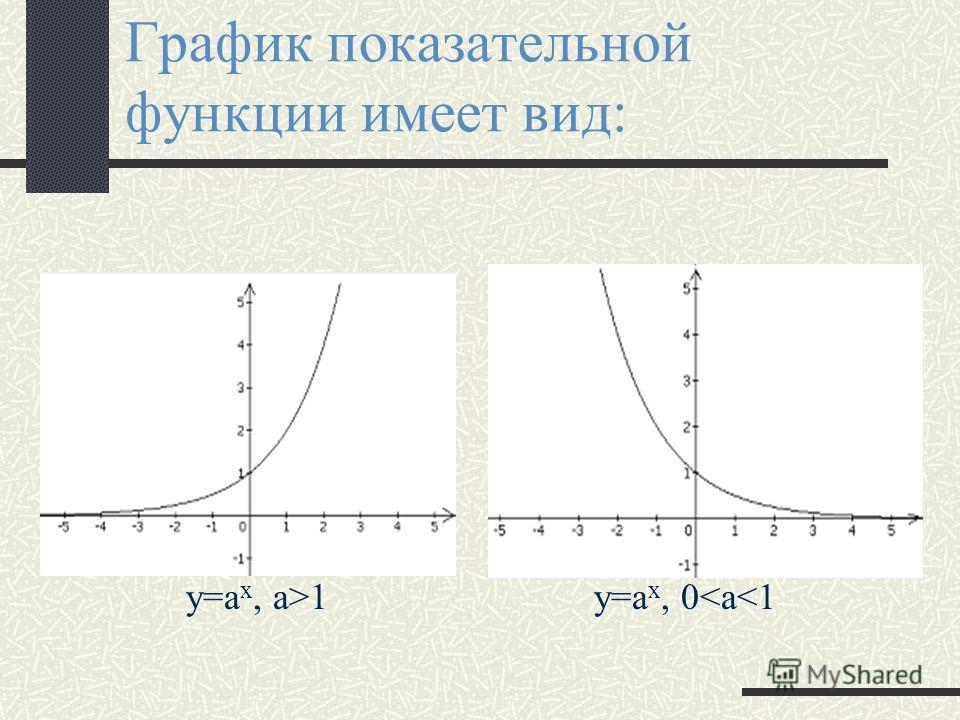

 то есть
то есть

 Основная экспоненциальная функция имеет вид f(x) = b x , где b > 0 и b ≠ 1,
Основная экспоненциальная функция имеет вид f(x) = b x , где b > 0 и b ≠ 1, Затем нанесите точки из таблицы и соедините их кривой. Наконец, удлините кривую на обоих концах.
Затем нанесите точки из таблицы и соедините их кривой. Наконец, удлините кривую на обоих концах.


 x}\]
x}\] 718…
718… 2} — 4\\ & = 5\влево( {7.389} \вправо) — 4\конец{выравнивание*}\]
2} — 4\\ & = 5\влево( {7.389} \вправо) — 4\конец{выравнивание*}\] е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
 {1 — \frac{t}{2}}}\).
Показать решение
{1 — \frac{t}{2}}}\).
Показать решение
 Это движение изменит и горизонтальную асимптоту графика. У родительской функции была горизонтальная асимптота в точке {eq}y=0 {/eq}, и теперь, после этого переноса, асимптота находится в точке {eq}y=-3 {/eq}. Родительская функция имела точку пересечения y в точке {eq}(0,1) {/eq}, а теперь точка пересечения находится в точке {eq}(0,-2) {/eq}. Это движение графика вниз на три позиции. Домен по-прежнему состоит из действительных чисел, но диапазон больше не равен {eq}y\geq 0 {/eq}. Теперь диапазон равен {eq}y\geq -3 {/eq}.{x+3} {/eq}
Это движение изменит и горизонтальную асимптоту графика. У родительской функции была горизонтальная асимптота в точке {eq}y=0 {/eq}, и теперь, после этого переноса, асимптота находится в точке {eq}y=-3 {/eq}. Родительская функция имела точку пересечения y в точке {eq}(0,1) {/eq}, а теперь точка пересечения находится в точке {eq}(0,-2) {/eq}. Это движение графика вниз на три позиции. Домен по-прежнему состоит из действительных чисел, но диапазон больше не равен {eq}y\geq 0 {/eq}. Теперь диапазон равен {eq}y\geq -3 {/eq}.{x+3} {/eq}
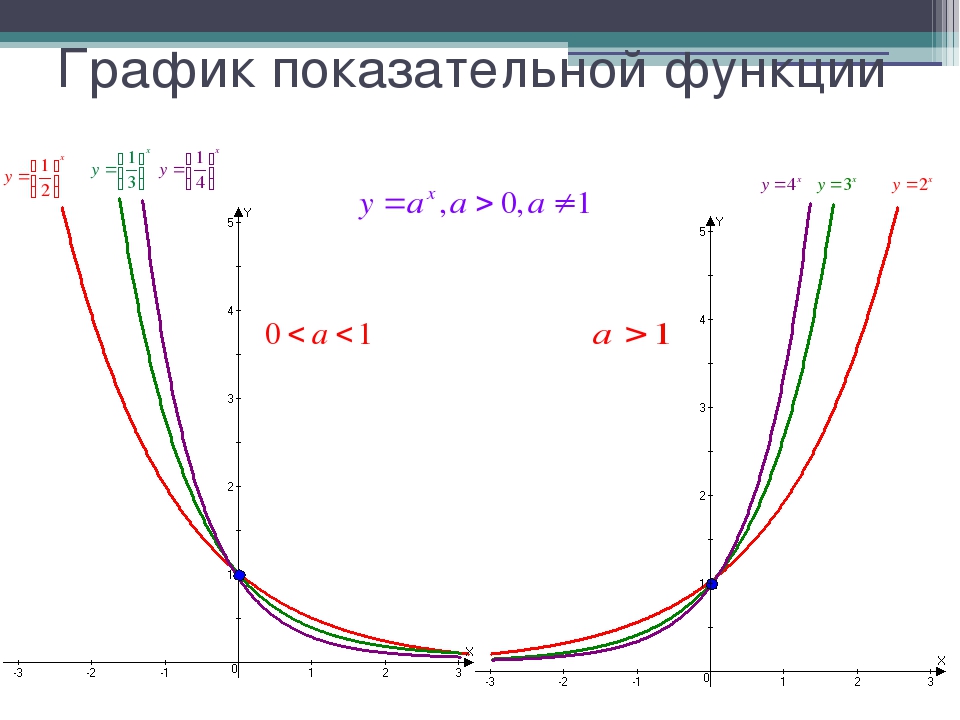 Обратите внимание, является ли функция отрицательной или независимая переменная отрицательна, чтобы также помочь вам узнать положение или направление графика. Если либо функция, либо независимая переменная отрицательны, функция будет уменьшаться по всей своей области определения.
Обратите внимание, является ли функция отрицательной или независимая переменная отрицательна, чтобы также помочь вам узнать положение или направление графика. Если либо функция, либо независимая переменная отрицательны, функция будет уменьшаться по всей своей области определения.
 Если родительская функция имеет асимптоту в точке {eq}y=0 {/eq} и к функции добавлено {eq}2 {/eq}, добавьте {eq}2 {/eq} к исходной асимптоте. Новая асимптота будет расположена в точке {eq}y=2 {/eq}. Если родительская функция имеет асимптоту при {eq}y=-2 {/eq}, а {eq}3 {/eq} было вычтено из функции, то вычтите {eq}3 {/eq} из исходной асимптоты. Новая асимптота будет расположена в точке {eq}y=-5 {/eq}.
Если родительская функция имеет асимптоту в точке {eq}y=0 {/eq} и к функции добавлено {eq}2 {/eq}, добавьте {eq}2 {/eq} к исходной асимптоте. Новая асимптота будет расположена в точке {eq}y=2 {/eq}. Если родительская функция имеет асимптоту при {eq}y=-2 {/eq}, а {eq}3 {/eq} было вычтено из функции, то вычтите {eq}3 {/eq} из исходной асимптоты. Новая асимптота будет расположена в точке {eq}y=-5 {/eq}. {x-2}-3 {/экв}.
{x-2}-3 {/экв}. Диапазон относится ко всем значениям y. Функция либо возрастает на всей своей области определения, либо убывает, и она вогнута вверх или вогнута вниз . Вогнутость описывает кривизну графика.Ключевые функции могут изменяться в зависимости от преобразований , которые происходят с функцией. Этот урок был посвящен преобразованиям отражений и переводов . Отражения, или отрицательные экспоненциальные функции, переворачивают график по оси x или y, когда перед базовым числом стоит отрицательное значение или перед независимой переменной стоит отрицательное значение. Переводы перемещают графики вверх, вниз, влево или вправо, когда число прибавляется или вычитается из функции или независимой переменной.
Диапазон относится ко всем значениям y. Функция либо возрастает на всей своей области определения, либо убывает, и она вогнута вверх или вогнута вниз . Вогнутость описывает кривизну графика.Ключевые функции могут изменяться в зависимости от преобразований , которые происходят с функцией. Этот урок был посвящен преобразованиям отражений и переводов . Отражения, или отрицательные экспоненциальные функции, переворачивают график по оси x или y, когда перед базовым числом стоит отрицательное значение или перед независимой переменной стоит отрицательное значение. Переводы перемещают графики вверх, вниз, влево или вправо, когда число прибавляется или вычитается из функции или независимой переменной.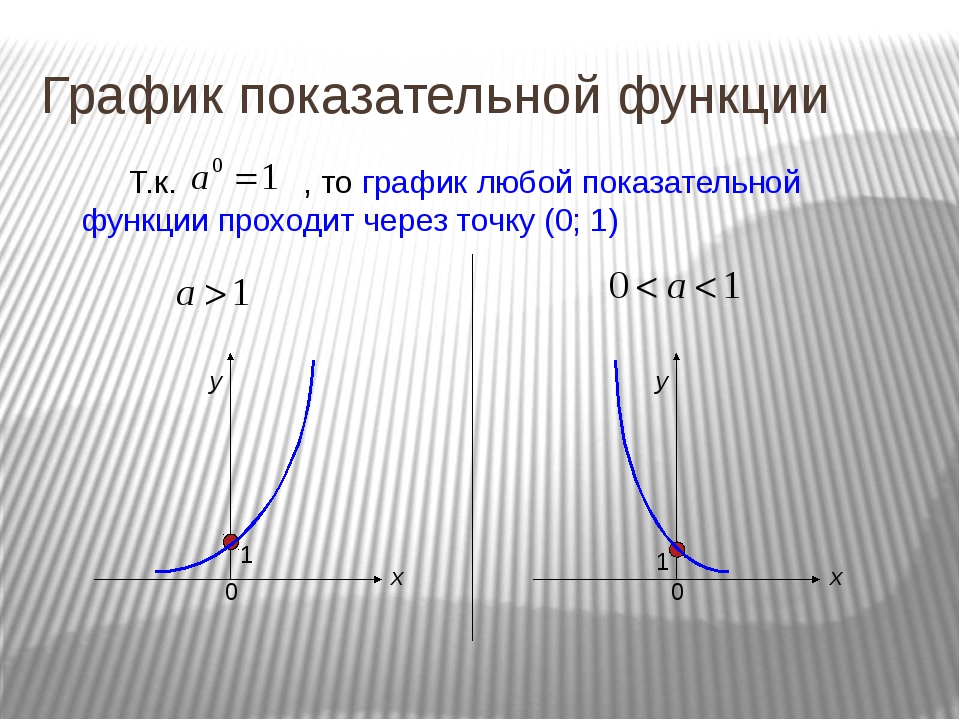 Мы изучали функции с переменным основанием и постоянными показателями, такими как x2 или y−3. В этом разделе мы исследуем функции с постоянным основанием и переменными показателями. При заданном вещественном числе b>0, где b≠1, экспоненциальная функцияЛюбая функция с определением вида f(x)=bx, где b>0 и b≠1.имеет вид,
Мы изучали функции с переменным основанием и постоянными показателями, такими как x2 или y−3. В этом разделе мы исследуем функции с постоянным основанием и переменными показателями. При заданном вещественном числе b>0, где b≠1, экспоненциальная функцияЛюбая функция с определением вида f(x)=bx, где b>0 и b≠1.имеет вид,
 Это связано с тем, что f(0)=b0=1 для любой функции, определенной с помощью формы f(x)=bx. Поскольку функции читаются слева направо, они интерпретируются как возрастающие или растущие экспоненциально. Кроме того, любая экспоненциальная функция этой формы будет иметь область определения, состоящую из всех действительных чисел (−∞, ∞), и диапазон, состоящий из положительных значений (0, ∞), ограниченных горизонтальной асимптотой при y = 0.
Это связано с тем, что f(0)=b0=1 для любой функции, определенной с помощью формы f(x)=bx. Поскольку функции читаются слева направо, они интерпретируются как возрастающие или растущие экспоненциально. Кроме того, любая экспоненциальная функция этой формы будет иметь область определения, состоящую из всех действительных чисел (−∞, ∞), и диапазон, состоящий из положительных значений (0, ∞), ограниченных горизонтальной асимптотой при y = 0.
 Ниже мы изобразили y=(12)x, y=(13)x и y=(110)x на одном и том же наборе осей.
Ниже мы изобразили y=(12)x, y=(13)x и y=(110)x на одном и том же наборе осей.
 Чтобы закончить, мы обычно хотим включить y -intercept. Помните, что для нахождения точки пересечения y мы устанавливаем x=0.
Чтобы закончить, мы обычно хотим включить y -intercept. Помните, что для нахождения точки пересечения y мы устанавливаем x=0. Другое важное число e возникает при работе с моделями экспоненциального роста и распада.Это иррациональное число, округленное до пяти знаков после запятой, e≈2,71828. Эта константа естественным образом встречается во многих реальных приложениях и поэтому называется естественным основанием . Иногда e называют постоянной Эйлера в честь Леонарда Эйлера (произносится как «Ойлер»).
Другое важное число e возникает при работе с моделями экспоненциального роста и распада.Это иррациональное число, округленное до пяти знаков после запятой, e≈2,71828. Эта константа естественным образом встречается во многих реальных приложениях и поэтому называется естественным основанием . Иногда e называют постоянной Эйлера в честь Леонарда Эйлера (произносится как «Ойлер»).


 44140
44140 Формула, которая дает сумму, накопленную за счет непрерывно начисленных процентов: A(t)=Pert.,
Формула, которая дает сумму, накопленную за счет непрерывно начисленных процентов: A(t)=Pert.,
 Кроме того, все экспоненциальные функции этой формы имеют точку пересечения y (0,1) и являются асимптотическими относительно оси x .
Кроме того, все экспоненциальные функции этой формы имеют точку пересечения y (0,1) и являются асимптотическими относительно оси x .


 Используйте калькулятор, где это уместно, чтобы округлить до ближайшей сотой.
Используйте калькулятор, где это уместно, чтобы округлить до ближайшей сотой.  2% годовых, которые начисляются ежемесячно. Сколько будет стоить компакт-диск в конце 3-летнего срока?
2% годовых, которые начисляются ежемесячно. Сколько будет стоить компакт-диск в конце 3-летнего срока? 8% годовых, начисляемых ежеквартально, то сколько процентов начисляется за первые 3 года?
8% годовых, начисляемых ежеквартально, то сколько процентов начисляется за первые 3 года? Сколько будет на счету через 212 лет?
Сколько будет на счету через 212 лет? 02)t, где t представляет время в годах с момента последней переписи. Используйте функцию для определения численности населения в день переписи (когда t = 0) и оцените численность населения через 6 лет с этого времени.
02)t, где t представляет время в годах с момента последней переписи. Используйте функцию для определения численности населения в день переписи (когда t = 0) и оцените численность населения через 6 лет с этого времени. Используйте формулу, чтобы определить стоимость автомобиля, когда он был новым ( t = 0) и стоимость через 4 года.
Используйте формулу, чтобы определить стоимость автомобиля, когда он был новым ( t = 0) и стоимость через 4 года.
 Какая часть образца остается через 10 дней?
Какая часть образца остается через 10 дней?
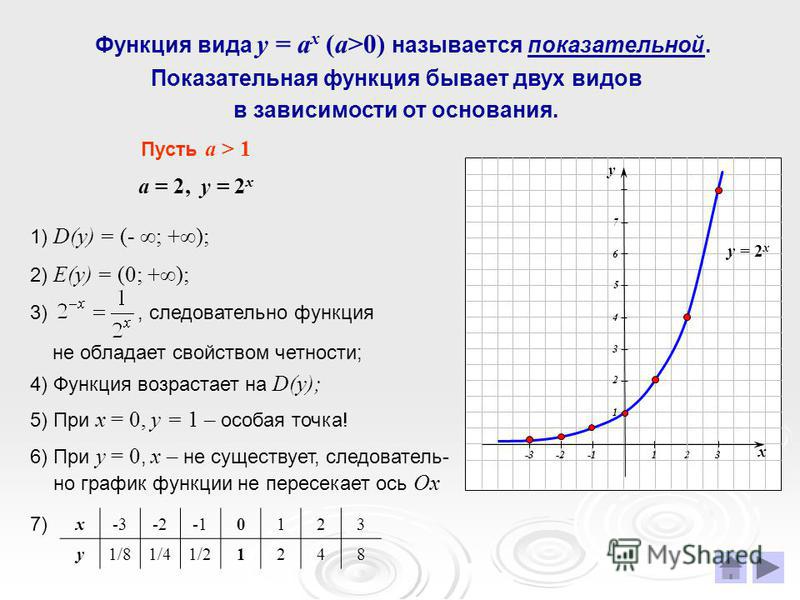 37, f(0)=3, f(32)≈6,48
37, f(0)=3, f(32)≈6,48 40
40
 В частности, важно изучить форму родительской функции. Из этого мы можем делать различные преобразования, в том числе сдвигать график влево и вправо, отражать его и растягивать.
В частности, важно изучить форму родительской функции. Из этого мы можем делать различные преобразования, в том числе сдвигать график влево и вправо, отражать его и растягивать.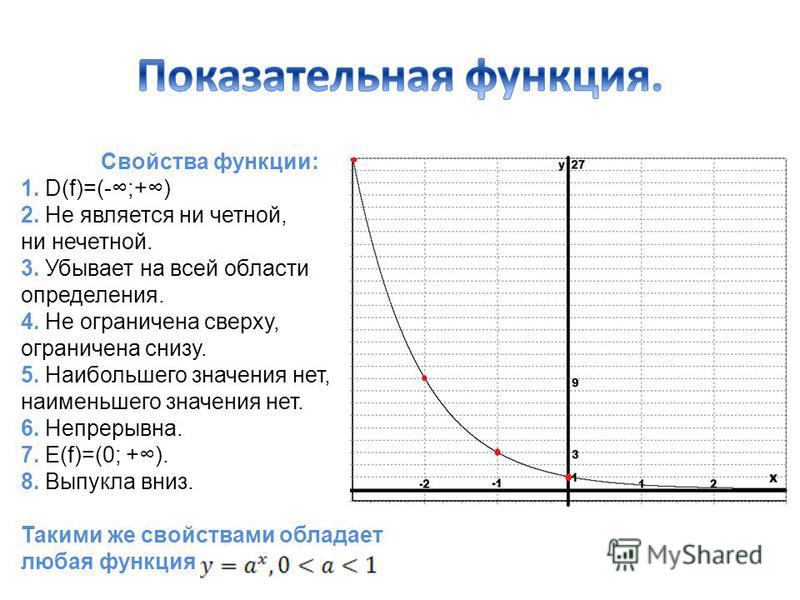 Но, что важно, они никогда не достигнут этого.Таким образом, асимптота — это линия, к которой функция приближается бесконечно близко, но на самом деле никогда не касается и не пересекает ее. В этом случае мы видим, что ось x является асимптотой любой экспоненциальной функции (при условии отсутствия вертикального смещения).
Но, что важно, они никогда не достигнут этого.Таким образом, асимптота — это линия, к которой функция приближается бесконечно близко, но на самом деле никогда не касается и не пересекает ее. В этом случае мы видим, что ось x является асимптотой любой экспоненциальной функции (при условии отсутствия вертикального смещения). В частности, если b положительно, функция сместит b единиц влево. Если b отрицательно, функция сдвинет |b| единиц вправо. Помните, что вы можете думать о числах, добавленных непосредственно к х, как о чем-то вроде «зеркального мира», где все противоположно тому, что вы ожидаете. Следовательно, отрицательные числа вызывают сдвиг вправо, а положительные числа вызывают сдвиг влево, что противоположно большинству вещей в математике.
В частности, если b положительно, функция сместит b единиц влево. Если b отрицательно, функция сдвинет |b| единиц вправо. Помните, что вы можете думать о числах, добавленных непосредственно к х, как о чем-то вроде «зеркального мира», где все противоположно тому, что вы ожидаете. Следовательно, отрицательные числа вызывают сдвиг вправо, а положительные числа вызывают сдвиг влево, что противоположно большинству вещей в математике.

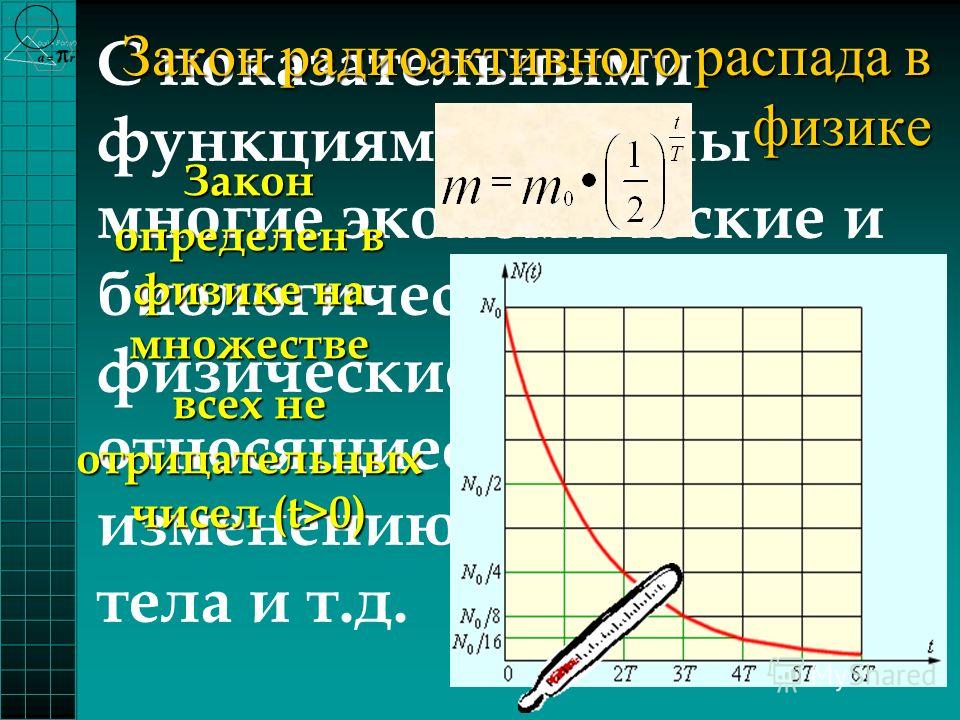 Логарифмы — это обратные экспоненциальные функции точно так же, как вычитание является обратным сложением, а деление — обратным умножению.
Логарифмы — это обратные экспоненциальные функции точно так же, как вычитание является обратным сложением, а деление — обратным умножению. Таким образом, как и все другие экспоненциальные функции, y=2 x будет иметь точку пересечения с точкой (0, 1).
Таким образом, как и все другие экспоненциальные функции, y=2 x будет иметь точку пересечения с точкой (0, 1). Используйте таблицу, чтобы помочь вам.
Используйте таблицу, чтобы помочь вам. Это то же самое, что 1/10+3 или 3,1.
Это то же самое, что 1/10+3 или 3,1. Это означает, что функция будет пересекать ось Y в точке (0, 1/5) вместо (0, 1). Однако его горизонтальная асимптота не изменится, поскольку не произошло никакого вертикального смещения.Следовательно, как и g(x), f(x) имеет горизонтальную асимптоту на линии y=0.
Это означает, что функция будет пересекать ось Y в точке (0, 1/5) вместо (0, 1). Однако его горизонтальная асимптота не изменится, поскольку не произошло никакого вертикального смещения.Следовательно, как и g(x), f(x) имеет горизонтальную асимптоту на линии y=0. Используйте таблицу, чтобы помочь вам.
Используйте таблицу, чтобы помочь вам.
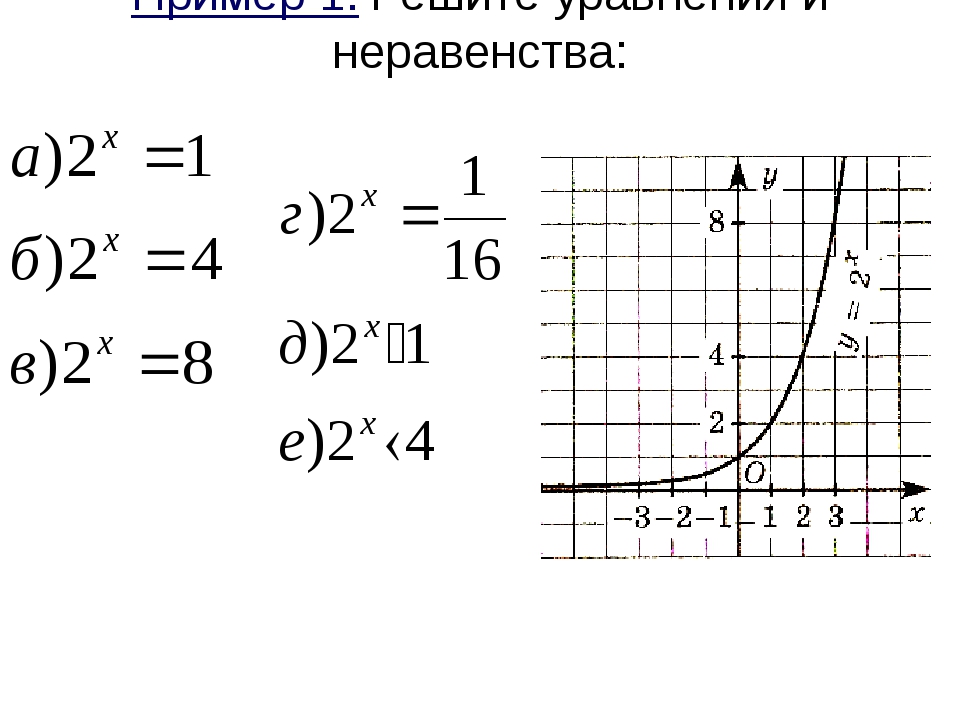 По мере того, как функция становится все больше и больше, значения y становятся все меньше и меньше. Следовательно, существует горизонтальная асимптота на линии y=0, оси x.
По мере того, как функция становится все больше и больше, значения y становятся все меньше и меньше. Следовательно, существует горизонтальная асимптота на линии y=0, оси x.

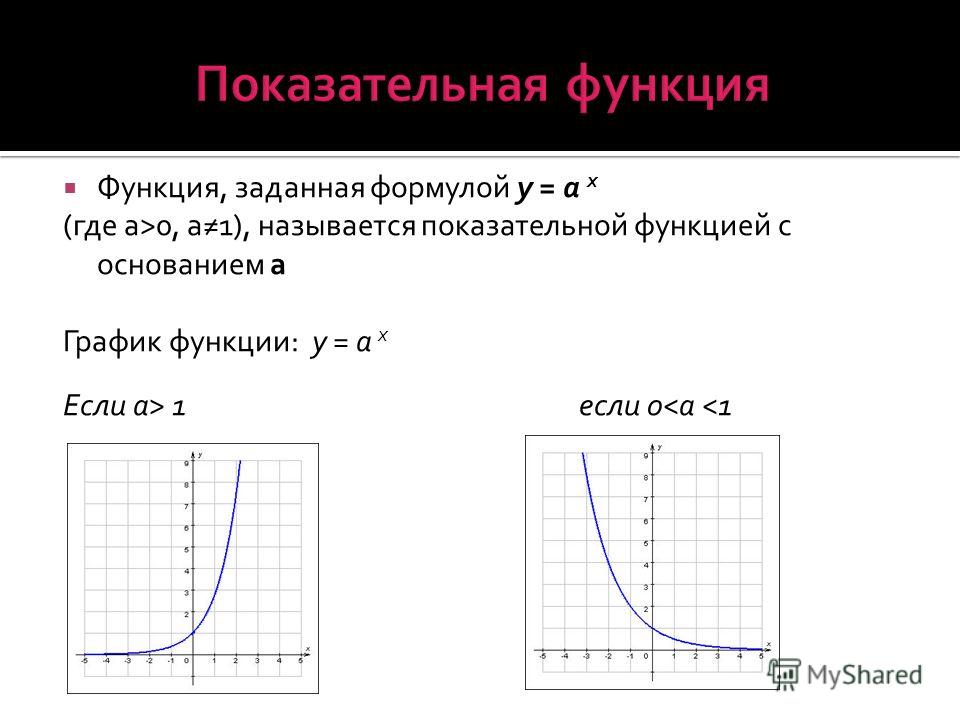 Мы будем использовать график, чтобы помочь.
Мы будем использовать график, чтобы помочь. Следовательно, мы были правы в том, что горизонтальная асимптота равна y = 0, но она существует, поскольку значения x становятся бесконечно большими, а не бесконечно малыми.
Следовательно, мы были правы в том, что горизонтальная асимптота равна y = 0, но она существует, поскольку значения x становятся бесконечно большими, а не бесконечно малыми. Каков график этой функции? Каково его алгебраическое представление?
Каков график этой функции? Каково его алгебраическое представление?
 Тогда либо они понятия не имеют, где
график идет с левой стороны, и оставьте его висеть там:
Тогда либо они понятия не имеют, где
график идет с левой стороны, и оставьте его висеть там: Когда х отрицательно, y = 2 х + 4 не будет
быть очень близким к нулю; вместо этого он будет очень близок к 4,
потому что значения будут «маленькими-маленькими числами,
плюс четыре», что получается чуть-чуть больше
чем четыре.
Когда х отрицательно, y = 2 х + 4 не будет
быть очень близким к нулю; вместо этого он будет очень близок к 4,
потому что значения будут «маленькими-маленькими числами,
плюс четыре», что получается чуть-чуть больше
чем четыре.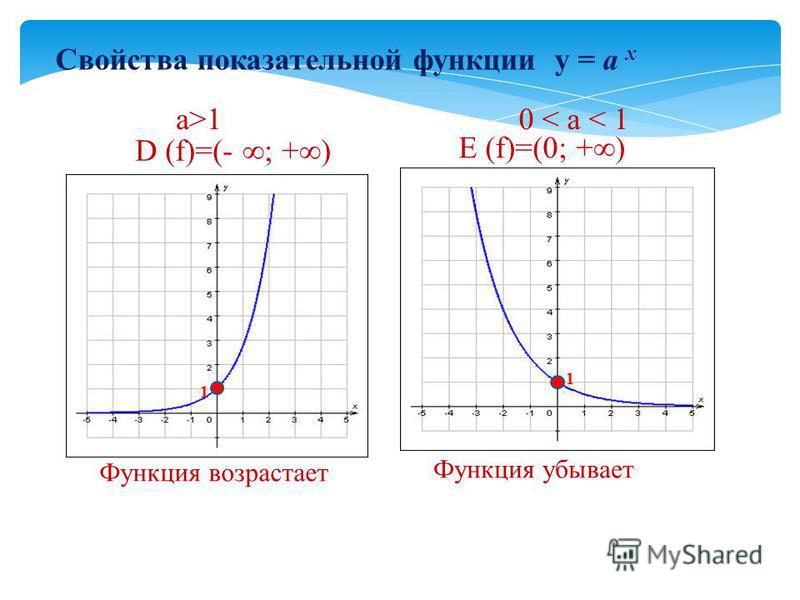 Не обязательно рисовать его, но это может быть полезно,
и можете указать учителю на тесте, что вы знаете
что ты делаешь.
Не обязательно рисовать его, но это может быть полезно,
и можете указать учителю на тесте, что вы знаете
что ты делаешь. Когда значения x отрицательны (то есть, когда я нахожусь в левой части графика),
значение х будет положительным, поэтому график будет быстро расти в левой части.
С другой стороны, когда значения x положительны (т. е. находятся в правой части графика), значение х будет отрицательным, поэтому график будет оставаться очень близко к оси x .
Когда значения x отрицательны (то есть, когда я нахожусь в левой части графика),
значение х будет положительным, поэтому график будет быстро расти в левой части.
С другой стороны, когда значения x положительны (т. е. находятся в правой части графика), значение х будет отрицательным, поэтому график будет оставаться очень близко к оси x . Чтобы график отображал экспоненциальное затухание, либо показатель степени
является «отрицательным», иначе основание находится между 0
и 1.
Вы должны ожидать, что вам нужно будет определить тип экспоненциального
уравнение из графика. Первые два проработанных примера отображали экспоненциальный
рост; последний пример выше показывает экспоненциальное затухание; и следующее
снова демонстрирует экспоненциальный рост.
Чтобы график отображал экспоненциальное затухание, либо показатель степени
является «отрицательным», иначе основание находится между 0
и 1.
Вы должны ожидать, что вам нужно будет определить тип экспоненциального
уравнение из графика. Первые два проработанных примера отображали экспоненциальный
рост; последний пример выше показывает экспоненциальное затухание; и следующее
снова демонстрирует экспоненциальный рост. Когда мощность равна нулю, экспонента
1.
Для «2 ( х +3) «,
когда мощность равна нулю? Когда х + 3 = 0, значит х = 3. То есть
основная сюжетная точка (0,
1) был сдвинут
в точку (3,
1), поэтому график
был сдвинут на три пункта влево:
Когда мощность равна нулю, экспонента
1.
Для «2 ( х +3) «,
когда мощность равна нулю? Когда х + 3 = 0, значит х = 3. То есть
основная сюжетная точка (0,
1) был сдвинут
в точку (3,
1), поэтому график
был сдвинут на три пункта влево: