Метод интервалов. Примеры
Продолжаем рассматривать метод интервалов. Примеры, в которых в ходе решения квадратного уравнения получаем дискриминант, равный нулю — следующие.
Используем алгоритм метода интервалов. Приравниваем к нулю левую часть:
Ищем дискриминант:
Поскольку дискриминант равен нулю, квадратное уравнение имеет один корень:
В точке x=3 на числовой прямой — «петля»:
Неравенство нестрогое, точка — закрашенная. Знак неравенства — больше либо равно, поэтому нам нужны промежутки с «+». Ответ:
От предыдущего неравенства это отличается только тем, что является строгим. Соответственно, точка x=3 — выколотая, и в ответ ее не включаем:
Ответ:
Поскольку знак неравенства — меньше либо равно, нам нужны промежутки с «-» а их нет. Отдельно стоящие закрашенные точки включаем в ответ. Здесь такая точка есть — x=3 (напоминаю, знак в петле — «виртуальный», на самом деле при x=3 выражение, стоящее в правой части, равно нулю, а нуль не является ни положительным, ни отрицательным числом).
Ответ:
Здесь нет ни одной точки удовлетворяющей условию неравенства.
Ответ:
Приравниваем к нулю левую часть. Получаем:
Поскольку в ходе решения уравнения x²-10x+25=0 получили дискриминант, равный нулю, в соответствующей точке x=5 — «петля». Отмечаем полученные точки на числовой прямой:
Знак неравенства — меньше либо равно, поэтому выбираем промежутки со знаком «-«. Точка х=5 — закрашенная, поэтому ее включаем в ответ (то есть разрывать промежуток от -3 до 6 не нужно).
Ответ: х∈(-3;6).
От предыдущего примера данный отличается только тем, что неравенство — строгое. Соответственно, все точки выколотые и в ответ х=5 уже не входит (промежуток от -3 до 6 разбивается на два).
Ответ: х∈(-3;5)U(5;6).
Здесь выбираем промежутки с «+». Отдельно стоящую закрашенную точку также включаем в ответ:
Ответ:
Поскольку неравенство — строгое, ни одну из точек в ответ не включаем:
Ответ:
Следует заметить, что если бы мы решали квадратные уравнения, в которых дискриминант равен нулю, используя теорему Виета, то получили бы два одинаковых корня (то есть один и тот же корень встречается четное число раз). Если бы свернули квадратный трехчлен по формулам квадрата суммы или квадрата разности, то получили бы кратный корень четной степени. То есть, при любом подходе пришли бы к «петле».
Примеры решений неравенств методом интервалов
I. Примеры решения иррациональных неравенств
1. 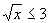
Решение. Введем функцию f(x) =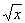 – 3. Необходимо определить промежутки, на которых f(x) 0. Очевидно, что D(f) = [0;). Нули f(x): x = 9.
– 3. Необходимо определить промежутки, на которых f(x) 0. Очевидно, что D(f) = [0;). Нули f(x): x = 9.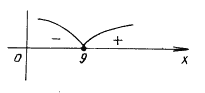
f(16) >0,
f(4) < 0.
Ответ: [0; 9].
2. 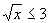 < 2 – x.
< 2 – x.
Решение. Традиционное решение этого неравенства приводит к системе неравенств

Решение этого неравенства можно осуществить, положив 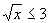
y < 20 – y2, y2 + y – 20 < 0, (y + 5)(y – 4) < 0,
откуда y < 4, поскольку y0. Итак, 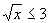 < 4 и – 18 x –2.
< 4 и – 18 x –2.
Интересен и такой вариант (графический) решения примера. Если заметить, что f(x) =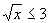 – функция возрастающая на луче [– 18; + ), а g(x) = 2 – x – убывающая на R и x = 2 – абсцисса их точки пересечения и при этом f(– 14) < g(– 14), то ясен и
– функция возрастающая на луче [– 18; + ), а g(x) = 2 – x – убывающая на R и x = 2 – абсцисса их точки пересечения и при этом f(– 14) < g(– 14), то ясен и
ответ: [– 18; – 2).
Обратимся к теме статьи. Пусть
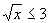 + x – 2. Надо решить неравенство f(x)< 0. Заметим, что D(f)=[– 18; +). Нули функции найдем, решив уравнение
+ x – 2. Надо решить неравенство f(x)< 0. Заметим, что D(f)=[– 18; +). Нули функции найдем, решив уравнение 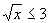 = 2 – x, откуда x = – 2.
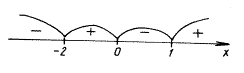
= 2 – x, откуда x = – 2. Применяем метод интервалов: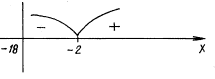
f(– 14) < 0,
f(7) > 0.
Ответ: [– 18; – 2).
3.  < 20.
< 20.
Решение. Область допустимых значений определяется системой неравенств
.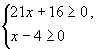
Для функции f(x) =  – 20 D(f) = [4; +). Далее находим нули f(x):
– 20 D(f) = [4; +). Далее находим нули f(x):
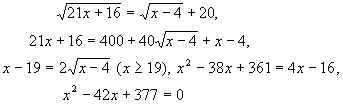
откуда x = 29 и x = 13 – посторонний корень.
f(30) =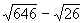 – 20 = 0,3 > 0,
– 20 = 0,3 > 0,
f(5) =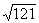 – 1 – 20 = – 10 < 0.
– 1 – 20 = – 10 < 0.
Ответ: [4; 29).
Примечание. Это неравенство можно решить, например, выполнив замену переменной 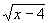 = y, где y 0.
= y, где y 0.
4. 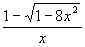 < 1.
< 1.
Решение. Область определения функции f(x) =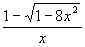 – 1 найдем, решив систему неравенств
– 1 найдем, решив систему неравенств
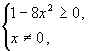
Легко видеть, что 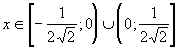 .
.
Находим нули функции f(x):
1 – 2x = 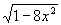 , – 4x + 12x2 = 0, x = 0 – посторонний корень, x =
, – 4x + 12x2 = 0, x = 0 – посторонний корень, x =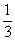 ;
;
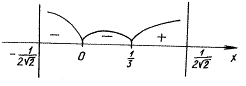
f(– 0,1) =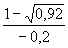 – 1 =
– 1 =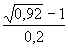 – 1 < 0,
– 1 < 0,
f(0,1) = 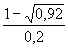 – 1 =
– 1 =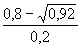
f(0,34) =
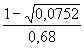 – 1 =
– 1 = 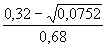 > 0.
> 0. Ответ: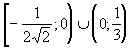 .
.
Примечание. Этот пример показывает, что для двух чисел, «близко» расположенных на координатной прямой, применение метода интервалов осуществимо.
5. 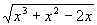 >x – 1.
>x – 1.
Решение. Пусть f(x) = 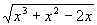
D(f) =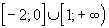 .
.
Ищем нули функции f, решив уравнение
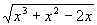 = x – 1, x3 = 1 и x = 1,
= x – 1, x3 = 1 и x = 1,
где x = 1 удовлетворяет уравнению, но не удовлетворяет исходному неравенству.
Далее применяем метод интервалов: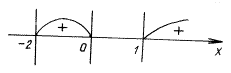
f(– 1) =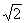 + 2 > 0,
+ 2 > 0,
f(2) = 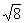 – 1 > 0.
– 1 > 0.
Ответ: 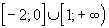 .
.
Традиционное решение данного неравенства сводится к совокупности двух систем:
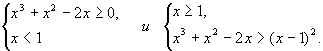
Примечание. Отметим, что не идет речь о преимуществах того или иного способа решения неравенств, а показывается применение метода интервалов на более широком классе неравенств.
Упражнения
Решите неравенства методом интервалов:
1. 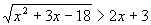 .
.
2. 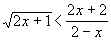 .
.
3. 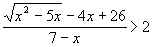 .
.
4. 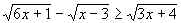 .
.
II. Примеры решения показательных неравенств
1. 4x < 2x+1 + 3.
Решение. Если f(x) = 4x – 2•2x – 3, то D(f) = R и необходимо решить неравенство f(x) < 0. Найдем нули
f: 4x–2•2x – 3 = 0, откуда 2x = 3, x = log23.
Далее применяем метод интервалов: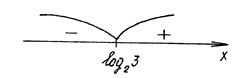
f(0) < 0, f(2) > 0.
Ответ: (– ; log23).
2. 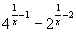 – 3 0.
– 3 0.
Решение. Пусть f(x) =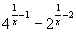 – 3. Решаем неравенство f(x) 0. Заметим, что D(f) = (– ; 0)(0; + ). Для нахождения нулей функции f решаем уравнение:
– 3. Решаем неравенство f(x) 0. Заметим, что D(f) = (– ; 0)(0; + ). Для нахождения нулей функции f решаем уравнение:
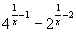 – 3 = 0.
– 3 = 0.
Полагая  = t, где t > 0, приходим к уравнению t2 –
= t, где t > 0, приходим к уравнению t2 – 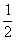 t – 3 = 0 с положительным корнем t = 2. Следовательно,
t – 3 = 0 с положительным корнем t = 2. Следовательно,  = 2 и x =
= 2 и x =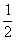 .
.
Применяем метод интервалов: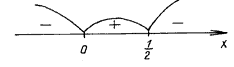
f(1) < 0,
f 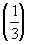 > 0,
> 0,
f(– 1) < 0.
Ответ: (– ; 0) 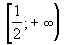 .
.
3. 4x 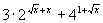 .
.
Решение. Рассмотрим функцию
f(x) = 4x – (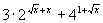 ) .
) .
Область определения функции f есть луч [0; + ). Найдем теперь нули функции f:
4x – (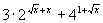 ) = 0.
) = 0.
Разделив обе части последнего уравнения на 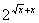 , получим
, получим
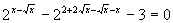 ,
, 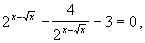
откуда 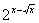 = 4, x–
= 4, x–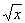 = 2, а это уравнение имеет единственный корень x = 4.
= 2, а это уравнение имеет единственный корень x = 4.
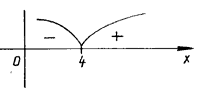
f(1) < 0, f(9) = 49 – 3•212 – 44 = 28(210 – 2•24 – 1) > 0.
Ответ: [0; 4].
4. 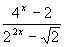 < 1.
< 1.
Решение. Введем в рассмотрение функцию f(x) =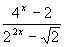 – 1. Легко видеть, что D(f) =
– 1. Легко видеть, что D(f) =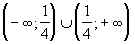 . Находим нули функции f(x): 4x – 2 – 22x +
. Находим нули функции f(x): 4x – 2 – 22x +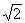 = 0. Уравнение корней не имеет.
= 0. Уравнение корней не имеет.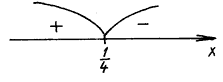
f(0) =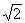 > 0,
> 0,
f(1) = 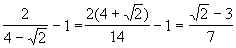 < 0.
< 0.
Ответ: 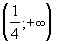 .
.
Упражнения
Решите методом интервалов неравенства:
5. 9x < 3x + 2.
6. 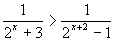 .
.
7. 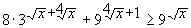 .
.
8. 3•4x – 7•10x + 2•25x > 0.
9.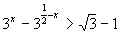 .
.
III. Примеры решения логарифмических
неравенств методов интервалов.
1. lg2 x – 2lg x – 8 0.
Решение. f(x) = lg2 x – 2lg x – 8, D(f) = (0; +). Для нахождения нулей функции f решаем уравнение
lg2 x – 2lg x – 8 = 0,
откуда lg x = – 2, lg x = 4 и x =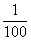 , x = 10000.
, x = 10000.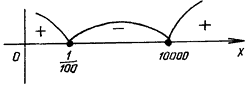
f(105) = 25 – 10 – 8 = 7 > 0,
f(1) < 0,
f(10–3) = 9 + 6 – 8 = 7 > 0.
Ответ: 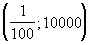 .
.
2. log0,3 (x2 – x – 20) – log0,3 (x + 4) > 0.
Решение. Найдем область определения функции f в левой части неравенства, решив систему неравенств
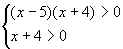 x > 5.
x > 5.
Решая уравнение log 0,3 (x2 – x – 20) – log0,3 (x + 4) = 0, находим нули функции f: x2 – x – 20 = x + 4, x2 – 2x – 24 = 0, x = – 4 – посторонний корень и x = 6.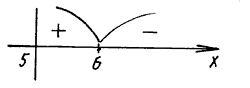
f(7) = log0,3 22 – log0,3 7 <0,
f(5,5) = log0,3 4,75 – log0,3 9,5>5.
Ответ: (5; 6).
3. 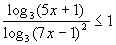 .
.
Решение. Пусть f(x) = 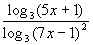 – 1. Необходимо решить неравенство f(x) 0.
– 1. Необходимо решить неравенство f(x) 0.
Область определения функции f определяется системой неравенств
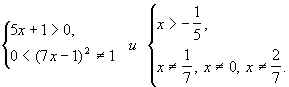
Итак, D(f) = 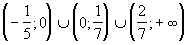 .
.
Найдем нули функции f:
log3 (5x + 1) = log3 (7x – 1)2,
откуда 49x2 – 19x = 0, x = 0 – посторонний корень, x =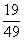 – корень уравнения.
– корень уравнения.
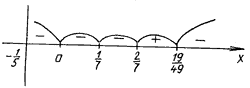
f(1) = 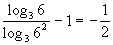 < 0,
< 0,
f(0,3) = 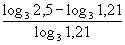 > 0,
> 0,
f(0,2) = 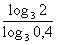 – 1 < 0, так как log3 2 > 0, log3 0,4 < 0.
– 1 < 0, так как log3 2 > 0, log3 0,4 < 0.
f(0,1) =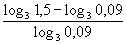 < 0,
< 0,
f(– 0,1) =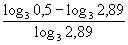 < 0.
< 0.
Ответ: 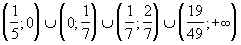 .
.
4. log3x+1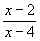 0.
0.
Решение. Для функции f(x) = log3x+1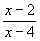 находим область определения. Решаем систему неравенств:
находим область определения. Решаем систему неравенств:
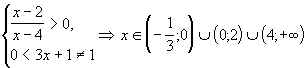 .
.
Найдем нули функции: log3x+1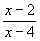 = 0,
= 0, 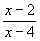 = 1, но последнее уравнение корней не имеет.
= 1, но последнее уравнение корней не имеет.
Применяем метод интервалов:
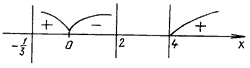
f(5) = log16 3 > 0,
f(1) = log4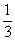 < 0,
< 0,
f(– 0,2) = log0,4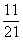 > 0.
> 0.
Ответ: 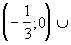 (4; + ).
(4; + ).
5. logx2 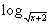 2.
2.
Решение. Для функции f(x) = logx 2 – 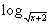 2 имеем D(f) = (0; 1) (1; + ). Очевидно, что для нахождения нулей f необходимо решить уравнение x =
2 имеем D(f) = (0; 1) (1; + ). Очевидно, что для нахождения нулей f необходимо решить уравнение x =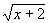 , откуда x = 2.
, откуда x = 2.
Применяем метод интервалов:
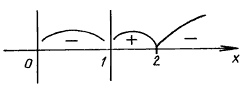
f(4) = log4 2 – log2 2 < 0,
f(1,5) = 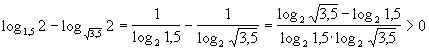 ,
,
f = 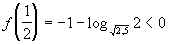 .
.
Ответ: (0; 1) [2; +).
Упражнения
Решите методом интервалов неравенства:
10. 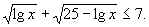
11. log2 (x + 1) < 1 – 2log4 x.
12. 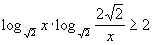 .
.
13. logx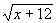 < 1.
< 1.
14. logx 3 log2x+3 9.
15. logx (1 – 2x) < 1.
16. log3 log27 log2 (x2 + x + 2) –1.
IV. Примеры на применение метода интервалов
к неравенствам, содержащим знак модуля.
1. x2 > | 5x + 6 |.
Решение. Функция f(x) = x2 – | 5x + 6 | определена при любом x. Найдем ее нули, решив уравнение
x2=| 5x + 6 |, откуда x2 = 5x + 6 или x2 = – (5x + 6), т. е.
x2 – 5x – 6 = 0 или x2 + 5x + 6 = 0.
Корни этих уравнений – 1, 6, – 2, – 3.
Далее применяем метод интервалов:
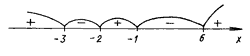
f(7) > 0, f(0) < 0, f(– 1,5) > 0, f(– 2,5) < 0, f(– 4) > 0.
Ответ: (–; – 3) (– 2; – 1) (6; + ).
Примечание. Неравенство можно также решить, заменив его на равносильное (x2 – 5x – 6)(x2 + 5x + 6) > 0.
2. y2 – 4| y | < 12.
Решение. Здесь положим f(y) = y2 – 4| y | – 12. Заметим, что D(y) = R и найдем нули функции f: y2 – 4| y | – 12=0, откуда | y | = 6, | y | = – 2. Последнее уравнение корней не имеет.
Ответ: – 6 < y < 6.
3. 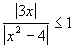 .
.
Решение. Заменим неравенство на равносильное 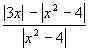 0 и положим f(x) =
0 и положим f(x) =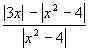 . Ясно, что D(f) = (– ; – 2) (– 2; 2) (2; + ). Находим нули функции f, решая уравнение | 3x | = | x2 – 4 |, которое распадается на два:
. Ясно, что D(f) = (– ; – 2) (– 2; 2) (2; + ). Находим нули функции f, решая уравнение | 3x | = | x2 – 4 |, которое распадается на два:
x2 – 3x – 4 = 0 и x2 + 3x – 4 = 0.
Корни этих уравнений соответственно равны – 1; 4 и 1; – 4.
Далее применяем метод интервалов:
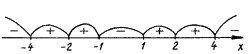
Ответ: (– ; – 4] [ – 1; 1] [4; + ).
Замечание. Конечно, при решении этого неравенства можно было учесть, что |x2 – 4 | > 0 при x ±2.
4. x2 + 2| x – 1 | + 7 4| x – 2 |.
Решение. Если f(x) = x2 + 2| x – 1 | + 7 – 4| x – 2 |, то D(f) = R и необходимо решить неравенство f(x) 0.
Находим нули f:
а) 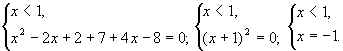
x = – 1 – нуль функции;
б) 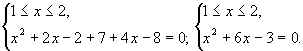
система решений не имеет;
в) 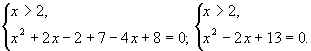
система не имеет решений.
Применяем метод интервалов:
f(0) > 0,
f(– 2) > 0.
Ответ: – 1.
5.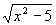 + 3 > | x – 1 |.
+ 3 > | x – 1 |.
Решение. Для f(x) = 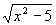 + 3 – | x – 1 | находим D(f) =
+ 3 – | x – 1 | находим D(f) =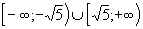 .
.
Находим нули функции f(x).
Если x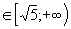 , то
, то
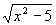 +3 – x + 1 = 0,
+3 – x + 1 = 0, 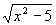 = x – 4, 8x = 21,
= x – 4, 8x = 21,
x = 2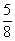 – не корень.
– не корень.
Если x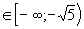 , то
, то
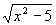 +3+x–1 = 0,
+3+x–1 = 0, 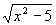 = – x – 2, 4x = – 9,
= – x – 2, 4x = – 9,
x = – 2,25 – корень.
Итак, функция f имеет один нуль x = –2,25.
Применяем метод интервалов:
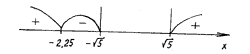
f(3) >0,
f(– 2,24) =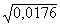 + 3 – 3,24 < 0,1 – 0,24 < 0,
+ 3 – 3,24 < 0,1 – 0,24 < 0,
f(– 3) > 0.
Ответ: (– ; – 2,25) [5; + ).
Упражнения
Решите методом интервалов неравенства:
17. | x – 6 | > x2 – 5x + 9.
18. 16| x2 – 2(x + | x | + 1 | < 1.
19. | x2 – | x + 1 || 2x – 3.
20. 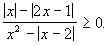
Ответы
1. (– ; – 6]
2. 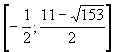 [0; 2).
[0; 2).
3. (– ; 0] [5; 7) (9; + ).
4. [3; 4].
5. (– ; log3 2).
6. (– ; 2) 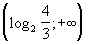 .
.
7. [0; 16].
8.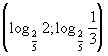
9.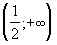
10.;1025]
11. (0;1)
12.[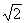 ;2]
;2]
13.(0;1)
14. (0;1) (3;+)
15.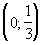
16.[-3;-1)
17.(1;3)
18. 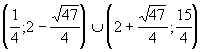
19. 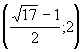
20.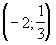
А. Смоляков,
г. Нефтекумск

Применение метода интервалов для решения неравенств. 9-й класс
Цель урока: рассмотреть применение метода интервалов для решения неравенств различных типов.
Задачи урока:
1. Сформировать у школьников мотивацию к изучению данной темы.
2. Развивать у учащихся умение пользоваться опорными знаниями, для их применения в новой ситуации.
3. Развивать у учащихся математическое мышление (умение наблюдать, выделять существенные признаки и делать обобщения).
4. Развивать у учащихся навыки творческого подхода к решению задач.
Оборудование и материалы: компьютер, проектор, экран, презентация для сопровождения занятия, раздаточный материал для учащихся.
Ход урока
1. Сообщение темы и цели урока.
2. Повторение и закрепление пройденного материала.
1) Ответы на вопросы по домашнему заданию (разбор задач, вызвавших затруднения).
2) Повторение применения метода интервалов для решения неравенств (слайд 2).
3) Контроль усвоения материала (самостоятельная работа). (Слайд 3).
Вариант 1.
№1. Решите методом интервалов неравенства:
а) б)
№2. Найдите область определения функции:
Вариант 2.
№1. Решите методом интервалов неравенства:
а) б)
№2. Найдите область определения функции:
Самопроверка самостоятельной работы (слайды 4-5), с оцениванием (слайд 6).
3. Изучение нового материала.
Нами уже рассматривался метод интервалов для решения квадратных неравенств. Применим тот же метод к решению неравенств высоких степеней. Рассмотрим схему решения на следующем примере.
Пример 1. Решим неравенство
Решение (слайд 7):
Прежде всего, отметим, что если в разложении многочлена на множители входит сомножитель , то говорят, что — корень многочлена кратности .
Данный многочлен имеет корни: кратности 6; кратности 3; кратности 1; кратности 2; кратности 5.
Нанесем эти корни на числовую ось. Отметим корни четной кратности двумя черточками, нечетной кратности — одной чертой.
Определим знак многочлена на каждом интервале, при любом значении х не совпадающем с корнями и взятом из данного интервала. Получим полную диаграмму знаков многочлена на всей числовой оси:
Теперь легко ответить на вопрос задачи, при каких значениях х знак многочлена неотрицательный. Отметим на рисунке нужные нам области, получим:
Из рисунка видно, что такими х являются .
Проанализируем смену знаков в корнях различной кратности.
Посмотрите внимательно на диаграмму знаков, что можно заметить? (предполагаемый ответ: в корнях четной кратности смена знаков не произошла, а в корнях нечетной кратности — знак меняется).
Давайте проверим, подтвердится ли данное наблюдение при решении других неравенств.
Решите неравенство (слайд 8).
1 вариант:
2 вариант:
(Два ученика решают неравенства на откидной доске не видной классу, остальные выполняют задание самостоятельно, затем проверяем полученное решение по вариантам и снова делаем выводы о смене знака в зависимости от степени кратности корня).
Обобщая ваши наблюдения, приходим к важным выводам (слайд 9):
- Для решения неравенства важно знать, является ли k четным или нечетным числом.
- При четном k многочлен справа и слева от имеет один и тот же знак (т.е. знак многочлена не меняется),
- При нечетном k многочлен справа и слева от имеет противоположные знаки (т.е. знак многочлена изменяется).
Еще небольшое замечание, что бы применять метод интервалов, нужно сначала привести в неравенство к указанному виду (т.е. разложить на множители).
Рассмотрим способы решения рациональных неравенств методом интервалов (слайд 10).
Заметим, что рациональные неравенства легко сводятся к решению неравенств высоких степеней. Умножим обе части такого неравенства на многочлен , который положителен при всех допустимых значениях х (т.к. ). Тогда знак исходного неравенства не меняется, и получаем неравенство , эквивалентное данному неравенству.
Итак,: эквивалентно системе неравенств которая далее решается методом интервалов.
Пример 2. (слайд 11) Решим неравенство
Отметим, прежде всего, что знаменатель неравенства не может быть равен нулю и найдем область определения неравенства:
откуда
Сведем данное рациональное неравенство к алгебраическому. Для этого умножим обе части неравенства на положительное выражение - квадрат знаменателя (замети, что при этом знак неравенства не меняется). Получаем: . Разложив квадратный трехчлен на множители, имеем: . Решаем это неравенство методом интервалов. Находим корни многочлена и определяем их кратность: х =1 (четная кратность), остальные корни 3, -1, 0, 5, -2 (нечетной кратности). Отмечаем корни на числовой оси с учетом области определения неравенства и определяем знаки на промежутках с учетом кратности корней.
Ответ: .
(слайд 12) Задание на уроке (первичное закрепление материала).
4. Фронтальная работа с классом №389 (а, в), № 390 (в, г), №393(а), №394(а).
№389. Решите неравенство, разложив его левую часть на множители:
а) в)
№ 390. Решите неравенство:
в) г)
№393. Решите неравенство: а)
№394. Решите неравенство: а)
5. Задание на дом (слайд 13).
Повторить параграф 15 (глава II), №389 (б), № 390 (б), №393(б), №394(б).
Подумайте, как имея готовую диаграмму знаков построить эскиз графика функции.
6. Подведение итогов урока, рефлексия.
1. Что вы ожидали от работы на данном уроке? Сравните свои предварительные цели и реально достигнутые результаты.
2. Какие чувства и ощущения возникали у вас в ходе работы? Что оказалось для вас самым неожиданным?
3. Что вам более всего удалось, какие моменты были выполнены наиболее успешно?
4. Перечислите в порядке убывания основные трудности, которые вы испытывали во время учебы. Как вы их преодолевали?
7. Задания (для тех, кто желает знать больше).
№1. Решите неравенство:
а)
б)
в)
№2. Постройте эскизы графиков функций:
а); б) .
Литература
1. Учебник: Алгебра-9 класс, Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, М.: Просвещение, 2009.
2. Рурукин А.Н., Полякова С.А., Поурочные разработки по алгебре: 9 класс. — М.: ВАКО, 2010 — (В помощь школьному учителю).
3. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg и шаблон с сайта http://aida.ucoz.ru
4. Изображение кота http://s39.radikal.ru/i084/1008/34/683cd4886d3f.jpg
Приложение 1
Приложение 2
Обобщенный метод интервалов | Подготовка к ЕГЭ по математике
Продолжение

Ранее мы рассмотрели как работает метод интервалов при решении рациональных (часть 1) и дробно-рациональных неравенств (часть 2).
Будем рассматривать неравенства вида  , где
, где  один из знаков
один из знаков  , а
, а  логарифмическая, показательная, иррациональная или тригонометрическая функция. И вот здесь самое время применить обобщенный метод интервалов.
логарифмическая, показательная, иррациональная или тригонометрическая функция. И вот здесь самое время применить обобщенный метод интервалов.
Наши действия будут такими:
1) Находим область определения 
2) Находим нули 
3) Определяем знаки  на ОДЗ (которая разделена на промежутки нулями функции), подставляя удобные значения, принадлежащие каждому промежутку.
на ОДЗ (которая разделена на промежутки нулями функции), подставляя удобные значения, принадлежащие каждому промежутку.
4) Записываем ответ, указывая объединение промежутков (из ОДЗ), на которых  имеет соответствующий знак.
имеет соответствующий знак.
Если же перед нами неравенство  , где
, где  логарифмические, показательные, иррациональные или тригонометрические функции, то мы будем переходить к неравенству:
логарифмические, показательные, иррациональные или тригонометрические функции, то мы будем переходить к неравенству:  , при условии, что
, при условии, что 
Пример 1.
Решить неравенство 
Решение: + показать Рассмотрим функцию Найдем ОДЗ данной функции: Найдем нули функции, решив уравнение: Из данного уравнения следует: Рассмотрим знаки функции на образовавшихся промежутках Находим знак на крайнем правом промежутке: Определяем знак на Определяем знак на Ответ:  .
.


![Rendered by QuickLaTeX.com x\in(-\infty;0]\cup[3;+\infty)](http://xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)




 :
:
 :
:
 :
:

![Rendered by QuickLaTeX.com (-\infty;0]\cup[3;3\frac{4}{7}]](http://xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
Пример 2.
Решить неравенство 
Решение: + показать (Этот метод не выигрышно смотрится на данного примере! Проще применить метод рационализации). Перейдем к равносильному неравенству: Рассмотрим функцию ОДЗ данной функции: Нули функции: Из равенства следует: Образовались следующие промежутки: Заметим, функция Определяем знак на Определяем знак на Определяем знак на Ответ: 
 .
. , то есть
, то есть 

 .
.


 – четная, поэтому нам достаточно определить знаки лишь на правой, например, половине рассматриваемых промежутков.
– четная, поэтому нам достаточно определить знаки лишь на правой, например, половине рассматриваемых промежутков. :
:
 :
:
 :
:


Надо сказать, что у обобщенного метода интервалов есть свои минусы. Потому что не всегда удобно определять знаки на промежутках, тем более когда они малы, когда на них нет целых значений.
Попробуйте, вот например, решить обобщенным методом интервалов следующее неравенство:

Вы столкнетесь с трудностями при определении знаков вот на таких промежутках:

Не из приятных занятие, правда? Поэтому, конечно, метод интервалов здесь неоправдан. Советую решить данное неравенство методом рационализации.
Да и еще, надеюсь вы понимаете, что  не есть
не есть  ? В данном случае
? В данном случае  . Поэтому, подумайте, нужно ли понижать степень в подлогарифмном выражении…
. Поэтому, подумайте, нужно ли понижать степень в подлогарифмном выражении…
Да, ответ такой: ![Rendered by QuickLaTeX.com (3;\frac{5+\sqrt7}{2}]\cup(4;4,5]](http://xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) (лучше порешать самостоятельно, но если что, – смотрим решение здесь).
(лучше порешать самостоятельно, но если что, – смотрим решение здесь).
Урок 20. решение неравенств методом интервалов — Алгебра — 9 класс
Рассмотрим функцию.
Нулями этой функции будут следующие значения переменной икс: минус один, два и семь
Областью определения данной функции является множество всех чисел, а нули функции будут разбивать это множество на промежутки, показанные на рисунке.
Задача состоит в том, чтобы определить, какое значение функция принимает на каждом из этих промежутков, ведь очевидно, внутри промежутка знак меняться не будет.
Так как выражение, задающее нашу функцию, является произведением трёх множителей, знак всего выражения будет зависеть от знаков этих множителей.
Для того чтобы определить знаки множителей на каждом из промежутков, составим таблицу, у которой в левом столбце указаны множители выражения, а в верхней строке промежутки.
Чтобы определить знак выражения на некотором промежутке достаточно подставить любое число из этого промежутка на место переменной и выполнить действие.
Например, чтобы определить, какой знак у суммы икс плюс один на промежутке от минус бесконечности до минус одного, достаточно подставить любое число из этого промежутка, допустим, минус четыре, и посчитать, чему равна сумма. Получим число минус три, значит, на всём этом промежутке сумма будет принимать отрицательные значения. Пометим это знаком минус в таблице.
Аналогично заполним остальные строки таблицы.
Из полученной таблицы видно, что на промежутке от минус бесконечности до минус одного функция принимает отрицательные значения.
На промежутке от минус одного до двух функция принимает положительные значения.
На промежутке от двух до семи функция принимает отрицательные значения.
И на промежутке от семи до плюс бесконечности функция принимает положительные значения.
Итак, функция подобного вида на каждом из промежутков, на которые разбивают область определения нули функции, принимает либо положительное, либо отрицательное значение, причём знак меняется только при переходе через нуль.
Это свойство применяют для решения неравенств, в которых требуется сравнить с нулём выражение, представленное в виде произведения нескольких множителей. Этот метод называют методом интервалов.
Разберём пример. Решим неравенство.
Рассмотрим соответствующую функцию.
Найдём нули данной функции и изобразим их на координатной прямой. Нетрудно определить, что нулями функции будут являться числа минус десять, минус четыре и двенадцать.
Чтобы определить, как ведёт себя функция в каждом из получившихся промежутков, достаточно узнать знак функции в одном из промежутков, например, в промежутке от двенадцати до плюс бесконечности. Для этого выберем любое число из данного промежутка и подставим в выражение, задающее функцию. Подставим, например, число двадцать.
Функция на данном промежутке принимает положительное значение, значит, мы можем расставить знаки на остальных промежутках, помня, что при переходе через нуль функция меняет свой знак.
Из рисунка мы видим, что множеством решений нашего неравенства будут промежутки от минус бесконечности до минус десяти и от минус четырёх до двенадцати.
Запишем ответ.