Степень с нулевым показателем. Алгебра, 7 класс: уроки, тесты, задания.

1.	Сравнение степеней (отрицательные целые числа) Сложность: лёгкое	1
2.	Сравнение степеней (десятичная дробь) Сложность: лёгкое	3
3.	Сравнение степеней (смешанное число и обыкновенная дробь) Сложность: лёгкое	2
4.	Сравнение степеней (обыкновенная дробь и -1) Сложность: лёгкое	3
5.	Действия со степенями (основание — бином) Сложность: среднее	3
6.	Действия со степенями (основание — обыкновенная дробь) Сложность: среднее	5
7.	Действия со степенями, основание — отрицательный одночлен (целые числа и переменные) Сложность: среднее	3
8.	Значение выражения (обыкновенные дроби) Сложность: среднее	6
9.	Значение выражения (целые числа и дроби) Сложность: среднее	7
10.	Числовое значение дроби Сложность: среднее	6

Урок алгебры в 7 классе «Все действия со степенями»

1. Древние славяне тоже умели записывать большие числа, для этого у них были специальные названия для большого счета

«тысяща» =

«легион» =

«ворон» =

«колода» =

2. Наш мозг состоит из нервных клеток и способен ежедневно

запомнить единиц информации. К концу жизни наша память

может хранить около единиц информации — число, о котором пока даже не мечтают создатели компьютерной техники.

2. Легенда о шахматной доске

Шахматы —одна из самых древних игр. Она существует уже многие века, и не удивительно, что с нею связаны предания, правдивость которых за давностью времени невозможно проверить. Одну из подобных легенд я и хочу рассказать. Чтобы понять ее, не нужно вовсе уметь играть в шахматы — достаточно знать, что игра происходит на доске, разграфленной на 64 клетки (попеременно черные и белые).

Шахматная игра была придумана в Индии, и когда индийский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что игра изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.

Изобретатель — его звали Сета — явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.

— Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал,— сказал царь.

Мудрец поклонился.

— Я достаточно богат, чтобы исполнить самое смелое твое пожелание,— продолжал царь.— Назови награду, которая тебя удовлетворит, и ты получишь ее.

Сета молчал.

— Не робей,— ободрил его царь.— Выскажи свое желание. Я не пожалею ничего, чтобы исполнить его!

— Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра, по зрелом размышлении, я сообщу тебе мою просьбу.

Когда на другой день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.

— Повелитель,— сказал Сета,— прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.

— Простое пшеничное зерно? — изумился царь.

— Да, повелитель. За вторую клетку прикажи выдать два зерна, за третью — четыре, за четвертую — 8, за пятую— 16, за шестую — 32…

— Довольно! — с раздражением прервал его царь.— Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Ступай! Слуги мои вынесут тебе мешок с пшеницей.

Сета улыбнулся, покинул залу и стал дожидаться у ворот дворца.

За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.

— Повелитель,— был ответ,— приказание твое, исполняется. Придворные математики исчисляют число следуемых зерен.

Царь нахмурился — он не привык, чтобы повеления его исполнялись так медлительно.

Вечером, отходя ко сну, царь Шерам еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.

— Повелитель,— ответили ему,— математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.

— Почему медлят с этим делом?! — гневно воскликнул царь.— Завтра, прежде чем я проснусь, всё до последнего зерна должно быть выдано Сете. Я дважды не приказываю!

Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.

— Прежде чем скажешь о твоем деле,— объявил Шерам.— я желаю услышать, выдана ли наконец Сете та ничтожная награда, которую он себе назначил.

— Ради этого я и осмелился явиться перед тобой в столь ранний’ час,— ответил старик.— Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…

— Как бы велико оно ни было,— надменно перебил царь,— житницы мои не оскудеют! Награда обещана и должна быть выдана…

— Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыри. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду.

С изумлением внимал царь словам старца.

— Назови же мне это чудовищное число,—сказал он в раздумье.

— Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!

Такова легенда. Действительно ли было то, что здесь рассказано, неизвестно, но что награда, о которой говорит предание, должна была выразиться именно таким числом, в этом вы сами можете убедиться терпеливым подсчетом. Начав с единицы, нужно сложить числа: 1, 2, 4, 8 и т. д.

Искомое число зерен: 18 446 744 073 709 551615.

Если желаете представить себе всю огромность этого числового великана, прикиньте, какой величины амбар потребовался бы для вмещения подобного количества зерен. Известно, что кубический метр пшеницы вмещает около 15 миллионов зерен. Значит, награда шахматного изобретателя должна была бы занять объем примерно в 12 000 000 000 000 куб. м, или 12 000 куб. км. При высоте амбара 4 м и ширине 10 м длина его должна была бы простираться на 300 000 000 км, то есть вдвое дальше, чем от Земли до Солнца!

Практика. Степени, одночлены, многочлены. Видеоурок. Алгебра 7 Класс

На этом уроке мы потренируемся решать различные задачи, связанные со степенями, одночленами и многочленами. В частности, потренируемся выполнять действия со степенями и одночленами, раскрывать скобки, раскладывать многочлены на множители.

Степенью с показателем 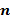 и основанием  называется произведение 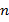 множителей, каждый из которых равен :

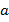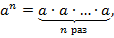
где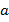

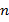 – основание степени,  – показатель степени, .

 

Свойства степени с натуральным показателем

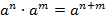
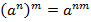
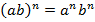
Задания на упрощение выражений со степенями за редким исключением решаются по одному алгоритму:

1. Разложить основания степеней на множители (те, которые можем).
2. Сгруппировать степени с одинаковыми основаниями.
3. Использовать свойства степени для упрощения полученного выражения.

Рассмотрим применение этого алгоритма на конкретных примерах.

 

Пример 1.

Упростить и вычислить:

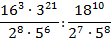
Решение:

Сначала разложим основания степеней на простые множители:

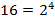
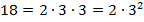
Тогда:

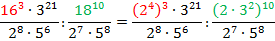
Воспользуемся свойствами:

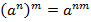
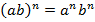
Получим:

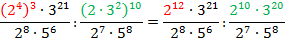
Мы получили отношение двух дробей. Вспомним, что деление на число можно заменить эквивалентным действием – умножением на число, ему обратное. А обратное число к дроби – это перевернутая дробь:

Cгруппируем степенис одинаковым основанием:

Используем свойство :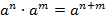

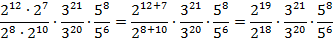
А теперь используем свойство :

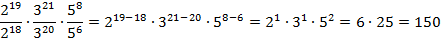
Ответ: .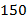

 

Пример 2.

Упростить и вычислить:

Решение:

Сначала разложим основания степеней на простые множители:

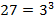
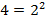
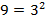
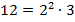
Перепишем выражение:

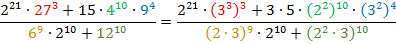
Воспользуемся следующими свойствами :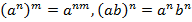

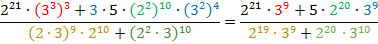
Вынесем общий множитель в числителе и знаменателе:

Ответ: .

Одночлен – это произведение чисел и степеней переменных с натуральными показателями (например: 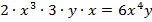). Если перемножить все числа (полученное в результате число называется коэффициентом одночлена), а также все степени с одинаковыми основаниями, то получится стандартная запись одночлена: 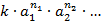, где  – числовой коэффициент, 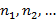 – натуральные числа.

Степень одночлена – это сумма показателей степени всех переменных, которые входят в стандартную запись одночлена (например, 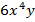:  – степень одночлена).

Рассмотрим несколько примеров, в которых необходимо выполнять действия с одночленами. В таких заданиях нам понадобится только умение работать со степенями.

 

Пример 3.

Представить одночлен в стандартном виде, указать его коэффициент и степень:

Решение:

Рассмотрим первый множитель:

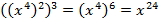
Рассмотрим второй множитель:

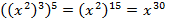
Перепишем выражение:

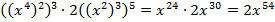
Коэффициент: , степень: .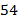

Ответ: .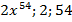

 

Пример 4.

Представить одночлен в стандартном виде, указать его коэффициент и степень:

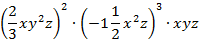
Решение:

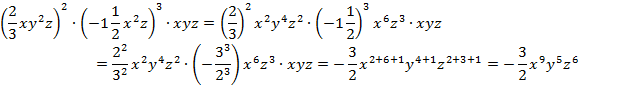
Коэффициент: 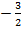, степень: .

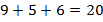Ответ: .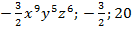

Многочлен – сумма одночленов, например: 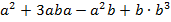 (одночлен – частный случай многочлена).

Чтобы привести многочлен к стандартному виду, нужно:

1. Привести к стандартному виду все одночлены, которые входят в состав многочлена: .
2. Привести подобные слагаемые – сложить одночлены с одинаковой буквенной частью: .

 

Степень многочлена – это наибольшая из степеней одночленов в стандартной записи многочлена: .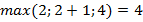

Рассмотрим несколько примеров, в которых необходимо выполнять действия с многочленами. В таких заданиях нам понадобится умение работать с одночленами, а также распределительный закон и следствия из него:

 

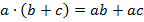
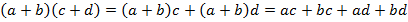
Пример 5.

Привести многочлен к стандартному виду и определить его степень:

1.        

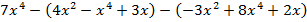
Раскроем скобки. Помним, что если перед скобками стоит знак «минус», то все слагаемые в скобках меняют свой знак на противоположный:

            Приведем подобные слагаемые:

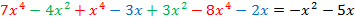
Степень: .

 

2.        

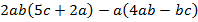
Раскроем скобки, используя распределительный закон:

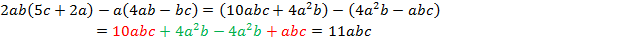
Степень: .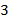

 

3.        

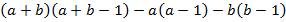
Раскроем скобки:

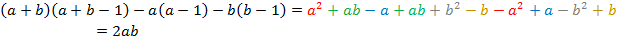
Степень: .

Ответ: .

 

Пример 6

Самостоятельная работа по теме «Действия со степенями», 7 класс.

Самостоятельная работа. Вариант 1.

1. Записать формулу возведения в степень произведения множителей.

2. Упростите:

а. a^5.a^4.a³:a⁷= г. (c²)^3.c⁵:(c⁴)²=

б. x⁴😡^3.x⁷= д. (2ab)⁴=

в. (a²)³= е. (5a^3. b⁵)⁴=

3. Вычислите:

а. 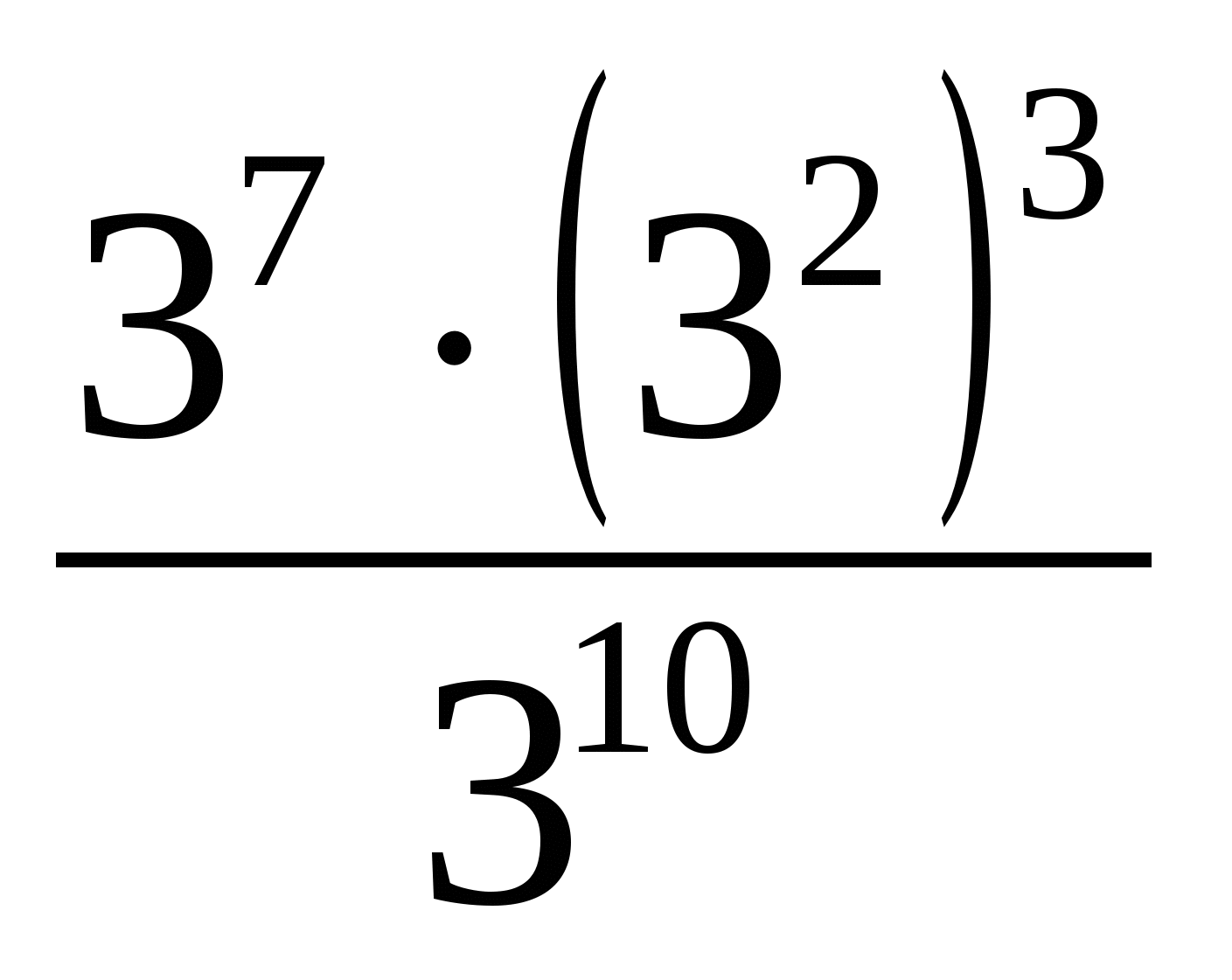= в. 27^.3⁴=

б. 5^5.0,2^5.4⁵=

Самостоятельная работа. Вариант 2.

1. Записать формулу возведения степени в степень.

2. Упростите:

а. b^4.b^6.b³:b⁵= г. (c⁵)^3.c⁴:(c⁷)²=

б. x^7.x³😡⁵= д. (3x^.y)³=

в. (a⁴)⁶= е. (2a^2.b⁶)⁵=

3. Вычислите:

а. 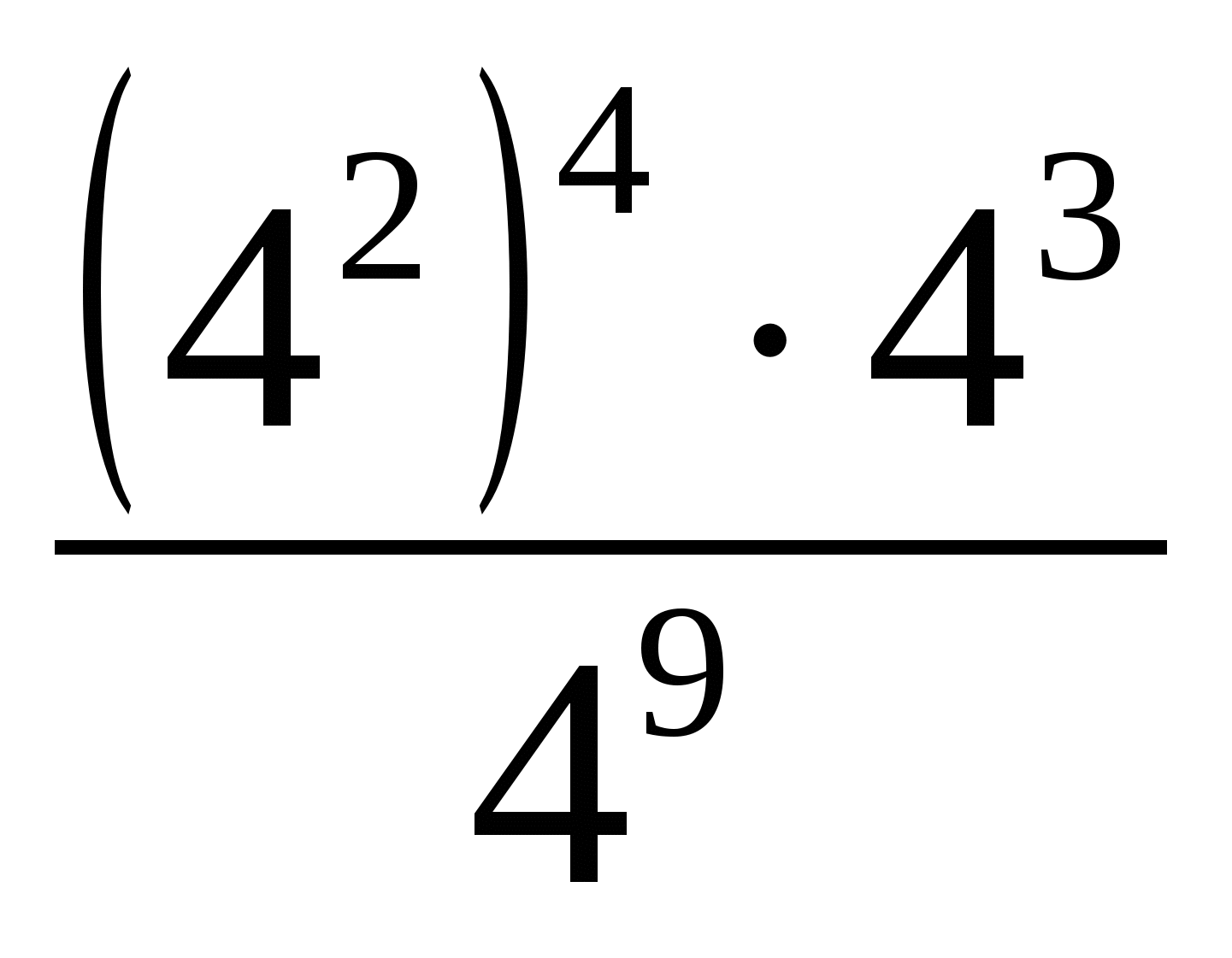= в. 8^.2⁴=

б. 10^3.0,1^3.5³=

Самостоятельная работа. Вариант 3.

1. Записать формулу умножения степеней.

2. Упростите:

а. a^4.a^7.a⁵:a⁸= г. (c⁸)^3.c⁴:(c²)⁵=

б. x¹¹😡^6.x⁴= д. (6ab)³=

в. (a⁷)⁹= е. (2a^6. b⁷)³=

3. Вычислите:

а. 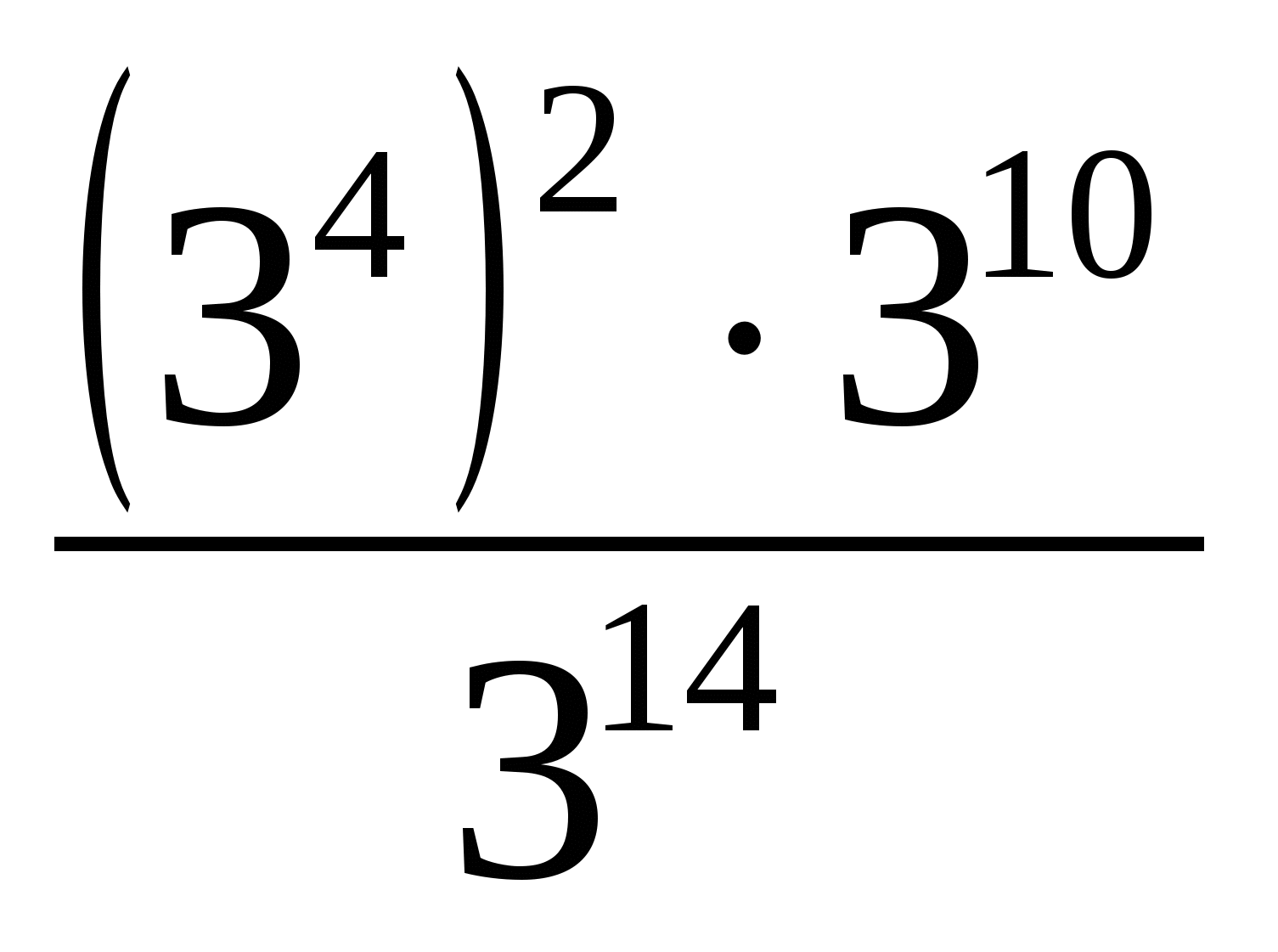= в. 81^.3³=

б. 5^6.0,2^6.3⁶=

Самостоятельная работа. Вариант4.

1. Записать формулу деления степеней.

2. Упростите:

а. b^6.b^7.b²:b⁸= г. (c⁵)^3.c⁴:(c⁴)²=

б. x^9.x⁵😡³= д. (4x^.y)³=

в. (a³)⁷= е. (3a^4.b⁶)³=

3. Вычислите:

а. =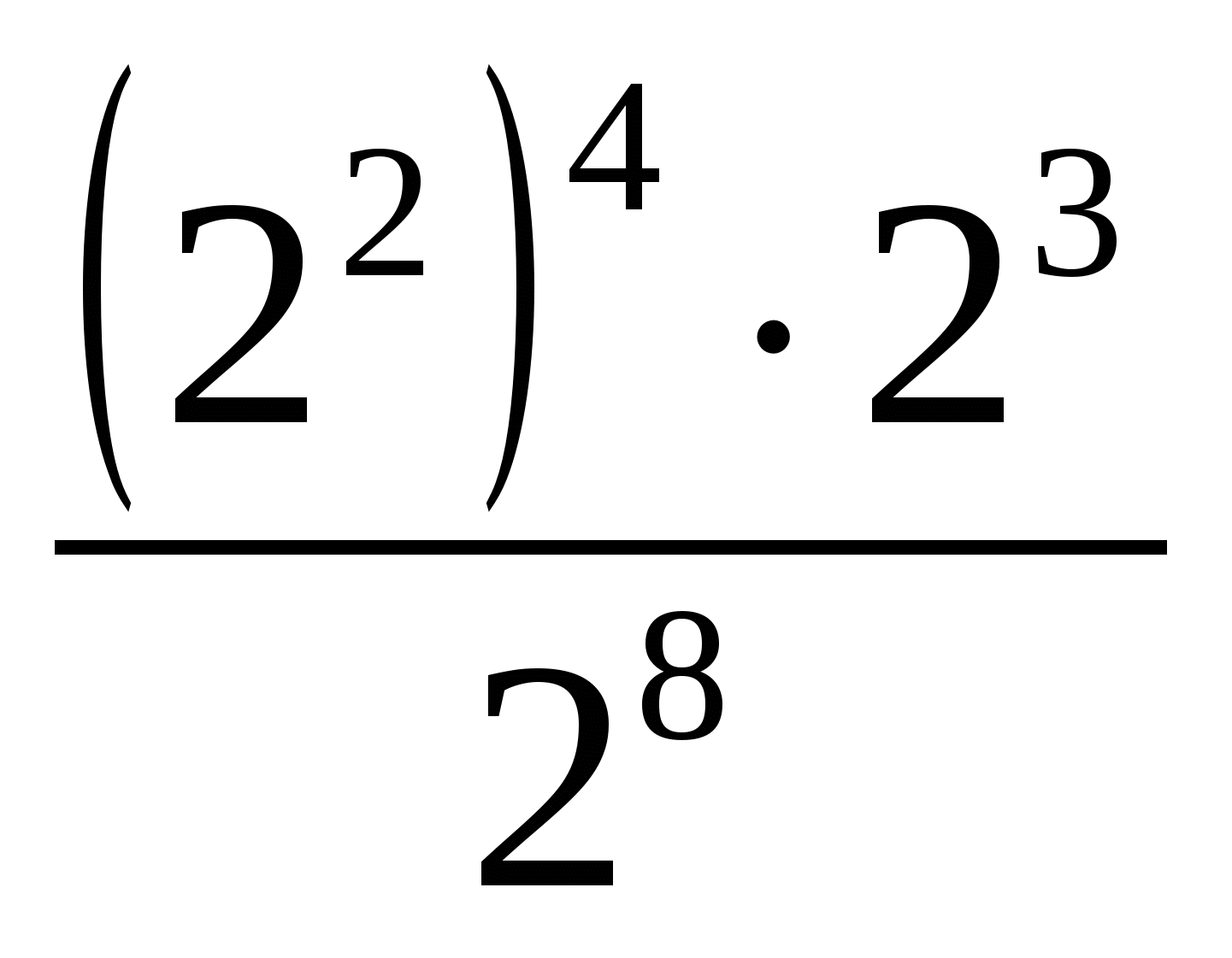

б. 10^5.0,1^5.3⁵=

в. 16^.2⁴=

Самостоятельная работа. Вариант 1.

1. Записать формулу возведения в степень произведения множителей.

2. Упростите:

а. a^5.a^4.a³:a⁷= г. (c²)^3.c⁵:(c⁴)²=

б. x⁴😡^3.x⁷= д. (2ab)⁴=

в. (a²)³= е. (5a^3. b⁵)⁴=

3. Вычислите:

а. 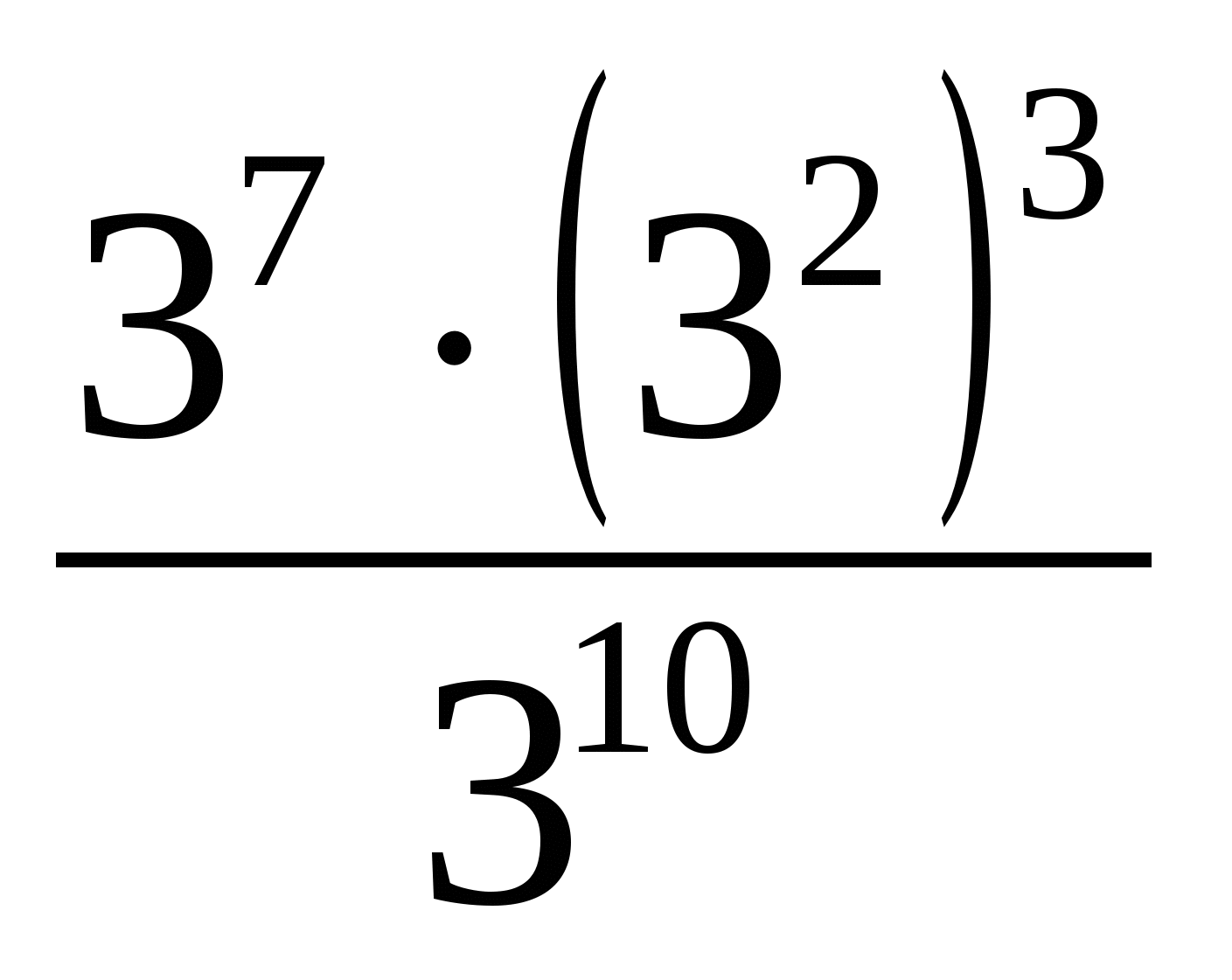= в. 27^.3⁴=

б. 5^5.0,2^5.4⁵=

Самостоятельная работа. Вариант 2.

1. Записать формулу возведения степени в степень.

2. Упростите:

а. b^4.b^6.b³:b⁵= г. (c⁵)^3.c⁴:(c⁷)²=

б. x^7.x³😡⁵= д. (3x^.y)³=

в. (a⁴)⁶= е. (2a^2.b⁶)⁵=

3. Вычислите:

а. 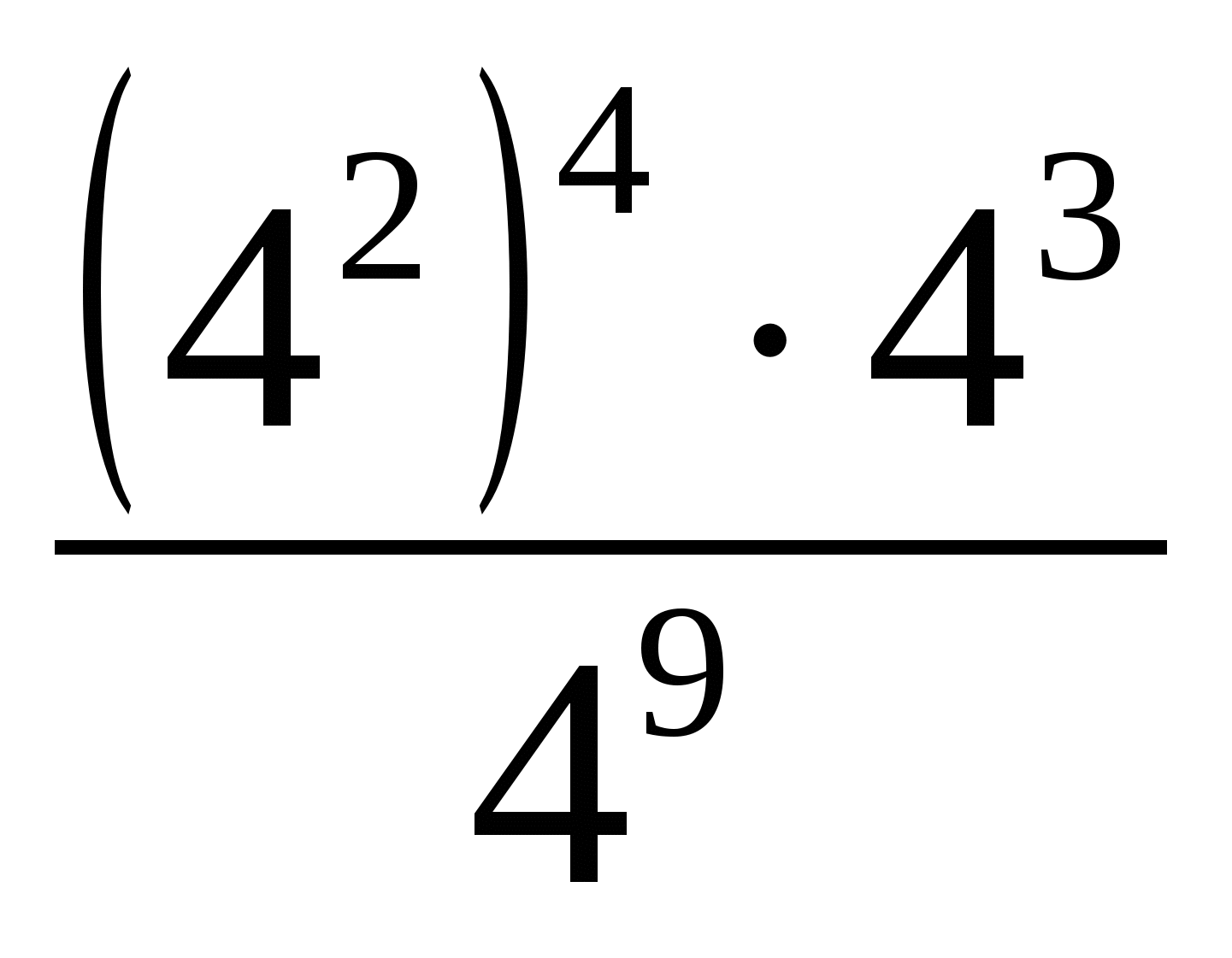= в. 8^.2⁴=

б. 10^3.0,1^3.5³=

Самостоятельная работа. Вариант 3.

1. Записать формулу умножения степеней.

2. Упростите:

а. a^4.a^7.a⁵:a⁸= г. (c⁸)^3.c⁴:(c²)⁵=

б. x¹¹😡^6.x⁴= д. (6ab)³=

в. (a⁷)⁹= е. (2a^6. b⁷)³=

3. Вычислите:

а. 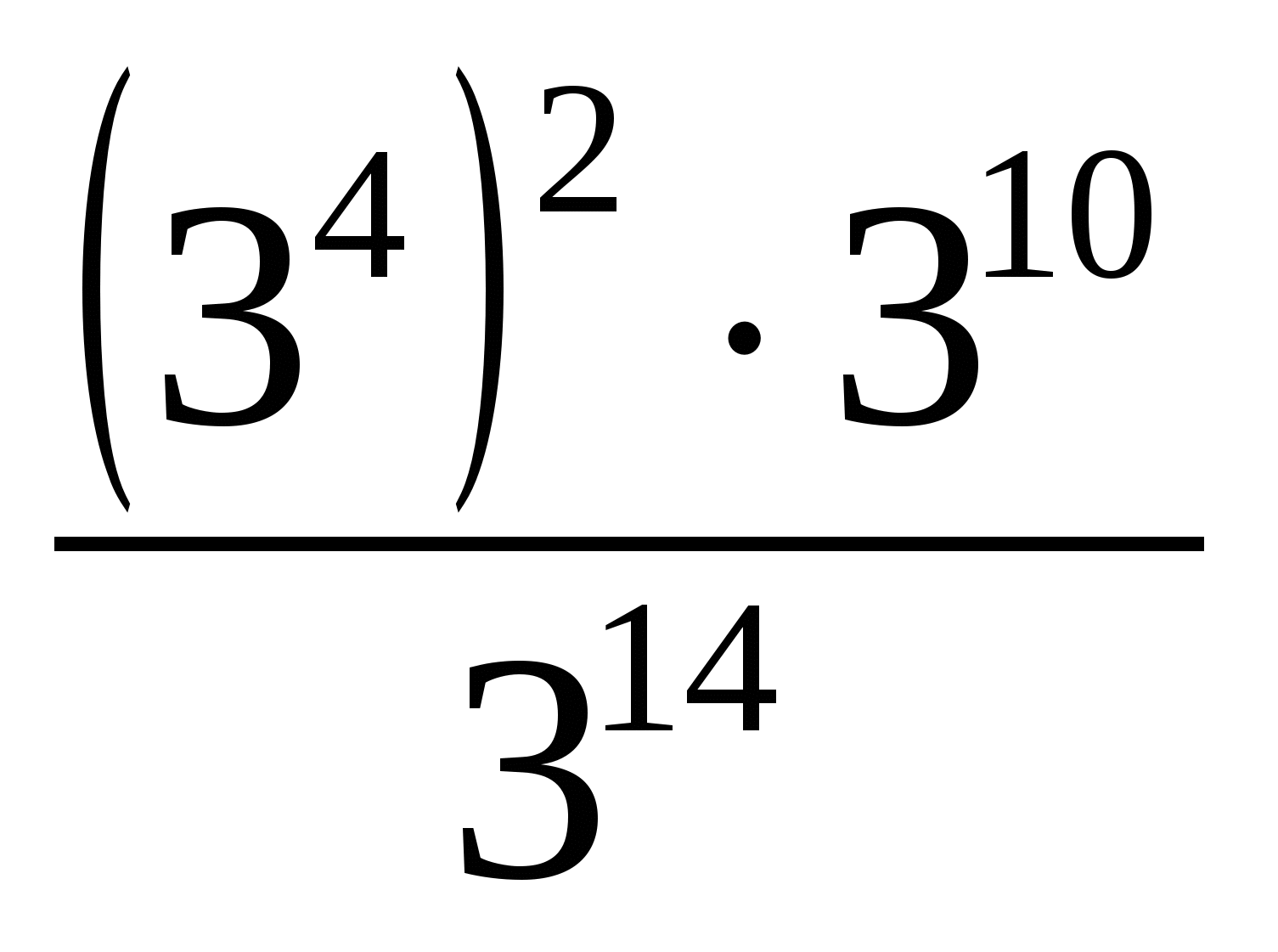= в. 81^.3³=

б. 5^6.0,2^6.3⁶=

Самостоятельная работа. Вариант4.

1. Записать формулу деления степеней.

2. Упростите:

а. b^6.b^7.b²:b⁸= г. (c⁵)^3.c⁴:(c⁴)²=

б. x^9.x⁵😡³= д. (4x^.y)³=

в. (a³)⁷= е. (3a^4.b⁶)³=

3. Вычислите:

а. =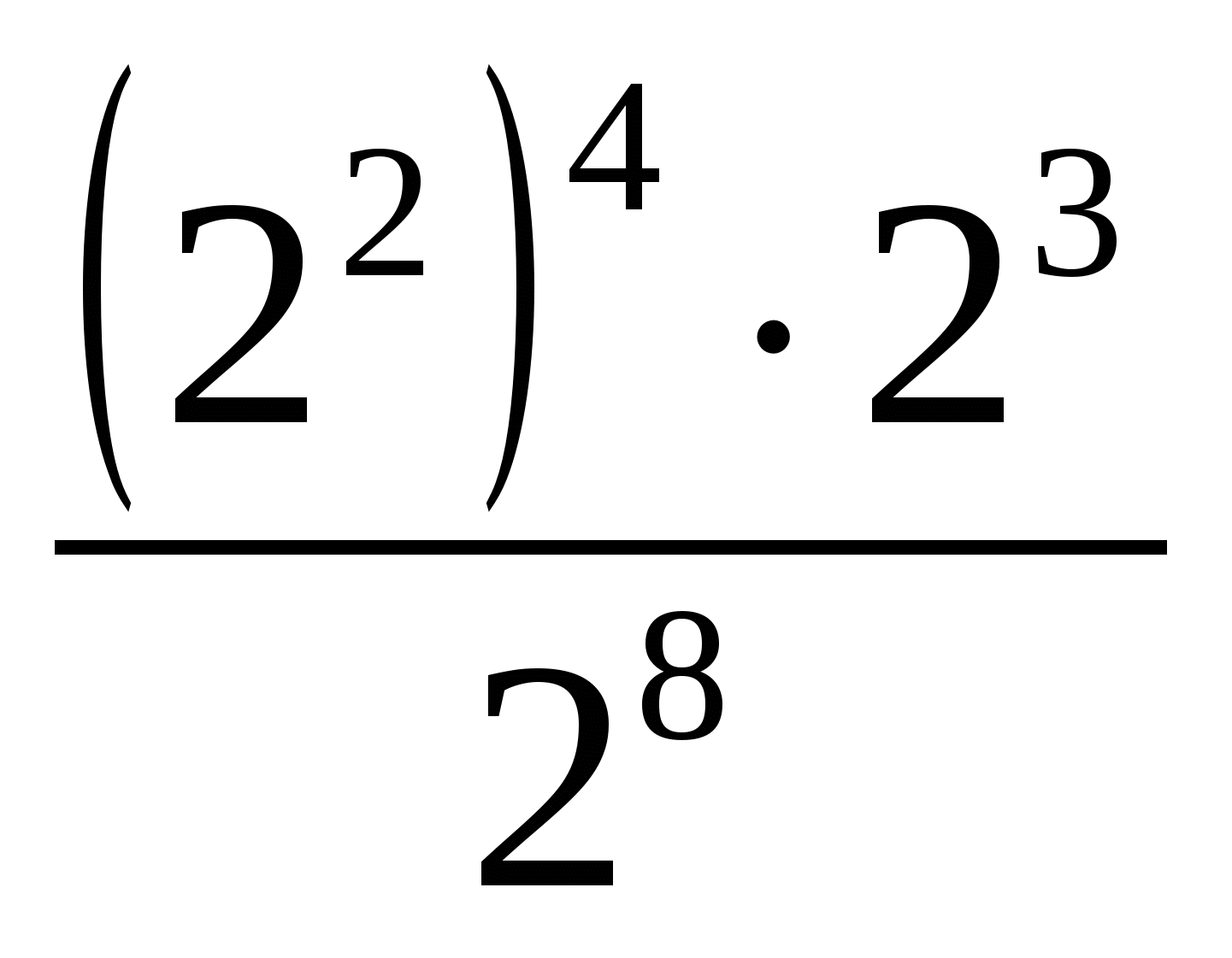

б. 10^5.0,1^5.3⁵=

в. 16^.2⁴=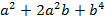