Уравнение касательной к графику функции
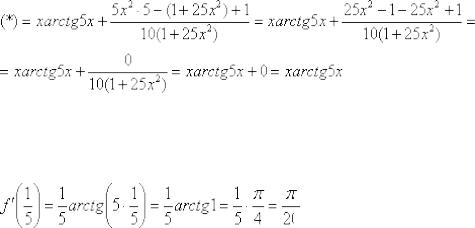
Ну вот, совсем другое дело. Вычислим значение производной в точке
:
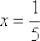В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно
изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому что арктангенсов на студенческий век ещё хватит.
Пример 4
Вычислить производную функции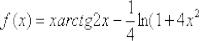 
в точке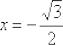 
Это пример для самостоятельного решения.
Чтобы закрепить предыдущий параграф, рассмотрим задачу нахождения касательной к графику функции в данной точке. Это задание встречалось нам в школе, и оно же встречается в курсе высшей математики.
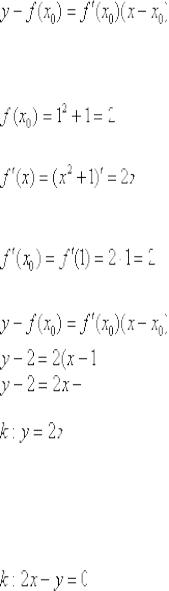
Как составить уравнение касательной в точке с абсциссой 
?
?Общая формула знакома нам еще со школы:
Значение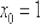 
нам уже дано в условии.
Теперь нужно вычислить, чему равна сама функция в точке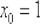 
:
На следующем этапе находим производную:
Находим производную в точке (задание, которое мы недавно рассмотрели):
Подставляем значения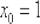 
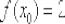и 
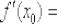в формулу:
Таким образом, уравнение касательной:
Это «школьный» вид уравнения прямой с угловым коэффициентом. В высшей математике уравнение прямой на плоскости принято записывать в так называемой общей форме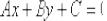 
, поэтому перепишем найденное уравнение касательной в соответствии с традицией:
Очевидно, что точка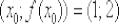 
должна удовлетворять данному
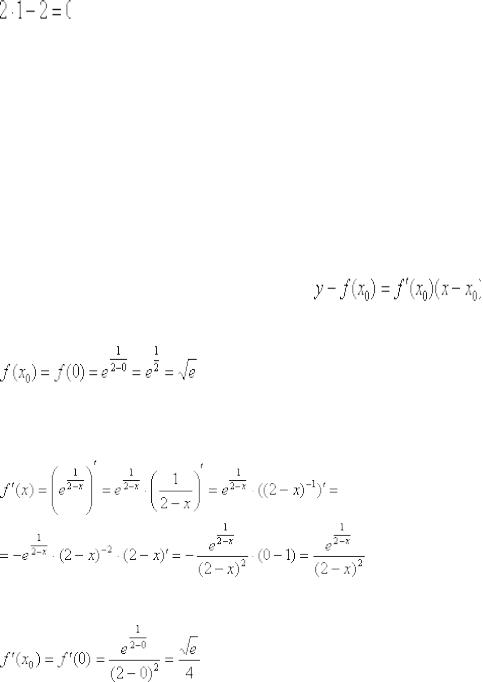
уравнению:
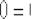
Следует отметить, что такая проверка является лишь частичной. Если мы неправильно вычислили производную в точке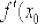 
, то выполненная подстановка нам ничем не поможет.
Рассмотрим еще два примера.
Пример 5
Составить уравнение касательной к графику функции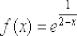 
в точке с абсциссой 
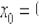Уравнение касательной составим по формуле
1)Вычислим значение функции в точке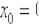 
:
2)Найдем производную. Дважды используем правило дифференцирования сложной функции:
3) Вычислим значение производной в точке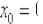 
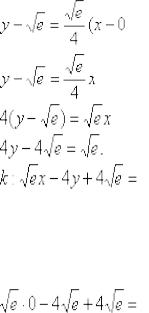
4) Подставим значения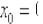 
, 
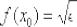и 
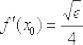в формулу
:
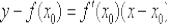Готово.
Выполним частичную проверку:
Подставим точку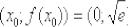 
в найденное уравнение:
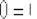– верное равенство. Пример 6
Составить уравнение касательной к графику функции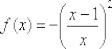 
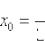
Полное решение и образец оформления в конце урока.
В задаче на нахождение уравнения касательной очень важно ВНИМАТЕЛЬНО и аккуратно выполнить вычисления, привести уравнение прямой к общему виду. И, конечно же, ознакомьтесь со
строгим определением касательной, после чего закрепите материал на уроке Уравнение нормали, где есть дополнительные примеры с касательной.
studfile.net
Уравнение касательной примеры. Уравнение касательной
В этой статье мы разберем все типы задач на нахождение
Вспомним геометрический смысл производной : если к графику функции в точке проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси ) равен производной функции в точке .
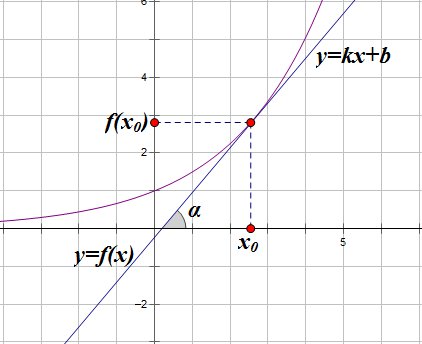
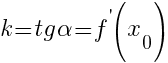
Возьмем на касательной произвольную точку с координатами :
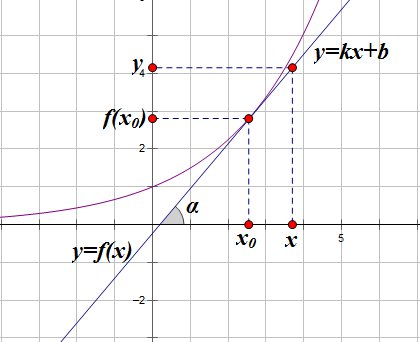
И рассмотрим прямоугольный треугольник :
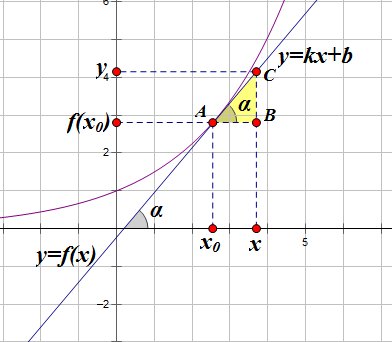
В этом треугольнике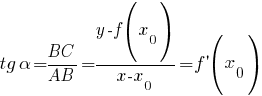 
Отсюда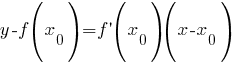 
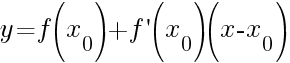
Это и есть уравнение касательной, проведенной к графику функции в точке .
Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти и .
Есть три основных типа задач на составление уравнения касательной.
1. Дана точка касания
2. Дан коэффициент наклона касательной, то есть значение производной функции в точке .
3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.
Рассмотрим каждый тип задач.
1
. Написать уравнение касательной к графику функции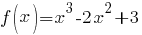 
в точке .
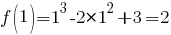
б) Найдем значение производной в точке . Сначала найдем производную функции
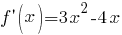
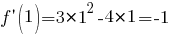
Подставим найденные значения в уравнение касательной:
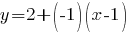
Раскроем скобки в правой части уравнения. Получим:
Ответ: .
2
. Найти абсциссы точек, в которых касательные к графику функции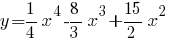 
ayunova.ru
уравнение касательной — 24 Августа 2013 — Примеры решений задач
Тема: Как найти уравнение касательной к графику функции
Уравнение касательной к графику функции y=f(x) в точке x0 имеет вид
в точке x0=2.
Алгоритм решения следующий:
1) Находим производную функции
2) Вычисляем значение производной в точке x0=2
3) Вычисляем значение функции в точке x0=2
4) Найденные значения подставляем в формулу уравнения касательной
Получаем уравнение касательной
Для наглядности рекомендуем построить график самой функции и касательной на координатной плоскости с помощью калькулятора. Для этого вводим в калькулятор функцию в виде 3x^2-5x+1 и касательную в виде 7x-11, задаем интервал построения графиков от x1=-2 до x2=4 (для данного примера функции вводить не требуется, они уже введены автором), нажимаем Ok, получаем ответ.
Разберем более сложный случай, когда касательная должна проходить через точку не принадлежащую кривой.
Пример 2. Напишите уравнения всех касательных к графику функции y = – x2 – 4x + 2, проходящих через точку M(– 3; 6).
Решение. Точка M(– 3; 6) не является точкой касания, так как f(– 3)=-9+12+2=5
1. a – абсцисса точки касания.
2. f(a) = – a2 – 4a + 2.
3. f ‘(x) = – 2x – 4, f ‘(a) = – 2a – 4.
4. y = – a2 – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.
Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.
6 = – a2 – 4a + 2 – 2(a + 2)(– 3 – a),
a2 + 6a + 8 = 0 ^ a1 = – 4, a2 = – 2.
Если a = – 4, то уравнение касательной имеет вид y = 4x + 18.
Если a = – 2, то уравнение касательной имеет вид y = 6.
www.reshim.su
Касательная плоскость и нормаль к поверхности: вывод уравнений, примеры
Определение. Касательной плоскостьью к поверхности z = f(x,y) в точке P0(x0,y0,f(x0,y0)) называется плоскость, содержащие все касательные к поверхности, проведённые в точке P0.
Определение. Нормалью к поверхности в точке P называется прямая, проходящая через эту точку перпендикулярно касательной плоскости, проведённой через точку P.
Чтобы найти уравнения касательной плоскости и нормали к поверхности, нужно выполнить следующее:
- найти частные производные функции, которой задана поверхность;
- найти значения найденных частных производных в точке P0;
- найденные значения частных производных и координаты точки P0 подставить в уравнения касательной плоскости и нормали в общем виде.
Прежде чем решать примеры, выведем уравнения касательной плоскости и нормали к поверхности: их вывод может быть включён в экзаменационные билеты.
Пусть дана поверхность z = f(x,y) и точка P0(x0,y0,f(x0,y0)) на этой поверхности.
Чтобы получить уравнение касательной плоскости, достаточно составить уравнение плоскости, на которой находятся две касательные прямые, проведённые через точку P0(x0,y0,f(x0,y0)). Одна из касательных прямых пусть будет параллельна плоскости xOz, другая — параллельна плоскости yOz (поэтому x — константа). Уравнения этих прямых будут следующими:
1) 
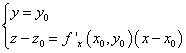
2) 
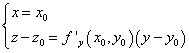
где z0 = f(x0,y0)
В последнем уравнении A и B — произвольные константы. Эта плоскость
перпендикулярна вектору нормали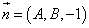 
.
Принимая в уравнении плоскости y = y0, получим уравнение пучка прямых, проходящих через точку P0(x0,y0,z0) и лежащих в плоскости y = y0:
.
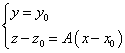Чтобы касательная прямая принадлежала этому пучку прямых, должно быть
.
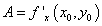Принимая в уравнении плоскости x = x0, получим уравнение пучка прямых, проходящих через точку P0(x0,y0,z0) и лежащих в плоскости x = x0:
.
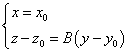Чтобы касательная прямая принадлежала этому пучку прямых, должно быть
.
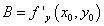Подставляя полученные коэффициенты A и B в уравнение плоскости, получаем уравнение касательной плоскости:
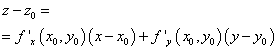
Это и есть уравнение касательной плоскости к поверхности z = f(x,y) в точке P0(x0,y0,z0).
Так как вектор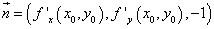 
перпендикулярен касательной плоскости к поверхности, то он параллелен нормали и может служить вектором
её направления. Таким образом, уравнение нормали к поверхности
z = f(x,y) в точке
P0(x0,y0,z0):
.
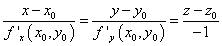Рассмотрим также случай, когда уравнение поверхности дано в неявной форме:
.
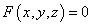Это уравнение определяет неявную функцию z = f(x,y), частные производные которой в точке P0(x0,y0,z0)
,
,
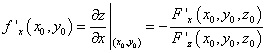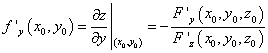при условии, что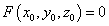 
,
а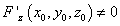 
. Подставляя эти производные
в уравнение касательной плоскости, получаем
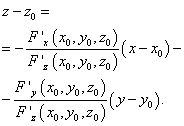
Перенеся все слагаемые в левую часть и умножив на
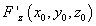, получаем уравнение касательной
плоскости для случая, когда поверхность задана в неявном виде:
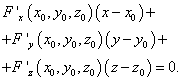
Соответствующие уравнения нормали к поверхности:
.
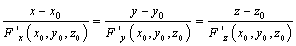Пример 1. Составить уравнения касательной плоскости и нормали к поверхности
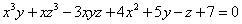
в точке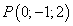 
.
Решение. Функция, которой задана поверхность:
.
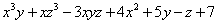Найдём частные производные этой функции:
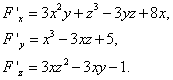
Вычислим значения частных производных в точке :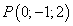
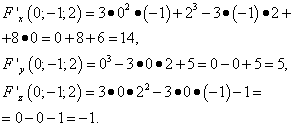
Найденные значения частных производных и координаты точки подставим в уравнения касательнной плоскости и нормали к поверхности. Получаем уравнение касательной плоскости:
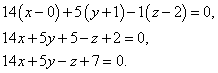
Уравнение нормали:
.
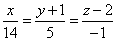Пример 2. Составить уравнения касательной плоскости и нормали к поверхности
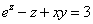
в точке P0(x0,y0,z0), если y0 = 1, z0 = 0.
Решение. Эта задача уже посложнее, так как в ней не дано x0 и эту координату требуется найти. Для этого подставим y0 и z0 в уравнение поверхности:
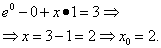
Найдём частные производные функции, которой задана поверхность:
.
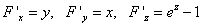Вычислим значения частных производных в точке P0(x0,y0,z0):
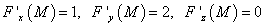
Найденные значения частных производных и координаты точки подставим в уравнения касательнной плосоксти и нормали к поверхности. Получаем уравнение касательной плоскости:
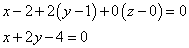
Уравнение нормали:
.
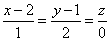Пример 3. Составить уравнения касательной плоскости и нормали к поверхности
,
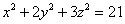которая параллельна плоскости
.
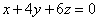Решение. Сначала нужно найти точку поверхности, проведённая через которую касательная плоскость будет параллельна заданной плоскости. Если касательная плоскость и данная плоскость параллельны, то векторы нормалей будут коллинеарны.
Вектором нормали касательной плоскости будет
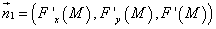, где
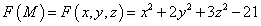. Вектором нормали данной
плоскости является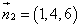 
.
Если векторы коллинеарны, то их координаты пропорциональны, то есть
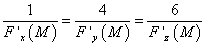
Так как частные производные
,
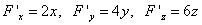то получим
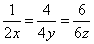
или
.
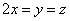Чтобы найти координаты точки M, к последним равенствам нужно присоединить уравнение поверхности. В результате получим систему уравнений, которую и решаем:
.
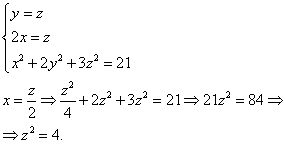Таким образом,
,
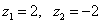следовательно,
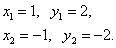
Вот мы и нашли две точк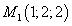и 
и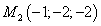 
, проведённая через
которые касательная плоскость параллельна данной плоскости.
Вычислим значения частных производных в точке :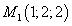
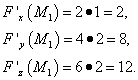
Теперь уже можем составить уравнение касательной плоскости, проведённой через точку
:
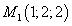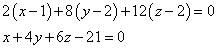
Вычислим значения частных производных в точке :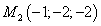
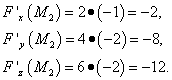
И, наконец, уравнение касательной плоскости, проведённой через точку
:
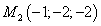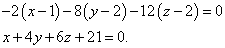
Поделиться с друзьями
Производные
Функции нескольких переменных
function-x.ru
4.1.3 Уравнение касательной к графику функции
Видеоурок: Уравнение касательной к графику функции
Лекция: Уравнение касательной к графику функции
Если некоторая прямая проходит через точку с координатами (х0; f (х0)), а угол наклона данной прямой равен производной функции в данной токе, то такую прямую называют касательной к графику.
Обратите внимание, если не существует производной графика в данной точке, то и не может существовать касательной, или же данная касательная перпендикулярна к оси ОХ. Второй случай можно наблюдать в результате проведения касательной для графика функции арксинуса.
Итак, давайте рассмотрим задание касательной. Мы знаем, что для задания любой прямой, необходимо воспользоваться формулой y = kx + b.
Коэффициент k показывает, под каким углом будет располагаться прямая относительно оси ОХ. Если данный коэффициент больше нуля, то угол наклона между касательной и осью ОХ острый, если же коэффициент отрицательный, то угол между осью ОХ и касательной тупой.
Но давайте возвратимся к тому, что такое угловой коэффициент и как он находится. С прошлых вопросов мы помним, что угловой коэффициент – это производная функции в некоторой точке х0.
Чтобы задать уравнение касательной, необходимо воспользоваться формулой:
Итак, давайте рассмотрим подробнее, для этого необходимо провести аналогию между первоначальным уравнением прямой и уравнением касательной.
Отсюда следует, что для нахождения коэффициента k, необходимо найти производную в рассматриваемой точке.
Давайте найдем уравнение прямой для функции у = х3 в точке х0 = 3.
1. Находим производную данной функции:
y’ = 3x2.
2. Как уже было сказано ранее, коэффициент – это производная функции в некоторой точке, поэтому
y'(3) = 3* 32 = 27.
3. Как видно из уравнения касательной, нам так же необходимо найти и значение функции в рассматриваемой точке f(x0):
f(3) = 33 = 27.
Совершенно случайно получилось так, что значение производной в точке совпало со значением функции в заданной точке. Обратите внимание, что это просто совпадения и НЕ обязательно y’ = f(x0).
4. Теперь давайте составим уравнение касательной по заданной формуле:
у = 27 * (х – 3) + 27.
Чтобы получить конечно уравнение, необходимо сделать некоторые преобразования:
у = 27 * (х – 3) + 27 = 27х – 81 + 27 = 27х — 54.
То есть уравнение касательной:
у = 27х — 54.
Найти уравнение касательной достаточно просто, главное не запутаться в формуле. Для этого её необходимо просто выучить.
cknow.ru
Как найти уравнение касательной и уравнение нормали, если функция задана неявно?
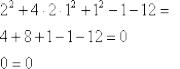
Формулы касательной и нормали остаются прежними, но меняется техника решения:
Пример 6
Найти уравнения касательной и нормали к кривой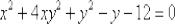 
в точке 
.
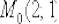Решение: судя по уравнению, это какая-то линия 3-го порядка, какая именно – нас сейчас совершенно не интересует.
В уравнении присутствует зловред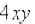 
, и поэтому перспектива выразить функция в явном виде 
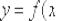выглядит весьма туманной.
Но этого и не требуется! Есть куда более остроумное решение. Уравнение касательной составим по той же формуле
.
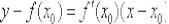Из условия известны значения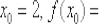 
, кстати, не помешает убедиться, что они действительно удовлетворяют предложенному уравнению:
Получено верное равенство, значит, с точкой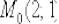 
всё в порядке.
Осталось вычислить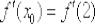 
. Сначала по стандартной схеме найдём производную от функции, заданной неявно:
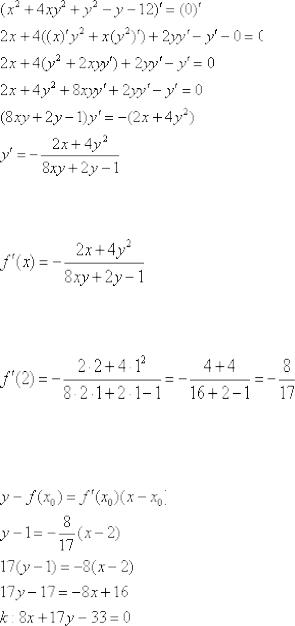
Перепишем результат с более подходящим для нашей задачи обозначением:
На 2-м шаге в найденное выражение производной подставим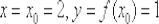 
:
Вот так-то!
Осталось аккуратно разобраться с уравнением:
Составим уравнение нормали:
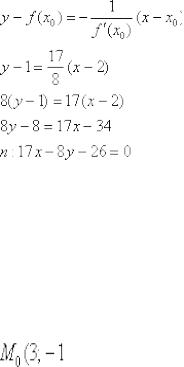
Ответ: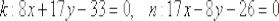 
Готово! А поначалу представлялось всё непросто. Хотя производная здесь, конечно, – место уязвимое. Миниатюра для самостоятельного решения:
Пример 7
Найти уравнение нормали к линии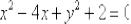 
в точке
Хватит уже вымучивать касательную =)
В данном случае легко выяснить, что это окружность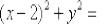 
центром в точке 
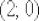радиуса 
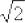и даже выразить нужную функцию 
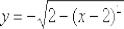. Но зачем?! Ведь найти производную от неявно
заданной функции на порядок легче! Она тут чуть ли не самая примитивная.
Краткое решение и ответ в конце урока.
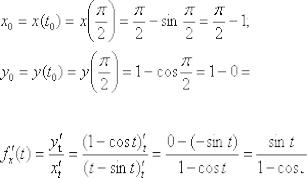
Как найти уравнение касательной и уравнение нормали, если функция задана параметрически?
Ещё проще. Но для этого нужно потренироваться в нахождении
производной от параметрически заданной функции. А так – почти халява:
Пример 8
Составить уравнения касательной и нормали к циклоиде 
, проведенные в точке, для которой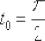 
.
Чертёж циклоиды можно найти на странице S и V, если линия задана параметрически (так получилось, что эта статья была создана раньше). Там даже изображена точка касания.
Решение: абсцисса и ордината точки касания рассчитываются непосредственно из параметрических уравнений кривой:
Найдём 1-ую производную от параметрически заданной функции:
И вычислим её значение при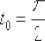 
:
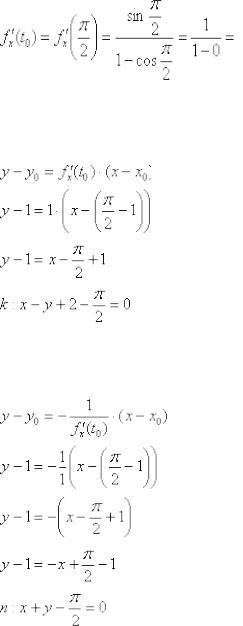
Уравнение касательной составим по обычной формуле с поправкой на несколько другие обозначения:
Уравнение нормали:
Ответ: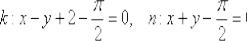 
В заключение предлагаю познакомиться с ещё одной интересной
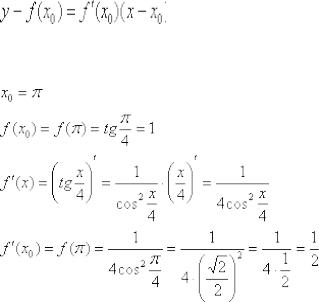
линией: Пример 9
Составить уравнение нормали к полукубической параболе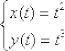 
, проведенной в точке, для которой 
.
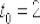Это пример для самостоятельного решения. Напоминаю, что графики параметрически заданных функций можно построить, например, с помощью моего расчётного геометрического макета.
Ну а наш урок подошёл к концу, и я надеюсь, что изложенный материал прошёл для вас не по касательной, а нормально =)
Спасибо за внимание и успехов!
Решения и ответы:
Пример 2: Решение: уравнение касательной составим по формуле:
В данном случае:
Таким образом:
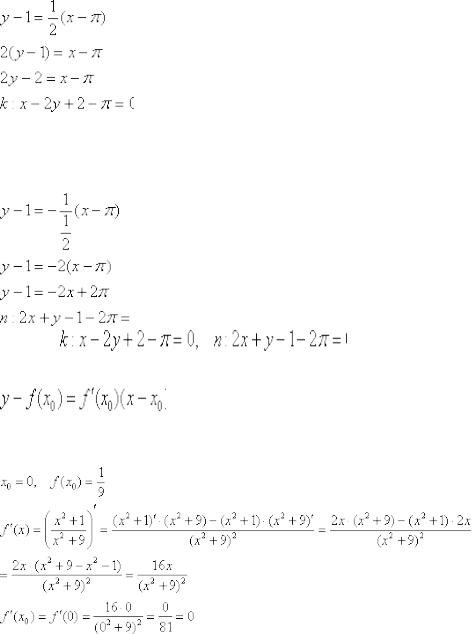
Уравнение нормали составим по формуле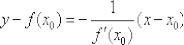 
:
Ответ:
Пример 4: Решение: уравнение касательной составим по формуле:
В данной задаче:
Таким образом:
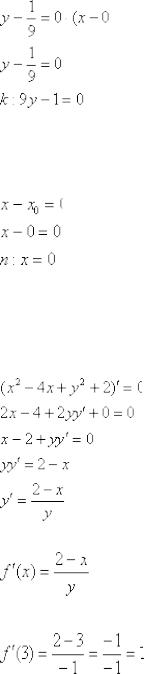
В точке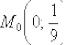 
касательная параллельна оси 
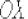, поэтому соответствующее уравнение нормали:
Ответ: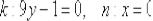 
Пример 7: Решение: в данной задаче: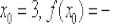 
. Найдём производную:
Или:
Подставим в выражение производной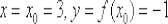 
:
Искомое уравнение нормали:
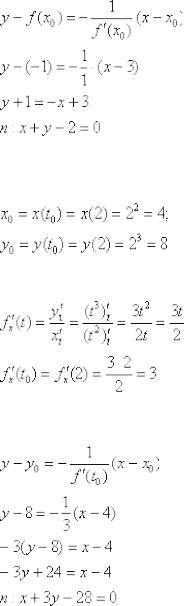
Ответ: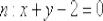 
Пример 9: Решение: в данном случае:
Найдём производную и вычислим её значение при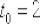 
:
Уравнение нормали:
Ответ: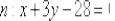 
studfile.net
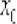