Абсолютная величина — Википедия

Материал из Википедии — свободной энциклопедии

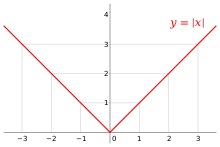График вещественной функции 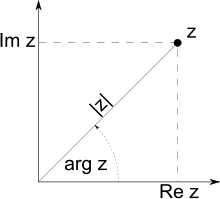Модуль |z|{\displaystyle |z|} и другие характеристики комплексного числа z{\displaystyle z}

Абсолю́тная величина́, или мо́дуль числа x{\displaystyle x} (в математике) — неотрицательное число, определение которого зависит от типа числа x{\displaystyle x}. Обозначается: |x|{\displaystyle |x|}.

В случае вещественного x{\displaystyle x} абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:

 |x|={  x,x⩾0−x, x<0{\displaystyle \ |x|={\begin{cases}\ \ x,&x\geqslant 0\\-x,&\ x<0\end{cases}}}

Обобщением этого понятия является модуль комплексного числа z=x+iy,{\displaystyle z=x+iy,} также иногда называемый абсолютной величиной

[1]. Он определяется по формуле:

|z|=|x+iy|=x2+y2{\displaystyle |z|=|x+iy|={\sqrt {x^{2}+y^{2}}}}

С геометрической точки зрения, модуль вещественного или комплексного числа есть расстояние между числом и началом координат. В математике широко используется тот факт, что геометрически величина |x1−x2|{\displaystyle |x_{1}-x_{2}|} означает расстояние между точками x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}} и, таким образом, может быть использована как мера близости одной (вещественной или комплексной) величины к другой.

Вещественные числа[править | править код]

• Область определения: (−∞;+∞){\displaystyle (-\infty ;+\infty )}.
• Область значений: [0;+∞){\displaystyle [0;+\infty )}.
• Функция чётная.
• Функция дифференцируема всюду, кроме нуля. В точке x=0{\displaystyle x=0} функция претерпевает излом.

Комплексные числа[править | править код]

Для любых вещественных чисел a,b{\displaystyle a,b} имеют место следующие соотношения:

•  |x|=x2=x⋅sgn⁡x=max{x,−x}{\displaystyle \ |x|={\sqrt {x^{2}}}=x\cdot \operatorname {sgn} x={\rm {max}}\,\{x,\,-x\}} (см. Функция sgn(x)).
• a⩽|a|{\displaystyle a\leqslant |a|}
• −|a|⩽a{\displaystyle -|a|\leqslant a}.
• Квадрат модуля числа равен квадрату этого числа: |a|2=a2{\displaystyle |a|^{2}=a^{2}}

Как для вещественных, так и для комплексных a,b{\displaystyle a,b} имеют место соотношения:

Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в начале XIX века.

Поскольку эта функция вычисляется достаточно просто (только сравнениями и присваиванием), то обычно она входит в стандартный список функций во все языки программирования. Например, в Pascal есть функция abs(x), а в C fabs(x) для вещественного типа. В программе Wolfram Mathematica Abs[x].

Понятие абсолютной величины можно ввести в произвольном упорядоченном кольце или упорядоченном поле, и свойства её будут аналогичны приведенным выше.

Обобщением понятия модуля можно считать норму элемента многомерного векторного пространства, обозначаемую ‖x‖{\displaystyle \|x\|}. Норма вектора в евклидовом пространстве иногда тоже называется модулем. По аналогии с модулем разности чисел, норма разности двух векторов является мерой близости между ними. В отличие от модуля числа, норма вектора может определяться различными способами, однако в случае одномерного пространства норма вектора пропорциональна (часто и равна) модулю его единственной координаты.

ru.wikipedia.org

Порядок числа по модулю — Википедия

Материал из Википедии — свободной энциклопедии

Показателем, или мультипликативным порядком, целого числа a{\displaystyle a} по модулю m{\displaystyle m} называется наименьшее положительное целое число ℓ{\displaystyle \ell }, такое, что^[1][2]

aℓ≡1(modm).{\displaystyle a^{\ell }\equiv 1{\pmod {m}}.}

Показатель определен только для чисел a{\displaystyle a}, взаимно простых с модулем m{\displaystyle m}, то есть для элементов группы обратимых элементов кольца вычетов по модулю m{\displaystyle m}. При этом, если показатель числа a{\displaystyle a} по модулю m{\displaystyle m} определен, то он является делителем значения функции Эйлера φ(m){\displaystyle \varphi (m)} (следствие теоремы Лагранжа) и значения функции Кармайкла λ(m){\displaystyle \lambda (m)}.

Чтобы показать зависимость показателя ℓ{\displaystyle \ell } от a{\displaystyle a} и m{\displaystyle m}, его также обозначают Pm(a){\displaystyle P_{m}(a)}, а если m{\displaystyle m} фиксировано, то просто P(a){\displaystyle P(a)}.

• a≡b(modm)⇒P(a)=P(b){\displaystyle a\equiv b{\pmod {m}}\Rightarrow P(a)=P(b)}, поэтому можно считать, что показатель задан на классе вычетов a¯{\displaystyle {\bar {a}}} по модулю m{\displaystyle m}.
• an≡1(modm)⇒P(a)∣n{\displaystyle a^{n}\equiv 1{\pmod {m}}\Rightarrow P(a)\mid n}. В частности, P(a)∣λ(m){\displaystyle P(a)\mid \lambda (m)} и P(a)∣φ(m){\displaystyle P(a)\mid \varphi (m)}, где λ(m){\displaystyle \lambda (m)} — функция Кармайкла, а φ(m){\displaystyle \varphi (m)} — функция Эйлера.
• at≡as(modm)⇔t≡s(modP(a)).{\displaystyle a^{t}\equiv a^{s}{\pmod {m}}\Leftrightarrow t\equiv s{\pmod {P(a)}}.}
• P(as)∣P(a){\displaystyle P(a^{s})\mid P(a)}; если gcd(s,P(a))=1{\displaystyle \gcd(s,P(a))=1}, то P(as)=P(a).{\displaystyle P(a^{s})=P(a).}
• Если p{\displaystyle p} — простое число и P(a)=k{\displaystyle P(a)=k}, то a,…,ak{\displaystyle a,\;\ldots ,\;a^{k}} — все решения сравнения xk≡1(modp){\displaystyle x^{k}\equiv 1{\pmod {p}}}.
• Если p{\displaystyle p} — простое число, то P(a)=p−1⇔a{\displaystyle P(a)=p-1\Leftrightarrow a} — образующая группы Zp{\displaystyle \mathbb {Z} _{p}}.
• Если ψ(k){\displaystyle \psi (k)} — количество классов вычетов с показателем k{\displaystyle k}, то ∑k∣φ(m)ψ(k)=φ(m){\displaystyle \sum \limits _{k\,\mid \,\varphi (m)}\psi (k)=\varphi (m)}. А для простых модулей даже ψ(k)=φ(k){\displaystyle \psi (k)=\varphi (k)}.
• Если p{\displaystyle p} — простое число, то группа вычетов Zp×{\displaystyle \mathbb {Z} _{p}^{\times }} циклична и потому, если a=gdk{\displaystyle a=g^{dk}}, где g{\displaystyle g} — образующая, d∣p−1{\displaystyle d\mid p-1}, а k{\displaystyle k} — взаимно просто с p−1{\displaystyle p-1}, то P(a)=p−1d{\displaystyle P(a)={\frac {p-1}{d}}}. В общем случае для произвольного модуля m{\displaystyle m} можно вывести аналогичную формулу, пользуясь теоремой о структуре мультипликативной группы вычетов Zm×{\displaystyle \mathbb {Z} _{m}^{\times }}.

Так как 24≡1(mod15){\displaystyle 2^{4}\equiv 1{\pmod {15}}}, но 21≢1(mod15){\displaystyle 2^{1}\not \equiv 1{\pmod {15}}}, 22≢1(mod15){\displaystyle 2^{2}\not \equiv 1{\pmod {15}}}, 23≢1(mod15){\displaystyle 2^{3}\not \equiv 1{\pmod {15}}}, то порядок числа 2 по модулю 15 равен 4.

Если известно разложение модуля m{\displaystyle m} на простые множители pj{\displaystyle p_{j}} и известно разложение чисел pj−1{\displaystyle p_{j}-1} на простые множители, то показатель заданного числа a{\displaystyle a} может быть найден за полиномиальное время от ln⁡m{\displaystyle \ln m}. Для вычисления достаточно найти разложение на множители функции Кармайкла λ(m){\displaystyle \lambda (m)} и вычислить все admodm{\displaystyle a^{d}\mod m} для всех d∣λ(m){\displaystyle d\mid \lambda (m)}. Поскольку число делителей ограничено многочленом от ln⁡m{\displaystyle \ln m}, а возведение в степень по модулю происходит за полиномиальное время, то алгоритм поиска будет полиномиальным.

Характеры Дирихле[править | править код]

Характер Дирихле χ{\displaystyle \chi } по модулю m{\displaystyle m} определяется обязательными соотношениями χ(ab)=χ(a)χ(b){\displaystyle \chi (ab)=\chi (a)\chi (b)} и χ(a)=χ(a+m){\displaystyle \chi (a)=\chi (a+m)}. Чтобы эти соотношения выполнялись, необходимо, чтобы χ(a){\displaystyle \chi (a)} был равен какому-либо комплексному корню из единицы степени Pm(a){\displaystyle P_{m}(a)}.

ru.wikipedia.org

Модуль числа в Python 3 — Функция abs библиотеки math

Очень часто возникает необходимость вычисления модуля числа в Python. Рассмотрим, что такое модуль числа, какие есть способы его вычисления. Так же отдельно коснемся комплексных чисел.

Модуль числа

Часто в программировании требуется вычислить абсолютное значение числа. Иначе говоря, отбросить знак.

При вычислении модуля возможны 3 ситуации:

• Когда число больше 0. Если взять его по модулю — не изменится.
• Модуль нуля так же равен нулю.
• У отрицательного числа отбрасываем знак. То есть умножаем его на -1.

Но это все справедливо только для действительных чисел. Чему же тогда будет равен модуль комплексных?

Комплексное число состоит из действительной составляющей и мнимой. Геометрически это можно представить как 2 ортогональные оси: действительную и мнимую. Отмечаем на координатных осях требуемую точку. Модулем будет длина отрезка, проведенного из начала координат в эту точку.

Исходя из теоремы Пифагора получаем, что модуль комплексного числа это корень квадратный из суммы квадратов мнимой и действительной частей.

Вычисление

Вычислять модуль можно следующими способами:

• Используя стандартную функцию abs.
• С помощью функции fabs библиотеки math.
• При помощи самостоятельно написанной функции.

Все эти функции работают как в Python 2, так и в Python 3.

abs

Для вычисления в Python модуля числа используется функция abs. Результат функции того же типа, которого был аргумент.

a = -10
b = abs(a)
print(b)
print(type(b))

10
<class 'int'>

fabs

Можно так же воспользоваться функцией fabs из библиотеки math. Библиотеку можно подключить с помощью from math import fabs.

from math import fabs
a = -10
b = fabs(a)
print(b)
print(type(b))

10.0
<class 'float'>

Отличие abs от fabs заключается в том, что функция abs возвращает значение того же типа, что и аргумент. Функция же fabs вначале преобразует тип аргумента к вещественному числу.

Свое решение

Если по каким то причинам нет возможности или желания использовать стандартные функции, то можно написать свое решение.

Например, можно вычислить воспользоваться тернарным оператором.

a = -10
b = a if a > 0 else -a
print(b)

10

На основе такого условия сделаем свою функцию.

def my_abs(a):
    return a if a > 0 else -a
print(my_abs(-3))

3

Модуль комплексного числа

Мы разобрались как происходит вычисление с действительными числами. Теперь посмотрим, как в языке программирования Python можно получить модуль комплексного.

Функцией fabs мы не сможем воспользоваться. Если попытаемся это сделать, то получим ошибку приведения комплексного числа к действительному (TypeError).

from math import fabs
a = -10-2j
b = fabs(a)
print(b)

Traceback (most recent call last):
  File "main.py", line 3, in <module>
    b = fabs(a)
TypeError: can't convert complex to float

А вот с помощью abs преобразование удается.

a = -10-2j
b = abs(a)
print(b)

10.19803902718557

Или же напишем свою функцию:

from math import sqrt
def my_abs_complex(c):
    return sqrt(c.real**2 + c.imag**2)
a = -10-2j
b = my_abs_complex(a)
print(b)

10.198039027185569

Результаты получились одинаковыми. Но нам все равно пришлось подключить библиотеку math для вычисления квадратного корня.

all-python.ru

вычисление модуля

Вы искали вычисление модуля? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить модуль, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление модуля».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вычисление модуля,вычислить модуль,вычислить модуль онлайн,калькулятор модулей числа,калькулятор модуль числа онлайн,калькулятор онлайн модуль числа,модуль как посчитать,модуль онлайн,модуль числа калькулятор онлайн,модуль числа онлайн калькулятор,найти модуль числа онлайн,онлайн вычислить модуль,онлайн калькулятор модулей,онлайн калькулятор модуль числа,онлайн модуль,раскрыть модуль онлайн калькулятор. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вычисление модуля. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислить модуль онлайн).

Где можно решить любую задачу по математике, а так же вычисление модуля Онлайн?

Решить задачу вычисление модуля вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

www.pocketteacher.ru

Модуль числа в 1С 8.3, запрос, функция

Редактор статьи:

Михаил  Сайко 

Сервис-инженер 1С Получить консультацию

Актуальность статьи проверена:
27.09.2018

Задача получения модуля числа часто встречается на практике. Суть этой операции обычно заключается в том, чтобы получить абсолютное значение числа. Непосредственной функции для вычисления модуля в платформе 1С нет, но специалисты по доработке 1С нашли несколько вариантов, решающих эту задачу. Запоминать эти алгоритмы нет необходимости, они логичны, и их достаточно легко построить самостоятельно.

Вычисление модуля числа в 1С

Обычно используются три варианта вычисления модуля: два для встроенного языка 1С, и последний – внутри запросов:

1. Функция Макс().Берем максимальное значение из двух: числа и его же, умноженного на 1; 

   
   МодульЧисла = Макс(Число, число * -1)
   

2. Применение конструкции «Если» или краткого аналога;

    
   Если число > 0 тогда
          МодульЧисла = число;
   иначе
          МодульЧисла = число * -1;
   конецЕсли;
   
   Модульчисла = ?(число > 0,число, число * -1)
   

3. Для запросов есть аналог конструкции «Если – Выбор».

   
   ВЫБОР
             КОГДА число > 0
                        ТОГДА число
             ИНАЧЕ число * -1
   КОНЕЦ
   

Мы видим, что это достаточно простые действия, но если у вас остались вопросы, обратитесь к нашим специалистам, предоставляющим консультационные услуги по 1С, мы с радостью вам поможем.

wiseadvice-it.ru

Аргумент и модуль комплексного числа

Вычислить аргумент и модуль комплексного числа.
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ

Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ

Из определения следуют следующие формулы:

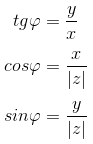
Для числа z = 0 аргумент не определен.

Главным значением аргумента называется такое значение φ, что 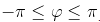. Обозначается: arg(z).

Свойства аргумента:

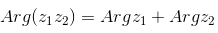	— аргумент от произведения двух комплексных чисел равен сумме аргументов этих чисел
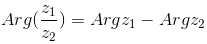	— аргумент частного двух комплексных чисел равен разности аргументов этих чисел
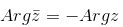	— аргумент от сопряженного комплексного числа равен отрицательному значению аргумента от этого числа.

Модулем комплексного числа z = x + iy называется вещественное число |z| равное:

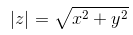
Для любых комплексных чисел z, z₁, z₂ имеют место следующие свойства модуля:

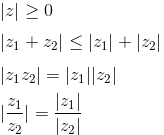для пары комплексных чисел z1 и z2 модуль их разности |z1 − z2| равен расстоянию между соответствующими точками комплексной плоскости.

allcalc.ru

Остаток числа в степени по модулю

Полученный результат

Рассмотрим одну из задач часто встречающейся в арифметике и теории чисел, которую можно выразить  несколькими примерами.

Какой остаток  будет у следующих чисел

если их попытаться разделить на число 31?

И если первый пример  можно решить на калькуляторе, так сказать » в лоб, не думая», то как Вы будете решать третий пример, это для некоторых очень не тривиальная задача.

Что же такое остаток? Остаток в данном случае — это такое число(по абсолютному значению меньше модуля!), отняв которое из исходного числа, полученный результат будет делится нацело на модуль ( в нашем примере модуль это число 31)

То есть, если обозначим остаток буквой Х получим  (в первом примере ) что число  делится нацело (без остатка) на модуль

Или в другой, записи более привычной 

 где M — модуль

Как же решать подобные задачи?

Для этого нам надо знать несколько  свойств из теории чисел, которые покажем на втором примере  

1. 

Даже объяснять неохота, выносим -1 за «скобки» ( отдельным множителем) и можем сразу посчитать. Если степень числа (321) четная то результат равен 1, если нечетная то -1.

2.

Если  число можно представить в виде двух и более сомножителей то, остаток от этого числа будет равен произведению остатков от сомножителей по этому же модулю.

3.

Прибавив или отняв от любого сомножителя  целое количество модуля — остаток не изменится.

4. 

Тоже ничего сложного, просто преобразовали степень. Обычное свойство степеней.

5. 

Здесь мы возвели -5 в куб и воспользовались 3 правилом, прибавив к нему 4 раза модуль

6. 

Воспользовавшись  первым правилом, получили что наш ответ 1

То есть можем утверждать что   есть целое число.

7. Последнее правило гласит, что формально, всегда существует два остатка и они равноценны. В нашем примере это 1 и -30, так как  тоже целое число.

 

Надеюсь это небольшой пример разбора, дал Вам методику решения подобных задач.

А бот, который создан, поможет  Вам легко узнавать правильность решения подобных задач или,  если Вы преподаватель, легко и точно генерировать задачи для учеников.

Синтакис для XMPP клиентов

modul число степень модуль

число — отрицательное или положительное, целое число

степень — только положительная целая степень.

модуль — положительное целое число.

каждый элемент может содержать до 19 цифр ( вообще я не знаю на какой длине, могут возникнуть ошибки, но при (до) 19 символах все работает хорошо)

поэтому нет ничего страшного найти остаток вот от такого «монстра»

кто хочет может умножать на калькуляторе 🙂

ответ 3848922529426

Если же Вы вдруг  нашли ошибку или у Вас есть пожелания или вопросы, не стесняйтесь обращайтесь Обратная связь с разработчиками бота.

Интересные факты

Утверждается, что если P — число простое то выполняется вот такое равенство

Это условие необходимое(то есть применимо ко всем простым числам) но не достаточное ( то есть есть составные числа для которых эта формула тоже действительна)

Красивое выражение было найдено пока тестировал бота ( для 2014 года) 🙂

На 31 мая 2018 года еще нашлось кое что интересное

Смотрите

Удачных расчетов!

• Пересечение окружности и прямой.Координаты. >>

abakbot.ru