Принцип Дирихле | Социальная сеть работников образования
Слайд 1
Презентация на тему: Принцип Дирихле Выполнил: ученик 7 «В» класса МКОУ Таловская СОШ Новиков Алексей Ноябрь 2015г.Слайд 2
Цель: Познакомиться с новым математическим методом решения задач; Научиться решать задачи с помощью принципа Дирихле; Показать его применение для решения разнообразных задач.
Слайд 3
При решении различных математических задач применяется специальный метод, получивший название: принцип Дирихле . Петер Густав Лежен Дирихле (13.02.1805 — 05.05.1859)
Слайд 4
Дирихле Петер Август Лежён (1805-1859) — немецкий математик, иностранный член-корреспондент Петербургской Академии наук (1837), член многих других академий Дирихле родился в вестфальском городе Дюрене в семье почтмейстера. В 12 лет Дирихле начал учиться в гимназии в Бонне, спустя два года в иезуитской гимназии в Кёльне, где в числе прочих преподавателей его учил Георг Ом. С 1822 по 1827 г. жил в качестве домашнего учителя в Париже, где вращался в кругу Фурье. — В 1827г. устраивается на должность приватдоцента университета Бреслау (Вроцлав). В 1829 г. он перебирается в Берлин, где проработал непрерывно 26 лет, сначала как доцент. Затем с 1831 г. Как экстраординарный профессор. С 1839 г. как ординарный профессор Берлинского университета. В 1855 г. Дирихле становится в качестве преемника Гаусса профессором высшей математики в Гёттингенском университете.
Слайд 5
При́нцип Дирихле́ ( нем . Schubfachprinzip , « принцип ящиков » ) — утверждение, сформулированное немецким математиком Дирихле в 1834 году, устанавливающее связь между объектами ( « кроликами » ) и контейнерами ( « клетками » ) при выполнении определённых условий. В английском и некоторых других языках утверждение известно как « принцип голубей и ящиков » (англ. Pigeonhole principle ), когда объектами являются голуби, а контейнерами — ящики. 9 клеток содержат 7 голубей, по принципу Дирихле хотя бы 9-7= 2 клетки свободны 9 клеток содержат 10 голубей, по принципу Дирихле хотя бы в одной клетке находятся более одного голубя
Слайд 6
Формулировки Наиболее распространена следующая формулировка этого принципа: Если в N клетках сидят не менее N + 1 кроликов, то в какой-то из клеток сидит не менее двух кроликов. Более общая формулировка звучит так : Если в N клетках сидят не менее kN + 1 кроликов, то в какой-то из клеток сидит по крайней мере k + 1 кролик. Возможны также формулировки для частных случаев: Если число клеток больше, чем число кроликов, то как минимум одна клетка пуста.
Слайд 7
Рассмотрим примеры различных задач, решаемых с помощью принципа Дирихле 1. В классе 15 учеников. Докажите, что найдутся как минимум 2 ученика, отмечающих дни рождения в один месяц. РЕШЕНИЕ: Пусть 15 учеников будут «зайцы». Тогда «клетками» будут месяцы года, их 12. Так как 15 > 12, то, по принципу Дирихле, найдется, как минимум, одна клетка, в которой будет сидеть, по крайней мере, 2 «зайца». То есть, найдется месяц, в котором будут отмечать дни рождения не менее 2 учеников класса.
Слайд 8
2. Внутри равностороннего треугольника со стороной 1 см расположено 5 точек. Докажите, что расстояние между некоторыми двумя из них меньше 0,5 см РЕШЕНИЕ: Это наиболее трудная задача на принцип Дирихле . Но на примере ее решения очень хорошо видны все достоинства принципа Дирихле. Итак, при решении сначала надо выбрать что-то за «зайцев». Так как в условии задачи фигурирует число «5», то пусть 5 точек будут «зайцами». Так как «клеток» должно быть меньше, и чаще всего на 1, то их должно быть 4. Как получить эти 4 «клетки»? Так как в условии задачи есть еще 2 числа; 1 и 0,5; причем второе меньше первого в 2 раза, то можно получить 4 « клетки », разбив равносторонний треугольник с помощью проведения отрезков, соединяющих середины сторон. Тогда получим 4 равносторонних треугольника со сторонами по 0,5 см, которые и будут у нас «клетками». Так как «зайцев» — 5, «клеток» — 4 и 5 > 4,то, по принципу Дирихле, найдется «клетка» — равносторонний треугольник со стороной 0,5 см, в который попадут не менее двух «зайцев» — точек. Так как 4 треугольника равны и расстояние между точками в любом треугольнике меньше, чем 0,5 см. т.е. некоторыми двумя точками из пяти расстояние будет меньше, чем 0,5. 2 4 1 3
Слайд 9
Дано 12 целых чисел. Докажите, что из них можно выбрать 2, разность которых делится на 11. РЕШЕНИЕ Примем числа за «зайцев». Так как их 12, то «клеток» должно быть меньше. Пусть «клетки» —это остатки от деления целого числа на 11. Всего «клеток» будет 11: О, 1, 2, 3, 4, 5, 6, 7, 8, 9,10. Тогда, по принципу Дирихле, найдется «клетка», в которой будут сидеть не менее чем 2 «зайца», то есть найдутся 2 целых числа с одним остатком. А разность двух чисел с одинаковым остатком от деления на 11, будет делиться на 11
Слайд 10
В ковре размером 3×3 метра Коля проделал 8 дырок. Докажите, что из него можно вырезать коврик размером 1×1 метр, не содержащий внутри себя дырок (Дырки можно считать точечными.) РЕШЕНИЕ Здесь дырки будут «зайцами». Разрежем ковер на 9 ковриков размерами 1×1 метр. Так как ковриков-«клеток» — 9, а дырок-«зайцев» — 8, то найдется хотя бы одна «клетка», в которой не будет «зайцев», то есть найдется коврик без дырок внутри.
Слайд 11
Таким образом, применяя данный метод, надо: Определить, что удобно в задаче принять за « клетки » , а что за « зайцев » . Получить « клетки » ; чаще всего « клеток » меньше (больше), чем « зайцев » на одну (или более). Выбрать для решения требуемую формулировку принципа Дирихле. Принцип Дирихле важен, интересен, полезен. Его можно применять в повседневной жизни, что развивает логическое мышление. Многие олимпиадные задачи решаются, используя это специальный метод. Он дает возможность обобщать.
Слайд 12
Применение принципа Дирихле В шкафу лежат вперемежку 5 пар светлых и 5 пар темных ботинок одинакового размера и фасона. Какое наименьшее количество ботинок надо взять наугад из шкафа, чтобы среди них была хоть одна пара (левый и правый) одного цвета? В классе 35 учеников. Можно ли утверждать, что среди них найдутся хотя бы два ученика, фамилии которых начинаются с одной буквы? Имеется 5 чемоданов и 5 ключей к ним, но неизвестно какой ключ от какого. Сколько проб придется сделать в самом худшем случае, чтобы подобрать к каждому чемодану свой ключ? В коробке лежат 7 красных и 5 синих карандашей. Сколько надо взять карандашей, чтобы среди них было не меньше 2 красных и не меньше 3 синих. В классе 30 человек. В диктанте Витя сделал 12 ошибок, а каждый остальной не больше. Докажите, что по крайней мере трое сделали одинаковое количество (может быть ноль) ошибок.
Слайд 13
При каком наименьшем количестве учеников школы среди них обязательно найдутся двое, у которых день и месяц рождения совпадает? В квадрате со стороной 5 см размещено 126 точек. Докажите, что среди них существуют 6 точек, которые лежат в круге радиуса 1 м. В классе 25 человек. 20 занимаются английским, 17 плаванием, 14 посещают математический кружок. Докажите, что найдется хотя бы один человек, посещающий все сразу. В квадрат со стороной 1 м бросили 51 точку. Докажите, что какие-то три из них можно покрыть квадратом со стороной 20 см. На дискотеку в студенческое общежитие, в котором 42 комнаты. Пришло 36 гостей. Докажите, что найдется комната, в которую не пришел ни один гость.
Слайд 14
Литература А.В. Спивак «Математический праздник» . С.А. Генкин, И.В. Итенберг, Д.В. Фомин «Ленинградские математические кружки» А.Я. Канель-Белов, А.К. Ковальджи «Как решают нестандартные задачи» . С.А. Дориченко, И.В.Ященко «57 Московская математическая олимпиада. Сборник подготовительных задач».
Принцип Дирихле. | Социальная сеть работников образования
Слайд 1
ТЕМА: «Принцип Дирихле» Выполнила: Зверева Екатерина Александровна Учащаяся 8 «а» класса Научный руководитель: Кирпичева Е.Е. 2011 — 2012 учебный годСлайд 2
Цели работы: 1. Ознакомиться с биографией Дирихле 2. Рассмотреть различные формулировки принципа Дирихле 3. Научиться применять изученный принцип к решению задач 4. Классифицировать задачи в соответствии с их содержанием: а) геометрические задачи; б) задачи на пары; в) задачи на знакомства и дни рождений; г) задачи на среднее арифметическое; д) задачи на делимость; е) задачи на комбинаторику; ж) задачи на теорию чисел; 5. Придумать свои задачи, и решить их используя принцип Дирихле
Слайд 3
Биография ДИРИХЛЕ Петер Густав Лежен(13.2.1805-5.5.1859) — немецкий математик. Род. в Дюрене. В 1822-1827 Д. был домашним учителем в Париже. Входил в кружок молодых ученых, которые группировались вокруг Ж. Фурье. В 1827 Д. занял место доцента в Бреславле; с 1829 работал в Берлине. В 1831-1855 — профессор Берлинского ун-та, а после смерти К. Гаусса (1855) — Геттингенского ун-та.
Слайд 4
Биография Д. создал общую теорию алгебраических единиц в алгебраическом числовом поле. В области математического анализа Д. впервые точно сформулировал и исследовал понятие условной сходимости ряда, дал строгое доказательство возможности разложения в ряд Фурье кусочно-непрерывной и монотонной функции, что послужило обоснованием для многих дальнейших исследований. Значительны труды Д. в механике и математической физике, в частности в теории потенциала.
Слайд 5
Биография Д. сделал ряд крупных открытий в теории чисел: установил формулы для числа классов бинарных квадратичных форм с заданным определителем и доказал теорему о бесконечности количества простых чисел в арифметической прогрессии из целых чисел, первый член и разность которой — взаимно просты. К решению этих задач Д. применил аналитические функции, названные функциями (рядами) Дирихле.
Слайд 6
Принцип Дирихле Наиболее применяемая формулировка: «Если в n клетках сидят n + 1 «кроликов», то есть клетка, в которой не менее 2-х «кроликов » « Дирихле по частоте упоминаний школьниками навсегда обеспечено одно из самых высших мест.»
Слайд 7
Несколько утверждений: У1. «Если в n клетках сидят не более n-1 «кроликов», то есть пустая клетка» У2. «Если в n клетках сидят n + 1 «кроликов», то есть клетка, в которой не менее 2-х «кроликов» У3. «Если в n клетках сидят не более nk-1 «кроликов», то в какой-то из клеток сидят не более k-1 «кроликов» У4. «Если в n клетках сидят не менее n k+1 «кроликов», то в какой-то из клеток сидят не менее k+1 «кроликов»
Слайд 8
У5. Непрерывный принцип Дирихле. «Если среднее арифметическое нескольких чисел больше a, то, хотя бы одно из этих чисел больше a»; У6. «Если сумма n чисел меньше S, то по крайней мере одно из этих чисел меньше S/n». У7. «Среди p + 1 целых чисел найдутся два числа, дающие при делении на p один и тот же остаток».
Слайд 9
1 ) Геометрические задачи
Слайд 11
Задача №3. («на пары») На планете Земля океан занимает больше половины площади поверхности. Докажите, что в мировом океане можно указать две диаметрально противоположные точки. Континент расположен между примерно 9° з. д. и 169° з. д., 12° ю. ш. 81° с. ш. Африка расположена между 37 ° с. ш. и 35 ° ю. ш., между 17 ° з.д., 51 ° з. д.
Слайд 12
Решение. Будем считать «кроликами» точки океана, а «клетками» — пары диаметрально противоположных точек планеты. Количество «кроликов» в данном случае — это площадь океана, а количество «клеток» — половина площади планеты. Поскольку площадь океана больше половины площади планеты, то «кроликов» больше, чем «клеток». Тогда есть «клетка», в которой сидит не менее двух «кроликов», т.е. пара противоположных точек, обе из которых — океан. У2
Слайд 13
Задача №4. В хвойном лесу растут 800000 елей. На каждой ели — не более 500000 иголок. Доказать, что существуют хотя бы две ели с одинаковым числом иголок.
Слайд 14
Решение. Число «клеток» – 500000 (на каждой ели может быть от 1 иголки до 500000 иголок, 800000 ели – число «кроликов», так как, «кроликов» больше чем клеток, значит, есть «клетка», в которой сидит не менее двух «кроликов». Значит, существуют хотя бы две ели с одинаковым числом иголок. (У2)
Слайд 15
Задача №5. («на делимость») Задача . Дано 11 различных целых чисел. Доказать, что из них можно выбрать два числа, разность которых делится на 10. Решение. По крайней мере, два числа из 11 дают одинаковый остаток при делении на 10 . Пусть это будут A = 10a + r и B = 10b + r. Тогда их разность делится на 10: A — B = 10(a — b). (У2)
Слайд 16
Задача №6. («на делимость») Доказать, что число N 5 оканчивается на ту же цифру, что число N. Решение. Докажем, что N 5 -N кратно 10. N(N-1 ) кратно 5 кратно 2
Слайд 17
Задача №7. («на комбинаторику») В коробке лежат шарики 4-х разных цветов (много белых, много черных, много синих, много красных). Какое наименьшее количество шариков надо наощупь вынуть из мешка, чтобы среди них заведомо оказались два одного цвета? Решение Возьмем за «кроликов» шары, а за «клетки» — черный, белый, синий, красный цвета. Клеток 4, поэтому если кроликов, хотя бы 5, то какие-то два попадут в одну клетку (будет 2 одноцветных шарика).
Слайд 18
Задача «на комбинаторику» № 8. Маленький брат Андрея раскрасил шашки в восемь цветов. Сколькими способами Андрей может поставить на доску 8 разноцветных шашек так, чтобы в каждом столбце и в каждой строке было по одной шашке? Сколькими способами Андрей может поставить на доску 8 белых шашек так, чтобы в каждом столбце и в каждой строке было по одной шашке?
Слайд 19
Решение задачи. Рассмотрим сначала случай, когда шашки белые. Будем расставлять шашки. В первом столбце мы можем поставить шашку в любую из 8 клеток. Во втором столбце — в любую из 7 клеток. (Т. к. нельзя ставить в ту же строку, в которой стоит первая шашка.) Аналогично в третьей строке мы можем поставить шашку в любую из 6 клеток, в четвёртой строке — в любую из пяти и т. д. Итого получаем 8 способов. 2) Теперь рассмотрим случай цветных шашек. Возьмём произвольную расстановку белых шашек. Будем раскрашивать эти шашки в 8 цветов, так чтобы любые две из них были покрашены в разные цвета. Первую мы можем покрасить в один из 8 цветов, вторую — в один из 7 оставшихся и.т. д. Т. е. всего 8 способов раскраски. Поскольку способов расстановки тоже 8 , и каждую из этих расстановок мы можем раскрасить 8 способами, то всего способов в этом случае 8·8=8². Ответ: 8² способов, 8 способов.
Слайд 20
Задача (метод от «противного») № 9. В Москве проживает более 10 000 000 людей. На голове у каждого человека не может быть более 300 000 волос. Докажите, что наверняка найдутся 34 москвича с одинаковым числом волос на голове.
Слайд 21
Решение 1) На голове может быть 0, 1, …, 300 000 волос — всего 300 001 вариант. Каждого москвича отнесём к одной из 300 001 групп в зависимости от количества волос. 2) Если 34 москвича с одинаковым количеством волос не найдутся, то это значит, что в любую из созданных групп входит не более 33 человек. 3)Тогда всего в Москве живёт не более 33·300 001=9 900 033
Слайд 22
Используемые интернет-ресурсы: images.yandex.ru (фото Дирихле, картинки о школе) http://bars-minsk.narod.ru/teachers/dirichle.html http://www.bestreferat.ru/referat-4776.html
Презентация на тему: «Принцип Дирихле»

ТЕМА: «Принцип Дирихле»
Выполнила:
Зверева Екатерина Александровна
Учащаяся 8 «а» класса
Научный руководитель: Кирпичева Е.Е.
2011 — 2012 учебный год

Цели работы:
1. Ознакомиться с биографией Дирихле
2. Рассмотреть различные формулировки принципа Дирихле
3. Научиться применять изученный принцип к решению задач
4. Классифицировать задачи в соответствии с их содержанием:
а) геометрические задачи;
б) задачи на пары;
в) задачи на знакомства и дни рождений;
г) задачи на среднее арифметическое;
д) задачи на делимость;
е) задачи на комбинаторику;
ж) задачи на теорию чисел;
5. Придумать свои задачи, и решить их используя принцип Дирихле

Биография
- ДИРИХЛЕ Петер Густав Лежен(13.2.1805-5.5.1859) — немецкий математик. Род. в Дюрене. В 1822-1827 Д. был домашним учителем в Париже. Входил в кружок молодых ученых, которые группировались вокруг Ж. Фурье. В 1827 Д. занял место доцента в Бреславле; с 1829 работал в Берлине. В 1831-1855 — профессор Берлинского ун-та, а после смерти К. Гаусса (1855) — Геттингенского ун-та.

Биография
- Д. создал общую теорию алгебраических единиц в алгебраическом числовом поле.
- В области математического анализа Д. впервые точно сформулировал и исследовал понятие условной сходимости ряда, дал строгое доказательство возможности разложения в ряд Фурье кусочно-непрерывной и монотонной функции, что послужило обоснованием для многих дальнейших исследований.
- Значительны труды Д. в механике и математической физике, в частности в теории потенциала.

Биография
- Д. сделал ряд крупных открытий в теории чисел: установил формулы для числа классов бинарных квадратичных форм с заданным определителем и доказал теорему о бесконечности количества простых чисел в арифметической прогрессии из целых чисел, первый член и разность которой — взаимно просты. К решению этих задач Д. применил аналитические функции, названные функциями (рядами) Дирихле.

Принцип Дирихле
« Дирихле по частоте упоминаний школьниками навсегда обеспечено одно из самых высших мест.»
Наиболее применяемая формулировка:
«Если в n клетках сидят
n + 1 «кроликов»,
то есть клетка, в которой не менее 2-х «кроликов »
- Наиболее применяемая формулировка: «Если в n клетках сидят n + 1 «кроликов», то есть клетка, в которой не менее 2-х «кроликов »

Несколько утверждений:
У1. «Если в n клетках сидят не более n-1 «кроликов», то есть пустая клетка»
У2. «Если в n клетках сидят n + 1 «кроликов», то есть клетка, в которой не менее 2-х «кроликов»
У3. «Если в n клетках сидят не более nk-1 «кроликов», то в какой-то из клеток сидят не более k-1 «кроликов»
У4. «Если в n клетках сидят не менее n k+1 «кроликов», то в какой-то из клеток сидят не менее k+1 «кроликов»

У5. Непрерывный принцип Дирихле.
«Если среднее арифметическое нескольких чисел больше a, то, хотя бы одно из этих чисел больше a»;
У6. «Если сумма n чисел меньше S, то по крайней мере одно из этих чисел меньше S/n».
У7. «Среди p + 1 целых чисел найдутся два числа, дающие при делении на p один и тот же остаток».

1 ) Геометрические задачи
Задача 1. Доказать, что если прямая l , расположенная в плоскости треугольника ABC , не проходит ни через одну из его вершин, то она не может пересечь все три стороны треугольника. Решение
Полуплоскости, на которые прямая l разбивает плоскость треугольника ABC , обозначим через q 1 и q 2 ; эти полуплоскости будем считать открытыми (то есть не содержащими точек прямой l ). Вершины рассматриваемого треугольника (точки A , B , C ) будут «зайцами», а полуплоскости q 1 и q 2 — «клетками». Каждый «заяц» попадает в какую-нибудь «клетку» (ведь прямая l не проходит ни через одну из точек A , B , C ). Так как «зайцев» три, а «клеток» только две, то найдутся два «зайца», попавшие в одну «клетку»; иначе говоря, найдутся такие две вершины треугольника ABC , которые принадлежат одной полуплоскости.
Пусть, скажем, точки A и B находятся в одной полуплоскости, то есть лежат по одну сторону от прямой l . Тогда отрезок AB не пересекается с l . Итак, в треугольнике ABC нашлась сторона, которая не пересекается с прямой l .

Задача 2. Внутри равностороннего треугольника со стороной 1 расположено 5 точек. Доказать, что расстояние между некоторыми двумя из них меньше 0,5
считать «зайцами».
По принципу Дирихле из пяти точек хотя бы две окажутся
в одном из четырёх треугольничков. Расстояние между этими точками
меньше 0,5, поскольку точки не лежат в вершинах треугольничков.
(Здесь использована известная лемма о том, что длина отрезка, расположенного внутри треугольника, меньше длины его наибольшей стороны.)

Задача №3. («на пары»)
На планете Земля океан занимает больше половины площади поверхности. Докажите, что в мировом океане можно указать две диаметрально противоположные точки.Африка расположена между
37 ° с. ш. и 35 ° ю. ш., между 17 ° з.д., 51 ° з. д.
Континент расположен между примерно
9° з. д. и 169° з. д., 12° ю. ш. 81° с. ш.

- Решение. Будем считать «кроликами» точки океана, а «клетками» — пары диаметрально противоположных точек планеты. Количество «кроликов» в данном случае — это площадь океана, а количество «клеток» — половина площади планеты. Поскольку площадь океана больше половины площади планеты, то «кроликов» больше, чем «клеток». Тогда есть «клетка», в которой сидит не менее двух «кроликов», т.е. пара противоположных точек, обе из которых — океан. У2

Задача №4. В хвойном лесу растут 800000 елей. На каждой ели — не более 500000 иголок. Доказать, что существуют хотя бы две ели с одинаковым числом иголок.

- Решение. Число «клеток» – 500000 (на каждой ели может быть от 1 иголки до 500000 иголок, 800000 ели – число «кроликов», так как, «кроликов» больше чем клеток, значит, есть «клетка», в которой сидит не менее двух «кроликов». Значит, существуют хотя бы две ели с одинаковым числом иголок. (У2)

Решение. По крайней мере, два числа из 11 дают одинаковый
остаток при делении на 10 . Пусть это будут A = 10a + r и B = 10b + r.
Тогда их разность делится на 10: A — B = 10(a — b). (У2)
Задача №5. («на делимость»)
Задача . Дано 11 различных целых чисел. Доказать, что из них можно выбрать два числа, разность которых делится на 10.

Задача №6. («на делимость»)
Доказать, что число N 5 оканчивается на ту же цифру, что число N.
Решение.
Докажем, что N 5 -N кратно 10.
N(N-1 )
кратно 2
кратно 5

Задача №7. («на комбинаторику») В коробке лежат шарики 4-х разных цветов (много белых, много черных, много синих, много красных). Какое наименьшее количество шариков надо наощупь вынуть из мешка, чтобы среди них заведомо оказались два одного цвета?
Решение
Возьмем за «кроликов» шары, а за «клетки» — черный, белый, синий, красный цвета. Клеток 4, поэтому если кроликов, хотя бы 5, то какие-то два попадут в одну клетку (будет 2 одноцветных шарика).

Задача «на комбинаторику»
№ 8. Маленький брат Андрея раскрасил шашки в восемь цветов. Сколькими способами Андрей может поставить на доску 8 разноцветных шашек так, чтобы в каждом столбце и в каждой строке было по одной шашке?
Сколькими способами Андрей может поставить на доску 8 белых шашек так, чтобы в каждом столбце и в каждой строке было по одной шашке?

Решение задачи.
- Рассмотрим сначала случай, когда шашки белые. Будем расставлять шашки. В первом столбце мы можем поставить шашку в любую из 8 клеток. Во втором столбце — в любую из 7 клеток. (Т. к. нельзя ставить в ту же строку, в которой стоит первая шашка.) Аналогично в третьей строке мы можем поставить шашку в любую из 6 клеток, в четвёртой строке — в любую из пяти и т. д. Итого получаем 8 способов.
2) Теперь рассмотрим случай цветных шашек. Возьмём произвольную расстановку белых шашек. Будем раскрашивать эти шашки в 8 цветов, так чтобы любые две из них были покрашены в разные цвета. Первую мы можем покрасить в один из 8 цветов, вторую — в один из 7 оставшихся и.т. д. Т. е. всего 8 способов раскраски. Поскольку способов расстановки тоже 8 , и каждую из этих расстановок мы можем раскрасить 8 способами, то всего способов в этом случае 8·8=8².
Ответ: 8² способов, 8 способов.

Задача (метод от «противного»)
№ 9. В Москве проживает более 10 000 000 людей. На голове у каждого человека не может быть более 300 000 волос. Докажите, что наверняка найдутся 34 москвича с одинаковым числом волос на голове.

Решение
1) На голове может быть 0, 1, …, 300 000 волос — всего 300 001 вариант. Каждого москвича отнесём к одной из 300 001 групп в зависимости от количества волос.
2) Если 34 москвича с одинаковым количеством волос не найдутся, то это значит, что в любую из созданных групп входит не более 33 человек.
3)Тогда всего в Москве живёт не более
33·300 001=9 900 033
4) Значит, такие 34 москвича обязательно найдутся.

Используемые интернет-ресурсы:
- images.yandex.ru (фото Дирихле, картинки о школе)
- http://bars-minsk.narod.ru/teachers/dirichle.html
- http://www.bestreferat.ru/referat-4776.html
План внеаудиторного занятия в 5-6 классах по теме «Принцип Дирихле»
План внеаудиторного занятия
Тема: Принцип Дирихле.
Класс: 5,6
Тип урока: урок внеклассного занятия.
Цель: Сформировать представление о принципе Дирихле.
Задачи: 1. Ознакомить учащихся с методом доказательства «от противного».
2. Развивать умение различать в задаче условие и заключение.
3. Ознакомить обучающихся с задачами, где при расплывчатых формулировках удается получить некоторую достоверную информацию.
4. Воспитывать умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем.
Форма работы: индивидуальная, групповая.
Организация деятельности учащихся:
— работают с рабочим листом
— отвечают на вопросы
— решают самостоятельно задачи
— оценивают себя, друг друга
№
Этап урока
Задачи этапа
Деятельность учителя
Деятельность ученика
Время
(в мин.)
Формируемые УУД
Познаватель-
ные
Регулятивные
Коммуникатив-
ные
Личностные
1
2
3
5
6
7
8
9
10
Этап мотивации
1
Организацион-ный этап
Создать благоприятный психологический настрой на работу
Приветствие учащихся.
Проверка учителем готовности класса к уроку; организация внимания;
Осознанное и произвольное построение речевого высказывания
Прогнозирование своей деятельности
Умение слушать и вступать в диалог
Умение выделять нравственный аспект поведения.
2
Актуализация знаний
Актуализация опорных знаний и способов действий
Вступительное слово учителя.
Решение логических задач.
Решают примеры логических задач.
Участвуют в беседе с учителем, отвечают на поставленные вопросы.
Логический анализ объектов с целью выделения признаков.
Поиск и выделение необходимой информации.
Выделение и осознание того, что уже пройдено.
Постановка учебной задачи на основе известного.
Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог
Самоопределение
Этап целеполагании
3
Постановка целей, задач урока, мотивационная деятельность учащихся
Обеспечение мотивации учения детьми, принятие ими целей урока
Вместе с учениками определяет цель урока.
Определяют цель урока.
Самостоятельное выделение-формулирование познавательной цели.
Целеполагание
Постановка вопросов
Самоопределение
4
Первичное усвоение новых знаний
Обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы: сложение натуральных чисел и его свойства.
Создает ситуацию, входе решения которой учащиеся делают необходимый вывод.
(коробка 3х3, кубики).
Вместе с учителем делают необходимый вывод.
Поиск и выделение необходимой информации. Структурирование знаний. Анализ объектов.
Построение логической цепи рассуждений.
Планирование, прогнозирование
Умение слушать и вступать в диалог
Самоопределение
5
Физкультминутка
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.
Учащиеся сменили вид деятельности (отдохнули) и готовы продолжать работу.
6
Первичная проверка понимания
Установление правильности и осознанности изучения темы. Выявление первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу.
Направляет работу учащихся.
Самостоятельно решают задачи. Отвечают на вопрос.
Выделение и формулирование познавательной цели, рефлексия способов и условий действия.
Анализ объектов и синтез
Планирование своей деятельности для решения поставленной задачи и контроль полученного результата
Умение слушать и вступать в диалог,
Коллективное обсуждение проблем (при необходимости)
Ориента-
ция в межлично-стных отношениях
6
Первичное закрепление
Установление правильности и осознанности изучения темы.
Выступает в роли тьютора для слабых учащихся при выполнении творческого задания.
Историческая справка о Дирихле.
Учащиеся выполняют в группах творческое задание Делают записи в тетрадь. После выполнения задания выполняют взаимную проверку.
Выделение и формулирование познавательной цели, рефлексия способов и условий действия.
Анализ и синтез объектов
Планирование своей деятельности для решения поставленной задачи, контроль полученного результата, коррекция полученного результата, саморегуляция
Умение слушать и вступать в диалог,
Интегрироваться в группу;
Поддержание здорового духа соперничества для поддержания мотивации учебной деятельности; планирование учебного сотрудничества со сверстниками; участие в коллективном обсуждении проблем.
Профессионалное самоопределение,
смыслообразование
7
Подведение итогов урока
Самооценка результатов своей деятельности и всего класса
Учитель предлагает учащимся обобщить приобретенные знания на уроке.
Вступают диалог с учителем Отвечают на поставленные вопросы.
Выделение и формулирование познавательной цели, рефлексия способов и условий действия.
Анализ и синтез объектов
Планирование своей деятельности для решения поставленной задачи, контроль полученного результата, коррекция полученного результата, саморегуляция
Поддержание здорового духа соперничества для поддержания мотивации учебной деятельности; планирование учебного сотрудничества со сверстниками; участие в коллективном обсуждении проблем.
Жизненное самоопределение, ценносто-смысловая ориентация обучающихся
8
Информация о домашнем задании, инструктаж по его выполнению.
Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания.
Задает дозированное домашнее задание
Учащиеся записывают домашнее задание в зависимости от уровня освоения темы урока
2
Оценка промежуточных результатов и саморегуляция для повышения мотивации учебной деятельности
управление поведением партнёра- контроль, коррекция, оценкна
Нравственно -этическая ориентация
9.
Рефлексия.
Инициировать рефлексию детей по поводу психоэмоционального состояния,
мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе.
-Кто работал на уроке лучше всех?
-Кому еще надо стараться?
-С каким настроением вы уйдете с урока?
По листу самоконтроля оценивают свою работу и работу одноклассников.
1-2
Оценка своей деятельности и других людей
Смыслообразование
Деятельность учителя
I. Организационный этап
Учитель приветствует учащихся, проверяет их готовность к уроку; Добрый день, ребята! Улыбнитесь друг другу, пожелайте хорошего настроения! С каким настроением вы пришли на урок математики? Сегодня необычное занятие. У нас сегодня пришли гости, и они будут на вас смотреть как вы работаете на занятии. Поздороваемся с гостями.
И так, начинаем.
Математика, друзья,
Абсолютно всем нужна.
На уроке работай старательно
И успех тебя ждет обязательно!
Деятельность учеников
«Здравствуйте».
— настроение хорошее;
— не очень
«Здравствуйте»
Учащиеся все вместе читают стихотворение.
II . Актуализация знаний.
О чем идет речь в этом стихотворении?
Как вы сказали что на уроках вы должны работать аккуратно, с усердием и еще?
А для того чтобы вы узнать как вы поняли это стихотворение я даю вам задание.
Эти задания вы выполняете на рабочих листах.
Задание №1
Определи закономерность и найди неизвестное число:
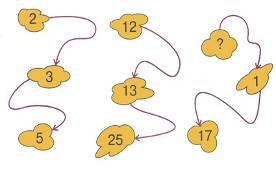
Какая буква должна быть следующей в этой последовательности: О, Д, Т, Ч, П, Ш, С…
Найти сумму последовательных чисел от 1 до 30
Заполните таблицу натуральными числами от 1 до 9
Для чего нужны эти задания?
Ответы учащихся:
— о математике;
— о том, что надо хорошо работать на уроке;
— математика нужна в жизни человека;
— чтобы подсчитать деньги.
Ответы учащихся
Ситуации разрыва:
В классе 15 учеников. Можно ли утверждать что найдутся как минимум 2 ученика, отмечающих дни рождения в один месяц?
III. Постановка целей, задач урока, мотивационная деятельность учащихся.
Как вы думаете чем мы будем заниматься сегодня на уроке?
Какова цель нашего урока?
Цель урока: Научиться решать логические задачи.
IV. Первичное усвоение темы:
В каждой группе учитель дает коробку с кубиками. (по 12 штук):
Взяли рабочий лист и решаем задание №2.
Задание №2
Заполните коробку 3х3 кубиками:
А. 8 кубиками
Б. 10 кубиками
В. 15 кубиками.
Обсуждение.
Работа в группах
V. Физкультминутка
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.
Устали?
После каждой умственной работы на уроке математики что нужно делать? А как можно отдыхать на уроке?
Так давайте делаем физкульминутку. Все встали.
Раз — подняли руки вверх.
Два — их опустили.
И еще раз повторили.
Три – налево наклонились
А затем – направо.
На четыре мы присели,
Встали, поклонились,
На места тихонько сели.
Учащиеся сменили вид деятельности (отдохнули) и готовы продолжать работу.
Да
Нет
Не очень
Отдыхать
Делать зарядку.
VI. Первичная проверка понимания: Самостоятельная работа в группах
Решают самостоятельно задачу в группах, из каждой команды по одному выходят к доске .
VII. Первичное закрепление . Историческая справка
Вывод учащихся: Таким образом, применяя данный метод, надо:
Определить, что удобно в задаче принять за «клетки», а что за «зайцев».
Получить «клетки»; чаще всего «клеток» меньше (больше), чем «зайцев» на одну (или более).
Выбрать для решения требуемую формулировку принципа Дирихле.
Принцип Дирихле важен, интересен, полезен. Его можно применять в повседневной жизни, что развивает логическое мышление.
Многие олимпиадные задачи решаются, используя это специальный метод. Он дает возможность обобщать.
VIII. Подведение итогов урока.
IX. Рефлексия.
Лист самоконтроля.
Оценивают свою работу и и свое настроение в конце урока
IX. Информация о домашнем задании, инструктаж по его выполнению.
Спасибо за работу на уроке!