Числовые и алгебраические выражения (Г. Г. Гаицгори). Видеоурок. Алгебра 7 Класс
Рассмотрим следующие примеры.
Пример 1. Чему равна площадь квадрата со стороной 2? (Рис. 1)
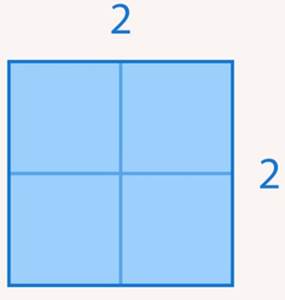
Рис. 1. Иллюстрация к примеру 1
Решение. Очевидно, что площадь квадрата со стороной 2 равна:  .
.
Ответ: 4.
Пример 2. Чему равна площадь квадрата со стороной 3? (Рис. 2)
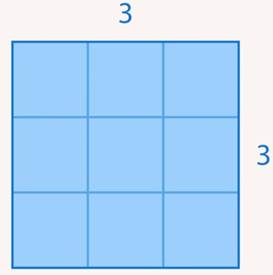
Рис. 2. Иллюстрация к примеру 2
Решение. Очевидно, что площадь квадрата со стороной 3 равна: 
Ответ: 9.
Запишем формулу для вычисления площади квадрата в общем случае при условии, что задана длина стороны квадрата. Для этого необходимо длину стороны умножить на саму себя. Записать это можно так: 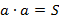 , где
, где 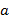 – сторона квадрата.
– сторона квадрата.
Рассмотрим пример, когда нужно посчитать, сколько машин понадобится для перевозки груза, если известно количество мешков, которые нужно перевезти, масса каждого мешка и грузоподъемность одной машины.
Пример 3. Пусть имеется 15 мешков, масса каждого 40 килограммов, а грузоподъемность машины – 200 кг. Сколько машин понадобится для перевозки всех мешков? (Рис. 3)

Рис. 3. Иллюстрация к примеру 3
Решение: Для нахождения количества машин, необходимых для перевозки всех мешков, умножим количество мешков на массу одного мешка и разделим на грузоподъемность одной машины: 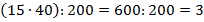 .
.
Ответ: 3 машины.
В условии задачи количество мешков может быть другим, например: 20, 57, 100. Тогда каждый раз нужно будет заново решать задачу и выполнять одни и те же действия. Чтобы этого избежать, можно один раз составить формулу, по которой всегда можно будет производить вычисления.
Количество машин должно быть не меньше, чем 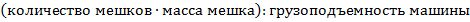

Рис. 4. Иллюстрация выведения формулы для многократного вычисления
Теперь по этой формуле любой сможет произвести расчеты, не задумываясь, как она была получена, а просто подставляя значения. Кроме того, можно запрограммировать компьютер, тогда можно подставлять конкретные данные, а вычисления будет производить он.
Составленное выше выражение можно записать короче, например, так: 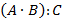 , где
, где 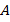 – количество мешков,
– количество мешков, 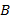
 – грузоподъемность одной машины.
– грузоподъемность одной машины.Переместительный закон сложения звучит так: от перемены мест слагаемых сумма не меняется. Например,  или
или  .
.
Слагаемые могут быть любыми числами. Т.е. формулировку закона можно переписать так:  , где
, где 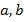
Как видно, в некоторых случаях удобнее заменять числа буквами, которые ещё называют переменными (их значения можно «переменять»).
Пример 4. Необходимо посчитать количество цветов в двух комнатах. В одной комнате их 5, а во второй – 3 (Рис. 5).

Рис. 5. Иллюстрация к примеру 4
Решение. Очевидно, для нахождения общего количества цветов достаточно сложить следующие числа:  .
.
Ответ: 8.
В примере 4 запись 
Определение: числовое выражение – это запись, составленная только с помощью чисел, знаков действий и скобок, при этом запись должна быть составлена со смыслом.
Что значит «составлена со смыслом»? В языке есть фразы, которые понятны другим людям (предложения). Так и в математике: если понятно, что делать c выражением, как вычислить его значение, то запись составлена со смыслом.
Например, запись  состоит из чисел, знаков действий и скобок, однако его значение нельзя вычислить (как числовое выражение оно не имеет смысла), поэтому оно не является числовым выражением.
состоит из чисел, знаков действий и скобок, однако его значение нельзя вычислить (как числовое выражение оно не имеет смысла), поэтому оно не является числовым выражением.
Запись 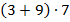
В условии задачи могут быть не цветы, а 5 машин и 3 машины  , пять восьмых
, пять восьмых  и три восьмых
и три восьмых 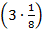
 . И это не повлияет на результат.
. И это не повлияет на результат.
Можно записать так: 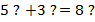 (5 чего-то и 3 чего-то равно 8 чего-то), где вместо
(5 чего-то и 3 чего-то равно 8 чего-то), где вместо 
В математике обычно в таких случаях используют буквы  , например,
, например, 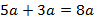 . Заменяя объекты буквами, можно работать не с самими объектами, а с математическими выражениями. Т.е. после выполнения действий с некоторой абстрактной переменной
. Заменяя объекты буквами, можно работать не с самими объектами, а с математическими выражениями. Т.е. после выполнения действий с некоторой абстрактной переменной 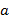 полученный результат будет верен для любых объектов (цветов, машин, деталей и т.д.). Тогда выражение
полученный результат будет верен для любых объектов (цветов, машин, деталей и т.д.). Тогда выражение 
Определение: алгебраическое выражение – это всякая составленная со смыслом запись, которая может содержать только числа, буквы, знаки действия и скобки. Из определения следует, что любое числовое выражение одновременно является и алгебраическим.
Примеры алгебраических выражений:  .
.
Задание 1 (алгебраические выражения)
Выберите алгебраические выражения:

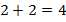
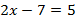



Решение.
 является алгебраическим выражением (вместо
является алгебраическим выражением (вместо 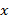 можно подставить какое-нибудь число и вычислить значение выражения).
можно подставить какое-нибудь число и вычислить значение выражения).
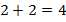
 .
.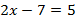 не является алгебраическим выражением, т.к. содержит знак равно
не является алгебраическим выражением, т.к. содержит знак равно  .
.
 не является алгебраическим выражением, т.к. нельзя вычислить его значение (не имеет смысла).
не является алгебраическим выражением, т.к. нельзя вычислить его значение (не имеет смысла).
 является алгебраическим выражением (вместо
является алгебраическим выражением (вместо  можно подставить какие-нибудь числа и вычислить значение выражения).
можно подставить какие-нибудь числа и вычислить значение выражения).
 является и алгебраическим выражением, и числовым (его значение можно вычислить
является и алгебраическим выражением, и числовым (его значение можно вычислить  ).
).
Ответ:  .
.
Чему равно значение выражения 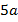 , если
, если  ? Подставим вместо
? Подставим вместо 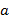 число 3 и посчитаем:
число 3 и посчитаем:  .
.
Так можно поступить с любым алгебраическим выражением – найти его значение при заданных значениях переменных.
Пример 5. Найти значение выражения 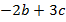 , если
, если 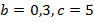 .
.
Решение. Подставим значения переменных  в выражение:
в выражение:  .
.
Ответ:  .
.
Пример 6. Найти значение выражения  , если
, если  .
.
Решение. Подставим значения переменных  в выражение:
в выражение:  .
.
Ответ:  .
.
Задание 2. Запишите формулу целых чисел, которые при делении на 9 дают остаток 2. Найдите количество таких чисел в пределах от 100 до 300.
Решение.
Пусть  – некоторое число. Если
– некоторое число. Если  делится на 9, то в его разложении на множители 9 было бы одним из них, т.е.
делится на 9, то в его разложении на множители 9 было бы одним из них, т.е.  . Т.к. число должно иметь остаток 2 при делении на 9, то тогда его можно записать так:
. Т.к. число должно иметь остаток 2 при делении на 9, то тогда его можно записать так:  .
.
Первое такое число, большее 100, – это 101 (при 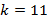 ), а последнее число – это 299 (при
), а последнее число – это 299 (при  ). Значит, всего таких чисел:
). Значит, всего таких чисел:  .
.
Ответ:  .
.
Заключение
На этом уроке мы познакомились с алгебраическими и числовыми выражениями, научились вычислять значение алгебраических выражений. На следующем уроке мы узнаем, как работать с алгебраическими выражениями.
Список рекомендованной литературы
- Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 7 класс. Учебник. ФГОС, «Просвещение», 2017.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра. 7 класс. Учебник. «Просвещение», 2014.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 7 класс. Учебник. «Просвещение», 2013.
Рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «yaklass.ru» (Источник)
- Интернет-портал «school-assistant.ru» (Источник)
- Интернет-портал «scienceland.info» (Источник)
Домашнее задание
- Найдите значения следующих числовых выражений:
 ;
; 
- Найдите значение алгебраического выражения
 , если
, если  .
. - Найдите
 от числа
от числа  .
.
Числовые и алгебраические выражения. Часть 1. Числовые и алгебраические выражения
Мы начинаем изучение алгебры. Если раньше мы работали преимущественно с числами (выполняли различные арифметические операции с ними, решали различные задачи), то теперь мы будем учиться работать с более абстрактными объектами – переменными. Преимущество этих объектов в том, что, решив в общем виде задачу один раз, можно находить ответ для всех задач такого типа, подставляя вместо переменных конкретные числовые значения.
На этом уроке мы вспомним, что такое числовое выражение, а также дадим определение алгебраическому выражению. Кроме того, научимся находить значение алгебраического выражения для данных числовых значений переменных.
Рассмотрим следующие примеры.
Пример 1. Чему равна площадь квадрата со стороной 2? (Рис. 1)

Рис. 1. Иллюстрация к примеру 1
Решение: Очевидно, что площадь квадрата со стороной 2 равна:  .
.
Ответ: 4.
Пример 2. Чему равна площадь квадрата со стороной 3? (Рис. 2)

Рис. 2. Иллюстрация к примеру 2
Решение: Очевидно, что площадь квадрата со стороной 3 равна:  .
.
Ответ: 9.
Запишем формулу для вычисления площади квадрата в общем случае при условии, что задана длина стороны квадрата. Для этого необходимо длину стороны умножить на саму себя. Записать это можно так: 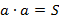 , где
, где 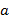 – сторона квадрата.
– сторона квадрата.
Рассмотрим пример, когда нужно посчитать, сколько машин понадобится для перевозки груза, если известно количество мешков, которые нужно перевезти, масса каждого мешка и грузоподъемность одной машины.
Пример 3. Пусть имеется 15 мешков, масса каждого 40 килограммов, а грузоподъемность машины – 200 кг. Сколько машин понадобится для перевозки всех мешков? (Рис. 3)

Рис. 3. Иллюстрация к примеру 3
Решение: Для нахождения количества машин, необходимых для перевозки всех мешков, умножим количество мешков на массу одного мешка и разделим на грузоподъемность одной машины: 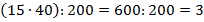 .
.
Ответ: 3 машины.
В условии задачи количество мешков может быть другим, например: 20, 57, 100. Тогда каждый раз нужно будет заново решать задачу и выполнять одни и те же действия. Чтобы этого избежать, можно один раз составить формулу, по которой всегда можно будет производить вычисления.
Количество машин должно быть не меньше, чем 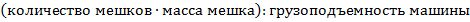 (Рис. 4).
(Рис. 4).

Рис. 4. Иллюстрация выведения формулы для многократного вычисления
Теперь по этой формуле любой сможет произвести расчеты, не задумываясь, как она была получена, а просто подставляя значения. Кроме того, можно запрограммировать компьютер, тогда можно подставлять конкретные данные, а вычисления будет производить он.
Составленное выше выражение можно записать короче, например, так: 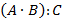 , где
, где 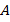 – количество мешков,
– количество мешков, 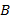 – масса каждого мешка,
– масса каждого мешка,  – грузоподъемность одной машины.
– грузоподъемность одной машины.
Переместительный закон сложения звучит так: от перемены мест слагаемых сумма не меняется. Например,  или
или  .
.
Слагаемые могут быть любыми числами. Т.е. формулировку закона можно переписать так:  , где
, где 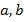 – любые числа. Эта запись несет ту же информацию, только в более компактной форме.
– любые числа. Эта запись несет ту же информацию, только в более компактной форме.
Как видно, в некоторых случаях удобнее заменять числа буквами, которые ещё называют переменными (их значения можно «переменять»).
Пример 4. Необходимо посчитать количество цветов в двух комнатах. В одной комнате их 5, а во второй – 3 (Рис. 5).

Рис. 5. Иллюстрация к примеру 4
Решение. Очевидно, для нахождения общего количества цветов достаточно сложить следующие числа:  .
.
Ответ: 8.
В примере 4 запись  является числовым выражением.
является числовым выражением.
Определение: числовое выражение – это запись, составленная только с помощью чисел, знаков действий и скобок, при этом запись должна быть составлена со смыслом.
Что значит «составлена со смыслом»? В языке есть фразы, которые понятны другим людям (предложения). Так и в математике: если понятно, что делать c выражением, как вычислить его значение, то запись составлена со смыслом.
Например, запись  состоит из чисел, знаков действий и скобок, однако его значение нельзя вычислить (как числовое выражение оно не имеет смысла), поэтому оно не является числовым выражением.
состоит из чисел, знаков действий и скобок, однако его значение нельзя вычислить (как числовое выражение оно не имеет смысла), поэтому оно не является числовым выражением.
Запись 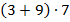 является числовым выражением, т.к. его значение можно вычислить.
является числовым выражением, т.к. его значение можно вычислить.
В условии задачи могут быть не цветы, а 5 машин и 3 машины  , пять восьмых
, пять восьмых  и три восьмых
и три восьмых 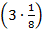
 . И это не повлияет на результат.
. И это не повлияет на результат.
Можно записать так: 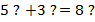 (5 чего-то и 3 чего-то равно 8 чего-то), где вместо
(5 чего-то и 3 чего-то равно 8 чего-то), где вместо  может быть любой предмет (цветы, машины, книги, ящики и т.д.).
может быть любой предмет (цветы, машины, книги, ящики и т.д.).
В математике обычно в таких случаях используют буквы  , например,
, например, 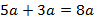 . Заменяя объекты буквами, можно работать не с самими объектами, а с математическими выражениями. Т.е. после выполнения действий с некоторой абстрактной переменной
. Заменяя объекты буквами, можно работать не с самими объектами, а с математическими выражениями. Т.е. после выполнения действий с некоторой абстрактной переменной 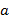 полученный результат будет верен для любых объектов (цветов, машин, деталей и т.д.). Тогда выражение
полученный результат будет верен для любых объектов (цветов, машин, деталей и т.д.). Тогда выражение  называется алгебраическим выражением.
называется алгебраическим выражением.
Определение: алгебраическое выражение – это всякая составленная со смыслом запись, которая может содержать только числа, буквы, знаки действия и скобки. Из определения следует, что любое числовое выражение одновременно является и алгебраическим.
Примеры алгебраических выражений:  .
.
М-1. Числовые и алгебраические выражения (теория)
Числовые выражения. В младших классах вы учились оперировать с целыми и дробными числами, решали уравнения, знакомились с геометрическими фигурами, с координатной прямой и координатной плоскостью. Всё это составляло содержание одного школьного предмета «Математика». В действительности такая важная область науки как математика подразделяется на огромное число самостоятельных дисциплин: алгебру, геометрию, теорию вероятностей, математический анализ, математическую логику, математическую статистику, теорию игр и т.д. У каждой дисциплины — свои объекты изучения, свои методы познания реальной действительности. Алгебра, к изучению которой мы приступаем, даёт человеку возможность не только выполнять различные вычисления, по и учит его делать это как можно быстрее, рациональнее. Человек, владеющий алгебраическими методами, имеет преимущество перед теми, кто не владеет этими методами: он быстрее считает, успешнее ориентируется в жизненных ситуациях, чётче принимает решения, лучше мыслит. Наша задача — помочь вам овладеть алгебраическими методами, ваша задача — не противиться обучению, с готовностью следовать за нами, преодолевая возникающие трудности. На самом деле в младших классах вам уже приоткрыли окно в волшебный мир алгебры, ведь алгебра в первую очередь изучает числовые и алгебраические выражения. Напомним, что числовым выражением называют всякую запись, составленную из чисел и знаков арифметических действий (составленную, разумеется, со смыслом: например, 3 + 5-7 — числовое выражение, тогда как 3 + : — не числовое выражение, а бессмысленный набор символов). По некоторым причинам (о них мы будем говорить в дальнейшем) часто вместо конкретных чисел употребляются буквы (преимущественно из латинского алфавита), тогда получается алгебраическое выражение. Эти выражения могут быть очень громоздкими. Алгебра учит упрощать их, используя разные правила, законы, свойства, формулы. Найти значение числового выражения (2,73 +4,81 + 3,27 — 2,81) 25-37-0,4 Сейчас мы вместе с вами кое-что вспомним, и вы увидите, как много алгебраических фактов вы уже знаете. Прежде всего нужно выработать план осуществления вычислений. Для удобства введём следующие обозначения. Числитель данного дробного выражения обозначим буквой А, а знаменатель — буквой В: А = (2,73 + 4,81 + 3,27 — 2,81) : В = 25 • 37 • 0,4. В выражении А обозначим делимое буквой С, а делитель — буквой D. Тогда план наших действий будет выглядеть так: 1) найдём значение с выражения С; 2) найдём значение d выражения D; 3) разделив с на d, найдём значение а выражения А; 4) найдём значение b выражения В; 5) разделив а на В, найдём значение заданного числового выражения. Итак, план вычислений есть (а наличие плана — половина успеха!), приступим к его реализации. 1) С = 2,73 + 4,81 + 3,27 — 2,81. Конечно, можно считать подряд или, как иногда говорят, «в лоб»: 2,73 + 4,81, затем к этому числу прибавить 3,27, затем вычесть 2,81. Но культурный человек так вычислять не будет. Он вспомнит переместительный и сочетательный законы сложения (впрочем, ему их и не надо вспоминать, они у него всегда в голове) и будет вычислять так: Здесь нам придётся вспомнить, как действовать с обыкновенными дробями. Сначала надо привести дроби к общему знаменателю. Наименьшим общим кратным 5 и 15 является число 15, оно и будет общим знаменателем. Для дроби получаем. Далее находим 3) Разделим с на d: 4) В = 25-37 ■ 0,4. Опять-таки можно проводить вычисления «и лоб», т. е. вычислить 25 • 37, затем то, что получится,, ум по жить на 0,4. Но думающий человек (а таким всегда является культурный человек) воспользуется переместительным и сочетательным законами умножения и будет вычислять так: 25 • 37 • 0,4 = (25 • 0,4) • 37 = 10 • 37 = 370. Итак, b = 370. 5) Осталось разделить числитель а на знаменатель Ь. ПолучимА теперь вместе проанализируем, какие сведения из математики нам пришлось вспомнить в процессе решения примера (причём не просто вспомнить, но и использовать). 1. Порядок арифметических действий. 2. Переместительный закон сложения: а + b = b + а. 3. Переместительный закон умножения: ab = bа. 4. Сочетательный закон сложения: а + b + с = (а + b) + с = а + (Ь + с). 5. Сочетательный закон умножения: abc = (ab)c = а(bс). 6. Понятия обыкновенной дроби, десятичной дроби, отрицательного числа. 7. Арифметические операции с десятичными дробями. 8. Арифметические операции с обыкновенными дробями. 9. Основное свойство обыкновенной дроби: (значение дроби не изменится, если её числитель и знаменатель одновременно умножить на одно и то же число или разделить на одно и то же число, отличное от нуля). Это свойство позволило нам преобразовать дробь — к виду — (числитель и знаменатель дроби — одновременно умножили на одно и то же число 3). Оно же позволило нам сократить дробь (числитель и знаменатель дроби одновременно разделили на одно и то же число 5). 10. Правила действий с положительными и отрицательными числами. Всё это вы знаете, но ведь всё это — алгебраические факты. Таким образом, некоторое знакомство с алгеброй у вас уже состоялось в младших классах. Основная трудность, как видно уже из примера 1, заключается в том, что таких фактов довольно много, причём их надо не только знать, но и уметь использовать, как говорят, «в нужное время и в нужном месте». Вот этому и будем учиться. И последнее, чтобы закончить обсуждение примера 1. То число, которое получается в результате упрощений числового выражения (в данном примере это было число ), называют значением числового выражения. И Алгебраические выражения Если дано алгебраическое выражение, то можно говорить о значении алгебраического выражения, но только при конкретных значениях входящих в него букв. Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т.е. можно менять значения букв), эти буквы называют переменными. Найти значение алгебраического выражения Решение а) Соблюдая порядок действий, последовательно находим: 1) а2 + 2аЬ + b2 = I2 + 2 • 1 • 2 + 22 = 1 + 4 + 4 = 9; 2) а + Ь=1 + 2 = 3; 3) а — b = 1 — 2 = -1; 4) (а + b)(а — Ь) = 3 • (-1) = -3; е-ч а2 + 2аЬ + й2 _ 9 _ о ’ (а + &)(а — Ь) -3 б) Аналогично, соблюдая порядок действий, последовательно находим: в) Снова, соблюдая порядок действий, последовательно находим: Смотрите, знаменатель равен нулю, а на нуль делить нельзя! Что это значит в данном случае (и в других аналогичных случаях)? Это значит, что при а — b = — заданное алгебраическое выражение не имеет смысла. Используется такая терминология: если при конкретных значениях букв (переменных) алгебраическое выражение имеет числовое значение, то указанные значения переменных называют допустимыми; если же при конкретных значениях букв (переменных) алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми. Так, в примере 2 значения а = 1 и 6 = 2, а — 3,7 и b = -1,7 — допустимые, тогда как значения а и b — недопустимые (более точно: первые две пары значений — допустимые, а третья пара значений — недопустимая). Вообще в примере 2 недопустимыми будут такие значения переменных а, Ь, при которых либо а + b = 0, либо а — b = 0. Например, а = 7, b = -7 или а = 28,3, b = 28,3 — недопустимые пары значений; в первом случае а + Ь = 0, а во втором случае а — b = 0. В обоих случаях знаменатель заданного в этом примере выражения обращается в нуль, а на нуль, повторим ещё раз, делить нельзя. Теперь, наверное, вы и сами сможете придумать как допустимые пары значений для переменных а, Ь, так и недопустимые пары значений этих переменных в примере 2. Попробуйте! Пример 2в) на самом деле мы решали плохо (некультурно), поскольку сделали ряд лишних, ненужных вычислений. Надо было сразу заметить, что при а — и b — — знаменатель обращается в нуль, и объявить: выражение не имеет смысла! Но, как говорится, сразу замечает тот, кто знает, что надо замечать. Этому и учит алгебра. Если бы мы с вами решали пример 2 позднее, то сделали бы это лучше. Мы бы смогли преобразовать выражение к более простому виду , а тогда, согласитесь, гораздо проще было бы и вычислять. А вот почему верно равенство пока мы сказать не можем. На этот вопрос ответим позднее (см. § 41).
Вопросы для самопроверки 1. Сформулируйте определение числового выражения. 2. Приведите три примера числового выражения. 3. Что называют алгебраическим выражением? 4. Используя переменные тип, составьте два алгебраических выражения. 5. Что такое значение числового выражения? 6. Что такое значение алгебраического выражения? 7. Найдите значение выражения — — при х = 1, х = 2,5. 8. Сформулируйте переместительный закон сложения. 9. Сформулируйте переместительный закон умножения. 10. Сформулируйте сочетательный закон сложения. 11. Сформулируйте сочетательный закон умножения. 12. Сформулируйте основное свойство дроби. 13. В чём состоит правило сложения отрицательных чисел? 14. В чём состоит правило сложения чисел с разными знаками? 15. Как вы понимаете фразу: «Заданное алгебраическое выражение не имеет смысла»? Приведите пример такого выражения. 16. Какие значения переменных называют допустимыми? 17. Какие значения переменных называют недопустимыми?
Числовые и алгебраические выражения, математические модели
Напомним, что числовым выражением называют всякую запись, составленную из чисел и знаков арифметических действий. Если же вместо чисел употребляют буквы, то получают алгебраическое выражение. Важнейшая типовая задача и для числовых, и для алгебраических выражений – это упрощение. Рассмотрим пример:
Пример 1:
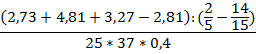
Первым действием является сложение в скобках. Но выполнять сложение сразу не очень удобно, так как в первой скобке стоят не самые простые десятичные дроби, поэтому нужно подумать, как удобнее выполнить данное действие. Несложно заметить, что при сложении первого числа с третьим получится круглое число, как и при вычитании из второго числа четвертого. Выполним действие:
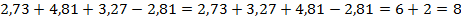
Таким образом, наше выражение теперь выглядит так:

Теперь выполним вычитание дробей во второй скобке, напомним, что для этого дроби нужно привести к общему знаменателю. Пользуясь основным свойством дроби, умножим числитель и знаменатель первой дроби на три:
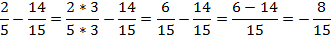
Перепишем исходное выражение:
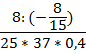
Далее упростим числитель, в котором теперь число умножается на дробь, напомним, что при этом число умножают на перевернутую дробь, и, если есть возможность, выполняется сокращение дроби:
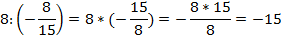
Исходное выражение приобретает вид:

Последнее действие – сократить полученную дробь, для этого выполним некоторые преобразования:
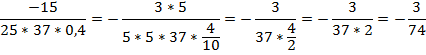
Но не всегда нам задано алгебраическое выражение, часто бывает нужно текстовую задачу перевести на математический язык и в результате получить необходимое выражение.
Пример 2: при каком значении k выражение  в два раза меньше, чем
в два раза меньше, чем 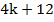
Итак, у нас есть два выражения и соотношение между ними. Составим уравнение:
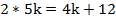
По существу, мы получили математическую модель – линейное уравнение с одной неизвестной. Решим его:
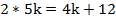
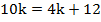



Ответ: при  выражение
выражение  в два раза меньше, чем
в два раза меньше, чем 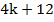 .
.
Пример 3: на вопрос о том, сколько у него учеников, древнегреческий математик Пифагор ответил так: «Половина моих учеников изучает математику, четверть изучает природу, седьмая часть проводит время в молчаливом размышлении. Остальную часть составляют три девы». Сколько учеников было у Пифагора?
Примем количество учеников за n, при чем  , то есть является натуральным числом. Запишем количество учеников Пифагора:
, то есть является натуральным числом. Запишем количество учеников Пифагора:  – те, которые изучают математику
– те, которые изучают математику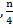 – те, кто изучают природу
– те, кто изучают природу — те, кто проводят время в размышлении и
— те, кто проводят время в размышлении и 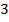 девы.
девы.
Найдем суммарное количество учеников Пифагора:

Таким образом, мы получили математическую модель – линейное уравнение с одной неизвестной. Найдем его корень:

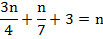
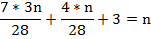







Ответ: у Пифагора было 28 учеников.
Напомним, что математическое моделирование включает три этапа – составление математической модели, работа с математической моделью, ответ на вопрос, поставленный в задаче.
Пример 4: спросил некто у учителя: «Скажи, сколько у тебя учеников, так как я хочу отдать тебе в ученье сына». Учитель ответил: «Если придут еще столько же, сколько имею, и полстолько, и четвертая часть и твой сын, то будет у меня сто учеников». Сколько было у учителя учеников?
Этап 1: пусть у учителя было х учеников, причем х – число натуральное; опишем количество учеников выражением:
Было  учеников, придет еще столько – то есть
учеников, придет еще столько – то есть  , еще полстолько –
, еще полстолько – 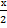 , и четвертая часть –
, и четвертая часть –  и еще
и еще  , то будет
, то будет  . Запишем уравнение:
. Запишем уравнение:

Математическая модель составлена.
Этап 2: приведем в левой части уравнения подобные члены, все свободные члены перенесем вправо и приведем подобные там, из элементарного уравнения найдем х:


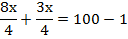
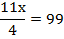
Разделим обе часть уравнения на 11:
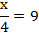
Умножим обе части на 4:

Этап 3: в задаче спрашивалось, сколько учеников было у учителя, мы получили  , за х было принято количество учеников, таким образом, у учителя было 36 учеников.
, за х было принято количество учеников, таким образом, у учителя было 36 учеников.
Вывод: на данном уроке мы вспомнили понятие числового и алгебраического выражения, выполнили пример на упрощение выражения, решили несколько текстовых задач методом математического моделирования.
Список литературы
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. – 6 изд. – М.: Просвещение, 2010.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. – М.: ВЕНТАНА-ГРАФ.
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Школьный помощник (Источник).
- Математическое моделирование (Источник).
Домашнее задание
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, №7, ст. 11;
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, №16, ст. 16;
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, №41, ст. 28.
Алгебраические выражения
Алгебраические выражения составляются из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень и извлечения корня и с помощью скобок.
 Рассмотрим некоторые примеры алгебраических выражений:
Рассмотрим некоторые примеры алгебраических выражений:
2a2b – 3ab2(a + b)
a + b + c/5
(1/a + 1/b – c/3)3.
Существует несколько видов алгебраических выражений.
Целым называется такое алгебраическое выражение, которое не содержит деления на переменные и извлечения корня из переменных (в том числе, возведения в степень с дробным показателем).
2a2b – 3ab2(a + b) является целым алгебраическим выражением.
(1/a + 1/b – c/3)3 не является целым алгебраическим выражением, т.к. содержит деление на переменную.
Дробным называется такое алгебраическое выражение, которое составлено из чисел и переменных с помощью действий сложения, вычитания, умножения, возведения в степень с натуральным показателем и деления.
(1/a + 1/b – c/3)3 является дробным алгебраическим выражением.
Рациональными алгебраическими выражениями называются целые и дробные выражения.
Значит, и 2a2b – 3ab2(a + b), и (1/a + 1/b – c/3)3 – это рациональные алгебраические выражения.
Иррациональное алгебраическое выражение – это такое алгебраическое выражение, в котором используются извлечение корня из переменных (или возведение переменных в дробную степень).
a 2/3 – b 2/3 – иррациональное алгебраическое выражение.
Иными словами, все алгебраические выражения делятся на две большие группы: рациональные и иррациональные алгебраические выражения. Рациональные выражения, в свою очередь, делятся на целые и дробные.
Допустимым значением переменных называется такое значение переменных, при котором алгебраическое выражение имеет смысл. Множество всех допустимых значений переменной – это область определения алгебраического выражения.
Целые выражения имеют смысл при любых значениях его переменных. Например, 2a2b – 3ab2(a + b) имеет смысл и при a = 0, b = 1, и при a = 3, b = 6 и др.
Предположим, что a = 0, b = 1, и попробуем найти решение выражения
2a2b – 3ab2(a + b).
Если a = 0, b = 1, то 2 ∙ 02 ∙ 1 – 3 ∙ 0 ∙ 12 ∙ (0 + 1) = 0 ∙ 0 = 0.
Значит, при a = 0, b = 1 выражение равно 0.
Дробные выражения имеют смысл только в том случае, если значения не обращают переменные в нуль: вспомним наше «золотое правило» – на нуль делить нельзя.
Выражение (1/a + 1/b – c/3)3 имеет смысл при a и b не равных нулю (а ≠ 0, b ≠ 0). В противном случае мы получим деление на нуль.
Иррациональное выражение не будет иметь смысл при значениях переменных, которые обращают в отрицательное число выражение, содержащееся под знаком корня четной степени или под знаком возведения в дробную степень.
Выражение a 2/3 – b 2/3 имеет смысл при a ≥ 0 и b ≥ 0. В противном случае мы столкнемся с возведением в дробную степень отрицательного числа.
Значением алгебраического выражения называется числовое выражение, получившееся в результате того, что переменным придали допустимые значения.
Найдем значение алгебраического выражения
a + b + c/5 при a = 6, b = 3, c = 5.
1. Выражение a + b + c/5 является целым алгебраическим выражением → все значения являются допустимыми.
2. Подставим числовые значения переменных и получим:
6 + 3 + 5/5 = 9 + 1 = 10.
Итак, ответ: 10.
Тождеством называют равенство, которое верно при всех допустимых значениях входящих в него переменных.
Тождественно равными называются выражения, соответственные значения которых совпадают при всех допустимых значениях переменных. Так, выражения x5 и x2 ∙ x3, a + b + c и b + c + a являются тождественно равными между собой.
Понятие тождественно равных выражений приводит нас к еще одному важному понятию – тождественное преобразование выражений.
Тождественным преобразованием выражения называется замена одного выражения другим, тождественно равным ему.
Это значит, выражение x5 можно тождественно преобразовать в выражение x2 ∙ x3.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Алгебраические выражения, коэффициент, виды выражений
Алгебраическое выражение
Алгебраическое выражение — это запись, составленная со смыслом, в которой числа могут быть обозначены и буквами, и цифрами. Также она может содержать знаки арифметических действий и скобки.
Любую букву, обозначающую число, и любое число, изображённое с помощью цифр, принято считать в алгебре также алгебраическим выражением.
Алгебраические выражения, входящие в состав формул, могут применяться к решению частных арифметических задач, если в них заменить буквы данными числами и произвести указанные действия. Число, которое получится, если взять вместо букв какие-либо числа и произвести над ними указанные действия, называется численной величиной алгебраического выражения. Из этого легко сделать вывод, что одно и то же алгебраическое выражение при различных значениях входящих в него букв может иметь различные числовые величины. Так, например, выражение
am+bn
при a=2, m=5, b=1, n=4 вычисляется: 2 · 5 + 1 · 4 = 14, а при a=3, m=4, b=5, n=1 вычисляется: 3 · 4 + 5 · 1 = 17 и т.д.; выражение
abс
при a=1, b=2, c=3, равно 6, а a=2, b=3, c=4, равно 24, и т.д.
Коэффициент
Произведение нескольких сомножителей a, b, c, d, пишется abcd. Если, кроме буквенных множителей, есть и численный (всё равно, целый или дробный), то он обычно ставится впереди и называется коэффициентом. Таким образом,
произведение величин a, b, c, d, 4 пишут так: 4abcd
произведение величин m, n,  , p пишут так:
, p пишут так:  .
.
Числа 4 и  — это коэффициенты. Очевидно, что 4abcd = abcd + abcd + abcd + abcd и точно также
— это коэффициенты. Очевидно, что 4abcd = abcd + abcd + abcd + abcd и точно также  . Итак, коэффициент показывает, сколько раз целое алгебраическое выражение или известная его часть берется слагаемым.
. Итак, коэффициент показывает, сколько раз целое алгебраическое выражение или известная его часть берется слагаемым.
Если при алгебраическом выражении нет коэффициента, то подразумевается, что он равен единице, так как a = 1 · a; bc = 1 · bc и так далее.
Виды выражений
Алгебраическое выражение, в которое не входят буквенные делители, называется целым, в противном случае дробным или алгебраической дробью.
Например, 7a2b,  — целые выражения;
— целые выражения;  ,
,  — дробные выражения.
— дробные выражения.
Выражения, не содержащие корней, называются рациональными, а содержащие корни — иррациональными или радикальными. Например, все выражения, приведённые выше, являющиеся целыми или дробными, так же можно назвать и рациональными.
 ,
,  — иррациональные или радикальные выражения.
— иррациональные или радикальные выражения.
Люди!!!Помогите привести пример числового выражения!?Заранеи спс.
Числовые выражения содержат только числа и математические знаки действий — это обычные примеры. Сам пример — числовое выражение, а его ответ называют значением числового выражения. Например: (25 — 15) : 4 = 2,5 Выражения с переменными содержат числа, буквы (переменные) и математические знаки действий. Например, буквенное выражение: 2х +7, или 5 / х, или 4 — у / 5…. У таких выражений нельзя найти один ответ как у числовых (у примеров) . Если будет дано значение переменой (буквы) , тогда можно найти значение выражения с переменной. Например: Если х = 10, то 2х+7 = 2*10 + 7 = 27
да любое 2+ 3 или (17*5 -8) :7
Числовые выражения содержат только числа и математические знаки действий — это обычные примеры. Сам пример — числовое выражение, а его ответ называют значением числового выражения. Например: (25 — 15) : 4 = 2,5 Выражения с переменными содержат числа, буквы (переменные) и математические знаки действий. Например, буквенное выражение: 2х +7, или 5 / х, или 4 — у / 5…. У таких выражений нельзя найти один ответ как у числовых (у примеров) . Если будет дано значение переменой (буквы) , тогда можно найти значение выражения с переменной. Например: Если х = 10, то 2х+7 = 2*10 + 7 = 27
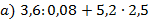 ;
; 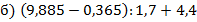
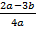 , если
, если  .
. от числа
от числа  .
.