Признаки однородности: Тема: Однородные члены предложения

Posted on by alexxlab

Содержание

Однородные члены предложения — примеры, определения, правила

Теперь покажем в виде схем, как однородное подлежащее, однородное сказуемое, однородное обстоятельство, однородное дополнение, однородное определение взаимосвязаны с другими членами предложения.

Отработать новый материал на практике помогут онлайн-курсы по русскому языку в школе Skysmart.

В таблице есть примеры использования разных членов предложения в качестве однородных.

Член предложения На какой вопрос отвечают Примеры
Подлежащее Кто? Что? Вика, Таня и Леша качались на качеле. На моей даче живут черепаха и кошка.
Сказуемое Что делать? Что сделать? Вчера в школе мы рисовали, пели и играли. Аня хорошо читает, пишет и говорит по-английски.
Определение Какой? Который? Я отдал кислую и горькую конфету. У стены стояла не большая, а маленькая тумбочка.
Дополнение Кого? Чего? Кому? Чему? Кого? Что? Кем? Чем? О ком? О чём? (вопросы косвенных падежей) Дедушка починил лук и стрелы. На холсте художник отразил небо и океан.
Обстоятельство Как? Где? Куда? Откуда? Когда? Зачем? Почему? Зимой и осенью нужно надевать более теплые вещи. Дорога идет то направо, то налево.

Теперь мы знаем на какие вопросы отвечают однородные члены предложения.

Способы определения однородных членов предложения

Давайте разберемся, как найти однородные члены предложения.

Алгоритм определения однородных членов предложения:

  1. Определить главные и второстепенные члены предложения. Отметить подлежащее и сказуемое;

  2. Установить, есть ли в предложении члены, которые отвечают на один и тот же вопрос и относятся к одному и тому же слову;

  3. Определить, какой связью они связаны:

    • сочинительной, которая выражена союзами,

    • бессоюзной, которая выражена с помощью перечислительной интонации.

Примеры:

  • Я выбрала букет из белых, розовых и зеленых хризантем.

    Хризантем (каких?) белых, розовых и зеленых — однородные определения, так как они отвечают на один вопрос, относятся к одному слову (хризантем) и связаны сочинительной связью (сочинительный союз и).

В предложении может быть несколько однородных членов:

  • Артем и Маша много смеялись, пели и танцевали.

    Артем и Маша — однородные подлежащие; смеялись, пели и танцевали — однородные сказуемые.

Теперь мы знаем, как определить однородные члены предложения.

А сейчас расскажем, какие члены предложения не являются однородными.

Если члены предложения относятся к одному и тому же слову, но отвечают на разные вопросы — их нельзя назвать однородными:

  • Я приду в гости завтра.

    Я приду (куда?) в гости (когда?) завтра.

    Обстоятельства относятся к сказуемому «приду», но отвечают на разные вопросы, поэтому их нельзя назвать однородными.

Однородными членами предложения не являются

  • Повторяющиеся слова, которые выступают в роли единого члена предложения: мы точно плавали в воздухе и кружились, кружились, кружились.

  • Повторяющиеся одинаковые формы, соединенные частицей «не», «так»: хочешь не хочешь; гулять так гулять.

  • Сочетания двух глаголов, из которых первый лексически неполный: возьму и закричу; пойду переверну.

  • Устойчивые сочетания с двойными союзами без запятой между ними: ни взад ни вперёд; ни за что ни про что; ни сном ни духом; и смех и грех; и так и сяк.

  • Уточняющие члены предложения, которые отвечают на вопросы «где именно?», «как именно?», «кто именно?» и произносятся с интонацией обособления. Часто в их роли выступают обстоятельства времени и места:

    Я мечтаю побывать на Эльбрусе, на Кавказе.

    Побывать (где?) на Эльбрусе, на Кавказе — не однородные обстоятельства. На Кавказе — уточняющее обстоятельство, которое объясняет, где именно находится Эльбрус.

Знаки препинания в предложениях с однородными членами

Чтобы правильно использовать ОЧ, нужно знать правила расстановки знаков препинания между ними. Рассмотрим тему пунктуации при однородных членах предложения.

Однородные члены могут сочетаться с обобщающим словом. Обобщающее слово является тем же членом предложения, что и другие однородные члены, отвечает на тот же вопрос, но имеет обобщающее значение:

  • обобщающее слово обозначает целое, а однородные члены — части этого целого:

    За деревней с холма был виден город: квадраты кварталов, кирпичные здания, разлив садов, шпили костёлов. (Шолохов)

  • обобщающее слово обозначает общее понятие, а однородные члены — более частные понятия:

    Пронзительно кричала птица: петухи, гуси, индейки. (Фадеев)

Запятая ставится:

  1. Если есть повторяющиеся соединительные или разделительные союзы:

    Я выполнила задание и по русскому, и по математике.

  2. Если есть два и более ОЧ без союзов:

    В парке было свежо, тихо, спокойно.

  3. Если ОЧ связаны противительными союзами в значении но:

    • а, но, хотя, да, однако же, зато.

    Эти конфеты дешевые, но очень вкусные.

Запятая НЕ ставится:

  1. Если между двух ОЧ есть союз:

    Из всех занятий на свете больше всего я люблю читать и танцевать.

  2. В устойчивых выражениях с повторяющимися союзами и. .. и, ни… ни:

    • ни конца ни края; ни то ни сё; ни рыба ни мясо; ни тот ни другой; и холод и голод; и туда и сюда; и день и ночь.

    • Ни тот ни другой не помог мне решить задачу.

  3. Если группы однородных членов разбиты на пары:

    В магазине мы купили все к столу: фрукты и овощи, рыбу и мясо, конфеты и печенье.

Кроме запятых в предложениях с ОЧ могут быть и другие знаки: двоеточие и тире.

Тире ставится:

  1. Когда обобщающее слово находится после ОЧ:

    Одежда, обувь, документы — все необходимое уже лежит в чемодане.

  2. Когда обобщающее слово стоит перед ОЧ, а после предложение продолжается:

    Везде: в гостинной, на кухне, в ванной — лежали ее вещи.

Двоеточие ставится:

  • когда обобщающее слово стоит перед ОЧ:

    Он всю неделю удивлял меня: убирался в квартире, готовил завтраки.

Теперь мы знаем все про однородные члены предложения в русском языке.

Повторим

  • однородные члены — это одинаковые члены предложения;

  • однородные члены зависят от одного и того же слова;

  • однородные члены связаны между собой сочинительной связью и интонацией.

Признаки однородных членов

  • отвечают на один и тот же вопрос;

  • являются одним членом предложения;

  • относятся к одному члену предложения;

  • часто выражены одной частью речи;

  • произносятся с перечислительной интонацией.

Вопросы для самопроверки

Объясните пунктуацию в предложениях с однородными членами.

  1. Усы, лапы и хвост — вот мои документы.

  2. Мама подарила Маше новую куклу и мячик.

  3. Я не сделал домашнее задание ни по физике, ни по химии.

  4. Картины висели повсюду: в гостиной, спальне и даже ванной.

  5. Заказ выполнили быстро, но плохо.

Испытание по критериям идентификации

Согласно Закона Республики Беларусь «О семеноводстве» государственное испытание сортов включает установление отличимости, однородности и стабильности (ООС).

Сорт считается отличимым, если он явно отличается от любого другого сорта, существование которого к моменту подачи заявки считается общеизвестным.

Сорт считается однородным, если с учетом особенностей его размножения растения этого сорта достаточно однородны по своим признакам.

Сорт считается стабильным, если его основные признаки  остаются неизменными после неоднократного размножения или в конце каждого цикла размножения.

Соответствие сортов условиям отличимости, однородности и стабильности является одним из главных показателей при включении их в Государственный реестр сортов, а также при получении патентов на сорта в Республике Беларусь

Испытание на ООС проводится на участках патентной экспертизы  сортоиспытательных станций в соответствии с их специализацией.

На сегодняшний день на 6 государственных сортоиспытательных станциях имеются участки патентной экспертизы:

ГСХУ «Горецкая СС»,

ГСХУ «Кобринская СС»,

ГСХУ «Молодечненская СС»,

ГСХУ «Несвижская СС»,

ГСХУ «Турская СС»,

ГСХУ «Жировичская СС».

Испытание проводится, как правило, параллельно на двух сортоиспытательных станциях, в течение не менее двух независимых полных вегетационных периодов при условиях, обеспечивающих нормальное развитие растений.

Помимо испытания сортов растений на ООС, ГУ «Государственная инспекция по испытанию и охране сортов растений» проводится испытание сортов на патентоспособность.

Данный вид испытания проводится, если заявителем подана заявка в Национальный центр интеллектуальной собственности на  предоставление сорту охраны в Республике Беларусь.

По результатам испытания сортов на ООС и патентоспособность, составляется их официальное описание, которое в случае получения патента на сорт определяет объем его правовой охраны  в течение 25 лет и регистрируется в Государственном реестре охраняемых сортов.

Однородность встречных требований — Сейчас.ру

О. ВИЛЕСОВА, А. КАЗАКОВА
Ольга Вилесова, юрист ООО «Бюро правовых экспертиз», г. Пермь.
Анна Казакова, юрист ООО «Бюро правовых экспертиз», г. Пермь.
Если ранее, в период бурного развития рыночных отношений, практика проведения зачетов безжалостно расходилась с теорией, то сейчас стороны чтут нормы ГК РФ и стараются следовать им. Нарушения все же встречаются, и судебная практика знает немало случаев оспаривания проведенных зачетов. Это говорит как о невнимательном отношении к существующим правилам со стороны предпринимателей, так и о том, что не все положения законодательства понятны и толкуются всеми одинаково.
Казалось бы, вполне четкая и лаконичная формулировка ст. 410 ГК РФ: «Обязательство прекращается полностью или частично зачетом встречного однородного требования, срок которого наступил либо срок которого не указан или определен моментом востребования. Для зачета достаточно заявления одной стороны» — вызывает на практике целый ряд вопросов. О том, что эти вопросы являются совсем не праздными, говорит хотя бы тот факт, что Президиумом ВАС РФ было выпущено информационное письмо N 65 от 29.12.2001 «Обзор практики разрешения споров, связанных с прекращением обязательств зачетом встречных однородных требований». В этом письме Президиум уделил немало внимания формированию единообразной практики правоприменения при проведении зачетов.
Возможно, это обстоятельство свидетельствует о том, что короткой формулировки статьи 410 ГК РФ явно недостаточно и некоторые использованные в ней термины нуждаются в раскрытии. В результате в гражданском обороте нередко возникают спорные ситуации, связанные именно с толкованием и применением положений статьи 410 ГК РФ. Разрешать их стало делом судов.
Одним из примеров такой неясности или, если быть точнее, неоднозначно истолкованного термина стало понятие однородности встречных требований.
Точки зрения
Уже на заре применения нового ГК РФ сразу же достаточно четко были обозначены две позиции в отношении определения однородности зачитываемых требований. Первую точку зрению представляла в том числе ленинградская школа права. Ее последователи считают, что однородность требования означает «однородность предмета обязательства (деньги, вещи одного и того же рода и прочее) с тем, чтобы зачету не предшествовало соглашение сторон об изменении предмета обязательства» <*>.
———————————
<*> Гражданское право. Часть 1: Учебник / Под ред. Ю.К. Толстого, А.П. Сергеева. М.: ТЕИС, 1996. С. 542.
Такой же точки зрения придерживается и В. Ю. Бакшинскас. Единственно, он рассматривает понятие однородности встречных требований, отмечая, что «предметом встречных обязательств должны быть вещи, определяемые родовыми признаками, в том числе деньги» <*>.
———————————
<*> Правовое регулирование хозяйственной деятельности. Информационное агентство ИПБ-БИНФА, 2002.
Второй подход к проблеме определения однородности встречных требований раскрыт в работах М.И. Брагинского, который исходит из того, что зачитываемые требования должны отвечать признаку однородности не только предмета, но и существа обязательств, из которых эти требования вытекают <*>.
———————————
<*> Комментарий к Гражданскому кодексу Российской Федерации, части первой (постатейный) / Рук. авт. кол. и отв. ред. О.Н. Садиков. М.: КОНТРАКТ; ИНФРА-М, 1997. С. 663.
См. также: Договорное право: Общие положения. М.: Статут, 1998. С. 362, 363.
Монография М.И. Брагинского, В.В. Витрянского «Договорное право. Общие положения» (Книга 1) включена в информационный банк согласно публикации — М.: Издательство «Статут», 2001 (издание 3-е, стереотипное).Однородность предмета требования
Поскольку, когда мы говорим о зачете встречных однородных требований, речь идет о прекращении обязательств исключительно гражданско-правового характера, то отталкиваться следует от самого определения обязательства.
Согласно п. 1 ст. 307 ГК РФ обязательство представляет собой правоотношение, в силу которого одно лицо (должник) обязано совершить в пользу другого лица (кредитора) определенное действие: передать имущество, выполнить работу, уплатить деньги и т.п., либо воздержаться от определенного действия, а кредитор имеет право требовать от должника исполнения его обязанности.
С юридическим явлением «обязательство» тесно связано понятие «сделка». Сделка есть одно из оснований возникновения обязательств. Как известно, двух- и многосторонние сделки именуются договорами. И если термин «предмет обязательства» в российском гражданском праве встречается достаточно редко, то термин «предмет договора» является одним из основополагающих терминов договорного права.
Предмет договора — это то, на достижение чего направлены действия сторон последнего, важнейшее существенное условие договора. Недостижение согласия сторон по поводу предмета договора автоматически низводит договор в ранг незаключенного.
Предмет различных видов договоров определен законом по-разному: передача вещи (купля-продажа, дарение, мена, аренда), выполнение определенной работы и передача ее результата (подряд), оказание услуг (возмездное оказание услуг), передача денег или других вещей, определенные родовыми признаками (заем), и т.д.
Если речь идет исключительно о том, что для проведения зачета встречных требований необходима однородность предмета встречных договоров, то сам процесс проведения зачетов стал бы весьма затруднительным. Для зачетов требовалось бы отбирать только такие требования, которые вытекают из встречных договоров, имеющих однородный предмет.
Зачет же по договорам, имеющим различный предмет (договору купли-продажи и договору оказания услуг, например), был бы невозможен. Тем не менее такое положение вещей вряд ли следует признать справедливым, ведь речь в ст. 410 ГК РФ идет не об однородности предмета договоров, а об однородности предмета требований.
ВАС РФ в своем информационном письме N 65 специально указал, что ст. 410 ГК РФ не требует, чтобы предъявляемое к зачету требование вытекало из того же обязательства или из обязательств одного вида (п. 7). Именно поэтому он посчитал возможным проведение зачета встречных однородных требований, вытекающих из обязательства по оплате работ, с одной стороны, и обязательства по возврату уплаченных процентов за пользование кредитом по договору поручительства, так как предметом обоих требований являлись деньги, хотя обязательства были разными.
Требование одной стороны к другой — составляющее содержания обязательства в виде права одной стороны и корреспондирующей ей обязанности другой стороны. Исходя из этого, полагаем, что обсуждать следует в первую очередь не однородность предмета обязательств в понимании обязательства как договора, а однородность требований как однородность взаимных прав участников обязательств.
Обязательства же в данном случае следует понимать исключительно как правоотношения, в которых одна сторона имеет определенное право, а другая — корреспондирующую ему обязанность. Тогда понятие «однородные требования» становится простым и определенным: одна сторона зачета имеет по отношению к другой стороне право требовать «нечто», другая сторона — к первой — право требовать то же самое.
Подтверждением этой точки зрения может служить вывод, сделанный ФАС СЗО в Постановлении от 18.06.2001 по делу N А56-2581/01: «…понятие однородности требования предполагает наличие одного и того же объекта различных требований (деньги, передача одинаковых вещей и т.п.)». А также тот факт, что в ряде случаев законодатель предусматривает возможность проведения зачета требований в рамках одного и того же обязательства.
К примеру, в силу п. 2 ст. 623 ГК РФ арендатор вправе после прекращения договора аренды зачесть в счет арендных платежей стоимость неотделимых улучшений, произведенных с согласия арендодателя за счет собственных средств.
Другой аналогичный пример — комиссионер вправе в соответствии со ст. 410 ГК РФ удержать причитающиеся ему по договору комиссии суммы из всех сумм, поступивших к нему за счет комитента (ст. 997 ГК РФ), а также заявить о зачете на основании иных встречных денежных требований к комитенту. Равно и как агент, заключивший от имени принципала договор с третьим лицом, имеет право на прекращение обязательства по передаче полученных от третьего лица денежных сумм зачетом встречного требования к принципалу по оплате вознаграждения.
Относительно же предмета зачитываемых требований можно, на наш взгляд, отметить следующее. Практика применения ст. 410 ГК РФ свидетельствует о том, что предметом зачитываемых требований всегда являются вещи, определенные родовыми признаками, в первую очередь — деньги. Теория ничего не говорит о невозможности проведения зачета требований, предметом которых являются не вещи, определенные родовыми признаками, а, например, работы или услуги.
Однородность существа обязательств
Что же касается позиции, согласно которой однородность должна проявляться не только в однородности предмета, но и в природе обязательств, то это серьезная тема для дискуссии. Начнем с того, что понятие правовой природы обязательств, существа обязательств нигде не зафиксировано.
Римские юристы исходили из того, что к зачету способны только обязательства одного и того же вида. Современный российский законодатель такого ограничения не ввел, и это стало началом практики проведения зачетов разных видов обязательств, в том числе обязательств, как вытекающих из договоров, так и внедоговорных.
Такой подход современного законодателя был обусловлен тем, что в нынешних условиях развития товарно-рыночных отношений ограничение в виде запрета на проведение зачетов по разным видам обязательств, даже гражданско-правовых, привело бы к усложнению расчетов и вынужденному излишнему перемещению денежных средств и товарно-материальных ценностей.
Поэтому в своем Постановлении от 09.06.1997 по делу N Ф09-418/97-ГК ФАС Уральского округа счел однородными встречные требования, вытекающие из обязательства по поставке оборудования и договора аренды. Если требования, происходящие из обязательств разного вида, могут зачитываться между собой и на это указывают даже те правоведы, которые считают их разнородными, то какие же обязательства имеют разную правовую природу?
В качестве примера приведем спор, предметом которого стал вопрос о возможности проведения зачета требования о перечислении авансового платежа на полученные товары — по одному договору и требования о взыскании пеней за недопоставку — по другому. Разрешая конфликт, ВАС РФ признал неоднородными и не способными к зачету обязательства возвратить полученную сумму кредита одной стороны и возникшее из поручительства субсидиарное по своему характеру обязательство другой стороны (Вестник ВАС РФ. 1996. N 4. С. 14 — 15) <*>.
———————————
<*> Комментарий к Гражданскому кодексу Российской Федерации, части первой (постатейный) / Рук. авт. кол. и отв. ред. О.Н. Садиков. М.: КОНТРАКТ; ИНФРА-М, 1997. С. 663.
Таким образом, требования, вытекающие из основного и субсидиарного обязательств, имеющих разную правовую природу, были сочтены не подлежащими зачету. Кроется ли вся загвоздка в разном существе обязательств? Является ли невозможным зачет требований о взыскании, скажем, пеней, с одной стороны, и основного долга — с другой? Полагаем, что нет.
В частности, в уже известном нам информационном письме от 29.12.2001 N 65 Президиумом ВАС РФ указывается: «Окончание исполнительного производства, основанное на сделанном одной из сторон заявлении о зачете, при наличии встречных исполнительных листов не противоречит закону».
Там же приводится судебное дело, в ходе которого суд счел однородными и подлежащими зачету требования, одно из которых вытекало из договора, а другое основывалось на исполнительном листе. При этом требование по исполнительному листу было охарактеризовано судом как требование, которое «подтверждено судом и по которому также выдан исполнительный лист».
Имело ли значение в данном случае, какое именно гражданско-правовое обязательство подтверждал исполнительный лист — основное или субсидиарное, договорное или внедоговорное? Пожалуй, нет, если только законодатель напрямую, как в ст. 411 ГК РФ, не запретил зачитывать такие требования.
Самое главное, что в обозначенном случае предмет требований был однороден, размер требования четко установлен и ни само требование, ни его размер не оспаривались.
В каких же случаях имеет значение разная правовая природа обязательств? Как ни странно, эти случаи оговорены самим законодателем. Например, п. 1 ст. 16 ФЗ «Об обществах с ограниченной ответственностью» устанавливается запрет на проведение зачета требований учредителя к обществу с ограниченной ответственностью в качестве исполнения обязанности по внесению вклада.
Действительно, обязательство по внесению вклада в целях оплаты уставного капитала и обязательство общества перед учредителем, возникшее из какого-либо гражданско-правового обязательства, имеют разную правовую природу. Но законодатель не руководствуется тем, что такие требования не могут быть зачтены просто потому, что они неодинаковы по своей природе, он специально прописывает запрет.
Существует и другая ситуация, в которой действующее законодательство не оговаривает все возможные случаи невозможности проводить зачеты встречных требований, но вводит одно общее ограничение. Согласно п. 3 ст. 2 ГК РФ к имущественным отношениям, основанным на административном или ином властном подчинении одной стороны другой, в том числе к налоговым и другим финансовым и административным отношениям, гражданское законодательство не применяется, если иное не предусмотрено законодательством.
Исходя из этого общего правила, зачет требований, проистекающих из обязательств, основанных на разных отношениях — административных, налоговых, гражданско-правовых, невозможен. Опять же, такой вывод мы делаем не только и не столько вследствие того, что обязательства, из которых вытекают требования, имеют разную правовую природу, а потому, что законодатель предписывает нам разграничивать имущественные отношения и не применять к любым таким отношениям гражданско-правовое регулирование.
Судебная практика также не восприняла жестко правило о невозможности зачета требований, вытекающих из обязательств с разной правовой природой, например из основных обязательств и обязательств, обеспечивающих их исполнение. Примером тому может служить одно из дел ФАС Уральского округа от 11.03.96 (дело N У-98/96-ГК).
При его рассмотрении ФАС УО признал необоснованным вывод суда предыдущей инстанции о неоднородности взаимных денежных требований сторон по оплате товара и выплате штрафа. Нижестоящему суду было предписано проверить обоснованность доводов ответчика о некачественности поставленных товаров и возникновении у него

Оспаривание дарения акций  »
Комментарии к законам »

Признаки однородности членов предложения — презентация онлайн

1.

Признаки однородности членов предложения: 1) отвечают на один и тот же
вопрос
2) относятся к одному и тому же
слову (члену предложения)
3) являются одним и тем же членом
предложения

2. Способы выражения однородных членов:

Одна часть речи:
где?
х
Около дома и в саду виднелись
цветы.
и
Разные части речи:
где?
И около дома, и вдалеке
цветы.
и
, и
х
виднелись

3. Укажите однородные члены предложения:

1) Безоблачное небо и лучи восходящего
солнца предвещали хороший день.

4. Подлежащие:

Безоблачное небо и лучи
восходящего солнца предвещали
хороший день.

5. Укажите однородные члены предложения:

2) С утра нужно покормить кошку и собаку.

6. Дополнения:

кого?
С утра нужно покормить кошку и собаку.

7. Укажите однородные члены предложения:

3) В субботу и в воскресенье пройдут
дожди.

8. Обстоятельства:

когда?
В субботу и в воскресенье пройдут
дожди.

9. Укажите однородные члены предложения:

4) В субботу мы не отдыхали, а работали.

10. Сказуемые:

что делали?
В субботу мы не отдыхали, а работали.

11. Укажите однородные члены предложения:

5) Корюшка – маленькая, но вкусная рыбка.

12. Определения:

какая?
Корюшка – маленькая, но вкусная рыбка.

13. Обобщающие слова при однородных членах Установите соответствие между обобщающими словами и рядами однородных членов:

Обобщающие слова
Школьная мебель
Однородные члены
Подлежащее и сказуемое
Родственники
Кошки, собаки, хомяки и
морские свинки
Грамматическая основа
предложения
Парта, стул, стол, шкаф
Домашние животные
Пирожки, булки, пирожные
Выпечка
Мама, сестра, папа, дедушка и
бабушка

14. Обобщающие слова при однородных членах:

Обобщающие слова
Однородные члены
Школьная мебель
Парта, стул, стол, шкаф
Родственники
Мама, сестра, папа, дедушка и
бабушка
Грамматическая основа
предложения
Подлежащее и сказуемое
Домашние животные
Кошки, собаки, хомяки и
морские свинки
Пирожки, булки, пирожные
Выпечка

15.

Закончите предложения, использовав подходящие обобщающее слово и ряд однородных членов: • При разборе предложения по членам
сначала выделяется …
• Мои одноклассники держат разных …

16. Закончите предложения, использовав подходящие обобщающее слово и ряд однородных членов:

При разборе предложения по членам сначала
выделяется
грамматическая
основа
предложения: подлежащее и сказуемое.
Мои
одноклассники
держат
домашних животных: кошек,
хомяков, морских свинок.
разных
собак,

Южное таможенное управление

Нелегальные духи и косметика

Опубликовано: 18 октября 2016 10:43

 

На пешеходной составляющей таможенного поста МАПП Адлер при проведении таможенного контроля лиц, следующих из России в Республику Абхазия, инспекторы обратили внимание на женщину с большими дорожными сумками.

К сотрудникам таможни за разъяснением правил перемещения товаров через границу гражданка не обращалась, таможенную декларацию не подавала. На вопрос инспектора таможни о наличии предметов, подлежащих обязательному письменному декларированию, она ответила отрицательно. В ходе таможенного контроля ее багажа с использованием досмотровой рентгентехники были установлены признаки однородности товара. Женщина пояснила, что перевозит «немного парфюмерии и косметики».

В результате таможенного досмотра в багаже гражданки было обнаружено множество парфюмерной и косметической продукции в коробках и упаковках: тушь для ресниц, помаду, гель, косметическое масло, духи. Общее количество единиц товара составило 844 штуки.

Нарушительница пояснила, что данную продукцию она приобрела на оптовом складе в г. Нальчике. О том, что ее необходимо было декларировать, она «не знала», так как ранее границу с товаром не пересекала. Со слов гражданки, данную продукцию она планировала подарить подругам и родственникам, которые проживают в Республике Абхазия.

Весь товар изъят, образцы направлены на экспертизу. В отношении гражданки возбуждено дело об административном правонарушении по ч. 1 ст. 16.2 КоАП РФ (недекларирование либо недостоверное декларирование товаров). Проводится административное расследование.

Сочинские таможенники задержали незадекларированную парфюмерную и косметическую продукцию.

Однородные и однородные — в чем разница?

Если вы описываете общество, состоящее из очень похожих людей, вы бы описали это общество как однородное или однородное ?

Несмотря на сходство написания, эти слова не являются синонимами. Один — устаревший термин из биологии, а другой — прилагательное, обозначающее тождество. Они настолько сбивают с толку, что даже профессиональные журналисты часто злоупотребляют ими.

Однако вы разборчивый писатель и понимаете, что правильный выбор слов может сохранить доверие к вам. Эта статья объяснит, какое из этих слов является правильным в вашем письме.

В чем разница между однородным и однородным?

В этом посте я сравню однородный и однородный . Я буду включать примеры предложений для каждого слова, чтобы вы могли увидеть их правильное использование в контексте.

Наконец, я покажу вам мнемонический прием, который позволяет легко выбрать гомогенный или гомогенный в вашем собственном письме.

Когда использовать гомогенный продукт

Что означает однородный? Гомогенный (произносится как huh- mah -je-nus) — устаревший биологический термин, обозначающий органов или тканей тела с генетическим сходством .

Сегодня большинство научных авторов использовали бы вместо этого более свежий термин гомологичный .

Тем не менее, если вы читаете старые научные тексты, время от времени вы можете встретить однородных .

Вот возможный пример:

  • Организм-хозяин отклонил даже имплантаты из однородной ткани.

Обычная ошибка с этими словами — использование слова однородный , когда автор действительно имеет в виду однородный . Поскольку гомогенный все меньше используется даже в научном сообществе, этой ошибки должно быть легко избежать.

Когда использовать гомогенный продукт

Что означает однородный? Однородный (произносится как hoh-muh- jeen -ee-us) — прилагательное.Это не является синонимом однородного , , несмотря на его написание схожесть с этим словом.

Однородный означает , имеющий аналогичные или однородные характеристики . Сообщество, большинство членов которого имеют схожие характеристики, например, байкерская банда, состоящая из мужчин с низким доходом в возрасте от 20 до 30 лет, у всех одинаковые татуировки, можно назвать однородным. Коробка цветных карандашей, в которой есть только синие мелки, также будет однородной.

Вот еще несколько примеров:

  • Тесто для торта сначала представляет собой набор разрозненных ингредиентов, но вскоре становится липкой однородной смесью.
  • Показатели продаж существующих и новых филиалов удивительно однородны; статистически значимых различий между филиалами за последний квартал нет.
  • Чистый результат — партии, которые гораздо более однородны внутри, чем это было поколение назад. — The Washington Post

Однородный появился на английском языке с 17 века. Он в некоторой степени уникален тем, что его этимологию можно проследить как на латинском, так и на греческом языках.Оно должно произноситься с использованием пяти отдельных слогов, хо-мух- jen -ee-us.

Связанное существительное с гомогенизировать — это однородность , и его глагол гомогенизировать . Вы, вероятно, видели этикетки на молоке, рекламирующие продукт как гомогенизированный . Однородный также имеет антоним неоднородный , что означает с разными характеристиками .

Как произнести слово «однородный» и «однородный»

Эти слова имеют разное произношение, и правильное произношение каждого слова является ключом к использованию правильного слова в вашем письме.

Как произносится homogenous: В произношении homogenous (huh- mah -je-nus) четыре слога.

Как произносится homogen: В произношении homogen (hoh-muh- jeen -ee-us) пять слогов. Однородный, как и его антоним, гетерогенный, оба содержат больше слогов, чем однородные.

  • Однородный = четыре слога.
  • Однородный = пять слогов.
  • Гетерогенный = шесть слогов.

Как запомнить разницу

Если вы не биолог 19 века, вам следует избегать использования гомогенного . Сегодня ученые с большей вероятностью будут использовать гомологичного вместо этого архаичного термина.

Для всех ситуаций, когда вам нужно описать что-то как имеющее похожие или однородные характеристики, выберите однородный .

Однородный и однородный чек: Поскольку однородный имеет дополнительный E , как и слово характеристики , вы можете помнить, что однородный описывает аналогичные характеристики.

Сводка

Он однородный или однородный? Гомогенный — это старый научный термин, описывающий похожие ткани или органы. Он был заменен на гомологичный . Однородный — прилагательное, описывающее сходных или однородных характеристик .

Таким образом,

  • Однородный все еще используется в современной письменности.
  • Однородный в основном заменен гомологичным .

Однородность — обзор | Темы ScienceDirect

2.4 Извлечение кластера

В методе SHOPIN мы определяем извлечение кластера как итерационный процесс нахождения разбиения матрицы расстояний PIN, который максимизирует функцию качества кластера, определяемую как:

(12) Q = BPi / WPi

, где Pi = C1C2… CNCi — заданное разбиение графика, B ( P i ) — функция, которая количественно определяет «расстояние» между кластерами, т.е.е., дисперсия между кластерами, и W ( P i ) — это функция, которая количественно определяет диапазон кластеров, то есть дисперсию внутри кластера.

Есть много способов определить расстояние между группами объектов, учитывая попарное расстояние между двумя объектами. Мы выбрали самый простой подход; мы моделируем расстояние между двумя кластерами как среднее всех попарных расстояний между узлами разных кластеров. Запишем это как:

(13) DCiCj = 1Ci || Cj∑v∈Ci∑w∈Cjdvw

Поскольку уравнение. (11) моделирует расстояние как обратное сродству, мы можем интерпретировать попарное расстояние между узлами как меру «отталкиваемости» узлов. Следовательно, уравнение. (13) моделирует межкластерную отталкиваемость в разделенном ПИН-графе. Определим

(14) BPi = 2NCiNCi − 1∑i = 1NCi − 1∑j = i + 1NCiDCiCj

, где NCi — общее количество кластеров в разбиении P i .

Максимально возможное значение дисперсии между кластерами, B ( P i ), равно 1, что соответствует случаю каждой пары кластеров, имеющих расстояние 1 (если мы рассмотрим простейший случай разбиения P приводит только к двум кластерам, B ( P ) = 1 тогда и только тогда, когда два кластера находятся в полной противоположности, например.g., все узлы в одном кластере все белые, а все узлы в другом кластере все черные).

Мы определяем протяженность кластера (или однородность одного кластера) как среднее расстояние между всеми парами узлов в этом кластере

(15) SCi = 2 | Ci | ⋅ | Ci | + 1∑v, w∈Cidvw

Внутрикластерная дисперсия разбиения P i теперь определяется как:

(16) WPi = 1NCi∑Ci∈PiSCi

, где NCi — общее количество кластеров в разбиении P i .

Детально определив функцию качества, мы можем ее оптимизировать, то есть максимизировать соотношение дисперсии между / внутри кластера. При инициализации оптимизации мы помещаем каждый узел в отдельный кластер. Мы определяем случайный порядок узлов и используем его для итерации. Для каждого узла и выполняется проверка, повысит ли какое-либо возможное смещение функцию качества. Смещение возможно, если соседний узел j , ( i , j ) ∈ E , принадлежит кластеру C j , отличному от кластера C i узла i .Смещение удаляет узел i из кластера C i и добавляет его в кластер C j . Для заданного смещения функция качества пересчитывается, и смещение считается положительным, если функция качества увеличивается. Если для узла и возможно более одного положительного смещения, мы выбираем то, которое дает наибольшее увеличение функции качества, и узел перемещается в соответствующий кластер. Если смещение невозможно или все смещения снижают функцию качества, узел и остается в своем текущем кластере.Когда узел перемещается в новый кластер, он автоматически покидает свой исходный кластер, и если в исходном кластере был единственный узел, мы имеем дело с объединением кластеров. Чтобы ускорить сходимость алгоритма, мы перебираем список узлов графа PIN, отсортированный по их степени (совокупный вес ребер, прикрепленных к узлу для взвешенного графа PIN) в порядке убывания. После того, как все узлы из списка будут проверены, мы вернемся к начальному узлу, то есть к узлу с наивысшей степенью.Алгоритм сходится, если все узлы проверены (в любом заданном порядке) и значение функции качества не увеличивается. Мы производим иерархическую кластеризацию (модульную структуру), используя подход (Blondel, Guillaume, Lambiotte, & Lefebvre, 2008), в котором алгоритм запускается несколько раз, используя разделение в устойчивом состоянии предыдущего запуска в качестве входных данных для следующего, каждый кластер из одного прогона заменяется одним узлом в следующем прогоне. Чтобы иметь возможность выполнить следующий запуск, нам нужно определить веса графа, полученного путем замены кластеров отдельными узлами.Мы используем следующее:

(17) WCk = ∑i, j∈Ckdij

(18) WCkl = ∑i∈Ck∑j∈Cldij

, где WC k — сумма всех весов ребер внутри кластера C k , WC kl — сумма всех весов ребер между кластерами C l и C k и d ( i , j ) — элемент матрицы расстояний. Новая матрица расстояний определяется как:

(19) dij = WCi, i = jlooponnewnodeWCij, i ≠ jedgebetweennewnodes

Эта новая матрица теперь используется в процессе оптимизации семантической однородности так же, как объяснялось ранее.Этот процесс может продолжаться до тех пор, пока мы не достигнем одного кластера, предопределенного порога для количества кластеров или если увеличение функции качества между последовательными уровнями в иерархии кластеризации будет ниже предопределенного порога (мы используем 0,1).

Однородность — обзор | Темы ScienceDirect

8.8.1 Ценообразование опционов

Привлекательность формулы ценообразования Блэка и Скоулза (1973) для практиков часто возникает из-за ее аналитической простоты для определения цены европейского опциона на актив, не приносящий дивидендов, по

(8.35) Ct = StN (d1) −Ke − rτN (d2)

с

d1 = [ln (St / K) + (r + 0.5σ2) τ] / (στ) d2 = d1 − στ,

где N — кумулятивное нормальное распределение, S t — цена базовой ценной бумаги, K — цена исполнения, r — преобладающая безрисковая процентная ставка, τ — время до -зрелость, а σ — волатильность базового актива. Уравнение 8.35 не содержит ни предпочтений отдельных лиц, ни предпочтений совокупного рынка.

Вывод Блэка-Шоулза в основном подвергался критике за допущения о распределении базовой ценной бумаги. Эмпирические исследования цены акций обнаруживают слишком много выбросов для простого логнормального распределения с постоянной дисперсией (Merton, 1976). Многие исследователи предлагали альтернативные объяснения. Олдфилд и др. . (1977) и Болл и Тороус (1985) применили сочетание непрерывных и скачкообразных процессов к данным о ценах на акции. Попытки согласовать стохастическую волатильность и стохастические процентные ставки в рамках анализа Блэка-Шоулза были осложнены сложностью оценки рыночной цены риска.Бакши и др. . (1997) предоставили закрытые решения для оценки опционов при стохастической волатильности и стохастических процентных ставках с использованием метода инверсии Фурье Хестона (1993) для расчета премий за волатильность и рыночный риск процентной ставки. Их результаты документально подтвердили, что модели стохастической волатильности и стохастической процентной ставки структурно неверно определены. Однако добавление функции стохастической волатильности к модели Блэка-Шоулза улучшает ценообразование вне выборки и эффективность модели хеджирования.В более поздней работе Сарвар и Крехбиль (2000) сообщили, что модель Блэка-Шоулза, рассчитанная с ежедневной пересмотренной подразумеваемой волатильностью, работает так же, как модель стохастической волатильности для опционов колл в европейской валюте. Дерман и Кани (1994), Дюпир (1994) и Рубинштейн (1994) разработали модель оценки опционов с функцией детерминированной волатильности (DVF) в попытке точно объяснить наблюдаемое сечение цен опционов. Однако Дюма и др. . (1998) сообщили, что модель оценки опционов DVF не лучше, чем специальная процедура, которая просто сглаживает подразумеваемую волатильность Блэка-Шоулза по ценам исполнения и времени до погашения.

Непараметрические модели оценки являются естественным продолжением, поскольку легче ослабить допущения о распределении. Естественная непараметрическая функция для определения цены европейского опциона колл на актив, выплачивающий неделимый доход, связывает цену опциона с набором переменных, которые характеризуют опцион, а именно с ценой базового актива S t , страйк-ценой K , а время до погашения τ. Следовательно, функцию оценки опционов можно записать как

(8.36) Ct = f (St, K, τ).

Этого подхода придерживаются Хатчинсон и др. . (1994). Функция также будет действительна для изучения цен, созданных моделью Блэка-Шоулза, поскольку параметры процентной ставки и волатильности, представленные в формуле, являются постоянными и не могут быть идентифицированы с помощью непараметрической оценки функции f . Обычно сложнее непараметрически оценить такую ​​функцию, когда число входных переменных велико. Чтобы уменьшить количество вводимых данных, Hutchinson et al .(1994) разделили функцию и ее аргументы на K и записали функцию ценообразования следующим образом:

(8,37) CtK = f (StK, l, τ).

Эта форма предполагает однородность первой степени 16 цены актива и цены исполнения функции ценообразования f .

Гарсия и Рено (1995) предложили модель равновесия, которая обеспечивает свойство однородности, которое сохраняет функциональную форму Блэка-Шоулза. Гарсия и Генчай (2000) использовали обобщенную формулу Блэка-Шоулза, предложенную в работе Garcia and Renault (1995),

(8. 38) CtK = StKf1 (StK, τ) −b (τ) f2 (StK, τ),

, где теоретические ограничения, вытекающие из отсутствия арбитража или равновесия, ограничивают функции f 1 и f 2 , чтобы аппроксимировать ту же функцию (например, функцию нормального распределения в формуле Блэка-Шоулза), возможно, с разными аргументами. Эти теоретические ограничения объясняются тем, что структура нейронной сети должна быть одинаковой для f 1 и f 2 , где b (τ) является функцией зрелости опциона.

Функция определения цены опциона в уравнении 8.37 и обобщенная форма в уравнении 8.38 оцениваются с помощью следующих упреждающих регрессий:

(8.39) fnh (StK, τ; θ) = β0 + Σj = 1dβj1 + exp [−γj0− γj1 (StK) −γj2τ]

(8.40) fwh (StK, τ; θ) = β0 + StK (Σj = 1dβj11 + exp [−γj10 − γj11 (StK) −γj12τ]) — e-ατ (Σj = 1dβj21 + exp [−γj20 − γj21 (StK) −γj22τ]),

, где f wh и f nh относятся к моделям с подсказкой и без подсказки соответственно.

Метод с подсказками описывает ситуацию, когда в дополнение к набору пар ввода-вывода неизвестной функции имеется дополнительная априорная информация о свойствах неизвестной функции, которая предоставляется алгоритму обучения. Как правило, подсказки предоставляют вспомогательную информацию о неизвестной функции, которую можно использовать для руководства процессом обучения. Идея использования вспомогательной информации о целевой функции для облегчения процесса обучения, несомненно, является базовой и использовалась в литературе под разными названиями, такими как подсказки, предварительные знания и явные правила.Поскольку подсказки накладывают дополнительные ограничения на набор допустимых решений, к которым может сходиться процесс обучения, подсказки могут иметь тенденцию ухудшать производительность в выборке, исключая некоторые решения, которые в противном случае могли бы лучше соответствовать данным. Это явно помогает избежать переобучения алгоритмов обучения. Основная цель использования подсказок — улучшить производительность алгоритмов обучения вне выборки.

Существуют разные типы подсказок, общие для разных приложений.Указания на инвариантность Ху (1962), Дуды и Харта (1973), Хинтона (1987), Мински и Паперта (1988) являются наиболее распространенными типами подсказок в приложениях распознавания образов. Подсказка инвариантности утверждает, что целевая функция инвариантна при определенных преобразованиях входных данных. Намеки на монотонность, как у Абу-Мостафа (1993), распространены в таких приложениях, как медицинская диагностика и кредитный рейтинг, где целевая функция предполагается монотонной по определенным переменным. Подсказки симметрии обычно используются техническими аналитиками при прогнозировании валютных курсов.Абу-Мостафа (1994, 1995) указал, что правильно установленные ограничения приведут к улучшенным обобщениям вне выборки. Абу-Мостафа (2001) дополнил функцию потерь функциями подсказки согласованности, основанными на расстоянии Кульбака-Лейблера, для калибровки финансовой модели.

Данные представляют собой ежедневные европейские опционы индекса S&P 500 от Чикагской биржи опционов за период с 1990 по 1993 год. Рынок опционов на индекс S&P 500 чрезвычайно ликвиден и является одним из самых активных рынков опционов в Соединенных Штатах.Этот рынок наиболее близок к теоретической установке модели Блэка-Шоулза. При построении данных, используемых в оценке, варианты с нулевым объемом не используются. Для каждого года выборка делится на три части: первая половина года (период обучения), третий квартал (период проверки) и четвертый квартал (период прогнозирования). Сложность сетей основана на их производительности в период проверки вне выборки. Уравнения 8.39 и 8.40 показывают, что сети для модели с подсказкой всегда будут иметь примерно вдвое больше параметров, чем сети без подсказки для данного количества скрытых единиц.Для справедливого сравнения производительности двух сетей принята трехэтапная стратегия. Во-первых, f nh оценивается с помощью от 1 до 10 скрытых единиц, а f wh оценивается с помощью от 1 до 5 скрытых единиц по половине точек данных для конкретной выборки, периода обучения. Затем выбирается сеть в каждом семействе, которая дает лучшую MSPE за период валидации. Наконец, эффективность прогнозирования (MSPE) оценивается для данных в выборке прогнозирования.

Результаты представлены в таблице 8.1. Для каждого года сообщается среднее значение MSPE, полученное в ходе пяти экспериментов для каждого семейства сетей, и среднее количество выбранных скрытых блоков. Неудивительно, что линейная модель обеспечивает худшую производительность с точки зрения MSPE. Производительность MSPE модели Блэка-Шоулза значительно лучше, чем у линейной модели, но хуже, чем у сетевых моделей с прямой связью. Между сетевыми моделями с прямой связью средний MSPE для моделей с подсказкой однородности всегда меньше, чем MSPE моделей без подсказки.Средние значения MSPE моделей с подсказкой и без нее за период с 1990 по 1993 год составляют 92, 93, 92 и 72% соответственно. Кроме того, соотношение стандартных отклонений MSPE по пяти экспериментам существенно благоприятствует модели с намеком на однородность. В большинстве лет это соотношение ниже 50%. Все значения статистики Diebold and Mariano (1995) (D&M) большие и положительные, что означает, что мы категорически отвергаем равенство ошибок прогноза в пользу нейронных сетей с прямой связью с подсказкой.

ТАБЛИЦА 8.1. Среднеквадратичные ошибки прогноза вне выборки опционов колл S & amp; P-500. В этой таблице представлены показатели среднеквадратичной ошибки прогнозирования вне выборки (MSPE) нейронной сети с подсказкой и без нее, а также линейная модель для цен опционов колл из опционов колл S & amp; P-500. В таблице приведены средние значения (U¯) пяти MSPE, соответствующих пяти сетям, оцененным по разным начальным значениям. Среднее количество скрытых единиц из пяти прогонов указано в скобках рядом со средними значениями MSPE.σ — стандартное отклонение пяти MSPE оцененных сетей. «Отношение» — это соотношение между соответствующими статистическими данными модели прямой связи с подсказкой и без подсказки. D & amp; M относится к тесту Diebold and Mariano (1995) для дифференциала средних потерь (Mizrach, 1995, имеет аналогичный тест для дифференциала средних потерь). Эта статистика теста распределяется стандартно нормально для больших выборок. Вся статистика тестов D&M рассчитывается из разницы потерь MSPE между моделями прямой связи с указанием на однородность и без него.Представленные цифры MSPE были умножены на 10 4 .

)
Статистика MSPE с подсказкой MSPE без подсказки Ratio MSPE Linear / BS
( 1990, всего: 3605, оценка 4: 20
x ¯ 0,6761 (3) 0,7253 (6) 0,92 8,15 / 2,62
σ 0,0763 0.1222 0,62
D & amp; M 5,04
( 1991, Всего: 4481, Проверка: 1922, Прогноз: 2061 ) x
0,3775 (8) 0,93 3,45 / 1,73
σ 0,0148 0,0336 0,44
D & amp; М , Всего: 4374, Проверка: 1922, Прогноз: 1848 )
x¯ 0. 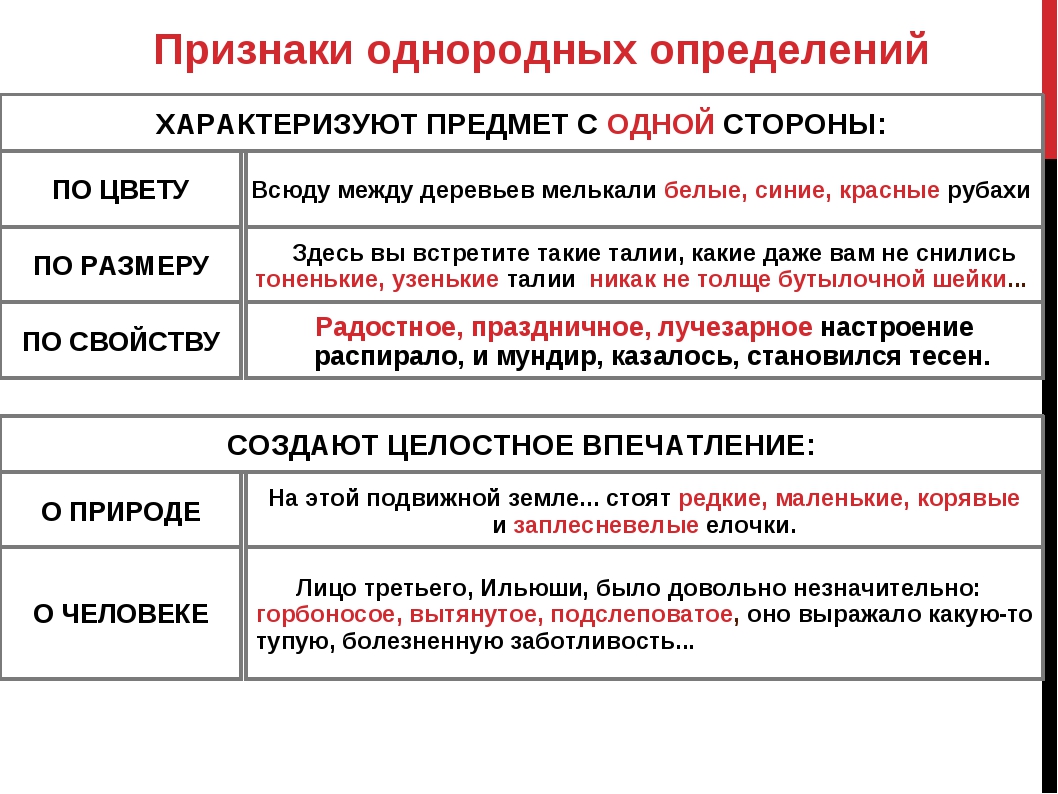1511 (4) 0,1649 (7) 0,92 2,39 / 1,36
σ 0,0115 0,0126 0,91
0,91
D & amp; M ( 1993, всего: 4214, проверка: 1973, прогноз: 2030 )
x¯ 0,1054 (4) 0,1453 (6) 0,72 2,28 / 0,74
0.0222 0,0498 0,44
D&M 11,24

Чтобы выяснить, какие варианты этих двух типов сетей различаются по ценовым характеристикам вне выборки, см. Таблицу 8.2. MSPE вне выборки для различных категорий опционов на основе зрелости и денежности на 1993 год. Соотношения средних и стандартных отклонений сетей с прямой связью с указанием на однородность и без него являются самыми низкими для двух концов диапазона, короткого -срочные опционы «при деньгах» и долгосрочные опционы «при деньгах». Сети прогнозируют с наименьшей разницей для среднесрочных опционов, близких к деньгам. Гарсиа и Генчай (2000) представили доказательства того, что такая разбивка прогнозов по зрелости и денежности подчеркивает, что намек на однородность оказывается наиболее полезным для обобщения вне выборки, когда в обучающей выборке меньше наблюдений. Результаты, представленные за 1993 год, являются репрезентативными для результатов, полученных за другие годы.

ТАБЛИЦА 8.2. Среднеквадратичные ошибки прогноза вне выборки по срокам погашения и денежным средствам.В этой таблице представлено сравнение показателей вневыборочной среднеквадратичной ошибки предсказания (MSPE) нейронной сети с подсказкой однородности (WH) и обычной сети прямого распространения (NN) для опций звонков S&P 500 в Европе разная зрелость и денежность. Средние значения и стандартные отклонения вычисляются по пяти MSPE, полученным из пяти оцененных сетей, начиная с пяти различных начальных значений. Пороговые значения по срокам погашения составляют менее 0,1 (краткосрочный), от 0,1 до 0,2 (среднесрочный) и выше 0. 2 (долгосрочный). Точки отсечения денежности меньше 0,97 (в деньгах), между 0,97 и 1,05 (около денег) и выше 1,05 (в деньгах).

9047 9047 9047 9047 9047 9047 904 902 904 904
MSPE × 10 4 Количество опций Среднее значение Нет подсказки Среднее значение Соотношение St. Короткий
Срок
Выход 128 0.0720 0,0492 0,68 0,0271 0,0149 0,55
Ближайший 473 0,1168 0,0910 0,78 0,0910 0,78 0,2160 0,2323 1,08 0,0834 0,0385 0,46
Средний Выход 198 0. 0292 0,0216 0,74 0,0068 0,0064 0,94
Около 409 0,0511 0,0503 0,91 0,1962 0,1907 0,97 0,0140 0,0176 1,25
Длинный Выход 186 0.0672 0,0512 0,76 0,0131 0,0193 1,47
Ат 337 0,0526 0,0439 0,84 0,0439 0,84 1,5109 0,8149 0,54 1,0780 0,3484 0,32

Ценовая эффективность конкурирующих сетевых моделей с прямой связью показывает, что сети с подсказкой предсказывают лучше, чем сети без подсказки. В этом разделе показано, что повышение точности ценообразования может быть достигнуто за счет использования последствий свойства однородности цен опционов в структуре нейронной сети. Вместо создания обучающей сети, отображающей соотношение S t / K и время до погашения (τ) непосредственно в цене производного финансового инструмента, Гарсия и Генчай (2000) разделили функцию ценообразования на две части: одна контролируется соотношением S t / K , другое — функцией времени до погашения.Результаты показывают, что подсказка однородности всегда уменьшает среднеквадратичную ошибку предсказания вне выборки по сравнению с нейронной сетью с прямой связью без подсказки.

Тест на однородность — вводная статистика

Распределение хи-квадрат

Тест согласия может использоваться для определения того, соответствует ли совокупность заданному распределению, но этого недостаточно для определения того, следуют ли две популяции одному и тому же неизвестному распределению. Другой тест, называемый тестом на однородность, может использоваться, чтобы сделать вывод о том, имеют ли две популяции одинаковое распределение.Чтобы вычислить статистику теста для теста на однородность, выполните ту же процедуру, что и с тестом независимости.

Примечание

Ожидаемое значение для каждой ячейки должно быть не менее пяти, чтобы вы могли использовать этот тест.

Гипотезы
H 0 : Распределение двух популяций одинаково.

H a : Распределение двух популяций не одинаково.

Тестовая статистика Используйте тестовую статистику.Он рассчитывается так же, как и тест на независимость.

степеней свободы ( df ) df = количество столбцов — 1

Требования Все значения в таблице должны быть больше или равны пяти.

Общее использование Сравнение двух популяций. Например: мужчины против женщин, до или после, восток против запада. Переменная является категориальной с более чем двумя возможными значениями ответа.

Распределены ли жилищные условия у студентов мужского и женского пола в колледжах одинаково? Используйте уровень значимости 0.05. Предположим, что 250 случайно выбранных студентов колледжа мужского пола и 300 случайно выбранных студенток колледжа спросили об их жилищных условиях: общежитие, квартира, с родителями, другое. Результаты показаны на (Рисунок). Распределены ли студенты мужского и женского пола по жилищным условиям одинаково?

Распределение жилищных условий для мужчин и женщин колледжей
Общежитие Квартира С родителями Прочие
Мужчины 72 84 49 45
Самки 91 86 88 35

H 0 : Распределение жилищных условий для студентов мужского пола такое же, как распределение жилищных условий для студенток колледжа.

H a : Распределение жилищных условий для студентов колледжей мужского пола не то же самое, что распределение жилищных условий для студенток колледжа.

степеней свободы ( df ):
df = количество столбцов — 1 = 4 — 1 = 3

Распределение для теста:

Рассчитайте статистику теста: χ 2 = 10,1287 (калькулятор или компьютер)

Утверждение вероятности: p -значение = P ( χ 2 > 10.1287) = 0,0175

Нажмите кнопку MATRX и перейдите к EDIT . Наберите 1: [A] . Нажмите 2 ENTER 4 ENTER . Введите значения таблицы по строкам. Нажимайте ENTER после каждого. Нажмите 2nd QUIT . Нажмите STAT и перейдите к TESTS . Стрелка вниз к C: χ2-TEST . Нажмите ENTER . Вы должны увидеть Наблюдаемое: [A] и Ожидаемое: [B] . Стрелка вниз к Рассчитать . Нажмите ENTER .Статистика теста составляет 10,1287, а значение p = 0,0175. Повторите процедуру еще раз, но стрелкой вниз на Нарисуйте вместо , рассчитайте .


Сравните α и p -значение: Поскольку α не указан, предположим, что α = 0,05. p -значение = 0,0175. α > p -знач.

Принять решение: Поскольку α > p -значение, отклонить H 0 . Это означает, что дистрибутивы не совпадают.

Заключение: При уровне значимости 5%, исходя из данных, имеется достаточно доказательств, чтобы сделать вывод о том, что распределение условий жизни для студентов мужского и женского пола неодинаково.

Обратите внимание, что вывод состоит только в том, что распределения не совпадают. Мы не можем использовать тест на однородность, чтобы делать какие-либо выводы о том, чем они различаются.

Попробуйте

Распределение автомобилей между семьями и одинокими одинаково? Используйте уровень значимости 0.05. Предположим, что 100 случайно выбранных семей и 200 случайно выбранных одиноких людей спросили, какой тип автомобиля они водят: спорткар, седан, хэтчбек, грузовик, фургон / внедорожник. Результаты показаны на (Рисунок). Распределение автомобилей между семьями и одинокими одинаково? Тест на уровне значимости 0,05.

Спорт Седан Хэтчбек Грузовик Фургон / Внедорожник
Семья 5 15 35 17 28
Одиночный 45 65 37 46 7

Как до, так и после недавнего землетрясения проводились опросы избирателей, за которых из трех кандидатов они планировали голосовать на предстоящих выборах в городской совет. Изменилось ли что-то после землетрясения? Используйте уровень значимости 0,05. (Рисунок) показывает результаты опроса. Изменилось ли распределение предпочтений избирателей после землетрясения?

Перес Чанг Стивенс
До 167 128 135
После 214 197 225

H 0 : Распределение предпочтений избирателей было одинаковым до и после землетрясения.

H a : Распределение предпочтений избирателей не было одинаковым до и после землетрясения.

степеней свободы ( df ):
df = количество столбцов — 1 = 3 — 1 = 2

Распределение для теста:

Вычислить статистику теста : χ 2 = 3,2603 (калькулятор или компьютер)

Отчет о вероятности: p -значение = P ( χ 2 > 3.2603) = 0,1959

Нажмите кнопку MATRX и перейдите к EDIT . Наберите 1: [A] . Нажмите 2 ENTER 3 ENTER . Введите значения таблицы по строкам. Нажимайте ENTER после каждого. Нажмите 2nd QUIT . Нажмите STAT и перейдите к TESTS . Стрелка вниз к C: χ2-TEST . Нажмите ENTER . Вы должны увидеть Наблюдаемое: [A] и Ожидаемое: [B] . Стрелка вниз к Рассчитать . Нажмите ENTER .Статистический показатель теста составляет 3,2603, а значение p = 0,1959. Повторите процедуру еще раз, но стрелкой вниз на Нарисуйте вместо , рассчитайте .

Сравните α и p -значение: α = 0,05 и p -значение = 0,1959. α < p -знач.

Примите решение: Поскольку α < p -значение, не отклонять H o .

Заключение: При уровне значимости 5%, исходя из данных, недостаточно доказательств, чтобы сделать вывод о том, что распределение предпочтений избирателей не было одинаковым до и после землетрясения.

Попробуйте

Школы Лиги плюща получают много заявлений, но только некоторые из них могут быть приняты. В школах, перечисленных на (Рисунок), принимаются два типа заявлений: обычное и досрочное решение.

Тип приложения принят коричневый Колумбия Корнелл Дартмут Пенн Йель
Обычный 2115 1,792 5,306 1,734 2 685 1,245
Раннее решение 577 627 1,228 444 1,195 761

Мы хотим знать, соответствует ли количество принятых обычных заявок тому же распределению, что и количество принятых ранее заявок.Сформулируйте нулевую и альтернативную гипотезы, степени свободы и статистику теста, нарисуйте график значения p и сделайте вывод о тесте на однородность.

Обзор главы

Чтобы оценить, получены ли два набора данных из одного и того же распределения — что необязательно знать, вы можете применить тест на однородность, который использует распределение хи-квадрат. Нулевая гипотеза для этого теста утверждает, что совокупности двух наборов данных происходят из одного и того же распределения.Тест сравнивает наблюдаемые значения с ожидаемыми, если две популяции следовали одинаковому распределению. Тест правосторонний. Каждое наблюдение или категория ячейки должны иметь ожидаемое значение не менее пяти.

Обзор формулы

Статистика теста на однородность, где: O = наблюдаемые значения
E = ожидаемые значения
i = количество строк в таблице сопряженности данных
j = количество столбцов в таблице сопряженности данных

df = ( i −1) ( j −1) Степени свободы

Учительница математики хочет проверить, одинаково ли распределение результатов тестов в двух ее классах. Какой тест ей следует использовать?

Каковы нулевая и альтернативная гипотезы (рисунок)?

Исследователь рынка хочет узнать, одинаково ли распределение продаж в двух разных магазинах в течение года. Какой тип теста ему следует использовать?

Метеоролог хочет знать, одинаково ли распределение штормов в Восточной и Западной Австралии. Какой тест ей следует использовать?

Какое условие должно быть выполнено для использования теста на однородность?

Все значения в таблице должны быть больше или равны пяти.

Используйте следующую информацию, чтобы ответить на следующие пять упражнений: Распределение рабочего времени у частных врачей и врачей больниц одинаковое? Предположим, что случайным образом выбрана выборка из 100 частных практикующих врачей и 150 врачей в больницах, которым задается вопрос о том, сколько часов в неделю они работают. Результаты показаны на (Рисунок).

.»>
20–30 30–40 40–50 50–60
Частная практика 16 40 38 6
Больница 8 44 59 39

Сформулируйте нулевую и альтернативную гипотезы.

Что такое статистика теста?

Что вы можете сделать на уровне значимости 5%?

Домашнее задание

Для каждой задачи со словом используйте лист решения, чтобы решить задачу проверки гипотезы. Перейдите к (Рисунок), чтобы получить лист решения хи-квадрат. Округлите ожидаемую частоту до двух десятичных знаков.

Психолог заинтересован в том, чтобы проверить, есть ли разница в распределении типов личности для студентов бизнес-специальностей и специальностей социальных наук.Результаты исследования представлены на (Рисунок). Проведите тест на однородность. Проверьте уровень значимости 5%.

Открыть Добросовестный Экстраверт Согласен Невротик
Бизнес 41 52 46 61 58
Социальные науки 72 75 63 80 65
  1. H 0 : Распределение типов личности одинаково для обоих основных направлений
  2. H a : Распределение типов личности неодинаково для обоих основных направлений
  3. df = 4
  4. хи-квадрат с df = 4
    5. Статистика теста
  5. = 3. 01
  6. p -значение = 0,5568
  7. Проверить решение учащегося.
    1. Альфа: 0,05
    2. Решение: Не отвергать нулевую гипотезу.
    3. Причина решения: р -значение> альфа
    4. Заключение. Недостаточно доказательств, чтобы сделать вывод о различии распределения типов личности для студентов, специализирующихся в сфере бизнеса и социальных наук.

Выбирают ли мужчины и женщины разные завтраки? Завтраки, заказанные случайно выбранными мужчинами и женщинами в популярном месте для завтрака, показаны на (Рисунок).Проведите тест на однородность с уровнем значимости 5%.

Французские тосты Блины Вафли Омлеты
Мужчины 47 35 28 53
Женщины 65 59 55 60

Рыбака интересует, совпадает ли распределение рыбы, пойманной в озере Зеленая долина, с распределением рыбы, пойманной в озере Эхо. Из 191 случайно выбранной рыбы, пойманной в озере Грин-Вэлли, 105 были радужной форелью, 27 — другой форелью, 35 — окунем и 24 — сомом. Из 293 случайно выбранных рыб, пойманных в озере Эхо, 115 были радужной форелью, 58 — другой форелью, 67 — окунем и 53 — сомом. Выполните тест на однородность с уровнем значимости 5%.

  1. H 0 : Распределение выловленной рыбы одинаково в озере Зеленая долина и в озере Эхо.
  2. H a : Распределение выловленной рыбы в озере Зеленая долина и в озере Эхо неодинаково.
  3. 3
  4. хи-квадрат с df = 3
  5. 11,75
  6. p -значение = 0,0083
  7. Проверить решение учащегося.
    1. Альфа: 0,05
    2. Решение: отклонить нулевую гипотезу.
    3. Причина решения: р -значение <альфа
    4. Заключение: есть основания полагать, что распределение пойманной рыбы отличается в озере Зеленая долина и в озере Эхо.

В 2007 году в США было 1.По данным Национального центра статистики образования США, 5 миллионов учащихся, обучающихся на дому. На (Рисунок) вы можете видеть, что родители решают обучать своих детей на дому по разным причинам, и некоторые причины оцениваются родителями как более важные, чем другие. Согласно результатам опроса, приведенным в таблице, соответствует ли распределение применимых причин распределению наиболее важной причины? Дайте свою оценку на уровне значимости 5%. Вы ожидали полученного результата?

Причины для обучения на дому Применимая причина (в тысячах респондентов) Самая важная причина (в тысячах респондентов) Всего строк
Забота об окружающей среде в других школах 1,321 309 1,630
Неудовлетворенность академическим обучением в других школах 1,096 258 1,354
Давать религиозные или нравственные наставления 1,257 540 1,797
У ребенка есть особые потребности, кроме физических или психических 315 55 370
Нетрадиционный подход к обучению детей 984 99 1,083
Другие причины (e. г., финансы, путешествия, время с семьей и т. д.) 485 216 701
Итого по столбцу 5,458 1,477 6 935

При изучении энергопотребления нас часто интересует выявление тенденций во времени и их корреляции между разными странами. Информация на (Рисунок) показывает среднее потребление энергии (в килограммах нефтяного эквивалента на душу населения) в США и совместных странах Европейского союза (ЕС) за шестилетний период с 2005 по 2010 год.Приводятся ли значения энергопотребления в этих двух областях из одного и того же распределения? Проведите анализ на уровне значимости 5%.

Год Европейский Союз США Всего строк
2010 3 413 7 164 10,557
2009 3 302 7 057 10 359
2008 3 505 7 488 90 472 10 993
2007 3,537 7,758 11 295
2006 3,595 7 697 11 292
2005 3 613 7 847 11 460
Итого по столбцу 20 965 45011 65 976
  1. H 0 : Распределение среднего потребления энергии в США такое же, как и в Европе в период с 2005 по 2010 год.
  2. H a : Распределение среднего энергопотребления в США не такое, как в Европе в период с 2005 по 2010 год.
  3. df = 4
  4. хи-квадрат с df = 4
    5. Статистика теста
  5. = 2,7434
  6. p -значение = 0,7395
  7. Проверить решение учащегося.
    1. Альфа: 0,05
    2. Решение: Не отвергать нулевую гипотезу.
    3. Причина решения: р -значение> альфа
    4. Заключение: на уровне значимости 5% недостаточно доказательств, чтобы сделать вывод о том, что средние значения энергопотребления в США и ЕС не получены из различных распределений за период с 2005 по 2010 год.

Страховой институт дорожной безопасности ежегодно собирает информацию о безопасности всех типов автомобилей и публикует отчет о лучших вариантах безопасности для всех автомобилей, марок и моделей. (Рисунок) представляет количество автомобилей, получивших награду Top Safety Picks в шести категориях автомобилей за два года — 2009 и 2013. Проанализируйте данные таблицы, чтобы сделать вывод, осталось ли распределение автомобилей, получивших награду Top Safety Picks, на прежнем уровне в период с 2009 по 2013 годы. Получите свои результаты на уровне значимости 5%.

Год \ Тип автомобиля Малый Средний Большой Маленький внедорожник Среднеразмерный внедорожник Большой внедорожник Всего строк
2009 12 22 10 10 27 6 87
2013 31 30 19 11 29 4 124
Итого по столбцу 43 52 29 21 56 10 211

Однородные дифференциальные уравнения

Здесь мы рассмотрим специальный метод решения «Однородных дифференциальных уравнений»

Однородные дифференциальные уравнения

Дифференциальное уравнение первого порядка — это Однородное , когда оно может иметь следующую форму:

dy dx = F ( y x )

Мы можем решить эту проблему, используя разделение переменных, но сначала мы создаем новую переменную v = y x

v = y x , что также равно y = vx

И dy dx = d (vx) dx = v dx dx + x dv dx (в соответствии с Правилом продукта)

Что можно упростить до dy dx = v + x dv dx

Используя y = vx и dy dx = v + x dv dx , мы можем решить дифференциальное уравнение.

Пример покажет, как это все делается:

Пример: Решить

dy dx = x 2 + y 2 xy

Можно ли сделать это в стиле F ( y x )?

Начать с: x 2 + y 2 xy

Отдельные термины: x 2 xy + y 2 xy

Упростить: x y + y x

, величина, обратная первому члену: ( y x ) -1 + y x

Да, у нас есть функция y x .

Итак, вперед:

Начать с: dy dx = ( y x ) -1 + y x

y = vx и dy dx = v + x dv dx : v + x dv dx = v -1 + v

Вычтите v с обеих сторон: x dv dx = v -1

Теперь используйте разделение переменных:

Разделите переменные: v dv = 1 x dx

Поставьте знак интеграла впереди: ∫v dv = ∫ 1 x dx

Интегрировать: v 2 2 = ln (x) + C

Тогда получаем C = ln (k) : v 2 2 = ln (x) + ln (k)

Линия комбайна: v 2 2 = ln (kx)

Упростить: v = ± √ (2 ln (kx))

Теперь подставляем обратно v = y x

Заменитель v = y x : y x = ± √ (2 ln (kx))

Упростить: y = ± x √ (2 ln (kx))

И у нас есть решение.

Положительная часть выглядит так:

Другой пример:

Пример: Решить

dy dx = y (x − y) x 2

Можно ли сделать это в стиле F ( y x )?

Начать с: y (x − y) x 2

Отдельные термины: xy x 2 — y 2 x 2

Упростить: y x — ( y x ) 2

Да! Итак, вперед:

Начать с: dy dx = y x — ( y x ) 2

y = vx и dy dx = v + x dv dx v + x dv dx = v — v 2

Вычтем v с обеих сторон: x dv dx = −v 2

Теперь используйте разделение переменных:

Разделите переменные: — 1 v 2 dv = 1 x dx

Поставьте знак интеграла впереди: ∫− 1 v 2 dv = ∫ 1 x dx

Интегрировать: 1 v = ln (x) + C

Затем получаем C = ln (k) : 1 v = ln (x) + ln (k)

Линия комбайна: 1 v = ln (kx)

Упростить: v = 1 ln (kx)

Теперь подставляем обратно v = y x

Заменитель v = y x : y x = 1 ln (kx)

Упростить: y = x ln (kx)

И у нас есть решение.

Вот несколько примеров значений k:

И последний пример:

Пример: Решить

dy dx = x − y x + y

Можно ли сделать это в стиле F ( y x )?

Начать с: x − y x + y

Разделить на x: x / x − y / x x / x + y / x

Упростить: 1 − y / x 1 + y / x

Да! Итак, вперед:

Начать с: dy dx = 1 − y / x 1 + y / x

y = vx и dy dx = v + x dv dx v + x dv dx = 1 − v 1 + v

Вычтите v с обеих сторон: x dv dx = 1 − v 1 + v — v

Тогда: x dv dx = 1 − v 1 + v — v + v 2 1 + v

Упростить: x dv dx = 1−2v − v 2 1 + v

Теперь используйте разделение переменных:

Разделите переменные: 1 + v 1−2v − v 2 dv = 1 x dx

Поставьте знак интеграла впереди: ∫ 1 + v 1−2v − v 2 dv = ∫ 1 x dx

Интегрировать: — 1 2 ln (1−2v − v 2 ) = ln (x) + C

Тогда получаем C = ln (k) : — 1 2 ln (1−2v − v 2 ) = ln (x) + ln (k)

Линия комбайна: (1−2v − v 2 ) -½ = kx

Квадратное и обратное: 1−2v − v 2 = 1 k 2 x 2

Теперь подставляем обратно v = y x

Заменитель v = y x : 1-2 ( y x ) — ( y x ) 2 = 1 k 2 x 2

Умножить на x 2 : x 2 −2xy − y 2 = 1 k 2

Мы почти у цели. .. хотя приятно выделить y!
Мы можем попытаться разложить на множители x 2 −2xy − y 2 , но сначала мы должны немного изменить порядок:

Изменить знаки: y 2 + 2xy − x 2 = — 1 k 2

Заменить — 1 k 2 на c: y 2 + 2xy − x 2 = c

Добавьте 2x 2 к обеим сторонам: y 2 + 2xy + x 2 = 2x 2 + c

Фактор: (y + x) 2 = 2x 2 + c

Квадратный корень: y + x = ± √ (2x 2 + c)

Вычтем x из обеих частей: y = ± √ (2x 2 + c) — x

И у нас есть решение.

Положительная часть выглядит так:

МакНемар, Маргинальная однородность, знак, тесты Вилкоксона

Непараметрические критерии значимости для двух зависимых выборок используются, когда исследователь хочет изучить коррелированные или согласованные выборки. Это включает в себя эффект «до и после» и соответствующие парные исследования: Тест Макнемара , Тест на предельную однородность, Знак тест и знаковый ранговый тест Уилкоксона. Тест Макнемара — лучший тест для дихотомических переменных с двумя зависимыми выборочными исследованиями. Если категория образца больше двух, подходят тесты на предельную однородность; по сути, они являются расширением теста Макнемара для зависимых выборок. Если выборки зависимых переменных являются непрерывными по своей природе, то критерий знака и критерий Вилкоксона подходят для двух исследований зависимых выборок.

Тест МакНемара: Этот тест также называется критерием симметрии хи-квадрат Макнемара.Тест Макнемара оценивает, произошло ли статистически значимое изменение пропорций дихотомического признака в двух временных точках одной и той же популяции.

В тесте Макнемара используется распределение хи-квадрат, основанное на следующей формуле:

степеней свободы = (строки — 1) (столбцы — 1) = 1

Узнайте, как мы помогаем редактировать главы вашей диссертации

Согласование теоретической основы, сбор статей, обобщение пробелов, формулирование четкой методологии и плана данных, а также описание теоретических и практических последствий вашего исследования — это часть наших комплексных услуг по редактированию диссертаций.

  • Своевременно вносить экспертизу по редактированию диссертаций на главы 1-5.
  • Отслеживайте все изменения, а затем работайте с вами, чтобы писать научные статьи.
  • Постоянная поддержка по ответам комитета, сокращение количества исправлений.

Интерпретация значимости теста Макнемара: Если вычисленное значение теста Макнемара меньше критического значения с использованием степени свободы, то оно не будет значимым. Если значение p , показанное на выходе, меньше желаемого значимого уровня, то разница между двумя зависимыми выборками будет статистически значимой; в противном случае это не будет иметь значения.

Ответов на вопросы:

Изменилась ли доля избирателей до и после пресс-конференции?

Тест на предельную однородность: Тест на предельную однородность во многом похож на тест МакНемара, но в тесте на предельную однородность переменные могут относиться к более чем двум категориям. Это оценивает предельные частоты различных строк и соответствующих столбцов. Тест на предельную однородность интерпретируется как тест Макнемара: если значение p меньше желаемого значимого значения, то средние значения зависимой выборки будут другими, а если значение p больше желаемого уровня, то среднее значение зависимых выборок будет таким же.

Ответов на вопросы:

Изменилось ли соотношение между оценками согласия (низкое, среднее или высокое) после лекции?

Знаковый тест: Знаковый тест используется, когда зависимые выборки упорядочены попарно, где двумерные случайные величины взаимно независимы. Тест знака преобразует регистр переменной в знаки плюс или минус (или связи, если применимо) и проверяет, отличается ли знак плюс от знака минус. Основываясь на результате, мы можем сделать вывод, совпадают ли два средних значения зависимой выборки или разные.Масштаб измерения по крайней мере порядковый в каждой паре. Знаковый тест считается более слабым тестом, потому что он проверяет значение пары ниже или выше медианы и не измеряет разницу пар. Знаковый тест доступен в SPSS: нажмите «меню», выберите «анализ», затем нажмите «непараметрический» и выберите «два связанных образца» и «знаковый тест».

Интерпретация критерия знака: Если значение p теста знака меньше желаемого значения, то два зависимых средних значения будут разными (отклонение нулевой гипотезы).Если значение p критерия знака больше, чем желаемый уровень значимости, то два выборочных средних будут считаться одинаковыми (не отвергая нулевую гипотезу).

Ответов на вопросы:

Какой продукт из газированных напитков (Pepsi или Coke) предпочитает группа из 10 потребителей?

Тест со знаком рангов Уилкоксона: Этот тест, также называемый тестом рангов со знаком согласованных пар Уилкоксона, используется для непрерывных переменных, которые измеряются дважды и время от времени оцениваются, существуют ли статистически значимые различия в баллах. 2.В SPSS знаковый ранговый тест Уилкоксона доступен, выполнив следующие действия: в меню нажмите «анализ», затем выберите «непараметрический» и выберите «две связанные выборки» и «Уилкоксон». Выходные данные SPSS также предоставят информацию о среднем ранге и сумме рангов для положительного и отрицательного знака. Если значение вероятности больше желаемого значения, то значение критерия ранжирования со знаком Уилкоксона не будет значимым (без отклонения нулевой гипотезы). Если это так, мы можем сказать, что средний ранг двух зависимых выборок одинаков.Если значение p меньше установленного значения значимости, то средний ранг двух зависимых выборок будет одинаковым (отклонение нулевой гипотезы)

Ответов на вопросы:

Отличаются ли показатели IQ от детского сада до 1 -го класса в одной и той же группе из 15 учеников?

Ключевые термины и понятия

  • Зависимая выборка: Две коррелированные выборки или исследование до и после выборки являются примерами зависимой выборки.Существует два типа зависимости: (1) до после выборки с одними и теми же людьми в разные моменты времени и (2) согласованное парное исследование с одними и теми же людьми в разные моменты времени.
  • Тип оценки значимости: Асимптотические, точные или методы оценки Монте-Карло используются для проверки значимости критериев Макнемара, предельной однородности, знака и Вилкоксона.
  • Интерфейс SPSS: Эти методы доступны в SPSS, к которым можно получить доступ, выбрав «анализ», затем «непараметрический», а затем две связанные выборки.Обратите внимание, что точные тесты доступны в дополнительном модуле SPSS.

Допущения:

  • Распределение данных: МакНемар, Маргинальная однородность, Знак и Знаковый ранговый тест Уилкоксона — это непараметрические (свободные от распределения) тесты, поэтому мы не предполагаем, что данные имеют нормальное распределение.
  • Два образца: Данные должны быть из двух образцов. Популяция может отличаться для двух выборок.
  • Зависимая выборка: Зависимые выборки должны быть парными или совпадающими.Также известен как образец «до – после».
  • Соответствующий размер выборки: Для теста Макнемара номер корпуса должен быть равен диагонали a-d. Если мы используем биномиальный тест, то он должен быть равен диагонали a + d.

Связанные страницы:

2.6: Гомогенная смесь — Chemistry LibreTexts

Введение

Многие люди наслаждаются чашечкой кофе в какой-то момент в течение дня. Кто-то может пить его черным, а кто-то может добавлять в кофе сливки (или заменитель молока) и сахар.Элитные кофейные напитки можно приобрести в киосках эспрессо (сидячих или проезжающих). Какими бы ни были предпочтения любителя кофе, они хотят, чтобы кофе в начале был таким же, как и в конце напитка. Они не хотят, чтобы компоненты разделялись, но хотят, чтобы их напиток был однородным сверху вниз.

Смеси

Обычная поваренная соль называется хлоридом натрия. Считается веществом , потому что имеет однородный и определенный состав.Все образцы хлорида натрия химически идентичны. Вода также является чистым веществом. Соль легко растворяется в воде, но соленую воду нельзя классифицировать как вещество, поскольку ее состав может варьироваться. Вы можете растворить небольшое или большое количество соли в определенном количестве воды. Смесь представляет собой физическую смесь двух или более компонентов, каждый из которых сохраняет свою индивидуальность и свойства в смеси . Меняется только форма соли, когда она растворяется в воде. Он сохраняет свой состав и свойства.

Гомогенные смеси

Гомогенная смесь представляет собой смесь, состав которой однороден по всей смеси. Вышеописанная соленая вода однородна, поскольку растворенная соль равномерно распределяется по всей пробе соленой воды. Часто легко спутать однородную смесь с чистым веществом, потому что они оба однородны. Разница в том, что состав вещества всегда одинаковый. Количество соли в соленой воде может варьироваться от образца к образцу.Все растворы будут считаться однородными, поскольку растворенный материал присутствует в одном и том же количестве во всем растворе.

Одной из характеристик смесей является то, что они могут быть разделены на компоненты. Поскольку каждая часть смеси не прореагировала с другой частью смеси, идентичность различных материалов не изменилась.

Сводка

  • Гомогенная смесь — это смесь, состав которой однороден по всей смеси.
  • Все решения будут считаться однородными.

Узнать больше

Воспользуйтесь ссылкой ниже, чтобы ответить на следующие вопросы:

1. В чем разница между гетерогенными и гомогенными смесями?

2. Приведите три примера однородных смесей.

3. Опишите, как разделить компоненты однородной смеси.

Авторы и авторство

  • Фонд CK-12 Шэрон Бьюик, Ричард Парсонс, Тереза ​​Форсайт, Шонна Робинсон и Жан Дюпон.

.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *