Для нахождения значения переменной, при котором квадратный многочлен обращается в ноль, используется вспомогательная конструкция, построенная на его коэффициентах и названная дискриминантом. Эта конструкция рассчитывается согласно формуле D равняется j * j — 4 * i * k. Зачем она используется?
- Она говорит, имеются ли действительные результаты.
- Она помогает их высчитать.
Как это значение показывает наличие вещественных корней:
- Если оно положительное, то можно найти два корня в области действительных чисел.
 (1/2).
(1/2). - Нахождение результата в соответствии с формулой (-j +/- d) / (2 * i).
- Подстановка полученного результата в исходное равенство для проверки.
- многочлен раскладывается в разность квадратов при отрицательном свободном члене;
- при положительной константе действительных решений найти нельзя.
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.

- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x
2 − 6x
+ 9 = 0.

- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
- x 2 + 9x = 0;
- x 2 − 16 = 0.
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
- 5x 2 − 14x + 17 = 0
- −x 2 + x + = 0
- x 2 + 0,25x = 0
- x 2 − 8 = 0
- «a » — первый или старший коэффициент;
- «b » — второй коэффициент;
- «c » — свободный член.
- a = −7
- b = −13
- с = 8
- привести квадратное уравнение к общему виду «ax 2 + bx + c = 0 ». То есть в правой части должен остаться только «0 »;
- использовать формулу для корней:
- с помощью факторизации;
- используя формулу для полного квадрата;
- применяя график соответствующей квадратичной функции;
- используя уравнение дискриминанта.
- D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
- D=0: у уравнения всего один корень, и он является действительным числом.

- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.

- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x
2 − 6x
+ 9 = 0.

- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
- x 2 + 9x = 0;
- x 2 − 16 = 0.
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
- x 2 + 9x = 0;
- x 2 − 16 = 0.
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
- Решите квадратные уравнения факторизацией.

- Решите квадратные уравнения методом квадратного корня.
- Решите квадратные уравнения, заполнив квадрат.
- Решите квадратные уравнения, используя квадратичные уравнения. формула.
- Найдите дискриминант квадратного уравнения и используйте это сказать как многие и какой тип решения имеет уравнение.
Некоторые частные случаи
В зависимости от коэффициентов решение может несколько упрощаться. Очевидно, что если коэффициент перед переменной во второй степени равен нулю, то получается линейное равенство. Когда коэффициент перед переменной в первой степени нулевой, то возможны два варианта:
Если свободный член нулевой, то корни будут {0; -j}
Но есть и другие частные случаи, упрощающие нахождение решения.
Приведенное уравнение второй степени
Приведенным именуют такой квадратный трёхчлен, где коэффициент перед старшим членом — единица. Для данной ситуации применима теорема Виета, гласящая, что сумма корней равняется коэффициенту при переменной в первой степени, помноженному на -1, а произведение соответствует константе «k». 2 + 18 * i * j * k * m.
2 + 18 * i * j * k * m.
Допустим, дискриминант превосходит ноль . Это значит, что имеется три корня в области действительных чисел. При нулевом есть кратные решения. Если D
Видео
Наше видео подробно расскажет о вычислении дискриминанта.
Не получили ответ на свой вопрос? Предложите авторам тему.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Виды квадратных уравнений
Что такое квадратное уравнение? Как оно выглядит? В термине
Говоря математическим языком, квадратное уравнение — это уравнение вида:
Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:
b и c – совсем любые, а а – любое, кроме нуля. Например:
Здесь а =1; b = 3; c = -4
Здесь а =2; b = -0,5; c = 2,2
Здесь а =-3; b = 6; c = -18
Ну, вы поняли…
В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.
Такие квадратные уравнения называются полными.
А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:
5х 2 -25 = 0,
2х 2 -6х=0,
-х 2 +4х=0
И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:
2х 2 =0,
-0,3х 2 =0
Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.
Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.
Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…
Вот и все главные виды квадратных уравнений. Полные и неполные.
Решение квадратных уравнений.
Решение полных квадратных уравнений.
Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:
Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а , b и c .
Формула для нахождения корней квадратного уравнения выглядит так:
Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:
Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:
а =1; b = 3; c = -4. Вот и записываем:
Пример практически решён:
Это ответ.
Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !
Предположим, надо вот такой примерчик решить:
Здесь a = -6; b = -5; c = -1
Допустим, вы знаете, что ответы у вас редко с первого раза получаются.
Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:
А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:
Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:
Узнали?) Да! Это неполные квадратные уравнения .
Решение неполных квадратных уравнений.
Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .
Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё.
Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.
И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .
Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку,

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:
Остаётся корень извлечь из 9, и всё. Получится:
Тоже два корня. х 1 = -3 , х 2 = 3 .
Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…
Дискриминант. Формула дискриминанта.
Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:
Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:
Обычно дискриминант обозначается буквой D . Формула дискриминанта:
D = b 2 — 4ac
И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.
Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю.
3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.
Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.
Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)
Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?
А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности. … За которые потом бывает больно и обидно…
… За которые потом бывает больно и обидно…
Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:
Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:
И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:
А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.
Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.
Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.
Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.
Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…
При работе с дробями ошибки, почему-то так и лезут…
Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.
Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:
Вот и всё! Решать – одно удовольствие!
Итак, подытожим тему.
Практические советы:
1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .
2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.
3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.
4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!
Теперь можно и порешать.)
Решить уравнения:
8х 2 — 6x + 1 = 0
х 2 + 3x + 8 = 0
х 2 — 4x + 4 = 0
(х+1) 2 + x + 1 = (x+1)(x+2)
Ответы (в беспорядке):
х 1 = 0
х 2 = 5
х 1,2 = 2
х 1 = 2
х 2 = -0,5
х — любое число
х 1 = -3
х 2 = 3
решений нет
х 1 = 0,25
х 2 = 0,5
Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.
Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.
Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Квадратное уравнение – решается просто! *Далее в тексте «КУ».
Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:
Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:
Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.
Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим! Содержание статьи:
Квадратное уравнение – это уравнение вида:
где коэффициенты a, b и с произвольные числа, при чём a≠0.
В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:
1. Имеют два корня.
2. *Имеют только один корень.
3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней
Как вычисляются корни? Просто!
Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:
Формулы корней имеют следующий вид:
*Эти формулы нужно знать наизусть.
Можно сразу записывать и решать:
Пример:
1. Если D > 0, то уравнение имеет два корня.
2. Если D = 0, то уравнение имеет один корень.
3. Если D
Давайте рассмотрим уравнение:
По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…
Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:
Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:
х 1 = 3 х 2 = 3
Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.
Теперь следующий пример:
Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.
Вот и весь процесс решения.
Квадратичная функция.
Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).
Это функция вида:
где х и у — переменные
a, b, с – заданные числа, при чём a ≠ 0
Графиком является парабола:
То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть
статью у Инны Фельдман.
Подробно о квадратичной функции можете посмотреть
статью у Инны Фельдман.
Рассмотрим примеры:
Пример 1: Решить 2x 2 +8 x –192=0
а=2 b=8 c= –192
D = b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600
Ответ: х 1 = 8 х 2 = –12
*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.
Пример 2: Решить x 2 –22 x+121 = 0
а=1 b=–22 c=121
D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0
Получили, что х 1 = 11 и х 2 = 11
В ответе допустимо записать х = 11.
Ответ: х = 11
Пример 3: Решить x 2 –8x+72 = 0
а=1 b= –8 c=72
D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224
Дискриминант отрицательный, решения в действительных числах нет.
Ответ: решения нет
Дискриминант отрицательный. Решение есть!
Решение есть!
Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.
Понятие комплексного числа.
Немного теории.
Комплексным числом z называется число вида
z = a + bi
где a и b – действительные числа, i – так называемая мнимая единица.
a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение.
Мнимая единица равна корню из минус единицы:
Теперь рассмотрим уравнение:
Получили два сопряжённых корня.
Неполное квадратное уравнение.
Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.
Случай 1. Коэффициент b = 0.
Уравнение приобретает вид:
Преобразуем:
Пример:
4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2
Случай 2. Коэффициент с = 0.
Коэффициент с = 0.
Уравнение приобретает вид:
Преобразуем, раскладываем на множители:
*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.
Пример:
9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0
x 1 = 0 x 2 = 5
Случай 3. Коэффициенты b = 0 и c = 0.
Здесь понятно, что решением уравнения всегда будет х = 0.
Полезные свойства и закономерности коэффициентов.
Есть свойства, которые позволяют решить уравнения с большими коэффициентами.
а x 2 + bx + c =0 выполняется равенство
a + b + с = 0, то
— если для коэффициентов уравнения а x 2 + bx + c =0 выполняется равенство
a + с = b , то
Данные свойства помогают решить определённого вида уравнения.
Пример 1: 5001 x 2 –4995 x – 6=0
Сумма коэффициентов равна 5001+(– 4995)+(– 6) = 0, значит
Пример 2: 2501 x 2 +2507 x +6=0
Выполняется равенство a + с = b , значит
Закономерности коэффициентов.
1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны
аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.
Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.
х 1 = –6 х 2 = –1/6.
2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны
аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.
Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.
х 1 = 15 х 2 = 1/15.
3. Если в уравнении ax 2 + bx – c = 0 коэффициент «b» равен (a 2 – 1), а коэффициент «c» численно равен коэффициенту «a» , то его корни равны
аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.
Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.
х 1 = – 17 х 2 = 1/17.
4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны
аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.
Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.
х 1 = 10 х 2 = – 1/10
Теорема Виета.
Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.
45 = 1∙45 45 = 3∙15 45 = 5∙9.
В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.
Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.
СПОСОБ ПЕРЕБРОСКИ
При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Если а ± b+c ≠ 0, то используется прием переброски, например:
2х 2 – 11х+ 5 = 0 (1) => х 2 – 11х+ 10 = 0 (2)
По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1
Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим
х 1 = 5 х 2 = 0,5.
Каково обоснование? Посмотрите что происходит.
Дискриминанты уравнений (1) и (2) равны:
Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:
У второго (изменённого) корни получаются в 2 раза больше.
Потому результат и делим на 2.
*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.
Ответ: х 1 = 5 х 2 = 0,5
Кв. ур-ие и ЕГЭ.
О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).
Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).
Что стоит отметить!
1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:
15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.
Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).
2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c
/a
) ≥ 0. Достаточно выразить величину x
2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Как вычисляется корень если дискриминант равен нулю. Как решать квадратные уравнения
», то есть
уравнения первой степени. В этом уроке мы разберем, что называют квадратным
уравнением и как его решать.
В этом уроке мы разберем, что называют квадратным
уравнением и как его решать.
Что называют квадратным уравнением
Важно!
Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.
Если максимальная степень, в которой стоит неизвестное — «2 », значит, перед вами квадратное уравнение.
Примеры квадратных уравнений
Важно! Общий вид квадратного уравнения выглядит так:
A x 2 + b x + c = 0
«a », «b » и «c » — заданные числа.Чтобы найти «a », «b » и «c » нужно сравнить свое уравнение с общим видом квадратного уравнения «ax 2 + bx + c = 0 ».
Давайте потренируемся определять коэффициенты «a », «b » и «c » в квадратных уравнениях.
| Уравнение | Коэффициенты |
|---|---|
| x 2 − 8 = 0 |
Как решать квадратные уравнения
В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней .
Запомните!
Чтобы решить квадратное уравнение нужно:
Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.
X 2 − 3x − 4 = 0
Уравнение « x 2 − 3x − 4 = 0 » уже приведено к общему виду «ax 2 + bx + c = 0 » и не требует дополнительных упрощений. Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения .
Определим коэффициенты «a », «b » и «c » для этого уравнения.
x 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
С её помощью решается любое квадратное уравнение.
В формуле «x 1;2 =
» часто заменяют подкоренное выражение
«b 2 − 4ac
» на букву «D
» и называют
дискриминантом
. Более подробно понятие дискриминанта рассматривается в уроке
«Что такое дискриминант ».
Рассмотрим другой пример квадратного уравнения.
x 2 + 9 + x = 7x
В данном виде определить коэффициенты «a », «b » и «c » довольно сложно. Давайте вначале приведем уравнение к общему виду «ax 2 + bx + c = 0 ».
X 2 + 9 + x = 7x
x 2 + 9 + x − 7x = 0
x 2 + 9 − 6x = 0
x 2 − 6x + 9 = 0
Теперь можно использовать формулу для корней.
X 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
x =
x = 3
Ответ: x = 3
Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем оказывается отрицательное число.
Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом «через дискриминант». Примеры использования полученных знаний также даются в статье.
О каких уравнениях пойдет речь?
На рисунке ниже изображена формула, в которой x — неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.
Каждый из этих символов называется коэффициентом. Как можно заметить, число «a» стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.
Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.
Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса — это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.
Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.
Способы решения уравнений второго порядка
Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:
Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким. Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта — это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка.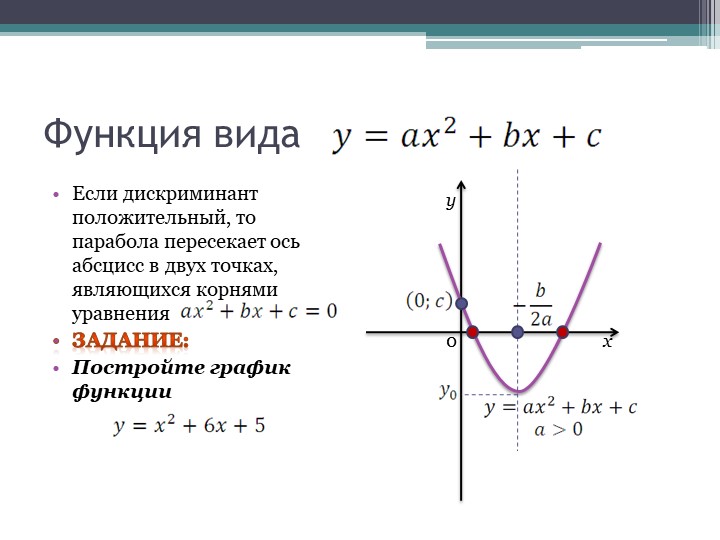 Поэтому в статье рассмотрим только его.
Поэтому в статье рассмотрим только его.
Формула для получения корней уравнения
Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).
Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.
В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).
В примере выше a = 6, b=4, c=-8. Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак «-«, то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.
Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.
Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак «±»). Для этого в него достаточно подставить коэффициенты b, c, и a.
Понятие о дискриминанте
В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.
Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:
Задача на определение дискриминанта
Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.
Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.
Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.
Пример неравенства через дискриминант
Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.
В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.
Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.
Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.
Пример решения уравнения
Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.
В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.
Геометрическая задача
Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.
У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.
Пусть полоса будет иметь толщину x м, тогда площадь ткани по длинной стороне одеяла составит (5+2*x)*x, а поскольку длинных сторон 2, то имеем: 2*x*(5+2*x). По короткой стороне площадь пришитой ткани составит 4*x, так как этих сторон 2, то получаем значение 8*x. Отметим, что к длинной стороне было добавлено значение 2*x, поскольку длина одеяла увеличилась на это число. Общая пришитая к одеялу площадь ткани равна 10 м². Поэтому получаем равенство: 2*x*(5+2*x) + 8*x = 10 => 4*x²+18*x-10 = 0.
Для этого примера дискриминант равен: D = 18²-4*4*(-10) = 484. Его корень равен 22. Воспользовавшись формулой, находим искомые корни: x = (-18±22)/(2*4) = (-5; 0,5). Очевидно, что из двух корней подходит по условию задачи только число 0,5.
Таким образом, полоса из ткани, которую пришьет Боб к своему одеялу, будет иметь ширину 50 см. 2 + b*x + c = 0
,где x
—
переменная, a,b,c
– константы; a0
. Задача состоит в отыскании корней уравнения.
2 + b*x + c = 0
,где x
—
переменная, a,b,c
– константы; a0
. Задача состоит в отыскании корней уравнения.
Геометрический смысл квадратного уравнения
Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х)
. Из этого следует, что есть три возможных случая:
1)
парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).
2) парабола имеет одну точку пересечения с осью Ох . Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).
3)
Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс. 2
и осуществим преобразование
2
и осуществим преобразование
Отсюда находим
Формула дискриминанта и корней квадратного уравнения
Дискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0 При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле
Теорема Виета
Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p
, взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q
. Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а
отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета. 2+x-6=0
.
2+x-6=0
.
Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения
С второго условия получаем, что произведение должно быть равно -6
. Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2}
. С учетом первого условия вторую пару решений отвергаем.
Корни уравнения равны
Задача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см 2 .
Решение:
Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х
– большую сторону, тогда 18-x
меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
х(18-х)=77;
или
х 2 -18х+77=0.
Найдем дискриминант уравнения
Вычисляем корни уравнения
Если х=11
,
то 18-х=7
,
наоборот тоже справедливо (если х=7
, то 21-х=9
).
Задача 6. Разложить квадратное 10x 2 -11x+3=0 уравнения на множители.
Решение:
Вычислим корни уравнения, для этого находим дискриминант
Подставляем найденное значение в формулу корней и вычисляем
Применяем формулу разложения квадратного уравнения по корнями
Раскрыв скобки получим тождество. 2+(2а+6)х-3а-9=0
имеет более одного корня?
2+(2а+6)х-3а-9=0
имеет более одного корня?
Решение:
Рассмотрим сначала особые точки, ими будут значения а=0
и а=-3
. При а=0
уравнение упростится до вида 6х-9=0; х=3/2
и будет один корень. При а= -3
получим тождество 0=0
.
Вычислим дискриминант
и найдем значения а
при котором оно положительно
С первого условия получим а>3
. Для второго находим дискриминант и корни уравнения
Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0
получим 3>0
.
Итак, за пределами промежутка (-3;1/3)
функция отрицательная. Не стоит забывать о точке а=0
,
которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
В результате получим два интервала, которые удовлетворяют условию задачи
Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках. 2–4*a*c.
2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D)
:
D>0
– уравнение имеет 2
различных действительных корня;
D=0
— уравнение имеет 1
корень (2
совпадающих корня):
D Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.
.
Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле
Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни
До 4
уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6,
следовательно корнями могут быть значения (1, 6)
и (2, 3)
или пары с противоположным знаком. Сумма корней равна 7
(коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».
Давайте попробуем разобраться,
что описывает дискриминант?В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0)
,
Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0)
,
или парабола ветвями вниз (a
Вершина параболы лежит посередине между корнями
Физический смысл дискриминанта:
Если дискриминант больше нуля (D>0)
парабола имеет две точки пересечения с осью Ox
.
Если дискриминант равен нулю (D=0)
то парабола в вершине касается оси абсцисс.
И последний случай, когда дискриминант меньше нуля (D
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c
/a
) ≥ 0. Достаточно выразить величину x
2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Решение квадратных уравнений если дискриминант меньше нуля. Дискриминант квадратного уравнения
Задачи на квадратное уравнение изучаются и в школьной программе и в ВУЗах. 2 + b*x + c = 0
,где x
—
переменная, a,b,c
– константы; a0
. Задача состоит в отыскании корней уравнения.
2 + b*x + c = 0
,где x
—
переменная, a,b,c
– константы; a0
. Задача состоит в отыскании корней уравнения.
Геометрический смысл квадратного уравнения
Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х)
. Из этого следует, что есть три возможных случая:
1)
парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).
2) парабола имеет одну точку пересечения с осью Ох . Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).
3)
Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс. 2
и осуществим преобразование
2
и осуществим преобразование
Отсюда находим
Формула дискриминанта и корней квадратного уравнения
Дискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0 При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле
Теорема Виета
Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p
, взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q
. Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а
отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета. 2+x-6=0
.
2+x-6=0
.
Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения
С второго условия получаем, что произведение должно быть равно -6
. Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2}
. С учетом первого условия вторую пару решений отвергаем.
Корни уравнения равны
Задача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см 2 .
Решение:
Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х
– большую сторону, тогда 18-x
меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
х(18-х)=77;
или
х 2 -18х+77=0.
Найдем дискриминант уравнения
Вычисляем корни уравнения
Если х=11
,
то 18-х=7
,
наоборот тоже справедливо (если х=7
, то 21-х=9
).
Задача 6. Разложить квадратное 10x 2 -11x+3=0 уравнения на множители.
Решение:
Вычислим корни уравнения, для этого находим дискриминант
Подставляем найденное значение в формулу корней и вычисляем
Применяем формулу разложения квадратного уравнения по корнями
Раскрыв скобки получим тождество. 2+(2а+6)х-3а-9=0
имеет более одного корня?
2+(2а+6)х-3а-9=0
имеет более одного корня?
Решение:
Рассмотрим сначала особые точки, ими будут значения а=0
и а=-3
. При а=0
уравнение упростится до вида 6х-9=0; х=3/2
и будет один корень. При а= -3
получим тождество 0=0
.
Вычислим дискриминант
и найдем значения а
при котором оно положительно
С первого условия получим а>3
. Для второго находим дискриминант и корни уравнения
Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0
получим 3>0
.
Итак, за пределами промежутка (-3;1/3)
функция отрицательная. Не стоит забывать о точке а=0
,
которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
В результате получим два интервала, которые удовлетворяют условию задачи
Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках.
Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».
Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.
D = b 2 – 4ас.
В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.
Если дискриминант отрицательное число (D
Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),
тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .
Например. Решить уравнение х 2 – 4х + 4= 0.
D = 4 2 – 4 · 4 = 0
x = (- (-4))/2 = 2
Ответ: 2.
Решить уравнение 2х 2 + х + 3 = 0.
D = 1 2 – 4 · 2 · 3 = – 23
Ответ: корней нет .
Решить уравнение 2х 2 + 5х – 7 = 0 .
D = 5 2 – 4 · 2 · (–7) = 81
х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5
х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1
Ответ: – 3,5 ; 1 .
Итак представим решение полных квадратных уравнений схемой на рисунке1.
По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида
ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что
а = 1, b = 3 и с = 2. Тогда
D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).
Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.
При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.
Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .
На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.
Пример. Решить уравнение
3х 2 + 6х – 6 = 0.
Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.
D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108
√D = √108 = √(36 · 3) = 6√3
х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3
х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3
Ответ: –1 – √3; –1 + √3
Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27
√(D 1) = √27 = √(9 · 3) = 3√3
х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3
х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3
Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.
D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12
√(D 2) = √12 = √(4 · 3) = 2√3
х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3
х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3
Ответ: –1 – √3; –1 + √3.
Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D
= 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
Наконец, если D
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:
Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Квадратное уравнение – решается просто! *Далее в тексте «КУ». Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:
Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.
Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.
Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим! Содержание статьи:
Квадратное уравнение – это уравнение вида:
где коэффициенты a, b и с произвольные числа, при чём a≠0.
В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:
1. Имеют два корня.
2. *Имеют только один корень.
3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней
Как вычисляются корни? Просто!
Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:
Под этим «страшным» словом лежит вполне простая формула:
Формулы корней имеют следующий вид:
*Эти формулы нужно знать наизусть.
Можно сразу записывать и решать:
Пример:
1. Если D > 0, то уравнение имеет два корня.
2. Если D = 0, то уравнение имеет один корень.
3. Если D
Давайте рассмотрим уравнение:
По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…
Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:
х 1 = 3 х 2 = 3
Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.
Теперь следующий пример:
Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.
Вот и весь процесс решения.
Квадратичная функция.
Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).
Это функция вида:
где х и у — переменные
a, b, с – заданные числа, при чём a ≠ 0
Графиком является парабола:
То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть статью у Инны Фельдман.
Рассмотрим примеры:
Пример 1: Решить 2x 2 +8 x –192=0
а=2 b=8 c= –192
D = b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600
Ответ: х 1 = 8 х 2 = –12
*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.
Вычисления будут проще.
Пример 2: Решить x 2 –22 x+121 = 0
а=1 b=–22 c=121
D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0
Получили, что х 1 = 11 и х 2 = 11
В ответе допустимо записать х = 11.
Ответ: х = 11
Пример 3: Решить x 2 –8x+72 = 0
а=1 b= –8 c=72
D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224
Дискриминант отрицательный, решения в действительных числах нет.
Ответ: решения нет
Дискриминант отрицательный. Решение есть!
Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.
Понятие комплексного числа.
Немного теории.
Комплексным числом z называется число вида
z = a + bi
где a и b – действительные числа, i – так называемая мнимая единица.
a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение.
Мнимая единица равна корню из минус единицы:
Теперь рассмотрим уравнение:
Получили два сопряжённых корня.
Неполное квадратное уравнение.
Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.
Случай 1. Коэффициент b = 0.
Уравнение приобретает вид:
Преобразуем:
Пример:
4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2
Случай 2. Коэффициент с = 0.
Уравнение приобретает вид:
Преобразуем, раскладываем на множители:
*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.
Пример:
9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0
x 1 = 0 x 2 = 5
Случай 3. Коэффициенты b = 0 и c = 0.
Здесь понятно, что решением уравнения всегда будет х = 0.
Полезные свойства и закономерности коэффициентов.
Есть свойства, которые позволяют решить уравнения с большими коэффициентами.
а x 2 + bx + c =0 выполняется равенство
a + b + с = 0, то
— если для коэффициентов уравнения а x 2 + bx + c =0 выполняется равенство
a + с = b , то
Данные свойства помогают решить определённого вида уравнения.
Пример 1: 5001 x 2 –4995 x – 6=0
Сумма коэффициентов равна 5001+(– 4995)+(– 6) = 0, значит
Пример 2: 2501 x 2 +2507 x +6=0
Выполняется равенство a + с = b , значит
Закономерности коэффициентов.
1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны
аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.
Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.
х 1 = –6 х 2 = –1/6.
2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны
аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.
Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.
х 1 = 15 х 2 = 1/15.
3. Если в уравнении ax 2 + bx – c = 0 коэффициент «b» равен (a 2 – 1), а коэффициент «c» численно равен коэффициенту «a» , то его корни равны
аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.
Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.
х 1 = – 17 х 2 = 1/17.
4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны
аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.
Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.
х 1 = 10 х 2 = – 1/10
Теорема Виета.
Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.
45 = 1∙45 45 = 3∙15 45 = 5∙9.
В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.
Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.
СПОСОБ ПЕРЕБРОСКИ
При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Если а ± b+c ≠ 0, то используется прием переброски, например:
2х 2 – 11х+ 5 = 0 (1) => х 2 – 11х+ 10 = 0 (2)
По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1
Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим
х 1
= 5 х 2
=
0,5.
Каково обоснование? Посмотрите что происходит.
Дискриминанты уравнений (1) и (2) равны:
Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:
У второго (изменённого) корни получаются в 2 раза больше.
Потому результат и делим на 2.
*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.
Ответ: х 1 = 5 х 2 = 0,5
Кв. ур-ие и ЕГЭ.
О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).
Что стоит отметить!
1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:
15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.
Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).
2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.
Поработаем с квадратными уравнениями . Это очень популярные уравнения! В самом общем виде квадратное уравнение выглядит так:
Например:
Здесь а =1; b = 3; c = -4
Здесь а =2; b = -0,5; c = 2,2
Здесь а =-3; b = 6; c = -18
Ну, вы поняли…
Как решать квадратные уравнения? Если перед вами квадратное уравнение именно в таком виде, дальше уже всё просто. Вспоминаем волшебное слово дискриминант . Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении. Итак, формула для нахождения корней квадратного уравнения выглядит так:
Выражение под знаком корня – и есть тот самый дискриминант . Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в это формулу и считаем. Подставляем со своими знаками! Например, для первого уравнения а =1; b = 3; c = -4. Вот и записываем:
Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в это формулу и считаем. Подставляем со своими знаками! Например, для первого уравнения а =1; b = 3; c = -4. Вот и записываем:
Пример практически решён:
Вот и всё.
Какие случаи возможны при использовании этой формулы? Всего три случая.
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых . Но это играет роль в неравенствах, там мы поподробнее вопрос изучим.
3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.
Ну и ладно. Это означает, что решений нет.
Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !
Предположим, надо вот такой примерчик решить:
Здесь a = -6; b = -5; c = -1
Допустим, вы знаете, что ответы у вас редко с первого раза получаются.
Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:
Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Итак, как решать квадратные уравнения через дискриминант мы вспомнили. Или научились, что тоже неплохо. Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?
Однако частенько квадратные уравнения выглядят слегка иначе. Например, вот так:
Это неполные квадратные уравнения . Их тоже можно решать через дискриминант. Надо только правильно сообразить, чему здесь равняются a, b и с .
Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !
Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !
Но неполные квадратные уравнения можно решать гораздо проще. Безо всякого дискриминанта. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.
И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х = 0 , или х = 4
Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем через дискриминант.
Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:
Остаётся корень извлечь из 9, и всё. Получится:
Тоже два корня. х = +3 и х = -3 .
х = +3 и х = -3 .
Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…
А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…
Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:
Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:
И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:
Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:
А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.
Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку. Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.
Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в предыдущем разделе. При работе с дробями ошибки, почему-то так и лезут…
Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.
Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:
Вот и всё! Решать – одно удовольствие!
Итак, подытожим тему.
Практические советы:
1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .
2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.
3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.
4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!
Дробные уравнения. ОДЗ.
Продолжаем осваивать уравнения. Мы уже в курсе, как работать с линейными уравнениями и квадратными. Остался последний вид – дробные уравнения . Или их ещё называют гораздо солиднее – дробные рациональные уравнения . Это одно и то же.
Дробные уравнения.
Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дроби, а дроби, у которых есть неизвестное в знаменателе . Хотя бы в одном. Например:
Напомню, если в знаменателях только числа , это линейные уравнения.
Как решать дробные уравнения ? Прежде всего – избавиться от дробей! После этого уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы знаем, что делать… В некоторых случаях оно может превратиться в тождество, типа 5=5 или неверное выражение, типа 7=2.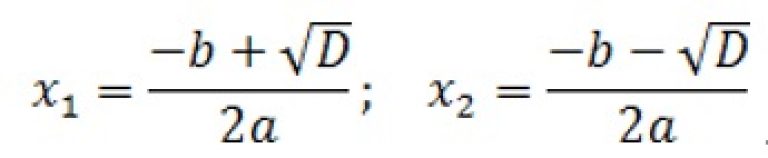 Но это редко случается. Ниже я про это упомяну.
Но это редко случается. Ниже я про это упомяну.
Но как избавиться от дробей!? Очень просто. Применяя всё те же тождественные преобразования.
Нам надо умножить всё уравнение на одно и то же выражение. Так, чтобы все знаменатели посокращались! Всё сразу станет проще. Поясняю на примере. Пусть нам требуется решить уравнение:
Как учили в младших классах? Переносим все в одну сторону, приводим к общему знаменателю и т.д. Забудьте, как страшный сон! Так нужно делать, когда вы складываете или вычитаете дробные выражения. Или работаете с неравенствами. А в уравнениях мы сразу умножаем обе части на выражение, которое даст нам возможность сократить все знаменатели (т.е., в сущности, на общий знаменатель). И какое же это выражение?
В левой части для сокращения знаменателя требуется умножение на х+2 . А в правой требуется умножение на 2. Значит, уравнение надо умножать на 2(х+2) . Умножаем:
Это обычное умножение дробей, но распишу подробно:
Обратите внимание, я пока не раскрываю скобку (х + 2) ! Так, целиком, её и пишу:
В левой части сокращается целиком (х+2) , а в правой 2. Что и требовалось! После сокращения получаем линейное уравнение:
Что и требовалось! После сокращения получаем линейное уравнение:
А это уравнение уже решит всякий! х = 2 .
Решим ещё один пример, чуть посложнее:
Если вспомнить, что 3 = 3/1, а 2х = 2х/ 1, можно записать:
И опять избавляемся от того, что нам не очень нравится – от дробей.
Видим, что для сокращения знаменателя с иксом, надо умножить дробь на (х – 2) . А единицы нам не помеха. Ну и умножаем. Всю левую часть и всю правую часть:
Опять скобки (х – 2) я не раскрываю. Работаю со скобкой в целом, как будто это одно число! Так надо делать всегда, иначе ничего не сократится.
С чувством глубокого удовлетворения сокращаем (х – 2) и получаем уравнение безо всяких дробей, в линеечку!
А вот теперь уже раскрываем скобки:
Приводим подобные, переносим всё в левую часть и получаем:
Классическое квадратное уравнение. Но минус впереди – нехорош. От него можно всегда избавиться, умножением или делением на -1. Но если присмотреться к примеру, можно заметить, что лучше всего это уравнение разделить на -2! Одним махом и минус исчезнет, и коэффициенты посимпатичнее станут! Делим на -2. В левой части – почленно, а в правой – просто ноль делим на -2, ноль и получим:
От него можно всегда избавиться, умножением или делением на -1. Но если присмотреться к примеру, можно заметить, что лучше всего это уравнение разделить на -2! Одним махом и минус исчезнет, и коэффициенты посимпатичнее станут! Делим на -2. В левой части – почленно, а в правой – просто ноль делим на -2, ноль и получим:
Решаем через дискриминант и проверяем по теореме Виета. Получаем х = 1 и х = 3 . Два корня.
Как видим, в первом случае уравнение после преобразования стало линейным, а здесь – квадратным. Бывает так, что после избавления от дробей, все иксы сокращаются. Остаётся что-нибудь, типа 5=5. Это означает, что икс может быть любым . Каким бы он не был, всё равно сократится. И получится чистая правда, 5=5. Но, после избавления от дробей, может получиться и совсем неправда, типа 2=7. А это означает, что решений нет ! При любом иксе получается неправда.
Осознали главный способ решения дробных уравнений ? Он прост и логичен. Мы меняем исходное выражение так, чтобы исчезло всё то, что нам не нравится. Или мешает. В данном случае это – дроби. Точно так же мы будем поступать и со всякими сложными примерами с логарифмами, синусами и прочими ужасами. Мы всегда будем от всего этого избавляться.
Мы меняем исходное выражение так, чтобы исчезло всё то, что нам не нравится. Или мешает. В данном случае это – дроби. Точно так же мы будем поступать и со всякими сложными примерами с логарифмами, синусами и прочими ужасами. Мы всегда будем от всего этого избавляться.
Однако менять исходное выражение в нужную нам сторону надо по правилам , да… Освоение которых и есть подготовка к ЕГЭ по математике. Вот и осваиваем.
Сейчас мы с вами научимся обходить одну из главных засад на ЕГЭ ! Но для начала посмотрим, попадаете вы в неё, или нет?
Разберём простой пример:
Дело уже знакомое, умножаем обе части на (х – 2) , получаем:
Напоминаю, со скобками (х – 2) работаем как с одним, цельным выражением!
Здесь я уже не писал единичку в знаменателях, несолидно… И скобки в знаменателях рисовать не стал, там кроме х – 2 ничего нет, можно и не рисовать. Сокращаем:
Раскрываем скобки, переносим всё влево, приводим подобные:
Решаем, проверяем, получаем два корня. х = 2 и х = 3 . Отлично.
х = 2 и х = 3 . Отлично.
Предположим в задании сказано записать корень, или их сумму, если корней больше одного. Что писать будем?
Если решите, что ответ 5, – вы попали в засаду . И задание вам не засчитают. Зря трудились… Правильный ответ 3.
В чём дело?! А вы попробуйте проверку сделать. Подставить значения неизвестного в исходный пример. И если при х = 3 у нас всё чудненько срастётся, получим 9 = 9, то при х = 2 получится деление на ноль! Чего делать нельзя категорически. Значит х = 2 решением не является, и в ответе никак не учитывается. Это так называемый посторонний или лишний корень. Мы его просто отбрасываем. Окончательный корень один. х = 3 .
Как так?! – слышу возмущённые возгласы. Нас учили, что уравнение можно умножать на выражение! Это тождественное преобразование!
Да, тождественное. При маленьком условии – выражение, на которое умножаем (делим) – отлично от нуля . А х – 2 при х = 2 равно нулю! Так что всё честно.
И что теперь делать?! Не умножать на выражение? Каждый раз проверку делать? Опять непонятно!
Спокойно! Без паники!
В этой тяжелой ситуации нас спасут три магических буквы. Я знаю, о чем вы подумали. Правильно! Это ОДЗ . Область Допустимых Значений.
БЕСПЛАТНЫЙ МАДЖОНГ — играть онлайн бесплатно
Играть онлайн бесплатно
Под игрой имеется описание, инструкции и правила, а также тематические ссылки на похожие материалы — рекомендуем ознакомиться.
Как играть — правила и описание
Классическое шанхайское исполнение с изображениями бамбуков, ванов, кругов, ветров, драконов, цветов и сезонов на поверхностях 144 костяшек, выкладываемых пирамидой-черепахой. Возможность играть на ПК, планшете или смартфоне. Все вышеперечисленное делает этот бесплатный маджонг по истине универсальным.
Игрок должен полностью очистить стол от костяшек, разобрав пирамиду. Извлекать из нее кости следует парами. Два одинаковых изображения или картинки одной из специальных подгрупп: цветы и времена года (сезоны) — дают основания считать несущие их кости порой. В игре предусмотрена следующая система подсчета очков. Самые дорогие пары — это времена года, множитель по таким костяшкам равен 14-ти. Подешевле — цветы с множителем 12, далее идут драконы и ветра с коэффициентами 10 и 8 соответственно, за ними бамбуки, круги и ваны (6, 4, 2). Важнейшим и существенным условием для уборки пары из пирамиды является открытость обоих выбранных костей. Если соседние фишки мешают извлечению, то кость не может быть сыграна.
Извлекать из нее кости следует парами. Два одинаковых изображения или картинки одной из специальных подгрупп: цветы и времена года (сезоны) — дают основания считать несущие их кости порой. В игре предусмотрена следующая система подсчета очков. Самые дорогие пары — это времена года, множитель по таким костяшкам равен 14-ти. Подешевле — цветы с множителем 12, далее идут драконы и ветра с коэффициентами 10 и 8 соответственно, за ними бамбуки, круги и ваны (6, 4, 2). Важнейшим и существенным условием для уборки пары из пирамиды является открытость обоих выбранных костей. Если соседние фишки мешают извлечению, то кость не может быть сыграна.
Вынуждены огорчить любителей неспешности. Этот маджонг вам придется разобрать за 10 минут, то есть время игры ограничено, увы. В игре присутствует система статистики (в верхней части), показывающая остаток костей на столе, число доступных совпадений для создания пар (open matches) и время до окончания партии.
Скачать игру БЕСПЛАТНЫЙ МАДЖОНГ нельзя, но подумайте, имеет ли смысл это делать, ведь здесь она всегда доступна, Вам достаточно лишь открыть эту страницу.
Сделайте перерыв и сыграйте в онлайн игры, которые развивают логику и воображение, позволяют приятно отдохнуть. Расслабьтесь и отвлекитесь от дел!
• Для планшета
Во весь экран
Игра БЕСПЛАТНЫЙ МАДЖОНГ в категориях Маджонги, Для планшета доступна бесплатно, круглосуточно и без регистрации с описанием на русском языке на Min2Win. Если возможности электронного рабочего стола позволяют, можно развернуть сюжет БЕСПЛАТНЫЙ МАДЖОНГ во весь экран и усилить эффект от прохождения сценариев. Многие вещи действительно имеет смысл рассмотреть детальнее.
2 + 4k + 24 = 4k + 24 #Чтобы иметь два решения для # x #:
# 4k + 24> 0 #, то есть #k> (- 6) #
Чтобы иметь одно решение для # x #:
# 4k + 24 = 0 #, то есть # k = -6 #
Более подробное объяснение:
‘ _ _ _ _ _ _ _ ___’
Помните, что ваша функция # y # как функция от # x #. 2 + 12x + 4 [-1,3145, 0,333, -0,136, 0,688]}
2 + 12x + 4 [-1,3145, 0,333, -0,136, 0,688]}
Как видите, график касается оси # x # только при найденном нами значении # x #. Следовательно, у вас есть только одно решение.
Что касается вашего вопроса о проверке значений # k # в уравнении, если вы это сделаете, это либо подтвердит, что у вас правильный ответ, либо сообщит, что вы, возможно, допустили ошибку. Это неплохая идея.
% PDF-1.4
%
388 0 объект
>
эндобдж
xref
388 168
0000000016 00000 н.
0000004866 00000 н.
0000004980 00000 н.
0000006585 00000 н.
0000006913 00000 п.
0000007027 00000 н.
0000007382 00000 п.
0000007764 00000 н.
0000012310 00000 п.
0000012667 00000 п.
0000012938 00000 п.
0000013050 00000 п.
0000013307 00000 п.
0000013478 00000 п.
0000013787 00000 п.
0000014139 00000 п.
0000014695 00000 п.
0000015083 00000 п.
0000015465 00000 п.
0000015902 00000 н.
0000020121 00000 п.
0000020391 00000 п.
0000020580 00000 п.
0000020843 00000 п.
0000021107 00000 п. 0000021196 00000 п.
0000021801 00000 п.
0000021970 00000 п.
0000022342 00000 п.
0000022781 00000 п.
0000022964 00000 п.
0000023082 00000 п.
0000023582 00000 п.
0000023775 00000 п.
0000027838 00000 п.
0000028203 00000 п.
0000028436 00000 п.
0000033482 00000 п.
0000033754 00000 п.
0000033884 00000 п.
0000034456 00000 п.
0000034752 00000 п.
0000034916 00000 п.
0000035294 00000 п.
0000035850 00000 п.
0000036043 00000 п.
0000036306 00000 п.
0000036587 00000 п.
0000036727 00000 н.
0000039197 00000 п.
0000039532 00000 п.
0000039935 00000 н.
0000044013 00000 п.
0000044463 00000 п.
0000044874 00000 п.
0000045177 00000 п.
0000045264 00000 п.
0000050093 00000 п.
0000050403 00000 п.
0000050584 00000 п.
0000050989 00000 п.
0000051191 00000 п.
0000055739 00000 п.
0000056221 00000 п.
0000056385 00000 п.
0000056655 00000 п.
0000057012 00000 п.
0000060099 00000 п.
0000064373 00000 п.
0000064540 00000 п.
0000064798 00000 п.
0000069033 00000 п.
0000069396 00000 п.
0000021196 00000 п.
0000021801 00000 п.
0000021970 00000 п.
0000022342 00000 п.
0000022781 00000 п.
0000022964 00000 п.
0000023082 00000 п.
0000023582 00000 п.
0000023775 00000 п.
0000027838 00000 п.
0000028203 00000 п.
0000028436 00000 п.
0000033482 00000 п.
0000033754 00000 п.
0000033884 00000 п.
0000034456 00000 п.
0000034752 00000 п.
0000034916 00000 п.
0000035294 00000 п.
0000035850 00000 п.
0000036043 00000 п.
0000036306 00000 п.
0000036587 00000 п.
0000036727 00000 н.
0000039197 00000 п.
0000039532 00000 п.
0000039935 00000 н.
0000044013 00000 п.
0000044463 00000 п.
0000044874 00000 п.
0000045177 00000 п.
0000045264 00000 п.
0000050093 00000 п.
0000050403 00000 п.
0000050584 00000 п.
0000050989 00000 п.
0000051191 00000 п.
0000055739 00000 п.
0000056221 00000 п.
0000056385 00000 п.
0000056655 00000 п.
0000057012 00000 п.
0000060099 00000 п.
0000064373 00000 п.
0000064540 00000 п.
0000064798 00000 п.
0000069033 00000 п.
0000069396 00000 п.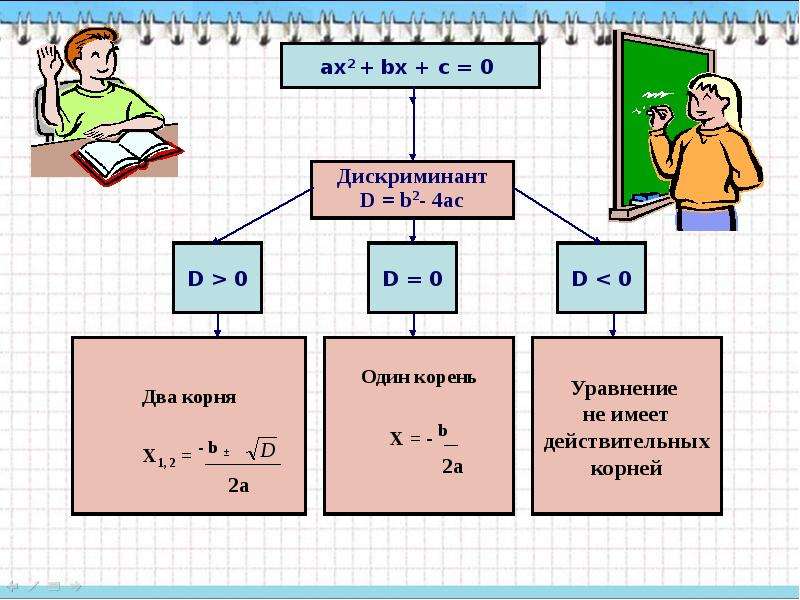 0000069806 00000 п.
0000070324 00000 п.
0000070686 00000 п.
0000070919 00000 п.
0000071307 00000 п.
0000071655 00000 п.
0000072073 00000 п.
0000072445 00000 п.
0000077290 00000 п.
0000081743 00000 п.
0000087153 00000 п.
0000112495 00000 н.
0000113277 00000 н.
0000113402 00000 н.
0000116210 00000 н.
0000118378 00000 н.
0000120651 00000 н.
0000121294 00000 н.
0000122976 00000 н.
0000123803 00000 н.
0000125315 00000 н.
0000150888 00000 н.
0000151622 00000 н.
0000152509 00000 н.
0000157047 00000 н.
0000157082 00000 н.
0000157160 00000 н.
0000171703 00000 н.
0000172034 00000 н.
0000172100 00000 н.
0000172216 00000 н.
0000172251 00000 н.
0000172329 00000 н.
00001
0000069806 00000 п.
0000070324 00000 п.
0000070686 00000 п.
0000070919 00000 п.
0000071307 00000 п.
0000071655 00000 п.
0000072073 00000 п.
0000072445 00000 п.
0000077290 00000 п.
0000081743 00000 п.
0000087153 00000 п.
0000112495 00000 н.
0000113277 00000 н.
0000113402 00000 н.
0000116210 00000 н.
0000118378 00000 н.
0000120651 00000 н.
0000121294 00000 н.
0000122976 00000 н.
0000123803 00000 н.
0000125315 00000 н.
0000150888 00000 н.
0000151622 00000 н.
0000152509 00000 н.
0000157047 00000 н.
0000157082 00000 н.
0000157160 00000 н.
0000171703 00000 н.
0000172034 00000 н.
0000172100 00000 н.
0000172216 00000 н.
0000172251 00000 н.
0000172329 00000 н.
00001
00000 н.
00001
00000 н.
00001 00000 н.
00001
00000 п. 00001 00000 н. 00001 00000 н. 00001 00000 н. 00001 00000 н. 00001 00000 н. 0000194278 00000 н. 0000194372 00000 н. 0000195070 00000 н. 0000195344 00000 н.
 0000195653 00000 н.
0000195740 00000 н.
0000196393 00000 н.
0000196656 00000 н.
0000196959 00000 н.
0000197152 00000 н.
0000197605 00000 н.
0000197915 00000 н.
0000198326 00000 н.
0000198765 00000 н.
0000199154 00000 н.
0000199490 00000 н.
0000199820 00000 н.
0000200238 00000 п.
0000200716 00000 н.
0000201026 00000 н.
0000201434 00000 н.
0000201858 00000 н.
0000203231 00000 н.
0000203568 00000 н.
0000203948 00000 н.
0000204430 00000 н.
0000204764 00000 н.
0000205082 00000 н.
0000206483 00000 н.
0000206783 00000 н.
0000246506 00000 н.
0000246545 00000 н.
0000249656 00000 н.
0000249695 00000 н.
0000252806 00000 н.
0000252845 00000 н.
0000253690 00000 н.
0000253755 00000 н.
0000256049 00000 н.
0000256114 00000 н.
0000256454 00000 н.
0000256764 00000 н.
0000257141 00000 н.
0000257547 00000 н.
0000258049 00000 н.
0000258471 00000 н.
0000258549 00000 н.
0000258817 00000 н.
0000258895 00000 н.
0000259163 00000 н.
0000003656 00000 н.
трейлер
] / Назад 761871 >>
startxref
0
%% EOF
555 0 объект
> поток
h kPUaeѽ «X, rE: # 4` Ը A]` eJd @ rAǑ Չ qLj: / Ϝ9 = 9s
Ln
0000195653 00000 н.
0000195740 00000 н.
0000196393 00000 н.
0000196656 00000 н.
0000196959 00000 н.
0000197152 00000 н.
0000197605 00000 н.
0000197915 00000 н.
0000198326 00000 н.
0000198765 00000 н.
0000199154 00000 н.
0000199490 00000 н.
0000199820 00000 н.
0000200238 00000 п.
0000200716 00000 н.
0000201026 00000 н.
0000201434 00000 н.
0000201858 00000 н.
0000203231 00000 н.
0000203568 00000 н.
0000203948 00000 н.
0000204430 00000 н.
0000204764 00000 н.
0000205082 00000 н.
0000206483 00000 н.
0000206783 00000 н.
0000246506 00000 н.
0000246545 00000 н.
0000249656 00000 н.
0000249695 00000 н.
0000252806 00000 н.
0000252845 00000 н.
0000253690 00000 н.
0000253755 00000 н.
0000256049 00000 н.
0000256114 00000 н.
0000256454 00000 н.
0000256764 00000 н.
0000257141 00000 н.
0000257547 00000 н.
0000258049 00000 н.
0000258471 00000 н.
0000258549 00000 н.
0000258817 00000 н.
0000258895 00000 н.
0000259163 00000 н.
0000003656 00000 н.
трейлер
] / Назад 761871 >>
startxref
0
%% EOF
555 0 объект
> поток
h kPUaeѽ «X, rE: # 4` Ը A]` eJd @ rAǑ Չ qLj: / Ϝ9 = 9s
LnКвадратные уравнения, это.
 2 + 7r = 3 .2 + bx + c = 0, a! = 0, завершив квадрат:
2 + 7r = 3 .2 + bx + c = 0, a! = 0, завершив квадрат:1. Если a! = 1, умножьте обе части уравнения на 1 / a.
2. Перепишите уравнение так, чтобы постоянный член находился только по одну сторону от знака равенства
.
3. Возвести в квадрат половину коэффициента при x и прибавить этот квадрат к обеим сторонам уравнения
.
4. Разложите полученный трехчлен на точный квадрат и сложите члены на другой стороне
.
5. Используйте свойство квадратного корня для завершения решения.2 = 5/9.
Теперь используйте свойство квадратного корня и свойство частного для радикалов, чтобы получить
z-2/3 = + — корень (5/9)
z-2/3 = + — корень (5) / (3)
z = 2/3 + — (корень (5)) / (3).
Эти два решения можно записать как
(2 + корень (5)) / (3)
с сокращенным набором решений {(2 + -root (5)) / (3)}.
Вот как наш пошаговый решатель квадратного уравнения решает указанную выше проблему. Вы можете увидеть, как похожие проблемы решены, нажав на кнопку «Решить похожие».2-2x + 4 = 0
Вы можете увидеть, как похожие проблемы решены, нажав на кнопку «Решить похожие».2-2x + 4 = 0
x = (2 + -корень (4-16)) / 2) a = 1, b = -2, c = 4
x = (2 + -корень (-12)) / (2)
x = (2 + -2i (корень (3))) / (2)
x = 1 + — (i) root (3) Выносим за скобки 2 в числителе и сокращаем до младших членов.
Набор решений — {-2,1 + — (i) root (3)}.
Давайте посмотрим, как наш решатель кубических уравнений решает эту и подобные проблемы. Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров.
Иногда необходимо решить буквальное уравнение для переменной, которая возведена в квадрат.2 — 4ac, называется дискриминантом. Когда числа a, b и c являются целыми числами (но не обязательно в противном случае), значение дискриминанта может использоваться для определения того, будут ли решения рациональными, иррациональными или мнимыми числами. Если дискриминант равен 0, будет только одно отличное решение. (Почему?)
Дискриминант квадратного уравнения дает следующую информацию о решениях уравнения. 2-9x-5)
2-9x-5)
Установите знаменатель равным 0 и решите.2-4 (3) (4))) / (2 (3)) = (1 + -корень (-47)) / (6)
Оба решения — мнимые числа, поэтому нет действительных чисел, делающих знаменатель равным нулю. Таким образом, на x нет ограничений на действительные числа.
2.5 ПРИМЕНЕНИЕ КВАДРАТИЧЕСКИХ УРАВНЕНИЙ
Многие прикладные задачи приводят к квадратным уравнениям. В этом разделе мы приводим примеры нескольких видов таких проблем.
ВНИМАНИЕ! При решении проблем, которые приводят к квадратным уравнениям, мы можем получить решение, которое не удовлетворяет физическим ограничениям проблемы.Например, если x представляет собой ширину, а два решения квадратного уравнения — -9 и 1. значение -9 должно быть отклонено, поскольку ширина должна быть положительным числом.
Пример 1
РЕШЕНИЕ ЗАДАЧИ ГЕОМЕТРИИ
Подрядчик по ландшафтному дизайну хочет сделать гравийный бордюр одинаковой ширины вокруг прямоугольного бассейна в саду. Бассейн 10 футов в длину и 6 футов в ширину. Материала хватит на 36 квадратных футов. Насколько широкой должна быть граница?
Бассейн 10 футов в длину и 6 футов в ширину. Материала хватит на 36 квадратных футов. Насколько широкой должна быть граница?
Схема пула с бордюром показана на рисунке 2.4. Поскольку нас просят найти ширину границы, пусть
x = ширина границы в футах.
Тогда 6 + 2x = ширина большего прямоугольника в футах,
и 10 + 2x = длина большего прямоугольника в футах.
Площадь большего прямоугольника составляет (6 + 2x) (10 + 2x) квадратных футов, а площадь бассейна составляет 6 * 10 = 60 квадратных футов. Площадь границы находится путем вычитания площади бассейна из площадь большего прямоугольника.2 + 8x-9 = 0
(х + 9) (х-1) = 0
Возможные варианты: -9 и 1. Ширина границы не может быть отрицательной. так что граница должна быть шириной 1 фут.
Проблемы, связанные с темпом работы, впервые были введены в разделе 2.2. Напомним, что если работа может быть выполнена за x единиц извести, скорость работы будет 1 / x работа за единицу времени.
Пример 2
РЕШЕНИЕ ПРОБЛЕМЫ РАБОТЫ
Пэт и Майк убирают офисы в офисном здании в центре города каждую ночь.Работаю в одиночку. Пэту требуется на 1 час меньше времени, чем Майку, чтобы выполнить задание. Работая вместе, они могут выполнить работу за 6 часов. Однажды ночью, Па! вызывает больной. Сколько времени нужно Майклу, чтобы справиться с работой в одиночку?
Пусть
x = время Майку сделать работу в одиночку
и
x-1 = время, когда Пэт выполняет работу в одиночку.
Ставки для Майка и Пэта равны. соответственно. 1 / x и 1 / (x — 1) работа в час. Если мы умножим время совместной работы, 6 часов, на каждую норму, мы получим дробную часть работы, выполненной каждым человеком.Это показано в следующей таблице.
| Оценка | Время | Часть | |
| Майк | 1 / х | 6 | 6 (1 / х) = 6 / х |
Пат. | 1 / (х — 1) | 6 | 6 (1 / (x-1)) = 6 / (x-1) |
Поскольку одно целое задание может быть выполнено двумя людьми, сумма сковород должна равняться 1, как показано уравнением
6 / х + 6 / (х-1) = 1
Чтобы очистить дроби, умножьте обе части уравнения на наименьший общий знаменатель, x (x — 1).2-4 (1) (6))) / (2 (1)) a = 1, b = -13, c = 6
x = (13 + -корень (169-24)) / (2)
x = (13 + -корень (145)) / (2)
х ≈ (13 + -12,04) / (2)
С помощью калькулятора найдите это значение с точностью до десятых, x = 12,5 или x = 0,5. Решение x = 0,5 не удовлетворяет условиям задачи, так как тогда Пату требуется x — 1 = -0,5 часа для завершения работы. Майку потребуется 12,5 часов, чтобы справиться с работой в одиночку.
Пример 3
РЕШЕНИЕ ПРОБЛЕМЫ ДВИЖЕНИЯ
Речной экскурсионный катер плыл вверх по течению от Галта до Ислтона.расстояние 12 миль. На обратном пути вниз по течению лодка двигалась быстрее на 3 мили в час. Если обратный путь занял на 8 минут меньше времени, как быстро лодка плыла вверх по течению?
На обратном пути вниз по течению лодка двигалась быстрее на 3 мили в час. Если обратный путь занял на 8 минут меньше времени, как быстро лодка плыла вверх по течению?
Таблица ниже суммирует информацию о проблеме, где x представляет скорость восходящего потока.
Записи в столбце для времени находятся в результате решения формулы расстояния. d = rt для t в каждом случае. Поскольку ставки указаны в милях в час, преобразуйте 8 минут в часы следующим образом, позволяя H представлять эквивалентное количество часов.
(ч) / (1 час) = (8 мин) / (60 мин)
H = 8/60 = 2/15
Теперь напишите уравнение, используя тот факт, что время обратного пути (нисходящего потока) было на 8 минут или на 2/15 часа меньше, чем время восходящего потока.
| Время на выходе | это | время до | меньше | 2/15 часа |
| 12 / (х + 3) | = | 12 / х | – | 15/2 |
Решите уравнение, сначала умножив обе части на общий знаменатель. 2 + 3x-270 = 0 Разделить на 2.
2 + 3x-270 = 0 Разделить на 2.
(х + 18) (х-15) = 0
x = -18 или x = 15
Отклонить отрицательное решение. Лодка двигалась вверх по течению со скоростью 15 миль в час.
ВНИМАНИЕ
Когда проблемы связаны с разными единицами времени (как в Примере 3, где скорость была указана в милях в час, а время было указано в минутах). перед настройкой уравнения необходимо преобразовать в те же единицы.
Пифагорейская теорема
В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы.2
Пример 4.
РЕШЕНИЕ ЗАДАЧИ ПИФАГОРЕЙСКОЙ ТЕОРЕМЫ
А вот! имеет форму прямоугольного треугольника. Более длинная ножка треугольника на 20 метров длиннее, чем в два раза длиннее более короткой ножки. Гипотенуза на 10 метров длиннее длинной ножки. Найдите длины трех сторон участка.
Пусть s = длина более короткого отрезка в метрах.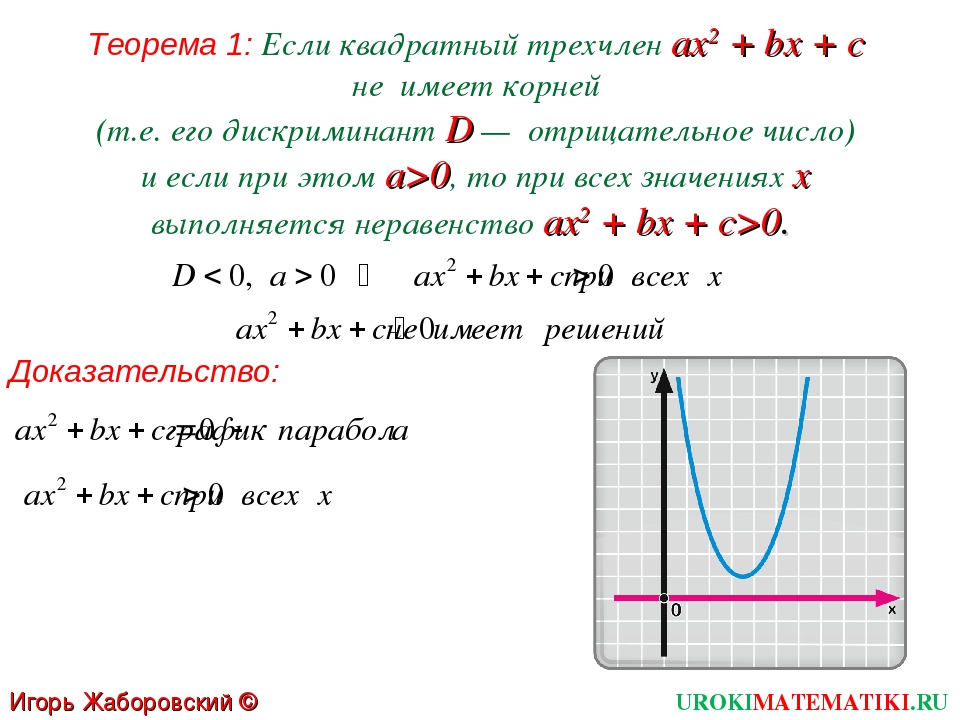 2 + 100 т
2 + 100 т
Это можно решить с помощью факторинга.
0 = -4т (4т-25)
-4т = 0 или 4т-25 = 0
т = 0 4т = 25
т = 6,25
Первое решение, 0, представляет время, в которое снаряд находился на земле перед запуском, поэтому оно не отвечает на вопрос. Снаряд вернется в землю через 6,25 секунды после запуска.
ДРУГИЕ ВИДЫ УРАВНЕНИЙ
Многие уравнения, которые на самом деле не являются квадратными, можно решить с помощью методов, описанных ранее в этой главе.2 + 2х-15 = 0
(х + 5) (х-3) = 0
x = -5 или xx = 3
Теперь предлагаемые решения необходимо проверить в исходном уравнении x = root (15-2x).
Если
х = -5
x = корень (15-2x)
-5 = корень (15-2 (-5))?
-5 = корень (15 + 10)?
-5 = корень (25)?
-5 = 5 Ложь
Если
х = 3
x = корень (15-2x)
3 = корень (15-2 (3))?
3 = корень (15-6)?
3 = корень (9)?
3 = 3 Истинно
Как показывает эта проверка, только 3 является решением, что дает набор решений {3}.
Чтобы решить уравнение, содержащее радикалы, выполните следующие действия.
РЕШЕНИЕ УРАВНЕНИЯ С РАДИКАЛАМИ
1. Выделите радикал на одной стороне уравнения.
2. Возвести каждую часть уравнения в степень, равную индексу радикала, чтобы радикал исключился.
3. Решите полученное уравнение. Если он все еще содержит радикал, повторите шаги 1 и 2.
4. Проверьте каждое предложенное решение в исходном уравнении.2-2x-3 = 0
(х-3) (х + 1) = 0
x = 3 или x = -1
Проверьте эти предложенные решения в исходном уравнении (Шаг 4)
Пусть x = 3.
корень (2x + 3) -корень (x + 1) = 1
корень (2 (3) +3) -корень (3 + 1) = 1?
корень (9) -корень (4) = 1?
3-2 = 1?
1 = 1 Истинно
Пусть x = -1
корень (2x + 3) -корень (x + 1) = 1
корень (2 (-1) +3) -корень (-1 + 1) = 1?
корень (1) -корень (0) = 1?
1-0 = 1?
1 = 1 Истинно
Оба предложенных решения 3 и -1 являются решениями исходного уравнения, что дает {3, -1} в качестве набора решений. (1/4) = root (4, b) — главный корень четвертой степени, поэтому правая часть x не может быть отрицательной. Следовательно. два предложенных отрицательных решения должны быть отклонены.
(1/4) = root (4, b) — главный корень четвертой степени, поэтому правая часть x не может быть отрицательной. Следовательно. два предложенных отрицательных решения должны быть отклонены.
Дискриминант квадратичной формулы
Дискриминант — это часть квадратичной формулы. Это позволяет нам определить, не решая квадратную формулу, как будут выглядеть решения. Положительный дискриминант означает, что существует два реальных решения, если он отрицательный, это означает, что реальных решений нет, а если он равен нулю, это означает, что существует только одно реальное решение.2-4 (1) (4) \\ = & \ quad 16-16 \\ = & \ quad 0 \ end {align} $$
Следовательно, поскольку дискриминант равен нулю, существует одно действительное решение для \ (x \).
Узнайте больше о наших темах Precalculus
Узнайте больше о наших темах о линейных и нелинейных уравнениях
| College Algebra Урок 17: Квадратичные уравнения WTAMU > Виртуальная математическая лаборатория> Алгебра колледжа Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам? WTAMU > Виртуальная математическая лаборатория> Алгебра колледжа |
Квадратичная формула — Бесплатная справка по математике
Что такое квадратное уравнение?
Квадратичная формула используется для решения очень специфического типа уравнения, называемого квадратным уравнением . Эти уравнения обычно записываются в следующей форме, где A, B и C — константы, а x — неизвестное. 4 \) термины и т. Д. В них могут присутствовать или не присутствовать все три члена (\ (Bx \) или \ (C \) могут отсутствовать). Есть несколько вариантов решения квадратного уравнения относительно x, включая факторизацию или завершение квадрата. В этом уроке мы будем использовать метко названную квадратную формулу , которая принимает три коэффициента (A, B и C) и предоставляет до двух решений, если они существуют.
4 \) термины и т. Д. В них могут присутствовать или не присутствовать все три члена (\ (Bx \) или \ (C \) могут отсутствовать). Есть несколько вариантов решения квадратного уравнения относительно x, включая факторизацию или завершение квадрата. В этом уроке мы будем использовать метко названную квадратную формулу , которая принимает три коэффициента (A, B и C) и предоставляет до двух решений, если они существуют.
Первым шагом к использованию квадратной формулы будет определение трех коэффициентов, A, B и C. В приведенном выше уравнении они удобно все вместе находятся на одной стороне упрощенного уравнения.2 + 5x = -8 $$
Решение уравнения для x
Как бы вы решили это уравнение относительно x? Мы упростили его до стандартной формы, но нет очевидного способа преобразовать это уравнение в форму x =. Вот здесь и пригодится квадратичная формула!
Квадратичная формула
Квадратичная формула — это инструмент, который мы можем использовать для решения квадратных уравнений для любых возможных решений. В конце концов мы обнаружим, что на самом деле может быть несколько уникальных решений, а может и не быть ни одного.2-4ac}} {2a} $$
В конце концов мы обнаружим, что на самом деле может быть несколько уникальных решений, а может и не быть ни одного.2-4ac}} {2a} $$
Я знаю, это выглядит очень сложно. Как только вы будете использовать его много, вы выучите формулу наизусть, но до тех пор продолжайте практиковаться. На самом деле с использованием не так уж и сложно — просто введите свои номера шаг за шагом. Мы уже научились находить три коэффициента A, B и C, и я сказал, что мы на полпути к решению. Теперь мы просто вставляем значения для A, B и C, и у нас остается два возможных решения для x, если они существуют. Почему два? Обратите внимание, что в формуле есть знак плюс / минус.2 + 12}} {2} $$ $$ x = \ frac {-2 \ pm \ sqrt {16}} {2} $$ $$ x = \ frac {-2 \ pm 4} {2} $$ $$ x = \ frac {-2 + 4} {2} = 1 \ text {OR} $$ $$ x = \ frac {-2-4} {2} = -3 $$
Как видите, у нас есть два решения для этого уравнения. Может показаться странным, что x может быть двумя разными значениями, но попробуйте их оба в исходном уравнении, и вы увидите, что оба они работают! Как такое возможно? Квадратное уравнение — это не прямая линия, соединяющая каждый x с одним значением y. Если вы посмотрите на график этого типа уравнения, вы поймете, почему может быть 0, 1 или 2 решения.2 + 2x-3 = y \), поэтому мы можем изобразить его на графике. Если мы это сделаем, мы увидим, что квадратные уравнения на графике выглядят как параболы, а парабола, безусловно, может пересекать ось x дважды (что означает y = 0 в двух местах). Например, следующее изображение представляет собой график уравнения, которое мы только что решили. Видите, как он дважды пересекает ось абсцисс? Для двух разных значений x значение y равно 0. Это два решения. Если кончик параболы просто касается оси x, то у нас есть единственное решение. Если он никогда не пересечется, у нас нет решений.2-x + 1 \) и нарисуйте график, мы увидим почему. Нет случаев, когда y = 0:
Если вы посмотрите на график этого типа уравнения, вы поймете, почему может быть 0, 1 или 2 решения.2 + 2x-3 = y \), поэтому мы можем изобразить его на графике. Если мы это сделаем, мы увидим, что квадратные уравнения на графике выглядят как параболы, а парабола, безусловно, может пересекать ось x дважды (что означает y = 0 в двух местах). Например, следующее изображение представляет собой график уравнения, которое мы только что решили. Видите, как он дважды пересекает ось абсцисс? Для двух разных значений x значение y равно 0. Это два решения. Если кончик параболы просто касается оси x, то у нас есть единственное решение. Если он никогда не пересечется, у нас нет решений.2-x + 1 \) и нарисуйте график, мы увидим почему. Нет случаев, когда y = 0:
Квадратичная формула сложна, но если вы просто будете следовать инструкциям, у вас не будет проблем. Обязательно проверьте дискриминант, чтобы знать, сколько решений ожидать, и не забудьте знак +/-. Запоминание самой формулы может занять некоторое время, но это очень пригодится.
Попробуйте дополнительные уроки с других сайтов: PurpleMath, SOSMath, wikipedia. Попробуйте обратиться за дополнительной помощью на нашу бесплатную доску сообщений — лучше всего подойдет начальная алгебраическая категория.
Связанные вопросы и ответы:
Связанные страницы
Использование и понимание дискриминанта — стало проще
”Здравствуйте! Пришло время снова сыграть в любимую викторину СТЕНА СЛАВЫ! » ”Первая участница сегодняшнего шоу — Тереза! Надеюсь, вы готовы сыграть в СТЕНУ СЛАВЫ! » Прежде чем мы начнем сегодняшнюю игру, давайте быстро рассмотрим наши правила игры. Тереза, ты собираешься увидеть сегодняшнюю стену. На стене 5 секретных дверей с одним уравнением , написанным над каждой дверью.Во время игры вы сможете открыть 3 из этих дверей. За каждую выбранную дверь вы получите приз, равный количеству решений уравнения. Если каждая дверь, которую вы выбираете, открывает приз, вы вернетесь на шоу завтра и получите шанс выиграть еще больший приз!
Понимание дискриминанта
Секрет этой игры в том, что понимает и , используя дискриминант . Если Тереза придумает, как использовать этот инструмент, у нее будет шанс выиграть все призы и вернуться завтра! Давайте взглянем на сегодняшнюю СТЕНУ СЛАВЫ! уравнения , которые у нас есть сегодня:
Если Тереза придумает, как использовать этот инструмент, у нее будет шанс выиграть все призы и вернуться завтра! Давайте взглянем на сегодняшнюю СТЕНУ СЛАВЫ! уравнения , которые у нас есть сегодня:
Уравнение 1: x-квадрат минус 10x плюс 34.
Уравнение 2: 3 x в квадрате минус 4x плюс 10.
Уравнение 3: x в квадрате минус 3x плюс 5.
Уравнение 4: x в квадрате плюс 2 корня 2x плюс 2.
Уравнение 5: x в квадрате плюс 6x минус 16
В качестве первого выбора Тереза выбирает дверь номер 4. Помните, мы говорили, что можем использовать дискриминант , чтобы быстро определить, выиграла ли Тереза один из наших невероятных призов. Дискриминант происходит от квадратной формулы , и ее формула представляет собой квадрат b минус 4ac, где a, b и c относятся к коэффициентам и константе квадратного уравнения в стандартной форме .
Когда дискриминант положительный , наше уравнение будет иметь 2 решения ; когда дискриминант равен 0 , наше уравнение имеет 1 решение , а когда наш дискриминант отрицательный , наше уравнение не будет иметь решений . Давайте посмотрим на уравнение , которое только что выбрала Тереза. В уравнении, которое только что выбрала Тереза, «a» равно 1, «b» равно двукратному квадратному корню из 2, а «c» равно 2.
Давайте посмотрим на уравнение , которое только что выбрала Тереза. В уравнении, которое только что выбрала Тереза, «a» равно 1, «b» равно двукратному квадратному корню из 2, а «c» равно 2.
Рассчитаем дискриминант ! Величина, умноженная на квадратный корень из 2 в квадрате, будет равна 8. 8 минус 8 будет равно 0. Поскольку дискриминант равен 0, это уравнение будет иметь одно решение. Тереза, вы только что выиграли 1 новенького единорога! Разве она не выглядит счастливой ?! Это самое хорошее начало, о котором вы можете мечтать!
Второй пример
При втором выборе Тереза выбирает пятое уравнение. Давайте познакомимся поближе! В этом уравнении «a» равно 1, «b» равно 6, а «c» равно отрицательному 16.Рассчитаем дискриминант! Подставляя наши значения, мы получаем 6 в квадрате минус 4 умножить на 1 отрицательное 16.
Используя PEMDAS , мы получаем 36 плюс 64, что равно 100. Вау! Посмотри на это! Тереза только что выиграла пару фигурок Позитрона и Негатрона! 2 приза за уравнение с 2 решениями! У Терезы пока все отлично! Если она выберет дверь с еще одним призом, ее снова пригласят на завтрашнее шоу и шанс выиграть главный приз!
И, сделав последний выбор, Тереза выбирает уравнение двери номер 2! Давайте посмотрим на ее уравнение! В этом уравнении «a» равно 3, «b» равно отрицательному 4, а «c» равно 10. Рассчитаем дискриминант! Подставляя наши значения , мы получаем отрицательные 4 в квадрате минус 4 умноженные на 3 умноженные на 10. Вычислив по нашему математическому уравнению , мы получаем 16 минус 120, что дает отрицательное значение 104. Как вы думаете, что это означает? Не только в отношении того, сколько решений имеет наше уравнение, но и в отношении шансов Терезы вернуться завтра?
Рассчитаем дискриминант! Подставляя наши значения , мы получаем отрицательные 4 в квадрате минус 4 умноженные на 3 умноженные на 10. Вычислив по нашему математическому уравнению , мы получаем 16 минус 120, что дает отрицательное значение 104. Как вы думаете, что это означает? Не только в отношении того, сколько решений имеет наше уравнение, но и в отношении шансов Терезы вернуться завтра?
Сводка
Помните, когда наш дискриминант на больше, чем 0 , это означает, что наше уравнение будет иметь 2 решения .Когда наш дискриминант равен 0 , наше уравнение будет иметь 1 решение . И когда наш дискриминант является отрицательным , наше уравнение не будет иметь реальных решений .
Ну, ребята! Это также означает, что приза нет! Хотя Тереза будет разочарована, по крайней мере, у нее есть фигурки и новый Единорог! Хотя этот Единорог выглядит немного подозрительно .
 (1/2).
(1/2).







 Так что
полезно знать различные способы решения квадратных уравнений, чтобы вы
будьте готовы к любой ситуации.После завершения
это
учебник, вы будете мастером решения квадратных уравнений.
Решение
уравнения в целом — очень важная часть алгебры. Так что я
предполагать
нам лучше добраться до этого.
Так что
полезно знать различные способы решения квадратных уравнений, чтобы вы
будьте готовы к любой ситуации.После завершения
это
учебник, вы будете мастером решения квадратных уравнений.
Решение
уравнения в целом — очень важная часть алгебры. Так что я
предполагать
нам лучше добраться до этого.


 Например, если ab = 1, то a = 5 и b = 1/5 или a = 3 и b = 1/3 и т. Д.Но с продуктом, установленным равным 0, мы можем гарантировать
найти решение, установив каждый коэффициент равным 0. То есть
Зачем
Важно для начала получить его в стандартной форме.
Например, если ab = 1, то a = 5 и b = 1/5 или a = 3 и b = 1/3 и т. Д.Но с продуктом, установленным равным 0, мы можем гарантировать
найти решение, установив каждый коэффициент равным 0. То есть
Зачем
Важно для начала получить его в стандартной форме.




 Поскольку как положительный, так и противоположный ему квадрат
результат
в том же ответе у вас будет два ответа плюс или минус
квадратный
корень B .
Поскольку как положительный, так и противоположный ему квадрат
результат
в том же ответе у вас будет два ответа плюс или минус
квадратный
корень B . Учебное пособие по .
14: Линейные уравнения с одной переменной.
Учебное пособие по .
14: Линейные уравнения с одной переменной.  корень 16 = 4
корень 16 = 4  из мульт. на 5 дел. по 5
из мульт. на 5 дел. по 5 
 кв. корень 20 = -2 кв.
корень 5
кв. корень 20 = -2 кв.
корень 5 

 Убедитесь, что вы не забыли добавить его с ОБЕИХ сторон, чтобы сохранить
уравнение
сбалансированный.
Убедитесь, что вы не забыли добавить его с ОБЕИХ сторон, чтобы сохранить
уравнение
сбалансированный.



 Это пригодится, когда
квадратное уравнение не учитывается или его трудно разложить на множители.
Это пригодится, когда
квадратное уравнение не учитывается или его трудно разложить на множители.


 Обратите внимание, что
мы только подставляем числа, мы также не подставляем переменную.
Обратите внимание, что
мы только подставляем числа, мы также не подставляем переменную.

 6 x является саб. 6 х
6 x является саб. 6 х  По возможности упростите.
По возможности упростите. 
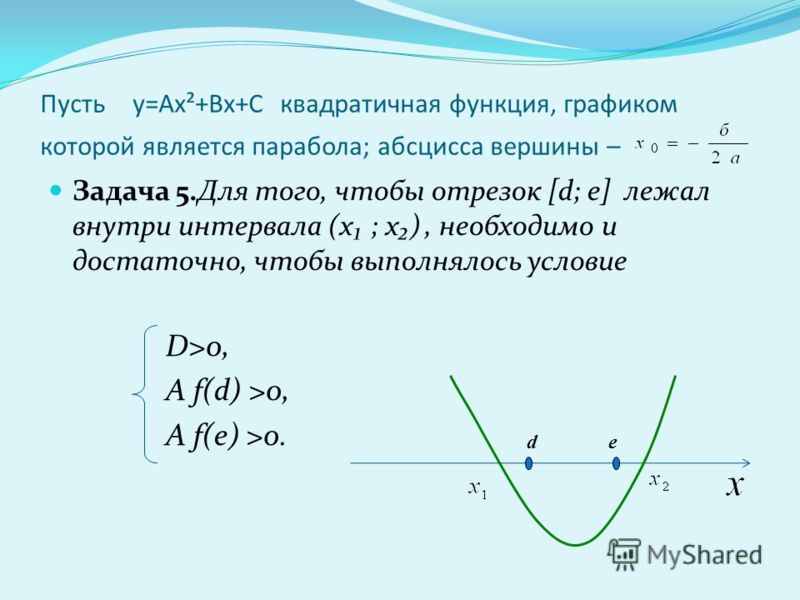




 16 доп. 16
16 доп. 16  По возможности упростите.
По возможности упростите. 


 По ссылке вы найдете ответ
а также любые шаги, которые привели к поиску этого ответа.
По ссылке вы найдете ответ
а также любые шаги, которые привели к поиску этого ответа. На основе дискриминации укажите, как
много и что
типа решения там не было бы.
На основе дискриминации укажите, как
много и что
типа решения там не было бы.