Признаки равенства прямоугольных треугольников

Треугольник называется прямоугольным, если у него есть прямой угол. Так как сумма углов треугольника равна 180˚, то у прямоугольного треугольника один угол прямой, а два других угла острые, причём их сумма равна 90˚. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.

Из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.

В прямоугольном треугольнике угол между двумя катетами – прямой, значит в двух любых прямоугольных треугольниках уже равные углы. Исходя из этого, можем сделать следующие выводы:

• если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны;
• если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Из второго признака равенства треугольников можно убрать прилежащий к катету прямой угол, потому что прямые углы в двух треугольниках равные, и получается:

• если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рассмотрим еще один признак равенства прямоугольных треугольников.

Из теоремы о сумме углов мы знаем, что сумма углов треугольника равна 180˚, один угол в прямоугольном треугольнике прямой. И если один острый угол в прямоугольнике соответственно равен острому углу второго треугольника, то и оставшиеся острые углы треугольников будут равны. Это второй признак равенства треугольников: по стороне и прилежащим к ней углам.

Значит, в прямоугольном треугольнике для определения равенства можно рассматривать только гипотенузу и один острый угол:

• если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.  

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Признаки равенства треугольников. Равнобедренный треугольник. Признаки равенства и свойства прямоугольных треугольников. Соотношения между сторонами и углами треугольника

Дата: 08.09.15

Тема: «Признаки равенства треугольников. Равнобедренный треугольник. Признаки равенства и свойства прямоугольных треугольников. Соотношения между сторонами и углами треугольника».

Цель урока: формировать умения применять полученные знания на практике

Задачи:

Образовательные:

— повторение, обобщение и проверка знаний по теме: «Признаки равенства треугольников. Равнобедренный треугольник. Признаки равенства и свойства прямоугольных треугольников. Соотношения между сторонами и углами треугольника».

Развивающие:

-развить внимание, усидчивость, настойчивость, логическое мышление, математическую речь.

Воспитательные:

-посредством урока воспитывать активность ,внимательное отношение друг к другу, прививать умение слушать одноклассников.

Тип урока: обобщения и систематизации знаний

Структура урока.

1. Организационный момент

2. Проверка домашнего задания

3. Актуализация опорных знаний

4. Диагностика знаний и умений учащихся

5. Подведение итогов

6. Постановка домашнего задания

Ход урока

1. Организационный момент.

Проверка готовности класса к уроку. Сообщение темы и цели урока.

2. Проверка домашнего задания

3. Актуализация опорных знаний.

1) Признаки равенства треугольников.

Первый признак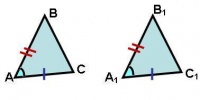

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак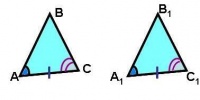 

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак

 

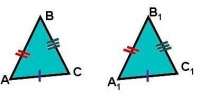
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя — основанием. По определению, правильный треугольник также является равнобедренным, но обратное утверждение неверно.

Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов).

Признаки равенства прямоугольных треугольников.

Признак равенства прямоугольных треугольников по двум катетам

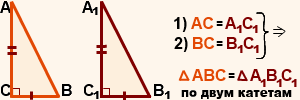
Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.

Признак равенства прямоугольных треугольников по катету и гипотенузе

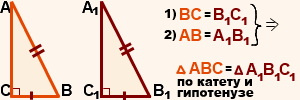
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

Признак равенства по гипотенузе и острому углу

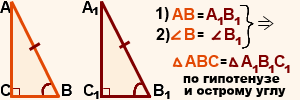
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Признак равенства прямоугольных треугольников по катету и острому углу

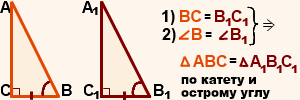
Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Свойства прямоугольных треугольников.

Свойство 1: Сумма острых углов треугольника равна 90^о.  

Свойство 2: АB > AC, АB > BC. 

Свойство 3: Катет, лежащий против угла 30^о, равен половине гипотенузы.

4. Диагностика знаний и умений учащихся.

а) по готовым чертежам ( готовые чертежи в буклетах и на интерактивной доске).

1. Найти: N 

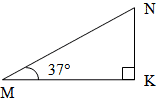
Сумма внутренних углов треугольника равна 180°.

2. АВ=12см. Найти: ВС

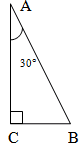
3. PD = 1,2cм. Найти: PQ

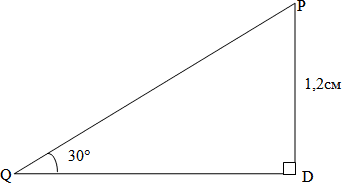
4. В прямоугольном треугольнике АВС 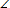С=90° и 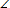А=30°, проведена медиана СМ и биссектриса MD ΔСМА. Найдите MD, если ВС=23см.

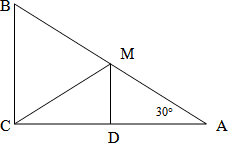
Дано: ΔАВС, 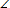С=90°, 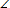А=30°, СМ-медиана 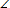С, МD – биссектриса ΔСМА, ВС=23см.
Найти: MD.
Решение:
Т.к. СМ – медиана, то СМ-ВМ=МА=0,5АВ
Т.к. 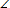А=30° и ВС=24см, то АВ=48см и = СМ=ВМ=МА=24см.
Т.к. СМ=МА, то ΔСМА равнобедренный, следовательно, МD – высота.
Т.к.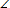 

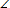А=30°, АDM= 90° и МА=24см, то MD=0,5МА= 12см.
Ответ: MD=12см.

5. Подведение итогов.

Выставление оценок за урок.

6. Постановка домашнего задания. Повторить правила.

Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 18 см. Найдите гипотенузу и меньший катет.

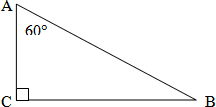
Дано: ΔАВС, 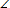С=90°,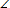 

А=60°, АВ+АС=18см
Найти: АВ, АС.
Решение:
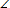В=90° – 60°=30°, значит, АС – меньший катет, тогда
АС=0,5АВ
АВ+0,5АВ=18
АВ=12см, АС=6см
Ответ: АВ=12см, АС=6см.

infourok.ru

Урок «Признаки равенства прямоугольных треугольников»

Технологическая карта урока по геометрии в 7 классе по теме «Признаки равенства прямоугольных треугольников»

учитель математики Крюкова Н.Н.

Л.С. Атанасян, В.Ф. Бутузова, М.: Просвещение, 2014г

Прямоугольные треугольники. Признаки равенства прямоугольных треугольников.

Урок «открытия» нового знания.

Создание условий для усвоения темы, развитие готовности мышления к усвоению нового способа деятельности, развитие мыслительных операций школьников, развитие навыков самоконтроля, схематичного мышления, развитие навыков адекватной самооценки.

Изучение признаков равенства прямоугольных треугольников; овладение знаниями и умениями, необходимыми для решения задач.

Формировать навык применения изученных признаков; развивать информационную компетентность учащихся, уметь извлекать и обрабатывать информацию.

Этап

Деятельность учителя

Деятельность учащихся

Планируемые результаты

УУД

Мотивация к деятельности

Цель этапа: включение учащихся

в деятельность.

Приветствует, проверяет готовность к уроку, желает успеха.

Включение в деловой ритм.

Подготовка класса к работе: наличие рабочей тетради, учебника, канцелярских принадлежностей.

Личностные результаты

Самоорганизация, самоопределение

Метапредметные результаты

Планирование учебного сотрудничества с учителем и сверстниками

Актуализация и пробное учебное действие

Цель этапа: подготовка мышления учащихся и организация осознания ими внутренней потребности к построению нового способа действий.

Организует повторение знаний, закрепление умений. Слайд1

— Какой треугольник называется прямоугольным?

— Чему равна сумма углов треугольника?

— Чему равна сумма острых углов прямоугольного треугольника?

— Чему равен катет, лежащий против угла в 30гр?

— Чему равны углы прямоугольного треугольника, если один из катетов равен половине гипотенузы?

— Первый признак равенства треугольников

— Второй признак равенства треугольников

— Третий признак равенства треугольников

— Какие треугольники называются равными?

— Свойство углов равнобедренного треугольника

— Свойство биссектрисы равнобедренного треугольника?

2.Тестовая работа

Работа на компьютерах с тестом 04.2 (интерактивное приложение к учебнику геометрия 7-9 кл. Атанасян Л.С.)

Отвечают на вопросы.

Решают задачи на применение свойств прямоугольного треугольника.

На данном этапе организуется подготовка учащихся к объяснению нового знания, выполнение ими пробного учебного действия и фиксация индивидуального затруднения.

Познавательные – анализ, обобщение, аналогия, классификация, извлечение необходимой информации; осознанное и произвольное построение речевого высказывания;

Регулятивные, включая действия саморегуляции: подведение под понятие выполнение пробного учебного действия фиксирование индивидуального затруднения в пробном действии; волевая саморегуляция в ситуации затруднения.

Коммуникативные выражение своих мыслей с достаточной полнотой и точностью; аргументация своего мнения и позиции в коммуникации; учет разных мнений; использование критериев для обоснования своего суждения

Постановка учебной задачи

Цель этапа: обсуждение затруднений (почему возникли затруднения, чего мы ещё не знаем).

— Определите признак, по которому равны треугольники?

Создает проблемную ситуацию (СЛАЙД 2)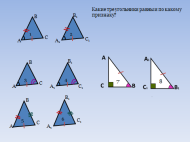

-Как вы думаете, можно ли доказать равенство данных прямоугольных треугольников ?

-Что вы использовали при решении данных задач?

-Что объединяет все эти задачи?

-Итак, сегодня на уроке мы изучаем «Признаки равенства прямоугольных треугольников» (СЛАЙД 3)

Запишите тему урока.

Какие же цели мы можем определить?

Изучить -признаки равенства прямоугольных треугольников,- решать задачи на их использование

— применение в жизни понятия, равенство прямоугольных треугольников

Анализ решения задач.

Вывод: признаки равенства треугольников применимы для доказательства равенства прямоугольных треугольников.

Ставят цели, формулируют проблему и тему урока.

Метапредметные результаты

Целеполагание

Постановка вопросов

Предметные результаты

Формулирование проблемы

Выявление места и причины затруднения

Цель этапа: постановка целей учебной деятельности

Организует учащихся по исследованию проблемной ситуации

Как вы думаете, зачем мы повторили признаки равенства треугольников ?

Чем отличается прямоугольный треугольник от всех остальных?

Какие признаки равенства треугольников мы можем применить к прямоугольным треугольникам, если нам известно, что один угол у них прямой? (1 и 2)

-Что и почему можно убрать из признака равенства треугольников, не меняя смысла теоремы?

-Почему?

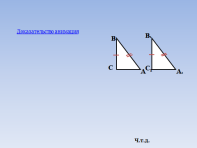
Работа с рабочим листом (СЛАЙД 4-6)

Интерактивная модель для доказательства теоремы 2

Работа с учебником стр.77-76

СЛАЙД 7

Соотносят полученное выражение с материалом, изученным ранее: сравнивают изученные ранее признаки равенства треугольников с решением задачи.

На основе выполненных действий

делают вывод о равенстве прямоугольных треугольников.

Делают записи в маршрутных листах.

Формулируют признаки равенства прямоугольных треугольников.

Метапредметные результаты

Соотнесение действия и правила.

Прогнозирование

Сотрудничество в поиске и действия.

Предметные результаты

Самостоятельное формулирование цели.

Решение проблемы, построение логической цепи рассуждений, доказательство, выдвижение гипотез и их обоснование

Физкультминутка

Читает упражнения в стихотворной форме

Выполняют упражнения

Первичное закрепление

Цель этапа: усвоение учащимися правильного применения признаков равенства прямоугольных треугольников.

Устанавливает осознанность восприятия, делает первичное обобщение.

Предлагает выполнить задания.

1.Найдите пары равных треугольников и запишите их номера в таблицу:

2. Определите количество равных элементов в треугольниках и выпишите номера рисунков и подпишите применяемый признак. Вычеркните треугольники, которые не являются равными.

СЛАЙД 8-9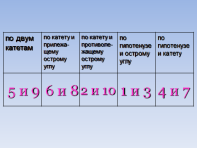

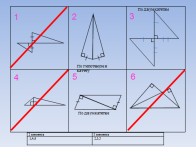
1.Устанавливают соответствие, обосновывают свой выбор.

2. Определяют количество равных элементов в треугольниках и выписывают номера рисунков и подписывают применяемый признак. Вычеркивают треугольники, которые не являются равными.

Взаимопроверка

Метапредметные результаты

Контроль

Оценка

Коррекция

Управление поведением партнера

Выражение своих мыслей и эмоций с достаточной полнотой и точностью

Предметные результаты

Действие по аналогии

Умение структурировать знания, выбор наиболее эффективных способов решения задач.

Контроль на этапе

окончания учебной цели

Цель этапа:

контроль

Организует самостоятельную коррекционную работу

(проверка документ камера)

1.Применяют признаки равенства прямоугольных треугольников при решении задачи

Метапредметные результаты

Контроль

Оценка

Коррекция

Выражение своих мыслей и эмоций с достаточной полнотой и точностью

Предметные результаты

Умение структурировать знания, выбор наиболее эффективных способов решения задач.

Личностные результаты

Выполняют работу, анализируют, контролируют и оценивают результат

Использование новых знаний

Цель этапа: получение дополнительных знаний

Историческая справка

Катафот (СЛАЙД 10-11)

1.Слушают, дополняют

Предметные результаты

уметь извлекать и обрабатывать информацию.

Домашняя работа

Учитель задает дифференцированное домашнее задание с учетом уровня подготовки учащихся.

1. П.36,решение задачи №262

Дополнительные

№ 1. Еще одно из свойств прямоугольного треугольника, доказанное Фалесом. Нарисуем прямоугольный треугольник АВС и разделим его гипотенузу АС точкой О пополам. Как вы думаете, какой отрезок длиннее: АО или ОВ. То есть куда ближе идти из середины гипотенузы — к острому углу или к прямому? 
№2. Жители трех домов, расположенных в вершинах равнобедренного прямоугольного треугольника, хотят выкопать общий колодец с таким расчетом, чтобы он был одинаково удален от всех трех домов. В каком месте надо копать. СЛАЙД (12)

Записывают домашнее задание с учетом своих возможностей

Личностные результаты

Умеют оценивать свои возможности при выборе домашнего задания

Рефлексия деятельности

Цель этапа: осознание учащимися своей учебной деятельности, самооценка результатов деятельности своей и всего класса.

Организует рефлексию, организует самооценку результатов учащихся.

Осуществляют оценку урока и самооценку, соотносят цель и результаты, степень их соответствия

Отвечают на вопросы:

• Какие знания помогли вам сегодня на уроке?

• Какая цель была у нашего урока и выполни ли мы ее?

• Проанализируйте свою работу на уроке. Оцените ее и отметьте в рабочем листе количество набранных баллов

• Поднимите руки те, кому было на уроке трудно, но интересно?

• Поднимите руки те, кому было на уроке понятно, но остались вопросы?

• Поднимите руки те, кому было все понятно.

Метапредметные результаты

Умение выражать свои мысли

Предметные результаты

Рефлексия

Контроль и оценка процесса и результатов деятельности

Личностные результаты

Самооценка на основе успешности

Адекватное понимание причин успехе/неуспеха в учебной деятельности

infourok.ru

«Прямоугольные треугольники. Свойства. Признаки равенства прямоугольных треугольников.»

Ларионова В.И. – учитель математики МБОУ Ставровская СОШ

Урок по теме:

«Прямоугольные треугольники.

Свойства.

Признаки равенства прямоугольных треугольников.»

Цель урока:

1. Рассмотреть свойства прямоугольных треугольников, исследовать признаки равенства прямоугольных треугольников с использованием аналогии.

2. Продолжить обучению этапам исследовательской работы на уроках математики.

3. Формирование коммуникативных умений слушать и слышать другого, аргументировано выражать свою точку зрения.

В самом начале первого урока детям предлагается выполнить исследовательскую работу по изучению свойств прямоугольных треугольников, о которых ученикам пока известно немного:

В

гипотенуза ∠ С = 90º

С катет А

Под руководством учителя начинается процедура исследования:

1. Вводится объект исследования – прямоугольный треугольник или два прямоугольных треугольника.

2. Определяется цель исследования – сформулировать гипотезы:

А) о свойствах прямоугольного треугольника;

Б) о признаках равенства прямоугольных треугольников.

3. Вместе с ребятами обсуждается тот факт, что всякая гипотеза требует проверки её истинности, т.е. предполагаемый факт должен быть либо строго доказан, либо опровергнут.

Для организации процедуры исследования ребятам предлагается объединиться в группы по 2 – 5 человек по их желанию. Время на выполнение работы заранее оговаривается (15 мин.). По завершении работы каждая группа должна доложить классу о результатах своей исследовательской работы.

По первой части работы выступили 3 группы.

Ребята сформулировали следующие свойства:

А m

1. ∠C=90º

2. ∠A+∠B=90 º

3. AC < AB

BC < AB

AC + CB > AC

C B

4. Если △ABC — равнобедренный, то ∠A =∠B = 45º

5. △ABC не может быть равносторонним

6. Если m  AC , то m CB

Все приведенные выше свойства были приведены с обоснованиями, и никаких разногласий по этому поводу не было.

Анализируя список приведенных свойств, можно заметить, что главный результат этой части работы — рефлексивно-осмысленный опыт совместной деятельности. Были применены в новой ситуации, ранее изученные свойства: сумма углов треугольника, признак параллельности прямых, соотношение между сторонами и углами треугольника, понятие о равностороннем треугольнике, свойство углов при основании равностороннем треугольнике, свойство углов при основании равнобедренного треугольника.

Вторая часть работы (исследование признаков равенства прямоугольных треугольников), как и ожидалось, вызвала различные затруднения:

А) трудности в выдвижении гипотезы;

Б) трудности в проверке истинности гипотезы.

Группами были предложены варианты гипотез.

Ι группа:

Два прямоугольных треугольника равны, если:

А) равны их гипотенузы;

Б) соответственно равны пары их острых углов.

Ребята получили возможность оценить истинность этих гипотез. Сразу же было высказано сомнение в верности этих предложении, что позволило обсудить один из способов опровержения гипотезы — контрпример.

А А₁ ∠A = ∠A₁

∠B = ∠B₁

∠C = ∠C₁ = 90º

△ABC ≠ △A₁B₁C₁

С В

С₁ В₁

Было предложено название этим треугольникам – подобные треугольники. Дали его сами ребята, опираясь на жизненный опыт.

ΙΙ и ΙΙΙ группы вышли на гипотезы о равенстве прямоугольных треугольников по двум катетам и по гипотенузе и острому углу. Только одна группа сумела самостоятельно доказать признак по двум катетам, а признак по гипотенузе и острому углу смогли доказать после небольшой дискуссии.

Возник вопрос о том, что мы применили для доказательства признака равенства прямоугольных треугольников по двум катетам. После обращения к признакам равенства треугольников появилась идея доказательства признака равенства прямоугольных треугольников по гипотенузе и острому углу при помощи второго признака равенства треугольников и использования свойства острых углов прямоугольного треугольника.

На этом первый урок был завершен.

Итог урока: процедура исследовательской деятельности учащихся выдержала до конца. Все выдвинутые гипотезы прошли проверку истинности, выполненную самими ребятами.

Второй урок по этой теме был начат с рефлексии итогов первого урока в части, касаемой признаков равенства прямоугольных треугольников, при доказательстве которых использовались признаки равенства треугольников.

Построение аналогии (различии), сопоставлении:

Признаки равенства треугольников.

Признаки равенства прямоугольных треугольников, найденные уч-ся

1. По двум сторонам и углу между ними.

2. По стороне и двум прилежащим углам.

3. По трем сторонам.

1) по двум катетам.

2) по гипотенузе и острому углу.

В результате выполненного анализа ребята вышли на необходимость отыскания только двух соответственно равных элементов для доказательства равенства прямоугольных треугольников.

Формируется цель следующего этапа исследовательской деятельности: отыскать другие признаки равенства прямоугольных треугольников. Форма работы опять групповая.

В результате исследования ребята приходят к гипотезам: возможно, существуют признаки равенства прямоугольных треугольников по катету и прилежащему острому углу, по гипотенузе и катету. Гипотеза о равенстве прямоугольных треугольников по двум соответственно равным острым углам отвергается сразу же, т.к. она возникла на предыдущем уроке.

А А₁ АС = А₁С₁

∠A = ∠A₁

∠C = ∠C₁ = 90º

△ABC = △A₁B₁C₁

С В

С₁ В₁

Этот признак легко доказывается учащимися. На этом признаке хорошо отрабатываются границы его применимости.

Что будет, если ситуация изменится?

AC = A₁C₁

∠B = ∠B₁

∠C = ∠C₁ = 90º

Будут ли по-прежнему равны треугольники △ABC и △A₁B₁C₁? Ребята быстро находят ответ на вопрос. Можно изменить название этого признака так: по катету и острому углу.

Признак равенства прямоугольных треугольников по гипотенузе и катету группы не смогли доказать самостоятельно. Была выяснена проблема: не хватает знания о равенстве соответствующих острых углов треугольников. В результате проведения аналогий с признаком равенства треугольников по трем сторонам и с его доказательством, возникает идея – использовать метод приложения треугольников. Один из учеников успешно ее реализует.

Итог двух уроков: самостоятельно сформулированы и самостоятельно доказаны учащимися свойства прямоугольного треугольника и четыре признака равенства прямоугольных треугольников.

Выход на практическое применение признаков:

Среди изображенных семи треугольников отыскать пары равных треугольников и ответить на вопрос: по какому признаку они равны.

15см

4см 3см

7,5см 4см

3см

60º

15см

3см

35º

15см

55º

3см 7,5см

Итак, признак равенства прямоугольных треугольников сформулированы, доказаны, применены в простейших случаях. Процедура исследовательской деятельности учащихся завершена.

На первом уроке объекты исследования и цель исследования были заданы учителем, на втором уроке уже определялись совместно учителем и учениками. Гипотезы были выдвинуты учениками самостоятельно, проверка их истинности производилась учениками самостоятельно. В случае необходимости учителю приходилось создавать ситуации, которые помогли ребятам найти логичное завершение совместного исследовательского поиска.

Конечно, не все дети класса вышли на уровень самостоятельного исследования.

Некоторые ученики лишь выдвигали гипотезы, доказать же их верность не могли. Некоторые смогли лишь сформулировать свойства прямоугольного треугольника, а признаки равенства не сумели. Ребята по формированию навыков исследовательской деятельности требует большого внимания, усилий и настойчивости в достижении этой цели со стороны учителя.

infourok.ru

План урока на тему «Признаки равенства прямоугольных треугольников. Свойства прямоугольного треугольника»

Этап актуализации знаний

Устный опрос

1. Формулировка 1 признака равенства треугольников

2. Формулировка 2 признака равенства треугольников

3. Формулировка 3 признака равенства треугольников

Какие темы мы изучали на последних уроках? ( сумма углов треугольника, неравенство треугольника, внешний угол треугольника..)

— какая фигура называется треугольником?

— по каким элементам мы классифицировали треугольников? ( по сторонам, по углам)

— какие существуют виды треугольников по сторонам? ( разносторонние, равнобедренные, равносторонние)

-на какие виды делятся треугольники по углам? ( остроугольные, тупоугольные, прямоугольные).

Учитель фиксирует на доске названные виды треугольников в два столбика с помощью табличек и магнитов.

Этап изучения нового материала

Треугольник называется прямоугольным, если у него есть прямой угол.

Сумма двух других углов прямоугольного треугольника равна

Сторона треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны- катетами.

Из истории математики

Прямоугольный треугольник занимал почетное место уже Вавилонской геометрии, упоминание о нем часто встречается в папирусе Ахмеса.

Термин «гипотенуза» происходит от греческого слова «hypoteinsa» (ипонейнуоза), обозначающее «тянущаяся над чем-либо», «стягивающая».

Термин «катет» происходит от греческого слова «катетос», которое означало отвес, перпендикуляр

Среди прямоугольных треугольников широкое распространение получил так называемый египетский треугольник. Кто из вас знает или слышал об этом?

Это треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов землемерами и архитекторами. Для построения прямого угла использовался шнур или веревка, разделенная отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.

В прямоугольных треугольниках мы имеем один общий элемент – прямой угол.

Поэтому признаки равенства прямоугольных треугольников можно переформулировать так:

1 признак. Если катеты одного треугольника соответственно равны катетам другого треугольника, то такие треугольники равны.

2 признак. Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого, то такие прямоугольные треугольники равны.

3 признак. Если гипотенуза и острый угол другого треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны.

4 признак. Если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого треугольника, то такие прямоугольные треугольники равны.

1 признак равенства прямоугольных треугольников является следствием 1 признака равенства треугольников. 2 и 3 признаки равенства прямоугольных треугольников непосредственно следуют из 2 признака равенства треугольников.

Свойства прямоугольного треугольника

1. Сумма двух острых углов прямоугольного треугольника равна 90⁰.

2. Катет прямоугольного треугольника, лежащий против угла в 30⁰,

равен половине гипотенузы.

3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30⁰.

Этап закрепления нового материала

Решение заданий у доски

Карточка

Задание. Найдите пары равных треугольников и запишите их номера в таблицу:

Найди пары равных треугольников и запишите их номера в таблицу:

infourok.ru