Урок математики на тему «Дроби и проценты», (6 класс)
Тема урока: « Дроби и проценты».
Цель: обобщить и систематизировать знания по темам: сложение и вычитание обыкновенных дробей, умножение и деление обыкновенных дробей, проценты;
развивать коммуникабельность, креативность, умение анализировать, обобщать, сравнивать, выделять главное;
воспитывать познавательный интерес к предмету и уверенность в своих силах.
Педагогические задачи:
Создать условия для повышения мотивации учащихся в потребности усвоения новых умений;
Организовать ситуацию постановки учебной проблемы;
Помочь учащимся в постановке цели урока и поиске путей решения данной проблемы;
Создать ситуацию самостоятельного поиска новых способов решения в группе, в паре;
Создать условия для самоконтроля и самооценивания.
Планируемые результаты:
предметные: формулировать и применять правила действий с обыкновенными дробями; формировать умение решать задачи на дроби, используя различные стратегии и способы рассуждений;
метапредметные: применять знания в различных ситуациях; предлагать разные варианты в зависимости от предложенной ситуации; применять приёмы самоконтроля при выполнении заданий;
личностные: организовывать свою деятельность, т.е. ставить личные цели, их достигать и оценивать результаты.
Тип урока: урок систематизации и обобщения знаний и умений.
Формы работы: самостоятельная, групповая, фронтальная работа.
Оборудование: мультимедийный проектор, компьютер, доска, задачники.
План урока:
Организационный этап.
Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Актуализация знаний.
Обобщение и систематизация знаний
Физкультминутка.
Применение знаний и умений в новой ситуации.
Контроль усвоения, обсуждение допущенных ошибок и их коррекция.
Информация о домашнем задании, инструктаж по его выполнению.
Рефлексия.
Ход урока.
Организационный этап.
Здравствуйте ребята. Посмотрите, какая сегодня замечательная погода, как ярко светит солнце. Я надеюсь, что после сегодняшнего урока ваше настроение будет таким же солнечным. Начнем урок.
Отгадайте загадку:
Без чего не могут обойтись математики, барабанщики и даже охотники? (Дробь) (Слайд 3 )
Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Ребята, а нужны ли дроби? Может быть, можно обойтись без них?
(Ответы детей)
Вы правы, конечно, нужны. На протяжении всей своей жизни мы постоянно сталкиваемся с дробями. А сейчас на уроках учимся выполнять различные действия с ними. Какова же тема сегодняшнего урока?
(Учащиеся формулируют тему урока).
А сейчас каждый ряд составит кластер: в центре — название дроби, а по сторонам — умения.
Составляют кластеры, передают друг другу по цепочке, дополняют, обсуждают (приложение 1). Вместе с учителем делают вывод, определяют цели урока.
Актуализация знаний.
— Давайте узнаем на деле, насколько дружим с дробями:
Правило вычитания дробей .(Ответы детей)
Соотнесите выражение и его значение: а) ; б) ; в) .
1) ; 2) ; 3). ( Слайд 4)
Правило сложения дробей. (Ответы детей)
Сложите дроби: а) ; б) ; в) . (Слайд 5)
Расставь числа так, чтобы получилось верное равенство. (Слайд 6 )
Как умножить дробь на дробь? (Ответы детей)
Как найти часть от числа? Как найти процент от числа? (Ответы детей)
Найдите: а) четвертую часть от 100; б) пятую часть от 80 ; в) 25% от 100; г)20% от 80. (Ответы детей)
(Ответы детей)
Ответы: а) 25 ; б) 16 ; в) 25 ; г) 16.
Обратить внимание детей на одинаковые ответы в заданиях. Ученики делают вывод: 25% = ; 20% = . (Слайд 7 )
Обобщение и систематизация знаний
Работа по учебнику. Анализируем и рассуждаем.
— Иногда нужное число процентов от величины можно найти совсем просто. Например, чтобы найти 10% от 100, нужно разделить 100 на 10.
Рассматривают таблицу. Приводят свои примеры.
Проценты | Дроби |
10% | |
20% | |
25% | |
50% | |
75% |
Вопрос: Как записать дробь в виде процентов?
стр. 27, № 114.
Решение задач.
Стакан вмещает 200 г молока. В него налили 160 г. Какая часть стакана осталась ненаполненной?
Обсуждается решение задачи. К доске идут два ученика, предложившие разные способы решения.
1 способ. 1) 160 : 200 = стакана наполнено.
2) 1 — стакана не наполнена.
Ответ: стакана.
2 способ. 1) 200 – 160 = 40 (г) – молока не долили в стакан.
2) 40 : 200 = стакана не наполнена.
Ответ: стакана.
— На сколько процентов наполнен стакан? (Ответы детей)
Записать на доске и в тетрадях :
В первый день туристы прошли 40% намеченного пути, во второй день 1/4 пути, а в третий день остальные 14 км.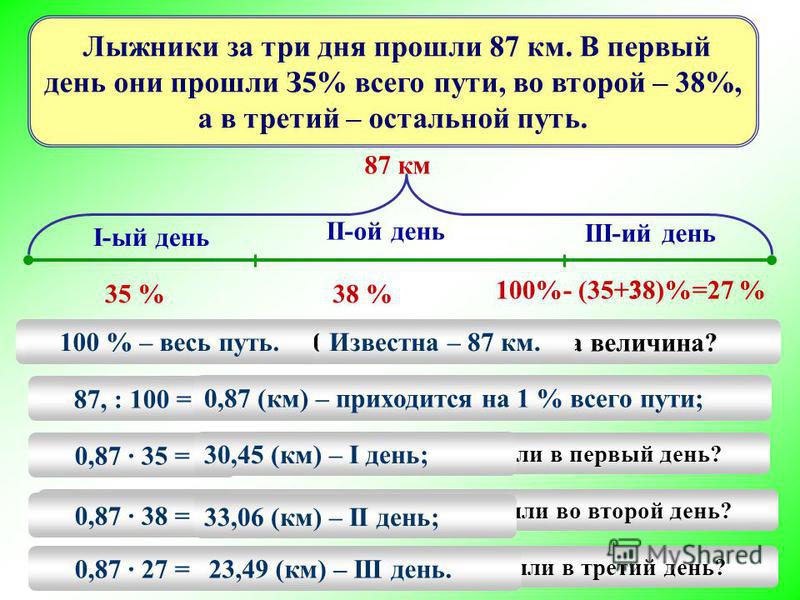 Чему равна длина всего пути?
Чему равна длина всего пути?
Один ученик решает задачу у доски с полным объяснением.
Решение: 40% =
пути прошли туристы за два дня.
пути прошли в третий день.
14 : (км) – длина всего пути.
Ответ: 40 км.
— Стр. 28 из учебника № 118.
Физкультминутка.
Ребята, давайте немного отдохнем. Все встали около своих парт. Выполним «Математическую зарядку».
Под музыку выполняют « Математическую зарядку». (Слайд 8 )
«Да» — руки вверх, «нет» — руки вниз.
В дроби знаменатель – 9.
В дроби числитель – 6.
Дробь — неправильная.
1 копейка – 1% рубля.
30 % — .
Молодцы! А теперь продолжим работу.
Применение знаний и умений в новой ситуации.
1. Осваивает алгоритмы.
Заполните самостоятельно таблицу. Затем выполните взаимопроверку.
Дробь | Дробь со знаменателем 100 | Проценты |
2.Анализируем и рассуждаем.
Следующее задание выполним в группах.
стр. 26 № 97(б)
Ученики работают в группах по 4 человека. Затем проверяется решение .
Контроль усвоения, обсуждение допущенных ошибок и их коррекция.
А сейчас выполним самостоятельную работу по вариантам
(приложение 2). У каждого на столе карточка с заданием. На выполнение работы 10 минут.
Выполняют самостоятельную работу в тетрадях. Четыре человека работают на ноутбуках, выполняют тест по теме «Дроби и проценты». Используется электронное приложение к учебнику.
По окончании выполняется проверка. Дети видят ответы на слайде. (Слайд 9 )
Каждый проверяет свою работу самостоятельно, исправляет ошибки. Проводится анализ наиболее распространенных ошибок.
Информация о домашнем задании, инструктаж по его выполнению.
Урок подходит к концу. Ребята, откройте дневники и запишите задание на дом.
На доске и слайде записано домашнее задание: Задачник: п. 1.6,
№ 97(а), 101(а-г), 108, 120
(Слайд 10 )
Откройте задачники. Найдите все номера, записанные на доске. Внимательно прочтите задания. Какие правила нужно вспомнить для выполнения домашнего задания? (Ответы детей)
IX.Рефлексия
Закончить урок мне бы хотелось словами знаменитого русского писателя Льва Толстого:
«Человек подобен дроби:
в знаменателе – то, что он о себе думает,
в числителе – то, что он есть на самом деле.
Чем больше знаменатель, тем меньше дробь».
Как вы понимаете эти слова? (Ответы детей)
Да, ребята, можно сказать, что Толстой вывел «формулу» для обозначения человеческого характера.
Из математики мы знаем, что если знаменатель равен числителю, то будет единица. Но также мы знаем, что знаменатель не должен равняться нулю, так как вся дробь не будет иметь смысла. И ещё, чем больше знаменатель, тем меньше дробь.
Очень редкое явление, когда «знаменатель» равен «числителю» , то есть мнение окружающих не всегда совпадает со своей самооценкой.
Родители с детства учили нас тому, что любить себя плохо, что приличный человек должен думать сначала о других, о потом уже о себе.
Я считаю, что уважать себя должен каждый. Это просто необходимо для сохранения чувства собственного достоинства. Но любить себя надо в меру. Если человек думает только о себе, то он эгоист. Нужно всегда думать о чувствах других.
Я надеюсь, что слова великого писателя запомнятся вам на всю жизнь.
Спасибо за урок! (Слайд 11)
Презентация к уроку математики «Дроби и проценты»
PPTX / 390.49 Кб
5.6.1. Проценты.
Автор Татьяна Андрющенко На чтение 1 мин. Просмотров 820 Опубликовано
Тема «Проценты» станет понятнее с книгой «Как решать задачи на проценты»! Узнать подробнее здесь!
- Процентом называется одна сотая часть.
- Чтобы выразить проценты дробью или натуральным числом, нужно число процентов разделить на 100%. (4%=0,04; 32%=0,32).
- Чтобы выразить число в процентах, нужно его умножить на 100%. (0,65=0,65·100%=65%; 1,5=1,5·100%=150%).
- Чтобы найти проценты от числа, нужно выразить проценты обыкновенной или десятичной дробью и умножить полученную дробь на данное число.
- Чтобы найти число по его процентам, нужно выразить проценты обыкновенной или десятичной дробью и разделить на эту дробь данное число.
- Чтобы найти, сколько процентов составляет первое число от второго, нужно разделить первое число на второе и результат умножить на 100%.
Пример 1. Выразить проценты дробью или натуральным числом: 130%, 65%, 4%, 200%.
- 130%=130%:100%=130:100=1,3;
- 65%=65%:100%=65:100=0,65;
- 4%=4%:100%=4:100=0,04;
- 200%=200%:100%=200:100=2.

Пример 2. Записать следующие числа в виде процентов: 1; 1,5; 0,4; 0,03.
- 1=1·100%=100%;
- 1,5=1,5·100%=150%;
- 0,4=0,4·100%=40%;
- 0,03=0,03·100%=3%.
Пример 3. Найти 15% от числа 400.
Решение.
1) 15%=15%:100%=15:100=0,15;
2) 0,15·400=60.
Ответ: 60.
Пример 4. Найти число, если 18% его равны 900.
Решение.
1) 18%=18%:100%=18:100=0,18;
2) 900:0,18=90000:18=5000.
Ответ: 5000.
Пример 5. Определить, сколько процентов составляет число 320 от числа 1600.
Решение.
(320:1600)·100%=0,2·100%=20%.
Ответ: 20%.
Тема: Обобщение и систематизация знаний по теме «Проценты».
Районный конкурс «Я расскажу вам о тыкве»
Муниципальное бюджетное общеобразовательное учреждение «Прелестненская средняя общеобразовательная школа» Районный конкурс «Я расскажу вам о тыкве» Номинация «Методическая разработка урока» Выполнила:
МАТЕМАТИКА И ЗДОРОВЬЕ
Проценты МАТЕМАТИКА И ЗДОРОВЬЕ на тему: «Решение задач на проценты» Здоровье все, но все без здоровья ничто Выразите в процентах. 7 100 = 29 100 = 125 100 = 7 % 29 % 125 % 30 % 0,3 = 3,7 = 21 % 0,21 =
ПодробнееДействия с рациональными числами (VI класс)
Действия с рациональными числами (VI класс) Е. В. Синютыч, учитель математики высшей категории СШ 16 г. Пинска Цель урока: отработка умений систематизировать знания правил по выполнению действий с рациональными
В. Синютыч, учитель математики высшей категории СШ 16 г. Пинска Цель урока: отработка умений систематизировать знания правил по выполнению действий с рациональными
3 класс (1-4). Программа Истоминой Н.Б.
3 класс (1-4). Программа Истоминой Н.Б. Тема: «ПЯТИЧНАЧНЫЕ И ШЕСТИЗНАЧНЫЕ ЧИСЛА». ( Первый урок.) Цель урока: ввести понятие «пятизначные» числа, научить читать и записывать такие числа. Задачи: ОБРАЗОВАТЕЛЬНЫЕ:
ПодробнееМетодическая разработка открытого урока
Довлатбегян Виктория Александровна, учитель математики МБОУ «Лицей» г.протвино, МО Методическая разработка открытого урока «Разложение многочлена на множители с помощью комбинации различных приемов» Алгебра.
ПодробнееТехнологическая карта урока математики.
Технологическая карта урока математики. Андреева Надежда Николаевна Тема урока «Умножение десятичных дробей на натуральное число» (5 класс) Цели (задачи) урока образовательные: Формировать умения выполнять
Подробнее Урок математики в 5 классе. Тема:
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа 7 города Алексеевки Белгородской области Урок математики в 5 классе Тема: Учитель математики: Васильченко Людмила Михайловна
ПодробнееСценарий конкурсной программы
Сценарий конкурсной программы «Наше здоровье в наших руках!» Цель конкурса: сформировать у обучающихся потребность в здоровом образе жизни. Задачи: помочь ученикам осознать важность разумного отношения
ПодробнееКонспект урока по математике 6 «б» класс
Конспект урока по математике 6 «б» класс «Умножение и деление обыкновенных дробей» (Слайд 1) Разработала учитель математики МБОУ СОШ 4 г. вязники Тимофеева Наталья Владимировна. Тип урока: урок обобщения
вязники Тимофеева Наталья Владимировна. Тип урока: урок обобщения
Урок 2 ( 14 22; с. 4, 5 учебника)
сумму? (Сложения.) разность? (Вычитания.) на сколько больше или меньше? (Вычитания.) VI. Домашнее задание 1. Выполнить задания 12, 13 (с. 4, учебник). 2. Индивидуальное задание на развитие внимания и сообразительности:
Подробнее6 урок из 7 части речи
Технологическая карта урока Предмет: русский язык класс: 3 Учитель: Корякова Анастасия Александровна Тема урока Место урока по теме (в разделе/главе) Разбор глагола как 6 урок из 7 части речи Тип урока
ПодробнееСТРУКТУРА И ХОД УРОКА
ПЛАН-КОНСПЕКТ УРОКА Умножение обыкновенных дробей. ФИО (полностью) Шишканова Наталья Алексеевна. Место работы Муниципальное бюджетное общеобразовательное учреждение городского округа Тольятти «Школа 7».
Тема урока: «Длина окружности».
Муниципальное общеобразовательное учреждение «Заречная средняя общеобразовательная школа» Открытый урок по математике в 6 классе Тема урока: «Длина окружности». Урок подготовила и провела учитель математики
Подробнее7. ПК с программой «Живая математика»
Урок-исследование 8 класс Тема: Площадь треугольника Дидактическая цель: создать условия для осознания и осмысления блока новой учебной информации средствами практической и исследовательской работ. Тип
ПодробнееТема урока: «Десятичные дроби»
Тема урока: «Десятичные дроби» 1 ФИО ХачетловаЗалинаСаадуловна Место работы МКОУ «Гимназия 1» го Нальчик Должность Учитель математики 4 Предмет Математика 5 Класс 5 6 Тема и номер урока в теме Дествия
Подробнее! Черный ящик Тест-прогноз
Длина окружности и площадь круга Цели: 1. Обобщить и систематизировать материал по данной теме. 2. Провести диагностику усвоения системы знаний и умений и ее применения для выполнения практических заданий
Обобщить и систематизировать материал по данной теме. 2. Провести диагностику усвоения системы знаний и умений и ее применения для выполнения практических заданий
Технологическая карта урока
Технологическая карта урока Предмет: математика Класс: 5 Учебник (УМК): Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 5 класс: Учебник для общеобразовательных учреждений. — М.:
Подробнее«Десятичная запись дробных чисел»
чисел.», ГОСУДАРСТВЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ЛИЦЕЙ 470 КАЛИНИНСКОГО АДМИНИСТРАТИВНОГО РАЙОНА САНКТ-ПЕТЕРБУРГА Методическое объединение учителей математики Математика Разработка урока математики
Конспект занятия по зубам.
Конспект занятия по зубам. Тема: «Здоровые зубы — здоровью любы». Цель: расширять представления детей об уходе за зубами, продолжать знакомить детей с функцией и строением зубов; формировать привычки следить
ПодробнееТехнологическая карта урока
Технологическая карта урока Ф.И.О. Ковалева Юлия Сергеевна Предмет: Математика Класс: 5 класс Автор УМК: Математика 5 класс: учебник для общеобразовательных учреждений А. Г. Мерзляк и др. Тема урока: Сложение
ПодробнееРазработка и проведение бинарного урока.
Разработка и проведение бинарного урока. Конспект урока Бинарный урок швейного дела и математики Класс 5 Тема: Построение чертежа наволочки с клапаном. Преобразование чисел, полученных при измерении длины.
ПодробнееОборудование: проектор, ноутбуки, рабочие листы, тетради, учебники, раздаточный материал
Достаточно часто в школах мы встречаем ситуацию, когда учитель прекрасно объясняет материал, учащиеся его внимательно слушают, но через несколько минут, выходя из кабинета, забывают, о чем шла речь на
ПодробнееНахождение числа по заданному значению его дроби
Представим себе такую историю…
–
Саша, чем ты занимаешься? – спросил у друга Паша.
– Да я вчера с родителями ездил на дачу, – начал Саша. – Папа сказал, что за поездку наш автомобиль израсходовал бака бензина, что составляет 36 литров. Вот мне и стало интересно, какой же тогда объём всего бака в литрах нашей машины.
– В 5-м классе мы решали похожие задачи, – вспомнил Паша. – Чтобы ответить на твой вопрос, сначала нужно вычислить, сколько литров составляет часть объёма бака машины. Получим литров. А затем уже посчитать объём всего бака. Получим литров.
– То есть объём бака нашей машины всего лишь 60 литров? – удивился Саша. – Паша, ты уверен, что всё правильно посчитал?
– Вроде бы, да… – задумался Паша. – Но давай лучше уточним у Мудряша.
– Ребята, прежде чем я расскажу вам о нахождении числа по заданному значению дроби, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!
– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Зная, что 36 литров составляют объёма всего бака машины, вы нашли весь объём бака в литрах Сашиной машины. Подобные задачи называют задачами на нахождение числа по заданному значению его дроби. Нахождение числа по заданному значению его дроби выполняется тогда, когда известно, сколько составляет часть от целого, и нужно «восстановить» само целое.
– Вы правильно вычислили объём в литрах бака машины, – продолжил Мудряш, – однако найденный ответ — 60 литров — можно было получить и другим способом. Сейчас мы с вами вместе его выведем. Итак, давайте объём всего бака машины, то есть целое, обозначим за х. Мы знаем, что всего бака, то есть часть от целого, равны 36 литрам.
–
Мне кажется я догадываюсь, – сказал Паша. – Нам поможет нахождение дроби от
числа. Чтобы найти дробь от числа, можно число умножить на эту дробь. Так
как х литров – это целое, а –
это часть от целого, то можем х умножить на и
получим 36.
Так
как х литров – это целое, а –
это часть от целого, то можем х умножить на и
получим 36.
– Правильно! – сказал Мудряш.
– Чтобы найти неизвестный множитель, – продолжил Саша, – нужно произведение разделить на известный множитель. Применим правило деления дробей. Тогда х = 60 литров.
– Молодцы! – похвалил ребят Мудряш. – А теперь давайте подумаем, что же мы сделали для того, чтобы узнать, чему равно наше целое?
– Мы известную нам часть разделили на долю, которую она составляла, – ответили мальчишки.
– Правильно! – согласился Мудряш. – То есть для того, чтобы выяснить, какой объём всего бака машины, достаточно число 36 разделить на дробь . Рассмотренный пример иллюстрирует следующее правило.
Запомните! – сказал Мудряш. – Чтобы найти число по заданному значению его дроби, можно данное значение разделить на эту дробь.
– Продолжу автомобильную тему, – улыбнулся Мудряш. – Давайте решим такую задачу: машина проехала 72 километра, что составило 30 % всего пути. Какой путь должна проехать машина?
– Запишем 30 % в виде десятичной дроби, – начал Паша. – Нам известно, что 72 километра – это 30 % всего пути. Значит, чтобы найти весь путь, который должна проехать машина, нужно 72 разделить на 0,3. Получим, что машина должна проехать 240 километров.
– Молодец! – похвалил Пашу Мудряш. – Рассмотренный пример иллюстрирует следующее правило. Запомните! Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь.
– А теперь давайте потренируемся и найдём следующие числа по известным их частям, – предложил Мудряш.
–
Нам нужно найти число, если известно, что от
него равны 3,6, – начал Паша. – Чтобы найти число по заданному значению его
дроби, можно данное значение разделить на эту дробь. Десятичную дробь 3,6
представим в виде смешанного числа .
Можем сократить числитель и знаменатель дробной части на 2. Затем смешанное
число представим в виде неправильной дроби .
Применим правило деления дробей. Сократим числитель и знаменатель на 2. Получим
дробь .
Это неправильная дробь, так как числитель больше знаменателя. Выделим целую
часть. Получим .
Десятичную дробь 3,6
представим в виде смешанного числа .
Можем сократить числитель и знаменатель дробной части на 2. Затем смешанное
число представим в виде неправильной дроби .
Применим правило деления дробей. Сократим числитель и знаменатель на 2. Получим
дробь .
Это неправильная дробь, так как числитель больше знаменателя. Выделим целую
часть. Получим .
– Перейдём к следующему пункту, – продолжил Саша. – Нам нужно найти число, если от него равно 0,7. Разделим 0,7 на дробь . Десятичную дробь 0,7 представим в виде обыкновенной дроби. Применим правило деления дробей. Сократим на 7. Получим дробь .
– В следующем пункте нам нужно найти число, если 25 % от него равно , – сказал Саша. – 25 % представим в виде обыкновенной дроби. Это будет . А теперь разделим на . Воспользуемся правилом деления дробей. Сократим на 4. И получим 1.
– В последнем пункте нужно найти число, если % от него равно 5, – сказал Паша. – % представим в виде обыкновенной дроби. Мы знаем, что для того, чтобы проценты перевести в число, нужно убрать знак процента и разделить число на 100. Тогда получим дробь . А теперь 5 разделим на . Воспользуемся правилом деления дробей. Получим 1250.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и решим несколько задач.
Задача первая: спортсмен пробежал 300 метров, что составило всей дистанции. Какова длина дистанции?
Решение: нам известно, что спортсмен пробежал 300 метров и это составляет всей дистанции. Чтобы найти число по заданному значению его дроби, можно данное значение разделить на эту дробь. Следовательно, 300 разделим на . Применим правило деления дробей. Сократим на 3. Получим, что вся дистанция равна 800 метрам. Не забудем записать ответ.
Задача
вторая: в киоске в первый день продали 40 % всех пакетов, во
второй день 53 % всех пакетов, а в третий день – остальные 847 пакетов. Сколько
пакетов продал киоск за три дня?
Сколько
пакетов продал киоск за три дня?
Решение: так как в первый день продали 40 % всех пакетов, а во второй день 53 % всех пакетов, то за два дня продали всех пакетов. Следовательно, в третий день продали всех пакетов. Мы знаем, что эти 7 % пакетов, проданных в третий день, равны 847. Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь. 7 % представим в виде обыкновенной дроби. Затем 847 разделим на . Применим правило деления дробей. Сократим дробь на 7. Получим, что за три дня в киоске продали 12 100 пакетов. Запишем ответ.
И последняя задача: на школьной выставке 220 рисунков выполнены красками, а остальные – карандашами. Сколько всего рисунков на выставке, если карандашами выполнено всех рисунков?
Решение: обозначим за х количество всех рисунков на выставке. Тогда – это количество рисунков, нарисованных карандашами. Нам известно, что карандашами нарисовано всех рисунков. Чтобы найти число по заданному значению его дроби, можно данное значение разделить на эту дробь. Следовательно, можем составить уравнение: . Решим это уравнение. Умножим левую и правую часть нашего равенства на . Получим уравнение . Перенесём все числа с переменной в левую часть равенства, а без переменной в правую. Упростим уравнение. Получим . Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Применим правило деления дробей. Сократим на 4. Отсюда . Получим, что всего 385 рисунков на выставке. Не забудем записать ответ.
Основы процента — бесплатный урок
Изучите основы концепции процентов в этом простом уроке! Процент (или процент) означает одну сотую. Следовательно, 1% означает 1/100 или одну сотую, а 7% означает 7/100 или семь сотых. Поскольку проценты — это всего лишь сотые части (что означает, что они ДРОБИ), мы можем очень легко записать их как дроби и как десятичные дроби.
Поскольку проценты — это всего лишь сотые части (что означает, что они ДРОБИ), мы можем очень легко записать их как дроби и как десятичные дроби.
Основные концепции и идеи этого урока также объясняются в этом видео:
| ||||||||||
| ||||||||||
1.Напишите заштрихованную часть и незатененная часть в виде дробей, десятичных знаков и процентов.
2. Запишите проценты, дроби и десятичные дроби.
|
|
3. Обычно семь из каждых 100
младенцев, рожденных в больнице Ривер-Крик, родилось
Обычно семь из каждых 100
младенцев, рожденных в больнице Ривер-Крик, родилось
дефект, большинство из них мелкие дефекты.
а. Какой типичный процент младенцев
врожденные дефекты?
г. Какой типичный процент младенцев у , а не у ?
врожденные дефекты?
г. О том, как
вы ожидаете найти
детей с врожденными дефектами в группе из 500
младенцы?
Прочие фракции в процентах
|
4.Напишите, какая часть
карандаши короткие, как в долях, так и в процентах.
Используйте эквивалентные дроби.
|
|
5. Преобразуйте дроби в эквивалентные дроби со знаминателем 100,
и запишите их
Преобразуйте дроби в эквивалентные дроби со знаминателем 100,
и запишите их
в процентах.
|
|
6.Напишите, какая часть
прямоугольник заштрихован и какая часть незатенена,
как дроби, так и
проценты.
| ||||||||||
| ||||||||||
7. Запишите дробями, десятичные дроби и проценты.
|
|
8. Записывайте проценты, дроби и десятичные дроби.
|
|
9. Запишите дроби в процентах.
а. Около 4/5 (_______%) населения США 14 лет или старшая.
г. Около 2/25 (_______%) населения мира проживает в Северная Америка.
г. Африканский континент занимает около 1/5 (_______%) Общая масса суши Земли.
10. Во дворе дома Сэнди растут два дерева. Более высокий
один на 5/4 высоты на
короче.
а. Напишите второе предложение, используя вместо этого проценты доли.
г. Если более короткое дерево 160 см, какова высота? более высокое дерево?
|
11.Запишите дроби в процентах. Используйте длинное деление. Округли свой
ответы с точностью до процента.
|
|
12.Запишите дроби в процентах.
Округлите ответы до
до ближайшего процента.
а. Около 1/20 (_________%) населения г.
Индии 65 лет и старше.
(оценка 2009 г.)
г. Около 13/100 (
________%) населения Австралии 65 лет и старше
(Оценка на 2009 год)
13. Напишите в процентах. Округлите свои ответы на ближайший процент.
а. 8/7
г. 1 3/8
|
См. Также
Процент числа с использованием мысленной математики — бесплатный урок
Как считать проценты чисел — бесплатный урок
Как считать проценты — бесплатное занятие
Основы процента сдачи — бесплатное занятие
Интерактивный инструмент дроби, десятичной дроби и процента
Этот инструмент показывает дробь визуально (столбик или круговая диаграмма) и преобразует дробь в проценты и десятичные дроби.Вы можете показать или скрыть эквивалентные процентные и десятичные дроби.
/interactives/fraction_decimal_percentage.php
Этот урок взят из книги Марии Миллер «Math Mammoth Percent» и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Урок шестого класса Преобразование с процентами
Учащиеся разработают алгоритмы преобразования дробей, десятичных знаков и процентов.
Что такое процент? Если вы заработали 90% на тесте, что это значит?
Студенты должны понимать, что проценты — «из 100», поэтому 90% будет означать, что они заработали 90 из 100.
Я дам студентам формальное определение процентов.
Процент — отношение части целого, разделенной на сотые, к 100
Это приведет нас к замене дробей на проценты.
Доли и проценты
Пример 1. Запишите 11/20 в процентах
Как мы можем применить определение процентов и использовать пропорцию, чтобы найти наш ответ?
Студенты должны установить пропорцию со знаминателем 100 и использовать свои знания эквивалентных дробей, чтобы найти числитель.
Десятичные числа и проценты
Пример 2 — Запишите 5/8 в процентах
Студенты могут заметить, что, хотя я упоминал, что мы перейдем от десятичных дробей к процентам, я привел им пример с дробью.
Можем ли мы легко использовать пропорцию для преобразования 5/8 в процент? Почему нет?
Студенты должны понимать, что, поскольку 8 не может быть легко разделено на 100, метод пропорции будет затруднен.
Как мы можем преобразовать 5/8 в десятичную дробь?
Студенты должны использовать свои предыдущие знания и преобразовать 5/8 в 0.625.
Я объясню, что для изменения десятичной дроби 0,625 на процент нам нужно умножить на 100, что даст нам 62,5%
Попробуем вместе еще один пример.
Пример 3 — Запишите 4/7 в процентах.
Какую стратегию лучше использовать для этой фракции?
Студенты должны предложить нам изменить дробь на десятичную, а затем умножить десятичную дробь на 100.
Есть ли ярлык вместо умножения десятичных знаков на 100?
Студенты могут заметить, что мы пришли бы к такому же ответу, если бы переместили десятичную запятую на 2 позиции вправо.
Процент числового урока
*** Для учащихся без доступа к Интернету: возьмите раздаточный материал с заметками в PowerPoint и распечатайте форму WSQ для заполнения. ****
В классе (весь класс):
I. Сделать сейчас — размещено по правому борту (5 минут)
II. Обзор видео-УРОКА: в группах обсудите следующие наводящие вопросы:
Напишите ответы вместе, а затем ПОСМОТРИТЕ МЕНЯ (7 минут):
1.Как вы рассчитываете ПРОЦЕНТ ОТ ИТОГО? Например, покажите, как вы вычисляете 25% от 160. Объясните 2 СПОСОБА:
2. КАК ВЫ НАЙТИ ИТОГО, КОГДА ИМЕЕТЕ заданное количество? Например, если в 6-м классе нашей школы 150 мальчиков, что составляет 20% мальчиков, сколько всего там детей? Объясните, как вы найдете этот ответ.
3. Как найти процентное соотношение, если дана общая и частичная сумма. Например: если вы правильно ответили на 18 вопросов из 25 в тесте, как вы рассчитаете процент правильных ответов? Какой процент вы ошиблись?
3.Как рассчитать цену со скидкой на товар? Если пара обуви стоит 50 долларов, а скидка в магазине составляет 20%, какова новая стоимость товара? Объяснять.
4. Как рассчитывается налог с продаж? Если вы покупаете пончики в магазине за 25 долларов, а налог составляет 7%, как вы вычисляете новую фактическую стоимость пончиков, которые вам нужно заплатить?
III. СОЗДАЙТЕ ПРАКТИЧЕСКИЙ ПАКЕТ И ЗАПОЛНИТЕ (только четные числа)!
IV. ВЫХОДНЫЕ БИЛЕТЫ (2)
V. Процент проблем с открытым текстом -RSL! Докажи, что ты Мастер Процентов!
В.ДЕЯТЕЛЬНОСТЬ:
Посетите: http://schools.mangahigh.com/lvmooremiddleschool. Пожалуйста, обратитесь ко мне, чтобы узнать ваше имя пользователя и пароль. Когда вы войдете в систему, вы увидите несколько «проблем», над которыми нужно поработать. Выберите следующее: преобразовать проценты в дроби и десятичные дроби, ИЛИ ПРОЦЕНТ ЧИСЛА, ИЛИ процентное изменение.
Прочтите инструкцию «как играть». Наберите не менее 5000 очков, чтобы перейти к следующему заданию!
VI. Магазин процентов — BREGMART!
VII. Проект Percents — Вы можете работать над этим в классе и дома!
Проценты — Введение | SkillsYouNeed
Термин «процент» означает «из ста».В математике проценты используются как дроби и десятичные дроби, как способы описания частей целого. Когда вы используете проценты, считается, что целое состоит из ста равных частей. Символ% используется для обозначения числа в процентах, реже может использоваться сокращение «pct».
Вы увидите проценты почти везде: в магазинах, в Интернете, в рекламе и в средствах массовой информации. Умение понимать, что означают проценты, — это ключевой навык, который потенциально сэкономит вам время и деньги, а также сделает вас более трудоспособным.
Значение процентов
Процент — это термин из латинского языка, означающий «из ста».
Таким образом, вы можете рассматривать каждое «целое» как разбитое на 100 равных частей, каждая из которых составляет один процент.
В поле ниже показано это для простой сетки, но это работает одинаково для всего: дети в классе, цены, галька на пляже и т. Д.
Визуализация в процентах
В приведенной ниже сетке 100 ячеек.
- Каждая ячейка равна 1% от целого (красная ячейка составляет 1%).
- Две ячейки равны 2% (зеленые ячейки).
- Пять ячеек равны 5% (синие ячейки).
- Двадцать пять ячеек (фиолетовые ячейки) равны 25% от целого или одной четверти (¼).
- Пятьдесят ячеек (желтые ячейки) равны 50% от целого или половины (½).
Сколько там незатененных (белых) ячеек? Каков процент незатененных ячеек?
Ответ: Есть два способа решить эту проблему.
- Подсчитайте белые клетки. Их 17 штук. Таким образом, из 100 ячеек 17% белые.
- Сложите количество других ячеек и возьмите их из 100. Есть одна красная ячейка, две зеленые, пять синих, 25 фиолетовых и 50 желтых. В сумме получается 83. 100−83 = 17. Опять же, из 100 ячеек 17 белые, или 17%.
Легко вычислить процентное соотношение, когда есть 100 отдельных «вещей», составляющих целое, как в таблице выше.Но что, если их больше или меньше?
Ответ состоит в том, что вы конвертируете отдельных элементов, составляющих целое, в проценты. Например, если бы в сетке было 200 ячеек, каждый процент (1%) составлял бы две ячейки, а каждая ячейка — полпроцента.
Мы используем проценты, чтобы упростить вычисления. Работать с частями от 100 намного проще, чем с третями, двенадцатыми и т. Д., Особенно потому, что довольно много дробей не имеют точного (неповторяющегося) десятичного эквивалента.Важно отметить, что это также значительно упрощает сравнение процентов (которые все имеют общий знаменатель 100), чем между дробями с разными знаменателями. Отчасти поэтому так много стран используют метрическую систему измерения и десятичную валюту.
Определение процента
Общее правило для нахождения заданного процента от данного целого:
Определите значение 1%, затем умножьте его на процент, который вам нужно найти.
Это легче всего понять на примере. Предположим, вы хотите купить новый портативный компьютер. Вы проверили местных поставщиков, и одна компания предложила вам скидку 20% от прейскурантной цены в 500 фунтов стерлингов. Сколько будет стоить ноутбук у этого поставщика?
В этом примере вся сумма составляет 500 фунтов стерлингов или стоимость портативного компьютера без учета скидки. Процент, который вам нужно найти, составляет 20% или скидку, предлагаемую поставщиком. Затем вы собираетесь снять это с полной цены, чтобы узнать, сколько вам будет стоить ноутбук.
Затем вы собираетесь снять это с полной цены, чтобы узнать, сколько вам будет стоить ноутбук.
Начните с вычисления значения 1%
Один процент от 500 фунтов стерлингов составляет 500 фунтов стерлингов ÷ 100 = 5 фунтов стерлингов.
Умножьте это на процент, который вы ищете
После того, как вы вычислили значение 1%, вы просто умножаете его на интересующий вас процент, в данном случае на 20%.
£ 5 × 20 = 100 £.
Теперь вы знаете, что скидка составляет 100 фунтов стерлингов.
Завершите расчет, добавляя или вычитая, если необходимо.
Цена ноутбука, включая скидку, составляет 500–20% фунтов стерлингов, или 500–100 фунтов стерлингов = 400 фунтов стерлингов .
Простой способ вычислить 1% от любого числа
1% — это целое (что бы это ни было), деленное на 100.
Когда мы делим что-то на 100, мы просто перемещаем значения разряда на два столбца вправо (или перемещаем десятичную точку на два разряда влево).
Вы можете узнать больше о числах и разрядах на нашей странице Числа , но вот краткое резюме:
500 фунтов стерлингов состоит из 5 сотен, ноль десятков и нулевых единиц.500 фунтов стерлингов также имеют ноль пенсов (центов, если вы работаете в долларах), поэтому их можно записать как 500,00 фунтов стерлингов с нулевыми десятыми или сотыми долями.
| Сот | Десятки | Квартир | Путевая точка | Десятые | сотых |
| 5 | 0 | 0 | . | 0 | 0 |
Когда мы делим на 100, мы перемещаем наш номер два столбца вправо.500, деленное на 100 = 005, или 5. Начальные нули (нули на «внешнем левом» числе, например, в 005, 02, 00014) не имеют значения, поэтому нам не нужно их записывать.
Вы также можете думать об этом как о перемещении десятичной запятой на два разряда влево.
| Сот | Десятки | Квартир | Путевая точка | Десятые | сотых |
| 0 | 0 | 5 | . | 0 | 0 |
Это правило применяется ко всем числам, поэтому 327 фунтов стерлингов, разделенные на 100, составляют 3,27 фунта стерлингов. Это то же самое, что сказать, что 3,27 фунта стерлингов составляют 1% от 327 фунтов стерлингов. 1 фунт стерлингов разделенный на 100 = 0,01 фунта стерлингов, или один пенс. Сто пенсов в фунте (и сто центов в долларе). Таким образом, 1p составляет 1% от 1 фунта стерлингов.
После того, как вы подсчитали 1% от целого, вы можете затем умножить свой ответ на процент, который вы ищете (помощь см. На нашей странице, посвященной умножению на ).
Ментальные математические приемы
По мере развития ваших математических навыков вы начнете видеть другие способы прийти к тому же ответу. Приведенный выше пример ноутбука довольно прост, и с практикой вы сможете использовать свои математические навыки, чтобы по-другому подумать об этой проблеме, чтобы облегчить ее. В этом случае вы пытаетесь найти 20%, поэтому вместо того, чтобы найти 1% и затем умножить его на 20, вы можете найти 10%, а затем просто удвоить его. Мы знаем, что 10% — это то же самое, что 1/10, и мы можем разделить число на 10, переместив десятичный знак на одну позицию влево (удалив ноль из 500).Следовательно, 10% от 500 фунтов стерлингов составляют 50 фунтов стерлингов, а 20% — 100 фунтов стерлингов.
Полезный прием в умственной математике состоит в том, что проценты обратимы, поэтому 16% от 25 равно 25% от 16. Неизменно один из них будет намного легче вычислить в нашей голове… попробуйте!
Воспользуйтесь нашим калькулятором процентов , чтобы быстро решить свои проблемы с процентами.
Работа с процентами
Мы рассчитали скидку 20% в приведенном выше примере, а затем вычли ее из целого, чтобы определить, сколько будет стоить новый ноутбук.
Мы можем не только убрать процент, но и добавить процент к числу. Это работает точно так же, но на последнем этапе вы просто добавляете, а не вычитаете.
Например: Джордж повышен в должности и получает повышение заработной платы на 5%. В настоящее время Джордж зарабатывает 24 000 фунтов стерлингов в год, так сколько он будет зарабатывать после повышения зарплаты?
Тренировка 1% от всего
Целое в этом примере представляет собой текущую зарплату Джорджа, 24 000 фунтов стерлингов.1% от 24 000 фунтов стерлингов составляет 24 000 ÷ 100 = 240 фунтов стерлингов.
Умножьте это на процент, который вы ищете
Джордж получает повышение заработной платы на 5%, поэтому нам нужно знать значение 5%, или 5 раз по 1%.
240 фунтов стерлингов × 5 = 1200 фунтов стерлингов.
Завершите расчет, добавив к исходной сумме
Повышение заработной платы Джорджа составляет 1200 фунтов стерлингов в год. Таким образом, его новая зарплата составит 24 000 фунтов стерлингов + 1 200 фунтов стерлингов = 25 200 фунтов стерлингов.
Процент более 100%
Процент может быть больше 100%. Этот пример один: новая зарплата Джорджа на самом деле составляет 105% от его старой.
Однако его старая зарплата не на 100% от его новой. Вместо этого он составляет чуть более 95%.
Когда вы рассчитываете проценты, главное — убедиться, что вы работаете с правильным целым. В данном случае «целое» — это старая зарплата Джорджа.
Десятичные и дробные проценты
Один процент — это одна сотая от целого.Следовательно, его можно записать как десятичную дробь, так и дробь.
Чтобы записать процент в виде десятичной дроби, просто разделите его на 100.
Например, 50% становится 0,5, 20% становится 0,2, 1% становится 0,01 и т. Д.
Д.
Мы можем вычислить проценты, используя эти знания. 50% равно половине, поэтому 50% от 10 равно 5, потому что пять — это половина от 10 (10 ÷ 2). Десятичная дробь 50% равна 0,5. Итак, другой способ найти 50% от 10 — это сказать 10 × 0,5 или 10 половин.
20% от 50 — это то же самое, что сказать 50 × 0.2, что равно 10.
17,5% от 380 = 380 × 0,175, что равно 66,5.
Увеличение зарплаты Джорджа составило 5% от 24 000 фунтов стерлингов. 24000 фунтов стерлингов × 0,05 = 1200 фунтов стерлингов.
Преобразование десятичного числа в процентное — это просто обратный расчет: умножьте десятичное число на 100.
0,5 = 50%
0,875 = 87,5%
Чтобы записать процент в виде дроби, поместите процентное значение над знаменателем 100 и разделите его на наименьшую возможную форму.
50% = 50/100 = 5/10 = ½
20% = 20/100 = 2/10 = 1/5
30% = 30/100 = 3/10
ВНИМАНИЕ!
Можно преобразовать дроби в проценты, преобразовав знаменатель (нижнее число дроби) в 100.
Однако преобразовать дроби в проценты труднее, чем проценты в дроби, потому что не каждая дробь имеет точное (неповторяющееся) десятичное число или процент.
Если знаменатель вашей дроби не делит целое число раз на 100, то простого преобразования не будет.Например, 1/3, 1/6 и 1/9 не дают «точных» процентов (это 33,33333%, 16,66666% и 11,11111%).
Расчет в процентах от целого
До сих пор мы рассмотрели основы процентов и то, как добавить или вычесть процент от целого.
Иногда бывает полезно вычислить проценты от целого, когда вам даны соответствующие числа.
Например, предположим, что в организации работают 9 менеджеров, 12 администраторов, 5 бухгалтеров, 3 специалиста по персоналу, 7 уборщиков и 4 работника общественного питания.Какой процент сотрудников каждого типа он нанимает?
Начните с проработки всего.

В этом случае вам неизвестно «целое» или общее количество сотрудников в организации. Поэтому первым шагом является сложение различных типов персонала.
9 менеджеров + 12 администраторов + 5 бухгалтеров + 3 специалиста по персоналу + 7 уборщиков + 4 работника общественного питания = 40 сотрудников.
Определите долю (или долю) персонала в каждой категории.
Нам известно количество сотрудников в каждой категории, но нам нужно преобразовать это число в дробную часть целого числа, выраженную в виде десятичной дроби. Расчет, который нам нужно сделать:
Персонал в категории ÷ Всего (См. Нашу страницу раздела , , чтобы получить помощь по суммам деления или воспользоваться калькулятором)
В качестве примера можно использовать менеджеров:
9 менеджеров ÷ 40 = 0,225
В этом случае может быть полезно, если вместо того, чтобы думать о символе деления «÷» как о значении «делится на», мы можем заменить слова «вне».Мы часто используем это в контексте результатов тестирования, например 8/10 или «8 из 10» правильных ответов. Итак, мы вычисляем «количество менеджеров из всего штата». Когда мы используем слова для описания вычислений, это может сделать их более понятными.
Преобразование доли целого в проценты
0,225 — это доля сотрудников, являющихся руководителями, выраженная в десятичном формате. Чтобы преобразовать это число в процент, нам нужно умножить его на 100.Умножение на 100 аналогично делению на сотню, за исключением того, что вы перемещаете числа в другую сторону по шкале значений разряда. Таким образом, 0,225 становится 22,5.
Другими словами, 22,5% сотрудников организации — менеджеры.
Затем мы делаем те же два вычисления для каждой другой категории.
- 12 администраторов ÷ 40 = 0,3. 0,3 × 100 = 30%.
- 5 бухгалтеров ÷ 40 = 0,125. 0,125 × 100 = 12,5%.
- 3 специалиста по персоналу ÷ 40 = 0.075. 0,075 × 100 = 7,5%.
- 7 очистителей ÷ 40 = 0,175. 0,175 × 100 = 17,5%.
- 4 работника общепита ÷ 40 = 0,1. 0,1 × 100 = 10%.
СОВЕТ! Убедитесь, что у вас всего 100%
Когда вы закончите вычислять свои проценты, рекомендуется сложить их вместе, чтобы убедиться, что они равны 100%. Если нет, проверьте свои расчеты.
Таким образом, мы можем сказать, что организация состоит из:
| Роли | Кол-во сотрудников | % персонала |
| Менеджеры | 9 | 22.5% |
| Администраторы | 12 | 30% |
| Бухгалтеры | 5 | 12,5% |
| Специалисты по персоналу | 3 | 7,5% |
| Очистители | 7 | 17,5% |
| Кейтеринг | 4 | 10% |
| Всего | 40 | 100% |
Может быть полезно отобразить процентные данные, представляющие целое, на круговой диаграмме.Вы можете быстро увидеть пропорции категорий персонала в примере.
Подробнее о круговых диаграммах и других типах графиков и диаграмм см. На нашей странице: Графики и диаграммы .
Следует помнить
- Проценты — это способ описания частей целого.
- Они немного похожи на десятичные дроби, за исключением того, что целое всегда делится на 100, а не на десятые, сотые, тысячные и т.д. единицы.
- Проценты предназначены для упрощения расчетов.
Дополнительная литература по навыкам, которые вам нужны
Пропорция
Часть необходимых навыков Руководство по счету
Эта электронная книга описывает пропорции, когда числа рассматриваются как части других чисел, как части большего целого или по отношению к другим числам. В книге описаны дроби и десятичные дроби, отношения и проценты с рабочими примерами, которые помогут вам развить свои навыки.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Преобразование дробей в проценты
Помните, что процент — это просто особый способ выражения дроби как числа из 100 .
Чтобы преобразовать дробь в проценты, сначала разделите числитель на знаменатель. Затем умножьте десятичную дробь на 100 .
То есть дробь 4 8 может быть преобразован в десятичный разделив 4 от 8 .Его можно преобразовать в проценты, умножив десятичную дробь на 100 .
4 ÷ 8 знак равно 0,5 0,5 × 100 знак равно 50
Итак, дробь 4 8 эквивалентно 50 % .
Пример 1:
Писать 2 25 в процентах.
С 25 больше чем 2 , чтобы разделить, мы должны добавить десятичную точку и несколько нулей после 2 . Мы можем не знать, сколько нулей добавить, но это не имеет значения. Если мы добавим слишком много, мы сможем стереть лишнее; если мы не добавим достаточно, мы можем добавить еще.Так,
2 25 знак равно 0,08 0,08 × 100 знак равно 8
Следовательно, дробь 2 25 эквивалентно 8 % .
Посмотрите на изображение ниже, оно показывает, что дробь 2 25 такой же как 8 снаружи 100 , это, 8 % .
Пример 2:
Писать 7 4 в процентах.
Делить 7 от 4 .Так,
7 4 знак равно 1.75 1,75 × 100 знак равно 175
Следовательно, дробь 7 4 эквивалентно 175 % .
Пример 3:
Писать 1 8 в процентах.
Делить 1 от .
Так,
1 8 знак равно 0.125 0,125 × 100 знак равно 12,5
Следовательно, дробь 1 8 эквивалентно 12,5 % .
Система счисления | |||
Номера | Prime против Composite | Интерактивная числовая линия | Мультифракционные игры! |
ФРАКЦИИ Абсолютное значение | Сравнение целых чисел (xP Math) Наименьшее общее кратное | Наименьшее общее число пиратов \ Наименьший общий знаменатель — Fruit Splat | Эквивалентные дроби Упрощение дробей Футбол Упрощение дробей Бейсбол |
Фракционные спиннеры — что вы знаете? | Боулинг для фракций | Вычисление дробей Морозные фракции | Добавление фруктов со знаками или вычитание знаков с фруктами |
Все о дробях | Действие сложения дробей | Основы дробей | Знакомство с дробями с одинаковыми знаменателями |
| Правила делимости дробей Представление правил делимости | Практика делимости (правила) | Сложение дробей (как знаменатели) | Добавление дробей Racing |
| Все о дробях | Порядок дробей | Эквивалентные доли Эквивалентные доли (ppt) | Больше аналогов! |
| Наименьший общий знаменатель | Сравнение и заказ дробей | Сложение и вычитание дробей (в отличие от) Сложение и вычитание дробей (в отличие от) (ppt) | Сопоставьте дроби |
| Умножение дробей | Умножение смешанных чисел (опасность) | Умножение и деление дробей (задачи со словами) | Упрощение дробей — Math Man: сокращение и упрощение |
| Баскетбол на деление дробей | Math Man: сложение дробей с разными знаменателями | Взаимные | Вычитание смешанных чисел |
| Уменьшить дроби: Splat! | Преобразование неправильных дробей в смешанные числа | Преобразование неправильного в смешанное (xP Math) | Головоломки с дробями |
| Дроби и десятичные числа Преобразование дробей в десятичные (Puppy Chase) | Линия номеров линкора (числовые строки с дробями, десятичными, целыми числами и смешанные числа) | Animal Rescue Number Line (Расширенная игра с числовой линией — Найдите и освободите пойманных животных) | НОМЕРНЫЕ ЛИНИИ Pearl Diver… Номерные строки |
| DECIMALS Таблица значений (печать или сохранение) | Число десятичных знаков и многое другое! Сравнение десятичных знаков | Сравнение и порядок десятичных знаков 1 Сравнение и округление десятичных знаков | Опасность десятичных и целых чисел Десятичные значения |
| Вычитание десятичных знаков Футбол | Десятичные знаки со спортом @ math-play | Футбольные десятичные знаки | Решение: сложение и вычитание десятичных знаков |
Ланч-леди (десятичное вычисление) г.Десятичные игры N | Веб-сайт NumberNut для десятичных знаков | Десятичные знаки BBC | Все о десятичных дробях |
| Пример: деление на целое число | Научитесь делить на целые числа | Деление на десятичные дроби Видео | Обзор игры для десятичных вычислений |
| Длинное деление с десятичными знаками (пошагово) | Практика деления десятичных знаков на десятичные | Практика деления десятичных чисел (целыми числами) | Процесс длинного деления, шаг за шагом |
| Десятичные дроби (дробилка) | НАСТОЯЩИЕ ДЕСЯТНЫЕ ЧАСТИ МИРА | Brain Pop: сравнение цен | |
| АБСОЛЮТНОЕ ЗНАЧЕНИЕ Абсолютное значение (FYI) | Абсолютное значение «Ячейки» (наименьшее / наибольшее) | Абсолютное значение (тест) | Практика абсолютных ценностей |
| Абсолютное значение «Сотня» | ГРАФИК Координаты | Найдите пришельцев (координаты) | |
| Полки на складе (заказываются парами) | |||
Расчет процентов | Помощь с математикой
Приведенные ниже инструкции помогут вам справиться с проблемами вычисления процентов, в том числе обнаруженными на странице процентных листов.
По мере того, как вы ведете своего ребенка, вы также должны воспользоваться возможностью, чтобы объяснить важность и актуальность процентных расчетов: повышение заработной платы, повышение пособий, процентные ставки, скидки на распродажные товары и т. Д. Обучение всегда улучшается, когда актуальность того, что изучается, оценен.
Что такое процент?
Процент означает «на каждые 100» или «из 100». Символ (%) как быстрый способ записать дробь со знаменателем 100. Например, вместо того, чтобы сказать «дождь шел 14 дней из каждых 100», мы говорим «дождь шел 14% времени».«
Проценты можно записать в виде десятичных дробей, переместив десятичную запятую на два разряда влево:
Десятичные дроби можно записать в процентах, переместив десятичную запятую на два разряда вправо:
Формула для расчета процентов
Формулы для расчета процентов или преобразования из процентов относительно просты.
Чтобы преобразовать дробную или десятичную дробь в процент, умножьте на 100:
Чтобы преобразовать процент в дробь, разделите на 100 и уменьшите дробь (если возможно):
Примеры процентного расчета
Следующие два примера показывают, как рассчитывать проценты.
1) 12 человек из 25 были женщинами. Какой процент составляли женщины?
2) Цена моноблока 1,50 $ увеличена на 20%. Какая была новая цена?
3) Налог на товар составляет 6 долларов США. Ставка налога составляет 15%. Какая цена без налога?
Задачи, аналогичные приведенным в примерах выше, решаются в серии из трех мини-уроков по Расчет с процентами . Они перечислены ниже.
# 1: Введение
# 2: Расчет с процентами e.грамм. 12% от 80?
# 3: Расчет с процентами, например 6 из 8 — какие%, а 15 — 30% из чего?
График в процентах
Эта процентная диаграмма показывает, что составляет 15% от 1 до 100 долларов, хотя она настраивается, поэтому вы можете установить процент и числа по своему усмотрению.

 08
08 Вы получите
Вы получите 
