Первообразная и неопределенный интеграл, их свойства

Определение первообразной

Для начала, дадим определение понятиям, которые будут использоваться в данном разделе. В первую очередь это первообразная функции. Для этого введем константу C.

Определение 1

Первообразная функции f(x) на промежутке (a; b) это такая функция F(x), при которое формула F'(x)=f(x) превращается в равенство для любого x из заданного промежутка.

Следует учитывать тот факт, что производная от константы C будет равна нулю, что позволяет нам считать верным следующее равенство F(x)+C’=f(x).

Получается, что функция f(x) имеет множество первообразных F(x)+C, для произвольной константы C. Эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла

Все множество первообразных функции f(x) можно назвать неопределенным интегралом этой функции. С учетом этого формула будет иметь вид ∫f(x)dx=F(x)+C. При этом, выражение f(x)dx является подынтегральным выражением, а f(x) – это подынтегральная функция. Подынтегральное выражение представляет собой дифференциал функции f(x).

Имея заданный дифференциал функции, мы можем найти неизвестную функцию.

Результатом неопределенного интегрирования будет не одна функция F(x), а множество ее первообразных F(x)+C.

• Зная свойства производной, мы можем сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

∫f(x)dx’=F(x)+C’=f(x)

• Производная результата интегрирования равна подынтегральной функции.

∫d(F(x))=∫F'(x)dx=∫f(x)dx=F(x)+C

• Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

∫k·f(x)dx=k·∫f(x)dx, где k – произвольная константа. Коэффициент можно выносить за знак неопределенного интеграла.

• Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.

∫f(x)±g(x))dx=∫f(x)dx±∫g(

«Как найти первообразную функции?» – Яндекс.Кью

Ох какой сложный вопрос.

Вообще, в политической науке (да пожалуй как и в любой другой общественной) самые ожесточенные дискуссии и непонятки вызывает именно анализ и синтез понятийно-категориального аппарата.

Можно конечно диссертации писать, заниматься графоманией и словоблудием, быть бесценных слов транжирой и мотом по данной тематике — никогда не иссякнет вопрос: а почему это мы не можем прийти к общему знаменателю? Да потому что абсурдно, наука ценна плюрализмом мнений и дифференцированными дефинициями.

Кто-то, как первый автор, отождествляет политический строй с формой государственного устройства, кто-то, как в комментариях, утверждает, что строй — это про институциональный дизайн. Если загуглить термин, то первая ссылка приведет нас к понятию «политический режим».

Совершенно верно дано определение политического режима — совокупность форм и методов управления в государстве. Однако, американская политология, например, подобную совокупность называет политической системой, в то время как в европейской традиции система — это совокупность вообще политических характеристик государства.

Типологии политических режимов также кто только не предлагал, один литературный обзор выйдет страниц на 30. Классическим считается деление режимов на демократические/недемократические, а далее уже кто во что горазд — это типология Голосова-Блонделя, которая есть в Википедии, типология Роберта Даля, типология Алмонда-Пауэлла, которые очень легко гуглятся и абсолютно доступны в любом скачиваемом учебнике по общей политологии.

Если коротко подвести итоги: да хрен его знает, сколько научных направлений, столько и определений и разграничений. Подобного рода смешение коней и людей в кучу создает создает изрядные затруднения в однозначном ответе на вопрос.

Что же касается политического строя, то в отечественной науке именно такого понятия просто нет, таким образом, можно назвать политическим строем что угодно — систему, режим, форму гос.устройства и прочее, хоть садовое товарищество.

Задание №7. Производная. Поведение функции. Первообразная

Необходимая теория:

Производная функции

Таблица производных

Первообразная функции

Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих встречаются вопросы о первообразной.

Геометрический смысл производной 

Вспомним, что производная — это скорость изменения функции.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .

Достроив до прямоугольного треугольника АВС, получим:

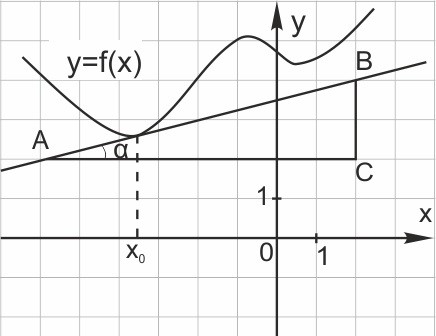
Ответ: 0,25.

2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке

Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .

Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:

Ответ: −0, 25.

Касательная к графику функции

3. Прямая является касательной к графику функции

Найдите абсциссу точки касания.

Запишем условие касания функции и прямой в точке

При значения выражений и равны.

При этом производная функции равна угловому коэффициенту касательной, то есть .

Из второго уравнения находим или Первому уравнению удовлетворяет только .

Физический смысл производной

Мы помним, что производная — это скорость изменения функции.

Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.

Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.

4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени с.

Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:

Найдем скорость материальной точки как производную от координаты по времени:

В момент времени получим:

Ответ: 3

Применение производной к исследованию функций

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если , то функция возрастает.

Если , то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

 

5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.

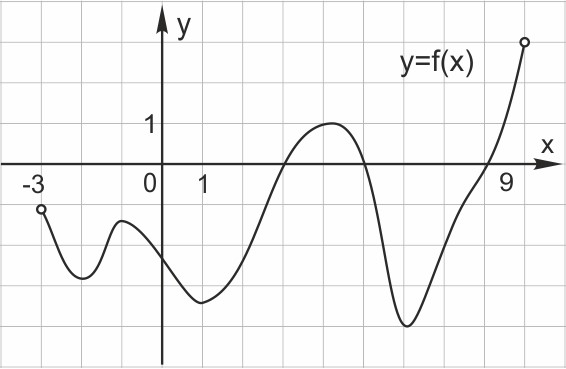
Производная функции в точках максимума и минимума функции Таких точек на графике 5.

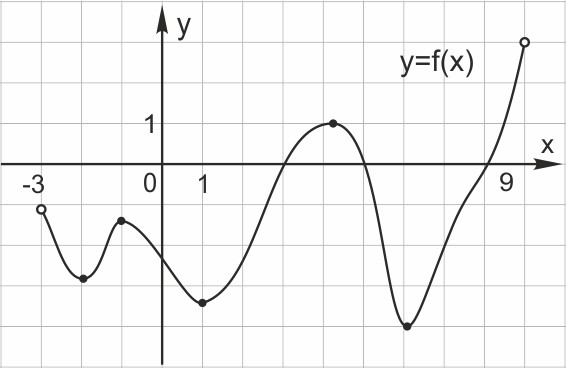
Ответ: 5.

6. На рисунке изображён график — производной функции , определённой на интервале . В какой точке отрезка функция принимает наибольшее значение?

Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?

Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.

На отрезке производная функции положительна.

Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.

Ответ: 3.

7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой

Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.

Ответ: 7.

8. На рисунке изображен график производной функции , определенной на интервале Найдите количество точек максимума функции на отрезке

Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это

Ответ: 1.

9. На рисунке изображен график производной функции , определенной на интервале Найдите точку экстремума функции на отрезке

Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.

Значит, является точкой экстремума.

Первообразная и формула Ньютона-Лейбница

Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции

10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Функция для которой является производной, называется

первообразной функции

Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.

Ответ: 4.

Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье

Первообразная функции. Формула Ньютона-Лейбница.

 

Mathway | Популярные задачи

1	Найти производную — d/dx	квадратный корень x
2	Найти производную — d/dx	натуральный логарифм x
3	Вычислить	интеграл натурального логарифма x по x
4	Найти производную — d/dx	e^x
5	Вычислить	интеграл e^(2x) относительно x
6	Найти производную — d/dx	1/x
7	Найти производную — d/dx	x^2
8	Вычислить	интеграл e^(-x) относительно x
9	Найти производную — d/dx	1/(x^2)
10	Найти производную — d/dx	sin(x)^2
11	Найти производную — d/dx	sec(x)
12	Вычислить	интеграл e^x относительно x
13	Вычислить	интеграл x^2 относительно x
14	Вычислить	интеграл квадратного корня x по x
15	Вычислить	натуральный логарифм 1
16	Вычислить	e^0
17	Вычислить	sin(0)
18	Найти производную — d/dx	cos(x)^2
19	Вычислить	интеграл 1/x относительно x
20	Вычислить	cos(0)
21	Вычислить	интеграл sin(x)^2 относительно x
22	Найти производную — d/dx	x^3
23	Найти производную — d/dx	sec(x)^2
24	Найти производную — d/dx	1/(x^2)
25	Вычислить	интеграл arcsin(x) относительно x
26	Вычислить	интеграл cos(x)^2 относительно x
27	Вычислить	интеграл sec(x)^2 относительно x
28	Найти производную — d/dx	e^(x^2)
29	Вычислить	интеграл в пределах от 0 до 1 кубического корня 1+7x по x
30	Найти производную — d/dx	sin(2x)
31	Вычислить	интеграл натурального логарифма x по x
32	Найти производную — d/dx	tan(x)^2
33	Вычислить	интеграл e^(2x) относительно x
34	Вычислить	интеграл 1/(x^2) относительно x
35	Найти производную — d/dx	2^x
36	График	натуральный логарифм a
37	Вычислить	e^1
38	Вычислить	интеграл 1/(x^2) относительно x
39	Вычислить	натуральный логарифм 0
40	Найти производную — d/dx	cos(2x)
41	Найти производную — d/dx	xe^x
42	Вычислить	интеграл 1/x относительно x
43	Вычислить	интеграл 2x относительно x
44	Найти производную — d/dx	( натуральный логарифм x)^2
45	Найти производную — d/dx	натуральный логарифм (x)^2
46	Найти производную — d/dx	3x^2
47	Вычислить	натуральный логарифм 2
48	Вычислить	интеграл xe^(2x) относительно x
49	Найти производную — d/dx	2e^x
50	Найти производную — d/dx	натуральный логарифм 2x
51	Найти производную — d/dx	-sin(x)
52	Вычислить	tan(0)
53	Найти производную — d/dx	4x^2-x+5
54	Найти производную — d/dx	y=16 корень четвертой степени 4x^4+4
55	Найти производную — d/dx	2x^2
56	Вычислить	интеграл e^(3x) относительно x
57	Вычислить	интеграл cos(2x) относительно x
58	Вычислить	интеграл cos(x)^2 относительно x
59	Найти производную — d/dx	1/( квадратный корень x)
60	Вычислить	интеграл e^(x^2) относительно x
61	Вычислить	sec(0)
62	Вычислить	e^infinity
63	Вычислить	2^4
64	Найти производную — d/dx	x/2
65	Вычислить	4^3
66	Найти производную — d/dx	-cos(x)
67	Найти производную — d/dx	sin(3x)
68	Вычислить	натуральный логарифм 1/e
69	Вычислить	интеграл x^2 относительно x
70	Упростить	1/( кубический корень от x^4)
71	Найти производную — d/dx	1/(x^3)
72	Вычислить	интеграл e^x относительно x
73	Вычислить	интеграл tan(x)^2 относительно x
74	Вычислить	интеграл 1 относительно x
75	Найти производную — d/dx	x^x
76	Найти производную — d/dx	x натуральный логарифм x
77	Вычислить	интеграл sin(x)^2 относительно x
78	Найти производную — d/dx	x^4
79	Вычислить	предел (3x-5)/(x-3), если x стремится к 3
80	Вычислить	интеграл от x^2 натуральный логарифм x по x
81	Найти производную — d/dx	f(x) = square root of x
82	Найти производную — d/dx	x^2sin(x)
83	Вычислить	интеграл sin(2x) относительно x
84	Найти производную — d/dx	3e^x
85	Вычислить	интеграл xe^x относительно x
86	Найти производную — d/dx	y=x^2
87	Найти производную — d/dx	квадратный корень x^2+1
88	Найти производную — d/dx	sin(x^2)
89	Вычислить	интеграл e^(-2x) относительно x
90	Вычислить	интеграл натурального логарифма квадратного корня x по x
91	Вычислить	2^5
92	Найти производную — d/dx	e^2
93	Найти производную — d/dx	x^2+1
94	Вычислить	интеграл sin(x) относительно x
95	Вычислить	2^3
96	Найти производную — d/dx	arcsin(x)
97	Вычислить	предел (sin(x))/x, если x стремится к 0
98	Вычислить	e^2
99	Вычислить	интеграл e^(-x) относительно x
100	Вычислить	интеграл 1/x относительно x