План-конспект урока по алгебре (7 класс) по теме: Прямая и обратная пропорциональность
Алгебра 7 класс УМК Г.В.Дорофеев.
Тема: Прямая и обратная пропорциональность.
Цель урока: — ввести понятие прямой и обратной пропорциональности в рамках побуждающего диалога, подводящего учащихся к возможности самостоятельно сформулировать тему урока на завершающем этапе введения нового материала;
-развивать логическое мышление, умение анализировать, обобщать факты, выдвигать гипотезы, формировать математическую культуру;- формировать эмоционально- личностное отношение учащихся к выражению математических понятий;
— формировать умения пользоваться раннее полученными знаниями и применять знания в новой ситуации.
1. Актуализация опорных знаний.
Записать формулы: расстояния; скорости; площади прямоугольника; длины окружности; стоимости товара; количества, купленного товара; объёма, выполненной работы; производительности труда. ( Проверить с доской , учащиеся отмечают плюсом правильное выполнение)
C=π×d
Подчеркнуть одной ( двумя) чертами формулы, записанные одинаковым действием.
2. Изучение нового материала.
Рассмотрим формулы первого вида
Как можно назвать эти формулы ( произведение).
Назвать компоненты произведения.
Давайте вместе понаблюдаем как связаны между собой переменные, входящие в формулы.Пусть v=40км/ч
Как теперь будет выглядеть формула? S=40 t
1 вариант вычислить путь, если время равно 2 часа.
2 вариант вычислить путь, если время равно 4 часа.(отмечаем правильное решение)
Как изменяется путь, если мы изменили время? Во сколько раз изменилось время? ( в 2 раза). Во сколько раз изменился путь? ( в 2 раза). Как они изменились? (одинаково).
Такие величины в математике называют прямо пропорциональными.
Попробуйте дать определение. ( Ответы учащихся, обобщение учителя, подтверждение в учебнике).
Изменим задачу. S=240км.
Запишем формулу 240=vt выразим v v=240/t
Какие переменные входят в формулу, назвать их.
Давайте за ними понаблюдаем:
1 вариант t=4ч.
2 вариант t=8ч.
(отмечаем правильное решение)
Как ведут эти две величины? Во сколько раз каждая из них изменилась? ( в 2 раза) . Как они изменились? ( одна увеличилась, другая уменьшилась)
Эти величины связаны обратной зависимостью и называются обратно пропорциональными.
Попробуем дать определение.
Давайте сделаем обобщение для любой формулы произведения. В прямой пропорциональности , что является константой ( множитель)? Обозначим его k — коэффициент пропорциональности. Составим формулу в общем виде у=k.х
Какой зависимостью связаны переменные у и х?
В обратной пропорциональности константа- произведение k=у.х. Составим формулу у=k/х .
Запишем тему урока «Прямая и обратная пропорциональность»
3. Первичное закрепление.
Из предложенных формул (на листах напечатаны) составить схему для прямой и обратной пропорциональности.
№ 162(устно), № 161( с проверкой ), №164( устно)
Решить у доски с оформлением №163(а), 165.
4. Рефлексия.
— Что нового узнали на уроке?
— В каких формулах эти зависимости можно выразить?
— Какая зависимость называется прямой пропорциональностью? Обратной пропорциональностью?
5. Итог урока.
Оценивание учащихся (с учетом всех плюсов, набранных на уроке)
Домашняя работа №163(б), 166.
nsportal.ru
АРМ для 7 класса «Прямая и обратная пропорциональная зависимость».
2017-2018 уч.год Лицей при КазГАСА математика Абдыкалыкова Г.Т.
ЛИЦЕЙ при КАЗАХСКОЙ ГОЛОВНОЙ АКАДЕМИИ АРХИТЕКТУРЫ И СТРОИТЕЛЬСТВААктивный раздаточный материал
Дисциплина : математика Класс : 6
Семестр: осенний
Преподаватель: Абдыкалыкова Г.Т.
Урок: 19-21 Учебный год: 2017-2018
Тема :Прямая и обратная пропорциональная зависимость.
Краткое содержание темы:
Алгоритм решения задач на прямую
и обратную пропорциональные зависимости
Неизвестное число обозначается буквой х.
Условие записывается в виде таблицы.
Устанавливается вид зависимости между величинами.
Прямо пропорциональная зависимость обозначается одинаково направленными стрелками, а обратно пропорциональная зависимость — противоположно направленными стрелками.
Записывается пропорция.
Находится её неизвестный член.
СРСП:
Решите задачи, составляя пропорции.
№1. На путь от одного поселка до другого со скоростью 12,5 км/ч велосипедист затратил 0,7 ч. С какой скоростью он должен был ехать, чтобы преодолеть этот путь за 0,5 ч?
Решение:

Составим пропорцию:
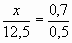 ;
; 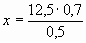 ;
; 
Ответ: 17,5 км/ч
№2. Из 5 кг свежих слив получается 1,5 кг чернослив. Сколько чернослива получится их 17,5 кг свежих слив?
Решение:
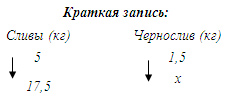
Составим пропорцию:
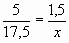 ;
; 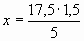 ;
; 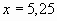 кг
кг
Ответ: 5,25 кг
№3. Автомобиль проехал 500 км, истратив 35 л бензина. Сколько литров бензина потребуется, чтобы проехать 420 км?
Решение:

Составим пропорцию:
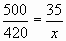 ;
; 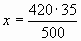 ;
; 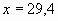 л
л
Ответ: 29,4 л.
СРС:
Составить пропорции для решения задач: (Работают в тетрадях)
а) Велосипедист за 3 ч проезжает 75 км. За сколько времени проедет велосипедист 125 км с той же скоростью?
б) 8 одинаковых труб заполняют бассейн за 25 минуты. За сколько минут заполнят бассейн 10 таких труб?
в) Бригада из 8 рабочих выполняет задание за 15 дней. Сколько рабочих сможет выполнить это задание за 10 дней, работая с той же производительностью?
г) Из 5,6 кг помидоров получают 2 л томатного соуса. Сколько литров соуса можно получить из 54 кг помидоров?
(Самооценка: поставить + или – карандашом в тетради; проанализировать ошибки)
Glossary
numberотношение
қатынас
attitudes
равенство
теңдік
equality
пропорция
пропорция
proportion
Основное свойство
basic property
негізгі қасиеті
Прямая зависимость
тікелей тәуелділік
direct dependency
Обратная зависимость
кері тәуелділік
inverse relationship
Крайний член
шеткі мүше
extreme member
Средний член
Ортанғы мүше
middle term
шартты
condition
задача
есеп
a task
Homework :
Literature:
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
infourok.ru
Конспект урока » Прямая и обратная пропорциональность»
Урок в 6 классе.
Тема урока: Прямая и обратная пропорциональность.
Обучающая цель: закрепить, обобщить и систематизировать полученные знания при решении задач на свойство пропорции и пропорциональные зависимости величин;
Развивающая цель: развитие логического мышления, сообразительности и познавательного интереса учащихся к предмету, умение практического применения темы в жизни;
Воспитательная цель: доброжелательное отношение друг другу, любознательность и добросовестность.
Оборудование: мультимедийный комплекс, компьютеры.
Ничто не нравится, кроме красоты,
В красоте-ничто, кроме форм,
В формах-ничто. Кроме пропорций,
В пропорциях-ничто, кроме пропорций,
В пропорциях-ничто, кроме числа.
(Аврелий Август)
Ход урока
Орг.момент.
Проверка домашнего задания.
Устная работа
Найдите неизвестный член пропорции
3:5=x:15; x=9
x:3=2:6; x=1
10x:=5:7; x=14
Верна ли пропорция
3:6=9:18
9:3=18:6
4:5=10:8
Опишите зависимость между …
а) Количеством булочек, которые можно купить в нашей столовой, и их общей стоимостью;
б) Между ростом ученика и его возрастом;
в) Путь, пройденный машиной с постоянной скоростью и время ее движения.
— Какие зависимости мы получили? (те, в которых с увеличением (уменьшением) одной величины в некоторое количество раз вторая величина увеличивается (уменьшается) в то же количество раз)
— Такие величины называются прямо пропорциональными величинами.
4. Исследовательская работа
(учащимся групп были даны задачи на исследование, ребята выполнили работу, сделали расчеты и представили в виде презентаций)
Задача 1
Маша съедает 4 яблока за пять минут. Определить, какое количество времени затратит она на поедание 8яблок.
Задача 2
За перемену между первым и вторым уроками по лестнице с первого на второй этаж поднялись 97 учащихся. Какое количество учащихся поднимутся с первого на второй этаж за все перемены с первого по шестой урок (мощность потока учащихся остается постоянной).
Задача 3
Из двух килограммов нечищеного картофеля у Кати при чистке в отходы ушло 0,3кг. Какой процент составляет масса чищеного картофеля от массы не чищенного?
Задача 4
Расстояние от дома до школы 2000м Саша проходит за 30 мин, за сколько мин. он пройдет расстояние 5 км, если скорость у него будет постоянной?
Работа в группах: задания на карточках
Карточка 1:
В 800 г раствора содержится 50 г соли. Сколько соли содержится в 240 г раствора?
Карточка 2:
При сжигании 1кг горючего в воздух автомобилем выбрасываются 0,8 кг угарного газа. Сколько угарного газа будет выброшено автомобилем при сжигании 50 кг горючего.
Карточка 3:
Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?
Карточка 4:
Из 400 кг молока получили 84кг сливок. Сколько сливок получится из 100 кг молока?
6. Работа на компьютере: задание в электронном варианте:
Задача 1.
Масса 8 одинаковых деталей равна 18 кг. Найти массу 24 таких же деталей.
Задача 2.
За 9 дней машинистка напечатала 126 рукописи. Сколько страниц рукописи напечатает она за 18 дней, если будет работать с такой же производительностью.
Решите уравнение:
х: 96=7:8
Решите уравнение:
5:7=x:91
Тесты:
Выберите правильный ответ:
1) Верна ли пропорция: 3:32=9:6
А) да Б) нет
Верна ли пропорция: 4:5=40:50
А) да Б) нет
2) Решите уравнение:
х: 5=9:15
А) 4 Б) 5 В) 3
7. Историческая справка
8. Рефлексия. Итог урока:
— Что мы сегодня на уроке повторили?
— Что узнали нового?
— Какой алгоритм для решения задач, содержащих прямо пропорциональную зависимость, мы вывели?
— Достигли ли мы поставленной цели?
9. Задача на размышление:
2 рабочих могут выполнить некоторую работу за 6 дней, за сколько дней выполнят эту же работу 4 рабочих, если будут работать с такой же производительностью
infourok.ru
Открытый урок на тему «Прямая и обратная пропорциональность»
Прямая и обратная пропорциональная зависимости
Цель урока: обобщение и закрепление материала по теме «Прямая и обратная пропорциональная зависимости».
Личностные результаты: способность к эмоциональному восприятию математических объектов, умение ясно и точно излагать свои мысли.
Предметные результаты: научиться различать прямые и обратные зависимости и решать с их помощью задачи.
Метапредметные результаты:развить умение работать в команде, осознать важность значения роли каждого в работе группы, умение делать выводы от частного к общему.
Технологии: элементы квест-технологии, здровьесберегающей технологии, витагенной технологии (обращение к жизненному опыту обучающихся).
Оборудование: презентация, компьютер, проектор, аудио и видеозаписи, раздаточный материал: 1) на группу: памятка «Правила работы в группе», конверты с заданиями 2) на каждого: рабочие листы , учебник, рабочая тетрадь.
Ход урока
1. Самоопределение к учебной деятельности.(1 мин)
Создать благоприятный психологический настрой на работу
Предмет математики столь серьезен,
что не следует упускать ни одной
возможности сделать его более
занимательным.
(Б. Паскаль)
Сегодняшний урок мы проведём в виде квест-игры. Работать мы будем в группах. На столах у вас лежат памятки «Правила работы в группе».
Каждый делает вклад в выполнение общего задания.
Внимательно слушать друг друга, не перебивая.
Приходить к общему решению.
Только выполнив одно задание, можно переходить к следующему.
Подавать сигнал о выполнении задания всем вместе.
Помнить о правиле «трёх мушкетеров».
УУД:
личностные: самоопределение, смыслообразование;
регулятивные: целеполагание;
коммуникативные: учебное сотрудничество с учителем и сверстниками.
2.Целеполагание и мотивация
Обеспечение мотивации учения детьми, принятие ими целей урока
На экране представлены пословицы, давайте их прочтём. Какие слова встречаются в пословицах, связанные с математикой и как они с ней связаны? (обучающиеся отвечают).
В каждой пословице две величины, которые связаны между собой зависимостью. Какие вы знаете зависимости? Какие зависимости встречаются в пословицах? (обучающиеся отвечают).
-Итак, сформулируйте тему урока. (Прямая и обратная пропорциональная зависимость).
– Молодцы! Запишите тему урока в тетрадях. (Учитель записывает тему на доске.)
Фронтальный опрос:
— Давайте определимся исходя из темы, что вы хотите на уроке сегодня научиться делать? (Различать прямую и обратную зависимости, решать с их помощью задачи)
–Сформулируйте цель сегодняшнего урока (Научиться различать прямые и обратные зависимости и решать с их помощью задачи.)
УУД:
регулятивные: целеполагание
коммуникативные: постановка вопросов
личностные: умение ясно и точно излагать свои мысли
познавательные: самостоятельное выделение-формулирование познавательной цели
3.Решение задач (квест-игра).
Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу.
— Сейчас мы с вами отправимся на экскурсию в музей, музей математический, и чтобы попасть в первый зал музея, вы должны отгадать его название.
Каждая группа получает конверт с заданием (собрать пазл). В результате получается 3 портрета древних математиков. Обучающиеся называют название 1 зала «Зал великих математиков».
-В этом зале хранится древнее письмо, но с потёртостями, чтобы восстановить стёртые числа нужно решить задачи.
Каждой группе раздаётся задача, в результате решения которых получаются числа из письма. Зачитывается письмо, в котором говорится об истории возникновения пропорции.
Чтобы попасть в следующий зал обучающиеся получают конверты с заданиями, в которых находятся ребусы. Разгадав ребусы обучающиеся озвучивают название зала «Зал старинных единиц измерений».
— А сейчас я предлагаю вам почувствовать себя исследователями и заняться исследовательской работой . Переведите свой рост в старинные меры длины, 1 группа – сажень, 2 группа-аршин, 3 группа-локоть. Обучающиеся озвучивают свой рост.
УУД:
личностные: умение ясно и точно излагать свои мысли
познавательные: умение анализировать
регулятивные: контроль, оценка, коррекция
коммуникативные: умение слушать и вступать в диалог, отстаивать свою точку зрения .
4. Физкультминутка
— К следующему залу нас проводит мальчик Петя, который уже был в этом музее, а вы повторяйте за ним все движения (видеозапись).
5.Организация контроля.
Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков.
— Для того, чтобы попасть в следующий зал, вам предстоит отгадать , что лежит в ящике у каждой группы. Для этого отгадайте загадки.
Обучающиеся разгадывают загадки, достают предметы: циркуль, линейка, рулетка. Озвучивают название зала «Зал измерительных приборов».
— Измерительных приборов очень много, применяются они не только в математике, но и в разных других профессиях. А кем вы хотели бы стать в будущем? (обучающиеся отвечают).
-Давайте сейчас вы себя попробуете в роли разных профессий, решив математический тест, где представлены задачи на пропорции.
УУД:
личностные: самоопределение
познавательные: оценивание результатов деятельности партнёра
регулятивные: осознание качества и уровня усвоения
7. Подведение итогов урока. Рефлексия учебной деятельности
Осуществляют самооценку собственной учебной деятельности, соотносят цель и результаты, степень их соответствия.Намечают перспективу последующей работы.
Рефлексия. Какие цели мы ставили в начале урока? Достигли их? Что нового для себя открыли? Как действовали?
сегодня я узнал…
сегодня я повторил…
я выполнял задания…
мне было немного трудно…
теперь я умею…
мне было интересно…
— Предлагаю Вам оценить свою работу, используя критерии оценки за сегодняшний урок (оценочный лист). Выставление оценок. По тем же критериям оцените работу своей группы. Каждого члена группы.
УУД:
личностные: критичность мышления, интерес к учебному материалу
регулятивные: оценка-осознание качества и уровня усвоения
8.Домашнее задание.
Дифференцированные карточки с заданиями.
— Вы были замечательными, активными, думающими и эмоционально открытыми сегодня. У каждого из нас своя роль в жизни. Но сегодня со своей ролью активных, замечательных, думающих и эмоционально открытых исследователей вы справились превосходно!
infourok.ru
План-конспект урока алгебры в 7 классе по теме Модуль числа. Прямая и обратная пропорциональная зависимости.
ГУ « Средняя общеобразовательная школа №5» отдела образования
акимата г. Костаная
ПЛАН-КОСПЕКТ УРОКА
ФИО (полностью) Пластун Сергей Владимирович
Предмет математика
Класс 7В
Дата 05.09.18
Источники Алматы «Мектеп-2012»
Базовый учебник
Дополнительная литература
Модуль числа. Прямая и обратная пропорциональная зависимости.
1. Цель урока: повторить и закрепить основные понятия по теме «Модуль числа. Прямая и обратная пропорциональная зависимости».
-закрепление следующих основных понятий: модуль рационального числа, пропорция, основное свойство пропорции, прямо пропорциональные величины, обратно пропорциональные величины;
-закрепить умение решать задачи с помощью пропорции
Развивающие:
— развить внимание, усидчивость, настойчивость, логическое мышление, математическую речь.
Воспитательные:
— посредством урока воспитывать активность ,внимательное отношение друг к другу, прививать умение слушать одноклассников.
2. Тип урока: урок повторения и закрепления
3. Формы работы с учащимися: фронтальная, индивидуальная.
4. Необходимое техническое оборудование.
5. Наглядные пособия, дидактические материалы, используемые на уроке.
6. Структура и ход урока.
СТРУКТУРА И ХОД УРОКА
(например,
иллюстрация, демонстрация и т. д.)
Деятельность ученика
Время
(в мин.)
1
2
3
4
5
1
Организационный момент
2 мин
2
Актуализация знаний
Отвечают на вопросы
10 мин
3
Проверка знаний и умений.
Работа у доски, задание для инклюзива
28 мин
4
Подведение итогов
3 мин
5
Постановка домашнего задания
2 мин
Ход урока
1. Организационный момент.
Проверка готовности урока. Сообщение темы и цели урока.
2. Актуализация знаний.
1) Модулем рационального числа называют расстояние (в единичных отрезках) от начала отсчета до точки координатной прямой, соответствующей этому числу.
Модуль числа а обозначается |a|.
Значит, число 4 называют модулем числа -4. Пишут:
|-4| = 4.
Читают: «модуль числа -4 равен 4».
Модуль от латинского слова modulus в переводе означает «мера», « величина».
Иногда вместо «модуля» говорят «абсолютная величина».
|-2,5| = 2,5.
Модуль отрицательного числа равен числу, ему противоположному.
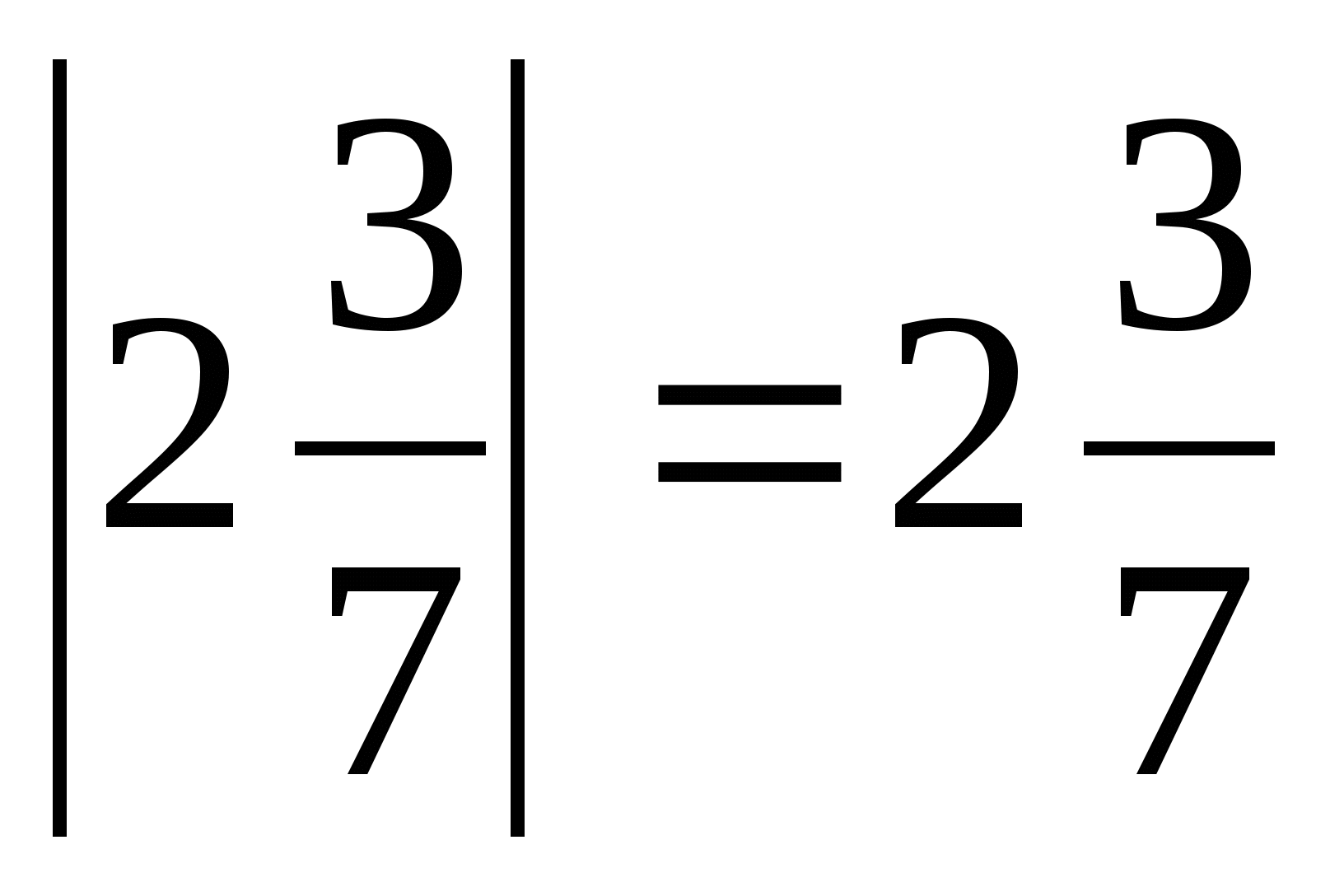 ; |8,7| = 8,7.
; |8,7| = 8,7.
Модуль положительного числа равен самому числу.
|0| = 0.
Модуль числа нуль равен нулю.
|-3| = |3|.
Противоположные числа имеют равные модули: |-а| = |а|. Например,
2) Теоретический опрос учащихся.
Какие величины называются прямо пропорциональными? Что можно сказать об отношениях соответствующих значений таких величин?
Какие величины называют обратно пропорциональными? Что можно сказать об отношениях соответствующих значениях таких величин?
Приведите примеры прямо пропорциональных величин.
Приведите примеры обратно пропорциональных величин.
Приведите примеры величин, у которых зависимость не является ни прямо, ни обратно пропорциональной
3. Проверка знаний и умений.
1) Найдите значения выражения |х|, если х=18; -15; -7,8; 16,5; —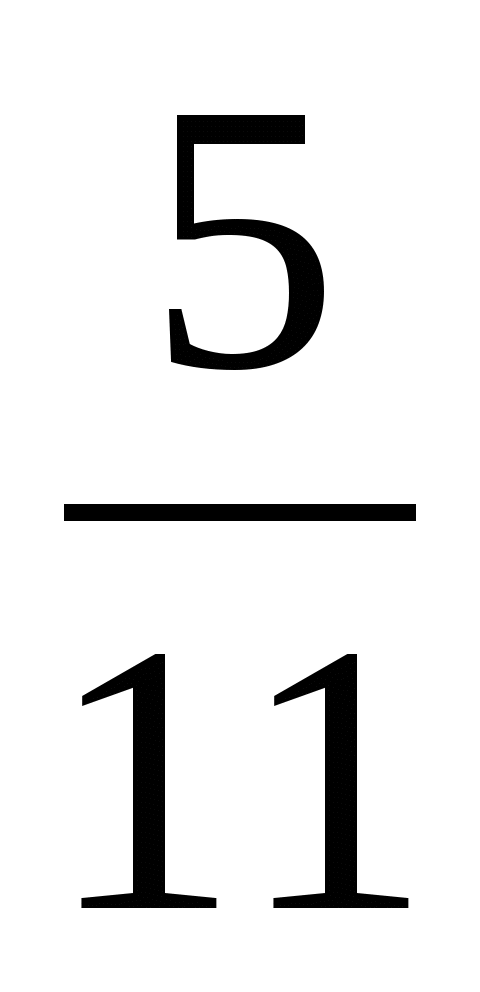 ; —
; — ; 9,2.
; 9,2.
х=18 х=-15 х=-7,8 х=16,5 х=-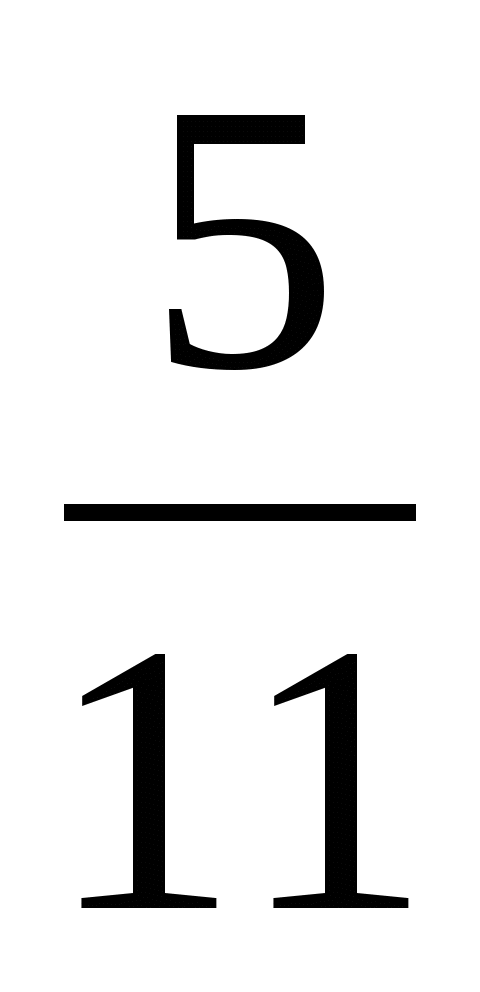 х=-
х=- х=9,2
х=9,2
|х|=18 |х|=15 |х|=7,8 |х|=16,5 |х|=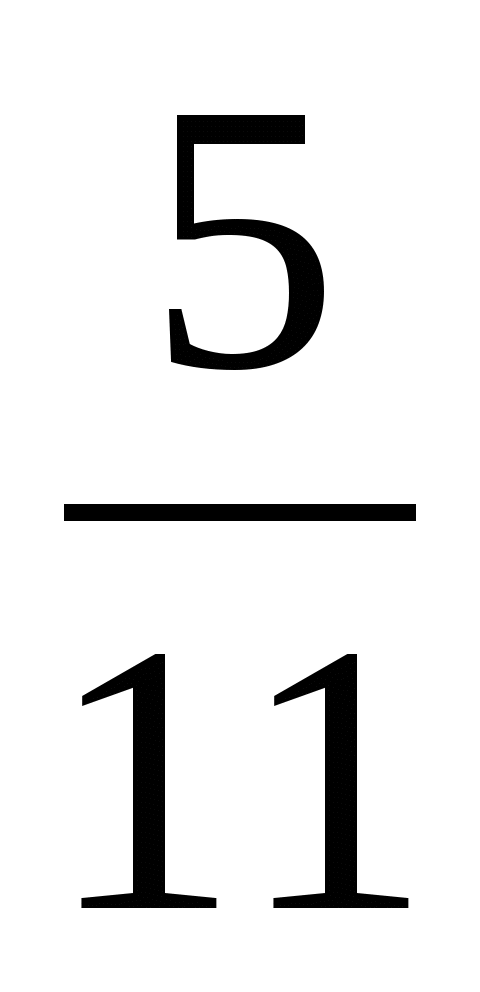 |х|=
|х|= |х|=9,2.
|х|=9,2.
2) Выберите уравнение, которое имеет решения. Найдите значения букв, такие, чтобы равенство было верным.
1) |х|=-3; 2) |х|=3,9; 3) |у|=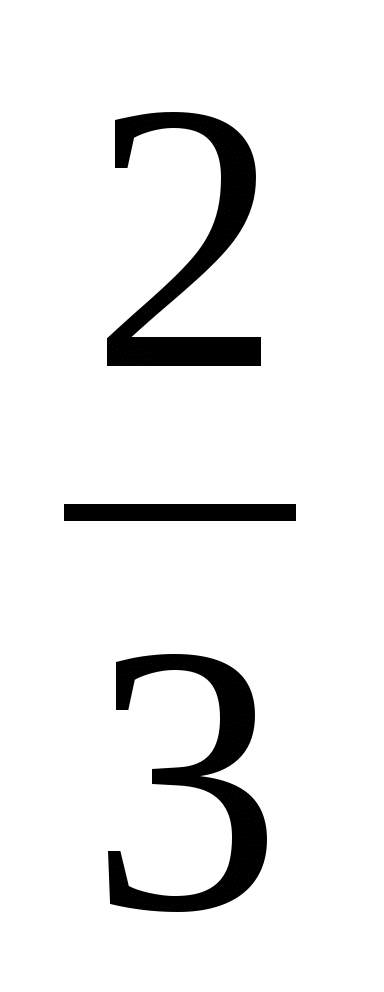 ; 4) |у|=-
; 4) |у|=-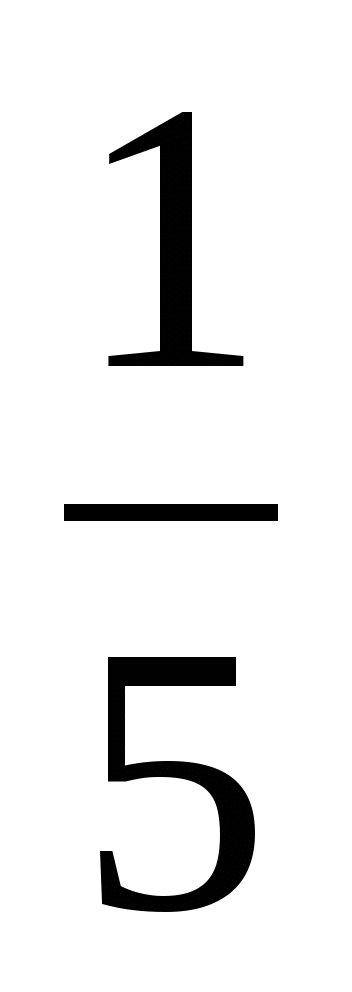 ;
;
5) |т|=-8; 6) |п|=6; 7) |х|=0,9; 8) |х|=-1.
|х|=3,9; |у|=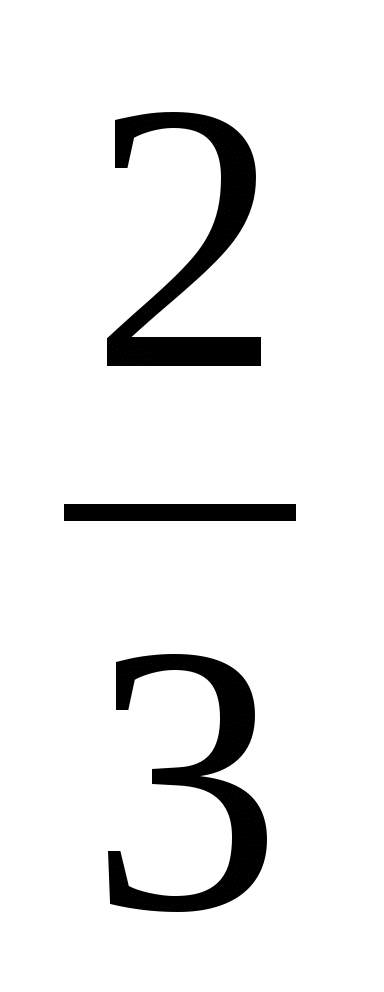 ; |п|=6; |х|=0,9; |п|=6
; |п|=6; |х|=0,9; |п|=6
3) Устная работа.
1. За 2 кг картошки заплатили 100 тенге. Сколько стоят 8 кг картошки?
В процессе устного обсуждения выясняем, что стоимость и количество товара при данной цене являются величинами прямо пропорциональными.
Значит, при увеличении количества товара, стоимость товара увеличится в то же число раз.
Ответ: 400 тенге
2. Два трактора вспахали поле за 6 дней. За сколько дней вспашут это поле 4 трактора, если будут работать с той же производительностью?
В процессе устного обсуждения выясняем, что время работы и количество рабочей силы являются величинами обратно пропорциональными. Значит, при увеличении количества рабочей силы, время работы уменьшится в то же число раз.
Ответ: 3 дня.
4) В растворе массой 500 г имеется 40 г соли. Сколько граммов соли в 200 г раствора?
500 г-40 г
200 г-х г
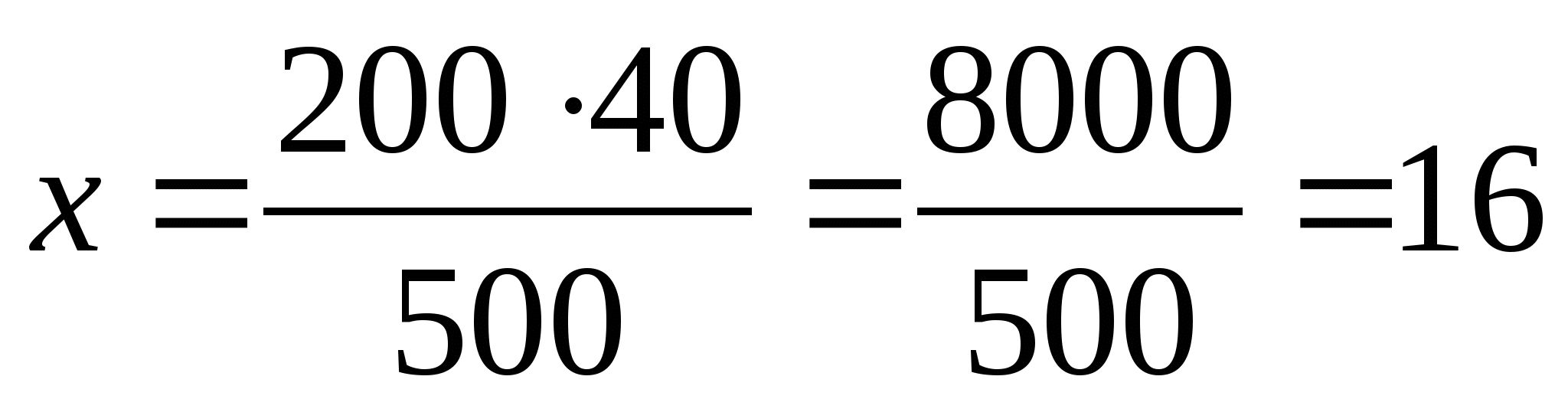
Ответ: 16 г
Крестьянским хозяйством заготовлено корма на 184 дня для 75 коров. На сколько дней хватит этого корма, если увеличить поголовье на 40 коров?
184 дня – 75 коров
х дней– 115 коров
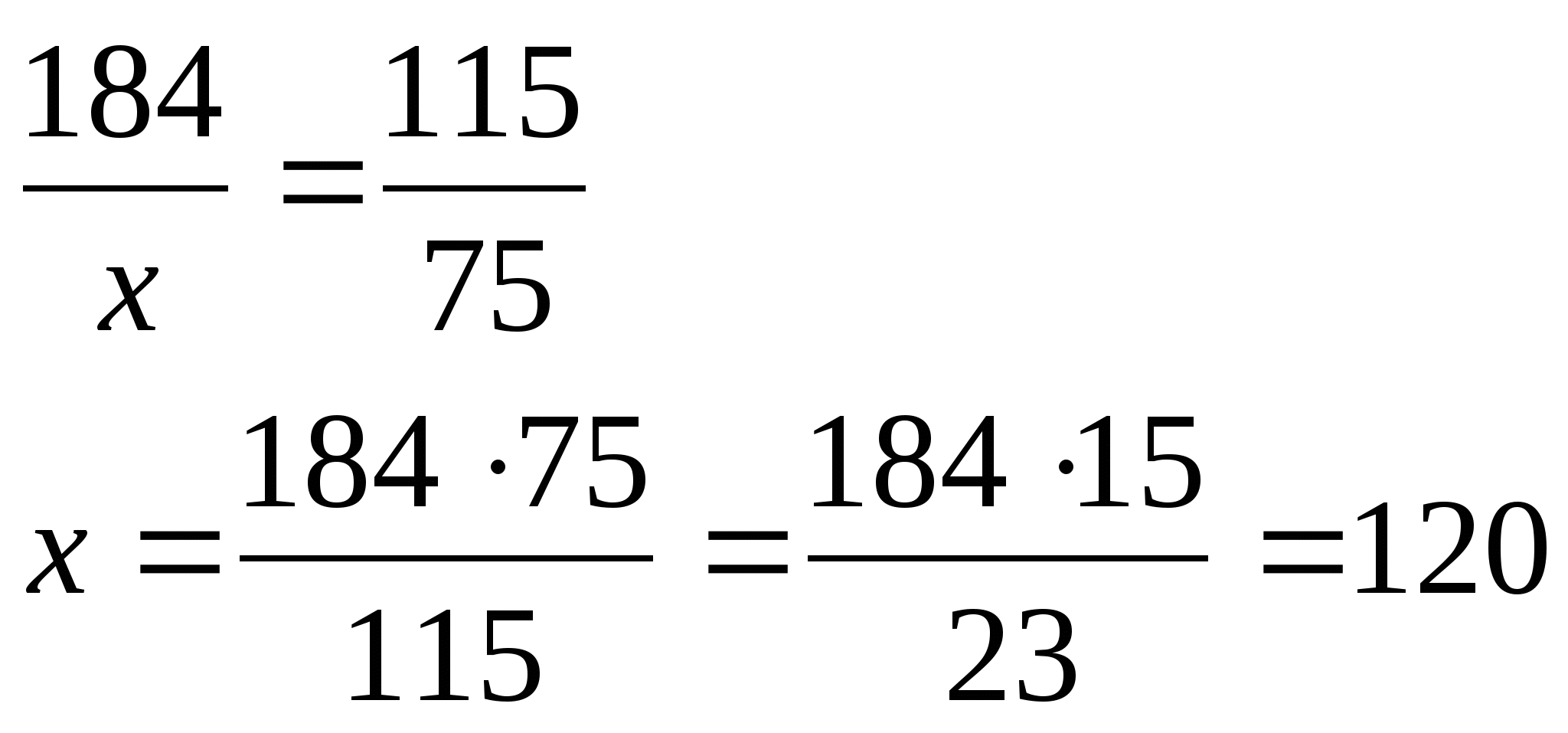
Ответ: 120 дней.
Задание для инклюзива:
х=2 х=-3 х=-2,8 х=20,5 х=-69,3
|х|=2 |х|=3 |х|=2,8 |х|=20,5 |х|=69,3
4. Подведение итогов.
5. Постановка домашнего задания.
Найдите значения выражения:
|-4,2| + 3 = 4,2 + 3=7,2;
|-90| : 15 = 90 : 15=6;
 ;
;|-100| + 5,4 : 3 = 100 + 1,8 = 101,8;
5) Станок-автомат изготовил 348 деталей по 58 деталей в час. Сколько деталей он изготовит за это же время, если будет изготавливать по 75 деталей в час?
348-58
х-75
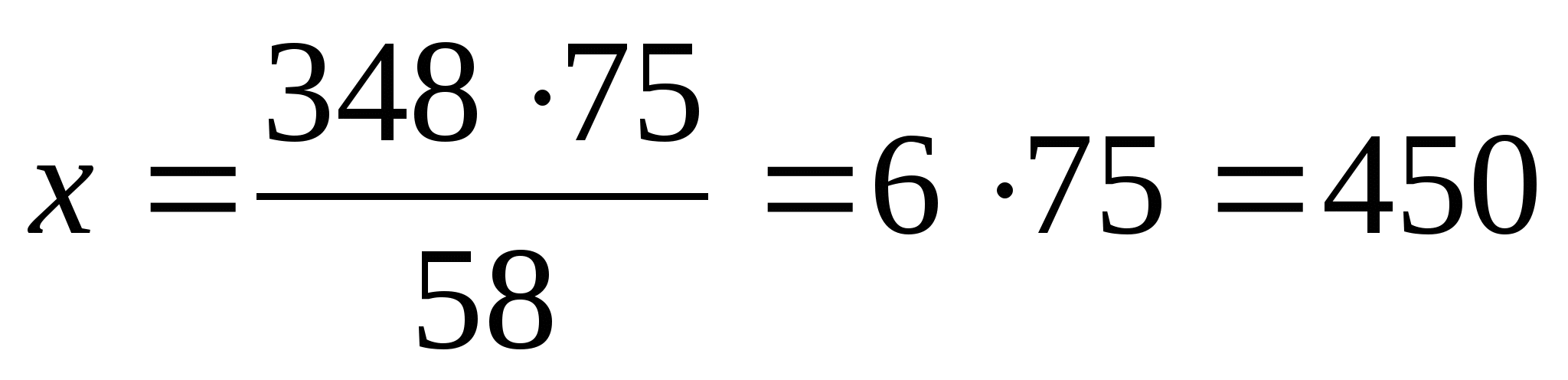
Ответ: 450 деталей
6) Бауржан купил для своего аквариума 9 рыбок по цене 120 тенге. Сколько рыбок купит Бауржан на эту сумму, если цена одной рыбки будет снижена на 25%?
9 р – 120т
х р – 90 т

Ответ: 12 рыбок
infourok.ru
Проверочный тест по алгебре по теме «Прямая пропорциональность», (7 класс)
Проверочный тест по теме
«Прямая пропорциональность» (7 класс)
I вариант:
Обязательная часть.
А1. Прямая пропорциональность задана формулой у = -2х. Найдите значение у при х = -5.
Варианты ответов:
а) -10
б) 10
в) -7
г) 7
Ответ: ______
А2.Прямая пропорциональность задана формулой у = 0,25х. Найдите значение х при котором у = -1.
Варианты ответов:
а) 4
б) -4
в) 0,25
г) -0,25
Ответ: _____
А3. На рисунке изображены графики трёх функций, задаваемых формулами вида 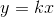 . Укажите для каждого графика соответствующую ему формулу, выбрав её из числа приведённых ниже.
. Укажите для каждого графика соответствующую ему формулу, выбрав её из числа приведённых ниже.
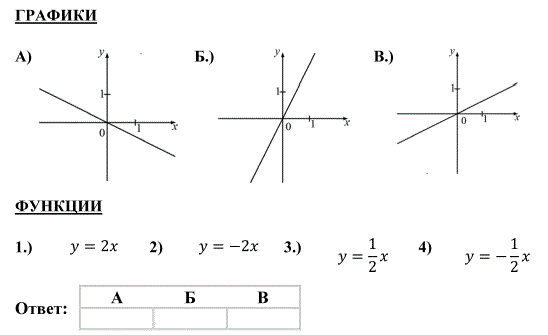
А4. Найдите координаты точки пересечения графика функции у = -1,2х с осью ординат.
Варианты ответов:
а) (-1,2; 0)
б) (0;0)
в) (0; -1,2)
г) (1,2; 0)
Ответ: ____
Дополнительная часть.
В1. Найдите координаты точки пересечения графиков функций у = 16,4 и у = — 2,01х аналитическим методом.
Решение: ______________________________________________________________________________________________________________________________________________________
Ответ:
В2. Сколько различных трехзначных чисел можно составить из цифр 1; 2; 3; 4, если цифры в числе не повторяются?
Решение: ______________________________________________________________________________________________________________________________________________________
II вариант:
Обязательная часть.
А1. Прямая пропорциональность задана формулой у = -5х. Найдите значение у при х = 3.
Варианты ответов:
а) -15
б) 15
в) -8
г) 8
Ответ: ______
А2.Прямая пропорциональность задана формулой у = -0,15х. Найдите значение х при котором у = 6.
Варианты ответов:
а) 40
б) -40
в) 0,9
г) -0,9
Ответ: _____
А3. На рисунке изображены графики трёх функций, задаваемых формулами вида 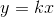 . Укажите для каждого графика соответствующую ему формулу, выбрав её из числа приведённых ниже.
. Укажите для каждого графика соответствующую ему формулу, выбрав её из числа приведённых ниже.
А4. Найдите координаты точки пересечения графика функции у = -2,3х с осью ординат.
Варианты ответов:
а) (-2,3; 0)
б) (0;0)
в) (0; -2,3)
г) (2,3; 0)
Ответ: ____
Дополнительная часть.
В1. Найдите координаты точки пересечения графиков функций у = 5,2 и у = — 1,04х аналитическим методом.
Решение: ______________________________________________________________________________________________________________________________________________________
Ответ:
В2. Сколько различных двухзначных чисел можно составить из цифр 1; 2; 3; 4; 5, если цифры в числе не повторяются?
Решение: ______________________________________________________________________________________________________________________________________________________
xn--j1ahfl.xn--p1ai
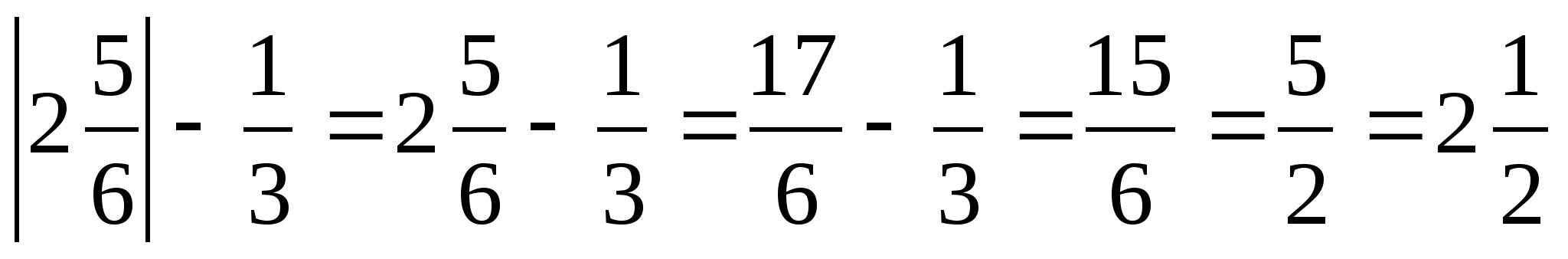 ;
;