Обратно пропорциональная зависимость | Математика
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз. Соответственно, при уменьшении одной из них в несколько раз другая увеличивается во столько же раз.
Зависимость между такими величинами — обратно пропорциональная зависимость. Примеры обратной пропорциональной зависимости:
1) время, затраченное на прохождение определенного пути, и скорость, с которой этот путь был пройден — обратно пропорциональные величины;
2) при одинаковой производительности труда количество рабочих, выполняющих определенную работу, обратно пропорционально времени выполнения этой работы;
3) количество товара, купленного на определенную сумму денег, обратно пропорционально его цене.
Чтобы отличить обратно пропорциональную зависимость от прямой, можно использовать пословицу: «Тише едешь — дальше будешь».
Задачи на обратно пропорциональные величины удобно решать с помощью пропорции.
Рассмотрим примеры задач на обратно пропорциональную зависимость.
1) 24 человека за 5 дней пропололи участок. За сколько дней выполнит ту же работу 30 человек, если будут работать с той же производительностью?
(Рассуждаем так:
1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы. Значит, это — обратно пропорциональная зависимость.
3. Поэтому вторая стрелка имеет противоположное направление).
Решение:
Пусть за х дней могут прополоть участок 30 человек. Составляем пропорцию (в направлении от начала стрелки к ее концу):
Чтобы найти неизвестный крайний член пропорции, надо произведение средних членов разделить на известный крайний член:
24 и 30 сокращаем на 6, 5 и 5 — на 5:
Значит, 30 человек выполнят эту работу за 4 дня.
Ответ: за 4 дня.
2) Для перевозки груза автомашине грузоподъемностью 7,5 тонн пришлось сделать 12 рейсов. Сколько рейсов понадобится сделать автомашине грузоподъемностью 9 тонн для перевозки этого же груза?
(1. В заполненном столбце ставим стрелку в направлении от большего числа к меньшему.
2. Чем больше грузоподъемность машины, тем меньше рейсов ей нужно сделать, чтобы перевезти груз. Значит, это — обратно пропорциональная зависимость.
3. Поэтому вторая стрелка имеет противоположное направление).
Решение:
Пусть х рейсов потребуется машине грузоподъемностью 9 тонн, чтобы перевезти груз. Составляем пропорцию (от начала стрелки к ее концу):
Значит, понадобится 10 рейсов.
Ответ: 10 рейсов.
www.for6cl.uznateshe.ru
Конспект урока и презентация по математике на тему «Прямая и обратная пропорциональность» (6 класс)
УРОК № 12. Глава 1. Отношения, пропорции, проценты (26 часов)
Тема. Прямая и обратная пропорциональность. С/р № 3.
Цель. Проверить знания учащихся по теме «Пропорции». Дать определение прямо пропорциональных и обратно пропорциональных величин. Научится решать задачи по данной теме.
Ход урока.
Организационный момент.
Проверка домашнего задания.
С
амостоятельная работа по теме «Пропорции». (10 min)
амостоятельная работа по теме «Пропорции». (10 min)Вариант 1. Вариант 1.
Решить пропорцию: Решить пропорцию:
1) 
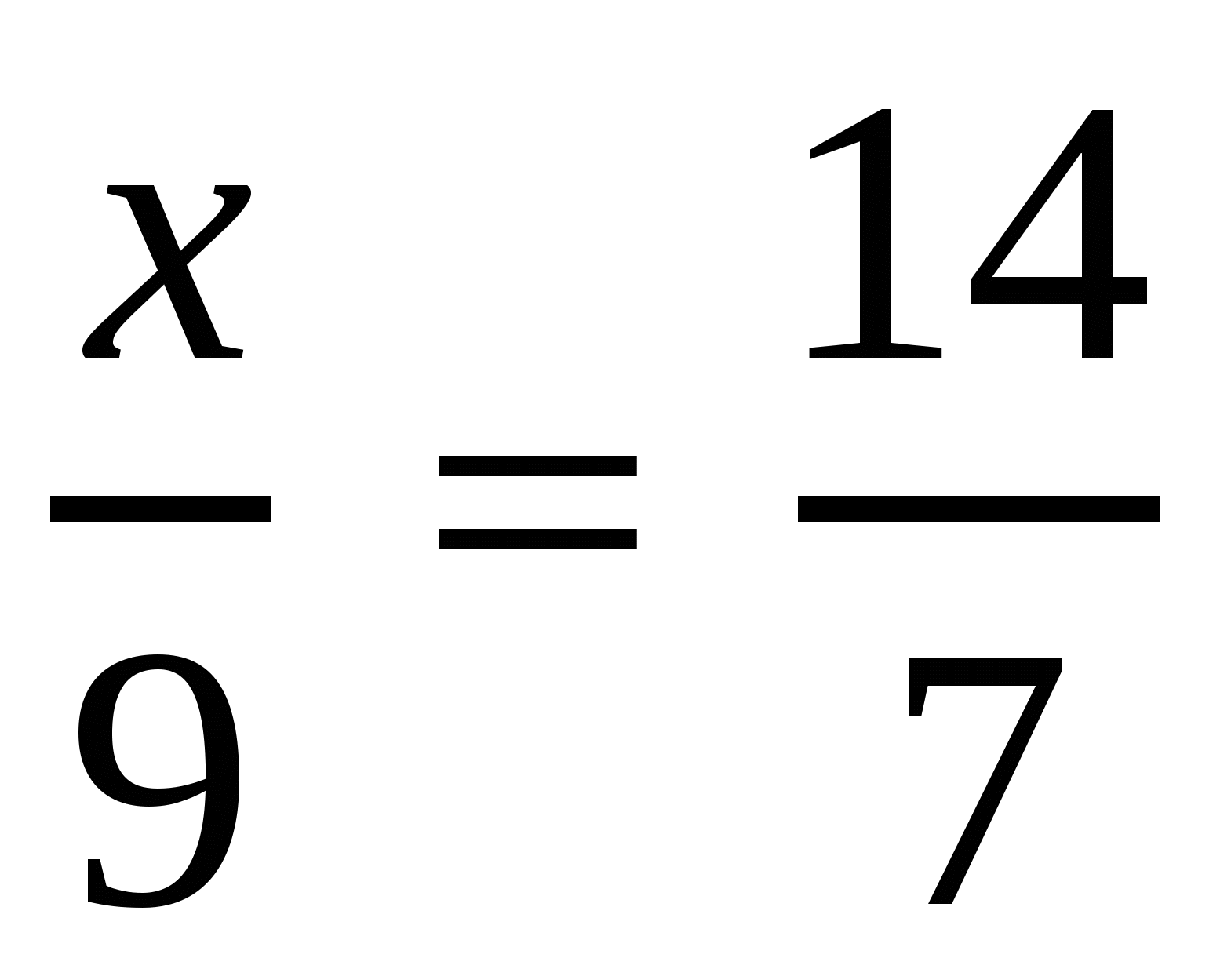, 1) 
, 
,
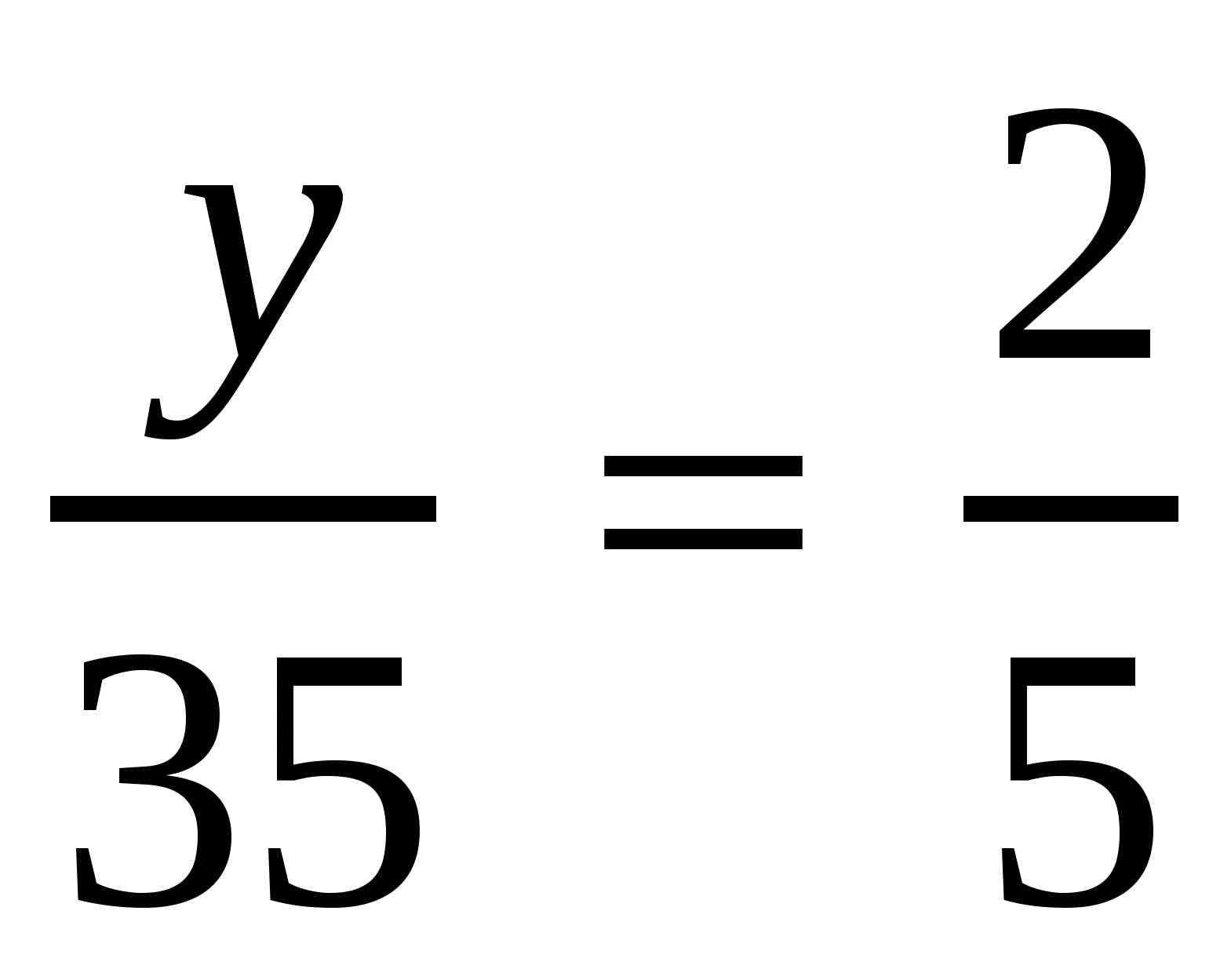
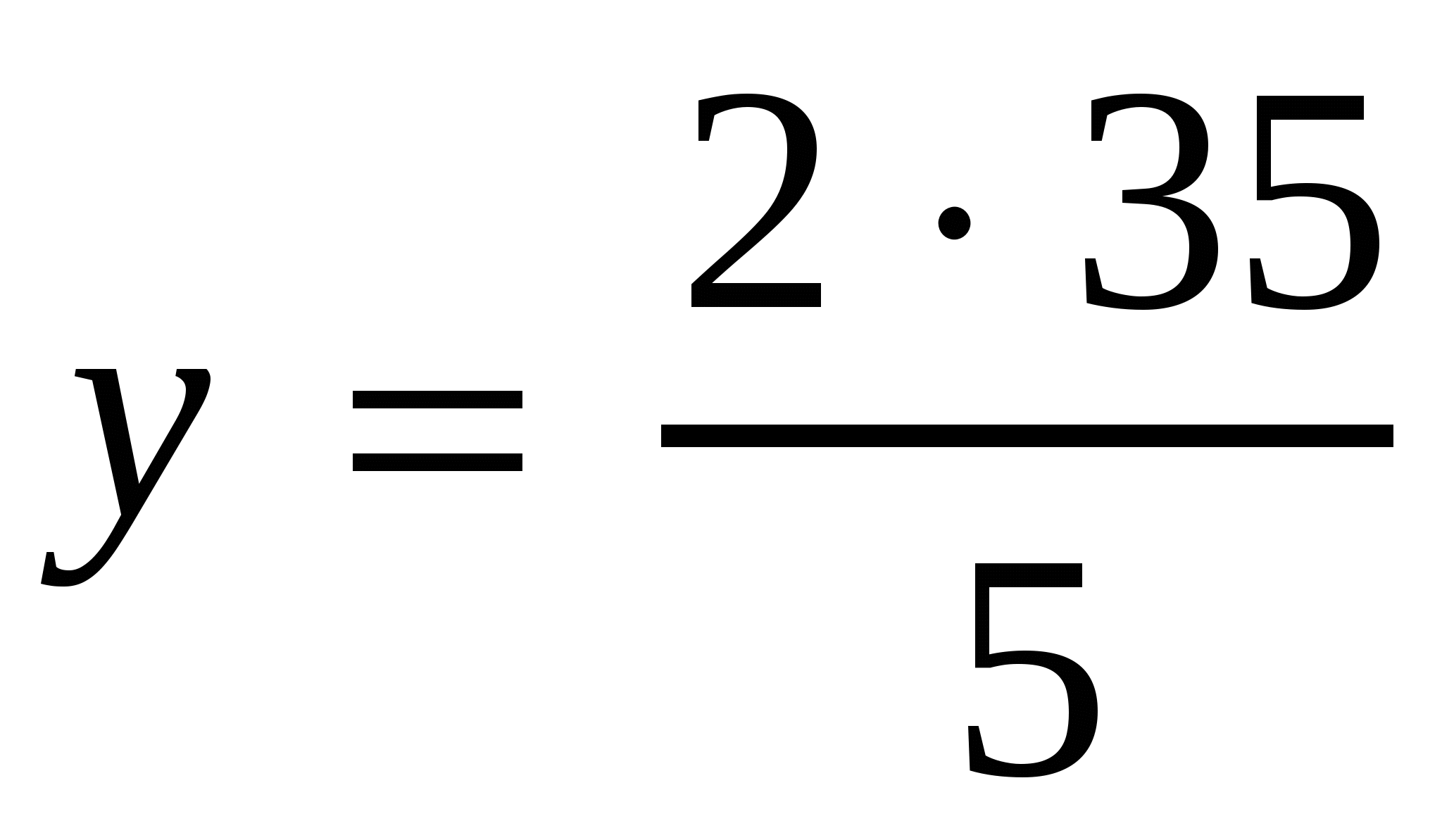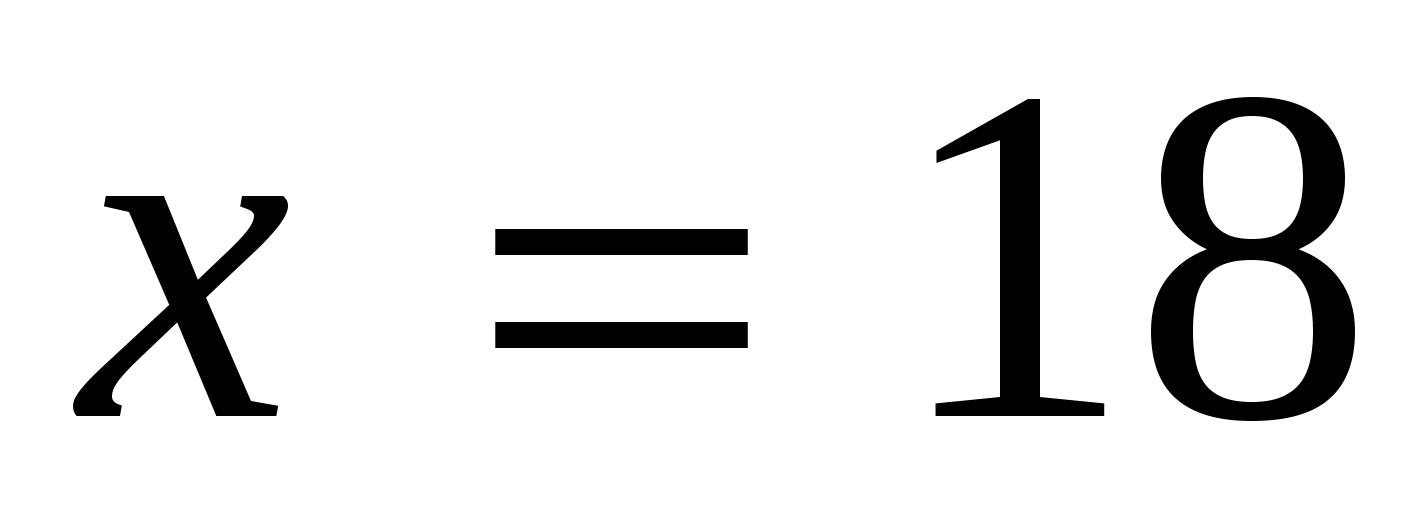. Ответ: 
. 
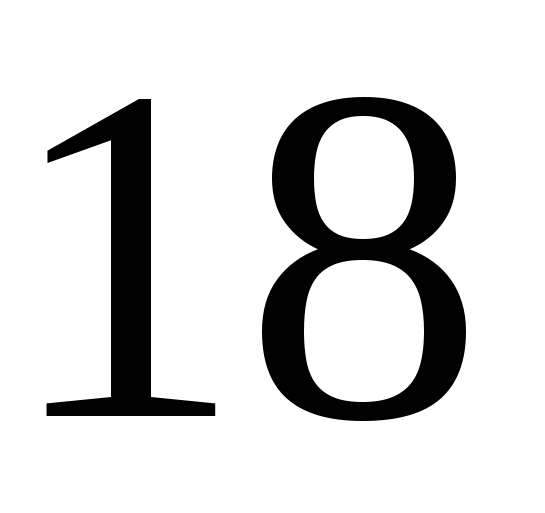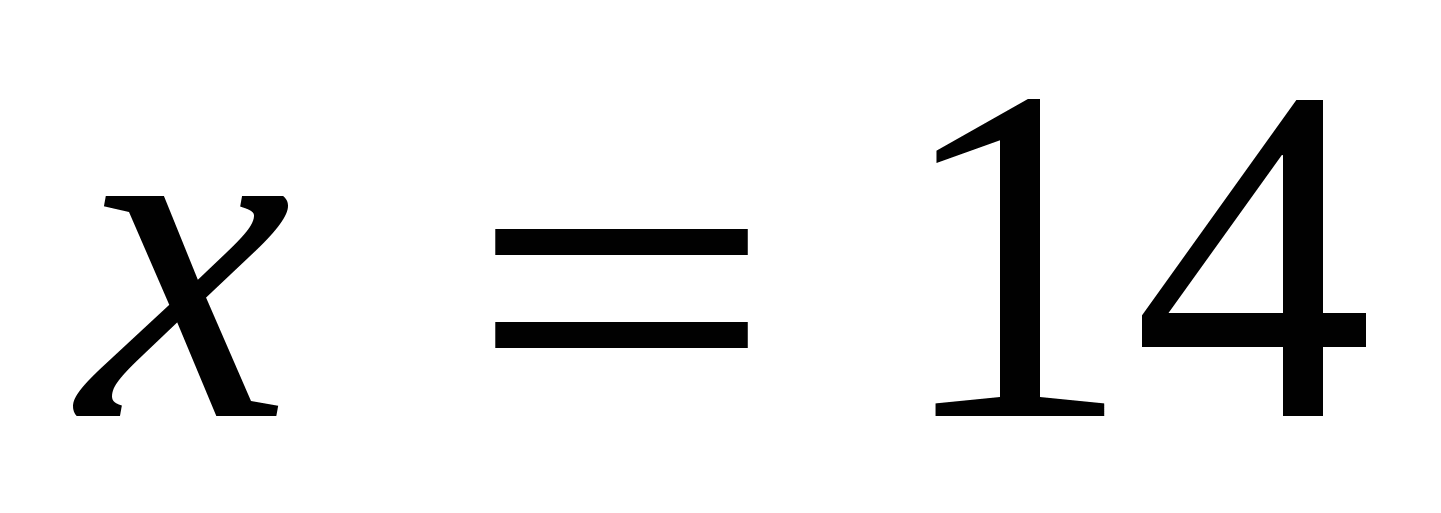. Ответ: 
.
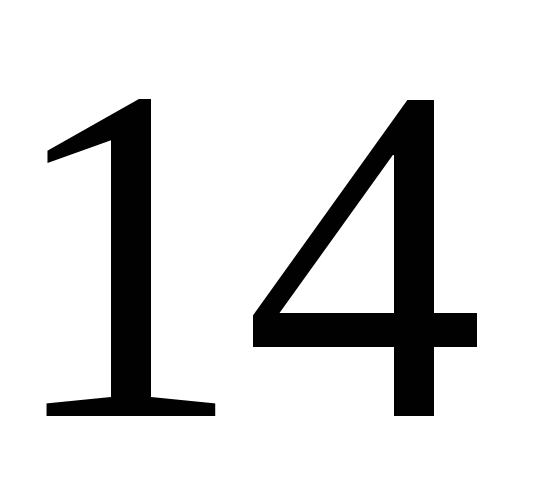2) 
,
, 
,
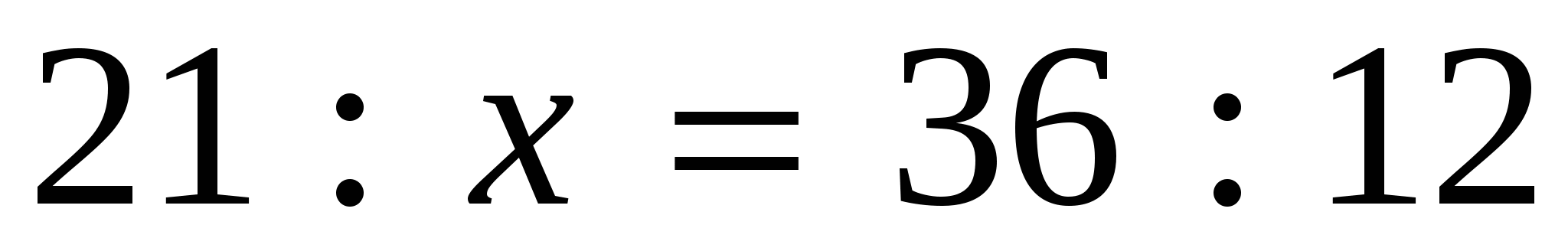
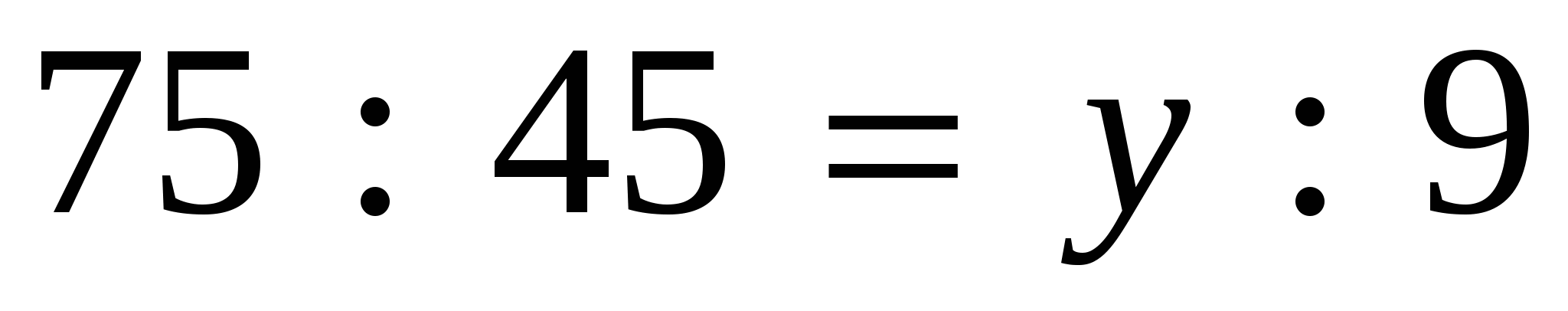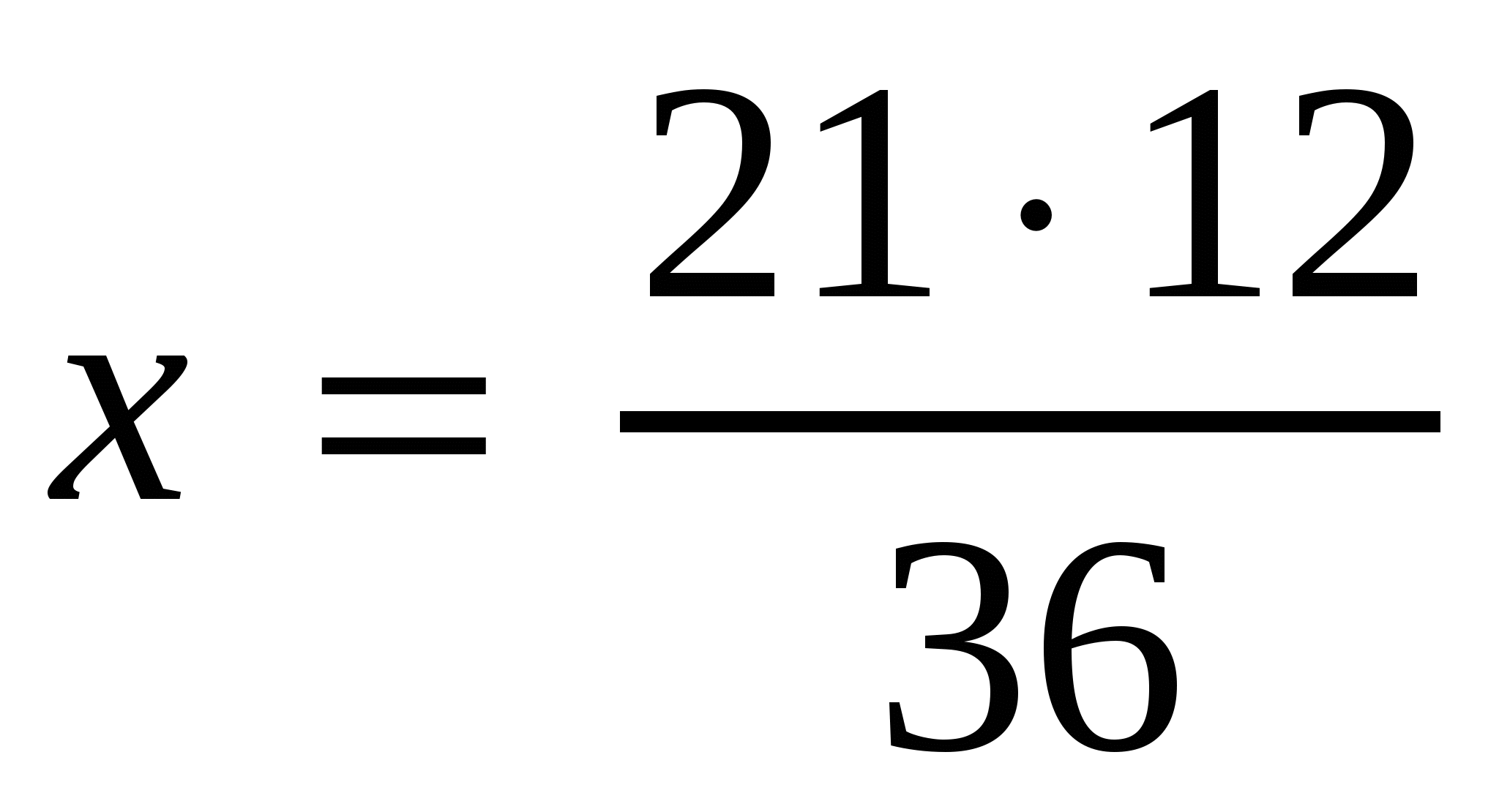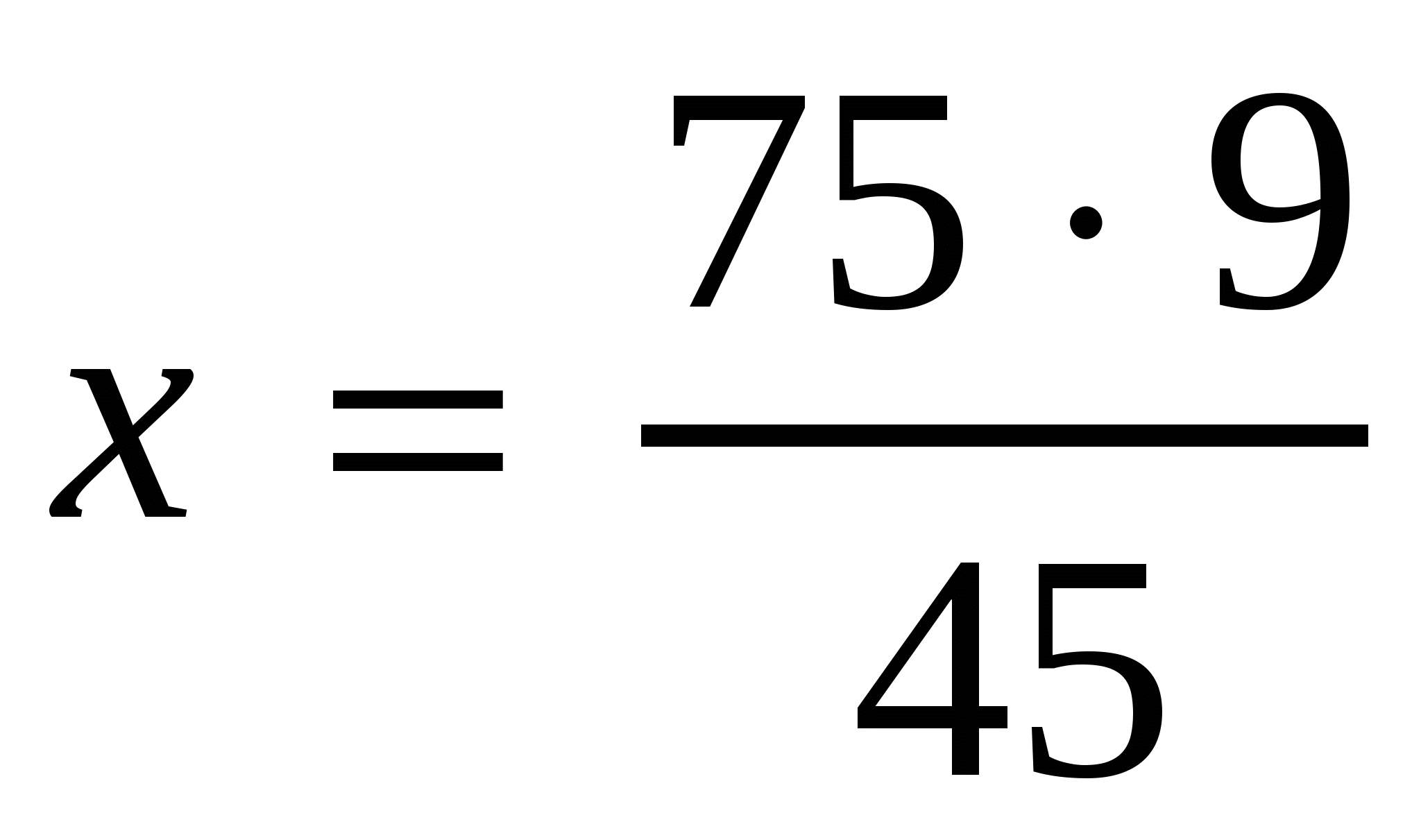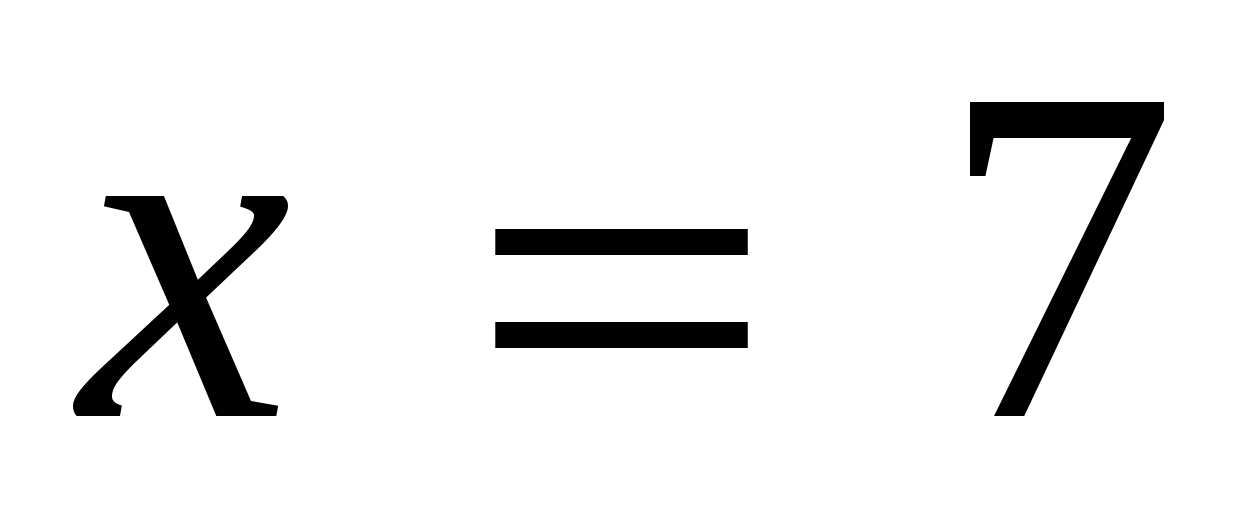. Ответ: 
. 
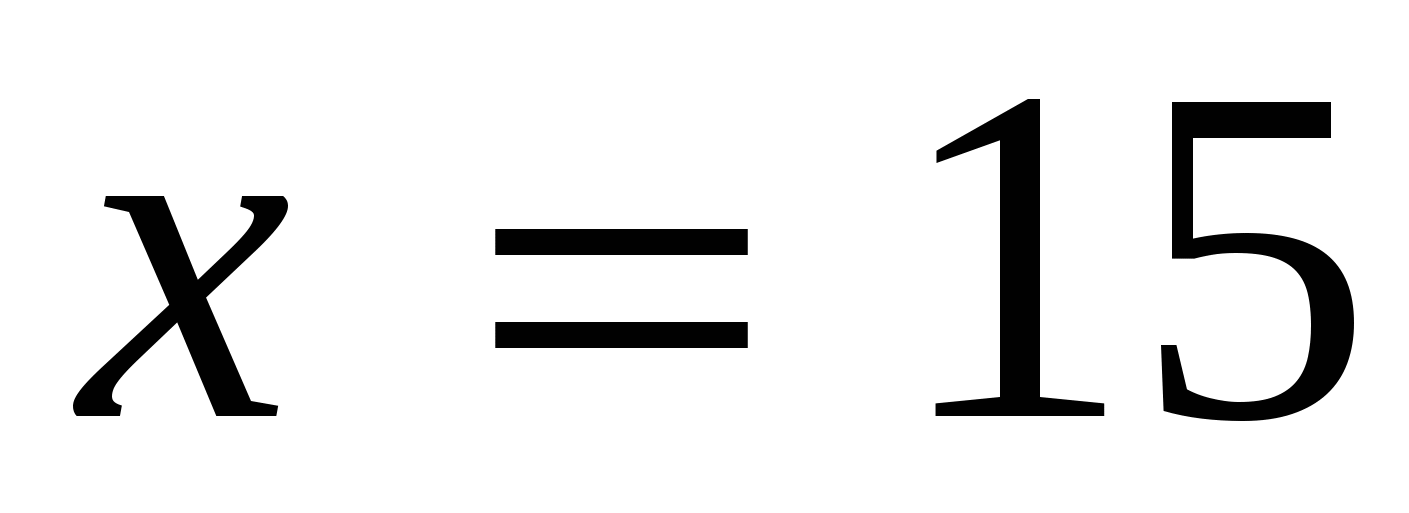. Ответ: 
.
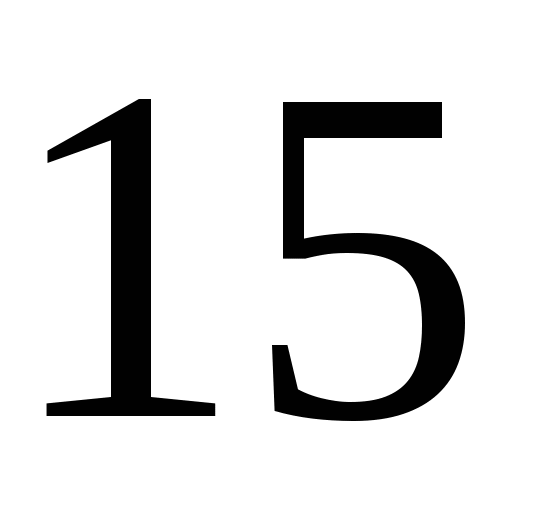3) 
,
, 
,
, 
,
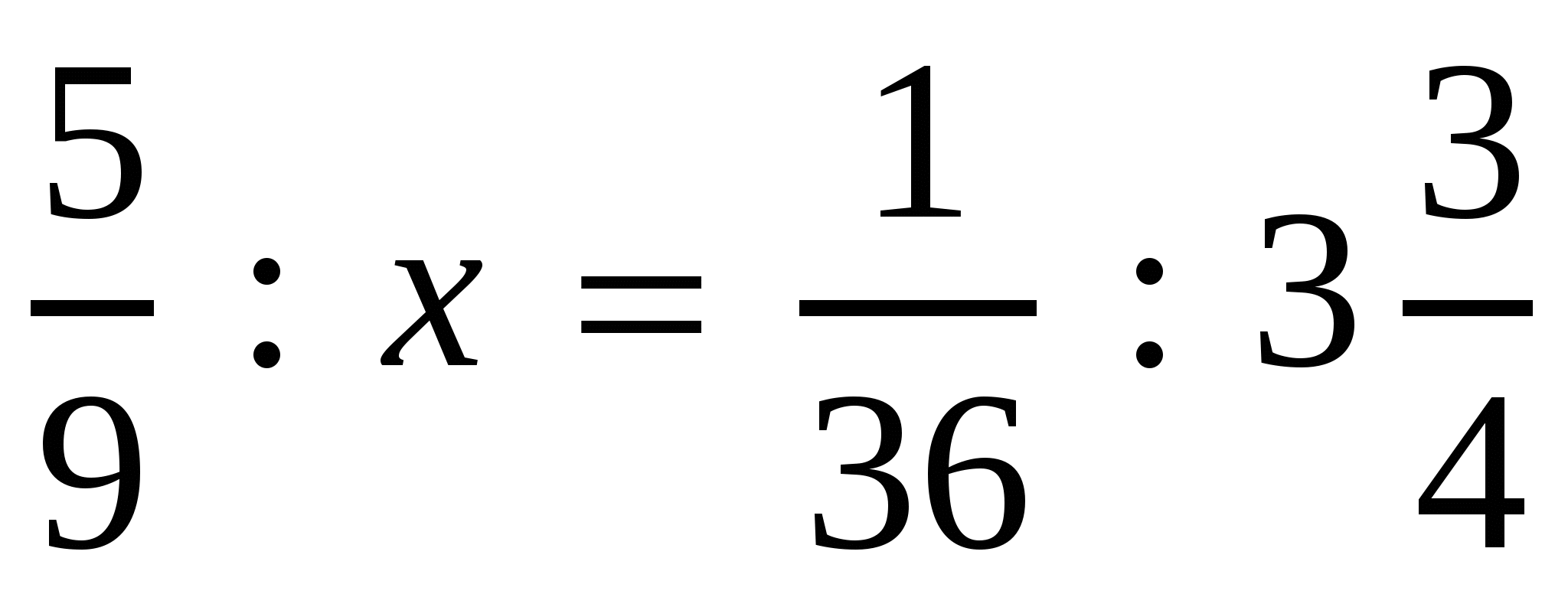
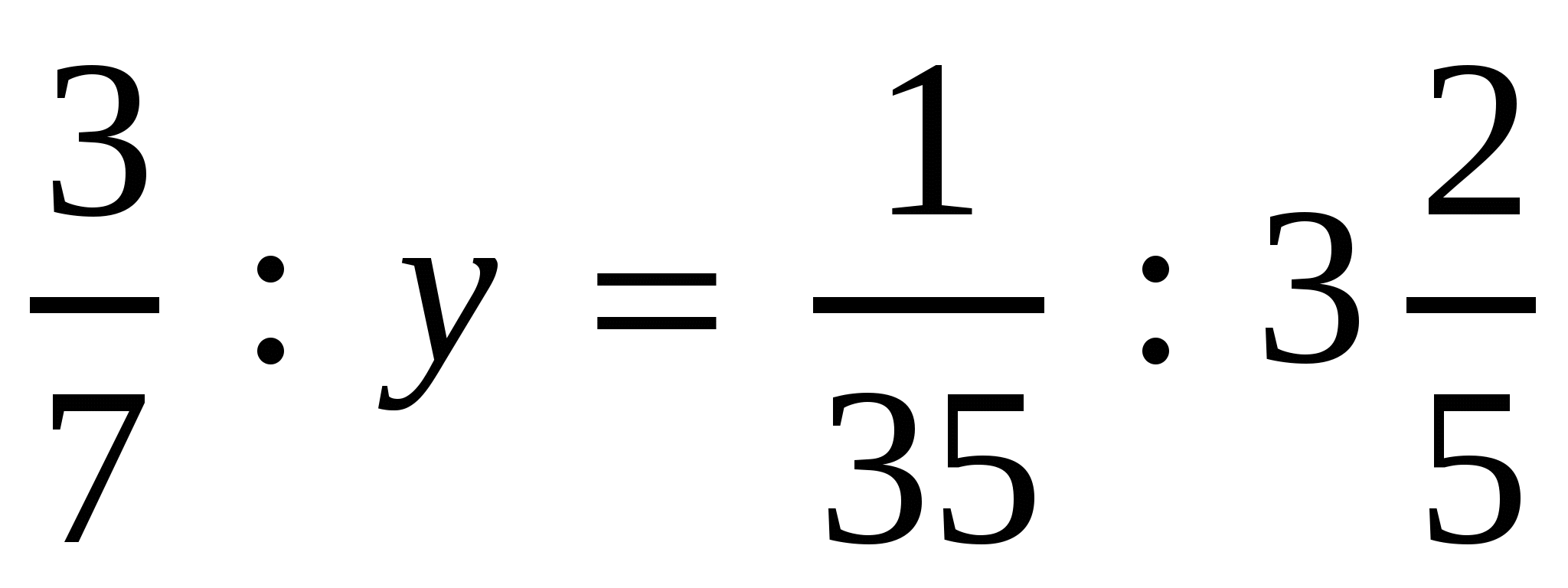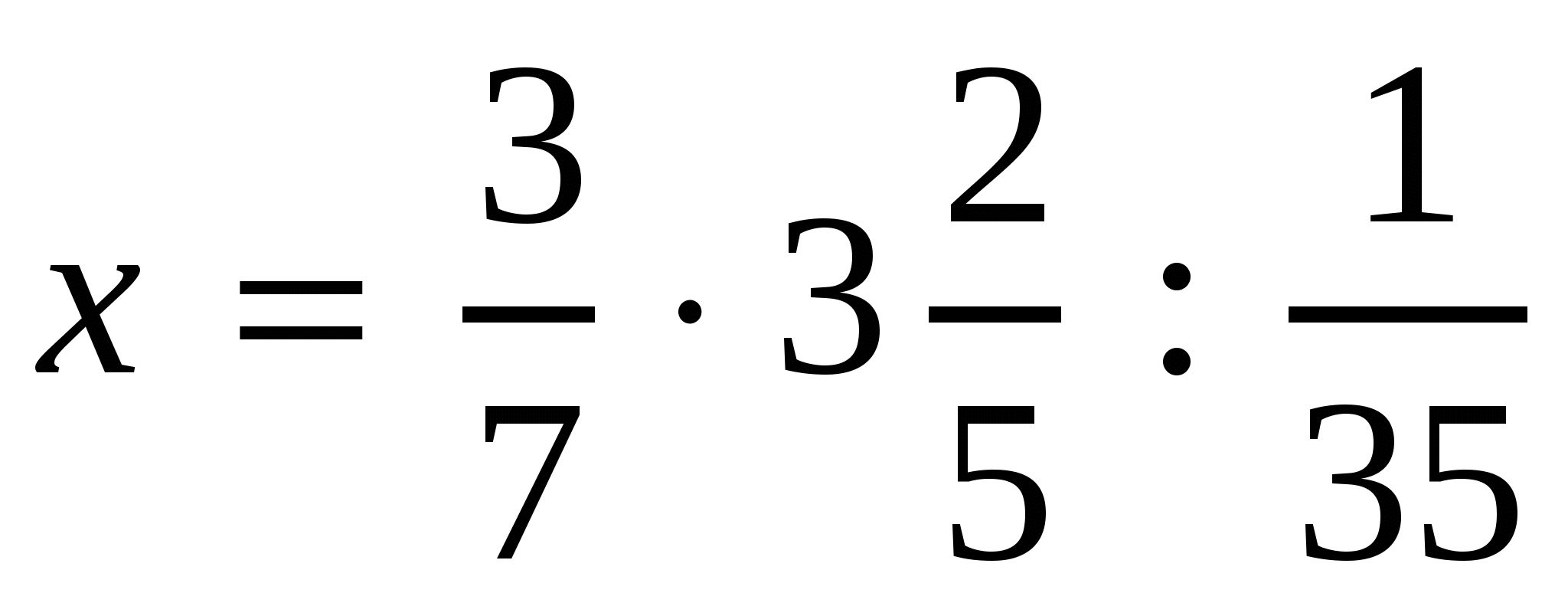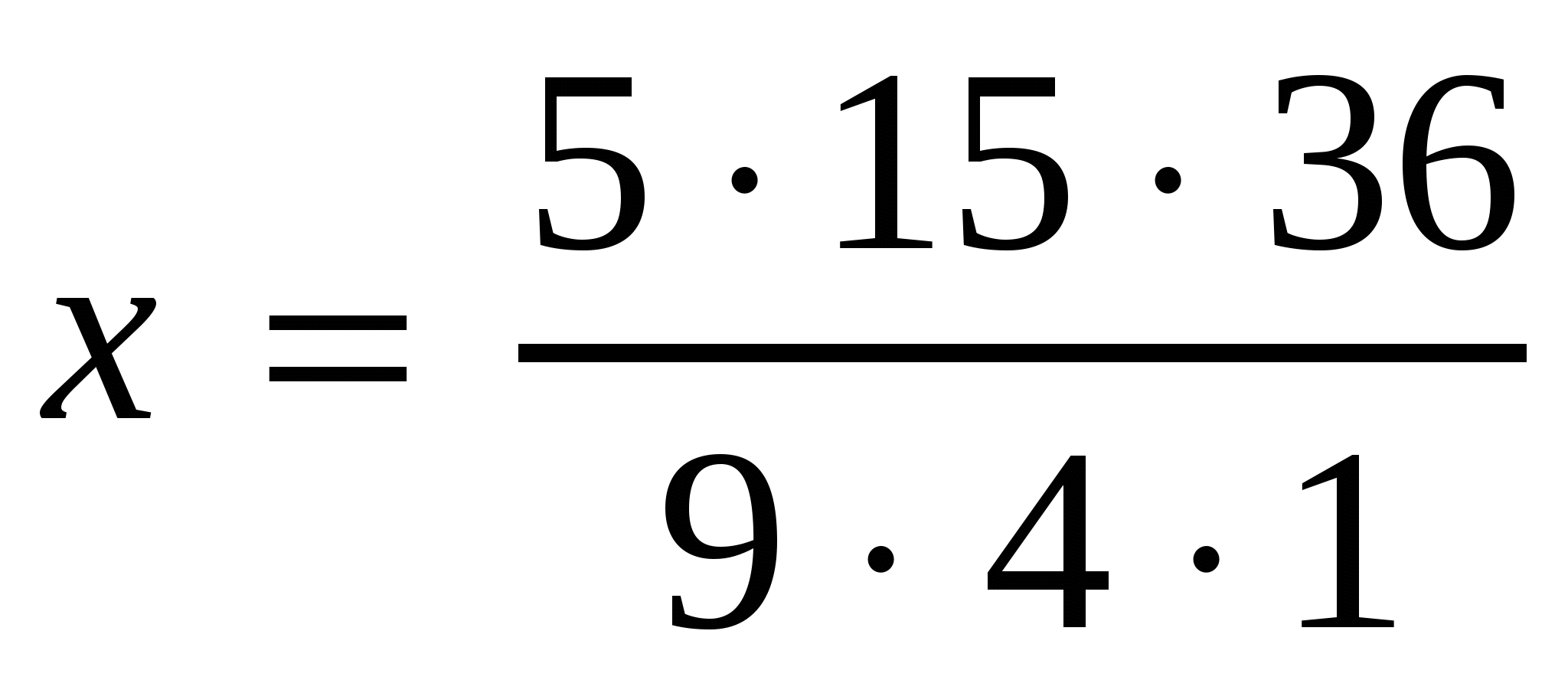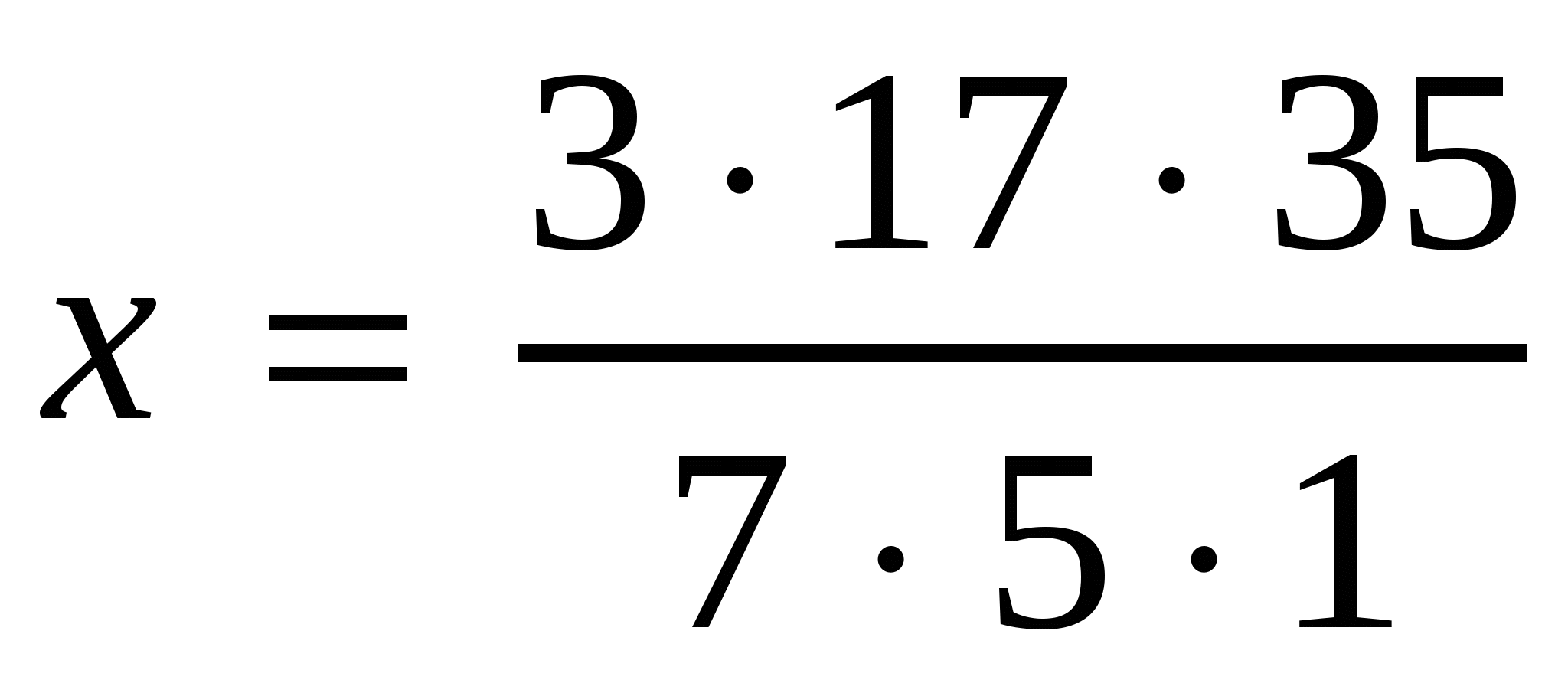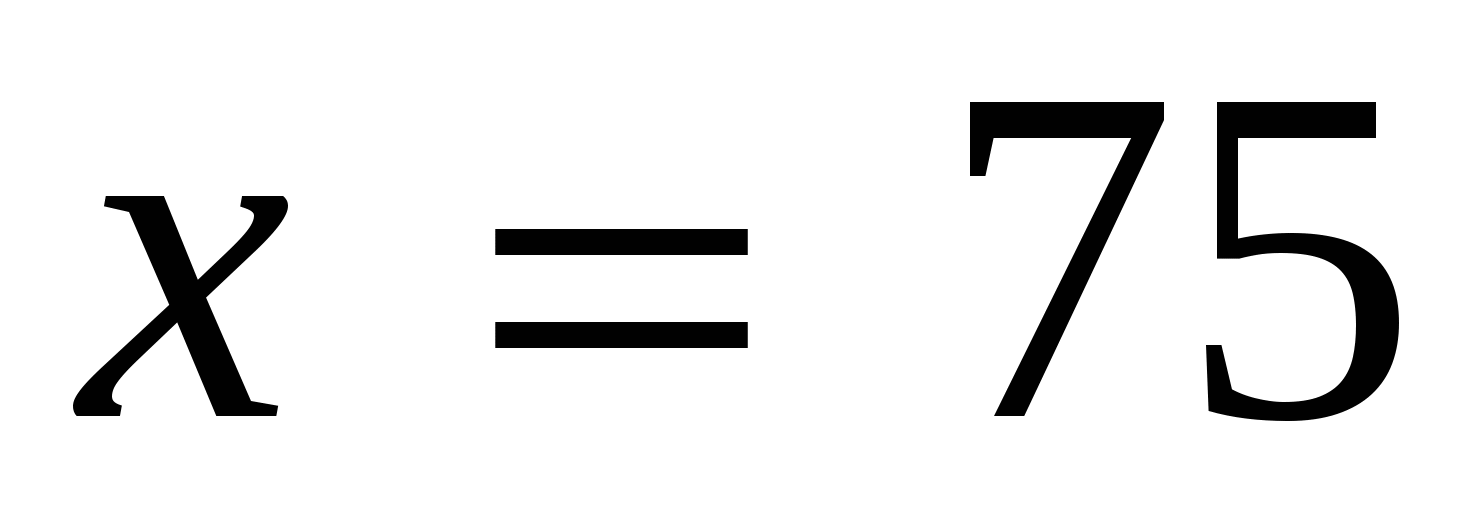. Ответ: 
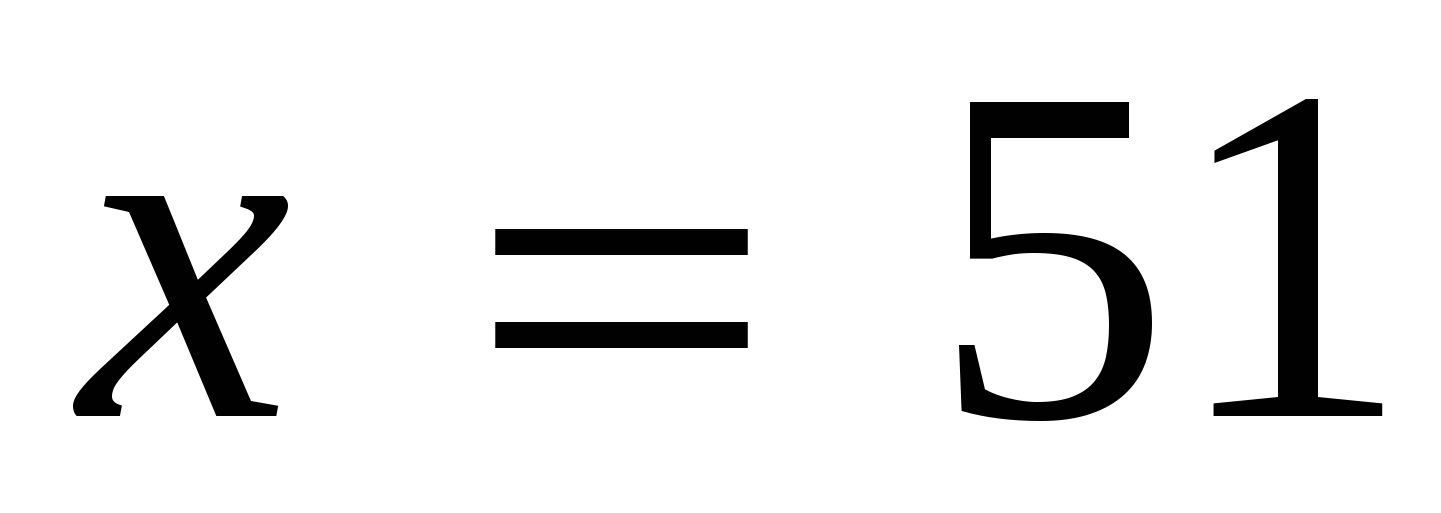. Ответ: 
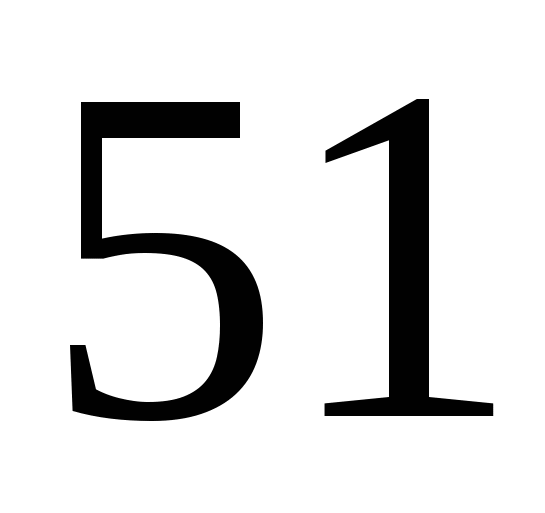.Объяснение нового материала.
Прямая и обратная пропорциональность.
Мультимедийная доска. Электронное приложение. Каталог. Анимация. Расход электроэнергии в квартире. (1 мин 31 секунды)
(Слайд 2). Пусть ручка стоит 3 р. (это цена). Тогда легко рассчитать стоимость двух, трех и т.д. ручек по формуле: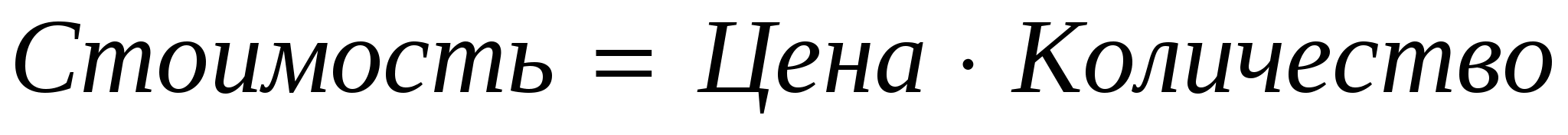 
.
Количество ручек, шт.
1
2
3
4
Стоимость, р.
36
9
12
Заметим, что с увеличением количества ручек в несколько раз их стоимость увеличивается во столько же раз.
Говорят, что стоимость покупки прямо пропорциональна количеству купленных ручек.
(Слайд 3). Определение. Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
(Слайд 4). Примеры прямо пропорциональных величин:
1. Периметр квадрата и длина стороны квадрата – прямо пропорциональные величины.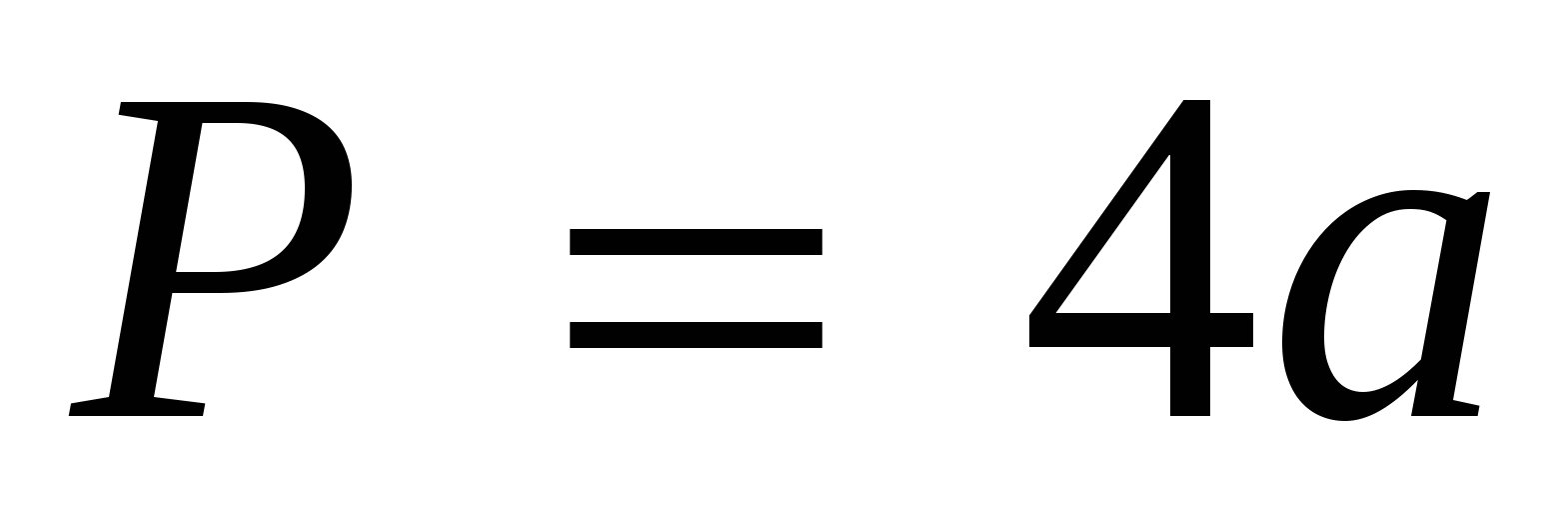 
.
2. Если скорость движения постоянна, то пройденный путь и время движения – прямо пропорциональные величины.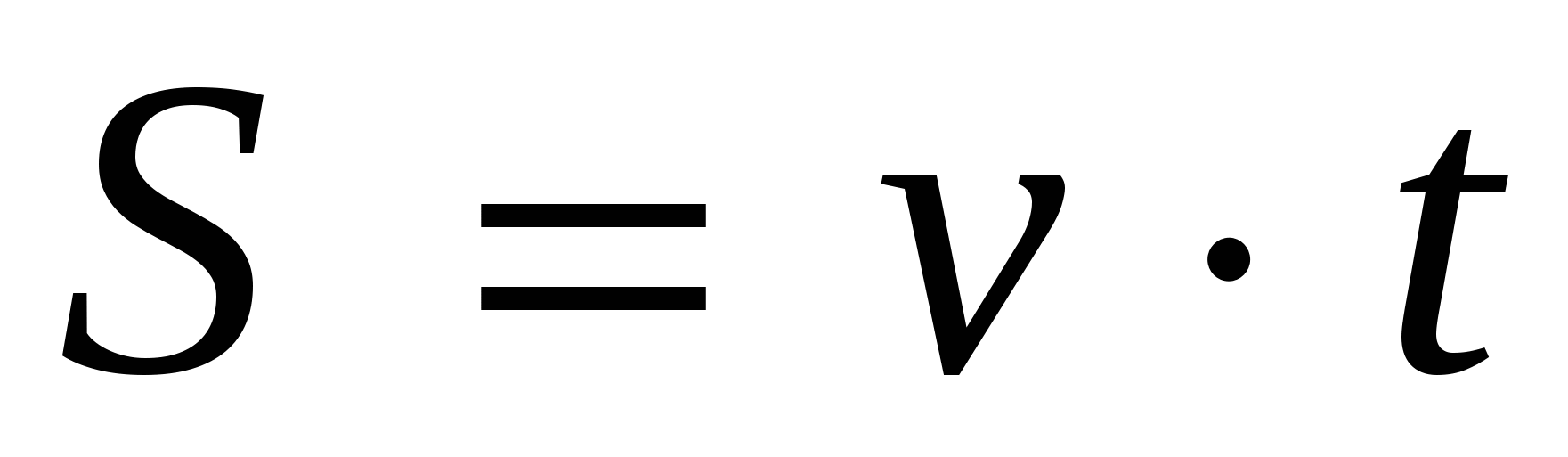 
3. Если производительность труда постоянна, то объём выполненных работ и время – прямо пропорциональные величины.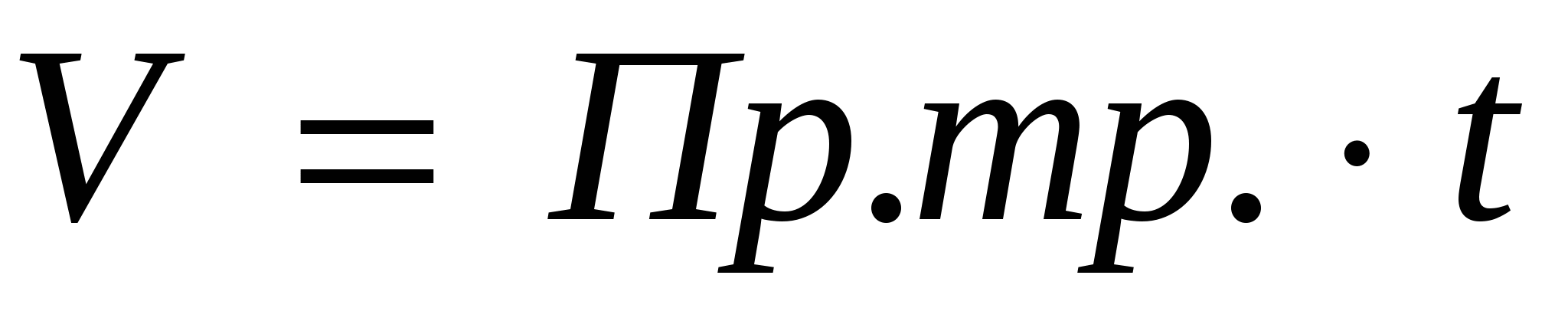 
.
4. Выручка кассы кинотеатра прямо пропорциональна количеству проданных билетов при одинаковой цене. И т.д.
(Слайд 5). Задача 1. За 5 тетрадей в клетку заплатили 40 р. Сколько заплатят за 12 таких же тетрадей?
Кол-во Стоимость
5
тетрадей – 40 р. Прямая пропорциональность
12 тетрадей – х р.
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
,
,
.
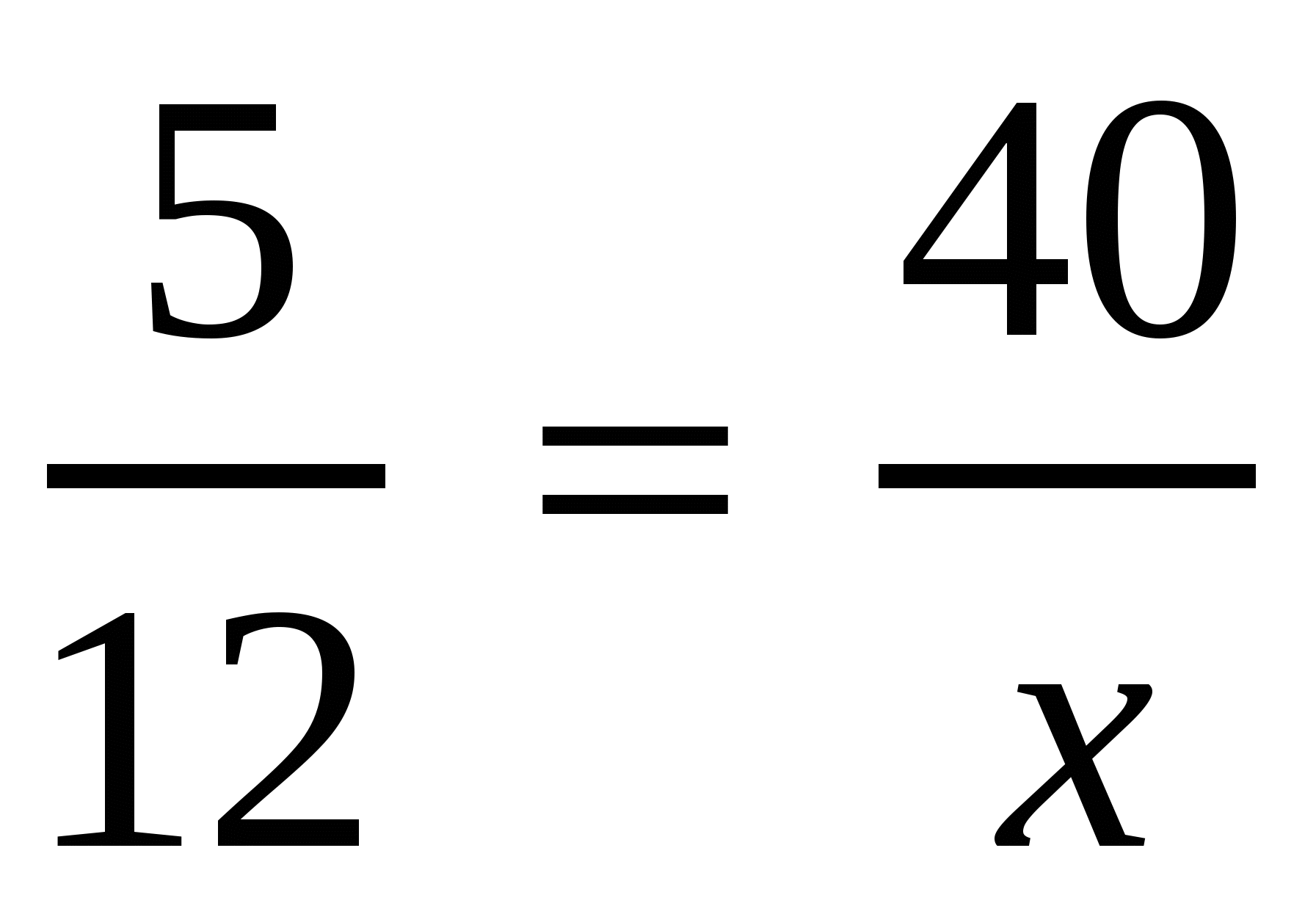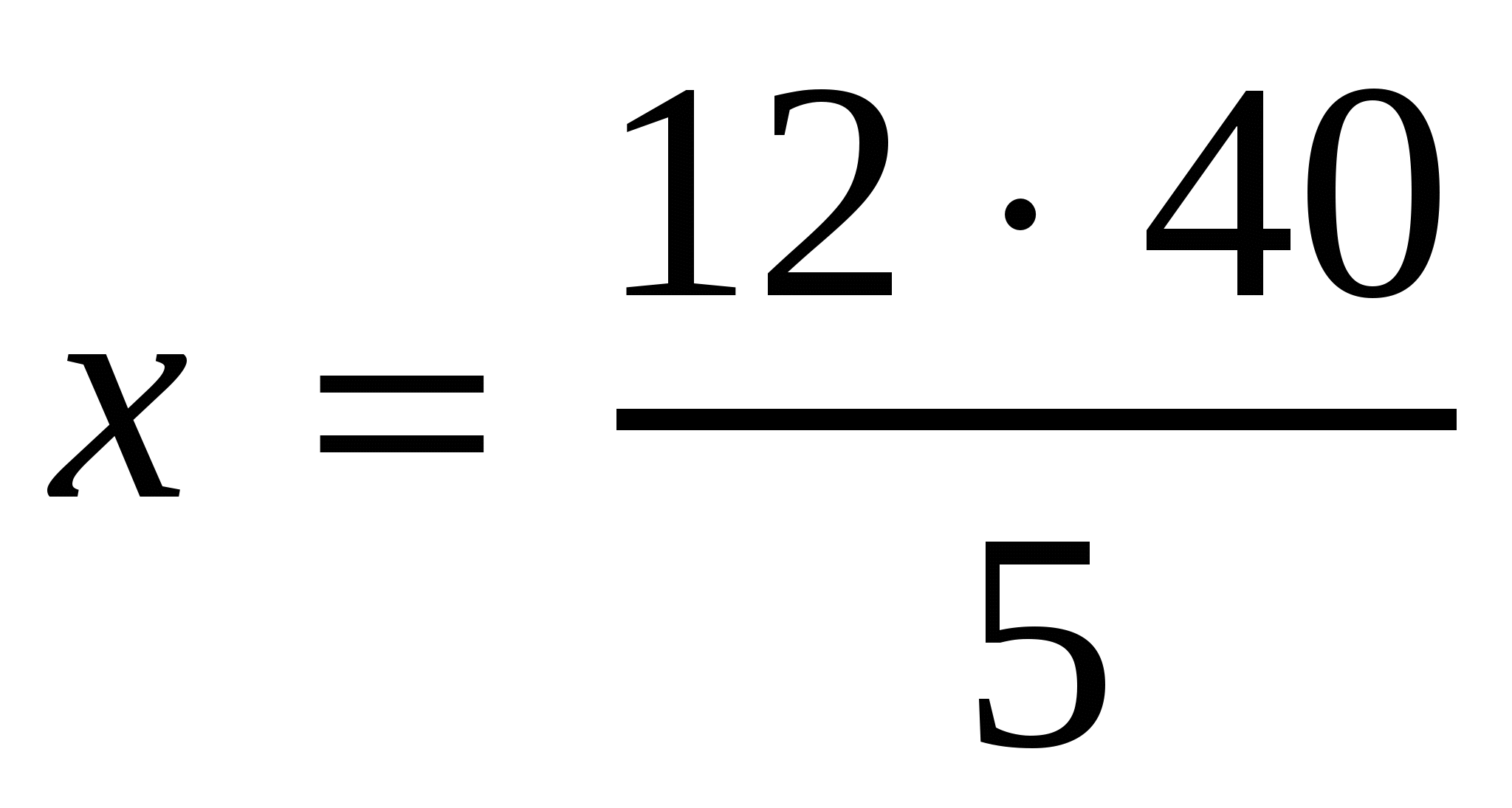96 р. заплатят за 12 тетрадей. Ответ: 96 р.
(Слайд 6). Хотят купить на 120 р. несколько одинаковых книг. Тогда легко рассчитать количество книг по 10 р., 20 р., 30 р. 40 р. и т.д. по формуле: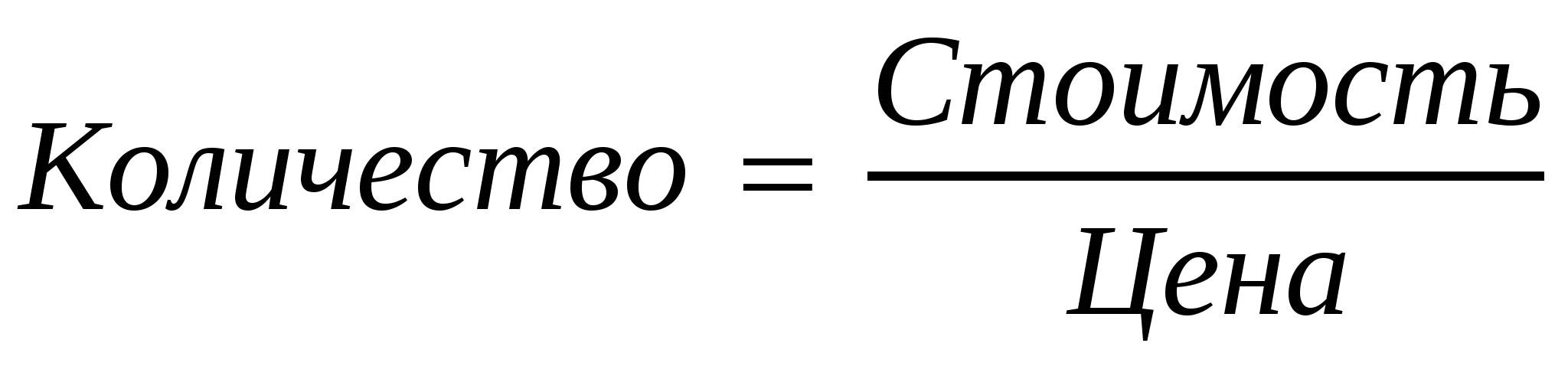 
.
Цена, р.
10
30
40
Количество книг, шт.
12
6
4
3
Заметим, что с увеличением цены книги в несколько раз их количество уменьшается во столько же раз.
Говорят, что количество купленных книг обратно пропорционально их цене.
(Слайд 7). Определение. Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению значений другой величины.
(Слайд 8). Примеры обратно пропорциональных величин:
1. Если пройденный путь постоянен, то скорость движения и время движения – обратно пропорциональные величины.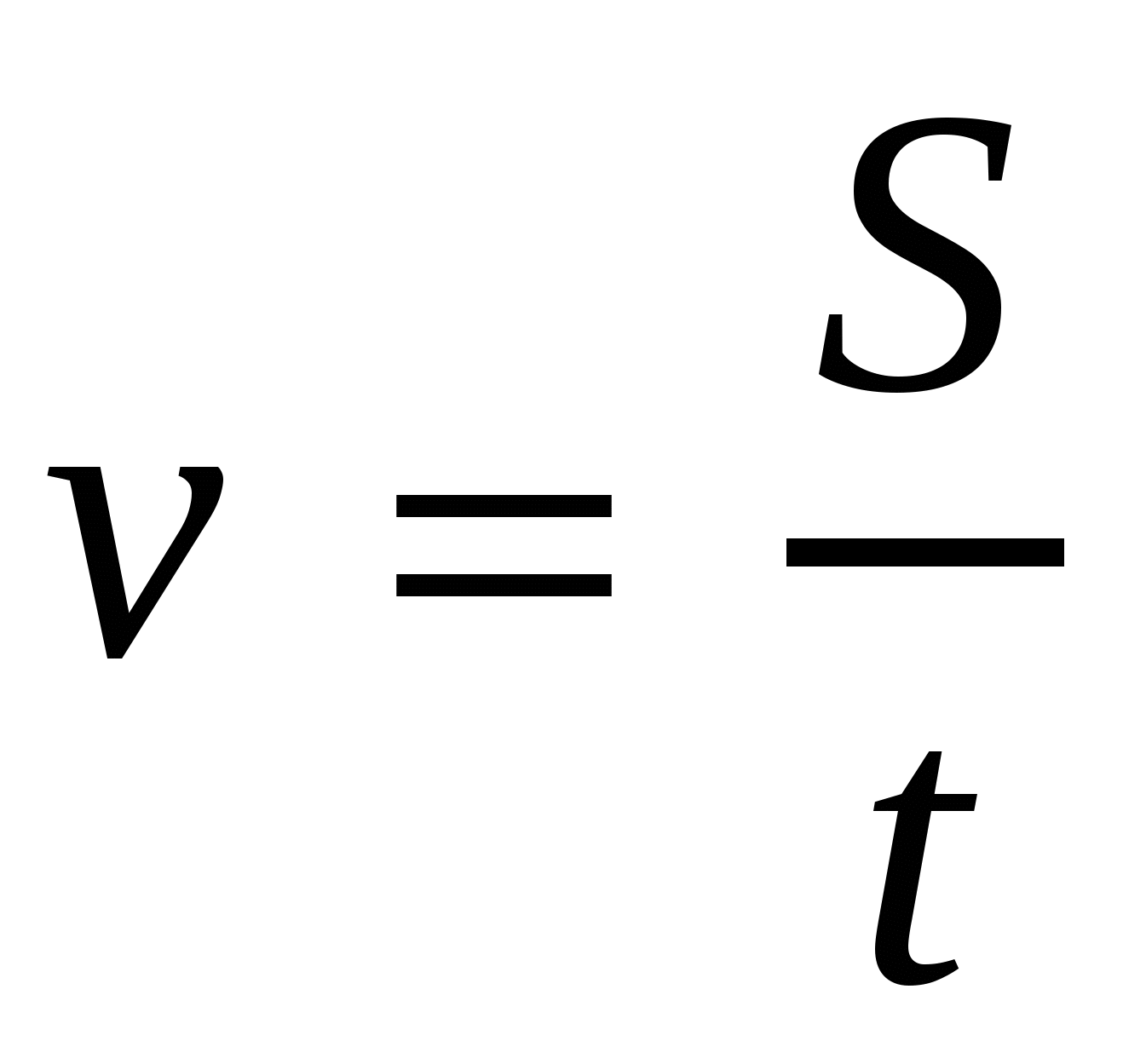 
.
2. Если производительность труда постоянна, то объём выполненных работ и время – обратно пропорциональные величины.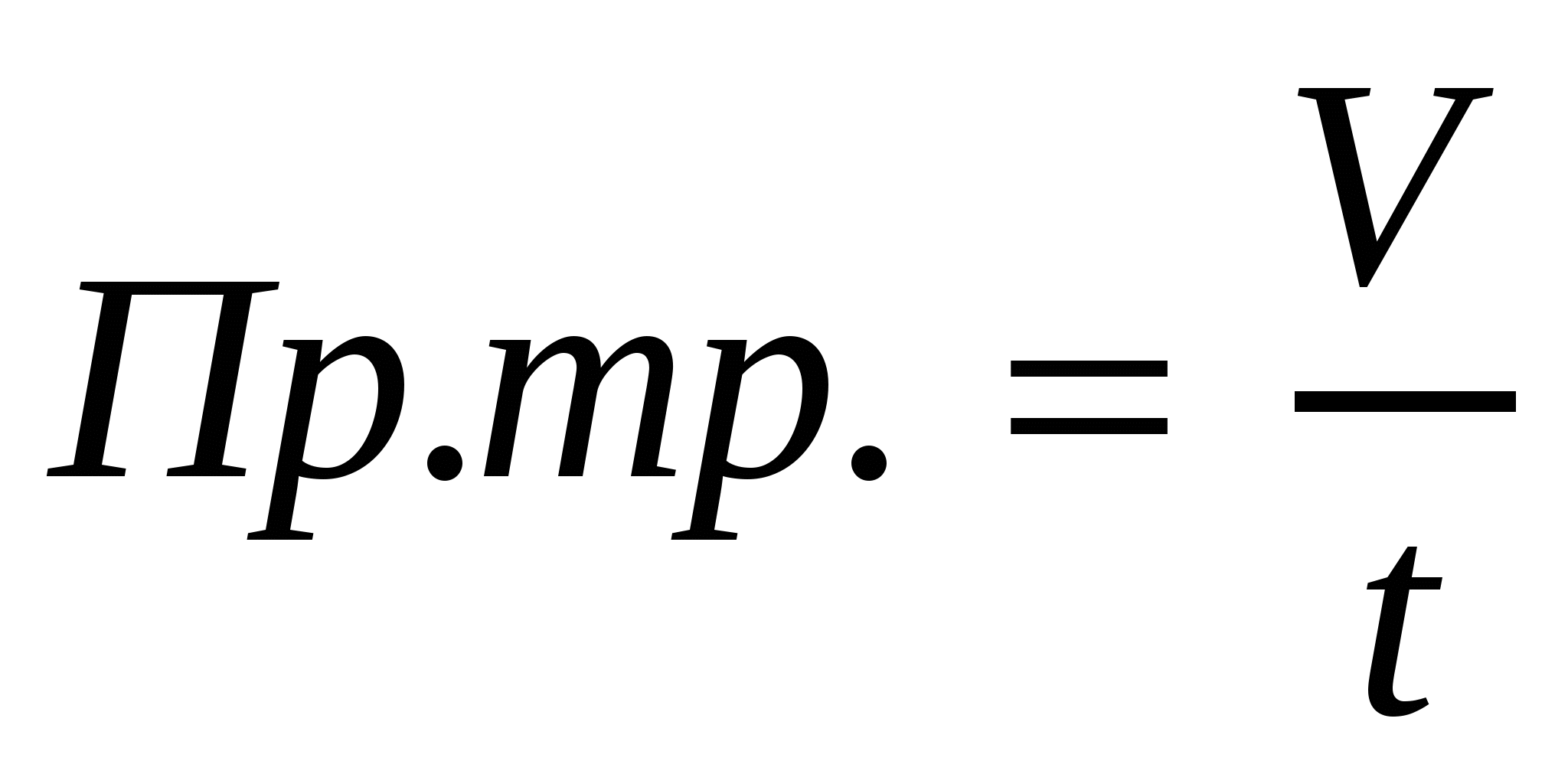 
.
(Слайд 9). Задача 2. 6 рабочих выполнят работу за 5 часов. За какое время справятся с этой работой 3 рабочих?
Кол-во Время
6 рабочих – 5 ч Обратная пропорциональность
3 рабочих – х ч
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
,
,
.
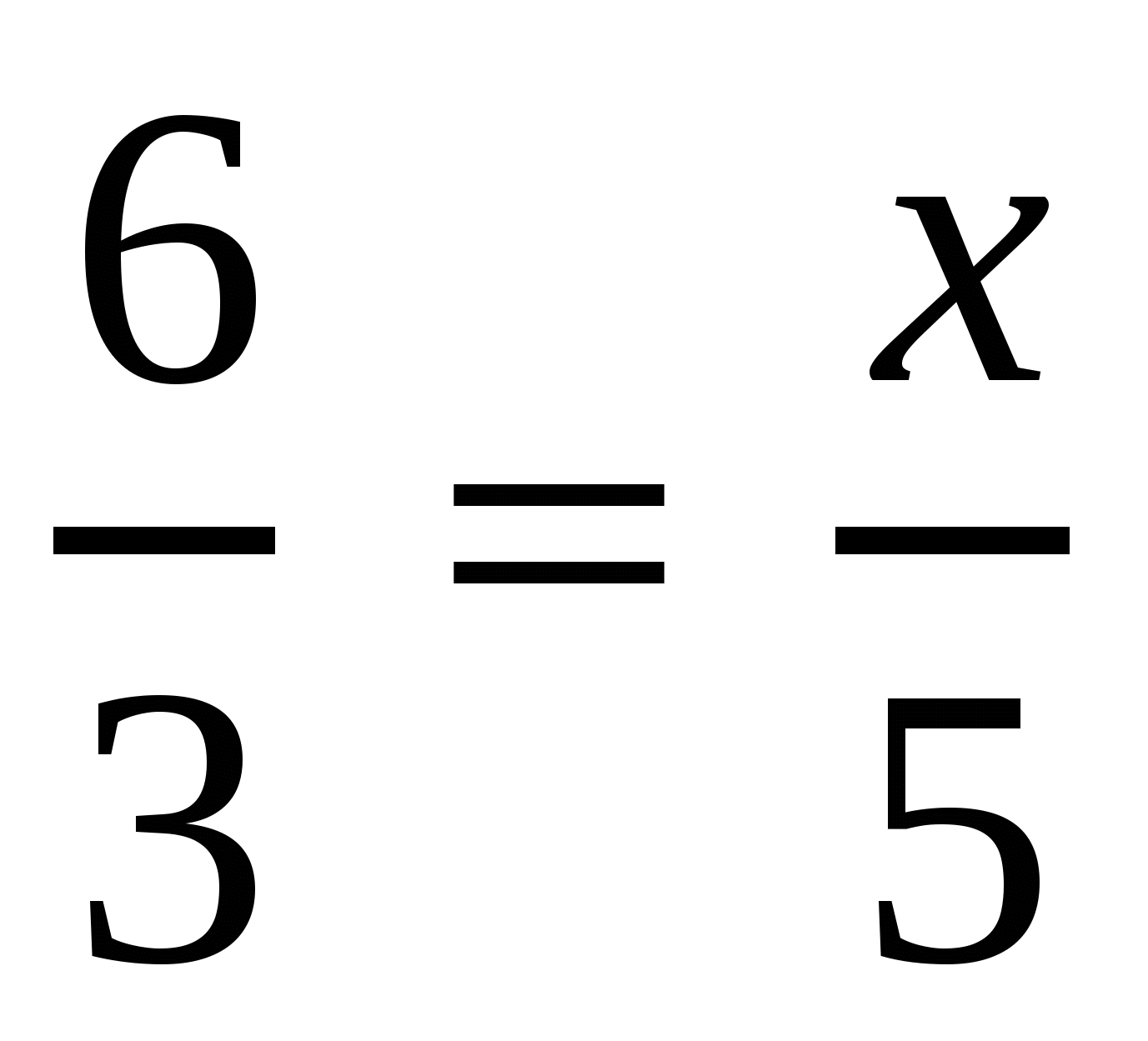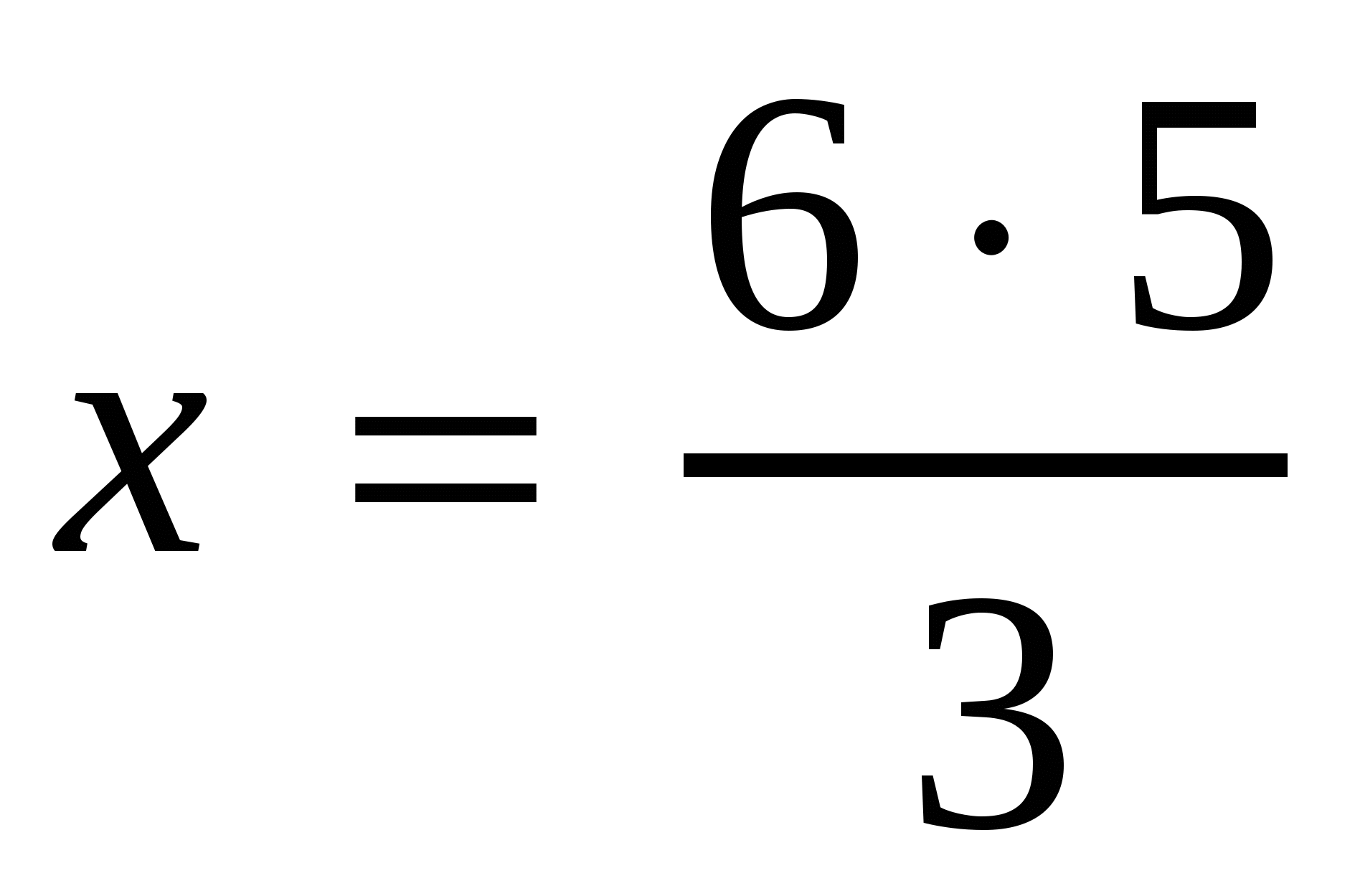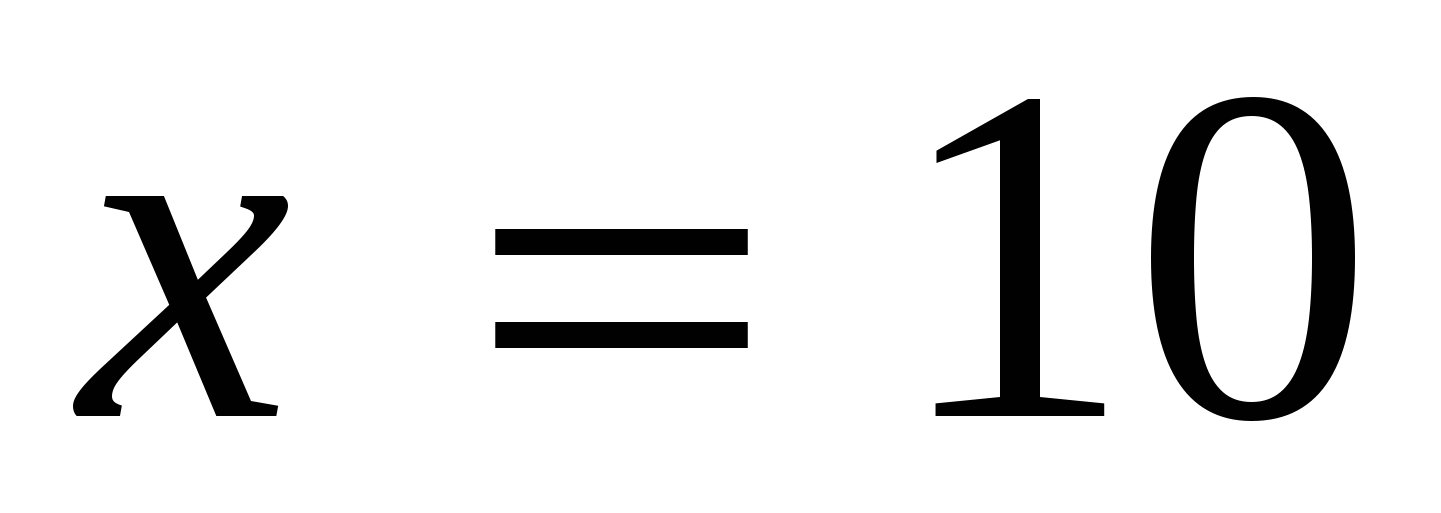За 10 ч справятся с этой работой 3 рабочих. Ответ: 10 ч.
Алгоритм решения задач.
Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом)
Составить пропорцию.
Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Найти неизвестный член пропорции.
Проанализировать полученный результат и записать ответ.
Решение упражнений.
Уч.с.21 № 75(а). В 100 г раствора содержится 4 г соли. Сколько соли содержится в 300 г этого раствора?
Р-р Соль
100 г – 4 г Прямая пропорциональность
300 г – х г
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
,
,
.
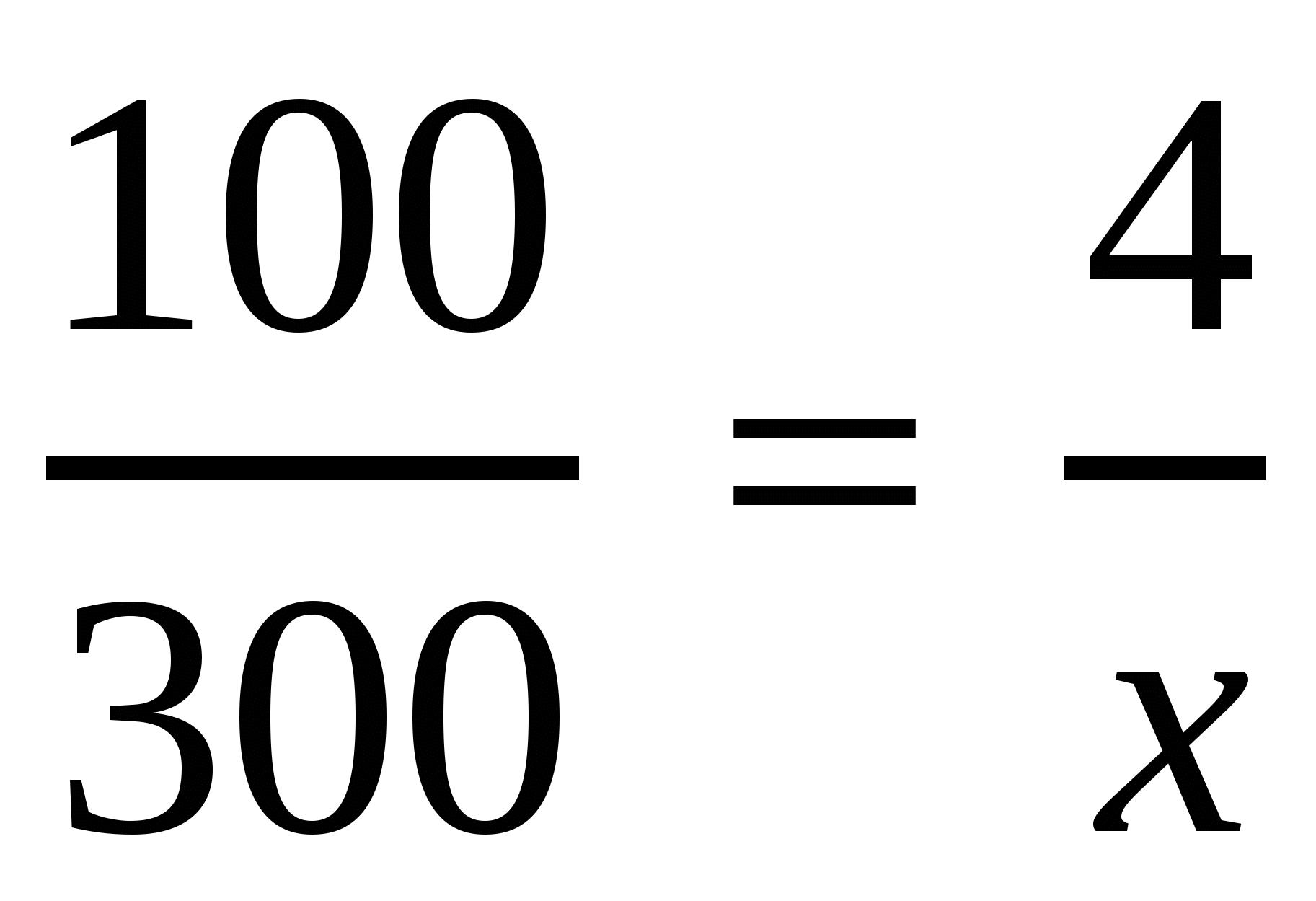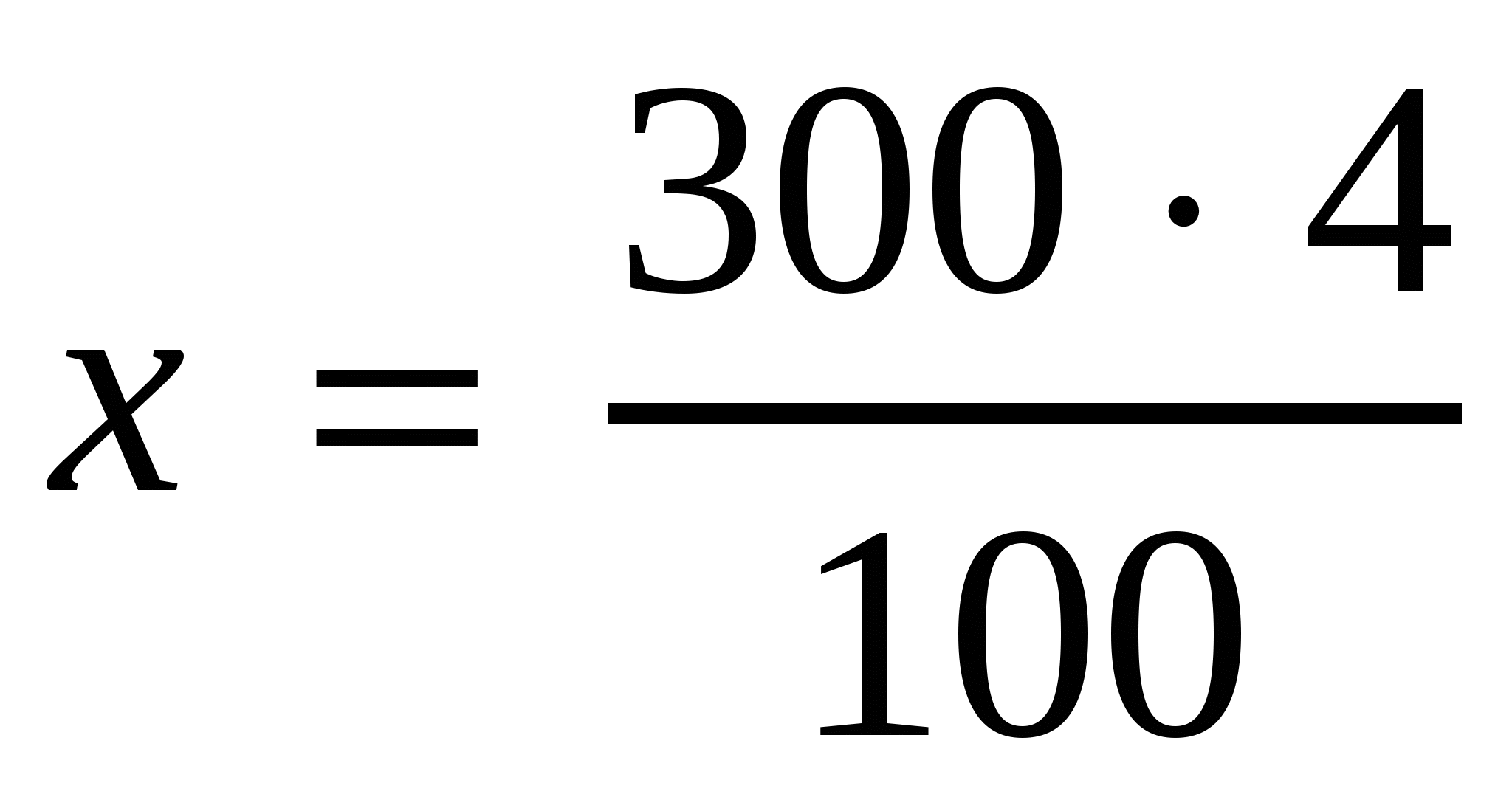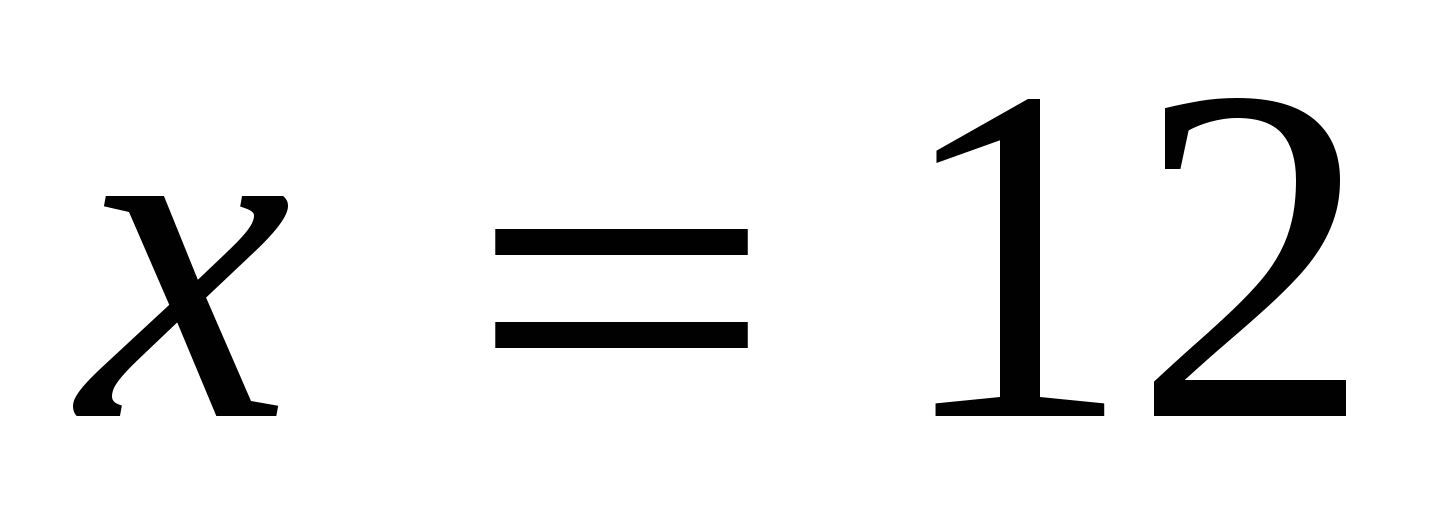12 г соли содержится в 300 г этого раствора. Ответ: 12 г.
Уч.с.22 № 88. Некоторую работу 6 человек сделают за 18 дней. За сколько дней сделают эту же работу 9 человек, работающие так же успешно, как и первые?
Кол-во Время
6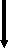 человек – 18 дн. Обратная пропорциональность
9 человек – х дн.
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
,
,
.
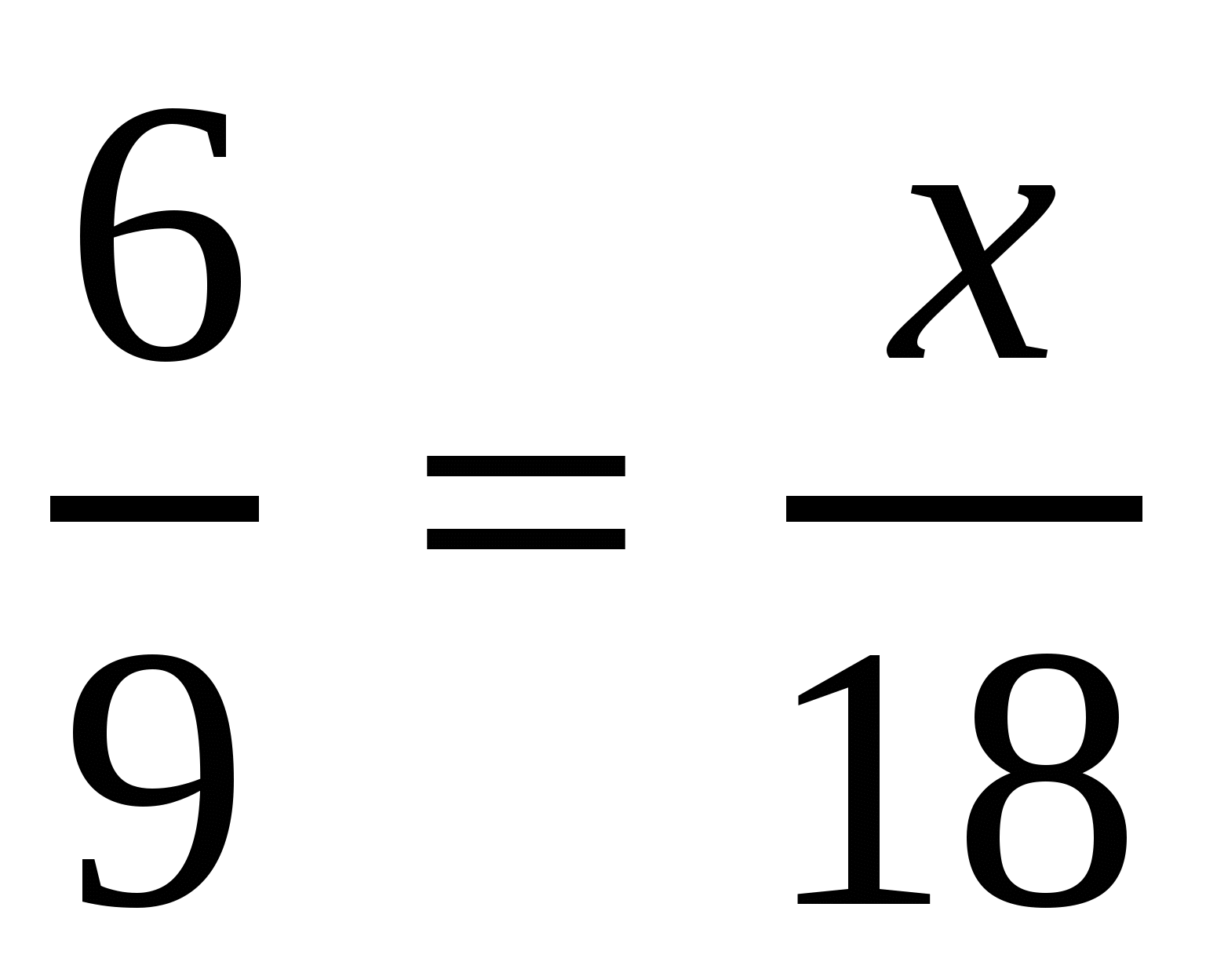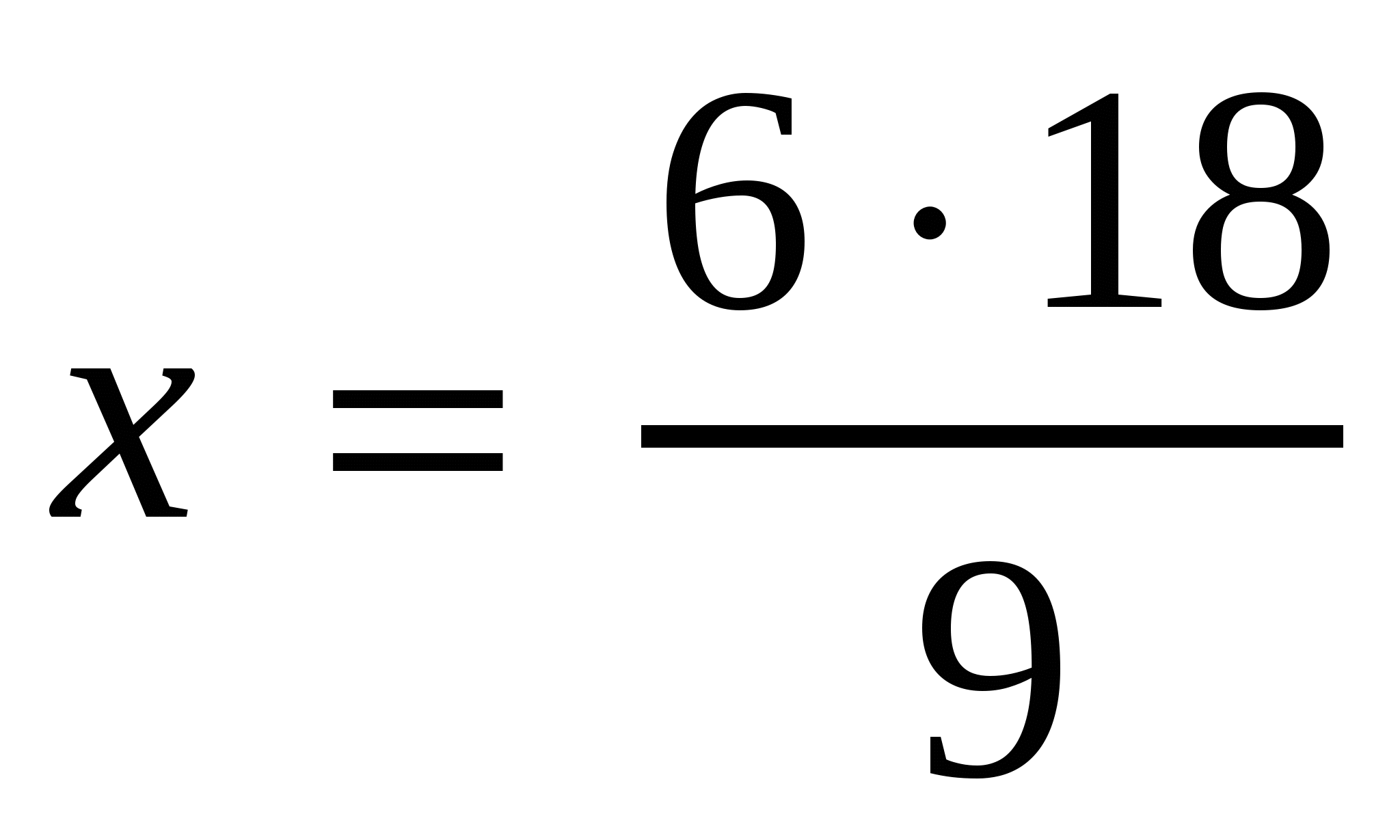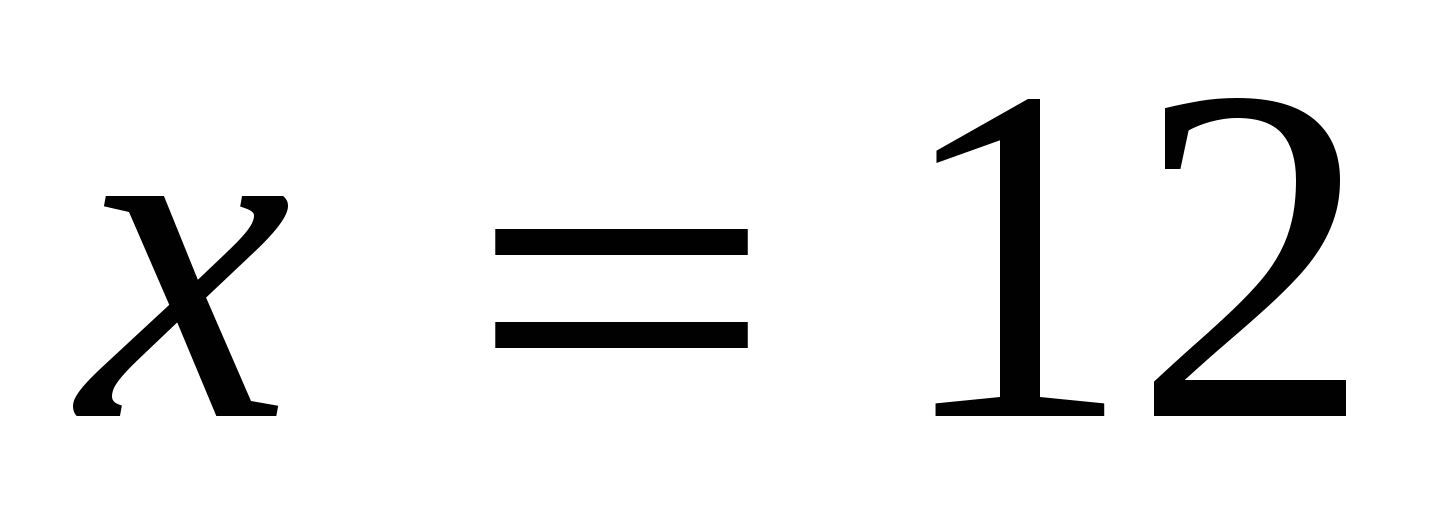За 12 дней сделают эту же работу 9 человек. Ответ: 12 дней.
Уч.с.22 № 83. Один килограмм металлолома заменяет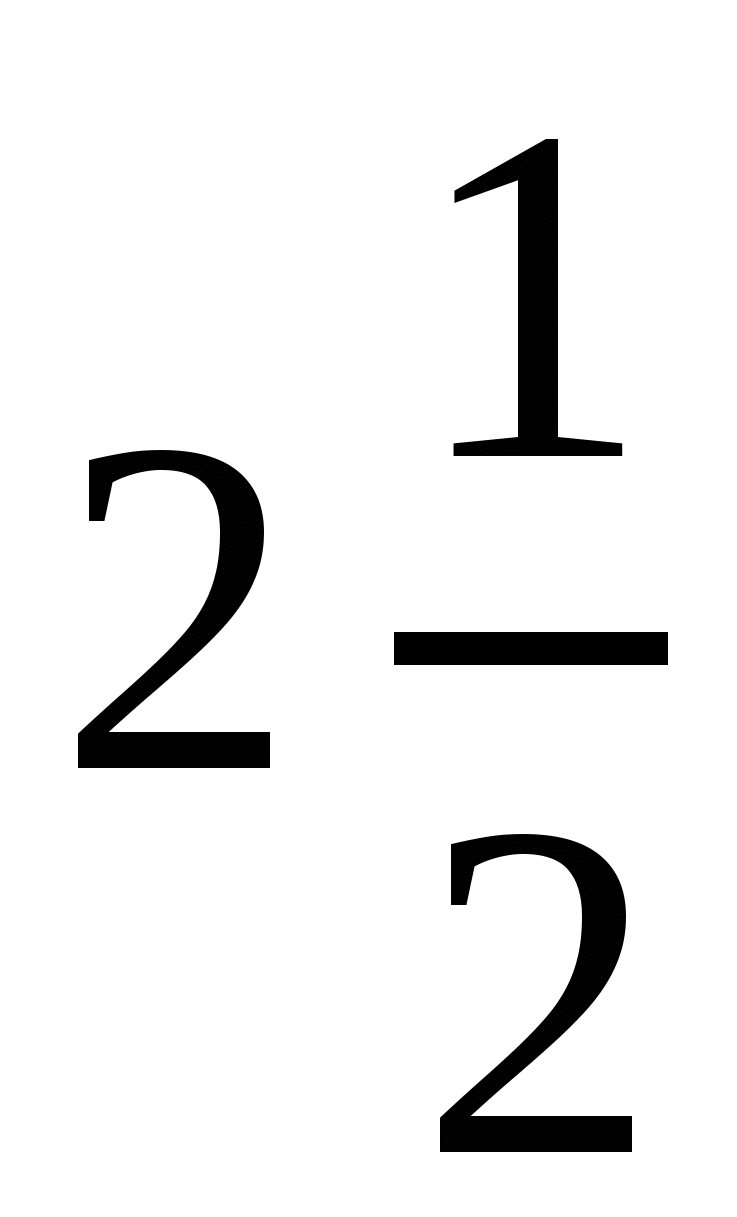 
кг богатой железом руды. Сколько руды заменяют 4 т металлолома?
Металлолом Руда
1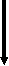
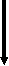кг – 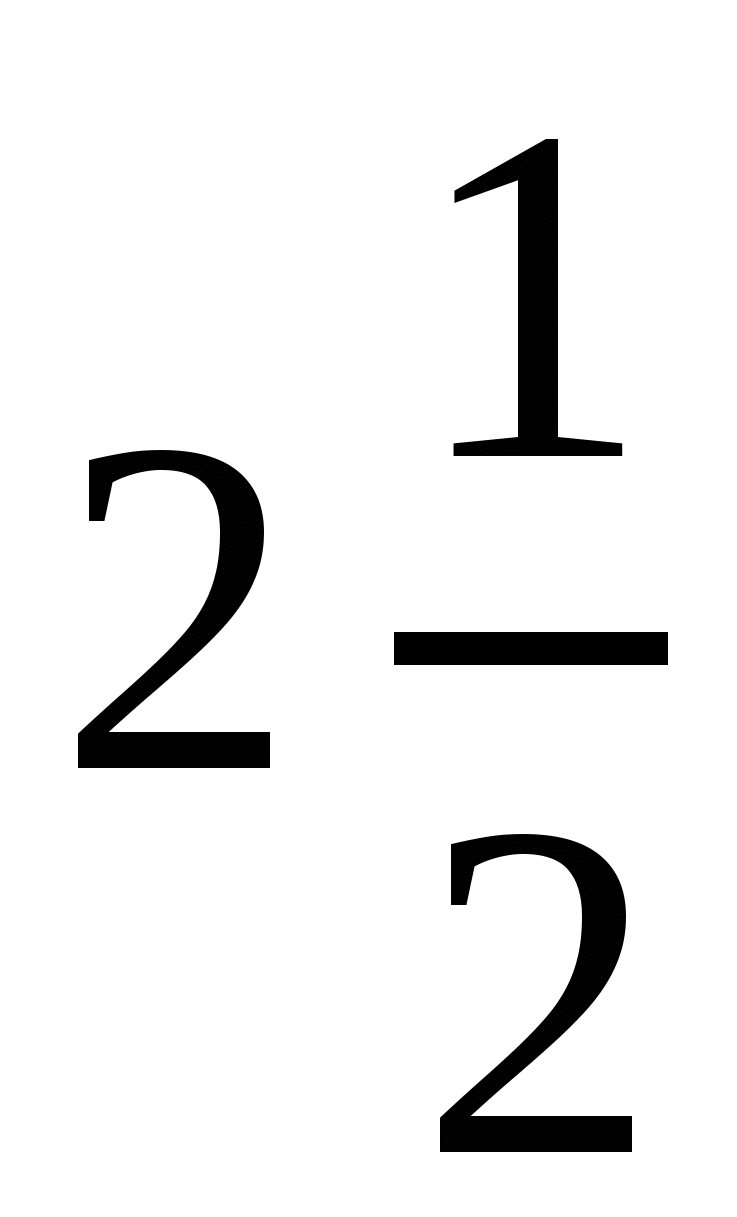кг Прямая пропорциональность
4 т – х кг
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
1) 4 т = 4000 кг;
2) 
,
,
.
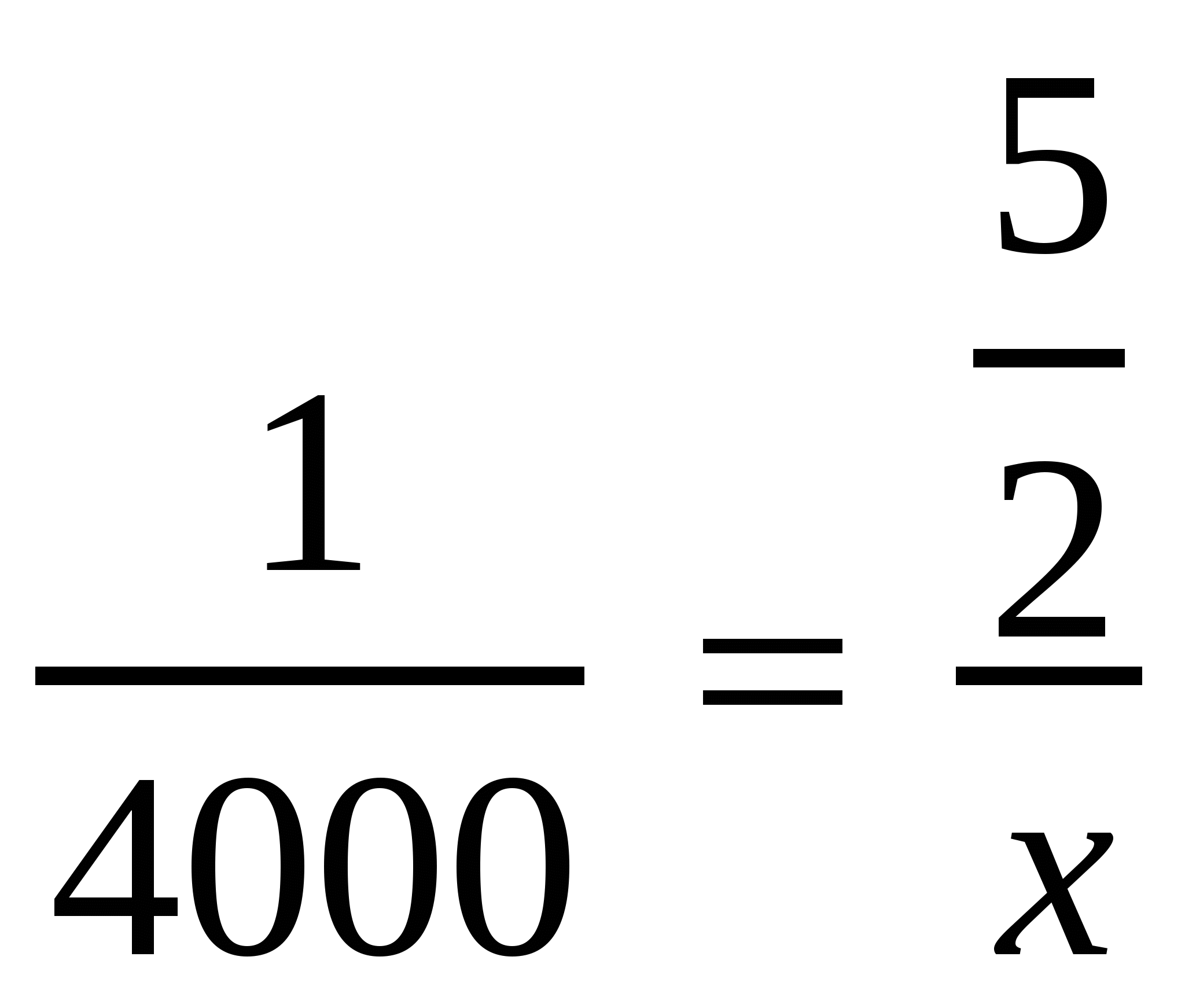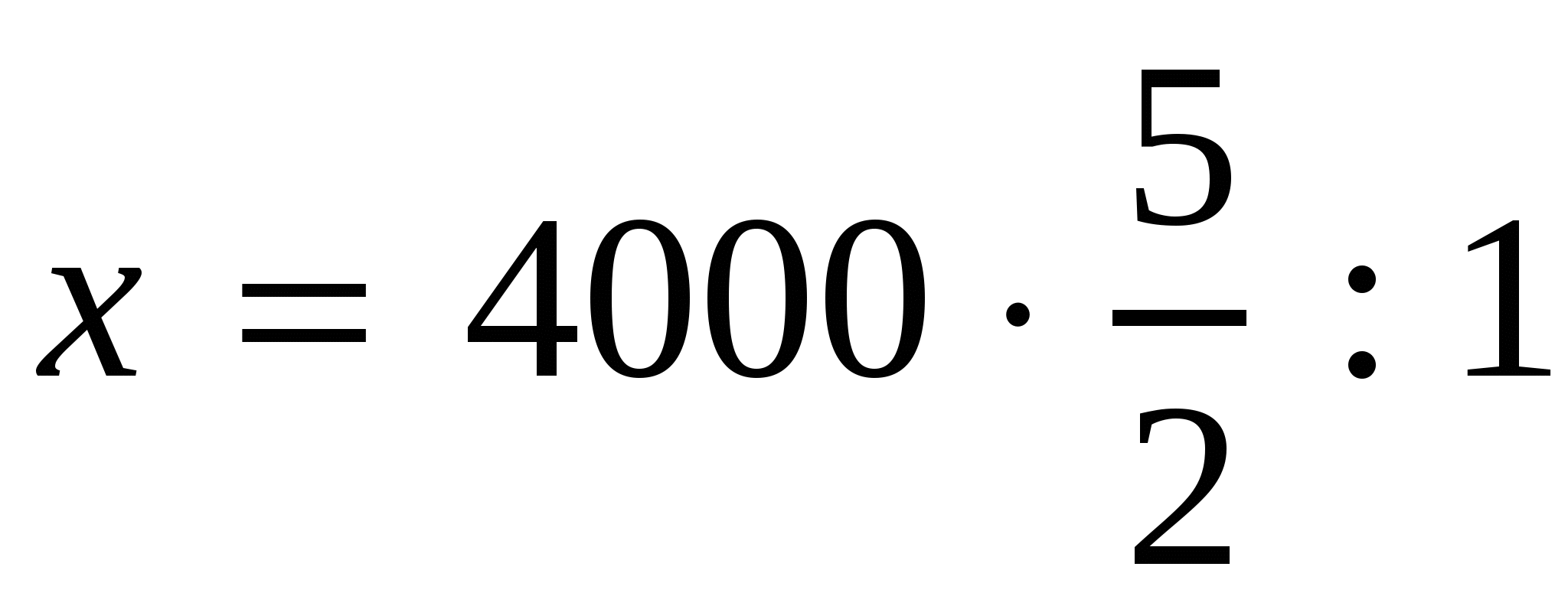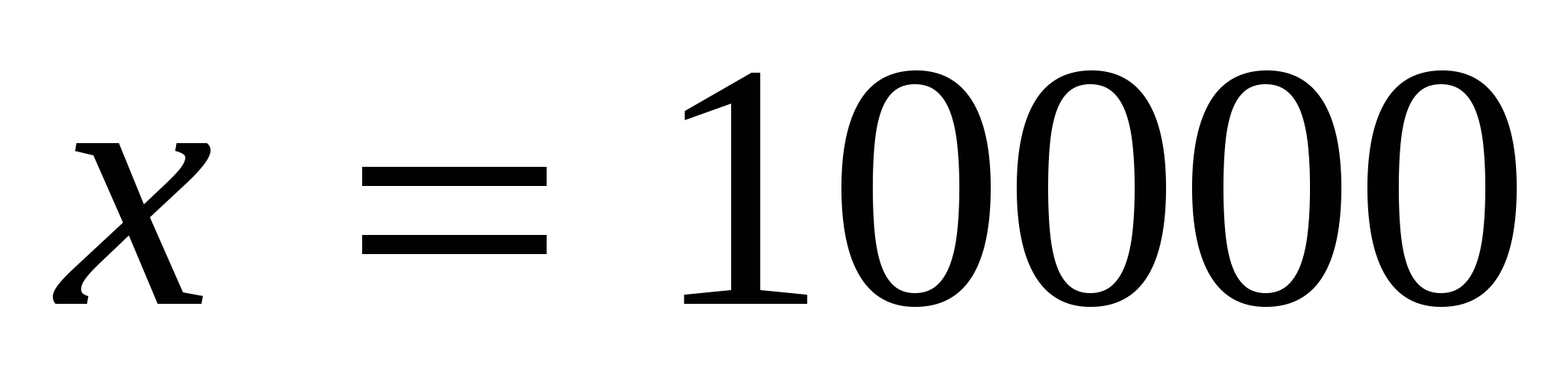10 000 кг руды заменяют 4 т металлолома. Ответ: 10 000 кг.
Уч.с.22 № 84(а). Автомобилист заметил, что со скоростью 60 км/ч он проехал мост через реку за 40 с. На обратном пути он проехал этот же мост за 30 с. Определите скорость автомобиля на обратном пути?
v t
60 км/ч – 40 с Обратная пропорциональность
х км/ч – 30 с
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
,
,
.
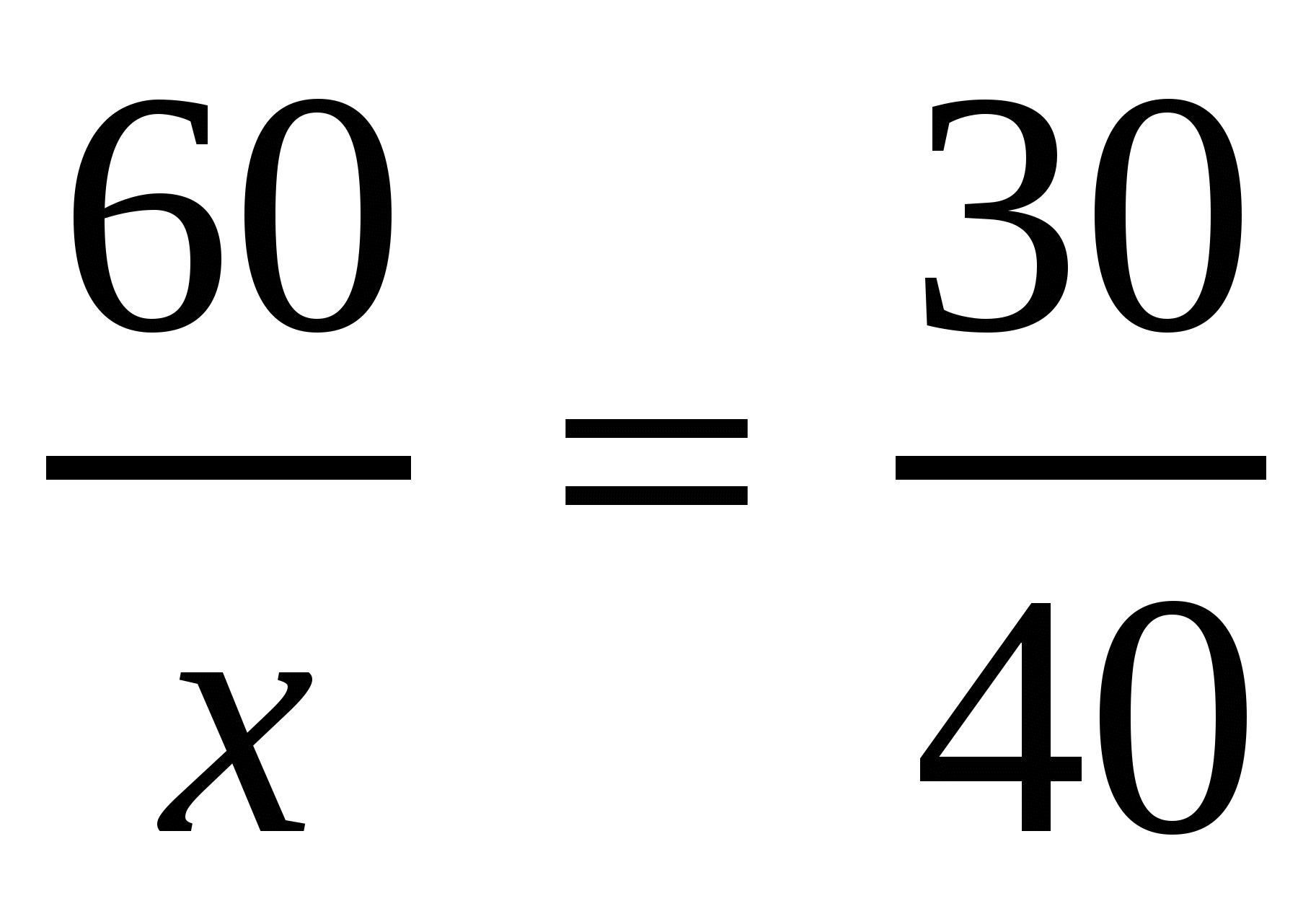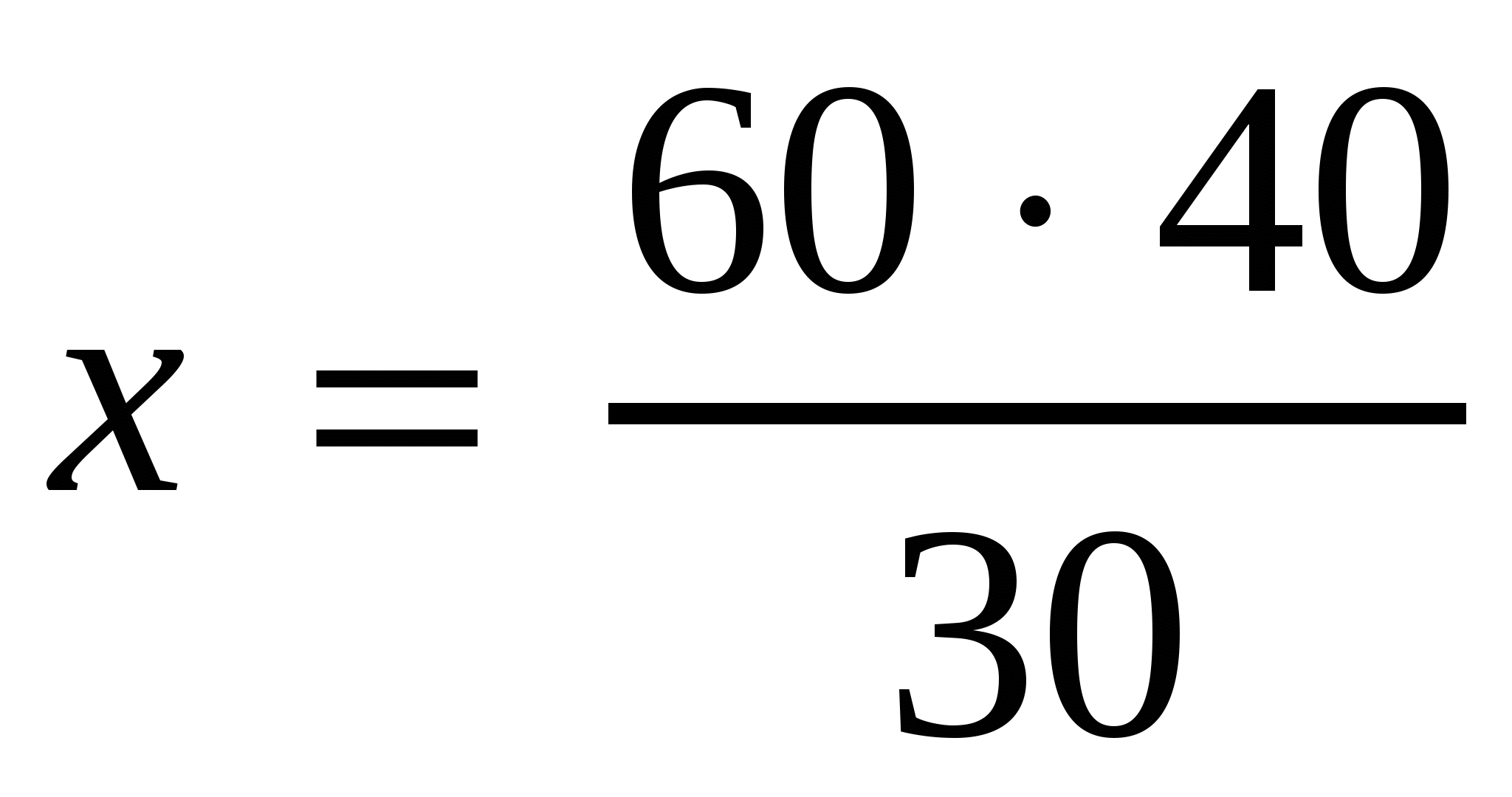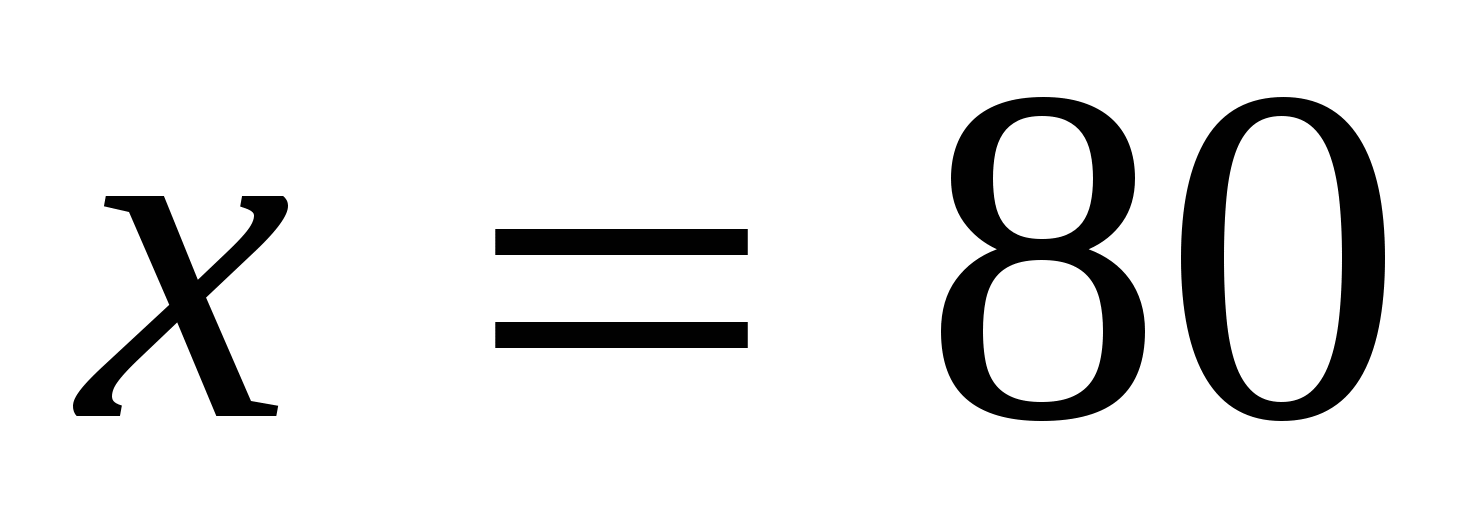80 км/ч скорость автомобиля на обратном пути. Ответ: 80 км/ч.
Подведение итогов урока
Домашнее задание. § 1.5 (выучить теорию). № 73, 75(б), 77(а), 84(б).
infourok.ru
| 1. | Пропорциональные и непропорциональные величины | 2 вид — интерпретация | лёгкое | 1 Б. | Следует определить, является ли пропорциональной зависимость между величинами. |
| 2. | Зависимость между величинами | 2 вид — интерпретация | лёгкое | 1 Б. | Необходимо определить, является ли прямо пропорциональной, обратно пропорциональной или не является пропорциональной зависимость между величинами. |
| 3. | Величины | 2 вид — интерпретация | лёгкое | 2 Б. | Необходимо выбрать величины, между которыми существует прямо/обратно пропорциональная зависимость. |
| 4. | Формулы. Прямая пропорциональность | 2 вид — интерпретация | среднее | 3 Б. | Формулы. Прямая пропорциональность. |
| 5. | Формулы. Обратная пропорциональность | 2 вид — интерпретация | среднее | 3 Б. | Формулы. Обратная пропорциональность. |
| 6. | Лишняя формула | 2 вид — интерпретация | среднее | 2 Б. | Из данных формул следует исключить «лишнюю», обратная пропорциональность. |
| 7. | Прямо пропорциональные величины, таблица | 2 вид — интерпретация | среднее | 4 Б. | Прямо пропорциональные величины, таблица. |
| 8. | Таблица и формула (десятичные дроби) | 2 вид — интерпретация | среднее | 4 Б. | Следует определить зависимость между величинами, записать формулу и заполнить таблицу. Прямая пропорциональность. |
| 9. | Таблица, формула (целые числа) | 2 вид — интерпретация | среднее | 5 Б. | Необходимо определить зависимость между величинами, записать формулу и заполнить таблицу. Обратная пропорциональность. |
www.yaklass.ru
6.1.3. Прямо пропорциональные величины математика-повторение
I. Прямо пропорциональные величины.
Пусть величина y зависит от величины х. Если при увеличении х в несколько раз величина у увеличивается во столько же раз, то такие величины х и у называются прямо пропорциональными.
Примеры.
1. Количество купленного товара и стоимость покупки (при фиксированной цене одной единицы товара — 1 штуки или 1 кг и т. д.) Во сколько раз больше товара купили, во столько раз больше и заплатили.
2. Пройденный путь и затраченное на него время (при постоянной скорости). Во сколько раз длиннее путь, во столько раз больше потратим времени на то, чтобы его пройти.
3. Объем какого-либо тела и его масса. (Если один арбуз в 2 раза больше другого, то и масса его будет в 2 раза больше)
II. Свойство прямой пропорциональности величин.
Если две величины прямо пропорциональны, то отношение двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
Задача 1. Для малинового варенья взяли 12 кг малины и 8 кг сахара. Сколько сахара потребуется, если взяли 9 кг малины?
Решение.
Рассуждаем так: пусть потребуется х кг сахара на 9 кг малины. Масса малины и масса сахара — прямо пропорциональные величины: во сколько раз меньше малины, во столько же раз нужно меньше сахара. Следовательно, отношение взятой (по массе) малины (12:9) будет равно отношению взятого сахара (8:х). Получаем пропорцию:
12:9=8:х;
х=9·8:12;
х=6. Ответ: на 9 кг малины нужно взять 6 кг сахара.
Решение задачи можно было оформить и так:
Пусть на 9 кг малины нужно взять х кг сахара.
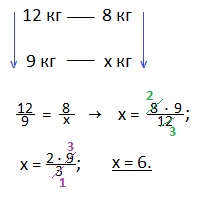(Стрелки на рисунке направлены в одну сторону, а вверх или вниз — не имеет значения. Смысл: во сколько раз число 12 больше числа 9, во столько же раз число 8 больше числа х, т. е. здесь прямая зависимость).
Ответ: на 9 кг малины надо взять 6 кг сахара.
Задача 2. Автомобиль за 3 часа проехал расстояние 264 км. За какое время он проедет 440 км, если будет ехать с той же скоростью?
Решение.
Пусть за х часов автомобиль пройдет расстояние 440 км.
Ответ: автомобиль пройдет 440 км за 5 часов.
Задача 3. Из трубы поступает вода в бассейн. За 2 часа она заполняет 1/5 бассейна. Какая часть бассейна заполняется водой за 5 часов?
Решение.
Отвечаем на вопрос задачи: за 5 часов наполнится 1/х часть бассейна. (Весь бассейн принимается за одну целую).
www.mathematics-repetition.com
Прямо пропорциональные величины — урок. Математика, 6 класс.
Задача. Сторона квадрата равна \(2\) дм. Определи, как изменится периметр квадрата, если его сторону увеличить в \(3\) раза, в \(4\) раза, в \(5\) раз?
| Сторона квадрата, дм | \(2\) | \(6\) | \(8\) | \(10\) |
| Периметр квадрата, дм | \(8\) | \(24\) | \(32\) | \(40\) |
Заметим, что при увеличении стороны квадрата в \(3\) раза (была \(2\) дм, стала — \(6\) дм) периметр увеличился тоже в \(3\) раза (был \(8\) дм, стал — \(24\) дм).
Аналогично, при увеличении стороны квадрата в \(4\) раза (была \(2\) дм, стала — \(8\) дм) периметр увеличился тоже в \(4\) раза (был \(8\) дм, стал — \(32\) дм).
Вывод: при увеличении стороны квадрата в несколько раз периметр увеличивается во столько же раз.
Говорят, что сторона квадрата прямо пропорциональна его периметру.
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Обрати внимание!
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Проверим это утверждение на приведённой выше задаче.
Найдём в каждом случае отношение стороны квадрата к периметру:
28=624=832=1040=14.
Прямую пропорциональность можно задать формулой.
Формулу \(y=kx\), где \(y\) и \(x\) — переменные величины, а \(k\) — постоянная величина, называют формулой прямой пропорциональности.
Источники:
Математика. 6 класс. Часть 2. — Изд. 2-е, перераб. / Г. В. Дорофеев, Л. Г. Петерсон. — М.: Издательство «Ювента», 2010. — 128 с.: ил.
www.yaklass.ru
6.1.5. Обратно пропорциональные величины математика-повторение
I. Обратно пропорциональные величины.
Пусть величина у зависит от величины х. Если при увеличении х в несколько раз величина у уменьшается во столько же раз, то такие величины х и у называются обратно пропорциональными.
Примеры.
1. Скорость и время при одинаковой длине пути. Если от А до В 200 км, то при скорости 50 км/ч понадобится 4 часа, а при скорости 40 км/ч понадобится 5 часов, т.е. если скорость уменьшается, то время увеличивается, а если скорость увеличивается, то время уменьшается. Это изобразится так:
2. Количество рабочих и время при определенном объеме работ. Если шести рабочим нужно на выполнение определенной работы 4 часа, то трем рабочим на выполнение той же работы потребуется 8 часов, т.е. чем меньше работников, тем больше нужно времени, чтобы выполнить определенную работу.
Смысл: во сколько раз стало меньше рабочих (в 2 раза), во столько же раз больше (в 2 раза) времени потребуется.
3) Длина и ширина прямоугольника при постоянной площади прямоугольника. Если площадь участка прямоугольной формы с длиной 8 м, равна 48 м², то его ширина будет равна (48:8=6)м. Если же длину взять больше в 2 раза (16 м), то ширина уменьшится тоже в 2 раза (48:16=3)м.
II. Свойство обратной пропорциональности величин.
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Задача 1. Изготавливая по 42 детали в час, рабочий трудился 8 часов. Сколько времени ему понадобилось бы на эту же работу, если бы он делал в час по 48 деталей?
Решение. Составим схему по условию задачи:
42 детали в час ——— 8 часов.
48 деталей в час ——- х часов.
Имеем обратно пропорциональную зависимость: во сколько раз больше деталей в час рабочий будет изготавливать, во столько же раз меньше ему потребуется времени на одну и ту же работу. Используя свойство обратной пропорциональности, запишем:
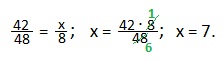
Ответ: рабочий выполнит ту же работу за 7 часов.
Задача 2. Бассейн можно наполнять через одну из двух труб.Через первую трубу, со скоростью 2 литра в 1 секунду, бассейн наполняется за 45 минут. Какова скорость наполнения бассейна через вторую трубу, если весь бассейн наполняется через вторую трубу за 1 час 15 минут.
Решение.
По условию задачи через первую трубу в бассейн вытекает 2 литра за 1 секунду или 2·60=120 литров за 1 минуту (1 минута=60 секунд), и бассейн наполняется за 45 минут.
Через вторую трубу бассейн наполняется за 1 час 15 минут. Времени требуется больше, значит, скорость наполнения меньше. Имеем обратно пропорциональные величины: скорость наполнения и время наполнения бассейна. Обозначим скорость наполнения бассейна через вторую трубу через х.
120 литров в минуту ——— 45 минут;
х литров в минуту ——— 75 минут. (1 час 15 минут = 60 минут + 15 минут = 75 минут).
Во сколько раз скорость наполнения меньше, во столько раз больше потребуется времени для заполнения бассейна.
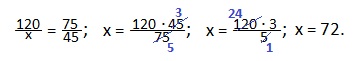
Мы нашли скорость наполнения бассейна через вторую трубу в литрах в минуту. Итак, через вторую трубу бассейн наполняется со скоростью 72 литра в минуту или 72:60=1,2 литров в секунду.
Ответ: через вторую трубу в бассейн вливается 1,2 литра в 1 секунду.
www.mathematics-repetition.com
Конспект по теме » Прямая и обратная пропорциональность»
Дата______ УРОК № 14.
Тема. Прямая и обратная пропорциональность.
Цель. Проверить знания учащихся по теме «Пропорции». Дать определение прямо пропорциональных и обратно пропорциональных величин. Научится решать задачи по данной теме.
Ход урока.
Организационный момент.
Проверка домашнего задания.
Самостоятельная работа по теме «Пропорции». (10 min)
Вариант 1. Вариант 1.
Решить пропорцию: Решить пропорцию:
1) , 1) ,
2) , 2) ,
3) , 3) ,
Объяснение нового материала.
Прямая и обратная пропорциональность.
Пусть ручка стоит 3 р. (это цена). Тогда легко рассчитать стоимость двух, трех и т.д. ручек по формуле: .
Заметим, что с увеличением количества ручек в несколько раз их стоимость увеличивается во столько же раз.Говорят, что стоимость покупки прямо пропорциональна количеству купленных ручек.
Определение. Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональных величин:
1. Периметр квадрата и длина стороны квадрата – прямо пропорциональные величины. .
2. Если скорость движения постоянна, то пройденный путь и время движения – прямо пропорциональные величины. .
3. Если производительность труда постоянна, то объём выполненных работ и время – прямо пропорциональные величины. .
4. Выручка кассы кинотеатра прямо пропорциональна количеству проданных билетов при одинаковой цене. И т.д.
Задача 1. За 5 тетрадей в клетку заплатили 40 р. Сколько заплатят за 12 таких же тетрадей?
Кол-во Стоимость
5 тетрадей – 40 р. Прямая пропорциональность
12 тетрадей – х р.
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
,
,
.
96 р. заплатят за 12 тетрадей. Ответ: 96 р.
Хотят купить на 120 р. несколько одинаковых книг. Тогда легко рассчитать количество книг по 10 р., 20 р., 30 р. 40 р. и т.д. по формуле: .
Заметим, что с увеличением цены книги в несколько раз их количество уменьшается во столько же раз.Говорят, что количество купленных книг обратно пропорционально их цене.
Определение. Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению значений другой величины.
Примеры обратно пропорциональных величин:
1. Если пройденный путь постоянен, то скорость движения и время движения – обратно пропорциональные величины. .
2. Если производительность труда постоянна, то объём выполненных работ и время – обратно пропорциональные величины. .
Задача 2. 6 рабочих выполнят работу за 5 часов. За какое время справятся с этой работой 3 рабочих?
Кол-во Время
6 рабочих – 5 ч Обратная пропорциональность
3 рабочих – х ч
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
,
,
.
За 10 ч справятся с этой работой 3 рабочих. Ответ: 10 ч.
Алгоритм решения задач.
Составить краткую запись и определить вид пропорциональности. (Одноименные величины записываются друг под другом)
Составить пропорцию.
Если две величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
Если две величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Найти неизвестный член пропорции.
Проанализировать полученный результат и записать ответ.
Решение упражнений.
Уч.с.21 № 75(а). В 100 г раствора содержится 4 г соли. Сколько соли содержится в 300 г этого раствора?
Р-р Соль
100 г – 4 г Прямая пропорциональность
300 г – х г
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
,
,
.
12 г соли содержится в 300 г этого раствора. Ответ: 12 г.
Уч.с.22 № 88. Некоторую работу 6 человек сделают за 18 дней. За сколько дней сделают эту же работу 9 человек, работающие так же успешно, как и первые?
Кол-во Время
6 человек – 18 дн. Обратная пропорциональность
9 человек – х дн.
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
,
,
.
За 12 дней сделают эту же работу 9 человек. Ответ: 12 дней.
Уч.с.22 № 83. Один килограмм металлолома заменяет кг богатой железом руды. Сколько руды заменяют 4 т металлолома?
Металлолом Руда
1 кг – кг Прямая пропорциональность
4 т – х кг
Решение.
Т.к. величины прямо пропорциональны, то отношения двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
1) 4 т = 4000 кг;
2) ,
,
.
10 000 кг руды заменяют 4 т металлолома. Ответ: 10 000 кг.
Уч.с.22 № 84(а). Автомобилист заметил, что со скоростью 60 км/ч он проехал мост через реку за 40 с. На обратном пути он проехал этот же мост за 30 с. Определите скорость автомобиля на обратном пути?
v t
60 км/ч – 40 с Обратная пропорциональность
х км/ч – 30 с
Решение.
Т.к. величины обратно пропорциональны, то отношения двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
,
,
.
80 км/ч скорость автомобиля на обратном пути. Ответ: 80 км/ч.
Подведение итогов урока
Домашнее задание. § 1.5 (выучить теорию). № 73, 75(б), 77(а), 84(б).
infourok.ru