Прямая и обратная пропорциональность величин: Урок 7. прямая и обратная пропорциональность. решение задач — Математика — 6 класс — Детская игровая комната «Волшебный лес»

Posted on 06.02.197127.12.2021 by alexxlab

Содержание

Урок 7. прямая и обратная пропорциональность. решение задач — Математика — 6 класс

Математика

6 класс

Урок № 7

Прямая и обратная пропорциональность. Решение задач

Перечень рассматриваемых вопросов:

Понятия прямой и обратной пропорциональной зависимости.
Краткая запись условия задачи.
Составление и решение пропорций по условию задачи.
Решение задач на прямую и обратную пропорциональную зависимость.

Тезаурус

Равенство двух отношений называют пропорцией.

Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.

Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.

Основная литература

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

Дополнительная литература

Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Прямая пропорциональность.

Обратная пропорциональность.

Для решения задач на пропорциональную зависимость, удобно составить таблицу или сделать краткую запись условия.

Столбцы таблицы соответствуют наименованиям зависимых величин.

Строки таблицы соответствуют значениям величин при первом и втором измерении.

Одинаково направленные стрелки показывают прямо пропорциональную зависимость, противоположно направленные – обратно пропорциональную.

Задача.

Поезд, скорость которого 55 км/ч, был в пути 5 часов. За сколько часов пройдёт этот же участок пути товарный поезд, скорость которого 45 км/ч?

Решение.

При постоянном пути скорость и время движения обратно пропорциональны.

Допустим, товарный поезд пройдёт этот же путь со скоростью 45 км/ч за x ч.

Сделаем краткую запись условия.

Задача.

Двигаясь с постоянной скоростью, велогонщик проезжает 40 метров за 3 с. Какой путь проедет велогонщик за 45 с?

Решение.

При постоянной скорости путь прямо пропорционален времени движения.

Пусть х м проедет велогонщик за 45 с.

Сделаем краткую запись условия.

Задача.

Усилие при восхождении на высоту 600 м равно усилию, требуемому для перехода 25 км по равнине. Турист поднялся в горы на 792 м. Какому расстоянию на равнине соответствует этот подъём?

Решение:

Решение.

Задача.

Четыре программиста могут написать игру за 12 месяцев. За сколько месяцев эту работу могут выполнить три программиста?

Решение.

Количество программистов и скорость написания игры – это обратно пропорциональная зависимость.

Разбор заданий тренировочного модуля

№ 1. Подстановка элементов в пропуски в тексте.

Подставьте нужные элементы в пропуски.

Пешеход шёл 3 часа со скоростью 8 км/ч. За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?

Решение:

При фиксированном расстоянии время в пути и скорость – ______ пропорциональны.

Пусть _____ часов – пешеход идёт со скоростью 6 км/ч.

Составим пропорцию:

_________

х=_______

х=_______(ч).

Правильный ответ.

Решение:

При фиксированном расстоянии время в пути и скорость – обратно пропорциональны.

Пусть х часов – пешеход идёт со скоростью 6 км/ч.

№ 2. Подстановка элементов в пропуски в таблице.

Заполните таблицу.

Поезд движется со скоростью 45 км/ч. Какое расстояние он пройдёт, если будет в пути 3 ч; 4 ч; 5 ч; 6 ч.

Варианты ответов:

135 км;

180 км;

225 км;

270 км.

Решение.

При постоянной скорости пройденный путь и время прямо пропорциональны. Скорость движения поезда 45 км/ч означает, что за 1 час поезд преодолевает расстояние в 45 км. Обозначим за x км – расстояние, которое поезд пройдёт за 3, 4, 5 и 6 часов.

Таким же способом находим расстояние, которое пройдёт поезд за 4, 5 и 6 часов, и подставляем соответствующие варианты в таблицу.

Ответ:

Прямая и обратная пропорциональность. Формулы, обозначение, примеры

Основные определения

Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

Виды зависимостей:

Прямая зависимость. Чем больше одна величина, тем больше вторая. Чем меньше одна величина, тем меньше вторая величина.
Обратная зависимость. Чем больше одна величина, тем меньше вторая. Чем меньше одна величина, тем больше вторая.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.

Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.

Есть две разновидности пропорциональностей:

Прямая пропорциональность. Это зависимость, при которой увеличение одного числа ведет к увеличению другого во столько же раз. А уменьшение одного числа ведет к уменьшению другого во столько же раз.
Обратная пропорциональность. Это зависимость, при которой уменьшение одного числа ведет к увеличению другого во столько же раз. А увеличение числа наоборот ведет к уменьшению другого во столько же раз.

Коэффициент пропорциональности

— это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

a и d называются крайними членами, b и c — средними.

Основное свойство пропорции

Произведение крайних членов равно произведению средних членов.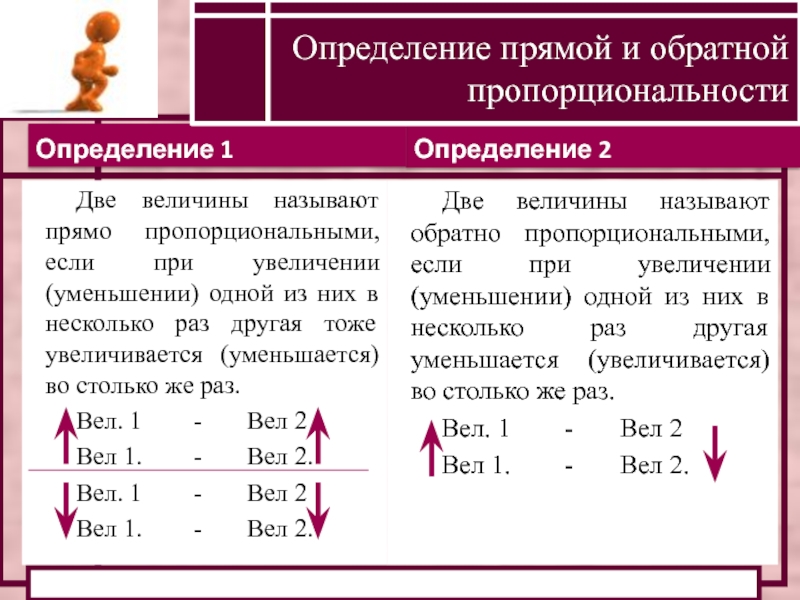

Свойство прямо пропорциональной зависимости:

Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Примеры прямо пропорциональной зависимости:

при постоянной скорости пройденный маршрут прямо-пропорционально зависит от времени;
периметр квадрата и его сторона — прямо-пропорциональные величины;
стоимость конфет, купленных по одной цене, прямо-пропорционально зависит от их количества.

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

Формула прямой пропорциональности

y = kx,

где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

y/x = k

Пример 1.

В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

Как решаем:

Вспомним формулу для определения пути через скорость и время: S = V * t.

Так как оба автомобиля проделали одинаковый путь, можно составить пропорцию из двух выражений: 70 * 2 = V * 7

Найдем скорость второго автомобиля: V = 70 * 2/7 = 20

Ответ: 20 км/ч.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Пример 2.

Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?

Как рассуждаем:

Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.

Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:

х = 1 (блогер) * 30 (раз) : 12/8 (дней).
х = 1 * 30 : 12/8
х = 20

Ответ: 20 человек напишут 420 постов за 12 дней.

Обратно пропорциональные величины

Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

Свойство обратной пропорциональности величин:

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины;
при одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи;
количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене.

Формула обратной пропорциональности

y = k/x

где y и x — это переменные величины,

k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

xy = k.

Потренируемся

Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Как рассуждаем:

В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.

Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

Как решаем:

Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию: 30 : 24 = 5 : х

Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член: х = 24 * 5 : 30; х = 4

Значит, 30 человек раскрутят канал за 4 дня.

Ответ: за 4 дня.

Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Как рассуждаем:

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Обозначим:

v1 = 75 км/ч

v2 = 52 км/ч

t1 = 13 ч

t2 = х

Как решаем:

Составим пропорцию: v1/v2 = t2/t1.
Соотношения равны, но перевернуты относительно друг друга.

Подставим известные значения: 75/52 = t2/13

Ответ: 18 часов 45 минут.

Обратная пропорциональность в математике и в жизни

Сегодня мы рассмотрим, какие величины называются обратно пропорциональными, как выглядит график обратной пропорциональности и как все это может вам пригодится не только на уроках математики, но и вне школьных стен.

Такие разные пропорциональности

Пропорциональностью называют две величины, которые взаимно зависимы друг от друга.

Зависимость может быть прямой и обратной. Следовательно, отношения между величинами описывают прямая и обратная пропорциональность.

Прямая пропорциональность – это такая зависимость двух величин, при которой увеличение либо уменьшение одной из них ведет к увеличению либо уменьшению другой. Т.е. их отношение не изменяется.

Например, чем больше усилий вы прилагаете для подготовки к экзаменам, тем выше ваши оценки. Или чем больше вещей вы берете с собой в поход, тем тяжелее нести ваш рюкзак. Т.е. количество затраченных на подготовку к экзаменам усилий прямо пропорционально полученным оценкам. И количество запакованных в рюкзак вещей прямо пропорционально его весу.

Обратная пропорциональность – это функциональная зависимость, при которой уменьшение либо увеличение в несколько раз независимой величины (ее называют аргументом) вызывает пропорциональное (т.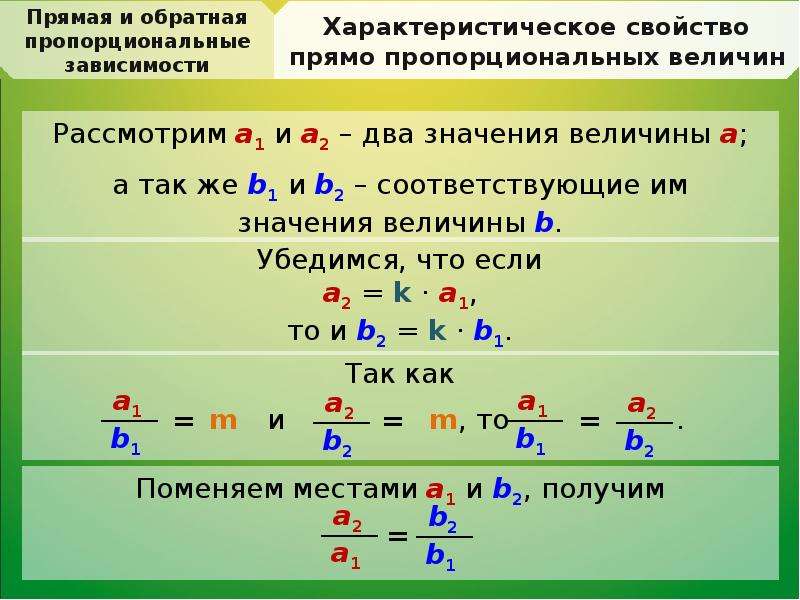 е. во столько же раз) увеличение либо уменьшение зависимой величины (ее называют функцией).

Проиллюстрируем простым примером. Вы хотите купить на рынке яблок. Яблоки на прилавке и количество денег в вашем кошельке находятся в обратной пропорциональности. Т.е. чем больше вы купите яблок, тем меньше денег у вас останется.

Функция и ее график

Функцию обратной пропорциональности можно описать как y = k/x. В котором x ≠ 0 и k ≠ 0.

Эта функция обладает следующими свойствами:

Областью ее определения является множество всех действительных чисел, кроме x = 0. D(y): (-∞; 0) U (0; +∞).
Областью значений являются все действительные числа, кроме y = 0. Е(у): (-∞; 0) U (0; +∞).
Не имеет наибольших и наименьших значений.
Является нечетной и ее график симметричен относительно начала координат.
Непериодическая.
Ее график не пересекает оси координат.
Не имеет нулей.
Если k > 0 (т.е. аргумент возрастает), функция пропорционально убывает на каждом из своих промежутков. Если k < 0 (т.е. аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
При возрастании аргумента (k > 0) отрицательные значения функции находятся в промежутке (-∞; 0), а положительные – (0; +∞). При убывании аргумента (k < 0) отрицательные значения расположены на промежутке (0; +∞), положительные – (-∞; 0).

График функции обратной пропорциональности называется гиперболой. Изображается следующим образом:

Задачи на обратную пропорциональность

Чтобы стало понятнее, давайте разберем несколько задач. Они не слишком сложные, а их решение поможет вам наглядно представить, что такое обратная пропорциональность и как эти знания могут пригодиться в вашей обычной жизни.

Задача №1. Автомобиль движется со скоростью 60 км/ч. Чтобы доехать до места назначения, ему потребовалось 6 часов. Сколько времени ему потребуется, чтобы преодолеть такое же расстояние, если он будет двигаться со скоростью в 2 раза выше?

Можем начать с того, что запишем формулу, которая описывает отношения времени, расстояния и скорости: t = S/V. Согласитесь, она очень напоминает нам функцию обратной пропорциональности. И свидетельствует о том, что время, которое автомобиль проводит в пути, и скорость, с которой он движется, находятся в обратной пропорциональности.

Чтобы убедиться в этом, давайте найдем V₂, которая по условию выше в 2 раза: V₂ = 60 * 2 = 120 км/ч. Затем рассчитаем расстояние по формуле S = V * t = 60 * 6 = 360 км. Теперь совсем несложно узнать время t₂, которое требуется от нас по условию задачи: t₂ = 360/120 = 3 ч.

Как видите время в пути и скорость движения действительно обратно пропорциональны: со скоростью в 2 раза выше изначальной автомобиль потратит в 2 раза меньше времени на дорогу.

Решение этой задачи можно записать и в виде пропорции. Для чего сначала составим такую схему:

↓ 60 км/ч – 6 ч ↑

↓120 км/ч – х ч ↑

Стрелки обозначают обратно пропорциональную зависимость. А также подсказывают, что при составлении пропорции правую часть записи надо перевернуть: 60/120 = х/6. Откуда получаем х = 60 * 6/120 = 3 ч.

Задача №2. В мастерской трудятся 6 рабочих, которые с заданным объемом работы справляются за 4 часа. Если количество рабочих сократить в 2 раза, сколько времени потребуется оставшимся, чтобы выполнить тот же объем работы?

Запишем условия задачи в виде наглядной схемы:

↓ 6 рабочих – 4 ч ↑

↓ 3 рабочих – х ч ↑

Запишем это в виде пропорции: 6/3 = х/4. И получим х = 6 * 4/3 = 8 ч. Если рабочих станет в 2 раза меньше, оставшиеся затратят на выполнение всей работы в 2 раза больше времени.

Задача №3. В бассейн ведут две трубы. Через одну трубу вода поступает со скоростью 2 л/с и наполняет бассейн за 45 минут. Через другую трубу бассейн наполнится за 75 минут. С какой скоростью вода поступает в бассейн через эту трубу?

Для начала приведем все данные нам по условию задачи величины к одинаковым единицам измерения. Для этого выразим скорость наполнения бассейна в литрах в минуту: 2 л/с = 2 * 60 = 120 л/мин.

Поскольку из условия следует, что через вторую трубу бассейн заполняется медленнее, значит, и скорость поступления воды ниже. На лицо обратная пропорциональность. Неизвестную нам скорость выразим через х и составим такую схему:

↓ 120 л/мин – 45 мин ↑

↓ х л/мин – 75 мин ↑

А затем составим пропорцию: 120/х = 75/45, откуда х = 120 * 45/75 = 72 л/мин.

В задаче скорость наполнения бассейна выражена в литрах в секунду, приведем полученный нами ответ к такому же виду: 72/60 = 1,2 л/с.

Задача №4. В небольшой частной типографии печатают визитки. Сотрудник типографии работает со скоростью 42 визитки в час и трудится полный рабочий день – 8 часов. Если бы он работал быстрее и печатал 48 визиток за час, насколько раньше он смог бы уйти домой?

Идем проверенным путем и составляем по условию задачи схему, обозначив искомую величину как х:

↓ 42 визитки/ч – 8 ч ↑

↓ 48 визитки/ч – х ч ↑

Перед нами обратно пропорциональная зависимость: во сколько раз больше визиток в час напечатает сотрудник типографии, во столько же раз меньше времени ему потребуется на выполнение одной и той же работы. Зная это, составим пропорцию:

42/48 = х/8, х = 42 * 8/48 = 7ч.

Таким образом, справившись с работой за 7 часов, сотрудник типографии смогу бы уйти домой на час раньше.

Заключение

Нам кажется, что эти задачи на обратную пропорциональность действительно несложные. Надеемся, что теперь вы тоже считаете их такими. А главное, что знание об обратно пропорциональной зависимости величин действительно может оказаться для вас полезным еще не раз.

Не только на уроках математики и экзаменах. Но и тогда, когда вы соберетесь отправиться в путешествие, пойдете за покупками, решите немного подработать в каникулы и т. п.

Расскажите нам в комментариях, какие примеры обратной и прямой пропорциональной зависимости вы замечаете вокруг себя. Пускай это будет такая игра. Вот увидите, как это увлекательно. Не забудьте «расшарить» эту статью в социальных сетях, чтобы ваши друзья и одноклассники тоже смогли поиграть.

Прямая и обратная пропорциональность — методическая рекомендация. Математика, 6 класс.

1.	Пропорциональные и непропорциональные величины	2 вид — интерпретация	лёгкое	1 Б.	Следует определить, является ли пропорциональной зависимость между величинами.
2.	Зависимость между величинами	2 вид — интерпретация	лёгкое	1 Б.	Необходимо определить, является ли прямо пропорциональной, обратно пропорциональной или не является пропорциональной зависимость между величинами.
3.	Величины	2 вид — интерпретация	лёгкое	2 Б.	Необходимо выбрать величины, между которыми существует прямо/обратно пропорциональная зависимость.
4.	Формулы. Прямая пропорциональность	2 вид — интерпретация	среднее	3 Б.	Формулы. Прямая пропорциональность.
5.	Формулы. Обратная пропорциональность	2 вид — интерпретация	среднее	3 Б.	Формулы. Обратная пропорциональность.
6.	Лишняя формула	2 вид — интерпретация	среднее	2 Б.	Из данных формул следует исключить «лишнюю», обратная пропорциональность.
7.	Прямо пропорциональные величины, таблица	2 вид — интерпретация	среднее	4 Б.	Прямо пропорциональные величины, таблица.
8.	Таблица и формула (десятичные дроби)	2 вид — интерпретация	среднее	4 Б.	Следует определить зависимость между величинами, записать формулу и заполнить таблицу. Прямая пропорциональность.
9.	Таблица, формула (целые числа)	2 вид — интерпретация	среднее	5 Б.	Необходимо определить зависимость между величинами, записать формулу и заполнить таблицу. Обратная пропорциональность.

Прямая и обратная пропорциональность. Математика, 6 класс: уроки, тесты, задания.

1.	Пропорциональные и непропорциональные величины Сложность: лёгкое	1
2.	Зависимость между величинами Сложность: лёгкое	1
3.	Величины Сложность: лёгкое	2
4.	Формулы. Прямая пропорциональность Сложность: среднее	3
5.	Формулы. Обратная пропорциональность Сложность: среднее	3
6.	Лишняя формула Сложность: среднее	2
7.	Прямо пропорциональные величины, таблица Сложность: среднее	4
8.	Таблица и формула (десятичные дроби) Сложность: среднее	4
9.	Таблица, формула (целые числа) Сложность: среднее	5

Прямая и обратная пропорциональная зависимость — Kid-mama

Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.

Проще всего понять прямо пропорциональную зависимость на примере станка, изготавливающего детали с постоянной скоростью. Если за два часа он делает 25 деталей, то за 4 часа он изготовит деталей вдвое больше — 50. Во сколько раз дольше времени он будет работать, во столько же раз больше деталей он изготовит.

Математически это выглядит так:

4 : 2 = 50 : 25 или так: 2 : 4 = 25 : 50

Прямо пропорциональными величинами тут являются время работы станка и число изготовленных деталей.

Говорят: Число деталей прямо пропорционально времени работы станка.

Если две величины прямо пропорциональны, то отношения соответствующих величин равны. (В нашем примере — это отношение времени 1 к времени 2 = отношению количества деталей за время 1 к количеству деталей за время 2)

Обратная пропорциональность

Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.

Обратно пропорциональная зависимость часто встречается в задачах на скорость. Скорость и время являются обратно пропорциональными величинами. Действительно, чем быстрее движется объект, тем меньше времени у него уйдет на путь.

Например:

Если величины обратно пропорциональны, то отношение значений одной величины (скорости в нашем примере) равно обратному отношению другой величины ( времени в нашем примере). ( В нашем примере — отношение первой скорости к второй скорости равно отношению второго времени к первому времени.

Задача 1:

Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?

Решение:

Запишем краткое условие задачи:

Задача 2:

Для перевозки груза потребовалось 24 машины грузоподъемностью 7,5 тонн. Сколько нужно машин грузоподъемностью 4,5 т, чтобы перевезти тот же груз?

Решение:

Краткая запись:

Онлайн урок: Прямая и обратная пропорциональные зависимости по предмету Математика 6 класс

Рассмотрим некоторые варианты задач на пропорциональную зависимость, в которых величины зависят прямо пропорционально одна от другой.

Задача 1

Для приготовления из 3 кг черной смородины по рецепту требуется 3,3 кг сахара.

Сколько сахара потребуется для приготовления варенья из 5 кг черной смородины?

Решение:

Пусть х (кг) сахара потребуется для приготовления варенья из 5 кг ягод.

Составим краткую запись задачи в виде таблицы:

Определим, как зависят масса сахара и масса ягод.

Чем больше ягод, тем больше нужно сахара, следовательно, между величинами прямо пропорциональная зависимость.

В таблице вертикальными стрелками изображаем прямо пропорциональную зависимость величин.

Так как зависимость величин прямо пропорциональная, составим пропорцию в точном соответствии с таблицей.

Отношение значений одной величины равно отношению соответствующих значений другой величины.

Получим $\mathbf{\frac{3,3}{x} = \frac{3}{5}}$

Составим уравнение, используя основное свойство пропорции:

$\mathbf{{3}\cdot{x} = {5}\cdot{3,3}}$

$\mathbf{ {x} = {(5}\cdot{3,3)}\div{3}}$

$\mathbf{ {x} = {5,5}}$ (кг) сахара потребуется для приготовления варенья из 5 кг ягод.

Ответ: $\mathbf{ {x} = {5,5}}$ (кг)

Задача 2

Автомобиль, двигаясь с постоянной скоростью, проехал 400 км за 5 часов.

За какое время автомобиль проедет 600 км?

Решение:

Пусть х (ч) – время, за которое автомобиль проедет 600 км.

Составим краткую запись задачи в виде таблицы:

Определим, как зависят величины S от t, где S — это путь, а t — это время.

Так как движение происходит с постоянной скоростью, то $\mathbf{ {S} = {V}\cdot{t}}$.

Чем больше расстояние, тем больше требуется времени для преодоления этого расстояния, значит, зависимость между величинами S и t прямо пропорциональная.

Изображаем в таблице краткой записи задачи вертикальными стрелками прямо пропорциональную зависимость величин.

Так как зависимость величин прямо пропорциональная, составим пропорцию в точном соответствии с таблицей.

Отношение значений одной величины равно отношению соответствующих значений другой величины.

Получим $\mathbf{\frac{5}{x} = \frac{400}{600}}$

Составим уравнение, используя основное свойство пропорции:

$\mathbf{ {400}\cdot{x} = {5}\cdot{600}}$

$\mathbf{ {x} = {(5}\cdot{600)}\div{400}}$

$\mathbf{ {x} = {7,5}}$ (ч) время, за которое автомобиль проедет 600 км

Ответ: $\mathbf{ {x} = {7,5}}$ (ч)

Примеры решения задач, в которых величины зависят обратно пропорционально одна от другой.

Задача 1

Для перевозки гравия потребовалось 42 машины грузоподъемностью 5 т.

Сколько нужно машин грузоподъемностью 7 т, чтобы перевезти тот же объем гравия?

Решение:

Пусть х (шт) — это количество машин грузоподъемностью 7 т, необходимых для перевозки груза.

Краткую запись задачи оформим в виде таблицы:

Определим, как зависят величины друг от друга.

Чем больше грузоподъемность машины, тем меньше машин потребуется для перевозки груза.

Получаем обратно пропорциональную зависимость.

Изображаем на краткой записи задачи вертикальными стрелками, направленными в разные стороны, обратно пропорциональную зависимость величин.

При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.

А это значит, что при составлении пропорции одно из отношений получится перевернутым.

Получим $\mathbf{\frac{42}{x} = \frac{7}{5}}$

Составим уравнение, используя основное свойство пропорции:

$\mathbf{ {7}\cdot{x} = {42}\cdot{5}}$

$\mathbf{ {x} = {(42}\cdot{5)}\div{7}}$

$\mathbf{ {x} = {30}}$ (шт. ) машин грузоподъёмностью 7 т понадобится для перевозки гравия.

Ответ: $\mathbf{ {x} = {30}}$ (шт.)

Задача 2

Велосипедист проехал путь от дачи до дома за час со скоростью 10 км/ч. Сколько понадобится времени велосипедисту на преодоление этого пути со скоростью 20 км/ч?

Решение:

Пусть х (ч) время велосипедиста, если он будет двигаться со скоростью 20 км/ч. Составим краткую запись задачи в виде таблицы:

Определим, как зависят V и t, где V— скорость движения велосипедиста, t— время движения.

Чем больше скорость велосипедиста, тем меньше времени ему потребуется для преодоления пути.

Получаем обратно пропорциональную зависимость величин друг от друга.

А это значит, при составлении пропорции одно из отношений получаем перевернутым.

Получим $\mathbf{\frac{x}{1} = \frac{10}{20}}$

Составим уравнение, используя основное свойство пропорции:

$\mathbf{ {20}\cdot{x} = {10}\cdot{1}}$

$\mathbf{ {x} = {(10}\cdot{1)}\div{20}}$

$\mathbf{ {x} = {0,5}}$ (ч) время велосипедиста, если он будет двигаться со скоростью 20 км/ч.

Ответ: $\mathbf{ {x} = {0,5}}$ (ч)

У меня есть дополнительная информация к этой части урока!

ЗакрытьРассмотрим некоторые, часто встречающиеся, варианты прямой и обратной пропорциональной зависимости величин в решении задач
Примеры задач, в которых величины зависят прямо пропорционально одна от другой.
Величины, зависящие друг от друга
Величина постоянная
Величина дроби и ее числитель
Знаменатель дроби
Объем выполненной работы и затраченное время
Производительность труда
Производительность труда и объем выполненной работы
Время работы
Длина пути и время прохождения этого пути
Скорость движения
Пройденный путь и скорость движения
Время движения
Количество товара и стоимость
Цена товара
Длина (ширина) прямоугольника и его площадь
Ширина (длина)

Примеры задач, в которых величины зависят обратно пропорционально одна от другой
Знаменатель дроби и значение дроби
Числитель дроби
Число рабочих и время выполнения ими заданной работы
Производительность всех рабочих
Производительность труда и время потраченное на работу
Объем работы
Скорость движения и время
Путь
Количество товара и его цена
Стоимость покупки
Обратная пропорция — Формула, Примеры, Определение, График
Когда две величины связаны друг с другом обратно пропорционально, т. Е. Когда увеличение одной величины приводит к уменьшению другой, и наоборот, то говорят, что они находятся в обратной пропорции. В обратной пропорции произведение двух данных величин равно постоянной величине. Давайте узнаем об этом подробнее в этой статье.
Что такое обратная пропорция?
Определение обратной пропорции гласит, что «две величины находятся в обратной пропорции, если увеличение одной приводит к уменьшению другой величины, а уменьшение одной приводит к увеличению другой величины».Другими словами, если произведение обеих величин, независимо от изменения их значений, равно постоянному значению, то говорят, что они находятся в обратной пропорции. Например, возьмем количество рабочих и количество дней, необходимое им для выполнения заданного объема работы, как x и y соответственно.
Количество рабочих (x) Количество необходимых дней (г)
16 3
12 4
8 6
4 12
Являются ли количество рабочих и количество дней обратной пропорциональной зависимостью? Давайте разберемся.
Тщательно соблюдайте значения, указанные в таблице. Вы обнаружите, что для каждой строки произведение x и y одинаково. Это означает, что если будет 16 рабочих, они выполнят работу за 3 дня. Итак, здесь x × y = 16 × 3 = 48. Теперь мы уменьшаем количество рабочих, очевидно, что меньшее количество рабочих будет выполнять ту же работу за большее время. Но здесь мы видим произведение x и y, это 12 × 4 = 48. Опять же, для 8 рабочих за 6 дней продукт равен 48. То же самое для 4 рабочих за 12 дней.Итак, произведение двух величин в обратной пропорции всегда равно.
Формула обратной пропорции
Формула обратной пропорции помогает установить связь между двумя обратно пропорциональными величинами. Пусть x и y — две величины, и предположим, что x уменьшается, когда y увеличивается, и наоборот. Пример: скорость обратно пропорциональна времени. По мере увеличения скорости время, необходимое нам для преодоления того же расстояния, уменьшается.Принимая скорость как y и время как x, мы можем сказать, что y обратно пропорционален x и математически записывается как формула обратной пропорции.
Формула обратной пропорциональности записывается как
y = k / x
где
Здесь символ ∝ обозначает пропорциональную зависимость между двумя величинами.
График обратной пропорции
График обратной пропорции обычно представляет собой кривую, которая изгибается к началу координат, образуя форму гиперболы.Если есть любые две случайные точки на оси x и оси y на графике обратной пропорции \ (x_ {1} \), \ (x_ {2} \), \ (y_ {1} \) и \ (y_ {2} \), такой, что \ (x_ {1} \) <\ (x_ {2} \) и \ (y_ {1} \) <\ (y_ {2} \), график будет отображаться так:
Это означает, что если мы увеличиваем значение x с \ (x_ {1} \) до \ (x_ {2} \), значение y уменьшается с \ (y_ {2} \) до \ (y_ {1 } \).
Прямая и обратная пропорция
Существует два основных типа пропорциональности — прямая пропорция и обратная пропорциональность.Говорят, что две переменные x и y находятся в прямой зависимости, когда y ∝ x (или x ∝ y). Это означает, что y = kx для постоянного k. В то время как две переменные x и y считаются обратно пропорциональными, если y ∝ 1 / x (или x ∝ 1 / y). Это означает, что y = k / x для постоянного k. В прямой пропорциональной зависимости соотношение двух переменных равно для любых значений, в то время как в обратной пропорции произведение двух переменных равно для любых значений. Посмотрите на изображение ниже, чтобы наглядно понять разницу между прямой и обратной пропорцией.
Темы, связанные с обратной пропорцией
Ознакомьтесь с этими интересными статьями, связанными с концепцией обратной пропорции.
Часто задаваемые вопросы об обратной пропорции
Что такое косвенная пропорция?
Косвенная или обратная пропорция — это отношение между двумя величинами, при котором увеличение одной ведет к уменьшению другой, и наоборот. Это полная противоположность прямой пропорции.
Что означает символ ∝ в формуле обратной пропорции?
В формуле обратной пропорции символ пропорциональности ∝ обозначает соотношение между двумя величинами. Это выражается как x ∝ 1 / y. Отсюда следует, что x = k / y, где k — коэффициент пропорциональности.
Как найти K в обратной пропорции?
K в обратной пропорции представляет собой константу пропорциональности, которая одинакова независимо от значений данных переменных. Чтобы найти k в обратной пропорции, найдите произведение x и y. Формула y = k / x, что дает нам k = xy.
Как представить формулу обратной пропорциональности?
Формула обратной пропорциональности отображает соотношение между двумя величинами, которое можно понять с помощью формулы, приведенной ниже:
Определите две величины, которые различаются в данной задаче.
Определите, что существует обратная вариация. х ∝ 1 / у
Примените формулу обратной пропорции x = k / y.
В чем разница между прямой и обратной пропорцией?
Разница между прямой и обратной пропорцией состоит в том, что прямая пропорция показывает прямую взаимосвязь между двумя величинами, где увеличение одного также приводит к увеличению другого количества, и наоборот. С другой стороны, обратная пропорция представляет собой косвенную связь между двумя величинами или переменными, где увеличение одной ведет к уменьшению другой переменной, и наоборот.
Что такое формула обратной пропорции?
Формула обратной пропорции: y = k / x, где x и y — две величины в обратной пропорции, а k — константа пропорциональности.
Как показать взаимосвязь между двумя величинами, используя формулу обратной пропорции?
Обратная пропорциональная зависимость между двумя величинами может быть показана, если произведение двух величин (x × y) является постоянным, тогда они отображают обратно пропорциональную зависимость.Он выражается как x ∝ 1 / y или x = k / y, где k — коэффициент пропорциональности.
Обратно пропорционально — Объяснение и примеры
Что означает «обратно пропорциональная величина»?
В нашей повседневной жизни мы часто сталкиваемся с ситуациями, когда на изменение значений одной величины влияет изменение значений другой величины.
Например, , сирена приближающейся пожарной машины или машины скорой помощи становится громче по мере приближения к вам автомобиля и тише по мере удаления.Вы заметили, что чем меньше расстояние между вами и автомобилем, тем громче сирена и чем больше расстояние, тем тише становится сирена. Этот тип ситуации называется обратной пропорцией, а иногда и косвенной пропорцией.
Прямая и косвенная пропорция — это два понятия, с которыми мы все знакомы, но, возможно, не на математическом уровне. И прямая, и обратная пропорция используются, чтобы показать, как две величины связаны друг с другом.
В этой статье мы узнаем об обратной и косвенной пропорции и о том, как эти концепции важны в реальных жизненных ситуациях.но прежде чем мы начнем, давайте вспомним о концепции прямой пропорции.
Прямая пропорция
Две переменные a и b считаются прямо пропорциональными, если увеличение одной переменной вызывает увеличение другой переменной, и наоборот. Это означает, что прямо пропорционально соотношение соответствующих значений переменных остается постоянным. В этом случае, если значения b; b ₁, b ₂ соответствует значениям a; a ₁, a ₂ соответственно, тогда их соотношение будет постоянным;
a _1/ / b ₁ = a ₂ / b ₂
Прямая пропорция представлена знаком пропорциональности ‘∝’ как a ∝ b.Формула прямого изменения имеет следующий вид:
a / b = k
, где k называется константой пропорциональности.
Обратная пропорция
В отличие от прямой пропорции, когда одна величина изменяется прямо пропорционально изменениям другой величины, в обратной пропорции, увеличение одной переменной вызывает уменьшение другой переменной, и наоборот. Говорят, что две переменные a и b обратно пропорциональны, если; а∝1 / б. В этом случае увеличение переменной b вызывает уменьшение значения переменной a. Точно так же уменьшение переменной b вызывает увеличение значения переменной a.
Формула косвенной пропорциональности
Если переменная a обратно пропорциональна переменной b, то это можно представить формулой:
a∝1 / b
ab = k; где k — пропорциональная постоянная.
Чтобы создать обратное пропорциональное уравнение, необходимо выполнить следующие шаги:
Запишите пропорциональное соотношение
Напишите уравнение, используя константу пропорциональности
Теперь найдите значение константы, используя заданные значения
Подставьте значение константы в уравнении.
Примеры из реальной жизни концепции обратной пропорции
Время, затрачиваемое определенным количеством рабочих на выполнение части работы, обратно пропорционально количеству рабочих на работе. Это означает, что чем меньше рабочих, тем больше времени требуется на завершение работы, и наоборот.
Скорость движущегося судна, такого как поезд, транспортное средство или корабль, обратно пропорциональна времени, необходимому для преодоления определенного расстояния. Чем выше скорость, тем меньше времени требуется на преодоление дистанции.

Пример 1
35 рабочих собирают урожай кофе на плантации за 8 дней. Сколько времени потребуется 20 работникам, чтобы собрать урожай кофе на одной и той же плантации.
Раствор
35 рабочих собирают кофе за 8 дней
Продолжительность, занятая одним рабочим = (35 × 8) дней
Теперь вычислите продолжительность, занятую 20 рабочими
= (35 × 8) / 20
= 14 дней
Следовательно, на 20 рабочих потребуется 14 дней.

Пример 2
6 коз или 8 овец пасутся на поле в течение 28 дней. Сколько времени понадобится 9 козам и 2 овцам, чтобы пасти одно и то же поле.
Решение
6 коз = 8 овец
⇒ 1 коза = 8/6 овец
⇒ 9 коз ≡ (8/6 × 9) овец = 12 овец
⇒ (9 коз + 2 овцы) ≡ (12 овец + 2 овец) = 14 овец
Итак, 8 овец => 28 дней
Одна овца будет пастись за (28 × 8) дней
⇒ 14 овец займет (28 × 8) / 14 дней
= 16 дней
Следовательно, 9 коз и 2 овцы будут пасти поле 16 дней.

Пример 3
Девять кранов могут заполнить бак за четыре часа. Сколько времени потребуется двенадцать кранов с одинаковым расходом, чтобы заполнить один и тот же резервуар?
Решение
Пусть отношения;
x ₁ / x ₂ = y _2/ y ₁
⇒ 9 / x = 12/4
x = 3
Таким образом, 12 кранов заполнят бак за 3 часа .
Практические вопросы
В армейской казарме достаточно еды, чтобы прокормить 80 солдат в течение 60 дней.Подсчитайте, на сколько еды хватит, когда через 15 дней в казарму войдут еще 20 солдат.
8 кранов с одинаковым расходом могут заполнить бак за 27 минут. Если не открывать два крана, сколько времени понадобится для заполнения бака оставшимися трубами?
Общая недельная заработная плата 6 рабочих, работающих по 8 часов в день, составляет 8400 долларов США. Какова будет недельная заработная плата 9 рабочих, работающих по 6 часов в день?
1350 литров молока могут выпить 70 студентов за 30 дней. Сколько учеников выпьют 1710 литров молока за 28 дней?
15 женщин или 12 мужчин могут выполнить определенную задачу за 66 дней.Сколько времени потребуется 3 и 24 женщинам и мужчинам соответственно, чтобы выполнить одну и ту же задачу?
Ответы
51 день
36 минут
$ 9450
95 студентов
30 дней
Предыдущий урок | Главная страница | Следующий урок
Обратно пропорционально — Определение, формула и примеры
Говорят, что две величины обратно пропорциональны, когда значение одной величины увеличивается по сравнению с уменьшением другой, или наоборот.Это означает, что эти две величины ведут себя противоположно по своей природе. Например, время, необходимое для выполнения задачи, уменьшается с увеличением количества рабочих, выполняющих ее, и увеличивается с уменьшением количества рабочих. Здесь время и количество рабочих обратно пропорциональны друг другу.
Другие термины, которые могут быть использованы здесь для этого типа пропорции, — это обратная пропорция или обратное изменение, или обратное изменение, или обратная пропорция. Две переменные говорят x и y, которые находятся в обратно пропорциональном отношении и представлены как x ∝ 1 / y или x ∝ y ^-1.Прямо пропорциональные и обратно пропорциональные отношения противоположны друг другу.
Что обратно пропорционально?
Изучая математику и физику, мы узнаем о величинах, которые зависят друг от друга, и такие величины называются пропорциональными друг другу. Другими словами, две переменные или величины пропорциональны друг другу, если одна изменяется, то другая также изменяется на фиксированную величину. Это свойство переменных называется пропорциональностью, а символ, используемый для представления пропорциональности, — «∝».«Есть два типа пропорциональности переменных. Их:
Прямо пропорциональный
Обратно пропорциональный
Когда две величины связаны друг с другом обратно пропорционально, т. Е. Когда увеличение одной величины приводит к уменьшению другой, и наоборот, то говорят, что они обратно пропорциональны. При этом, если одна переменная уменьшается, другая увеличивается в той же пропорции. Это противоположно прямой пропорции. Или говорят, что две величины обратно пропорциональны , когда одна величина прямо пропорциональна обратной величине другой.Например, соотношение между скоростью и временем. Скорость и время в пути обратно пропорциональны, потому что чем быстрее мы путешествуем, тем меньше времени требуется, то есть чем больше скорость, тем меньше время.
По мере увеличения скорости время в пути уменьшается.
И с уменьшением скорости время в пути увеличивается.
Общая формула обратно пропорциональной
Символ «∝» обозначает пропорциональную зависимость между двумя величинами. Пусть x и y — две величины. Тогда y обратно пропорционален x — это то же самое, что y прямо пропорционален 1 / x. Математически это записывается как y ∝ 1 / x.
Общее уравнение обратной вариации y = k / x, где k — постоянная пропорциональности. Мы также можем записать это как y × x = k или y × x = Constant. Если x и y находятся в обратной вариации и x имеет два значения x ₁ и x ₂, соответствующие y, который также имеет два значения y ₁ и y ₂ соответственно, то по определению обратной вариации, имеем x ₁ y ₁ = x ₂ y ₂ = k.
В этом случае это становится x ₁ / x ₂ = y ₂ / y ₁ = k.
Графическое представление обратной пропорциональности
График обратной пропорциональности выглядит следующим образом.
Например, ниже показан график уравнений y = 1 / x и y = -1 / x, имеющих обратно пропорциональную зависимость.
Применения обратно пропорциональной системы
Понятие обратно пропорционального широко используется в повседневной жизни, а также при решении многих задач в области науки, статистики и т. Д.В физике существует множество формул, которые выводятся с использованием концепции обратной пропорциональности. Закон Ома, соотношение скорости и времени, длина волны звука и его частота — это несколько.
Важные примечания по обратно пропорциональной системе
Для обратной пропорциональности необходимо помнить следующие моменты:
Если одно количество увеличивается, другое уменьшается.
x ∝ 1 / y или y ∝ 1 / x.
x × y = k, где k называется константой пропорциональности.
Связанные темы об обратно пропорциональной системе
Проверьте эти интересные статьи, связанные с обратно пропорциональными.
Часто задаваемые вопросы об обратно пропорциональной системе
Что означает «обратно пропорциональная величина»?
Обратно пропорциональные переменные или величины — это переменные, в которых, если одна переменная увеличивается, другая уменьшается, а если одна переменная уменьшается, другая увеличивается. Это означает, что когда увеличение одного количества приводит к уменьшению другого, и наоборот, говорят, что они обратно пропорциональны.Например, время, затрачиваемое на выполнение работы, обратно пропорционально количеству рабочих.
Как узнать, пропорционально оно прямо или обратно?
Обратно пропорциональное соотношение между двумя величинами можно понять, как показано ниже,
Определите две величины, которые различаются в данной задаче.
Если x / y постоянный, то он прямо пропорционален.
Если x × y постоянно, то обратно пропорционально.
Какая формула для обратно пропорциональной?
Формула обратной связи помогает математически представить обратно пропорциональную зависимость. Формула обратной вариации: x × y = k или y = k / x, где x и y — две переменные, а k — константа пропорциональности.
Что противоположно обратно пропорциональному?
Обратно пропорционально противоположно прямо пропорционально. Это означает, что когда увеличение одного количества приводит к увеличению другого, и наоборот, они говорят, что они прямо пропорциональны.
Что это значит, если две вещи обратно пропорциональны?
Говорят, что две величины обратно пропорциональны, когда значение одной величины увеличивается по сравнению с уменьшением другой, или наоборот. Это означает, что эти две величины ведут себя противоположно по своей природе. Например, соотношение скорости и времени. Скорость и время в пути обратно пропорциональны, потому что чем быстрее мы путешествуем, то есть чем больше скорость, тем меньше время.
Что означает символ обратной пропорциональности?
Символ, используемый для обозначения пропорциональности, — «∝».«Обратная пропорциональность относится к одной величине, которая прямо пропорциональна обратной величине другой величины. Мы представляем любые две величины в обратной пропорции как, x ∝ 1 / y или x ∝ y ^-1.
Что такое пример обратно пропорциональной зависимости?
Обратно пропорциональная зависимость возникает, когда одно значение увеличивается, а другое уменьшается, и наоборот. Например, большее количество рабочих сокращает время, необходимое для выполнения задачи. Таким образом, они обратно пропорциональны.
Прямая и обратная пропорция — Прямая и обратная пропорция — Edexcel — GCSE Maths Revision — Edexcel
Прямая пропорция
Существует прямая пропорция между двумя значениями, когда одно кратно другому. Например, \ (1 \: \ text {cm} = 10 \: \ text {mm} \). При переводе сантиметров в миллиметры множитель всегда равен 10. Прямая пропорция используется для расчета стоимости бензина или обменных курсов иностранных денег.
Символ прямой пропорции — \ (\ propto \).
Выражение ‘t прямо пропорционально r’ можно записать с помощью символа пропорциональности:
z4b4kz976.0.0.0.1:0.1.0.$0.$1.$4″> \ [t \ propto r \]
Если \ (y = 2p \), то \ (y \) пропорционально \ (p \) и \ (y \) могут быть вычислены для \ (p = 7 \):
\ [y = 2 \ times 7 = 14 \]
Аналогично, если \ (y = 60 \), то \ (p \) можно вычислить:
\ [60 = 2p \]
Чтобы найти \ (p \), разделите 60 на 2:
\ [60 \ div 2 = 30 \]
Прямая пропорция — выше
Пропорциональность можно использовать для создания уравнения.
Для этого есть четыре шага:
0.$0.$2.$3″>
запишите пропорциональную зависимость
преобразовать в уравнение с использованием константы пропорциональности
использовать данную информацию, чтобы найти константу пропорциональности
заменить константу пропорциональности в уравнение
Пример
Значение \ (e \) прямо пропорционально \ (п\). Когда \ (e = 20 \), \ (p = 10 \). Найдите уравнение, связывающее \ (e \) и \ (p \).
\ [e \ propto p \]
\ [e = kp \]
0.0.0.1:0.1.0.$0.$2.$6.$2″> \ (20 = 10k \), поэтому \ (k = 20 \ div 10 = 2 \)
\ [e = 2p \ ]
Это уравнение теперь можно использовать для вычисления других значений \ (e \) и \ (p \).
Если \ (p = 6 \), то \ (e = 2 \ times 6 = 12 \).
Обратная пропорция
Если одно значение обратно пропорционально другому, то оно записывается с использованием символа пропорциональности \ (\ propto \) по-другому. Обратная пропорция возникает, когда одно значение увеличивается, а другое уменьшается. Например, большее количество рабочих сократит время на выполнение задачи. Они обратно пропорциональны.
0.$0.$3.$2″> Утверждение «b обратно пропорционально m» записывается:
\ [b \ propto \ frac {1} {m} \]
Уравнения, содержащие обратные пропорции, могут использоваться для вычисления других значений.
Использование: \ (g = \ frac {36} {w} \) (поэтому \ (g \) обратно пропорционально \ (w \)).
Если \ (g = 8 \), найти \ (w \).
\ [8 = \ frac {36} {w} \]
\ [w = \ frac {36} {8} = 4.5 \]
Аналогично, если \ (w = 6 \), найти \ ( г\).
\ [g = \ frac {36} {6} \]
\ [g = 6 \]
z4b4kz976.0.0.0.1:0.1.0.$0.$4.$0″> Обратная пропорция — выше
Пропорциональность может использоваться для создания уравнения.
Для этого есть четыре шага:
запишите пропорциональную зависимость
преобразовать в уравнение с использованием константы пропорциональности
использовать данную информацию, чтобы найти константу пропорциональности
заменить константу пропорциональности в уравнение
Пример
Если \ (g \) обратно пропорционально w и когда \ (g = 4 \), \ (w = 9 \), то сформируйте уравнение, связывающее \ (g \) с \ (w \).
\ [g \ propto \ frac {1} {w} \]
\ [g = k \ times \ frac {1} {w} = \ frac {k} {w} \]
\ ( 4 = \ frac {k} {9} \), поэтому \ (k = 4 \ times 9 = 36 \)
\ [g = \ frac {36} {w} \]
Это уравнение можно использовать для вычислить новые значения \ (g \) и \ (w \).
Если \ (g = 8 \), найти \ (w \).
\ [8 = \ frac {36} {w} \]
\ [w = \ frac {36} {8} = 4.5 \]
Аналогично, если \ (w = 6 \), найти \ ( г\).
z4b4kz976.0.0.0.1:0.1.0.$0.$4.$12″> \ [g = \ frac {36} {6} \]
\ [g = 6 \]
Объяснение прямой и обратной пропорции
Введение
По крайней мере, один из моих постов Как расстояние уменьшает мощность радиоволн (еще не опубликовано) требует понимания математической пропорциональности.В частности, требуется понимание Обратной пропорции . Итак, я написал эту статью, чтобы попытаться прояснить ее. Он дает объяснение двух типов пропорции , иначе известной как вариант , вариация , а именно:
Прямая пропорция ,
Обратная пропорция , также известная как Непрямая пропорция .
Символ, используемый для обозначения пропорции
В математике есть символ пропорциональности, например:
∝
Итак, если y пропорционально x , это отображается как:
y ∝ x
1.
Прямая пропорция
Все, что находится в , прямо пропорционально чему-то еще, поднимается и опускается вместе с ним, то есть если одно увеличивается в размере вдвое, то же самое и другое.
Итак, если y ∝ x , то 2y ∝ 2x и y / 2 ∝ x / 2 .
На графиках ниже y ∝ x (линейная функция)
Рис. 1. Диаграмма с тремя графиками, каждый из которых использует линейную функцию для демонстрации пропорциональности.
На рис. 1 выше показана диаграмма с тремя графиками, где значения на оси y идут вверх и вниз в прямо пропорционально значениям на оси x .
, т.е. y ∝ x
или y = kx , где k — постоянная.
Примеры прямой пропорции
Мои первые три примера взяты из каждого из графиков в Рис. 1 . Я использовал одно и то же значение для x , т. Е. x = 3 , повсюду. Каждый использует другую константу k , таким образом:
Пример 1: Пусть k = 1 в этом примере, что делает y = 1x .Итак, y = (1 × 3) = 3 .
Пример 2: Пусть k = 3 в этом примере, что делает y = 3x . Итак, y = (3 × 3) = 9 .
Пример 3: Пусть в этом примере k = 6 , в результате y = 6x . Итак, y = (6 × 3) = 18 .
Мои следующие три примера, от 4 до 6 , предполагают, что значение x удваивается до 6 . y , будучи в пропорции, тоже удваивается:
Пример 4: Когда k = 1 , y = (1 × 6) = 6 . (Ранее в примере 1 , y было 3 .)
Пример 5: Когда k = 3 , y = (3 × 6) = 18 . (Ранее в примере 2 , y было 9 .)
Пример 6: Когда k = 6 , y = (6 × 6) = 36 . (Ранее в примере 3 , y было 18 .)
В приведенных выше примерах y поднимается и опускается синхронно с x и, таким образом, повышается в прямо пропорционально от до х .
Поскольку y = kx , x и y имеют постоянное соотношение k , таким образом: y / x = k
На графике ниже y ∝ x
² (нелинейная функция) Рис. 2. График, демонстрирующий нелинейную функцию x ² .
На рис. 2 выше показан график, на котором значения по оси y идут вверх и вниз по прямо пропорционально квадратам значений по оси x .
т.е. y ∝ x ² (x в квадрате)
или y = kx ² , где k — постоянная.
k = 1 , в этом примере y = 1x ² .
Итак, если x = 5 , то y = 1 × (5 × 5) = 25 .
Тогда, если x удвоится с 5 до 10 , y будет умножится на четыре от 25 до 100 ,
и.е. y = 1 × (5 × 2) × (5 × 2) .
Таким образом, y теперь поднимается и опускается в соответствии с x ² и больше не в прямо пропорционально только до x , но теперь находится в прямо пропорционально до x ² .
См. Объяснения других людей:
2. Обратная или косвенная пропорция
Все, что обратно пропорционально (или косвенно) чему-то другому, упадет, когда другая вещь поднимется, и поднимется, когда она упадет, т.е.е. если одна из них вдвое больше других половин.
Итак, если y ∝ 1 / x , то 2y ∝ 2 / x и y / 2 ∝ 1 / (2x) .
На графике ниже y ∝ 1 / x (нелинейная функция)
Рис. 3. График с использованием линейной функции для демонстрации обратной пропорциональности.
На рис. 3 выше показан график, на котором значения на оси y идут вверх и вниз в , обратно пропорционально значениям на оси x .
, т.е. y ∝ 1 / x
или y = k / x , где k — постоянная.
k = 1 , в этом примере y = 1 / x .
Итак, если x = 5 , y = 1/5 = 0,2
Затем, если x удвоится до 10 , y уменьшится вдвое до 0,1 ,
т.е. y = 1 / (2 × 5) = 1/10 = 0,1
Таким образом, y падает вместе с ростом x и возрастает вместе с падением x , поскольку y находится в обратной пропорции от до x .
На графике ниже y ∝ 1 / x
² (нелинейная функция) Рис. 4. График, демонстрирующий обратную пропорциональность функции квадрата.
На рис. 4 выше показан график, на котором значения по оси y идут вниз в обратной пропорции к квадратам значений по оси x .
т. е. y ∝ 1 / x ²
или y = k / x ² , где k — постоянная.
k = 1 , в этом примере y = 1 / x ² .
Итак, если x = 5 , y = 1 / (5 × 5) = 1/25 = 0,04 .
Затем, если x удвоить до 10 , y будет с разделением на четыре части до 0,01 ,
, т.е. y = 1 / (2 × 5) × (2 × 5) = 1 / (10 × 10) = 1/100 = 0,01 .
Таким образом, y падает вместе с x ² возрастает и поднимается вместе с x ² падает, поскольку y больше не находится в обратно пропорционально до x , но теперь в обратная пропорция до x ² .
См. Объяснения других людей:
Сравнение обратной пропорции 1 / x с 1 / x
²
Это то же самое, что и сравнение изменения видимого размера объектов, видимых на выбранном расстоянии, с их видимыми областями на этих расстояниях.
Если бы я сказал, что видимый размер объекта (высота и ширина) равен , обратно пропорционален его расстоянию (x) , я бы имел в виду, что чем дальше он становится, тем меньше он будет выглядеть как по высоте, так и по ширине ( 1 / х) .Таким образом, если расстояние было увеличено вдвое, его видимый размер уменьшился бы вдвое: (1 / 2x) , а если расстояние снова удвоить, его видимый размер снова уменьшился бы вдвое: (1 / 4x) . Тогда он будет составлять четверть своего первоначального размера, потому что расстояние до него будет в четыре раза больше исходного расстояния.
Эта обратная пропорциональность , связывающая видимый размер с расстоянием, поддерживается Кейси Правилом , программистом и композитором, в его цитате ниже.
Видимый размер объекта в поле зрения линейно уменьшается по мере увеличения расстояния от зрителя. Таким образом, круг диаметром 1 дюйм на расстоянии 5 метров от камеры будет выглядеть как 5 дюймов на расстоянии 1 метра от камеры.
, автор Casey Rule re Взаимосвязь между размером объекта и расстоянием до камеры
Я проверил, что 1 / x или x ^-1 — нелинейная функция. Единственная линейная степень x — x ¹ .Я цитирую Инес Уолстон из Brainly. Я проверил это, потому что правило Кейси гласит: Видимый размер объекта в поле зрения линейно уменьшается по мере увеличения расстояния от зрителя. И его использование слова «линейно» может сбивать с толку. Я думаю, что приведенная ниже диаграмма может показать, что он имеет в виду.
Теперь вспомним все эти формулы для расчета площадей различных форм, таких как прямоугольники, круги, треугольники, параллелограммы и т. Д., Станет очевидным, что площади этих фигур не обратно пропорциональны расстоянию от них наблюдателя, поскольку их размеры ( высота и ширина) есть.Эти площади на самом деле обратно пропорциональны квадрату расстояния от наблюдателя (1 / x ²) .
Сравнение графиков обратной пропорции на рис. 3 и 4.
Рис. 5. Сравнение графиков для y = 1 / x и y = 1 / x ² .
Рис. 5 сравнивает { y , когда он обратно пропорционален x } с { y , когда он обратно пропорционален x ² }.
, то есть сравнивает y = k / x с y = k / x ² , когда k = 1 .
Из этих графиков ясно видно, что график 1 / x ² быстро падает для небольших значений x по сравнению с графиком 1 / x . Это хорошая новость для всех, кого беспокоит излучаемая мощность, так как это обычно приводит к тому, что принимаемая мощность в любой момент оказывается меньше ожидаемой.
ПРИМЕЧАНИЕ: Графики на Рис.5 основаны на концепции, согласно которой уровни мощности на реальном графике y = (k / x ²) и предполагаемом графике y = (k / x) совпадают, когда единица измерения расстояния от источник — 1 , в соответствии с единицами измерения x , например:
1 метр , если x измеряется в метрах,
1 ярд , когда x измеряется в ярдах,
1 фут , когда x измеряется в футах.
ПРИМЕЧАНИЕ: Во всех приведенных здесь примерах и обсуждениях x, y и k могут иметь отрицательные значения с математической точки зрения. Однако я пытаюсь направить дискуссию на излучение положительной силы и энергии, где отрицательные значения обычно не играют роли.
Примечание: Раздел ниже может быть удален из этого сообщения и вставлен в мой будущий пост Как расстояние уменьшает мощность радиоволн .
Как эти наблюдения связаны с излучением энергии
В физике мощность излучаемых сигналов, содержащих энергию, таких как радиоволны, свет и звук, уменьшается так же, как видимая площадь удаленного объекта. Их мощность уменьшается на обратно пропорционально квадрату расстояния, на которое они передаются. Это означает, что удвоение расстояния снижает мощность не только до половины, но и до , половина от половины, что составляет четверть от того, что было, а удвоение снова снижает ее до , четверть четверти, что составляет четверть. шестнадцатая какая то была.
Этот «квадратный закон» полностью определяет мощность получаемой энергии. Это снижает его до более низкого уровня, чем вы могли ожидать.
Если вы были отправлены на этот пост во время чтения Как расстояние уменьшает мощность радиоволн (еще не опубликовано), вам следует вернуться к нему и продолжить чтение.
КОНЕЦ СООБЩЕНИЯ
Просмотры сообщений: 874
Похожие сообщения
Обратно пропорционально: определение, формула и примеры — Видео и стенограмма урока
Что такое обратно пропорционально?
В математике количество может измениться, когда вы измените другое количество.Когда две величины или переменные связаны, мы говорим, что между ними существует связь. Переменные могут иметь одно из трех соотношений или вариантов: прямое, обратное и совместное .
В этом уроке мы сосредоточимся на понимании определения обратной вариации : если одна величина увеличивается в результате уменьшения другой величины или наоборот, то две величины обратно пропорциональны . Мы можем записать математическое определение обратно пропорциональной зависимости, как показано на рисунке 1.
Рисунок 1: y — это переменная, которая обратно пропорциональна переменной x в степени n, а k — ненулевое число.
Скажем, у нас есть n = 1, тогда определение можно упростить и записать как: y = k / x, где «y» обратно пропорционально «x».
Если x возведено во вторую степень, то мы говорим, что y обратно пропорционально квадрату x или кубу x в третьей степени, и так далее.Значение n также может быть дробью, например, 1/2 степени. Когда у вас есть показатель степени 1/2, он также известен как квадратный корень. В этом случае мы бы сказали, что y обратно пропорционально квадратному корню из x , и мы бы записали его следующим образом:
Давайте лучше поймем, что означает обратно пропорциональная величина, построив график значений x и y для различных значений n :
Посмотрите на график, где y обратно пропорционально x с константой k , равной 50. Обратите внимание, что по мере увеличения значения x значение y уменьшается. 50 делится на увеличивающееся значение x , в результате чего получаются все меньшие и меньшие значения y . Это происходит потому, что в знаменателе стоит x . Часто вы будете иметь отношение, которое обратно пропорционально, если независимая переменная находится в знаменателе.
Давайте посмотрим, что произойдет, если у вас будет x во второй степени в знаменателе, а не в первой степени.Обратите внимание, что первоначально, когда значение x увеличивается, значение y уменьшается очень быстро, но затем снижение происходит медленнее по сравнению с началом графика. Однако тенденция остается той же, что и раньше: по мере увеличения значения x значение y снижается.
Если бы вы построили график y как функцию 50, деленную на квадратный корень из x , даже тогда эта тенденция все равно останется прежней. Увеличение значения x приведет к уменьшению значения y или наоборот. Обычно, когда одна переменная движется в одном направлении, другая переменная обычно движется в противоположном направлении. Это причина, по которой этот тип отношений называется обратно пропорциональным.
Теперь, когда мы лучше понимаем эту взаимосвязь, давайте посмотрим, как мы можем применить ее для решения проблем.
Искусство решения проблем
Говорят, что два числа находятся в соотношении друг к другу, если между ними существует какое-то числовое отношение.Есть несколько типов пропорций, каждый из которых определяется отдельным классом функций.
Содержание
1 Прямая пропорция
2 Обратная пропорция
3 Экспоненциальная пропорция
4 Проблемы
4.1 Вводный
4.2 Средний
4,3 Олимпиада
5 См. Также
Прямая пропорция
Прямая пропорция — это пропорция, в которой одно число кратно другому. Прямая пропорция между двумя числами и может быть выражена как:
где — некоторое действительное число.
График прямой пропорции всегда линейный.
Часто это записывается как.
Обратная пропорция
Обратная пропорция — это пропорция, в которой по мере увеличения абсолютного значения одного числа, другого уменьшается прямо пропорционально. Это можно выразить как:
где — некоторое действительное число, не равное нулю.
График обратной пропорции всегда представляет собой гиперболу с асимптотами по осям x и y.
Экспоненциальная пропорция
Пропорция, в которой одно число равно константе, возведенной в степень другого, или логарифму другого, называется экспоненциальной пропорцией. Это можно выразить как:
или
для некоторого действительного числа, не равного нулю или единице.
Проблемы
Вводный
Предположим, что находится либо в следующей системе, либо в следующей:
Найдите возможные значения.