Теорема Виета. Теорема, обратная теореме Виета.
Краткосрочный план урока № 1
Школа: КГУ «Красносельская СШ»Дата:.19.12.2016
ФИО учителя: Даулбаева Дана Куанышкызы
Класс: 8
Количество присутствующих:
Количество отсутствующих:
Тема урока
Теорема Виета. Теорема, обратная теореме Виета
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
применять теорему Виета при решении квадратных уравнений
применять теорему, обратную теореме Виета
Цели урока
Все учащиеся научатся:
Применять теорему Виета для определения знаков корней уравнения, нахождения корней уравнения в несложных случаях; применять обратную теорему для составления квадратного уравнения
Большинство учащихся научится:
Применять теорему Виета для определения знаков корней уравнения, нахождения корней уравнения; применять обратную теорему для составления квадратного уравнения
Некоторые учащиеся научатся:
Доказывать теорему Виета; применять прямую и обратную теоремы Виета для решения более сложных задач
Критерии успеха
формулирует прямую и обратную теоремы Виета
применяет прямую теорему Виета для нахождения корней квадратного уравнения
применяет обратную теорему Виета для составления квадратного уравнения
Языковые цели
— квадратное уравнение;
— приведенное квадратное уравнение;
— теорема Виета
— обратная теорема Виета
Привитие ценностей
Открытость, сотрудничество, академическая честность
Воспитание глобальной гражданственности
понимание универсальности темы квадратные уравнения через сравнения заданий из различных международных источников.
Навыки использования ИКТ
1) использование программ MC Office.
2) использование ресурсов Internet
Аутентичность обучения
Достижимость целей обучения каждым учащимся через предоставляемые ресурсы
Межпредметные связи
английский язык, казахский язык
Предварительные знания
Приведенное квадратное уравнение, коэффициенты, дискриминант, формулы корней
Ход урока
Запланированные этапы урока
Запланированная деятельность на уроке
Ресурсы
1 урок
2 мин
12 мин
3 мин
5 мин
10 мин
4 мин
2 мин
Организационный момент
Приветствие учащихся
Сообщение темы урока, целей обучения, формулировка критериев успеха
Исследовательская работа в парах

Учащиеся делают выводы о связи корней приведенного квадратного уравнения и его коэффициентов
Изучение нового материала


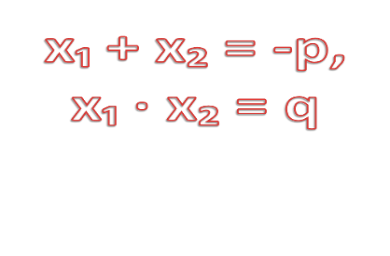
Актуализация изученного материала (устная работа)
Что называется квадратным уравнением?
Формула дискриминанта?
Как можно определить количество корней по дискриминанту?
Формула корней квадратного уравнения?
Какое уравнение называют приведенным?
Работа в парах
Мозговой штурм
Что такое обратная теорема?
Всякая ли теорема имеет обратную теорему?
А что же с теоремой Виета?
Кто может сформулировать теорему, обратную теореме Виета?
Изучение нового материала (продолжение)
Подведение итогов урока
Постановка дом. задания
1) Составьте квадратное уравнение, корнями которого являются числа:
а) -1 и 8; б) -0,5 и -3
2) Попытаться доказать (вывести) теорему Виета согласно приведенному плану:
План доказательства:
Записать формулы для нахождения x₁ и x₂;
Найти сумму корней: x₁+ x₂;
Найти произведение корней: x₁· x₂
Приложение 1
Приложение 2
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
Здоровье и соблюдение техники безопасности
Учащиеся в течение урока будут работать в парах, индивидуально. Более способным ученикам будет предоставлена возможность оказать помощь менее способным.
Проверка уровня усвоения материала будет проведена в форме фронтальной работы учащихся, а также через самооценивание, взаимооценивание.
В начале урока учащиеся ознакомлены с правилами поведения и техникой безопасности на уроке.
Рефлексия по уроку
Были ли цели урока/цели обучения реалистичными?
Все ли учащиеся достигли ЦО?
Если нет, то почему?
Правильно ли проведена дифференциация на уроке?
Выдержаны ли были временные этапы урока?
Какие отступления были от плана урока и почему?
Общая оценка
Какие два аспекта урока прошли хорошо (подумайте, как о преподавании, так и об обучении)?
1:
2:
Что могло бы способствовать улучшению урока (подумайте, как о преподавании, так и об обучении)?
1:
2:
Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
infourok.ru
[Билет 24] Квадратичная функция. Выделение полного квадрата. Вывод формулы корней квадратного уравнения, условия их существования и числа. Прямая и обратная теоремы Виета. Разложение квадратного трёхчлена на линейные множители.
Квадратичная функция.Функция, заданная формулой y = ax2 + bx + c , где x и y — переменные, а a, b, c — заданные числа, причем a не равно 0 ,
называется квадратичной функцией
Выделение полного квадрата.
Вывод формулы корней квадратного уравнения, условия их существования и числа.
– дискриминант квадратного уравнения.Прямая и обратная теоремы Виета.
3. Теорема ВиетаТеорема. Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.Доказательство. Рассмотрим приведённое квадратное уравнение. Обозначим второй коэффициент буквой p, а свободный член — буквой q.Пусть D>0 .Тогда это уравнение имеет два корня: и найдём сумму и произведение корней: |
3.1 Теорема, обратная теореме ВиетаТеорема. Если числа m и n таковы, что их сумма равна –p, а произведение равно q, то эти числа являются корнями уравненияДоказательство. По условию m+n=-p,а mn=q. Значит, уравнениеможно записать в виде: Подставив вместо x число m, получим: Значит, число m является корнем уравнения. Аналогично можно показать, что число n так же является корнем уравнения: |
Разложение квадратного трёхчлена на линейные множители.
Теорема. Пусть
x1 и x2 — корни квадратного трехчлена x2 + px + q. Тогда этот трехчлен раскладывается на линейные множители следующим образом: x2 + px + q = (x — x1) (x — x2).Доказательство. Подставим вместо
p и q их выражения через x1 и x2 и воспользуемся способом группировки:x2 + px + q = x2 — (x1 + x2) x + x1 x2 = x2 — x1 x — x2 x + x1 x2 = x (x — x1) — x2 (x — x1) = = ( x — x1) (x — x2). Теорема доказана.
Квадратное уравнение. График квадратного трехчлена
• Уравнение вида
называется квадратным уравнением. Число D = b2 — 4ac — дискриминант
этого уравнения.
Если
то числа
являются корнями (или решениями) квадратного уравнения. Если D = 0, то корни совпадают:
Если D < 0, то квадратное уравнение корней не имеет.
Справедливы формулы:
— формулы Виета; а
ах2 + bх + с = а(х — х1)(х — х2) —
формула разложения на множители.
Графиком квадратичной функции (квадратного трехчлена) у = ах2 + bх + с является парабола. Расположение параболы в зависимости от знаков коэффициента а и дискриминанта D приведено на рис.
Числа х1 и х2 на оси абсцисс — корни квадратного уравнения ах2 + bх + + с = 0; координаты вершины параболы (точки А) во всех случаях
точка пересечения параболы с осью ординат имеет координаты (0; с).
Подобно прямой и окружности парабола разбивает плоскость на две части. В одной из этих частей координаты всех точек удовлетворяют неравенству у > ах2 + bх + с, а в другой — противоположному. Знак неравенства в выбранной части плоскости определяем, найдя его в какой-либо точке этой части плоскости.
Рассмотрим понятие касательной к параболе (или окружности). Прямую у — kx + 1 назовем касательной к параболе (или окружности), если она имеет с этой кривой одну общую точку.
В точке касания М(х; у) для параболы выполняется равенство kx +1 = ах2 + bх + с (для окружности — равенство (х — х0)2 + (kx + 1 — у0)2 — R2). Приравнивая дискриминант полученного квадратного уравнения нулю (так как уравнение должно иметь единственное решение), приходим к условиям для вычисления коэффициентов касательной.
fizmatinf.blogspot.com
Урок 2. Теорема Виета
Урок математики №2 в 8 классе

Учитель МБОУ СОШ № 30
Маргиева Е.Ф.
Владикавказ
УРОК 2.
Цели урока:
Образовательная:
вывести теорему, обратную теореме Виета;
выработать у учащихся навыки решения задач, используя теорему Виета и обратную теореме Виета;
развить умение решать квадратные уравнения;
Развивающая:
развитие внимания, мышления, наблюдательности, активности;
развитие устной и письменной речи;
развитие умений применять полученные знания на практике;
Воспитательная:
воспитание самостоятельности, эстетичности;
воспитание интереса к предмету математики.
Метод урока: объяснительно-иллюстративный.
Тип урока: урок изучения и усвоения нового материала.
Оборудование: компьютер, мультимедийный проектор, раздаточный материал
Ход урока.
Ι. Организационный момент.
ΙΙ. Актуализация опорных знаний учащихся.
1. Выборочно проверить несколько тетрадей с домашним заданием у учащихся.
2. Устная работа.
1) Сформулируйте теорему Виета. Чему равны сумма и произведение корней квадратного уравнения 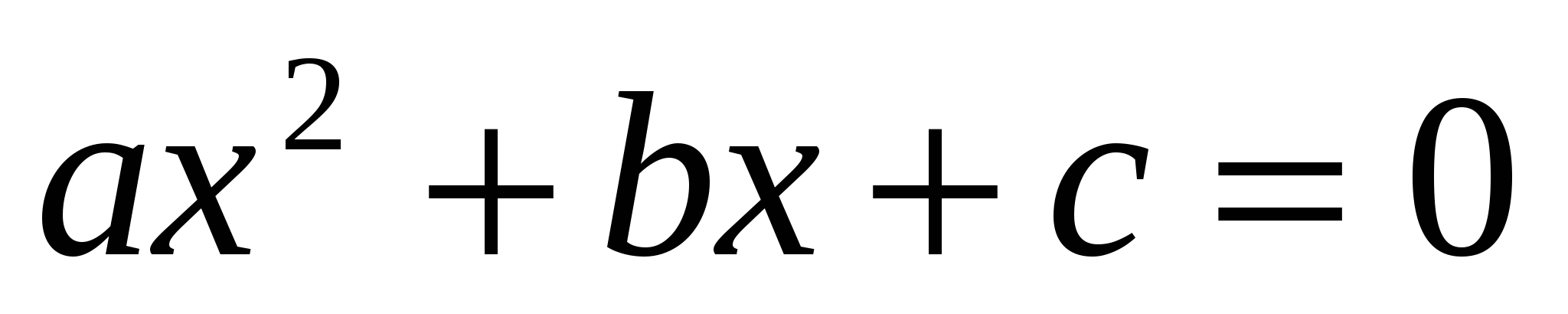 ?
?
2) Укажите сумму и произведение корней квадратного уравнения: а) 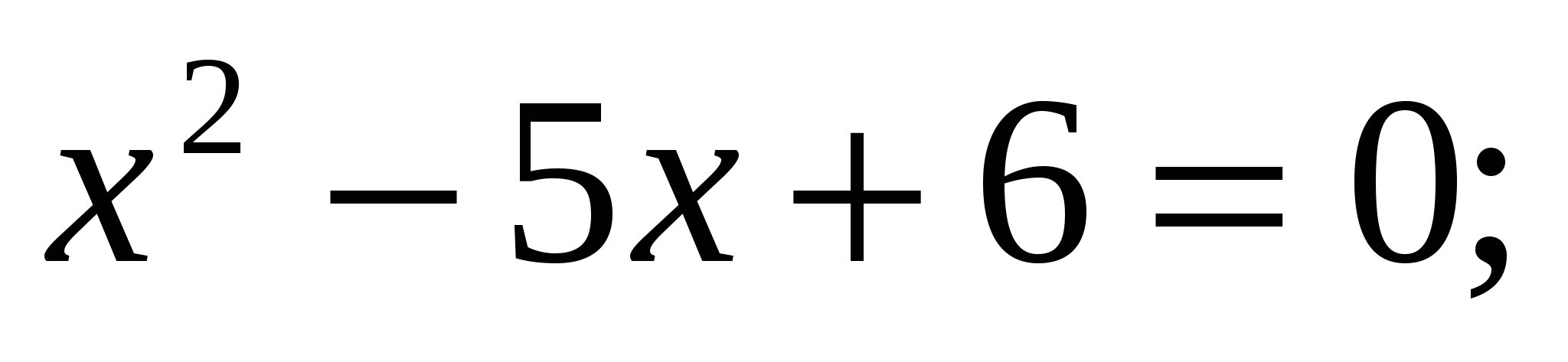 б)
б) 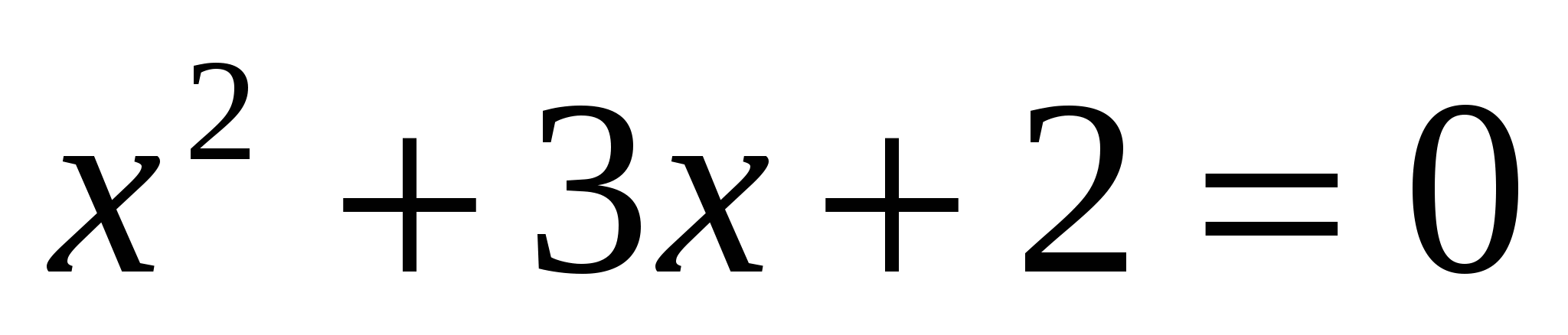 ; в)
; в) 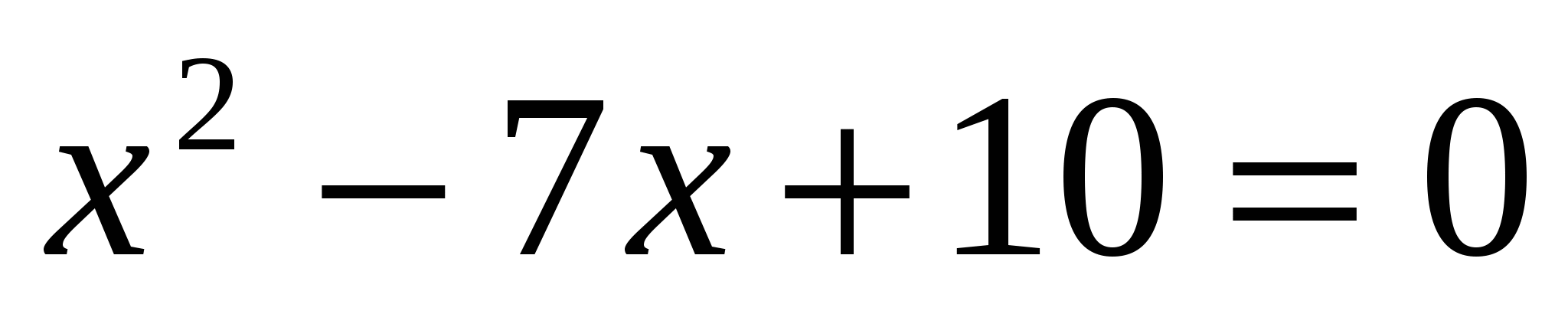 .
.
Ответ: а)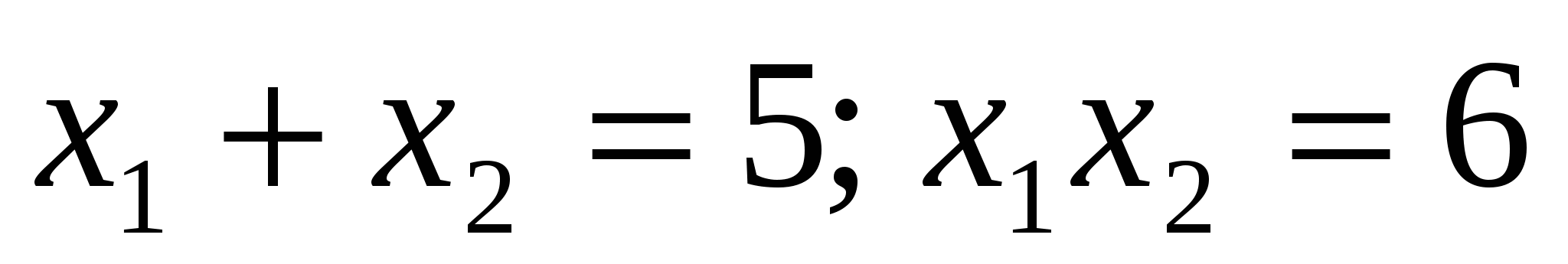 ; б)
; б) 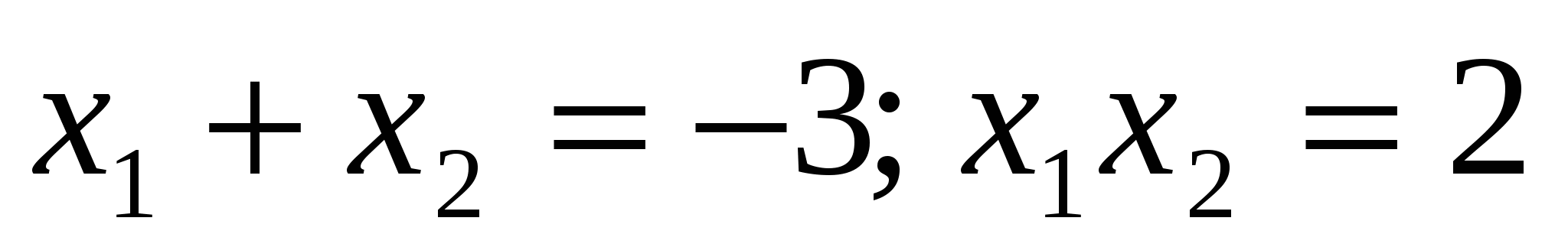 ; в)
; в) 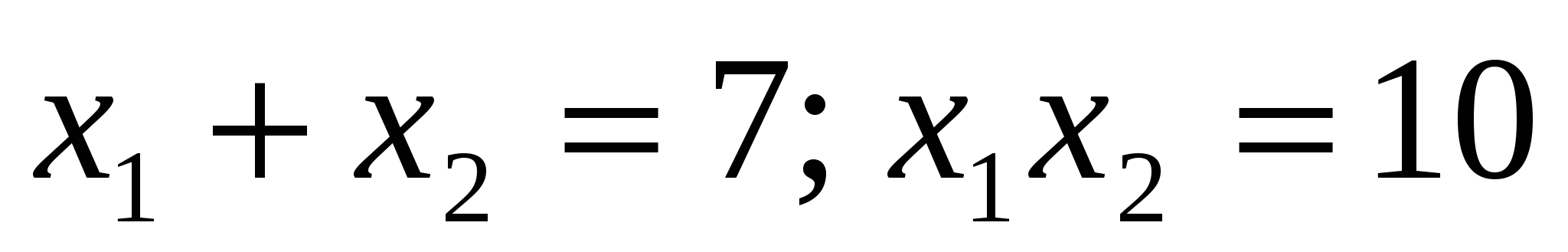
3) Составьте квадратное уравнение, зная его корни:
А) 3 и 5; б) 3 и –5; в) –3 и 5; г) –3 и –5.
ΙΙΙ. Новый материал.
ТЕОРЕМА, обратная теореме Виета. Если два числа m и n такого, что их сумма равна –b, произведение равно с, то эти числа являются корнями квадратного уравнения 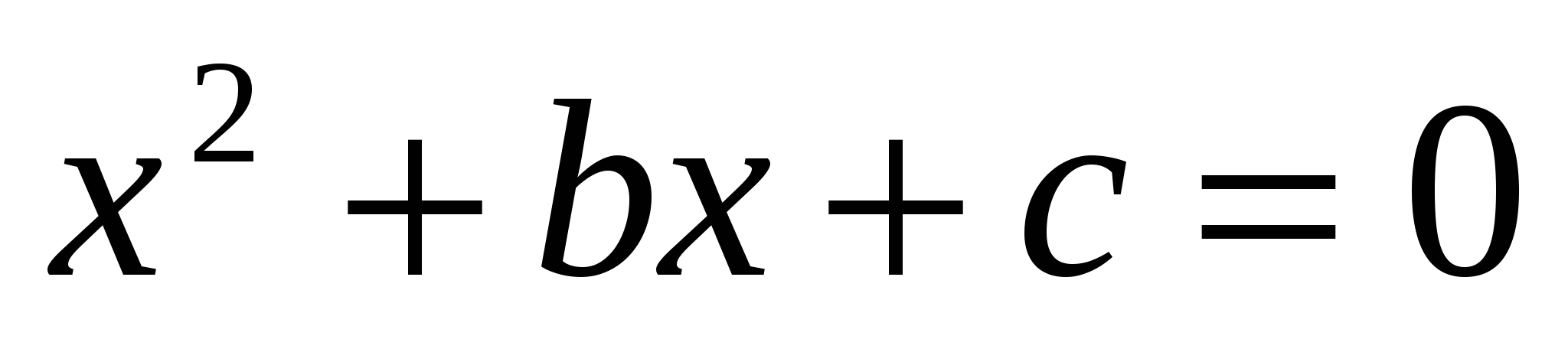 .
.
Оставить место для доказательства, которое учащиеся разбирают сами по учебнику дома.(стр.122)
Теорема, обратная теореме Виета позволяет решать приведенные квадратные уравнения, не используя формулы – методом подбора.
ΙV. Закрепление.
№ 576.
а) (Учитель решает у доски с подробным объяснением.)
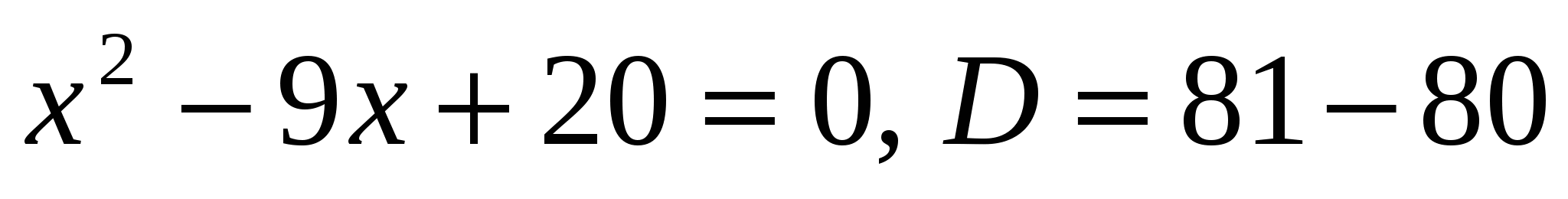 >
> 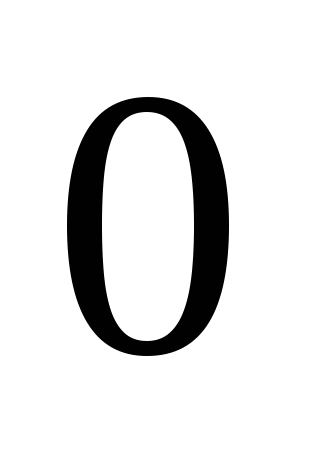
 по теореме Виета
по теореме Виета 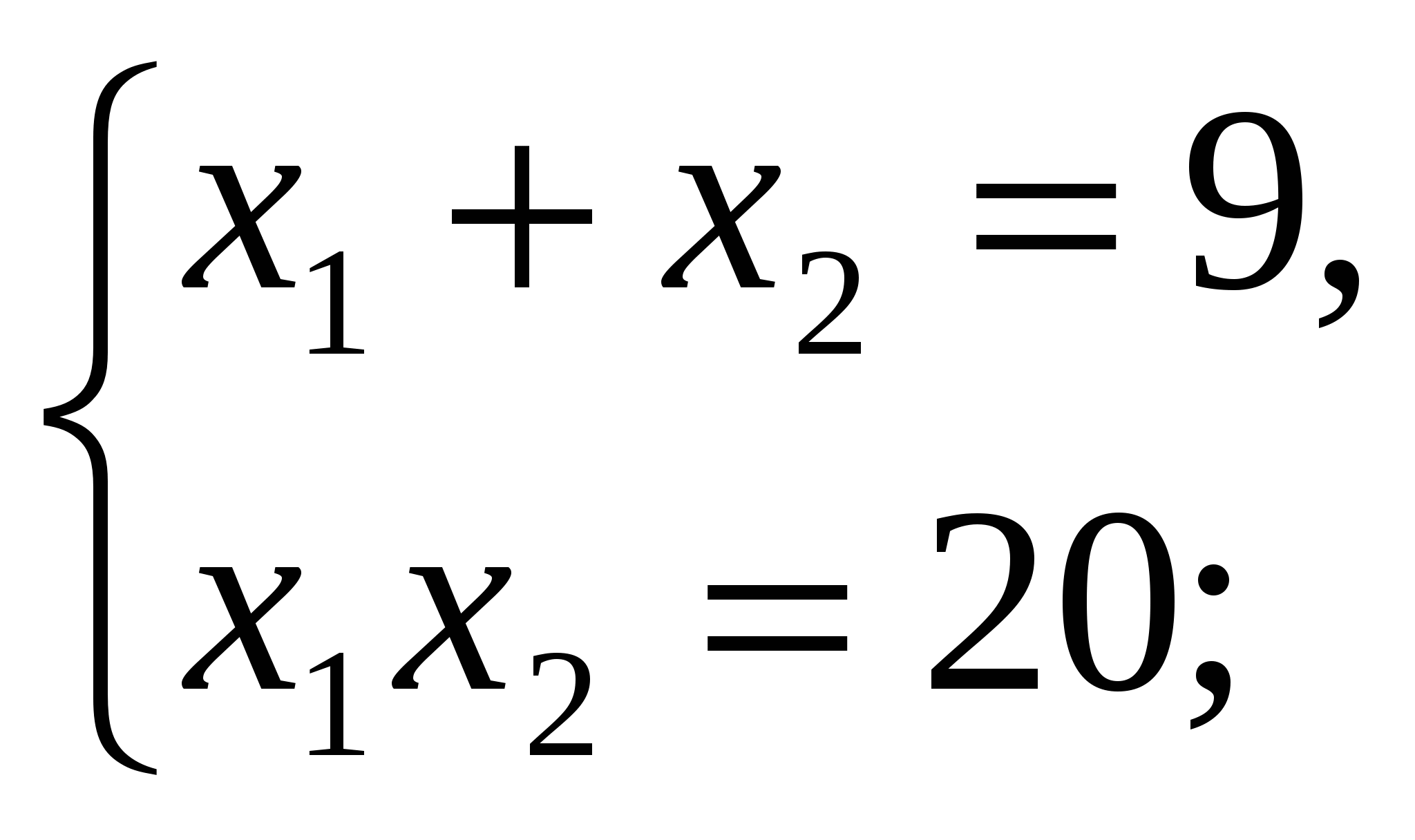
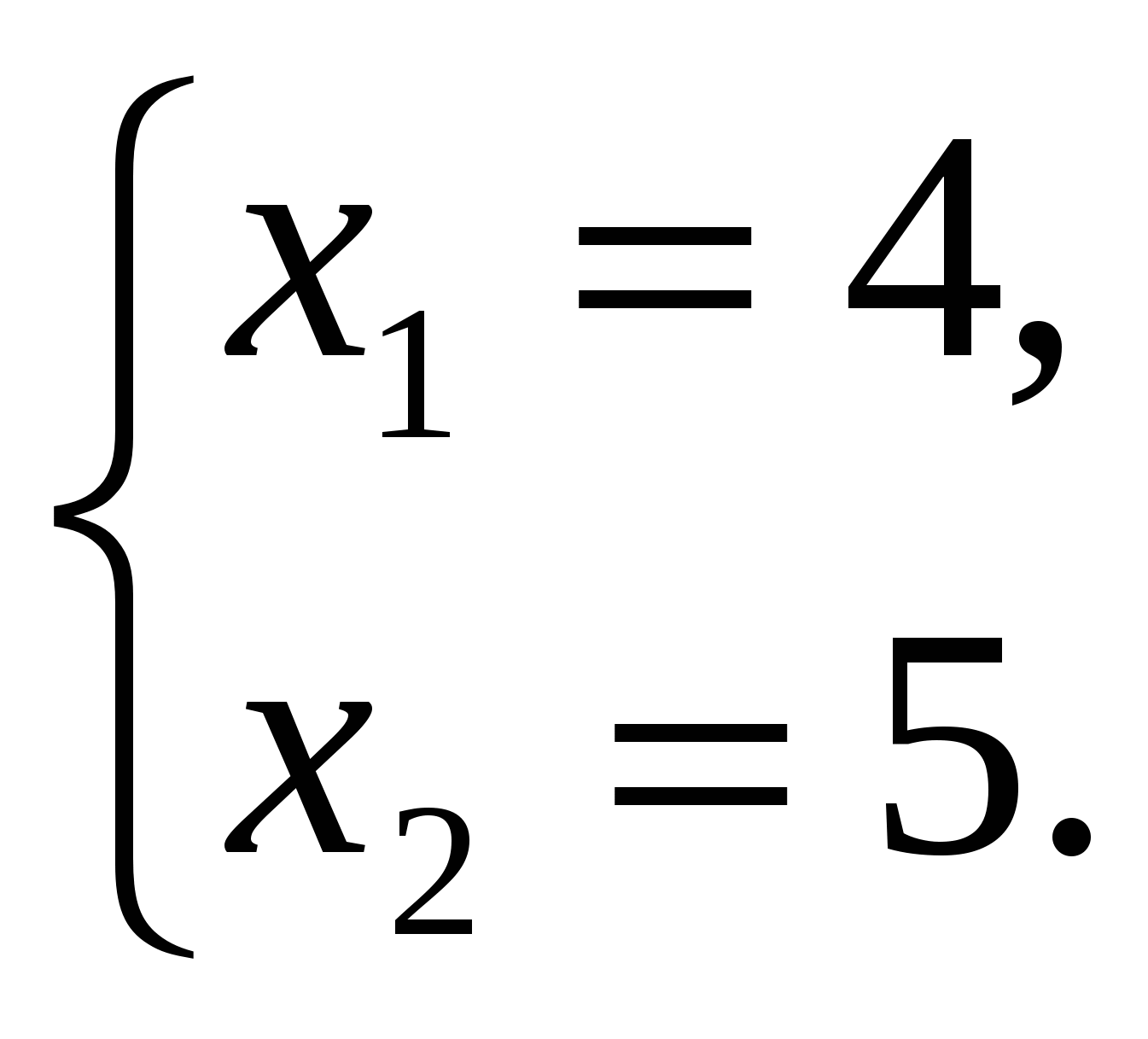
Проверка (устно): 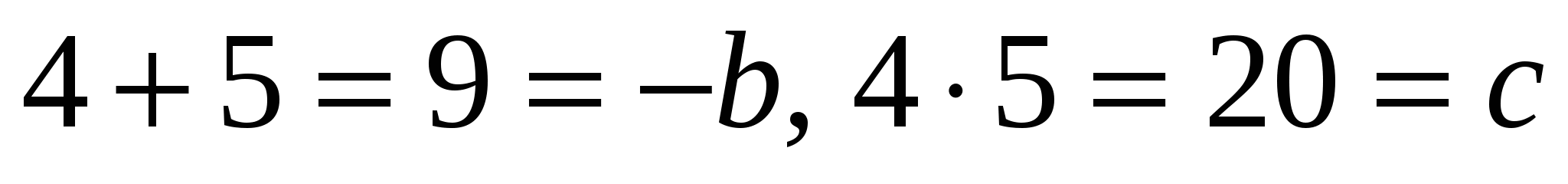 .
.
с >0, значит корни одного знака;
–b<0 – они положительны.
Следовательно, 4 и 5 – корни уравнения по теореме, обратной теореме Виета.
б) (Решает ученик с помощью учителя у доски).
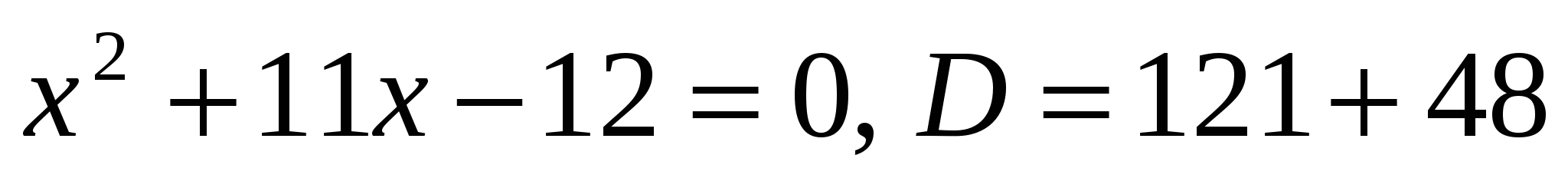 >
>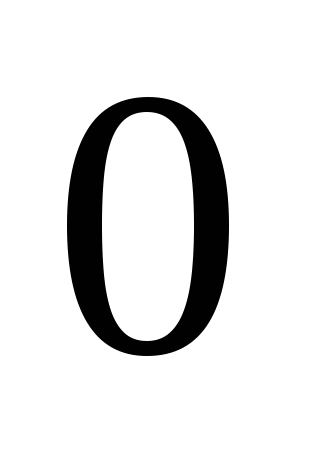
 по теореме Виета
по теореме Виета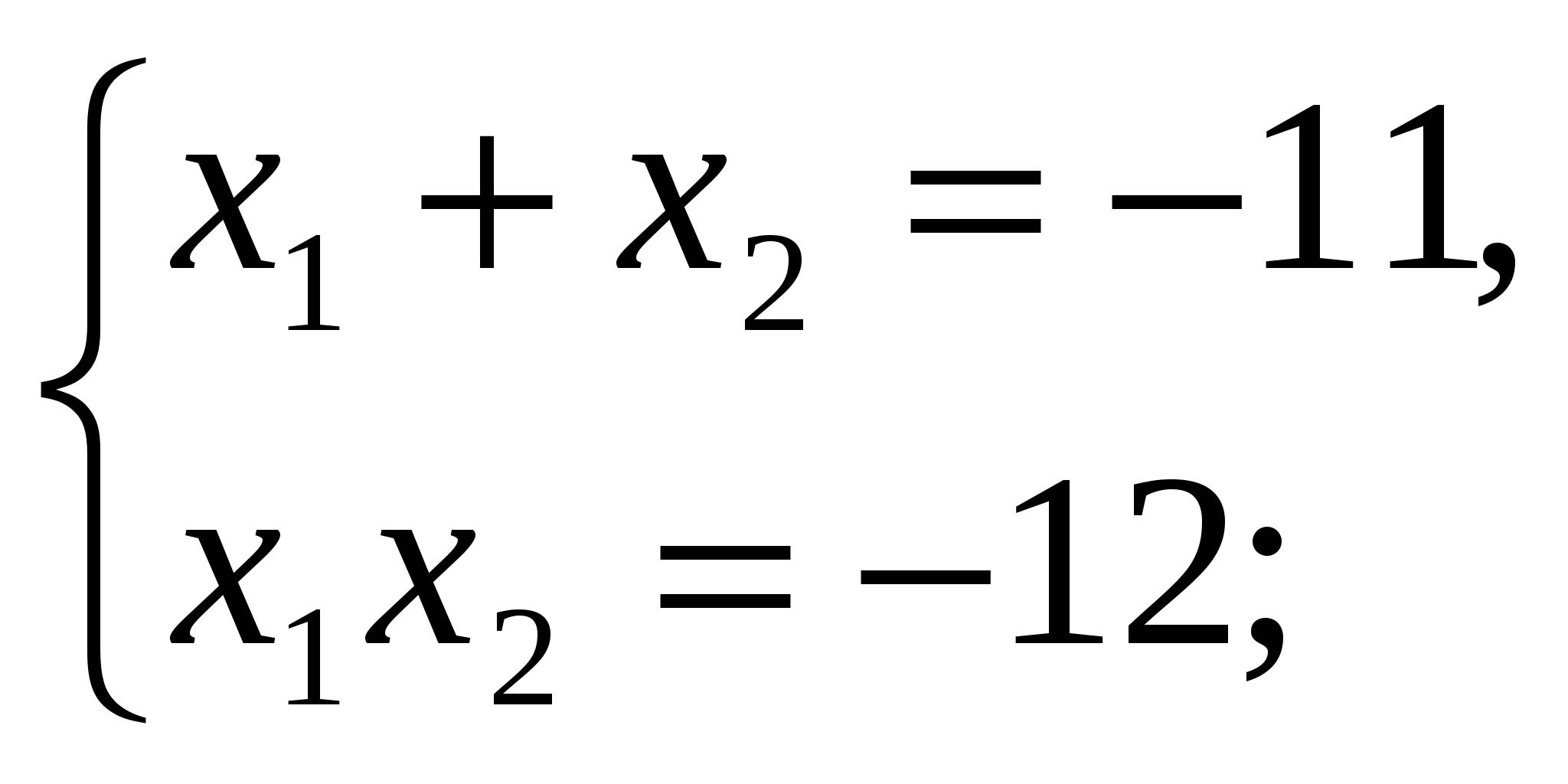
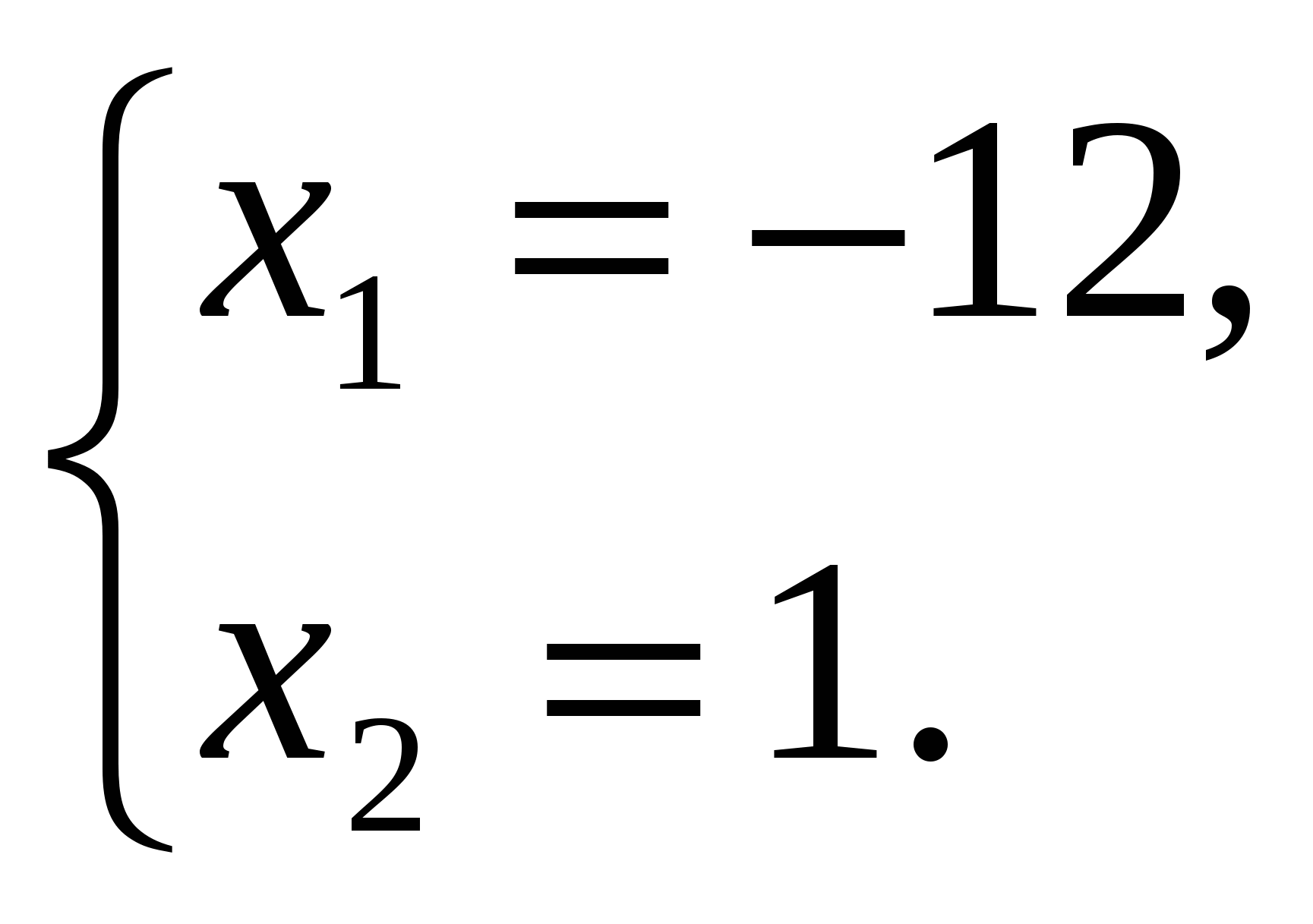
Проверка (устно): 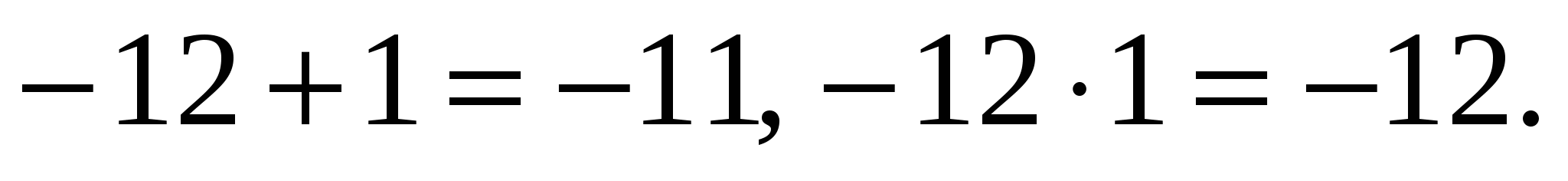 .
.
с<0, значит корни имеют разные знаки,
–b>0, значит минус у того числа, у которого модуль больше.
Следовательно, 1 и –12 – корни уравнения по теореме, обратной теореме Виета.
в) (Решает ученик у доски, объясняя, класс помогает.)
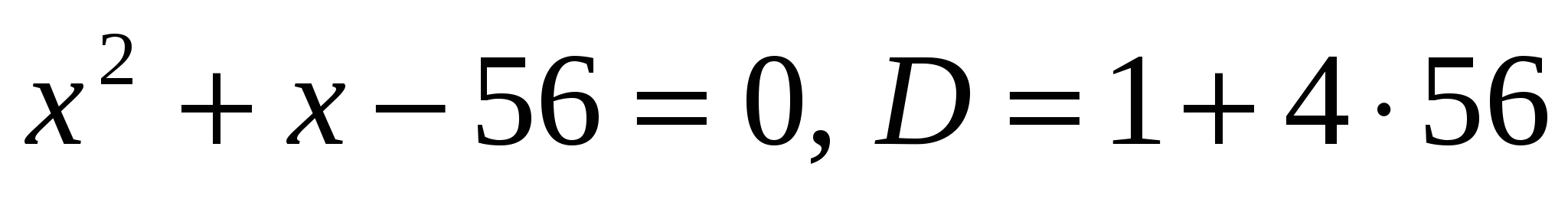 >
>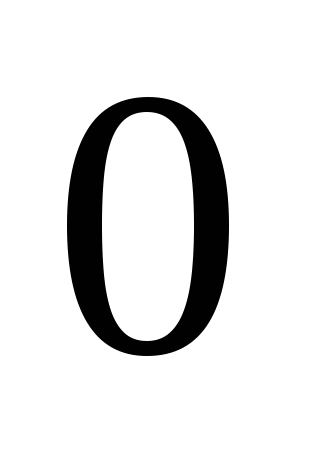
 по теореме Виета
по теореме Виета 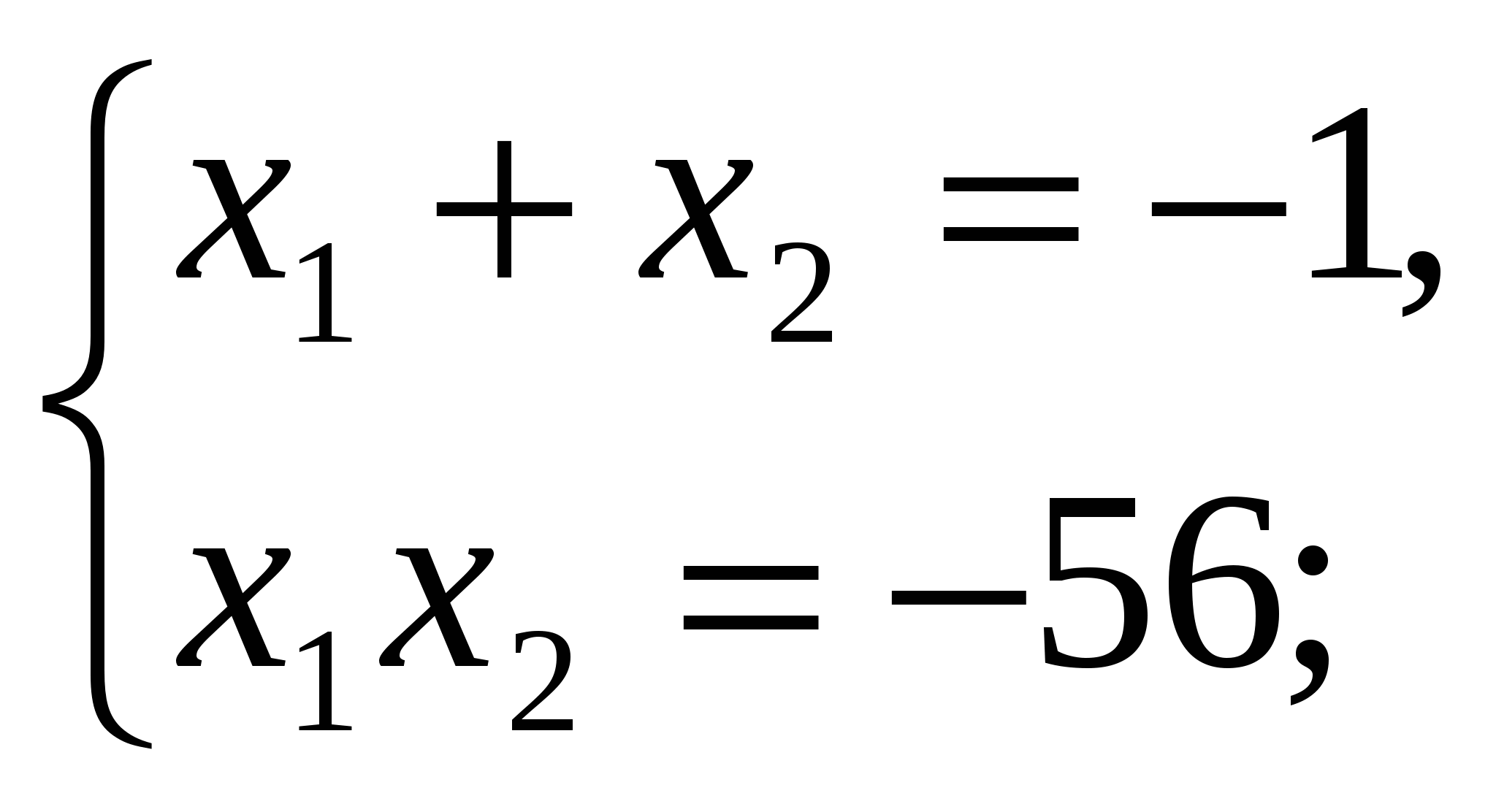
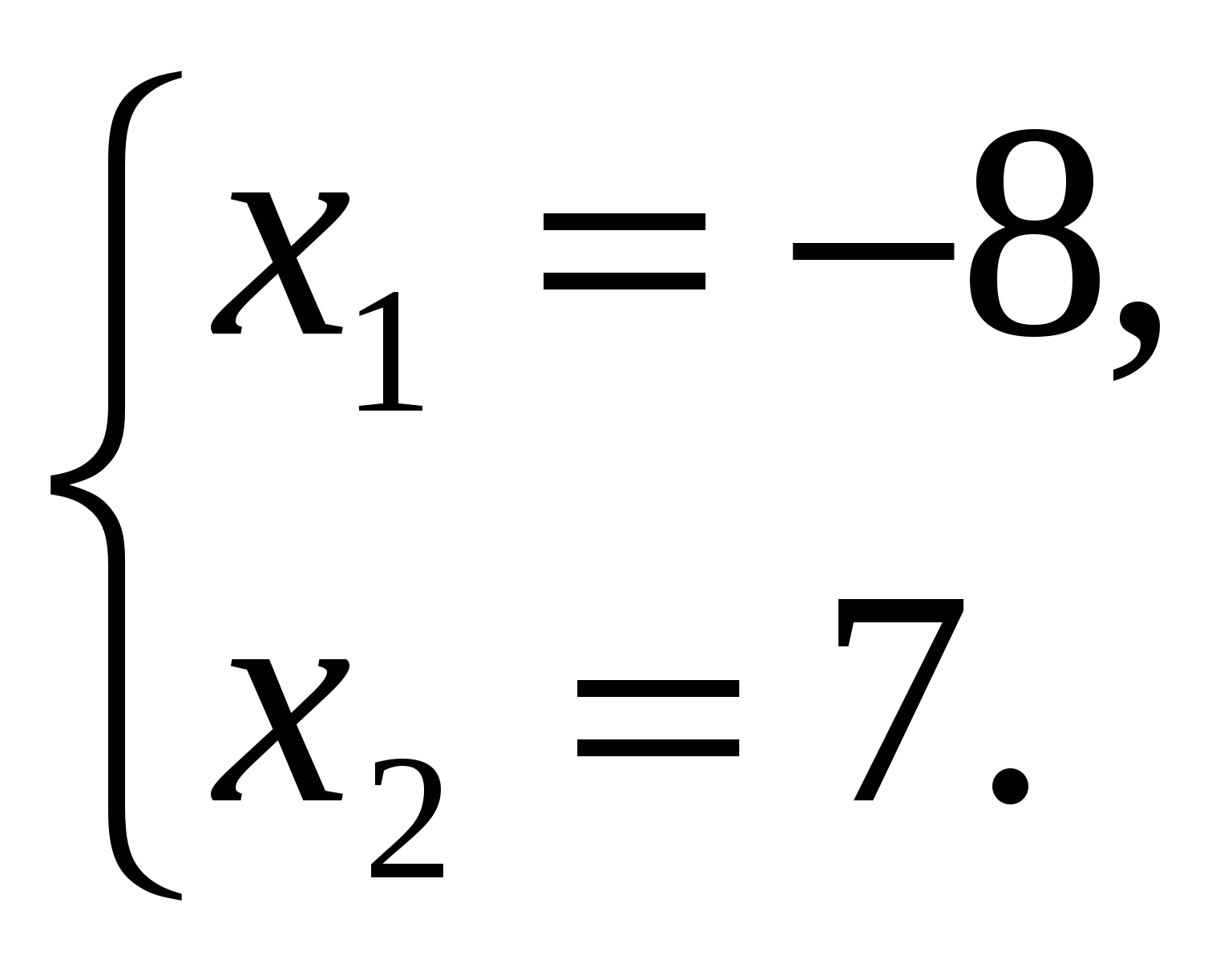
Проверка (устно): 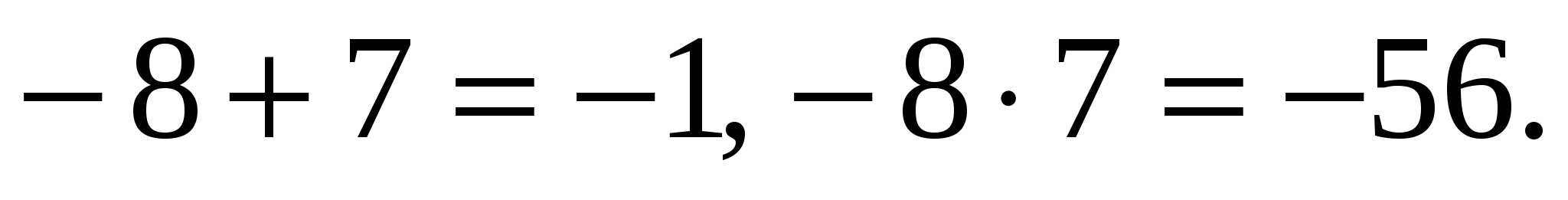 .
.
с<0, значит корни разных знаков,
–b>0, значит минус у того числа, у которого модуль больше.
Следовательно, –8 и 7 – корни уравнения по теореме, обратной теореме Виета.
г) (Ученик решает у доски молча, класс самостоятельно.)
 >
>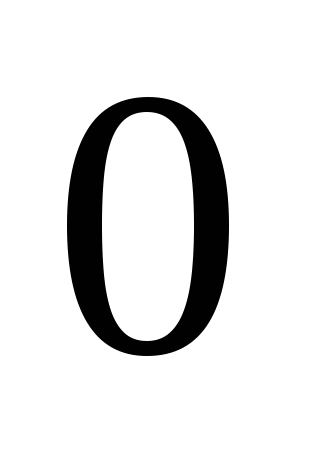
 по теореме Виета
по теореме Виета 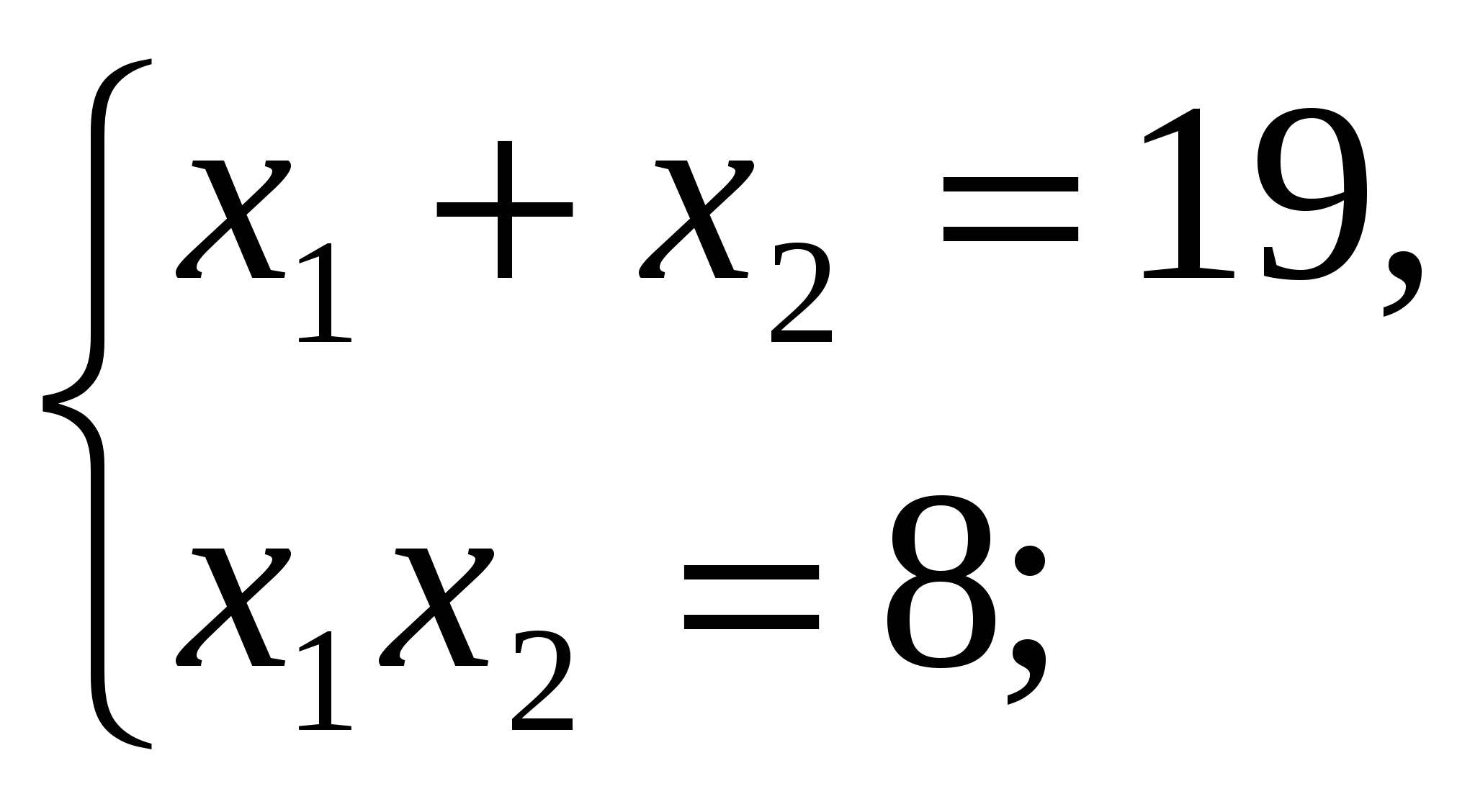
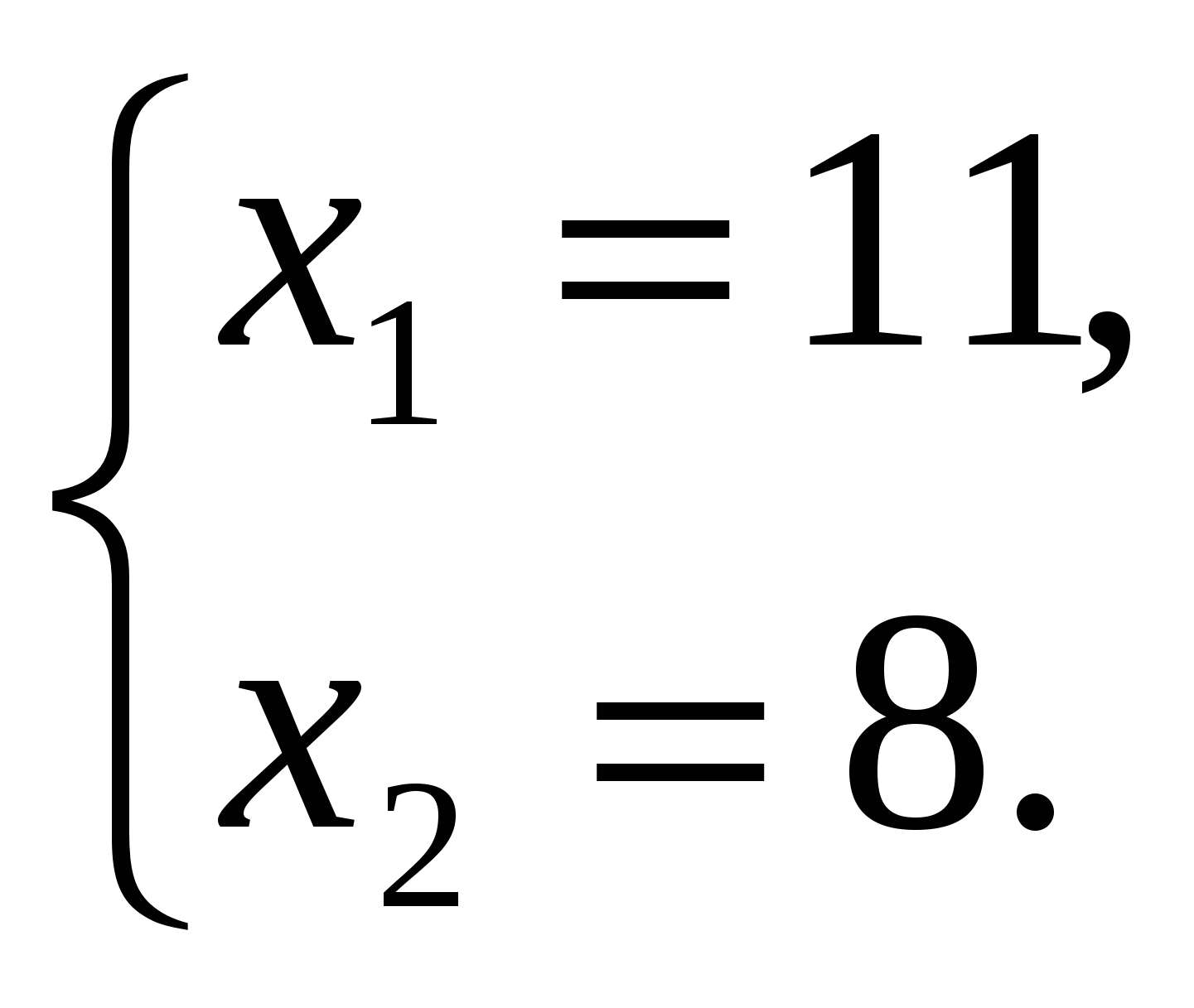
Проверка (устно): 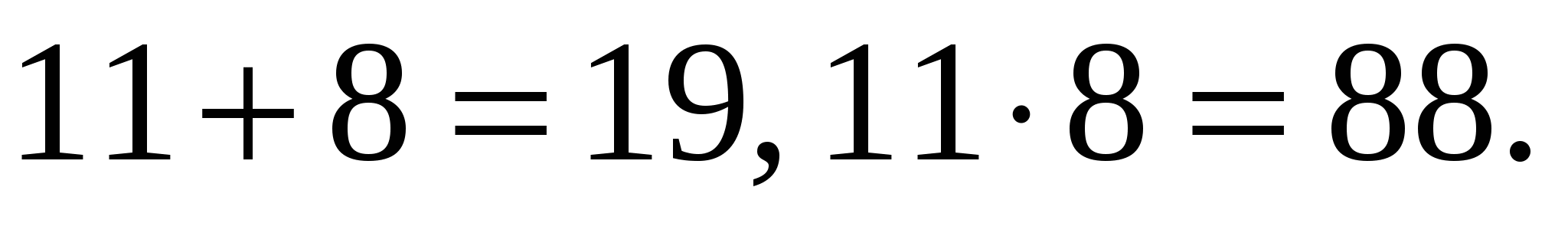 .
.
с>0, значит корни имеют один знак;
–b>0, значит корни положительны.
Следовательно, 11 и 8 – корни уравнения по теореме, обратной теореме Виета.
№ 578. 
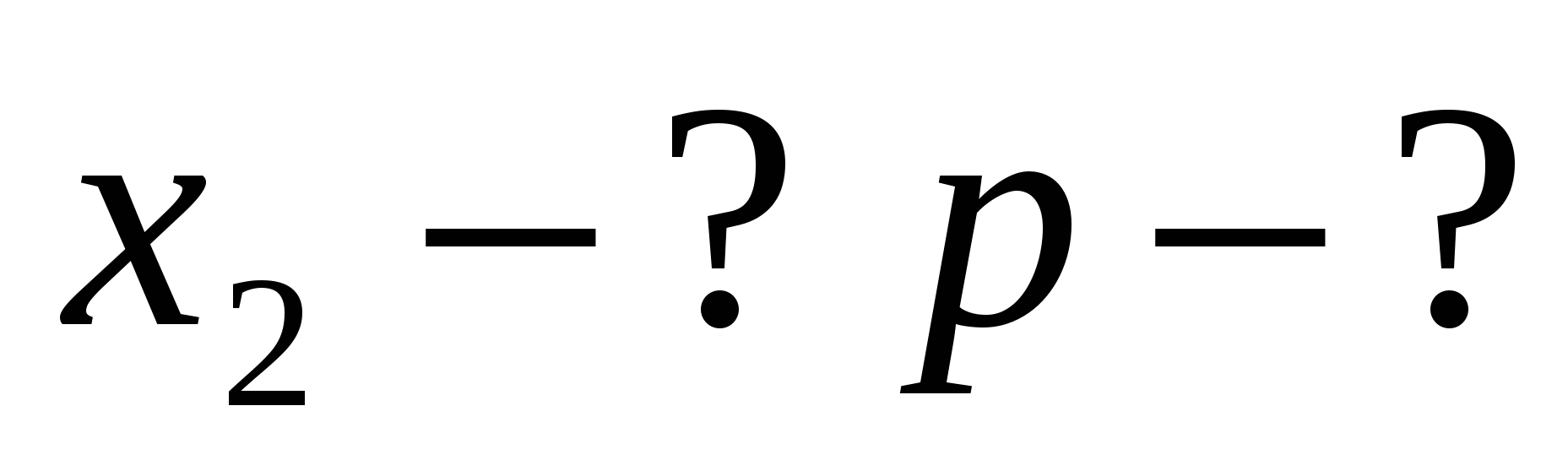
Два корня 
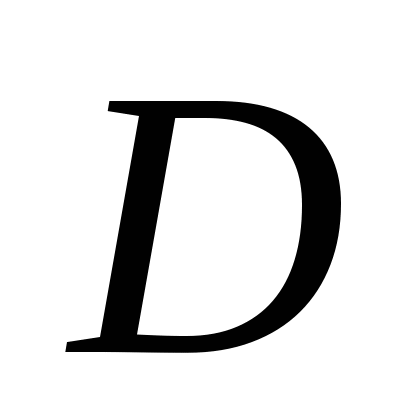 >
>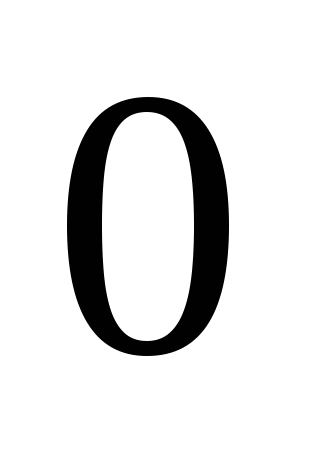
 по теореме Виета
по теореме Виета

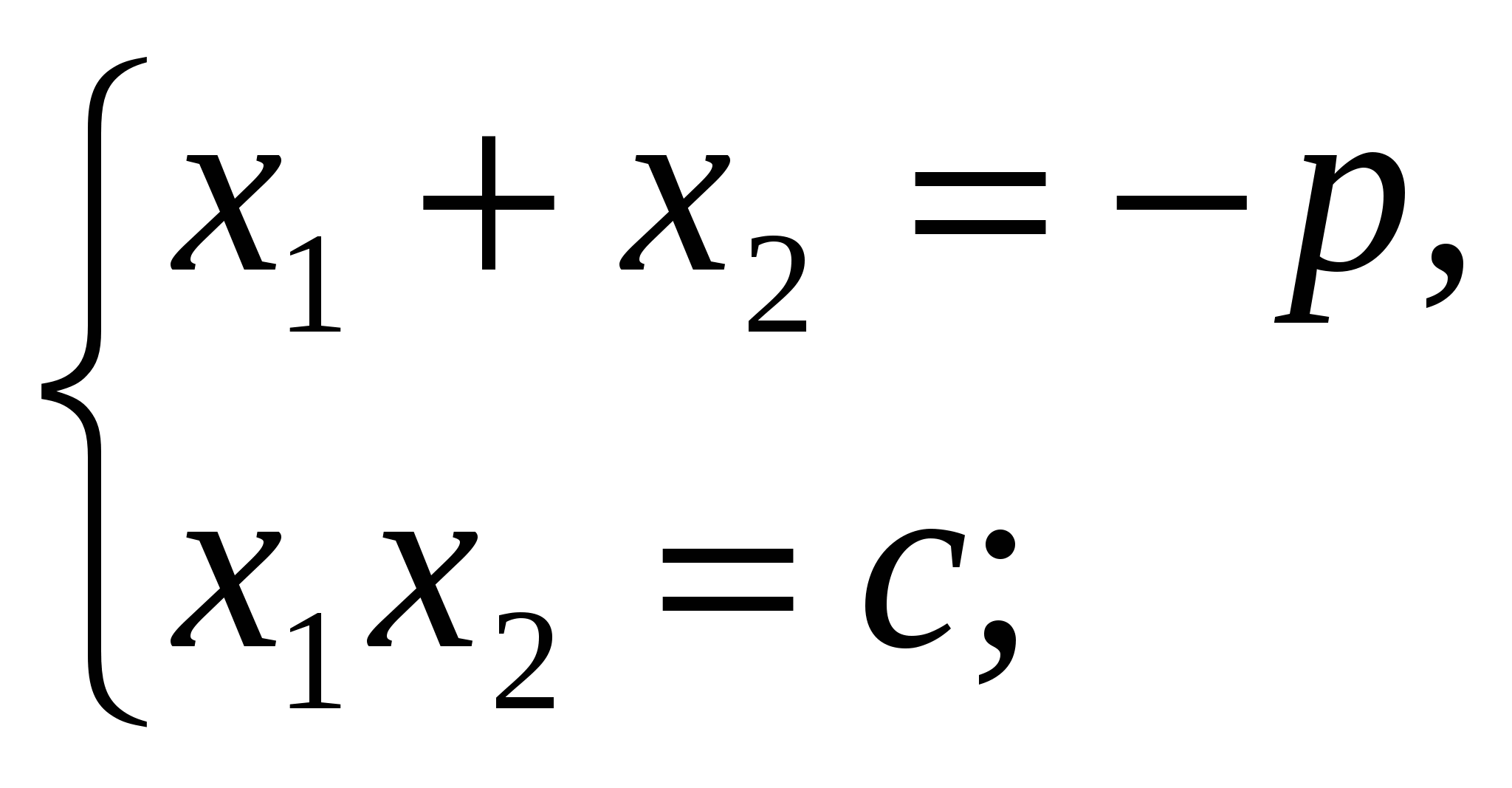

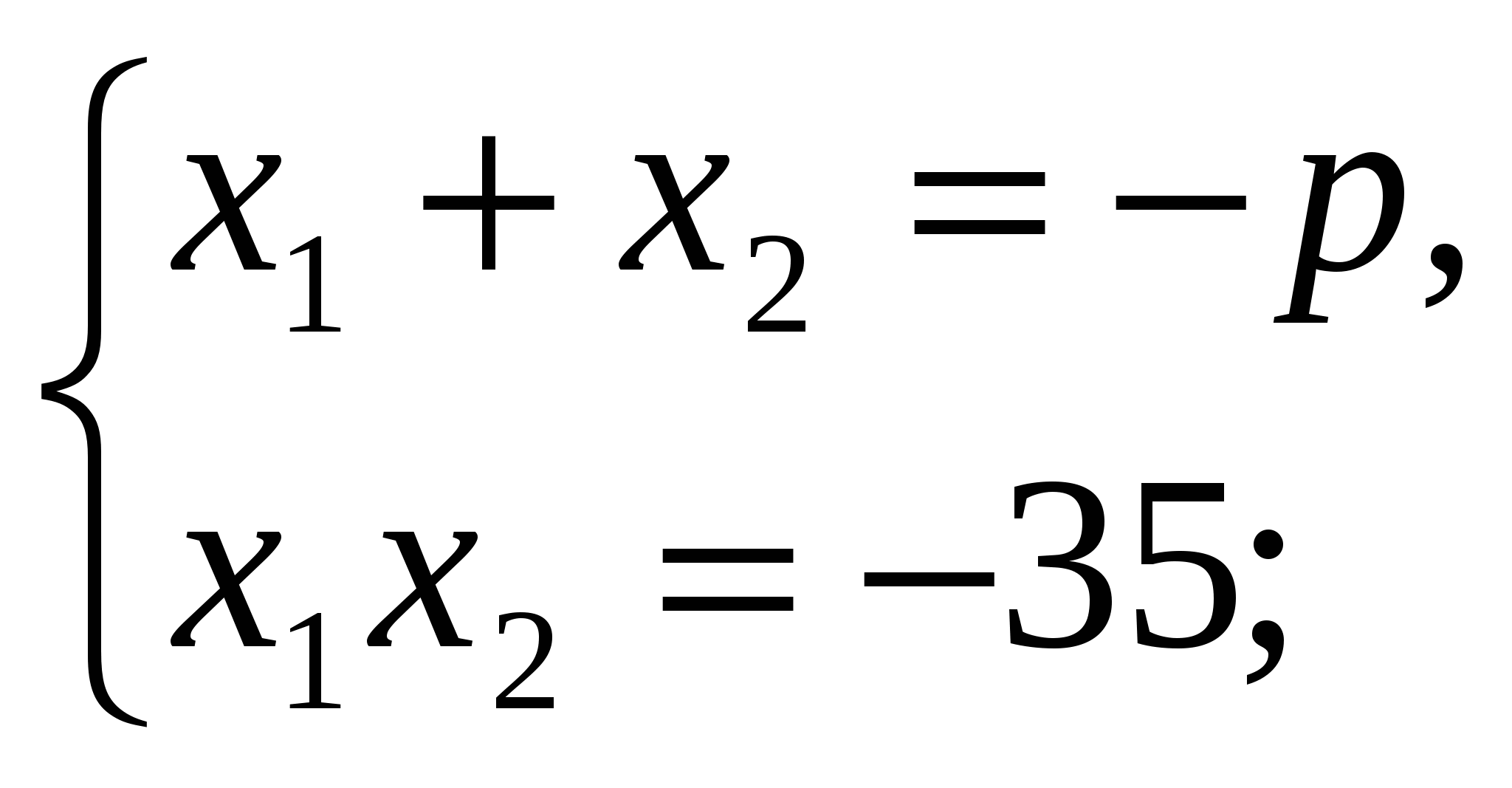

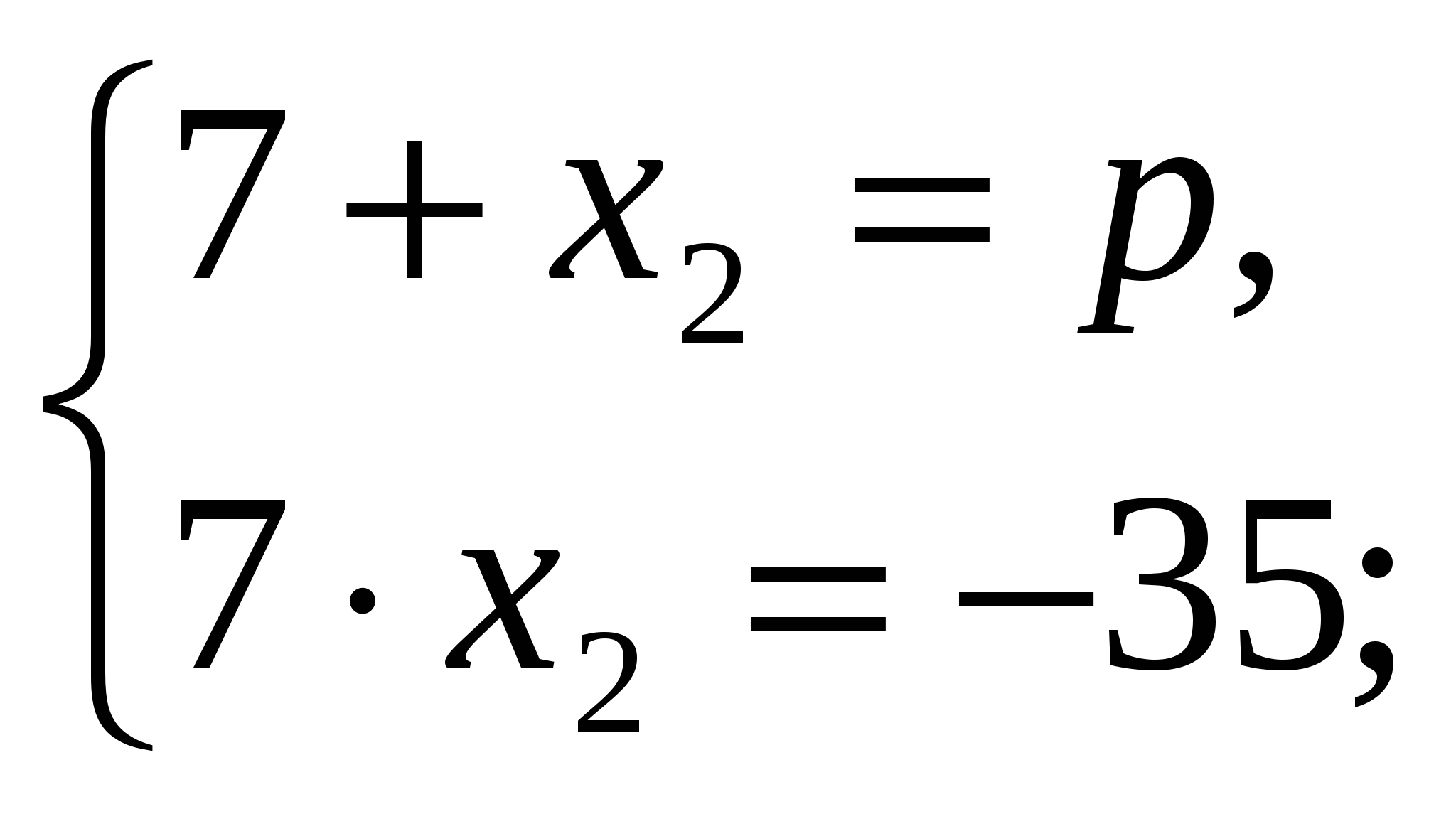

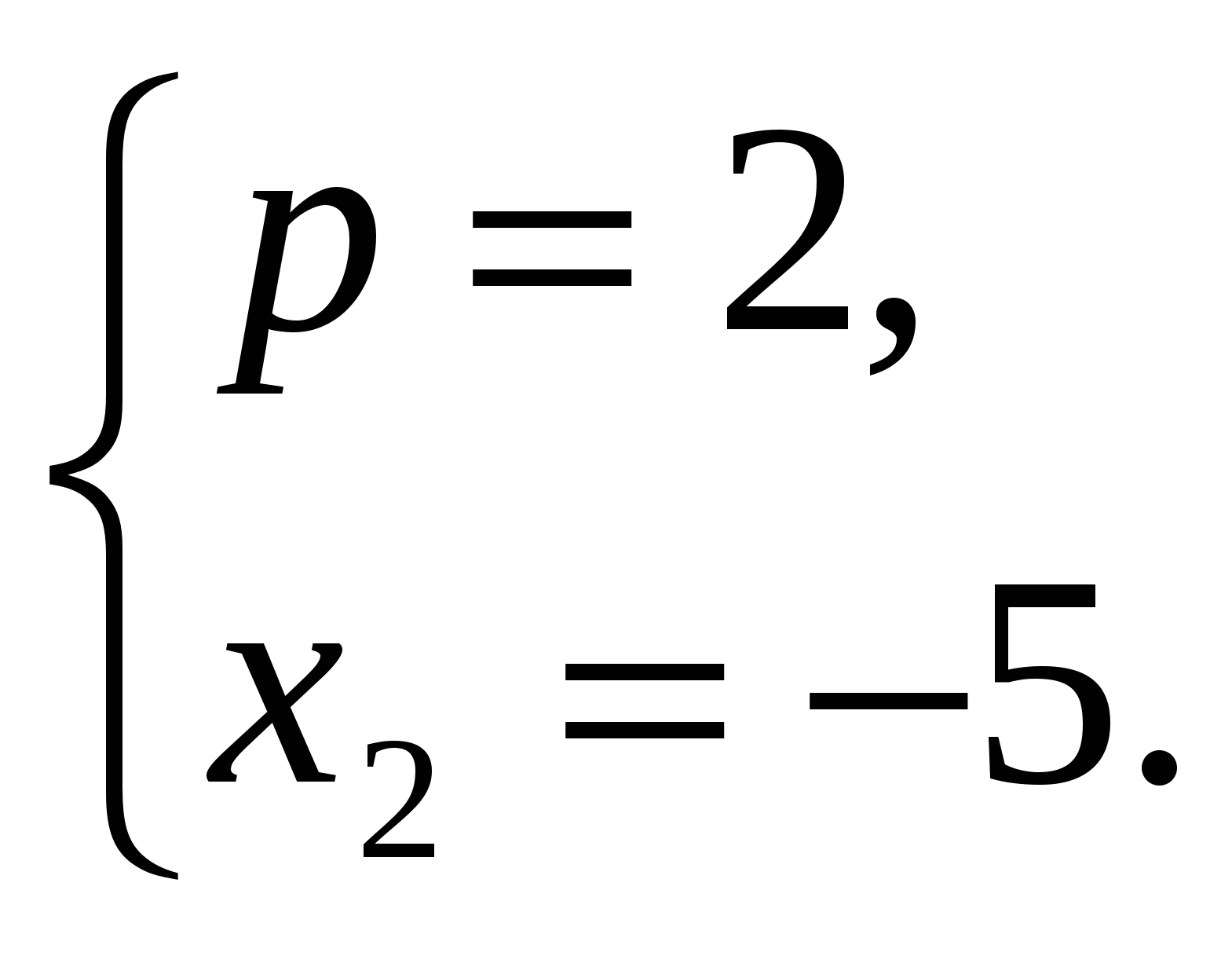
Ответ: 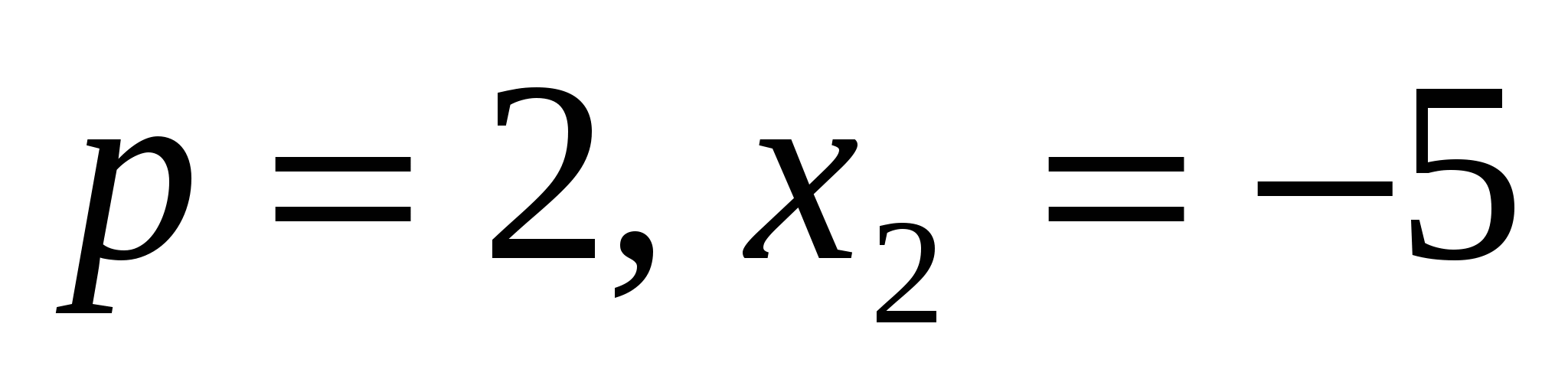 .
.
№ 581. 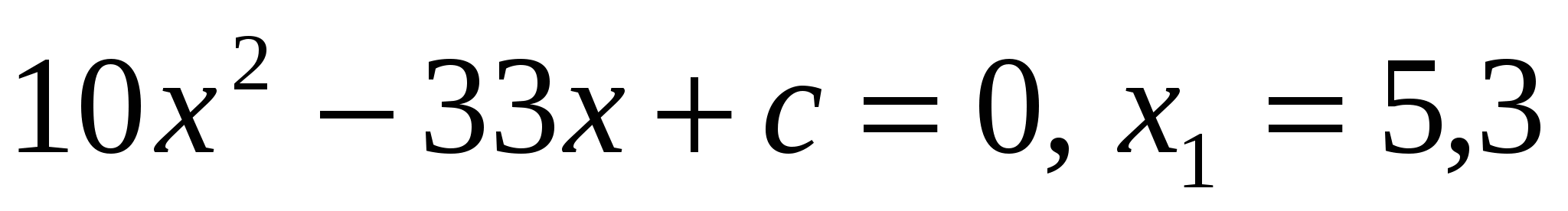
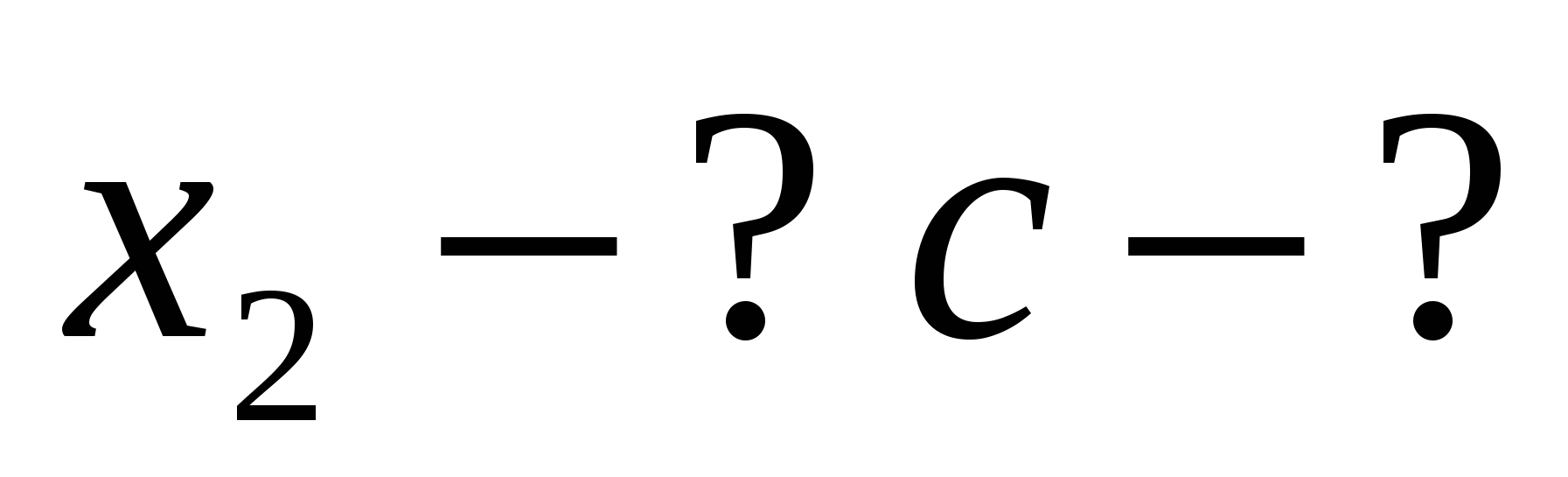
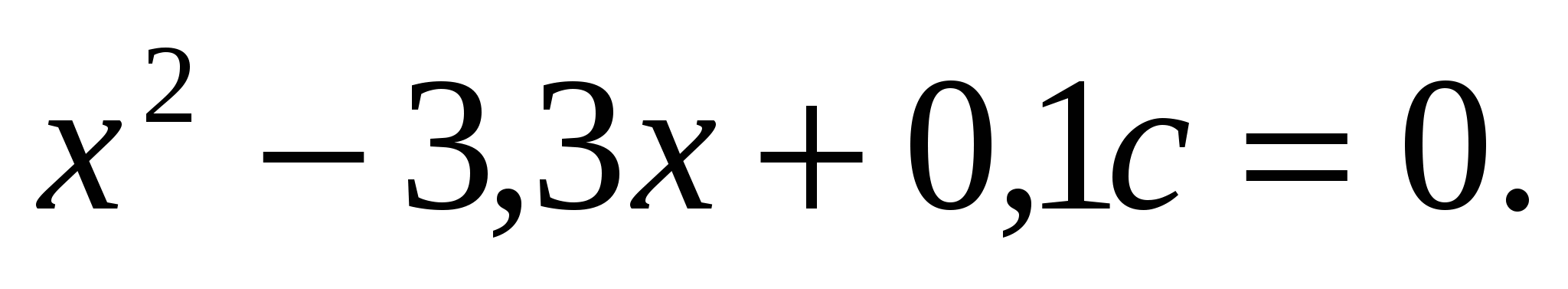
Уравнение имеет два решения 
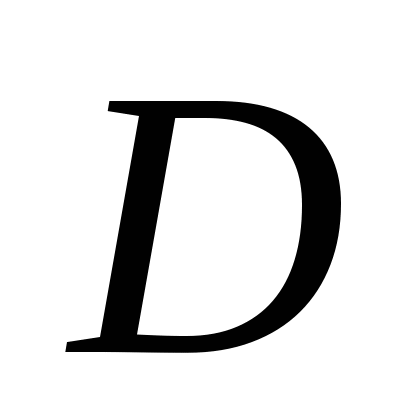 >
>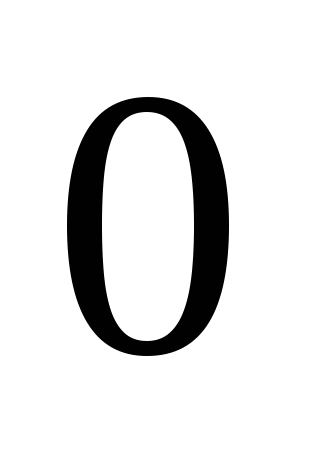
 по теореме Виета
по теореме Виета

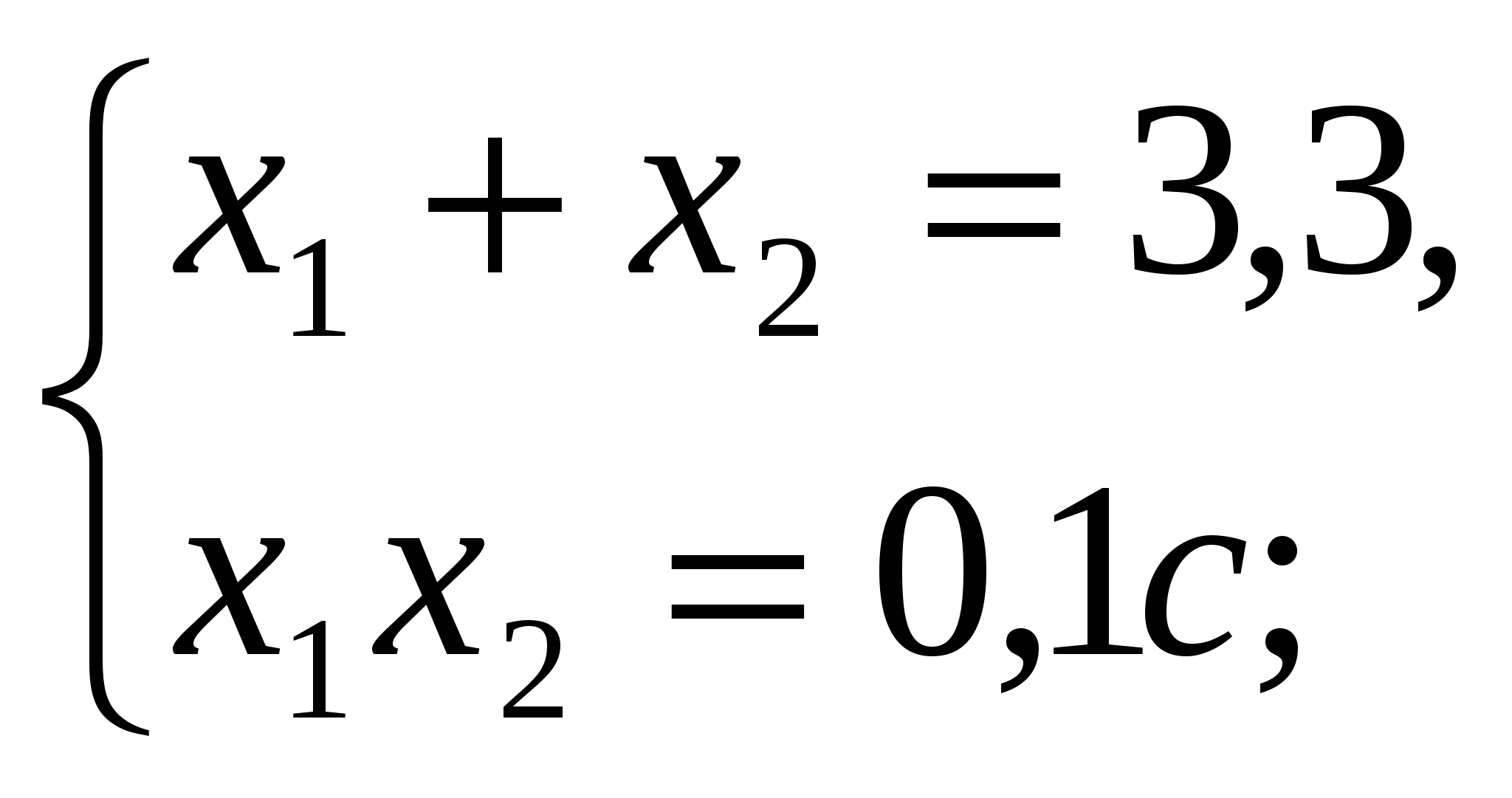

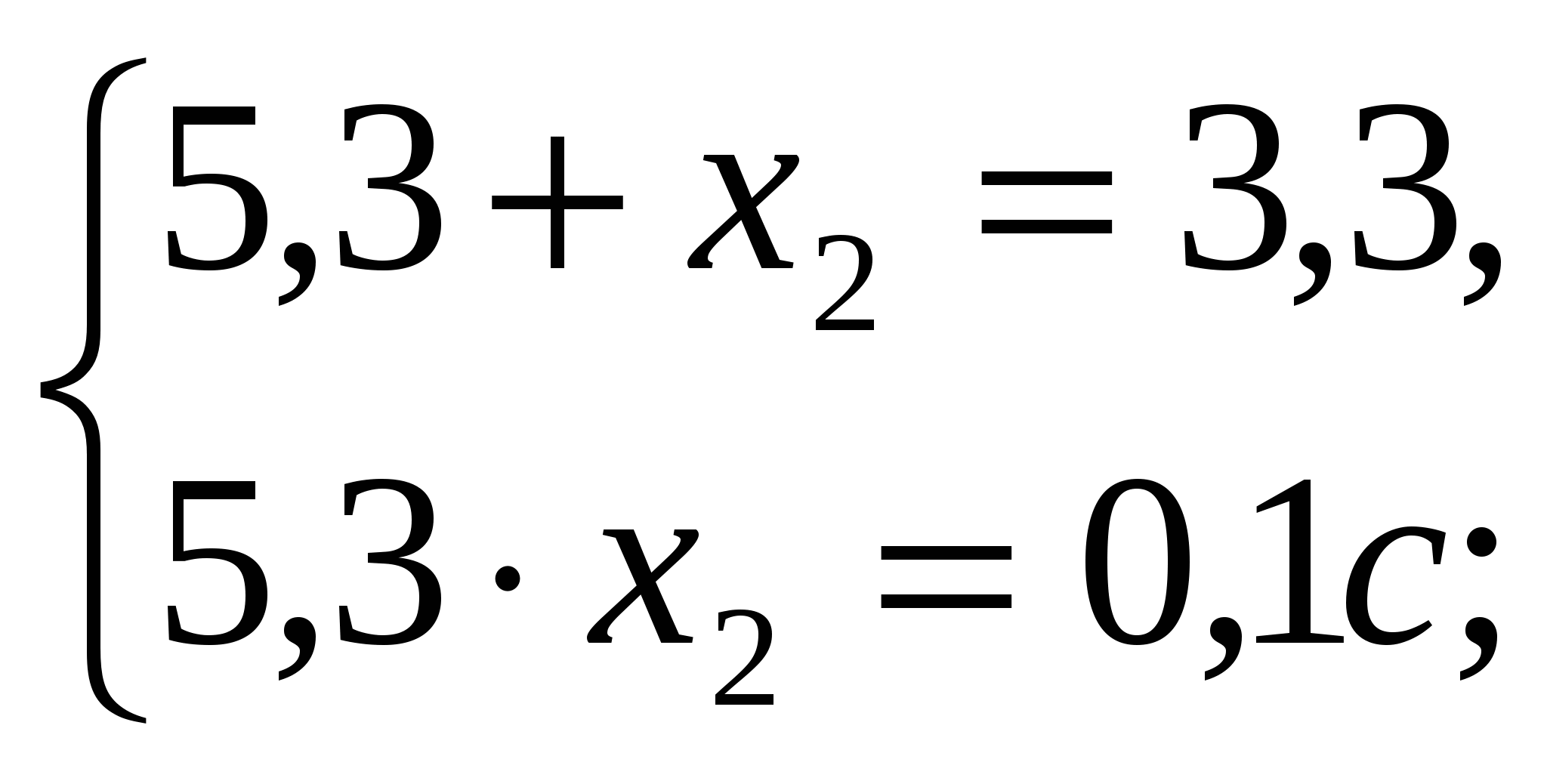

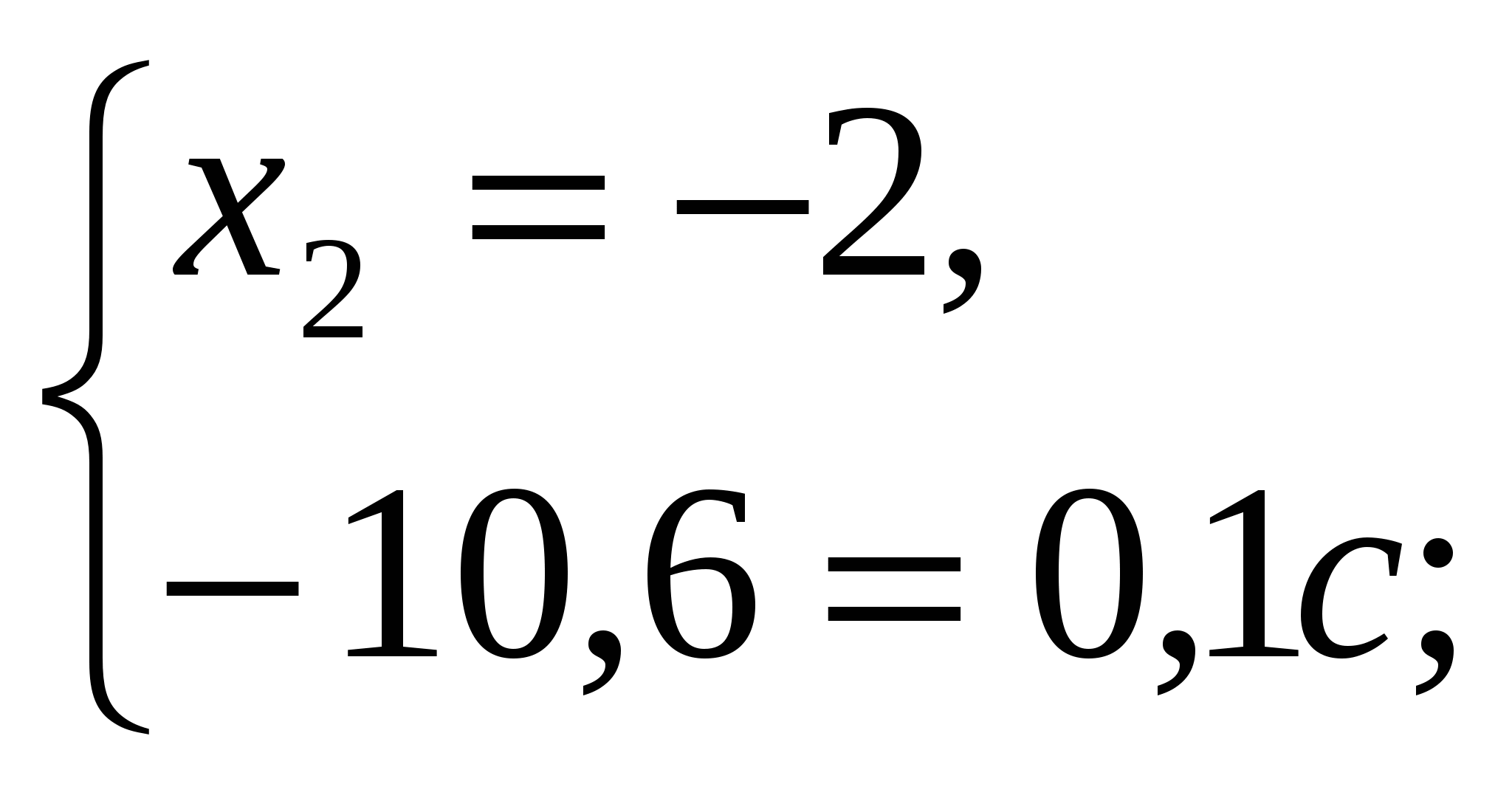

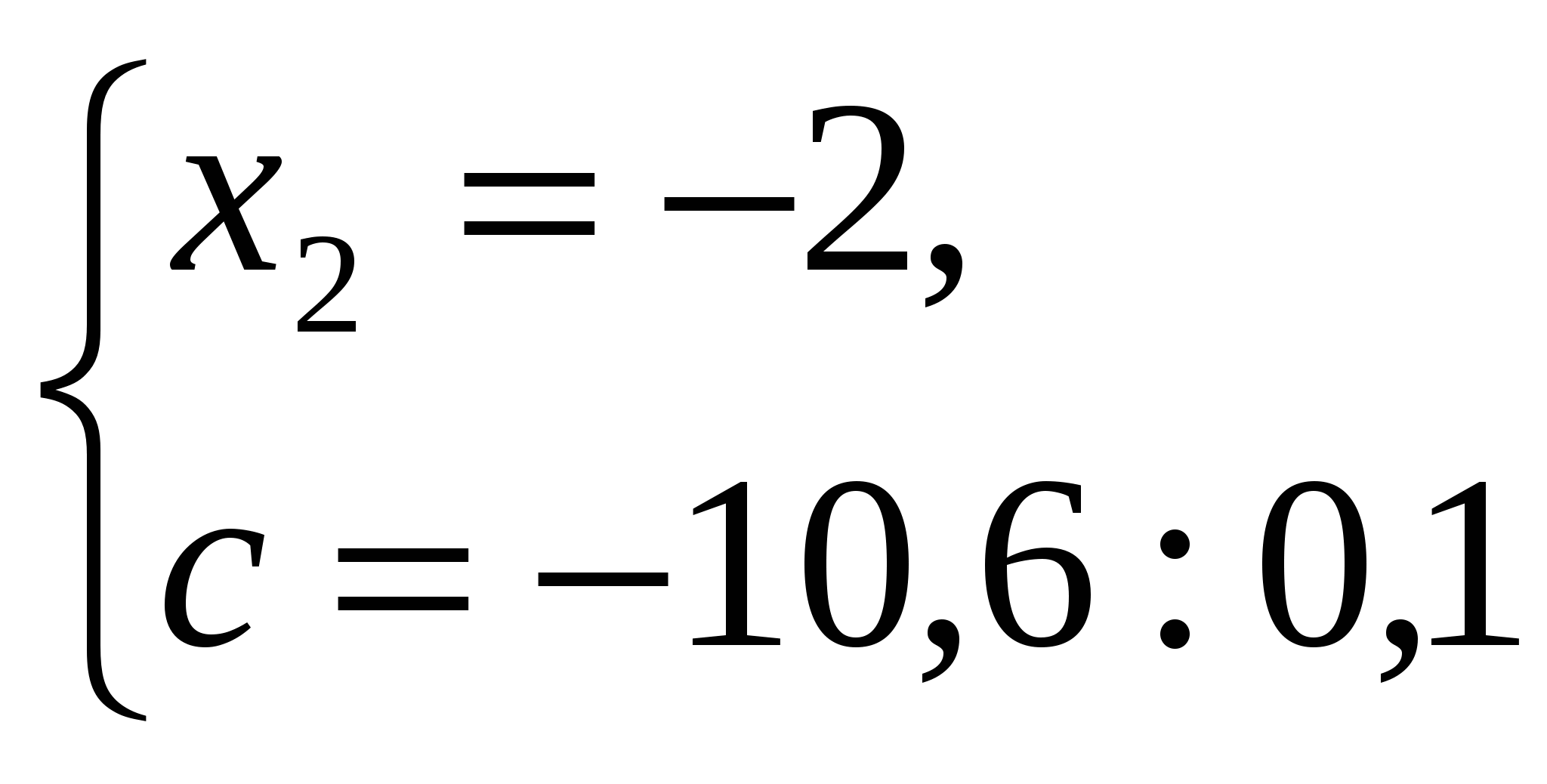

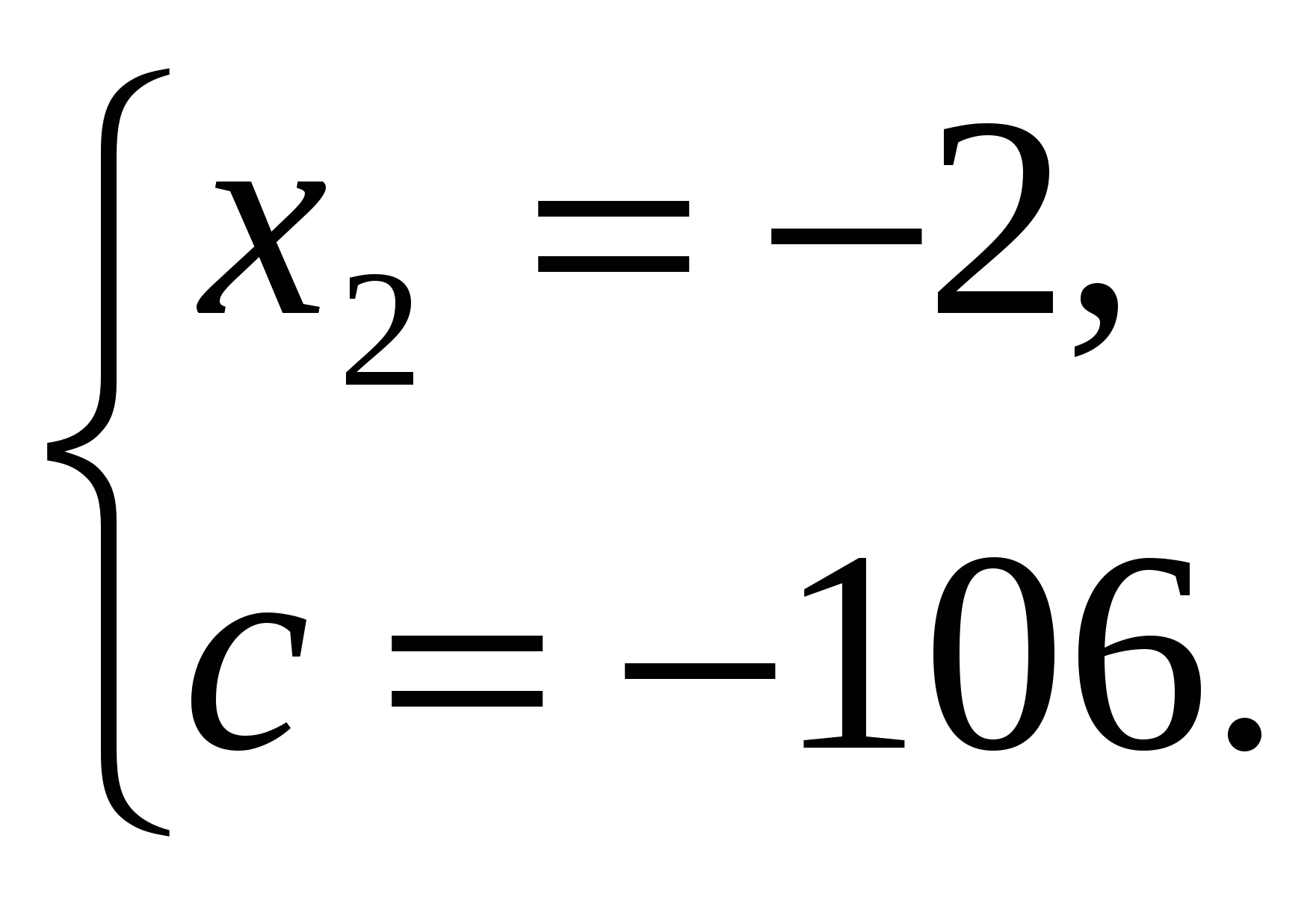
Ответ: 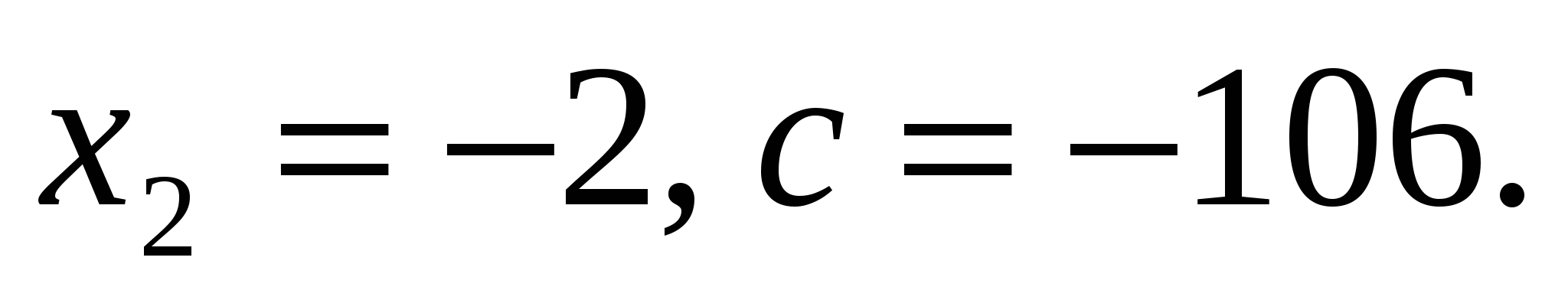 .
.
V. Итоги.
1. Сформулируйте прямую и обратную теоремы Виета.
2. Когда можно применять их?
3. В чем разница между прямой и обратной теоремами?
4. Каков алгоритм решения квадратного уравнения методом подбора?
1) Определить знак дискриминанта.
2) Выяснить знаки корней.
3) Подбором найти модули.
4) Сделать проверку.
5. В каких случаях неважно, модуль какого числа больше? Почему?
VΙ. Рефлексия учебной деятельности на уроке.
— Какую цель в поставили перед собой на уроке?
— Вы достигли поставленной цели?
— Что помогло выполнять задания?
— Проанализируйте свою работу, заполнив карточку.
Карточка для этапа рефлексии
Ответьте на вопросы:
1. Данная тема мне понятна.
2. Я хорошо понял теорему Виету и теорему, обратную теореме Виета.
3. Я знаю, как пользоваться данными теоремами.
Задание на дом: п.21-23; № 574 (б; в; г), № 580, № 583, № 586 (а; б; в).
infourok.ru
Теорема Виета и её применение
Цель:
- Обобщить и закрепить навыки решения квадратных уравнений ах2 + вх + с = 0, в которых а + в + с = 0; продолжить развивать навыки устного решения таких уравнений.
- Способствовать выработке у школьников желания и потребности обощения изучаемых фактов: развивать самостоятельность и творчество.
- Обеспечить закрепление теоремы на интересных примерах.
Оборудование:
- Кодоскоп
- Карточки тесты
- Карточки с индивидуальными заданиями для учащихся
- Сигнальные карточки.
Ход урока
I Повторение пройденного материала
1) Устная работа через кодоскоп с применением сигнальных карточек. Если ученик готов отвечать, то зеленая, нет – красная. Согласен с ответом – зеленая, не согласен – красная.
Доказательство теоремы Виета и свойств числовых коэффициентов уравнения.
Теорема Виета.
Сумма корней квадратного уравнения равна коэффициенту при х, взятому с противоположным знаком и деленному на коэффициент при х2; произведение корней этого уравнения равно свободному члену деленному на коэффициент при х2.
х1 + х2 = –
х1х2 = .
Доказательство.
Т.к. квадратное уравнение ах2 + вх + с = 0 имеет корни х1 и х2, то справедливо тождество ах2 + вх + с = а(х – х1)(х – х2).
Раскроем скобки в правой части этого тождества:
х2 + х – х2х + х1х2,
отсюда следует, что х1 + х2 = – и х1* х2 = . Что и требовалось доказать.
Обратная теорема Виета.
Если выполняются равенства х1 + х2 = – и х1х2 = , то числа х1 и х2 являются корнями уравнения ах2 + вх + с = 0.
Свойства коэффициентов 1.
Пусть дано квадратное уравнение ах2 + вх + с = 0, где а0. Если а + в + с = 0, то х1 = 1, х2 = .
Доказательство.
ах2 + вх + с = 0, а0
Разделим обе части уравнения на а0, получим приведенное квадратное уравнение х2 + .
| Согласно теореме Виета | х1 + х2 = – | |
| х1 |
| По условию а + в + с = 0, откуда в = – а – с. Значит | х1 + х2 = – = 1 + | |
| х1* х2 = 1 * |
Получим х1 = 1, х2 = .
Свойство коэффициентов 2.
Если в квадратном уравнении ах2 + вх + с = 0 а – в + с = 0, то х1 = – 1, х2 = – .
Доказывается аналогично.
В итоге на доске открывается таблица:
Связь между корнями и коэффициентами квадратного уравнения.
| Уравнение | Условие | Заключение | Пример |
| ах2 + вх + с = 0 | х1 и х2 | х1 + х2 = – , х1 * х2 = | х1 = 7 + ; х2 = 2 – х1 + х2 = 9; х1х2 = 11 – 5 |
| ах2 + вх + с = 0 | х1 + х2 = – , х1 * х2 = | х1 и х2 корни | х2 + 5х + 6 = 0 х1 = – 2, х2 = – 3 |
| ах2 + вх + с = 0 | а + в + с = 0 | х1 = 1, х1 = | 1998х2 – 907х – 1091 = 0 х1 = 1, х2 = |
| ах2 + вх + с = 0 | а – в + с = 0 | х1 = – 1, х1 = – | 127х2 + 250х + 123 = 0 х1 = – 1, х1 = – |
| ах2 + вх + с = 0 | а2х2 + авх + ас = 0 у2 + в1у + с1 = 0 у1, у2 |
х1 = х2 = |
4х2 + 12х + 5 = 0 у2 + 12у + 20 = 0 х1 = – , х2 = – ; у1 = – 2, у2 = – 10. |
Вывод:
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше скажи постоянства такого:
Умножишь ты корни – и дробь уж готова?!
В числителе с, в знаменателе а,
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда!
В числителе в, в знаменателе а.
II. Решение интересных заданий с применением теоремы Виета. Классу задается на дом подобрать по три интересных задания. Самые интересные решаются на уроке. №1 и №2 решаются на доске одновременно. №1 решается с полным комментированием, класс работает с учеником, который решает №1. №2 ученик рассказывает основные моменты.
1. Найдите сумму квадратов всех корней уравнения х2 – 3e х? + 1 = 0.
Решение.
| х2 + 3х + 1 = 0; | х1 + х2 = – 3; | х1 * х2 = 1; | |
| х2 – 3х + 1 = 0; | х3 + х4 = 3; | х1 * х2 = 1; |
х + х + х + х = (х1 + х2)2 – 2х1х2 + (х3х4)2 – 2х3х4 = 9 – 2 + 9 – 2 = 14.
2. Пусть х1 и х2 – корни уравнения 2х2 – 7х + 1 = 0. Составьте квадратное уравнение, корнями которого являются числа и .
Решение.
По теореме Виета х1 + х2 = 3,5; х1 * х2 = 0,5
Для составления квадратного уравнения с заданными корнями и воспользуемся теоремой, обратной теореме Виета, для этого необходимо найти их сумму и произведение:
+ = = = = 150,5
– = = = 2.
Искомое уравнение имеет вид
х2 + 150,5 + 2 = 0 или 2х2 – 301х + 4 = 0.
3. Корни уравнения х2 – вх – в = 0 таковы, что х + х + хх = 7,5.
Решение.
х1 + х2 = b;
х1 * х2 = – b;
х + х = (х)(( х) – 3х) + х = b(b + 3b) – b3 = b3 + 3b2 – b3 = 3b2 = 75.
3b2 = 75
b2 = 25
b1 = 5, b2 = – 5.
4. Пусть х1и х2 корни уравнения 3х2 + 14х – 4 = 0.
Установите, больше или меньше единицы значение дроби
.
Решение.
х1 + х2 = – ;
х1 * х2 = – ;
5. Для каких значений а разность корней уравнения 2х2 – (а + 1)х + а + 3 = 0 равна единице?
Решение.
х1 – х2 = 1 = > х1 = 1 + х2
х1 + х2 = = > 1 + х1 + х2 =
х1 * х2 = = > 2х2 + 1 = = > х2 = .
х1 = 1 +
х1 =
= ;
(а + 3)(а – 1) = 8а + 24
а2 + 3а – а – 3 – 8а – 24 = 0
а2 – 6а – 27 = 0
а1 = -3
а2 = 9.
Ответ: а1 = -3, а2 = 9.
III. Тест – самостоятельная по карточкам.
Вариант I.
Установите верный ответ из числа предложенных А), Б), В), Г).
Решите уравнение:
х2 + (
А) 2; ;
Б) —;
В); ;
Г) нет правильных ответов.
Не решая квадратного уравнения 3х2-х-11 = 0, составьте квадратное уравнение, корнями которого являются числа и .
А) х2—
Б) х2—
В) х2 +
Г) х2 +
Вариант II.
Установите верный ответ из числа предложенных А), Б), В), Г).
1) Решите уравнение:
х2-(
А) 5; ;
Б) —;
В) -; ;
Г) ; .
Не решая квадратного уравнения 2х2-5х-4 = 0, составьте квадратное уравнение, корнями которого являются числа и .
А) х2—
Б) х2—
В) х2 +
Г) х2 +
Проверка ответов через кодоскоп. Учащиеся меняются листочками с ответами, проверяют решение соседа и ставят оценку.
IV. Домашнее задание
Поменяться карточками с творческими заданиями.
VI. Итог урока
urok.1sept.ru
Теорема Виета (математика)
Урок-открытие новых знаний
Тема урока «Терема Виета»
Цели урока
Предметные результаты: наблюдать и анализировать связь между корнями и коэффициентами квадратного уравнения. Формулировать и доказывать теорему Виета, а также обратную теорему, применять теоремы для решения уравнений и задач.
Метапредметные результаты: использовать приемы умственной деятельности – анализ, классификация, обобщение и подведение под понятие; ставить цель исследования, выдвигать гипотезы представлять информацию в символической и табличной формах.
Личностные: формирование мотивации – интереса к изучению математики за счет включения примеров из биографии Виета, приема запоминания формулировки теоремы Виета, самостоятельного открытия знаний, выполнения заданий, раскрывающих все основные варианты соответствующей деятельности.
Ход урока:
I. Самостоятельная работа
Решить уравнения:
1) х2 – 6х + 8 = 0; 3) 3x2 = x + 2;
2) х2 – 2х = 5; 4) х2 + 4х – 7 = 5+3х–2х2.
II. Актуализация знаний
1. Что записано на доске? [Квадратные уравнения.]
2. Докажите, что данные уравнения квадратные.
3. Какие виды квадратных уравнений записаны? [Приведенные и неприведенные уравнения.]
Проводится взаимопроверка. Учитель называет правильные ответы. Ученики обмениваются тетрадями и делают проверку. Оценка 5 выставляется за все правильно решенные задания и т.д.
Уравнение | Корни | Сумма корней | Произведение корней |
х2–6х+8=0 | |||
х2–2х–5=0 | |||
3x2–x–2=0 | |||
3х2+х–2=0 | |||
х2+рх+q=0 | |||
ax2+bx+c=0 |
Уравнение | Корни | Сумма корней | Произведение корней |
х2–6х+8=0 | 4 и 2 | 6 | 8 |
х2–2х–5=0 | | 2 | –5 |
3x2–x–2=0 | | | |
3х2+х–2=0 | –1 и | – | |
х2+рх+q=0 |
| –р | q |
ax2+bx+c=0 |
| | |
III. Постановка проблемы и открытие нового знания
Найдите сумму и произведение корней. Какое предположение можно сделать? Сравните сумму и произведение корней с коэффициентами уравнения в первом столбце.
Какая существует зависимость между корнями приведенного квадратного уравнения и его коэффициентами? Сформулируйте утверждение.
[Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, произведение корней равно свободному члену.]
IV. Исторический материал
Впервые зависимость между корнями и коэффициентами квадратного уравнения установил знаменитый французский ученый Франсуа Виет (1540-1603 гг).
Франсуа Виет был по профессии адвокатом и много лет работал советником короля. И хотя математика была его увлечением, хобби, благодаря упорному труду он добился больших результатов. Виет в 1591 г. ввел буквенные обозначения для неизвестных и коэффициентов уравнений, стало возможным свойства уравнений и корней записывать общими формулами.
Недостатком алгебры Виета было то, что он признавал только положительные числа. Чтобы избежать отрицательных решений, он заменял уравнения или искал искусственные приемы решения, что отнимало много времени, и усложняло решение.
Много разных открытий сделал Виет, но сам он больше всего дорожил установлением зависимости между корнями и коэффициентами квадратного уравнения, т.е. той зависимостью, которая называется «теоремой Виета».
V. Доказательство теоремы Виета
1. Дано: х2 + рх + q = 0. Доказать:
1) х1 + х2 = –р; 2) х1 х2 = q.
2. Сформулируйте обратную теорему Виета.
Если числа m и n таковы, что их сумма равна –р, а произведение равно q, то эти числа являются корнями уравнения х2+рх+q=0.
3. Сформулируйте теорему Виета для произвольного квадратного уравнения.
ах2 + bx + c = 0, а 0, х2 +  .
.
1) х1 + х2=– ; 2) х1 х2 =
; 2) х1 х2 =  .
.
4. Проверьте равенства для уравнений 3 и 4 из самостоятельной работы.
VI. Способ запоминания теоремы Виета
Чтобы лучше запомнить эти формулы можно выучить стихотворение
«Теорема Виета».
По праву стихом быть достойным воспета
О свойствах корней теорема Виета.
Что лучше скажи постоянства такого
Умножишь ты корни и дробь уж готова:
В числителе С, в знаменателе А
И сумма корней тоже дроби равна,
Хоть с минусом дробь та, что за беда:
В числителе В, в знаменателе А.
VII. Первичное закрепление изученного материала
Показать примеры применения
прямой и обратной теорем Виета
1. Проверьте, правильно ли найдены корни квадратного уравнения:
а) х2 + 3х – 40 = 0, х1 = –8, х2 = 5;
б) х2 + 2х – 3 = 0, х1 = –1, х2 = 3;
в) 2х2 – 5х – 3 = 0, х1 = – , х2 = 3.
, х2 = 3.
2. Найдите корни квадратного уравнения, применяя теорему, обратную теореме Виета:
а) х2 – 6х + 5 = 0; б) х2 – 7х + 12 = 0; в) х2 – х – 12 = 0.
3. Составьте приведенные квадратные уравнения, если его корни равны:
а) х1 = –3, х2 = 1; б) х1 = –3, х2 = –4; в) х1 = 5, х2 = 6.
4. Проверьте выполнимость теоремы Виета для уравнения:
1) х2 – 2х – 9 = 0, р = –2, q = –9.
х1 =1 –  , х2 = 1 +
, х2 = 1 +  , х1 + х2 = 2, х1 х2 = –9.
, х1 + х2 = 2, х1 х2 = –9.
2) 2х2 + 7х – 6 = 0, р =  , q = –3.
, q = –3.
х1= , х2=
, х2= , х1 + х2=–
, х1 + х2=– , х1 х2 = –3.
, х1 х2 = –3.
5. Найдите: х2, р, если известно х2 + рх – 35 = 0, х1 = 7.
Решение. х1х2 = –35, 7х2 = –35, х2 = –5; х1 + х2= –р, 7–5=–р, р= –2.
Ответ: х2 = –5, р = –2.
VIII. Подведение итогов урока. Рефлексия.
Вопрос 1. Можно ли, не решая самого уравнения
x2–2x+3=0, сказать, чему равна сумма его корней?
Скорее всего, ученики скажут, что число 2. Однако этот ответ неверен, так как это уравнение вообще не имеет корней: x2–2x+3=x2–2x+1+2=(x–1)2+220.
Следовательно, прежде чем ответить на вопрос о сумме и произведении корней, необходимо проверить, существуют ли корни у заданного квадратного уравнения.
Вопрос 2. Каков по знаку дискриминант уравнения
х2–2x–9=0?
Вопрос 3. Могут ли оба корня уравнения х2–2x–9=0 быть положительными?
[Нет, х1х2 = –9, значит, корни разных знаков.]
Вопрос 4. Можно ли утверждать, что модуль положительного корня уравнения х2–2x–9=0 больше модуля отрицательного?
[Да, можно, потому что х1+х2=20.]
Домашнее задание. п.23, №329 (2), 330 (2), 332 (1,4), 333 (2,4).
Творческое задание для сильных учеников:
«Доказать, что если в квадратном уравнении ах2+bx+c=0:
1) а + b + c = 0, то х1 = 1, х2 =  ;
;
2) а – b + c = 0, то х1 = –1, х2= – ».
».
videouroki.net
План-конспект урока по алгебре (8 класс) по теме: Теорема Виета
Тема урока: Теорема Виета
Цели урока:
- «Открыть» зависимость между корнями уравнения и его коэффициентами; научить применять теорему Виета и обратную ей теорему в различных ситуациях при решении квадратных уравнений;
- Развивать творческое мышление учащихся и кругозор учащихся;
- Воспитание познавательного интереса к учебному предмету математика.
Средства обучения:
- приемы технологии УДЕ;
- презентация Power Point;
- таблицы;
- средства компьютерной технологии;
- интерактивная доска.
Ход урока
I. Проверка домашнего задания и постановка проблемы.
— Дома вы должны были заполнить таблицу. Давайте проверим, как вы справились.
(Под диктовку учащихся заполняется таблица на доске)
Уравнение | Корни | Произведение корней | Сумма корней |
4х2 + 7х + 3 = 0 | |||
x2 + х – 56 = 0 | |||
x2 – х – 56 = 0 | |||
x2 – х – 1 = 0 | |||
x2 + px + q = 0 | |||
ax2 + bx + c = 0 |
Уравнение | Корни | Произведение корней | Сумма корней |
4х2 + 7х + 3 = 0 | -1; — | -1- = — | |
x2 + х – 56 = 0 | -8; 7 | -56 | -1 |
x2 – х – 56 = 0 | -7; 8 | -56 | 1 |
x2 – х – 1 = 0 | ; | -1 | 1 |
x2 + px + q = 0 | x1 и x2 | q | -p |
ax2 + bx + c = 0 | x1 и x2 | c/а | — в / а |
II.I «Открытие» нового знания
— Сравните сумму и произведение корней с коэффициентами уравнений. Какое предположение можно сделать? Какая существует зависимость между корнями приведенного квадратного уравнения и его коэффициентами? Сформулируйте утверждение и запишите его.
II.II. Историческая справка.
Впервые зависимость между корнями и коэффициентами квадратного уравнения установил знаменитый французский ученый Франсуа Виет (1540-1603).
Франсуа Виет был по профессии адвокатом и много лет работал советником короля. И хотя математика была всего лишь его увлечением, благодаря упорному труду, он добился в ней больших результатов.
В 1591 году он ввел буквенные обозначения для коэффициентов при неизвестных в уравнениях, что дало возможность записать общими формулами корни уравнения, а также его свойства.
Виет сделал множество открытий, сам он больше всего дорожил установлением зависимости между корнями и коэффициентами квадратного уравнения, которое называется теоремой Виета.
II.III.Доказательство теоремы Виета и теоремы, обратной теореме Виета.
Наша с вами задача доказать, что эти соотношения выполняются для всех приведенных квадратных уравнений. Итак, запишем в тетради формулировку и доказательство теоремы Виета
Теорема Виета | Теорема, обратная теореме Виета |
Сумма корней приведенного квадратного уравнения х2+рх+q=0 равна второму коэффициенту взятому с противоположным знаком (-р), а произведение корней приведенного квадратного уравнения равно свободному члену (q ). Дано: х1 и х2 – корни уравнения х2+рх+q=0 (I) Доказать: х1+х2= -р х1*х2 =q Док-во. Составим квадратное уравнение вида (I), которое имеет корни х1 и х2: х2+рх+q=0. (I) х-х1=0, х-х2=0. (х-х1)(х-х2)=0•0, х2-х1х-х2х+х1х2=0, х2-(х1+х2)х+х1х2=0, (II) х2 +рх+q=0. (I) Приравнивая соответствующие коэффициенты выведенного уравнения (II) и исходного уравнения (I), мы находим доказываемые соотношения (III) и (IV): р= — (х1+х2), или х1+х2= — р х1 • х2 = q | Если в квадратном уравнении второй коэффициент (р) противоположен сумме некоторых двух чисел x1 и x2, а свободный член (q ) равен произведению тех же чисел, то числа x1 и x2 являются корнями данного квадратного уравнения. Дано: х1 и х2 – числа, такие что р= -(х1+х2), q=х1*х2 х2+рх+q=0 (I) Доказать: х1 и х2 – корни уравнения х2+рх+q=0 Док-во. Согласно условию теоремы напишем квадратное уравнение (II): х2-(х1+х2)х+х1х2=0 (II) Подставим х1, вместо х в уравнение (II), х2-(х1+х2)х1+х1х2?0 х21-х21+х1х2-х1х2=0 0=0 Значит, х1- корень уравнения (II). Подставим х2 вместо х в уравнение (II). х22 — (х1+х2) х2+ х1х2 = 0 х22 – х1х2 + х22 + х1х2 = 0 0=0 Следовательно, х1 и х2 – корни уравнения (II). |
III Отработка полученных знаний
№1. а) Проверить двойную таблицу сумм и произведений однозначных положительных чисел (рис.1).
Составим квадратное уравнение с корнями, указанными в одной из клеток этой таблицы; например, в пересечении столбца x2 = 5 и строки x1 = 4 мы находим два числа. Это означает:
— (a + b) = — (4 + 5) = -9 = p, 4 * 5 = 20 = q.
x1 + x2 = -p
x1 * x2 = q
x2 – px + q = 0
x2 x1 | 3 3 | 5 5 | 7 7 | 9 9 |
2 | 5 6 | 7 10 | 9 14 | 11 18 |
4 | 7 12 | 9 20 | 11 28 | 13 36 |
6 | 9 18 | 11 30 | 13 42 | 15 54 |
8 | 11 24 | 13 40 | 15 56 | 17 72 |
x2 – 9x + 20 = 0
x2 – 15x + 54 = 0
. . .
(x1 = 4; x2 = 5)
(x1 = 6; x2 = 9)
Рис.1
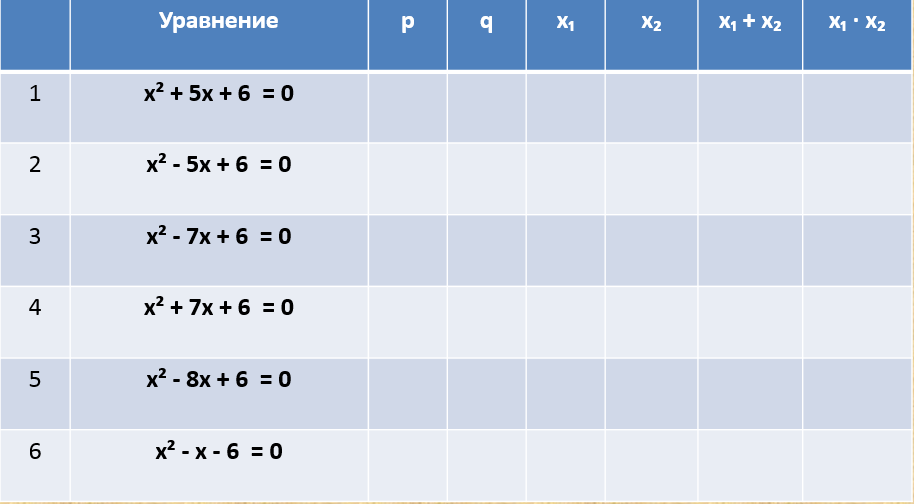
№2. Выясните, имеют ли данные уравнения корни. В случае утвердительного ответа найдите их, используя теорему, обратную теореме Виета (х12):
№ | Уравнения | Исследование существования корней | х1 • x2 | х1+ x2 | х1 | x2 |
1 | х2 — х — 6 = 0 | |||||
2 | х2 + х – 6 = 0 | |||||
3 | х2 + х + 6 = 0 | |||||
4 | х2 + 5х – 6 = 0 | |||||
5 | х2 + 5х + 6 = 0 | |||||
6 | х2 — 6х + 8 = 0 | |||||
7 | х2 — 2х + 3 = 0 | |||||
8 | х2 +2007 х – 2008 = 0 | |||||
9 | х2 – (1 — )х — = 0 | |||||
10 | -х2 + 8х – 12 = 0 |
№ | Уравнения | Исследование существования корней | х1 • x2 | х1+ x2 | х1 | x2 |
1 | х2 — х — 6 = 0 | + | -6 | 1 | 3 | -2 |
2 | х2 + х – 6 = 0 | + | -6 | -1 | -3 | 2 |
3 | х2 + х + 6 = 0 | _ | ||||
4 | х2 + 5х – 6 = 0 | + | -6 | -5 | -6 | 1 |
5 | х2 + 5х + 6 = 0 | + | 6 | -5 | -3 | 2 |
6 | х2 — 6х + 8 = 0 | + | 8 | 6 | 4 | 2 |
7 | х2 — 2х + 3 = 0 | _ | ||||
8 | х2 +2007 х – 2008 = 0 | + | -2008 | -2007 | -2008 | 1 |
9 | х2 – (1 — )х-= 0 | + | — | 1 — | — | 1 |
10 | -х2 + 8х – 12 = 0 x2-8x+12=0 | + | 8 -8 | -12 12 | 2 | 6 |
№3. Составьте квадратное уравнение, имеющее заданные корни х1 и x2:
№ | х1 | x2 | х1+ x2 | х1 • x2 | Квадратное уравнение |
1 | -3 | 5 | |||
2 | 4 | 7 | |||
3 | 0 | 7 | |||
4 | — | ||||
5 | -0,5 | -0,2 | _______________________________ _х2 ________х 1=0 | ||
6 | 1 | 2 | ______________________________ 3 х2 _______х ______= 0 |
№ | х1 | x2 | х1+ x2 | х1 • x2 | Квадратное уравнение |
1 | -3 | 5 | 2 | -15 | x2-2x-15=0 |
2 | 4 | 7 | 11 | 28 | x2 -11x+28=0 |
3 | 0 | 7 | 7 | 0 | x2-7x=0 |
4 | — | 0 | -2 | x2-2=0 | |
5 | -0,5 | -0,2 | -0.7 | 0,1 | x2+0,7x+0.1=0_________________ _х2 — _0,7х — 1=0 |
6 | 1 | 2 | х2 – 10 / 3 х + 8 / 3 = 0_________ 3 х2 ___10____х ___8___= 0 |
№ 4. Проанализируйте данные и заполните пропуски:
1) х2 _____ х _______ = 0, 2) х2 _____х –15 = 0,
х1 = — 2, х1 = — 5,
x2 = 8; x2 = _____;
3) х2 –15 х _____ = 0, 4) х2 ____х ______ = 0,
х1 = 5, х1 = x2 = -2;
x = _____;
5) х2 _____ = 0, 6) х2 – 12х _____= 0,
х1 = 8, х1 — x2 = 2;
х2 = -8.
1) х2 — _6х_ — __16__ = 0, 2) х2 + 2х – 15 = 0,
х1 = — 2, х1 = — 5,
x2 = 8; x2 = _3____;
3) х2 –15 х + _____ = 0, 4) х2 + __4__х + ____4__ = 0,
х1 = 5, х1 = x2 = -2;
x2 = 10__;
5) х2 — ___64__ = 0, 6) х2 – 12х + __35___= 0,
х1 = 8, х1 — x2 = 2;
х2 = -8. х1+х2=12
№ 5. Проанализировав первую и последнюю строку домашней таблицы, сформулируйте теорему Виета для квадратного уравнения общего вида.
№ 6. Заполните пропуски в стихотворении:
По праву достойна в стихах быть воспета
О свойстве корней теорема____________
Что лучше, скажи, постоянства такого?
Умножишь ты корни, и дробь уж готова:
В числителе «_____», в знаменателе «а».
И сумма корней тоже дроби равна.
Хоть с минусом дробь эта, что за беда
В числителе «____», в знаменателе – «_____»
По праву достойна в стихах быть воспета
О свойстве корней теорема _Виета_
Что лучше, скажи, постоянства такого?
Умножишь ты корни, и дробь уж готова:
В числителе «_с_», в знаменателе «а».
И сумма корней тоже дроби равна.
Хоть с минусом дробь эта, что за беда
В числителе «_в_», в знаменателе – «_а_»
IV.Итог урока: Итак, сегодня мы познакомились с теоремой знаменитого французского ученого Виета и научились ее использовать в простейших случаях.
V. Задание на дом.
1. В таблице даны параметры семи уравнений. Найти пропущенные числа, составив и решить соответствующие уравнения.
1 | 2 | 3 | 4 | 5 | 6 | 7 | |
х 1 | 0,5 | 3/4 | 0,2 | 0, 3 | 2 | — 3 | |
х 2 | 4 | ||||||
р | -8 | -0,7 | 3/5 | 8 | 5 | ||
q | 12 | 4 |
2. Найдите коэффициенты квадратных уравнений, учитывая, что один
из корней равен -3.
1) х2 – 5х _____ = 0 2) х2 _____х + 18 = 0
______________________ _____________________
______________________ _____________________
______________________ ______________________
______________________ ______________________
3) х2 _____х – 15 = 0 4) х2 _____ = 0
______________________ ______________________
______________________ ______________________
______________________ ______________________
______________________ ______________________
5) х2 _____ х = 0 6) 2х2 _____х – 3 = 0;
___________________
___________________
___________________
___________________
nsportal.ru






 и
и 
 и
и 

