Пропорции. Прямая и обратная пропорциональная зависимости 6 класс онлайн-подготовка на Ростелеком Лицей
56. Пропорции. Прямая и обратная пропорциональная зависимости.
Рассмотрим отношения 3,6:1,2=3 и 6,3:2,1=3.
Эти отношения равны. 3,6:1,2=6,3:2,1 или 3,61,2=6,32,1.
Равенство двух отношений называют пропорцией.
С помощью букв пропорцию записывают так:
a:b=c:d или аb=cd.
Эти записи читают так: «Отношение a к b равно отношению с к d» или «а так относится к b, как с относится к d».
Числа а и d называют крайними, а числа b и c – средними членами пропорции.
В пропорции 3,61,2=6,32,1 найдем произведение ее крайних членов и произведение ее средних членов: 3,6·2,1=7,56 и 1,2·6,3=7,56.
В верной пропорции произведение крайних членов равно произведению средних. Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.
Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.
ad=bc.
Это свойство называют основным свойством пропорции.
Пропорция 20:16=5:4 верна, так как 20·4=16·5=80.
Поменяем местами в этой пропорции средние члены, т.е. 20:5 = 16:4. Получилось верное равенство. Таким образом, при перестановке произведение крайних и произведение средних членов не меняется.
Если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны.
Используя основное свойство пропорции, можно найти ее неизвестный член, если все остальные члены известны.
Пример 1. Найдем в пропорции у:
у:51,6=11,2:34,4.
Используя основное свойство пропорции, получим: у·34,4=51,6·11,2. Значит,
у=51,6·11,234,4=16,8.
Пример 2. Решим уравнение 67,8а=7,626,35.
Решим уравнение 67,8а=7,626,35.
Используя основное свойство пропорции, получим: 7,62·а =6,35·67,8. Значит,
а=6,35·67,87,62=56,5.
Пример 3. Решим уравнение 0,2:x-2=12:212.
Используя основное свойство пропорции, получим:
x-2∙12=0,2∙212
x-2∙12=12
x-2=1
x=3.
Если станок с программным управлением за 2 ч изготовляет 28 деталей, то за 4 ч он изготовит 56 таких деталей. Во сколько раз больше времени будет работать станок, во столько же раз больше деталей он изготовит. Значит, равны отношения 4:2 = 56:28. Такие величины, как время работы станка и число изготовленных деталей, называют прямо пропорциональными величинами.
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Если величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Пример 4. Автомобиль за 2 ч проехал 180 км. За какое время автомобиль проедет вдвое большее расстояние, если будет двигаться с той же скоростью?
Найдем вдвое большее расстояние: 180·2=360 км.
Найдем скорость автомобиля: 180:2=90 км/ч.
Найдем время, требующееся на 360 км:360:90=4 ч.
Значит, автомобилю потребуется вдвое большее времядля прохождения вдвое большего расстояния.
Говорят: «Время прямо пропорционально расстоянию«. Во сколько раз увеличится расстояние, при постоянной скорости, во столько же раз увеличится время.
Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины.
Пример 5. Автомобилю, двигающемуся со скоростью 60 км/ч, потребовалось 6 часов на прохождение пути. За какое время автомобиль проедет это же расстояние, если будет двигаться с вдвое большей скоростью?
Автомобилю, двигающемуся со скоростью 60 км/ч, потребовалось 6 часов на прохождение пути. За какое время автомобиль проедет это же расстояние, если будет двигаться с вдвое большей скоростью?
Найдем вдвое большую скорость: 60·2=120 км/ч.
Найдем расстояние: 60·6=360 км.
Найдем время при скорости 120 км/ч:360:120=3 ч.
Значит, автомобилю потребуется вдвое меньшее время для прохождения расстояния с вдвое большей скоростью.
Говорят: «Время обратно пропорционально скорости». Во сколько раз увеличится скорость, при том же расстоянии, во столько же раз уменьшится время.
Прямая и обратная пропорциональные зависимости
Сегодня на уроке мы продолжим работать с
пропорциями, а точнее познакомимся с прямой и обратной
пропорциональными зависимостями.
Задача
Сколько нужно сахара, чтобы сварить варенье из 5 кг черешни, если по рецепту на 2 кг ягод нужно 3 кг сахара?
Решение:
Из решения видно, что во сколько раз больше имеется черешни, во столько раз больше понадобится сахара.
Эту же задачу можно решить и при помощи пропорции. Запишем кратко условие задачи в виде таблицы, обозначив за неизвестную нам массу сахара буквой х. Смотрите, у нас есть столбик, где мы будем записывать массу ягод, и столбик, где мы укажем соответствующую массу сахара на массу ягод. Итак, по условию задачи известно, что по рецепту на 2 кг ягод нужно 3 кг сахара. Нам нужно узнать, сколько кг сахара потребуется на 5 кг ягод.
Такая зависимость между массой ягод и массой сахара
условно обозначается в таблице одинаково направленными стрелками. Их
направление говорит о том, что если первая величина возрастает (стрелка вверх),
то и вторая тоже возрастает (стрелка тоже вверх).
Задача
Велосипедист, двигаясь с постоянной скоростью, проехал 10 км за 20 минут. Какой путь проедет велосипедист за 50 минут?
Решение: для наглядности запишем кратко условие задачи в виде таблицы.
Такие величины, как масса ягод для варенья и масса сахара, время и пройденный за это время при постоянной скорости путь, и т.д. называют прямо пропорциональными величинами.
Определение
Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Задача
Автомобиль ехал 3 часа со скоростью 60 км/ч. За какое время он продет это же расстояние, если будет ехать со скоростью 90 км/ч?
Решение:
Из решения видно, что во сколько раз скорость
автомобиля больше, во столько раз меньше времени тратится на этот же
путь.
Эту же задачу решим при помощи пропорции. Запишем в таблицу кратко условие задачи. За х обозначим неизвестное нам время.
Понятно, что чем больше скорость автомобиля, тем меньше времени ему понадобится на преодоление этого же пути. Такая зависимость между скоростью и временем, затраченным на пройденный путь, условно обозначается в таблице противоположно направленными стрелками. Их направление говорит о том, что если первая величина возрастает (стрелка вверх), то вторая убывает (стрелка вниз). Составим пропорцию. Т.к. стрелки направлены в разные стороны, то второе отношение перевернём.
Задача
5 рабочих выполнили заказ за 132 часа. За какое время этот же заказ смогут выполнить 12 рабочих?
Решение:
Понятно, что чем больше будет задействовано рабочих
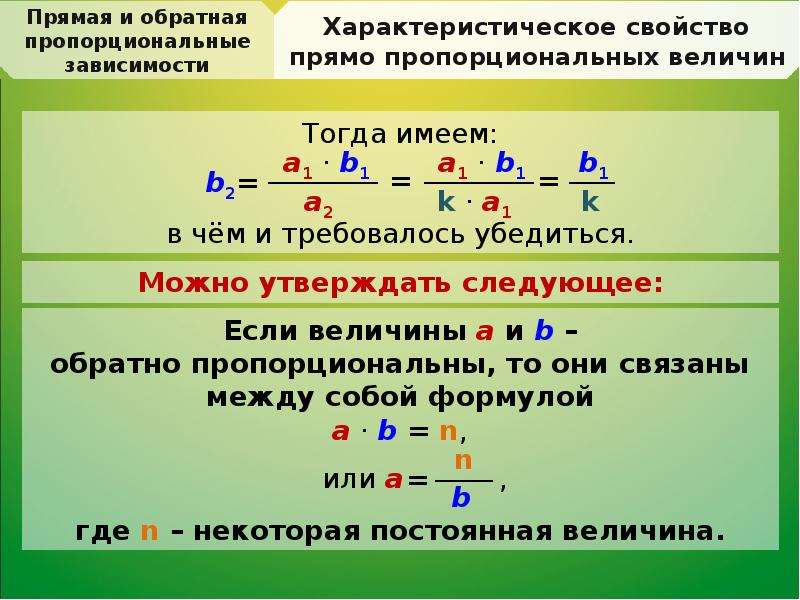 Составим пропорцию:
Составим пропорцию:Такие величины, как скорость автомобиля и время, за которое он проедет определённый путь, число работников и время, за которое они выполняют заказ, и т.д. называют обратно пропорциональными величинами.
Определение
Две величины называются обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
Не всякие две величины являются прямо пропорциональными или обратно пропорциональными.
Например, возраст человека и размер его обуви не связаны пропорциональной зависимостью. Зависимость между величинами есть. Размер обуви с возрастом увеличивается, но не во столько же раз.
Возраст дерева и его высота не связаны
пропорциональной зависимостью. В этом случае зависимость между величинами есть.
Действительно, высота дерева с возрастом увеличивается, но не во столько же
раз.
Прямая и обратная пропорциональные зависимости
Прямая пропорциональная зависимость
| Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз. |
Примеры:
1) — периметр квадрата, — его сторона.
= 4.
Если = 1 см, то = 41 = 4 (см).
Если = 2 см, то = 42 = 8 (см).
Если = 4 см, то = 44 = 16 (см).
Получаем, что каждый раз, увеличивая сторону квадрата в 2 раза, его периметр также будет увеличиваться в 2 раза. Аналогично, если сторону квадрата будем уменьшать в какое-то число раз, то и периметр квадрата будет уменьшаться в это же число раз. Следовательно, 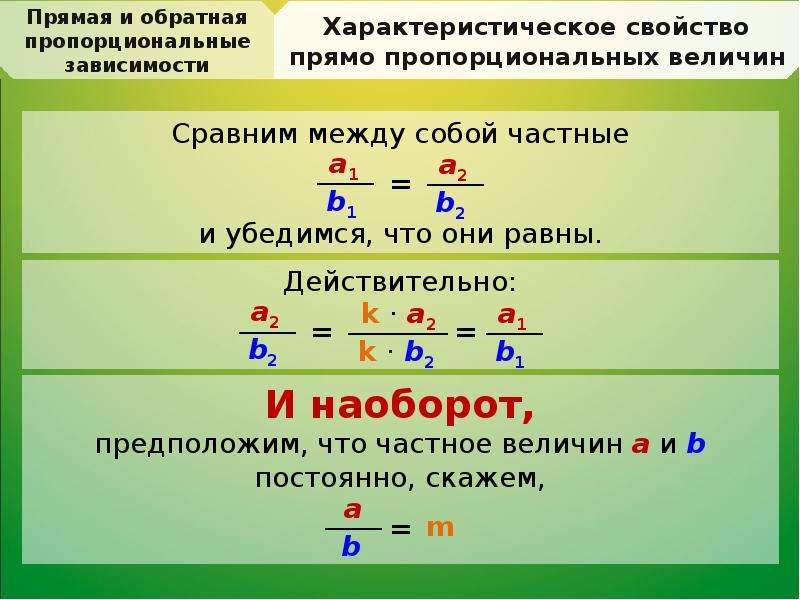
2) При движении с постоянной скоростью, пройденный путь и время движения прямо пропорциональны, т.к. пройденный путь равен произведению скорости и времени движения.
Пусть скорость движения пешехода 8 км/ч.
Если = 1 ч, то = 81 = 8 (км).
Если = 3 ч, то = 83 = 24 (км).
Если = 9 ч, то = 89 = 72 (км).
Получаем, что каждый раз, увеличивая время в пути в 3 раза, путь также будет увеличиваться в 3 раза, а это и говорит о том, что зависимость между величинами и является прямой пропорциональностью, при условии движения с постоянной скоростью.
Свойство прямо пропорциональных величин:
| Если две величины прямо пропорциональны, то отношение соответствующих значений этих величин равно одному и тому же, постоянному для данных величин, числу. |
В рассмотренных выше примерах для величин и это число равно 4, т. к. : = 4 : 1 = 8 : 2 = 16 : 4 = 4, а для величин и это число равно 8, т.к. : = 8 : 1 = 24 : 3 = 72 : 9 = 8.
к. : = 4 : 1 = 8 : 2 = 16 : 4 = 4, а для величин и это число равно 8, т.к. : = 8 : 1 = 24 : 3 = 72 : 9 = 8.
Обратная пропорциональная зависимость
| Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз. |
Примеры:
1) Если расстояние является постоянной величиной, то скорость и время движения обратно пропорциональны, т.к. время движения равно частному от деления расстояния на скорость движения.
Пусть расстояние равно 80 км.
Если = 10 км/ч, то = 80 : 10 = 8 (ч).
Если = 20 км/ч, то = 80 : 20 = 4 (ч).
Если = 40 км/ч, то = 80 : 40 = 2 (ч).
Получаем, что каждый раз, увеличивая скорость движения в 2 раза, время движения будет уменьшаться в 2 раза, а это и говорит о том, что зависимость между величинами и является обратной пропорциональностью, при том условии, что расстояние нужно проехать одинаковое.
2) и — стороны прямоугольника, а его площадь 36 см2.
Если = 3 см, то = 36 : 3 = 12 (см).
Если = 6 см, то = 36 : 6 = 6 (см).
Получаем, что величины и обратно пропорциональны, т.к. увеличивая (уменьшая) одну сторону прямоугольника в 2 раза, чтобы его площадь не изменилась, вторую сторону нужно уменьшить (увеличить) в 2 раза.
Свойство обратно пропорциональных величин:
| Если две величины обратно пропорциональны, то произведение соответствующих значений этих величин равно одному и тому же для данных величин числу. |
В рассмотренных выше примерах для величин и это число равно 80, т.к. = 108 = 204 = 402 = 80, а для величин и это число равно 12, т.к. = 312 = 66 = 36.
Не всякие величины являются прямо пропорциональными или обратно пропорциональными. Например, размер обуви человека увеличивается при увеличении его возраста, но эти величины не являются пропорциональными, т. к. при удвоении возраста размер обуви человека не удваивается.
к. при удвоении возраста размер обуви человека не удваивается.
Пусть нам дана задача:
Украшение состоит из белого и желтого золота массой 192 г. При этом масса белого золота относится к массе желтого золота как 5 : 7. Надо найти массу белого и желтого золота, из которых сделано украшение.
Решение:
Мы можем считать, что все украшение состоит из 5 + 7 = 12 частей одинаковой массы. По условию масса украшения равна 192 г, а значит, масса одной части украшения равна 192 : 12 = 16 г.
Белое золото соответствует 5 частям, то есть имеет массу 516 = 80 г, а желтое золото соответствует 7 частям, то есть имеет массу 716 = 112 г.
Итак мы получили, что украшение состоит из 80 г белого золота и 112 г желтого золота.
То есть мы число 192 (масса украшения) представить в виде суммы двух слагаемых — 80 и 112, отношение которых равно 5 : 7.
В этом случае говорят, что число 192 разделили в отношении 5 : 7, или по-другому, число 192 представили в виде суммы двух слагаемых, пропорциональных числам 5 и 7.
|
1 вариант №1 Решить пропорцию. 1) = ; 2) = ; 3) х : 2 = 3 : №2 Проверить, верно ли равенство. 1 : 2 = 1 : 2 №3 Задача Масса 9 одинаковых ящиков равна 24 кг. Найдите массу 39 таких же ящиков. №4 Задача Самолет со скоростью 200 км/ч преодолевает расстояние от Москвы до Тюмени за 2 часа, за сколько он преодолеет это же расстояние со скоростью 150 км/ч №5 Отношение – это…Пропорция – это…Основное свойство пропорции: … 1 вариант
№1 Решить пропорцию. 1) = ; 2) = ; 3) х : 2 = 3 : №2 Проверить, верно ли равенство. 1 : 2 = 1 : 2 №3 Задача Масса 9 одинаковых ящиков равна 24 кг. Найдите массу 39 таких же ящиков. №4 Задача Самолет со скоростью 200 км/ч преодолевает расстояние от Москвы до Тюмени за 2 часа, за сколько он преодолеет это же расстояние со скоростью 150 км/ч №5 Отношение – это…Пропорция – это…Основное свойство пропорции:… |
2 вариант №1 Решить пропорцию. 1) = ; 2) = ; 3) х : 1 = 7 :
№2 Проверить, верно ли равенство. 2 : 6 = : 2 №3 Задача За 9 дней машинистка напечатала 126 страниц. Сколько страниц напечатает она за 14 дней? №4 Задача Автобус со скоростью 80 км/ч преодолевает расстояние от Тобольска до Тюмени за 3 часа, за сколько он преодолеет это же расстояние со скоростью 60 км/ч №5 Отношение – это… Пропорция – это…Основное свойство пропорции: …. 2 вариант №1 Решить пропорцию. 1) = ; 2) = ; 3) х : 1 = 7 : №2 Проверить, верно ли равенство. 2 : 6 = : 2 №3 Задача
За 9 дней машинистка напечатала 126 страниц. №4 Задача Автобус со скоростью 80 км/ч преодолевает расстояние от Тобольска до Тюмени за 3 часа, за сколько он преодолеет это же расстояние со скоростью 60 км/ч №5 Отношение – это… Пропорция – это…Основное свойство пропорции: …. |
Урок математики по теме «Прямая пропорциональность», 6 класс — К уроку — Математика, алгебра, геометрия
Тема: Прямая пропорциональность, 6 класс
Цель:
1. Познакомиться с понятием прямой пропорциональности.
2. Сформировать навык решения задач на прямую пропорциональность.
3. Вывести алгоритм решения таких задач.
Ход урока:
1. Организационный момент. Класс делится
на 3 группы
Организационный момент. Класс делится
на 3 группы
2. Проверка домашнего задания.
Подготовительный этап
Цель: повторить понятие пропорции, основное свойство пропорции, способы решения уравнений с помощью пропорции.
Учитель: Здравствуйте, дорогие ребята! Сегодня мы приступаем к изучению новой темы (СЛАЙД 1). К вам я пришла не одна, а с “волшебным экраном”. Он вас научит решать задачи, а по какой теме, мы узнаем, если выполним условия нашего гостя. Ну что начнем? Смотрим на экран, какое испытание он предлагает нам в самом начале урока (СЛАЙД 2).
Ученики: Фронтально отвечают на вопросы “экрана”.
Учитель:
Итак, первое испытание мы прошли,
двигаемся дальше. (СЛАЙД 3). А теперь
поиграем в домино и разгадаем тему
(СЛАЙД 4). У вас на столах лежат плашки,
они разделены на две части: на одной
уравнение, на другой ответ. Ваша задача:
решить уравнение, найти плашку с ответом,
совместить их. Все плашки сложить в ряд.
Какая группа справится, поднимаем руку.
(Все плашки и правильное решение приведено
на СЛАЙДЕ 5).
Ваша задача:
решить уравнение, найти плашку с ответом,
совместить их. Все плашки сложить в ряд.
Какая группа справится, поднимаем руку.
(Все плашки и правильное решение приведено
на СЛАЙДЕ 5).
Ученики: Устно решают уравнения.
Объяснение нового материала
Цель: познакомиться с понятием прямой пропорциональности; сформировать навык решения задач на прямую пропорциональность; вывести алгоритм решения таких задач.
Учитель: Готово? Хорошо! Итак, проверим, как вы сложили плашки. Должно получится как у “волшебного экрана”.
Ученики: Проверяют.
Учитель:
Теперь, давайте перевернем плашки и
прочтем тему нашего урока. (СЛАЙД 5).
Проверим с экраном, так или нет. Все,
молодцы. Значит, мы сегодня решаем задачи
по теме “Прямая пропорциональность”.
Итак, (СЛАЙД 6), узнаем, какая пропорциональность
называется прямой, научимся решать
задачи, выведем план решения таких
задач. Записываем в тетрадях число,
классная работа.
Записываем в тетрадях число,
классная работа.
Ученики: Записывают.
Учитель: (На карточках задания каждой группе. По выполнению один учащийся из группы проверяет задание с экраном. СЛАЙДЫ 7, 8, 9.). Мы находимся в группах, для каждой группы “волшебный экран” приготовил задания. Нужно его выполнить, чтобы двигаться дальше.
По СЛАЙДУ 7: По какой формуле находим S?
Ученик: , следовательно, S= 20 км; 40 км; 120 км.
Учитель: Что происходит со временем?
Ученик: Время увеличивается.
Учитель: Одновременно со временем, что происходит с расстоянием?
Ученик: Оно также увеличивается.
Учитель: Давайте, проанализируем, как увеличивается время?
Ученик:
Сначала в 2 раза, потом в 3 раза.
Учитель: А расстояние как себя ведет?
Ученик: Увеличивается сначала в 2 раза, потом в 3 раза.
Учитель: Проверим, верно, ли мы рассуждаем или нет? (СЛАЙД 6).Молодцы!
По СЛАЙДУ 8: По какой формуле находим площадь?
Ученик: , следовательно, S= 4; 8; 16.
Учитель: Что происходит с шириной прямоугольника?
Ученик: Ширина прямоугольника увеличивается сначала в 2 раза, потом в 2 раза.
Учитель: Одновременно с шириной как изменяется площадь?
Ученик: Увеличивается сначала в 2 раза и потом еще в 2 раза.
Учитель: Проверим, верно, ли мы рассуждаем или нет? (СЛАЙД 7).Молодцы!
По СЛАЙДУ 9: По какой формуле находим периметр квадрата?
Ученик:
, следовательно, Р = 32 см; 16 см; 4 см.
Учитель: Что происходит со стороной квадрата?
Ученик: Сторона уменьшается сначала в 2 раза, потом в 4 раза.
Учитель: Одновременно, как изменяется периметр?
Ученик: Периметр уменьшается сначала в 2 раза, потом в 4 раза.
Учитель: Проверим, верно, ли мы рассуждаем или нет? (СЛАЙД 9).Молодцы!
Мы выслушали мнения всех трех групп, мнения все верные. Поэтому, какой вывод можно сделать по всему сказанному?
Ученик: Если одна величина увеличивается в несколько раз, то и другая увеличивается в это же число раз. Если одна уменьшается, то и другая уменьшается, в это же число раз.
Учитель: Давайте проверим, правильно ли мы рассуждаем или нет? (СЛАЙД 10) Итак, как вы думаете, как называются такие величины?
Ученик:
Затрудняются ответить.
Учитель: (СЛАЙД 11) Эти величины называются прямо пропорциональными? Обратите внимание, как направлены стрелочки?
Ученик: Стрелки направлены в одну сторону.
Закрепление нового материала
Цель: отработка навыка решения задач с помощью плана решения.
Учитель: Итак, наш “волшебный экран” приготовил первую задачу. (СЛАЙД12) Попробуем решить задачу с помощью уравнения. Что нужно сделать, решая задачу уравнением?
Ученик: Ввести неизвестную.
Учитель: Что обозначим за Х?
Ученик: Количество деталей, выполненное за 4 часа.
Учитель: Составим уравнение с помощью пропорции:
100 деталей 2 часа
Х деталей 4 часа
Определим
вид зависимости. Чем больше времени,
тем больше деталей сделаем за это время.
Следовательно, зависимость прямая. А
прямая зависимость обозначается
стрелками в одну сторону: либо вверх,
либо вниз.
Чем больше времени,
тем больше деталей сделаем за это время.
Следовательно, зависимость прямая. А
прямая зависимость обозначается
стрелками в одну сторону: либо вверх,
либо вниз.
Осталось составить уравнение по стрелкам и решить его.
Ученик: Решают.
Учитель: Проверим, правильно ли мы решили задачу. (СЛАЙД 13)
Давайте, теперь по решению первой задачи выделим шаги алгоритма или план решения задачи.
Ученик: Стараются выделить шаги алгоритма.
Учитель: Проверим, правильно ли мы мыслим или нет. (СЛАЙД 14)
Следующее задание (СЛАЙД 15), выполняем проговаривая шаги алгоритма вслух.(Один у доски)
Ученик: Читают условие задачи и решают ее по шагам алгоритма.
Учитель: Проверим, правильно ли мы решили? (СЛАЙД 16)
Следующее
задание (СЛАЙД 17) , выполняем, проговаривая
шаги алгоритма про себя.
Ученик: Решают сами.
Учитель: Проверим, правильно ли мы решили? (СЛАЙД 18). Молодцы, все у нас сегодня получилось.
Итог:
Учитель: Давайте подведем итог нашего необычного урока, на этом задания “волшебного экрана” еще не закончились. (СЛАЙД 19).
Ученик: Отвечают фронтально на вопросы “экрана”.
Учитель: (СЛАЙД 20) Запишите домашнее задание, которое предлагает ваш гость. Давайте попрощаемся с ним и позовем еще раз в гости. Все были молодцы, всем спасибо и до скорой встречи. (СЛАЙДЫ 21, 22).
Прямая пропорция — Промежуточный и Высший уровень — Соотношение — WJEC — GCSE Maths Numeracy (WJEC) Revision
Говорят, что две величины прямо пропорциональны, если они увеличиваются или уменьшаются в одном и том же отношении.
Если две суммы прямо пропорциональны, мы можем увеличить их путем умножения.
- Вопрос
Если три карандаша стоят 75 пенсов, сколько стоят девять карандашей?
- Показать ответ
Мы знаем, что три лота по три дают девять.
Итак, если мы умножим стоимость трех карандашей на 3, мы получим стоимость девяти карандашей:
75p × 3 = 225p
pu8go7moxq.0.0.0.1:0.1.0.$0.$2.$1.3.$3″> Девять карандашей стоят 2,25 фунта стерлингов
Возможно, вам придется использовать общий множитель. найти новое количество.
- Вопрос
В рецепте четырех блинов используется 300 мл молока. Сколько молока нужно на десять блинов?
- Раскройте ответ
Из двух частей рецепта получится восемь блинов:
2 × 300 мл = 600 мл
Из половины рецепта получится два блина:
pu8go7moxq.0.0.0.1:0.1.0.$0.$3.$1.3.$3″> ½90 × 300 мл = 0503 0508 чтобы испечь десять блинчиков:
600 + 150 = нужно 750 мл молока.
Наконец, может быть проще использовать деление, чтобы найти, сколько стоит одна единица, а затем умножить, чтобы найти окончательный ответ.
Пример 1
Семь апельсинов стоят 1,75 фунта стерлингов, сколько будут стоить три апельсина?
Решение
- Один апельсин будет стоить 1,75 фунта стерлингов ÷ 7 = 0,25 фунта стерлингов = 25 пенсов 0.1:0.1.0.$0.$4.$4.$1″> Таким образом, три апельсина будут стоить 25 пенсов × 3 = 75 пенсов
Символ прямой зависимости ∝.
A ∝ B означает, что A прямо пропорционально B.
Это можно преобразовать в формулу:
\[\text{A = k × B}\]
, где \(\text{k}\) — константа пропорциональности. Он показывает взаимосвязь между A и B.
Пример 2
Няня получает 6,25 фунтов стерлингов за каждый час работы. Здесь заработок прямо пропорционален количеству отработанных часов. Мы можем записать это как:
0.$0.$6.$2.$0″> заработок ∝ отработанных часов
Мы можем создать формулу, чтобы показать взаимосвязь между этими двумя значениями: заработок = 6 фунтов стерлингов.25 × отработанных часов.
Эта формула позволяет легко рассчитать заработок или количество отработанных часов, учитывая другое значение.
- Вопрос
Заработная плата строителя прямо пропорциональна количеству отработанных часов. Плата строителя за пять часов работы составляет 68 фунтов стерлингов.
a) Напишите формулу, показывающую связь между заработной платой и количеством отработанных часов, и используйте ее для расчета константы пропорциональности
pu8go7moxq.0.0.0.1:0.1.0.$0.$7.$0.1.$2″> b) Используйте эту формулу для расчета заработной платы строителя, если они отработали три часа- Покажите ответ
а) 68 фунтов стерлингов = почасовая оплата × пять часов.
68 фунтов стерлингов ÷ 5 часов = почасовая оплата.
Почасовая оплата = 13,60 фунтов стерлингов в час.
Формула: заработная плата = 13,60 фунтов стерлингов × отработанные часы .
pu8go7moxq.0.0.0.1:0.1.0.$0.$7.$0.3.$4″> b) Заработная плата = 13,60 ф. ст. × 3 = 40,80 ф. ст. Для чего они используются?Сегодня мы узнаем, что такое прямые пропорции и для чего они используются.
Прежде чем мы продолжим, нам нужно знать, что такое величина .
Величина — это количество, которое можно измерить или подсчитать . Например, вес человека, количество работающих строителей, количество бананов, количество собачьего корма, съеденного собакой, расстояние между двумя городами или скорость лошади на полном галопе.
Все это может быть связано с другими типами величин.
Прямые пропорции- Вес человека может быть связан с размером одежды, которую он может носить.
- Количество работающих строителей может быть связано со временем, которое требуется для завершения проекта.
- Количество бананов можно соотнести с количеством ящиков, необходимых для их хранения.

- Расстояние между двумя городами может быть связано со временем, затрачиваемым на путешествие между ними.
- Скорость скачущей лошади может быть связана со временем, которое требуется лошади, чтобы добраться из одной точки в другую.
Существуют различные виды отношений.Сегодня мы рассмотрим одну из них: прямых пропорции.
Чтобы между двумя величинами сохранялась прямо пропорциональная связь, они должны быть связаны таким образом, что если мы удвоим одну, то другая также удвоит . Точно так же, если мы утроим один, другая величина тоже должна быть утроена . Тот же случай для уменьшения, если мы уменьшаем одно наполовину, то и другое нужно уменьшить наполовину. Таким образом, в основном, если мы увеличиваем количество одного, другой должен делать это «пропорционально».Какую связь мы можем увидеть между количеством бананов и количеством ящиков, которые нам нужны для того, чтобы их хранить?
Как видите, сколько бы бананов у нас ни было, нам нужно больше коробок, верно? Эти две величины поддерживают отношения, которые прямо пропорциональны.

Важно знать, что отношение между двумя прямо пропорциональными величинами всегда постоянно. В нашем примере это соотношение равно 3 .
Отношения прямой пропорциональности часто встречаются в нашей повседневной жизни.
Примеры
Вы когда-нибудь покупали конфеты? Как рассчитать сумму денег, которую нужно заплатить за конфету?
Что вы можете сказать, ребята, об этих двух величинах: количестве свиней и количестве стогов сена, которые нужны, чтобы их накормить?
Можно ли сказать, что они сохраняют прямую пропорциональность?
Если вы хотите научиться решать задачи на пропорциональность, помните, что в Smartick у вас есть гораздо больше упражнений и задач на пропорциональность для практики.
Узнать больше:
Веселье — любимый способ обучения нашего мозга
Дайан Акерман
Smartick — увлекательный способ изучения математики- 15 минут веселья в день
- Адаптируется к уровню вашего ребенка
- Миллионы учеников с 2009 года
Группа создания контента.
МОДУЛЬ
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.РАЗ M35 — Пропорция
Проект улучшения математического образования в школах (TIMES)
вернуться к индексу
ПРЕДПОЛАГАЕМЫЕ ЗНАНИЯ
- Свободное владение арифметикой целых чисел и дробей.
- Знакомство с основными единицами расстояния, времени, массы и объема.
- Рисование прямых графиков.
- Определение градиента прямолинейного графика.
- Знакомство с коэффициентами и ставками.
- Простые формулы и уравнения.
МОТИВАЦИЯ
Врачи и медсестры рассчитывают, сколько лекарства нужно ввести, используя
идеи пропорции. Например, предположим, что лекарство должно вводиться со скоростью
20 микрограммов на кг в минуту. Если больной весит 56 кг, сколько миллиграммов он должен получить за один час?Люди, работающие в науке, финансах и многих других областях, ищут отношения между различными величинами интереса.
 Эти отношения часто оказываются либо линейными, либо гиперболическими. То есть график, связывающий эти величины, представляет собой либо прямую линию, либо гиперболу.
Эти отношения часто оказываются либо линейными, либо гиперболическими. То есть график, связывающий эти величины, представляет собой либо прямую линию, либо гиперболу.В этом модуле мы в основном занимаемся формулами (см. модуль «Формулы»), для которых соответствующие графики представляют собой либо прямые линии, либо прямоугольные гиперболы. В первом случае имеем прямую пропорцию, а во втором обратно пропорциональную.
Возьмем очень простой пример: I = закон Ома, связывающий V напряжение (разность потенциалов), I ток и R сопротивление проводника.
Закон Ома является фундаментальным в изучении электричества. Если R — константа, I прямо пропорциональна V. Если V — константа, I обратно пропорциональна R. В модуле «Коэффициенты и отношения» формула d = vt соединяет пройденное расстояние d, затраченное время t и скорость V. было представлено и обсуждено. При постоянной скорости пройденное расстояние пропорционально пройденному времени, а при фиксированном расстоянии затраченное время обратно пропорционально скорости.

Более сложные ситуации также рассматриваются с использованием пропорции.Известный пример из науки: для тела, движущегося с постоянным ускорением, пройденное расстояние 90 247 пропорционально квадрату времени, пройденного в пути.
Существует огромное разнообразие применений пропорций, и это станет очевидным из множества примеров, приведенных в разделе содержания модуля.
В этом модуле будет представлен ряд формул из физики, однако читателю не обязательно знать связанные с ними физические принципы.
СОДЕРЖАНИЕ
В этом модуле мы будем использовать слова «переменная» и «постоянная» вместо одного слова
«пронумеральный».Прямая пропорция
Определение
Говорят, что переменная y прямо пропорциональна x, если
y = kx для некоторой ненулевой константы k.
Константа k называется константой пропорциональности.
Утверждение «у прямо пропорционально х» символически записывается как
у х.
Иногда в литературе вместо пропорции используется слово вариация.

График y = kx представляет собой прямую линию, проходящую через начало координат. Его градиент k является константой пропорциональности. (Значения, которые может принимать x, часто являются положительными действительными числами, но это не всегда так.)
Вот простой пример прямой пропорциональности.
Дэвид едет из дома с постоянной скоростью 100 км/ч.
Формула для расстояния d км, пройденного за t часов, равна
.д = 100т.
Дэвид пройдет в два раза дальше за удвоенное время, в три раза дальше за три раза и так далее.
График зависимости d от t представляет собой прямую линию, проходящую через начало координат. В этом примере d прямо пропорционально t, и мы пишем d t. Константа 100 — это константа пропорциональности, и это градиент линии.
Обратите внимание, что в этом примере константой пропорциональности является скорость, то есть скорость. Ставки являются одним из наиболее распространенных примеров пропорции.

Коэффициенты, соотношения и пропорции
Ставки и коэффициенты учитывались в модуле Ставки и коэффициенты. Идеи этого модуля
получили дальнейшее развитие и рассматриваются с другой точки зрения.Ставки
Все ситуации с постоянной скоростью, подобные приведенному выше примеру с автомобилем, движущимся с постоянной скоростью, представляют собой примеры прямой зависимости.
Например, если вода поступает в бак со скоростью 5 литров в минуту, то количество воды V литров, влившееся в бак через t минут, определяется по формуле V = 5t.Таким образом, объем воды прямо пропорционален времени, в течение которого вода в нее втекает.
Вот таблица значений для этой ситуации.
Из таблицы видно, что это константа.
= = = = = 5.
Таким образом, отношение V : t постоянно.
В : т = 5 : 1 = 10 : 2 = 15 : 3 = 20 : 4.
Из этого примера видно, как связаны постоянные ставки, постоянные отношения и прямая пропорция.
Соотношения
Предположим, что размеры прямоугольника относятся к 3 : 2.
 Пусть х — длина прямоугольника, а у — ширина. Затем
Пусть х — длина прямоугольника, а у — ширина. Затему : х = 3 : 2 или = или у = .
Ширина прямоугольника y прямо пропорциональна длине прямоугольника.
Константа пропорциональности равна . График зависимости y от x представляет собой прямую линию, проходящую через 90 247 начала координат с градиентом .ПРИМЕР
Отрезана лента шириной 3 см и длиной 1 см. Площадь отрезанной ленты Acm2 определяется по формуле A = 3l.Напишите заявление о пропорции словами и символами, укажите константу пропорциональности и нарисуйте график зависимости А от l.
Решение
Поскольку A = 3l, A прямо пропорционально
l, и мы можем написать A l. Константа пропорциональности
равна 3.Свойства прямой зависимости
Ниже приведены три важных свойства пропорции.
Применение свойств
Существует множество приложений, иллюстрирующих второе и третье свойства
прямой зависимости.
Пример свойства 2
Если автомобиль движется со скоростью 60 км/ч, то расстояние, пройденное Skkm за t часов, равно
.S = 60т. Здесь S t и константа пропорциональности равна 60. Перестановка дает
t = S. Следовательно, t S и коэффициент пропорциональности равен .
Пример свойства 3
Для выращивания риса требуется 40 кг азотных удобрений на гектар, а стоимость
кг составляет 50 центов. Пусть A гектаров будет площадь, n будет количество килограммов необходимых удобрений, а
$C будет общая стоимость удобрений.Имеем n = 40A и C = 0,5n. Это означает n A и
C n. Следовательно, C A. Мы видим, что C = 20 A, поэтому C A.Другие примеры прямой пропорциональности
Есть много примеров прямой пропорциональности. Вот несколько элементарных примеров, показывающих повсеместность этой идеи.
Из торговли
- Когда мы читаем цену на нефть 72 доллара за баррель, мы предполагаем, что цена количества нефти прямо пропорциональна количеству баррелей.
 Большинство проблем, связанных с затратами на единицу продукции, связаны с прямой зависимостью.
Большинство проблем, связанных с затратами на единицу продукции, связаны с прямой зависимостью. - Сумма налога на товары и услуги, подлежащая уплате за товар, прямо пропорциональна стоимости товара. Константа пропорциональности равна 10%.
- При заданной процентной ставке, например 6% годовых, сумма процентов, полученных за фиксированный период времени, прямо пропорциональна сумме инвестиций.
- Курсы валют. Стоимость предмета в евро пропорциональна его стоимости в долларах.
Из измерения
- Преобразование между единицами измерения обычно связано с прямой пропорцией.Например, перевод сантиметров в метры или футов в метры. Есть примеры, когда преобразование единиц не связано с прямой пропорцией, например, преобразование Фаренгейта в Цельсия.
- Глубина воды в сосуде, который представляет собой прямую призму с горизонтальным «основанием», прямо пропорциональна объему воды, а объем прямо пропорционален глубине воды
- Периметр правильного многоугольника прямо пропорционален длине одной стороны.

- Длина окружности прямо пропорциональна радиусу окружности с коэффициентом пропорциональности 2π. И наоборот, радиус круга прямо пропорционален длине окружности. (C = 2πr и r = )
- На карте, нарисованной в масштабе, расстояние между любыми двумя точками на карте пропорционально расстоянию между двумя местоположениями, которые представляют точки,
с константой пропорциональности, являющейся масштабом карты.
Из науки
- Масса тела пропорциональна его объему. Константа пропорциональности равна
плотности тела. Например, плотность воды 1 грамм/см3. (Формула m = ρV) - Ускорение тела пропорционально действующей на него равнодействующей силе.
Константа пропорциональности — масса. (Формула = ) - Сила, действующая на определенный объект из-за гравитации, пропорциональна массе объекта.Константа пропорциональности между массой и силой известна как гравитационное ускорение.
- Для постоянной силы, действующей на тело, работа, совершаемая силой, пропорциональна расстоянию, на которое перемещается тело.
 (Формула W = Fd)
(Формула W = Fd) - Гравитационная потенциальная энергия тела над земной поверхностью пропорциональна высоте тела над земной поверхностью. Константа пропорциональности является произведением массы и ускорения свободного падения.
- Для тела, движущегося по окружности с постоянной угловой скоростью, линейная скорость (тангенциальная скорость) пропорциональна угловой скорости. Константой пропорциональности является радиус окружности. (Формула v = ωr)
- Закон Архимеда: вес вытесненной жидкости прямо пропорционален объему вытесненной жидкости. Проще говоря, принцип гласит, что выталкивающая сила, действующая на объект, равна весу жидкости, вытесненной объектом.
- Закон Шарля: при постоянном давлении объем V заданной массы идеального газа увеличивается или уменьшается на тот же коэффициент, что и его температура T по абсолютной шкале температур (т. е. газ расширяется при повышении температуры).
Свойства прямой зависимости можно с пользой применять в каждом из приведенных выше примеров.
 Вот еще два важных примера.
Вот еще два важных примера.Обмен валюты (пример свойства 2): конвертировать австралийские доллары в доллары США и доллары США в австралийские доллары.(Обратное значение константы пропорциональности, используемой для первого преобразования, применяется для второго.)
Преобразование единиц измерения (пример свойства 3): Измените метры на миллиметры, сначала заменив метры на сантиметры, а затем заменив сантиметры на миллиметры.
УПРАЖНЕНИЕ 1
Медицинский пример, с которого начинается раздел мотивации, также использует свойство 3.
Лекарство вводят пациенту со скоростью 20 мкг/кг/мин.Если пациент весит 56 кг, сколько миллиграммов он должен получить за один час?
УПРАЖНЕНИЕ 2
В 2008 году во время мирового финансового кризиса один австралийский доллар стоил 0,618 доллара США. Сколько стоил один доллар США в австралийских долларах?
(После этого подумайте о золотом сечении.)Нахождение константы пропорциональности
Если y пропорционально x, константу пропорциональности можно найти, если задано только одно значение x и соответствующее значение y.

ПРИМЕР
Переменная y пропорциональна переменной x. Когда x = 4, y = 11. Найдите константу пропорциональности и, следовательно, запишите формулу для y через x.
Решение
Поскольку y пропорциональна x, существует константа k такая, что y = kx.
Когда x = 4, y = 11, поэтому 11 = 4k и k = .
Следовательно, у = х.
Порядок решения этого вопроса был следующим.
- Запишите оператор пропорции в виде уравнения, содержащего константу k.
- Используйте информацию в вопросе, чтобы найти значение k.
- Перепишите формулу с вычисленным значением k.
Пропорциональность квадрату или кубу
Металлический шар падает с вершины высокого здания, и расстояние, на которое он падает, записывается каждую секунду.
Из физики формула для расстояния d m, на которое мяч упал за t секунд, равна
.d = 4,9t2.
В этом случае мы говорим, что d прямо пропорционально
квадрату t.Когда мы строим график зависимости d
от t, график представляет собой половину параболы.
Но что случилось с нашей прямой линией, проходящей через начало координат, которую мы ожидаем от прямой пропорциональности? Мы можем получить прямую линию, нанеся график зависимости d от t2, а не от t.
т 0 1 2 3 т 2 0 1 4 9 д 0 4.9 19,6 44,1 Градиент этой линии равен 4,9.
Теперь это прямая линия, проходящая через начало координат с градиентом 4,9.

Мы видим, что d пропорционально t2, и запишем это как d t2.Это означает, что для любых двух значений t1 и t2 с соответствующими значениями d1 и d2,
= = 4,9.
Таким образом, еще раз соотношение является константой, а градиент линии является константой пропорциональности.
Есть много примеров, когда одна величина пропорциональна квадрату
или кубу другой. Вот еще несколько элементарных примеров:Как мы видели выше, для нахождения константы пропорциональности нужна всего одна пара значений
.ПРИМЕР
Масса, m грамм пластического материала, необходимая для формования твердого шара, прямо пропорциональна кубу радиуса r см шара. Если нужно 40 грамм пластика
, чтобы сделать шар радиусом 2.5 см, какого размера мяч можно сделать из 200 граммов такого же пластика?Решение
Мы знаем, что m = kr3, где k — константа и
м = 40 при r = 2,5 Так 40 = к × (2,5)3 к = 2,56. 
Итак, формула m = 2,56r3
При m = 200, 200 = 2,56r3 г3 = 78,125 г = г ≈ 4,27 см УПРАЖНЕНИЕ 3
Мощность p кВт, необходимая для движения лодки, зависит от куба ее скорости s м/с.Если мощность 400 кВт позволяет лодке двигаться со скоростью 3 м/с, то какая мощность потребуется для того, чтобы та же лодка двигалась со скоростью 5 м/с?
Увеличение и уменьшение
Если одна величина пропорциональна другой, мы можем понять, что происходит с одной из величин при изменении другой.
Пусть y = kx для положительной константы k.
Если значение x удваивается, то значение y удваивается. Лучший способ продемонстрировать это — подставить конкретное значение x.
Например, если мы подставим x = 7, тогда y = 7k, а когда x = 14, получится y = 14k.

Аналогично, если значение x утроится, то значение y утроится. Мы можем использовать это с любым вопросом пропорции.
Сводка по прямой пропорции
- y прямо пропорционально x, если существует положительная константа k такая, что y = kx.
- Для обозначения «пропорционально» используется символ . Пишем у х.
- Если y прямо пропорционально x, то график зависимости y от x представляет собой прямую линию,
проходящую через начало координат.Градиент линии является константой пропорциональности.
Обратная пропорция
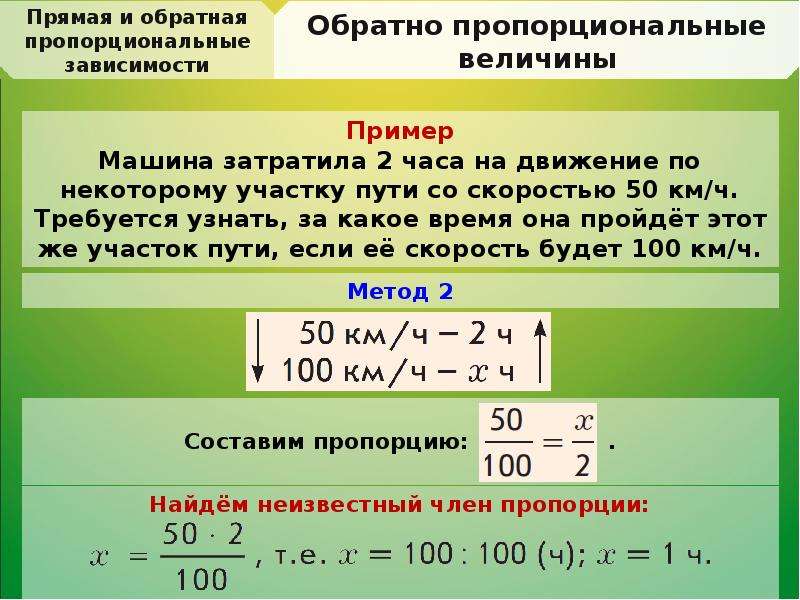
Определение
Говорят, что переменная y обратно пропорциональна x, если
г =
для константы k. Число k называется константой пропорциональности.
Утверждение, что «y обратно пропорционально x», записывается символически как y .
Обратите внимание, что это также может быть прочитано как «у прямо пропорционально».Полезные свойства обратной пропорциональности отличаются от свойств прямой пропорциональности.
 Здесь мы перечисляем три важных свойства.
Здесь мы перечисляем три важных свойства.Скорость и время являются хорошим примером обратной пропорциональности.
Мы знаем, что расстояние = скорость × время или д = vt Перестановка дает время = или т = Пусть расстояние между двумя городами равно 72 км.Время t часов, необходимое для преодоления этого расстояния со скоростью v км/ч, определяется по формуле
.т =
Это пример обратной пропорции. Мы пишем t и говорим, что t обратно пропорционально v с коэффициентом пропорциональности 72,
.График зависимости t от v является частью прямоугольной гиперболы, но график зависимости t от
представляет собой прямую линию с градиентом 72.ПРИМЕР
Предположим, что два города А и В находятся на расстоянии 144 км друг от друга.
а Запишите формулу для времени t часов, затрачиваемого на поездку из А в В со скоростью v км/ч.

b Нарисуйте график зависимости t от v.
c Если автомобиль движется со скоростью 24 км/ч, сколько времени потребуется, чтобы завершить поездку?
d Если поездка занимает 90 минут, с какой постоянной скоростью
должен двигаться автомобиль?Решение
с При v = 24, т
=
= 6 часов
д При t = =
, =
Так в
= 144 ×
= 96 км/ч
Есть много примеров обратной пропорциональности тем, изучаемых в школе.
 Например,
Например,- Лента длиной 100 м должна быть разделена между n людьми. Длина, которую получает каждый человек, обратно пропорциональна количеству людей.
- Для цилиндров объемом 2 м3 высота цилиндра обратно пропорциональна площади основания.
- Сила между двумя заряженными объектами обратно пропорциональна квадрату расстояния между их центрами.
- Освещенность от источника света обратно пропорциональна квадрату расстояния от источника.
УПРАЖНЕНИЕ 4
Объем V см3 газа при постоянной температуре обратно пропорционален давлению P кПа. Если объем равен 500 см3 при давлении 80 кПа, найдите объем при давлении 25 кПа. (Это пример закона Бойля)
УПРАЖНЕНИЕ 5
Если a обратно пропорционально кубу b и a = 2 при b = 3, найдите
и
а при b = 2
б
б, когда а =
Как и в случае с прямой пропорцией, мы можем рассчитать влияние на одну переменную изменения другой.

Сводная информация об обратной пропорции
х1 у1 = х2у2 = к.
ССЫЛКИ ВПЕРЕД
Пропорциональность по нескольким переменным
Часто конкретная физическая величина зависит от нескольких других переменных. Например, расстояние d, которое проезжает автомобилист, зависит как от скорости v, с которой он едет, так и от времени t, которое он проезжает, d = vt.
В более общем смысле, если y = kxz для положительной константы k, мы говорим, что y прямо пропорциональна x и z.Точно так же, если a = для положительной константы k, мы говорим, что a прямо пропорционально b3 и обратно пропорционально c2.
ПРИМЕР
Предположим, что a прямо пропорционально b и квадрату c. Если a = 36 при b = 3 и
c = 2, найти a при b = 4 и c = 1Решение
и BC2 так и = kbc2 для некоторой константы k Подстановка известных значений для нахождения k.

36 = к × 3 × 22 к = 3, Отсюда и = 3bc2 Когда b = 4 и c = 1, a = 3 × 4 × 12 = 12
УПРАЖНЕНИЕ 7
Электрическое сопротивление R ом в проводе прямо пропорционально его длине L м и обратно пропорционально квадрату его диаметра d мм.Некий провод длиной 100 м с
диаметром 0,4 мм имеет сопротивление 1,4 Ом.a Найдите уравнение, связывающее R, L и D.
b Найти сопротивление (с точностью до одного десятичного знака) провода из того же материала, если его длина 150 м, а диаметр 0,25 мм.
c Если длину и диаметр увеличить вдвое, как изменится сопротивление?
d Если длину увеличить на 10 %, а диаметр уменьшить на 5 %, как изменится сопротивление в процентах? (Ваш ответ дайте с точностью до одного десятичного знака.
 )
)Два очень важных случая прямой зависимости от нескольких переменных — это два правила обратных квадратов.
Первый — это фундаментальный закон силы тяготения, а второй — закон Кулона для электростатической силы между двумя электрическими зарядами. Для основного закона тяготения R — это расстояние между массами m1 и m2, а для закона Кулона — расстояние между зарядами q1 и q2.
Другие применения пропорции
Важные примеры возникают в математике, где существует прямая зависимость от функции.Одним из важных случаев является случай, когда y 2 x , что обеспечивает модель как для экспоненциального роста, так и для экспоненциального затухания.
Интересным случаем пропорции является закон Снеллиуса. Когда свет преломляется через прозрачное вещество, угол падения θ связан с углом преломления Φ
уравнениемsin θ = k sin Φ для некоторой константы k, называемой показателем преломления.
Таким образом, нужно взять синус обоих углов, чтобы получить утверждение о пропорциональности.

Функции и вычисления
Эта тема является началом понимания учащимися приложений функций и должна показать степень применения математики во многих различных областях. Это ведет ко всем аспектам изучения функций и исчисления. Графическое представление о ставках дает идея пропорции.
ИСТОРИЯ
История пропорции начинается с древних греков. Он был разработан в Книге V Евклида и использован для геометрии в Книге VI.Многие вопросы, поднятые у Евклида, не были удовлетворительно решены до работ Вейерштрасса, Кантора и Дедекинда в 19 веке. Кое-что из этого обсуждается в модуле «Коэффициенты и коэффициенты».
Пропорция — настолько фундаментальная идея, что она проявлялась в более приземленных проявлениях.
Один из таких случаев следующий:Правило трех
Правило трех было сокращенной версией особой формы перекрестного умножения, которую часто заучивали ученики наизусть.Вот пример типа проблемы.
Если три банана стоят 60 центов, сколько будут стоить 7 бананов? Используя правило трех, вы должны умножить 60 на 7 и разделить на 3.

Метод эквивалентен решению уравнения = . Без современных алгебраических обозначений язык, объясняющий, почему правило трех произведений было трудно объяснить.
Правило трех было создано индусскими математиками Брахмагуптой (около 628 г. н.э.) и Бхаскарой (около 1150 г. н.э.).Он появился в Европе с 15 века и пользовался огромной популярностью у торговцев. Английский арифметик XVII века писал: «Правило трех обычно называют золотым правилом; и действительно, это можно было бы так назвать; ибо, как золото превосходит все другие металлы, так и этот закон превосходит все остальные в арифметике».
Конечно, мы можем переписать решение этого вопроса в терминах пропорции «Стоимость n бананов в центах = 20n».
Греческая наука
Идеи отношений использовались и в греческой науке.Например, Архимед
(287–212 гг. до н. э.) добился результатов, касающихся балансировки однородного стержня. Проиллюстрируем это на примере.Груз массой 3 кг находится на расстоянии 120 см от точки опоры, на которой балансирует штанга.
 Равновесие может быть достигнуто, если поместить груз массой m килограммов на расстоянии x см от точки опоры с другой стороны от точки опоры, так что mx = 120 × 3. Следовательно, расстояние, на котором находится вес от точки опоры, необходимое для равновесия, обратно пропорционально пропорциональна весу.Современный термин для этого продукта – момент.
Равновесие может быть достигнуто, если поместить груз массой m килограммов на расстоянии x см от точки опоры с другой стороны от точки опоры, так что mx = 120 × 3. Следовательно, расстояние, на котором находится вес от точки опоры, необходимое для равновесия, обратно пропорционально пропорциональна весу.Современный термин для этого продукта – момент.Трактат Архимеда «О плавающих телах» также содержит материал, в котором используются пропорции. Принцип Архимеда, упомянутый ранее в этом модуле, является примером его результатов в этой области.
Пропорция, наука и математика
Мы кратко обсудим развитие некоторых аспектов математики и естественных наук вплоть до начала 18 века. Мы не можем попытаться дать какую-либо полную картину этого, но отметим, что наука и математика развивались очень тесно вместе вплоть до Нового времени, и пропорция была центральным понятием в этом развитии.
Корни многих математических наук лежат в физических науках.
Некоторый прогресс был достигнут в средние века.
 Ученые Мертона в Оксфорде в середине четырнадцатого века изучали движение с постоянным ускорением, и им приписывалось следующее.
Ученые Мертона в Оксфорде в середине четырнадцатого века изучали движение с постоянным ускорением, и им приписывалось следующее.Тело, движущееся с равноускоренным движением в данное время точно такое же расстояние, которое оно двигалось бы с постоянной скоростью, равной его мгновенной скорости, в середине рассматриваемого периода времени.
90 132 Николь Оремская (1323–1382) разработала схематическое изображение движения. Он пришел к представлению пройденного расстояния в виде области, двумя измерениями которой (представленными перпендикулярными линиями) были время, а другое — скорость. Таким образом, он представил идею, очень похожую на прямоугольные координаты. Его выводы должны были быть повторены и развиты Галилеем. Эта работа была проделана задолго до того, как появилось четкое представление о координатной геометрии.Пропорция была частью языка математики и физики со времен Галилея (1564 − 1642). Многие рукописи, происходящие от греков, пришли из Византийской империи и от арабов, и многие считали, что эти рукописи стали катализатором возрождения научной мысли в Европе.
 Галилей добился того, что для тела, движущегося с постоянным ускорением, пройденный путь пропорционален квадрату времени движения.
Галилей добился того, что для тела, движущегося с постоянным ускорением, пройденный путь пропорционален квадрату времени движения.Кеплер (1571 − 1630) также был знаком с работами древних греков.Он последовал за Коперником и развил его теории дальше. Его законы планетарного движения используют язык пропорций.
Законы Кеплера:
- Орбита каждой планеты представляет собой эллипс с Солнцем в одном из двух фокусов.
- Линия, соединяющая планету и Солнце, заметает равные площади за равные промежутки времени. С точки зрения пропорций это можно записать так: «Площадь, очерченная за данный промежуток времени линией, соединяющей Солнце с планетой, пропорциональна длине временного интервала».
- Квадрат периода обращения планеты прямо пропорционален кубу большой полуоси ее орбиты.
Гюйгенс (1629 − 95) получил дальнейшие результаты и обнаружил, что для тела, движущегося по круговой траектории с постоянной скоростью v, ускорение направлено к центру окружности .
 Сила, действующая на частицу, пропорциональна квадрату скорости и обратно пропорциональна радиусу окружности.
Сила, действующая на частицу, пропорциональна квадрату скорости и обратно пропорциональна радиусу окружности.Работа сэра Исаака Ньютона (1642 − 1727) последовала за работами более ранних ученых, о которых говорилось выше.Он родился в год смерти Галилея. Он математически объяснил результаты, полученные Галилеем и Кеплером. Для достижения этих результатов он использовал разработанное им исчисление. Он получил фундаментальный закон гравитационных сил F = G, который можно прочитать так: «Каждая точечная масса притягивает любую другую точечную массу силой, направленной вдоль линии, пересекающей обе точки». Сила прямо пропорциональна произведению двух масс и обратно пропорциональна квадрату расстояния между точечными массами.
Второй закон движения Ньютона также сформулирован в терминах пропорции.
«Изменение в движении пропорционально приложенной движущей силе и происходит на прямой линии, по которой приложена эта сила» (F = ma).
Пропорция оставалась ключевой идеей на протяжении 18-го и 19-го веков, и ее значение, конечно же, сохраняется и по сей день.

ОТВЕТЫ НА УПРАЖНЕНИЯ
УПРАЖНЕНИЕ 1
67,2 миллиграмма
УПРАЖНЕНИЕ 2
1.618 (десятичная аппроксимация золотого сечения)
УПРАЖНЕНИЕ 3
1852 кВт
УПРАЖНЕНИЕ 4
1600см3
УПРАЖНЕНИЕ 5
и 6,75 б 4 УПРАЖНЕНИЕ 6
и y увеличивается примерно на 23.5% б x уменьшился примерно на 4,7% УПРАЖНЕНИЕ 7
и Р = б 5,4 Ом с сопротивление уменьшено вдвое д сопротивление увеличено на 21.9% Проект «Улучшение математического образования в школах» (TIMES) на 2009–2011 годы финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.

Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Министерства образования, занятости и трудовых отношений правительства Австралии.
© Мельбурнский университет от имени Международного центра передового опыта в области образования по математике (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное).Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/Прямая и обратная пропорция
Пропорция — это просто равенство двух или более дробей :
$$$\dfrac{a}{b}=\dfrac{c}{d}$$$
, где $$a$$ и $$d$$ — названные концы, а $$b$$ и $$c$$ — середины.
Прямая пропорция
Мы скажем, что пропорция прямая, если они относятся к величинам, в которых при увеличении одной возрастает и другая, и наоборот .

В этом случае правило трех будет применяться следующим образом:
Если поезду требуется $$3$$ часа, чтобы пройти $$400$$ километров: сколько времени потребуется, чтобы преодолеть вдвое большее расстояние?
Для начала заметим, что это случай прямой зависимости, так как чем больше часов мы проводим, тем больше километров проедет поезд. Ответ можно вывести мысленно, поскольку, если поезд должен пройти в два раза большее расстояние, он также займет в два раза больше времени, поэтому ему потребуется $6$$ ч, чтобы пройти $$800$$ км.Вывод правильный, но давайте посмотрим, как он решается, применяя правило трех для прямых пропорций.
Имеем следующее отношение:
$$$\begin{eqnarray} 3 \\mbox{h} & \rightarrow & 400 \ \mbox{км}\\ х \ \mbox{h} & \rightarrow & 800 \ \mbox{км} \end{eqnarray}$$$
То есть, если за $3$$ ч будет пройдено $400$$ км, то за $$x$$ ч будет пройдено $800$$.
Мы видим, что отношение может быть также выражено в соответствии с моделью равенства между дробями, используемой для описания понятия пропорции:
$$$\dfrac{3}{x}=\dfrac{400}{800}$$$
Где обе величины упражнения остаются в разных дробях: время в одной части равенства и расстояние в другой.

Теперь нам нужно только изолировать $$x$$, чтобы найти решение:
$$$x=\dfrac{800\cdot3}{400}=\dfrac{2400}{400}=6$$$
Следовательно, поезду потребуется $$6$$ часов, чтобы пройти $$800$$ км.
Если килограмм вишни стоит $4,5$$ €: сколько будет стоить полкило?
У нас есть прямая зависимость, так как чем меньше килограммов мы покупаем, тем меньше они будут стоить.
Имеем отношение пропорциональности:
$$$\begin{eqnarray} 1 \ \mbox{кг} & \rightarrow & 4,5 \ \mbox{€}\\ \frac{1}{2} \\mbox{кг} & \rightarrow & x \ \mbox{€} \end{eqnarray}$$$
Применяя правило трех имеем:
$$$x=\dfrac{\frac{1}{2}\cdot4,5}{1}=\dfrac{1}{2}\cdot4,5=2,25$$$ €
Значит, полкило вишни будет стоить вдвое дешевле килограмма.
Обратная пропорция
Мы будем говорить, что пропорция обратная, если она включает отношение величин, при котором, когда мы увеличиваем одну из них, другая уменьшается, и наоборот .
 В этом случае правило трех будет применяться следующим образом:
В этом случае правило трех будет применяться следующим образом:Если фермеру с $2$$ требуется $$10$$ дней, чтобы вспахать поле: сколько потребуется той же работы для фермера с $$5$$?
Это явный пример обратной пропорциональности, поскольку чем больше фермеров работает, тем меньше времени потребуется для вспашки одного и того же поля.
Для ее решения применяется правило трех, как учили:
$$$\begin{eqnarray} 2 \\mbox{фермеры} & \rightarrow & 10 \ \mbox{дни}\\ 5 \ \mbox{фермеров} & \rightarrow & x \ \mbox{дней} \end{eqnarray}$$$
И решено:
$$$x=\dfrac{2\cdot10}{5}=\dfrac{20}{5}=4$$$ дней
Таким образом, несмотря на то, что двум фермерам требуется $$10$$ дней, с помощью еще $$3$$ партнеров они смогут выполнить ту же работу всего за $$4$$ дней.
Международный журнал научных и технологических исследований
ДОБРО ПОЖАЛОВАТЬ В IJSTR (ISSN 2277-8616) —
International Journal of Scientific & Technology Research — это международный журнал с открытым доступом, посвященный различным областям науки, техники и технологий, в котором особое внимание уделяется новым исследованиям, разработкам и их применению. 
Приветствуются статьи, сообщающие об оригинальных исследованиях или расширенных версиях уже опубликованных статей для конференций/журналов. Статьи для публикации отбираются на основе рецензирования, чтобы гарантировать оригинальность, актуальность и удобочитаемость.
IJSTR обеспечивает широкую политику индексации, чтобы сделать опубликованные статьи заметными для научного сообщества.
IJSTR является частью экологически чистого сообщества и предпочитает режим электронной публикации как онлайновый «ЗЕЛЕНЫЙ журнал».
Приглашаем вас представить высококачественные статьи для рецензирования и возможной публикации во всех областях техники, науки и техники.Все авторы должны согласовать содержание рукописи и ее представление для публикации в этом журнале, прежде чем она будет передана нам.
 Рукописи должны быть представлены через онлайн-подачу
Рукописи должны быть представлены через онлайн-подачуIJSTR приветствует ученых, которые заинтересованы в работе в качестве добровольных рецензентов. Рецензенты должны проявить интерес, отправив нам свои полные биографические данные. Рецензенты определяют качество материалов.Поскольку ожидается, что они будут экспертами в своих областях, они должны прокомментировать значимость рецензируемой рукописи и то, способствует ли исследование знаниям и продвижению как теории, так и практики в этой области. Заинтересованным рецензентам предлагается отправить свое резюме и краткое изложение конкретных знаний и интересов по адресу [email protected]
.IJSTR публикует статьи, посвященные исследованиям, разработкам и применению в области техники, науки и технологий.Все рукописи предварительно рецензируются редакционной комиссией.
 Вклады должны быть оригинальными, ранее или одновременно не публиковавшимися в других местах, и подвергаться критическому анализу перед публикацией. Статьи, которые должны быть написаны на английском языке, должны иметь правильную грамматику и правильную терминологию.
Вклады должны быть оригинальными, ранее или одновременно не публиковавшимися в других местах, и подвергаться критическому анализу перед публикацией. Статьи, которые должны быть написаны на английском языке, должны иметь правильную грамматику и правильную терминологию.IJSTR — международный рецензируемый электронный онлайн-журнал, публикуемый ежемесячно. Цель и сфера деятельности журнала — предоставить академическую среду и важную ссылку для продвижения и распространения результатов исследований, которые поддерживают обучение, преподавание и исследования на высоком уровне в области инженерии, науки и технологий.Приветствуются оригинальные теоретические работы и прикладные исследования, которые способствуют лучшему пониманию инженерных, научных и технологических задач.
прямо пропорционально в предложении
Эти примеры взяты из корпусов и из источников в Интернете.
 Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.Выходная амплитуда системы в основном прямая пропорция к энергии входного жеста.
Независимо от природы стимула дисперсия ответов была в прямой пропорциональной средней частоте возбуждения этой реакции.
В обеих странах значимость концепции была функцией образования, при этом демократия имела значение в прямой пропорциональной продолжительности обучения респондента в школе.
Если и есть что-то близкое к надежной корреляции в социальных науках, так это то, что перья растут в 90 141 прямой 90 142 90 141 пропорционально 90 142 близости к линии гоминидов.

Однако можно предсказать важное свойство их распределения: частота, с которой гласные неправильно интерпретируются как удлиненные, будет возрастать в прямой пропорциональной их внутренней длительности.
Количество и стоимость проб почвы увеличиваются в прямой пропорциональной размеру интересующей области, и данные будут доступны только после лабораторных анализов.
Они не просят ни гроша из общего фонда, который не прямо пропорционален их текущим расходам.
Но поскольку они сконцентрировались на подоходном налоге, выгода, полученная физическими лицами от сокращения налога, была прямо пропорциональна их доходам.

Количество заболеваемости варьировалось в прямой пропорциональной степени и продолжительности паводков в течение зимы.
Лучше, чтобы власти начисляли прямую пропорцию к количеству представлений.
Политика будет успешной в прямой пропорции силы ввода в эксплуатацию и относительно ограниченного характера системы лицензирования.
По мере того, как все больше и больше людей вовлекается в его сферу действия, число тех, кто выступает против него, растет в прямой пропорции .

Однако следует помнить, что их способность делать это прямо пропорциональна зависимости экономики от экспорта.
Возврат на вложенные деньги находится в прямой пропорции к количеству купленных единиц.
Мы пытаемся получить цифры прямой пропорции к количеству образования и возможностям зданий.
На самом деле это не так, и никогда не было так, что уменьшение в прямо пропорционально уменьшению ствола.
Если мой благородный друг простит мои слова, посещаемость не должна быть прямой пропорциональной доброте или дурности меры.

Я сам обнаружил, что моя структура увеличивается в прямой пропорциональной зависимости от удовольствия от еды.
Не увеличилась ли заболеваемость астмой и другими серьезными респираторными заболеваниями прямо пропорционально увеличению автомобильного движения?
Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Что такое прямая пропорция, Формула прямой пропорции
Вслед за отношение математики , прямая пропорция включает использование соотношений для сравнения и установления значений и сумм.
Что такое прямая пропорция?
Если два или более отношения равны, то они находятся в прямой пропорциональности.
1 : 4 , 2 : 8 , 3 : 12
Все вышеперечисленные коэффициенты прямо пропорциональны, обе части коэффициента увеличиваются с одинаковой скоростью.
Каждый раз, когда левая часть увеличивается на 1 , правая часть увеличивается на 4 .
Примеры
(1.1)
Сотрудник компании зарабатывает 16 долларов США за 2 часов работы.
Сколько долларов они заработают за 7 часов работы?
Оплата с тем же соотношением долларов и часов.Решение
Мы можем записать соотношение как Часы : Доллары => 2 : 16 .

Который можно упростить до 1 : 8 .
8 долларов за  1 час работы.
Теперь, умножив обе части коэффициента на 7 , вы получите коэффициент для  7 оплаченных часов. Работа.
1 × 7 = 7 , 8 × 7 = 56 => 7 : 56
За 7 часов работы сотрудник заработает 56 долларов США .
(1.2)
Для приготовления молочных коктейлей 4 девушка использует следующие ингредиенты.
800 мл Молоко: 28 г Клубника : 4 г сахара .
Сколько каждого ингредиента потребуется для приготовления  13 молочных коктейлей из тех же ингредиентов соотношение?
Решение
Разделив на 4 , вы получите отношение молочного коктейля 1 .

800 &дел 4 = 200 , 28 &дел 4 = 7 , 4 &div 4 = 1Теперь, когда у нас есть количество ингредиентов для 1 молочного коктейля.
Умножение на  13 даст количество ингредиентов для 13 молочных коктейлей.200 × 13 = 2600 , 7 × 13 = 91 , 1 × 13 = 13
Соотношение ингредиентов, необходимых для приготовления 13 молочных коктейлей, составляет,
2600 мл Молоко : 91 г Клубника : 13 г Сахар .
Формула прямой пропорцииКогда одно значение прямо пропорционально другому, например, в примере (1.
 1), где заработанные деньги
была прямо пропорциональна количеству отработанных часов.
1), где заработанные деньги
была прямо пропорциональна количеству отработанных часов.Можно написать, что M ∝ H ,
означает, что M прямо пропорционально H .В примере (1.1), заработанные деньги были прямо пропорциональны отработанным часам.
Заработанные деньги = долларов × часов
Это соединение может быть записано как M = k H .
Где k – константа, специально называемая «константой соразмерность».
Нам просто нужны два соответствующих значения M и H для определения значения k.
Нам дали это в примере (1.1) с » 2 Часов и » 16 » Долларов.16 = k 2 => \\boldsymbol{\\frac{16}{2}} = k => 8 = к
В результате получается полная формула прямой зависимости в примере (1.
 1):
1):
М = 8 ННапример (1.1), в любое время, когда вы захотите узнать сумму Денег, заработанных сотрудником, вы просто умножаете количество отработанных часов на 8 .
- Домой ›
- Соотношение и пропорция › Что такое прямая пропорция
Вернуться к НАЧАЛУ страницы .


 Сколько страниц напечатает она за 14 дней?
Сколько страниц напечатает она за 14 дней?



 Эти отношения часто оказываются либо линейными, либо гиперболическими. То есть график, связывающий эти величины, представляет собой либо прямую линию, либо гиперболу.
Эти отношения часто оказываются либо линейными, либо гиперболическими. То есть график, связывающий эти величины, представляет собой либо прямую линию, либо гиперболу.


 Пусть х — длина прямоугольника, а у — ширина. Затем
Пусть х — длина прямоугольника, а у — ширина. Затем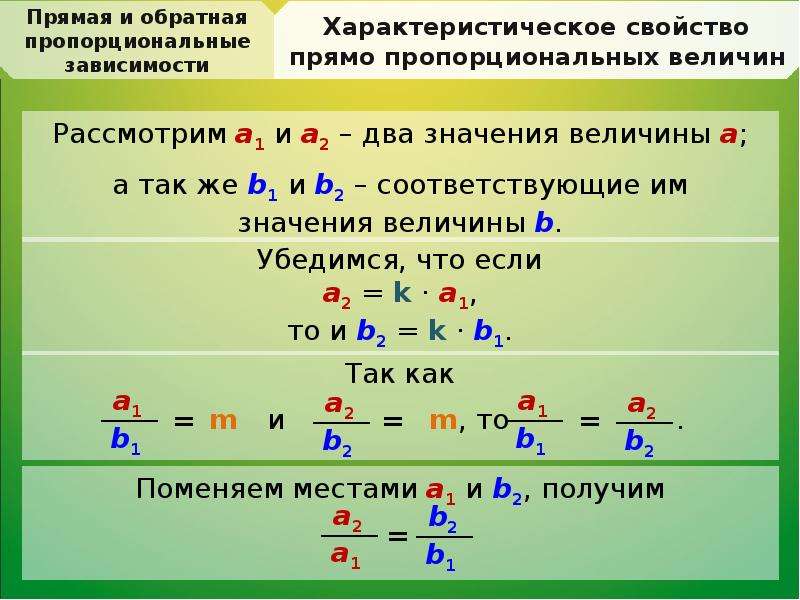
 Большинство проблем, связанных с затратами на единицу продукции, связаны с прямой зависимостью.
Большинство проблем, связанных с затратами на единицу продукции, связаны с прямой зависимостью.
 (Формула W = Fd)
(Формула W = Fd) Вот еще два важных примера.
Вот еще два важных примера.




 Здесь мы перечисляем три важных свойства.
Здесь мы перечисляем три важных свойства.
 Например,
Например,

 )
)

 Равновесие может быть достигнуто, если поместить груз массой m килограммов на расстоянии x см от точки опоры с другой стороны от точки опоры, так что mx = 120 × 3. Следовательно, расстояние, на котором находится вес от точки опоры, необходимое для равновесия, обратно пропорционально пропорциональна весу.Современный термин для этого продукта – момент.
Равновесие может быть достигнуто, если поместить груз массой m килограммов на расстоянии x см от точки опоры с другой стороны от точки опоры, так что mx = 120 × 3. Следовательно, расстояние, на котором находится вес от точки опоры, необходимое для равновесия, обратно пропорционально пропорциональна весу.Современный термин для этого продукта – момент. Ученые Мертона в Оксфорде в середине четырнадцатого века изучали движение с постоянным ускорением, и им приписывалось следующее.
Ученые Мертона в Оксфорде в середине четырнадцатого века изучали движение с постоянным ускорением, и им приписывалось следующее. Галилей добился того, что для тела, движущегося с постоянным ускорением, пройденный путь пропорционален квадрату времени движения.
Галилей добился того, что для тела, движущегося с постоянным ускорением, пройденный путь пропорционален квадрату времени движения. Сила, действующая на частицу, пропорциональна квадрату скорости и обратно пропорциональна радиусу окружности.
Сила, действующая на частицу, пропорциональна квадрату скорости и обратно пропорциональна радиусу окружности.



 В этом случае правило трех будет применяться следующим образом:
В этом случае правило трех будет применяться следующим образом:
 Рукописи должны быть представлены через онлайн-подачу
Рукописи должны быть представлены через онлайн-подачу Вклады должны быть оригинальными, ранее или одновременно не публиковавшимися в других местах, и подвергаться критическому анализу перед публикацией. Статьи, которые должны быть написаны на английском языке, должны иметь правильную грамматику и правильную терминологию.
Вклады должны быть оригинальными, ранее или одновременно не публиковавшимися в других местах, и подвергаться критическому анализу перед публикацией. Статьи, которые должны быть написаны на английском языке, должны иметь правильную грамматику и правильную терминологию. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.





 1), где заработанные деньги
была прямо пропорциональна количеству отработанных часов.
1), где заработанные деньги
была прямо пропорциональна количеству отработанных часов. 1):
1):