Решение систем линейных уравнений методом Гаусса

1. Решение систем линейных уравнений методом Гаусса

2. Метод Гаусса – это метод последовательного исключения переменных

• Систему уравнений приводят к
эквивалентной ей системе с
треугольной матрицей. Это называется
прямым ходом.
• Из полученной треугольной системы
переменные находят с помощью
последовательных подстановок. Это
называется обратным ходом.

3. При выполнении прямого хода используют следующие преобразования:

1. Умножение или деление коэффициентов
свободных членов на одно и то же число;
2. Сложение и вычитание уравнений;
3. Перестановка уравнений системы;
4. Исключение из системы уравнений, в
которых все коэффициенты при
неизвестных и свободные члены равны
нулю.

4. Решить систему уравнений методом Гаусса

x y 5
2 x y 7
Нужно записать расширенную матрицу системы
1 1 5
2 1 7
Вертикальная черта внутри матрицы не несёт
никакого математического смысла – это
просто отчеркивание для удобства
оформления.
Матрица системы – это матрица,
составленная только из
коэффициентов при неизвестных.
Расширенная матрица системы – это
та же матрица системы плюс
столбец свободных членов, в
данном случае.

6. Решение. Умножим первую строку на (-2)

1 1 5
2 1 7
2 2 10
2 1 7

7. ко второй строке прибавим первую строку умноженную на -2

1 1 5
2 1 7
2 2 10
0 3 3
2 2 10
2 1 7

8. Разделим опять первую строку на (-2)

1 1 5
2 1 7
2 2 10
0 3 3
2 2 10
2 1 7
1 1 5
0 3 3
строка, которую ПРИБАВЛЯЛИ – не изменилась.
Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.

9. Цель элементарных преобразований –

Цель элементарных преобразований
–
привести матрицу к ступенчатому виду.
Сам термин «ступенчатый вид» не
вполне теоретический, в научной и
учебной литературе он часто
называется трапециевидный
вид или треугольный

10.

В результате элементарных преобразований получена эквивалентная исходной система уравнений В результате элементарных преобразований
получена эквивалентная исходной система уравнений
x y 5
2 x y 7
x y 5
y 1
Выполняем обратный ход, т.е. подстановку в первое
уравнение вместо у,
х =-5+у
х=-5+1
х=-4
Ответ: (-4; 1)

11. Решить систему уравнений методом Гаусса

3 x 2 y z 4
2 x y 3z 9
x 2 y 2z 3
Решение.
Переставим третье уравнение на место первого и запишем расширенную
матрицу:
x 2 y 2z 3
3 x 2 y z 4
2 x y 3z 9
1 2 2 3
3 2 1 4
2 1 3 9

12. Чтобы в первом столбце получить а2=а3=0, умножим 1-ю строку сначала на 3, а затем на 2 и вычтем результаты из 2-й и 3-й строк

1 2 2 3
3 2 1 4
2 1 3 9
1 2 2 3
0 8 7 5
0 3 1 3

13. Разделим 2-ю строку на 8, полученные результаты умножим на 3 и вычтем из 3-й строки

1 2 2 3
3 2 1 4
2 1 3 9
1 2 2 3
0 1 7 5
8 8
0 3 1 3
1 2 2 3
0 8 7 5
0 3 1 3
1 2 2 3
0 3 21 15
8
8
0 3 1 3
1 2 2
3
21
15
0
3
8
8
39
0 0 13
8
8

14. Запишем новую эквивалентную систему с учетом расширенной матрицы

x 2 y 2z 3
7
5
y z
8
8
13
39
z
8
8
x 2 y 2z 3
7
5
y z
8
8
13
39
z
8
8
Выполняем обратный ход, с помощью
последовательных подстановок находим
неизвестные
13
39
z
z 3
8
8
7
5
5 21 16
y 3
y
2
8
8
8 8
8
x 2 2 2 3 3 x 3 4 6 1
Ответ: (1; 2; 3)

Вычислить определитель матрицы системы методом гаусса онлайн. Вычисление определителя

Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.

О методе

При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.

1. Записываем расширенную матрицу.
2. Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
3. Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.

Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите «очень подробное решение» и посмотрите его решение онлайн.

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

Обозначения : Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два» :

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 — нормальные.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Пример:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ .

Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке , очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:

Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу :

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя .

БУДЬТЕ ВНИМАТЕЛЬНЫ!

Содержание

Введение…………………………………………………………………………………………….. 2

1. Постановка задачи………………………………………………………………………….. 3

2. Математические и алгоритмические основы решения задачи……………… 5

2.1 Определитель матрицы………………………………………………………………….. 5

2.2 Метод Гаусса для решения систем линейных уравнений…………………… 6

2.3 Метод Гаусса для вычисления определителя……………………………………. 8

3. Функциональные модели и блок-схемы решения задачи…………………….. 9

4. Программная реализация решения задачи………………………………………. 11

5. Пример выполнения программы…………………………………………………….. 16

Заключение………………………………………………………………………………………. 18

Список использованных источников и литературы……………………………… 19

Введение

Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему алгебраических уравнений.

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.

При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.

Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы и нахождения определителя.

Целью данной курсовой работы является реализация вычисления определителя методом исключения Гаусса.

1. Постановка задачи

Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную матрицу, её определитель равен произведению элементов, стоящих на диагонали.

. ~. . .

Вычислить определитель матрицы методом A исключения Гаусса.

.

Приведем матрицу к диагональному виду методом Гаусса.

~.

Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:

.

Знак определяется количеством обменов строк, следовательно определитель матрицы

.

2. Математические и алгоритмические основы решения задачи

2.1 Определитель матрицы

Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка n, нужно уже знать, что такое определитель матрицы порядка n-1. Отметим также, что определитель существует только у квадратных матриц.

Определитель квадратной матрицы A будем обозначать

или det A.

Определение. Определителем квадратной матрицы

второго порядка называется число

.

Определителем

квадратной матрицы порядка n,

, называется число — определитель матрицы порядка n-1, полученной из матрицы A вычеркиванием первой строки и столбца с номером k.

2.2 Метод Гаусса для решения систем линейных уравнений

Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.

Воспользуемся идеями метода Гаусса решения систем линейных уравнений.

Дана система:

a11 x1 + a12 x2 + … + a1n xn = b1

a21 x1 + a22 x2 + … + a2n xn = b2

an1 x1 + an2 x2 + … + ann xn = bn

Выполним следующий алгоритм.

На первом шаге найдём в первом столбце наибольший по модулю элемент, поставим уравнение с этим элементом на первую строчку (обменяв две соответствующие строки матрицы A и два соответствующих элемента вектора B), а затем будем отнимать это уравнение от всех остальных, чтобы в первом столбце все элементы (кроме первого) обратились в ноль. Например, при прибавлении ко второй строке будем домножать первую строку на -a21/a11, при добавлении к третьей — на -a31/a11, и т.д.

На втором шаге найдём во втором столбце, начиная со второго элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на вторую строчку, и будем отнимать это уравнение от всех остальных (в том числе и от первого), чтобы во втором столбце все элементы (кроме второго) обратились в ноль. Понятно, что эта операция никак не изменит первый столбец — ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.

Т.е. на i-ом шаге найдём в i-ом столбце, начиная с i-го элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на i-ю строчку, и будем отнимать это уравнение от всех остальных. Понятно, что это никак не повлияет на все предыдущие столбцы (с первого по (i-1)-ый).

В конце концов, мы приведём систему к так называемому диагональному виду:

Т.е. мы нашли решение системы.

Замечание 1. На каждой итерации найдётся хотя бы один ненулевой элемент, иначе система бы имела нулевой определитель, что противоречит условию.

Замечание 2. Требование, что на каждом шаге мы выбираем наибольший по модулю элемент, очень важно в смысле численной устойчивости метода. Если выбирать произвольный ненулевой элемент, то это может привести к гигантской погрешности, когда получившееся решение будет отличаться в разы от правильного.

2.3 Метод Гаусса для вычисления определителя

Будем выполнять те же самые действия, что и при решении системы линейных уравнений, исключив только деление текущей строки на a[i][i] (точнее, само деление можно выполнять, но подразумевая, что число выносится за знак определителя). Тогда все операции, которые мы будем производить с матрицей, не будут изменять величину определителя матрицы, за исключением, быть может, знака (мы только обмениваем местами две строки, что меняет знак на противоположный, или прибавляем одну строку к другой, что не меняет величину определителя).

Но матрица, к которой мы приходим после выполнения алгоритма Гаусса, является диагональной, и определитель её равен произведению элементов, стоящих на диагонали. Знак, как уже говорилось, будет определяться количеством обменов строк (если их нечётное, то знак определителя следует изменить на противоположный). Таким образом, мы можем с помощью алгоритма Гаусса вычислять определитель матрицы за O(N3).

Осталось только заметить, что если в какой-то момент мы не найдём в текущем столбце ненулевого элемента, то алгоритм следует остановить и вернуть 0.

3. Функциональные модели и блок-схемы решения задачи

Блок-схема решения задачи представлена на рисунке 1.

Рисунок 1 – Блок-схема решения задачи для функции DETERMINATE

4 Программная реализация решения задачи

;ФУНКЦИЯ, ВЫЧИСЛЯЮЩАЯ ОПРЕДЕЛИТЕЛЬ

(DEFUN DETERMINANT (MATRIX SIZE)

;ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ

;ОПРЕДЕЛИТЕЛЬ

(DECLARE (SPECIAL DET))

;ВСПОМОГАТЕЛЬНЫЕ МАССИВЫ И ПЕРЕМЕННЫЕ

(DECLARE (SPECIAL PAR))

(DECLARE (SPECIAL R))

(DECLARE (SPECIAL T_))

(DECLARE (SPECIAL I))

(DECLARE (SPECIAL II))

;*********************

(SETQ R (MAKE-ARRAY SIZE:ELEMENT-TYPE «FLOAT:INITIAL-ELEMENT 0))

((>= J (- SIZE 1)))

;ИСКЛЮЧАЕМ ДЕЛЕНИЕ НА 0

(IF (= (AREF MATRIX J J) 0)

(SETQ II (+ J 1))

;ИЩЕМ СТРОКУ В КОТОРОЙ J-Й ЭЛЕМЕНТ НЕ 0

((OR (/= (AREF MATRIX II J) 0) (= II (- SIZE 1))))

(SETQ II (+ II 1))

;ЕСЛИ НЕТ ТАКОЙ СТРОКИ ОПРЕДЕЛИТЕЛЬ РАВЕН 0

(IF (AND (= (AREF MATRIX II J) 0) (= II (- SIZE 1))) (SETQ T_ 0))

Вычислим определитель методом Гаусса.

Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.

Идея метода состоит в следующем: пусть дан определитель третьего порядка

элементдолжен быть равен
, для этого первую строку разделим на.

Получим определитель вида
(2)

Обнулим элементы, стоящие в первом столбце, кроме первого. Для этого из второй строки вычтем первую, умноженную на
, далее из третьей строки вычтем первую, умноженную на. Получим определитель вида
.

Обозначим его элементы буквой с, тогда

(3)

Теперь надо обнулить элемент . Элемент
должен быть равен
, для этого вторую строку разделим на
. Получим определитель вида
.

.

Обозначим его элементы буквой t, тогда

(4)

Вот мы привели определитель к треугольному виду, теперь он равен
.

Разберем теперь это на конкретном примере.

Пример 4: Вычислить определительметодом Гаусса.

Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).

Получили

Из второй строки вычтем первую, умноженную на 2, далее из третьей строки вычтем первую, умноженную на 3. Получили

Получили —

§2.Матрицы Виды матриц

Определение 7: Если в матрицеmстрок иnстолбцов, то она называетсяразмерностью mnи пишут
.

Определение 8: Если
, то матрица называется квадратной.

Определение 9: Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).

Определение 10: Матрица, состоящая из нулей, называется нулевой матрицей.

Определение 11: Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.

Определение 12: Единичной матрицей называется диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице.

Определение 13: Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.

Действиянад матрицами.

Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.

Пример 5:

Матрицы А и В равны, т.е.

Определение 15: Суммой (разностью) матриц А и В называется такая матрица С, у которой каждый элемент равен
.

Пример 6: Найти матрицу
, если

Решение:

Cвойства сложения

А+В=В+А(переместительное)

2 0 А+О=А, где О-нулевая матрица

3 0 А+(В+С)=(А+В)+С (дистрибутивное)

4 0 А+(-А)=О, где – А противоположная матрица

(т.е. элементы имеют противоположные знаки)

Определение 16: Произведением матрицы А на число
называется матрица, полученная из данной умножением всех ее элементов на число.

Пример 7:

Умножение матиц

Это действие распространяется на так называемые согласованные матрицы.

Определение 17: Матрица А называетсясогласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.

Пример 8:
и
— согласованные

и
— несогласованные

и
несогласованные

Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементовiстроки матрицы А на соответствующие элементыj-го столбца матрицы В.

Если матрица А имеет размерность
, а матрица В
, то
.

Пример 9: Умножить матрицы

Метод Гаусса — определение с примерами решения

Содержание:

1. Опишем метод Гаусса подробнее
2. Примеры с решением
3. Пример 4.4.
4. Пример 4.5.
5. Пример 1.18.
6. Пример 1.7.
7. Пример 1.8.

Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.

Пусть дана система уравнений (4.3)

Процесс решения по методу Гаусса состоит из двух этапов. На нервом этапе (прямой ход) система приводится к i ступенчатому (в частности, треугольному) виду.

Приведенная ниже система имеет ступенчатый вид

где

Коэффициенты называются главными элементами системы. На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Опишем метод Гаусса подробнее

Прямой ход. Будем считать, что элемент (если то первым в системе запишем уравнение, в котором коэффициент при отличен от нуля). Преобразуем систему (4.3), исключив неизвестное во всех уравнениях, кроме первого (используя элементарные преобразования системы).

Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы.

Затем умножим обе части первого уравнения на и сложим с третьим уравнением сиап стемы. Продолжая этот процесс, получим эквивалентную систему

Здесь

новые значения коэффициентов и правых частей, которые полу чаю юя после первого шага. Аналогичным образом, считая главным элементом исключим неизвестное из всех уравнений системы, кроме первого и второго, и так далее.

Продолжаем этот процесс, пока это возможно. Если в процессе приведения системы (4.3) к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида их отбрасывают. Если же появится уравнение вида то это свидетельствует о несовместности системы. Второй этап {обратный ход) заключается в решении ступенчатой системы.

Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное через остальные неизвестные Затем подставляем значение в предпоследнее уравнение системы и выражаем затем находим Придавая свободным неизвестным произвольные значения, получим бесчисленное множество решений системы.

Возможно вам будут полезны данные страницы:

Замечания: 1. Если ступенчатая система оказывается треугольной, т. е. то исходная система имеет единственное решение. Из последнего уравнения находим хп, из предпоследнего уравнения далее поднимаясь по системе вверх, найдем все остальные неизвестные На практике удобнее работать не с системой (4.3), а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на ).

Примеры с решением

Пример 4.4.

Решить систему методом Гаусса:

Решение:

В результате элементарных преобразований над расширенной матрицей системы

исходная система свелась к ступенчатой:

Поэтому общее решение системы: Если положить, например, то найдем одно из частных решений этой системы

Пример 4.5.

Решить систему методом Гаусса:

Решение:

Произведем элементарные преобразования над строчками расширенной матрицы системы:

Полученная матрица соответствует системе

Осуществляя обратный ход, находим Рассмотрим решение системы (1.25) т линейных уравнений с п неизвестными. Заметим, что матрица коэффициентов системы не обязательно должна быть квадратной.

Предлагаемые методы решения систем линейных алгебраических уравнений сводятся к элементарным преобразованиям над уравнениями системы.

Преобразования Гаусса удобно проводить, осуществляя преобразования не самих уравнений, а строк матрицы их коэффициентов.

Рассмотрим матрицу

(1. 33) называемую расширенной матрицей системы (1.25), так как в нее, кроме коэффициентов матрицы А системы (1.25), дополнительно включен столбец свободных членов В. Метод Гаусса (метод последовательного исключения неизвестных. Рассмотрим систему (1.25) в случае

Суть метода Гаусса заключается в том, что с помощью элементарных преобразований расширенная матрица системы (1.33) приводится к равносильной матрице ступенчатого вида по алгоритму поиска ранга матрицы (см. пример 1.13). Это и есть прямой ход метода Гаусса.

На основании полученной ступенчатой матрицы составляется новая система уравнений, равносильная исходной, из которой последовательно, начиная с последнего уравнения, находятся все неизвестные; это суть обратного хода метода Гаусса.

Пример 1.18.

Решить систему уравнений методом Гаусса:

Решение:

Расширенная матрица системы имеет вид

Используя элементарные преобразования (см. пример 1.14), сведем эту матрицу к ступенчатой, не забывая при этом, что теперь в строке уже не три, а четыре элемента.

Вспомнив, что до черты стоят коэффициенты системы уравнений, а после нее — столбец свободных членов, выпишем получившуюся систему уравнений:

Теперь применим обратный ход метода Гаусса. Из последнего 4 2 тл уравнения полученной системы найдем

Из второго уравнения найдем Аналогично найдем из первого уравнения, подставив в него уже наиденные два неизвестных

Получим решение системы

Предлагаем читателю убедиться, что найденные числа образуют решение данной системы. Расширенная матрица системы. Ступенчатая матрица. Метод Гаусса. Коэффициенты системы (1.1) удобно объединить в прямоугольную таблицу, называемую матрицей системы. Для матрицы принято обозначение:

Матрица содержит т горизонтальных рядов, называемых строками, и вертикальных рядов, называемых столбцами, числа называются ее элементами. Таким образом, первый индекс элемента — это номер строки (номер уравнения системы (1. 1)), а второй индекс — номер столбца (или номер неизвестного коэффициентом при котором является уравнении системы (1.1)).

Например, матрица

квадратная матрица 3-го — единичная матрица 2-го порядка. Если к матрице А добавить столбец из свободных членов, то получим так называемую расширенную матрицу А* системы, содержащую всю информацию о системе:

Для системы из примера 1.1 матрицей системы является а расширенной матрицей этой системы является матрица На практике элементарным преобразованиям подвергают не саму систему, а ее расширенную матрицу.

Преобразованиям двух типов над системой (1.1) соответствуют два типа элементарных преобразований над строками матрицы 1-й тип — перестановка местами двух любых ее строк; 2-й тип — сложение соответствующих элементов двух любых строк, все элементы одной из которых предварительно умножены на одно и то же число.

Целью элементарных преобразований является приведение расширенной матрицы системы (1.1) к так называемой ступенчатой форме.

Определение 1.6. Матрица называется ступенчатой, если для нее выполняются следующие условия: 1) если какая-либо строка данной матрицы состоит из нулей, то и все последующие строки также состоят из нулей; 2) если — первый ненулевой элемент строки, а — первый ненулевой элемент строки,то Так, например, матрица

является ступенчатой.

Матрица из одной строки считается ступенчатой по определению. Теорема 1.2. Любую матрицу Л конечным числом элементарных преобразований первого и второго типов можно преобразовать в ступенчатую матрицу.

Пример 1.7.

Привести к ступенчатому виду матрицу

Решение:

Выполним следующие элементарные преобразования над матрицей

1) к элементам второй строки прибавим элементы первой строки и из элементов третьей строки вычтем элементы первой строки, в результате преобразуется к виду: — расширенная матрица системы.

2) переставим вторую и третью строки:

3) из третьей строки полученной матрицы вычтем вторую строку, умноженную на 3, получим:

На приведении расширенной матрицы системы (1. 1) к ступенчатой матрице основан метод Гаусса, или метод последовательного исключения неизвестных. Система линейных уравнений с расширенной ступенчатой матрицей называется ступенчатой системой, по теореме 1.1 она будет равносильна соответствующей системе в форме (1.1). Приведение системы (1.1) к ступенчатой форме называется прямым ходом метода Гаусса.

Решение полученной ступенчатой системы называется обратным ходом метода Гаусса. Он может быть выполнен как в форме последовательного определения неизвестных, начиная с последнего уравнения ступенчатой системы, так и в форме преобразования матрицы к ступенчатой матрице специального вида.

Пример 1.8.

Решить методом Гаусса систему уравнений

Решение:

Прямой ход метода Гаусса. В примере 1.7 матрица при помощи элементарных преобразований приведена к ступенчатой матрице

Теперь матрице сопоставим систему, для которой она будет расширенной матрицей:

Обратный ход метода Гаусса. 1-й способ. Имеем: . 2-й способ.

Умножим последнюю строку матрицы на 1 /5, сложим со второй строкой, после чего к первой строке прибавим последнюю, умноженную на (-2), с целью получить нули в третьем столбце:

Напишем систему с расширенной матрицей

Ответ: система совместная и определенная, она имеет единственное решение:

Решение уравнений в Excel методом итераций Крамера и Гаусса

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х² + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
2. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
3. После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».



Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

1. Значения элементов введем в ячейки Excel в виде таблицы.
2. Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
3. Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
4. Умножим обратную матрицу Ах^-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
5. Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

1. Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
2. Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
3. Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
4. Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
5. В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х³ + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

Х_n+1 = X_n– F (X_n) / M, n = 0, 1, 2, … .

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х³ – 1. М = 11.

В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Скачать решения уравнений в Excel

Корень на заданном промежутке один.

Метод Гаусса — Жордана — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения ко

Пользователи также искали:

метод гаусса онлайн, метод гаусса пример, метод гаусса — жордана обратная матрица, метод гаусса жордана онлайн, метод гаусса — жордана python, метод гаусса — жордана с выбором ведущего элемента, метод жордана — гаусса c++, отличие метода гаусса от метода жордана — гаусса, Гаусса, гаусса, метода, Метод, метод, жордана, Жордана, онлайн, отличие, python, матрица, обратная, ведущего, элемента, пример, выбором, метод гаусса пример, метод гаусса онлайн, метод жордана — гаусса c, Метод Гаусса — Жордана, метод гаусса — жордана python, отличие от метода жордана — гаусса, метод гаусса — жордана обратная матрица, метод гаусса — жордана с выбором ведущего элемента, метод гаусса жордана онлайн, метод гаусса — жордана, методы решения слау. метод гаусса — жордана, метод гаусса — жордана,

Билеты по курсу «Введение в численные методы» 2 поток.

Билеты по курсу «Введение в численные методы» (2 –ой поток)
(2019)

Билет 1. Прямые методы решения СЛАУ. Метод Гаусса.
Билет 2. Трехдиагональные системы линейных алгебраических уравнений. Метод
прогонки.
Билет 3. Обусловленность системы линейных алгебраических уравнений. Число
обусловленности.
Билет 4. Одношаговые итерационные методы решения системы линейных
алгебраических уравнений. Достаточные условия сходимости.
Билет 5. Метод простой итерации.
Билет 6. Метод Зейделя.
Билет 7. Метод верхней релаксации.
Билет 8. Интерполирование полиномами. Интерполяционные формулы Лагранжа
и Ньютона.
Билет 9. Погрешность интерполяционного полинома.
Билет 10. Интерполирование с кратными узлами. Полиномы Эрмита
Билет 11. Интерполирование сплайнами.
Билет 12. Квадратурные формулы прямоугольников и трапеций.
Билет 13. Квадратурные формулы Симпсона.
Билет 14. Квадратурные формулы Гаусса.
Билет 15. Сеточные функции. Разностная аппроксимация первой и второй
производной.
Билет 16. Метод Эйлера.
Билет 17. Метод Рунге-Кута.
Билет 18. Метод Адамса.
Билет 19. Разностная аппроксимация краевой задачи для линейного
дифференциального уравнения второго порядка.
Билет 20. Разностная задача на собственные значения.

Дополнительные вопросы и задачи

Содержание курса

Глава 2 Численное решение систем линейных алгебраических уравнений.

Билет 1. Прямые методы решения СЛАУ. Метод Гаусса.
Постановка задачи численного решения СЛАУ.
§ 1. Прямые методы.
1. Правило Крамера
Формулы Крамера (без вывода). Оценка количества действий (с использованием формулы
Стирлинга).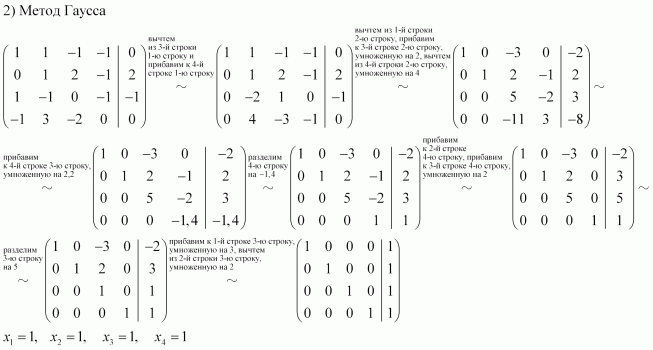
2. Метод Гаусса
Прямой ход, формулы прямого хода, получение треугольной матрицы. Обратный ход,
формулы обратного хода. Оценка количества действий.
3. Метод Гаусса с выбором главного элемента
Оценка роста погрешности вычислений в процессе обратного хода. Выбор главного
элемента, ограниченность погрешности.
4. Система с диагональным преобладанием .
Определение, теорема о существовании и единственности решения системы с
диагональным преобладанием.
Билет 2. Трехдиагональные системы линейных алгебраических
уравнений. Метод прогонки.
5. Системы с трехдиагональной матрицей. Метод прогонки.
Запись системы с трехдиагональной матрицей в виде системы «трехточечных» уравнений.
Формулы метода прогонки – прямого и обратного хода. Теорема о корректности метода
прогонки. Устойчивость метода прогонки.
Билет 3. Обусловленность системы линейных алгебраических уравнений.
Число обусловленности.
§ 2. Обусловленность СЛАУ. Число обусловленности.
Непрерывная зависимость погрешности решения от погрешности правой части для
системы с невырожденной матрицей. Определения абсолютной и относительной погрешности.
Оценка относительной погрешности решения через относительную погрешность правой части.
Определение числа обусловленности, роль числа обусловленности. Примеры.
Лемма об оценке числа обусловленности через собственные значения невырожденной
матрицы. Лемма о числе обусловленности самосопряженной невырожденной матрицы.
Билет 4. Одношаговые итерационные методы решения системы
линейных алгебраических уравнений. Достаточные условия сходимости.
§ 3. Итерационные методы.
Постановка задачи .
1. Одношаговые итерационные методы. Сходимость.
Определение одношагового итерационного метода. Канонический вид. Определение
сходимости, невязки. Лемма о связи погрешности решения и невязки для линейного
одношагового метода. Свойства самосопряженных положительных операторов, лемма о
положительности собственных значений, лемма об оценке (Ах,х) через собственные значения.
Лемма об оценке (Ах,х) снизу для невырожденной матрицы.
2. Достаточные сходимости одношагового итерационного процесса.
Теорема Самарского.
Билет 5. Метод простой итерации.
3. Метод простой итерации.
Каноническая запись метода. Теорема о достаточном условии сходимости. Теорема о
необходимом и достаточном условии сходимости (условие на оператор перехода). Оптимальное
значение итерационного параметра.
Билет 6. Метод Зейделя.
4. Метод Зейделя.
Каноническая запись метода Зейделя. Теорема о сходимости метода Зейделя. Индексная
запись метода. Теорема о сходимости при диагональном преобладании. Скорость сходимости.
Билет 7. Метод верхней релаксации.
5. Метод верхней релаксации.
Каноническая запись. Индексный вид. Теорема о достаточном условии сходимости.
 

Глава 3 Интерполирование.

 

Билет 8. Интерполирование полиномами. Интерполяционные формулы
Лагранжа и Ньютона.
1. Постановка задачи.
Постановка задачи интерполяции . Чебышевская система функций.
2. Интерполирование полиномами
Постановка задачи, разрешимость задачи интерполирования полиномами.
3. Интерполяционный многочлен в форме Лагранжа.
Построение общего вида интерполяционного многочлена в форме Лагранжа.
4. Интерполяционный многочлен в форме Ньютона.
Построение общего вида интерполяционного многочлена в форме Ньютона.
Билет 9. Погрешность интерполяционного полинома.
5. Погрешность интерполяции.
Теорема о погрешности интерполяции полиномом. Следствия (оценка погрешности,
равномерная сходимость).
Билет 10. Интерполирование с кратными узлами. Полиномы Эрмита
6. Интерполяционный многочлен Эрмита.
Определение полинома Эрмита. Теорема о существовании и единственности полинома
Эрмита. Оценка погрешности интерполяции полиномом Эрмита.
Билет 11. Интерполирование сплайнами.
7. Интерполирование сплайнами.
Определение кубического сплайна. Теорема о существовании и единственности
кубического сплайна (сведение задачи построения кубического сплайна к системе линейных
алгебраических уравнений с трехдиагональной матрицей, существование и единственность
решения).
Теоремы о сходимости и скорости сходимости (без доказательств).
Билет 12. Квадратурные формулы прямоугольников и трапеций.

 

Глава 4. Численное интегрирование

Постановка задачи численного интегрирования
§ 1. Квадратурные формулы прямоугольников, трапеций и Симпсона.
1. Метод прямоугольников
Квадратурные формулы прямоугольников. Оценка погрешности.
2. Метод трапеций
Квадратурные формулы трапеций. Оценка погрешности.
Билет 13. Квадратурные формулы Симпсона.
3. Метод Симпсона.
Квадратурные формулы парабол.
Погрешность квадратурной формулы с тремя точками на отрезке [-с,с]  (без вывода). Оценка
погрешности составной формулы.
Билет 14. Квадратурные формулы Гаусса.
§ 2. Квадратурные формулы Гаусса.
1. Постановка задачи.
2. Полиномы Лежандра.
Свойства полиномов Лежандра (четность, значения в точках 1 и -1, свойства корней,
свойство ортогональности полиномов Лежандра).
3. Узлы и коэффициенты квадратуры Гаусса.
Способ построения узлов, способ вычисления коэффициентов.
4. Точность формулы Гаусса для полиномов степени 2n-1.
Доказательство того, что построенная по указанным узлам и коэффициентам формулам
есть формула Гаусса. Пример.

 

Глава 5. Численное интегрирование обыкновенных дифференциальных
уравнений.

Билет 15. Сеточные функции. Разностная аппроксимация первой и второй
производной.
§ 1. Сеточные функции, аппроксимация.
1. Постановка задачи.
2. Сетка , сеточные функции.
Определение сетки, сеточной функции. Пространство сеточных функций. Разностная
схема. Погрешность решения разностной схемы, погрешность аппроксимации
дифференциального оператора, погрешность аппроксимации правой части, сходимость,
порядок сходимости и аппроксимации.
§ 2. Разностная аппроксимация первой и второй производной.
1. Первая производная.
Правая, левая и центральная производная. Погрешность аппроксимации.
2. Вторая производная.
Аппроксимация второй производной, погрешность аппроксимации.
Билет 16. Метод Эйлера.
§ 3. Численное решение задачи Коши.
1. Метод Эйлера
Формула явного метода Эйлера. Погрешность аппроксимации. Доказательство
сходимости, оценка скорости сходимости.
Билет 17. Метод Рунге-Кута.
2. Метод Рунге-Кутта.
Однопараметрическая схема Рунге-Кутта второго порядка. Погрешность аппроксимации.
Сходимость, скорость сходимости. Схема Рунге-Кутта четвертого порядка (без
доказательства)
Билет 18. Метод Адамса.
3. Метод Адамса.
Построение общей формулы явного метода Адамса по m точкам. Погрешность
аппроксимации для схемы с m=1.
Билет 19. Разностная аппроксимация краевой задачи для линейного
дифференциального уравнения второго порядка.
§ 4. Численное решение краевой задачи для ОДУ второго порядка.
1. Постановка задачи, разностная схема
Краевая задача. Разностная схема для ОДУ второго порядка. Сведение разностной схемы к системе с трехдиагональной матрицей. Диагональное преобладание. Применимость метода прогонки.
2. Аппроксимация и сходимость.
Погрешность аппроксимации разностной задачи. Доказательство сходимости, скорость
ходимости.
Билет 20. Разностная задача на собственные значения.
3. Разностная задача на собственные значения.
Краевая задача на собственные значения для дифференциального уравнения второго
порядка, собственные числа, собственные функции. Разностная задача, собственные
значения и собственные функции.

Базовый учебник

Костомаров Д.П., Фаворский А.П. Вводные лекции по численным методам . –М.: Логос, 2004, 184с

Основная литература

Самарский А.А. Введение в численные методы. –М.: Наука, 1987, 288 с.

Самарский А.А., Гулин А.В. Численные методы. –М.: Наука, 1978, 432 с.

 

Дополнительная литература

Самарский А. А. Теория разностных схем. М.: Наука. 1989.

 

 

Решение высшей математики онлайн

‹— Назад

Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса) Пусть дана система линейных уравнений с неизвестными . Требуется найти ее общее решение, если она совместна, или установить ее несовместность. Метод, который будет изложен в этом разделе, близок к методу вычисления определителя 5.1.с и к методу нахождения ранга матрицы (раздел 5.8). Предлагаемый алгоритм называется методом Гаусса или методом последовательного исключения неизвестных.

Выпишем расширенную матрицу системы

Назовем элементарными операциями следующие действия с матрицами:

1. перестановка строк;
2. умножение строки на число, отличное от нуля;
3. сложение строки с другой строкой, умноженной на число.

Отметим, что при решении системы уравнений, в отличие от вычисления определителя и нахождения ранга, нельзя оперировать со столбцами.

Читатель легко проверит, что если по матрице, полученной из выполнением элементарной операции, восстановить систему уравнений, то новая система будет равносильна исходной.

Цель алгоритма — с помощью применения последовательности элементарных операций к матрице добиться, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.

Шаг алгоритма заключается в следующем. Находим первый ненулевой столбец в матрице . Пусть это будет столбец с номером . Находим в нем ненулевой элемент и строку с этим элементом меняем местами с первой строкой. Чтобы не нагромождать дополнительных обозначений, будем считать, что такая смена строк в матрице уже произведена, то есть . Тогда ко второй строке прибавим первую, умноженную на число , к третьей строке прибавим первую, умноженную на число , и т. д. В результате получим матрицу

(Первые нулевые столбцы, как правило, отсутствуют.)

Если в матрице встретилась строка с номером , в которой все элементы равны нулю, а , то выполнение алгоритма останавливаем и делаем вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что -ое уравнение будет иметь вид

Этому уравнению не удовлетворяет ни один набор чисел .

Матрицу можно записать в виде

где По отношению к матрице выполняем описанный шаг алгоритма. Получаем матрицу где , . Эту матрицу снова можно записать в виде и к матрице снова применим описанный выше шаг алгоритма.

Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее.

Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида

Далее выполняется так называемый обратный ход метода Гаусса. По матрице составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть . Заметим, что . Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части.

Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные решения исходной системы . Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами , включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин (в частности, просто произвольной величиной ). Эта запись и будет общим решением системы.

Если система была однородной, то получим общее решение однородной системы. Коэффициенты при , взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при  — второе решение и т.д.

Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одному переменному, перенесенному в правую часть, нужно присвоить значение 1, а остальным — нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другому переменному в правой части значение 1, а остальным — нули, получим второе решение из фундаментальной системы и т.д.

        Замечание 15.4   У читателя может возникнуть вопрос: «Зачем рассматривать случай, когда некоторые столбцы матрицы нулевые? Ведь в этом случае соответствующие им переменные в системе уравнений в явном виде отсутствуют.» Но дело том, что в некоторых задачах, например, при нахождении собственных чисел матрицы, такие системы возникают, и игнорировать отсутствующие переменные нельзя, так как при этом происходит потеря важных для задачи решений.                  Пример 15.2   Найдите общее решение системы уравнений где неизвестными являются .

Решение. Выпишем расширенную матрицу системы

Прибавим ко второй строке первую, умноженную на число , к третьей строке прибавим первую, умноженную на . В результате получим Прибавим к третьей строке вторую, умноженную на число . Получим Прямой ход метода Гаусса закончен. Выписываем по матрице систему уравнений Переносим в правую часть неизвестные (неизвестное реально в ней присутствовать не будет, коэффициент перед ним равен нулю). Получаем Пусть , , , . Из уравнений находим:

Ответ: , , , , , , где , , ,  — произвольные числа.         

        Замечание 15.5   В процессе решения можно также установить, какие ранги у матриц и и где расположены их базисные миноры. В предыдущем примере , базисный минор расположен в строках с номерами 1, 2, столбцах с номерами 2, 5.                  Пример 15.3   Найдите общее решение системы уравнений

Решение. Запишем расширенную матрицу системы:

Ко второй строке прибавим первую, умноженную на , к третьей строке прибавим первую, умноженную на , к четвертой строке прибавим первую, умноженную на : Вторую строку, умноженную на , прибавим к третьей: В третьей строке все элементы равны нулю, а элемент . Значит, система несовместна.

Ответ: Система несовместна.         

        Пример 15.4   Решите систему

Решение. Имеем:

Первую строку, умноженную на числа , , , прибавим соответственно ко второй, третьей и четвертой строкам: К третьей строке прибавим вторую, умноженную на . Получим К четвертой строке прибавим третью, умноженную на : Выписываем по матрице систему уравнений: Находим последовательно значения неизвестных:

Ответ: .         

        Замечание 15.6   Так же, как и при решении системы уравнений по правилу Крамера, при использовании метода Гаусса приходится выполнять большой объем вычислительной работы. Из-за этого вполне возможно, что будет допущена какая-либо ошибка в вычислениях. Поэтому желательно после решения системы выполнить проверку, то есть подставить полученные значения неизвестных в уравнения системы. Для выполнения полной проверки подстановку нужно произвести во все уравнения системы. Если же по каким-то причинам это не выполнимо, то можно подставить найденные значения в одно уравнение. В отличие от правила Крамера в методе Гаусса эту подстановку нужно производить в ПОСЛЕДНЕЕ уравнение исходной системы. При наличии в этом уравнении всех неизвестных эта подстановка почти всегда покажет наличие ошибки, если таковая была допущена.         

        Пример 15.5   Найдите фундаментальную систему решений и общее решение однородной системы линейных уравнений:

Решение. Составляем расширенную матрицу системы:

Умножим первую строку последовательно на , 5 и 1 и прибавим соответственно ко второй, третьей и четвертой строкам. Получим матрицу Вторую строку умножим последовательно на числа 4 и 2 и прибавим соответственно к третьей и четвертой строкам. Получим матрицу Прямой ход метода Гаусса закончен. У полученной матрицы легко определить ранг, ее базисный минор . Отсюда следует, что . По  теореме 15.3 число решений в фундаментальной системе равно разности между числом неизвестных и рангом матрицы, в нашем случае фундаментальная система состоит из трех решений.

Переходим к системе уравнений

Неизвестные и оставляем в левой части, остальные переносим в правую часть:

Положим , . Получим , . Первое решение из фундаментальной системы: .

Положим , . Получим , . Второе решение из фундаментальной системы решений: .

Положим , . Получим , . Третье решение из фундаментальной системы решений: . Фундаментальная система решений найдена. Общее решение имеет вид

Ответ: Фундаментальная система решений:
, , , общее решение: .         

        Замечание 15.7   Если решения, составляющие фундаментальную систему, умножить на любые ненулевые числа, то вновь полученные решения снова будут образовывать фундаментальную систему. Поэтому в предыдущем примере фундаментальную систему образуют и такие решения:
, , . Общее решение можно записать так: .         

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Онлайн калькулятор: Метод исключения Гаусса

Система линейных уравнений:

может быть решена методом исключения Гаусса с помощью калькулятора.

В методе исключения Гаусса система линейных уравнений представлена ​​как расширенная матрица, то есть матрица, содержащая коэффициенты уравнения и постоянные члены с размерами [n: n + 1]:

Исключение по Гауссу

8 3 4 5 31 14 4 33 23 17 15 4 23 7 22 4 11 17 1 51

Матрица системы линейных уравнений

Точность вычислений

Цифры после десятичной точки: 2

Файл очень большой. Во время загрузки и создания может произойти замедление работы браузера.

Скачать закрыть

content_copy Ссылка сохранить Сохранить расширение Виджет

Исключение по Гауссу

Метод назван в честь Карла Фридриха Гаусса, гениального немецкого математика 19 века. Сам Гаусс не изобрел этот метод. Метод сокращения строк был известен древним китайским математикам; он был описан в «Девяти главах математического искусства», китайской книге по математике, изданной во II веке.

Ликвидация вперед

Первым шагом исключения Гаусса является получение матрицы строковой формы. Левая нижняя часть этой матрицы содержит только нули, и все нулевые строки находятся ниже ненулевых строк:

Матрица приводится к этой форме с помощью элементарных операций со строками: поменять местами две строки, умножить строку на константу, добавить к одной строке скалярное число, кратное другой.
Наш калькулятор получает форму эшелона путем последовательного вычитания верхних строк, умножения на нижние строки, умножения на, где i — ведущая строка коэффициентов (ведущая строка).
Важно, чтобы старший коэффициент отличался от нуля. Если он становится равным нулю, строка заменяется более низкой строкой с ненулевым коэффициентом в той же позиции.

Обратная замена

На этом этапе операции с элементарными строками продолжаются до тех пор, пока не будет найдено решение. Наконец, он преобразует матрицу в сокращенную форму эшелона строк:
,

Метод исключения Гаусса, алгоритм и блок-схема

.

Метод исключения Гаусса может быть использован для решения линейных одновременных уравнений, возникающих в инженерных задачах.В методе уравнения решаются последовательной процедурой исключения неизвестных.

В целом метод сводит систему линейных одновременных уравнений к верхнетреугольной матрице. Затем используется обратная подстановка для получения неизвестных. Это ключевая концепция при написании алгоритма или программы или рисовании блок-схемы для исключения Гаусса.

Частичное или полное вращение может быть использовано в методе исключения Гаусса. Таким образом, этот метод считается более совершенным по сравнению с методом Гаусса Джордана.

В алгоритме метода исключения Гаусса и блок-схеме, приведенной ниже, процесс исключения выполняется до тех пор, пока в последнем уравнении не останется только одно неизвестное. Его легко запрограммировать, и для контроля ошибок округления можно использовать частичное вращение.

Алгоритм исключения Гаусса:

1. Пуск
2. Объявите переменные и прочтите порядок матрицы n.
3. Возьмите коэффициенты линейного уравнения как:
   Do для k = от 1 до n
   Do для j = от 1 до n + 1
   Считайте a [k] [j]
   Конец для j
   Конец для k
4. Сделать для k = от 1 до n-1
   Сделать для i = от k + 1 до n
   Сделать для j = k + 1 до n + 1
   a [i] [j] = a [i] [j] — a [i] [k] / a [k] [k] * a [k] [j]
   Конец для j
   Конец для i
   Конец для k
5. Вычислить x [n] = a [n] [n + 1] / a [n] [n]
6. Do для k = n-1 до 1
   sum = 0
   Do for j = k + 1 to n
   sum = sum + a [k] [j] * x [j]
   End for j
   x [k] = 1 / a [k] [k] * (a [k] [n + 1] — сумма)
   Конец для k
7. Показать результат x [k]
8. Остановка

Блок-схема исключения Гаусса:

Вот базовая схема блок-схемы исключения Гаусса, которая включает ввод, прямое исключение, обратную замену и вывод.

Ниже показана процедура поворота и исключения.

Вот приложение, показывающее, как происходит прямое исключение и обратная замена.

См. Также,
Программа исключения Гаусса C
Программа исключения Гаусса MATLAB

При решении одновременных линейных уравнений аналитические методы часто терпят неудачу в сложных задачах. Эти алгоритм и блок-схема могут использоваться для написания исходного кода для метода исключения Гаусса на любом языке программирования высокого уровня.

Он завершен, и хотя он несколько длинен для кодирования, он четко разграничен для фазы исключения и фазы обратной замены. Если возникнут вопросы, обсудите их в комментариях.

Калькулятор метода исключения Гаусса

— Онлайн-программа для сокращения строк

Поиск инструмента

Исключение по Гауссу

Инструмент для применения метода исключения Гаусса и получения формы сокращенного эшелона строки с шагами, деталями, обратной матрицей и векторным решением.

Результаты

Исключение Гаусса — dCode

Тег (и): Матрица, символьное вычисление

Поделиться

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Калькулятор исключения по Гауссу

Преобразователь системы уравнений в матрицу

Ответы на вопросы (FAQ)

Что такое метод исключения Гаусса?

Алгоритм исключения Гаусса (также называемый методом Гаусса-Жордана или методом поворота) позволяет находить решения системы линейных уравнений и определять обратную матрицу.

Алгоритм работает со строками матрицы путем обмена или умножения строк между ними (с точностью до множителя).

На каждом шаге алгоритм стремится ввести в матрицу на элементах за пределами диагонали нулевые значения.

Как вычислить решения системы линейных уравнений с Гауссом?

Первым шагом из системы линейных уравнений является преобразование уравнений в матрицу.

Пример: $$ \ left \ {\ begin {array} {} x & — & y & + & 2z & = & 5 \\ 3x & + & 2y & + & z & = & 10 \\ 2x & — & 3y & — & 2z & = & — 10 \\\ end {массив} \ право.$$ можно записать в форме умножения «> матричного умножения: $$ \ left (\ begin {array} {ccc} 1 & -1 & 2 \\ 3 & 2 & 1 \\ 2 & -3 & 2 \ end { array} \ right). \ left (\ begin {array} {c} x \\ y \\ z \ end {array} \ right) = \ left (\ begin {array} {c} 5 \\ 10 \\ -10 \ end {array} \ right) $$, который соответствует (расширенной) матрице $$ \ left (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 3 & 2 & 1 & 10 \\ 2 & -3 & 2 & -10 \ end {array} \ right) $$

Затем для каждого элемента за пределами ненулевой диагонали выполните соответствующие вычисления, добавив или вычтя другие строки, чтобы элемент стал 0.

Пример: Вычтите 3 раза (строка 1) из (строка 2), например, элемент в строке 2, столбец 1 станет 0: $$ \ left (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 0 & 5 & -5 & -5 \\ 2 & -3 & -2 & -10 \ end {array} \ right) $$
Вычтите 2 раза (строка 1) до (строка 3) например, элемент в строке 3, столбец 1 становится 0: $$ \ left (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 0 & 5 & -5 & -5 \\ 0 & -1 & -6 & -20 \ end {array} \ right) $$
Вычтите 1/5 раз (строка 2) из ​​(строка 3), например, элемент в строке 3, столбец 2 станет 0: $$ \ слева (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 0 & 5 & -5 & -5 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$
Вычтите 1/5 раз (строка 2) из ​​(строка 1), например, элемент в строке 1, столбец 2 станет 0: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 1 & 4 \\ 0 & 5 & -5 & -5 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$
Отнимите 1/7 раз (строка 3) до (строка 1), например как элемент в строке 1, столбец 3 становится 0: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 0 & 1 \\ 0 & 5 & -5 & -5 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$
Вычтите 5/7 раз (строка 3) из (строка 2), например, элемент в строке 2, столбец 3 станет 0: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 0 & 1 \\ 0 & 5 & 0 & 10 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$

Упростите каждую линию, разделив значение по диагонали.

Пример: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 2 \\ 0 & 0 & 1 & 3 \ end {array } \ right) $$

Вектор результата — последний столбец.

Пример: $ {1,2,3} $, что соответствует $ {x, y, z} $, поэтому $ x = 1, y = 2, z = 3 $

Задайте новый вопрос

Исходный код

dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Исключение Гаусса». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент алгоритма исключения Гаусса (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой алгоритм исключения Гаусса ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Исключения Гаусса» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для получения помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

исключение, точка поворота, гаусс, иордан, матрица, система, уравнение

Ссылки

Источник: https: // www.dcode.fr/gaussian-elimination

© 2021 dCode — Лучший «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.

Веб-сервер Delphi

Веб-сервер Delphi

Помните, что веб-сервер DelPhi использует DelPhiPKa для добавления протонов в соответствии с указанным пользователем pH. Следовательно, выполнение заданий Delphi может занять двадцать минут. Пожалуйста, проявите терпение.
Если вы хотите, чтобы вычисления выполнялись быстро, предоставьте вместо этого файл PQR.

DelPhi — это программа электростатики белков, первоначально разработанная в ДокторЛаборатория Барри Хонига и в настоящее время поддерживается командой разработчиков Delphi. Он использует метод конечных разностей для решить уравнение Пуассона-Больцмана для биомолекул и объектов в данной системе. Его Преимущества заключаются в способности решать линейные или нелинейные уравнения ПБ, будучи быстрым, универсальным, и точный. Этот веб-сервер обеспечивает простой, понятный и пошаговый процесс для используя DelPhi в своих интересах.Автономный пакет Delphi доступен бесплатно для Скачать здесь.

Краткий обзор того, как все работает:

• Необходим файл координат биомолекулы (например, формат файла PDB). Этот PDB-файл может последовательно быть исправлены для отсутствующих атомов / остатков и протонированы, или пользователь может загрузить уже исправленные и протонированный файл.
• DelPhi использует файлы заряда и размера для сбора информации о необходимых атомах для вашего биомолекула. Мы предоставляем эти файлы по умолчанию, поскольку они создаются для charmm, янтарь, или совместимость olpsaa. Тем не менее, вы можете загрузить свой собственный файл заряда или размера, если нужно быть.
• Для успешной отправки также необходим файл параметров DelPhi.Мы предоставляем файл параметров по умолчанию . Однако, опять же, вы можете загрузить свой собственный файл параметров.
• Что касается результатов, вам предлагаются варианты расчета различных энергий вместе с различные карты визуального отображения. Чтобы результаты выдавались автоматически, пользователь должен указать имя и адрес электронной почты.

DelPhi работает на суперкомпьютерном кластере Palmetto Университета Клемсона. Мы хотели бы поблагодарить Команда пальметто за размещение этой услуги. Мы также хотели бы поблагодарить NIH-Grant № 1R01GM093937 за поддержку этой работы.

Наконец, если эти результаты появятся в опубликованных статьях, мы смиренно просим включить ссылку на наши сервис, как определено здесь.

Начинать

Эмпирический байесовский кригинг

Осенний выпуск 2012 г.

Эмпирический байесовский кригинг

Реализовано в ArcGIS Geostatistical Analyst

Константин Криворучко, старший научный сотрудник, группа разработки программного обеспечения, Esri

Эта статья в формате PDF.

Рисунок 1a: Значения вариограммы для пар точек (красный), их средние значения (синие кресты) и расчетная модель вариограммы (синяя линия.)

Получение надежных экологических измерений может быть дорогостоящим и трудоемким, и во многих случаях пробы загрязнителей окружающей среды не собираются там, где люди живут или работают. Следовательно, очень важна способность предсказывать значения там, где нет наблюдений. Интерполяция — это процесс получения значения интересующей переменной в месте, где данные не наблюдались, с использованием данных из мест, где данные были собраны.

Существует множество методов интерполяции пространственных данных.Они делятся на два широких класса: детерминированные и вероятностные. Детерминированные методы используют предопределенные функции расстояния между точками наблюдения и местоположения, для которого требуется интерполяция (например, интерполяция обратного расстояния). Вероятностные методы основаны на статистической теории. Эти предикторы количественно определяют неопределенность, связанную с интерполированными значениями. Требование предоставления информации о неопределенности прогноза ограничивает выбор интерполяторов статистическими.

Разработка надежных моделей автоматической статистической интерполяции долгое время была актуальной проблемой в сообществе ГИС. Однако это очень сложная задача, потому что каждая статистическая модель основана на данных пользователей, а данные часто настолько сложны, что их чрезвычайно сложно описать математически без взаимодействия.

Рисунок 1b: Спектр моделей вариограмм, произведенных EBK

В этой статье кратко обсуждаются функции статистической интерполяции, а затем приводятся некоторые подробности об эмпирической модели байесовского кригинга (EBK), реализованной в ArcGIS 10.1 Геостатистический аналитик. Обширные испытания с использованием большого количества данных показали, что EBK является надежным автоматическим интерполятором. Эта модель кригинга также доступна как инструмент геообработки, который можно использовать в сценариях ModelBuilder и Python.

Кригинг

Кригинг — это класс статистических методов для оптимального пространственного прогнозирования. Он был разработан Львом Гандиным в 1959 году для метеорологических приложений. Он использовался во многих других дисциплинах, включая сельское хозяйство, горное дело и науки об окружающей среде.

Кригинг является вероятностным предсказателем и, как таковой, предполагает наличие статистической модели для данных. Предикторы кригинга имеют стандартные ошибки, которые количественно определяют неопределенность, связанную с предсказанными значениями. Предикторы кригинга называются оптимальными предикторами, потому что ошибка прогнозирования минимизирована, и в среднем прогнозируемое значение и истинное значение совпадают. Предикторы кригинга:

• Имеют меньшую неопределенность прогноза, чем другие модели прогнозирования
• Имеют возможность отфильтровывать ошибки измерения
• Использовать информацию о корреляции между интересующей переменной и ковариатами

Рисунок 2: Пространственные данные, смоделированные с использованием модели вариограммы мощности со значениями мощности 0.1, 1.0 и 1.9 (сверху вниз)

Когда предикторы кригинга применяются к анализу радиоактивного загрязнения, они могут ответить на такие вопросы, как: Какова вероятность того, что загрязнение пищевых продуктов превышает радиоэкологический стандарт в указанном месте? и предоставить оценки среднего и общего загрязнения в определенных областях.

Kriging использует вариограмму — функцию расстояния и направления, разделяющего два местоположения, — для количественной оценки пространственной зависимости в данных.Вариограмма строится путем вычисления половины среднего квадрата разности значений всех пар измерений в точках, разделенных заданным расстоянием ч. Вариограмма отложена по оси y в зависимости от разделительного расстояния h.

На рис. 1а показаны значения вариограммы для пар точек (показаны красным) и их средние значения для набора интервалов расстояний между точками (показаны синими крестиками). Синяя линия на рисунке 1a показывает расчетную модель вариограммы.Затем эта модель вариограммы используется для определения весов, которые определяют вклад каждой наблюдаемой точки данных в предсказание новых значений в местах без выборки.

Кригинг основан на некоторых статистических допущениях. Основное предположение — стационарность (пространственная однородность). Если данные являются стационарными, среднее значение данных и вариограмма одинаковы во всех местах экстента данных. Если это предположение выполняется, для получения оптимальных прогнозов и достоверных статистических выводов необходимо оценить лишь несколько параметров модели кригинга.

Если распределение данных гауссово, лучший предсказатель — это тот, который использует линейную комбинацию ближайших значений данных. Однако для других распределений лучший предсказатель часто бывает нелинейным и, следовательно, более сложным. Данные могут быть преобразованы в соответствии с распределением Гаусса. Затем можно точно преобразовать прогнозы кригинга в исходную шкалу данных, что можно сделать в ArcGIS Geostatistical Analyst.

Классический кригинг также предполагает, что оценочная вариограмма является истинной вариограммой наблюдаемых данных.Это означает, что данные были сгенерированы на основе распределения Гаусса с корреляционной структурой, определенной оценочной вариограммой. Это очень сильное предположение, и на практике оно редко выполняется. Следовательно, необходимо предпринять действия, чтобы сделать статистическую модель более реалистичной.

Введение в эмпирический байесовский кригинг

EBK отличается от классических методов кригинга тем, что учитывает ошибку, вносимую при оценке модели вариограммы. Это делается путем оценки и последующего использования многих моделей вариограммы, а не одной вариограммы.Этот процесс включает в себя следующие шаги:

1. Модель вариограммы рассчитывается на основе данных.
2. Используя эту вариограмму, новое значение моделируется в каждой ячейке входных данных.
3. Новая модель вариограммы оценивается на основе смоделированных данных. Затем рассчитывается вес для этой вариограммы с использованием правила Байеса, которое показывает, насколько вероятно, что наблюдаемые данные могут быть получены из вариограммы.

Рисунок 3a: Прогнозы загрязнения почвы радиоцезием в шести подмножествах данных

Шаги 2 и 3 повторяются.При каждом повторении вариограмма, оцененная на шаге 1, используется для моделирования нового набора значений во входных точках. Смоделированные данные используются для оценки новой модели вариограммы и ее веса. Прогнозы и стандартные ошибки предсказания затем производятся в местах без выборки с использованием этих весов.

Этот процесс создает спектр вариограмм. Каждая вариограмма — это оценка истинной вариограммы, на основе которой может быть создан наблюдаемый процесс. На рисунке 1b показан спектр построенных вместе моделей вариограммы.Медиана распределения показана сплошной красной линией. 25-й и 75-й процентили выделены красными пунктирными линиями. Ширина синих линий пропорциональна весам вариограммы, поэтому модели с меньшими весами показаны более тонкими линиями.

Модель кригинга по умолчанию в EBK называется внутренней случайной функцией порядка 0, а модель пространственной корреляции — это модель мощности, где b, c, и α (допустимое значение значения мощности α находится между 0 и 2). параметры модели.Эта корреляционная модель соответствует дробному броуновскому движению, также известному как процесс случайного блуждания. Он состоит из шагов в случайном направлении и отфильтровывает умеренный тренд в данных.

Рисунок 3b: Корзина с фруктами Джузеппе Арчимбольдо (ок. 1527–1593)

На рис. 2 показаны смоделированные поверхности с тремя различными значениями мощности α: α = 0,1 (вверху), α = 1 (в центре) и α = 1,9 (внизу). Увеличение масштаба любой части поверхности показывает аналогичную поверхность случайного блуждания.Модель корреляции с α = 1, линейная модель, показанная на среднем изображении, соответствует регулярному броуновскому движению, процессу с независимыми приращениями шага. Однако приращения зависят от дробного броуновского движения. Если на предыдущих этапах наблюдается возрастающая картина, то, вероятно, текущий шаг будет увеличиваться, когда значение мощности α больше 1, и уменьшаться, когда α меньше 1. На рисунке 2 смоделированная поверхность с малым α (верхнее изображение) выглядит как смесь умеренного тренда и случайного шума, в то время как смоделированная поверхность с большим α (нижнее изображение) показывает практически бесшумные крупномасштабные вариации данных.

Для демонстрации использования EBK были смоделированы шесть подмножеств данных по измеренному загрязнению почвы радиоцезием ( ¹³⁷ Cs) для местоположений вблизи АЭС Фукусима-Дайити в Японии после аварии, произошедшей на этом объекте в 2011 году. Они показаны на Рисунок 3а. Карты результатов каждого подмножества качественно схожи: они показывают те же характеристики, что и карты на Рисунке 2. Это демонстрирует, что модель EBK по умолчанию обеспечивает хороший метод для прогнозирования радиоактивного загрязнения для небольших территорий.

Использование распределения моделей вариограммы вместо одной модели дает большое преимущество перед классическими моделями кригинга. Однако EBK имеет несколько дополнительных преимуществ: модель можно использовать для интерполяции нестационарных данных для больших площадей, а данные можно локально преобразовать в распределение Гаусса.

Рис. 4a: Распределение данных о загрязнении почвы радиоцезием по шести подмножествам данных

В модели EBK в случае больших наборов данных входные данные сначала разделяются на подмножества заданного размера, которые могут перекрываться, а могут и не перекрываться.В каждом подмножестве производятся распределения вариограмм. Затем для каждого местоположения создается прогноз с использованием распределения вариограммы из одного или нескольких подмножеств. Каждое подмножество данных использует модели, определяемые близкими значениями, а не подверженные влиянию очень отдаленных факторов, но когда все модели объединены, они создают полную картину, точно так же, как «лицо» на картине Джузеппе Арчимбольдо под названием Корзина с фруктами . создается путем объединения групп фруктов (рис. 3b).

Хотя модель EBK по умолчанию приближает распределение данных остатков к гауссовскому распределению за счет удаления локального тренда, распределение остатков все же может быть негауссовым. В этом случае модель с опцией преобразования данных может давать более точные прогнозы. В Geostatistical Analyst это можно определить с помощью диагностики модели.

Рисунок 4b: Процесс преобразования данных

Построение графика распределения загрязнения почвы ¹³⁷ Cs в нескольких областях экстента данных показывает, что они явно не гауссовы и различаются по регионам, как показано на Рисунке 4a.Следовательно, изменяющееся локальное распределение данных явно является важной особенностью оптимальной модели интерполяции. EBK предоставляет возможность преобразовать наблюдаемый процесс в гауссовский процесс, используя оценочную функцию преобразования данных, как показано на рисунке 4b.

EBK с опцией преобразования данных многократно оценивает распределение данных, используя следующий алгоритм:

1. Данные преобразуются в распределение Гаусса, и модель вариограммы одновременно оценивается на основе данных.
2. Используя эту вариограмму, новые данные безоговорочно моделируются, а затем снова преобразуются в каждом из местоположений входных данных.
3. Новые данные преобразуются, и новая модель вариограммы одновременно оценивается на основе смоделированных данных.
4. Шаги 2 и 3 повторяются указанное количество раз. Каждое повторение создает новую трансформацию и вариограмму.
5. Вес вариограмм рассчитывается с использованием правила Байеса.
6. Прогнозы и стандартные ошибки предсказания делаются с использованием весов, а затем обратно преобразуются с коррекцией смещения.

Эти связанные неопределенности прогнозов следует учитывать при использовании этих результатов для принятия решений. На рис. 5а показан прогноз загрязнения почвы ¹³⁷ Cs (Ки / км ² ) и карты стандартной ошибки прогноза, составленные EBK для районов вблизи АЭС Фукусима-Дайити. [Кюри (Ки) — единица, используемая для измерения интенсивности радиоактивности образца.] На рисунке 5b показаны оценочные распределения ¹³⁷ Cs (медиана показана красным цветом) для одного местоположения внутри экстента данных.

Рисунок 5a: ¹³⁷ Cs прогноз загрязнения почвы и карты стандартной ошибки прогнозирования; 95-процентные интервалы прогноза для местоположений, обозначенных 1 и 2, составляют [7,82, 21,62] и [1,17, 3,21] Ки / км2.

Радиоактивный распад представляет собой интересный пример, потому что это процесс Пуассона, а не более простой гауссовский процесс. Существенным свойством любого пуассоновского процесса является то, что его среднее значение равно его дисперсии. Следовательно, вариабельность прогнозов, как правило, меньше для наблюдаемых данных с более низкими значениями и больше для наблюдаемых данных с более высокими значениями.Это показано на рисунке 5а.

Интерпретация прогнозов вместе со стандартными ошибками прогнозов обеспечивает лучшее понимание возможных уровней загрязнения. Более подробный анализ двух отмеченных местоположений на рисунке 5a показывает, что прогнозы и связанные с ними стандартные ошибки прогнозов составляют (1) 14,72 и 3,52 и (2) 2,19 и 0,52.

Радиоактивное загрязнение почвы в этих местах составляет приблизительно (95-процентный интервал прогноза) 14,72 ± 3,52 × 1.96 ≈ 14,72 ± 6,9 Ки / км ² и 2,19 ± 0,52 × 1,96 ≈ 2,19 ± 1,02 Ки / км ² соответственно. Следовательно, «истинное» загрязнение в первом местоположении может быть больше 20 Ки / км ² , хотя прогнозируемое значение меньше 15 Ки / км ² . Если верхний допустимый предел загрязнения почвы составляет 15 Ки / км ² (как это было в бывшем Советском Союзе), проживание в первом месте небезопасно и людей, живущих поблизости, следует эвакуировать. Во втором месте «истинное» загрязнение может достигать 3 Ки / км ² , учитывая прогнозируемое значение, близкое к 2 Ки / км ² .

Заключение

Эмпирический байесовский кригинг, реализованный в дополнительном модуле ArcGIS 10.1 Geostatistical Analyst, обеспечивает как простой, так и надежный метод интерполяции данных. Для получения дополнительной информации об использовании EBK см. Интерактивную справку по дополнительному модулю ArcGIS Geostatistical Analyst. Чтобы узнать больше о пространственной статистике, прочтите «Анализ пространственных статистических данных для пользователей ГИС», опубликованный Esri Press.

Рис. 5b: Расчетное распределение загрязнения почвы ¹³⁷ Cs в одном месте недалеко от АЭС «Фукусима-дайити».

Об авторе

Константин Криворучко — старший научный сотрудник группы разработчиков программного обеспечения Esri, сыгравший центральную роль в разработке дополнительного модуля ArcGIS Geostatistical Analyst. До прихода в Esri в 1998 году он был директором лаборатории ГИС в Институте радиоэкологии им. Сахарова в Минске, Беларусь, где он разрабатывал учебные программы по ГИС и пространственной статистике, а также руководил исследованиями кандидатов в докторантуру и аспирантуру, касающихся приложений ГИС и анализа пространственных статистических данных. .Он провел множество курсов по прикладной пространственной статистике и ГИС. Эти действия кратко описаны в Анализ пространственных статистических данных для пользователей ГИС .

Дополнительная литература

Грибов А., Криворучко К. (2012). «Новое гибкое непараметрическое преобразование данных для трансгауссовского кригинга». Geostatistics Oslo 2012, Количественная геология и геостатистика, Том 17, Часть 1, стр. 51–65, Нидерланды: Springer.

Криворучко К. (2011). Анализ пространственных статистических данных для пользователей ГИС. Редлендс, Калифорния: Esri Press, 928 с.

3 Методы решения систем уравнений

Три метода, наиболее часто используемые для решения систем уравнений, — это подстановка, исключение и расширенные матрицы. Замена и исключение — это простые методы, с помощью которых можно эффективно решить большинство систем двух уравнений за несколько простых шагов. Метод расширенных матриц требует большего количества шагов, но его применение распространяется на большее количество систем.

Замена

Замена — это метод решения систем уравнений путем удаления всех переменных, кроме одной, в одном из уравнений, а затем решения этого уравнения. Это достигается путем выделения другой переменной в уравнении и последующей подстановки значений этих переменных в другое уравнение. Например, чтобы решить систему уравнений x + y = 4, 2x — 3y = 3, выделите переменную x в первом уравнении, чтобы получить x = 4 — y, затем подставьте это значение y во второе уравнение, чтобы получить 2 (4 — у) — 3у = 3.Это уравнение упрощается до -5y = -5 или y = 1. Подставьте это значение во второе уравнение, чтобы найти значение x: x + 1 = 4 или x = 3.

Исключение

Исключение — еще один способ решения системы уравнений, переписав одно из уравнений в терминах только одной переменной. Метод исключения достигает этого путем сложения или вычитания уравнений друг из друга, чтобы сократить одну из переменных. Например, сложение уравнений x + 2y = 3 и 2x — 2y = 3 дает новое уравнение 3x = 6 (обратите внимание, что члены y сокращены).Затем система решается с использованием тех же методов, что и для замены. Если невозможно сократить переменные в уравнениях, необходимо будет умножить все уравнение на коэффициент, чтобы коэффициенты совпали.

Расширенная матрица

Расширенные матрицы также могут использоваться для решения систем уравнений. Расширенная матрица состоит из строк для каждого уравнения, столбцов для каждой переменной и расширенного столбца, который содержит постоянный член с другой стороны уравнения.Например, расширенная матрица для системы уравнений 2x + y = 4, 2x — y = 0 имеет вид [[2 1], [2 -1] … [4, 0]].

Определение решения

Следующий шаг включает использование элементарных операций со строками, таких как умножение или деление строки на константу, отличную от нуля, и добавление или вычитание строк. Цель этих операций — преобразовать матрицу в форму строки-эшелона, в которой первая ненулевая запись в каждой строке — это 1, записи выше и ниже этой записи — все нули, а первая ненулевая запись для каждого row всегда находится справа от всех таких записей в строках над ней.Строчно-эшелонированная форма для указанной выше матрицы — [[1 0], [0 1] … [1, 2]]. Значение первой переменной задается первой строкой (1x + 0y = 1 или x = 1). Значение второй переменной задается второй строкой (0x + 1y = 2 или y = 2).

Приложения

Подстановка и исключение — это более простые методы решения уравнений, которые используются гораздо чаще, чем расширенные матрицы в базовой алгебре. Метод подстановки особенно полезен, когда одна из переменных уже изолирована в одном из уравнений.Метод исключения полезен, когда коэффициент одной из переменных одинаков (или его отрицательный эквивалент) во всех уравнениях. Основное преимущество расширенных матриц состоит в том, что их можно использовать для решения систем из трех или более уравнений в ситуациях, когда подстановка и исключение либо невозможны, либо невозможны.

Последние достижения в области машинного обучения

Руководство для читателей

Что это за страница? На этой странице слева показаны таблицы, извлеченные из документов arXiv.Он показывает извлеченные результаты с правой стороны, которые соответствуют таксономии в Papers With Code.

Какие цветные прямоугольники справа? Здесь показаны результаты, извлеченные из бумаги и связанные с таблицами слева. Результат состоит из значения метрики, имени модели, имени набора данных и имени задачи.

Что означают цвета? Зеленый означает, что результат одобрен и показан на сайте. Желтый — это результат того, что вы добавили, но еще не сохранили.Синий — это результат ссылки, полученный из другой бумаги.

Откуда берутся предлагаемые результаты? У нас есть модель машинного обучения, работающая в фоновом режиме, которая дает рекомендации по статьям.

Откуда берутся ссылочные результаты? Если мы находим в таблице результаты со ссылками на другие статьи, мы показываем проанализированный справочный блок, который редакторы могут использовать для аннотирования, чтобы получить эти дополнительные результаты из других статей.

Руководство для редактора

Я впервые редактирую и боюсь ошибиться.Помощь! Не волнуйтесь! Если вы сделаете ошибки, мы можем исправить их: все версионировано! Так что просто сообщите нам на канале Slack, если вы что-то случайно удалили (и так далее) — это вообще не проблема, так что дерзайте!

Как добавить новый результат из таблицы? Щелкните ячейку в таблице слева, откуда берется результат. Затем выберите одно из 5 лучших предложений. Вы можете вручную отредактировать неправильные или отсутствующие поля. Затем выберите задачу, набор данных и название метрики из таксономии «Документы с кодом».Вы должны проверить, существует ли уже эталонный тест, чтобы предотвратить дублирование; если его не существует, вы можете создать новый набор данных. Например. ImageNet по классификации изображений уже существует с показателями Top 1 Accuracy и Top 5 Accuracy.

Каковы соглашения об именах моделей? Название модели должно быть простым, как указано в документе. Обратите внимание, что вы можете использовать круглые скобки для выделения деталей, например: BERT Large (12 слоев), FoveaBox (ResNeXt-101), EfficientNet-B7 (NoisyStudent).

Другие советы и рекомендации

• Если эталонный тест для введенной пары набор данных / задача уже существует, вы увидите ссылку.
• Если эталонный тест не существует, появится значок «новый», обозначающий новую таблицу лидеров.