Рациональные неравенства. Алгебра, 9 класс: уроки, тесты, задания.

1.	Рациональное неравенство (знаменатель — число) Сложность: лёгкое	2
2.	Числа, которые являются решением дробного неравенства Сложность: лёгкое	3
3.	Замена рационального неравенства системами неравенств Сложность: лёгкое	1
4.	Рациональное неравенство (линейное уравнение) Сложность: среднее	3
5.	Рациональное неравенство (общий знаменатель) Сложность: среднее	3
6.	Рациональное неравенство (неполный квадратный трёхчлен) Сложность: среднее	4
7.	Рациональное неравенство (три множителя) Сложность: среднее	4
8.	Дробное рациональное неравенство (знаменатель — бином) Сложность: среднее	5
9.	Дробь и единица Сложность: среднее	5
10.	Дробное рациональное неравенство (знаменатель — неполный квадратный трёхчлен) Сложность: среднее	6
11.	Дробное рациональное неравенство (разность квадратов) Сложность: сложное	8
12.	Дробное рациональное неравенство (теорема Виета) Сложность: сложное	7
13.	Значения выражения, переменная x Сложность: сложное	2

Рациональные неравенства — методическая рекомендация. Алгебра, 9 класс.

1.	Рациональное неравенство (знаменатель — число)	1 вид — рецептивный	лёгкое	2 Б.	Решение неравенства, знаменатель дроби которого — число
2.	Числа, которые являются решением дробного неравенства	1 вид — рецептивный	лёгкое	3 Б.	Выбор чисел, которые являются решением неравенства
3.	Замена рационального неравенства системами неравенств	1 вид — рецептивный	лёгкое	1 Б.	Замена рационального неравенства системами неравенств.
4.	Рациональное неравенство (линейное уравнение)	1 вид — рецептивный	среднее	3 Б.	Метод интервалов (нахождение общего знаменателя — в правой части число).
5.	Рациональное неравенство (общий знаменатель)	1 вид — рецептивный	среднее	3 Б.	Метод интервалов (нахождение общего знаменателя).
6.	Рациональное неравенство (неполный квадратный трехчлен)	1 вид — рецептивный	среднее	4 Б.	Решение неравенства методом интервалов, вынесение общего множителя за скобки
7.	Рациональное неравенство (три множителя)	1 вид — рецептивный	среднее	4 Б.	Решение неравенства методом интервалов
8.	Дробное рациональное неравенство (знаменатель — бином)	1 вид — рецептивный	среднее	5 Б.	Решение неравенства методом интервалов
9.	Дробь и единица	1 вид — рецептивный	среднее	5 Б.	Решение неравенства, приведение к общему знаменателю
10.	Дробное рациональное неравенство (знаменатель — неполный квадратный трёхчлен)	1 вид — рецептивный	среднее	6 Б.	Решение неравенства методом интервалов, вынесение общего множителя за скобки
11.	Дробное рациональное неравенство (разность квадратов)	2 вид — интерпретация	сложное	8 Б.	Решение неравенства методом интервалов, деление на положительное выражение, примениение формулы сокращённого умножения
12.	Дробное рациональное неравенство (теорема Виета)	2 вид — интерпретация	сложное	7 Б.	Решение неравенства методом интервалов, разложение на множители числителя и знаменателя с применением теоремы Виета
13.	Значения выражения, переменная x	1 вид — рецептивный	сложное	2 Б.	О положительных и отрицательных величинах всех значений переменной x.

Рациональное неравенство знаменатель число. Числовые промежутки на координатной прямой. Понятие рациональных равенств

>>Математика:Рациональные неравенства

Рациональное неравенство с одной переменной х — это неравенство вида — рациональные выражения, т.е. алгебраические выражения, составленные из чисел и переменной х с помощью операций сложения, вычитания, умножения, деления и возведения в натуральную степень . Разумеется, переменная может быть обозначена любой другой буквой, но в математике чаще всего предпочтение отдается букве х.

При решении рациональных неравенств используются те три правила, которые были сформулированы выше в § 1. С помощью этих правил обычно преобразуют заданное рациональное неравенство к виду / (ж) > 0, где / (х) — алгебраическая дробь (или многочлен). Далее разлагают числитель и знаменатель дроби f (х) на множители вида х — а (если, конечно, это возможно) и применяют метод интервалов, который мы уже упоминали выше (см. в предыдущем параграфе пример 3).

Пример 1. Решить неравенство (х — 1) (х + 1) (х — 2) > 0.

Решение. Рассмотрим выражение f(х) = (х-1)(х + 1)(х-2).

Оно обращается в 0 в точках 1,-1,2; отметим эти точки на числовой прямой. Числовая прямая разбивается указанными точками на четыре промежутка (рис. 6), на каждом из которых выражение f (x) сохраняет постоянный знак. Чтобы в этом убедиться, проведем четыре рассуждения (для каждого из указанных промежутков в отдельности).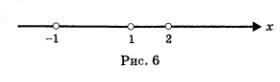

Возьмем любую точку х из промежутка (2, Эта точка расположена на числовой прямой правее точки -1, правее точки 1 и правее точки 2. Это значит, что х > -1, х >1, х > 2 (рис. 7). Но тогда x-1>0, х+1>0, х — 2 > 0, а значит, и f (х) > 0 (как произведение рациональное неравенство трех положительных чисел). Итак, на всем промежутке выполняется неравенство f (x) > 0.

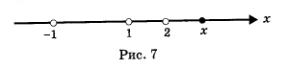
Возьмем любую точку х из интервала (1,2). Эта точка расположена на числовой прямой правее точки-1, правее точки 1, но левее точки 2. Значит, х > -1, х > 1, но х 0,x-1>0,x-2

Возьмем любую точку х из интервала (-1,1). Эта точка расположена на числовой прямой правее точки -1, левее точки 1 и левее точки 2. Значит, х >-1, но х 0, х -1 0 (как произведение двух отрицательных и одного положительного числа). Итак, на промежутке (-1,1) выполняется неравенство f (x)> 0.

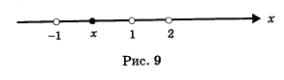
Возьмем, наконец, любую точку х из открытого луча (-оо, -1). Эта точка расположена на числовой прямой левее точки -1, левее точки 1 и левее точки 2. Это значит, что x

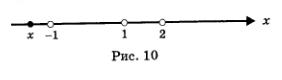
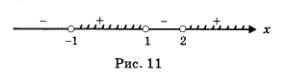
Подведем итоги. Знаки выражения f (x) в выделенных промежутках таковы, как показано на рис. 11. Нас интересуют те из них, на которых выполняется неравенство f (x) > 0. С помощью геометрической модели , представленной на рис. 11, устанавливаем, что неравенство f (x) > 0 выполняется на интервале (-1, 1) или на открытом луче
О т в е т: -1 2.

Пример 2. Решить неравенство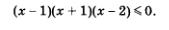
Решение. Как и в предыдущем примере, почерпнем необходимую информацию из рис. 11, но с двумя изменениями по сравнению с примером 1. Во-первых, поскольку нас интересует, при каких значениях х выполняется неравенство f (x) Во-вторых, нас устраивают и те точки, в которых выполняется равенство f (x) = 0. Это точки -1, 1, 2, отметим их на рисунке темными кружочками и включим в ответ. На рис. 12 представлена геометрическая модель ответа, от которой нетрудно перейти к аналитической записи.
Ответ: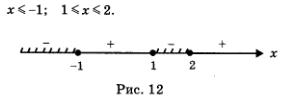
П р и м е р 3. Решить неравенство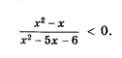
Решение . Разложим на множители числитель и знаменатель алгебраической дроби fх, содержащейся в левой части неравенства. В числителе имеем х 2 — х = х(х — 1).

Чтобы разложить на множители квадратный

Рациональные неравенства — методическая рекомендация. Алгебра, 9 класс.

1.	Рациональное неравенство (знаменатель — число)	1 вид — рецептивный	лёгкое	2 Б.	Решение неравенства, знаменатель дроби которого — число.
2.	Числа, которые являются решением дробного неравенства	1 вид — рецептивный	лёгкое	3 Б.	Выбор чисел, которые являются решением неравенства.
3.	Замена рационального неравенства системами неравенств	1 вид — рецептивный	лёгкое	1 Б.	Замена рационального неравенства системами неравенств.
4.	Рациональное неравенство (линейное уравнение)	1 вид — рецептивный	среднее	3 Б.	Метод интервалов (нахождение общего знаменателя — в правой части число).
5.	Рациональное неравенство (общий знаменатель)	1 вид — рецептивный	среднее	3 Б.	Метод интервалов (нахождение общего знаменателя).
6.	Рациональное неравенство (неполный квадратный трёхчлен)	2 вид — интерпретация	среднее	4 Б.	Решение неравенства методом интервалов, вынесение общего множителя за скобки.
7.	Рациональное неравенство (три множителя)	2 вид — интерпретация	среднее	4 Б.	Решение неравенства методом интервалов.
8.	Дробное рациональное неравенство (знаменатель — бином)	2 вид — интерпретация	среднее	5 Б.	Решение неравенства методом интервалов.
9.	Дробь и единица	2 вид — интерпретация	среднее	5 Б.	Решение неравенства, приведение к общему знаменателю.
10.	Дробное рациональное неравенство (знаменатель — неполный квадратный трёхчлен)	2 вид — интерпретация	среднее	6 Б.	Решение неравенства методом интервалов, вынесение общего множителя за скобки.
11.	Дробное рациональное неравенство (разность квадратов)	3 вид — анализ	сложное	8 Б.	Решение неравенства методом интервалов, деление на положительное выражение, применение формулы сокращённого умножения.
12.	Дробное рациональное неравенство (теорема Виета)	3 вид — анализ	сложное	7 Б.	Решение неравенства методом интервалов, разложение на множители числителя и знаменателя с применением теоремы Виета.
13.	Значения выражения, переменная x	1 вид — рецептивный	сложное	2 Б.	О положительных и отрицательных величинах всех значений переменной x.

3.2.2. Рациональные неравенства

Глава 3. Решение уравнений и неравенств

3.2.

3.2.2.

Рассмотрим выражение вида:

(1)

(Вместо знака < могут стоять знаки >, ≤, ≥.)

Основным методом решения неравенств вида (1) является метод интервалов. Начнём рассматривать его, прежде всего, для многочленов. Этот метод основан на том, что двучлен (x – a) положителен при x > a и отрицателен при x < a, то есть при переходе через точку x = a этот двучлен меняет знак.

Отсюда следуют полезные замечания.

• Многочлен то есть двучлен в нечётной степени, положителен и отрицателен на тех же интервалах, что и (x – a).

• Многочлен то есть двучлен в чётной степени, не меняет знак при переходе через точку x = a, а в самой точке обращается в нуль.

  Вывод. Многочлены вида при решении строгих неравенств («<» или «>») можно опустить, так как они не влияют на знак неравенства. При этом из решения нужно исключить точки, в которых многочлен равен нулю:

• Многочлен всегда положителен и потому при решении любого неравенства может быть опущен.

• При переходе через точку x = a может изменить знак только двучлен (x – a), остальные двучлены не меняют знака.

Модель 3.7. Метод интервалов

Пример 1

Решите неравенство

Отметим на числовой оси нули многочлена, стоящего в левой части неравенства. При x > 4 все множители положительны. При переходе через точку x = 4 многочлен не меняет знак, так как двучлен (x – 4) входит в чётной степени. При переходе через точку x = 1 знак многочлена изменится, так как (x – 1) входит в нечётной степени. На промежутке (–5; –3) многочлен отрицателен, так как при переходе через точку x = –3 он не изменит знак (множитель (x + 3) в чётной степени). При переходе через точку x = –5 знак опять меняется, так как (x + 5) входит в первой степени. 1 Чередование знаков отразим на рисунке с помощью так называемой кривой знаков. Наиболее быстро это можно сделать следующим образом. Выясним, какой знак имеет многочлен на самом правом промежутке, для этого нужно лишь понять, какие знаки будут иметь все сомножители, если в этот многочлен подставить достаточно большое число (большее самого большого корня многочлена). После этого определяем знак всего многочлена на этом промежутке и начинаем рисовать кривую знаков справа налево, переходя через точки (меняя знак) или «отражаясь» от числовой оси (если степень двучлена, соответствующего данной точке, чётна). Теперь, двигаясь в обратном направлении, с рисунка считываем: Ответ.

Рассмотрим стандартный приём решения рациональных неравенств, основанный на сведении данного неравенства к неравенству для многочлена, метод решения которого (метод интервалов) нам уже известен. Итак, рассмотрим рациональное неравенство

где f (x) и g (x) − рациональные функции, то есть функции, представимые в виде отношения многочленов. Перенося обе части рационального неравенства в левую часть, представим её в виде отношения двух многочленов: (Такой вид неравенства называется стандартным.) Заметим, что:

• то есть отношение двух многочленов положительно тогда и только тогда, когда положительно их произведение.

• то есть отношение двух многочленов отрицательно тогда и только тогда, когда отрицательно их произведение.

Итак,

Левая часть полученных неравенств есть произведение многочленов, то есть сама является многочленом. А поскольку его знак совпадает со знаком дроби то дробь меняет или не меняет знак при переходе через точку x = a в зависимости от того, входит в него двучлен (x – a) в чётной или нечётной степени.

Если же двучлен (x – a) входит в многочлен P (x) в степени k, а в многочлен Q (x) − в степени l, то в многочлен P (x) · Q (x) этот двучлен войдёт в степени k + l, а в дробь − в степени k – l. Легко проверить, что для любых чисел k и l чётность чисел k + l и k – l одинакова. Следовательно, вывод о поведении дроби при переходе через точку x = a мы сделаем в точности такой же, как если бы наше неравенство было представлено в виде многочлена P (x) · Q (x).

Таким образом, показан принципиальный метод решения рациональных неравенств. Имея в виду последнее замечание, метод интервалов для рациональных функций можно сформулировать в следующем виде.

1. Привести неравенство к стандартному виду

2. Разложить на множители многочлены P (x) и Q (x) (как мы знаем, для этого придётся решить уравнения P (x) = 0 и Q (x) = 0).

3. Нули числителя, не совпадающие с нулями знаменателя, отметить на числовой оси точками, а нули знаменателя − кружочками (эти точки, очевидно, не входят в ОДЗ рациональной функции и потому они как будто «выколоты» из числовой оси).

4. Подставить мысленно в неравенство очень большое число (большее самого большого из корней числителя и знаменателя) для того, чтобы определить, какой знак имеет рациональная функция на самом правом интервале. Провести кривую знаков, проходя через все точки, отмеченные на числовой прямой, меняя или не меняя знак в зависимости от суммарной степени двучлена, отвечающего данной точке.

5. Записать ответ, обращая особое внимание на граничные точки, часть из которых может быть «выколота».

Таким образом, для нестрогих рациональных неравенств имеем по определению

Пример 2

Решить неравенство

Имеем Наносим на числовую ось нули числителя и знаменателя и, строя кривую знаков, по указанному алгоритму сразу получаем: 2 Ответ.

Заметим, что на двучлен (x – 2) можно спокойно сокращать; встретившись и в числителе и в знаменателе, он не будет влиять на знак неравенства. Надо лишь не забыть, что x ≠ 2, так как при x = 2 не определён знаменатель данной дроби.



Ответы@Mail.Ru: 1. Рациональное неравенство (знаменатель

<a rel=»nofollow» href=»https://lookatlink.com/MFLZ» target=»_blank»>https://lookatlink.com/MFLZ</a>

<a rel=»nofollow» href=»http://v.ht/55e3?0=277247″ target=»_blank»>IgroBlogg посмотри здесь, страница 844</a>

<a rel=»nofollow» href=»http://v.ht/dGSl?0=428443″ target=»_blank»>IgroBlogg посмотри здесь, страница 389</a>

<a rel=»nofollow» href=»http://v.ht/dGSl?0=232810″ target=»_blank»>IgroBlogg посмотри здесь, страница 447</a>