Рациональные неравенства — теория и формулы, подготовка к ЕГЭ по математике
Рациональное неравенство — это неравенство, которое можно свести к виду \[\Large{\dfrac{P(x)}{Q(x)}\lor 0}\]где \(P(x),\
Q(x)\) — многочлены.
(\(\lor\) — один из знаков \(\geqslant,
\ \leqslant, \ >, \ <\))
Например, следующие неравенства являются рациональными: \[\dfrac1{x+1}>0,\qquad x+2+\dfrac{x-1}{x+3}<1,\qquad x^2+x-2\leqslant 0\]
\[{\Large{\text{Линейные неравенства}}}\] Линейные неравенства – это неравенства вида \[ax+b \lor 0, \qquad
\lor — \text{ один из знаков } \geqslant, \ \leqslant, \ >, \
<;\quad a,b — \text{ числа,}\]или сводящиеся к такому виду.
Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа (\(x\in \mathbb{R}\)).
Общее правило решения линейных неравенств:
1) Для того, чтобы решить данное неравенство, необходимо привести его к виду \(ax\lor -b\), то есть перенести число \(b\) в правую часть.
2) Если коэффициент \(a\) перед \(x\) – положительный, то неравенство равносильно \(x\lor -\dfrac ba\), то есть после деления обеих частей неравенства на \(a\) знак неравенства не меняется.
3) Если коэффициент \(a\) перед \(x\) – отрицательный, то неравенство равносильно \(x\land -\dfrac ba\), то есть после деления обеих частей неравенства на \(a\) знак неравенства меняется на противоположный
4) Если \(a=0\), то неравенство равносильно \(0\lor -b\), что либо верно при всех значениях переменной \(x\) (например, если это \(0>-1\)), либо неверно ни при каких значениях \(x\) (например, если это \(0\leqslant -3\)).
То есть ответом будут либо \(x\in\mathbb{R}\), либо \(x\in
\varnothing\).
Замечание
Заметим, что знаку \(\leqslant\) противоположен знак \(\geqslant\), а знаку \(<\) – знак \(>\). И наоборот.
Пример 1
Решить неравенство \(5-3x>-1\).
Решение. I способ
Сделаем цепочку преобразований:
\[5-3x>-1 \ \Rightarrow \ -3x>-1-5 \ \Rightarrow \ -3x>-6 \
\Rightarrow \ x<\dfrac 63 \ \Rightarrow \ x<2\] Таким образом, ответом будет \(x\in(-\infty;2)\).
Заметим, что т.к. мы делили неравенство на \(-3\), то знак неравенства поменялся.
Решение. II способ
Можно перенести слагаемое \(-3x\) в правую часть, а \(-1\) – в левую:
\[5-3x>-1 \ \Rightarrow \ 5+1>3x \ \Rightarrow \ 3x<6 \ \Rightarrow \ x<2\]
Пример 2
Решить неравенство \((1-\sqrt2)x+2\leqslant 0\).
Решение
Заметим, что перед \(x\) находится отрицательный коэффициент. Поэтому:
\[(1-\sqrt2)x\leqslant -2 \Rightarrow x\geqslant -\dfrac 2{1-\sqrt2}\] Преобразуем число \(-\dfrac 2{1-\sqrt2}\): домножим числитель и знаменатель дроби на сопряженное к \(1-\sqrt2\), то есть на \(1+\sqrt2\), чтобы избавиться от иррациональности в знаменателе:
\[-\dfrac 2{1-\sqrt2}=-\dfrac{2(1+\sqrt2)}{(1-\sqrt2)(1+\sqrt2)}=
-\dfrac{2(1+\sqrt2)}{1-2}=2(1+\sqrt2)\]
Таким образом, ответ \(x\in [2+2\sqrt2;+\infty)\).
Перейдем к квадратичным неравенствам, которые являются очень важным инструментом в решении задач.
\[{\Large{\text{Метод интервалов}}}\]
Приступим к рассмотрению общего метода для решения любого рационального неравенства, то есть неравенства вида
\[(**)\qquad \dfrac{P(x)}{Q(x)}\geqslant 0 \qquad (\text{на месте }\geqslant \text{может стоять любой из} \leqslant, \ <, \ >)\]
Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа, кроме нулей знаменателя.
Существует два способа решения таких неравенств:
1 способ: Классический. Т.к. дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель дроби одного знака (разных знаков), то неравенство \((*)\) равносильно совокупности: \[{\large{\left[\begin{gathered} \begin{aligned} &\begin{cases} P(x)\geqslant 0\\ Q(x)>0 \end{cases}\\ &\begin{cases} P(x)\leqslant 0\\ Q(x)<0 \end{cases} \end{aligned} \end{gathered} \right.}}\]
Такой способ подойдет для решения любого неравенства, где слева стоит дробь, а справа — \(0\).
Но, как правило, для решения большинства рациональных неравенств он неудобен. Почему? Вы сможете убедиться в этом после того, как мы рассмотрим метод интервалов.
2 способ: Удобный. Метод интервалов (будем рассматривать этот метод на примере конкретного неравенства, чтобы было понятней).
Заметим, что первые три шага созданы для того, чтобы преобразовать неравенство к более простому виду, что поможет вам не допустить ошибку в решении подобных задач. Метод интервалов – это всего лишь удобный инструмент для решения рациональных неравенств, и если вы будете всегда пользоваться одним и тем же алгоритмом, то вероятность допустить ошибку при решении таких неравенств будет минимальной.
Данный алгоритм специально расписан подробно, чтобы у вас не возникло вопросов; всего после нескольких использований этого алгоритма вы будете решать рациональные неравенства очень быстро и без ошибок!
1 ШАГ. Необходимо перенести все слагаемые в одну часть (пусть это будет левая часть) неравенства так, чтобы в другой части неравенства остался \(0\), и привести эти слагаемые к общему знаменателю так, чтобы в левой части неравенства получилась дробь. Затем нужно разложить числитель и знаменатель полученной дроби, то есть многочлены \(P(x), \ Q(x)\), на множители.
Например, неравенство \(\dfrac1{x+1}<1\) нужно переписать в виде \(\dfrac1{x+1}-1<0\), затем привести к общему
знаменателю \(\dfrac1{x+1}-\dfrac{x+1}{x+1}<0\), затем записать в виде одной дроби левую часть: \(\dfrac{1-(x+1)}{x+1}<0\) и
привести подобные слагаемые: \(\dfrac{-x}{x+1}<0\).
Итак, пусть после разложения на множители неравенство приняло вид \[\dfrac{x^2(x-1)^3(x+1)(2x^2+3x+5)(2x-x^2-3)}{(x+1)^3(3-x)(2-3x)^2} \geqslant0\]
Заметим, что любой многочлен можно (а в нашем способе НУЖНО) разложить до произведения только линейных скобок (\(ax+b\)) и квадратичных скобок с отрицательным дискриминантом \((ax^2+bx+c), \ D<0\).
2 ШАГ. Рассмотрим скобки, в которых остался квадратичный трехчлен с \(D<0\).
\(\bullet\) Если при \(x^2\) находится положительный коэффициент \(a>0\), то при всех значениях \(x\) выражение \(ax^2+bx+c\) положительно (не может быть равно нулю!). Т.к. мы имеем право делить неравенство на любое число/выражение, не равное \(0\), то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является \((2x^2+3x+5)\)). Причем заметим, что т.к. мы делим на положительное выражение, то знак неравенства не меняется!
\(\bullet\) Если при \(x^2\) находится отрицательный коэффициент \(a<0\), то при всех значениях \(x\) выражение \(ax^2+bx+c\) отрицательно. Т.к. мы имеем право делить неравенство на любое число/выражение, не равное \(0\), то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является \((2x-x^2-3)\)). Причем заметим, что т.к. мы делим на отрицательное выражение, то знак неравенства должен измениться на противоположный!
Итак, обобщим 2 шаг: квадратичные скобки с отрицательным дискриминантом можно просто вычеркнуть, причем при вычеркивании скобок с \(a>0\) знак неравенства остается прежним, а вот при вычеркивании скобок с \(a<0\) знак неравенства меняется на противоположный столько раз, сколько было таких скобок. Лучше вычеркивать их последовательно по одной, каждый раз меняя знак неравенства на противоположный.
Таким образом, неравенство примет вид \[\dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(3-x)(2-3x)^2} \leqslant 0\]
3 ШАГ. Рассмотрим линейные скобки \((ax+b)\).
Назовем скобку хорошей, если при \(x\) находится положительный коэффициент (такие скобки мы трогать не будем), и плохой, если при \(x\) находится отрицательный коэффициент (в таких скобках необходимо поменять все знаки на противоположные, то есть сделать их хорошими).
Для того, чтобы в одной плохой скобке поменять все знаки на противоположные, необходимо домножить правую и левую части неравенства на \(-1\). Таким образом, после одного такого действия знак неравенства сменится на противоположный. Значит, если плохих скобок четное количество, то знак неравенства не изменится, если нечетное – то знак неравенства изменится на противоположный.
Заметим, что выражение \((ax+b)^n\) — это не что иное, как произведение \(n\) скобок \((ax+b)\).
В нашем неравенстве среди плохих одна скобка \((3-x)\) и две скобки \((2-3x)\) (т.к. \((2-3x)^2=(2-3x)(2-3x)\)), то есть всего три плохих скобки, следовательно, знак неравенства изменится и неравенство примет вид: \[\dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(x-3)(3x-2)^2} \geqslant0\quad (***)\]
Заметим, что множитель \(x^2\) — это скобка \((x-0)^2\), или, что то же самое, \((x-0)(x-0)\) – произведение двух одинаковых линейных скобок.
4 ШАГ. Теперь, когда левая часть неравенства состоит из произведения только хороших линейных скобок (в каких-то степенях), можно приступить к самому методу интервалов.
Его суть состоит в том, что левая часть неравенства — всюду непрерывная функция, кроме тех точек, где знаменатель дроби равен нулю. Поэтому точки, в которых эта функция равна нулю (то есть ее числитель равен нулю) и точки, в которых эта функция не существует (то есть ее знаменатель равен нулю), разбивают область определения этой функции на промежутки, причем на каждом промежутке функция принимает значения строго одного знака.
А нам как раз нужно найти те значения \(x\), при которых функция \(\geqslant 0\). Причем, т.к. наша функция — рациональная, то ее область определения — это все действительные числа (\(\mathbb{R}\)), кроме нулей знаменателя. Поэтому отметим нули каждой скобки на вещественной прямой (а ноль каждой скобки – это как раз ноль числителя или знаменателя), причем нули знаменателя – выколотые, нули числителя – закрашенные (если знак неравенства нестрогий, как в примере, то есть \(\geqslant \) или \(\leqslant \)) или выколотые (если знак неравенства строгий, то есть \(>\) или \(<\)).
Заметим, что если мы отметили \(n\) точек, то числовая прямая разобьется на \(n+1\) промежутков.
Расставим знак на каждом промежутке \(\color{red}{{\Large{\text{справа налево}}}}\). Будем ставить “\(+\)”, если функция на этом промежутке принимает положительные значения, и “\(-\)” — если отрицательные. Нулю функция равна в закрашенных точках.
Первые три шага мы делали для того, чтобы не подставлять точки из каждого промежутка и не вычислять, какого знака будет левая часть неравенства (что бывает неудобно, если числа, которые нужно отмечать на прямой, “некрасивые”). Знаки мы будем расставлять, выявив некоторую закономерность. Какую – вы узнаете дальше.
Но в любом случае способ расстановки знаков путем подстановки чисел остается в нашем арсенале.
Т.к. все скобки – хорошие, то первый знак всегда будет “\(+\,\)” (именно для этого мы и приводили неравенство к такому виду!). Действительно, если подставить любое число, превышающее самый большой корень (у нас самый большой корень \(x=3\)), то каждая скобка будет положительна, значит, и произведение таких скобок будет всегда положительно.
Если какой-то корень входит в четное количество скобок, то при переходе через него (справа налево!) знак меняться не будет. В нашем неравенстве это точки \(-1, \ 0, \ \dfrac23\) (например, точка \(-1\) входит в четное количество скобок: одна в числителе \((x+1)\) и три в знаменателе \((x+1)^3\)).
Если точка входит в нечетное количество скобок, то при переходе через эту точку (справа налево!) знак будет меняться (в нашем неравенстве это точки \(3\) и \(1\)).
Объясним, почему так происходит. Каждая линейная скобка в нечетной степени \((x-a)^{2n+1}\) имеет ровно один корень \(x=a\), причем, т.к. мы сделали ее хорошей, то для всех \(x>a\) она будет положительной, для всех \(x<a\) она будет отрицательной (а для \(x=a\), естественно, равной нулю). Значит, когда \(x\in (1;3)\), то все скобки, кроме \((x-3)\), будут оставаться положительными, и лишь эта скобка \((x-3)\) станет отрицательной. Значит, их произведение также станет отрицательным. Аналогично при переходе через точку \(x=1\).
Каждая линейная скобка в четной степени \((x-b)^{2n}\) также имеет ровно один корень \(x=b\), но т.к. она в четной степени, то при всех \(x\ne b\) она всегда будет положительной! И только при \(x=b\) она будет равна нулю. Именно поэтому при переходе через точку \(x=\dfrac23\), т.е. на \(x\in(0;\frac23)\), скобка \((3x-2)^2\) не сменит свой знак на отрицательный, поэтому вся левая часть останется по знаку такой же, как и была на \((\frac23;1)\) (т.е. положительной). Аналогично при переходе через точки \(0, -1\).
5 ШАГ. Неравенство практически решено и нам остается только записать ответ. В нашем случае, т.к. знак преобразованного \((***)\) неравенства \(\geqslant 0\) (нестрогий), то в ответ пойдут промежутки со знаком “\(+\,\)” (где значение функции больше нуля) и закрашенные точки (где значение функции равно нулю): \[x\in \Big(-\infty;-1\Big)\cup \left(-1;\dfrac23\right)\cup \left(\dfrac23;1\right]\cup\Big(3;+\infty\Big)\]Напоминаем, что если точка не входит в ответ, то она пишется в круглой скобке “\((\)” или “\()\)”, если входит в ответ – то в квадратной скобке “\([\)” или “\(]\)”. Бесконечности всегда пишутся в круглых скобках.
\[{\Large{\text{Квадратичные неравенства}}}\]
Квадратичным неравенством называется любое неравенство вида \[ax^2+bx+c \lor 0, \quad a\ne 0,\]
или сводящееся к такому виду.
Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа (\(x\in \mathbb{R}\)).
Квадратичные неравенства – это те же самые рациональные неравенства, следовательно, их также можно решать с помощью метода интервалов. Но давайте рассмотрим еще один способ, при помощи которого, как правило, удобнее решать квадратичные неравенства. Для этого нам понадобится вспомнить про параболу.
Замечание
Вспомним, как преобразуется квадратичный трехчлен \(ax^2+bx+c\) в зависимости от того, сколько корней он имеет.
Если квадратное уравнение \(ax^2+bx+c=0\)
\(\bullet\) имеет два корня \(x_1\) и \(x_2\) (дискриминант \(D>0\)), то \(ax^2+bx+c=a(x-x_1)(x-x_2)\).
\(\bullet\) имеет один корень \(x_1\) (\(D=0\)), то \(ax^2+bx+c=a(x-x_1)^2\).
\(\bullet\) не имеет корней (\(D<0\)), то квадратный трехчлен \(ax^2+bc+c\) никогда не может быть равен нулю и не разлагается на линейные множители.
Шаг 1. Рассмотрим функцию \(f(x)=ax^2+bx+c\). Графиком такой функции является парабола.
Для того, чтобы решить квадратичное неравенство, изобразим схематично параболу: то есть определим, куда направлены ее ветви и в каких точках она пересекает ось \(Ox\).
Если \(a>0\), то ветви направлены вверх, если \(a<0\), то ветви направлены вниз. Корни уравнения \(ax^2+bx+c=0 \ (*)\) и есть абсциссы точек, в которых парабола пересекает ось \(Ox\).
Шаг 2. Таким образом, наша парабола будет одного из 6 видов: 
\((1)\) и \((4)\) — когда уравнение \((*)\) имеет один корень;
\((2)\) и \((5)\) — когда уравнение \((*)\) имеет два корня;
\((3)\) и \((6)\) — когда уравнение \((*)\) не имеет корней.
Часть параболы, находящая выше оси \(Ox\), отвечает за \(f(x)>0\);
часть параболы, находящаяся ниже оси \(Ox\), отвечает за \(f(x)<0\);
точки, в которых парабола пересекает ось \(Ox\), отвечают за \(f(x)=0\).
Пример 1.
Решить неравенство \(x^2+3x+2\geqslant 0\).
Решение
Решим уравнение \(x^2+3x+2=0 \Leftrightarrow x_1=-2, x_2=-1\). Таким образом, неравенство можно переписать в виде: \((x+1)(x+2)\geqslant
0\). Ветви параболы направлены вверх, следовательно, схематично она выглядит как \((2)\). Т.к. знак неравенства \(\geqslant\), то решением неравенства будут те значения \(x\), для которых график находится выше оси \(Ox\), а именно \(x\in (-\infty;-2]\cup[-1;+\infty)\).
Заметим, что точки \(-2, -1\) входят в ответ, потому что знак “больше или равно”.
Пример 2.
Решить неравенство \(11x-3x^2-6>0\)
Решение
Решим уравнение \(11x-3x^2-6=0 \quad\Leftrightarrow\quad
x_1=\dfrac23, x_2=3\). Таким образом, неравенство можно переписать в виде: \(-3(x-3)(x-\frac23)>0\).
1 способ. Ветви параболы направлены вниз, следовательно, схематично она выглядит как \((5)\). Т.к. знак неравенства \(>\), то решением неравенства будут \(x\in \left(\dfrac23;3\right)\).
2 способ. Домножим правую и левую части неравенства на \(-1\), получим \(3(x-3)(x-\frac23)<0\) (заметим, что знак сменился на противоположный). У новой параболы \(\Big(f(x)=3(x-3)(x-\frac23)\Big)\) ветви направлены вверх, следовательно, схематично она выглядит как \((2)\). Но знак неравенства уже \(<\). Решением нового неравенства, естественно, будут те же \(x\in \left(\dfrac23;3\right)\).
Таким образом, если в квадратичном неравенстве отрицательный знак при \(x^2\), то можно сначала домножить неравенство на \(-1\) (и не забыть поменять знак неравенства), чтобы ветви параболы всегда были направлены вверх.
Пример 3.
Решить неравенство \(x^2+4x+4 \geqslant 0\).
Решение
Вспомнив формулу сокращенного умножения, получаем \((x+2)^2\geqslant
0\) (это быстрее, чем находить корни через дискриминант :)). Таким образом, парабола пересекает ось \(Ox\) в единственной точке \(x_1=-2\) и выглядит как \((1)\). А т.к. нам нужны те \(x\), для которых график находится не ниже оси \(Ox\), то решением неравенства будут \(x\in
\mathbb{R}\), то есть выражение \((x+2)^2\) всегда больше или равно \(0\).
shkolkovo.net
«Решение неравенств». 10-й класс
Цели:
- Систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения рациональных неравенств.
- Содействовать развитию математического мышления учащихся,умению комментировать,тренировать память.
- Воспитание ответственного отношения к учебному труду,чувства товарищества и взаимопомощи.
Оборудование: интерактивная доска, раздаточный материал(разноуровневые карточки с практическими заданиями).
Структура урока:
- Сообщение темы и цели урока (1 мин.)
- Проверка домашнего задания (5 мин.)
- Систематизация знаний и умений по пройденному материалу (10 мин.)
- Инструктирование по выполнению заданий в группах (3 мин.)
- Выполнение заданий в группах (15 мин.)
- Проверка и обсуждение полученных результатов (8 мин.)
- Постановка домашнего задания (2 мин.)
- Подведение итогов урока (1 мин.)
Ход урока
I. Сообщение темы и цели урока.
Сегодня на уроке мы будем решать неравенства методом интервалов и методом замены переменных. Эпиграфом к сегодняшнему уроку будут слова Ньютона:“При изучении наукпримеры не менее поучительны,нежели правила” и слова Ломоносова: “Примеры учат больше,чем теория”.
II. Проверка домашнего задания.
На дом были даны неравенства. Проверьте ваше решение по интерактивной доске.
Слайд №1
№1.
Отметим на числовой оси корни числителя и знаменателя.
Ответ: Є (-3; 1]
№2.
Ответ: x Є [1; 2] U (3; +∞)
№3.
Ответ: x Є (-6; 1)
№4.
≥
Преобразуем исходное неравенство
– ≥ 0
≥ 0
≥ 0
≥ 0
Применим метод интервалов.
Ответ: (-∞; 1) U (2; +∞).
III. Систематизация знаний и умений по пройденному материалу.
Решим методом интервалов следующее неравенство. (Учитель на доске дает образец решения неравенств).
№1.
≥ 0
Решение.
Рассмотрим функцию
1. Область определения функции f(x)находим из системы неравенств
Область определения: [-4; 3) U (3; 4]
2. Уравнение f (x) ═ 0 имеет корни: -4; 4; 3,5
Ответ: [-4; 3) U [3,5; 4]
Следующее неравенство решим методом замены переменных.
№2.
()² + 7 () +12 < 0
Решение
Замена ═ t
Решим его методом интервалов.
-4 <t< -3
Решим систему:
Решим 1-е неравенство
xЄ( 1; 3)
Решим 2-е неравенство
xЄ (- ∞ ; 2) U (2 ; +∞)
Окончательный ответ: xЄ (1; 2) U (2; 3)
IV. Инструктирование по выполнению самостоятельной работы.
Учитель передает задания каждой группе из 4-5 учащихся и двойные листы с копиркой для оформления решения каждым учеником, раздаточный материал с заданиями для групп.Содержание одного из вариантов задания.
Решите неравенства:
- >0
- ≤ 0
- ≥ 0
V. Выполнение заданий в группах.
VI. Проверка и обсуждение полученных результатов.
Проверьте по интерактивной доске решение работы.
Учащиеся осуществляют самопроверку и самооценку заданий. Получают разъяснения по возникающим при этом вопросам.
Ответы к рассмотренному варианту.
Слайд №2
1.
Решение:
Воспользуемся методом интервалов, получим :
Ответ: (1; 5) U (5; + ∞)
2.
≤ 0
Решение:
Замена
Тогда t-1 — ≤ 0
Решим неравенство методом интервалов
t≤ -4; 0 <t≤ 5
Вернемся к замене
0 <
Решим 1-е неравенство:
Д ═49 -84 ═-35 <0
Неравенство решений не имеет.
Решим 2-е неравенство.
0 <
Решим систему:
Решим 1-е неравенство системы:
Д < 0, значит x Є R
Решим 2-е неравенство системы:
Ответ: [3;4]
3.
≥ 0
Рассмотрим функцию: f (x)═
1) Область определения находим из системы неравенств
x ≥ -11;
Область определения:
[-11; -3) U (-3; 0) U (0; +∞)
2) Уравнение f(x)═0 имеет корень -11
Ответ: [-11; -3) U (0; +∞)
VII. Постановка домашнего задания.
Запишите домашнее задание. Решить неравенства:
≤ 0
- ≥ 0
- ≥0
VIII. Подведение итогов урока.
urok.1sept.ru
Рациональные неравенства и их системы. Системы рациональных неравенств
С помощью данного урока вы узнаете о рациональных неравенствах и их системах. Решается система рациональных неравенств с помощью эквивалентных преобразований. Рассматривается определение эквивалентности, способ замены дробно-рационального неравенства — квадратным,а также разбирается в чем отличие неравенства от уравнения и как осуществляются равносильные преобразования.
Алгебра 9 класс
Итоговое повторение курса алгебры 9-го класса
Рациональные неравенства и их системы. Системы рациональных неравенств.
1.1 Конспект.
1. Эквивалентные преобразования рациональных неравенств.
Решить рациональное неравенство означает – найти все его решения. В отличии от уравнения, при решении неравенства, как правило, возникает бесчисленное множество решений. Бесчисленное множество решений нельзя проверить методом подстановки. Поэтому, нужно так преобразовывать исходное неравенство, чтобы в каждой следующей строчке получалось неравенство с тем же множеством решений.
Рациональные неравенства решаются только с помощью эквивалентных или равносильных преобразований. Такие преобразования не искажают множество решений.
Определение. Рациональные неравенства называют эквивалентными, если множества их решений совпадают.
Для обозначения эквивалентности используют знак
2. Решение системы неравенств 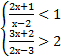
Первое и второе неравенство – это дробно-рациональные неравенства. Методы их решения являются естественным продолжением методов решения линейных и квадратных неравенств.

Перенесем числа, стоящие в правой части, в левую с противоположным знаком.
В итоге в правой части останется 0. Это преобразование является эквивалентным. На это указывает знак 
Выполним действия, которые предписывает алгебра. Вычтем «1» в первом неравенстве и «2» во втором.

Упростим полученные неравенства. Далее будем решать каждое неравенство по- очереди.
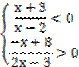
3. Решение неравенства 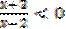 методом интервалов
методом интервалов
1) 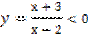 Введем функцию. Нам нужно узнать, когда эта функция меньше 0.
Введем функцию. Нам нужно узнать, когда эта функция меньше 0.
2) 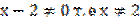 Найдем область определения функции: в знаменателе не должен стоять 0. «2» — точка разрыва. При х=2 функция неопределенна.
Найдем область определения функции: в знаменателе не должен стоять 0. «2» — точка разрыва. При х=2 функция неопределенна.
3) 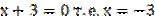 Найдем корни функции. Функция равна 0,если в числителе стоит 0.
Найдем корни функции. Функция равна 0,если в числителе стоит 0.

Поставленные точки разбивают числовую ось на три интервала – это интервалы знакопостоянства. На каждом интервале функция сохраняет знак. Определим знак на первом интервале. Подставим какое-нибудь значение. Например, 100. Ясно, что и числитель, и знаменатель больше 0. Значит и вся дробь положительна.

Определим знаки на остальных промежутках. При переходе через точку х=2 только знаменатель меняет знак. Значит, и вся дробь поменяет знак, и будет отрицательной. Проведем аналогичное рассуждение. При переходе через точку х=-3 только числитель меняет знак. Значит, дробь поменяет знак и будет положительной.
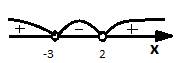
Выберем интервал соответствующий условию неравенства. Заштрихуем его и запишем в виде неравенства


4. Решение неравенства  с помощью квадратичного неравенства
с помощью квадратичного неравенства
Важный факт.
При сравнении с 0 ( в случае строгого неравенства) дробь можно заменить на произведение числителя на знаменатель или поменять числитель или знаменатель местами.
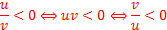

Это так, потому, что все три неравенства выполняются при условии, что u и v разного знака. Эти три неравенства эквивалентны.
Используем это факт и заменим дробно-рациональное неравенство квадратным.
 . Решим квадратное неравенство.
. Решим квадратное неравенство.
Введем квадратичную функцию. Найдем ее корни и построим эскиз ее графика.


 Значит, ветви параболы вверх. Внутри интервала корней функция сохраняет знак. Она отрицательна.
Значит, ветви параболы вверх. Внутри интервала корней функция сохраняет знак. Она отрицательна.
Вне интервала корней функция положительна.
Решение первого неравенства: 
5. Решение неравенства 
Введем функцию:

Найдем ее интервалы знакопостоянства:
Для этого найдем корни и точки разрыва области определения функции. Точки разрыва выкалываем всегда. (х=3/2) Корни выкалываем в зависимости от знака неравенства. Наше неравенство строгое. Поэтому корень выкалываем.

Расставим знаки:
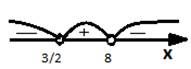
Запишем решение:

Закончим решение системы. Найдем пересечение множества решений первого неравенства и множества решений второго неравенства.
Решить систему неравенств означает найти пересечение множества решений первого неравенства и множества решений второго неравенства. Поэтому, решив первое и второе неравенство по отдельности нужно записать полученные результаты в одну систему.

Изобразим решение первого неравенства над осью Ох.

Решение же второго неравенства изобразим под осью.
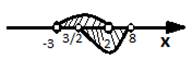
Решением системы будут те значения переменной, которые удовлетворяют как первому, так и второму неравенству. Итак, решение системы:
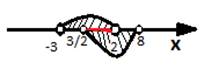

1.2. Список рекомендованной литературы
- Алгебра, 9 класс. Часть 1 из 2. Учебник (А. Г. Мордкович, П. В. Семенов) 2010
- Алгебра, 9 класс. Часть 2 из 2. Задачник (А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.) 2010
- Алгебра, 9 класс (Л. В. Кузнецова, С. Б. Суворова, Е. А. Бунимович и др.) 2010
- Алгебра, 9 класс. Задачник (Л. И. Звавич, А. Р. Рязановский, П. В. Семенов) 2008
- Алгебра, 9 класс (Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова) 2009
- Алгебра, 9 класс (Л. В. Кузнецова, С. Б. Суворова, Е. А. Бунимович и др.) 2010
1.3. Дополнительные веб-ресурсы
http://slovo.ws/urok/algebra -Учебные материалы (учебники, статьи) по алгебре для 9 класса. Все учебники, указанные в списке можно посмотреть в режиме онлайн , без скачивания.
http://math-portal.ru/matematika-shkolnaya/
1.4. Сделай дома
Алгебра, 9 класс. Часть 2 из 2. Задачник (А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.) 2010
Домашнее задание: 4.24; 4.28
Другие задания: 4.25; 4.26
interneturok.ru
Метод интервалов в рациональных неравенствах. Примеры, тест
Чтобы оценить все могущество метода интервалов, давайте сначала решим несложное неравенство так, как если бы мы его решали, не зная метода интервалов. + показать
Решим неравенство  .
.
Как мы будем рассуждать?
Произведение двух множителей дает знак «+», когда
1) оба множителя положительны;
2) оба множителя отрицательны.
Поэтому предстоит решить совокупность двух систем неравенств:

Решение первой системы:


Решение второй системы:


Итак, нам осталось объединить решения первой и второй систем:
Ответ: 
А теперь представьте, если бы у нас было не два множителя, как выше, а три-четыре, а если бы при этом множители представляли из себя многочлены второй степени, например.
Представляете, сколько было бы перебора различных ситуаций?
Метод интервалов для рациональных неравенств
Метод интервалов выручит! Избавит нас от рутины! + показать
Мы ведь понимаем, что любое число – либо отрицательное (-), либо положительное (+), либо ноль. Где «переход» из одной зоны (+или – ) в другую (- или +)? В нуле!


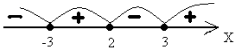
На рисунке 1 функция обращается в нуль в точках -2; 1; 5 и 7. Именно при переходе через них она и меняет свой знак с одного на другой.
Функция может также коснуться оси (ох), и «не перескочить» в другую зону (как на рисунке 2). В данном случае точка  – корень четной кратности (мы еще поговорим об этом).
– корень четной кратности (мы еще поговорим об этом).
В любом случае, если функция попала из одной «зоны» («+,-») в другую («-,+»), – значит она в какой-то точке должна была обратиться в ноль.
Поэтому-то нули функции и помогут нам!
Итак, давайте выработаем алгоритм, которого будем придерживаться при решении рациональных неравенств.
Алгоритм решения рациональных неравенств
Пусть нам дано неравенство вида  , где
, где  – один из знаков
– один из знаков  .
.
1. Раскладываем  на множители (если это возможно*).
на множители (если это возможно*).
2. Находим нули  .
.
3. Отмечаем корни (нули) функции на оси в порядке возрастания. Эти числа разбивают числовую ось на интервалы. На каждом из этих интервалов выражение сохраняет знак, а, переходя через отмеченные точки, меняет знак на противоположный (или не меняет, если корень – четной кратности, например, в неравенстве 
 – корень четной кратности, корень
– корень четной кратности, корень  – обычный).
– обычный).
4. Расставляем знаки на интервалах, начиная от крайнего правого. Советую брать «миллиончик» – не промахнетесь (шучу). Нам не важно само значение функции в выбранной точке, но только ЗНАК в ней, поэтому не утруждайте себя подсчетами – только грубая прикидка.
5. Выбираем подходящие нам промежутки, записываем ответ. Например, если неравенство со знаком «>», то берем интервалы со знаком «+», если неравенство со знаком «<», то берем интервалы со знаком «-», если неравенство со знаком  (
( ), то берем промежутки со знаком «+» («-») c закрытыми концами.
), то берем промежутки со знаком «+» («-») c закрытыми концами.
Практика
Пример 1.
Решить неравенство: 
Решение: + показать
1) Разложим вторую скобку неравенства на множители по формуле «разность квадратов»: 
2) Нули: 
3)

4) Взяв «миллиончик» и «подставив» в  , конечно же будем иметь знак «-». Далее знаки чередуются.
, конечно же будем иметь знак «-». Далее знаки чередуются.

5) Выбираем подходящие нам промежутки, записываем ответ:

Ответ:  .
.
Пример 2.
Решить неравенство: 
Решение: + показать
1) Попадаем в ситуацию (*) – на множители-то не раскладывается, так как  .
.
2) –
3) А отмечать-то нечего на оси 🙁
4) Так значит, меняться знаку негде! Он – либо «+» либо «-» всюду! Берем любое число, например, 0 и смотрим, какой знак в нем принимает выражение  . Очевидно, это «+». Поэтому
. Очевидно, это «+». Поэтому 
5) Ответ:  .
.
Пример 3.
Решить неравенство: 
Решение: + показать
1) Раскладываем первую скобку на множители по формуле разность кубов:
 . Заметим,
. Заметим,  дальше на множители не раскладывается, так как
дальше на множители не раскладывается, так как  для этого квадратного трехчлена. А значит, эта скобка несет в себе только один знак (не трудно понять, что «+»). То есть, вообще говоря, мы можем поделить обе части исходного неравенства на
для этого квадратного трехчлена. А значит, эта скобка несет в себе только один знак (не трудно понять, что «+»). То есть, вообще говоря, мы можем поделить обе части исходного неравенства на  . Полученное тогда неравенство
. Полученное тогда неравенство  равносильно исходному.
равносильно исходному.
Будем дальше решать именно это неравенство:

2) Нули:  .
.
3)-4) Обратите внимание: корень  – четной кратности, при переходе через него не будет происходить смена знаков! Ну действительно, знак неравенства определяется только выражением
– четной кратности, при переходе через него не будет происходить смена знаков! Ну действительно, знак неравенства определяется только выражением  , ведь
, ведь  принимает только «+» (то есть не влияет на знак произведения) или обращается в ноль.
принимает только «+» (то есть не влияет на знак произведения) или обращается в ноль.

Далее

Обратите внимание – в ответ пойдет и точка {-5}! Так как знак неравенства нестрогий, мы должны взять и все точки, лежащие на оси.
5) Ответ:  {
{ }
}![Rendered by QuickLaTeX.com \cup[3;+\infty]](http://xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) .
.
Пример 4.
Решить неравенство: 
Решение: + показать
Пример 5.
Решить неравенство: 
Решение: + показать
Надеюсь, у вас не возникает желания разложить на множители каждую из скобок? Ни в коем случае! Должен быть «0» справа!
Поэтому, первое, что нужно сделать, – перенести «-5» в левую сторону. Но раскрывать скобки и выходить на 4-ю степень не хотелось бы.
Замечаем, что есть одинаковые компоненты ( ) в скобках, поэтому, можно сделать замену переменной. Обозначим
) в скобках, поэтому, можно сделать замену переменной. Обозначим  за
за  . Тогда получаем следующее неравенство:
. Тогда получаем следующее неравенство:  .
.
Далее:  .
.
1) Раскладываем на множители: 
2) Нули: 1; 5
3)-5) Ось у нас будет называться  :
:

 .
.
Теперь нам предстоит сделать обратную замену:  .
.
Перепишем двойное неравенство в виде системы:


Нам предстоит решить два неравенства, а потом пересечь их решения.
Решаем первое неравенство: 
Раскладываем на множители:  .
.

Решение первого неравенства: 
Решаем второе неравенство: 
Раскладываем на множители: 

Решение второго неравества:  .
.
Пересекаем решения неравенств:

Ответ:  .
.
Пример 6.
Решить неравенство:  .
.
Решение: + показать
Введем переменную:  , заметим, при этом
, заметим, при этом  .
.


Или, что тоже самое:

Обратная замена:

Тогда (как раскрывать модуль)


Ответ:  .
.
! Возможно, вам будет интересно ВИДЕО по данной теме.
А также смотри это видео
Здесь предлагаю ознакомиться с решением дробно-рациональных неравенств методом интервалов.

Вы можете пройти тест тест по теме «Метод интервалов для рациональных неравенств»
egemaximum.ru
Конспект урока на тему «Рациональные неравенства».
Алгебра и начала математического анализа. 10-А класс
Урок № 18 «Рациональные неравенства»
Тип урока: комбинированный
Цель: формировать навыки решения рациональных неравенств, применение метода интервалов, поиск области применения рациональных неравенств.
Задачи урока:
— проверить умения и навыки в решении рациональных неравенств и их систем;
— показать учащимся возможности применения свойств функции при решении неравенств;
— формировать логическое мышление;
— формировать у учащихся положительный мотив обучения;
— развить самостоятельность учащихся.
Ход урока.
1. Организационный момент. Целеполагания.
2. Устная работа. Найдите область определения функций.
Показываю карточку, учащиеся комментируют с места.
Какие навыки нам понадобились при нахождении области определения функции?
(решать уравнения и неравенства). На прошлом уроке мы решали рациональные уравнения, а сегодня рассмотрим способы решения рациональных неравенства и их практическое применение.
Учитель: Рациональными называют неравенства, содержащие только целые рациональные или дробно-рациональные функции. Наша задача рассмотреть особые случаи-корни четной кратности и точки разрыва.
I.Творческое задание: Составьте рациональные неравенства решения которых являются данные числовые промежутки
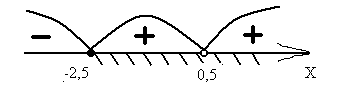
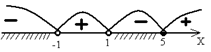
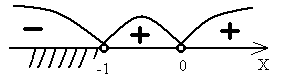
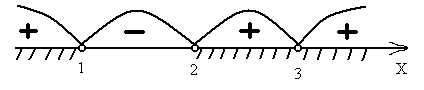

II. Найти область определения функции .Что называется областью определения функции?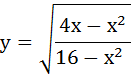 Ответ: (-∞; -4) [0;4) (4; +∞)
Ответ: (-∞; -4) [0;4) (4; +∞)
III. Найти промежутки на которых функция принимает отрицательные значения
у= (х-5)2(2-х)(х+3)3 Ответ: (-∞;- 3] ᴗ [2; +∞)
IV. Рассмотрим несколько задач с практическим содержанием из банка заданий ЕГЭ которые решаются с помощью рациональных неравенств.
Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1,6+8t-5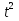 , где h – высота в метрах, t –время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров? Составьте неравенство.
, где h – высота в метрах, t –время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров? Составьте неравенство.Решение: t +
t +  ,
, 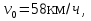
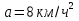 .
.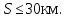
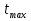 -? (мин)
-? (мин)
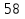 t +
t + 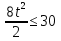
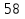 t +
t +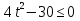 /:2
/:2
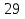 t +
t +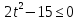
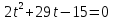
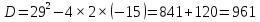
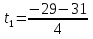 =
=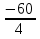 = -15
= -15
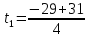 =
=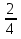 =
=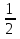 = 0,5
= 0,5
2 (t+15) (t-0,5) ≤ 0
-15 ≤ t ≤ 0,5
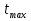 = 0,5 ч = 30 мин
= 0,5 ч = 30 мин
Ответ: 30
Решение:
h(t)=1,6+8t-5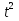 , h ≥ 3, t-?
, h ≥ 3, t-?
1,6+8t-5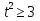
-5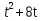 -1,4
-1,4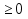 /:(-1)
/:(-1)
5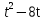 +1,4 ≤
+1,4 ≤ 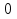
5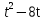 +1,4 =
+1,4 = 
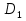 =
= 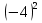 -5×1,4=16-7=9
-5×1,4=16-7=9
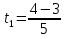 =
=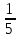 = 0,2
= 0,2
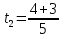 =
=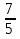 = 1,4
= 1,4
5(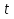 -0,2) (
-0,2) (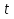 -1,4) ≤
-1,4) ≤ 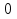
0,2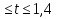
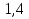 -0,2=1,2
-0,2=1,2
Ответ: 1,2
V. Самостоятельная работа с самопроверкой. Сопоставить числовые промежутки с решениемданных неравенств.
Решение неравенств по дидактическим материалам (Алгебра и начала математического анализа 10 класс А.Г.Мерзляк, В.Б.Полонский )
Страница 81: № 38 (2, 5), № 39 (5), № 41 (7), № 43(1).
а) (х+12)(х-4)(х-20) ˃ 0б) (х+7,2)(3-х)(6-х) ≤ 0
в) 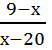 ≥ 0
≥ 0
г) (х-2)2(х2 — 4х +3)≥0
д) 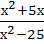 ≥ 0
≥ 0
(-∞; -5) ᴗ (-5;0] ᴗ (5; +∞)
(-12;4) ᴗ (20; +∞)
[9;20)
(-∞; 1] ᴗ {2} ᴗ [3; +∞)
(-∞; -7,2] ᴗ [3;6]
На доске ответы. Сверяем, анализируем ошибки.
VI. Рефлексия. Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
V II. Домашнее задание. (Алгебра и начала математического анализа 10 класс А.Г.Мерзляк, В.Б.Полонский )
Страница 32: № 38 (2, 5), № 39 (5), № 41 (7), № 43(1).
Что называется функцией?
Перечислите основные свойства функций.
Что называется областью определения функции?
Что называется множеством значений функции?
Приведите пример ограниченной функции.
Какая функция называется монотонной?
Приведите пример функции возрастающей на всей области определения.
А вы знаете что современные знаки неравенства появились лишь в 17 веке, причем английский математик Томас Гарриот (1560-1621) ввел строгие неравенства, а француз Пьер Буге (1698-1758) нестрогие.
умение решать рациональные неравенства необходимы при исследовании функций, но и свойства функций можно использовать при решении неравенств. Решение показательных неравенств основано на монотонности показательной функции y aх , которая при a>1 монотонно возрастает, при (0;1)a монотонно убывает 1 0,a const,a a 1,a 0
Суть метода замены множителей (МЗМ) состоит в том, чтобы с помощью равносильных преобразований заменить каждый множитель в области его существования на более простой множитель, в конечном счете, рациональный и имеющий те же интервалы знакопостоянства (на множитель равного знака).

Пример 3. Решить неравенство 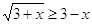 . Существует стандартный прием решения: возведение в квадрат (при условии
. Существует стандартный прием решения: возведение в квадрат (при условии 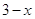
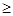 0). Мы рассмотрим решение данного неравенства с использованием свойства монотонности. Функция, расположенная в левой части неравенства, монотонно возрастает, в правой части — убывает. Из этого следует, что уравнение
0). Мы рассмотрим решение данного неравенства с использованием свойства монотонности. Функция, расположенная в левой части неравенства, монотонно возрастает, в правой части — убывает. Из этого следует, что уравнение 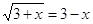 имеет не более одного решения, причем если x0 – решение этого уравнения, то при
имеет не более одного решения, причем если x0 – решение этого уравнения, то при 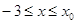 будет
будет 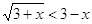 , а решением данного неравенства будет
, а решением данного неравенства будет 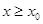 . Значение
. Значение 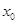 легко подбирается:
легко подбирается: 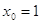 .
.
Ответ: 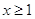 .
.
Что называется функцией?
Перечислите основные свойства функций.
Что называется областью определения функции?
Что называется множеством значений функции?
Приведите пример ограниченной функции.
Какая функция называется монотонной?
Приведите пример функции возрастающей на всей области определения.
А вы знаете что современные знаки неравенства появились лишь в 17 веке, причем английский математик Томас Гарриот (1560-1621) ввел строгие неравенства, а француз Пьер Буге (1698-1758) нестрогие.
2. Устная работа. Укажите область допустимых значений выражений
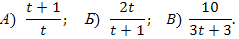
Найди и исправь ошибку 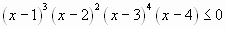

Верно, ли расставлены знаки произведения на числовых интервалах?
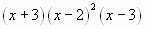
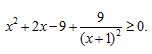
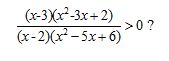
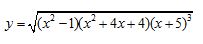
Тест. “Метод интервалов”
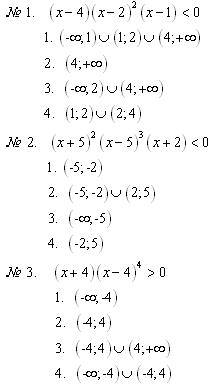
ОТВЕТЫ к тесту: № 1 — 4. № 2 — 4. № 3 — 3
Задание 1. Найти промежутки на которых функция принимает отрицательные значения
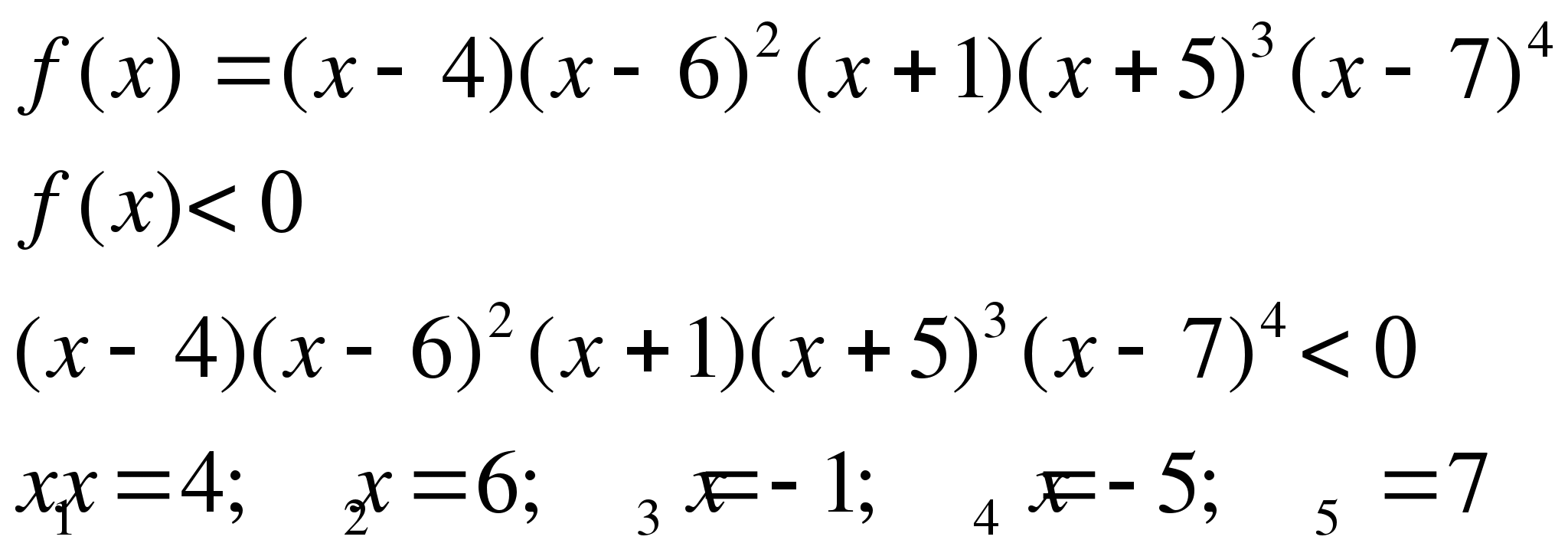

Ответ: 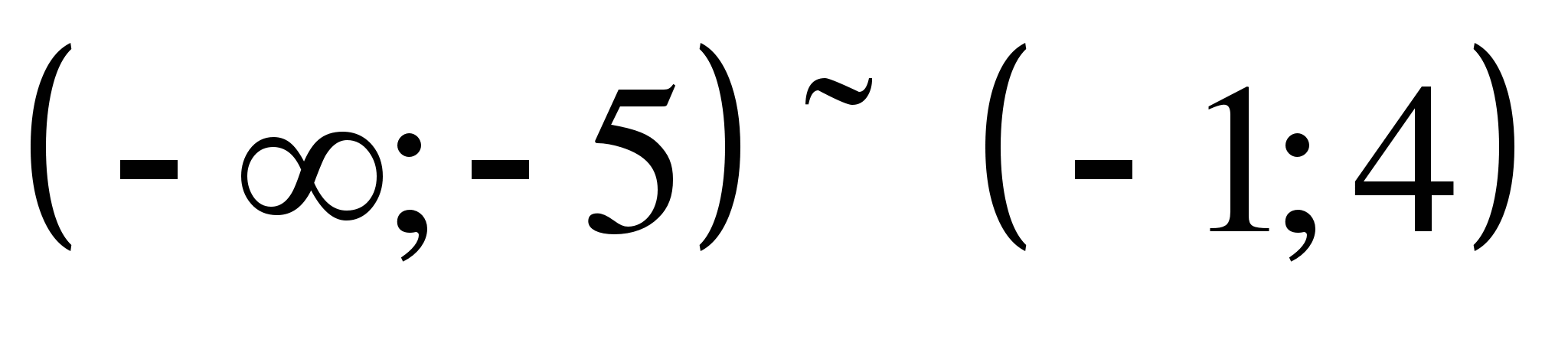
Задание 2. Найти область определения функции
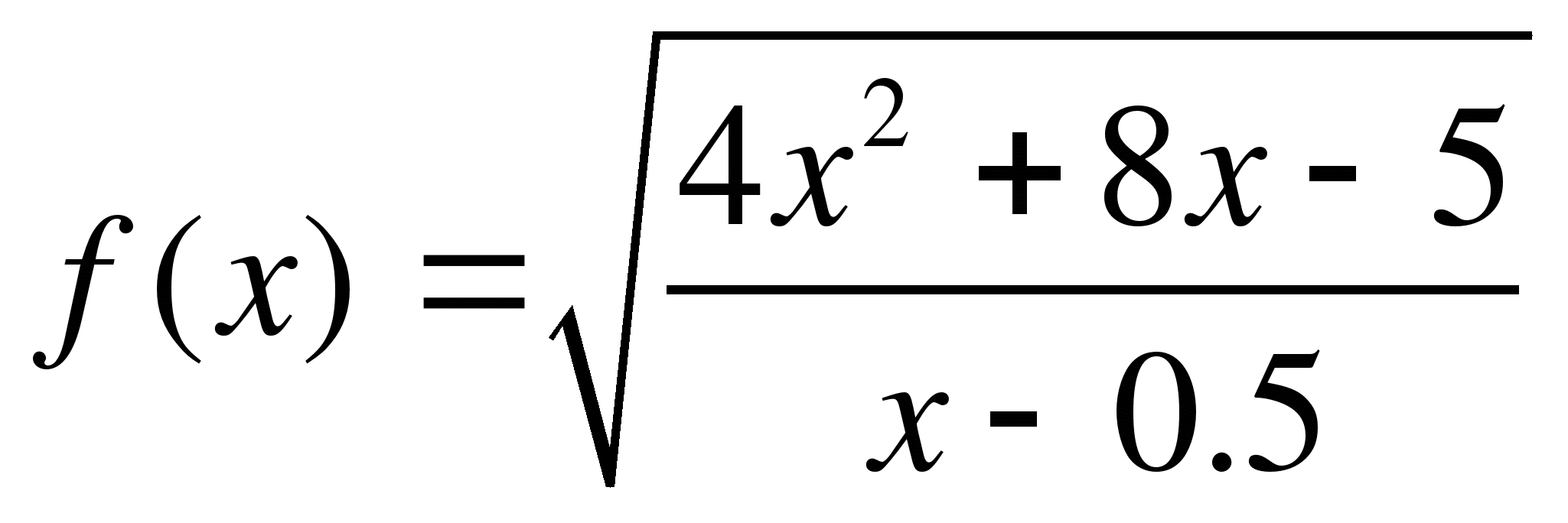
Так как подкоренное выражение должно быть неотрицательным, то
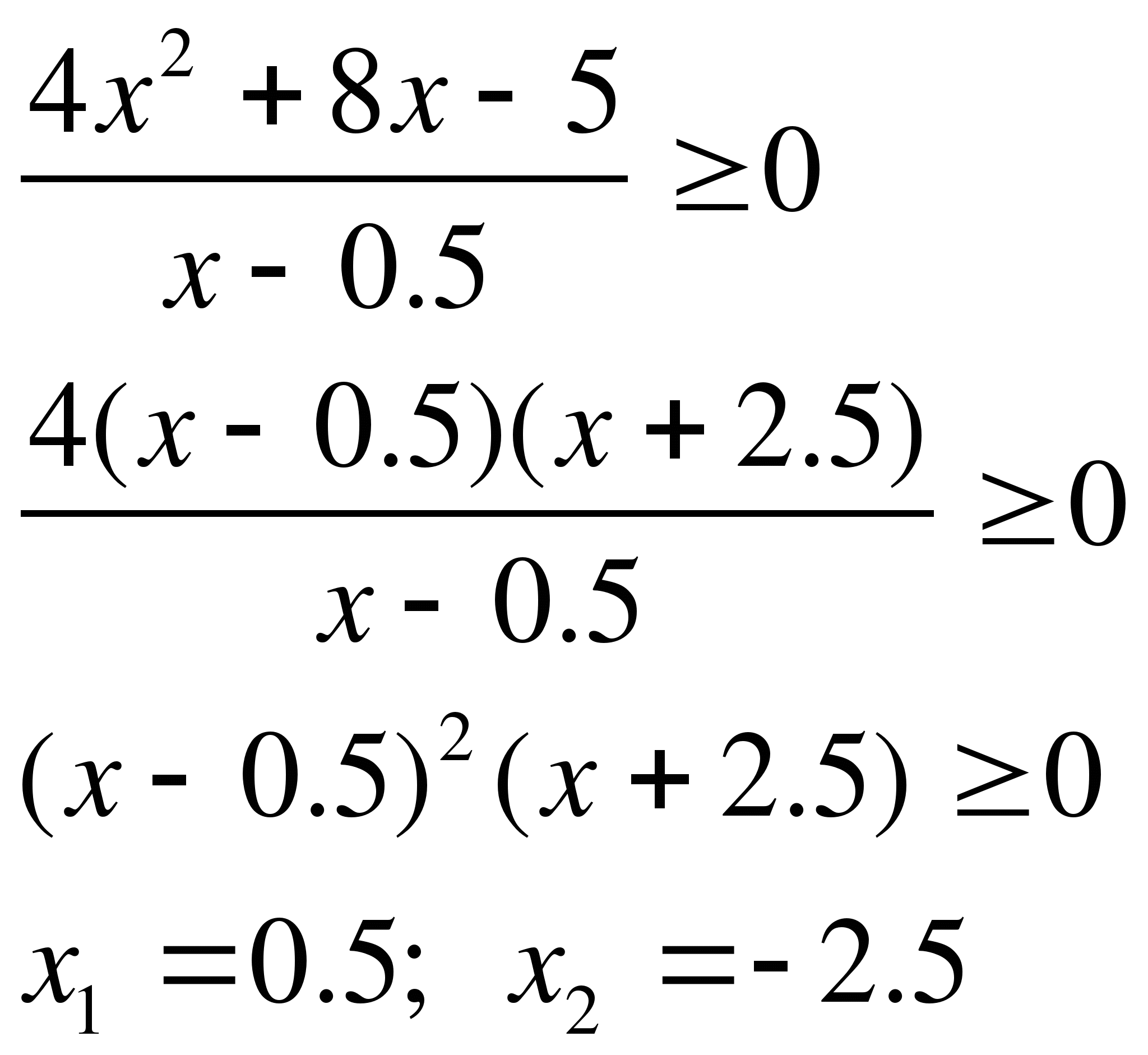
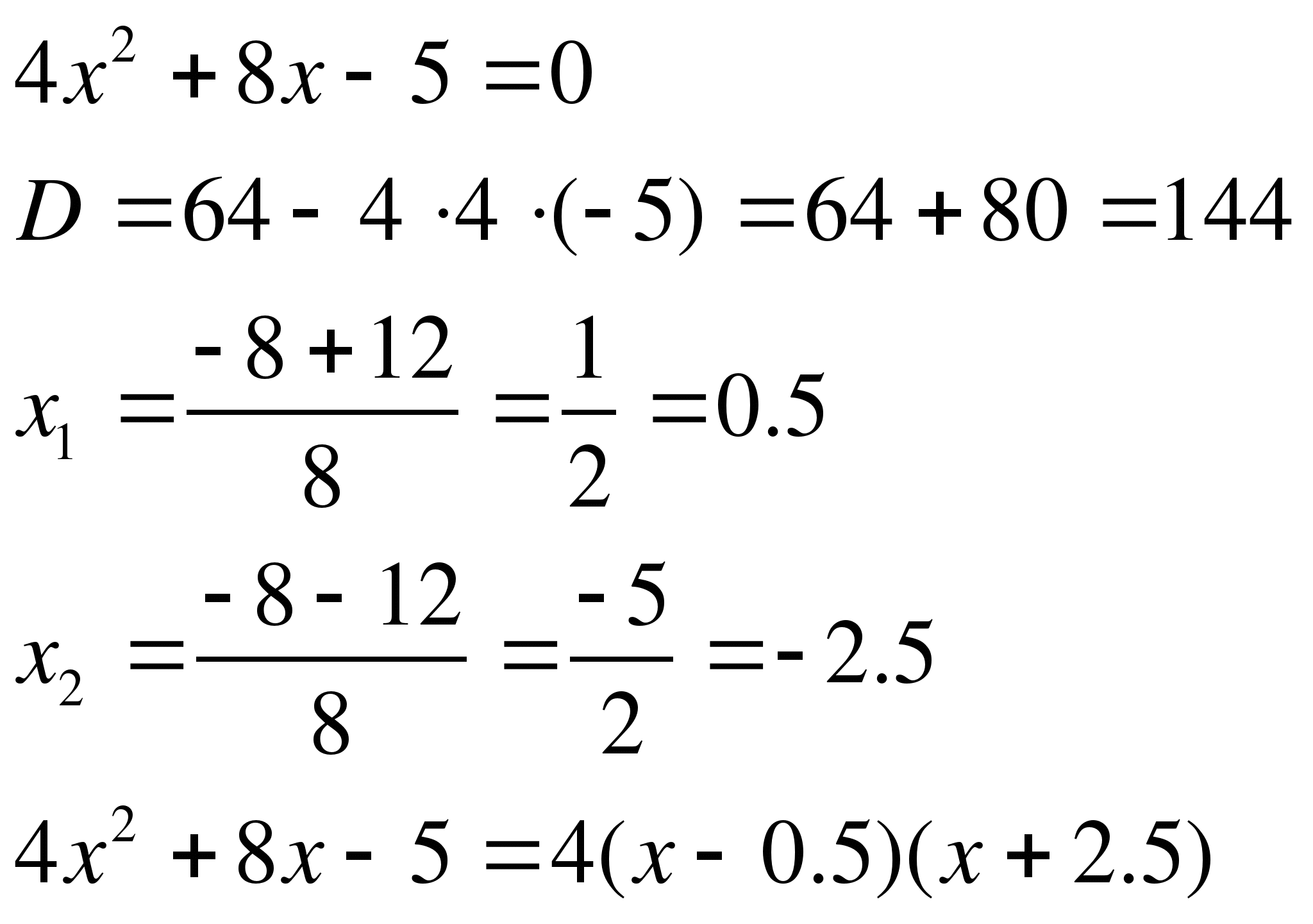

Ответ: 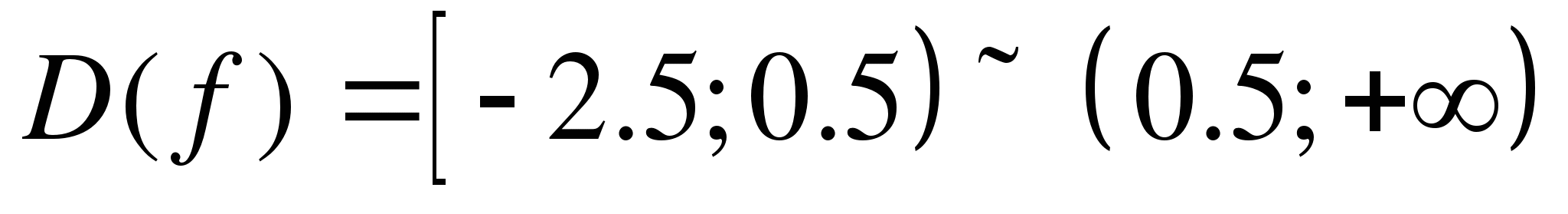
Задание 3. Найти область определения функции
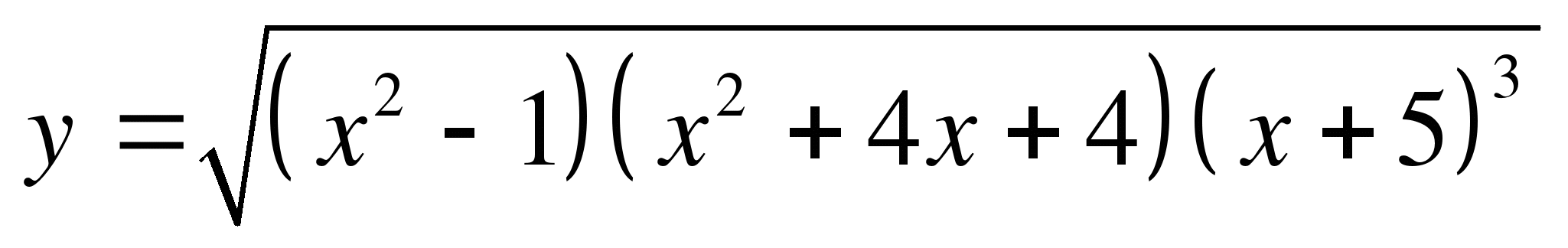
Так как подкоренное выражение должно быть неотрицательным, то
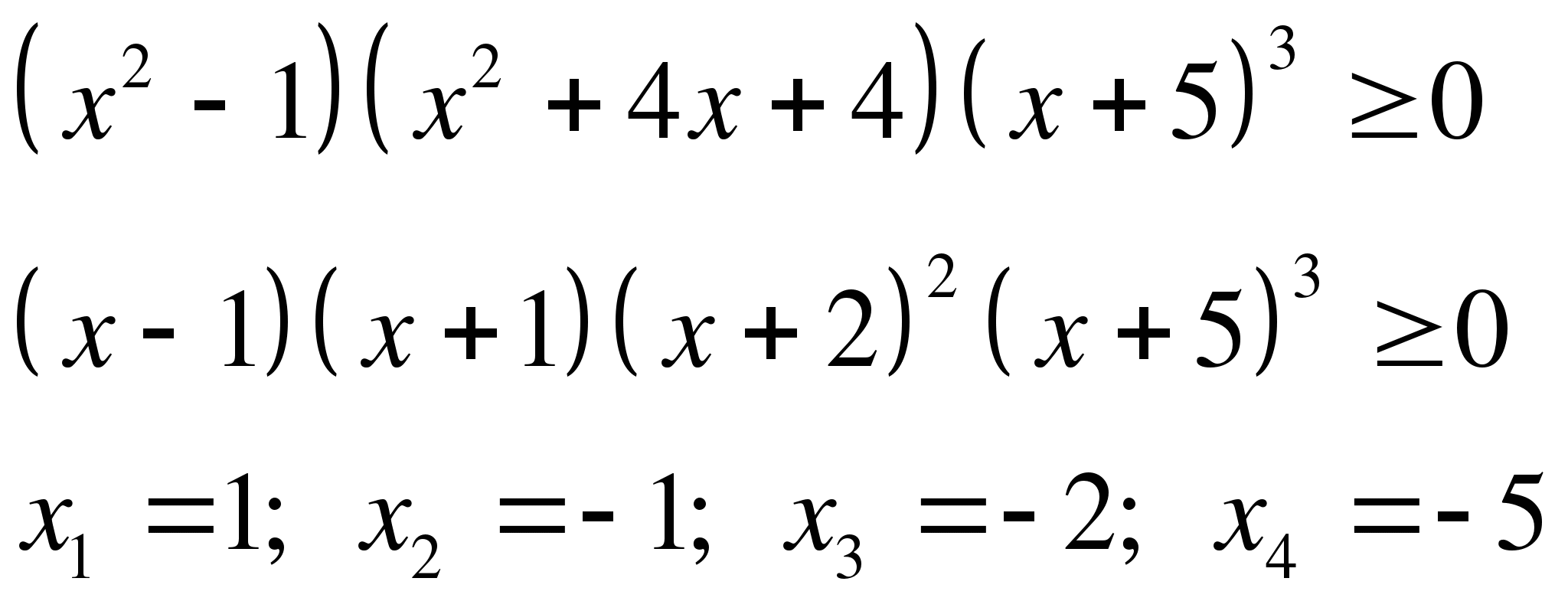

Ответ: 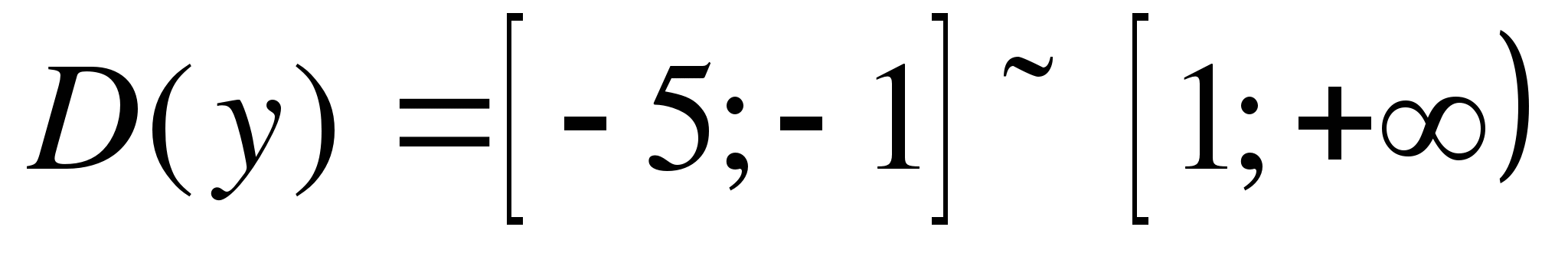
Задание 3. Решить неравенство методом интервалов
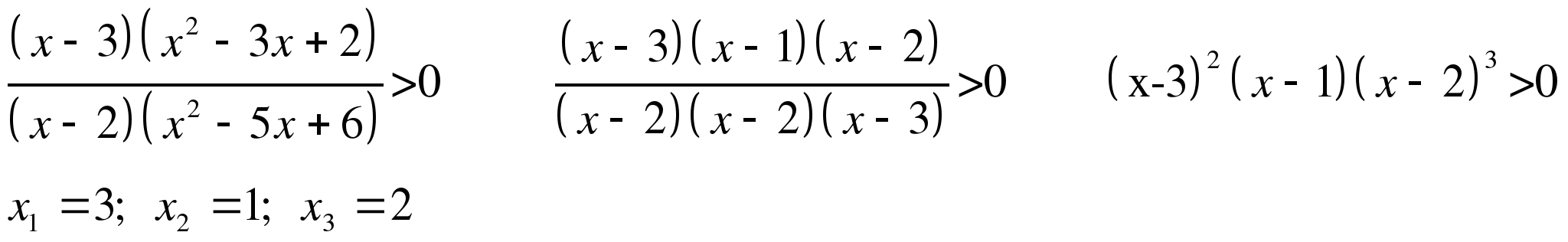

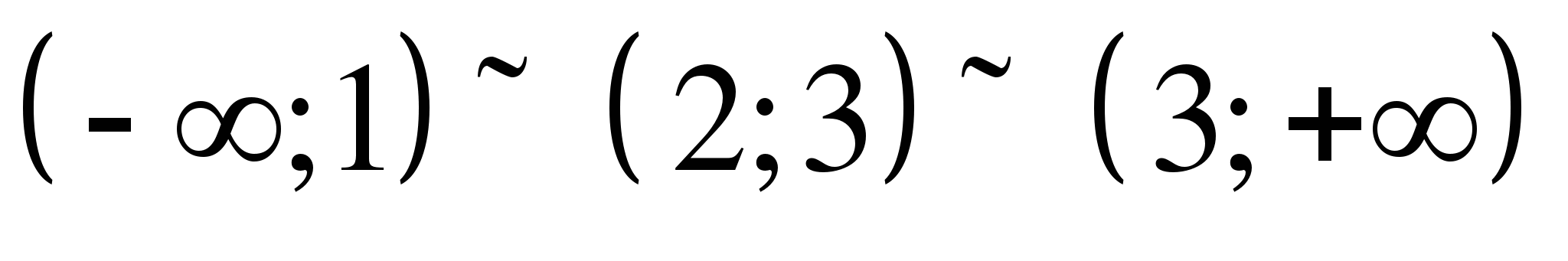
Задание 4.
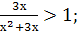
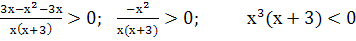


Ответ: (-3; 0)
Задание 5.
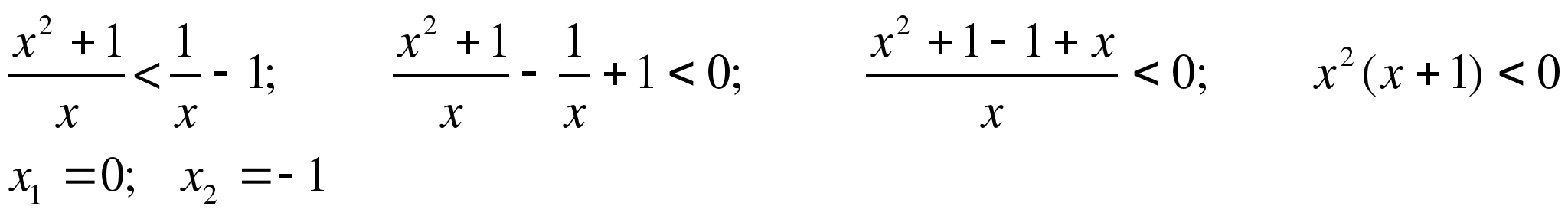

Ответ: (-∞; -1)
Задание 6. Найти область определения функции
у=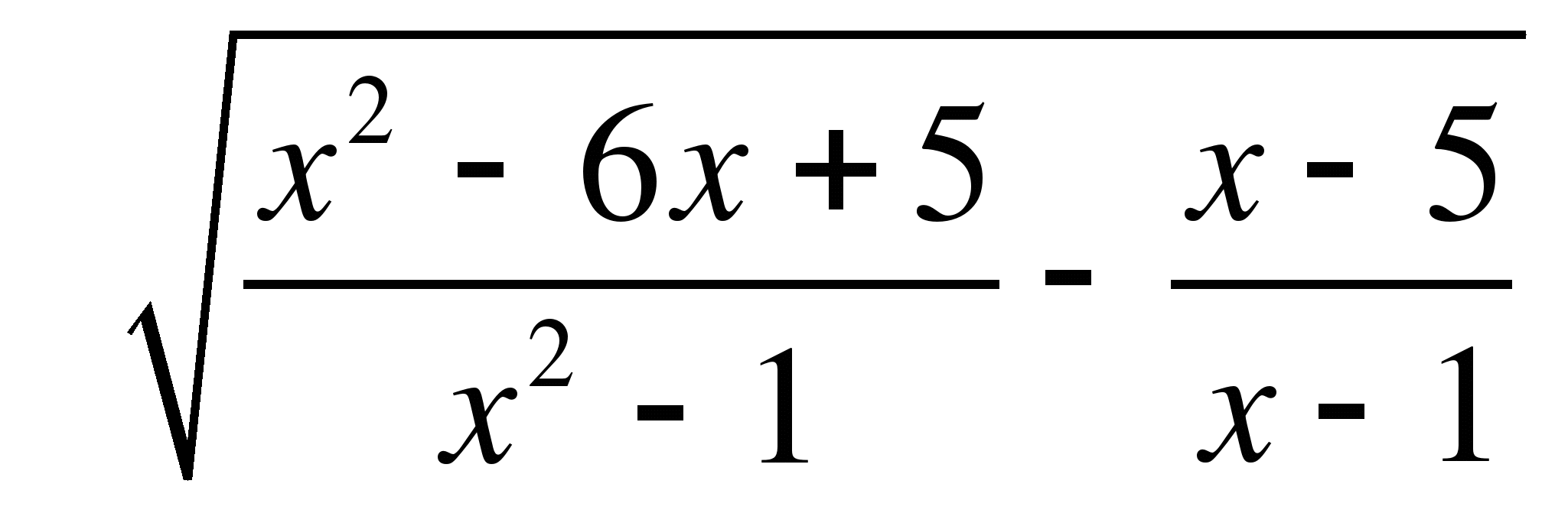 Так как подкоренное выражение должно быть неотрицательным, то
Так как подкоренное выражение должно быть неотрицательным, то
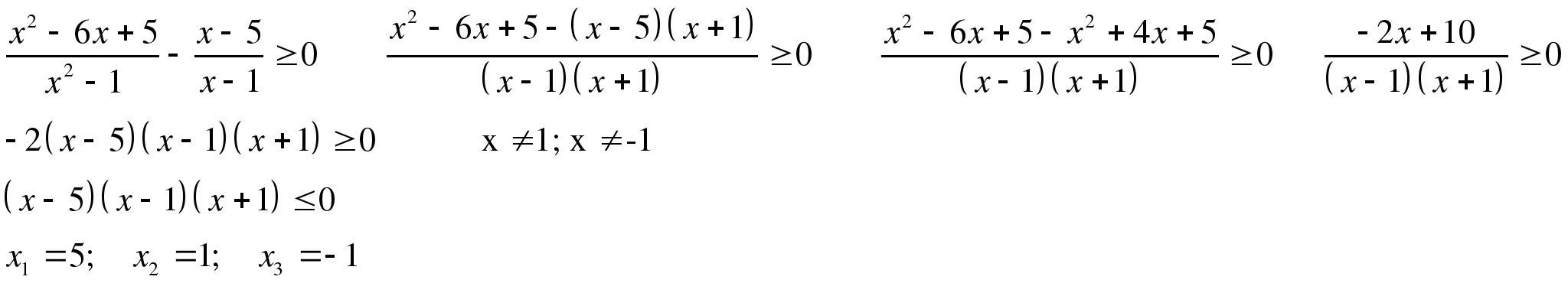
 2+3+4+5 = 14 Ответ: 14
2+3+4+5 = 14 Ответ: 14

Рассмотрим методику решения экономических задач, сводящихся к системе неравенств с несколькими неизвестными. Часто то или иное неравенство в экономике является важным вспомогательным средством, опорным пунктом, позволяющим доказать или опровергнуть возможность выполнения того или иного плана или действия, рассчитать прибыль от реализации товара или ресурса, вывести наиболее экономный вариант перевозок при максимальном количестве клиентов. Наглядно показать доход от экспорта и расход на импорт. Наиболее часто приходится решать экономистам задачи об использовании сырья и задачи о транспортировке сырья и грузов(транспортные задачи).
infourok.ru
Рациональные уравнения и неравенства | LAMPA
Рациональное уравнение
Уравнение вида A(x)B(x)=0\frac{A(x)}{B(x)}=0B(x)A(x)=0, где A,BA,BA,B — , называется рациональным уравнением.
- — вся ось, кроме точек, в которых B(x)=0B(x)=0B(x)=0;
- Решения уравнения в области определения совпадают с решениями уравнения A(x)=0A(x)=0A(x)=0.
2x+33x+2=0⇔{2x+3=03x+2≠0⇔x=−32.\frac{2 x+ 3}{3x+2}=0 \,\,\,\, \Leftrightarrow \,\,\,\, \left\{\begin{array}{lr} 2x+3=0 \\ 3x+2\neq 0 \end{array}\right. \,\,\,\,\Leftrightarrow \,\,\,\, x=-\frac{3}{2} .3x+22x+3=0⇔{2x+3=03x+2≠0⇔x=−23.
Рациональное неравенство
Неравенство вида A(x)B(x)≤0\frac{A(x)}{B(x)}\le 0B(x)A(x)≤0, где A,BA,BA,B — , называется рациональным неравенством.
Как решать?
- Найдите корни уравнений A(x)=0A(x)=0A(x)=0 и B(x)=0B(x)=0B(x)=0.
- Отметьте корни обоих уравнений на числовой прямой.
- Примените .
- Обратите внимание на то, что при B(x)=0B(x)=0B(x)=0 левая часть неравенства не определена, поэтому корни уравнения B(x)=0B(x)=0B(x)=0 не включаются в решение.
2x+33x+2≤0.\frac{2 x+ 3}{3x+2}\le 0.3x+22x+3≤0. Корень уравнения 2x+3=02x+3=02x+3=0 равен x=−32x=-\frac{3}{2}x=−23.
Корень уравнения 3x+2=03x+2=03x+2=0 равен x=−23x=-\frac{2}{3}x=−32.
Применим метод интервалов. Неравенство выполняется при значениях xxx, лежащих между корнями двух уравнений: −32≤x<−23-\frac{3}{2}\le x\lt -\frac{2}{3}−23≤x<−32 или x∈[−32;−23)x\in[-\frac{3}{2};-\frac{2}{3})x∈[−23;−32).
Обратите внимание на то, что корень −23-\frac{2}{3}−32 не включен в решение неравенства.
lampa.io
Урок алгебры (совместно 9-й 10-й классы – профильная группа) по теме «Рациональные неравенства»
ХАРАКТЕРИСТИКА ТЕМЫ.
ЗАВЕРШАЮЩИЙ УРОК ПО ТЕМАМ:
- 9 класс: “Уравнения и неравенства с одной переменной” УМК к учебнику “Алгебра,9”, Ю.А. Макарычев, Н.Г. Миндюк и др. М.:Просвещение, 2009
- 10 класс: “Рациональные уравнения и неравенства” УМК к учебнику “Алгебра и начала анализа 10” С.М. Никольский, Н.Н. Решетников, А.В. Шевкин М.: Просвещение. 2008
ДОМИНИРУЮЩАЯ ДИДАКТИЧЕСКАЯ ЦЕЛЬ:
- Расширение представлений учащихся девятого класса о неравенствах с одной переменной и методах их решения;
- Вторичное осмысление учащимися десятого класса методов решения рациональных неравенств.
ТРИЕДИНАЯ ДИДАКТИЧЕСКАЯ ЦЕЛЬ:
Развивающий аспект
- Развитие интеллектуальных, коммуникативных способностей, творческого мышления, речи учащихся в процессе обсуждения проблемных заданий.
Воспитательный аспект
- Создание условий для воспитания делового сотрудничества, культуры учебной деятельности;
- Создание условий для осознанного выбора профиля обучения в старшей школе.
Образовательный аспект
- Создание условий для ознакомления учащихся девятого класса с общим методом интервалов;
- Формирование умений решать рациональные неравенства.
СОГЛАСНО ПРОЕКТУ, УРОК ОЖИДАЕТСЯ
По содержанию
Урок повторения и качественного повышения уровня сложности изучаемого материала.
По применяемым технологиям
Урок интерактивного обучения в разновозрастных группах с учетом индивидуального стиля учебной деятельности. (Приложение 2)
По форме организации познавательной деятельности
Урок фронтальной, индивидуальной, парной учебной деятельности.
Ход урока.
1. Организационный момент.
Сообщаются тема, цели и основная форма урока (работа в динамических парах, ученик 9 и ученик 10 класса).
2. Устная работа. (Учащиеся показывают номера ответов, с помощью сигнальных карточек).
1. Даны выражения:
Какие из выражение не имеют смысла при t=-1?
2. Укажите промежуток, которому принадлежит значение выражения
3. Из чисел выберите наибольшее.
4). Из формулы длины окружности , выразите число .
5). Сократите дробь .
6. На каком рисунке изображено множество решений неравенства (x-3)(x+4)>0
ОТВЕТЫ.
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
ответ |
4 |
4 |
2 |
3 |
1 |
4 |
3.Решение заданий по теме.
Приложение 3-задания, Приложение 4- решения и ответы.
1) Ученик 10 класса решает задание №1 (Приложение 3) на доске с подробными пояснениями, остальные работают в тетрадях.
2) Ученик 10 класса решает задание №2 (Приложение 3) на доске с подробными пояснениями, остальные работают в тетрадях.
3) Задание №3 (Приложение 3) учащиеся решают в парах. При этом учащийся 10 класса выступает в роли консультанта. Одновременно на закрытой доске это задание выполняет ученик 10 класса, для последующей проверки.
4) Ученик 9 класса решает задание №4 (Приложение 3) на доске с подробными пояснениями, остальные работают в тетрадях.
5) Смена состава пар.
Первый состав пар учитывал особенности темперамента, а второй — доминирующее полушарие головного мозга.
6) Ученик 10 класса решает задание №5 (Приложение 3) на доске с подробными пояснениями, остальные работают в тетрадях.
7) Задание №6 (Приложение 3) учащиеся решают в парах. При этом учащийся 10 класса выступает в роли консультанта. Одновременно на закрытой доске это задание выполняет ученик 9 класса, для последующей проверки.
8) Ученик 10 класса решает задание №12 (Приложение 3) на доске, остальные учащиеся 10 класса выполняют его в тетрадях.
В это же время три ученика 9 класса работают на доске по карточкам, остальные самостоятельно работают над тестом “Метод интервалов”.
Карточка 1.
Найди и исправь ошибку
Карточка 2.
Верно, ли расставлены знаки произведения на числовых интервалах?
Карточка 3.
- Найдите все числа х, для каждого из которых .
- Изобразите эти числа на координатной оси.
- Определите знак произведения на каждом из полученных интервалов.
Тест. “Метод интервалов”
ОТВЕТЫ к тесту: № 1 — 4. № 2 — 4. № 3 — 3
4. Домашнее задание.
10 класс: задания №№ 7,8,9,10,11 (Приложение 3)- любые четыре задания.
9 класс: №№ 338 (а, б), 389 (в), 391 (а) из учебника; дополнительно: задания №№ 13,14 (Приложение 3)-по выбору.
5. Итог урока.
Оценку за урок получают все учащиеся, которые работали у доски, и ученики 9 класса за тест.
Приложение 1
urok.1sept.ru