Рациональные неравенства 10 класс как решать: Рациональные неравенства — теория и формулы, подготовка к ЕГЭ по математике

Posted on by alexxlab
2+x-2\leqslant 0\]

\[{\Large{\text{Линейные неравенства}}}\] Линейные неравенства – это неравенства вида \[ax+b \lor 0, \qquad \lor — \text{ один из знаков } \geqslant, \ \leqslant, \ >, \ <;\quad a,b — \text{ числа,}\]или сводящиеся к такому виду.
Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа (\(x\in \mathbb{R}\)).

 

Общее правило решения линейных неравенств:

1) Для того, чтобы решить данное неравенство, необходимо привести его к виду \(ax\lor -b\), то есть перенести число \(b\) в правую часть.

2) Если коэффициент \(a\) перед \(x\) – положительный, то неравенство равносильно \(x\lor -\dfrac ba\), то есть после деления обеих частей неравенства на \(a\) знак неравенства не меняется.

3) Если коэффициент \(a\) перед \(x\) – отрицательный, то неравенство равносильно \(x\land -\dfrac ba\), то есть после деления обеих частей неравенства на \(a\) знак неравенства меняется на противоположный

.

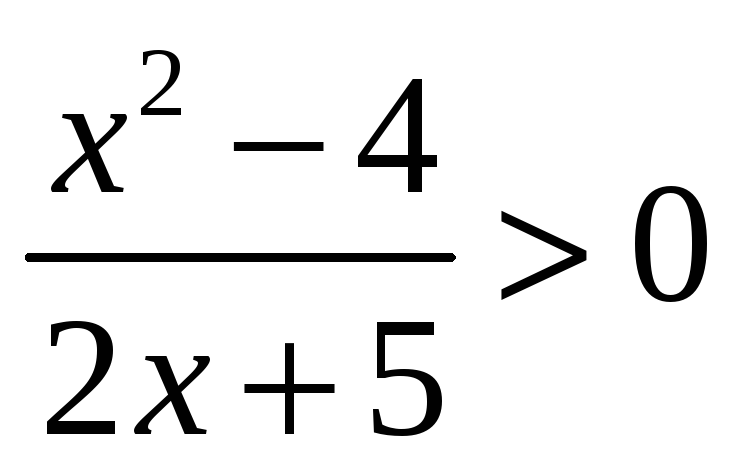
4) Если \(a=0\), то неравенство равносильно \(0\lor -b\), что либо верно при всех значениях переменной \(x\) (например, если это \(0>-1\)), либо неверно ни при каких значениях \(x\) (например, если это \(0\leqslant -3\)).
То есть ответом будут либо \(x\in\mathbb{R}\), либо \(x\in \varnothing\).

 

Замечание
Заметим, что знаку \(\leqslant\) противоположен знак \(\geqslant\), а знаку \(<\) – знак \(>\). И наоборот.

 

Пример 1
Решить неравенство \(5-3x>-1\).

 

Решение. I способ
Сделаем цепочку преобразований:

\[5-3x>-1 \ \Rightarrow \ -3x>-1-5 \ \Rightarrow \ -3x>-6 \ \Rightarrow \ x<\dfrac 63 \ \Rightarrow \ x<2\] Таким образом, ответом будет \(x\in(-\infty;2)\).
Заметим, что т.к. мы делили неравенство на \(-3\), то знак неравенства поменялся.

 

Решение. II способ
Можно перенести слагаемое \(-3x\) в правую часть, а \(-1\) – в левую:

\[5-3x>-1 \ \Rightarrow \ 5+1>3x \ \Rightarrow \ 3x<6 \ \Rightarrow \ x<2\]

Пример 2
Решить неравенство \((1-\sqrt2)x+2\leqslant 0\).

 

Решение
Заметим, что перед \(x\) находится отрицательный коэффициент. Поэтому:

\[(1-\sqrt2)x\leqslant -2 \Rightarrow x\geqslant -\dfrac 2{1-\sqrt2}\] Преобразуем число \(-\dfrac 2{1-\sqrt2}\): домножим числитель и знаменатель дроби на сопряженное к \(1-\sqrt2\), то есть на \(1+\sqrt2\), чтобы избавиться от иррациональности в знаменателе:

\[-\dfrac 2{1-\sqrt2}=-\dfrac{2(1+\sqrt2)}{(1-\sqrt2)(1+\sqrt2)}= -\dfrac{2(1+\sqrt2)}{1-2}=2(1+\sqrt2)\]
Таким образом, ответ \(x\in [2+2\sqrt2;+\infty)\).
Перейдем к квадратичным неравенствам, которые являются очень важным инструментом в решении задач.

 

\[{\Large{\text{Метод интервалов}}}\]

Приступим к рассмотрению общего метода для решения любого рационального неравенства, то есть неравенства вида

\[(**)\qquad \dfrac{P(x)}{Q(x)}\geqslant 0 \qquad (\text{на месте }\geqslant \text{может стоять любой из} \leqslant, \ <, \ >)\]

Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа, кроме нулей знаменателя.

 

Существует два способа решения таких неравенств:

 

1 способ: Классический. Т.к. дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель дроби одного знака (разных знаков), то неравенство \((*)\) равносильно совокупности: \[{\large{\left[\begin{gathered} \begin{aligned} &\begin{cases} P(x)\geqslant 0\\ Q(x)>0 \end{cases}\\ &\begin{cases} P(x)\leqslant 0\\ Q(x)<0 \end{cases} \end{aligned} \end{gathered} \right.}}\]

 

Такой способ подойдет для решения любого неравенства, где слева стоит дробь, а справа — \(0\).
Но, как правило, для решения большинства рациональных неравенств он неудобен. Почему? Вы сможете убедиться в этом после того, как мы рассмотрим метод интервалов.

 

2 способ: Удобный. Метод интервалов (будем рассматривать этот метод на примере конкретного неравенства, чтобы было понятней).
Заметим, что первые три шага созданы для того, чтобы преобразовать неравенство к более простому виду, что поможет вам не допустить ошибку в решении подобных задач. Метод интервалов – это всего лишь удобный инструмент для решения рациональных неравенств, и если вы будете всегда пользоваться одним и тем же алгоритмом, то вероятность допустить ошибку при решении таких неравенств будет минимальной.

Данный алгоритм специально расписан подробно, чтобы у вас не возникло вопросов; всего после нескольких использований этого алгоритма вы будете решать рациональные неравенства очень быстро и без ошибок!

 

1 ШАГ. Необходимо перенести все слагаемые в одну часть (пусть это будет левая часть) неравенства так, чтобы в другой части неравенства остался \(0\), и привести эти слагаемые к общему знаменателю так, чтобы в левой части неравенства получилась дробь. Затем нужно разложить числитель и знаменатель полученной дроби, то есть многочлены \(P(x), \ Q(x)\), на множители.   Например, неравенство \(\dfrac1{x+1}<1\) нужно переписать в виде \(\dfrac1{x+1}-1<0\), затем привести к общему   знаменателю \(\dfrac1{x+1}-\dfrac{x+1}{x+1}<0\), затем записать в виде одной дроби левую часть: \(\dfrac{1-(x+1)}{x+1}<0\) и   привести подобные слагаемые: \(\dfrac{-x}{x+1}<0\).

2\), или, что то же самое, \((x-0)(x-0)\) – произведение двух одинаковых линейных скобок.

 

4 ШАГ. Теперь, когда левая часть неравенства состоит из произведения только хороших линейных скобок (в каких-то степенях), можно приступить к самому методу интервалов.

 

Его суть состоит в том, что левая часть неравенства — всюду непрерывная функция, кроме тех точек, где знаменатель дроби равен нулю. Поэтому точки, в которых эта функция равна нулю (то есть ее числитель равен нулю) и точки, в которых эта функция не существует (то есть ее знаменатель равен нулю), разбивают область определения этой функции на промежутки, причем на каждом промежутке функция принимает значения строго одного знака.

 

А нам как раз нужно найти те значения \(x\), при которых функция \(\geqslant 0\). Причем, т.к. наша функция — рациональная, то ее область определения — это все действительные числа (\(\mathbb{R}\)), кроме нулей знаменателя.

Поэтому отметим нули каждой скобки на вещественной прямой (а ноль каждой скобки – это как раз ноль числителя или знаменателя), причем нули знаменателя – выколотые, нули числителя – закрашенные (если знак неравенства нестрогий, как в примере, то есть \(\geqslant \) или \(\leqslant \)) или выколотые (если знак неравенства строгий, то есть \(>\) или \(<\)).
Заметим, что если мы отметили \(n\) точек, то числовая прямая разобьется на \(n+1\) промежутков.

 

Расставим знак на каждом промежутке \(\color{red}{{\Large{\text{справа налево}}}}\). Будем ставить “\(+\)”, если функция на этом промежутке принимает положительные значения, и “\(-\)” — если отрицательные. Нулю функция равна в закрашенных точках.
Первые три шага мы делали для того, чтобы не подставлять точки из каждого промежутка и не вычислять, какого знака будет левая часть неравенства (что бывает неудобно, если числа, которые нужно отмечать на прямой, “некрасивые”). Знаки мы будем расставлять, выявив некоторую закономерность.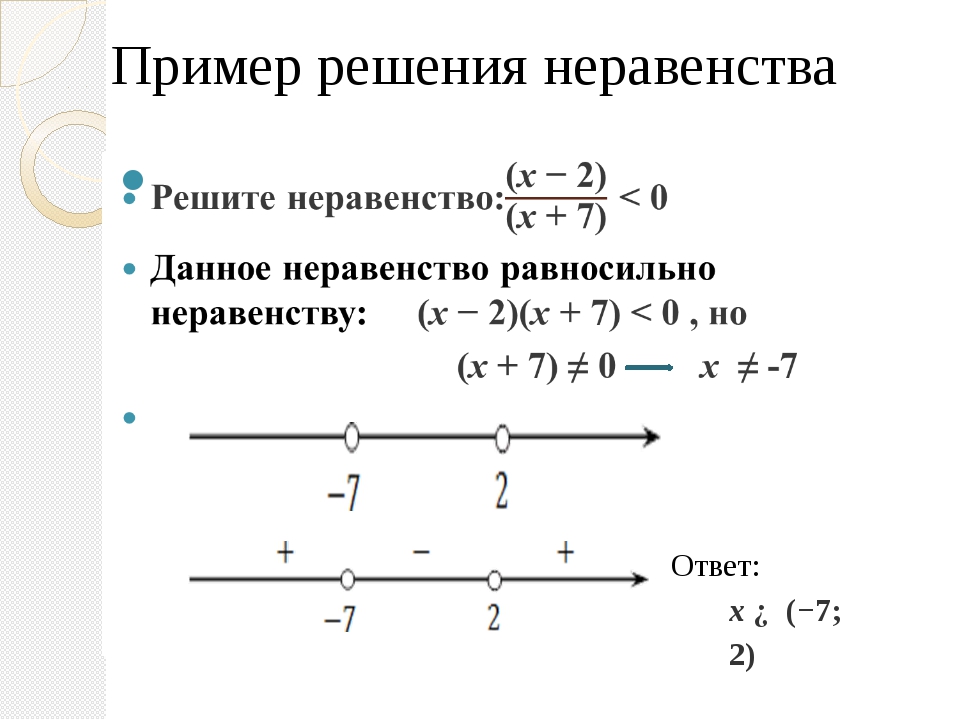

2\) не сменит свой знак на отрицательный, поэтому вся левая часть останется по знаку такой же, как и была на \((\frac23;1)\) (т.е. положительной). Аналогично при переходе через точки \(0, -1\).

 

5 ШАГ. Неравенство практически решено и нам остается только записать ответ. В нашем случае, т.к. знак преобразованного \((***)\) неравенства \(\geqslant 0\) (нестрогий), то в ответ пойдут промежутки со знаком “\(+\,\)” (где значение функции больше нуля) и закрашенные точки (где значение функции равно нулю): \[x\in \Big(-\infty;-1\Big)\cup \left(-1;\dfrac23\right)\cup \left(\dfrac23;1\right]\cup\Big(3;+\infty\Big)\]Напоминаем, что если точка не входит в ответ, то она пишется в круглой скобке “\((\)” или “\()\)”, если входит в ответ – то в квадратной скобке “\([\)” или “\(]\)”. Бесконечности всегда пишутся в круглых скобках.

 

\[{\Large{\text{Квадратичные неравенства}}}\]

Квадратичным неравенством называется любое неравенство вида \[ax^2+bx+c \lor 0, \quad a\ne 0,\]

или сводящееся к такому виду. {2}}-{x}-1=\left( {x}-\frac{-1+\sqrt{5}}{2} \right)\left( {x}-\frac{-1-\sqrt{5}}{2} \right)\)

Вернемся к неравенству. Оно принимает вид:

\(\displaystyle \frac{\left( {x}-\frac{-1+\sqrt{5}}{2} \right)\left( {x}-\frac{-1-\sqrt{5}}{2} \right)}{\left( {x}-1 \right)\left( x+2 \right)\left( x+3 \right)}\ge 0\)

Теперь нужно расположить эти корни на числовой оси, а для этого надо понять, где находятся числа \(\displaystyle \frac{-1-\sqrt{5}}{2}\) и \(\displaystyle \frac{-1+\sqrt{5}}{2}\) относительно \(\displaystyle 1\), \(\displaystyle -2\) и \(\displaystyle -3\).

Подробно о том, как это делается, читай в теме «Сравнение чисел».

\(\displaystyle \begin{array}{l}2<\sqrt{5}<3\text{ }\Leftrightarrow \text{ }\\1<-1+\sqrt{5}<2\text{ }\Leftrightarrow \\\frac{1}{2}<\frac{-1+\sqrt{5}}{2}<1\end{array}\)

\(\displaystyle \begin{array}{l}2<\sqrt{5}<3\text{ }\Leftrightarrow \\-3<-\sqrt{5}<-2\text{ }\Leftrightarrow \\-4<-1-\sqrt{5}<-3\text{ }\Leftrightarrow \\-2<\frac{-1-\sqrt{5}}{2}<-\frac{3}{2}\end{array}\)

Содержание

Урок 23.

показательные неравенства — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №23. Показательные неравенства.

Перечень вопросов, рассматриваемых в теме

  • простейшие показательные неравенства;
  • решение показательных неравенств замена переменной, разложение на множители;
  • метод рационализации при решении показательных неравенств;
  • метод интервалов при решении показательных неравенств;
  • графический метод решения показательных неравенств.

Глоссарий по теме

Показательным называется неравенство, в котором переменная входит только в показатели степеней, при постоянном основании.

Неравенства вида , называются простейшими показательными неравенствами.

Метод рационализации для решения показательных неравенств – переход от неравенства, содержащего показательные выражения, к равносильному рациональному неравенству (или равносильной системе рациональных неравенств).

Основная литература:

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е.,  Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс. 216—220, 223-230.

Дополнительная литература:

Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики — 4-е изд. — М.: Просвещение, 1995. — 288 с.: ил. — ISBN 5-09-0066565-9, сс. 70-74.

Открытые электронные ресурсы:

https://ege.sdamgia.ru/ — решу ЕГЭ образовательный портал для подготовки к экзаменам

http://fcior.edu.ru/ — Федеральный центр информационно-образовательных ресурсов

http://school-collection.edu.ru/ — Единая коллекция цифровых образовательных ресурсов

Теоретический материал для самостоятельного изучения

1. Рассмотрим показательные неравенства.

Показательным называется неравенство, в котором переменная входит только в показатели степеней, при постоянном основании.

Неравенства вида , называются простейшими показательными неравенствами.

В самом простом случае неравенство принимает вид: . Очевидно, что знак неравенства может быть любым (<, >, , ).

Множество решения неравенства будет зависеть и от знака неравенства, и от основания степени, и от значения b.

Так как множество значений показательной функции – множество положительных чисел, то при неравенства: и решений не имеют, независимо от значения основания а. В то же время множеством решения неравенств и является все множество действительных чисел, независимо от значения основания а (см. Рисунок 1).

Рисунок 1 – иллюстрация решения простейшего показательного неравенства при b<0

Теперь рассмотрим случай b>0, a>1.

В том случае, когда основание степени a>1, то при переходе от исходного неравенства к неравенству с показателями знак неравенства не изменяется (см. Рисунки 2 и 3).

Рисунок 2 – иллюстрация решения простейшего показательного неравенства или при b>0, a>1.

Рисунок 3 – иллюстрация решения простейшего показательного неравенства или при b>0, a>1.

Теперь рассмотрим случай b>0, 0<a<1.

В том случае, когда основание степени 0<a<1, то при переходе от исходного неравенства к неравенству с показателями знак неравенства изменяется на противоположный (см. Рисунки 4 и 5).

Рисунок 4 – иллюстрация решения простейшего показательного неравенства или при b>0, 0<a<1.

Рисунок 5 – иллюстрация решения простейшего показательного неравенства илипри b>0, 0<a<1.

Для того чтобы решить простейшее показательное неравенство , нужно число b представить в виде степени числа a.

Рассмотрим пример: .

Представим в виде степени числа 5: .

Теперь перепишем данное неравенство в виде: .

Так как основание степени больше 1, то при переходе к показателям знак неравенства сохраняется, поэтому x>3/7.

Ответ: x>3/7.

Рассмотрим еще один пример: .

Перепишем его в виде

.

Так как основание степени меньше 1, то при переходе к показателям знак неравенства изменяется на противоположный:

,

,

.

Ответ: .

2. Теперь перейдем к решению более сложных показательных неравенств.

2.1) Рассмотрим пример: .

Преобразуем показатель первого слагаемого: .

Теперь в левой части вынесем за скобку общий множитель: .

Разделим обе части неравенства на 4: . Получили простейшее показательное неравенство. Так как основание степени больше 1, то при переходе к показателям знак неравенства сохраняется, получаем: . Решение этого неравенства является полуинтервал (0; 1].

Ответ: (0; 1].

2.2) Рассмотрим еще один пример: .

Заметим, что , поэтому введем новую переменную . Получим вспомогательное неравенство: .

Решим его:

.

Вернемся к исходной переменной:

, .

Так как основание степени меньше 1, то при переходе к показателям знак неравенства изменится на противоположный:

.

Ответ: .

2.3) Рассмотрим еще одной показательное неравенство, которое решается методом замены переменной.

.

Видим, что неравенство зависит от выражения , поэтому введем новую переменную и запишем вспомогательное неравенство: .

Преобразуем полученное неравенство к виду: F(t)<0.

, приведем левую часть к общему знаменателю:

, . Так как , то , поэтому решение полученного неравенства сводится к: , то есть .

Вернемся к исходной переменной: , то есть x<0.

Ответ:

Примеры и разбор решения заданий тренировочного модуля

1. .

Решение:

Введем новую переменную .

Запишем вспомогательное неравенство: .

1) Если , то решением неравенства является любое значение t, которое удовлетворяет области определения: .

Решив систему: , получаем: .

2) Если (), возведем обе части неравенства в квадрат:

.

Решим его: ,

,

,

0<t<9.

Учитывая условие , получаем: . ((x+5)/(x+2))

Решение:

Используем метод рационализации и перепишем неравенство в виде:

,

.

Получили неравенство: .

Упростим его и решим методом интервалов:

,

.

Запишем ответ: .

Ответ: .

Разработка темы «Рациональные неравенства. Системы рациональных неравенств. Рациональные неравенства с параметрами» в профильном классе

Рациональные неравенства.  Системы рациональных неравенств. Рациональные неравенства с параметрами.

 Нестандартные методы решения неравенств и их систем (МЗМ). Решение неравенств с двумя переменными.

1

Повторить теорию:  Никольский п. 2.9, 2.10, 2.11

На оценку проверяется:

2

Решить задачи: Никольский  — № 2.70, — 2.72, 2.78, 2.79, 2.88-2.92, 2.98-2.100,  2.101 — 2.107, 

№  84, 85, 89, 94,  101, 102, 105 (стр. 373 — 376).

  1. умение решать рациональные неравенства и системы неравенств

3*

Изучить теорию и разобрать примеры:

 Коропец п. 1, 2, 3

4*

Решить задачи:  Коропец: №1-31 стр. 19-20, № 1-49 стр. 37-39.

  1.  умение решать рациональные неравенства заменой неизвестного

 

 

  1. умение решать иррациональные неравенства заменой неизвестного

  1. умение решать неравенства с параметрами

 

 

 

 

 

 

 

 

РЕШЕНИЕ ДРОБНО-РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ.

10 КЛАСС. | Презентация к уроку (алгебра, 10 класс) по теме:

ИСАКОВА СИРЕНЬ ХИКАМУТДИНОВНА

Учитель математики высшей категории

МБОУ «Средняя общеобразовательная школа №8»ЕМР

ТЕМА: «РЕШЕНИЕ ДРОБНО-РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ»

Цель: формирование системы по решению дробно-рациональных неравенств методом интервалов.

Литература:

  1. Никольский С.М., Алгебра и начала анализа: учебник для 10 класса общеобразовательных учреждений, М., «Просвещение», 2007
  2. Колмогоров А.Н., Алгебра и начала анализа: учебник для 10-11 класса общеобразовательных учреждений, М., «Просвещение», 2006
  3. Н.В. Александрова, «Математические термины», «Высшая школа», 1978
  4. Макарычев Ю.Н., Алгебра 8 класс: учебник для школ и классов с углубленным изучением математики, М., «Мнемозина», 2006

Материалы: обобщающие таблицы, компьютер, проектор.

Ход урока:

  1. Организационный момент.

Сообщение темы, цели урока.

  1. Актуализация.

Слайд 2, слайд 3

Какое неравенство называется рациональным?

( Неравенство, левая и правая части которого есть рациональные выражения относительно х, называют рациональным неравенством с неизвестным x)
Что значит решить неравенство?

(Решить неравенство – значит найти все его решения или показать, что их нет)

Какого вида неравенства решают методом интервалов?

(, , , , где  и  — целые выражения с одним неизвестным)

Метод интервалов?

(Метод интервалов – метод решения неравенств с одной переменной, который позволяет решать любые неравенства одна часть которых – нуль, а другая является произведением или частным функций, не меняющих знак на известном промежутке)

Слайд 4

  1. Вводная беседа.

3.1 Разбор метода интервалов на примере функции которая является произведением линейных множителей.

Слайд 5

Нули функции:

 или  или  

3.2 Ознакомление с алгоритмом применения метода интервалов.

Слайд 6

Алгоритм применения метода интервалов

  1. Ввести функцию
  2. Указать область определения функции
  3. Найти нули функции
  4. Отметить на координатной прямой нули функции и область определения, учитывая строгость неравенства
  5. Выяснить знак функции на каждом промежутке подсчетом или рассуждением
  6. Записать ответ
  1. Закрепление

4.1 Слайд 7

  3. ,

          .

Ответ:

4.2 Слайд 8

        

        

Ответ: .

4.3 Слайд 9

 

Ответ:

4.4 Слайд 10

        

Ответ:

4.5 Слайд 11

Слайд 12

        

— корень четной кратности

Для решения таких неравенств обычно применяют общий метод интервалов. Это метод решения неравенств с одной переменной, который позволяет решать неравенства, имеющие  в произведении или в дроби одинаковые двучлены.

Итак, если корень повторяется четное число раз, то при переходе через него знак дроби (произведения) не меняется.

 

Ответ:

4.6 Слайд 13

— корень нечётной кратности

— корень чётной кратности

— корень нечётной кратности

Ответ:

4.7 Слайд 14

 — корень чётной кратности

— корень чётной кратности

— корень нечётной кратности

Ответ:

  1. Итог урока.

Неравенства какого вида называются дробно-рациональными?

Каким методом можно решать дробно-рациональные неравенства?
В чем заключается суть метода интервалов?
В каких случаях применяется общий метод интервалов?

  1. Домашнее задание.

№ 2.87 (б,е), №2.91 (г), №2.92 (е)

(Никольский С.М. , Алгебра и начала анализа: учебник для 10 класса общеобразовательных учреждений, М., «Просвещение», 2007)

РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА — PDF Free Download

Знаки линейной функции

И. В. Яковлев Материалы по математике MathUs.ru Метод интервалов Метод интервалов это метод решения так называемых рациональных неравенств. Общее понятие рационального неравенства мы обсудим позже, а сейчас

Подробнее

(a 1)(a + 2) (a + 4)(a 3) = (a 2 + a 2) (a 2 + a 6).

3.. Методы решения рациональных неравенств 3..1. Числовые неравенства Сначала определим, что мы понимаем под утверждением a > b. Определение 3..1. Число a больше числа b, если разность между ними положительна.

Подробнее

Ягубов.РФ. решаем неравенства

С. ШЕСТАКОВ [email protected] г. Москва решаем неравенства П О В Ы Ш Е Н И Е КВАЛИФИК А Ц И И / ЛЕКТО Р И Й 1.. Метод интервалов Перейдем теперь к описанию наиболее общих методов решения неравенств с одной

Подробнее

Иррациональные неравенства

Иррациональные неравенства Неравенства, в которых переменная содержится под знаком корня, называются иррациональными Основным методом решения иррациональных неравенств является метод сведения исходного

Подробнее

МАТЕМАТИЧЕСКИЙ ПРАКТИКУМ

МАТЕМАТИЧЕСКИЙ ПРАКТИКУМ Ю.Л.Калиновский Введение Решение квадратных уравнений Решение квадратных уравнений c помощью разложения на множители. Решение квадратных уравнений c помощью дополнения до полного

Подробнее

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА

Гущин Д. Д. http://www.mthnet.spb.ru ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА Основные факты. Показательными уравнениями (неравенствами) называются уравнения (неравенства), содержащие переменную в показателе

Подробнее

1 Решение квадратных уравнений

Введение Решение квадратных уравнений Решение квадратных уравнений c помощью разложения на множители. Решение квадратных уравнений c помощью дополнения до полного квадрата Решение квадратных уравнений

Подробнее

Уравнения высших порядков

И. В. Яковлев Материалы по математике MathUs.ru Содержание Уравнения высших порядков 1 Непосредственная группировка……………………….. 1 2 Подбор корня………………………………….

Подробнее

Алгоритм решения квадратных неравенств

Алгоритм решения квадратных неравенств 1) Привести неравенство к стандартному виду : 2) Решить квадратное уравнение (т.е. найти точки пересечения параболы с осью Ох):,, если D > 0, то (две точки пересечения

Подробнее

Дробно-рациональные выражения

Дробно-рациональные выражения Выражения содержащие деление на выражение с переменными называются дробными (дробно-рациональными) выражениями Дробные выражения при некоторых значениях переменных не имеют

Подробнее

РАЗДЕЛ 14. ЗАДАЧИ С ПАРАМЕТРАМИ

РАЗДЕЛ ЗАДАЧИ С ПАРАМЕТРАМИ Комментарий Задачи с параметрами традиционно являются сложными заданиями в структуре ЕГЭ, требующими от абитуриента не только владения всеми методами и приемам решения различных

Подробнее

Логарифмические неравенства

Логарифмические неравенства 1. 1. Решите неравенство: Решим неравенство:. 2. 2. Решите неравенство: Найдём значения, при которых определены обе части неравенства: Для таких получаем: Тогда исходное неравенство

Подробнее

x 4 ; x log 6 — логарифмические неравенства

Вопрос. Неравенства, система линейных неравенств Рассмотрим выражения, которые содержат знак неравенства и переменную:. >, — +х -это линейные неравенств с одной переменной х.. 0 — квадратное неравенство.

Подробнее

Иррациональные неравенства

Содержание И. В. Яковлев Материалы по математике MathUs.ru Иррациональные неравенства Учёт ОДЗ…………………………………… Равносильные преобразования………………………… Двукратное

Подробнее

МАТЕМАТИКА НЕРАВЕНСТВА

Агентство образования администрации Красноярского края Красноярский государственный университет Заочная естественно-научная школа при КрасГУ Математика: Неравенства Модуль для 0 класса Учебно-методическая

Подробнее

= — (2mn) 12 ( 2mn) 22 ( 2mn) ( 2mn) ( 2mn) 2

Автор: Фильчев Э.Г. Адрес:Россия.188760.Ленинградская область г.приозерск.ул.привокзальная 5. кв.60. кубического уравнения в системе mn параметров кубического уравнения на основе современных методов не

Подробнее

4.6. Иррациональные уравнения

4.6. Иррациональные уравнения Иррациональным уравнением называют уравнение, содержащее под знаком радикала переменную, относительно которой оно решается. Областью допустимых значений уравнения являются

Подробнее

РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ

РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ Оглавление РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ I Рациональные алгебраические уравнения Равносильность уравнений Равносильность уравнений на множестве Равносильность

Подробнее

Е. Н. ФИЛАТОВ АЛГЕБРА

Заочный физико-математический лицей «Авангард» Е. Н. ФИЛАТОВ АЛГЕБРА 8 Экспериментальный учебник Часть МОСКВА 06 Заочный физико-математический лицей «Авангард» Е. Н. Филатов АЛГЕБРА 8 Экспериментальный

Подробнее

Многочлены и их корни

Многочлены и их корни 2018 г. Гущина Елена Николаевна Определение: Многочленом степени n n N называется всякое выражение вида: P & z = a & z & + a &+, z &+, + + a, z + a., где a &, a &+,, a,, a. R, a &

Подробнее

Тема 03. Уравнения с модулем

Тема. Уравнения с модулем Содержание.. Модуль.. Простейшие уравнения с модулем.. Метод интервалов.. Модуль Абсолютной величиной (модулем) числа называется расстояние на координатной прямой от точки до

Подробнее

г. Классная работа.

5.0. 014 г. Классная работа. Уравнения и системы уравнений с параметрами. Опыт вступительных экзаменов в вузы показывает, что решение уравнений и неравенств, содержащих параметры, вызывает большие затруднения

Подробнее

ISBN К 22.14я721 ISBN

ДК 373:512 К 22.14721 49 49 аа, аьяа Маа.. 7 9 /.М.. М : Э, 2018. 128. (. ). ISBN 978-5-04-093533-8, 7 9-. П ё -. П,. П 7 9-,, -. ДК 373:512 К 22.14я721 ISBN 978-5-04-093533-8 аа.м., 2018 О. ООО «Иаь «Э»,

Подробнее

МАТЕМАТИКА Задачи типа С3

Большая перемена Э.Н. Балаян МАТЕМАТИКА Задачи типа С3 Неравенства и системы неравенств Ростов-на-Дону еникс 013 УДК 373.167.1:51 ББК.1я71 КТК 444 Б0 Б0 Балаян Э.Н. Математика. Задачи типа С3 : неравенства

Подробнее

Многочлены и их корни

Многочлены и их корни Определение: Многочленом степени n (n N) называется всякое выражение вида: P n (z) = a n z n + a n 1 z n 1 + + a 1 z + a 0, где a n, a n 1, a 1, a 0 R, a n старший коэффициент, a

Подробнее

Математика 8 класс Многочлены

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 8 класс Многочлены Новосибирск Многочлены Рациональными

Подробнее

Учебный центр «Резольвента»

ООО «Резольвента», www.resolventa.ru, [email protected], (495) 59-8- Учебный центр «Резольвента» Кандидат физико-математических наук, доцент С. С. САМАРОВА РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ Учебно-методическое

Подробнее

Примеры и комментарии

72 Глава2 Многочлены Примеры и комментарии Алгоритмы А-01 Запись многочлена в стандартном виде А-02 Действия над многочленами А-03 Устные преобразования А-04 Формулы сокращенного умножения А-05 Бином Ньютона

Подробнее

Показательные неравенства

Показательные неравенства Решение показательных неравенств основано на строгой монотонности показательной функции Известно, что при основании, большем единицы, показательная функция возрастает, при положительном

Подробнее

Решение уравнений в целых числах

Решение уравнений в целых числах Линейные уравнения. Метод прямого перебора Пример. В клетке сидят кролики и фазаны. Всего у них 8 ног. Узнать сколько в клетке тех и других. Укажите все решения. Решение.

Подробнее

Уравнения высших порядков

И. В. Яковлев Материалы по математике MathUs.ru Содержание Уравнения высших порядков 1 Непосредственная группировка……………………….. 1 2 Подбор корня………………………………….

Подробнее

Иррациональные уравнения и неравенства 2

Иррациональные уравнения и неравенства Оглавление Иррациональные уравнения Метод возведения обеих частей уравнения в одну и ту же степень Задание Задание Задание Замена иррационального уравнения смешанной

Подробнее

Рабочая программа по алгебре 8 А класса

Государственное бюджетное общеобразовательное учреждение Республики Хакасия «Хакасская национальная гимназия интернат им. Н.Ф.Катанова» «СОГЛАСОВАНО» на заседании кафедры математики и информатики Протокол

Подробнее

МАТЕМАТИКА. Квадратные корни

МАТЕМАТИКА Квадратные корни Задание для 8-х классов (006-00 учебный год) 4 Введение Дорогие ребята! Вы получили очередное задание по математике. В этом задании мы знакомим вас с важным математическим понятием

Подробнее

Содержание. Неравенства… 20

Содержание Уравнение…………………………………….. Целые выражения………………………………. Выражения со степенями……………………….. 3 Одночлен………………………………………

Подробнее

Иррациональные уравнения

Иррациональные уравнения Уравнения, в которых переменная содержится под знаком корня, называются иррациональными. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному

Подробнее

Решение рациональных неравенств методом интервалов. Алгебра, 9 класс: уроки, тесты, задания.

1. Рациональное неравенство (знаменатель — число)

Сложность: лёгкое

2
2. Числа, которые являются решением дробного неравенства

Сложность: лёгкое

3
3. Замена рационального неравенства системами неравенств

Сложность: лёгкое

1
4. Рациональное неравенство (линейное уравнение)

Сложность: среднее

3
5. Рациональное неравенство (общий знаменатель)

Сложность: среднее

3
6. Рациональное неравенство (неполный квадратный трёхчлен)

Сложность: среднее

4
7. Рациональное неравенство (три множителя)

Сложность: среднее

4
8. Дробное рациональное неравенство (знаменатель — бином)

Сложность: среднее

5
9. Дробь и единица

Сложность: среднее

5
10. Дробное рациональное неравенство (знаменатель — неполный квадратный трёхчлен)

Сложность: среднее

6
11. Дробное рациональное неравенство (разность квадратов)

Сложность: сложное

8
12. Дробное рациональное неравенство (теорема Виета)

Сложность: сложное

7
13. Значения выражения, переменная x

Сложность: сложное

2

Решение рациональных неравенств — ChiliMath

Ключевой подход к решению рациональных неравенств основан на нахождении критических значений рационального выражения, которые делят числовую прямую на отдельные открытые интервалы.

Критические значения — это просто нули числителя и знаменателя. Вы должны помнить, что нули знаменателя делают рациональное выражение неопределенным, поэтому их следует немедленно игнорировать или исключать как возможное решение.Однако нули числителя также необходимо проверять на предмет его возможного включения в общее решение.

В этом уроке я рассмотрю пять (5) рабочих примеров с разным уровнем сложности, чтобы проиллюстрировать как процедуры, так и концепции.

Примеры решения рациональных неравенств

Пример 1: Решите приведенное ниже рациональное неравенство.

Я начинаю решать это рациональное неравенство с написания его в общем виде. Общая форма подразумевает, что рациональное выражение расположено слева от неравенства, а ноль остается справа.

Общая форма имеет четыре (4) типа.

Приятно знать, что эта проблема уже в общей форме. Мой следующий шаг — найти нулей числителя и знаменателя .

Я могу найти нули числителя, полностью вычленив его, а затем отдельно установить каждый множитель равным нулю и решить относительно x. Точно так же поиск нулей знаменателя выполняется таким же образом.

Теперь я буду использовать нули, чтобы разделить числовую строку на интервалы.Нули числителя и знаменателя также известны как критические числа . В этом случае два критических числа делят числовую прямую на три отдельных интервала.

Следующий шаг — выбрать или выбрать число в каждом интервале и вычислить его обратно в исходное рациональное неравенство; чтобы определить, истинное это утверждение или ложное. Истинное утверждение означает, что интервал является частью решения, в противном случае это не так.

Как видите, числа, которые я выбрал для каждого интервала, выделены желтым.

Обратите внимание, что открытый интервал между -1 и 3, записанный как \ left ({- 1,3} \ right), дает истинное утверждение, которое подразумевает, что оно является частью решения.

Итак, где еще нам искать возможные решения, чтобы покончить с этим?

Проверяйте нули или критические числа числителей только в исходном уравнении. Если это верно, включите это критическое число как часть общего решения.

Нулей в числителе 3. Сейчас проверю.

Использование квадратной скобки указывает, что это часть решения, а открытая скобка (скобка) означает, что это не так. Я напишу свой окончательный ответ как \ left ({- 1, \ left. 3 \ right]} \ right ..

Пример 2: Решите приведенное ниже рациональное неравенство.

Во-первых, данное рациональное неравенство имеет общий вид, потому что рациональное выражение находится слева, а ноль — справа. Это хорошо!

Далее я вынесу за скобки числитель и знаменатель.После этого у вас должно получиться что-то вроде этого.

Теперь я могу найти нули числителя и знаменателя.

Эти нули или критические числа делят числовую строку на отдельные интервалы или части.

Выберите номер теста для каждого интервала и верните исходное рациональное неравенство.

Используйте факторизованную форму исходного рационального неравенства , чтобы оценить числа тестов для упрощения вычислений.

Цифры желтого цвета — это те числа, которые я выбрал для проверки достоверности каждого интервала.

Интервалы, дающие истинные утверждения, равны

.

Чтобы найти остальную часть решения, проверьте правильность нулей числителя только в исходное рациональное неравенство.

Если вы сделали это правильно, вы должны согласиться с тем, что −4 и 2 — это недействительные ответы , потому что они не дают истинных утверждений после проверки.

Окончательный ответ на эту проблему в интервальной записи:

.

Пример 3: Решите приведенное ниже рациональное неравенство.

Я бы сначала вычленил числитель и знаменатель, чтобы найти их нули. В факторизованном виде я получил

Затем определите нули рационального неравенства, установив каждый множитель равным нулю, а затем решив относительно x.

  • Нули числителя: –1 и 4
  • Нули знаменателя: 4

Используйте нули как критические числа, чтобы разделить числовую строку на отдельные интервалы. Я начинаю проверять достоверность каждого интервала, выбирая тестовые значения и оценивая их в соответствии с исходным рациональным неравенством.Желтым — числа, которые я выбрал.

Обратите внимание, что единственный интервал, дающий истинное утверждение, — это \ left ({- 1,4} \ right).

Более того, нули числителя не согласуются с исходным рациональным неравенством, поэтому я должен их игнорировать.

Окончательный ответ — \ left ({- 1,4} \ right).

Пример 4: Решите приведенное ниже рациональное неравенство.

Это рациональное неравенство не в общем виде . Правая часть должна быть равна нулю.Первый шаг — избавиться от константы на этой стороне путем вычитания обеих частей на 1. После этого сведите к одному рациональному выражению. У вас должен быть аналогичный предварительный шаг, вот так.

Затем найдите нули числителя и знаменателя.

  • Нули в числителе: -7
  • Нули в знаменателе: -3

Используйте нули как критические числа для разделения числовой прямой на участки или интервалы.

Затем выберите номера тестов для каждого интервала и оцените их в общей форме, чтобы определить их истинностные значения.Желтым цветом обозначены выбранные значения. Вы можете выбрать другие числа, если они находятся в проверяемом интервале.

Интервалы, дающие истинные утверждения, равны

.

Между тем, после проверки нуля числителя при x = — \, 7 это также приводит к истинному утверждению. Используйте квадратную скобку, чтобы указать, что он включен в качестве решения.

Окончательный ответ в интервальной записи должен быть

.

Пример 5: Решите приведенное ниже рациональное неравенство.

Мне нужно обнулить правую часть рационального неравенства. Для этого я буду одновременно прибавлять x и вычитать 5 с обеих сторон. Однако моя конечная цель — выразить это в едином рациональном выражении. Здесь вам пригодятся ваши навыки складывания и вычитания рациональных выражений. У вас должны быть аналогичные шаги ниже.

Затем найдите нули числителя и знаменателя.

  • Нули в числителе: -3 и 5
  • Нули в знаменателе: 0

Используйте нули, чтобы разделить числовую прямую на отдельные интервалы.Выберите номера тестов для каждого интервала, чтобы проверить, приводит ли он к истинным утверждениям. Выбранные тестовые значения для x выделены желтым цветом.

«Истинные» интервалы — это \ left ({- \, \ infty, — 3} \ right) и \ left ({0,5} \ right). Более того, нули числителя также сверяются с общим видом данного рационального неравенства. Следовательно, я должен включить -3 и 5 как часть решения с использованием квадратных скобок.

Окончательный ответ теперь становится

Практика с рабочими листами

Возможно, вас заинтересует:

Решение рациональных уравнений

Сложение и вычитание рациональных выражений

Умножение рациональных выражений

Решение рациональных неравенств

Rational

Рациональное выражение выглядит так:

Неравенства

Иногда нам нужно решить такие рациональные неравенства:

Обозначение

слов

Пример




>

больше

(х + 1) / (3-х)> 2

<

менее

х / (х + 7) <−3

≥

больше или равно

(x − 1) / (5 − x) ≥ 0

≤

меньше или равно

(3−2x) / (x − 1) ≤ 2

Решение

Решение неравенств очень похоже на решение уравнений… вы делаете почти то же самое.

Когда мы решаем неравенств
, мы пытаемся найти интервалов ,
, например, отмеченные «<0» или «> 0»

Это шаги:

  • найти «достопримечательности»:
    • точки «= 0» (корни) и
    • «вертикальные асимптоты» (где функция не определена)
  • между «точками интереса», функция либо больше нуля (> 0), либо меньше нуля (<0)
  • затем выберите тестовое значение, чтобы узнать, какое оно (> 0 или <0)

Вот пример:

Пример:

3x − 10 x − 4 > 2

Первый , давайте упростим!

Но вы не можете умножить на (x − 4)

Потому что «x − 4» может быть положительным или отрицательным…. мы не знаем, следует ли нам менять направление неравенства или нет. Все это объясняется в разделе «Устранение неравенств».

Вместо этого переместите «2» влево:

3x − 10 x − 4 -2> 0

Затем умножьте 2 на (x − 4) / (x − 4):

3x − 10 x − 4 -2 x − 4 x − 4 > 0

Теперь у нас есть общий знаменатель, давайте все вместе:

3x − 10-2 (x − 4) x − 4 > 0

Упростить:

x − 2 x − 4 > 0

Второй , давайте найдем «достопримечательности».

При x = 2 имеем: (0) / (x − 4)> 0, что является точкой «= 0», или корень

При x = 4 имеем: (x − 2) / (0)> 0, что равно undefined

Третий , сделайте контрольные точки, чтобы увидеть, что он делает между:

При x = 0:

  • x − 2 = −2, что составляет отрицательное значение
  • x − 4 = −4, что также является отрицательным
  • Итак, (x − 2) / (x − 4) должно быть положительным

Мы можем сделать то же самое для x = 3 и x = 5 и получить следующие результаты:

х = 0 х = 2 х = 3 х = 4 х = 5
х − 2 <0 х − 2> 0 х − 2> 0
х − 4 <0 х − 4 <0 х − 4> 0
(x − 2) / (x − 4) равно> 0 0 <0 undefined> 0

Это дает нам полную картину!

А где это> 0?

Итак, наш результат:

(−∞, 2) U (4, + ∞)

Все это мы сделали без рисования сюжета!

Но вот график (x − 2) / (x − 4), поэтому вы можете видеть:

Решение рациональных неравенств

Решение рациональных неравенств Вот шаги, необходимые для решения рациональных неравенств:
Шаг 1 : Напишите неравенство в правильной форме.Одна сторона должна быть равна нулю, а другая может иметь только одну дробь, поэтому упростите дроби, если дробей больше одной.
Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, установите числитель и знаменатель дроби равными нулю и решите.
Шаг 3 : Сделайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки.
Шаг 4 : Выполните анализ знаков. Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. Знак этого ответа (положительный или отрицательный) будет знаком всего раздела. Вы можете проверить другой номер из того же раздела, если хотите проверить свой ответ.
Шаг 5 : Используйте диаграмму знакового анализа, чтобы определить, какие разделы удовлетворяют неравенству.Если неравенство меньше нуля или меньше или равно нулю, тогда вы хотите, чтобы все отрицательные участки были найдены в диаграмме анализа знаков. Если неравенство больше нуля или больше или равно нулю, тогда вы хотите, чтобы все положительные участки были найдены в диаграмме анализа знаков.
Шаг 6 : Используйте интервальную запись, чтобы написать окончательный ответ.

Пример 1 — График:

Шаг 1 : Запишите неравенство в правильной форме.Одна сторона должна быть равна нулю, а другая может иметь только одну дробь, поэтому упростите дроби, если дробей больше одной.
Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, установите числитель и знаменатель дроби равными нулю и решите.
Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки.
Шаг 4 : Выполните анализ знаков. Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –5, что дает –1,333, x = 0, что дает +12, x = 2, что дает –6, и x = 4, что дает +2,666.
Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству.В этом случае у нас меньше или равно нулю, поэтому нам нужны все отрицательные секции. Обратите внимание, что x ≠ 1, потому что это сделало бы исходную задачу неопределенной, поэтому вы должны использовать открытый кружок при x = 1 вместо замкнутого круга для рисования графика.
Шаг 6 : Используйте нотацию интервалов для записи окончательного ответа.

Пример 2 — График:

Шаг 1 : Запишите неравенство в правильной форме.Одна сторона должна быть равна нулю, а другая может иметь только одну дробь, поэтому упростите дроби, если дробей больше одной.
Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, установите числитель и знаменатель дроби равными нулю и решите.
Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки.
Шаг 4 : Выполните анализ знаков. Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –4, что дает –0,025, x = 0, что дает +0,75, x = 2, что дает –2,5, и x = 4, что дает +2.
Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству.В этом случае у нас больше или равно нулю, поэтому нам нужны все положительные секции. Обратите внимание, что x ≠ 1 и x ≠ 4, потому что это сделает исходную задачу неопределенной, поэтому вы должны использовать открытый кружок при x = 1 и x = 4 вместо замкнутого круга для рисования графика.
Шаг 6 : Используйте нотацию интервалов для записи окончательного ответа.

Щелкните здесь для практических задач

Пример 3 — График: График:

Шаг 1 : Запишите неравенство в правильной форме.Одна сторона должна быть равна нулю, а другая может иметь только одну дробь, поэтому упростите дроби, если дробей больше одной.
Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, установите числитель и знаменатель дроби равными нулю и решите.
Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки.
Шаг 4 : Выполните анализ знаков. Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –6, что дает –0,031, x = –3, что дает +0,4, x = 0, что дает –1,25, и x = 3, что дает +1,6.
Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству.В этом случае у нас меньше нуля, поэтому нам нужны все отрицательные секции.
Шаг 6 : Используйте нотацию интервалов для записи окончательного ответа.

Щелкните здесь для практических задач

Пример 4 — График: График:

Шаг 1 : Запишите неравенство в правильной форме. Одна сторона должна быть равна нулю, а другая может иметь только одну дробь, поэтому упростите дроби, если дробей больше одной.
Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, установите числитель и знаменатель дроби равными нулю и решите.
Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки.
Шаг 4 : Выполните анализ знаков.Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –2, что дает +0,25, x = 0, что дает –0,5, и x = 3, что дает +4.
Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству. В этом случае у нас меньше или равно нулю, поэтому нам нужен отрицательный участок.Обратите внимание, что x ≠ 2, потому что это сделало бы исходную задачу неопределенной, поэтому вы должны использовать открытый кружок при x = 2 вместо замкнутого круга, чтобы нарисовать график.
Шаг 6 : Используйте нотацию интервалов для записи окончательного ответа.

Щелкните здесь для практических задач

Пример 5 — График: График:

Шаг 1 : Запишите неравенство в правильной форме.Одна сторона должна быть равна нулю, а другая может иметь только одну дробь, поэтому упростите дроби, если дробей больше одной.
Шаг 2 : Найдите ключевые или критические значения. Чтобы найти ключевые / критические значения, установите числитель и знаменатель дроби равными нулю и решите.
Шаг 3 : Создайте диаграмму анализа знаков. Чтобы создать диаграмму анализа знаков, используйте ключевые / критические значения, найденные на шаге 2, чтобы разделить числовую линию на участки.
Шаг 4 : Выполните анализ знаков. Чтобы провести анализ знаков, выберите по одному числу из каждого раздела, созданного на шаге 3, и вставьте это число в многочлен, чтобы определить знак полученного ответа. В этом случае вы можете выбрать x = –4, что дает +0,2, x = 0, что дает –3, и x = 2, что дает +5.
Шаг 5 : Используйте диаграмму анализа знаков, чтобы определить, какие разделы удовлетворяют неравенству.В этом случае у нас больше или равно нулю, поэтому нам нужны все положительные секции. Обратите внимание, что x ≠ 1, потому что это сделало бы исходную задачу неопределенной, поэтому вы должны использовать открытый кружок при x = 1 вместо замкнутого круга, чтобы нарисовать график.
Шаг 6 : Используйте нотацию интервалов для записи окончательного ответа.

Щелкните здесь для практических задач

Решение рациональных неравенств

Решение Рациональное неравенство (стр. 1 из 2)

Решение рационального неравенства очень похоже на решение полинома неравенства.Но потому что рационально выражения имеют знаменатели (и, следовательно, могут иметь места, где они не определены), вы должны быть немного осторожнее в поиске решений.

Чтобы решить рациональное неравенство, вы сначала находите нули (из числителя) и неопределенные точки (от знаменателя). Вы используете эти нули и неопределенные точки для деления числовую строку на интервалы. Тогда вы найдете знак рационального на каждом интервале.

  • Решите следующее:

    Сначала учту все:

    Эта полиномиальная дробь будет нулем везде, где числитель равен нулю, поэтому я установлю числитель равным нулю и решаем:

    Дробь будет undefined там, где знаменатель равен нулю, поэтому я установлю знаменатель равным нулю и решаем:

    Эти четыре значения, 4, 2, 1, и 4, разделите числовую строку на пять интервалов, а именно:

      (бесконечность, 4), (4, 2), (2, 1), (1, 4) и (4, + бесконечность).

    Я мог бы использовать «тест» точек », чтобы найти решение неравенства, выбрав значение x в каждом интервале, вставляя его в исходное рациональное выражение, упрощая получение числового ответа, а затем проверяя знак, но этот процесс становится долгим и утомительным (и подвержен ошибкам), поэтому я вместо этого используйте более простой и быстрый метод таблицы факторов.


    Моя таблица коэффициентов выглядит так:

    В моем столе одна строка для каждого фактора, строка для числовой строки и строка для рационального выражения.Каждая строка разбита на столбцы, с каждым столбцом, соответствующим одному из интервалов на числовая строка.

    Знак рационального выражение является результатом признаков его различных факторов, поэтому мне нужно чтобы узнать, где каждый фактор положителен: Авторское право Элизабет Стапель 2005-2011 Все права защищены

      x + 4> 0 для x > 4
      x + 2> 0 для x > 2
      x + 1> 0 для x > 1
      x 4> 0 для x > 4

    Теперь могу поставить «плюс» знаки на интервалах в каждой строке, где коэффициент этой строки положительный:

    Где фактор не положительный, это отрицательный, поэтому я поставлю знак «минус» в остальные интервалы каждого ряда:

    Умножение знаков вниз по столбцам я получаю общий знак исходного рационального выражения на каждом интервале:

    Тогда рациональное положительный на интервалах (бесконечность, 4), (2, 1), и (4, + бесконечность).

    Оглядываясь на оригинал упражнения, это неравенство «или равно», поэтому мне нужно также учитывайте конечные точки интервала. Если бы это было полиномиальное неравенство, Я мог бы просто добавить в решение все конечные точки интервала и Я бы сделал. Однако для рационального использования я должен быть осторожен, чтобы не включать любые x -значения это вызовет деление на ноль.

    Конечные точки интервалов 4 года, 2, 1, и 4.Могу включить 2 и 1 дюйм решение, потому что они просто делают выражение равным нулю обнуление числителя. Но подключив 4 или 4 будет вызвать разделение на ноль, что делает рациональное выражение неопределенным, поэтому я не могу включить эти значения в решении.

    Тогда полное решение это:

Если вам нужно написать свой решение в нотации «неравенство» будет выглядеть так:

    x < 4, 2 < x < 1, и x > 4

Не забудьте: «Бесконечность» не является «числом» в том смысле, как, скажем, «2» является.«Бесконечность» не может быть «включена» в ваше решение, поэтому никогда не рисуйте квадратную скобку рядом с конечной точкой «бесконечности».

Вверх | 1 | 2 | Возвращаться к указателю Вперед >>

Цитируйте эту статью как:

Стапель, Елизавета. «Решение рациональных неравенств». Пурпурная Математика .Имеется в наличии из
https://www.purplemath.com/modules/ineqrtnl.htm . Дата обращения [Дата] [Месяц] 2016 г.

Алгебра — рациональные неравенства

Прежде чем мы перейдем к их решению, мы должны указать, что они НЕ решают так же, как мы решаем уравнения, содержащие рациональные выражения.В случае с уравнениями первое, что мы всегда делали, это очищали знаменатели, умножая их на наименьший общий знаменатель. Однако с ними это не сработает.

Поскольку мы не знаем значение \ (x \), мы не можем умножить обе части на что-либо, содержащее \ (x \). Напомним, что если мы умножим обе части неравенства на отрицательное число, нам нужно будет изменить направление неравенства. Однако, поскольку мы не знаем значение \ (x \), мы не знаем, положительный или отрицательный знаменатель, и поэтому мы не знаем, нужно ли нам менять направление неравенства или нет.Фактически, что еще хуже, знаменатель будет как положительным, так и отрицательным для значений \ (x \) в решении, и это создаст реальные проблемы.

Итак, нам нужно оставить рациональное выражение в неравенстве.

Теперь основной процесс здесь тот же, что и с полиномиальными неравенствами. Первый шаг — получить ноль на одной стороне и записать другую сторону как единое рациональное неравенство. Здесь для нас это уже сделано.

Следующим шагом будет максимально возможное разложение числителя и знаменателя. Опять же, в данном случае это уже было сделано для нас.

Следующий шаг — определить, где числитель и знаменатель равны нулю. В данном случае это значения.

\ [{\ mbox {числитель:}} x = — 1 \ hspace {0,5 дюйма} {\ mbox {знаменатель:}} x = 5 \]

Эти числа нам нужны по нескольким причинам.Во-первых, как и в случае с полиномиальными неравенствами, это единственные числа, у которых рациональное выражение может изменить знак . Итак, мы построим числовую линию, используя эти точки, чтобы определить диапазоны, из которых следует выбирать контрольные точки, как мы это делали с полиномиальными неравенствами.

Однако есть еще одна причина, по которой требуется значение \ (x \), делающее знаменатель равным нулю. Независимо от того, что еще здесь происходит, у нас есть рациональное выражение, а это означает, что нам нужно избегать деления на ноль, и поэтому знание того, где знаменатель равен нулю, даст нам значения \ (x \), которых следует избегать для этого.

Вот числовая прямая этого неравенства.

Итак, нам нужны области, которые делают рациональное выражение отрицательным. Это означает средний регион. Кроме того, поскольку в неравенстве есть часть «или равно», нам также необходимо указать, где неравенство равно нулю, это означает, что мы включаем \ (x = — 1 \). Обратите внимание, что нам также нужно избегать \ (x = 5 \), поскольку это дает деление на ноль.

Решение этого неравенства:

\ [- 1 \ le x

Решение рациональных неравенств — Видео и стенограмма урока

Шаги для решения

Чтобы решить рациональное неравенство, мы выполняем следующие шаги:

  1. Обозначьте неравенство в общем виде.
  2. Установите числитель и знаменатель равными нулю и решите. Полученные вами значения называются критическими значениями . Критические значения функции — это когда функция не определена или равна 0. Когда числитель равен 0, функция равна 0. Когда знаменатель равен 0, функция не определена.
  3. Нанесите критические значения на числовую прямую, разбив числовую прямую на интервалы.
  4. Возьмите номер теста из каждого интервала и подставьте его в исходное неравенство.Если это истинное утверждение, то интервал, из которого оно пришло, находится в решении. Если он делает ложное утверждение, то интервал, из которого оно пришло, не входит в решение.
  5. Определите, следует ли включать конечные точки интервалов в растворе в интервалы.

Давайте покончим с сомнением в отношении того, сколько велосипедов вы должны продать, чтобы заработать немного денег, приняв рациональное неравенство, представляющее вашу прибыль, с помощью этих шагов.

Первое, что мы хотим сделать, это изложить его в общем виде.Хорошие новости! В данном случае это было сделано за нас. У нас есть рациональное выражение в левой части неравенства и 0 в правой части.

Затем мы хотим установить числитель и знаменатель равными 0 и решить.

Это дает нам критические значения x = -30, x = 30 и x = 0. Давайте изобразим их на числовой прямой, разбив числовую прямую на интервалы.

Теперь найдем тестовые значения для каждого интервала. Мы можем использовать любое число, попадающее в каждый интервал, в качестве тестового значения. Обычно рекомендуется использовать числа, с которыми легко работать. В этом случае давайте использовать -40 из интервала I, -1 из интервала II, 1 из интервала III и 40 из интервала IV.

Мы приближаемся! Теперь нам просто нужно вставить эти тестовые значения в исходное неравенство, чтобы увидеть, получим ли мы истинное или ложное утверждение для каждого из них.

Мы видим, что интервалы, которые делают наше неравенство истинным, составляют от -30 до 0 и от 30 до бесконечности.

Следующее, что нам нужно сделать, это определить, должны ли конечные точки этих интервалов быть включены в наше решение. Неравенство больше 0. Мы знаем, что если мы подставим -30 или 30, то рациональное выражение будет равно нулю, поэтому их не следует включать в интервалы. Точно так же, если мы подставим 0 для x , рациональное выражение будет неопределенным, поскольку у нас не может быть 0 в знаменателе.Таким образом, 0 не следует включать в интервалы.

Мы пришли к решению для нашего неравенства: решение — это все действительные числа x , такие что -30 < x <0 или x > 30. Мы также можем записать решение, используя интервальную нотацию . Запись интервала — это способ записи интервала чисел. В обозначении интервалов мы записываем интервал как ( a , b ), что означает все числа между a и b .Когда мы не хотим включать конечную точку, мы используем круглые скобки, а когда мы действительно хотим включить конечную точку, мы используем скобки.

Теперь, когда дело доходит до нашей реальной проблемы, мы хотим знать, сколько велосипедов нужно продать, чтобы получить прибыль. Поскольку нельзя продать отрицательное количество велосипедов, мы можем не учитывать интервал (-30, 0). Это говорит нам о том, что для получения прибыли вам необходимо продать более 30 велосипедов — лучше начните!

Итоги урока

Давайте рассмотрим. Рациональные неравенства — это неравенства, содержащие рациональное выражение. Чтобы решить рациональные неравенства, выполните следующие действия:

  1. Приведите неравенство в общем виде.
  2. Установите числитель и знаменатель равными 0 и решите, чтобы получить критических значений .
  3. Нанесите критические значения на числовую прямую, разбив числовую прямую на интервалы.
  4. Возьмите номер теста из каждого интервала и подставьте его в исходное неравенство.Если это истинное утверждение, то интервал, из которого оно пришло, находится в решении. Если он делает ложное утверждение, то интервал, из которого оно пришло, не входит в решение.
  5. Определите, следует ли включать конечные точки интервалов в растворе в интервалы.

Эти виды неравенства могут проявляться во многих различных областях, таких как финансы, инженерия и медицина. Вот почему полезно знать, как с ними работать и решать.

Решение рациональных неравенств — различные способы решения, решенный пример и часто задаваемые вопросы

Ключевой подход к решению рационального неравенства зависит от определения критических значений рационального выражения, которое делит числовую прямую на отчетливые открытые интервалы.Критические значения — это нули (0) как в числителе, так и в знаменателе. Обратите внимание, что нули знаменателя делают рациональное выражение неопределенным, поэтому их следует немедленно исключить или отклонить как вероятное решение. Однако нули числителей также требуют проверки на возможность их включения во все решение.

Различные способы решения рационального неравенства

Борьба со способами поиска рационального неравенства? Хорошо! Существуют различные способы решения рациональных неравенств, которые приведены ниже:

  • Алгебраическое решение рациональных неравенств.

  • Решение неравенств с рациональными выражениями.

  • Решение рациональных неравенств с помощью построения графиков.

Как решить рациональные неравенства

Ниже приведены краткие инструкции по поиску рациональных неравенств и их решению.

Шаг 1. Запишите выражение неравенства в виде одного частного слева и нуля (0) справа.

Шаг 2: определите критические точки — точки, в которых рациональное выражение будет либо неопределенным, либо нулевым.

Шаг 3: Используйте критические точки для разделения числовой прямой на интервалы.

Шаг 4: Проверьте значение каждого интервала. В числовой строке отображается знак каждого множителя числителя, а также знаменатель в каждом интервале. В числовой строке также указан знак частного.

Шаг 5: определите интервалы, в которых неравенство уместно.

Шаг 6: Запишите решение в виде интервальной записи.

Rational

Вот как выглядит рациональное выражение, имеющее отношение двух многочленов.

(Изображение будет загружено в ближайшее время)

Иногда нам может потребоваться решить такие рациональные неравенства, как это:

003 Пример 9200003

Symbol

Слова

3

больше

(x + 1) / (3 — x)> 2

<

меньше

x / (x + 7) <−3

≥

больше или равно

(x − 1) / (5 − x) ≥ 0

≤

меньше или равно

(3 — 2x) / (x — 1) ≤ 2

Решенный пример

Пример: Решите и упростите данное рациональное неравенство:

(x 2 — 3x — 4) / ( x 2 — 8x + 16) <0

Решение:

Шаг 1. Выносим за скобки числитель и знаменатель, чтобы найти их нули.В факторизованной форме получим:

(x + 1) (x — 4) / (x — 4) (x — 4) <0

Шаг 2: определите нули рационального неравенства, установив каждый множитель равным к нулю

Шаг 3: Найдите x. Мы получаем:

Нулей числителей: –1 и 4

Нулей знаменателей: 4

Шаг 4: Рассмотрите возможность принятия нулей в качестве критических чисел, чтобы разделить числовую линию на отдельные интервалы.

Шаг 5: Проверьте достоверность каждого интервала, выбрав тестовое значение и оценив их в исходное рациональное неравенство.Обратите внимание, что желтым цветом обозначены выбранные нами числа.

(Изображение будет скоро загружено)

Если вы заметили, единственный интервал, обеспечивающий истинное утверждение, — это (- 1, 4).

Кроме того, нули числителя не совпадают с исходным рациональным неравенством, поэтому мы должны их не учитывать.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *