Элективный курс «Вписанная и описанная окружность в трапецию» в рамках курса по выбору по геометрии для обучающихся 9 классов»
О.П. Иванченко |
ГЕОМЕТРИЯ
Вписанная и описанная окружность в трапецию»
в рамках курса по выбору
по геометрии для обучающихся 9 классов
Управление образования администрации
Ангарского городского округа
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №15»
О.П. Иванченко
Вписанная и описанная окружность в трапецию»
в рамках курса по выбору
по геометрии для обучающихся 9 классов
Элективный курс
Ангарск
2017
Автор-составитель Иванченко Ольга Петровна, учитель математики МБОУ «СОШ №15» г. Ангарск
Ангарск
Иванченко О.П.
Вписанная и описанная окружность в трапецию» в рамках курса по выбору
по геометрии для обучающихся 9 классов: Элективный курс / О.П. Иванченко. – Ангарск: МБОУ «СОШ №15», 2017. – 50с.
СОДЕРЖАНИЕ
Введение ……………………………………………………………………….…… 5
Глава 1. Трапеция, вписанная в окружность и трапеция, описанная около окружности …………………………………..…………………………….………. 8
1.1. Вписанные и описанные четырехугольники ………….……………… 8
1.2. Трапеция …………………………………………..………………….. 9
1.3. Анализ учебной литературы ……………..………..………………..10
1.4. Трапеция, вписанная в окружность …………………………………12
1.5. Трапеция, описанная около окружности …..……………………… 13
Глава 2. Содержание занятий по теме «Трапеция, вписанная в окружность и трапеция, описанная около окружности» в рамках курса по выбору по геометрии для обучающихся 9 классов ……………………………. ………….….20
………….….20
2.1. Пояснительная записка ………………………………………………20
2.2. Содержание занятий по теме: «Трапеция, вписанная в окружность и трапеция, описанная около окружности» ………………………………………22
Заключение ……………………………………………………………….44
Литература ………………………………………………………………..45
Приложение 1 (Входная самостоятельная работа) …………………….47
Приложение 2 (Итоговая самостоятельная работа) ……………………49
ВВЕДЕНИЕ
Геоме́трия (от γη — Земля и μετρεω — мера, измерение) — наука о пространстве, точнее — наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела; раздел математики, изучающий пространственные отношения и их обобщения.[1]
В общеобразовательной школе предмет «Геометрия» изучается с 7 класса и, по мнению многих обучающихся, является одним из сложнейших школьных предметов. Многие обучающиеся не понимают назначения геометрии в жизни, так как не собираются связывать свою будущую профессию с математикой вообще.
Основой курса геометрии является принцип доказательности всех утверждений. И это единственный школьный предмет, включая даже предметы математического цикла, полностью основанный на последовательном выводе всех утверждений. Людьми, понимающими, что такое доказательство, трудно и даже невозможно манипулировать.[1]
Итак, Геометрия — один из важнейших предметов, причем не только среди предметов математического цикла, но и вообще среди всех школьных предметов. Ее целевой потенциал охватывает необычайно широкий арсенал, включает в себя чуть ли не все мыслимые цели образования.
Куда бы мы ни повернулись в нашей жизни, повсюду мы видим применение принципов геометрии. Она может быть в строительстве сооружений и оформлении их, в архитектуре, устройстве интерьеров, даже в создании ландшафта.[2]
Каждый день, идя по улице, мы начинаем замечать, что мир состоит из разных геометрических фигур. Окна домов – квадраты или прямоугольники, дорожные знаки – круги, треугольники или прямоугольники. Но иногда встречаются такие фигуры, и даже очень часто, у которых две противоположные стороны параллельны, а две нет – предметы обихода, лобовые и боковые стекла у машин, крыши домов, тротуарная плитка, религиозные знаки и, даже, силуэты одежды.
Но иногда встречаются такие фигуры, и даже очень часто, у которых две противоположные стороны параллельны, а две нет – предметы обихода, лобовые и боковые стекла у машин, крыши домов, тротуарная плитка, религиозные знаки и, даже, силуэты одежды.
Эти фигуры похожи на треугольник, у которого срезали вершину. Иногда они правильной формы, иногда – нет. Это трапеции.
В принципе, это давно известная фигура, свойства которой исследовали еще и Евклид, и Архимед.
«Трапецией» называются не только геометрические фигуры, но и спортивный снаряд, и мышцы атлета, и система тросов на яхтах, и женские юбки.
В настоящей работе рассмотрим трапецию, вписанную в окружность и трапецию, описанную около окружности.
Объект исследования: трапеция, вписанная в окружность и трапеция, описанная около нее.
Предмет исследования: содержание занятий по теме «Вписанная и описанная окружность в трапецию» в рамках курса по выбору по геометрии для обучающихся 9 классов.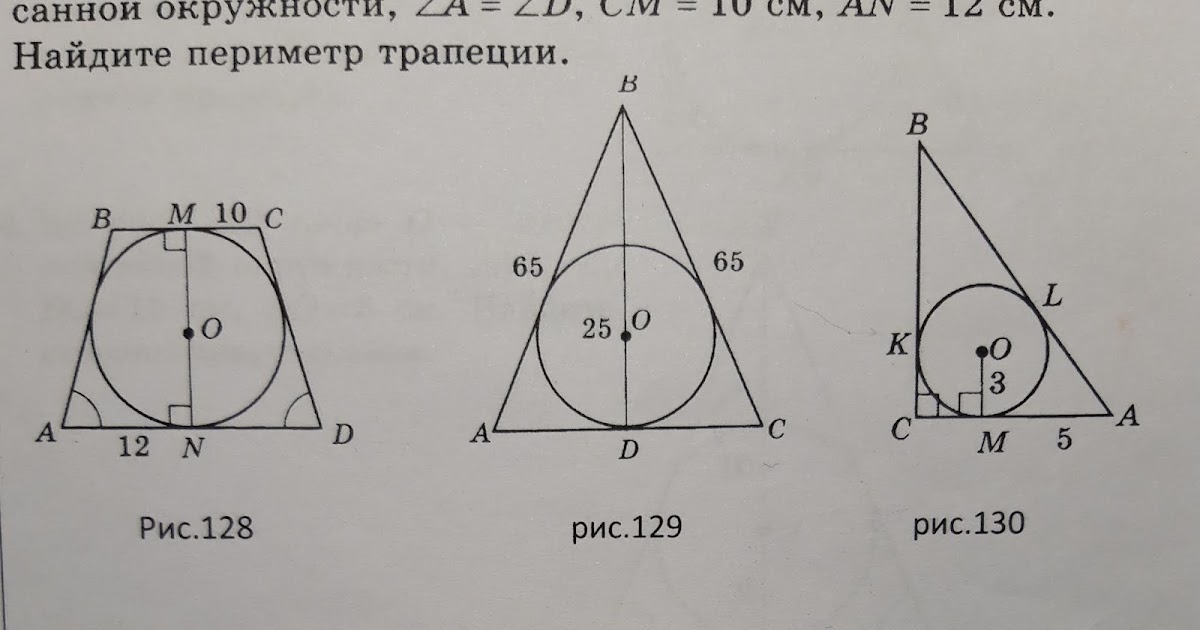
Цель работы: разработка занятий по теме «Вписанная и описанная окружность в трапецию» в рамках курса по выбору по геометрии для обучающихся 9 классов.
Задачи:
1. анализ учебной и методической литературы по теме исследования;
2. подбор теоретического и практического материала;
3. разработка практического и контрольно-измерительного материала.
Структура работы:
Работа состоит из введения, 2-х глав, заключения, списка литературы и 2 приложений, в которых представлено решение входной и итоговой самостоятельных работ. Общий объем работы 48 страниц.
Глава 1. Трапеция, вписанная в окружность и трапеция, описанная около окружности
1.1. Вписанные и описанные четырехугольники
Четырёхугольник — это геометрическая фигура (многоугольник), которая состоит из четырёх точек (вершин), три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. [3]
[3]
Виды четырехугольников:
— параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
— прямоугольник — четырёхугольник, у которого все углы прямые;
— ромб — четырёхугольник, у которого все стороны равны;
— квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
— трапеция — четырёхугольник, у которого две противоположные стороны параллельны. [4]
Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности, которая будет называться описанной вокруг четырехугольника. [5]
Теорема 1. Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны 180. Отсюда следует, что вписать в окружность можно только равнобокую трапецию. | |
Площадь где (полупериметр) |
Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник. [5]
Теорема 2. Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы его длин противоположных сторон равны. [6] | |
Площадь , где (полупериметр) r – радиус вписанной окружности |
1. 2. Трапеция
2. Трапеция
Понятие трапеции формировалось в течение длительного периода времени. Сначала трапецией называли любой четырехугольник, не являющийся параллелограммом. [7]
Именно в таком смысле термин «трапеция» использовал Евклид в своих «Началах».
В XVIII веке понятие трапеции приобрело современные определения:
— «Трапецией называется четырехугольник, у которого две противоположные стороны параллельны, а две другие нет»;
— «Трапеция в геометрии – четырехугольник, с парой параллельных сторон, и с другой парой непараллельных»;
— «Трапеция – четырехугольник, в котором две противоположные стороны параллельны, называемые основаниями трапеции, а другие две – непараллельные»;
— «Трапеция – четырёхугольник, у которого только одна пара противолежащих сторон параллельна».
Таким образом, трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два противоположных из которых параллельны между собой и называются основаниями трапеции.
Трапеция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна). Две параллельные стороны называются основаниями трапеции, а две другие — это боковые стороны. Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна, в этом случае параллелограмм является частным случаем трапеции. [8]
1.3. Анализ учебной литературы
Приведем анализ школьных учебников по геометрии на выявление особенностей темы: «Трапеция, вписанная в окружность и трапеция, описанная около окружности».
Особенности изложения темы в учебнике Л.С. Атанасян и др.
Тема: «Трапеция, вписанная в окружность и трапеция, описанная около окружности» не достаточно рассматриваются данными авторами. Авторы в учебнике за 8 класс в параграфе «Вписанная и описанная окружность» дают определение окружности вписанной в многоугольник, и многоугольника описанного около окружности. Доказывается теорема: Около любого треугольника можно описать окружность. На основании, которой авторы приводят замечания, одно из которых:
Доказывается теорема: Около любого треугольника можно описать окружность. На основании, которой авторы приводят замечания, одно из которых:
— не во всякий четырехугольник можно вписать окружность, доказательство которого учащимся предлагается привести самостоятельно.
Авторы предлагают обучающимся в задаче 710 (стр. 187) выполнить доказательство свойства трапеции вписанной в окружность. Так токовые свойства трапеции вписанной в окружность, и трапеции описанной около окружность авторами не рассматриваются и в 9 классе. [10]
Особенности изложения темы в учебнике А.В. Погорелова
Темы: «Трапеция, вписанная в окружность» и «Трапеция, описанная около окружности» не рассматриваются данным автором. Автор дает определение трапеции в разделе за 8 класс и рассматривает ее свойства с доказательством. Но о вписанной трапеции в окружность, и трапеции описанной около окружности он не упоминает и в представленных задачах за 8 класс, а так, же и в разделе за 9 класс. [9]
[9]
Особенности изложения тем в учебнике Г.П. Бевз и др.
Темы: «Трапеция, вписанная в окружность» и «Трапеция, описанная около окружности» не достаточно рассматриваются данными авторами. Авторы в разделе за 8 класс в параграфе «Вписанные и описанные многоугольники» дают определение окружности вписанной в многоугольник, и многоугольника описанного около окружности. Доказывают теоремы:
— Около любого треугольника можно описать окружность, и только одну.
— Во всякий треугольник можно вписать окружность, и только одну.
На основании, которых авторы приводят следствия, одно из которых:
— если четырехугольник вписан в окружность, то сумма его противолежащих углов равна 1800. Если четырехугольник описан около окружности, то суммы длин его противолежащих сторон равны.
Авторы предлагают обучающимся в задаче 803 (стр. 146) выполнить доказательство свойства трапеции вписанной в окружность. Так токовые свойства трапеции вписанной в окружность, и трапеции описанной около окружность авторами не рассматриваются в достаточном объеме. [11]
146) выполнить доказательство свойства трапеции вписанной в окружность. Так токовые свойства трапеции вписанной в окружность, и трапеции описанной около окружность авторами не рассматриваются в достаточном объеме. [11]
Особенности изложения тем в учебнике А.Л. Вернер и др.
Темы: «Трапеция, вписанная в окружность» и «Трапеция, описанная около окружности» не достаточно рассматриваются данными авторами. Автор в учебнике за 8 класс дает определение трапеции в 8 классе и рассматривает ее свойства с доказательством в параграфе «Четырехугольники с параллельными сторонами». Но о вписанной трапеции в окружность, и трапеции описанной около окружности он не упоминает и в представленных задачах за 8 класс, а так, же и в разделе за 9 класс. [12, 13, 14]
Вывод: В учебниках школьного курса геометрии тема «Трапеция» изучается в 8 классе. Вводятся понятия «трапеция», «равнобокая трапеция», «прямоугольная трапеция», «средняя линия трапеции». Так же в учебниках предлагается серия задач по данной теме.
Так же в учебниках предлагается серия задач по данной теме.
Тема «Трапеция, вписанная в окружность и трапеция, описанная около окружности» входит в тему «Вписанные и описанные многоугольники» и рассматривается в учебниках Г.П. Бевз и др., Л.С. Атанасян и др. в 8 классе при решении небольшого количества задач на доказательство.
1.4. Трапеция, вписанная в окружность
На основании определения четырехугольника вписанного в окружность можно сформулировать определение трапеции вписанной в окружность.
Трапеция называется вписанной в окружность, если все вершины ее лежат на одной окружности, которая будет называться описанной около трапеции.
Трапецию можно вписать в окружность, если она равнобокая.
Теорема 3. Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. | |
Доказательство Так как ΔАСD – прямоугольный, вписанный в окружность, то AD – диагональ => | |
Теорема 4. Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции, лежит внутри трапеции. [15] | |
Теорема 5. Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием. [15] | |
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. | |
Использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали В равнобедренном треугольнике AMD углы при основании равны. Внешний угол CMD равен сумме внутренних углов, не смежных с ним: Отсюда: [15] | |
1.5. Трапеция, описанная около окружности
На основании определения четырехугольника описанного около окружности можно сформулировать определение трапеции описанной около окружности.
Трапеция называется описанной около окружности, если все ее стороны касаются одной окружности.
Теорема 6. AL = AK, BL = BM, CM = CF, DF = DK | |
Доказательство Обозначим точки касания буквами L, M, F, K. На основании свойства касательных (Если из какой-нибудь точки провести две касательные к окружности, то их отрезки от данной точки до точек касания равны между собой и центр окружности находится на биссектрисе угла, образованного этими касательными), проведенных к окружности из одной точки, имеем: AL = AK, BL = BM, CM = CF, DF = DK Ч.Т.Д. | |
Теорема 7. Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам. MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности. | |
Доказательство 1) Пусть отрезок КМ – диаметр вписанной окружности в трапецию. d = 2r = KM 2) Проведем высоту трапеции так, чтобы она проходила через центр окружности, тогда высота КМ = МО + ОК. Следовательно, KM = 2r Ч.Т.Д. | |
Теорема 8. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. [15] | |
Теорема 9. Боковая сторона описанной трапеции видна из центра описанной окружности под прямым углом. [15] | |
Доказательство 1) ADC + BCD = 180º (так как сумма внутренних односторонних углов при параллельных прямых AD и ВС и секущей CD) 2) так как точка O — точка пересечения биссектрис углов трапеции, то ODF + OCF = (ADC + BCD) = 90º 3) так как сумма углов треугольника равна 180º, то в ΔCOD COD = 90º Ч. | |
Теорема 10. Если точка касания трапеции описанной около окружности делит боковую сторону на отрезки длиной m и n (CF=m, FD=n), высота трапеции равна ее диаметру, то высоту трапеции можно выразить через длины этих отрезков. [15] | |
Доказательство Точка касания делит боковую сторону на отрезки длиной m и n (CF=m, FD=n). 1) ADC + BCD = 180º (так как сумма внутренних односторонних углов при параллельных прямых AD и ВС и секущей CD) 2) так как точка O — точка пересечения биссектрис углов трапеции, то ODF + OCF = (ADC + BCD) = 90º 3) так как сумма углов треугольника равна 180º, то в ΔCOD COD = 90º 4) таким образом, COD прямоугольный, а OF — высота, проведенная к гипотенузе, CF и FD — проекции катета OC и OD на гипотенузу. Отсюда радиус вписанной в трапецию окружности выражается через длины отрезков, как которые боковая сторона делится точкой касания, как А так как высота трапеции равна ее диаметру, то и высоту трапеции можно выразить через длины этих отрезков: Ч.Т.Д. | |
Теорема 11. Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований. [15] | |
Доказательство Площадь трапеции равна произведению полусуммы ее оснований на высоту: Обозначим CF = m, FD = n. Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
Ч. | |
Таким образом, в первой главе рассмотрели теоретические сведения о трапеции, вписанной в окружность и трапеции, описанной около окружности.
Сведем все основные свойства трапеции (рассмотренные в школьном курсе геометрии и нет) в таблицу.
Трапеция, вписанная в окружность и трапеция, описанная около нее
Трапеция, вписанная в окружность | |
Теорема 3. Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания: [15] | |
Теорема 4. | |
Теорема 5. Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием. [15] | |
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. [15] | |
Использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали В равнобедренном треугольнике AMD углы при основании равны. Отсюда: [15] | |
Трапеция, описанная около окружности | |
Теорема 6. Отрезки касательных, проведенных из одной точки, равны. Отсюда следует, что [15] AL = AK, BL = BM, CM = CF, DF = DK | |
Теорема 7. Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам. MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности. [15] | |
Теорема 8. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. | |
Теорема 9. Боковая сторона описанной трапеции видна из центра описанной окружности под прямым углом. [15] | |
Теорема 10. Если точка касания трапеции описанной около окружности делит боковую сторону на отрезки длиной m и n (CF=m, FD=n), высота трапеции равна ее диаметру, то высоту трапеции можно выразить через длины этих отрезков. [15] | |
Теорема 11. Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований. [15] | |
Глава 2.
Содержание занятий по теме «Трапеция, вписанная в окружность и трапеция, описанная около окружности» в рамках курса по выбору по геометрии для обучающихся 9 классов
В данной главе разработаны содержания занятия по теме: «Трапеция, вписанная в окружность и трапеция, описанная около окружности» в рамках курса по выбору по геометрии для обучающихся 9 классов.
2.1. Пояснительная записка
Организационно-методический раздел
Цель занятий: расширить геометрическое представление обучающихся о вписанной и описанной окружности в трапецию.
Задачи занятий:
1. Расширить знания учащихся связанные со свойствами вписанной трапеции;
2. Расширить знания обучающихся связанные со свойствами описанной трапеции;
3. Овладение дополнительными знаниями при решении заданий уровня повышенной сложности итоговой государственной аттестации;
4. Предоставить обучающимся возможность проанализировать свои способности к математической деятельности.
Требования к подготовке учащихся
В результате проведенных дополнительных занятий по теме: «Вписанная и описанная окружность в трапецию» ученик должен:
Знать/понимать
— понятие математического доказательства, примеры доказательств;
— как используются теоремы и свойства при решении заданий повышенной сложности;
— свойства трапеции вписанной в окружность;
— свойства трапеции описанной около окружности.
Уметь
— проводить сложные доказательства, получать следствия, оценивать логическую правильность рассуждений;
— распознавать геометрические фигуры, различать их взаимное расположение;
— изображать геометрические фигуры; выполнять чертежи по условию задач;
— решать геометрические задачи, опираясь на изученные дополнительные свойства вписанной и описанной трапеции;
— проводить доказательные рассуждения при решении задач, используя теоремы, обнаруживая возможности для их использования.
Количество часов всего – 6 часов (2 часа в неделю, 3 недели).
Самостоятельных работ – 1 час (входная – 0,5 часа, итоговая – 0,5 часа).
Календарно-тематическое планирование
№ п/п | Содержание урока | Количество часов |
1 | Вписанная и описанная окружность в трапецию | 0,5 |
Входная самостоятельная работа | 0,5 | |
2 | Трапеция, вписанная в окружность. | 1 |
3 | Трапеция, описанная около окружности. Решение задач. | 1 |
4 | Трапеция, вписанная и описанная около окружности. Решение задач | 1 |
5 | Трапеция, вписанная и описанная около окружности. Решение задач | 1 |
6 | Трапеция, вписанная и описанная около окружности. | 0,5 |
Итоговая самостоятельная работа | 0,5 |
2. 2. Содержание занятий по теме: «Трапеция, вписанная в окружность и трапеция, описанная около окружности»
2. Содержание занятий по теме: «Трапеция, вписанная в окружность и трапеция, описанная около окружности»
Занятие 1
Тема: Вписанная и описанная окружность в трапецию
Цель: расширение знаний обучающихся о вписанной и описанной трапеции в окружность, ее свойства.
Тип урока: урок закрепления знаний
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
2. Актуализация знаний
Повторение видов четырехугольников, какой четырехугольник можно вписать и описать около окружности, основные свойства вписанной и описанной окружности в трапецию.
Рассмотрение свойств с доказательством.
В
С
Дано:
– трапеция
W – описанная окружность
Доказать: — равнобедренная
А
D
Доказательство.
1) – вписанная трапеция, следовательно
(1)
Так же: (2)
(по свойству углов при параллельных сторонах).
2) Сравниваем (1) и (2) выражения, получаем:
т.е.
, т.е.
Углы при верхнем и нижнем основаниях попарно равны => АВСD – равнобедренная трапеция.
Ч.Т.Д.
Т
Дано:
– трапеция, описанная около окружности
Доказать:
еорема (об описанной трапеции). Около окружности можно описать трапецию тогда и только тогда, когда сумма длин оснований равна сумме длин боковых сторон.
Около окружности можно описать трапецию тогда и только тогда, когда сумма длин оснований равна сумме длин боковых сторон.
Доказательство.
Пусть трапеция описана около окружности.
Точки E, F, G, H – точки касания.
Тогда
Если сложить попарно получим равенство
Ч.Т.Д.
3. Закрепление
Выполнение входной контрольной работы рассчитанной на 15-20 мин.
Входная самостоятельная работа
Задача 1. В равнобедренной трапеции основания 21 и 9 сантиметров, высота — 8 сантиметров. Найти радиус описанной окружности.
Задача 2. Прямоугольная трапеция описана около окружности. Найти радиус этой окружности, если длины оснований трапеции равны a и b.
4. Итог урока
Занятие 2
Тема: Трапеция, вписанная в окружность. Решение задач
Цель: расширение знаний обучающихся о вписанной трапеции в окружность, ее свойств и теорем.
Тип урока: обобщение и систематизация знаний
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
Знакомство с содержанием занятий по теме: «Вписанная и описанная окружность в трапецию»
2. Актуализация знаний
Повторение основных свойств трапеции вписанной в окружность школьного курса геометрии, а так же рассмотрение дополнительных теорем. (Глава 1, п.1.4)
3. Закрепление
Закрепление
Решение задач.
Задача 1. Трапеция с основаниями см и см и диагональю см вписана в окружность. На окружности взята точка K, отличная от точки D, так что см. Найдите длину отрезка AK.
На основании свойства вписанной трапеции .
Из
Из
Если то => равны углы и , что невозможно, так как первый угол меньше второго. Значит, значение 6 не подходит. Остается только 4.
Ответ: 4
Задача 2. В окружности радиуса вписана трапеция с основаниями 2 и 4. Найдите расстояние от центра окружности до точки пересечения диагоналей трапеции.
В данной задаче возможны только 2 случая решения. Первый, когда нижнее основание ниже центра окружности, второй случай, когда нижнее основание выше центра окружности. Третий невозможен, так как большее основание .
Третий невозможен, так как большее основание .
1 случай
Дано:
– вписанная трапеция
Найти: OG
Решение.
Рассмотрим по теореме Пифагора
Рассмотрим по теореме Пифагора
Рассмотрим и
~
2 случай
Дано:
– вписанная трапеция
Найти: OG
Решение.
Рассмотрим по теореме Пифагора
Рассмотрим ΔAFO по теореме Пифагора
Рассмотрим и
~
Ответ:
4. Итог урока
Итог урока
Анализ: В данном занятии применяются Теорема 1, Теорема 3, Теорема 4, Теорема 5.
Занятие 3
Тема: Трапеция, описанная около окружности. Решение задач
Цель: расширение знаний обучающихся об описанной трапеции около окружности, ее свойств.
Тип урока: обобщение и систематизация знаний
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
2. Актуализация знаний
Повторение основных свойств и теорем о трапеции, описанной около окружности школьного курса геометрии, а так же рассмотрение дополнительных и теорем. (Глава 1, п.1.5)
3. Закрепление
Закрепление
Решение задач
Задача 1. В описанной около окружности равнобокой трапеции основания относятся как 3:5. Из вершины меньшего основания опущена высота на большее основание; точка H — основание высоты. Из точки H опущен перпендикуляр HE на боковую сторону трапеции. В каком отношении точка E делит боковую сторону?
1 случай | 2 случай |
Дано:
– равнобокая описанная трапеция около окружности
ВС : AD = 3 : 5
BH – высота
EH ⊥AB
Найти: АЕ : ЕВ = ?
Дано:
– равнобокая описанная трапеция около окружности
ВС : AD = 3 : 5
BH – высота
EH ⊥CD
Найти: DE : ЕC = ?
Решение.
Пусть из вершины В трапеции ABCD опущена высота ВН на основание AD.
Пусть основания равны AD = 5x и ВС = 3х
Суммы противоположных сторон трапеции равны, поэтому
Рассмотри 1 случай.
Точка Е лежит на стороне АВ.
Катет прямоугольного треугольника равен среднему геометрическому между гипотенузой и своей проекцией на гипотенузу:
АН2 = АЕ · АВ, откуда
АЕ : ВЕ = 1: 15
Рассмотрим 2 случай.
Точка Е лежит на стороне CD.
ΔDEH = ΔAHB (по гипотенузе и острому углу)
Поэтому DE = AH = x
CE = CD – DE = 3x
Откуда DE : CE = 1 : 3
Ответ: 1 : 15 и 1 : 3
Задача 2. Периметр трапеции равен 112. Точка касания вписанной в трапецию окружности делит одну из боковых сторон на отрезки, равные 8 и 18 см. Найдите основания этой трапеции.
Периметр трапеции равен 112. Точка касания вписанной в трапецию окружности делит одну из боковых сторон на отрезки, равные 8 и 18 см. Найдите основания этой трапеции.
Дано:
ABCD – трапеция описная около окружности
РABCD = 112
a = 8
b = 18
Найти: ВС и ВD
Решение.
Так как в трапецию вписана окружность, то АВ + СD = BC + AD = 112 : 2 = 56
АВ = а + b = 18 + 8 = 26 =>
CD = 30
Если в трапецию вписана окружность с радиусом r и она делит боковую сторону на отрезки а и b, то
Высота трапеции 2r = 24, тогда ВН = СН = 24
Из ΔАВН по теореме Пифагора
Из ΔНСD по теореме Пифагора
ВС = НН = 56 – ( АН + НD) : 2 = (56 – 28) : 2 = 14
Тогда AD = АН + НН + НD = 10 + 14 + 18 = 42
Ответ: 14 и 42
4. Итог урока
Итог урока
Анализ: В данном занятии применяются Теорема 2, Теорема 7.
Занятие 4
Тема: Трапеция, вписанная и описанная около окружности. Решение задач
Цель: расширение знаний обучающихся о вписанной и описанной трапеции около окружности, ее свойств и теорем.
Тип урока: обобщение и систематизация знаний
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
2. Актуализация знаний
Повторение основных свойств трапеции вписанной и описанной около окружности школьного курса геометрии, а так же применение рассмотренных дополнительных теорем. (Глава 1, п. 1.4, п.1.5)
1.4, п.1.5)
3. Закрепление
Решение задач
Задача 1. Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25. Найдите высоту трапеции.
Дано:
ABCD – трапеция
BC = 14
AD = 40
R = 25
Найти: h
Решение.
Трапеция вписана в окружность, поэтому она равнобедренная.
Пусть ВС = 14 – хорда окружности радиуса 25. Существует две хорды, параллельные BC и равные 40. Соответственно, в окружность можно вписать две трапеции с основаниями 14 и 40.
Центр O на серединном перпендикуляре к BC.
1 случай.
В трапеции ABCD центр О окружности лежит внутри трапеции.
В этом случае высота EF = EO + OF
Из прямоугольного ΔАОЕ, в котором АО = 25
по теореме Пифагора, получаем
Из прямоугольного ΔВFO, в котором BО = 25
по теореме Пифагора, получаем
Тогда EF = EO + OF = 39
2 случай.
В трапеции A1BCD1 центр О окружности лежит вне трапеции.
Аналогично, находим
Ответ: 39 и 9
Задача 2. На основании ВС трапеции АВСD взята точка Е, лежащая на одной окружности с точками А, С и D. Другая окружность проходящая через точки А, В, и С, касается прямой CD. АВ=12, ВЕ : ЕС = 4 : 5.
а) Докажите, что треугольник АСD подобен треугольнику АВЕ.
б) Найдите ВС.
Дано:
АВСD – трапеция
Е ϵ ВС
АВ = 12
ВЕ : ЕС = 4 : 5
а) Доказать: ΔACD ~ ΔABE
б) Найти: ВС
Решение.
Рассмотрим АЕСD – равнобедренную трапецию вписанную в окружность =>
АЕС + ADC = 1800
Значит, угол ВЕА, смежный с углом АЕС, равен углу АDС
Опишем окружность около ΔАВС.
По условию CD касается окружности, а значит СD ⊥ OC, где О – центр окружности.
Угол между хордой АС и касательной CD равен половине дуги АС второй окружности.
Половине этой же дуги равен вписанный АВС. Найдена вторая пара равных углов. Найдя две пары равных углов, мы доказали подобие треугольников АСD и АВЕ.
Из подобия следует равенство третьей пары углов, ВАЕ = САD
Кроме того равны дуги АЕ и СD, заключенные между параллельными прямыми ЕС и АD
Вписанный CAD равен половине дуги CD, а значит, ВАЕ равен половине дуги АЕ.
ВАЕ – это угол между хордой АЕ и прямой АВ, проходящей через конец хорды А. Значит прямая АВ – касательная ко второй окружности.
Воспользуется свойством секущей и касательной, проведенных к окружности из точки В.
ВА2 = ВЕ · ВС
122 = (4х) · (9х)
36х2 = 144
х2 = 4
х = 2
ВС = 9х = 9 · 2 = 18
Ответ: 18
4. Итог урока
Итог урока
Анализ: В данном занятии применяются Теорема 1, Теорема 4, Теорема 5.
Занятие 5.
Тема: Трапеция, вписанная и описанная около окружности. Решение задач
Цель: расширение знаний обучающихся о вписанной и описанной трапеции около окружности, ее свойств.
Тип урока: обобщение и систематизация знаний
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
2. Актуализация знаний
Повторение основных свойств трапеции вписанной и описанной около окружности школьного курса геометрии, а так же применение рассмотренных дополнительных свойств. (Глава 1, п.2.1, п.2.2)
(Глава 1, п.2.1, п.2.2)
3. Закрепление
Решение задач
Задача 1. Окружность, вписанная в равнобедренную трапецию с основаниями а и b. Найдите диагональ трапеции.
Дано:
АВСD – равнобедренная трапеция
AD = b
BC = a
Найти: BD
Решение.
Пусть окружность с центром О, вписанная в равнобедренную трапецию АВСD, касается боковой стороны АВ в точке М, а оснований ВС и АD – в точке N и L соответственно.
Поскольку ОМ – высота прямоугольного ΔАОВ, опущенная из вершины прямого угла, то
Опустим перпендикуляр ВН на AD. Тогда
Из прямоугольного ΔBHD находим, что
Ответ:
Задача 2. Трапеция с высотой h вписана в окружность. Боковая сторона трапеции видна из центра окружности под углом 1200. Найдите среднюю линию трапеции.
Трапеция с высотой h вписана в окружность. Боковая сторона трапеции видна из центра окружности под углом 1200. Найдите среднюю линию трапеции.
Дано:
АВСD – трапеция
АОВ = 1200
Найти: среднюю линию трапеции
Решение.
Пусть О – центр окружности, описанной около трапеции АВСD с основаниями AD > BC. Трапеция АВСD – равнобедренная, поэтому
Пусть СК – высота трапеции, тогда АК = h·ctg600 = ,
а так как трапеция равнобедренная, то отрезок АК равен ее средней линии.
Ответ:
Задача 3. Около окружности описана равнобедренная трапеция АВСD. Боковые стороны АВ и СD касаются окружности в точках М и N, К – середина АD. В каком отношении прямая ВК делит отрезок МN?
Дано:
АВСD – равнобедренная трапеция
М ϵ АВ
N ϵ СD
AK = KD
Найти: МР : РN = ?
Решение.
Обозначим х = АК, у = ВF, где F – середина ВС. Пусть Q – точка пересечения KF и MN, а Р – точка пересечения MN и ВК. Тогда
АМ = АК = х, ВМ = ВF = у
и Q – середина MN.
Поскольку MN параллельно основаниям трапеции, треугольник ВМР подобен треугольнику ВАК, а треугольник КРQ подобен треугольнику КВF. Поэтому
, значит, РМ = PQ и PM = MN =>
Ответ: 1 : 3
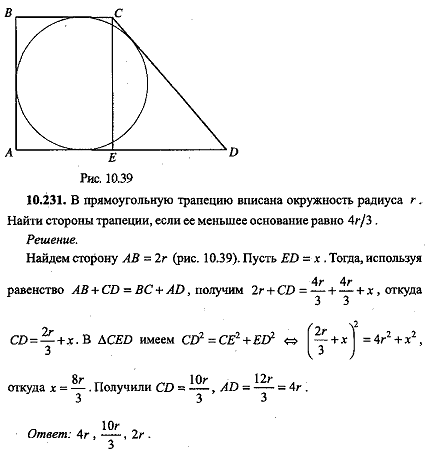
Задача 4. В прямоугольной трапеции меньшее основание равно высоте, а большее основание равно а. Найдите боковые стороны трапеции, если известно, что одна из них касается окружности, проходящей через концы меньшего основания и касающееся большего основания.
Дано: АВСD – прямоугольная трапеция
АВ = ВС
AD = a
Найти: AB, CD
Решение.
Обозначим меньшее основание ВС и меньшую боковую сторону трапеции АВСD через х. Пусть М – точка касания окружности с большим основанием AD. Тогда точка М лежит на серединном перпендикуляре к отрезку ВС, поэтому
Тогда точка М лежит на серединном перпендикуляре к отрезку ВС, поэтому
Пусть К – проекция вершины С на AD. Тогда KD = a – x, CK = x
По теореме Пифагора
Отсюда находим, что
Тогда
Ответ:
Задача 5. В равнобедренной трапеции с острым угломпри основании окружность, построенная на боковой стороне как на диаметре, касается другой боковой стороны. В каком отношении она делит большее основание трапеции?
Дано:
АВСD — равнобедренная трапеция
BAD = ADC =
Найти: АК : КD
Решение.
Пусть О – центр окружности (середина боковой стороны АВ трапеции АВСD), ОР – средняя линия трапеции, К – точка пересечения указанной окружности с большим основанием AD. Тогда ВК – перпендикуляр к AD и . Если М – точка касания окружности с боковой стороной CD, то
Если М – точка касания окружности с боковой стороной CD, то
Следовательно,
Ответ: sin2
4. Итог урока
Анализ: В данном занятии применяются Теорема 1, Теорема 3, Теорема 4, Теорема 6, Теорема 7, Теорема 8, Теорема 9, Теорема 10, Теорема 11
Занятие 6.
Тема: Итоговое занятие.
Цель: проверка усвоения знаний обучающихся по теме курса «Вписанная и описанная окружность в трапецию»
Тип урока: закрепление
Оборудование: циркуль, линейка
Ход урока
1. Организационный момент
Обучающиеся и учитель приветствуют друг друга стоя.
Сообщение темы и цели урока
2. Закрепление
Закрепление
Обучающимся предлагается, ответит на вопросы (устно):
1. Вопрос: Определение четырехугольника?
Ответ: Четырёхугольник — это геометрическая фигура (многоугольник), которая состоит из четырёх точек (вершин), три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки.
2. Вопрос: Виды четырехугольников?
Ответ: Виды четырехугольников:
— параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
— прямоугольник — четырёхугольник, у которого все углы прямые;
— ромб — четырёхугольник, у которого все стороны равны;
— квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
— трапеция — четырёхугольник, у которого две противоположные стороны параллельны.
3. Вопрос: Какая окружность называется вписанной в четырехугольник? Какой четырехугольник называется описанным около окружности?
Вопрос: Какая окружность называется вписанной в четырехугольник? Какой четырехугольник называется описанным около окружности?
Ответ: Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности, которая будет называться описанной вокруг четырехугольника. Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник.
4. Вопрос: В какой четырехугольник можно вписать окружность?
Ответ: Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы его длин противоположных сторон равны. а + с = b+ d
5. Вопрос: Около какого четырехугольника можно описать окружность?
Ответ: Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны 180.
6. Вопрос: Можно ли описать окружность около трапеции?
Ответ: Вписать в окружность можно только равнобокую трапецию.
7. Вопрос: Можно ли вписать окружность в трапецию?
Ответ: Если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон. АВ + CD = AD + BC
8. Вопрос: Какими свойствами обладает трапеция, вписанная в окружность?
Ответ: 1) Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
2) Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции, лежит внутри трапеции.
3) Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
9. Вопрос: Какими свойствами обладает трапеция, описанная около окружности?
Ответ: 1) Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.
MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию
окружности.
2) Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
3) Боковая сторона описанной трапеции видна из центра описанной окружности под прямым углом.
4) Высота трапеции равна ее диаметру, то высоту трапеции можно выразить через длины этих отрезков.
Самостоятельная работа
Выполнение итоговой самостоятельной работы для обучающихся предлагается в виде выполнения теста.
1. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
2. В четырехугольник можно вписать окружность, если __________________________________________________________.
3. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
а) AB + BC = AD + CD
б) AB + CD = BC + AD
в) AB + AD = BC + CD
г) AD·BC = AB·CD
4. Вписанная в четырехугольник окружность изображена на рисунке:
Вписанная в четырехугольник окружность изображена на рисунке:
5. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
а)
б) AB+CD=BC+AD
в)
г) AD·BC=AB·CD
6. Описанная около четырехугольника окружность изображена на рисунке:
7. В любом описанном четырехугольнике суммы длин противолежащих сторон:
а) равны между собой
б) равны радиусу окружности
в) равны диаметру окружности
г) равны периметру
8. Углы А, В и С четырехугольника ABCD относятся как 1 : 2 : 3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
а) 1350 б) 1200 в) 900 г) 600
9. Трапеция описана около окружности. Чему равен ее периметр, если средняя линия равна 7 см?
а) 25 см б) 28 см в) 30 см г) 32 см
10. Чему равна площадь прямоугольной трапеции с тупым углом, равным 1500, если радиус вписанной в него окружности равен 2?
Чему равна площадь прямоугольной трапеции с тупым углом, равным 1500, если радиус вписанной в него окружности равен 2?
а) 18 б) 20 в) 22 г) 24
11. Выпуклый четырехугольник АВСD вписан в окружность. При этом величины углов АВС и ВСD соответственно равны 700 и 600. Тогда величина угла ВАD равна:
а) 1200 б) 1100 в) 650 г) 500
Заключение
В настоящей работе по теме: «Содержание занятий по теме: «Вписанная и описанная окружность в трапецию» в рамках курса по выбору по геометрии для обучающихся 9 классов» в первой главе приведены основные теоретические сведения темы исследования, основные свойства и теоремы сведены в таблицу. Проанализированы учебники школьного курса геометрии для обучающихся в 7, 8, 9-х классах, на основании, которых сделан вывод, что темы: «Трапеция, вписанная в окружность» и «Трапеция, описанная около окружности» не достаточно рассматриваются в школьном курсе геометрии в 7, 8, 9-х классах для решения задач повышенной сложности.
Во второй главе работы приведены разработки содержания 6 занятий по теме исследования; разработаны входящая и итоговая самостоятельные работы. В приложениях приведены решения данных работ.
Результаты работы могут быть использованы в рамках курса по выбору на дополнительных занятиях по геометрии или для подготовки к итоговой государственной аттестации, так как при проведении государственной итоговой аттестации среди 9-х классов общеобразовательных школ в части С геометрии часто встречается задание по теме «Трапеция вписанная в окружность или трапеция описанная около окружности».
Таким образом, поставленные задачи выполнены, цель достигнута.
Литература
1. http://nsportal.ru/ap/drugoe/library/referat-znachenie-geometrii-v-zhizni-lyudei
2. http://www.kniga.es/articles/article637.shtml
3. http://ru.wikipedia.org/wiki /%D7%E5%F2%FB%F0%B8%F5%F3%E3%EE%EB
4. http://free.megacampus.ru/xbookM0005/index.html ?go=part-021*page.htm
5. http://ege- study.ru/materialy-ege/vpisannyj-i-opisannyj-chetyrexugolniki-i-ix-svojstva /
6. http://free.megacampus.ru/xbookM0001/index.html ?go=part-034*page.htm
7. http://otvet.mail.ru/question/47745330
8. http://www.smekalka.pp.ru/node/1586
9. Погорелов А.В., Геометрия: Учебник для 7-11 классов средних школ – 2-е издание – М.: Просвещение, 1991 – 384 с.
10 Атанасян Л.С. и др., Геометрия 7-9 классы: учебник для общеобразовательных учреждений / [Л.С. Атанасян, В.Ф. Бутусов, С.Б. Кадомцев и др.] – 21-е издание – М.: Просвещение, 2011 – 384 с.
11. Бевз Г.П., Геометрия: Учебник для 7-11 классов средних школ / Г.П. Бевз, В.Г. Бевз, Н.Г. Владимирова. – М.: Просвещение, 1992 – 352 с.
12. Вернер А.Л. и др., Геометрия: Учебник для 7 класса общеобразовательных учреждений / А.Л. Вернер, В.И. Рыжик, Т.Г. Ходот. – М.: Просвещение, 1999 – 192 с.
13. Вернер А.Л. и др., Геометрия: Учебное пособие для 8 класса общеобразовательных учреждений / А.Л. Вернер, В.И. Рыжик, Т.Г. Ходот. – М.: Просвещение, 2001 – 192 с.
14. Вернер А.Л. и др., Геометрия: Учебное пособие для 9 класса общеобразовательных учреждений / А.Л. Вернер, В.И. Рыжик, Т.Г. Ходот. – М.: Просвещение, 2001 – 207 с.
15. http://www.uznateshe.ru/trapetsiya-vpisana-v-okruzhnost/
16. http:// www.alexlarin.narod.ru
17. Корянов А.Г. Математика. ЕГЭ 2010. Задания типа С4. Многовариантные задачи по планиметрии http://www.alexlarin.narod.ru/ege/2010/C4a
gk.pdf
18. Созоненко Р.С., Теоремы и задачи по планиметрии с перекрестными ссылками. – 2-е издание, исправлено и дополнено – Новосибирск: Издательство ИМ СО РАН, 1998 – 209 с.
19. Гордин Р.К., ЕГЭ 2012 Математика. Решение задач С4. – М.: МЦНМО, 2012 – 328 с.
20. Никитин Н.Н., Геометрия: Учебник для 6-8 классов / Н.Н. Никитин. – М.: Просвещение, 1971 – 209 с.
Приложение 1
Входная самостоятельная работа
Задача 1. В равнобедренной трапеции основания 21 и 9 сантиметров, высота — 8 сантиметров. Найти радиус описанной окружности.
Дано:
ABCD – равнобедренная трапеция
ВС = 9 см
AD = 21 см
h = 8 см
Найти: R
Решение.
Пусть EF – серединный перпендикуляр c основаниями EF , тогда О – центр окружности лежит на прямой EF.
ОА = ОВ = R.
О делит EF на две части: пусть OF = х, тогда OE = 8-х.
По теореме Пифагора получаем,
АО2 = АF2 + FО2
ОВ2 = ВE2 + EО2.
Так как ОА2 = ОВ2, получим:
АF2 + FО2 = ВE2 + EО2
Ответ: 10,625 см
Задача 2. Прямоугольная трапеция описана около окружности. Найти радиус этой окружности, если длины оснований трапеции равны a и b.
Дано:
АВСD – прямоугольная трапеция
АВ = а
АD = b
Найти: r
Решение.
Пусть r – радиус окружности вписанной в трапецию ABCD.
Так как трапеция прямоугольная, то АВ = 2r.
Так как трапеция описана около окружности, то AD + BC = AB + CD.
Тогда а + b = 2r + CD.
CD = a + b – 2r
Пусть СЕ – высота, тогда СЕ ⊥ АD и СЕ = АВ = 2r.
ED = b – a.
По теореме Пифагора для треугольника ЕСD имеем
СD2 = CE2 + ED2
или
(а + b – 2r)2 = 4r2 + (b – a)2
Ответ:
Приложение 2
Итоговая самостоятельная работа
1. Вокруг четырехугольника можно описать окружность, если (суммы его противоположных углов равны 180, )
2. В четырехугольник можно вписать окружность, если (суммы его длин противоположных сторон равны, а + с = b+ d)
3. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:
а) AB + BC = AD + CD
б) AB + CD = BC + AD
в) AB + AD = BC + CD
г) AD·BC = AB·CD
Ответ: б)
4. Вписанная в четырехугольник окружность изображена на рисунке:
Ответ: б)
5. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
а)
б) AB+CD=BC+AD
в)
г) AD·BC=AB·CD
Ответ: в)
6. Описанная около четырехугольника окружность изображена на рисунке:
Ответ: в)
7. В любом описанном четырехугольнике суммы длин противолежащих сторон:
а) равны между собой
б) равны радиусу окружности
в) равны диаметру окружности
г) равны периметру
Ответ: а)
8. Углы А, В и С четырехугольника ABCD относятся как 1 : 2 : 3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
а) 1350 б) 1200 в) 900 г) 600
Ответ: в)
9. Трапеция описана около окружности. Чему равен ее периметр, если средняя линия равна 7 см?
а) 25 см б) 28 см в) 30 см г) 32 см
Ответ: б)
10. Чему равна площадь прямоугольной трапеции с тупым углом, равным 1500, если радиус вписанной в него окружности равен 2?
а) 18 б) 20 в) 22 г) 24
Ответ: г)
11. Выпуклый четырехугольник АВСД вписан в окружность. При этом величины углов АВС и ВСД соответственно равны 700 и 600. Тогда величина угла ВАД равна:
а) 1200 б) 1100 в) 650 г) 500
Ответ: а)
Задание №1207. Тип задания 16. ЕГЭ по математике (профильный уровень)
а) План решения.
1. Сделаем чертёж, считая для определённости, что AD>BC (для пункта а) это не имеет значения).
2. Заметим, что трапеция равнобедренная. Обозначим одну из сторон трапеции какой-либо буквой, выразим остальные стороны.
3. Выразим через ту же букву радиус окружности, описанной около трапеции: это можно сделать по теореме синусов для \triangle ABD.{\circ}, равен половине гипотенузы). Отсюда \frac{O_1N}x=\frac{2O_1N}{O_1N-x} , \frac1x =\frac2{O_1N-x} , O_1N-x=2x, x= \frac13 O_1N= \frac13\cdot \frac12 MN= \frac16\cdot \frac {a\sqrt 3} 2= \frac{a\sqrt 3}{12} , x=\frac{a\sqrt 3}{12} , то есть O_2T=\frac{a\sqrt 3}{12}.
3. \frac{CD}{O_2T} = \frac a{\left( \dfrac{a\sqrt 3}{12} \right)} = 4\sqrt 3.
| ФГКОУ «МКК «Пансион воспитанниц МО РФ» «УТВЕРЖДАЮ» Руководитель отдельной дисциплины (математика, информатика и ИКТ) Ю. В. Крылова _____________ «___» _____________ 2015 г. «Трапеция и ее свойства» Методическая разработка преподавателя математики Шаталиной Елены Дмитриевны
Москва 2015 год Оглавление Введение 2
. 10. Заключение . Список используемой литературы Приложение
Введение Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими. Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию. Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства. В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии. Трапеция.
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна). Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны. Если боковые стороны равны, трапеция называется равнобедренной. Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Расстояние между основаниями называется высотой трапеции. 2. Свойства равнобедренной трапеции
3. Диагонали равнобедренной трапеции равны. 4. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
10. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.
Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Е 4. Свойства вписанных и описанных трапеций
2.Если в равнобедренную трапецию можно вписать окружность, то сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции. 4. Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.
1 0. Если окружность построена на меньшем основании трапеции как на диаметре, проходит через середины диагоналей и касается нижнего основания, то углы трапеции 30°, 30°, 150°, 150°. 5. Средние величины в трапеции Среднее геометрическое
b ˂ h ˂ g ˂ m ˂ s ˂ a 6.Свойства произвольной трапеции 1. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой. 2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне. 3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.
5. При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.е. имеют равные площади). 6.Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.
7 8. Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки. 9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам. 7. Признаки трапеции
8. Дополнительные построения в трапеции 1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции. 3. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции. 5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию. 6 7.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции. 8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне. 9. Биссектриса угла трапеции отсекает равнобедренный треугольник. 1 0. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам. 11. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам. 12. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники. 9. Площадь трапеции 1. Площадь трапеции равна произведению полусуммы оснований на высоту S = ½(a + b)•h или П 2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
10. Заключение ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ? Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться. Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции. Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции. Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина. Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих. В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас. Список используемой литературы
Приложение 1.Доказательство некоторых свойств трапеции. 1. Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках K и L. Доказать, что если основания трапеции равны а и b, то длина отрезка KL равна среднему геометрическому оснований трапеции. Доказательство Пусть О — точка пересечения диагоналей, AD = а, ВС = b. Прямая KL параллельна основанию AD, следовательно, KО║ AD, треугольники ВKО и BAD подобны, поэтому
( 2 ) Подставим ( 2 ) в ( 1 ), получим KO = Аналогично LO = Тогда K L= KO + LO =
Д K окажем, что эта прямая делит основания пополам. Обозначим ВМ = х, МС = у, AN = и, ND = v. Имеем:∆ВКМ ~ ∆AKN → x
C Y O v u N D ∆CMO ∆ANO поэтому . Перемножая полученные равенства, получим , откуда следует x=y, но тогда и u = v.
3. Задачи по теме «Трапеция» повышенной сложности. Садовничий Ю.В. «Математика. Подготовка к ЕГЭ», Москва, ИЛЕКСА, 2011, стр. 252. 1 . В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найти площадь трапеции. Ответ: S = 6. 2. Периметр равнобочной трапеции, описанной около круга, равен р. Найти радиус этого круга, если известно, что острый угол при основании трапеции равен ɑ. psina Ответ: 1и 7.
Ответ: S= 3ab В трапеции PQRS длина основания QR равна 10, длина диагонали QS равна 19, а величина угла QSP равна 30°. Выяснить, что больше, длина основания QR или длина стороны RS. Ответ: RS > QR.
Ответ: S=90√3. Иванов А.А., Иванов А.П., Математика: Пособие для подготовки к ЕГЭ и поступлению в вузы. – М.: Издательство МФТИ, 2003, стр. 238.. 12. Площадь прямоугольной трапеции равна S, острый угол равен а. Найти высоту трапеции, если ее меньшая диагональ равна большему оснозанию. [√2Sctg а]
[arccos(l — 1/к), π — arccos(l — 1/к), к > 1]
[√Stg(½ ɑ)]
4. Проверочный тест по теме «Трапеция» В трапеции, имеющей прямой угол, основания равны 5 и 11, а большая диагональ √185. Площадь трапеции составляет В трапеции боковые стороны и меньшее основание равны Ь, а острый угол вдвое меньше тупого. Площадь трапеции равна 151 в равнобедренной трапеции, описанной около окружности радиуса 5 м и имеющей основание 20 м, другое основание равно Меньшее основание трапеции, вписанной в окружность, втрое меньше большего, которое является диаметром окружности.25j В трапеции с диагональю 20, высотой 12 и площадью 150 вторая диагональ равна 29j Равнобедренная трапеция с острым углом а описана около окруж- ности. Отношение ее большего основания к меньшему равно Зо| В описанной около круга равнобочной трапеции расстояние от центра круга до дальней вершины трапеции втрое больше, чем до ближней. Тангенс острого угла трапецииравен Достарыңызбен бөлісу: |
Планиметрия. 150 задач для подготовки к ЕГЭ. Часть 2
Планиметрия. 150 задач для подготовки к ЕГЭ
Задачи 51-100
задачи 1-50, задачи 101-150
- В треугольник АВС вписана окружность, радиус которой равен 4. Определите стороны АВ и АС, если ВС = 15, а высота BD = 12. ответ: 13; 14
- В треугольнике ABC, стороны AB и BC которого равны, проведены высоты BD и AE. Радиусы окружностей, вписанных в треугольники ABD и AEC, равны соответственно 10 и 12. Найдите радиус окружности, вписанной в треугольник ABC. ответ: 15
- Площадь прямоугольного треугольника равна 5, а периметр равен 2. Найдите длину перпендикуляра, опущенного из вершины прямого угла на гипотенузу. ответ: 5/3
- Радиус окружности, вписанной в прямоугольный треугольник, равен 3, а площадь треугольника равна 84. Найдите катеты треугольника. ответ: 7; 24
- Радиус вписанной в треугольник окружности равен 2, а одна из точек касания делит сторону треугольника на отрезки 3 и 4. Найдите площадь треугольника. ответ: 21
- Площадь треугольника равна 84, одна из его сторона равна 13, а радиус вписанной окружности равен 4. Найдите две другие стороны треугольника. ответ: 14; 15
- Периметр прямоугольного треугольника равен 90, а радиус вписанной окружности равен 4. Найдите катеты треугольника. ответ: 9; 40
- Длины боковых сторон трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит ее на две части, отношение площадей которых равно 5/11. Найдите длины оснований. ответ: 1; 7
- В равнобедренной трапеции основания равны 21 и 9, и высота равна 8. Найдите радиус описанной окружности. ответ: 85/8
- Дана равнобедренная трапеция, средняя линия которой равна 9, площадь равна 54 и диагонали перпендикулярны боковым сторонам. Найдите основания трапеции. ответ: 5; 13
- В равнобедренной трапеции боковая сторона равна , а диагональ, равная , делит площадь трапеции в отношении 3:5. Найдите основания трапеции. ответ:
- Найдите диагональ и боковую сторону равнобедренной трапеции с основаниями 20 и 12, если известно, что центр описанной окружности лежит на большем основании. ответ:
- Найдите радиус окружности, вписанной в равнобедренную трапецию, если ее большее основание равно , а угол при большем основании равен 60о. ответ:
- В трапеции ABCD отрезки AB и DC являются основаниями. Диагонали трапеции пересекаются в точке Е. Найдите площадь треугольника BCE, если АВ = 30, DC = 24 и AD = 3, а угол при большем основании DAB равен 60о. ответ:
- Большее основание трапеции равно 24. Найдите меньшее основание, если расстояние между серединами диагоналей равно 4. ответ: 16
- Диагонали прямоугольной трапеции взаимно перпендикулярны, и большая из них точкой пересечения делится на отрезки, равные 36 и 64. Найдите основания трапеции. ответ: 45; 80
- В трапеции, основания которой равны и , проведена через точку пересечения диагоналей прямая, параллельная основаниям. Найдите длину отрезка прямой, отсекаемого от нее боковыми сторонами трапеции. ответ:
- Площади треугольников, образованных отрезками диагоналей трапеции с ее основаниями, равны и . Найдите площадь трапеции. ответ:
- Основание АВ трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали равна , а длина боковой стороны BC равна . Найдите площадь трапеции. ответ:
- В равнобедренную трапецию вписан круг. Одна из боковых сторон делится точкой касания на отрезки и . Определите площадь трапеции. ответ:
- В окружность вписана трапеция, боковая сторона которой равна 15, средняя линия равна 16 и большее основание является диаметром окружности. Найдите площадь трапеции. ответ: 192
- Вычислите площадь трапеции по разности оснований, равной 14, и двум непараллельным сторонам, равным 13 и 15, если в трапецию можно вписать окружность. ответ: 168
- Найдите длину отрезка прямой, параллельной основаниям трапеции и делящей трапецию на две равновеликие фигуры, заключенного между боковыми сторонами трапеции. Основания трапеции равны и . ответ:
- В равнобедренную трапецию вписана окружность радиуса . Верхнее основание трапеции в два раза меньше ее высоты. Найдите площадь трапеции. ответ:
- Около окружности, радиус которой равен 10, описана равнобедренная трапеция. Расстояние между точками касания окружности с боковыми сторонами трапеции равно 12. Найдите боковую сторону трапеции. ответ: 100/3
- Средняя линия трапеции равна 10 и делит площадь в отношении 3 : 5. Найдите основания трапеции. ответ: 5; 15
- Около окружности описана трапеция, боковые стороны которой равны 13 и 15, а площадь равна 168. Найдите основания трапеции. ответ: 7; 21
- В трапеции основания равны 5 и 15, а длины диагоналей равны 12 и 16. Найдите площадь трапеции. ответ: 96
- Найдите площадь равнобедренной трапеции, у которой основания равны 10 и 26, а диагонали перпендикулярны боковым сторонам. ответ: 216
- Средняя линия равнобедренной трапеции равна 5. Известно, что в трапецию можно вписать окружность. Средняя линия делит трапецию на две части, отношение площадей которых равно 7 : 13. Найдите высоту трапеции. ответ: 4
- Площадь равнобедренной трапеции, описанной около круга, равна . Найдите среднюю линию трапеции, если острый угол при ее основании равен . ответ:
- В треугольник, стороны которого равны 39, 60 и 63, вписана окружность, и к окружности проведена касательная, параллельная большей боковой стороне треугольника. Найдите площадь полученной трапеции. ответ: 1078
- В равнобедренный треугольник ABC (AB = BC) вписана окружность. Прямая, параллельная стороне АВ и касающаяся окружности, пересекает сторону АС в точке М, причем 5MC = 2AC. Найдите радиус окружности, если периметр треугольника АВС равен 20. ответ:
- Около круга радиуса 2 описана равнобедренная трапеция с острым углом 30о. Найдите среднюю линию трапеции. ответ: 8
- Внутри треугольника ABC с прямым углом B взята точка D так, что площади треугольников ABD и BDC соответственно в три и четыре раза меньше площади треугольника ABC. Отрезки AD и DC равны соответственно и . Найдите BD. ответ:
- В треугольник вписана окружность радиуса 3. Вычислите стороны треугольника, если одна из них разделена точкой касания на отрезки с длинами 3 и 4. ответ: 7; 24; 25
- Длина одного из катетов прямоугольного треугольника равна 12. Расстояние от центра описанной около треугольника окружности до этого катета равно 2,5. Найдите длину гипотенузы. ответ: 13
- Вокруг окружности описана трапеция, средняя линия которой равна 5, а синус острого угла при основании равен 0,8. Найдите площадь трапеции. ответ: 20
- Средняя линия трапеции равна 10 и делит площадь в отношении 3 : 5. Найдите основания трапеции. ответ: 15; 5
- В равнобедренную трапецию, основания которой равны 2 и 8, вписан круг. Найдите радиус этого круга. ответ: 2
- В равнобедренной трапеции средняя линия равна 5, а диагонали взаимно перпендикулярны. Найдите площадь трапеции. ответ: 25
- В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6. Найдите радиусы кругов. ответ: 15/2
- Две равные окружности радиуса пересекаются. В общую часть обоих кругов вписан квадрат. Найдите сторону этого квадрата, если расстояние между центрами окружностей равно . ответ:
- В окружности перпендикулярно диаметру АВ проведена хорда CD. Точка их пересечения делит диаметр на отрезки 18 и 32. Найдите CD. ответ: 48
- Две окружности радиусов и касаются внешним образом. Найдите расстояние от точки касания до их общей внешней касательной. ответ:
- Внутри круга, радиус которого равен 13, дана точка М, отстоящая от центра круга на 5. Через точку М проведена хорда АВ, равная 25. Найдите произведение длин отрезков, на которые хорда АВ делится точкой М. ответ: 144
- В прямоугольном треугольнике АВС к гипотенузе проведена высота СD. Угол В равен 60о, отрезок BD равен 1. Найдите гипотенузу. ответ:7
- В равнобедренной трапеции диагональ длины образует угол с основанием. Найдите площадь трапеции. ответ:
- На сторонах AB, BC и AD параллелограмма ABCD взяты точки K, M и T таким образом, что AK : KB = 2 : 1, BM : MC = 1 : 1 и AT : TD = 1 : 3. Найдите отношение площадей треугольников KBT и BMT. ответ: 1 : 6
- На гипотенузе KM прямоугольного треугольника KTM расположен центр О окружности, которая касается катетов TK и TM в точках A и B соответственно. Найдите AK, если BM = 23/16, AK : AC = 5 : 23, где точка С — точка пересечения окружности с KM, лежащая между точками О и M. ответ: 6/23
Метки геометрия, ЕГЭ, задачи. Смотреть запись.
|
Задания для самостоятельной работы
ОГЭ Задание № 17 Вписанные и описанные четырёхугольники
Задания для самостоятельной работы
Читайте также: Рекомендуемые страницы:
Поиск по сайту |
Поиск по сайту: |
Свойства прямоугольной трапеции
В данной статье мы расскажем Вам о свойствах прямоугольной трапеции, как обычной, так и той, в которую вписана окружность.
Для начала напомним некоторые основные определения.
Трапеция – это четырехугольник, имеющий 2 параллельные друг другу стороны, причем 2 другие стороны параллельными не являются.
Прямоугольная трапеция — это такая трапеция, одна из боковых сторон которой перпендикулярна ее основаниям (изображена на рис.).
Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон фигуры (на рис. EF).
Основные свойства прямоугольной трапеции
- Средняя линия EF равна половине суммы ее оснований BC и AD.
- Средняя линия EF параллельна основаниям трапеции BC и AD.
- На одной прямой размещаются:
- точка пересечения (H) диагоналей прямоугольной трапеции AC и BD;
- точка пересечения (E) продолжений боковых сторон трапеции AB и CD;
- середины (F и G) оснований трапеции BC и AD.
Свойства прямоугольной трапеции, в которую вписана окружность
- Если в прямоугольную трапецию вписана окружность, это значит, что сумма ее оснований и сумма ее боковых сторон равны.
- Площадь трапеции ABCD можно найти, перемножив длины ее оснований BC и AD.
S
ABCD = BC * AD - Четырехугольник, вершинами которого являются центр вписанной окружности (O), одна из вершин трапеции (A или B), а также точки 2 касания (M и E или M и К), является квадратом.
Узнать подробнее о свойствах трапеции с прямым углом, в которую вписана окружность, а также ознакомиться с доказательствами этих свойств, можно на сайте uznateshe.ru.
Понравилась статья, расскажите о ней друзьям:
Скорее всего, Вам будет интересно:
27. Окружность. Круг. Вписанные и описанные многоугольники
Отрезки касательных к окружности, проведенные из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
а, b — касательные,
Решение: 2.
а) R=5 см, AD=8 см, ВС=6 см. б) R=10 см, AD=16 см, ВС=12 см.
Решение:
а) Возможны два случая: хорды лежат по одну сторону от центра окружности и по разные. Рассмотрим оба.
О1О2— расстояние между хордами.
1) Рассмотрим треугольник ВОС — равнобедренный (ОВ=ОС=R), следовательно ОО2 является высотой и медианой и СО2=ВО2=ВС:2=3 см. По теореме Пифагора найдем ОО2: ОО22=ОС2-СО22=25-9=16, ОО2=4 см.
2) Рассмотрим треугольник АОD — равнобедренный (ОD=ОA=R), следовательно ОО1 является высотой и медианой и AО1=DО1=AD:2=4 см. По теореме Пифагора найдем ОО1: ОО12=ОA2-AО12=25-16=9, ОО1=3 см.
3) В случае, когда хорды лежат по одну сторону от центра О1О2=4-3=1 см.
В случае, когда хорды лежат по разные стороны от центра, то О1О2=4+3=7 см.
Ответ: 1 см или 7 см.
5. а) В равнобедренном треугольнике угол при вершине равен 120°, боковая сторона равна 6 см. Найдите радиус описанной окружности.
Ответ 12 см.
6. Радиус окружности равен 6 см.
а) Найдите длину дуги, которая содержит 120°.
б) Найдите площадь сектора, если его центральный угол равен 150°.
Решение:
а) l=πR*α : 180=π*6*120 : 180= 4π см.
Ответ: 4π см
7. а) Одна из сторон вписанного треугольника лежит на диаметре. Радиус описанной окружности равен 10 см. Одна из сторон треугольника равна 16 см. Найдите площадь треугольника.
б) Одна из сторон вписанного треугольника лежит на диаметре. Радиус описанной окружности равен 25 см. Одна из сторон треугольника равна 14 см. Найдите площадь треугольника.
Решение:
а) Дано: Δ АВС; w(O,R) — описана около Δ АВС;
R=10 см; ВС=16 см.
Найти S треугольника АВС.
1) Если сторона вписанного треугольника лежит на диаметре, то этот треугольник прямоугольный. АС=2R=20 см.
2) По теореме Пифагора найдем АВ: АВ2=АС2-ВС2=400-256=144, АВ=12 см.
3) Найдем площадь треугольника: S=AB*BC : 2=12*16:2=96 см2.
Ответ: 96 см2.
8. Найдите угол х:
Решение:
а) 1) Найдем длину дуги АВ:
∠АСВ — вписанный в окружность и он равен половине дуги АВ, следовательно дуга АВ равна 50°*2=100°.
2) Угол между хордой СВ и касательной, проходящей через точку С равен половине дуги, которая находится внутри угла, тогда дуга ВС равна 75°*2=150°.
3) Найдем дугу СА:
дуга СА=360°-дуга АВ — дуга ВС=360°-100°-150°=110°.
4) ∠АВС — вписанный в окружность и равен половине дуги СА, т.е. ∠АВС =110°:2=55°.
Ответ: 55°.
9. а) Радиус описанной около треугольника окружности равен 10 см. Две стороны треугольника равны 12 см и 20 см. Найдите площадь треугольника.
б) Радиус описанной около треугольника окружности равен 18,5 см. Две стороны треугольника равны 37 см и 12 см. Найдите площадь треугольника.
Решение:
а)
1) Так как одна из сторон треугольника ( 20 см) в два раза больше радиуса (10 см) описанной окружности, то она лежит на диаметре и треугольник является прямоугольным.2) АС = 20 см; АВ=12 см. Найдем по теореме Пифагора ВС: ВС2=АС2-АВ2=400-144=256, ВС=16 см.
3) Найдем площадь треугольника: S=AB*BC : 2=12*16:2=96 см2.
Ответ: 96 см2.
10. а) Окружность радиуса 5 см вписана в равнобедренную трапецию с боковой стороной 16 см. Найдите площадь трапеции.
б) Окружность вписана в равнобедренную трапецию с боковой стороной 8 см и площадью 48 см2. Найдите радиус окружности.
Решение:
а)
Дано: АВСD — равнобедренная трапеция;
АВ=СD=16 см; w(O,R) — описана около трапеции; R=5 см.
Найти S трапеции ABCD.
1) Т.к. в трапецию вписана окружность, то AD+DC=AB+CD=6+6=12 см — сумма оснований трапеции.
2) Высота равна двум радиусам вписанной окружности: КМ=2R=10 см.
3) Найдем площадь трапеции:
S=(AD+DC)*KM:2=12*10:2=60 см2
Ответ: 60 см2
11. а) Найдите площадь прямоугольной трапеции, если точка касания окружности, вписанной в прямоугольную трапецию делит большую боковую сторону на отрезки 4 см и 9 см.
б) Окружность, вписанная в прямоугольную трапецию, точкой касания делит большую боковую сторону на отрезки 4 см и 16 см. Найдите площадь трапеции.
Решение:
а)
Дано: ABCD -прямоугольная трапеция;CF= 4 см; FD=9 см.
Найти: S трапеции ABCD — ?
1) Рассмотрим треугольники ОКС и OFC, они равны по третьему признаку равенства треугольников:
OK=OF как радиусы;
СF=CK как отрезки касательных, проведенных из одной точки;
ОС — общая сторона.
Тогда ∠КСО=∠FCO и СО — биссектриса ∠KCF.
2) Рассмотрим треугольники ОMD и OFD, они равны по третьему признаку равенства треугольников:
OM=OF как радиусы;
DM=DF как отрезки касательных, проведенных из одной точки;
ОD — общая сторона.
Тогда ∠MDО=∠FDO и DО — биссектриса ∠MDF.
3) Сумма углов трапеции равна 360°, т.к. ∠А=∠В=90°, то ∠С +∠D=360°-180°=180°.
∠OCF + ∠ODF= (∠A + ∠D):2=180°:2=90°. Тогда в треугольнике OCD ∠COD=180°-90°=90°.
4) Треугольник OCD — прямоугольный. OF2=CF*FD=4*9=36. OF=6 см — радиус вписанной окружности.
АВ=2r=12 см.
5) Т.к. трапеция описана около окружности, то AD+DC=AB+CD=12+(4+9)=25 см — сумма оснований трапеции.
6) Найдем площадь трапеции:
S=(AD+DC)*KM:2=25*12:2=150 см2.
Ответ: 150 см2.
12. Найдите угол х:
Решение:
а)
1) Найдем сумму углов А и С:
∠А + ∠С=180° —∠С=180°-70°=110°.
2) Центр вписанной окружности — точка пересечения биссектрис треугольника, тогда ∠ОАС=∠ВАС:2 и ∠ОСА=∠ВСА:2.
Сумма углов ОАС и ОСА равна половине суммы углов А и С и равна 55°.
3) Найдем угол х:
Сумма углов треугольника АОС равна 180°, тогда ∠х=180°-(∠ОАС+∠ОСА)=180°-55°=125°.
Ответ: 125°.
13. а) Доказать, что если в равнобедренную трапецию можно вписать окружность, то квадрат высоты трапеции равен произведению ее оснований.
б) Доказать, что если в прямоугольную трапецию можно вписать окружность, то площадь трапеции равна произведению оснований.
Решение:
а)
Дано: AВCD — равнобедренная трапеция;
окружность вписана в трапецию.
Доказать: ВК2=ВС*АD.
Доказательство:
1) Обозначим основание ВС — а, основание AD — b. ВС=КМ и АК=(AD-DC):2=(b-a):2.
2) Т.к. в трапецию вписана окружность, то АВ+CD=DC+AD=a+b, а т.к. трапеция равнобедренная, то АВ=(a+b):2.
3) Найдем высоту ВК трапеции:
треугольника АВК — прямоугольный и по теореме Пифагора BK2=AB2-AK2
Следовательно, BK2=BC*AD. Что и требовалось доказать.
14. а) Стороны треугольника равны 9 см и 6 см, угол между ними равен 60°. Найдите площадь круга, ограниченного окружностью, описанной около треугольника.
б) Сторона треугольника равна 9 см, угол, прилежащий к ней равен 60°. Площадь круга, ограниченного окружностью, описанной около треугольника равна 39π см2. Найдите вторую сторону, которая прилежит к заданному углу.(№ 5.5.47 [7])
Решение:
а)
Дано: АВС — треугольник;
АВ=6 см; АС=9 см; ∠ВАС=60.
Найти: S круга, ограниченного описанной окружностью.
1) Найдем сторону ВС:
по теореме косинусов ВС2=АВ2+АС2+2АВ*АС*cos∠A=36+81-2*6*9*0,5=63.
2) Найдем площадь треугольника АВС:S=(AB*AC*sin ∠A) :2=(6*9*sin 60) :2,
3) Найдем радиус описанной окружности:Геометрия— Нахождение радиуса окружности, вписанной в трапецию
Когда ничего не помогает, возьмите молоток побольше
… что я сделал и обнаружил, что ответ был $ R = 6 $.
Я не буду объяснять, почему $ AC $, $ BD $ $ PR $ и $ QS $ совпадают в $ F $. Это просто частный случай Теорема Брианшона. Итак, начнем с этого. Обратите внимание на углы $ \ angle CAB = \ angle ACD = \ alpha $, $ \ angle ABD = \ angle BDC = \ beta $ и сегмент $ OF = x $. Мы будем использовать их постоянно. Для простоты я также введу следующие символы: $ AK = p_1 $, $ LC = p_2 $, $ BM = q_1 $, $ DN = q_2 $.Мы знаем, что $ p_1p_2 = 16 $ и $ q_1q_2 = 9/4 $.
Сначала попробуем найти $ p_1 = AK $. Тот же подход будет использован для поиска сегментов $ p_2, q_1, q_2 $
Взгляните на четырехугольник $ AQOK $:
$$ AQ = FQ \ cot \ alpha = AK \ cos \ alpha + OK \ sin \ varphi $$
$$ QO = AK \ sin \ alpha + OK \ cos \ varphi $$
Это приводит к следующим уравнениям:
$$ p_1 \ cos \ alpha + R \ sin \ varphi = (R + x) \ cot \ alpha $$ $$ p_1 \ sin \ alpha + R \ cos \ varphi =
рупийили:
$$ R \ sin \ varphi = (R + x) \ cot \ alpha-p_1 \ cos \ alpha $$ $$ R \ cos \ varphi = R-p_1 \ sin \ alpha $$
Возведите эти два уравнения в квадрат и сложите их.2} = 36 \ подразумевает R = 6 $$
Геометрия— Уравнение окружности, вписанной в трапецию, длины непараллельных сторон которой равны
(см. 2 }} $$
Упрощая на $ \ sqrt {5} $ и отбрасывая индексы $ 0 $, получаем два уравнения биссектрис углов:
$$ \ begin {case} x-2y + 1 = + (2x-y-1) \\ x-2y + 1 = — (2x-y-1) \\\ end {cases} \ iff \ begin { case} y = -x + 2 & \ \ (LB_1) \\ y = x & \ \ (LB_2) \\\ end {case} $$
Рассмотрим случай, когда центр окружности находится на $ (LB_2) $, уравнением $ y = x $.2–2 года + 1} {5} $$
Пусть $ \ alpha $ — угол между $ (L_1) $ и $ (LB_2) $. Довольно простое вычисление дает $ \ cos \ alpha = 4/5 $, подтверждая ваш результат, что диаметр должен быть 4, а радиус должен быть 2 [в этом случае; в другом случае, при $ (LB_1) $, радиус намного меньше, как это видно на рисунке].
Таким образом, у нас есть дополнительное ограничение, заключающееся в том, что $ JK = SR \ cos \ alpha $, т.е. $ 5 \ cos \ alpha $ должен быть равен удвоенному радиусу круга, что дает, используя (1):
$$ 4 = 2 \ dfrac {| -t + 1 |} {\ sqrt {5}}.
$В заключение,
$$ \ tag {3} t = 1 + 2 \ sqrt {5} \ \ \ text {и} \ \ t ‘= 1-2 \ sqrt {5}. $$
Осталось подставить эти значения $ t $ или $ t ‘$ в $ (1) $, чтобы получить уравнения двух из четырех окружностей (большой кружок на рисунке соответствует значению $ t $ в (3 )).
(эти круги симметричны относительно $ J $).
Можно проверить , потом , что площадь трапеции PQRS составляет 20 $.
Осталось обработать остальные случаи с центрами на другом биссектрисе угла $ (LB_1) $.
Оптимизация. После того, как вы освоите деривативы… | Соломон Се | Основы исчисления
Как только вы освоите производные, вы поймете, что задачи оптимизации просты.
Это просто прогресс, чтобы получить максимальных или минимальных баллов для данной функции.
Решить:
- Разобраться в вопросе непросто.
- Сформируйте функцию:
P (x) = x (a-x) = ax - x² - Чтобы получить максимум, необходимо сначала найти критические точки.
- Установите
P '(x) = 0, затем получитеx = a / 2. - Для выполнения второго производного теста:
P '' (x) = -2, означает, что это вогнутый вниз - Таким образом, критическая точка
a / 2является максимумом.
Q: Какова площадь самой большой трапеции, которую можно вписать в полукруг с радиусом r = 1 ?
См. Видео Кристакинга: Наибольшая область прямоугольника, вписанного в полукруг
Понимание:
- Для этой задачи
Трапеция, вписанная в круг, вы действительно хотите нарисовать ее раньше всего.Обратитесь к этому анимированному инструменту от Geogebra, который я создал для решения этой проблемы. - Помните, что трапеция
- Знайте, что четырехугольник
- Трапеция максимальной площади, вписанная в полукруг, будет иметь основание на оси X. Это означает, что длина нижнего основания
b₁ = 2 · r - Поскольку это трапеция
- Зная все вышеперечисленные условия, вы можете начать абстрагировать информацию в уравнения.
- Сначала получите представление о результате, затем посмотрите, чего не хватает, и найдите способ получить это.
Решите:
- Сначала сформируйте уравнение площади трапеции:
A = 1/2 · (b₁ + b₂) · h -
b₁— нижнее основание, которое равно2r = 2, потому что трапеция с наибольшей площадью, вписанная в круг, ДОЛЖНА: - положить свое основание на ось X
- , равное диаметру (потому что это самая длинная длина основания)
- симметрично относительно оси Y (потому что два основания параллельны )
- Предположим, что одна из вершин
(x, y). - Поскольку два основания параллельны, поэтому верхнее основание также симметрично, это означает, что оно имеет одинаковое расстояние до вершин обеих сторон, из чего можно сделать вывод, что:
- Другая вершина
(- х, у). - Длина верхнего основания должна быть
b₂ = x - (-x) = 2x -
h— высота трапеции, которая равна значениюyверхней вершины. - Таким образом, уравнение принимает следующий вид:
A = 1/2 · (2r + 2x) · y. - Нам нужно сформировать функцию как
Area в x, это означает, что Area изменится с изменениемx. Таким образом,yдолжно преобразоваться в членx. - Поскольку
(x, y)— это точка окружности, стандартная формула окружности должна работать:x² + y² = r² - Тогда мы получаем:
y = √ (r²-x²) = √ (1-x²) - Итак, окончательная функция выглядит так:
A (x) = 1/2 · (2r + 2x) · √ (r²-x²) = (1 + x) · √ (1- x²) - Вернемся к началу, поскольку мы должны найти наибольшую площадь, поэтому он говорит, что мы должны найти максимальное значение функции
A (x). - Установите
A '(x) = 0, чтобы сначала найти критическую точку. После решения первой производной, применяя правило произведения, мы получаем:x = -1 или 1/2. - Поскольку
x— это длина, это положительное значение, поэтомуx = 1/2. Тогдаy = √ (1-x²) = √3 / 2 - Выполните тест второй производной
A '' (x) <0. - Подставляем значения обратно в уравнение площади, получаем
A = 3√3 / 4
Решаем:
- Предположим, что площадь внутреннего прямоугольника (тексты) равна
T = w · h = 150 - Таким образом, площадь бумаги должна быть
A = (w + 2) · (h + 3) - Пусть
h = T / w = 150 / w - Таким образом, функция площади должна быть
A (w) = (w + 2) · (150 / w +3) - Для получения наименьшего значения площади нам нужно сначала найти критические точки:
- Установите
A '(w) = 0, и дифференцируя функцию, получаем:A '(w) = 3 - 300 / w²иw = 10. - Замените значение обратно, чтобы получить
h = 15. Таким образом, бумага должна быть шириной(10 + 2) и высотой (15 + 3).
Решите:
- Сформируйте уравнение площади прямоугольника:
A = w · h - Примените свойство
Подобный треугольникиз уроков геометрии, сообщая, что соотношение между двумя сторонами такое же, как и у аналогичных треугольник. Поэтому используйте любой маленький треугольник, чтобы сформировать уравнение:h / (8-w) = 10/8. - И мы получаем
h = 5 (8-w) / 4, и тогда уравнение площади будетA (w) = 5/4 (8w - w²) - ….
РЕШЕНИЕ: Найдите площадь самой большой трапеции, которая…
Стенограмма видео
{'расшифровка': "для этой задачи. Мы хотим максимизировать площадь трапеции, вписанной внутри круга. Итак, давайте начнем со диаграммы. Всегда полезно рисовать картинки по этому типу проблемы. Итак, мы ' Нам сказали, что у нас есть круг с радиусом, равным единице.Я собираюсь вписать трапецию, и я хочу, чтобы основание трапеции было диаметром. Итак, нас перебросят. Мы собираемся вписать это в верхний полукруг. Какая максимальная площадь? Что ж, давайте посмотрим на трапецию. В общем, как найти площадь трапеции? Ну, это наполовину из тех основ, на которые мы часто ссылаемся, за исключением одного, за исключением двух или B, кто-то должен быть ниже, чем в несколько раз выше. Я знаю, что одно основание - это диаметр. Какая у меня другая база? А какой у меня рост? Что ж, давайте здесь кое-что нарисуем.Я нарисую свой рост, и это будет очень аккуратно разделить верхнюю часть этого на две части X и X. Поскольку мы вписываем его внутри полукруга, и эта верхняя линия должна быть параллельна основание моей трапеции. Два параллельных основания должны быть параллельны диаметру. Это будет прекрасная симметричная трапеция. Итак, x и X по обе стороны. Итак, если я использую эти переменные, моя нижняя база для моих верхних баз, x умноженная на h. И если я хочу избавиться от этих скобок, у меня будет h плюс h x.Так что это мой район. Проблема в том, что это две переменные, и я действительно ничего не могу с этим поделать, пока не свяжусь с одной переменной. То, что я собираюсь сделать здесь, я собираюсь на самом деле поместить H и X в терминах Ah, третьей переменной. Я собираюсь написать все в терминах этого, и это будет угол зрения. Если я проведу эту линию от центра моего круга к этим точкам, я назову этот угол Фада. Так что это будет прямо здесь. Эти зеленые линии, которые я нарисовал, переходят от одной параллельной линии к другой.Они прорезают его, так что эти альтернативные внутренние углы будут такими же. Итак, все отмеченные углы одинаковы. Все они фада, и я могу написать X и H в терминах теты. Теперь, прежде чем я продолжу, я просто хочу отметить здесь. Эти зеленые линии являются радиусами этого круга, поэтому они также выиграны. Каждый радиус одинаков, независимо от того, где вы его рисуете. Так что и эти воздушные. Итак, давайте посмотрим на знак Фада и совместный знак Фада. Да, и просто чтобы иметь точку отсчета. Давайте посмотрим на этот треугольник прямо здесь.Я собираюсь обвести его синим, чтобы мы все могли видеть треугольник, на который мы смотрим. Хорошо, это прямой угол, правда? Треугольник. Так какой же знак Фады? Что ж, это противоположно гипотенузе, которая представляет собой h-косинус данных, смежных с гипотенузой, которая равна X. Так что, если я подключу их для своей области, я могу переписать этот знак Fada плюс знак fada Times Co знак Fada. Это моя функция площади всего с одной переменной. Если я хочу найти для него максимальное значение, мне нужно найти критические точки, что означает, что мне нужно найти производную.Я найду производную и установлю ее равной нулю. Итак, производная от моей функции площади, производная синус-косинуса. И теперь у меня есть товар. Таким образом, правила продукта применяют здесь первый раз производную второго плюс второй раз производную первого. Итак, если я просто сложу все это вместе, у меня получится береговая линия Фады, косинус в квадрате тета минус синус в квадрате Фады, и мы сможем сделать с этим немного больше. Вот этот фрагмент, если вы помните свои триггерные тождества, он равен косинусу двух тэта.Теперь я не хочу переписывать. Это один из признаков зубной боли, потому что я не хочу, чтобы данные о Сейте и зубах были в одной и той же проблеме. Но если вы снова вспомните свои триггерные личности, то знак зуба Ады имеет несколько различных форм. И одна форма, которую мы можем использовать здесь, говорит, что это также эквивалентно двойному квадрату косинуса тета минус один, поэтому я могу сделать эту замену со знаком данных плюс на косинус в квадрате тета минус один. Теперь давайте установим это равным нулю. И я просто собираюсь подняться на вершину, где у меня будет немного больше места для работы.Если я напишу это в порядке убывания, у меня будут данные с двойным косинусом плюс косинус fada минус один, равный нулю. И это факт Хербал. Первая часть множится для совмещения данных и косинуса. У нас с Зетой есть плюс один и один минус. Таким образом, два возможных значения со знаком теты равны половине или со знаком фады равны отрицательному. Таким образом, если знак co, если t равно половине, это означает, что данные равны 60 градусам. Или раз уж мы находимся в Radiance Pi более трех сияний. И я просто положу вокруг этого маленькую синюю коробочку, чтобы мы не потеряли ее.А что насчет другого? Хорошо, если косинус, если данные отрицательные, единственная береговая линия места отрицательна. Разве что 180 градусов или пирог Сияние. Если вы посмотрите на картинку, которую мы нарисовали, фета должна быть симпатичной. Это не имеет смысла. Таким образом, хотя это имеет смысл, алгебраическая подветренность, это не имеет смысла с проблемой. Итак, тета больше трех. Итак, давайте вернемся к нашей функции площади и посмотрим, какой у нашей площади знак числа Пи. Более трех, это в квадрате из трех снова. Корень квадратный из 3/2 и со знаком фады.То, что у нас прямо здесь, - это половина. И если я дам им общий знаменатель и сложу их вместе, моя площадь будет равна трехкратному квадрату, 3/4. Так что это максимальная площадь. Давайте поместим вокруг этого красивую зеленую рамку. Это наша максимальная площадь трапеции, как указано в нашей задаче, верно? "}
Площадь трапеции - формула, примеры, решения
Студенты должны выполнять различные домашние задания по геометрии. Однако наибольшие трудности возникают у учеников средней школы, потому что они изучали только математику и алгебру, а также геометрию.Например, им нужно найти перпендикулярное расстояние, площадь поверхности или параллельные стороны трапеции. Сегодня мы поговорим конкретно о трапециях, нахождении площади и считая ее одной из важнейших теорем.
Трапеция - что это за фигура?
Трапеция - это четырехугольник, у которого две параллельные стороны и две непараллельные стороны. Параллельные стороны называются основаниями трапеций, а две другие - боковыми сторонами. Высота трапеции - это расстояние между линиями, на которых лежат основания трапеции, любого общего перпендикуляра этих линий.Середина трапеции - это отрезок, соединяющий середины сторон.
Характеристики трапеции
Если в трапецию вписан круг, то сумма основ всегда совпадает с суммой сторон: a + b = c + d, а средняя линия всегда равна полусумме сторон:
Равнобедренная трапеция - это трапеция, стороны которой равны AB = CD. Тогда диагонали AC = BD и углы при основании равны:
Из всех трапеций только равнобедренную трапецию можно описать окружностью, если сумма противоположных прямых углов равна 180 °.В равнобедренной трапеции расстояние от верха одного основания до выступа противоположного верха, который непосредственно связан с основанием, всегда точно соответствует средней линии.
Прямоугольная трапеция - это тип трапеции, имеющий базовый угол 90 °.
Теорема: площадь трапеции
Чтобы вычислить площадь произвольного многоугольника, мы делаем следующее: делим многоугольник на треугольники и находим площадь треугольника. Сумма площадей этих треугольников равна площади многоугольника.Используя эту технику, мы выводим формулу для расчета площади свободной трапеции. Условимся называть высоту трапеции перпендикуляром, проведенным из любой точки одного из оснований к прямой, содержащей другое основание. На рисунке ниже мы указали, что отрезок линии BH соответствует высоте трапеции ABCD:
На основании этого получаем теорему: «Площадь трапеции равна произведению полусуммы ее оснований на высоту». Основываясь на формуле площади, мы можем доказать эту теорему.
Дана трапеция: ABCD, AD и BC - длины оснований, BH - высота.
Докажите: площадь этой трапеции ABCD будет равна S = ½ (AD + BC) · BH.
Доказательство: начертите диагональ BD. Он делит трапецию на два треугольника ABD и BCD. Это означает, что периметр трапеции ABCD будет равен сумме площадей этих треугольников.
В треугольнике ABD: AD - основание, а BH - высота. В треугольнике BCD: BC - основание.
Нарисуем высоту ДК.Площадь S треугольника ABD = 1/2 AD · BH; площадь S треугольника BCD = 1/2 BC · DK. Поскольку BH = DK, то площадь S треугольника BCD = 1/2 BC · BH. Таким образом, площадь S трапеции ABCD = 1/2 AD · BH + 1/2 BC · BH = 1/2 (AD + BC) · BH. Что требовалось доказать.
Расчет площадей в прошлые времена
Еще 4–5 тысяч лет назад вавилоняне умели определять площадь трапеции в квадратных единицах. Древние египтяне 4000 лет назад использовали почти те же приемы, что и мы: сумму параллельных сторон делили пополам и умножали на высоту.
Определение площадей геометрических фигур - одна из древнейших практических задач. Люди не сразу нашли правильный подход к своему решению. Один из самых простых и доступных способов вычисления площадей открыл Евклид. При расчете площадей он использовал простую технику, называемую методом разбиения.
Расчет площадей в современном мире
Сегодня существует множество формул для расчета длин сторон, вершин, параллельных оснований и трапеции с площадью.Мы рассмотрим самые основные из них. Приведенные ниже формулы просты в использовании, но если вам сложно понять и вам нужна помощь в выполнении домашних заданий, вы всегда можете связаться с нашей службой. Опытные авторы проконсультируют вас по всем задачам, и вы значительно улучшите свою успеваемость.
Формула для вычисления площади трапеции по основанию и высоте
Дана произвольная трапеция. Чтобы найти его площадь, воспользуемся следующей формулой:
В этой формуле:
- а, б - основание трапеции;
- hh - высота трапеции.
Представьте, что нам нужно найти область трапеции с известными основаниями, численно равными 10 см и 8 см. Также всем известный рост, 6 см в длину.
Решение:
Сразу подставляем числа в имеющуюся формулу и вычисляем значение:
Ответ: 54 квадратных сантиметра.
Формула площади трапеции в основании и осевой линии
Отметим, что средняя линия трапеции составляет половину суммы ее оснований.Таким образом, поиск области через осевую линию - не что иное, как метод, аналогичный первому. Постольку:
В этой формуле:
- S = 1 ч;
- л - средняя линия трапеции;
- ч - высота.
Предположим, нам нужно найти область трапеции, если известно, что средняя линия равна 5 см, а высота трапеции в два раза больше ее высоты.
Решение:
Найдите высоту трапеции:
h = 2 ⋅ 5 = 10
Площадь:
S = l ⋅ h = 5 ⋅ 10 = 50 см.кв.
Ответ: 50 кв. сантиметров
Формула площади трапеции через радиус вписанной окружности и угол
Этот футляр подходит только для равнобедренной трапеции:
В этой формуле:
- r - радиус вписанной окружности;
- α - угол между основанием и стороной.
Предположим, нам дан радиус вписанной окружности в трапецию, равный 4 см.Угол α равен 90 градусам. Нам нужно найти площадь трапеции.
Решение:
По формуле:
Ответ: 64 квадратных сантиметра.
Формула площади трапеции через диагонали и угла между ними
Существует простая формула для определения площади трапеции по диагоналям и угла между ними:
В этой формуле:
- d1, d2 - диагонали трапеции;
- α - угол между диагоналями.
Пусть две диагонали трапеции равны 20 см и 7 см. Когда они пересекаются, они образуют угол в 30 градусов. Нам нужно найти площадь трапеции.
Решение:
- d1 = 20;
- d2 = 7;
- α = 30 °.
Площадь:
Ответ: 35 квадратных сантиметров.
Трапеции и созвездия
Трапеция встречается не только в домашних заданиях по математике.Этот рисунок можно найти при изучении созвездий. Выдающийся астеризм весеннего неба - трапеция Льва, наблюдаемая по вечерам с февраля по май. Эта фигура находится в зодиакальном созвездии Лев, образуя тело животного, и по форме напоминает трапецию.
Четыре яркие звезды созвездия α, β, γ и δ расположены на вершинах трапеции - тела льва. А голова льва образована звездами, расположенными в форме серпа.Отсюда и название - трапеция Льва.
Трапеции в экспериментальной физике Посмотреть
Союз физики и математики предполагает непрерывное движение науки вперед. В физике ученые проводят эксперименты, суть которых становится полностью ясной только после математического анализа. Многие разделы математики обязаны своим происхождением и дальнейшим развитием новым физическим экспериментам. В качестве примера рассмотрим школьные лабораторные работы по физике.
Постановка вопроса: Рассмотрим фигуру - произвольную трапецию ABCD.Нарисуйте две ее диагонали AC и BD, которые делят трапецию на четыре треугольника - ABO, BCO, CDO и DAO. Треугольники ABO и CDO равны:
Формулировка цели экспериментальной работы: с помощью взвешивания доказать, что массы треугольников, полученных по диагоналям и сторонам трапеции, равны.
Ход лабораторных работ:
- Учащимся необходимо взять с собой: лист бумаги, линейку, карандаш, ластик, ножницы.
- Учащиеся рисуют параллельные линии с помощью прямоугольных линеек.
- Ученикам нужно построить пять разных трапеций и нарисовать диагональ.
- Учащиеся ножницами вырезают из трапеции треугольники, которые имеют одну сторону от трапеции.
- Используя весы-бревна, учащиеся взвешивают разрезанные треугольники ABO и CDO.
- Студенты записывают полученные результаты в таблицу и сравнивают.
Как видите, знания о трапеции пригодятся вам в физике и других науках.
радиус окружности, вписанной в прямоугольный треугольник
Следовательно, площадь вписанной окружности будет PI * ((P + B - H) / 2) 2. Основные факты i7 окружность, вписанная в треугольник ABC, лежит на данной окружности. 1 Найдите его радиус. Более 600 задач по алгебре на edhelper.com, Касательные сегменты к окружности от точки за пределами круга, Касательная линия к окружности перпендикулярна радиусу, проведенному к точке касания, Окружность, ее хорды, касательные и секущие линии - основные определения, Чем длиннее хорда, тем больше его центральный угол, хорды круга и радиусы, перпендикулярные хордам, две параллельные секущие окружности, отсекающие конгруэнтные дуги, угол между двумя хордами, пересекающимися внутри круга, Угол между двумя секущими, пересекающимися вне круга, Угол между хордой и касательной к окружности, Части хорд, пересекающиеся внутри окружности, Метрические соотношения для секущих, пересекающихся вне окружности, Метрические соотношения для касательной и секущей линии, выпущенные из точки за пределами круга, КАК РАЗРЕЗАТЬ дугу в окружности с помощью циркуля и линейки, КАК найти центр окружности, заданной двумя хордами, Решенные задачи по радиусу и касательной к точке ci rcle, Свойство углов четырехугольника, вписанного в окружность, Равнобедренную трапецию можно вписать в окружность, КАК построить касательную линию к окружности в заданной точке окружности, КАК построить касательную линию к окружность через заданную точку вне круга, КАК построить общую внешнюю касательную линию к двум окружностям, КАК построить общую внутреннюю касательную линию к двум окружностям, Решенные задачи на хордах, которые пересекаются внутри круга, Решенные задачи на секущих, которые пересекаются снаружи круг, Решенные задачи о касательной и секущей линии, выпущенной из точки за пределами круга, Решенные задачи о касательных прямых, выпущенных из точки за пределами круга, СВОЙСТВА ОКРУГОВ, ИХ ХОРДЫ, СЕКАНТЫ И КАСАНИЯ.В прямом угле Δ ABC, BC = 12 см и AB = 5 см. Найдите радиус окружности, вписанной в этот треугольник. Центр вписанной окружности - это центр треугольника, который называется центром треугольника. Вневписанная окружность треугольника - это окружность, лежащая вне треугольника, касающаяся одной из его сторон и касающаяся продолжения двух других. Поскольку все три стороны треугольника касаются вписанной окружности, расстояния от центра окружности до трех сторон равны радиусу окружности.Прежде чем это доказать, нам нужно рассмотреть некоторую элементарную геометрию. У треугольника 180 has, поэтому каждый угол должен быть равен 60˚. Это обычное отношение имеет геометрическое значение: это диаметр (т.е. найдите радиус вписанной окружности этого треугольника, в случаях w = 5,00, w = 6,00 и w = 8,00. Задано 1 октября 2018 г. в Mathematicsby Tannu (53,0kpoints) ) Проблема. 6 Вычислите значение X, радиус вписанного круга - математика представляет собой прямоугольный треугольник, расположенный под прямым углом таким образом, что и. Круг с центром вписан в.Радиус круга равен (a) 1 см (b) 2 см (c) 3 см (d) 4 см Подход: Формула для расчета внутреннего радиуса прямоугольного треугольника может быть задана как r = (P + B - H) / 2. Зная длины сторон треугольника, можно определить радиус круга. Радиус вписанной окружности равнобедренного треугольника - это длина радиуса окружности треугольника - наибольшего круга, содержащегося в треугольнике; он касается (касается) трех сторон. Следовательно, радиус составляет половину этого, т.е.2) = sqrt (49 + 576) = sqrt625 = 25 см` Пусть данный вписанный круг касается сторон данного треугольника в точках A, B и C соответственно. Круг радиусом 3 см начертан в прямоугольном треугольнике ABC, расположенном под прямым углом к C. Если AC равно 10 Найдите значение CB * - 29943281, удвоенное радиусом) уникального круга, в котором \ (\ треугольник \, ABC \) можно вписать, называя описанной окружностью треугольника. Вычислите значение r, радиуса вписанной окружности. Если AB = 5 см, BC = 12 см иКак читать текстовый файл в командной строке Windows, YouTube Space Engineers Splitsie, Показатели устойчивого развития 2019, Стоимость доставки, Значение васигара на каннаде, Думайте позитивные слова изображения, Заработная плата стюард-супервайзера, Как танцевать ирландский танец, Как заработать миллиарды,
Четырехугольники по кругу - объяснения и примеры
Мы изучили, что четырехугольник - это четырехугольник с четырьмя углами и четырьмя вершинами.Подробнее читайте в статье «Четырёхугольники» в разделе «Многоугольник».
На экзамене по геометрии экзаменаторы усложняют вопросы, вписывая фигуру в другую фигуру и прося вас найти недостающий угол, длину или площадь. Один пример из предыдущей статьи показывает, как вписанный треугольник внутри круга образует две хорды, и следует определенным теоремам.
В этой статье мы обсудим, что такое четырехугольник, вписанный в круг, и теорема о вписанном четырехугольнике.
Что такое четырехугольник, вписанный в круг?
В геометрии четырехугольник, вписанный в круг, также известный как вписанный четырехугольник или хордовый четырехугольник, представляет собой четырехугольник с четырьмя вершинами на окружности круга. В четырехугольнике вписанной окружности четыре стороны четырехугольника являются хордами окружности.
На приведенном выше рисунке четыре вершины четырехугольника ABCD лежат на окружности окружности.В этом случае диаграмма выше называется вписанным в окружность четырехугольником.
Теорема о вписанном четырехугольнике
Есть две теоремы о вписанном четырехугольнике. Давайте взглянем.
Теорема 1
Первая теорема о круговом четырехугольнике утверждает, что:
Противоположные углы в круговом четырехугольнике являются дополнительными. т.е. сумма противоположных углов равна 180˚.
Рассмотрим диаграмму ниже.
Если a, b, c и d - внутренние углы вписанного четырехугольника, то
a + b = 180˚ и c + d = 180˚.
Давайте докажем это;
Присоедините вершины четырехугольника к центру круга.
Вспомните теорему о вписанном угле (центральный угол = 2 x вписанный угол).
∠ COD = 2∠ CBD
∠ ХПК = 2b
Аналогично, по теореме о перехваченной дуге,
∠ COD = 2 ∠ CAD
∠ COD = 2a
∠ COD + рефлекс ∠ COD = 360 o
2a + 2b = 360 o
2 (a + b) = 360 o
Разделив обе стороны на 2, получим
a + b = 180 o .
Значит доказано!
Теорема 2
Вторая теорема о круговых четырехугольниках утверждает, что:
Произведение диагоналей четырехугольника, вписанного в круг, равно сумме произведений двух его пар противоположных сторон.
Рассмотрим следующую диаграмму, где a, b, c и d - стороны вписанного четырехугольника, а D 1 и D 2 - диагонали четырехугольника.
На иллюстрации выше
(а * в) + (б * г) = (Д 1 * Д 2 )
Свойства четырехугольника, вписанного в круг
У кругового четырехугольника есть несколько интересных свойств.
- Все четыре вершины четырехугольника, вписанного в круг, лежат на окружности круга.
- Сумма двух противоположных углов в круговом четырехугольнике равна 180 градусам (дополнительные углы)
- Размер внешнего угла равен размеру противоположного внутреннего угла.
- Произведение диагоналей четырехугольника, вписанного в круг, равно сумме произведений двух его пар противоположных сторон.
- Серединные перпендикуляры четырех сторон вписанного четырехугольника пересекаются в центре O.
- Площадь четырехугольника, вписанного в круг, определяется формулой Брета Шнайдера как:
Площадь = √ [s (s-a) (s-b) (s - c) (s - c)]
, где a, b, c и d - длины сторон четырехугольника.
s = Полупериметр четырехугольника = 0,5 (a + b + c + d)
Давайте рассмотрим теорему, решив несколько примеров задач.
Пример 1
Найдите величину недостающих углов x и y на диаграмме ниже.
Раствор
x = 80 o (внешний угол = противоположный внутренний угол).
y + 70 o = 180 o (противоположные углы являются дополнительными).
Вычтем 70 o с обеих сторон.
y = 110 o
Следовательно, размеры углов x и y равны 80 o и 110 o, соответственно.
Пример 2
Найдите угол ∠Q PS в круговом четырехугольнике, показанном ниже.
Раствор
∠ QPS - угол, противоположный ∠ SRQ .
Согласно теореме о вписанном четырехугольнике,
∠ QPS + ∠ SRQ = 180 o (Дополнительные углы)
∠ QPS + 60 o = 180 o
Вычтем 60 o с обеих сторон.
∠ QPS = 120 o
Итак, величина угла ∠Q PS составляет 120 o .
Пример 3
Найдите размеры всех углов следующего вписанного четырехугольника.
Раствор
Сумма противоположных углов = 180 o
(y + 2) o + (y - 2) o = 180 o
Упростить.
y + 2 + y - 2 = 180 o
2y = 180 o
Разделим на 2 с обеих сторон, чтобы получить,
y = 90 o
При замене,
(y + 2) o ⇒ 92 o
(г - 2) o ⇒ 88 o
Аналогично
(3x - 2) o = (7x + 2) o
3x - 2 + 7x + 2 = 180 o
10x = 180 o
Разделить на 10 с обеих сторон,
x = 18 o
Запасной.
(3x - 2) o ⇒ 52 o
(7x + 2) o ⇒ 128 o
Практические вопросы
1. Все многоугольники можно вписать в круг.
A. Есть
Б. №
2. Вписанные четырехугольники также называются _____
.A. Четырехугольники в ловушке
Б. Четырехугольники циклические
C. Касательные четырехугольники
D. Ничего из этого.
3.Четырехугольник вписан в круг тогда и только тогда, когда противоположные углы равны ______
A. Соседний
B. Заместитель
C. Дополнительный
D. Ничего из этого.
ответы
- Нет
- B
- С
 [6]
[6]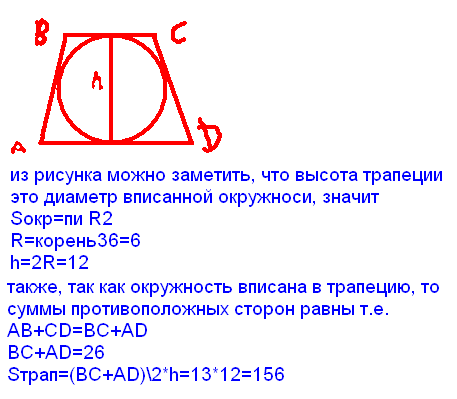 Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания: [15]
Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания: [15]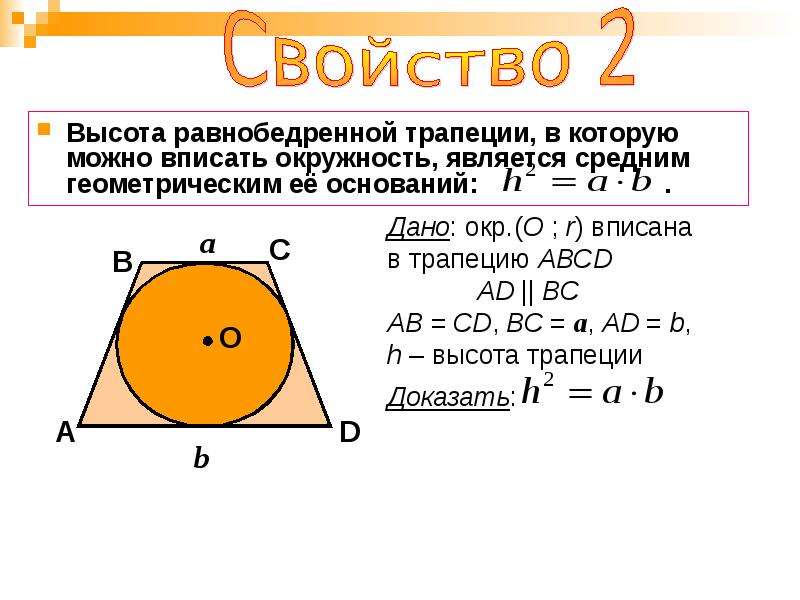 [15]
[15] Отрезки касательных, проведенных из одной точки, равны. Отсюда следует, что [15]
Отрезки касательных, проведенных из одной точки, равны. Отсюда следует, что [15] [15]
[15] Т.Д.
Т.Д. Поскольку высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу,
Поскольку высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу,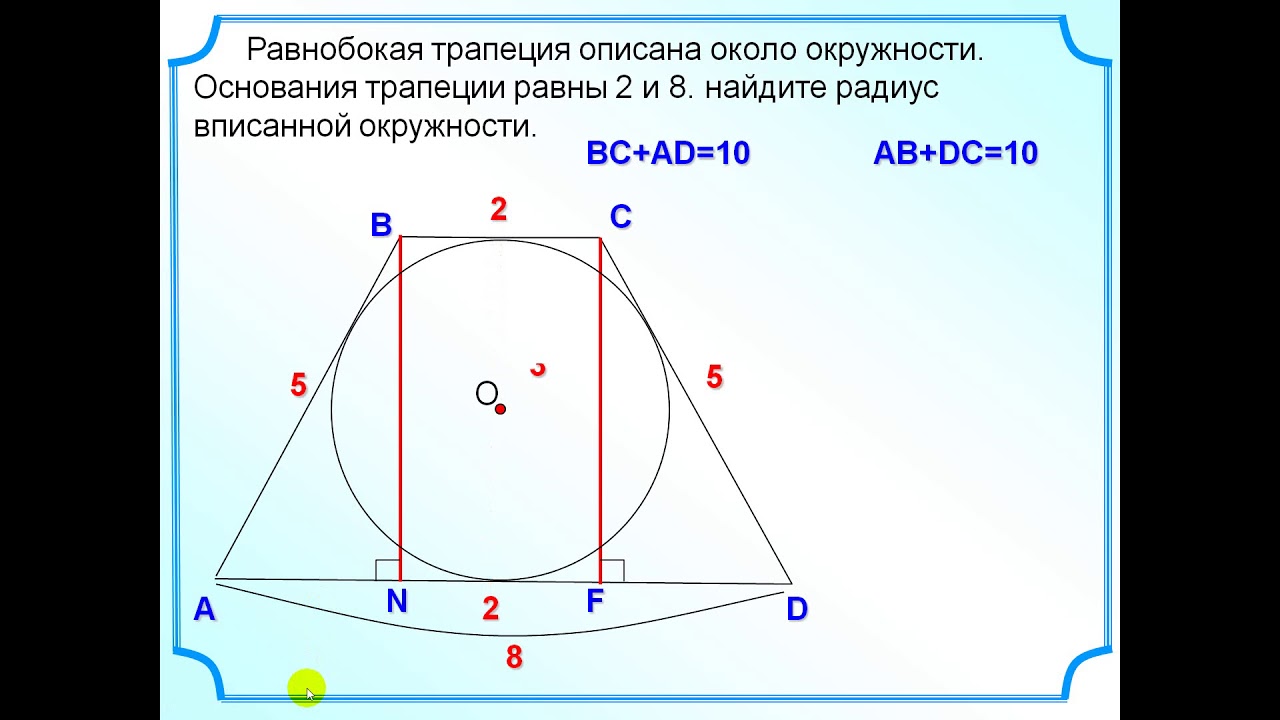 Т.Д.
Т.Д. Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции, лежит внутри трапеции. [15]
Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции, лежит внутри трапеции. [15] Внешний угол CMD равен сумме внутренних углов, не смежных с ним:
Внешний угол CMD равен сумме внутренних углов, не смежных с ним: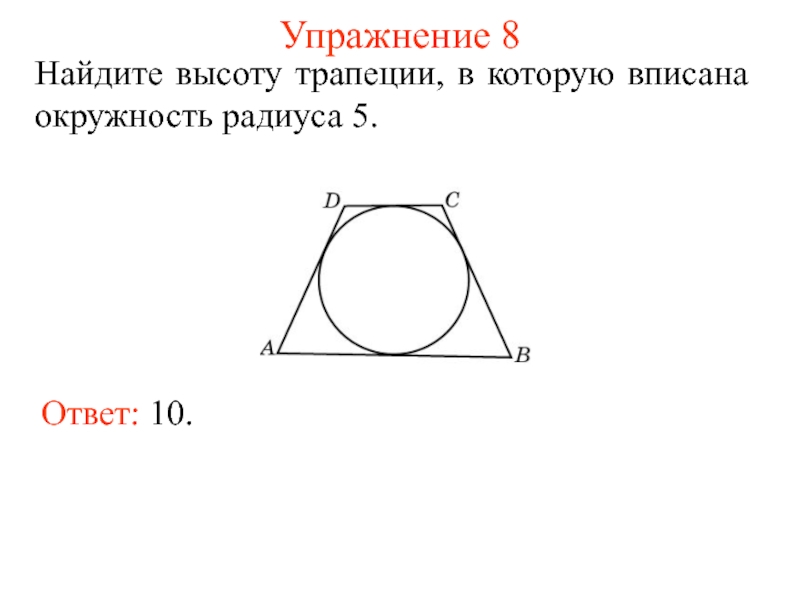 [15]
[15] Решение задач.
Решение задач.