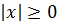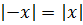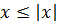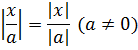«Кастинг чисел» или раскрытие модуля на занятиях с репетитором по математике
Модули — трудная тема для учеников. Приступая к работе с ней репетитор по математике должен понимать, что основные сложности учащиеся испытывают не при вычислении модуля, а при проведения алгебраических преобразований с ним. Причины всех трудностей — недостаточное внимание к данной теме со стороны школьных программ и невозможность в большинстве случаяв работать с «этими палочками» напрямую, за одну операцию, без разветвления применяемых алгоритмов. Знак модуля — это всего лишь оболочка, условное обозначения этого разветвления.
 Практика показывает, что большинство приходящих к репетитору учеников имеют крайне низкий уровень владения приемами раскрытия модуля, если под его знаком стоит переменная. В этом случае, репетитор по математике оказывается главным участником сражений за понимание, поскольку в школе толком ничего не объясняется, а самостоятельно разобраться в дебрях разветвлений дети часто не в состоянии.
Практика показывает, что большинство приходящих к репетитору учеников имеют крайне низкий уровень владения приемами раскрытия модуля, если под его знаком стоит переменная. В этом случае, репетитор по математике оказывается главным участником сражений за понимание, поскольку в школе толком ничего не объясняется, а самостоятельно разобраться в дебрях разветвлений дети часто не в состоянии.
Далеко не в каждом случае репетитор по математике способен научить ученика работать с модулем. Для этого необходмы не только способности репетитора давать точные комментарии к используемым алгоритмам, но и способности ребенка самостоятельно создавать, контролировать и обрабатывать несколько числовых потоков одновременно. Причем этот контроль имеет многоэтапный и даже виртуальный характер, без участия в нем самих чисел. Сложная задача для ученика.
Составление алгоритмов работы с модулем можно сравнить с запуском автоматизированной линии по выпуску рыбных консервов определенного вида без участия на всех этапах производства самого человека. Фантастика, но попробуем себе это предствить. Надо расставить определенные виды сетей и для каждой из них, в независимости от того, что в нее попадает, запланировать какой то способ дальнейшей сортировки и переработки пойманного. Тоже сложная задача. Учитывая тот факт, что не каждый ученик сможет правильно проанализировать влияние специфики уравнения (конечного продукта) для поиска таких алгоритмов, — задача вдвойне усложняется.
Спасаться учебниками не получается. Во всех книжках, которые попадались мне на глаза, объяснения велись сразу через записи систем, равносильных исходному уравнению.
Нельзя объяснять ребенку методы решений уравнений с модулем через равносильные системы.
Проблема заключается в том, что их появление — есть продукт мыслительной деятельности знающего человека и предназначены они для ПРОВЕРКИ РЕШЕНИЯ знающим человеком, но никак не для того, чтобы учить с их помощью ПОНИМАТЬ происходящеее. Ими демонстрируется только «вершина айсберга», большая часть которого, связанная с «демонстрацией передвижения чисел», скрыта. Ее нельзя как-либо полностью показать что то записывая, как нельзя, например заменить всю информацию на видео несколькими фотографиями. Донести до ученика суть можно только на словах. Это и должен сделать репетитор по математике.
В этой статье я хочу поделиться с вами собственной методикой объяснения основного способа снятия модуля : разбора случаев по подмодульному выражению. Для Начала посмотрим как решается базовое (линейное) уравнение с модулем в любом более-менее серьезном пособии по подготовке к экзамену в 11 классе.
Решить уравнение:
| x — 3 | = 2x+1
От учебника к учебнику пояснения будут в целом близки по духу, но несколько отличаться друг от друга комментариями. Вот некоторые из них:
1) Уравнение равносильно совокупности систем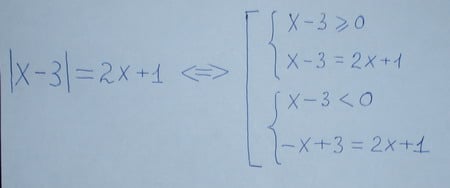
Далее, как правило, в том же виде (параллельно) демонстрируется решение каждой системы и записывается ответ. И все!!!!! Среднему и даже сильному ученику, порой, трудно в этом разобраться. Слабый ученик не поймет ровным счетом ничего. А у более толкового возникнет масса вопросов: почему именно так решается исходное уравнение? Почему надо включать в записи еще какие-то неравенства? Все ли уравнения с модулем можно решить этим способом?А если модулей несколько?. Некоторые учителя, не усложняя себе жизнь поиском подходящих разъяснений, пользуются этой схемой и считают, что она сама обо всем рассказывает и тратить лишнее время — только запутывать ученика. Но практика показывает, что большинство детей не способны на самостоятельный анализ участия в решении даже таких простых неравенств
2) Вторая разновидность демонстрации решения: рассмотрим случаи (уже не понятно, что значит «рассмотрим», зачем и что такое вообще «случаи» :
1) х — 3 ≥ 0
Тогда уравнение приводится к виду х-3=2х+1. Находим его корень х= −4. Он не удовлетворяет неравенству х — 3 ≥ 0
2) х — 3 < 0 Тогда решим уравнение —х+3= 2х+1. Его корень 2/3 очевидно удовлетворяет условию х — 3 < 0.
В итоге получаем ответ х=2/3.
Конечно, при таком подходе появляются попытки внести ясность, но все равно возникают вполне естественные вопросы :
1) как связаны два решаемых уравнения с первоначальным?
2) Почему надо делать еще какую то проверку?
Ни тот ни другой метод «разъяснений» не отражает главного — специфики объекта и особенности выполнения действий с ним. Все что показывают книжки — это всего лишь краткое оформление промежуточных и необходимых для получения ответа выкладок.
Предлагаю вам свой уникальный текст, разъясняющий ученику смысл фраз «рассмотрим случаи», «уравнение приводится к виду …» , «равносильно совокупности систем…».
Лучше всего подавать идею решения в виде следующего рассказа (более или менее подробного в зависимости от типа ученика).
Итак, надо решить уравнение |x — 3| = 2x+1, то есть найти все числа, которые при подстановке вместо буквы х превращают это уравнение в верное числовое равенство. (ученик, конечно, должен понимать, что такое корень уравнения и как его проверить). Мы не знаем этих чисел, но в любом случае они находятся где-то на числовой прямой.
Будем искать их также, как какие-нибудь нужные вещи в двухкомнатной квартире. Зайдем сначала в одную комнату и поищем в ней, затем в другую, а затем, соберем все, что найдено, в общий мешок для демонстрации результата поиска. Тоже самое сделаем с уравнением. Разрежем числовую ось на две части (аналоги комнат) разделительной точкой х=3 (почему бедется именно она — станет понятно позже).
Сначала поищем корни уравнения среди чисел, больших (или равных) чем 3. Если бы их все можно было бы проверить перебором, мы бы так и сделали. Сложность в том, что чисел бесконечное количество. Если мы начнем этот бесконечный процесс (представим себе такое) или захотим протестировать какое-нибудь конкретное число из этой комнаты на предмет попадания в ответ, то подставляя числа в исходное уравнение, внутри модуля, каждый раз будем получать неотрицательное число (это любой 11-ти классник поймет). В этом случае на знак модуля не окажет никакого влияния на вычисление результата всех действий в девой части, т.к. что модуль неотрицательного числа равен самому числу под его знаком. А раз так, то в выражении |x-3| будет получаться тот же самый результат, что и в выражении х—3. Поэтому нам НЕ ВАЖНО В КАКОЕ УРАВНЕНИЕ ДЛЯ ПРОВЕРКИ ВСТАВЛЯТЬ ЧИСЛА ИЗ ВЫБРАННОЙ КОМНАТЫ. Можно в |x—3| = 2x+1, а можно в x — 3 = 2x+1 (так как в их левых частях получаются равные результаты). Если одно равенство окажется верным, то и другое тоже.
Поэтому, для вылавливания чисел из промежутка х>3 я могу заменить проверку |x — 3| = 2x+1 на проверку равенства x — 3 = 2x+1. Если оно окажется верным — тестируемое число попадет в ответ. Чисел, которые обеспечивают выполнение этого условия не так много, более того оно одно и его можно найти просто решив линейное уравнение. Но оно может не находится в рассматриваемой части оси (в 1-ой комнате), поэтому этот корень еще требуется проверить на принадлежность к промежутку от 3 до +∞.
Именно поэтому тестируемое число должно отвечать двум требованиям х>3 и x — 3 = 2x+1, а значит должно быть решением следующей системы:
Ее ответ покажет, какие числа первой комнаты являются корнями исходного уравнения.
Аналогично можно объяснить как найти корни во второй комнате, то есть на промежутке (- ∞;3). Если тестировать любое число из этого промежутка, и вставлять его в исходное уравнение (представим себе этот бесконечный процесс), то под модулем будет каждый раз получаться отрицательное число, а в этом случае в выражении |x — 3| будет получаться тот же самый результат, что и в выражении —(х — 3), (этот факт лучше объяснить отдельно до темы уравнения с модулем). Поэтому для принятия решения о включении тестируемого числа в ответ не важно где его проверять: подставляя в |x — 3| = 2x+1 или в уравнение —(x — 3) = 2x+1 (раз в левых частях получается один и тот же результат). И опять, вместо того, чтобы проверять пербором все числа расположенные левее x=3, я могу просто решить это уравнение —(x — 3) = 2x+1. В его ответ «заползут» все числа обеспечивающее его верность. Среди них надо взять только те, которые левее 3, то есть проверить условие х<3). Итак, для попадания числа из второй комнаты в ответ нужно, чтобы оно отвечало двум требованиям
То есть являлось бы решением системы:
Решив обе полученные системы и собрав вместе все найденные числа мы получим ответ уравнения |x — 3| = 2x+1.
Репетитор по математике должен тщательно следить не только за порядком слов, которые он использует, но и за темпом изложения. Нельзя спешить и слишком много говорить.
 Через урок, после объяснения метода построения графика с модулем репетитору полезно вернуться к разобранному уравнению и решить его же графически.
Через урок, после объяснения метода построения графика с модулем репетитору полезно вернуться к разобранному уравнению и решить его же графически.
Аналогично объясняется метод решения неравенств с модулем. Фраза «проверка равенства» заменяется на фразу «проверку верности неравенства».
Если репетитор по математике смог разъяснить ученику, что линия, заданная на плоскости уравнением есть не что иное как его ответ в графической форме и отбирать для ответа уже нужно точки плоскости (вместо точек оси), то те же самые рассуждения годятся и для построения графика функции с модулем. Повторяя почти тот же самый текст с заменой слова «число» на «пару чисел» или на «точку плоскости» репетитор по математике сможет убить двух зайцев: и новое изучить и старое закрепить. Привожу этот текст в слегка сокращенном виде:
построить график функции у=|х-1|+2х
Разделим плоскость на две части, так чтобы в первую часть попали точки у которых х≥1, а у другой х<1. Репетитору по математике лучше нарисовать эти две «комнаты».
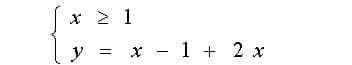 Она указывает на построенную часть финального графика. Аналогично дается пояснение для построения левой части, а затем объединяем построенные линии и получаем:
Она указывает на построенную часть финального графика. Аналогично дается пояснение для построения левой части, а затем объединяем построенные линии и получаем:
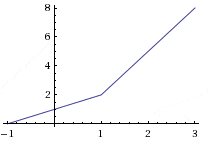 Как видите, репетитор по математике может предложить практически тот самый текст ученику, что и при решениии уравнений с одной перменной. Закрепление материала будет лишь вопросом времени при самостоятельной работе. Особое чутье репетитора здесь проявляется в способности понять когда можно с учеником переходить к последовательному чередованию объектов (уравнений, неравенств, графиков).
Как видите, репетитор по математике может предложить практически тот самый текст ученику, что и при решениии уравнений с одной перменной. Закрепление материала будет лишь вопросом времени при самостоятельной работе. Особое чутье репетитора здесь проявляется в способности понять когда можно с учеником переходить к последовательному чередованию объектов (уравнений, неравенств, графиков).
Модное на сегодняшний день слово «кастинг» как нельзя лучше подходит для описания работы алгоритмов решения уравнений с мордулями. Большинство подростком с ним знакомы и понимают его сымсл. Для Красиво зазвучит: «кастинг чисел» «кастинг точек плоскости».
Уяснив метод разбора случаев на простых линейных подмодульных выражениях, ученик может быть отправлен репетитором по математике в гости к нелинейным. В такой последовательности легче понять, что делать, если под модулем, например, стоит дробь или косинус. Стоит обратить внимание на то, что в первой строке систем вписывается неравенство, указывающее своим ответом на рассматриваемое множество. Именно этот ответ и есть первая комната. Записывая неравенство мы выделяем эту комнату. Поскольку ответ неравенств часто состоит их кусочков оси, то комната просто будет рваной, но принцип отбора (кастинга) ее чисел остается прежним. Все равно надо решать систему, просто вместо готового для изображения ответа х≥3 придется включать в первую строку системы неравенство «подмодульное выражение больше(меньше) либо равно нуля», решать его, а затем пересекать полученный ответ с ответом второй строчки системы.
Итак, с одним модулем разобрались. Что репетитор по математике предложит еще? Если по его ощущениям у ученика еще остался потенциал — можно перейти к уравнениям с двумя линейными модулям, например |x-3|+|2x+1|-4=0. Важно, чтобы на этом этапе ученик понимал как выбирается разделительная точка для каждого модуля. Можно назвать ее переломной.
Удобнее всего ось разделить двумя точками «обнуляющими» подмодульные выражения на 3 области и для отбора чисел из каждого множества заменить проверку исходного неравенства на проверку неравенства без модулей. Тремя системами получаем ответ.
Опытный репетитор по математике всегда знает, что наиболее вероятной ошибкой является потеря контроля за раскрытием модуля если он «обложен» со всех сторон действиями. Для уменьшения ошибок важно предложить какое-то единое опорное правило. Я всегда говорю так. В случае, когда под модулем получается «минус» модуль надо поменять на скобку, а перед скобкой поменять знак. Это очень удобно для запоминания, так как в голове ученика в этот момент сидит директива «что-то поменять». Легко запомнить, что если хочется «что-то поменять», то надо поменять все что только можно (слева от подмодульного выражения).
В заключение отмечу, что репетитор по математике может показать сильному ученику и другие способы раскрытия модуля. После изучения темы «возведение неравенств и уравнений в квадрат» легко объясняется, почему возведение в квадрат неравенства, обе части которого заключены под знак модуля не приводит ни к потере корней, ни к приобретению лишних корней. Репетитору желательно донести до сознания ученика тот факт,, что после возведения никаких проверок или дополнительных условий подмешивать к объекту не нужно, модули можно поменять на скобки, перенести все слагаемые в левую часть и разложить ее на множители. И ничего не надо возводить в степень… Сильному ученику можно показать расширенный метод интервалов для дробей с модулями, в котором, их раскрытие ведется по числителю и знаменателю независимо.
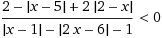 После раскрытия находят распределение знаков через графики (или через пробные точки в каждом промежутке) и уже по ним «читают» итоговые знаки всей дроби.
После раскрытия находят распределение знаков через графики (или через пробные точки в каждом промежутке) и уже по ним «читают» итоговые знаки всей дроби.
Стоит упомянуть, что репетитор по математике всегда выбирает глубину изложения темы в зависимости от ученика и разбирает с ним способы решения только до определенного уровня. К заданиям несколько более высокого уровня сложности обычно относят те, в которых или присутствует большое количество модулей, параметр, или модуль стоит поверх тригонометрической функции, или модули появляются при удалении квадратного корня вместе с полным квадратом какого-нибудь выражения, расположенным под его знаком.
К нестандартным я бы отнес функциональные приемы :
- использование области значений функции у=│f (х)|
- расширенный метод интервалов, применяемый к функциям с модулями.
Часто задаваемые вопросы учеников репетитору по теме «раскрытие модуля»
Колпаков Александр Николаевич, репетитор по математике.
Метки: Методики для репетиторов, Примеры объяснений, Раскрытие модуля, Решение уравнений
ankolpakov.ru
Решение уравнений с модулем ☑️ как раскрыть модуль квадратного уравнения, функции, свойства и виды неравенств, правила и способы решения, примеры, онлайн-калькулятор

Начало обучения
Теоретические знания нужно приобретать целенаправленно. Не имеет смысла запоминать огромные массивы информации, поскольку она не отложится в головном мозге. Объяснением этого является защита организма и нервной системы от переутомления. Однако следует обратить внимание на «лазейки», с помощью которых можно добиться успехов. При этом зубрить материал необязательно.
Математики рекомендуют не тратить время на заучивание материала. Они считают, что очень важно с ним ознакомиться и разобраться. Сегодня существует много информации, однако она часто изложена на непонятном языке или неправильно.
Перед изучением любой дисциплины следует составить подробный план. Эта операция довольно сложная, поскольку произвести ее может не каждый. Специалисты рекомендуют действовать по такому абстрактному алгоритму:
- Поставить задачу.
- Определить базовый минимум знаний.
- Найти информацию о каждом элементе второго пункта.
- Разобраться в терминах и теоретическом материале.
- Приступить к практике начиная с простых заданий.

Первый пункт должен быть подробно расписан. Необходимо точно описать проблему, а также последствия (например, научиться решать что-то). После этого нужно найти информацию, желательно использовать несколько источников. В некоторых случаях каждую задачу во втором пункте допускается разбивать на подзадачи.
Далее необходимо составить список всех необходимых знаний, которые нужны для достижения цели в первом пункте (например, решение квадратных уравнений с модулем). Их нужно расписать полностью. Можно воспользоваться любым текстовым процессором (Word, OpenOffice и т. д.). Основная задача третьего пункта заключается в полной систематизации информации.
Четвертый пункт — углубленное чтение. Нужно не просто прочитать материал, а попытаться в нем разобраться. Заучивать его нет смысла, поскольку такие действия очень часто приводят к разочарованию и усталости. После четвертого пункта следует приступить к решению простых примеров. Действия нужно выполнять до полного автоматизма. Основной принцип этого алгоритма — постепенное усваивание материала.
Базовые знания
Практическое применение описанного алгоритма следует разобрать на примере решения уравнений с модулем. Первый пункт — постановка задачи, формулировка которой следующая: научиться решать произвольные уравнения с модулем. На основании этого можно составить перечень элементов. Первым из них является модуль. Список пунктов по нему может быть следующим:
- Определение и обозначение.
- Геометрический и математический смысл.
- График функции y = |x|.
- Свойства.
Вторым пунктом является классификация уравнений, поскольку каждое из них может содержать модуль. Необходимо найти информацию о выражениях с неизвестным и их классификации. Третий пункт — способы и методы решения. В некоторых случаях потребуются алгоритмы нахождения корней. Если все систематизировать, то можно получить план такого вида:
- Модуль.
- Классификация уравнений.
- Алгоритмы и методы решения уравнений без модуля.
- Особенности решения выражений, содержащих неизвестные под знаком модуля.
Далее необходимо найти информацию об элементах плана. Нет необходимости включать в пункт 1 тыс. страниц печатного текста. Для этих целей следует воспользоваться и сравнить несколько источников. Объема, равного двум или трем листам, достаточно, но можно его сократить до одной страницы.
Общие сведения о модуле
Модулем числа называется абсолютная величина, представляющая неотрицательное число. Обозначается следующим образом: |любое число|. Следует отметить, что модуль рассматривается как два значения выражения (отрицательное и положительное). Это очень важно при решении уравнений. Запись |x| расписывается по формуле, которая состоит из кусочной линейной функции:

- х: x >= 0.
- -x: x < 0.
В результате этого нужно рассматривать два случая при решении: выражение принимает положительное и отрицательное значение. Алгебраическим смыслом модуля является положительная величина.
Геометрический смысл — расстояние от начала координат до искомой точки. Далее следует рассмотреть график функции y = |x|. Чтобы его начертить, нужно составить таблицу зависимости y от аргумента х.
| y | 2 | 1 | 0 | 1 | 2 |
| x | -2 | -1 | 0 | 1 | 2 |
Таблица 1. Зависимость значения функции y = |x| от ее аргумента.
Не имеет смысла использовать больше значений, поскольку графиком является прямая, зеркально отображенная относительно оси ординат ОУ. Далее нужно начертить декартовую прямоугольную систему координат и отметить на ней точки. Затем их следует соединить (рис. 1).
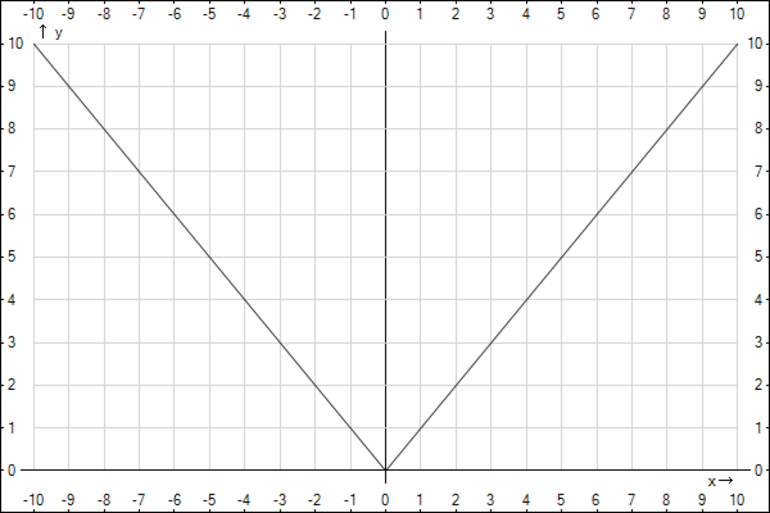
Рисунок 1. График y = |x|.
Необходимо знать также основные свойства абсолютной величины, которыми можно воспользоваться при решении соответствующих уравнений. К ним относятся следующие:

- Неотрицательное число: |x| >= 0.
- Модули чисел с разными знаками равны: |x| = |-x|.
- Произведение под знаком модуля равно произведению абсолютных величин: |x * y| = |x| * |y|.
- Частное двух чисел под знаком модуля равно частному их абсолютных значений: |x / y| = |x| / |y|. Необходимо учитывать, что y не равен нулю. Для пропорции тоже справедливо это утверждение: |x / y| = |z / w| = |x| / |y| = |z| / |w|.
- Модуль суммы равен или меньше суммы модулей значений: |x + y| <= |x| + |y|. Аналогично утверждение и для разности: |x – y| <= |x| – |y|.
- Константу (положительное число), умноженную на переменную, допускается выносить за знак модуля: |C * y| = C * |y|.
- Квадрат абсолютного значения равен квадрату числа, стоящего под модулем: |x|^2 = x 2.
- Корень четной степени 2n из числа a в степени 2n эквивалентен |a|: [a^(2n)]^(½n) = |a|.
Объем информации небольшой. Далее необходимо разобраться и приступить к сбору данных для следующего пункта.
Классификация уравнений
Существует огромное разнообразие уравнений и их частных случаев. Однако следует разобрать самые основные виды, которые встречаются в алгебраических задачах. Тождества с одним неизвестным бывают таких видов:
- линейные;
- квадратные;
- кубические;
- биквадратные (четвертая степень).
Первый тип является самым простым. Это уравнение вида Ay + B = 0. Для нахождения корня следует перенести известные величины в правую сторону относительно знака равенства, а неизвестный член оставляют в левой. В результате оно принимает такой вид: Ay = -B. Неизвестный аргумент можно найти по такой формуле: у = -В / А.
Квадратные уравнения вида Ay 2 + By + C = 0 (А не равно 0) решать немного сложнее, поскольку появляется новая величина. Она называется дискриминантом. Для нахождения корней следует применить такой алгоритм:
- Вычислить дискриминант: D = (-B)^2 – 4AC.
- Если D > 0, то решениями тождества считаются два корня: y1 = -B – D^(½) / 2A и y2 = -B + D^(½) / 2A.
- При D = 0 оно имеет всего один корень: y = -B / 2A.
- Если D < 0, то корней не существует.
- После нахождения корней или корня нужно проверить их, подставив в исходное тождество.
Если В = 0, то D считать нет смысла. Для решения достаточно перенести свободный член С в правую сторону тождества (Ay2 = C). Далее следует выполнить следующие шаги:
- Разделить С на А.
- Если (С / А) > 0, то извлечь квадратный корень из него: y = (С / А)^(½). Результат будет в виде двух решений, поскольку значение квадратного корня из числа являются положительной и отрицательной величинами.
- При (С / А) < 0 корней нет вообще.
Следует также рассмотреть случай, когда свободный член С = 0 (Ay 2 + By = 0). Уравнение решается при помощи вынесения общего множителя за скобку. Алгоритм решения довольно простой:
- Вынести неизвестную величину за скобку: y (Ay + B) = 0.
- Разобрать каждое уравнение: y1 = 0 и Ay2 + B = 0.
- Оба примера в пункте 2 решаются просто: первое — готовое решение, а второе — линейное.
Эти виды уравнений являются простыми. Отдельно следует описать принцип решения сложных тождеств с неизвестным.
Сложные типы
Сложнее решаются кубические тождества с неизвестным (Ay 3 + By 2 + Cy + D= 0). Они бывают нескольких типов, по которым и следует выбирать алгоритм решения:
- Ay 3 + D= 0.
- Ay 3 + By 2 + By + A = 0.
- Ay 3 + By 2 + Cy = 0.
- Ay 3 + By 2 + Cy + D = 0.
Для решения первого типа его следует привести к такому виду: y 3 + D/А= 0. Затем нужно воспользоваться формулой разложения на множители: y 3 + D/А = (y + (D/A)^(1/3)) * (y 2 — [(D/A)^(1/3)]y + [(D/A)^2]^(1/3)) = 0. В результате операции степень понижается, и получаются два уравнения.
Второй тип следует решать при помощи метода математических преобразований: Ay 3 + By 2 + By + A = A (y 3 + 1) + B (y 2 + x) = A (y + 1)(y 2 — y + 1) + By (y + 1) = (y + 1)(Ay 2 + y (B — A) + A) = 0. Получаются два тождества: линейное и квадратное. Для решения третьего вида следует просто вынести неизвестное за скобку: Ay 3 + By 2 + Cy = y (Ay 2 + By + C) = 0.
Сложно решить уравнение четвертого типа. Для этого следует воспользоваться формулой Кардана. Кроме того, необходимо придерживаться такого алгоритма:
- Ввести коэффициенты: Е1 = В/А, Е2 = С/А и Е3 = D/A.
- Параметры для формулы: u = -((E1)^2 / 3) + E2 и v = [2 (E1)^3 / 27] — [(E1 * E2) / 3] + E3.
- Формула Кардана: z = [(-v / 2) + ((v 2 / 4) + u 3 / 27)^(½)]^(1/3) + [(-v / 2) — (-(v 2 / 4) + u 3 / 27)^(½)]^(1/3).
- Найти корни: y1 = z – E1, y2 = z – E2 и y3 = z – E3.
Существуют также и биквадратные уравнения вида Ay 4 + By 2 + C = 0. Все они решаются при помощи замены. Суть методики сводится к понижению степени. Алгоритм решения имеет такой вид:
- Разделить все члены уравнения на А. Если А = 1, то этот пункт следует пропустить.
- Ввести параметр замены: t = y 2.
- Записать уравнение с учетом нового параметра: t 2 + (B/А)t + C/А = 0.
- Найти корни квадратного уравнения относительно t.
- Вернуться ко второму пункту, найти корни: y1 = t^(½) и y2 = -[t^(½)].
В пятом пункте следует учитывать, что корней может быть четыре, поскольку у квадратного тождества с неизвестным t есть один или два корня. Далее можно рассмотреть алгоритм для решения модульных уравнений.
Поиск корней
После изучения основных элементов, которые необходимы для решения равенств модульного типа с неизвестными, можно переходить к рассмотрению алгоритма. Следует на первоначальном этапе правильно раскрыть модуль в уравнении. Эту методику можно применить и к неравенствам такого же типа. Правила нахождения корней следующие:

- Раскрыть модуль.
- Упростить.
- Решить два уравнения по одной из методик.
- Проверить корни, подставив их в исходное выражение.
- Автоматизированная проверка.
При раскрытии модуля образуются выражения с противоположными знаками. Специалисты рекомендуют заключить их в квадратные скобки, а также указывать минус и плюс. Последний пункт — использование онлайн-калькулятора для решения уравнений с модулем. После теории можно приступить к практическому решению.

Пример решения
Необходимо решить уравнение биквадратного типа |4z 4 + 8z 2 — 20| = 4. Ошибочное утверждение, которое делают новички, заключается в упрощении (разделить обе части на 4). Однако это делать не рекомендуется, поскольку следует придерживаться алгоритма:

- Раскрытие модуля (двойное выражение): 4z 4 + 8z 2 — 20 = 4 и -[4z 4 + 8z 2 — 20] = 4.
- Упрощение: 4z 4 + 8z 2 — 20 — 4 = 4z 4 + 8z 2 — 24 = z 4 + 2z 2 — 6 = 0 и -4z 4 — 8z 2 + 20 — 4 = -z 4 + 2z 2 — 4 = 0.
- Решение z 4 + 2z 2 — 4 = 0 с вводом параметра замены t = z 2 : t 2 + 2t — 6 = 0.
- Дискриминант: D1 = (-B)^2 — 4AC = 4 — 4 * (-6) = 28 = [2 * (7)^(½)]^2.
- Корни: t1 = [-B — (D1)^(½)] / 2A = [2 — 2 * (7)^(½)] / 2 = -1 — (7)^(½) и t2 = -1 + (7)^(½).
- Окончательное решение первого уравнения: z1 = [-1 + (7)^(½)]^(½) и z2 = -[-1 + (7)^(½)]^(½).
- Решение второго уравнения с w = z 2 : w 2 + 2w — 4 = 0.
- Дискриминант: D2 = (-B)^2 — 4AC = 4 — 4 * (-4) = 20 = [2 * (5)^(½)]^2.
- Корни: w1 = [-B — (D1)^(½)] / 2A = [2 — 2 * (5)^(½)] / 2 = -1 — (5)^(½) и w2 = -1 + (5)^(½).
- Нахождение искомых корней: z3 = [-1 + (5)^(½)]^(½) и z4 = -[-1 + (5)^(½)]^(½).
Корнями являются четыре иррациональных значения. Если проверить при помощи онлайн-калькулятора, то ответы будут верными. В физике также можно встретить такой тип уравнений. Например, необходимо выполнить сравнение сил, направленных в противоположные стороны. В этом случае рекомендуется воспользоваться модулем для упрощения записи.
Задание любого типа следует решать, используя абстрактный алгоритм. Он позволяет произвести вычисления без ошибок, что позволит сэкономить много времени.
nauka.club
Решение уравнений с модулем
 Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа, и как правильно раскрывать выражения, содержащие знак модуля, то наличие в уравнении выражения, стоящего под знаком модуля, перестает быть препятствием для его решения.
Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа, и как правильно раскрывать выражения, содержащие знак модуля, то наличие в уравнении выражения, стоящего под знаком модуля, перестает быть препятствием для его решения.
Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.
Например, число +5, или просто 5 имеет знак «+» и абсолютное значение 5.
Число -5 имеет знак «-» и абсолютное значение 5.
Абсолютные значения чисел 5 и -5 равны 5.
Абсолютное значение числа х называется модулем числа и обозначается |x|.
Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.
Это же касается любых выражений, которые стоят под знаком модуля.
Правило раскрытия модуля выглядит так:
|f(x)|= f(x), если f(x) ≥ 0, и
|f(x)|= — f(x), если f(x) < 0
Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3<0.
Чтобы решить уравнение , содержащее выражение, стоящее под знаком модуля, нужно сначала раскрыть модуль по правилу раскрытия модуля.
Тогда наше уравнение или неравенство преобразуется в два различных уравнения, существующих на двух различных числовых промежутках.
Одно уравнение существует на числовом промежутке, на котором выражение, стоящее под знаком модуля неотрицательно.
А второе уравнение существует на промежутке, на котором выражение, стоящее под знаком модуля отрицательно.
Рассмотрим простой пример.
Решим уравнение:
|x-3|=-x2+4x-3
1. Раскроем модуль.
|x-3|=x-3, если x-3≥0, т.е. если х≥3
|x-3|=-(x-3)=3-x, если x-3<0, т.е. если х<3
2. Мы получили два числовых промежутка: х≥3 и х<3.
Рассмотрим, в какие уравнения преобразуется исходное уравнение на каждом промежутке:
А) При х≥3 |x-3|=x-3, и наше уранение имеет вид:
x-3=-x2+4x-3
Внимание! Это уравнение существует только на промежутке х≥3!
Раскроем скобки, приведем подобные члены:
x2 -3х=0
и решим это уравнение.
Это уравнение имеет корни:
х1=0, х2=3
Внимание! поскольку уравнение x-3=-x2+4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х2=3.
Б) При x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:
3-x=-x2+4x-3
Внимание! Это уравнение существует только на промежутке х<3!
Раскроем скобки, приведем подобные члены. Получим уравнение:
x2-5х+6=0
х1=2, х2=3
Внимание! поскольку уравнение 3-х=-x2+4x-3 существует только на промежутке x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х1=2.
Итак: из первого промежутка мы берем только корень х=3, из второго — корень х=2.
Ответ: х=3, х=2
ege-ok.ru
«Раскрытие модуля в тригонометрических уравнениях»
Открытый урок по теме:
«Раскрытие модуля по определению в тригонометрических уравнениях»
Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а < 0.
Согласно этому определению, в уравнениях модуль можно раскрывать следующим образом:
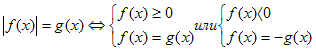
№1. Решить уравнение.
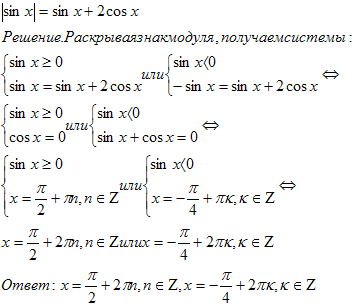
№2. Решить уравнение.
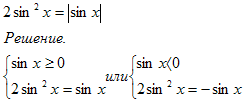
Решаем уравнение первой системы:
2sin2x-sinx=0
sinx(2sinx-1)=0
sinx=0 или sinx=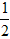 (оба уравнения удовлетворяют условию sinx≥0)
(оба уравнения удовлетворяют условию sinx≥0)
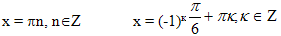
Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию sinx<0,
получаем х =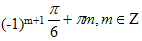
Серии ответов 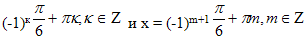 можно записать объединяя
можно записать объединяя
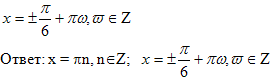
№3. Решить уравнение.
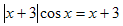
Решение. Раскрывая знак модуля, получаем системы:
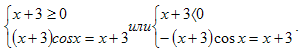
Решая уравнение первой системы, получим 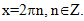 Из значений
Из значений 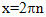 нужно выбрать те, которые удовлетворяют неравенству системы х ≥ -3. Это
нужно выбрать те, которые удовлетворяют неравенству системы х ≥ -3. Это 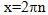 при n=0, 1, 2, 3…
при n=0, 1, 2, 3…
Решая уравнение второй системы, получим  Из этого множества значений нужно выбрать те, которые удовлетворяют неравенству х < -3. Это значения
Из этого множества значений нужно выбрать те, которые удовлетворяют неравенству х < -3. Это значения 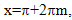 при m= -1, -2, -3…
при m= -1, -2, -3…
Ответ: 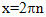 при n=0, 1, 2, 3…;
при n=0, 1, 2, 3…; 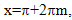 при m = -1, -2, -3…и х = -3
при m = -1, -2, -3…и х = -3
№4 Решить уравнение.
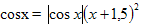
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, поэтому, раскрывая знак модуля, получим только одну систему 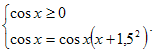
Решаем уравнение системы:
соsx=cosx(x+1,5)2
cosx(1-(x+1,5)2)=0
cosx=0 или x+1,5=1 или x-1,5 = -1
 х= -0,5 х = -2,5
х= -0,5 х = -2,5
Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)
Ответ: 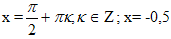
№5. Найти все решения уравнения 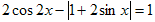 на отрезке [0;4].
на отрезке [0;4].
Решение. Перепишем уравнение в виде 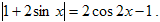
Раскрывая знак модуля, получаем системы:
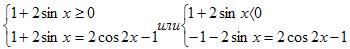
Решая первую систему, получим 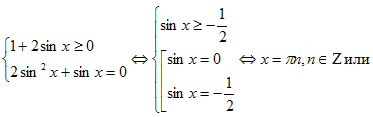
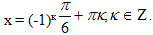
Из серии 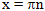 в нужном промежутке [0;4] лежат точки 0 и
в нужном промежутке [0;4] лежат точки 0 и 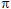 ; , а из серии
; , а из серии 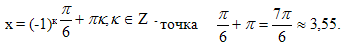
Решая вторую систему, получим систему  , которая не имеет решений.
, которая не имеет решений.
Ответ: 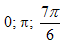
№6 Решить уравнение.
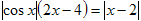
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия правого модуля по определению рассматривается только один случай: 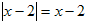
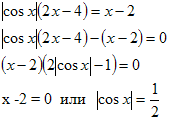
х=2 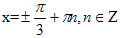
Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2
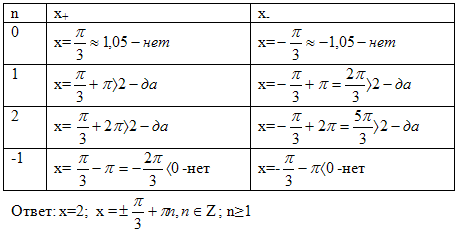
№7. Решить уравнение.
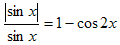
Решение. ОДЗ: 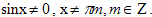
Раскрывая знак модуля, получаем системы: 
Решая первую систему, получим cos2x=0, и из решений 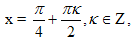 надо выбрать те, при которых sinx>0. На круге видно, что это точки вида
надо выбрать те, при которых sinx>0. На круге видно, что это точки вида 
Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.
Ответ: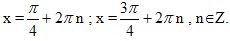
№8. Решить уравнение.
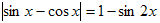
Решение. Преобразуем уравнение следующим образом:
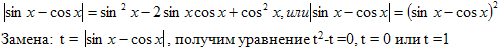
Обратная замена:
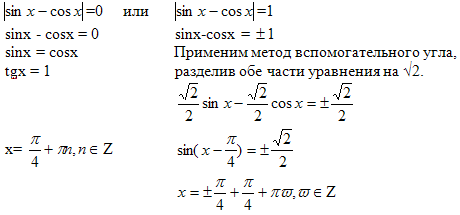
Ответ: 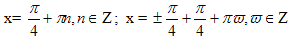
№9. Решить уравнение.
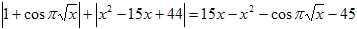
Решение. Выражение под первым модулем всегда неотрицательно, и его можно сразу отбросить. Второй модуль раскрываем по определению.
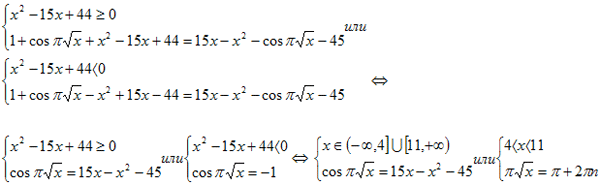
Решить уравнение первой система аналитически невозможно, исследуем поведение левой и правой частей на данных промежутках. Функция f(x) =-x2+15x-45=(-x2+15x-44)-1≤-1
при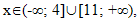 причем, f(х)= -1 в точках 4 и 11.Левая часть cos
причем, f(х)= -1 в точках 4 и 11.Левая часть cos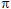
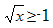 при любых х, причем, в точках 4 и 11 не равна -1, значит, система решений не имеет.
при любых х, причем, в точках 4 и 11 не равна -1, значит, система решений не имеет.
При решении уравнения второй системы получается:
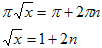 В промежутке
В промежутке  только одно целое нечетное число 3, т.е
только одно целое нечетное число 3, т.е 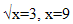
Ответ: 9
Другие способы раскрытия модулей.
Уравнения вида 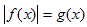 можно решать и следующим способом:
можно решать и следующим способом:
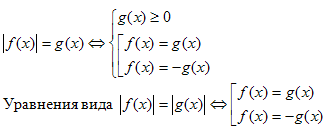
№10. Решить уравнение.
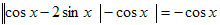
Решение. Левая часть уравнения неотрицательна, значит, неотрицательна и правая часть, тогда cosx <0, тогда уравнение равносильно системе 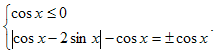
Рассмотрим две системы: 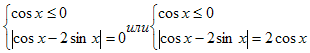
Решая уравнение первой системы получим: cosx-2sinx=0
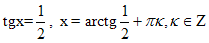
Учитывая, что cosx≤0, x = arctg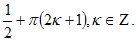 Вторая система решений не имеет.
Вторая система решений не имеет.
Ответ: x = arctg.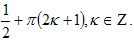
№11. Решить уравнение.
cosx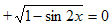
Решение.
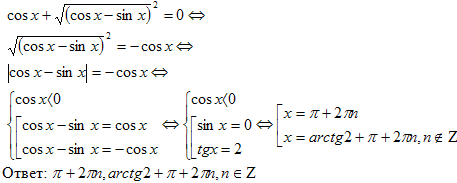
№12. Решить уравнение.
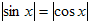
Решение. Уравнение равносильно sinx = ± cosx 
Ответ: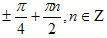
Задачи для самостоятельного решения:
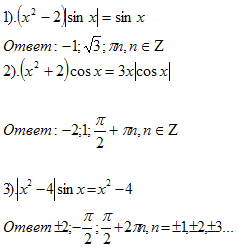
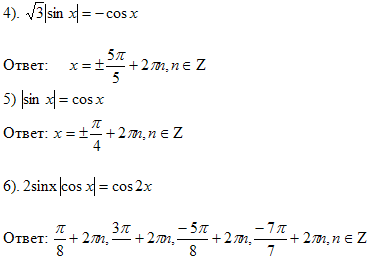
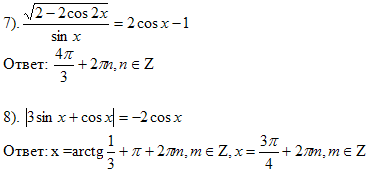
infourok.ru
Модуль числа, решение неравенств с модулем, свойства, как раскрыть, чему равен модуль отрицательного числа, как решать уравнения с модулем, примеры графиков
Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.
Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.
Что такое модуль в математике
Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.

Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.
Свойства модуля
Важно помнить о следующих свойствах:
- Правило раскрытия: абсолютная величина любого числа больше или равна нулю:

- Если абсолютные значения содержат выражения противоположных значений, они равны:

- Значение числа не превышает величину его модуля:

- Правило раскрытия при произведении:

- Правило, применимое при делении:

- При возведении в степень:

- Сумма величин:
- Двойной модуль:

Модуль комплексного числа
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).
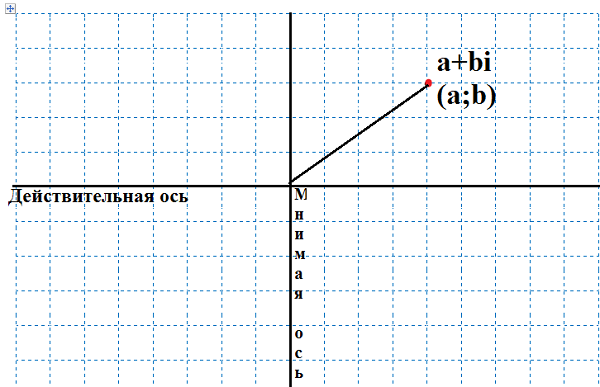
Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.
Как решать уравнения с модулем
Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.
Уравнения типа |x| = a
Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.
Равенство с абсолютной величиной не имеет решения, если величина отрицательная.
Если |x| <, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.
Уравнения типа |x| = |y|
Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.
Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).
Далее простая арифметика − нужно решить два равенства относительно x.
Уравнения типа |x| = y
Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.
Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:
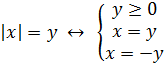
Решение неравенств с модулем
Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.
Уравнения вида |x| = a
Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.
Решение.
Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.
После перемещения константы вправо получено: |x| = 2.
Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.
Ответ: 2 и −2.
Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.
Решение.
Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.
Это означает, что –2 – поворотная точка.
Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.
Разделим интервал на 2 части:
- для x + 2 ≥ 0

Общим ответом для этих двух неравенств является интервал [−1, + ∞).
- для х + 2 <, 0
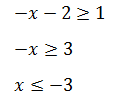
Общим ответом для этих двух неравенств является интервал (−∞, –3].
Окончательное решение – объединение ответов отдельных частей:
x ∈ (–∞, –3] ∪ [–1, + ∞).
Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).
Уравнения вида |x| = |y|
Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.
Решение:
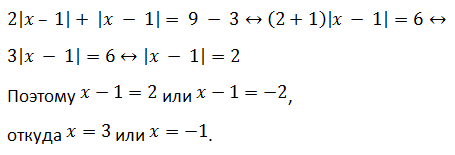
Ответ: x1 = 3, x2 = − 1.
Пример 2 (алгебра 8 класс). Решить неравенство:
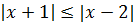
Решение:

Уравнения вида |x| = y
Пример 1 (алгебра 10 класс). Найти x:

Решение:
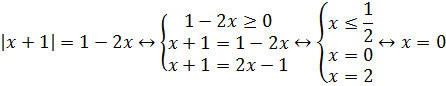
Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что не лежит в промежутке .
Ответ: x = 0.
Модуль суммы

Модуль разности
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.
Пример 1.
Пример 2.

Модуль отрицательного числа
Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,
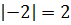
Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.
Модуль нуля
Известно свойство:
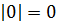
Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.
Модуль в квадрате
Модуль в квадрате всегда равен выражению в квадрате:
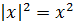
Примеры графиков с модулем
Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.
Пример 1.
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.
Решение:
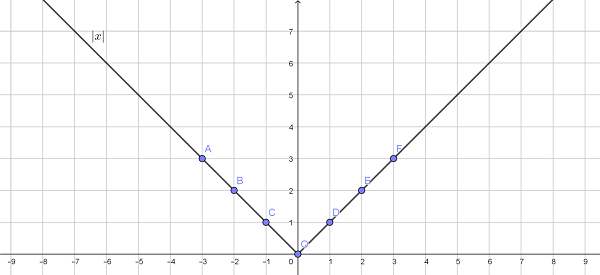
Объяснение: из рисунка видно, что график симметричен относительно оси Y.
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.
Решение:
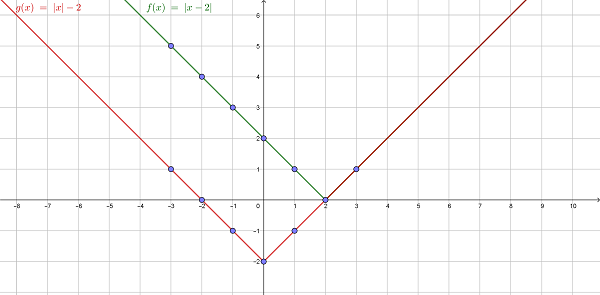
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).
Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.
Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.
Метод интервалов в задачах с модулем
Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.
Для использования метода нужно совершить следующие действия:
- Приравнять каждое выражение к нулю.
- Найти значения переменных.
- Нанести на числовую прямую точки, полученные в пункте 2.
- Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно. Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
- Решить неравенства с полученными знаками.
Пример 1. Решить методом интервалов.
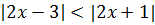
Решение:
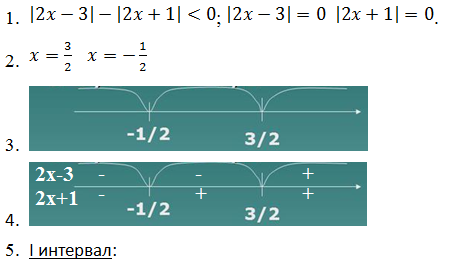

Результатом будет сумма всех подходящих интервалов.
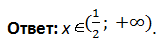
Модуль в модуле
Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.
Лучше всего понять принцип на примере.
Пример 1. Решить
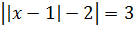
Решение:
Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:
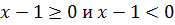
В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:

Нужно упростить два уравнения:
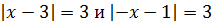
Далее каждое из равенств разделяется еще на два:
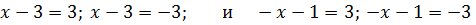
Получено четыре результата:
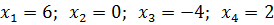

Заключение
Самое важное, что нужно знать: модуль не может быть отрицательным.
Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.
В качестве итогов, напомним все свойства, которые помогут в решении задач:
- когда положительное число находится внутри модуля, достаточно просто избавиться от него,
- если есть выражение, нужно его упростить, прежде чем найти абсолютное значение,
- если равенство содержит две переменные, нужно решать его с помощью системы уравнений и за основу брать методы решения выражений с абсолютными величинами.
Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.
tvercult.ru