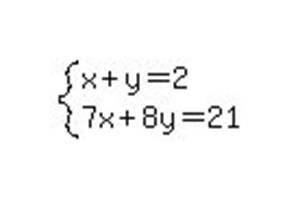6.А. Метод Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных, данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример 18. Решить систему уравнений методом Гаусса:

Решение. Выпишем расширенную матрицу данной системы

и произведем следующие элементарные преобразования над ее строками:
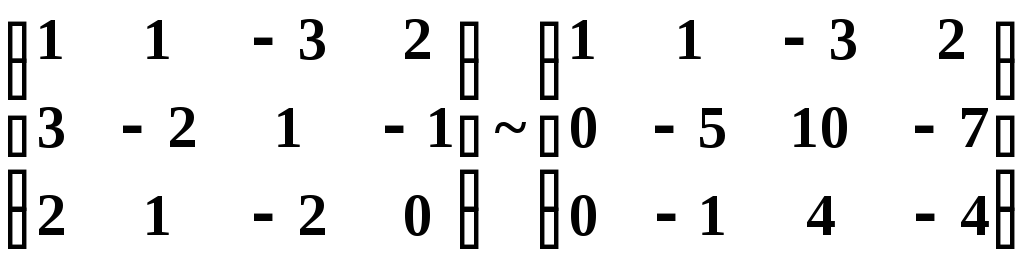
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
 ;
;
б) третью строку умножим на (- 5) и прибавим к ней вторую:
 .
.
В результате всех этих преобразований данная система приводится к треугольному виду:
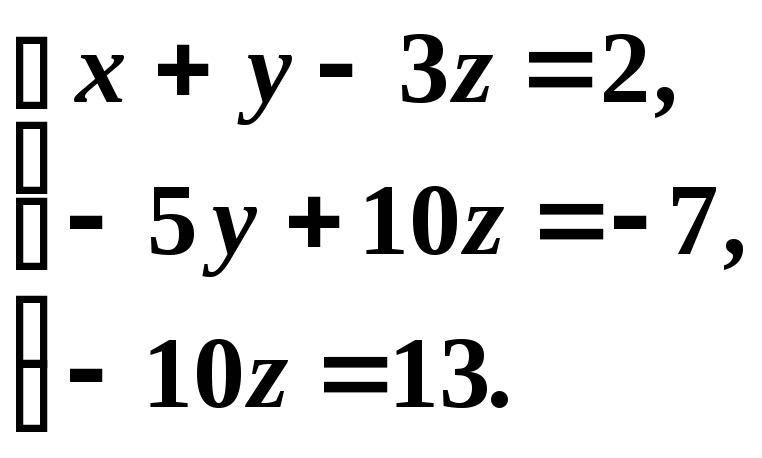
Из
последнего уравнения находим  .
Подставляя это значение во второе
уравнение, имеем
.
Подставляя это значение во второе
уравнение, имеем .
Далее из первого уравнения получим
.
Далее из первого уравнения получим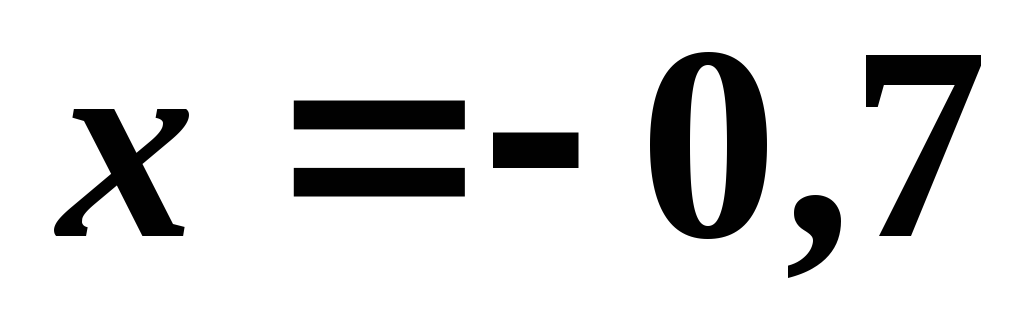 .
.
6.Б. Формулы Крамера
Назовем
столбцы матрицы  следующим образом: первый столбец —
следующим образом: первый столбец — ,
второй столбец —
,
второй столбец — ,
и т.д., последний столбец —
,
и т.д., последний столбец —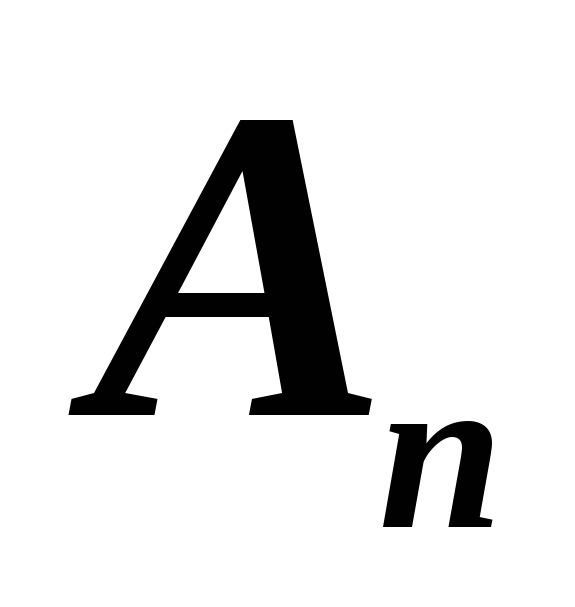 .
Тогда матрицу
.
Тогда матрицу
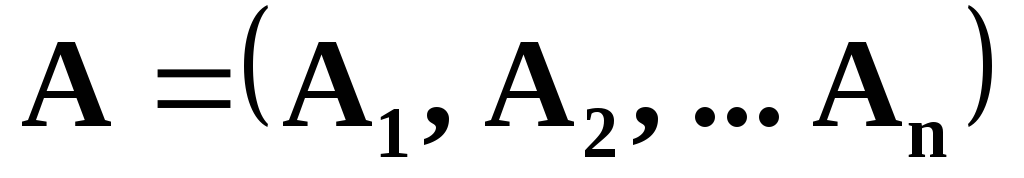 .
. Составим  дополнительных матриц:
дополнительных матриц:
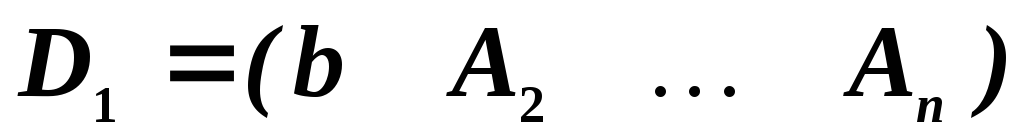 ,
, 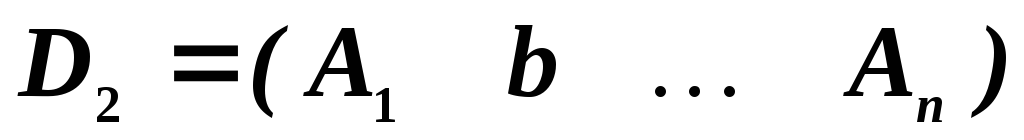 ,
…,
,
…, ,
,
и вычислим их определители и определитель исходной матрицы:
 ,
,  ,
, ,
…,
,
…,
Тогда значения неизвестных вычисляются по формулам Крамера:
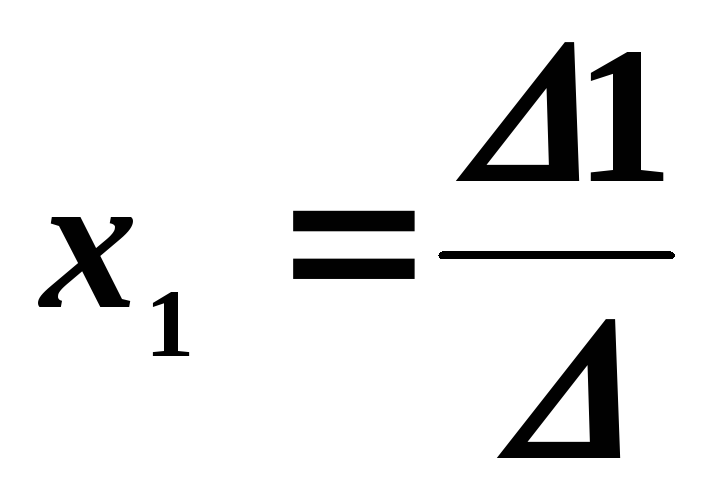 ,
,  ,
…,
,
…, .
.
Правило Крамера дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по вышеприведенным формулам.
Если
главный определитель системы  и все вспомогательные определители
и все вспомогательные определители равны нулю, то система имеет бесчисленное
множество решений.
равны нулю, то система имеет бесчисленное
множество решений.
Если
главный определитель системы 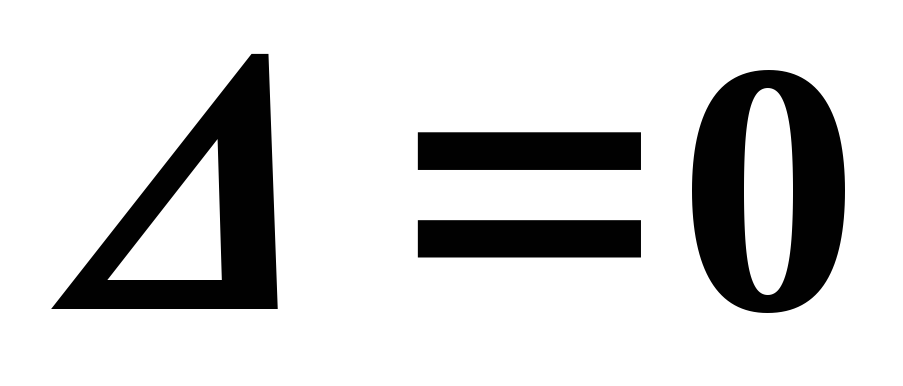 ,
а хотя бы один вспомогательный определитель
отличен от нуля, то система несовместна.
,
а хотя бы один вспомогательный определитель
отличен от нуля, то система несовместна.
Пример 19. Решить систему уравнений методом Крамера.
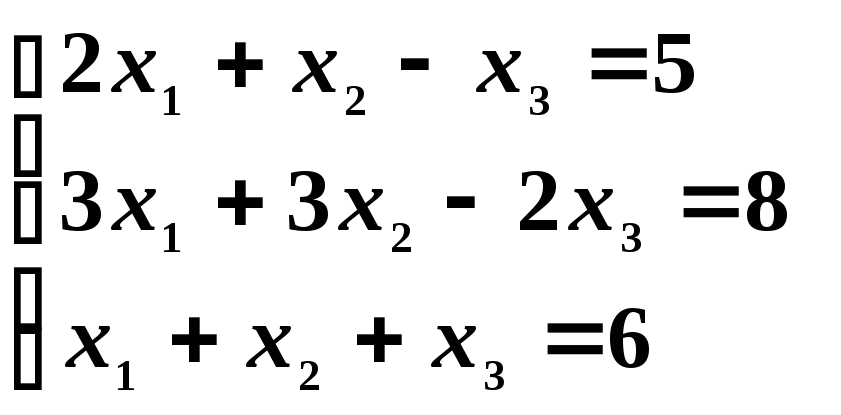
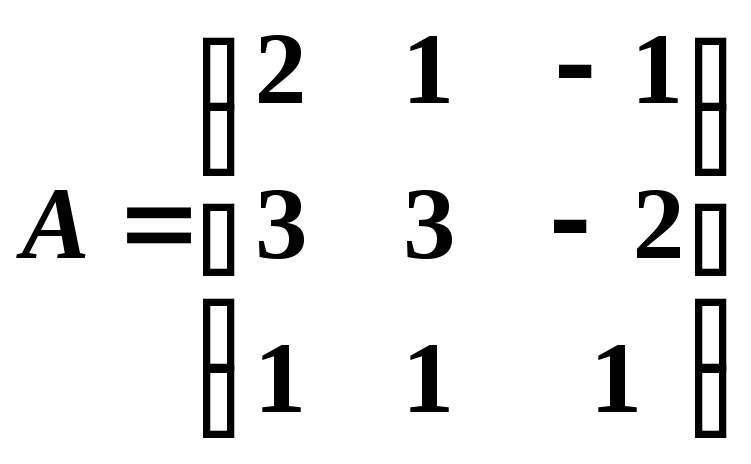 ,
, .
.
Тогда
 ,
, ,
,
Вычисляя определители этих
матриц, получаем 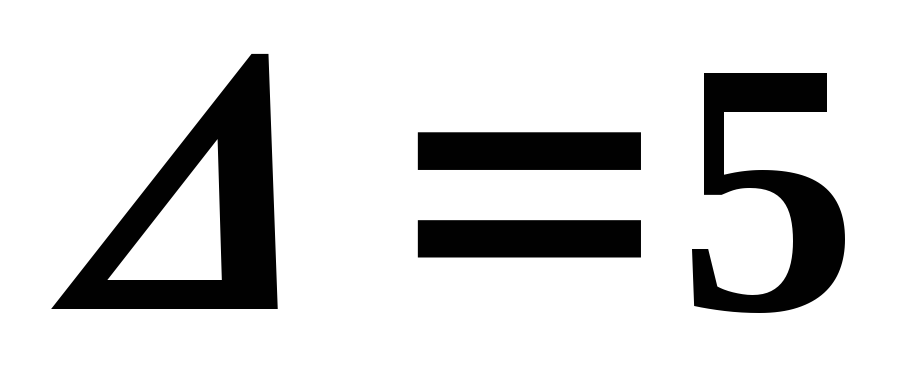 ,
, ,
, ,
, .
.
И по формулам Крамера
находим:  ,
, ,
, .
.
6.В. Матричный метод
Теперь,
рассмотрим матричное уравнение 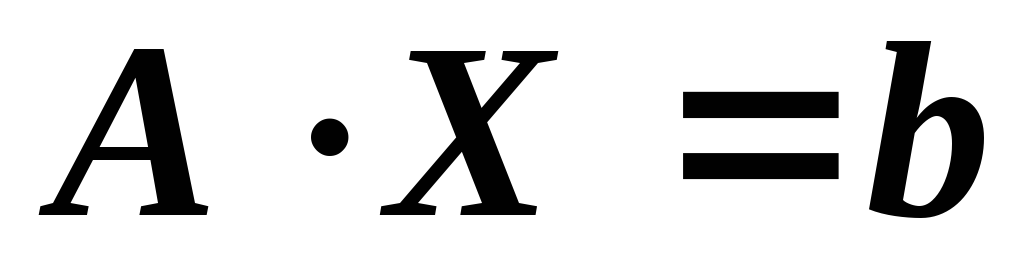 .
Если у матрицы
.
Если у матрицы
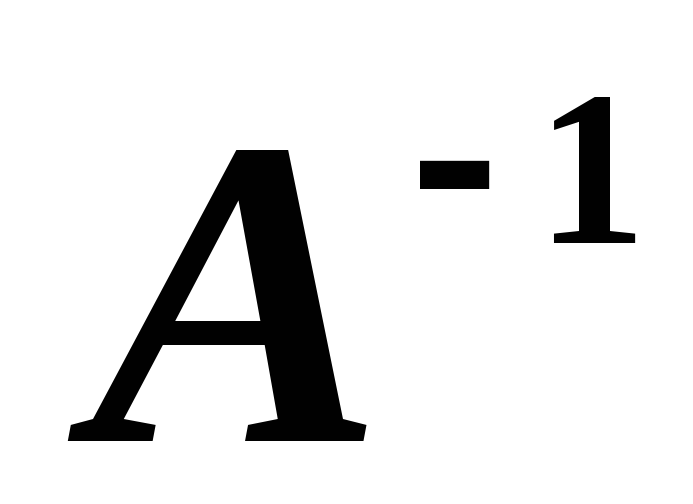 ,
то, умножая матричное уравнение на
,
то, умножая матричное уравнение на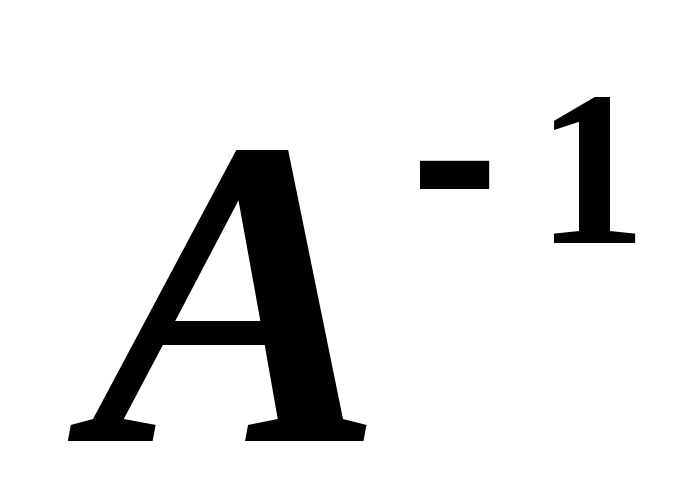 слева, получим:
слева, получим:  .
.
По
определению обратимости матрицы  и по свойству единичной
и по свойству единичной ,
получаем:
,
получаем:
 .
.
Пример 20. Решить систему уравнений с помощью обратной матрицы.

Имеем:
 ,
, .
.
Вычислим определитель
матрицы  ,
разлагая по первой строке:
,
разлагая по первой строке:

Значит, обратная матрица существует. Вычислим алгебраические дополнения элементов матрицы:
 ,
, ,
,
 ,
,
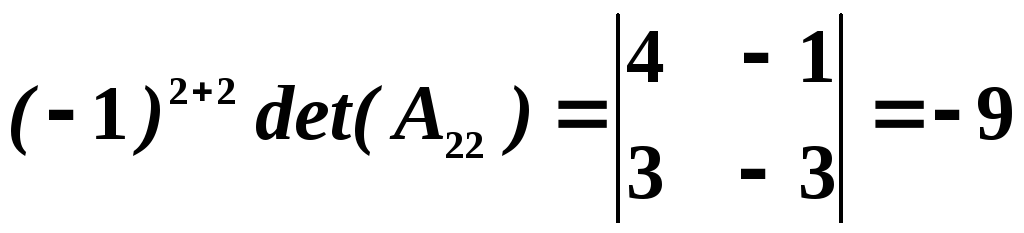 ,
,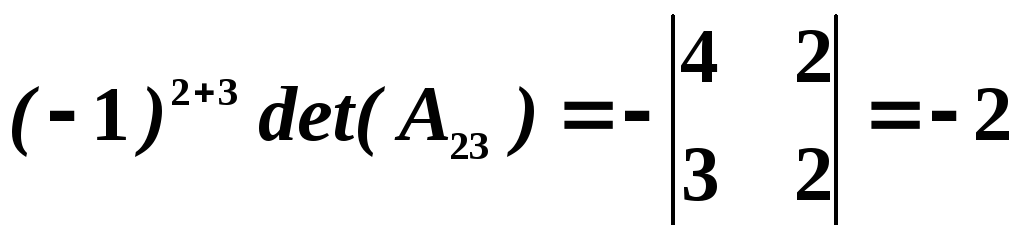 ,
,
 ,
, ,
,
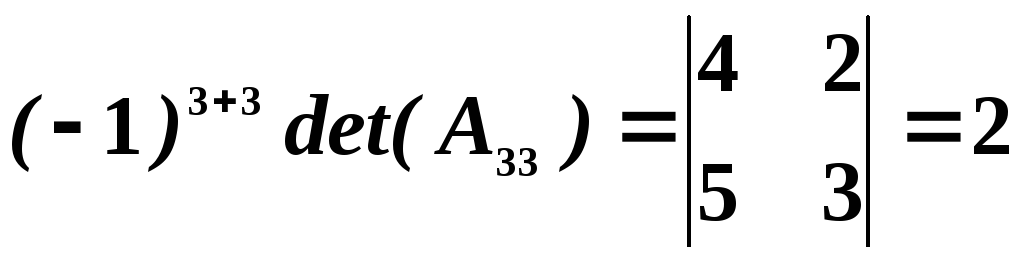 .
.
Тогда решение системы получается умножением обратной матрицы на столбец свободных членов

7. Системы линейных уравнений общего вида
Если
система уравнений оказалась совместной,
т. е. матрицы 
 имеют один и тот же ранг, то могут
представиться две возможности ‑ a)
имеют один и тот же ранг, то могут
представиться две возможности ‑ a)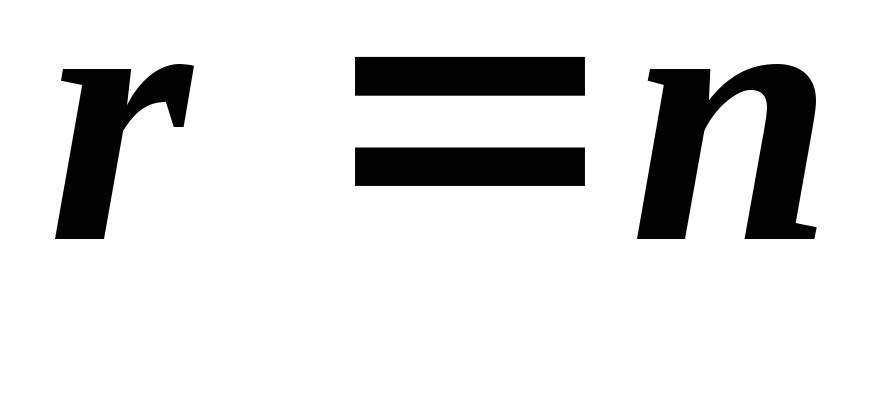 ,
б)
,
б) .
. а)
Если  ,
то имеем
,
то имеем независимых уравнений с
независимых уравнений с неизвестными, причем определитель
неизвестными, причем определитель этой системы отличен от нуля. Такая
система имеет единственное решение,
получаемое, например, по формулам
Крамера.
этой системы отличен от нуля. Такая
система имеет единственное решение,
получаемое, например, по формулам
Крамера.
б)
Если 
Перенесем
лишние неизвестные 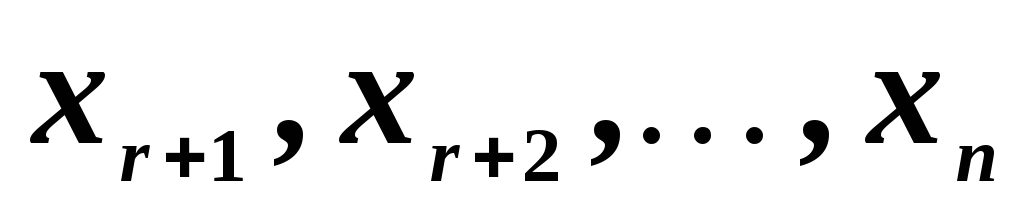 ,
которые принято называть свободными,
в правые части; наша система линейных
уравнений примет вид:
,
которые принято называть свободными,
в правые части; наша система линейных
уравнений примет вид:

Ее
можно решить относительно  ,
так как определитель этой системы (
,
так как определитель этой системы (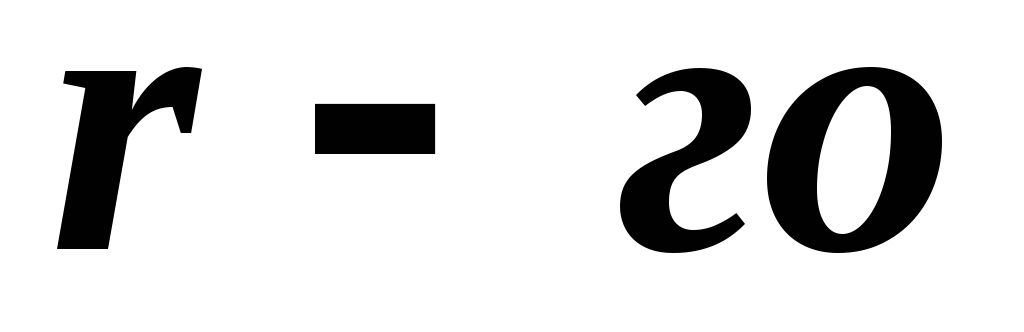 порядка) отличен от нуля. Придавая
свободным неизвестным произвольные
числовые значения, получим по формулам
Крамера соответствующие числовые
значения для
порядка) отличен от нуля. Придавая
свободным неизвестным произвольные
числовые значения, получим по формулам
Крамера соответствующие числовые
значения для .
Таким образом, при
.
Таким образом, при имеем бесчисленное множество решений.
имеем бесчисленное множество решений.
Система
уравнений называется однородной,
если все  ,
т. е. она имеет вид:
,
т. е. она имеет вид:

Из
теоремы Кронекера-Капелли следует, что
она всегда совместна, так как добавление
столбца из нулей не может повысить ранга
матрицы. Это, впрочем, видно и непосредственно
— система заведомо обладает нулевым,
или тривиальным, решением  .
Пусть матрица
.
Пусть матрица системы имеет ранг
системы имеет ранг .
.
Если 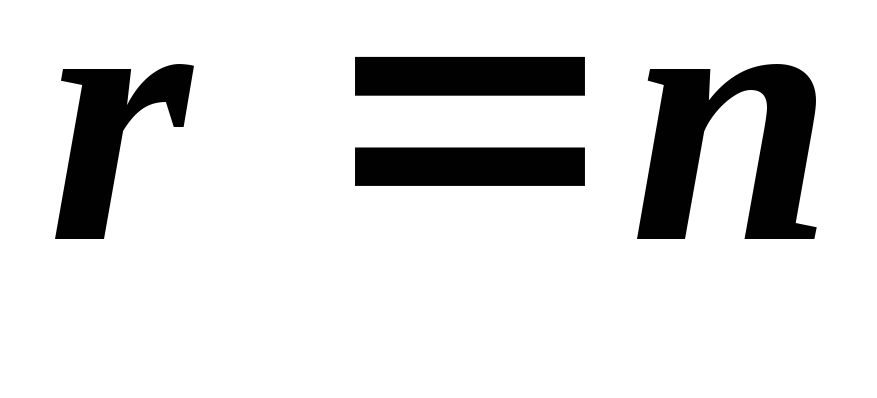 ,
то нулевое решение будет единственным
решением системы; при
,
то нулевое решение будет единственным
решением системы; при система обладает решениями, отличными
от нулевого, и для их разыскания применяют
тот же прием, как и в случае произвольной
системы уравнений.
система обладает решениями, отличными
от нулевого, и для их разыскания применяют
тот же прием, как и в случае произвольной
системы уравнений.
Всякий
ненулевой вектор ‑ столбец 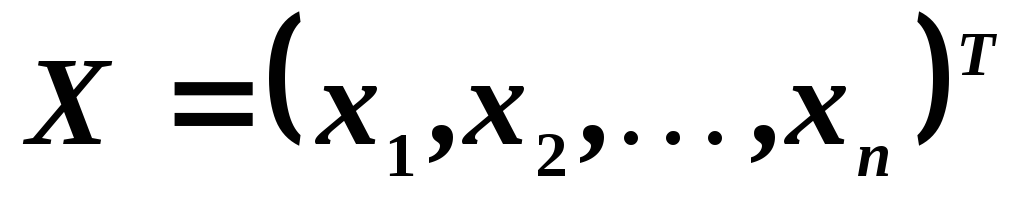 называетсясобственным
вектором линейного преобразования (квадратной
матрицы
называетсясобственным
вектором линейного преобразования (квадратной
матрицы  ), если
найдется такое число
), если
найдется такое число  ,
что будет выполняться равенство
,
что будет выполняться равенство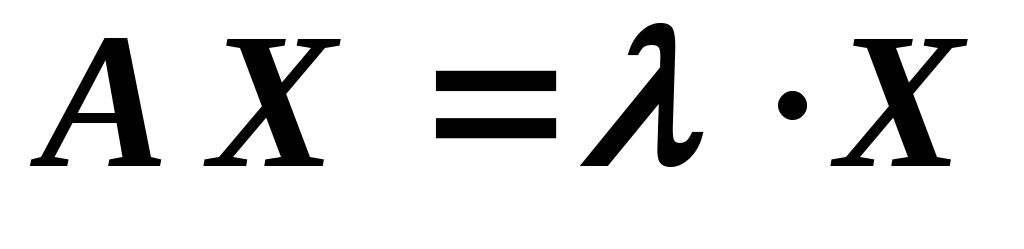 .
.
Число  называетсясобственным
значением линейного преобразования (матрицы
называетсясобственным
значением линейного преобразования (матрицы  ), соответствующим вектору
), соответствующим вектору  .
Матрица
.
Матрица имеет порядок
имеет порядок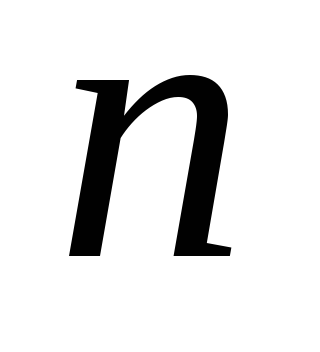 .
.
В
математической экономике большую роль
играют так называемые продуктивные
матрицы.
Доказано, что матрица  является продуктивной тогда и только
тогда, когда все собственные значения
матрицы
является продуктивной тогда и только
тогда, когда все собственные значения
матрицы по модулю меньше единицы.
по модулю меньше единицы.
Для
нахождения собственных значений матрицы  перепишем равенство
перепишем равенство в виде
в виде ,
где
,
где —
единичная матрица
—
единичная матрица 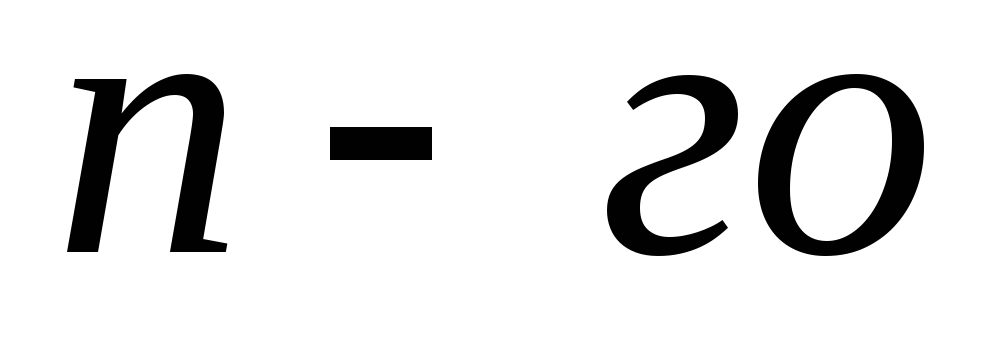 порядка или в координатной форме:
порядка или в координатной форме:
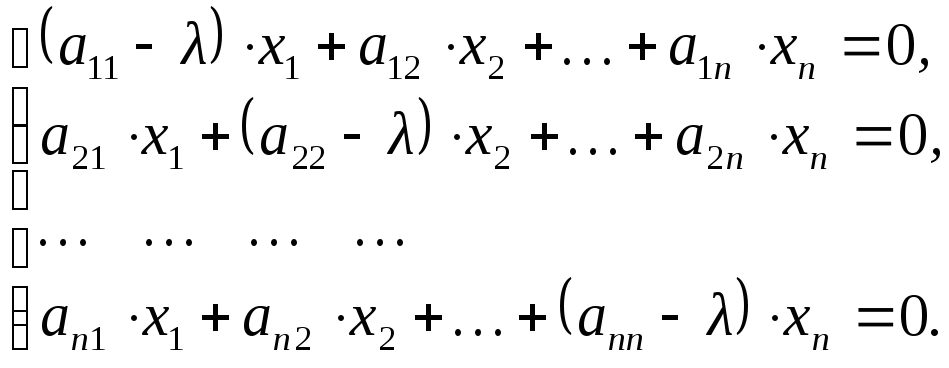
Получили систему линейных однородных уравнений, которая имеет ненулевые решения тогда и только тогда, когда определитель этой системы равен нулю, т.е.
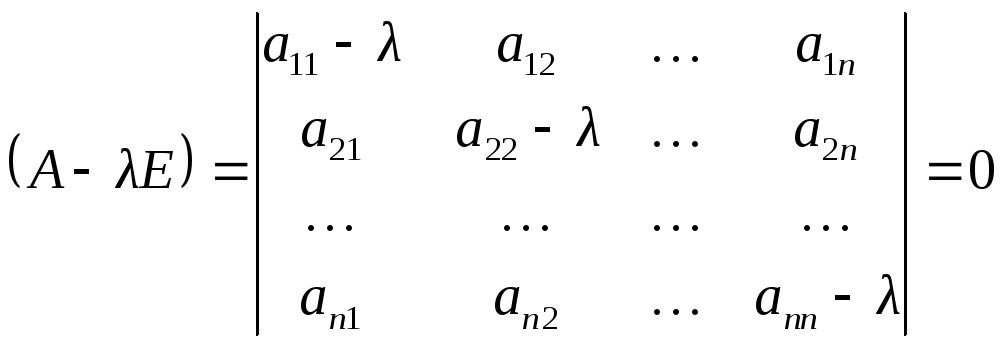 .
.
Получили
уравнение  степени относительно неизвестной
степени относительно неизвестной ,
которое называетсяхарактеристическим
уравнением матрицы
,
которое называетсяхарактеристическим
уравнением матрицы  ,
многочлен
,
многочлен называетсяхарактеристическим
многочленом матрицы
называетсяхарактеристическим
многочленом матрицы  ,
а его корни —характеристическими
числами, или собственными значениями,
матрицы
,
а его корни —характеристическими
числами, или собственными значениями,
матрицы  .
.
Для
нахождения собственных векторов матрицы  в векторное уравнение
в векторное уравнение или в соответствующую систему однородных
уравнений нужно подставить найденные
значения
или в соответствующую систему однородных
уравнений нужно подставить найденные
значения и решать обычным образом.
и решать обычным образом.
Пример 18. Исследовать систему уравнений и решить ее, если она совместна.
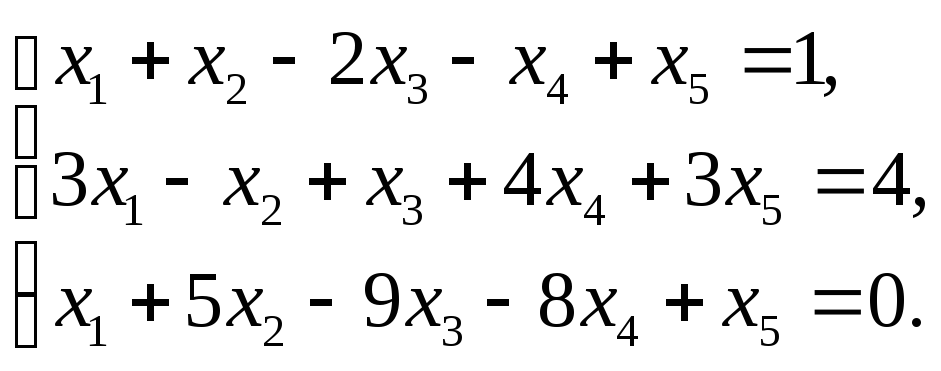
Решение. Будем
находить ранги матриц  и
и методом элементарных преобразований,
приводя одновременно систему к
ступенчатому виду:
методом элементарных преобразований,
приводя одновременно систему к
ступенчатому виду:
 .
.
Очевидно,
что  .
Исходная система равносильна следующей
системе, приведенной к ступенчатому
виду:
.
Исходная система равносильна следующей
системе, приведенной к ступенчатому
виду:

Поскольку определитель при неизвестных x1 и x2отличен от нуля, то их можно принять в качестве главных и переписать систему в виде:

откуда 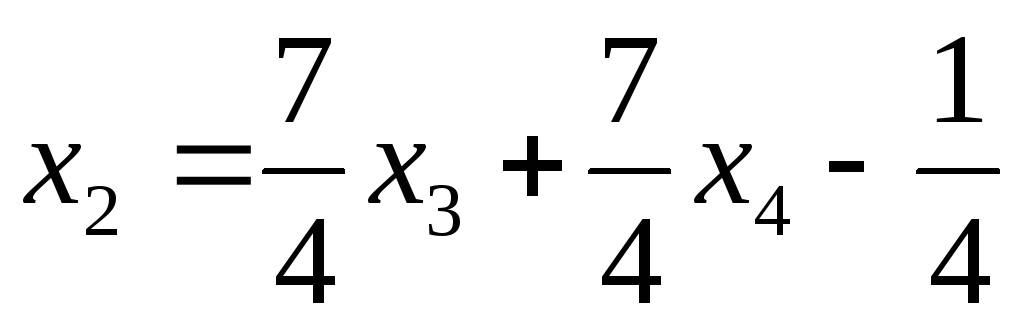 ,
,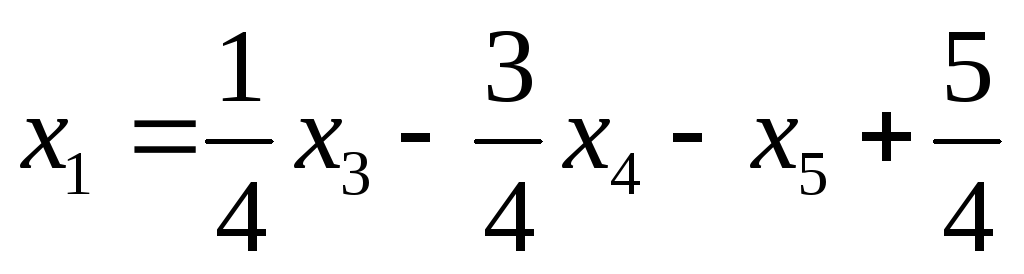 ‑ общее решение системы, имеющей
бесчисленное множество решений. Придавая
свободным неизвестнымx3,
x4,
x5конкретные
числовые значения, будем получать
частные решения. Например, при
‑ общее решение системы, имеющей
бесчисленное множество решений. Придавая
свободным неизвестнымx3,
x4,
x5конкретные
числовые значения, будем получать
частные решения. Например, при  ,
, ,
, .
Вектор
.
Вектор  является частным решением данной
системы.
является частным решением данной
системы.
Пример
19. Исследовать систему уравнений и найти
общее решение в зависимости от значения
параметра  .
.

Решение. Данной системе соответствует матрица
 .
.
Имеем
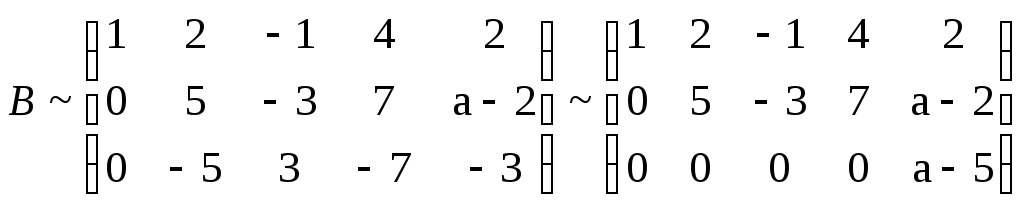
следовательно, исходная система равносильна такой:

Отсюда
видно, что система совместна только при  .
Общее решение в этом случае имеет вид:
.
Общее решение в этом случае имеет вид:
 ,
,  .
.
Пример 20. Выяснить, будет ли линейно зависимой система векторов:
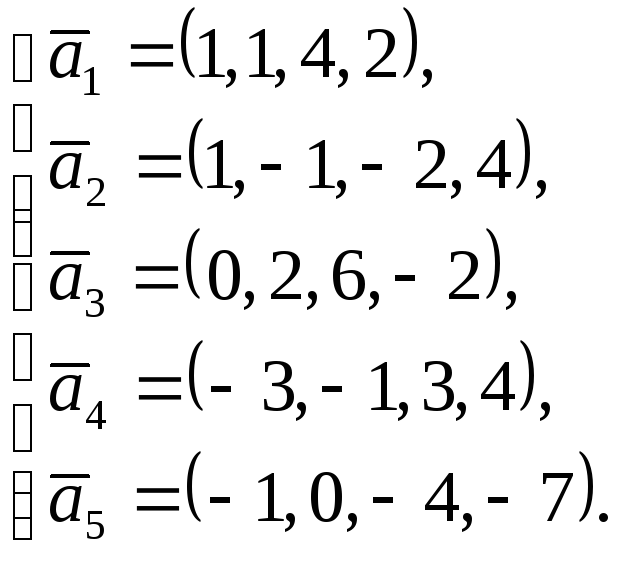
Решение. Система векторов является линейно зависимой, если найдутся такие числа x1, x2, x3, x4, x5, из которых хотя бы одно отлично от нуля, что выполняется векторное равенство:
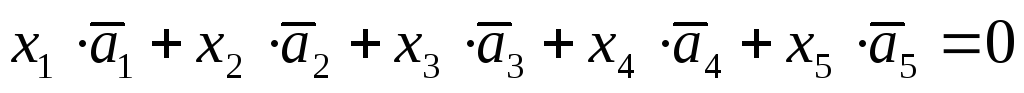 .
.
В координатной записи оно равносильно системе уравнений:

Итак, получили систему линейных однородных уравнений. Решаем ее методом исключения неизвестных:

Система
приведена к ступенчатому виду. Ранг
матрицы равен  ,
значит однородная система уравнений
имеет решения, отличные от нулевого
(
,
значит однородная система уравнений
имеет решения, отличные от нулевого
( ).
Определитель при неизвестныхx1,
x2,
x4 отличен от нуля, поэтому их можно выбрать
в качестве главных и переписать систему
в виде:
).
Определитель при неизвестныхx1,
x2,
x4 отличен от нуля, поэтому их можно выбрать
в качестве главных и переписать систему
в виде:

Имеем:
 ,
, 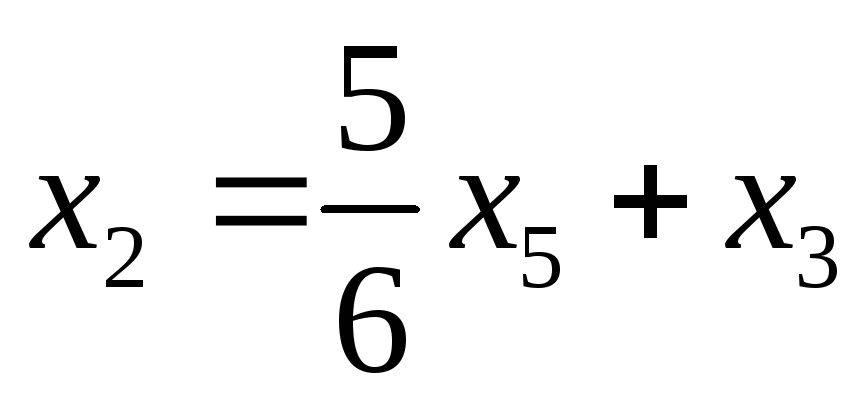 ,
, .
.
Система имеет бесчисленное множество решений; если свободные неизвестные x3и x5не равны нулю одновременно, то и главные неизвестные отличны от нуля. Следовательно, векторное уравнение
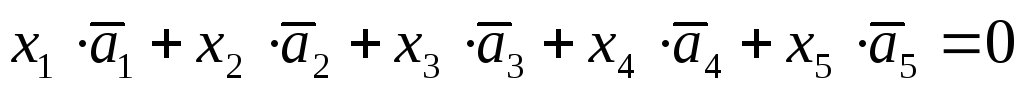
имеет
коэффициенты, не равные нулю одновременно;
пусть например, 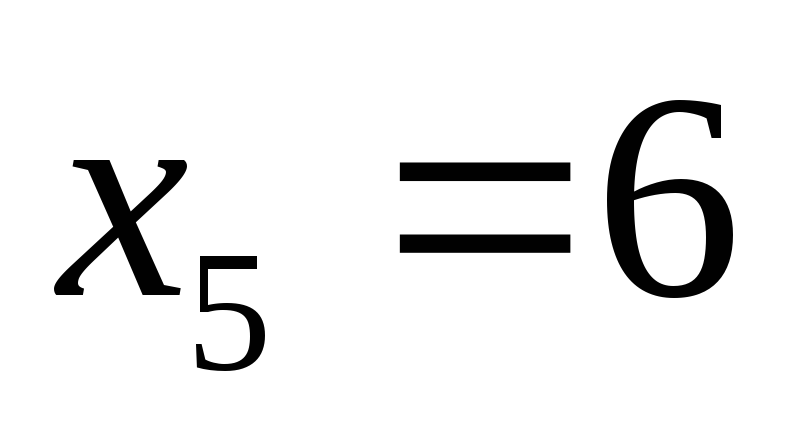 ,
, .
Тогда
.
Тогда ,
, ,
, и мы получим соотношение
и мы получим соотношение
 ,
,
т.е. данная система векторов линейно независима.
Пример 21. Найти собственные значения и собственные векторы матрицы
 .
.
Решение. Вычислим
определитель матрицы  :
:


Итак, 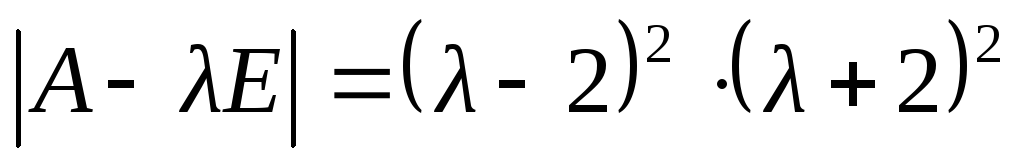 .
Корни характеристического уравнения
.
Корни характеристического уравнения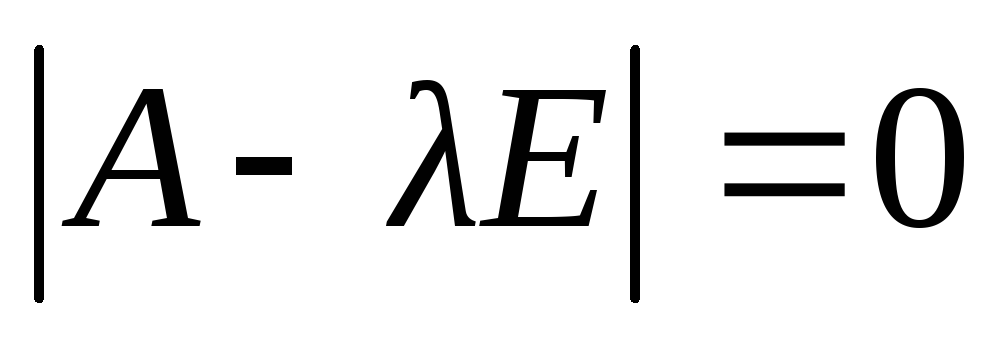 ‑ это числа
‑ это числа и
и .
Другими словами, мы нашли собственные
значения матрицы
.
Другими словами, мы нашли собственные
значения матрицы .
Для нахождения собственных векторов
матрицы
.
Для нахождения собственных векторов
матрицы подставим найденные значения
подставим найденные значения в систему: при
в систему: при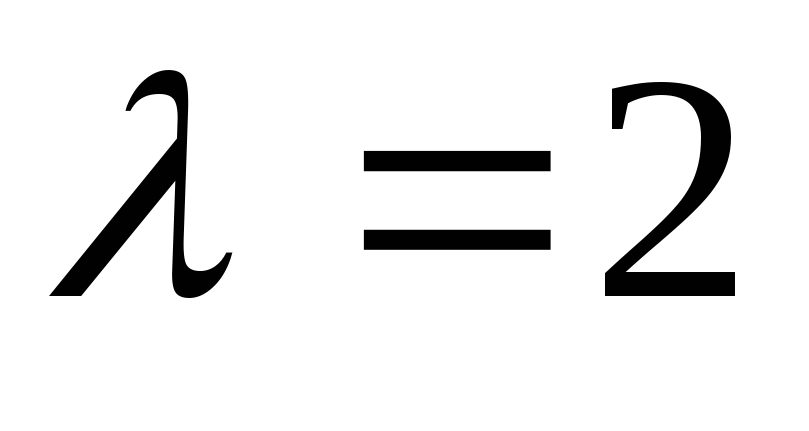 имеем систему линейных однородных
уравнений
имеем систему линейных однородных
уравнений

Следовательно,
собственному значению 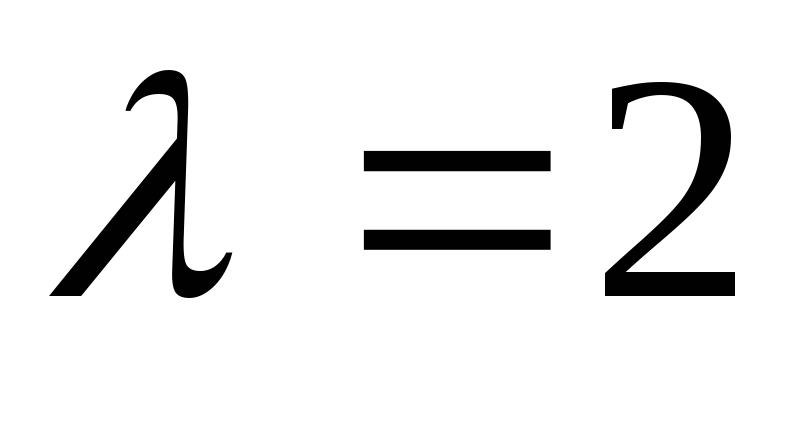 отвечают собственные векторы вида
отвечают собственные векторы вида (8, 8, -3, 15), где
(8, 8, -3, 15), где — любое отличное от нуля действительное
число. При
— любое отличное от нуля действительное
число. При имеем:
имеем:
 ,
,
и поэтому координаты собственных векторов должны удовлетворять системе уравнений
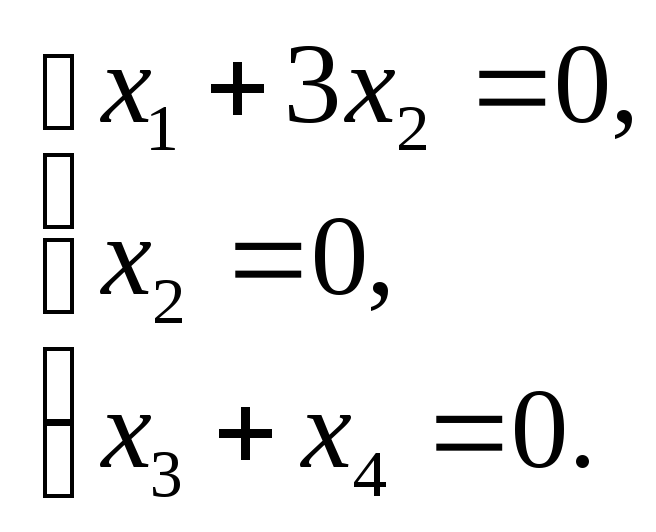
Поэтому
собственному значению  отвечают собственные векторы вида
отвечают собственные векторы вида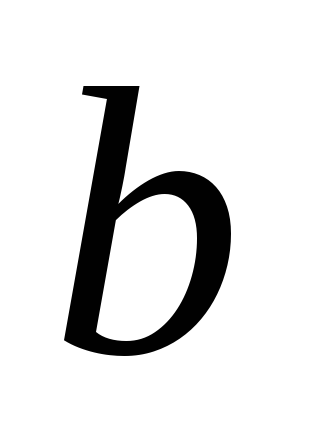 (0, 0,-1, 1), где
(0, 0,-1, 1), где — любое отличное от нуля действительное
число.
— любое отличное от нуля действительное
число.
FVB
studfile.net
Алгоритм метода Гаусса:
1) Составить расширенную матрицу системы, включающую столбец свободных членов.
2) Если а11 0, то первую строку делим на а11 и умножаем на (– a21) и прибавляем вторую строку. Аналогично дойти до m–той строки:
I стр. делим на а11 и умножаем на (– аm1) и прибавляем m – тую стр.
При этом из уравнений, начиная со второго по m – тое, исключится переменная x1.
3) На 3 ‒ м шаге вторая строка используется для аналогичных элементарных преобразований строк с 3 ‒ й по m – тую. При этом исключится переменная x2 , начиная с 3 ‒ й строки по m – тую, и т. д.
В результате этих преобразований система приведется к треугольной или ступенчатой форме (в случае треугольной формы под главной диагональю нули).
Приведение системы к треугольной или ступенчатой форме называется прямым ходом метода Гаусса, а нахождение неизвестных из полученной системы называется обратным ходом.
Пример:

Прямой ход. Приведём расширенную матрицу системы

с помощью элементарных преобразований к ступенчатому виду. Переставим первую и вторую строки матрицыAb, получим матрицу:

Сложим вторую строку полученной матрицы с первой, умноженной на (‒2), а её третью строку – с первой строкой, умноженной на (‒7). Получим матрицу

К третьей строке полученной матрицы прибавим вторую строку, умноженную на (‒3), в результате чего получим ступенчатую матрицу

Таким образом, мы привели данную систему уравнений к ступенчатому виду:
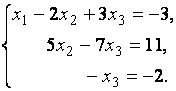 ,
,
Обратный
ход. Начиная с последнего уравнения
полученной ступенчатой системы уравнений,
последовательно найдём значения
неизвестных: 
Вопрос 2. Исследование систем линейных уравнений.
Теорема Кронекера — Капелли, базисные решения.
Теорема 1. Система m – линейных уравнений с n – неизвестными совместна только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
r (A) = r (Aв)
Пример:
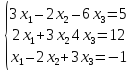
│А│= 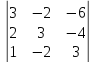 = 58
0, r (А) = 3;
= 58
0, r (А) = 3;
AB= 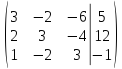 =r (AB)
≤ 3, так как
=r (AB)
≤ 3, так как
 =
‒ 8 + 45 + 144 ‒ 40 + 72 ‒ 18 = 195 =r (AB)
= 3 =
=
‒ 8 + 45 + 144 ‒ 40 + 72 ‒ 18 = 195 =r (AB)
= 3 =
r(A) = r (AB) => по теореме Кронекера ‒ Капелли система совместна.
Теорема 2. Если ранг матрицы совместной системы равен числу неизвестных, т. е. r(A) = n, то система имеет единственное решение.
Если ранг матрицы системы меньше числа неизвестных, т. е. r (A) <n, то переменные х1, х2, …, хrназываются базисными, если минор, составленный из коэффициентов при этих неизвестных 0.
Остальные (n – r) – неизвестных называются свободными.
Пример: найти базисное решение системы уравнений.
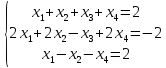
Решение:

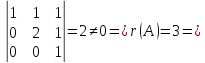 х1,
х2,
х3 –
базисные, х4 –
свободное.
х1,
х2,
х3 –
базисные, х4 –
свободное.

Пусть х4= C = const; х3= 2, тогда
2 х2+ 2 + 2 C= 0 | · 2
х2= – C – 1
х1 – C – 1 + 2 + C= 2;
х1= 1
Ответ:
х1= 1;
х2= – C – 1;
х3 = 2;
х4= C.
Найдем частное решение:
Пусть C = 1, тогда
х1= 1;
х2= – 2;
х3 = 2;
х4= 1.
Проверка:
Подставим значения х1, х2, х3, и х4 в систему уравнений
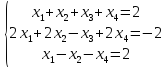 ,
,
Получим

Лекция № 6
Вопрос 1. Системы линейных однородных уравнений.
Исследование решений. Фундаментальная система решений.
Однородной системы m – линейных уравнений с n – неизвестными называется система уравнений вида:
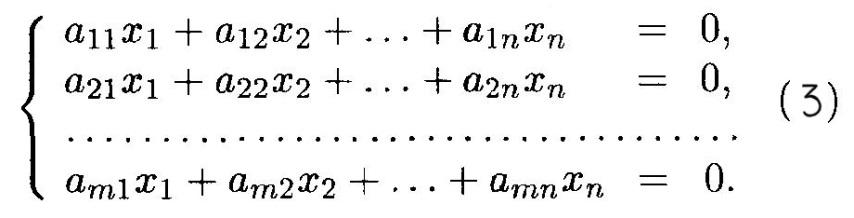
Теорема. Система (3) всегда имеет хотя бы одно тривиальное решение: х1= х2 = … = хn= 0.
При решении однороднойсистемылинейных уравнений возможны следующие случаи:
1) Если m = n и определитель матрицы системы ∆ 0, то ∆ x1 = ∆ x2 = = … = ∆ xn= 0. Тогда система (3) имеет единственное тривиальное решение по формулам Крамера.
2) Если m = n, но определитель матрицы системы ∆ = 0, то система (3) имеет множество решений.
3) Если m<n, то система (3) имеет множество решений.
Определение. Система линейно независимых решений el, е2, …, еk называется фундаментальной, если каждое решение системы (3) является линейной комбинацией решений el, е2 , …, еk.
Теорема. Если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений (3) меньше числа переменных n, то всякая фундаментальная система решений системы (3) состоит из n – r решений.
Пример:
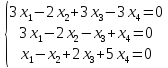
m = 3; n = 4.


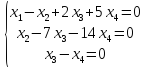
 х1,
х2,
х3 –
базисные, x4 –
свободное.
х1,
х2,
х3 –
базисные, x4 –
свободное.
Пустьх4= C, тогда
х3 = х4=>х3= C
х2– 7C– 14C= 0
х2= 21C
х1– 21C + 2C + 5C = 0
х1= 14C
Ответ:
х1= 14C;
х2= 21C;
х3= C;
х4= C.
studfile.net
Метод Гаусса для решения матриц. Решение системы линейных уравнений методом Гаусса :: SYL.ru
Еще с начала XVI-XVIII веков математики усиленно начали изучать функции, благодаря которым так много в нашей жизни изменилось. Компьютерная техника без этих знаний просто не существовала бы. Для решения сложных задач, линейных уравнений и функций были созданы различные концепции, теоремы и методики решения. Одним из таких универсальных и рациональных способов и методик решения линейных уравнений и их систем стал и метод Гаусса. Матрицы, их ранг, детерминант — все можно посчитать, не используя сложных операций.
Что представляет собой СЛАУ
В математике существует понятие СЛАУ — система линейных алгебраических уравнений. Что же она собой представляет? Это набор из m уравнений с искомыми n неизвестными величинами, обычно обозначающимися как x, y, z, или x1, x2… xn, или другими символами. Решить методом Гаусса данную систему — означает найти все искомые неизвестные. Если система имеет одинаковое число неизвестных и уравнений, тогда она называется системой n-го порядка.
Наиболее популярные методы решения СЛАУ
В учебных заведениях среднего образования изучают различные методики решения таких систем. Чаще всего это простые уравнения, состоящие из двух неизвестных, поэтому любой существующий метод для поиска ответа на них не займет много времени. Это может быть как метод подстановки, когда из одного уравнения выводится другое и подставляется в изначальное. Или метод почленного вычитания и сложения. Но наиболее легким и универсальным считается метод Гаусса. Он дает возможность решать уравнения с любым количеством неизвестных. Почему именно эта методика считается рациональной? Все просто. Матричный способ хорош тем, что здесь не требуется по несколько раз переписывать ненужные символы в виде неизвестных, достаточно проделать арифметические операции над коэффициентами — и получится достоверный результат.
Где используются СЛАУ на практике
Решением СЛАУ являются точки пересечения прямых на графиках функций. В наш высокотехнологический компьютерный век людям, которые тесно связаны с разработкой игр и прочих программ, необходимо знать, как решать такие системы, что они представляют и как проверить правильность получившегося результата. Наиболее часто программисты разрабатывают специальные программы-вычислители линейной алгебры, сюда входит и система линейных уравнений. Метод Гаусса позволяет высчитать все существующие решения. Также используются и другие упрощенные формулы и методики.
Критерий совместимости СЛАУ
Такую систему можно решить только в том случае, если она совместима. Для понятности представим СЛАУ в виде Ax=b. Она имеет решение, если rang(A) равняется rang(A,b). В этом случае (A,b) – это матрица расширенного вида, которую можно получить из матрицы А, переписав ее со свободными членами. Выходит, что решить линейные уравнения методом Гаусса достаточно легко.
Возможно, некоторые обозначения не совсем понятны, поэтому необходимо рассмотреть все на примере. Допустим, есть система: x+y=1; 2x-3y=6. Она состоит всего из двух уравнений, в которых 2 неизвестные. Система будет иметь решение только в том случае, если ранг ее матрицы будет равняться рангу расширенной матрицы. Что такое ранг? Это число независимых строк системы. В нашем случае ранг матрицы 2. Матрица А будет состоять из коэффициентов, находящихся возле неизвестных, а в расширенную матрицу вписываются и коэффициенты, находящиеся за знаком «=».
Почему СЛАУ можно представить в матричном виде
Исходя из критерия совместимости по доказанной теореме Кронекера-Капелли, систему линейных алгебраических уравнений можно представить в матричном виде. Применяя каскадный метод Гаусса, можно решить матрицу и получить единственный достоверный ответ на всю систему. Если ранг обычной матрицы равняется рангу ее расширенной матрицы, но при этом меньше количества неизвестных, тогда система имеет бесконечное количество ответов.
Преобразования матриц
Прежде чем переходить к решению матриц, необходимо знать, какие действия можно проводить над их элементами. Существует несколько элементарных преобразований:
- Переписывая систему в матричный вид и осуществляя ее решение, можно умножать все элементы ряда на один и тот же коэффициент.
- Для того чтобы преобразовать матрицу в канонический вид, можно менять местами два параллельных ряда. Канонический вид подразумевает, что все элементы матрицы, которые расположены по главной диагонали, становятся единицами, а оставшиеся — нулями.
- Соответствующие элементы параллельных рядов матрицы можно прибавлять один к другому.
Метод Жордана-Гаусса
Суть решения систем линейных однородных и неоднородных уравнений методом Гаусса в том, чтобы постепенно исключить неизвестные. Допустим, у нас есть система из двух уравнений, в которых две неизвестные. Чтобы их найти, необходимо проверить систему на совместимость. Уравнение методом Гаусса решается очень просто. Необходимо выписать коэффициенты, находящиеся возле каждого неизвестного в матричный вид. Для решения системы понадобится выписать расширенную матрицу. Если одно из уравнений содержит меньшее количество неизвестных, тогда на место пропущенного элемента необходимо поставить «0». К матрице применяются все известные методы преобразования: умножение, деление на число, прибавление соответствующих элементов рядов друг к другу и другие. Получается, что в каждом ряду необходимо оставить одну переменную со значением «1», остальные привести к нулевому виду. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.
Простой пример решения системы 2х2
Для начала возьмем простенькую систему алгебраических уравнений, в которой будет 2 неизвестных.
Перепишем ее в расширенную матрицу.
Чтобы решить данную систему линейных уравнений, требуется проделать всего две операции. Нам необходимо привести матрицу к каноническому виду, чтобы по главной диагонали стояли единицы. Так, переводя с матричного вида обратно в систему, мы получим уравнения: 1x+0y=b1 и 0x+1y=b2, где b1 и b2 — получившиеся ответы в процессе решения.

- Первое действие при решении расширенной матрицы будет таким: первый ряд необходимо умножить на -7 и прибавить соответственно отвечающие элементы ко второй строке, чтобы избавиться от одного неизвестного во втором уравнении.
- Так как решение уравнений методом Гаусса подразумевает приведение матрицы к каноническому виду, тогда необходимо и с первым уравнением проделать те же операции и убрать вторую переменную. Для этого вторую строку отнимаем от первой и получаем необходимый ответ — решение СЛАУ. Или, как показано на рисунке, вторую строку умножаем на коэффициент -1 и прибавляем к первой строке элементы второго ряда. Это одно и то же.
Как видим, наша система решена методом Жордана-Гаусса. Переписываем ее в необходимую форму: x=-5, y=7.
Пример решения СЛАУ 3х3
Предположим, что у нас есть более сложная система линейных уравнений. Метод Гаусса дает возможность высчитать ответ даже для самой, казалось бы, запутанной системы. Поэтому, чтобы более глубоко вникнуть в методику расчета, можно переходить к более сложному примеру с тремя неизвестными.
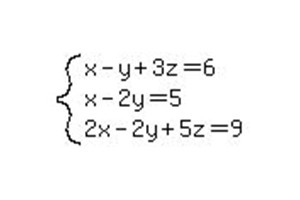
Как и в прежнем примере, переписываем систему в вид расширенной матрицы и начинаем приводить ее к каноническому виду.
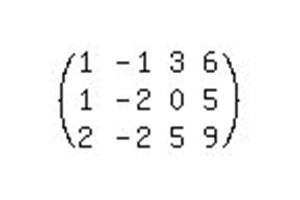
Для решения этой системы понадобится произвести гораздо больше действий, чем в предыдущем примере.
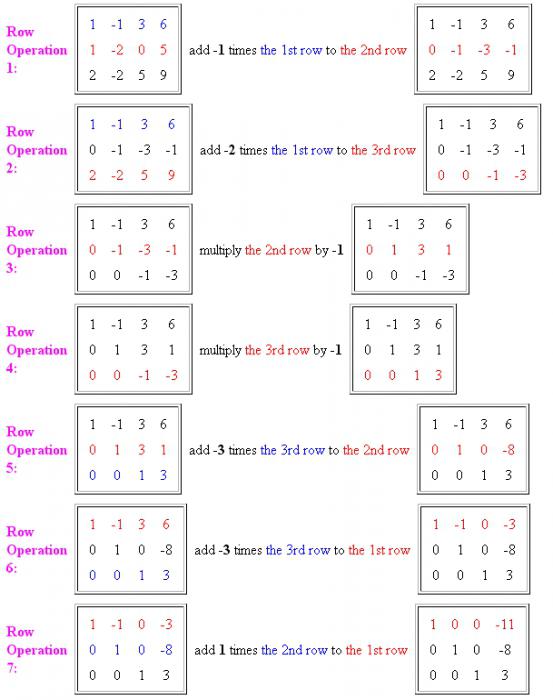
- Сначала необходимо сделать в первом столбце один единичный элемент и остальные нули. Для этого умножаем первое уравнение на -1 и прибавляем к нему второе уравнение. Важно запомнить, что первую строку мы переписываем в изначальном виде, а вторую — уже в измененном.
- Далее убираем эту же первую неизвестную из третьего уравнения. Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья — уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена.
- Теперь необходимо проделать операции и над другими элементами рядов. Третье и четвертое действие можно объединить в одно. Нужно разделить вторую и третью строку на -1, чтобы избавиться от минусовых единиц по диагонали. Третью строку мы уже привели к необходимому виду.
- Дальше приведем к каноническому виду вторую строку. Для этого элементы третьего ряда умножаем на -3 и прибавляем их ко второй строчке матрицы. Из результата видно, что вторая строка тоже приведена к необходимой нам форме. Осталось проделать еще несколько операций и убрать коэффициенты неизвестных из первой строки.
- Чтобы из второго элемента строки сделать 0, необходимо умножить третью строку на -3 и прибавить ее к первому ряду.
- Следующим решающим этапом будет прибавление к первой строке необходимые элементы второго ряда. Так мы получаем канонический вид матрицы, а, соответственно, и ответ.
Как видно, решение уравнений методом Гаусса довольно простое.
Пример решения системы уравнений 4х4
Некоторые более сложные системы уравнений можно решить методом Гаусса посредством компьютерных программ. Необходимо вбить в существующие пустые ячейки коэффициенты при неизвестных, и программа сама пошагово рассчитает необходимый результат, подробно описывая каждое действие.
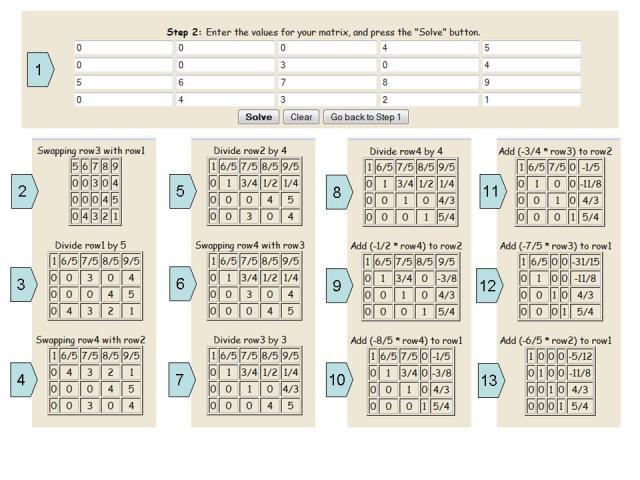
Ниже описана пошаговая инструкция решения такого примера.
• В первом действии в пустые ячейки вписываются свободные коэффициенты и числа при неизвестных. Таким образом, получается такая же расширенная матрица, которую мы пишем вручную.
• Далее меняются все строки местами, чтобы можно было выразить по главной диагонали единичные элементы.
• И производятся все необходимые арифметические операции, чтобы привести расширенную матрицу к каноническому виду. Необходимо понимать, что не всегда ответ на систему уравнений — это целые числа. Иногда решение может быть из дробных чисел.
Проверка правильности решения
Метод Жордана-Гаусса предусматривает проверку правильности результата. Для того чтобы узнать, правильно ли посчитаны коэффициенты, необходимо всего-навсего подставить результат в изначальную систему уравнений. Левая сторона уравнения должна соответствовать правой стороне, находящейся за знаком «равно». Если ответы не совпадают, тогда необходимо пересчитывать заново систему или попробовать применить к ней другой известный вам метод решения СЛАУ, такой как подстановка или почленное вычитание и сложение. Ведь математика – это наука, которая имеет огромное количество различных методик решения. Но помните: результат должен быть всегда один и тот же, независимо от того, какой метод решения вы использовали.
Метод Гаусса: наиболее часто встречающиеся ошибки при решении СЛАУ
Во время решения линейных систем уравнений чаще всего возникают такие ошибки, как неправильный перенос коэффициентов в матричный вид. Бывают системы, в которых отсутствуют в одном из уравнений некоторые неизвестные, тогда, перенося данные в расширенную матрицу, их можно потерять. В результате при решении данной системы результат может не соответствовать действительному.
Еще одной из главных ошибок может быть неправильное выписывание конечного результата. Нужно четко понимать, что первый коэффициент будет соответствовать первому неизвестному из системы, второй — второму, и так далее.
Метод Гаусса подробно описывает решение линейных уравнений. Благодаря ему легко произвести необходимые операции и найти верный результат. Кроме того, это универсальное средство для поиска достоверного ответа на уравнения любой сложности. Может быть, поэтому его так часто используют при решении СЛАУ.
www.syl.ru
Метод Гаусса
Метод Гаусса предназначен для решения систем линейных алгебраических уравнений (СЛАУ). Его описание приводится в предположении, что число неизвестных равно числу уравнений и что определитель матрицы коэффициентов системы отличен от нуля (матрица невырожденная).
Пусть задана СЛАУ (запись в матричном виде) Ax = b, где
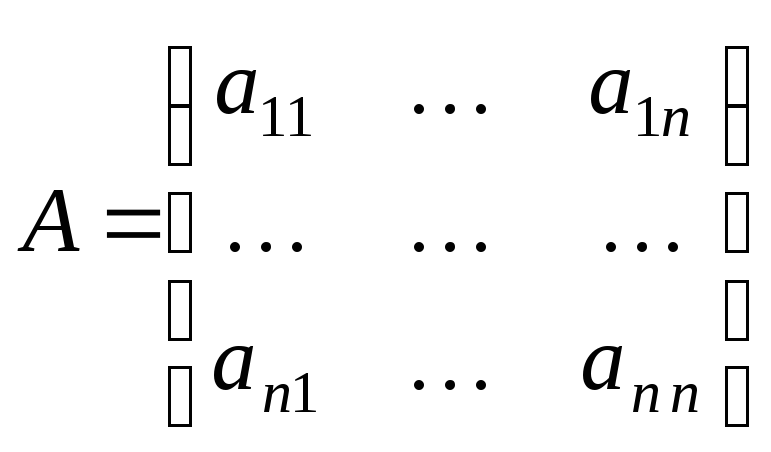 ,
,  ,
, .
.
Составляется
расширенная матрица системы  .
С элементами этой матрицы выполняются
следующие операции, которые обычно
называются элементарными:
.
С элементами этой матрицы выполняются
следующие операции, которые обычно
называются элементарными:
можно менять местами строки;
к одной строке можно прибавлять другую, умноженную на любое число;
можно умножать строку на любое число, отличное от нуля (используется в основном при вычислениях вручную, на бумаге).
Цель выполнения элементарных операций – получить под главной диагональю матрицы A нули. Этой цели добиваемся последовательными переходами от одной матрицы к другой после выполнения определенного цикла элементарных операций.
От
матрицы  переходим к матрице
переходим к матрице следующим образом. Пусть
следующим образом. Пусть .
Тогда первую строку матрицы
.
Тогда первую строку матрицы оставляем без изменения, т.е.
оставляем без изменения, т.е. ,
, ,
, .
Ко второй строке прибавляем первую
строку, умноженную на число
.
Ко второй строке прибавляем первую
строку, умноженную на число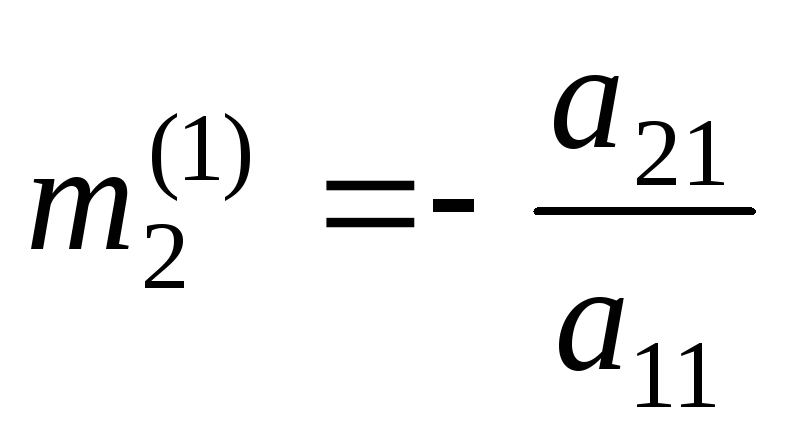 ,
т.е.
,
т.е.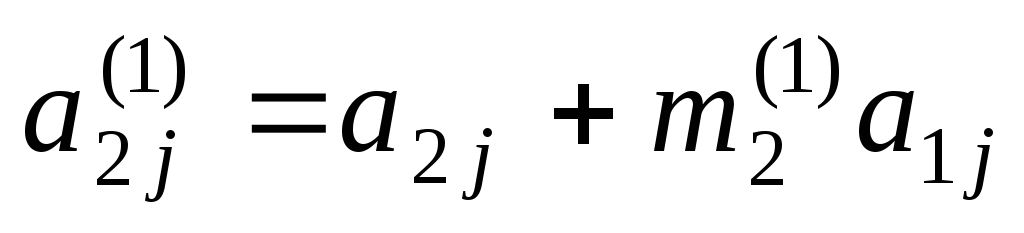 ,
, ,
, ,
при этом окажется, что
,
при этом окажется, что .
.
К
третьей строке прибавляем первую строку,
умноженную на число  ,
т.е.
,
т.е. ,
, ,
, ,
при этом окажется, что
,
при этом окажется, что .
Таким же образом преобразуем все строки,
т.е. к строке с номеромi прибавляется первая строка, умноженная
на число
.
Таким же образом преобразуем все строки,
т.е. к строке с номеромi прибавляется первая строка, умноженная
на число  ,
,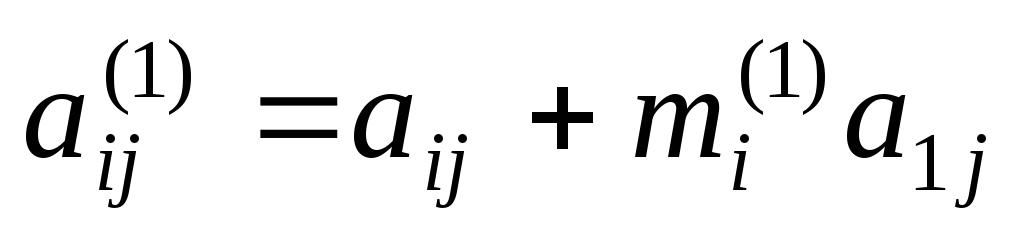 ,
, ,
, ,
,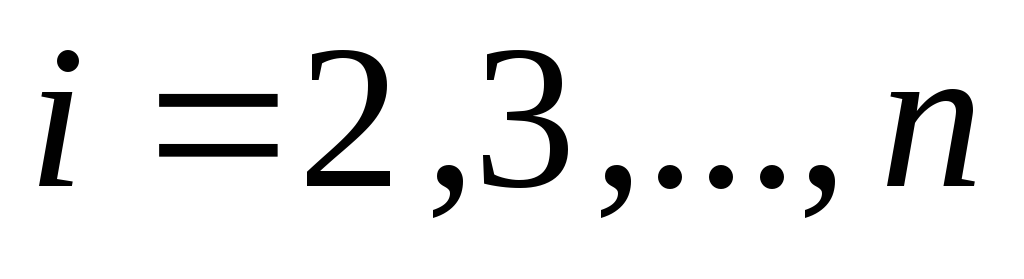 .
В результате этих вычислений получим
матрицу
.
В результате этих вычислений получим
матрицу
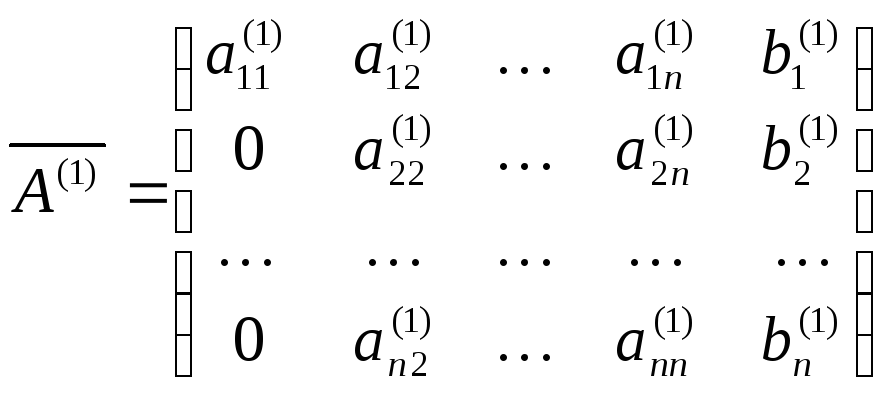 .
.
Первый шаг прямого хода метода Гаусса на этом закончен.
Далее
переходим к матрице 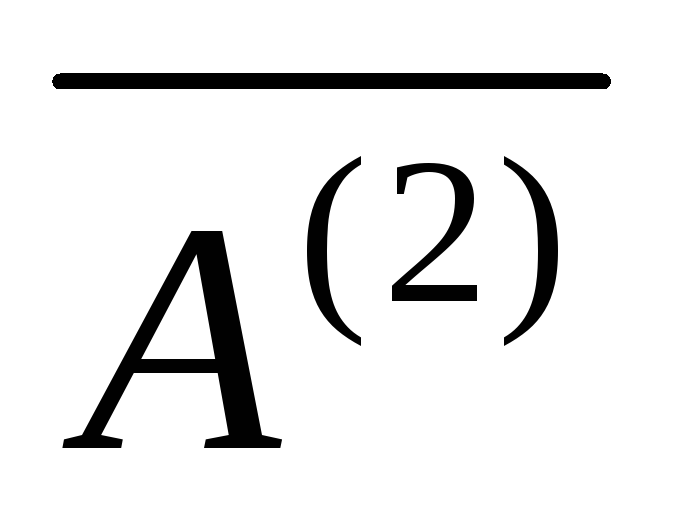 ,
добиваясь нулей во втором столбце,
начиная с третьей строки. Строки 1,2
оставим без изменений. Полагаем
,
добиваясь нулей во втором столбце,
начиная с третьей строки. Строки 1,2
оставим без изменений. Полагаем ,
, .
К строке с номером
.
К строке с номером матрицы
матрицы прибавляем вторую строку, умноженную
на число
прибавляем вторую строку, умноженную
на число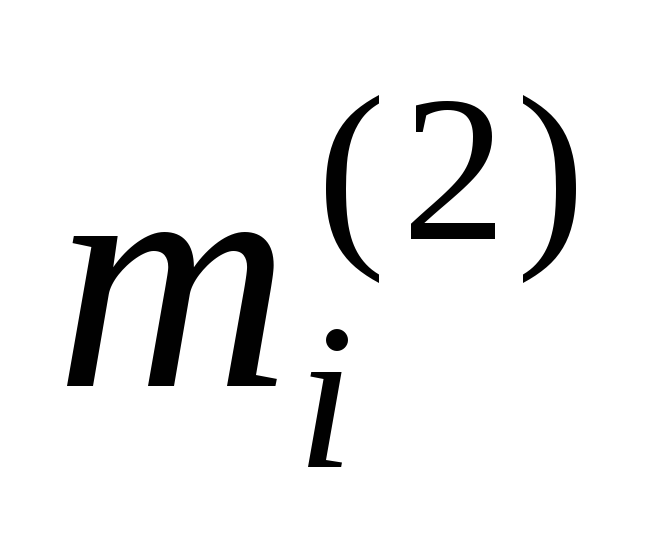 ,
,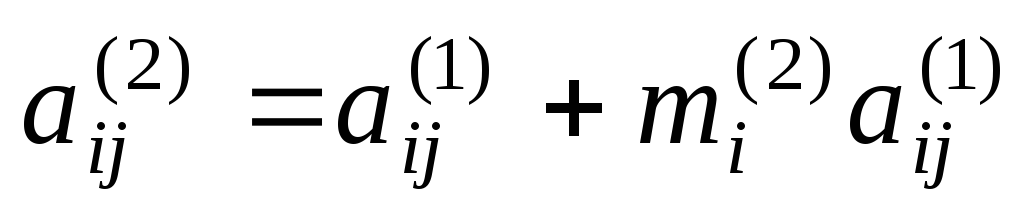 ,
, ,
,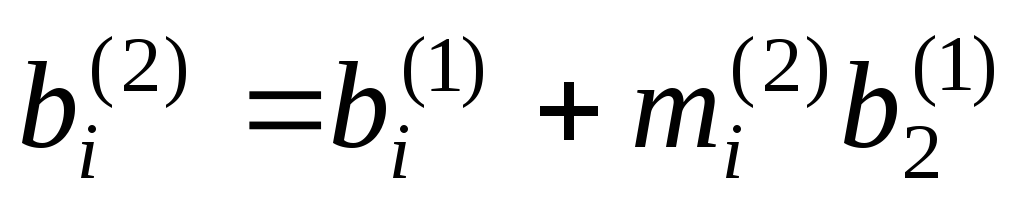 ,
, .
В действительностиj меняется
от 2 до n,
так как первый столбец в результате
этих действий останется без изменений.
Получим матрицу
.
В действительностиj меняется
от 2 до n,
так как первый столбец в результате
этих действий останется без изменений.
Получим матрицу
 .
.
На этом закончен второй шаг прямого хода метода Гаусса.
Продолжая
вычисления аналогичным образом,
переходим к матрице ,
где в третьем столбце, начиная с четвертой
позиции, будут стоять нули. Действуя
далее аналогично, придем к матрице
,
где в третьем столбце, начиная с четвертой
позиции, будут стоять нули. Действуя
далее аналогично, придем к матрице
 ,
,
у которой под главной диагональю стоят одни нули. Прямой ход метода Гаусса закончен.
Матрице  соответствует система уравнений
соответствует система уравнений
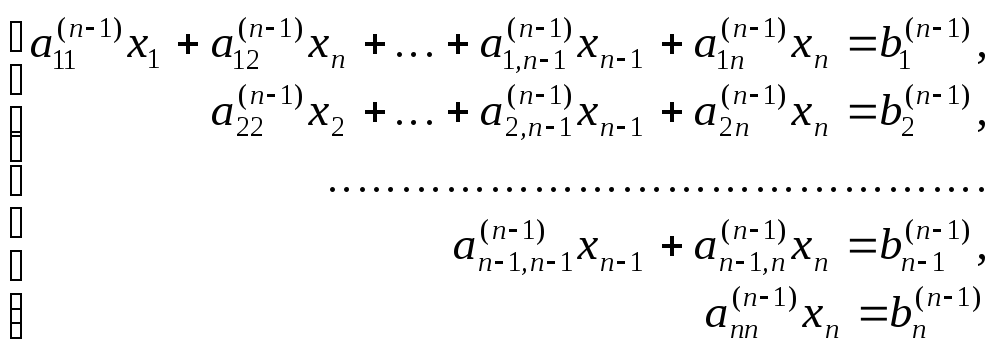
равносильная
исходной. Ее решения легко найти по
формулам  ,
,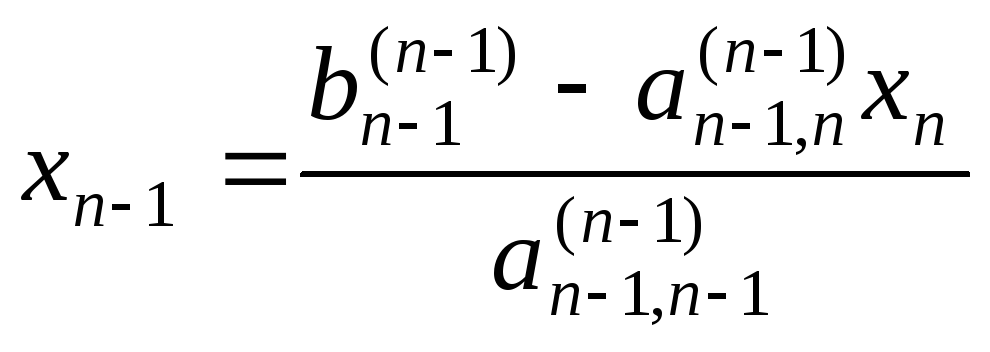 (значение
(значение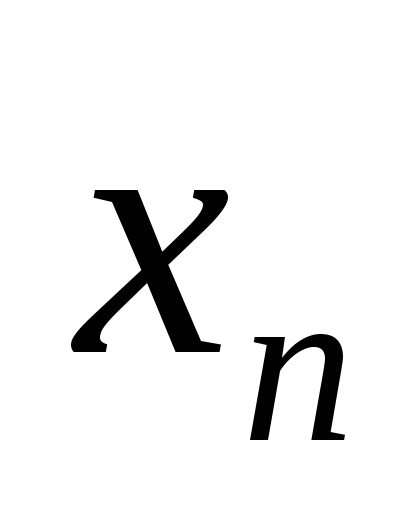 уже найдено) и так далее. Общая формула:
уже найдено) и так далее. Общая формула:
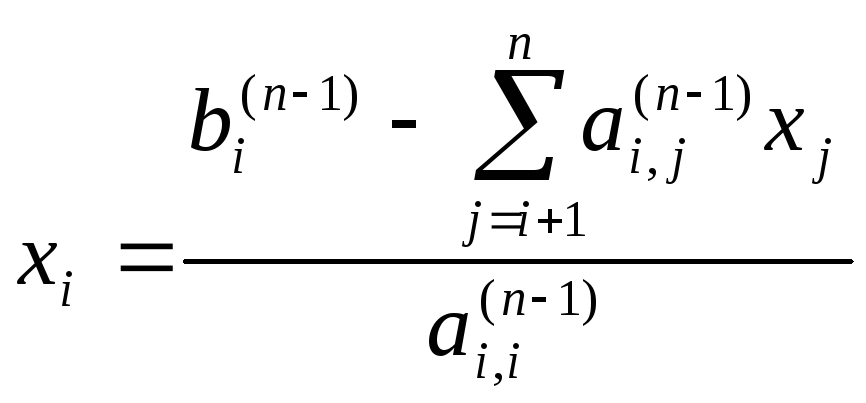 ,
, 
Метод
Гаусса требует выполнения порядка  арифметических операций. Это один из
самых экономичных методов.
арифметических операций. Это один из
самых экономичных методов.
Метод lu-разложения
Можно
показать, что применение метода Гаусса
эквивалентно LU-разложению
матрицы А,
т.е. ее представлению в виде произведения  ,
где
,
где
 .
.
Элементы этих матриц находятся по формулам в том порядке, в котором здесь эти формулы выписаны:
 ,
,


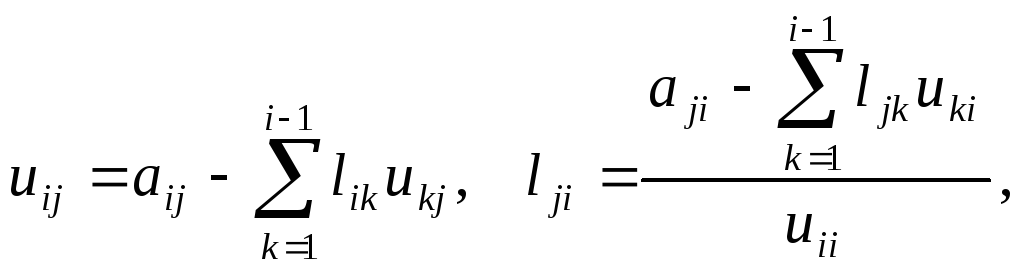

Такое разложение дает следующий результат:
 .
Положим
.
Положим 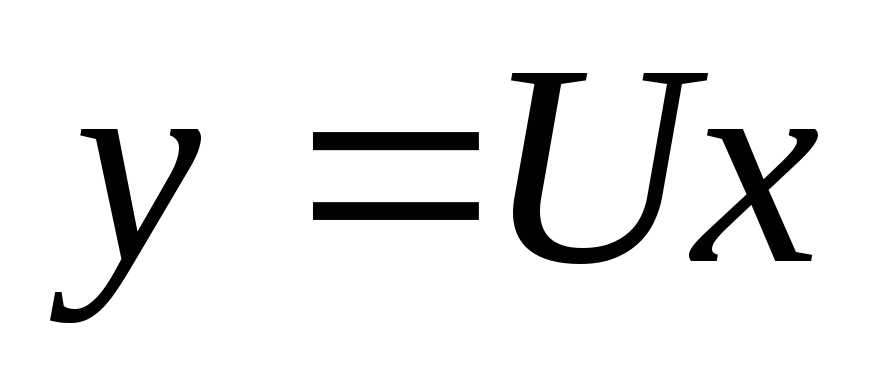 ,
тогда
,
тогда .
Получили треугольную систему уравнений
.
Получили треугольную систему уравнений

Из
этой системы последовательно находим 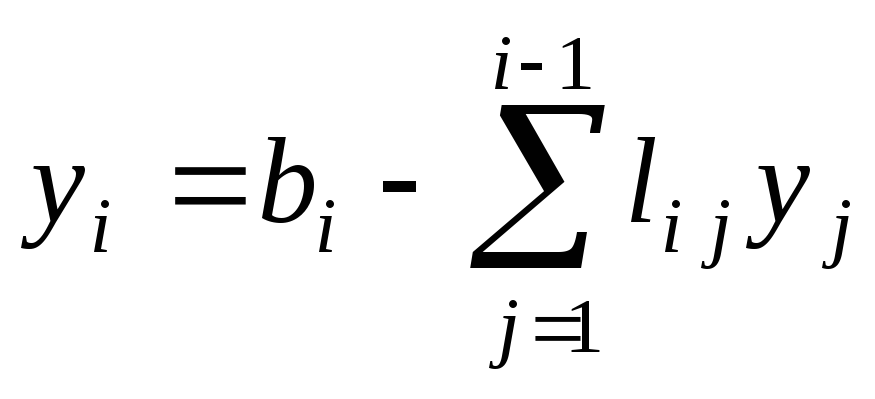 ,
, .
Знаяy,
находим x из треугольной системы
.
Знаяy,
находим x из треугольной системы
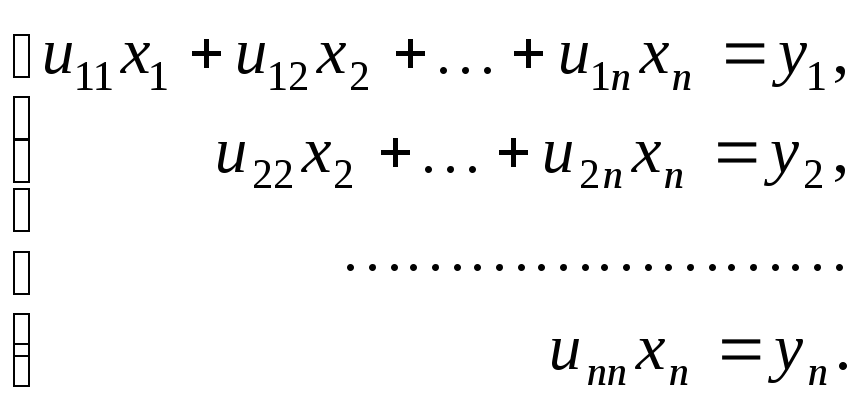
Откуда 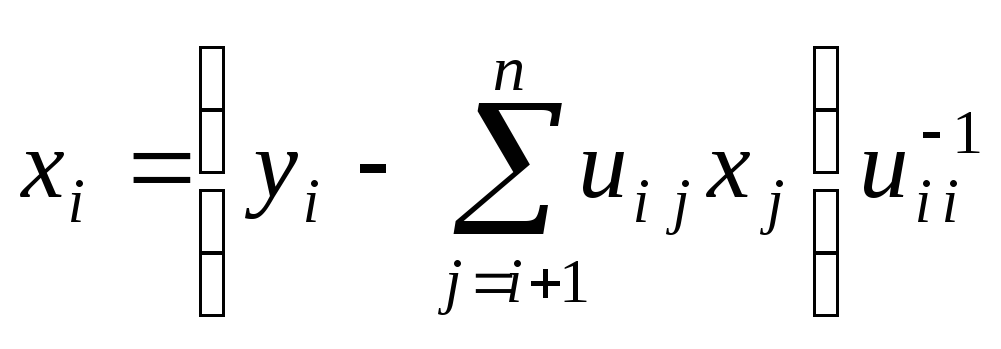 ,
, .
.
И в методе Гаусса при решении систем линейных уравнений, и в LU-разложении матрицы приходится выполнять деление на элемент матрицы. Если этот элемент нуль, то процесс остановится, хотя матрица А не вырождена, и решение системы существует. Проблемы возникают и в том случае, когда элемент, на который приходится делить, очень маленький. В этой ситуации предыдущие ошибки, возникающие неизбежно при округлении чисел компьютером, резко увеличиваются и могут стать недопустимо большими. Если действия выполняются на бумаге, то вы просто меняете строки матрицы местами. Аналогично поступают и при программировании метода Гаусса и LU-разложения. При этом обычно выбирают такую строку, где элемент, на который нужно делить, является наибольшим по модулю.
При
таком алгоритме при LU-разложении
уже получается три матрицы P, L, U.
Матрицы L, U – нижняя и верхняя треугольные
соответственно, 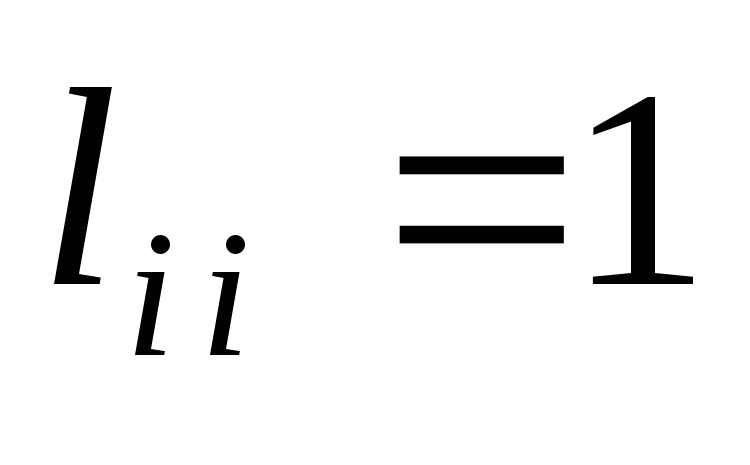 ,
, ,P – матрица перестановок, т.е. квадратная
матрица порядка n,
в каждой строке и в каждом столбце
которой только один элемент равен 1, а
все остальные элементы – нули. Эти
матрицы связаны соотношением
,P – матрица перестановок, т.е. квадратная
матрица порядка n,
в каждой строке и в каждом столбце
которой только один элемент равен 1, а
все остальные элементы – нули. Эти
матрицы связаны соотношением  .
Такое разложение всегда возможно, если
.
Такое разложение всегда возможно, если .
.
Если
мы получим такое разложение, то для
решения системы  обе части умножим слева на матрицуP,
обе части умножим слева на матрицуP, 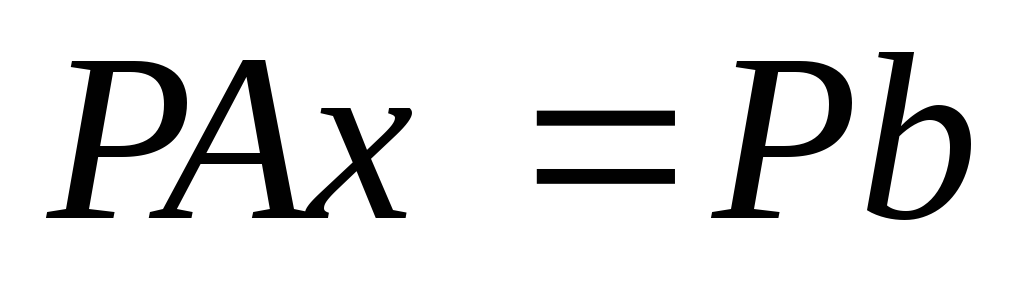 ,
и заменимPA на LU,
,
и заменимPA на LU,  .
Далее действия такие же, как описано
выше. ИменноLU-разложение
используется в системе MATHCAD
для решения систем линейных уравнений.
.
Далее действия такие же, как описано
выше. ИменноLU-разложение
используется в системе MATHCAD
для решения систем линейных уравнений.
studfile.net
Метод Жордана-Гаусса для решения СЛАУ: основные понятия, примеры, определения
В данной статье мы рассмотрим метод Жордана-Гаусса для решения систем линейных уравнений, отличие метода Гаусса от метода Жордана-Гаусса, алгоритм действий, а также приведем примеры решений СЛАУ.
Основные понятия
Определение 1Метод Жордана-Гаусса — один из методов, предназначенный для решения систем линейных алгебраических уравнений.
Этот метод является модификацией метода Гаусса — в отличие от исходного (метода Гаусса) метод Жордана-Гаусса позволяет решить СЛАУ в один этап (без использования прямого и обратного ходов).
ПримечаниеМатричная запись СЛАУ: вместо обозначения А в методе Жордана-Гаусса для записи используют обозначение Ã — обозначение расширенной матрицы системы.
Пример 1Решить СЛАУ методом Жордана-Гаусса:
4×1-7×2+8×3=-232×1-4×2+5×3=-13-3×1+11×2+x3=16
Как решить?
Записываем расширенную матрицу системы:
Ã=4-78|-232-45|-13-3111|16
Напоминаем, что слева от черты записывается матрица системы А:
A=4-782-45-3111
Замечание 1На каждом шаге решения необходимо выбирать разрешающие элементы матрицы. Процесс выбора может быть различным — в зависимости от того, как выбираются элементы, решения будут отличаться. Можно выбирать в качестве разрешающих элементов диагональные элементы матрицы, а можно выбирать произвольно.
В этой статье мы покажем оба способа решения.
Произвольный способ выбора разрешающих элементов
Следует обратиться к 1-му столбцу матрицы Ã — необходимо выбрать ненулевой (разрешающий) элемент.
В 1-ом столбце есть 3 ненулевых элемента: 4, 2, -3. Можно выбрать любой, но, по правилам, выбирается тот, чей модуль ближе всего к единице. В нашем примере таким числом является 2.
Цель: обнулить все элементы, кроме разрешающего, т.е. необходимо обнулить 4 и -3:
4-782-45-3111
Произведем преобразование: необходимо сделать разрешающий элемент равным единице. Для этого делим все элементы 2-ой строки на 2. Такое преобразование имеет обозначение: II:2:
4-78|-232-
zaochnik.com
Вычисление определителя методом Гаусса
Вычислим определитель методом Гаусса.
Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.
Идея метода состоит в следующем: пусть дан определитель третьего порядка
 (1)
(1)
элемент должен быть равен
должен быть равен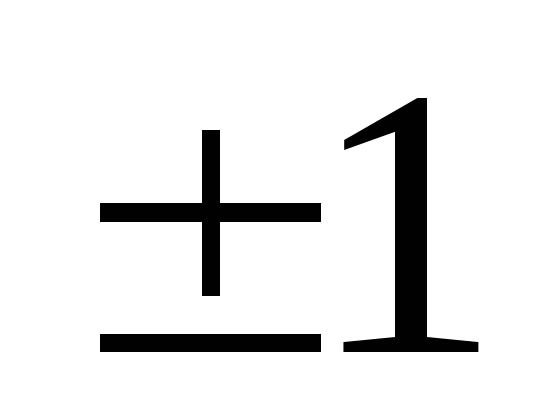 ,
для этого первую строку разделим на
,
для этого первую строку разделим на .
.
Получим определитель вида  (2)
(2)
Обнулим элементы, стоящие в первом
столбце, кроме первого. Для этого из
второй строки вычтем первую, умноженную
на 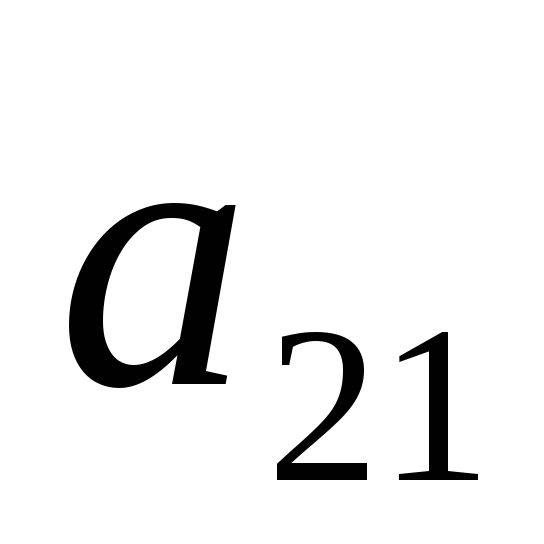 ,
далее из третьей строки вычтем первую,
умноженную на
,
далее из третьей строки вычтем первую,
умноженную на .
Получим определитель вида
.
Получим определитель вида .
.
Обозначим его элементы буквой с, тогда
 (3)
(3)
Теперь надо обнулить элемент  .
Элемент
.
Элемент должен быть равен
должен быть равен ,
для этого вторую строку разделим на
,
для этого вторую строку разделим на .
Получим определитель вида
.
Получим определитель вида .
.
Далее из третьей строки вычтем вторую,
умноженную на  .
.
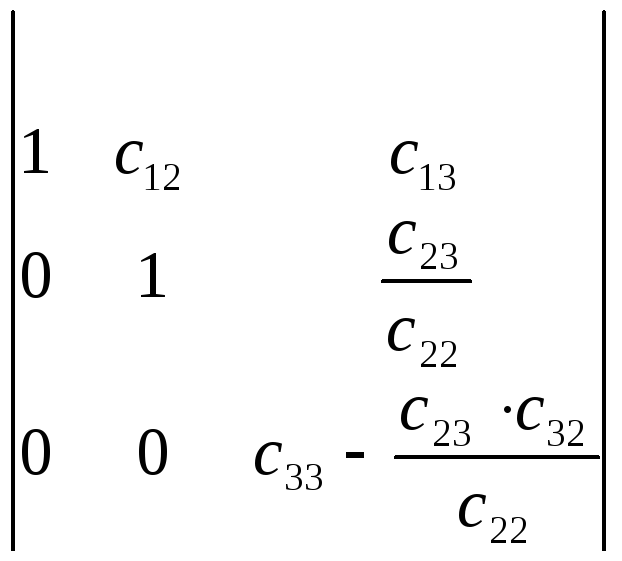 .
.
Обозначим его элементы буквой t, тогда
 (4)
(4)
Вот мы привели определитель к треугольному
виду, теперь он равен 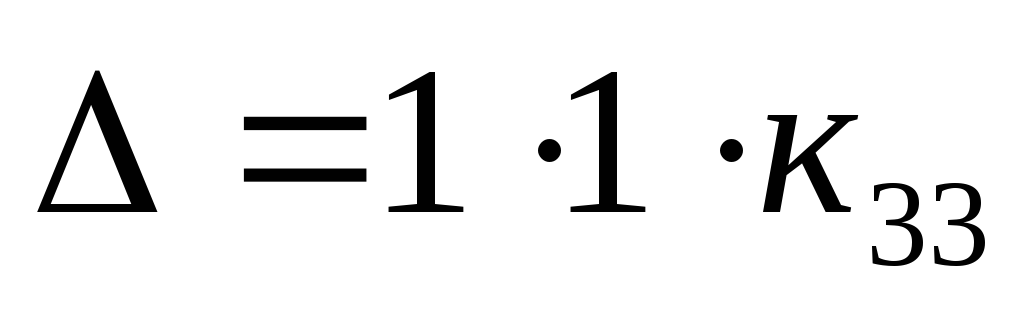 .
.
Разберем теперь это на конкретном примере.
Пример 4:Вычислить определитель методом Гаусса.
методом Гаусса.
Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).
Получили
Из второй строки вычтем первую, умноженную
на 2, далее из третьей строки вычтем
первую, умноженную на 3. Получили 
Далее из третьей строки вычтем вторую, умноженную на 3.
Получили — 
§2.Матрицы Виды матриц
Определение 7: Если в матрицеmстрок иnстолбцов, то она
называетсяразмерностьюm nи пишут
nи пишут .
.
Определение 8: Если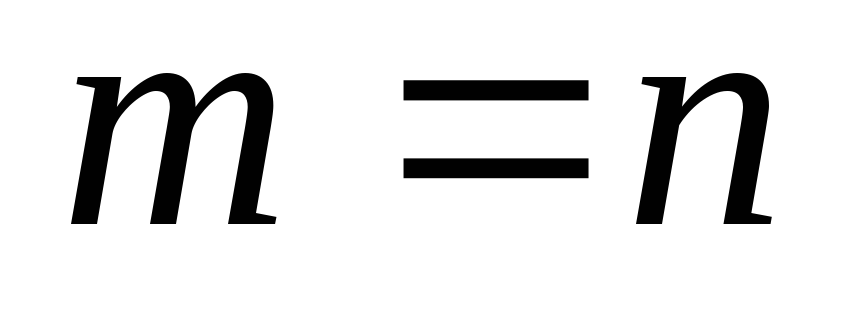 ,
то матрица называется квадратной.
,
то матрица называется квадратной.
Определение 9:Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).
Определение 10:Матрица, состоящая из нулей, называется нулевой матрицей.
Определение 11:Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.
Определение 12:Единичной матрицей называется диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице.
Определение 13:Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.
Действиянад матрицами.
Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.
Пример 5: 
Матрицы А и В равны, т.е. 
Определение 15: Суммой (разностью)
матриц А и В называется такая матрица
С, у которой каждый элемент равен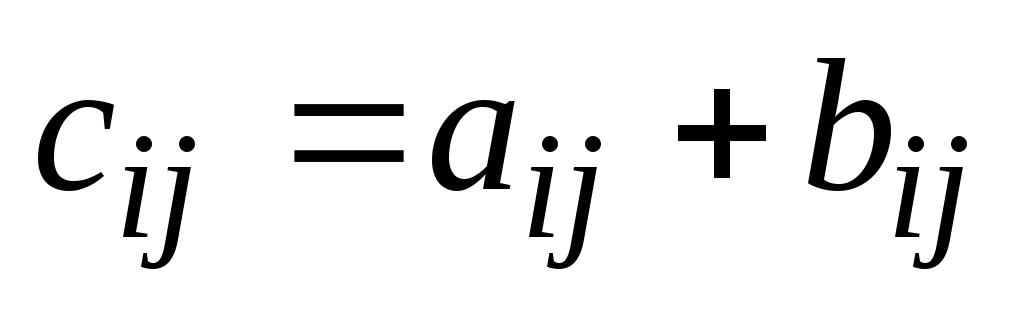 .
.
Пример 6: Найти матрицу ,
если
,
если 
Решение:
Cвойства сложения
 А+В=В+А(переместительное)
А+В=В+А(переместительное)
20А+О=А, где О-нулевая матрица
30 А+(В+С)=(А+В)+С (дистрибутивное)
40А+(-А)=О, где – А противоположная матрица
(т.е. элементы имеют противоположные знаки)
Определение 16: Произведением матрицы
А на число называется матрица, полученная из
данной умножением всех ее элементов на
число
называется матрица, полученная из
данной умножением всех ее элементов на
число .
.
Пример 7: 
Умножение матиц
Это действие распространяется на так называемые согласованные матрицы.
Определение 17: Матрица А называется согласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.
Пример 8: и
и — согласованные
— согласованные
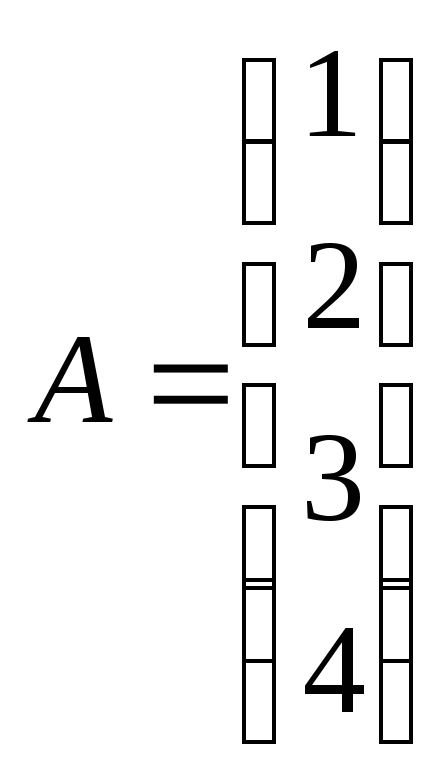 и
и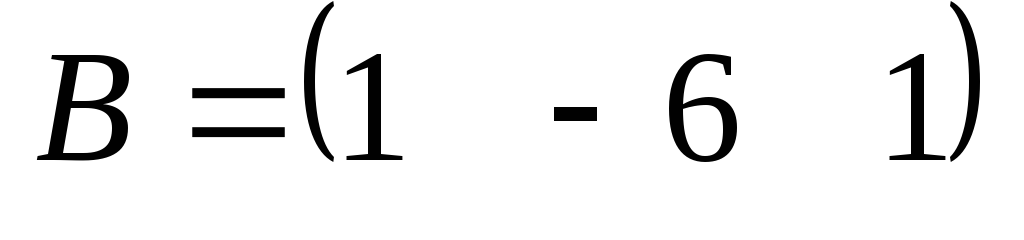 — несогласованные
— несогласованные
 и
и несогласованные
несогласованные
Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементовiстроки матрицы А на соответствующие элементыj-го столбца матрицы В.
Если матрица А имеет размерность 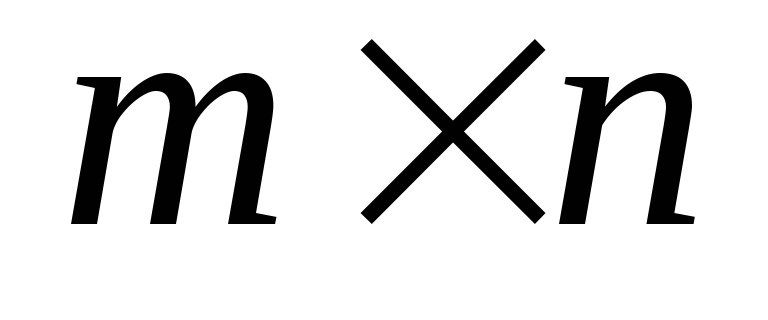 ,
а матрица В
,
а матрица В ,
то
,
то .
.
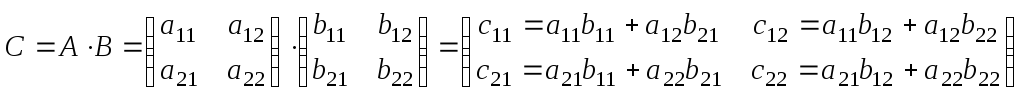
Пример 9: Умножить матрицы


studfile.net