c++ — Евклидова геометрия. Расстояние от точки до отрезка
Stack Overflow на русскомLoading…
- 0
- +0
- Тур Начните с этой страницы, чтобы быстро ознакомиться с сайтом
- Справка Подробные ответы на любые возможные вопросы
- Мета Обсудить принципы работы и политику сайта
- О нас Узнать больше о компании Stack Overflow
- Бизнес Узнать больше о поиске разработчиков или рекламе на сайте
- Войти Регистрация
-
текущее сообщество
1.Расстояние между двумя точками. Деление отрезка в данном отношении.

Деление отрезка в данном отношении.

3.Понятие об ур-нии линии.


Определение окружности и ее определение.
Окружность
радиуса R
с центром в начале координат представляется
уравнением 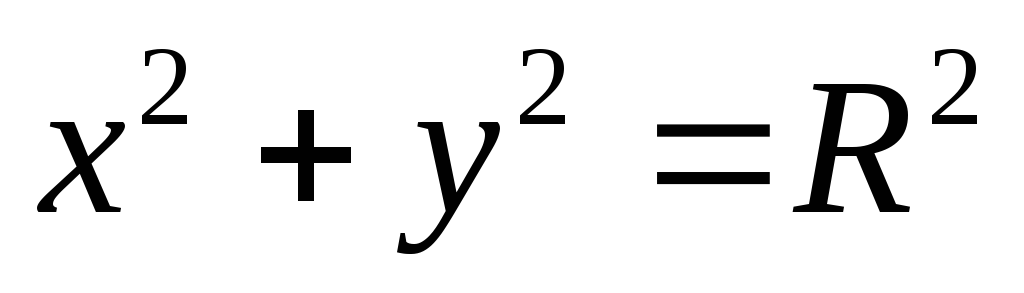

4.Уравнение прямой с угловым коэффициентом


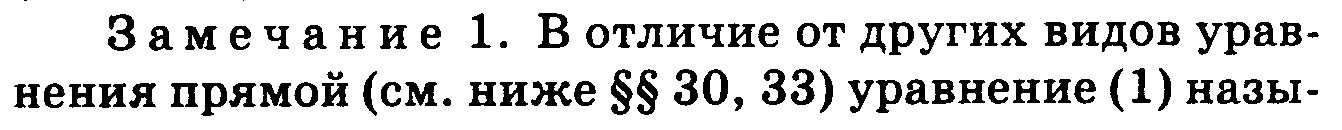


5.Общее уравнение прямой.


24. Метод обратной матрицы решения системы алгебраических уравнений.
m = n, det A ≠ 0
A×X = B
Умножаем систему 2 слева на матрицу А-1
А-1 × А × Х = А-1 × В
Е × Х = А-1 × В
Х = А-1 × В
6.Ур-ние прямой, проходящей через 2 точки. Ур-ние прямой в отрезках.

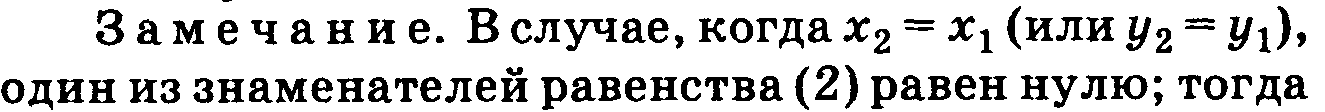
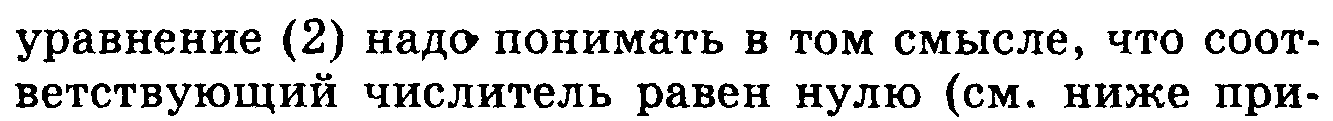



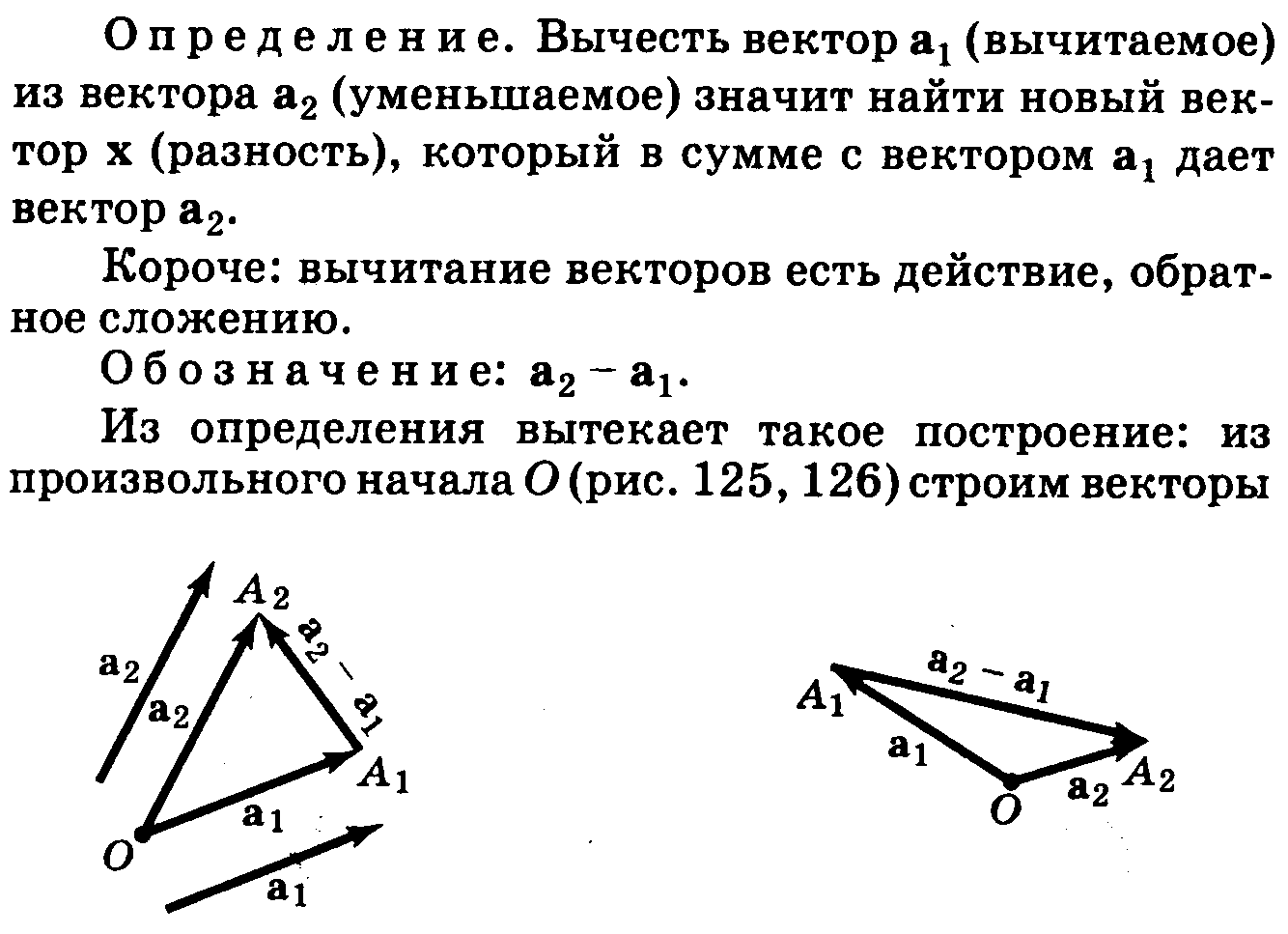
9.Скалярные и векторные велечины. Сложение, вычетание векторов, умножение вектора на число.



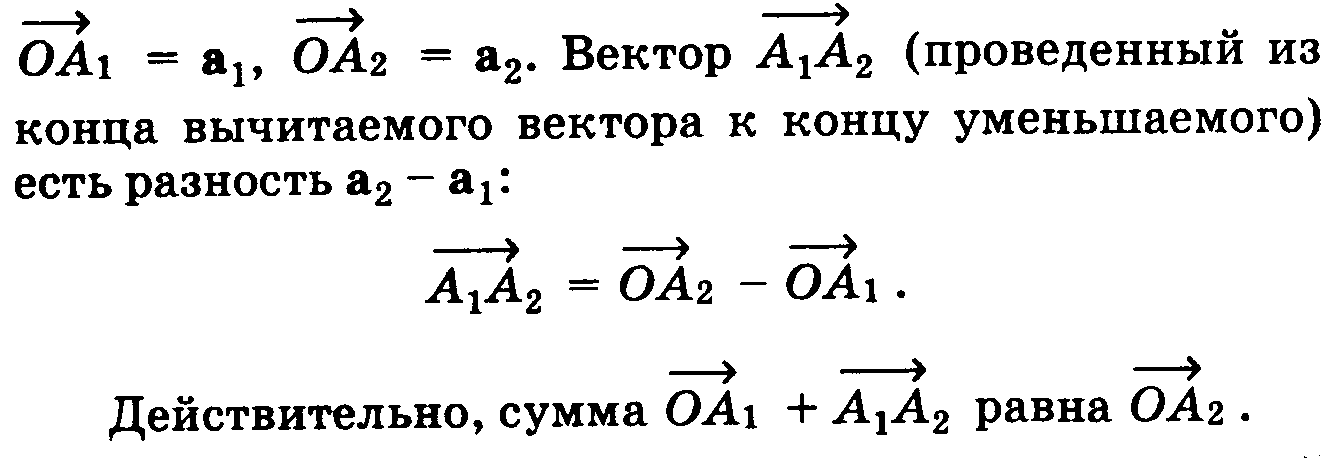

15.Общее уравнение плоскости:
Ах + Ву + Сz + D=0, где ABCD- некоторые числа, причем A2+B2+C2>0.
1. Уравнение плоскости
по точке и нормальному вектору: M0M
перпендикулярно 
 ×M0M=0,
M0M=(x-x0,y-y0,z-z0),
×M0M=0,
M0M=(x-x0,y-y0,z-z0),  ×M0M=A(x-x0)+B(y-y0)+C(z-z
×M0M=A(x-x0)+B(y-y0)+C(z-z
2. Уравнение плоскости
в отрезках на осях: Ax+By+Cz =D, —  —
—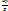 —
— 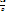 =
1,
=
1,  +
+ 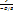 +
+  =1,
=1, 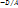 =a,
=a, 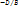
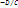 =c,
=c,  +
+ +
+  =
1.
=
1.3.Уравнение плоскасти по трем точкам: 0=[M1M, M1M2, M1M3]- компланарные, M1M=(x-x1, y-y1, z-z1), M1M2=(x2-x1, y2-y1, z2-z1), M1M3=(x3-x1, y3-y1, z3-z1).
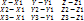
Угол между плоскостями: A1x + B1y + C1z + D1 = 0, A2x + B2y + C2z + D2 = 0.
 =(A1,
B1,
C1 ),
=(A1,
B1,
C1 ),  =(A2,
B2,
C2)
=(A2,
B2,
C2) 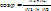 =
=
Плоскости будут
параллельны, если вектора калиниарны:
n1⃓⃓
n2  =
=
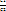 ≠
≠
A1x + B1y + C1z + D1=0.
Плоскости перпендикулярны, когда вектора ортогональные:
 =0,
A1×A2 + B1×B2 + C1×C2 =0
=0,
A1×A2 + B1×B2 + C1×C2 =0
7.Угол между 2-мя прямыми. Условия параллельности и перпендикулярности.


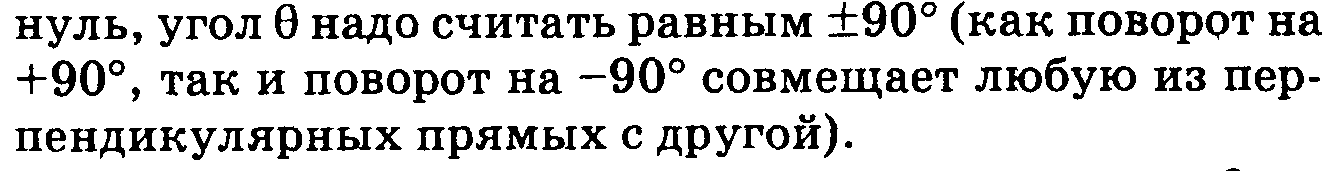

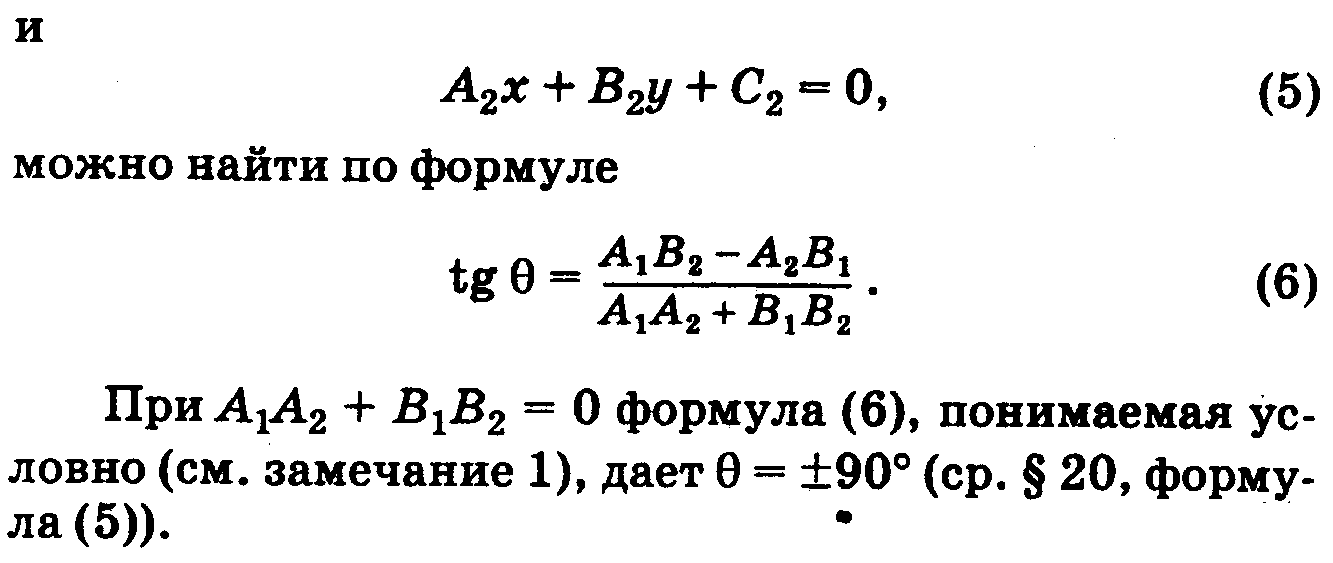


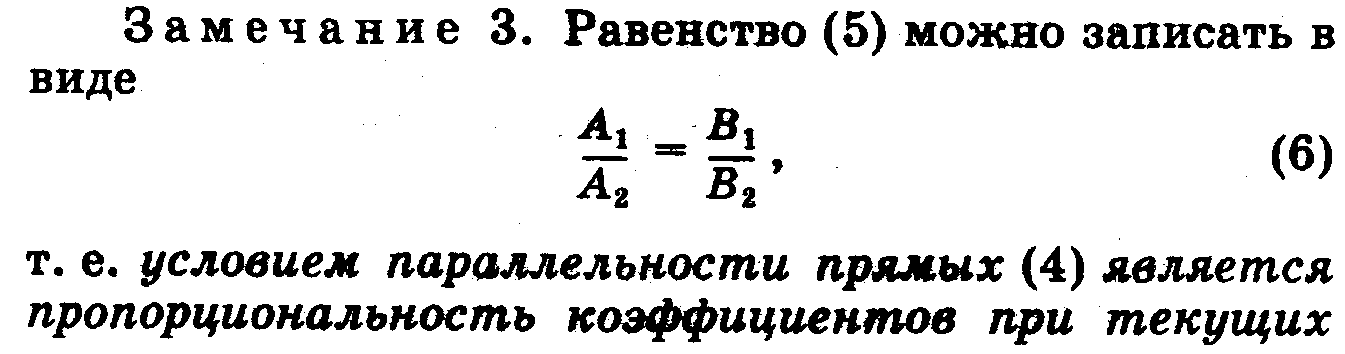
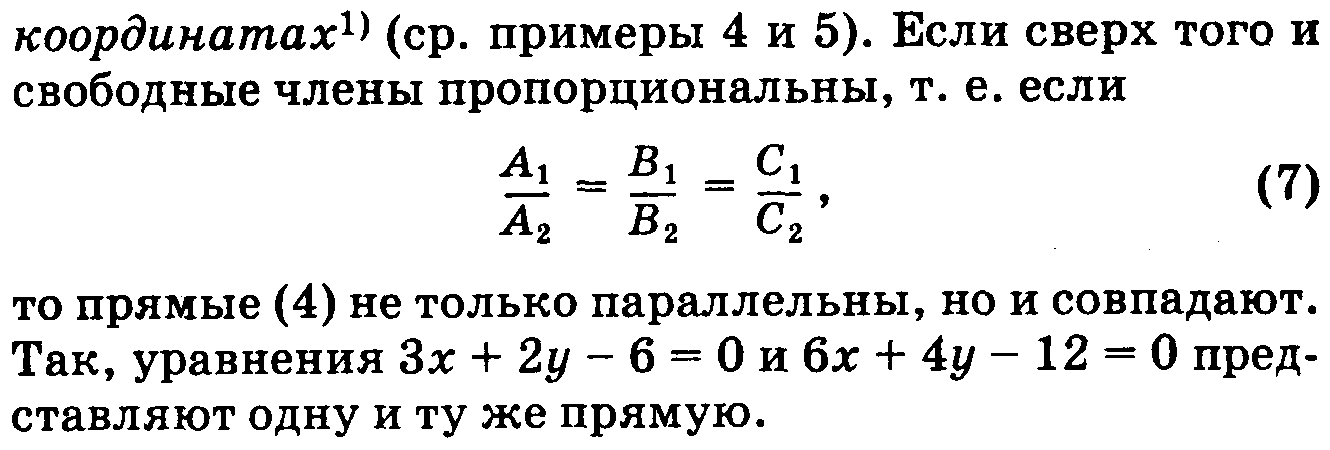
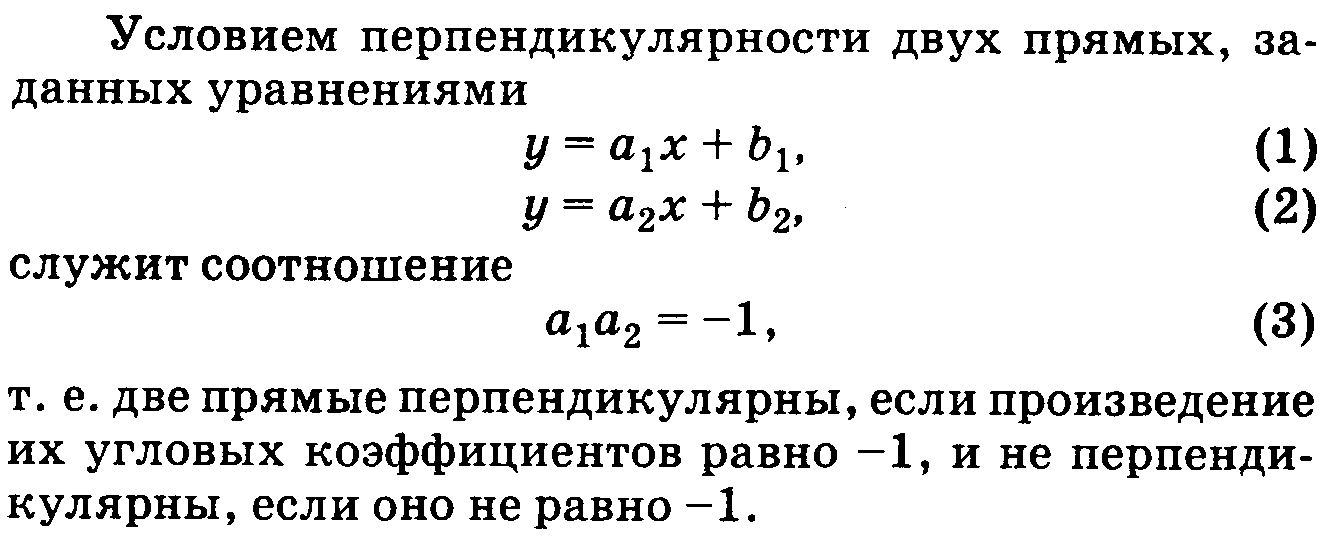

14. Угол между 2-мя векторами.
Угол между векторами a1{X1;Y1;Z1},a2{X2;Y2;Z2} можно найти по формуле

Условие коллинеарности:
Векторы назыв коллинеарными если они || одной плоскости
Если векторы a1{X1;Y1;Z1},a2{X2;Y2;Z2} коллинеарны, то их соответствующие координаты пропорциональны X2: X1= Y2: Y1= Z2: Z и обратно. Если коэффициент пропорциональности положителен, то векторы равнонаправлены, если отрицателен, то – противопол направ.
Условие компланарности:
Три вектора назыв компланарными, если они, будучи приведены к одному началу, лежат в одной плоскости
Условие (необходимое и достаточное) компланарности векторов a1{X1;Y1;Z1}, a2{X2;Y2;Z2},a3{X3;Y3;Z3} :
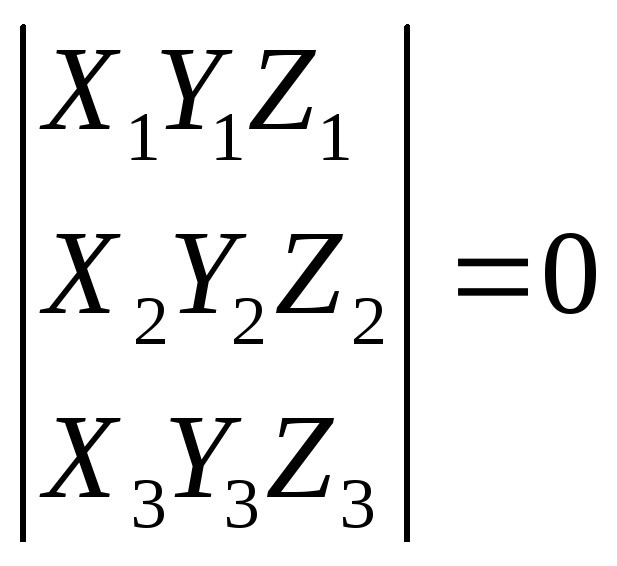
8. Кривые второго порядка (эллипс, парабола, гипербола)
Парабола и ее свойства.
Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax2, где х и у — текущие координаты, а- нек. число, наз. параболой.
Е сли
вершина нах. в О(0,0), то ур-е примет вид
сли
вершина нах. в О(0,0), то ур-е примет вид
y2=2px-симметрично отн. оси ОХ
х2=2pу-симметрично отн. оси ОУ
Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 — ее директриса.
Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2
Св-ва:
1. парабола предст. собой точек плоскости, равноотстающих от фокуса и от директрисы y=ax2.
Эллипс и его св-ва:
Кривая второго порядка наз. эллипсом если коэффициенты А и L имеют одинаковые знаки
Аx2+Cy2=
ур.-е 
наз. канонич. ур.-ем
эллипса, где 
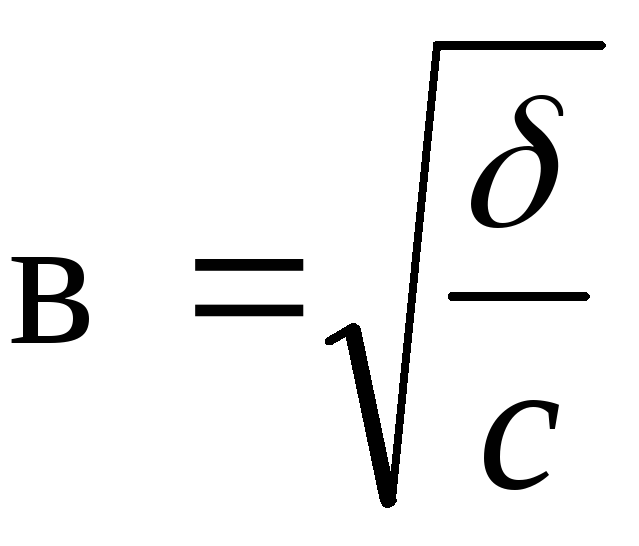 При а=в представляет собой ур-е окружности
х2+y2=а2
При а=в представляет собой ур-е окружности
х2+y2=а2

Точки F1(-c,0) и F2(c,0) — наз. фокусами эллипса а.
Отношение =с/а наз. его эксцентриситетом (0<=<=1)
Точки A1,A2,B1,B2 -вершины эллипса.
Св-во: Для любой точки эллипса сумма расстояний этой точки до фокусов есть величина постоянной, =2а.
Гипербола и ее св-ва.
Кривая 2го порядка наз. гиперболой, если в ур-ии Ax2+Cy2=, коэффициент А и С имеют противоположные знаки, т.е. А*С<0
б) Если >0, то каноническое ур-е гиперболы примет вид: x2/a2-y2/b2=1, F1(c,o) и F2(-c,0) — фокусы ее, >0, =c/a — эксцентриситет.
Св-во: для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная = 2а.
б) если =0, ур-е примет вид x2/a2-y2/b2=0, получаем 2 перекрестные прямые х/ау/b=0
в) если <0, то x2/a2-y2/b2=-1 — ур-е сопряженной гиперболы.
Метод координат на плоскости. Расстояние между точками. Расстояние до точки от начала координат. Координаты точки, делящей отрезок в отношении λ . Координаты середины отрезка. Координаты центра тяжести треугольника.
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Линейная алгебра. Вектора, матрицы, определители, миноры, детерминанты… / / Метод координат на плоскости. Расстояние между точками. Расстояние до точки от начала координат. Координаты точки, делящей отрезок в отношении λ . Координаты середины отрезка. Координаты центра тяжести треугольника. Поделиться:
| ||||||