Равнобедренная трапеция — Википедия

В евклидовой геометрии равнобедренная трапеция — это выпуклый четырёхугольник с осью симметрии, проходящей через середины двух противоположных сторон. Этот четырёхугольник является частным случаем трапеций. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (боковые) имеют одинаковые длины (свойство, которому удовлетворяет также параллелограмм). Диагонали также имеют одинаковые длины. Углы при каждом основании равны и углы при разных основаниях являются смежными (в сумме дающие 180º).

Специальные случаи

Прямоугольники и квадраты обычно считаются специальными случами равнобедренных трапеций, хотя в некоторых источниках они таковыми не считаются.

Другим специальным случаем является трапеция с 3 равными сторонами. В англоязычной литературе её называют trilateral trapezoid (трёхсторонняя трапеция) ^[1], trisosceles trapezoid (триравнобедренная трапеция) ^[2] или, реже,

symtra ^[3]. Такую трапецию можно рассматривать как отсечение 4 последовательных вершин от правильного многоугольника, имеющего 5 или более сторон.

Самопересечения

Любой несамопересекающийся четырёхугольник с единственной осью симметрии должен быть либо равнобедренной трапецией, либо дельтоидом^[3]. Однако, если разрешить самопересечение, множество симметричных четырёхугольников нужно расширить включением в него самопересекающиеся равнобедренные трапеции, в которых пересекающиеся стороны равны, а две другие стороны параллельны, и антипараллелограммы, у которых противоположные стороны имеют равные длины.

У любого антипараллелограмма выпуклая оболочка является равнобедренной трапецией и антипараллелограмм может быть получен из диагоналей равнобедренной трапеции^[4].

Выпуклая равнобедренная трапеция	Самопересекающаяся равнобедренная трапеция	антипараллелограмм

Описания

Если четырёхугольник является трапецией, не обязательно проверять, равны ли боковые стороны (и недостаточно, поскольку ромбы, являющиеся специальными случаями трапеций с боковыми сторонами равной длины, но у него нет осевой симметрии через середины оснований). Любое из следующих свойств выделяет равнобедренную трапецию от других трапеций:

• Диагонали имеют одинаковую длину.
• Углы при основании равны.
• Отрезок, соединяющий середины параллельных сторон, перпендикулярен им.
• Противоположные углы дополнительны (до 180º), из чего, в свою очередь, следует, что равнобедренные трапеции являются вписанными четырёхугольниками.
• Диагонали делятся точкой пересечения на попарно равные отрезки. В терминах рисунка ниже, AE = DE, BE = CE (и AE ≠ CE, если хотят исключить прямоугольники).

Если прямоугольники включаются в класс трапеций, то можно определить равнобедренную трапецию как «вписанный четырёхугольник с равными диагоналями»

[5], как «вписанный четырёхугольник с парой параллельных сторон», или как «выпуклый четырёхугольник с осью симметрии, проходящей через середины противоположных сторон».

Углы

В равнобедренной трапеции углы при основаниях попарно равны. На рисунке ниже углы ∠ABC и ∠DCB являются одинаковыми тупыми углами, а углы ∠BAD и ∠CDA являются одинаковыми острыми углами.

Поскольку прямые AD и BC параллельны, углы, принадлежащие противоположным основаниям, являются дополнительными, то есть ∠ABC + ∠BAD = 180°.

Диагонали и высота

Другая равнобедренная трапеция.

Диагонали равнобедренной трапеции равны. То есть любая равнобедренная трапеция является равнодиагональным четырёхугольником. Однако диагонали равнобедренной трапеции делятся в одной и той же пропорции. На рисунке диагонали AC и BD имеют одинаковую длину (

AC = BD) и делят друг друга на отрезки той же длины (AE = DE и BE = CE).

Отношение, в котором делятся диагонали, равно отношению длин параллельных сторон, то есть

AEEC=DEEB=ADBC.{\displaystyle {\frac {AE}{EC}}={\frac {DE}{EB}}={\frac {AD}{BC}}.}

Длина каждой диагонали, согласно теореме Птолемея, задаётся формулой

p=ab+c2{\displaystyle p={\sqrt {ab+c^{2}}}},

где a и b — длины параллельных сторон AD и BC, а c — длина каждой боковой стороны AB и CD.

Высота, согласно теореме Пифагора, задаётся формулой

h=p2−(a+b2)2=124c2−(a−b)2.{\displaystyle h={\sqrt {p^{2}-\left({\frac {a+b}{2}}\right)^{2}}}={\tfrac {1}{2}}{\sqrt {4c^{2}-(a-b)^{2}}}.}

Расстояние от точки E до основания AD задаётся формулой

d=aha+b{\displaystyle d={\frac {ah}{a+b}}},

где a и b — длины оснований AD и BC, а h — высота трапеции.

Площадь

Площадь равнобедренной (а также любой) трапеции равна половине произведения суммы оснований на высоту. На рисунке, если мы примем AD = a, BC = b, а высота h равна длине отрезка между прямыми AD и BC (перпендикулярного им), то площадь K задаётся формулой:

K=h3(a+b).{\displaystyle K={\frac {h}{2}}\left(a+b\right).}

Если вместо высоты трапеции известны длины боковых сторон AB =CD = c, то площадь можно вычислить по формуле Брахмагупты площади вписанных четырёхугольников. Равенство двух боковых сторон упрощает формулу до

K=(s−a)(s−b)(s−c)2,{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)^{2}}},}

где s=12(a+b+2c){\displaystyle s={\tfrac {1}{2}}(a+b+2c)} — полупериметр трапеции. Эта формула аналогична формуле Герона вычисления площади треугольника. Эту же формулу можно переписать в виде

K=14(a+b)2(a−b+2c)(b−a+2c).{\displaystyle K={\frac {1}{4}}{\sqrt {(a+b)^{2}(a-b+2c)(b-a+2c)}}.}

Радиус описанной окружности

Радиус описанной окружности задаётся формулой^[6]

R=cab+c24c2−(a−b)2.{\displaystyle R=c{\sqrt {\frac {ab+c^{2}}{4c^{2}-(a-b)^{2}}}}.}

Для прямоугольника, в котором a = b, формула упрощается до R=12a2+c2{\displaystyle R={\tfrac {1}{2}}{\sqrt {a^{2}+c^{2}}}}.

См. также

Примечания

Литература

• George Bruce Halsted. Elementary Synthetic Geometry. — J. Wiley & sons, 1896..
• William Dwight Whitney, Benjamin Eli Smith. The Century Dictionary and Cyclopedia. — The Century co., 1911..

Ссылки

Равнобедренная трапеция Википедия

В евклидовой геометрии равнобедренная трапеция — это выпуклый четырёхугольник с осью симметрии, проходящей через середины двух противоположных сторон. Этот четырёхугольник является частным случаем трапеций. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (боковые) имеют одинаковые длины (свойство, которому удовлетворяет также параллелограмм). Диагонали также имеют одинаковые длины. Углы при каждом основании равны и углы при разных основаниях являются смежными (в сумме дающие 180º).

Специальные случаи[ | ]

Прямоугольники и квадраты обычно считаются специальными случами равнобедренных трапеций, хотя в некоторых источниках они таковыми не считаются.

Другим специальным случаем является трапеция с 3 равными сторонами. В англоязычной литературе её называют trilateral trapezoid (трёхсторонняя трапеция) ^[1], trisosceles trapezoid (триравнобедренная трапеция) ^[2] или, реже, symtra ^[3]. Такую трапецию можно рассматривать как отсечение 4 последовательных вершин от правильного многоугольника, имеющего 5 или более сторон.

Самопересечения[ | ]

Любой несамопересекающийся четырёхугольник с единственной осью симметрии должен быть либо равнобедренной трапецией, либо дельтоидом^[3]. Однако, если разрешить самопересечение, множество симметричных четырёхугольников нужно расширить включением в него самопересекающиеся равнобедренные трапеции, в которых пересекающиеся стороны равны, а две другие стороны параллельны, и антипараллелограммы, у которых противоположные стороны имеют равные длины.

У любого антипараллелограмма выпуклая оболочка является равнобедренной трапецией и антипараллелограмм может быть получен из диагоналей равнобедренной трапеции^[4].

Равнобедренная трапеция Википедия

В евклидовой геометрии равнобедренная трапеция — это выпуклый четырёхугольник с осью симметрии, проходящей через середины двух противоположных сторон. Этот четырёхугольник является частным случаем трапеций. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (боковые) имеют одинаковые длины (свойство, которому удовлетворяет также параллелограмм). Диагонали также имеют одинаковые длины. Углы при каждом основании равны и углы при разных основаниях являются смежными (в сумме дающие 180º).

Специальные случаи

Прямоугольники и квадраты обычно считаются специальными случами равнобедренных трапеций, хотя в некоторых источниках они таковыми не считаются.

Другим специальным случаем является трапеция с 3 равными сторонами. В англоязычной литературе её называют trilateral trapezoid (трёхсторонняя трапеция) ^[1], trisosceles trapezoid (триравнобедренная трапеция) ^[2] или, реже, symtra ^[3]. Такую трапецию можно рассматривать как отсечение 4 последовательных вершин от правильного многоугольника, имеющего 5 или более сторон.

Самопересечения

Любой несамопересекающийся четырёхугольник с единственной осью симметрии должен быть либо равнобедренной трапецией, либо дельтоидом^[3]. Однако, если разрешить самопересечение, множество симметричных четырёхугольников нужно расширить включением в него самопересекающиеся равнобедренные трапеции, в которых пересекающиеся стороны равны, а две другие стороны параллельны, и антипараллелограммы, у которых противоположные стороны имеют равные длины.

У любого антипараллелограмма выпуклая оболочка является равнобедренной трапецией и антипараллелограмм может быть получен из диагоналей равнобедренной трапеции^[4].

Выпуклая равнобедренная трапеция	Самопересекающаяся равнобедренная трапеция	антипараллелограмм

Описания

Если четырёхугольник является трапецией, не обязательно проверять, равны ли боковые стороны (и недостаточно, поскольку ромбы, являющиеся специальными случаями трапеций с боковыми сторонами равной длины, но у него нет осевой симметрии через середины оснований). Любое из следующих свойств выделяет равнобедренную трапецию от других трапеций:

• Диагонали имеют одинаковую длину.
• Углы при основании равны.
• Отрезок, соединяющий середины параллельных сторон, перпендикулярен им.
• Противоположные углы дополнительны (до 180º), из чего, в свою очередь, следует, что равнобедренные трапеции являются вписанными четырёхугольниками.
• Диагонали делятся точкой пересечения на попарно равные отрезки. В терминах рисунка ниже, AE = DE, BE = CE (и AE ≠ CE, если хотят исключить прямоугольники).

Если прямоугольники включаются в класс трапеций, то можно определить равнобедренную трапецию как «вписанный четырёхугольник с равными диагоналями» ^[5], как «вписанный четырёхугольник с парой параллельных сторон», или как «выпуклый четырёхугольник с осью симметрии, проходящей через середины противоположных сторон».

Углы

В равнобедренной трапеции углы при основаниях попарно равны. На рисунке ниже углы ∠ABC и ∠DCB являются одинаковыми тупыми углами, а углы ∠BAD и ∠CDA являются одинаковыми острыми углами.

Поскольку прямые AD и BC параллельны, углы, принадлежащие противоположным основаниям, являются дополнительными, то есть ∠ABC + ∠BAD = 180°.

Диагонали и высота

Другая равнобедренная трапеция.

Диагонали равнобедренной трапеции равны. То есть любая равнобедренная трапеция является равнодиагональным четырёхугольником. Однако диагонали равнобедренной трапеции делятся в одной и той же пропорции. На рисунке диагонали AC и BD имеют одинаковую длину (AC = BD) и делят друг друга на отрезки той же длины (AE = DE и BE = CE).

Отношение, в котором делятся диагонали, равно отношению длин параллельных сторон, то есть

AEEC=DEEB=ADBC.{\displaystyle {\frac {AE}{EC}}={\frac {DE}{EB}}={\frac {AD}{BC}}.}

Длина каждой диагонали, согласно теореме Птолемея, задаётся формулой

p=ab+c2{\displaystyle p={\sqrt {ab+c^{2}}}},

где a и b — длины параллельных сторон AD и BC, а c — длина каждой боковой стороны AB и CD.

Высота, согласно теореме Пифагора, задаётся формулой

h=p2−(a+b2)2=124c2−(a−b)2.{\displaystyle h={\sqrt {p^{2}-\left({\frac {a+b}{2}}\right)^{2}}}={\tfrac {1}{2}}{\sqrt {4c^{2}-(a-b)^{2}}}.}

Расстояние от точки E до основания AD задаётся формулой

d=aha+b{\displaystyle d={\frac {ah}{a+b}}},

где a и b — длины оснований AD и BC, а h — высота трапеции.

Площадь

Площадь равнобедренной (а также любой) трапеции равна половине произведения суммы оснований на высоту. На рисунке, если мы примем AD = a, BC = b, а высота h равна длине отрезка между прямыми AD и BC (перпендикулярного им), то площадь K задаётся формулой:

K=h3(a+b).{\displaystyle K={\frac {h}{2}}\left(a+b\right).}

Если вместо высоты трапеции известны длины боковых сторон AB =CD = c, то площадь можно вычислить по формуле Брахмагупты площади вписанных четырёхугольников. Равенство двух боковых сторон упрощает формулу до

K=(s−a)(s−b)(s−c)2,{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)^{2}}},}

где s=12(a+b+2c){\displaystyle s={\tfrac {1}{2}}(a+b+2c)} — полупериметр трапеции. Эта формула аналогична формуле Герона вычисления площади треугольника. Эту же формулу можно переписать в виде

K=14(a+b)2(a−b+2c)(b−a+2c).{\displaystyle K={\frac {1}{4}}{\sqrt {(a+b)^{2}(a-b+2c)(b-a+2c)}}.}

Радиус описанной окружности

Радиус описанной окружности задаётся формулой^[6]

R=cab+c24c2−(a−b)2.{\displaystyle R=c{\sqrt {\frac {ab+c^{2}}{4c^{2}-(a-b)^{2}}}}.}

Для прямоугольника, в котором a = b, формула упрощается до R=12a2+c2{\displaystyle R={\tfrac {1}{2}}{\sqrt {a^{2}+c^{2}}}}.

См. также

Примечания

Литература

• George Bruce Halsted. Elementary Synthetic Geometry. — J. Wiley & sons, 1896..
• William Dwight Whitney, Benjamin Eli Smith. The Century Dictionary and Cyclopedia. — The Century co., 1911..

Ссылки

Равнобедренная трапеция — Википедия. Что такое Равнобедренная трапеция

В евклидовой геометрии равнобедренная трапеция — это выпуклый четырёхугольник с осью симметрии, проходящей через середины двух противоположных сторон. Этот четырёхугольник является частным случаем трапеций. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (боковые) имеют одинаковые длины (свойство, которому удовлетворяет также параллелограмм). Диагонали также имеют одинаковые длины. Углы при каждом основании равны и углы при разных основаниях являются смежными (в сумме дающие 180º).

Специальные случаи

Прямоугольники и квадраты обычно считаются специальными случами равнобедренных трапеций, хотя в некоторых источниках они таковыми не считаются.

Другим специальным случаем является трапеция с 3 равными сторонами. В англоязычной литературе её называют trilateral trapezoid (трёхсторонняя трапеция) ^[1], trisosceles trapezoid (триравнобедренная трапеция) ^[2] или, реже, symtra ^[3]. Такую трапецию можно рассматривать как отсечение 4 последовательных вершин от правильного многоугольника, имеющего 5 или более сторон.

Самопересечения

Любой несамопересекающийся четырёхугольник с единственной осью симметрии должен быть либо равнобедренной трапецией, либо дельтоидом^[3]. Однако, если разрешить самопересечение, множество симметричных четырёхугольников нужно расширить включением в него самопересекающиеся равнобедренные трапеции, в которых пересекающиеся стороны равны, а две другие стороны параллельны, и антипараллелограммы, у которых противоположные стороны имеют равные длины.

У любого антипараллелограмма выпуклая оболочка является равнобедренной трапецией и антипараллелограмм может быть получен из диагоналей равнобедренной трапеции^[4].

Выпуклая равнобедренная трапеция	Самопересекающаяся равнобедренная трапеция	антипараллелограмм

Описания

Если четырёхугольник является трапецией, не обязательно проверять, равны ли боковые стороны (и недостаточно, поскольку ромбы, являющиеся специальными случаями трапеций с боковыми сторонами равной длины, но у него нет осевой симметрии через середины оснований). Любое из следующих свойств выделяет равнобедренную трапецию от других трапеций:

• Диагонали имеют одинаковую длину.
• Углы при основании равны.
• Отрезок, соединяющий середины параллельных сторон, перпендикулярен им.
• Противоположные углы дополнительны (до 180º), из чего, в свою очередь, следует, что равнобедренные трапеции являются вписанными четырёхугольниками.
• Диагонали делятся точкой пересечения на попарно равные отрезки. В терминах рисунка ниже, AE = DE, BE = CE (и AE ≠ CE, если хотят исключить прямоугольники).

Если прямоугольники включаются в класс трапеций, то можно определить равнобедренную трапецию как «вписанный четырёхугольник с равными диагоналями» ^[5], как «вписанный четырёхугольник с парой параллельных сторон», или как «выпуклый четырёхугольник с осью симметрии, проходящей через середины противоположных сторон».

Углы

В равнобедренной трапеции углы при основаниях попарно равны. На рисунке ниже углы ∠ABC и ∠DCB являются одинаковыми тупыми углами, а углы ∠BAD и ∠CDA являются одинаковыми острыми углами.

Поскольку прямые AD и BC параллельны, углы, принадлежащие противоположным основаниям, являются дополнительными, то есть ∠ABC + ∠BAD = 180°.

Диагонали и высота

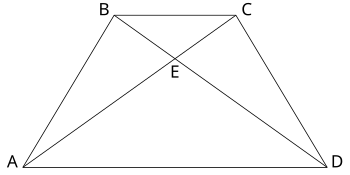Другая равнобедренная трапеция.

Диагонали равнобедренной трапеции равны. То есть любая равнобедренная трапеция является равнодиагональным четырёхугольником. Однако диагонали равнобедренной трапеции делятся в одной и той же пропорции. На рисунке диагонали AC и BD имеют одинаковую длину (AC = BD) и делят друг друга на отрезки той же длины (AE = DE и BE = CE).

Отношение, в котором делятся диагонали, равно отношению длин параллельных сторон, то есть

AEEC=DEEB=ADBC.{\displaystyle {\frac {AE}{EC}}={\frac {DE}{EB}}={\frac {AD}{BC}}.}

Длина каждой диагонали, согласно теореме Птолемея, задаётся формулой

p=ab+c2{\displaystyle p={\sqrt {ab+c^{2}}}},

где a и b — длины параллельных сторон AD и BC, а c — длина каждой боковой стороны AB и CD.

Высота, согласно теореме Пифагора, задаётся формулой

h=p2−(a+b2)2=124c2−(a−b)2.{\displaystyle h={\sqrt {p^{2}-\left({\frac {a+b}{2}}\right)^{2}}}={\tfrac {1}{2}}{\sqrt {4c^{2}-(a-b)^{2}}}.}

Расстояние от точки E до основания AD задаётся формулой

d=aha+b{\displaystyle d={\frac {ah}{a+b}}},

где a и b — длины оснований AD и BC, а h — высота трапеции.

Площадь

Площадь равнобедренной (а также любой) трапеции равна половине произведения суммы оснований на высоту. На рисунке, если мы примем AD = a, BC = b, а высота h равна длине отрезка между прямыми AD и BC (перпендикулярного им), то площадь K задаётся формулой:

K=h3(a+b).{\displaystyle K={\frac {h}{2}}\left(a+b\right).}

Если вместо высоты трапеции известны длины боковых сторон AB =CD = c, то площадь можно вычислить по формуле Брахмагупты площади вписанных четырёхугольников. Равенство двух боковых сторон упрощает формулу до

K=(s−a)(s−b)(s−c)2,{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)^{2}}},}

где s=12(a+b+2c){\displaystyle s={\tfrac {1}{2}}(a+b+2c)} — полупериметр трапеции. Эта формула аналогична формуле Герона вычисления площади треугольника. Эту же формулу можно переписать в виде

K=14(a+b)2(a−b+2c)(b−a+2c).{\displaystyle K={\frac {1}{4}}{\sqrt {(a+b)^{2}(a-b+2c)(b-a+2c)}}.}

Радиус описанной окружности

Радиус описанной окружности задаётся формулой^[6]

R=cab+c24c2−(a−b)2.{\displaystyle R=c{\sqrt {\frac {ab+c^{2}}{4c^{2}-(a-b)^{2}}}}.}

Для прямоугольника, в котором a = b, формула упрощается до R=12a2+c2{\displaystyle R={\tfrac {1}{2}}{\sqrt {a^{2}+c^{2}}}}.

См. также

Примечания

Литература

• George Bruce Halsted. Elementary Synthetic Geometry. — J. Wiley & sons, 1896..
• William Dwight Whitney, Benjamin Eli Smith. The Century Dictionary and Cyclopedia. — The Century co., 1911..

Ссылки

Равнобедренная трапеция — Википедия

Материал из Википедии — свободной энциклопедии

В евклидовой геометрии равнобедренная трапеция — это выпуклый четырёхугольник с осью симметрии, проходящей через середины двух противоположных сторон. Этот четырёхугольник является частным случаем трапеций. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (боковые) имеют одинаковые длины (свойство, которому удовлетворяет также параллелограмм). Диагонали также имеют одинаковые длины. Углы при каждом основании равны и углы при разных основаниях являются смежными (в сумме дающие 180º).

Специальные случаи

Прямоугольники и квадраты обычно считаются специальными случами равнобедренных трапеций, хотя в некоторых источниках они таковыми не считаются.

Другим специальным случаем является трапеция с 3 равными сторонами. В англоязычной литературе её называют trilateral trapezoid (трёхсторонняя трапеция) ^[1], trisosceles trapezoid (триравнобедренная трапеция) ^[2] или, реже, symtra ^[3]. Такую трапецию можно рассматривать как отсечение 4 последовательных вершин от правильного многоугольника, имеющего 5 или более сторон.

Самопересечения

Любой несамопересекающийся четырёхугольник с единственной осью симметрии должен быть либо равнобедренной трапецией, либо дельтоидом^[3]. Однако, если разрешить самопересечение, множество симметричных четырёхугольников нужно расширить включением в него самопересекающиеся равнобедренные трапеции, в которых пересекающиеся стороны равны, а две другие стороны параллельны, и антипараллелограммы, у которых противоположные стороны имеют равные длины.

У любого антипараллелограмма выпуклая оболочка является равнобедренной трапецией и антипараллелограмм может быть получен из диагоналей равнобедренной трапеции^[4].

Определение трапеции

Трапецией называется четырёхугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны трапеции называются её основаниями, а непараллельные – боковыми сторонами трапеции.

\(ABCD\) – трапеция;

\(AD, \, BC\) – основания, \(AB, \, CD\) – боковые стороны трапеции \(ABCD\)

Свойства трапеции

1. Сумма углов, прилежащих к боковой стороне трапеции, равна \(180^{\circ}\).
2. Каждая диагональ трапеции образует с её основаниями равные углы.
3. При пересечении диагоналей трапеции и продолжений её боковых сторон образуются подобные треугольники, прилежащие к основаниям.
4. Биссектрисы смежных углов трапеции перпендикулярны.

\(ABCD\) – трапеция \(\Rightarrow \, \angle{DAB}+\angle{ABC}=180^{\circ}, \, \angle{ADC}+\angle{DCB}=180^{\circ};\)
\(ABCD\) – трапеция \(\Rightarrow \, \angle{CAD}=\angle{ACB}, \, \angle{BDA}=\angle{DBC};\)
\(ABCD\) – трапеция, \(AC \cap BD=O\) \(\Rightarrow \, \triangle{AOD} \backsim \triangle{COB};\)
\(ABCD\) – трапеция, \(AB \cap CD=E\) \(\Rightarrow \, \triangle{AED} \backsim \triangle{BEC}\)

Средняя линия трапеции

Определение. Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.

Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.

\( AD||BC, \, M\) – середина \(AB, \, N\) – середина \(CD \, \Rightarrow \) $$ MN||AD, \, MN||BC, \, MN=\frac{1}{2}(AD+BC)$$

Свойства равнобедренной трапеции

1. В равнобедренной трапеции углы при каждом основании равны.
2. Диагонали равнобедренной трапеции равны.
3. Ранобедренную трапецию можно вписать в окружность.

\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, \angle{ABC}=\angle{DCB}, \, \angle{BAD}=\angle{CDA}; \)
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, AC=BD; \)
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, ABCD\) вписанная

Признаки равнобедренной трапеции

1. Если углы при некотором основании трапеции равны, то эта трапеция равнобедренная.
2. Если диагонали трапеции равны, то эта трапеция равнобедренная.
3. Если трапецию можно вписать в окружность, то эта трапеция равнобедренная.

\( AD||BC, \, M\) – середина \(AB, \, N\) – середина \(CD \, \Rightarrow \) $$ MN||AD, \, MN||BC, \, MN=\frac{1}{2}(AD+BC)$$

Площадь трапеции

1. Площадь трапеции равна половине произведения суммы её оснований на высоту трапеции.
2. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.

$$ S=\frac{1}{2}(a+b)h$$		$$ S=\frac{1}{2} d_1d_2\sin{\varphi}$$