Равнобедренный треугольник как найти – Равнобедренный треугольник. Подробная теория с примерами. — Детская игровая комната «Волшебный лес»

Posted on 09.11.202026.12.2019 by alexxlab

Содержание

Стороны равнобедренного треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Равнобедренный треугольник имеет две равные по значению боковые стороны a и основание b. Это позволяет рассчитать любые параметры треугольника, необходимые для решения задачи. Периметр равнобедренного треугольника равен удвоенной боковой стороне в сумме с основанием. (рис.88.1) P=2a+b

Высота, проведенная к основанию равнобедренного треугольника, делит его на два конгруэнтных прямоугольных треугольника, с половиной основания в качестве второго катета и боковой стороной как гипотенузой. Такая высота одновременно является и медианой и биссектрисой. Найти ее можно по теореме Пифагора из прямоугольного треугольника. (рис.88.2) h_b=m_b=l_b=√(a^2-(b/2)^2 )=√(4a^2-b^2 )/2

Остальные две высоты равны друг другу и считаются через формулу с произведением разностей полупериметров и сторон, где приравнены боковые стороны. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a

Зная высоту, найти площадь равнобедренного треугольника можно, подставив полученное выражение в формулу, по которой площадь равна половине основания, умноженной на его высоту. S=hb/2=(b√(4a^2-b^2 ))/4

Углы в равнобедренном треугольнике распределяются следующим образом – углы при основании друг другу конгруэнтны, также как и боковые стороны, а в сумме все три угла дают 180 градусов, поэтому найти их можно двумя видами разности. α=(180°-β)/2 β=180°-2α

Если ни один из углов не дан, но есть все стороны, то можно воспользоваться теоремой косинусов, чтобы найти любой угол. cos⁡α=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cos⁡β=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 )

Медиана и биссектриса, опущенные на основание, вычисляются по формуле высоты, приведенной выше, а оставшиеся две медианы (равно как и две биссектрисы) равны друг другу, поскольку строятся на равных боковых сторонах. Вычислить медиану можно, упростив формулу произвольного треугольника. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2

В формуле биссектрисы аналогично приравниваются боковые стороны, и ее становится возможным вычислить по упрощенной схеме. (рис. 88.4) l_a=√(ab(2a+b)(a+b-a) )/(a+b)=(b√(a(2a+b) ))/(a+b)

Средняя линия равнобедренного треугольника, параллельная основанию, равна его половине, а средние линии, параллельные боковым сторонам, равны между собой и также равны половинам самих боковых сторон. (рис. 88.5) M_b=b/2 M_a=a/2

Радиус окружности, вписанной в равнобедренной треугольник, является производной формулы для произвольного треугольника, и рассчитать его можно, зная боковую сторону и основание. (рис. 88.6) r=b/2 √((2a-b)/(2a+b))

Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы и выглядит упрощенно следующим образом. (рис. 88.7) R=a^2/√(4a^2-b^2 )

geleot.ru

Как посчитать стороны равнобедренного треугольника

Чтобы посчитать чему равны стороны равнобедренного треугольника воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

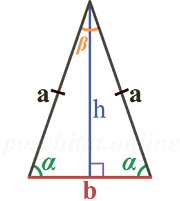
Чтобы вычислить длины сторон равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):

для стороны a:

длину основания (b) и угол α
длину основания (b) и угол β
длину основания (b) и высоту (h)

для стороны b:

длину двух равных сторон (a) и угол α
длину двух равных сторон (a) и угол β
длину двух равных сторон (a) и высоту (h)

Введите их в соответствующие поля и получите результат.

Как посчитать сторону a равнобедренного треугольника

Если известна сторона b и угол α

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол α?

Формула

a = ^b/_{2⋅cos α}

Пример

Если сторона b = 10 см, а ∠α = 30°, то:

a = ¹⁰/_{2⋅cos 30°} = 10/(2⋅0.8660) = 5.77см

Если известна сторона b и угол β

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол β?

Формула

a = ^b/_{2⋅sin ^β/₂}

Пример

Если сторона b = 10 см, а ∠β = 30°, то:

a = ¹⁰/_{2⋅sin 15} = 10/(2⋅0.2588) = 19.31см

Если известна сторона b и высота h

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и высота h?

Формула

a = √¹/_b² + h²

Пример

Если сторона b = 10 см, а высота h = 20 см, то:

a = √¹/_10² + 20² = √0.01+400 = 20.61см

Как посчитать сторону b (основание) равнобедренного треугольника

Если известна сторона a и угол α

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол α?

Формула

b = 2⋅a⋅cos α

Пример

Если сторона a = 10 см, а ∠α = 30°, то:

b = 2⋅10⋅cos 30° = 2⋅10⋅0.8660 = 17.32см

Если известна сторона a и угол β

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол β?

Формула

b = 2⋅a⋅sin ^β/₂

Пример

Если сторона a = 10 см, а ∠β = 40°, то:

b = 2⋅10⋅sin ⁴⁰/₂ = 2⋅10⋅0.342 = 6.84см

Если известна сторона a и высота h

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и высота h?

Формула

b = 2⋅√a² — h² , h

Пример

Если сторона a = 10 см, а высота h = 5 см, то:

b = 2⋅√10² — 5² = 2⋅√75 = 17.32см

См. также

poschitat.online

Конспект «Равнобедренный треугольник + ЗАДАЧИ»

«Равнобедренный треугольник + ЗАДАЧИ по теме»

Равнобедренный треугольник — треугольнику которого две стороны равны.
Равные стороны называют боковыми сторонами, а третью сторону — основанием.

Свойства равнобедренного треугольника были известны с давних времен. Еще древние вавилоняне (II в. до н.э.) знали, что углы у основания равнобедренного треугольника равны. Любой треугольник можно разрезать на равнобедренные треугольники.

Свойства и признаки равнобедренного треугольника

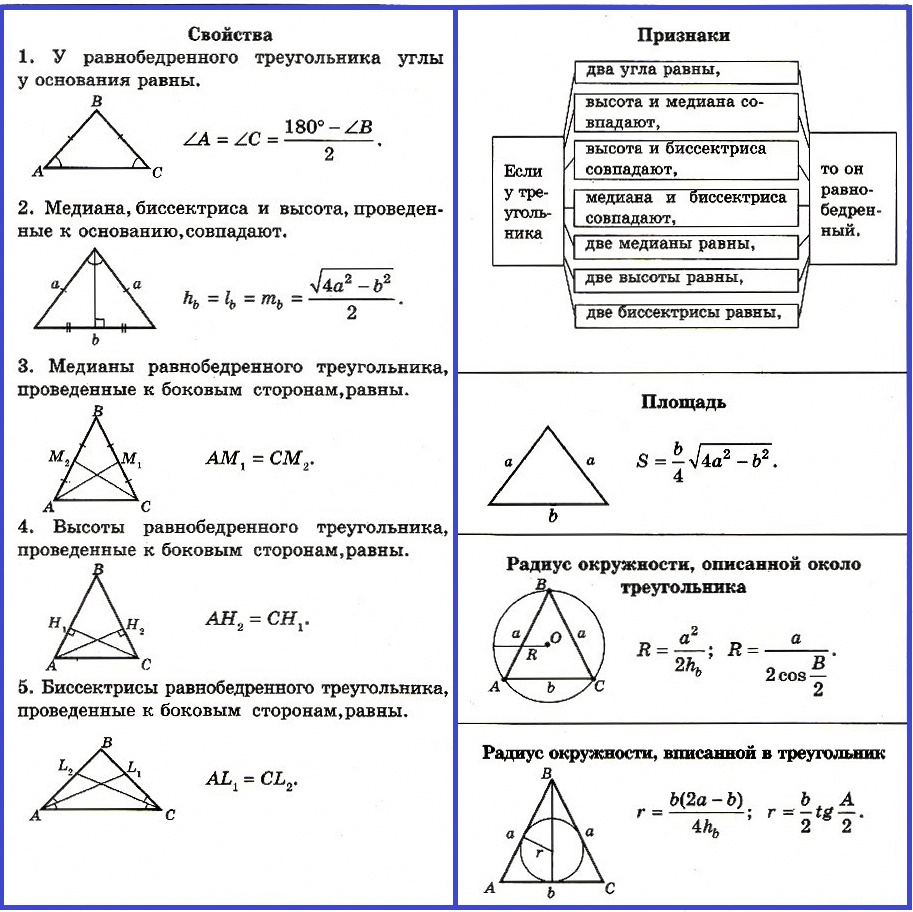
Свойства равнобедренного треугольника:
1. У равнобедренного треугольника углы у основания равны (теорема).
2. Медиана, биссектриса и высота, проведенные к основанию, совпадают (теорема).
3. Медианы равнобедренного треугольника, проведенные к боковым сторонам, равны.
4. Высоты равнобедренного треугольника, проведенные к боковым сторонам, равны.
5. Биссектрисы равнобедренного треугольника, проведенные к боковым сторонам, равны.

Признаки равнобедренного треугольника:
Если у треугольника есть один из нижеуказанных признаков, то он равнобедренный:
— два угла равны,
— высота и медиана совпадают,
— высота и биссектриса совпадают,
— медиана и биссектриса совпадают,
— две медианы равны,
— две высоты равны,
— две биссектрисы равны.

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ:

Задача № 1. Дано: ΔABC — равносторонний, ΔADC — равнобедренный (AD=CD), AC — общая сторона, BC = 8 см, P

ADC > P_ABC в 1,5 раза. Найти: CD.

Задача № 2. Дано: ΔABC — равнобедренный, AB = BC, AD — медиана, AB + BD = 27 см, AC + CD = 21 см. Найти: AB, BC, AC.

Задача № 3. Дано: ΔABC — равнобедренный, AB = BC, ∠1 = 130°. Найти: ∠2.

Это конспект по теме «Равнобедренный треугольник + ЗАДАЧИ по теме». Выберите дальнейшие действия:

uchitel.pro

Калькулятор расчета углов равнобедренного треугольника

Треугольник с одинаковыми боковыми сторонами называется равнобедренным. В нем равны и углы при основании. Если они известны, то вычислить третий угол не составит труда. Как известно, сумма всех углов треугольника равна 180°. Если из 180° вычесть сумму двух одинаковых углов при основании (а), то найдем третий угол β:

β = 180°-2α

Если известна величина угла b, противолежащего основанию и требуется найти угол (а) при основании, необходимо из 180° вычесть известный угол β. Полученную величину делим на два, т.к. углы при основании равны.

α= (180°-β)/2

Если известны стороны равнобедренного треугольника, можно рассчитать все его углы. Чтобы найти угол при основании, проведем к основанию высоту, которая делит основание пополам, а треугольник — на два одинаковых прямоугольных треугольника. Гипотенузой вновь образованных треугольников будет боковая сторона равнобедренного треугольника (а), а одним из катетов — половина длины основания (b/2). Используя теорему косинусов определяем косинус угла (а), как отношение прилежащего к искомому углу катета (b/2) к гипотенузе (а) по формуле:

cosα= b/2a

Рассчитать угол при основании равнобедренного треугольника можно также через катеты образованного в нем прямоугольного треугольника (например, abc). Одним из его катетов (b) будет половина длины основания равнобедренного треугольника, другим катетом (а) — высота равнобедренного треугольника. Найти угол α при основании треугольника можно через тангенс угла, как отношение противолежащего ему катета (а) к прилежащему катету (b).

tg (α) = a/b

В таблицк тангенсов находим угол α в градусах. Т.к. Углы при основании равнобедренного треугольника равны, то найти третий угол не составит труда, зная, что сумма всех его углов равна 180°.

Рассчитать углы равнобедренного треугольника зная длину катетов

infofaq.ru

Свойства и признаки равнобедренного треугольника.

Категория: Справочные материалы

Елена Репина 2013-07-22 2013-07-31

Равнобедренный треугольник – треугольник, у которого две стороны равны между собой.

Равные стороны называются боковыми, третья сторона называется основанием.

Свойства равнобедренного треугольника

1. Углы при основании равны

2. Биссектриса, медиана и высота, проведенные к основанию совпадают между собой

3. Углы при основании равнобедренного треугольника вычисляются по следующей формуле: $\alpha=\beta=90^{\circ}-\frac{\gamma}{2}$ , где $\gamma$ – угол напротив основания.

4. Биссектрисы, медианы и высоты, проведённые из углов при основании равны между собой

5. Центры вписанной и описанной окружностей лежат на медиане=высоте=биссектрисе, проведенной к основанию

Признаки равнобедренного треугольника

1. Если в треугольнике два угла равны, то он равнобедренный.

2. Если в треугольнике медиана является и высотой (биссектрисой), то такой треугольник равнобедренный.

Автор: egeMax | Нет комментариев

egemaximum.ru

Равнобедренный треугольник. Вычисление длин, углов. Синус угла

Продолжаем разбор Заданий №6 ЕГЭ по математике.

76н

Если вы научились находить значения синусов,

косинусов, тангенсов углов в прямоугольном треугольнике (статьи 1 и 2 ), то задачи, которые мы сегодня будем разбирать, не покажутся вам сложными.

Можете заглянуть и сюда, чтобы вспомнить свойства равнобедренного треугольника.

В категорию «Задания №6» входят также задачи следующих типов + показать

Задача 1.

В треугольнике ABC AC=BC . Внешний угол при вершине B равен $163^{\circ}$ . Найдите угол C. Ответ дайте в градусах.

Решение: + показать

Задача 2.

В треугольнике ABC угол A равен $62^{\circ}$ , угол C равен $50^{\circ}.$ На продолжении стороны AB отложен отрезок BD=BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.

Решение: + показать

Задача 3.

В треугольнике ABC $AC=BC=5\sqrt2, \;AB=10.$ Найдите tgA.

Решение: + показать

Задача 4.

В треугольнике $ABC\;AC=BC=5,\;sinA=\frac{3}{5}.$ Найдите AB.

Решение: + показать

Задача 5.

В треугольнике ABC AC=BC , AH — высота, $sinBAC=\frac{\sqrt3}{2}.$ Найдите sinBAH.

dfgv

Решение: + показать

Задача 6.

В треугольнике $ABC\;AC=BC,$ – высота, $AB=20,5,\;tgBAC=\frac{40}{9}.$ Найдите BH.

dfgv

Решение: + показать

Задача 7.

В треугольнике ABC $AC=BC,\;AB=20,$ высота AH=8. Найдите синус угла BAC.

Решение: + показать

, так как треугольник равнобедренный.

Из треугольника

$sinB=\frac{AH}{AB}=\frac{8}{20}=0,4.$

Ответ: 0,4.

Задача 8.
В треугольнике $ABC\;AC=BC=2\sqrt3,$ угол равен $120^{\circ}$ . Найдите высоту .
Решение: + показать
Задача 9.
В треугольнике ABC $AC=BC=15,\;AB=18.$ Найдите синус внешнего угла при вершине A.
Решение: + показать
Задача 10.
В треугольнике $ABC\;AC=BC,$ угол равен $120^{\circ},$ $AC=2\sqrt3.$ Найдите .

Решение: + показать
Если мы проведем медиану , то она будет и высотой, и биссектрисой для треугольника
$sinACH=sin60^{\circ}=\frac{\sqrt3}{2};$
По определению синуса для угла имеем:
$\frac{\sqrt3}{2}=\frac{AH}{AC};$
$\frac{\sqrt3}{2}=\frac{AH}{2\sqrt3};$
Значит
Ответ: 6.

Устали? Хотите немного посмеяться? + показать
* * *
Сын “нового русского” говорит отцу:
– Папа, ты мне обещал, что если я получу “пять”, то ты мне дашь 11 долларов. Вчера я получил “два”, а сегодня “три”, – итого – “пять”.
– Хорошо, говорит отец, – на тебе один доллар и еще один – итого одиннадцать. Учись дальше, сынок.
Остальное тут.

Вы можете пройти тест по теме «Равнобедренный треугольник. Вычисление углов и длин».

egemaximum.ru
Равнобедренный треугольник — это… Что такое Равнобедренный треугольник?
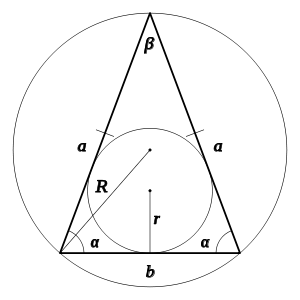Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Равные стороны называются боковыми, а последняя — основанием. По определению, правильный треугольник также является равнобедренным, но обратное утверждение неверно.
Свойства
Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.
Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию, совпадают между собой. Центры вписанной и описанной окружностей лежат на этой линии.
Углы, противолежащие равным сторонам, всегда острые (следует из их равенства).
Пусть a — длина двух равных сторон равнобедренного треугольника, b — длина третьей стороны, α и β — соответствующие углы, R — радиус описанной окружности, r — радиус вписанной.
Стороны могут быть найдены следующим образом:
Углы могут быть выражены следующими способами:
Периметр равнобедренного треугольника может быть вычислен любым из следующих способов:
Площадь треугольника может быть вычислена одним из следующих способов:
(формула Герона).
Признаки
Два угла треугольника равны.
Высота совпадает с медианой.
Высота совпадает с биссектрисой.
Биссектриса совпадает с медианой.
Две высоты равны.
Две медианы равны.
Две биссектрисы равны (теорема Штейнера — Лемуса).
См. также
academic.ru