Решение задач по теме «Неравномерное движение. Сложение скоростей»

План-конспект урока по теме «Решение задач по теме «Неравномерное движение. Сложение скоростей»»

Дата:

Тема: «Решение задач по теме «Неравномерное движение. Сложение скоростей»»

Цели:

Образовательная: формирование практических умений по решению задач на тему «Неравномерное движение. Сложение скоростей»;

Развивающая: совершенствовать интеллектуальные умения (наблюдать, сравнивать, размышлять, применять знания, делать выводы), развивать познавательный интерес;

Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.

Тип урока: обобщение и систематизация знаний

Оборудование и источники информации:

1. Исаченкова, Л. А. Физика : учеб. для 9 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский ; под ред. А. А. Сокольского. Минск : Народная асвета, 2015

2. Исаченкова, Л. А. Сборник задач по физике. 9 класс : пособие для учащихся учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, В. В. Дорофейчик. Минск : Аверсэв, 2016, 2017.

Структура урока:

1. Организационный момент (5 мин)

2. Актуализация опорных знаний (5 мин)

3. Закрепление знаний(30 мин)

4. Итоги урока (5 мин)

Содержание урока

1. Организационный момент

Здравствуйте, садитесь! (Проверка присутствующих). Сегодня на уроке мы должны научиться решать задачи по теме «Неравномерное движение. Сложение скоростей». А это значит, что

Тема урока: «Решение задач по теме «Неравномерное движение. Сложение скоростей»»

2. Актуализация опорных знаний

1. Какое движение называется неравномерным? Можно ли утверждать, что тело движется равномерно, если пути, проходимые телом за каждый час. одинаковы?

2. Что показывает средняя скорость пути? Средняя скорость перемещения? Как их вычисляют?

3. В чем смысл закона сложения скоростей Галилея?

3. Закрепление знаний

А сейчас перейдем к решению задач из сборника:

№ 111

Человек прошел первую часть пути = 3,2 км за промежуток времени Δ

t_t = 28 мин, а вторую часть s ₂ = 1,6 км— за промежуток времени Δt₂ = 20 мин. Определите среднюю скорость пути за весь промежуток времени движения человека.

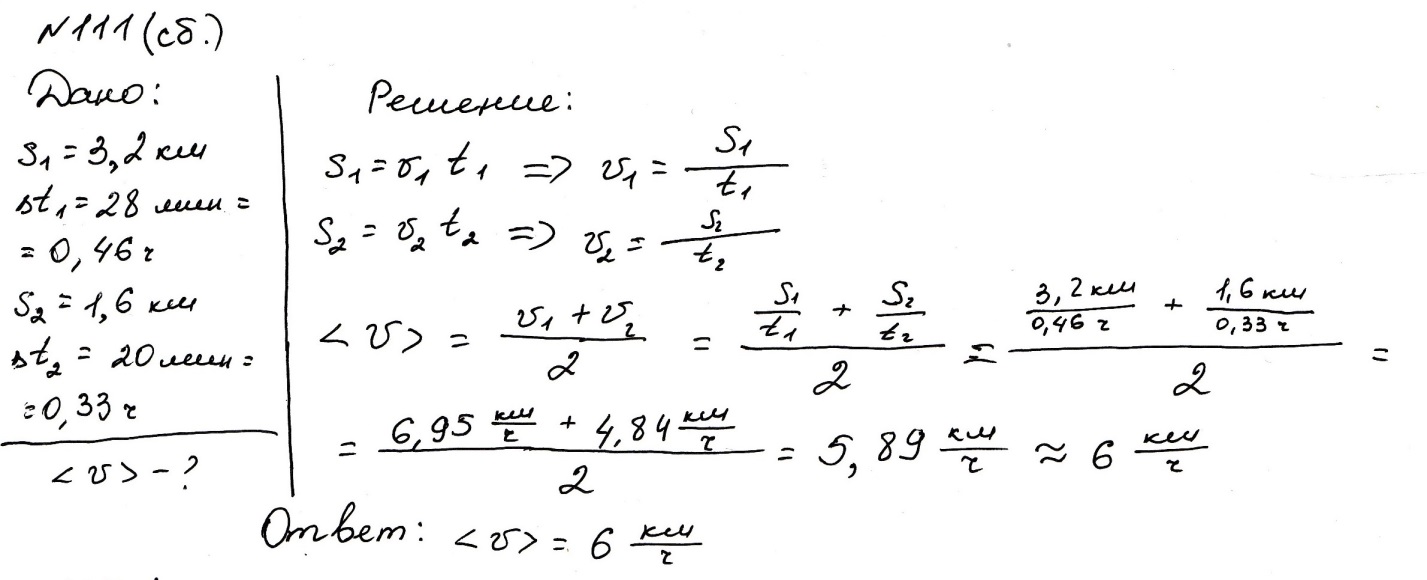
№ 112

Первую часть дистанции конькобежец пробежал за время Δ = 20 с со скоростью, модуль которой = 7,6, а вторую — за время Δt₂ = 36 с со скоростью, модуль которой v₂ = 9,0 . Определите среднюю скорость движения конькобежца на всей дистанции.

№ 113

Самолет пролетает путь = 500 км с постоянной скорость =1000, а затем попадает в зону действия встречного ветра и пролетает путь s₂ = 1200 км с постоянной скоростью v₂ = 800. Определите среднюю скорость пути за весь перелет.

№ 114

Мотоциклист проехал путь = 20 км за промежуток времени Δ = 30 мин, а далее ехал со скоростью v₂ = 60 в течение промежутка времени Δ=1,5ч. Найдите среднюю скорость движения мотоциклиста на всем пути.

№ 115

Велосипедист проехал путь = 10 км со скоростью = 20 , после чего путь s₂ = 50 км проехал за промежуток времени Δ= 2,0 ч. Найдите среднюю скорость движения велосипедиста на всем пути.

№ 116

Спортсмен пробегает N = 10 полных кругов по беговой дорожке длиной l= 0,33 км за промежуток времени Δt = 11 мин. Определите модуль средней скорости перемещения спортсмена и среднюю скорость пути на всей дистанции.

№ 117

Путь между начальной и конечной станциями маршрута автобуса s =210 км. Определите время, которое тратит автобус на остановки на промежуточных станциях, если средняя скорость его движения без учета остановок <> = 50 , а средняя скорость пути с учетом остановок

— <>= 42 .

№ 5 упр. 6( учебник)

Модуль скорости движения катера относительно воды =4, Какие значения может принять модуль скорости движения катера относительно берега, если модуль скорости течения воды = 1,5 ,?

№ 6 упр. 6( учебник)

Вертолет летит из Минска на юг. Модуль скорости движения вертолета относительно =5 4 . В направлении с севера на юг дует ветер, модуль

скорости которого = 10. Найдите модуль скорости вертолета относительно Земли и его перемещение за время t= 30 мин полета.

№ 7 упр. 6 (учебник)

Решите предыдущую задачу для случаев, когда ветер дует: а) с юга на север; б) с запада на восток. Решение подтвердите чертежом.

4. Закрепление знаний

1. Быстрота неравномерного движения на участке траектории характеризуется средней скоростью, а в данной точке траектории — .мгновенной скоростью.

2. Мгновенная скорость приближенно равна средней скорости, определенной за малый промежуток времени. Чем меньше этот промежуток времени, тем меньше отличие средней скорости от мгновенной.

3. Мгновенная скорость направлена по касательной к траектории движения.

4. Если модуль мгновенной скорости возрастает, то движение тела называют ускоренным, если он убывает — замедленным.

5. При равномерном прямолинейном движении мгновенная скорость одинакова в любой точке траектории.

6. Перемещение тела относительно неподвижной системы отсчета равно векторной сумме его перемещения относительно движущейся системы и перемещения движущейся системы относительно неподвижной.

7. Скорость тела в неподвижной системе отсчета равна векторной сумме его скорости относительно движущейся системы и скорости движущейся системы относительно неподвижной.

5. Итоги урока

Итак, подведем итоги. Что вы сегодня узнали на уроке?

Организация домашнего задания

§9,10, упр. 6 № 3, 6.

Рефлексия.

Продолжите фразы:

• Сегодня на уроке я узнал…

• Было интересно…

• Знания, которые я получил на уроке, пригодятся

Равномерное движение

Равномерное движение

Равномерное движение — движение вдоль прямой линии с постоянной (как по модулю, так и по направлению) скоростью. При равномерном движении пути, которые тело проходит за равные промежутки времени, также равны.

Для кинематического описания движения расположим ось OХ вдоль направления движения. Для определения перемещения тела при равномерном прямолинейном движении достаточно одной координаты Х. Проекции перемещения и скорости на координатную ось можно рассматривать, как алгебраические величины. 

Пусть в момент времени t1 тело находилось в точке с координатой x1, а в момент времени  t2 — в точке с координатой x2. Тогда проекция перемещения точки на ось OХ будет запишется в виде:

∆s=x2-x1.

В зависимости от направления оси и направления движения тела эта величина может быть как положительной, так и отрицательной. При прямолинейном и равномерном движении модуль перемещения тела совпадает с пройденным путем. Скорость равномерного прямолинейного движения определяется по формуле:

v=∆s∆t=x2-x1t2-t1

Если v>0, тело движется вдоль оси OX в положительном направлении. Иначе — в отрицательном. 

Математическое описание равномерного прямолинейного движения

Закон движения тела при равномерном прямолинейном движении описывается линейным алгебраическим уравнением.

Уравнение движения тела при равномерном прямолинейном движении

x(t)=x0+vt

v=const ; x0 — координата тела (точки) в момент времени t=0.

Пример графика равномерного движения — на рисунке ниже.

Здесь два графика, описывающих движение тел 1 и 2. Как видим, тело 1 во время t=0 находилось в точке x=-3.

От точки x1 до точки x2 тело переместилось за две секунды. Перемещение тела составило три метра.

∆t=t2-t1=6-4=2с

∆s=6-3=3м.

Зная это, можно найти скорость тела. 

v=∆s∆t=1,5мс2

Есть еще один способ определения скорости: из графика ее можно найти как отношение сторон BC и AC треугольника ABC. 

v=∆s∆t=BCAC.

Причем, чем больше угол, который образует график с осью времени, тем больше скорость. Говорят также, что скорость равн

Сложение скоростей. Самостоятельная работа по теме «Равномерное движение»

План-конспект урока по теме «Сложение скоростей. Самостоятельная работа по теме «Равномерное движение»

Дата:

Тема: «Сложение скоростей. Самостоятельная работа по теме «Равномерное движение»

Цели:

Образовательная: Обеспечить и сформировать осознанное усвоение знаний о неравномерном движении и мгновенной скорости;

Развивающая: Продолжить развитие навыков самостоятельной деятельности, навыков работы в группах.

Воспитательная: Формировать познавательный интерес к новым знаниям; воспитывать дисциплину поведения.

Тип урока: урок усвоения новых знаний

Оборудование и источники информации:

Исаченкова, Л. А. Физика : учеб. для 9 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский ; под ред. А. А. Сокольского. Минск : Народная асвета, 2015

Структура урока:

1. Организационный момент(2 мин)

2. Актуализация опорных знаний(2мин)

3. Изучение нового материала (15 мин)

4. Физкультминутка (2 мин)

5. Закрепление знаний (22 мин)

6. Итоги урока(2 мин)

Содержание урока

1. Организационный момент

Здравствуйте, садитесь! (Проверка присутствующих). Сегодня на уроке мы должны разобраться с понятием сложение скоростей. А это значит, что Тема урока: Сложение скоростей. Самостоятельная работа по теме «Равномерное движение»

2. Актуализация опорных знаний

В повседневной жизни мы часто видим, как одни тела движутся относительно других движущихся тел. Например, авиапассажир перемещается по салону летящего самолета, человек идет по движущемуся эскалатору, катер пересекает реку с быстрым течением и т. д.

Каковы закономерности таких движении?

3. Изучение нового материала

Проведем опыт. В вертикальную стеклянную трубку, заполненную сахарным сиропом, опустим металлический шарик (рис. 76). Трубку будем равномерно перемещать относительно школьной доски в горизонтальном направлении.

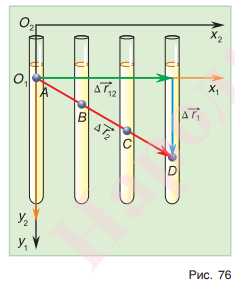
Систему отсчета с осями координат и , связанную с трубкой, назовем движущейся, а систему отсчета с осями и , связанную с доской, — неподвижной.

Наблюдая за движением шарика, будем отмечать на доске его положения через каждые 10 с (точки А, В, С, D).

Из рисунка 76 видно, что относительно трубки шарик за 30 с совершил перемещение Δ. За это время трубка совершила перемещение Δотносительно школьной доски. Видно также, что перемещение Δ шарика относительно доски равно векторной сумме перемещений Δ и Δ:

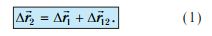
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме его перемещения относительно движущейся системы и перемещения движущейся системы относительно неподвижной.

Все эти перемещения произошли за один и тот же промежуток времени Δt. Разделив в формуле (1) каждое из перемещений на Δt, получим:

Вектор 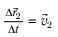— это скорость движения шарика относительно доски,

вектор — скорость движения шарика относительно трубки, а вектор 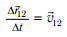— скорость, с которой трубка движется относительно доски

(см. рис. 76).

Таким образом,

Скорость тела в неподвижной системе отсчета равна векторной сумме его скорости относительно движущейся системы и скорости движущейся системы относительно неподвижной.

Это утверждение называют законом сложения скоростей Галилея.

Формула (3) справедлива и для тел, движущихся неравномерно. В этом случае векторы и , являются мгновенными скоростями.

Отметим, что неподвижной мы могли бы считать и систему отсчета, связанную с трубкой. Тогда система отсчета, связанная с доской, считалась бы движущейся. Докажите, что закон сложения скоростей от этого не изменится.

Закон сложения скоростей (3) используется при решении многих практически важных задач. Он позволяет найти скорость снаряда, выпущенного из движущегося танка, скорость самолета, заходящего на посадку при сильном ветре (рис. 77), и т. д.

4. Физкульминутка

Встали, глазками сделали 8-ку, потресли руками, потресли ногами, сели.

5. Закрепление знаний

Самостоятельная работа по теме «Равномерное движение»

Вариант 1

№ 1. Системой отсчета в механике называется:

а) тело отсчета, связанная с ним система координат и прибор для измерения времени;

б) система координат и прибор для измерения времени;

в) тело отсчета, связанная с ним система координат и прибор для измерения расстояний;

г) система координат и прибор для измерения расстояний.

№ 2. Кинематический закон движения материальной точки вдоль

оси Ох имеет вид х = А + Bt, где А = — 4 м, В = 6 . Определите координату точки через промежуток времени Δt = 8 с после начала отсчета времени.

№ 3. Мяч, брошенный вниз с балкона с высоты , =3м, отскочил от тротуара и поднялся на высоту h₂ = 4 м относительно земли. Определите модуль перемещения мяча.

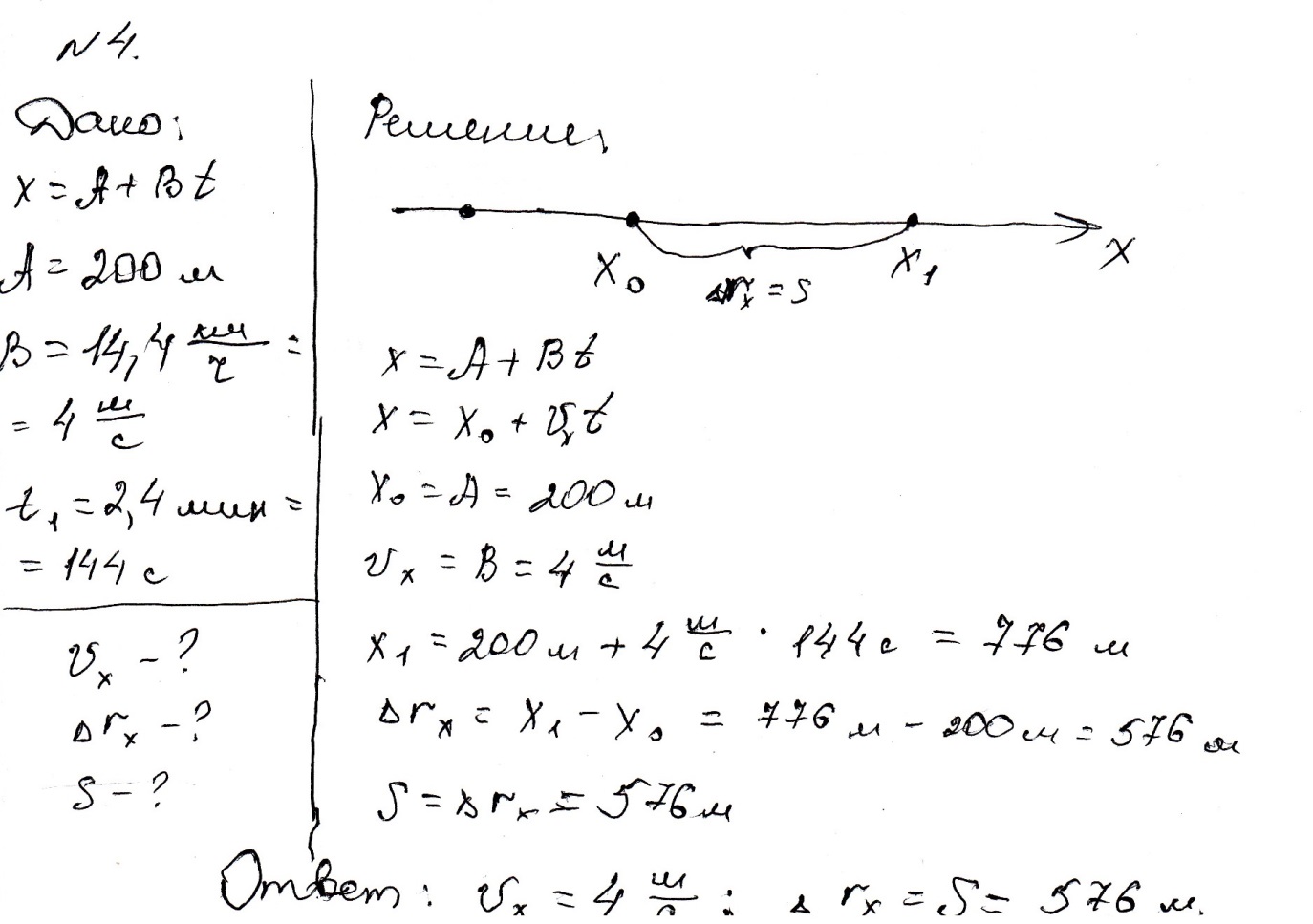
№ 4. Кинематический закон прямолинейного движения лодки вдоль оси Ох задан уравнением x = A + Bt, где А =200 м, В = 14,4 Определите проекции скорости и перемещения на ось Ох, а также путь, пройденный лодкой за время = 2,4 мин.

№ 5. Первую половину пути автомобиль проехал со средней скоростью v₁ = 60 км/ч, а вторую – со средней скоростью v₂ = 40 км/ч. Определить среднюю скорость автомобиля на всем пути.

Решение:

Проанализируем условие задачи: первую половину пути автомобиль проехал со скоростью 60 км/ч и затратил время равное вторую половину пути автомобиль проехал со скоростью 40 км/ч и затратил время равное По определению, средняя скорость при равномерном прямолинейном движении, равна отношению всего пройденного пути ко всему затраченному времени.

т. е.

Подставляя значения скорости, в формулу средней скорости, имеем:

Средняя скорость равна 48 км/ч.

Самостоятельная работа по теме «Равномерное движение»

Вариант 2

№ 1. Телом отсчета в механике называется:

а) тело, от которого удаляются другие тела;

б) тело, к которому приближаются другие тела;

в) тело, движение которого изучается;

г) тело, относительно которого рассматривается движение других тел.

№ 2. Кинематический закон движения материальной точки вдоль

оси Ох имеет вид х = А + Bt, где A = 2 м, В = — 8 . Определите координату точки через промежуток времени Δt = 3 с после начала отсчета времени.

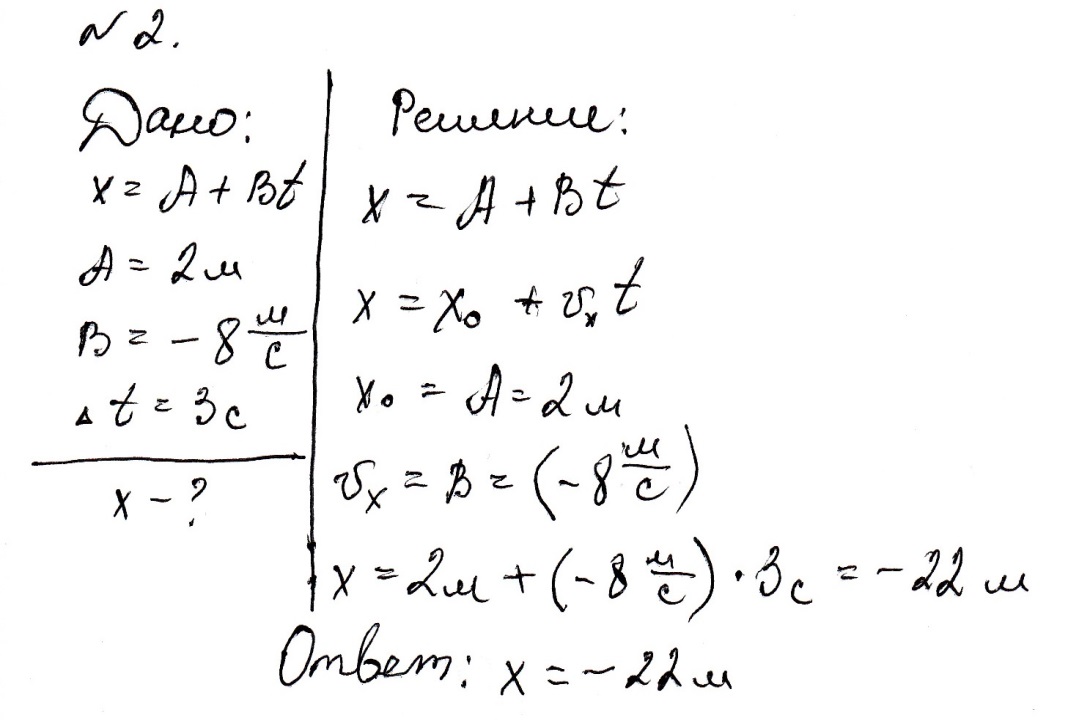
№ 3. Мяч, брошенный вверх с балкона с высоты = 3 м, поднялся на высоту h₂ = 4 м относительно балкона и упал на землю. Определите модуль перемещения мяча.

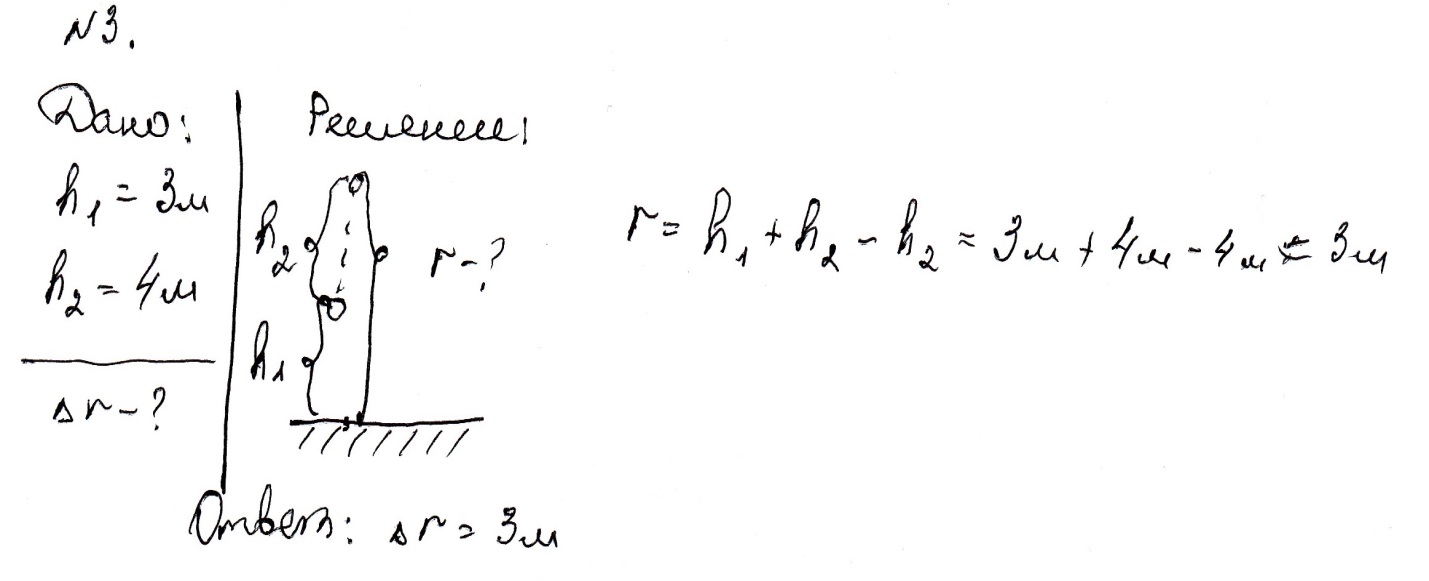
№ 4. Кинематический закон прямолинейного движения лодки вдоль оси Ох задан уравнением x = A + Bt, где А =150 м, В = 10,5 Определите проекции скорости и перемещения на ось Ох, а также путь, пройденный лодкой за время = 2 мин.

№ 5. Первую половину времени автомобиль двигался со средней скоростью v₁ = 40 км/ч, а вторую – со средней скоростью v₂ = 60 км/ч. Определить среднюю скорость автомобиля на всем пути.

Решение:

Автомобиль движется первую половину времени с одной скоростью 40 км/ч, а вторую половину времени со скоростью 60 км/ч. Следовательно, автомобиль проходит за равные промежутки времени разные расстояния.

и

тогда средняя скорость

Средняя скорость для этого случая оказалась равной среднему арифметическому значению скоростей.

Подставим значения скоростей и проведем вычисления:

Средняя скорость равна 50 км/ч.

6. Итоги урока

Итак, подведем итоги. Что вы сегодня узнали на уроке?

Организация домашнего задания

§ 10, упр. 6 № 2, 5, 6.

Рефлексия.

Продолжите фразы:

• Сегодня на уроке я узнал…

• Было интересно…

• Знания, которые я получил на уроке, пригодятся

Равномерное прямолинейное движение. Скорость

В прошлой теме говорилось о механическом движении, которое представляет собой изменение положения тел (или частей одного и того же тела) относительно друг друга в пространстве с течением времени.

Для описания механического движения необходимо выбрать тело отсчета, то есть тело или группу тел, которое в данном случае принимают за неподвижное и относительно которого рассматривается движение других тел, и связать с ним систему координат.

Так же было установлено, что для определения положения тела в какой-то момент времени, нужно знать вектор его перемещения. Действительно, для того, чтобы сказать, как переместилось тело, необходимо знать не только расстояние от начальной точки, но и направление, в котором тело переместилось.

Также довольно важной характеристикой любого движения является скорость. В данной теме разговор пойдёт о скорости при равномерном прямолинейном движении тела. Равномерное прямолинейное движение — это самый простой вид движения. При таком движении тело двигается только по прямой и за любые равные промежутки времени совершает равные перемещения. То есть это движение с постоянной по модулю и направлению скоростью.

Обратите внимание на то, что всегда необходимо задавать направление скорости. В прошлых темах было показано, что выбор системы отсчёта имеет решающее значение, а в разных системах отсчета скорости могут быть направлены по-разному.

Вообще скоростью называется физическая векторная величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения. Иными словами, это производная радиус-вектора точки по времени.

Уравнение скорости для равномерного прямолинейного движения имеет вид

По формулам, написанным в векторном виде, вычисления вести нельзя. Ведь векторная величина имеет не только численное значение, но и направление. При вычислениях удобно пользоваться формулами, в которые входят не векторы, а их проекции на оси координат, так как над проекциями можно производить алгебраические действия. И так, как же рассчитать проекцию скорости? Рассмотрим простой пример. Пусть в начальный момент времени координата тела была равна x₀, а в момент времени t – x.

Тогда за промежуток времени ∆tؚ, равный tؚ — tؚ₀, координата тела изменилась на величину равную разности между конечной и начальной координатой тела. Тогда проекция скорости тела в этом случае будет равна отношению изменения координаты тела к промежутку времени, в течении которого это изменение произошло.

Из записанной формулы, воспользовавшись известными математическими приемами, можно получить уравнение зависимости координаты тела от времени.

Полученное уравнение называют кинематическим уравнением равномерного движения.

Известно, что разность между начальной и конечной координатой тела есть ни что иное, как проекция перемещения на выбранную координатную ось.

Воспользуемся основным свойством пропорции, чтобы выразить проекцию перемещения.

Полученное уравнение называется уравнением перемещения.

При равномерном прямолинейном движении направление вектора скорости не изменяется, а значит путь и модуль проекции перемещения тела равны. На основании этого, получим уравнение пути при равномерном прямолинейном движении тела.

Обратите внимание, что проекция скорости тела взята под знак модуля. Это объясняется тем, что путь не может быть отрицательным, а вот знак проекции вектора скорости, как и проекции перемещения, будет зависеть от выбора направления координатной оси.

Рассмотрим графические зависимости скорости, координаты, пути и перемещения от времени при равномерном прямолинейном движении. При равномерном движении скорость постоянна, поэтому график зависимости скорости от времени будет представлять собой прямую линию, параллельную оси времени. Иными словами, при равномерном движении скорость не зависит от времени, так как является величиной постоянной.

Из графика скорости видно, что проекция скорости тел для оранжевой и зелёной прямых больше нуля, так как они располагаются выше оси времени. В случае с синей прямой, наблюдается противоположная картина: значит, тело двигается в обратном направлении, поэтому проекция скорости отрицательная.

Если рассмотреть конечный промежуток времени, то получим ограниченную область, имеющую форму прямоугольника. Площадь этого прямоугольника будет являться ничем иным, как изменением координаты «Икс», а, следовательно, пройденным телом путем. Действительно, ведь длина одной из сторон прямоугольника — это скорость, а длина другой — это промежуток времени.

Следующим рассмотрим график зависимости проекции перемещения от времени. Для этого еще раз вспомним уравнение перемещения:

Из уравнения видим, что проекция перемещения линейно зависит от времени. Следовательно, при равномерном движении графиком перемещения является прямая линия.

Направление и угол наклона графика зависимости проекции перемещения к оси времени будет зависеть от проекции вектора скорости на координатную ось.

Из рисунка видно, что тело 1 и тело 3 движутся в положительном направлении оси х, при этом скорость первого тела больше скорости третьего.

Тело 2 движется в направлении, противоположном направлению оси х, поэтому график перемещения располагается под осью времени.

Рассмотрим зависимость пройденного пути от времени.

Для равномерного движения график зависимости пути от времени представляет собой прямую линию, так как зависимость пути от времени, как и в случае с перемещением тела, линейная. Однако графики зависимости пути от времени для всех трех тел располагаются выше оси времени. Это объясняется тем, что пройденный путь — это длина траектории, а, следовательно, путь не может быть отрицательным.

Наклон графика пути к оси времени, как и в случае с графиком перемещения, зависит от модуля скорости: чем больше скорость движения тела, тем больший угол наклона.

Рассмотрим графики зависимости координаты от времени (их еще называют графиками движения).

На рисунке представлены три прямые, каждая из которых описывается одним и тем же уравнением. Точки пересечения этих графиков с осью x соответствуют значениям начального положения. Как видно из графика, для первого тела x₀<0, для второго x₀=0, а для третьего — x₀>0.

Так же на графике хорошо видно, что проекции скоростей для первого и третьего тел больше нуля. Действительно, ведь значение координаты x увеличивается с течением времени. Значит, тело двигается в направлении, совпадающем с положительным направлением оси икс. Это соответствует положительному перемещению, а, значит, положительной проекции скорости.

В случае с синей прямой, наблюдается противоположная картина: значит второе тело двигается в обратном направлении, поэтому его проекция скорости отрицательная.

Кроме того, из графиков можно судить о модуле скорости. Очевидно, что тело, движение которого описано оранжевой прямой, двигается быстрее остальных, так как за один и тот же промежуток времени оно проходит большее расстояние. Используя этот же аргумент, можно сказать, что модуль скорости второго тела больше, чем модуль скорости тела номер три.

При этом, как и в случае с перемещением, угол наклона графика к оси времени зависит от скорости тела. Из этих наблюдений можно сделать следующий вывод: чем больше угол между прямой и осью времени, тем больше скорость движения тела.

В случае прямолинейного равномерного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти положение тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту (если предположить, что тело двигалось с такой же скоростью и до начала отсчета времени).

С помощью графика движения можно определить:

1) координаты тела в любой момент времени;

2) путь, пройденный телом за некоторый промежуток времени;

3) время, за которое пройден какой-то путь;

4) кратчайшее расстояние между телами в любой момент времени;

5) момент и место встречи тел;

6) и так далее.

Необходимо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.

Очень часто наблюдаются довольно сложные типы движения, когда тело движется относительно системы отсчёта, которая в тоже время движется относительно Земли. На прошлых уроках говорилось о том, что любое механическое движение относительно, то есть в разных системах отсчета будут различны вид траектории, значение скорости, перемещения и других физических величин.

Было установлено, что в случае, когда тело участвует одновременно в нескольких движениях, результирующее перемещение тела равно векторной сумме перемещений, совершаемых им в каждом из движений.

В рассматриваемом примере очевидно, что все перемещения произошли за один и тот же промежуток времени. Разделив каждое перемещение в уравнении на этот промежуток времени, получим классический закон сложения скоростей, установленный Галилеем: скорость тела относительно неподвижной системы отсчета равна геометрической сумме скорости тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной.

Здесь следует помнить, что данный закон справедлив и для неравномерного движения. В этом случае вектора скорости — это мгновенные скорости, то есть скорости в данный момент времени или в данной точке траектории.

Основные выводы:

В данной теме были повторены некоторые важные понятия кинематики. Поговорили о равномерном прямолинейном движении тел и способах описания такого движения. Еще раз затронули относительность движения и вывели классический закон сложения скоростей.

Теория «Относительность движение и сложение скоростей для 9 кл. по физике»

В общем случае, при движениях систем отсчета с ускорением друг относительно друга, ускорения тела в различных системах отсчета оказываются различными.

В случае, когда вектора относительной скорости v ′ и переносной скорости v₀ параллельны друг другу, закон сложения скоростей можно записать в скалярной форме:

Относительность механического движения.

1. Механическое движение можно наблюдать только относительно других тел. Обнаружить изменение положения тела, если не с чем сравнивать невозможно.

2. В различных системах отсчета физические величины (скорость, ускорение, перемещение и т.д.), характеризующие движение одного и того же тела, могут быть различными.

3. Характер движения, траектория движения и т.п. могут быть различны в разных системах отсчета для одного и того же тела могут быть различны.

Пусть две СО движутся друг относительно друга с постоянной скоростью . Положение точки А в неподвижной системе К задано вектором , а в движущейся системе К₁ — вектором . Из чертежа видим, что . Это уравнение позволяет переходить из одной СО в другую.

При этом мы считаем, что время течет в обеих СО одинаково.

Будем условно называть систему К неподвижной, а систему К₁ — движущейся.

Тогда для случая, когда координаты y и z не меняются, получим:

— преобразования Галилея.

Из этих уравнений следует:

— расстояние между двумя точками абсолютно, т.е. не зависит от выбора СО. Пусть в неподвижной СО координаты точек x и x‘, а в подвижной соответственно x₁ и x₁‘. Тогда ;

Разделим правую и левую часть уравнения на промежуток времени, в течение которого шло перемещение.

Получим:

— закон сложения скоростей. Здесь скорость точки относительно неподвижной СО равна векторной сумме скорости точки относительно подвижной СО и скорости самой подвижной СО относительно неподвижной.

Скорость подвижной СО относительно неподвижной наз. переносной скоростью.

При решении задач часто бывает удобно принимать одно из движущихся относительно Земли тел за неподвижное. Тогда скорость Земли в этой СО будет равна по величине и противоположна по направлению скорости данного тела.

Если скорости v₁ и u сонаправлены (тела сближаются), то их проекции складываются, если противоположно направлены (тела удаляются) – вычитаются.

Если скорости направлены под прямым углом — ,

если угол произвольный, то необходимо пользоваться теоремой косинусов: .

Эти выводы справедливы для скоростей много меньших скорости света в вакууме (3^.10⁸м/с).

Механическое движение. Траектория. Путь и перемещение. Сложение скоростей

Раздел 1 МЕХАНИКА

Глава 1: О с н о в ы к и н е м а т и к и

Механическое движение. Траектория. Путь и перемещение. Сложение скоростей

Механическим движением теланазывается изменение его положения в пространстве относительно других тел с течением времени.

Механическое движение тел изучаетмеханика.Раздел механики, описывающий геометрические свойства движения без учёта масс тел и действующих сил, называется кинематикой.

Механическое движение относительно. Чтобы определить положение тела в пространстве, нужно знать его координаты. Для определения координат материальной точки следует, прежде всего, выбрать тело отсчёта и связать с ним систему координат.

Телом отсчёта называется тело, относительно которого определяется положение других тел. Тело отсчёта выбирают произвольно. Это может быть что угодно: Земля, здание, автомобиль, теплоход и т.д.

Система координат, тело отсчёта с которым она связана, и указание отсчёта времени образуют систему отсчёта,относительно которой рассматривается движение тела (рис.1.1).

Тело, размерами, формой и структурой которого можно пренебречь при изучении данного механического движения, называется материальной точкой.Материальной точкой можно считать тело, размеры которого намного меньше расстояний, характерных для рассматриваемого в задаче движения.

Траектория это линия, по которой движется тело.

В зависимости от вида траектории движения разделяются на прямолинейные и криволинейные

Путь – это длина траектории ℓ(м) (рис.1.2)

Вектор , проведенный из начального положения частицы в её конечное положение, называется перемещениемэтой частицыза данное время.

В отличие от пути, перемещение является не скалярной, а векторной величиной, так как оно показывает не только на какое расстояние, но и в каком направлении сместилось тело за данное время.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль перемещения не может быть больше пройденного пути. Например, если из точки А в точку Б автомобиль перемещается по криволинейной траектории, то модуль вектора перемещения меньше пройденного пути ℓ. Путь и модуль перемещения оказываются равными лишь в одном единственном случае, когда тело движется по прямой.

Скорость – это векторная количественная характеристика движения тела

Средняя скорость – это физическая величина, равная отношению вектора перемещения точки к промежутку времени

Направление вектора средней скорости совпадает с направлением вектора перемещения.

Мгновенная скорость, то есть скорость в данный момент времени – это векторная физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt.

 

Вектор мгновенной скорости направлен по касательной к траектории движения (рис. 1.3 ).

В системе СИ скорость измеряется в метрах в секунду (м/с), то есть единицей скорости принято считать скорость такого равномерного прямолинейного движения, при котором за одну секунду тело проходит путь в один метр. Часто скорость измеряют в километрах в час.

или 1

 

Сложение скоростей

Любые механические явления рассматриваются в какой-либо системе отсчета: движение имеет смысл только относительно других тел. При анализе движения одного и того же тела в разных системах отсчета все кинематические характеристики движения ( путь, траектория, перемещение, скорость, ускорение ) оказываются различными.

Например, пассажирский поезд движется по железной дороге со скоростью 60км/ч. По вагону этого поезда идёт человек со скоростью 5км/ч. Если считать железную дорогу неподвижной и принять её за систему отсчёта, то скорость человека относительно железной дороги, будет равна сложению скоростей поезда и человека, то есть

60км/ч + 5 км/ч = 65 км/ч, если человек идёт в том же направлении что и поезд и

60км/ч — 5 км/ч = 55 км/ч, если человек идёт против направления движения поезда.

Однако это справедливо только в этом случае, если человек и поезд движутся по одной линии. Если же человек будет двигаться под углом, то необходимо учитывать этот угол, и тот факт , что скорость – это векторная величина.

Рассмотрим описанный выше пример более подробно – с деталями и картинками.

Итак, в нашем случае железная дорога это неподвижная система отсчёта. Поезд, который движется по этой дороге – это подвижная система отсчёта. Вагон, по которому идёт человек, является частью поезда. Скорость человека относительно вагона (относительно подвижной системы отсчёта) равна 5км/ч. Обозначим её буквой . Скорость поезда, (а значит и вагона) относительно неподвижной системы отсчёта (то есть относительно железной дороги) равна 60 км/ч. Обозначим её буквой . Другими словами, скорость поезда – это скорость подвижной системы отсчёта относительно неподвижной системы отсчёта.

Скорость человека относительно железной дороги (относительно неподвижной системы отсчёта) нам пока неизвестна. Обозначим её буквой .

Свяжем с неподвижной системой отсчёта (рис.1.4) систему координат ХОY, а с подвижной систему отсчёта – Х_пО_пY_п. Определим теперь скорость человека относительно неподвижной системы отсчёта, то есть относительно железной дороги.

За малый промежуток времени Δt происходят следующие события:

· Человек перемещается относительно вагона на расстояние

· Вагон перемещается относительно железной дороги на расстояние

Тогда за этот промежуток времени перемещение человека относительно железной дороги:

= +

Это закон сложения перемещений. В нашем примере перемещение человека относительно железной дороги равно сумме перемещений человека относительно вагона и вагона относительно железной дороги.

Разделив обе части равенства на малый промежуток времени Dt, за которое произошло перемещение:

Получим:

Это закон сложения скоростей: скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и скорости самой подвижной системы отсчёта относительно неподвижной.

[Физика билет 1] Система отсчета. Траектория, путь и перемещение. Материальная точка. Средняя скорость. Относительность движения. Закон сложения скоростей в классической механике. Прямолинейное равномерное движение. Уравнения движения и графики x(t), vx(t), s(t) для равномерного прямолинейного движения.

Система отсчета.

Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел

Траектория, путь и перемещение.

Вектор перемещения — вектор начальная точка которого совпадает  с начальным положением движущейся точки и конец вектора с ее конечным положением.

Траектория движения материальной точки – линия, описываемая этой точкой в пространстве (прямолинейная или криволинейная).

Путь точки – сумма длин всех участков траектории, пройденных точкой за рассматриваемый участок времени.

Материальная точка.

Материа́льная то́чка  — тело, обладающее массой и скоростью, но размеры и формы которого в условиях данной задачи существенного значения не имеют.

Средняя скорость.

Сре́дняя ско́рость движущейся точки за промежуток времени t — векторная величина, равная отношению вектора перемещения к промежутку времени за которое это перемещение произошло.

Средняя (путевая) скорость

Средняя скорость по перемещению (средневекторная)

Относительность движения.

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.

Закон сложения скоростей в классической механике.

Vабс= Vотн + Vпер

Абсолютная скорость материальной точки равна векторной сумме переносной и относительной скорости.

Прямолинейное равномерное движение.

Прямолинейное равномерное движение — движения  с постоянной по модулю и направлению скоростью.

Уравнения движения и графики x(t), vx(t), s(t) для равномерного прямолинейного движения.

уравнение равномерного прямолинейного движения материальной точки:

(17) или

Формулы равномерного прямолинейного движения

Графики зависимости скорости, проекции скорости,пути и координаты от времени для равномерного прямолинейного движения

График скорости v = v(t)

Рис. 22

 = const
График скорости равномерного движения – прямая линия, параллельная оси абсцисс (оси t).
По графику v = v(t) можно найти пройденный путь за интервал времени t: он численно равен площади фигуры ОАВС (прямоугольника):
q (площадь прямоугольника OABC) = OA • OC  v₁ • t₁  S
График пути S = S(t)

Рис. 23

S = v • t, где v = const
График пути равномерного движения – прямая линия, которая образует угол  с осью времени.
На этом графике , но   v ~ tg (скорость равномерного движения пропорциональна тангенсу угла , который график пути составляет с осью времени).
График зависимости координаты точки от времени: x = x(t)
Уравнение x = x₀ + v_x (t – t₀) – линейная функция, поэтому график x = x(t) – прямая линия, которая образует угол  с осью времени.

Рис. 24

Рис. 25

На графике x = x(t): , где   v ~ tg.